Introduction

Natural convection plays a pivotal role in understanding the flow of heat in the absence of any mechanical device used to enhance the flow rate since the wear caused by this will be overlooked until the damage is irreparable. All electronic assemblies nowadays have huge heat dissipation due to their need for compaction and extensive miniaturization. Even though the usage of fans with higher capacities and cooling agents is being promoted but they would significantly increase manufacturing costs and production time. Not to mention these components would require special care, adding to the manpower costs. Hence, the most ideal way would be to optimize the geometry is to utilize the features of the components themselves to maximize heat dissipation. This methodology can be applied in choosing an optimum geometry in heat transfer applications and in the placement of cylindrical luminescent sources (tube light) to ensure the endurance of the product. In the placement of condenser coils too, the results obtained from our experiment can find use. Solar energy is the dominant renewable energy source in today’s generation, and our study of cylinders in enclosures will help us, better understand the heat flow between the liquid carrying tubes in the flat plate collectors. Even the petroleum industry, which employs tanks for the storage of crude oil, requires extremely long tubes for the transportation of fluid. One can optimize the geometry of these tubes to maintain the required temperature. Nuclear systems require the reaction to be constantly cooling to maintain an optimal temperature. Hence, a literature review has been carried out by considering natural convection in an enclosure with and without obstacles.

Saris et al. [1] studied the phenomenon of free convection in an enclosure with a sinusoidally varying temperature profile that is on the upper wall for the Rayleigh numbers 102–108 and found that the fluid recirculation pattern increases in intensity, shifts to the upper walls with the increase in Rayleigh number and the aspect ratio. This subsequently increased the rate of heat transfer. Lee et al. [2] numerically investigate a cylinder in an enclosure with an aspect ratio of one for the Rayleigh numbers 103–106 and notices peak values of Nusselt number on the cylinder surface and the boundaries when the position of the cylinder is varied horizontally and diagonally. Garrpeters [3] considered a horizontal cavity filled with inert fluid and took into account the periodic instabilities in the fluid. He analyzed the critical zone temperature, disturbances in steady flow for various spatial orientations and zone depths. Sadegh et al. [4] investigates isothermal cylinders arranged in vertical arrays for low Rayleigh numbers (Ra) and concluded that there exists an optimum separation distance for maximum possible heat transfer for each array, and the array Nusselt number depends upon diameter ratio, number of cylinders in the array and cylinder spacing. Bahrami and Safikhani [5] in their study of an “eccentric cylinder with an inner rotating wall using a porous media” were successful in determining a relationship between Rayleigh, Darcy, Richardson number and the heat transfer capability of the object. Marcel et al. [6] studied two horizontally heated cylinders, separated vertically in an enclosure with the horizontal walls maintained at the heat sink temperature for Rayleigh numbers 103–106. The Nusselt number depends on the thermal conductivity ratio of the wall, the fluid enclosed, and the Rayleigh number. The part of the top horizontal surface in the heat dissipation decreases as the Ra number keeps increasing while it’s vice versa for the bottom surface. Asan et al. [7] studied two isothermal concentric square ducts and the annular region enclosed by them and computed up to a Ra. number of 106 at three different dimension ratios. Kim et al. [8] considered the domain of a square enclosure consisting of a hot circular obstacle at multiple locations, vertically symmetric to the enclosure. The size and formation of the fluid cell are predominantly determined by the location of the cylinder within the enclosure and the Ra. number. Afzal et al. [9] analyzed the “effect of spacing on thermal performance characteristics of Li-ion battery cells”. When the heat generation was assumed to be uniform, the central battery temperature increased on increase of spacing. Bhowmick et al. [10] investigated square and round cylinders surrounded by an enclosure with sinusoidal temperature distribution on the walls. The streamlines start losing their regularity on increasing the wavelength, there’s the formation of two cells within the enclosure and one dominates (one near the cold wall) over the other (one near the hot wall) on increase in Ra. number.

TetsuFujii et al. [11], have justified the use of a thick boundary layer around a circular cylinder through the use of relevant equations employing the finite-difference method. It was found that the effect of convective terms was evident even at Gr = 10−4, as witnessed in the radial temperature distribution of the local Nusselt number. Bilgen [12] in his study considered an enclosure with isothermal vertical boundaries and adiabatic horizontal boundaries and accounting for partitions at various lengths and Rayleigh numbers 104–1011. The flow regime was found to be laminar for Ra up to 104 and thereafter turbulent. Dutta et al. [13] analyzed a porous rhombic enclosure at an inclination angle of 30° for heat transfer and entropy generation characteristics. The bottom and top walls of the enclosure are heated non-uniformly. Nusselt number increases but not before initially decreasing in its value when the phase angle increases. Girish et al. [14] studied mixed convection in an upright annular region which is double open-ended and consists of a perfectly conducting baffle in between the inner hot and the outer cylinder. The effect of viscous dissipation was taken into consideration. Littlefield et al. [15] considered a uniform annular section of a comparatively higher aspect ratio. The outer wall was specified to be isothermal, and constant flux was established. It was found that the changes in the Rayleigh number and heat flux ratio, significantly affect the rate of heat and mass transfer. Lee [16] examined a horizontal layer of fluid bounded by two parallel plates and an array, periodically arranged square cylinders enclosed by the layer. The horizontal extent of the enclosure is varied by including more square cylinders and a large aspect ratio is employed to overcome approximation errors. Pishkar et al. [17] investigated “unsteady natural convection of Newtonian and non-Newtonian fluids in a square enclosure”. They placed a “heat source with an oscillating heat flux on the bottom wall of the enclosure”. It was found that that the Nusselt number is inversely proportional to the power-law index, and the converse is true for the maximum temperature. Ho et al. [18] examined the fluid flow between two horizontal cylinders to understand the effect of insulated boundaries of the round enclosure wall on the heat transfer and flow field characteristics in the region enclosed by the horizontal cylinders and the wall. Basak et al. [19] studied the flow inside a trapezoidal enclosure with two different conditions. Minea [20] analyzed convection and radiation in a rectangular and oval enclosure. The heat was transferred from two lateral panels through natural convection. Mohammed Rabhi et al. [21] analyzed the heat transfer due to natural convection in an inclined rectangular enclosure with multiple partitions. It was found that the partitions contributed to a decrease in heat transfer within the enclosure since it disrupted the flow field and the radiative heat. Fusegi et al. [22] found that in their study differentially heated sidewalls were seen in the cavity, and a uniform internal heat generation was witnessed. Seyyedi et al. [23] studied a square cylinder enclosing a circular pipe, meant to model a hot pipe buried in the soil. The reduction in cylinder radius and the Darcy number caused the Nusselt number to reduce. Kim et al. [24] too conducted an immersed boundary study of natural convection in a square enclosure comprising of a circular cylinder for the Rayleigh numbers 103–106. On the further increase of temperature, the Nusselt number drops due to the formation of secondary vortices at the apex of the cylinder and then reaches its maximum value (for the study) at Ra = 106. Corvaro et al. [25] conducted an experimental interferometric analysis of natural convection in a square enclosure with partially active cold and hot walls at atmospheric pressure (Pr = 0.71). Shadlaghani et al. [26] studied “the serrated fins and their effect on annular spaces of varying cross-sections” and found that the inverted triangular section had the best rate of heat transfer. Paroncini et al. [27] conducted an experimental and numerical analysis on natural convective heat transfer in an enclosure with partially active sidewalls and air as a medium. They found that an increase in the number of heat sources has a direct impact on the velocity field and ultimately increased the heat transfer. Yuan et al. [28] analyzed horizontal concentric annuli of varying inner shapes with the inner and outer shape kept at a constant temperature. They witnessed that increasing space at the top and the presence of corners increase the rate of heat transfer. The surface radiation had a huge role to play in this phenomenon.

Previous studies had made the authors curious regarding the flow field interactions and natural convection heat dissipation if more than one obstacle existed in an enclosure. In today’s components and systems, where there are multiple heat emanating substances inside enclosures, and we are tasked with enhancing the heat dissipation and also keeping power & materials constraints in mind. This triggered the authors to visualize two heated circular obstacles at five different combinations and the fluid interactions between them inside a square enclosure to find the most optimum orientation of the heated bodies to ensure maximum heat dissipation.

Problem formulation

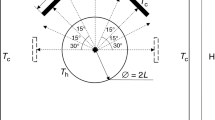
In this study, a two-dimensional enclosure with cold walls is studied, and enclosed within are two circular obstacles of constant dimensions, in varying positions. A total of five cases are considered and of which three are visible in Fig. 1. One of the obstacles is placed at a vertically symmetric position (Prime obstacle) with the other obstacle (case obstacle) being inline in one of the cases and inclined at 45° (mirrored) in the other two cases. The cases in which the 2nd obstacle is at an inclination are horizontally mirrored to obtain two more cases. The numerical analysis is carried out through ANSYS Fluent 18 employing suitable assumptions. The flow is steady, 2D, laminar, and incompressible. The physical properties are specified at the bulk mean temperature i.e., [(Tc + Th)/2]. The length of the square enclosure is 5d, and the diameter of both the obstacles is d. The (adiabatic) walls of the enclosure are at the constant cold wall temperature of Tc, and the obstacles are at a hot wall temperature of Th, which varies according to the Rayleigh Number as shown in Fig. 1.

Fig.1
figure 1

Physical domain of the study

Full size image

Governing equations and formulae

Appropriate boundary conditions are selected with keeping Fig. 1 as a reference, and the problem is solved by employing the finite volume method. The walls of the enclosure and circular obstacles are assigned a no-slip boundary condition and are kept at specified operating temperatures. The difference in these temperatures establishes the flow field. The Boussinesq approximation is used to account for the buoyancy effects. To reduce the approximation, 2nd order upwind scheme is employed. We make use of the SIMPLE algorithm to obtain a solution. The residuals set for the convergence criteria for the mass and momentum conservation are 10–6 and 10–12 for energy.

Continuity equation

$$\frac{{\partial {\text{u}}}}{{\partial {\text{x}}}} + \frac{{\partial {\text{v}}}}{{\partial {\text{y}}}} = 0$$
(1)

x—Momentum equation

$$\rho \left( {u\frac{\partial u}{{\partial t}} + v\frac{\partial u}{{\partial y}}} \right) = - \frac{\partial p}{{\partial x}} + \mu \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)$$
(2)

y—Momentum equation

$$\rho \left( {u\frac{\partial v}{{\partial t}} + v\frac{\partial v}{{\partial y}}} \right) = - \frac{\partial p}{{\partial y}} + \mu \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) + g\beta \left( {T - T_{\infty } } \right)$$
(3)

Energy equation

$$u\left( {\frac{\partial T}{{\partial x}}} \right) + v\left( {\frac{\partial T}{{\partial y}}} \right) = \alpha \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)$$
(4)

Formulae

$$T_{\rm{h}} = { }\frac{Ra \cdot \propto \cdot \vartheta }{{g \cdot \beta \cdot L^{3} }} + T_{\rm{c}}$$
(5)
$$Nu = \frac{hL}{k}$$
(6)
$$C_{\rm{p}} = \frac{{p - p_{\infty } }}{{\frac{1}{2}\rho_{\infty } V_{\infty }^{2} }} = \frac{{p - p_{\infty } }}{{p_{^\circ } - p_{\infty } }}$$
(7)
$$C_{\rm{f}} = \frac{{\tau_{\rm{w}} }}{{\frac{1}{2}\rho v^{2} }}$$
(8)
$${\text{U}}^{*} = { }\frac{{{\text{U}} \cdot {\text{ L}}}}{ \propto }$$
(9)
$${\text{W}}^{*} = \user2{ }\frac{{{\text{W}} \cdot {\text{L}}}}{{\text{U}}}$$
(10)

Grid generation and grid independence

In this study, due to the curvilinear design of the physical domain and the square enclosure around it, an unstructured mesh has been chosen for better computational results. In order to understand the flow physics and heat transfer on the boundary, we have made use of the edge sizing feature on the wall boundaries and the obstacles (Fig. 2).Grid independence study has been conducted in the field of interest (Table 1), where different number of grid elements are used. Convergence was achieved on nearly 14,696 elements, and it was found that successive iterations have the least impact on Nusselt number, which is a significant parameter in this study.

Fig. 2
figure 2

Unstructured mesh distribution of computational domain

Full size image
Table 1 Grid independence study
Full size table

Results and discussion

The square enclosure with two hot circular obstacles has been studied in different orientations. Their effects on flow and heat transfer characteristics are depicted and analyzed in detail in this section.

Verification of computational study

Kim et al. [7] examined the phenomenon of natural convection caused by a temperature difference between a cold enclosure and a hot inner circular obstacle. He further studied the effect of the location of the obstacle on the heat transfer and fluid flow when the temperature of the bottom wall is varied. The position of the obstacle is varied along the vertical line of symmetry and investigated for verification, which is presented in Table 2. The appropriate velocity and temperature contours are presented in Fig. 3.

Table 2 Validation of Nusselt Number from the study
Full size table
Fig. 3
figure 3

Velocity (a, b, c) and Temperature (a′, b′, c′) contours [7]

Full size image

Ramesh and Venkatesan [29] experimentally studied natural convection in a square enclosure with air as a medium. The domain comprised of differentially heated vertical walls and adiabatic horizontal walls. Ramesh and Venkatesan make use of a differential interferometer placed at the top and bottom walls and the trapezoidal rule to calculate the average heat transfer coefficient. Ramesh and Venkatesan found that the contribution of radiation was negligible to the flow owing to the low emissivity of the hot wall. The boundary conditions played a pivotal role in the flow regime and heat transfer characteristics. Ramesh and Venkatesan also recommended using extra insulation behind the walls to achieve adiabatic boundary conditions. Ramesh and Venkatesan had validated Ostrach’s [30] study of enclosures by comparing their experimentally found Local Nusselt number with the latter’s empirical calculation. The present study took this a step further by comparing the numerical values found with previous experimental and empirical results (Fig. 4).

Fig. 4
figure 4

Comparison of experimental [29], empirical [30], and numerical Nusselt number

Full size image

Heat Transfer enhancement of an enclosure with heated circular obstacle [8]

As one is aware that a hotter fluid is less dense as compared to a colder one and hence is quick to rise to the top in an enclosure whereas the colder fluid remains at the bottom owing to its mass. This phenomenon is also noticeable in B.S Kim’s [8] study when one analyses the velocity contour of an enclosure consisting of a single heated circular obstacle with no-slip boundary conditions applied to the walls of the enclosure. The rate of heat transfer was quantized in terms of Nusselt & Rayleigh numbers. Mathematically speaking, the Nusselt number is the ratio of convective and conductive heat transfer and a measure of comparison of the amount of heat transfer by the fluid and solid in the domain. Rayleigh number considered essential in characterizing the flow regime and is a product of Prandtl number (the ratio of momentum and thermal diffusivity) and Grashof number (the ratio of buoyant and viscous forces). With the increase in the Rayleigh number, fluid transitions from a laminar to turbulent flow. Present study was carried out for three Rayleigh Numbers 104,105 & 106. The pressure and skin friction coefficient maps for all the above cases were also obtained. The former is needed to describe the relative pressures throughout the flow domain, and the latter mathematically is a ratio of the skin shear stress on the surface of the body due to the viscous pressure and the dynamic pressure of the free stream. Once the fluid (air) starts gaining temperature after coming in contact with the obstacle, it starts rising toward the top of the enclosure and since the walls of the enclosure are at a lower temperature, the fluid loses its heat through convection. After which, the fluid moves to the bottom of the enclosure due to an increase in its density, and the entire cycle is repeated (Fig. 3a). One can witness a consistency in the flow owing to less variation in the density which in turn can be attributed to the small temperature difference between the walls & the obstacle at a low Ra. number[104](Fig. 3b).

As one goes on to increase the same (105), one finds that there’s a considerable increase in the magnitude of the vorticity in the upper regions of the enclosure and as the temperature difference increases so does the velocity. Also, the vortex formation is unevenly distributed with the majority of them occurring in the top half, and the flow pattern is still found to be symmetric to the vertical axis. (Fig. 3c) The contours are consistent at 106 too but a considerable increase in the velocity, and vorticity magnitude is noted. The bifurcation of flow moves even further away from the obstacle. The average Nusselt number obtained is very similar to those published in Table 2, with negligible deviations.

Velocity and Temperature contours of Present Study at Different Orientations

Bottom center configuration (inline arrangement at center)

Firstly, when one considers the case of the inline geometry (BC), one can easily point out that a major portion of fluid interaction is restricted to the space between both obstacles. Since both of them are heated and each prevent the heat transfer of the other from occurring smoothly. Hence, they mutually disrupt each other’s flow (Fig. 5a and a′). At Ra number 104, the bifurcation of the fluid layers occurs on the top of the upper obstacle (‘case’) and with marginal space between the two obstacles. As the Ra number (105) is increased, a predictable increase in the velocity and vortex formation rate is noticed due to the increased temperature gradient as mentioned earlier (Fig. 5b and b′). This is in agreement with H. Asan’s study on an annular region between two isothermal square ducts [7]. One is even able to observe pockets of hot regions on either side of the obstacles, which might indicate that a fraction of fluid particles move downwards after losing their energy to the upper wall. These can absorb the heat from the region formed by the interaction of fluids between the two obstacles. An evident larger bifurcation too is witnessed atop the upper obstacle. At Ra number 106 there is no such bifurcation owing to the considerable increase in the velocity and vorticity magnitude (Fig. 5c and c′). The same could even be stated as the reason for the pockets of spaces formed, where the fluid interaction seems to be absent since the increased velocity does not give time to the downward traveling fluid to come in contact with the hotter air around the obstacles. This phenomenon is even witnessed in J.M Lee’s analysis of a square enclosure with cold wall obstacles [2]

Fig. 5
figure 5

Velocity (a, b, c) and Temperature (a′, b′, c′) contours of BC

Full size image

Bottom inclined configuration (‘BR and BL’)

When the bottom right configuration (BR) is studied, it is noted that the flow of the fluid is quite evenly distributed throughout the enclosure for the Ra number 104 with the most high-speed regions of space present between both the heated circular obstacles. Upon close observation, it is found that the heated fluid rises from the lower ‘case’ obstacle. It comes in contact in quick succession with the ‘prime’ obstacle and then the adjacent walls. This makes the fluid lose energy quite drastically as compared to the previous cases. The air again comes in contact with the lower obstacle which makes it gain temperature (Fig. 6a and a′). This rapid transfer of energy occurs through convection, causing the air to diffuse almost immediately when it meets the lower obstacle and hence does not make it to the bottom corner, where the lower obstacle is present. At a higher Rayleigh number (105), this process speeds up even more due to the increase in the velocity and vorticity magnitude (Figs. 6b and b′). Another inference made is that as the velocity of the fluid inside the enclosure keeps increasing, it doesn’t find enough time to interact with the regions of enclosure beyond the ‘prime’ obstacle and hence leading to formation of low-speed regions of air in those areas. This phenomenon is most evident at Ra number 106, where the region beyond the ‘prime’ obstacle witnessed almost negligible fluid flow and the temperature contours too are uniform (Figs. 6c and 6c′). Similarly, when the orientation is changed from right to left, we could not observe any significant variations in the flow physics and heat transfer.

Fig. 6
figure 6

Velocity [a, b, c] and temperature [a′, b′, c′] contours of BR

Full size image

Top inclined configurations (‘UL and UR’)

When we consider the upper left configuration(‘UL’), in surprising contrast to the bottom inclined configurations, we notice that a major proportion of flow circulation occurs between the heated obstacles and the far vertical wall (Figs. 7a and a′), which wasn’t the case previously at Ra. number 104. This is remarkable as the fluid can disperse even more uniformly and has a lot of available space to spread out which in turn makes heat transfer more efficient.

Fig. 7
figure 7

Velocity (a, b, c) and Temperature (a′, b′, c′) contours of upper left orientation (UL)

Full size image

But here also one can witness the same successive transfer of energy between hot and cold boundaries which leads to quicker diffusion on the lower obstacle (‘prime’), though not as quick as in bottom inclined cases. The heated fluid rising from the prime obstacle to the case gets diffused toward the open space toward the upper wall and again to the adjacent one. This further pushes it downwards toward the lower obstacle but due to the availability of space the loss and gain of energy are gradual. (Fig. 7b and b′) On increasing the Rayleigh number, the rate of heat transfer increased drastically due to the increase in velocity and vorticity magnitude. This further enhances the heat transfer rate. There is hardly any region inside the enclosure where the flow circulation is negligible, though at Ra number 106, (Fig. 7c and c′) the flow circulation starts to follow a dedicated path and thus creating a pocket by encircling around it. The heat transfer is uniform otherwise, and there are possibilities of more pockets being created at higher Rayleigh numbers. Here also the top inclined right resembles the same fluid flow and heat transfer characteristics because its axis-symmetric in nature. When the heat transfer rate of UL & UR is compared with the validation study [8], there was an increase of 28.09%. This indicates that we should prefer to arrange heated obstacles at inclined configurations to obtain an enhanced heat dissipation rate. Furthermore, when the same configuration was compared to the bottom center arrangement, an increase of 70.08% was witnessed. We can gauge from this that the BC configuration would be the least suitable candidate when it comes to selecting the optimum arrangement to maximize heat dissipation.

Orientation effect on local and average pressure coefficients

When it comes to the BC configuration, the local pressure coefficients for all the three Rayleigh numbers are negative and in the range of − 0.005 to – 0.045 for the ‘case’ obstacle (Fig. 8). They show a steep decline around 200° of inclination. The values become more negative with the increase of the Rayleigh number. For the ‘prime’ obstacle one witnessed a contrasting phenomenon. All the values are positive and only increase in magnitude with the increase in the Rayleigh number (Fig. 9). They are in the range of + 0.004– + 0.0018 and also witness a steep increase at 200° of inclination. When it comes to the average pressure coefficient is seen that all the values are negative and positive for the ‘case’ and ‘prime’ obstacle, respectively. The magnitude (negative/positive) only increased with an increase in the Rayleigh number (Fig. 10). Hence the static pressure on the surface is found to be less than the free stream pressure for the ‘case’ obstacle and more for the ‘prime’ obstacle. This implied that the fluid velocity is more than the free stream velocity on the surface of the ‘case’ obstacle and doesn’t exceed free stream velocity in the case of the ‘prime’ obstacle. The values found are similar to other bottom inclined configurations. When it comes to the local skin friction coefficient, in the ‘case’ obstacle, the curve is periodic and witnesses the lowest values at around 200° for Ra. numbers 104 and 105 but also peaks in the same region when considering Ra. number 106 (Fig. 11). The values are in the range of 0.0001 to 0.0082 and witness a major increase with the increase in Ra. number. In the ‘prime’ obstacle, the decline is more prolonged, and the lowest peak obtained is constant for almost 100o (Fig. 12). When the average skin friction coefficient is considered, it is seen that the slope of the curve is steep between Ra. numbers 104 and 105 but there’s a drastic increase between 105 and 106(Fig. 13). So as the Rayleigh number keeps on increasing and fluid starts transitioning away from a laminar flow, the shear stress on the surface of heated obstacles increases.

Fig. 8
figure 8

a Local pressure coefficients of ‘case’ obstacle for Rayleigh number 104 b Local pressure coefficients of ‘case’ obstacle for Rayleigh number 105 c Local pressure coefficients of ‘case’ obstacle for Rayleigh number 106

Full size image
Fig. 9
figure 9

a Local pressure coefficients of ‘Prime’ obstacle for Rayleigh number 104 b Local pressure coefficients of ‘Prime’ obstacle for Rayleigh number 105 c Local pressure coefficients of ‘Prime’ obstacle for Rayleigh number 106

Full size image
Fig. 10
figure 10

a Average pressure coefficients of ‘case’ obstacles for different configurations at various Rayleigh numbers b Average pressure coefficients of ‘Prime’ obstacles for different configurations at various Rayleigh numbers

Full size image
Fig. 11
figure 11

a Local Skin friction coefficients of ‘case’ obstacle for Rayleigh number 104 b Local Skin friction coefficients of ‘case’ obstacle for Rayleigh number 105 c Local Skin friction coefficients of ‘case’ obstacle for Rayleigh number 106

Full size image
Fig. 12
figure 12

a Local Skin friction coefficients of ‘Prime’ obstacle for Rayleigh number 104 b Local Skin friction coefficients of ‘Prime’ obstacle for Rayleigh number 105 c Local Skin friction coefficients of ‘Prime’ obstacle for Rayleigh number 106

Full size image
Fig. 13
figure 13

a Average skin friction coefficients of ‘case’ obstacles for different configurations at various Rayleigh numbers b Average skin friction coefficients of ‘Prime’ obstacles for different configurations at various Rayleigh numbers

Full size image

In bottom inclined configurations, since the velocity and vorticity undergo a considerable increase, the bottom corner witnesses’ negligible fluid flow and the temperature contours are uniform. The local pressure coefficients for all the three Rayleigh numbers are negative and in the range of − 0.005 to − 0.04 for the ‘case’ obstacle (Fig. 8). Although ‘BL’ shows a steep decline around 200° of inclination, the curve shoots up to around the same value for ‘BR’ at Ra numbers 104 and 105. The values become more negative with the increase of the Rayleigh number. For the ‘prime’ obstacle, we witness a contrasting phenomenon. All the values are positive and only increase in magnitude with the increase in the Rayleigh number (Fig. 9).

They are in the range of + 0.004– + 0.082 and also witness a steep increase at 200° of inclination for Ra number 104 and 105. Although for Ra number 106 one notices that the pressure coefficient dips at around 100° and then rises steeply at around 200° in the case of ‘BL’ but for ‘BR’, the curve rises and falls. It finally peaks at around 300°.

When it comes to the average pressure coefficient it is seen that all the values are negative and positive for the ‘case’ and ‘prime’ obstacle, respectively, and the magnitude (negative/positive) only increases with an increase in the Rayleigh number (Fig. 10). Hence the static pressure on the surface is found to be less than the free stream pressure for the ‘case’ obstacle and more for the ‘prime’ obstacle. This implied that the fluid velocity is more than the free stream velocity on the surface of the ‘case’ obstacle and doesn’t exceed free stream velocity in the case of the ‘prime’ obstacle. The cause for this is attributed to the effective performance of the configuration. The values found are similar to the above inline configuration.

Orientation effect on local and average skin friction coefficients

For the local skin friction coefficient plot, in the case of the ‘case’ obstacle, the curve is periodic and witnessed the lowest values at around 200° for Ra. numbers 104 and 105 but also peaks in the same region when considering Ra. number 106 (Fig. 11). The values are in the range of 0.0001–0.0082 and witnessed a major increase with the increase in Ra. number. In the ‘prime’ obstacle, the decline is more prolonged, and the lowest peak obtained is constant for almost 100° (Fig. 12).

When the average skin friction coefficient is considered, it is observed that the slope of the curve is steep between Ra. numbers 104 and 105 but there’s a drastic increase between 105 and 106 (Fig. 13). So as the Rayleigh number keeps on increasing and fluid starts transitioning away from a laminar flow, the shear stress on the surface of heated obstacles increases. The ‘case’ (bottom) obstacle has the maximum values for every Ra number as the heat flow is restricted between both obstacles and thus increased the shear stress on the bodies. But in the case of the ‘prime’ obstacle, the skin friction coefficient is intermediate between upper and lower inclined configurations because of the enhanced heat transfer in the upper inclined configurations. This phenomenon is witnessed due to the effective performance of the configuration.

Orientation effect on local and average nusselt number

The local Nusselt number (104 and 105) plot of the ‘case’ (lower) obstacle further strengthens the point of view of rapid transfer of energy, when a serious dip at an angle of inclination around 200° (Fig. 14) is witnessed in the curve. The plot conforms to the previous study when 106 is considered, which is justified by the increased velocity and vorticity. The Local Nusselt number is conformal for all three Rayleigh numbers in the case of ‘prime’ obstacles with the validation (Fig. 15) results. The computed average Nusselt number values were close to those obtained during the validation, and hence, it can be deduced that this configuration does not give an edge over the others in terms of heat transfer enhancement (Fig. 16). The bottom right configuration ‘BR’ turned out to be a mirror image of the former case with respect to all the parameters considered for this study. This belief is further strengthened by the fact that the average Nusselt number plot of the same overlaps that of bottom right configuration ‘BR’ (Fig. 16).

Fig. 14
figure 14

a Local Nusselt number of ‘Case’ obstacles for Rayleigh number 104 b Local Nusselt number of ‘Case’ obstacles for Rayleigh number 105 c Local Nusselt number of ‘Case’ obstacles for Rayleigh number 106

Full size image
Fig. 15
figure 15

a Local Nusselt number of ‘Prime’ obstacles for Rayleigh number 104 b Local Nusselt number of ‘Prime’ obstacles for Rayleigh number 105 c Local Nusselt number of ‘Prime’ obstacles for Rayleigh number 106

Full size image
Fig. 16
figure 16

Average Nusselt Number at different Rayleigh numbers for different configurations

Full size image

Though one can notice a considerable dip in the local Nusselt number values of the ‘prime’ obstacle across all Rayleigh numbers as it has considerably way more available space to dissipate its heat through all directions. Since there’s no immediate obstruction in the path of its flow (Fig. 15). The uniform flow circulation helps in the dissipation of the heat from the ‘prime’ (lower) obstacle. On studying the average Nusselt number, it was found that the values are unimaginably high, and this was quite expected due to the above-stated reasons. The heat transfer rate even further kept increasing drastically when the Rayleigh numbers are increased (Fig. 16). The upper right configuration yields a result that is a mirror image of the upper left configuration for all the parameters considered. Although one noticeable fact is that the (Figs. 13 and 14) local Nusselt number curves give the inverse of those found in UL configuration. This is logical as the flow circulation direction too is mirrored.

Conclusions

By conducting this study, the authors gained considerable insights into what geometry configuration might be suitable or unsuitable to employ in compact electronic components as natural convection is only the ideal solution when it comes to optimizing the heat transfer rate of those compact components. It was realized that the placement of heated circular obstacles directly in the line of each other (BC) should be avoided since they mutually disrupt each other’s flow circulation, which acts quite detrimental to the objective of heat dissipation and the average Nusselt number plot approves of this notion. When the configurations in which the obstacles at the bottom are inclined (‘BL’ and ‘BR’) are considered, it is found that the proximity of the enclosing walls to the heated obstacle plays a key factor. It leads to a moderate rate of heat transfer, whose value is quite close to that of the validation study. Quick successive energy transfers are witnessed between the fluid and the obstacle first, followed by the fluid and the boundary walls and lastly with the obstacle in a repetitive manner. When the configurations in which the obstacles at the top are inclined (‘UL’ and ‘UR’) are considered, a quite significant improvement in the heat transfer rate was noted, owing to the gradual successive energy transfer and increased available space for flow circulation. This made way to achieve uniform heat dissipation and the hypothesis is confirmed by the surface Nusselt number plot of UL and UR (which are overlapping), found to be comparatively high with respect to the other configurations in this study. On analyzing the local pressure coefficients, it was found that in top inclined configurations the values of pressure coefficient are positive for ‘case’ obstacles and is negative for ‘prime’ obstacles. A contrasting phenomenon is witnessed in bottom inclined configurations, where the values are negative for ‘case’ obstacles and positive for ‘prime’ obstacles. It was gauged from this that the static pressure is less than the free stream pressure for ‘case’ obstacles in bottom inclined configurations and ‘prime’ obstacles in top inclined configurations. The local velocity is more than the free stream velocity near these surfaces. Similarly for the ‘case’ obstacles in top inclined configurations and ‘prime’ obstacles in bottom inclined configurations, the static pressure is more than the free stream pressure leading us to the conclusion that the local velocity is less than the free stream velocity near these surfaces. When the average skin friction coefficient in ‘case’ obstacles of BC configuration was studied, it was found that the slope of the curve is steep between Ra. numbers 104 and 105 but there’s a drastic increase between 105 and 106. So as the Ra. the number kept increasing and the fluid started transitioning away from a laminar flow, the shear stress on the surface of heated obstacles increased. In the ‘prime’ obstacle, the decline is more prolonged, and the lowest peak obtained is constant for almost 100°.In bottom inclined configurations, The ‘case’ (bottom) obstacle had the intermediate values for every Ra. number but the ‘prime’ obstacle had the least skin friction coefficient since the bottom obstacle prevented the heat from making it to the surface of the upper obstacle. The body, in turn, ended up having a comparatively lower value of skin friction coefficient. In top inclined configurations, The ‘case’ (bottom) obstacle had the lowest values for every Ra. number but the ‘prime’ obstacle had the highest skin friction coefficient. Although the heat could impinge on the lower obstacle due to gravity, the flow dissipated way faster to the surrounding space rather than the upper obstacle due to availability of space. The increase in Ra. number lead to an increase in the rate of heat transfer as indicated by the Local Nu. number plots, the magnitude of local pressure coefficients, and the order of local skin pressure friction coefficients.

To quantify heat transfer rate between the least and the most optimum geometry, the study found an increase of 28.09% when the UL configuration is compared with the validation results and found a staggering 70.08% increase when UL is compared to the least optimum inline configuration (BC).