Introduction

Gas flow modeling in micro-/nanoscale is dependent on various parameters, the most important of which include compressibility and rarefaction. These two parameters cannot be ignored in gas flow modeling when the gas molecules–wall interaction cannot be ignored at the molecular scale. For this reason, the impact of fluid molecules–solid wall collisions is more significant than intermolecular collisions in the fluid flow. The type of flow is of great importance for the advancement of microfluidic instruments, and numerous investigations have been recently conducted on rarefied gas flow simulation in microchannels of different geometries. The gas rarefaction in microfluidic devices considerably influences the molecular mean free path, which in turn may change the thermodynamic equilibrium in such devices. Rarefaction and non-equilibrium of fluid are measured by the dimensionless Knudsen number \(\left( {{\text{Kn}} = \frac{\lambda }{H}} \right)\), where \(\lambda\) and H are the molecular mean free path and the characteristic length, respectively. Gas flow in microfluidic devices, rarefaction and compressibility are interdependent, and their effects on each other cannot be neglected. This interdependency causes difficulties in the analysis of gas flow in such devices. Conventionally, the compressibility of gas flow is measured concerning its Mach number. When the Mach number of the gas flow approaches one, the compressibility turns into an effective factor in the fluid flow, such that it cannot be ignored for gas flows with a Mach number greater than 0.3. According to the gas kinetic theory, Knudsen, Reynolds and Mach numbers are related as \({\text{Kn}} = \sqrt {\frac{\gamma \pi }{2}} \frac{\hbox{Ma}}{\hbox{Re}}\), and the range of the Reynolds number can be related to flow compressibility or incompressibility [1].

At high Knudsen numbers, the compressibility of gas flow can be ignored only at very low Reynolds numbers. At low Knudsen numbers, the flow can be considered incompressible in a wide range of Reynolds numbers. Gas flow can be considered as a rarefied flow on a small scale and at high altitudes. The gas flow is classified into four types based on the Knudsen number: (1) continuous regime (Kn< 0.01): fluid continuity and thermodynamic equilibrium hypotheses hold in the Navier–Stokes equations. It is noteworthy that the Navier–Stokes equations with the no-slip condition can be used in microchannels. (2) Slip regime (0.01 < Kn< 0.1): thermodynamic equilibrium does not hold on the walls and in the Knudsen layer. Moreover, the Navier–Stokes equations (based on the flow continuity assumption) can be used assuming a fluid slip condition on the walls. (3) Transition regime (0.1 < Kn< 10): The Navier–Stokes equations do not hold under any condition, and rarefaction plays a key role in this case. The impact of Knudsen number in this regime is significant, posing a challenge for rarefied gas flow simulation in microchannels. The wall function or the modified Knudsen number based on the gas kinetic theory (because of the viscosity correction) for dealing with this problem should be employed. (4) Free molecular regime (Kn> 10): The collisions between gas molecules can be disregarded in comparison with gas molecules–solid wall collisions as a key factor in the gas flow modeling [2].

Lattice Boltzmann method (LBM) has recently become a good alternative to direct simulation Monte Carlo (DSMC) for studying rarefied gas flow in microchannels due to its lower computational time and the ability to simulate complex geometries. Numerous investigations have been carried out on gas flow in micro- and nanoscales. Dongari et al. [3] analytically studied gas flow in a long microchannel and found a direct relationship between the mass flow rate and pressure ratio. In accordance with their results, the normalized mass flow rate initially decreased up to a Knudsen number of 0.886, after which it started to increase. Dongari et al. [4] examined the influence of Knudsen layer variations in micro-/nanoscale on the gas flow. Providing an analytical function called power law, the impact of Knudsen number on transition gas flow was studied with reasonable accuracy.

Arkilic et al. [5] investigated gas flow in a long microchannel using the perturbation method. In accordance with pressure variations along the streamlines, they concluded that the pressure decreases with raising the Knudsen number, and pressure changes nonlinearly in the slip regime. They also found that the mass flow rate is boosted by growing the pressure. However, they considered the first-order derivative of velocity in the transverse direction to provide a relation for slip velocity. Armaly et al. [6] analyzed gas flow in a microchannel with a step both experimentally and theoretically and obtained transverse velocities in this geometry. They obtained the separation distance enhanced by increasing the Reynolds number up to 1200 in the laminar flow regime. A considerable rise in the Reynolds number formed oscillation as well as an increase in the velocity. Graur et al. [7] studied a relatively rarefied gas flow in a microchannel with a variable cross section both experimentally and theoretically. They found the mass flow rate increased as pressure increased in the nozzle and diffuser. Hemadri et al. [8] studied rarefied gas flow in a microchannel with a non-uniform cross-section experimentally. They proposed a correlation between the average Knudsen number and average rarefaction and reported a Knudsen minimum of roughly 0.9. They showed that the mass flow rate improved by enhancing the angle, whereas it was decreased as the aspect ratio increased.

Sazhin [9] scrutinized the rarefied gas flow in a rough microchannel utilizing the particle-based method called DSMC. In short/long channel, the mass flow rate at a broad range of Knudsen numbers from a free molecular regime to the near hydrodynamic was reported. The roughness has a significant impact on the flow rate in the free molecular and transitional regimes. Sabouri and Darbandi [10] investigated the species separation for rarefied gas mixture flow in a micronozzle using the DSMC scheme. They conceived two parameters that have an important effect on the separation of mixture flow, including lateral species separation and streamwise separation. Biswas et al. [11] studied a step flow at low and moderate Reynolds numbers and found a larger separation length with increasing the Reynolds number. Darbandi and Roohi [12] evaluated subsonic flow in stepped nanochannels in micro-/nanoscale by employing the DSMC method. According to their outcomes, pressure linearly decreased along the microchannel, and the pressure deviated parabolically from the linear pressure. The dimensionless velocity along y-direction (to wall velocity) was higher at higher x/l values, and the velocity was higher along the step because of a reduction in the cross section. The velocity also decreased with increasing the Knudsen number. The Mach number for the lower wall along the longitudinal direction decreased from the inlet to the step length and then increased up to the microchannel outlet, but again slightly decreased at the outlet. Hadjiconstantinou and Simek [13] simulated 2D thermal gas flow in a micro-/nanochannel by DSMC method and calculated the Knudsen number (for constant wall temperature) and Cf·Re values. They found that Cf·Re declines with the Knudsen number. Mozaffari and Roohi [14] studied the thermally driven flow inside a divergent micro-/nanochannel with divergence angle at the range of 0–7 degrees with two aspect ratios (L/H = 6 and 20) using DSMC method. They found that while the opening angle is small, the velocity and pressure distributions have a constant treatment approximately. Roohi et al. [15] extended the 2D solution of Navier–Stokes equations to the transition regime utilizing the information preservation method. They obtained the transverse velocities using the linear Boltzmann method and DSMC, IP (by models 1 and 2) and Beskok methods. The ratio of the mass flow rate obtained from the above methods to that obtained from the Navier–Stokes equations (the parameters) decreased with the Knudsen number at the outlet.

Chen and Tian [16] simulated gas flow in a microchannel applying the LBM and found an increase in the slip velocity by growing the Knudsen number. They presented the variations in dimensionless velocity along the transverse direction of the microchannel and showed that the non-dimensional velocity in terms of inlet velocity rises with growing the Knudsen number. Liu and Feng [17] examined the gas flow through a microchannel by using the cascade LBM. The Bosanquet-type effective viscosity is used to capture the rarefaction effect, and the BSR scheme plays a role as the wall boundary condition. The dimensionless parameters, such as velocity and mass flow rate, are reported and discussed in detail.

Bakhshan and Omidvar [18] studied fluid flow in a microchannel with a step for a broad range of Knudsen numbers using LBM with multiple relaxation times. They obtained velocities at various cross sections of the microchannel and found that the size of eddies increased with growing pressure ratio in the slip regime. They also found the transverse dimensionless velocities (in terms of average velocity) were inversely related to the Knudsen number. However, the changes in the cross section were represented by the relation \({\text{Kn}}\left( x \right) \cdot P\left( x \right) \cdot H\left( x \right) = {\text{const}}\). Ginzburg [19] proposed a model with two relaxation times (TRT) using symmetric distribution functions and symmetric equilibrium distribution function and also for asymmetric functions for the first time. This model considerably reduced computational cost compared to a model with multiple relaxation times in the LBM. Esfahani and Norouzi [20] investigated rarefied gas flow in a microchannel with two relaxation times applying the LBM and calculated transverse velocities up to a Knudsen number of 0.338. With the increasing Knudsen number, the slip velocities obtained from the LBM were different from those calculated by DSMC method due to neglecting the effect of Knudsen layer in the transition regime and applying the slip velocity up to the first derivative.

Guo et al. [21] simulated rarefied gas flow in microscale using the modified LBM with multiple relaxation times and obtained transverse velocities and mass flow rates at different Knudsen numbers. As reported, the mass flow rate initially decreased and then increased. The model was, however, unable to provide the correct slip velocity and produced different results compared to those obtained from the DSMC. He and Luo [22] provided the LBM theory and, additionally, provided an approximate velocity-based distribution function for low Much numbers by studying equilibrium distribution functions and their effective parameters. They also extended the LBM to two and three dimensions. Homayoon et al. [23] studied rarefied gas flow in a microchannel in a broad range of Knudsen numbers using the LBM. In this research, a single relaxation time was used, and the slip velocity was considered up to the first order. They reported transverse velocities in the microchannel up to a Knudsen number of 8. However, their model failed to provide the slip velocity with acceptable accuracy, and values obtained from LBM differed from those calculated by the DSMC method. Kharmiani and Roohi [24] studied rarefied gas flow in a convergent–divergent nano-/micronozzle using two relaxation times in the LBM and presented the diagrams for pressure and slip Mach numbers. Assigning individual slip coefficients for each regime (by trial and error), they obtained a pressure close to obtained outcomes from the direct simulation Monte Carlo. However, the Mach number was obtained with a significant deviation on account of disregarding the impact of Knudsen layer in the analytical power-law function. Although offering a good accuracy for two planar surfaces, this function lacks sufficient accuracy for geometries with a variable cross-section. Lim et al. [25] examined gas flow in microchannels using the LBM. They reported a relatively parabolic relation for pressure deviation from the linear pressure (\(\delta P\)) and an increase in the slip velocity along the channel. Bounce-back distribution functions were considered for the walls. The apparent difference in the \(\delta P\) was due to the inability of the relaxation time to provide the desired values.

Li et al. [26] simulated transitional flow in a microchannel by the LBM. Using multiple relaxation times and bounce-back/specular reflection distribution functions, they reported transverse velocities and mass flow rates in the microchannel in terms of the Knudsen number. The slip velocities were significantly different from those obtained from the DSMC at high Knudsen numbers (around 4.5). They reported a Knudsen minimum of 0.886. Ahangar et al. [27] studied the isothermal diluted gas flow in a microchannel with a backward-facing step employing the TRT-LBM and reported pressure and velocity at different points. Different slip coefficients were provided in the LBM for various regimes to obtain values close to those computed by the DSMC approach. According to their results, the size of eddies decreased with increasing the rarefaction parameter, and the length of separation zone approached zero at high Knudsen numbers (in the transition regime). They also investigated the rectangular barrier effect on the rarefied flow properties in the long microchannel utilizing the power-law analytical function approach [28]. Gokaltun and Dulikravich [29] simulated rarefied gas flow in a channel with heat transfer by LBM with single relaxation time. The temperature of the upper and lower walls was ten times that of the inlet temperature. They found the transverse dimensionless temperature (in terms of wall temperature) declined with the rising Knudsen number. The transverse dimensionless velocity (in terms of inlet velocity) also increased with increasing x/l. Since a first-order slip velocity was considered in the simulations, the proposed model showed an acceptable performance up to a Knudsen number of 0.14 and lacked a reasonable accuracy at higher Knudsen numbers, although no validation was performed to evaluate the accuracy of the calculated temperatures. Chen and Tian [30] investigated a thermal microscale flow under the slip regime by LBM and observed a higher temperature at the lower wall at high Knudsen numbers at Eckert number (Ec) = 2. The Nusselt number decreased with increasing the Knudsen number at two different Ec numbers so that the flow with a higher Ec showed a higher Knudsen number. They neglected the higher derivative orders in the calculation of velocity, leading to the low accuracy of the results. Other works can be addressed in this way, concerning fluid flow and heat transfer at the microscale level via LBM or molecular dynamic (MD) approach [31,32,33,34,35,36,37,38,39].

Previous researchers [23, 26, 29] considered single relaxation time and multiple relaxation times for solving the fluid flow. They also utilized three types of non-equilibrium distribution functions for particles in the D2Q9 lattice network to solve the thermal lattice Boltzmann equation against our proposed model. As novel research, the rarefied gaseous flow with heat transfer in a regular-shape microchannel was simulated by incorporating the LBM into a modified model (TRT_SRT solver). Two relaxation times, namely symmetric relaxation time and antisymmetric relaxation time, were used for the diluted gas flow by applying the Zou–He and BSR boundary conditions at the inlet–outlet and wall surfaces, respectively. Single relaxation time and the second-order implicit method (used for geometry walls) were adopted to handle the thermal treatment of rarefied flow. Non-equilibrium distribution functions and a fully developed temperature profile were, respectively, considered in inlet and outlet boundary conditions. The acceptable consistency between the DSMC and LBM results shows the accuracy of the proposed model.

Modified TRT_SRT model

Problem statement

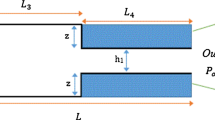
Figure 1 shows the gas flow in a microchannel with a height of H, length of L and an aspect ratio (L/H) of 20. A pressure ratio (\(\varPi = \frac{{P_{\text{in}} }}{{P_{\text{out}} }}\)) of 2 was considered in the simulations. The upper and lower microchannel walls were considered to be at the same temperature (\(T_{\text{bottom}} = T_{\text{top}} = T_{\text{w}} = 0 \,{\text{Tu}}\)), which were lower than the fluid inlet temperature (\(T_{\text{in}} = 1\,{\text{Tu}}\)). A fully developed temperature profile was considered at the microchannel outlet. The parameters H = 40, L = 800 and Pr = 0.7 were considered for simulation of the gas flow with heat transfer in the microchannel, and the dimensionless parameters X*, Y*, U* and T* were defined as X/L, Y/H, U/Umean and T/Tmean, respectively. Umean and Tmean, respectively, indicate the mean velocity and mean temperature.

Fig. 1
figure 1

2D gas flow with heat transfer in a microchannel at a pressure ratio of 2

Full size image

Governing equations of LB

Lattice Boltzmann simulation includes two steps, namely collision and streaming. The Boltzmann equation is impossible to solve directly due to its complexity and the nonlinearity of the collision operator. To simplify the collision operator, Bhatnagar–Gross–Krook (BGK) proposed a first-order linear model with a reasonable modeling accuracy [40]:

$$\varOmega = \omega \left( {f^{\text{eq}} - f} \right) = \frac{1}{\tau }\left( {f^{\text{eq}} - f} \right)$$
(1)

where \(\tau\) and \(\omega\), respectively, represent the relaxation time and collision frequency, \(f^{\text{eq}}\) is the equilibrium distribution function, also known as Maxwell–Boltzmann distribution function, showing the particle state precisely at the moment of collision. Relaxation time indicates conditions under which the distribution function \(f\) approaches the equilibrium distribution function (\(f^{\text{eq}}\)). Relaxation time is an indispensable parameter in the LBM simulation and should be within the range of 0.5–3 for the model to convergence. The equilibrium distribution function is defined as follows [40]:

$$f^{\text{eq}} = \frac{\rho }{{\left( {2\pi RT} \right)^{1.5} }}{ \exp }\left( { - \frac{{\left( {\vec{\varepsilon } - \vec{u}} \right)^{2} }}{2RT}} \right)$$
(2)

where \(\vec{\varepsilon }\) shows the microscopic velocity, ρ, vector u and T represent macroscopic density, velocity and temperature, respectively, and R is the ideal gas constant.

In recent years, both single and multiple relaxation times have been used in the LBM for rarefied gas flow simulations. The model with a single relaxation time lacks sufficient precision in calculating the slip velocity. In contrast, a model with multiple relaxation times suffers from extensive computational times. Ginzburg [19] provided a model with two relaxation times (TRT). Ahangar et al. [41] reported the lattice Boltzmann equation with two relaxation times as follows:

$$f_{\text{i}} \left( {\varvec{x} + \varvec{c}_{i} \delta t,t + \delta t} \right) - f_{\text{i}} \left( {\varvec{x},t} \right) = - \frac{1}{{\tau_{\text{s}} }}\left( {f_{\text{i}}^{\text{s}} \left( {\varvec{x},t} \right) - f_{\text{i}}^{\text{s,eq}} \left( {\varvec{x},t} \right)} \right) - \frac{1}{{\tau_{\text{a}} }}\left( {f_{i}^{\text{a}} \left( {\varvec{x},t} \right) - f_{\text{i}}^{\text{a,eq}} \left( {\varvec{x},t} \right)} \right)$$
(3)

where \(f_{\text{i}}\) represents the local distribution functions, \(f_{\text{i}}^{\text{s}}\) symmetric distribution functions, \(f_{\text{i}}^{\text{s,eq}}\) symmetric equilibrium distribution functions and \(f_{\text{i}}^{\text{a,eq}}\) asymmetric equilibrium distribution functions. Moreover, \(\tau_{\text{s}}\) denotes symmetric relaxation time (based on corrected viscosity), \(\tau_{\text{a}}\) asymmetric relaxation time (based on wall boundary conditions), x particle position, ci discretized velocity vectors for each particle and \(\delta t\) time step. The simulation used the D2Q9 grid with time and spatial steps of unity.

The following distribution function, g, with single relaxation time, was used to obtain the temperature profiles [40]:

$$g_{\text{i}} \left( {\varvec{x} + \varvec{c}_{\text{i}} \delta t,t + \delta t} \right) - g_{\text{i}} \left( {\varvec{x},t} \right) = - \frac{1}{{\tau_{\text{s}} }}\left( {g_{\text{i}}^{\text{s}} \left( {\varvec{x},t} \right) - g_{\text{i}}^{\text{seq}} \left( {\varvec{x},t} \right)} \right)$$
(4)

To use Eq. (2) in programming the LBM, its discretized form is written using the Taylor series expansion [40] as follows:

$$f_{\text{i}}^{\text{eq}} = \omega_{\text{i}} \rho \left[ {1 + \frac{{\varvec{c}_{\text{i}} \cdot \varvec{V}}}{{c_{\text{s}}^{2} }} + \frac{{(\varvec{c}_{\text{i}} \cdot \varvec{V})^{2} }}{{2c_{\text{s}}^{4} }} - \frac{{\varvec{V} \cdot \varvec{V}}}{{2c_{\text{s}}^{2} }}} \right]$$
(5)

where ρ is density, ωi mass coefficients for each particle, ci particle velocity equal to \(\frac{\delta x}{\delta t}\), V velocity vector and cs sound velocity, which is equal to \(\frac{c}{\surd 3}\).

The distribution function, g, is used in the simulations to obtain the temperature profiles. The equilibrium distribution functions \(g_{\text{i}}^{\text{eq}}\) are defined as follows [40]:

$$g_{\text{i}}^{\text{eq}} = \omega_{\text{i}} T\left[ {1 + \frac{{\varvec{c}_{\text{i}} \cdot \varvec{V}}}{{c_{\text{s}}^{2} }}} \right]$$
(6)

Ginzburg [19] defined local symmetric distribution functions (\(f_{\text{i}}^{\text{s}}\)), asymmetric distribution functions (\(f_{\text{i}}^{\text{a}}\)) and symmetric (\(f_{\text{i}}^{\text{s,eq}}\)) and asymmetric (\(f_{\text{i}}^{\text{a, eq}}\)) equilibrium distribution functions for each particle as follows:

$$\begin{aligned} f_{\text{i}}^{\text{s}} & = \frac{1}{2}\left( {f_{\text{i}} + f_{{ - {\text{i}}}} } \right),\, f_{\text{i}}^{\text{a}} = \frac{1}{2}\left( {f_{\text{i}} - f_{{ - {\text{i}}}} } \right) \\ f_{\text{i}}^{\text{s,eq}} & = \frac{1}{2}\left( {f_{\text{i}}^{\text{eq}} + f_{{ - {\text{i}}}}^{\text{eq}} } \right),\, f_{\text{i}}^{\text{a, eq}} = \frac{1}{2}\left( {f_{\text{i}}^{\text{eq}} - f_{{ - {\text{i}}}}^{\text{eq}} } \right) \\ \end{aligned}$$
(7)

The discretized velocities for the particles in the D2Q9 grid are defined as follows [42]:

$$c_{\text{i}} = \left\{ {\begin{array}{*{20}l} {\left( {0,0} \right)} \hfill & { i = 0} \hfill \\ {\left( {\cos \left[ {\frac{{\left( {i - 1} \right)\pi }}{2}} \right],\sin \left[ {\frac{{\left( {i - 1} \right)\pi }}{2}} \right]} \right)c } \hfill & {i = 1,2,3,4} \hfill \\ {\left( {\cos \left[ {\frac{{\left( {2i - 9} \right)\pi }}{4}} \right],\sin \left[ {\frac{{\left( {2i - 9} \right)\pi }}{4}} \right]} \right)\sqrt 2 c } \hfill & {i = 5,6,7,8} \hfill \\ \end{array} } \right.,c = 1$$
(8)

Any particle in the lattice grid has its mass coefficients indicating the effect of these particles on the local equilibrium distribution function. These coefficients for the D2Q9 grid are expressed as follows [27]:

$$\omega_{\text{i}} = \left\{ {\begin{array}{*{20}l} {\frac{4}{9}} \hfill & {i = 0} \hfill \\ {\frac{1}{9}} \hfill & {i = 1,2,3,4} \hfill \\ {\frac{1}{36} } \hfill & {i = 5,6,7,8} \hfill \\ \end{array} } \right.$$
(9)

Fluid properties such as macroscopic density, velocity and pressure can be calculated by the numerical LBM [40]:

$$\rho = \mathop \sum \limits_{i = 0}^{8} f_{\text{i}} , \rho \varvec{V} = \mathop \sum \limits_{i = 0}^{8} \varvec{c}_{\text{i}} f_{\text{i}} , T = \mathop \sum \limits_{i = 0}^{8} g_{\text{i}} , P = \rho c_{\text{s}}^{2}$$
(10)

As the primary assumption in the LBM, the intermolecular forces are disregarded, and the gas is considered to be an ideal gas. Hence, equating \(P = \rho RT\) with Eq. 10 gives \(RT = c_{\text{s}}^{2} = \frac{1}{3}\).

The kinematic viscosity (ν) related to the symmetric relaxation time of the gas flow (τf) and thermal diffusion (α) related to the relaxation time of heat transfer in gas (τg) are defined as follows [40], [43]:

$$\nu = \left( {\tau_{\text{f}} - 0.5} \right)c_{\text{s}}^{2} \cdot \delta t , \alpha = \left( {\tau_{\text{g}} - 0.5} \right)c_{\text{s}}^{2} \cdot \delta t$$
(11)

Effective relaxation times

Gas viscosity is a crucial parameter for momentum transfer between gas molecules. By utilizing the gas kinetic theory, the viscosity of gas flow is defined by Guo et al. [44] as follows:

$$\mu = 1.016 \times \frac{5}{16}\frac{m}{{d^{2} }}\sqrt {\frac{RT}{\pi }} \approx 0.5\rho \bar{c}\lambda , \;\lambda = \frac{m}{{\sqrt 2 \pi \rho d^{2} }}$$
(12)

where m is molecular weight, d molecular diameter and \(\bar{c} = \sqrt {\frac{8RT}{\pi }}\) mean molecular velocity. According to Eq. 12, the molecular mean free path equals \(\lambda = \frac{\mu }{P}\sqrt {\frac{\pi RT}{2}}\), in which the pressure (P) equals \(\rho RT\). This equation only holds for unconfined gas flows [44]. For the gas flows restricted by solid walls, the path of some molecules colliding the walls will be smaller than the mean free path as mentioned by Nie et al. [45], Guo et al. [21], Meng et al. [46] and Tang et al. [47]. In general, the collision between gas molecules and solid walls can be ignored in comparison with intermolecular collisions when the Knudsen number is considerably lower than one. According to Eq. 12, viscosity (µ0) equals \(a_{0} \rho \bar{c}\lambda\) for such conditions, where \(a_{0} = 0.5\) and the effective viscosity is equal to \(\mu_{0}\). For transition gas flow, intermolecular collisions significantly decrease with increasing rarefaction effects. Bosanquet interpolated the diffusion coefficients and obtained the Bosanquet-type correlation for rarefied gas flows at low Knudsen numbers [48]:

$$\frac{1}{{\mu_{e} }} = \frac{1}{{\mu_{0} }} + \frac{1}{{\mu_{\infty } }}$$
(13)

where \(\mu_{e}\), \(\mu_{0}\) and \(\mu_{\infty }\), respectively, denote the effective viscosity of gas flow in transition regime, slip regime and free molecular regime. Only the collisions between the gas molecules and the solid wall should be regarded in the free molecular regime, in which case \(\mu_{\infty } = a_{\infty } \rho \bar{c}H\). According to Beskok and Karniadakis [49], the effective viscosity of the gas flow in the transition regime is expressed as \(\mu_{\text{e}} = \frac{{\mu_{0} }}{{\left( {1 + a{\text{Kn}}} \right)}} = \frac{{a_{0} \rho \bar{c}\lambda }}{{\left( {1 + a{\text{Kn}}} \right)}}\), where \(a = \frac{{a_{0} }}{{a_{\infty } }}\) and a value of 2 was considered for a by Yuhong and Chan [50]. The next objective is to find the relationships between Knudsen number (Kn) and symmetric relaxation time (τs) to simulate the gas flow in slip and transition regimes. According to the above data, Li et al. [51] proposed the following correlations for slip and transition gas flows:

$$\tau_{\text{f}} = \tau_{\text{s}} = 0.5 + \sqrt {\frac{6}{\pi }} N \cdot {\text{Kn}} \,\left( {{\text{Slip}}\, {\text{flow }}\,{\text{regime}}} \right)$$
(14)
$$\tau_{\text{f}} = \tau_{\text{s}} = 0.5 + \sqrt {\frac{\pi }{6}} \frac{{N \cdot {\text{Kn}}}}{{\left( {1 + a{\text{Kn}}} \right)}} \,\left( {{\text{Transition }}\,{\text{flow }}\,{\text{regime}}} \right)$$
(15)

where \(N = \frac{H}{\delta x}\) represents the number of grids along the characteristic length, H is the characteristic length and \(\delta x\) shows the time step. The following single relaxation time was used to obtain the thermal solution [41]. \(\tau_{\text{g}}\) and \(\tau_{\text{f}}\) represent the relaxation times related to fluid flow and thermal fluid flow, respectively:

$$\tau_{\text{g}} = 0.5 + \frac{ \alpha }{{c_{\text{s}}^{2} \cdot \delta t}}$$
(16)

Boundary conditions

Boundary conditions used for simulation of rarefied gas flow with heat transfer are of great importance. A common relation called second-order slip boundary condition [27] and the temperature jump relation for the gas flow [29] were considered in the simulations:

$$u^{\text{slip}} = B_{1} \sigma_{\upnu} \lambda \left. {\frac{\partial u}{\partial y}} \right|_{\text{W}} - B_{2} \lambda^{2} \left. {\frac{{\partial^{2}_{\text{u}} }}{{\partial y^{2} }}} \right|_{\text{W}}$$
(17)
$$T^{\text{jump}} = \phi \left( {\frac{2\gamma }{\gamma + 1}} \right)\left( {\frac{\text{Kn}}{ \Pr }} \right)\left( {\frac{\partial T}{\partial y}} \right)$$
(18)

In Eq. 17, uslip represents slip velocity and \(\sigma_{\upnu}\) is the tangential momentum accommodation coefficient (TMAC) defined as \(\left( {\frac{2 - \sigma }{\sigma }} \right)\), where \(\sigma = 1\). The slip coefficients B1 and B2, respectively, assume values of 1 and 0.5, 0.8183 and 0.6531, and 1.11 and 0.61 according to Hsia and Domoto [52], Guo et al. [21] and Cercignani [53].

If it is equal to or even higher than 1, B1 is unable to express slip velocity with reasonable accuracy as it directly impacts the calculation of slip velocity. Accordingly, through correcting the first-order Maxwell slip coefficient, Loyalka et al. [54], and Loyalka [55] expressed this coefficient as \(B_{1} = \left( {\frac{2 - \sigma }{\sigma }} \right)\left( {1 - 0.1817\sigma } \right)\). Reported by Li et al. [51], the slip coefficients \(B_{1} = \left( {1 - 0.1817\sigma } \right)\) and \(B_{2} = 0.8\) were used in the simulations.

The temperature jump for the fluid on the wall is expressed using the first-order derivative of temperature (Eq. 18), where \(\gamma\) is specific heat ratio, Pr is Prandtl number and \(\phi = \left( {\frac{{2 - \sigma_{T} }}{{\sigma_{T} }}} \right)\), in which \(\sigma_{T}\) represents the thermal accommodation coefficient and is usually considered equal to 1 [56].

Zou–He boundary conditions were considered at the inlet and outlet of the microchannel as follows [57]:

The flow boundary condition at microchannel inlet is given as:

$$u\left( {0,j} \right) = 1 - \left( {\frac{{f_{0} + f_{2} + f_{4} + 2\left( {f_{3} + f_{6} + f_{7} } \right)}}{{\rho_{\text{in}} }}} \right)$$
(19)
$$f_{1} = f_{3} + \frac{2}{3}\rho_{\text{in}} u\left( {0,j} \right)$$
(20)
$$f_{5} = f_{7} - 0.5\left( {f_{2} - f_{4} } \right) + \frac{1}{6}\rho_{\text{in}} u\left( {0,j} \right)$$
(21)
$$f_{8} = f_{6} + 0.5\left( {f_{2} - f_{4} } \right) + \frac{1}{6}\rho_{\text{in}} u\left( {0,j} \right)$$
(22)

where \(\rho_{\text{in}}\) is flow density at the inlet, which equals \(\rho_{\text{in}} = 3P_{\text{in}}\) due to the pressure ratio (\(\varPi = \frac{{P_{\text{in}} }}{{P_{\text{out}} }} = 2\)) used in the problem under study.

The flow boundary condition at the microchannel outlet is given as:

$$u\left( {n,j} \right) = - 1 + \left( {\frac{{f_{0} + f_{2} + f_{4} + 2\left( {f_{1} + f_{5} + f_{8} } \right)}}{{\rho_{\text{out}} }}} \right)$$
(23)
$$f_{3} = f_{1} - \frac{2}{3}\rho_{\text{out}} u\left( {n,j} \right)$$
(24)
$$f_{7} = f_{5} + 0.5\left( {f_{2} - f_{4} } \right) - \frac{1}{6}\rho_{\text{out}} u\left( {n,j} \right)$$
(25)
$$f_{6} = f_{8} - 0.5\left( {f_{2} - f_{4} } \right) - \frac{1}{6}\rho_{\text{out}} u\left( {n,j} \right)$$
(26)

where \(\rho_{\text{out}}\) is flow density at the outlet, which equals \(\rho_{\text{out}} = 3P_{\text{out}}\) for the gas flow.

Bounce-back/specular reflection boundary conditions were used for the upper and lower walls [58].


For the upper wall,

$$f_{4} = f_{2}$$
(27)
$$f_{7} = rf_{5} + \left( {1 - r} \right)f_{6}$$
(28)
$$f_{8} = rf_{6} + \left( {1 - r} \right)f_{5}$$
(29)

For the lower wall,

$$f_{2} = f_{4}$$
(30)
$$f_{5} = rf_{7} + \left( {1 - r} \right)f_{8}$$
(31)
$$f_{6} = rf_{8} + \left( {1 - r} \right)f_{7}$$
(32)

Non-equilibrium distribution functions were used as a temperature boundary condition at the microchannel inlet. A fully developed temperature profile was also considered at the microchannel outlet [40].

The temperature boundary condition at the inlet is:

$$g_{1} = T_{\text{in}} \left( {\omega \left( 1 \right) + \omega \left( 3 \right)} \right) - g_{3}$$
(33)
$$g_{5} = T_{\text{in}} \left( {\omega \left( 5 \right) + \omega \left( 7 \right)} \right) - g_{7}$$
(34)
$$g_{8} = T_{\text{in}} \left( {\omega \left( 8 \right) + \omega \left( 6 \right)} \right) - g_{6}$$
(35)

The temperature boundary condition at the outlet (\(\frac{\partial T}{\partial x} = 0\)) is:

$$g_{i} \left( n \right) = g_{i} \left( {n - 1} \right),{\text{for}}\, \, i = 1 - 8$$
(36)

The temperature jump of the fluid on the walls is defined as follows. First, the fluid temperature on the wall is calculated using this coefficient, and then the temperature boundary conditions are employed at the microchannel inlet and outlet. The following relationships were obtained using the second-order implicit scheme [29].

\(T_{1}\) and \(T_{2}\) show the temperature at nodes near the wall surface (y = 0 and y = 1). The temperature boundary condition for the lower wall and the unknown distribution function related to thermal rarefied gas flow at the bottom wall are calculated as follows:

$$T_{{{\text{y}} = 0}} = \frac{{\left[ {C^{*} \left( {4T_{1} - T_{2} } \right) + 2T_{\text{w}} } \right]}}{{\left( {2 + 3C^{*} } \right)}}$$
(37)
$$g_{2} = T_{{{\text{y}} = 0}} \left( {\omega \left( 2 \right) + \omega \left( 4 \right)} \right) - g_{4}$$
(38)
$$g_{5} = T_{{{\text{y}} = 0}} \left( {\omega \left( 5 \right) + \omega \left( 7 \right)} \right) - g_{7}$$
(39)
$$g_{6} = T_{{{\text{y}} = 0}} \left( {\omega \left( 6 \right) + \omega \left( 8 \right)} \right) - g_{8}$$
(40)

\(T_{{{\text{m}} - 1}}\) and \(T_{{{\text{m}} - 2}}\) demonstrate the temperature at y = m and y = m − 1. The temperature boundary condition for the upper wall is:

$$T_{{{\text{y}} = {\text{m}}}} = \frac{{\left[ {C^{*} \left( {4T_{{{\text{m}} - 1}} - T_{{{\text{m}} - 2}} } \right) + 2T_{\text{w}} } \right]}}{{\left( {2 + 3C^{*} } \right)}}$$
(41)
$$g_{4} = T_{{{\text{y}} = {\text{m}}}} \left( {\omega \left( 2 \right) + \omega \left( 4 \right)} \right) - g_{2}$$
(42)
$$g_{8} = T_{{{\text{y}} = {\text{m}}}} \left( {\omega \left( 6 \right) + \omega \left( 8 \right)} \right) - g_{6}$$
(43)
$$g_{7} = T_{{{\text{y}} = {\text{m}}}} \left( {\omega \left( 7 \right) + \omega \left( 5 \right)} \right) - g_{5}$$
(44)

The temperature jump coefficient (\(C^{*}\)) used in the rarefied gas flow simulation in the microchannel with heat transfer is defined as follows [29]:

$$C^{*} = \phi {\text{Kn}}\left( {\frac{2\gamma }{{\left( {\gamma + 1} \right){ \Pr }}}} \right) = \left( K \right){\text{Kn}} ,\quad K = \phi \cdot \frac{2\gamma }{{\left( {\gamma + 1} \right) \cdot { \Pr }}} , \phi = 1$$
(45)

Guo and Shu [40] expressed the slip velocity of the gas flow between two planes based on the bounce-back/specular reflection boundary conditions for the wall, where flow rarefaction level plays a crucial role in Eq. 46. They also provided an analytical equation (Eq. 47) for the second-order slip velocity in terms of slip coefficients. Equating the relations from lattice Boltzmann and analytical solutions, the asymmetric relaxation time (based on wall boundary conditions) and the parameter (dependent on the slip coefficient B1) are obtained from Eqs. (48) and (49). The asymmetric relaxation time along with the symmetric relaxation time increases the accuracy of slip velocities for the gas flow:

$$u_{\text{s}} = \frac{{4\left( {1 - r} \right)}}{r}\sqrt {\frac{6}{\pi }} {\text{Kn}} + \frac{2\varpi }{{\pi \left( {\tau_{\text{s}} - 0.5} \right)^{2} }}{\text{Kn}}^{2}$$
(46)
$$u_{\text{s}} = 4B_{1} {\text{Kn}} + 8B_{2} {\text{Kn}}^{2}$$
(47)
$$r = \left( {1 + \sqrt {\frac{\pi }{6}} B_{1} } \right)^{ - 1}$$
(48)
$$\tau_{\text{a}} = 0.5 + \frac{{\pi B_{2} \left( {2\tau_{\text{s}} - 1} \right)^{2} + 3}}{{8\left( {2\tau_{\text{s}} - 1} \right)}}$$
(49)

where \(\varpi = 16\left( {\tau_{\text{s}} - 0.5} \right)\left( {\tau_{\text{a}} - 0.5} \right)\).

Results and discussion

Grid independency test

The optimal grid size plays a crucial role in reducing computational costs. The gas flow in the microchannel for obtaining the proper mesh size was simulated under conditions of aspect ratio (\({\text{AR}}) = \frac{L}{H} = 20\), pressure ratio \(\left( {{\text{PR}} = \varPi = 2} \right)\) and \({\text{Kn}}_{\text{in}} = 0.055\) with four mesh sizes of \(200 \times 10\), \(400 \times 20\), \(800 \times 40,\) and \(1600 \times 80\). The velocity was obtained in section Y* = 0.5. According to the results in Table 1, the lower difference between the mesh sizes of \(800 \times 40\) and \(1600 \times 80\) is acceptable, and the mesh size of \(800 \times 40\) is selected as the optimal choice reducing the computational cost.

Table 1 Velocities at y-direction at \({\text{Kn}}_{\text{in}} = 0.055\)
Full size table

DSMC–linear Boltzmann validations

The test case for validation of fluid flow and thermal fluid flow is different. The direct simulation Monte Carlo method was used to evaluate model accuracy. The helium flow in a microchannel with AR = 4, \({\text{Kn}}_{\text{in}} = 0.055\) and different pressure ratios was considered to evaluate the temperature accuracy according to Table 2. To examine the accuracy of transverse velocity in the microchannel, a pressure ratio of 2 and an aspect ratio of 20 were used.

Table 2 Details of the selected test case for thermal solution
Full size table

Figure 2 shows the accuracy of the proposed model. Figure 2a shows the dimensionless velocity at y-direction (relative to the average velocity) for the slip regime (Kn= 0.096). The values obtained from LBM are very close to the analytical solution [59]. In this regime, the influences of the Knudsen layer are considerably lower than the slip regime, and the symmetric relaxation time in Eq. 14 was used in the simulations. Figure 2b shows the dimensionless velocity in the transverse direction for the transition rarefied gas flow (Kn= 0.667). Due to the significant impact of the Knudsen layer in this regime and the correctness of the suggested model, the DSMC method [15] and linear Boltzmann method [60] were used to improve model accuracy. The transverse velocity is parabolic in both slip and transition regimes. The lowest slip velocities were observed on the walls, and the highest velocity was observed at the microchannel centerline. Figure 2c, d displays the dimensionless temperatures (related to Tin) along the microchannel and temperature jumps with different heat conditions of wall surfaces (300 K and 350 K) at an inlet Knudsen number of 0.055. As seen, the dimensionless temperature decreases along the microchannel, and a maximum error of 4% occurs about X* = 0.8. The DSMC method [61] was used to increase the accuracy of dimensionless temperature. The maximum error of temperature jump occurred at a microchannel inlet (Fig. 2d), and the value is roughly 7%. The diagrams show the excellent accuracy of the proposed model for gas flow in a microchannel with heat transfer.

Fig. 2
figure 2

Dimensionless velocity profiles for a slip regime and b transition regime. LBM solution compared with Sreekanth analytical solution [59], direct simulation Monte Carlo [15], Ohwada linear Boltzmann [60], c and d dimensionless centerline temperatures, temperature jumps and DSMC solution (Roohi et al. [61])

Full size image

Results

In this section, the parameters AR = 20, \(\varPi = 2\), different inlet Knudsen numbers, \(T_{\text{bottom}} = T_{\text{top}} = T_{\text{wall}}\) = 0 (Tu), \(T_{\text{inlet}}\) = 1 (Tu) and Pr= 0.7 are considered for the present simulation.

Figure 3 represents the dimensionless pressure (in terms of outlet pressure) and pressure deviation from the linear pressure as a function of the inlet Knudsen number. Figure 3a displays the dimensionless pressure along the microchannel. The pressure ratio of the microchannel is 2. As shown, the dimensionless pressure reduces with the growing inlet Knudsen number. The nonlinearity of the pressure profile decreases as the flow regime changes from the slip to the transition regime so that a linear pressure profile can be considered at an inlet Knudsen number of 0.5. Given the importance of deviation from linear pressure for rarefied gas flow in microchannels, Liu and Guo [62] expressed the linear pressure as \(P_{\text{l}} = P_{\text{in}} + \left( {x/l} \right)\left( {P_{\text{out}} - P_{\text{in}} } \right)\). They also expressed the dimensionless \(\delta P\) in terms of outlet pressure as \(\delta P = \left[ {P\left( x \right) - P_{l} } \right]/\left( {P_{\text{out}} } \right)\). Figure 3b represents the \(\delta P\) characteristic in terms of inlet Knudsen number with a parabolic trend. The \(\delta P\) parameter declines with the rising inlet Knudsen number. As seen, these two parameters are at a minimum at both the inlet and outlet and reach a maximum at a length of about 0.55.

Fig. 3
figure 3

a Dimensionless pressure profiles along the microchannel and b pressure deviation from the linear pressure along the longitudinal direction of the geometry at different inlet Knudsen numbers

Full size image

Figure 4 displays the transverse velocity profiles in terms of inlet Knudsen number, centerline velocity and slip velocities along the x-axis. Figure 4a shows the dimensionless transverse velocity (in terms of mean velocity) in slip and transition regimes concerning the inlet Knudsen number. With the increasing rarefaction parameter, the velocity decreases along the centerline while slip velocity on the wall increases at a specific length of the microchannel (\(x = 200 \,{\text{lu}}\)). As seen in Fig. 2b, the dimensionless centerline velocity decreases as the flow regime changes from the slip to the transition regime. However, the centerline velocity increases at the microchannel outlet. The gas flow with an inlet Knudsen number of 0.075 and a pressure ratio of 2 changes from a slip regime to a transition regime, leading to a decrease in the nonlinearity (relative to the slip regime). Figure 4c exhibits the effect of the rarefaction parameter on the dimensionless slip velocity along the microchannel. The slip velocity grows with the rising rarefaction parameter and slightly decreases at the end of the microchannel.

Fig. 4
figure 4

a Dimensionless transverse velocity profiles, b centerline velocity and c slip velocity in terms of inlet Knudsen numbers

Full size image

Figure 5 shows Cf·Re profiles at different Knudsen numbers for rarefied gas flow in a microchannel. Zhang et al. [63] introduced these values for a slip gas flow between two parallel plates using an analytical solution. They used the analytical relation \(\left[ {96/\left( {1 + 6A_{1} {\text{Kn}} + 12A_{2} {\text{Kn}}^{2} } \right)} \right]\) to report these values up to a Knudsen number of 0.1. \(A_{1}\) and \(A_{2}\) show the slip coefficient for fluid flow. Due to the lack of generalization for the transition regime, Bakhshan and Omidvar [18] proposed the relation \(C_{f} \cdot {\text{Re}} = 3.113 + \frac{2.915}{{1 + 2{\text{Kn}}}} + 0.641{ \exp }\left( {\frac{3.203}{{1 + 2{\text{Kn}}}}} \right)\) up to a Knudsen number of 10. This relation has been used in both transition and slip regimes for simulation of rarefied gas flows in microchannels.

Fig. 5
figure 5

Cf·Re profiles in a slip regime along the microchannel and b transition regime at different inlet Knudsen numbers

Full size image

Figure 5a displays the effect of the rarefaction parameter on Cf·Re along the microchannel in the slip regime. As seen, Cf·Re diminishes with improving the inlet Knudsen number. The nonlinearity of the Cf·Re profiles also diminishes with the growing Knudsen number of the gas flow in the slip regime. Figure 5b shows Cf·Re for the rarefied gas flow in the transition regime. As clearly seen, Cf·Re declines with the increasing rarefaction parameter. The range of variations for Cf·Re is larger at lower inlet Knudsen numbers (0.5) compared to large Knudsen numbers (Kn= 1.5), and a completely linear trend is observed with the increasing Knudsen number. The Knudsen number boosts along the microchannel (from the inlet to the outlet) according to the relation \({\text{Kn}}_{\text{out}} = {\text{Kn}}_{\text{in}} \cdot \varPi\) due to a decrease in the gas pressure (\(\varPi = \frac{{P_{\text{in}} }}{{P_{\text{out}} }} = 2\)). Consequently, Cf·Re decreases in both slip and transition regimes according to the correlation presented for this parameter.

Figure 6 shows the dimensionless temperature profiles (relative to the mean temperature) of the gas flow at different microchannel abscisses as a function of Knudsen and Prandtl numbers. In Fig. 6a, the Knudsen number is constant (Knin= 0.035), and transverse temperature profiles are shown along the microchannel. The dimensionless temperature decreases as the gas flow passes through the microchannel from the inlet to the outlet. Figure 6b shows the effect of rarefaction parameter at Kn= 1.667 in the transverse direction of the microchannel on the dimensionless temperatures. With the increasing inlet Knudsen number, temperature at X* = 0.02375 increases and reaches 0.0027, 0.00913 and 0.0118 on the upper wall at Knudsen numbers of 0.01, 0.035 and 0.045, respectively. Figure 6c shows the impact of Prandtl number on the transverse temperature profiles in the microchannel at the inlet Knudsen number of 0.05. As the Prandtl number increases, the temperature at the center in the transverse direction decreases, whereas the temperature on the walls increases. The dimensionless temperature at X* = 0.00875 and Y* = 0 equals 0.00896, 0.00933, 0.0108, 0.0121 and 0.0129 at Prandtl numbers of 0.7, 2, 5, 7.88 and 10, respectively.

Fig. 6
figure 6

a Dimensionless temperature profiles in y-direction at different microchannel lengths, b dimensionless temperature profile at different inlet Knudsen numbers and c the effect of Prandtl number on dimensionless temperature profile in y-direction at \({\text{Kn}}_{\text{in}} = 0.05\)

Full size image

Figure 7 shows the impact of inlet Knudsen number on the dimensionless temperature profiles (relative to mean temperature) at the centerline and on the microchannel walls. Figure 7a depicts temperature variations at the centerline along the microchannel as a function of the rarefaction parameter. As seen, the temperature at the centerline rises with the increasing Knudsen number. Figure 7b displays the temperature profiles of the gas flow on the microchannel walls. When the flow regime type shifts from slip (Knin= 0.035) to transition (according to \(\varPi = 2\)), the temperature jump profile declines along the microchannel at a given inlet Knudsen number despite the increasing trend of temperature profiles with the Knudsen number.

Fig. 7
figure 7

a Dimensionless temperature profiles at microchannel centerline at different rarefaction parameters and b temperature jump in the gas flow at different inlet Knudsen numbers along the microchannel

Full size image

Hadjiconstantinou and Simek [13] defined the Nusselt number for gas flow in a microchannel with a fully developed temperature profile as \({\text{Nu}} = \frac{{2H\left( {\frac{\partial T}{\partial y}} \right)_{\text{w}} }}{{\left( {T_{\text{w}} - T_{\text{B}} } \right)}}\) using the DSMC method, where TB (bulk temperature) and H represent the bulk temperature and channel width, respectively. In the simulations conducted using the proposed model, a Prandtl number of 0.7 was considered. Figure 8 indicates the impact of rarefaction, Prandtl number and k on the Nusselt number of a rarefied gas flow along the microchannel.

Fig. 8
figure 8

a Nusselt profiles at different inlet Knudsen numbers along the microchannel, b the effect of Prandtl number on the Nusselt number at \({\text{Kn}}_{\text{in}} = 0.08\) and c effect of k on the Nusselt number in the rarefied gas flow

Full size image

Figure 8a shows the Nusselt number at different inlet Knudsen numbers along the microchannel obtained from the numerical LBM. As the Knudsen number increases, the Nusselt number decreases along the microchannel. However, the Nusselt number remains unchanged due to a fully developed temperature profile from a certain length up to the end of the microchannel. Figure 8b illustrates the impact of Prandtl number on the Nusselt number along the microchannel at an inlet Knudsen number of 0.08. The Nusselt number of rarefied gas flow increases with the increasing Prandtl number. As previously pointed out by Shokouhmand and Esfahani [64], when the Prandtl number increases significantly, the Nusselt number of the gas flow experiences a sharp change at lengths close to the microchannel inlet as shown in Fig. 2b at the Prandtl numbers 7.88 and 10. Figure 8c shows the Nusselt number of the gas flow as a function of k along the microchannel. As seen, the Nusselt number decreases with increasing k. According to Eq. 45, k is dependent on the specific heat ratio (γ) and Prandtl number.

Mass flow rate and normalized mass flow rates have been reported in terms of Knudsen number [1], [20], [65], and Roohi and Darbandi [15] proposed the dimensionless mass flow rate as \({\text{Mn}} = \dot{m}/\left( {\rho_{\text{av}} \cdot \sqrt {2RT} \cdot H/2} \right)\), where \(\rho_{av}\) is the average density equal to \(\left( {\rho_{\text{in}} + \rho_{\text{out}} } \right)/2\), R gas constant, T temperature and H the characteristic length of the microchannel. The mass flow rate (\(\dot{m}\)) is defined as \(\mathop \smallint \nolimits_{0}^{H} \rho \left( y \right) \cdot u\left( y \right) \cdot {\text{d}}y\).

Figure 9 depicts the impact of the pressure ratio on the mass flow rate in terms of Knudsen number. Figure 9a shows the normalized mass flow rate up to an inlet Knudsen number of 10 for the gas flow obtained from the LBM and DSMC methods. The mass flow rate decreases up to an inlet Knudsen number of about 0.9 and then increases. This inflection point is defined as the Knudsen minimum. Gavasane et al. [66] reported an inflection point of \(\delta_{\text{m}} = 1\) based on the average rarefaction parameter (\(\delta_{\text{m}}\)) from the relation \(\delta_{\text{m}} = \sqrt \pi /\left( {2{\text{Kn}}_{\text{m}} } \right)\). Figure 9b illustrates the three pressure ratios effects on the mass flow rate. As seen in Table 3, the normalized mass flow rate of the gas in the microchannel rises with the rising pressure ratio. An aspect ratio of 20 was considered for the microchannel in Fig. 9a, b.

Fig. 9
figure 9

a Normalized mass flow rate in terms of Knudsen number obtained from LBM and DSMC methods, b pressure ratio effect on the dimensionless mass flow rate at different inlet Knudsen numbers

Full size image
Table 3 Mass flow rate at varying inlet Knudsen numbers for different pressure ratios
Full size table

Conclusions

Non-isothermal microscale gas flow \((T_{\text{w}} < T_{\text{in}} )\) was studied by a modified TRT_SRT model based on the LBM. A symmetric relaxation time was separately used in each regime. In the transitional regime, for considering the effect of the Knudsen layer, a single relaxation time based on viscosity correction (Bosanquet-type) was used. Bounce-back and specular-boundary conditions were considered at walls, and the accuracy of slip velocities was improved using the asymmetric relaxation time obtained based on this boundary condition. The fluid temperature jump was obtained by using a second-order implicit scheme and the temperature jump coefficient \(C^{*}\). The main results are summarized below:

  • With the increasing Knudsen number, the nonlinear pressure profiles along the microchannel turned into linear profiles, leading to a decrease in the \(\delta P\).

  • As the Knudsen number increased, the transverse dimensionless velocity decreased at the centerline, while the slip velocities on the wall increased.

  • The Cf·Re profiles in the slip and transition regimes were, respectively, nonlinear and linear and decreased with the rising rarefaction parameter.

  • With the increasing Prandtl number, the transverse dimensionless temperature decreased relative to the inlet temperature but increased on the walls.

  • The dimensionless temperature at the centerline (relative to the average temperature) increased with the increasing Knudsen number. The fluid temperature on the wall decreased from the slip regime to the transition regime with the increasing Knudsen number. Additionally, this temperature showed an increasing trend in the transition regime.

  • The Nusselt number declined with the rising rarefaction parameter, assuming a fully developed temperature profile for the gas flow. The Nusselt profiles increased with the increasing Prandtl number.

  • For different Knudsen numbers at the inlet, the normalized mass flow rate profile experienced a decreasing trend up to a point with the Knudsen minimum, after which it starts an increasing trend reaching \(\delta_{\text{m}} = 1\).