Introduction

Heat transfer in fluid occurs in industrial applications. The efficiency of thermal and cooling system involves heat transfer in fluid that depends upon the thermal conductivity of fluids. Therefore, thermal enhancement has been studied in many recent investigations. For instance, Sheikholeslami [1] performed a computational analysis for an enhancement of heat transfer in fluid by suspension of nanoparticles. Sheikholeslami et al. [2] did an experimental study for the application of nano-refrigerant for boiling of heat transfer in fluid flows. Sheikholeslami et al. [3] investigated an enhancement of heat transfer in fluid in a heat storage unit containing nanoparticles and cooling fin. Sheikholeslami and Ghasemi [4] performed heat transfer simulations in the presence of thermal radiation via finite element method (FEM). Sheikholeslami and Seyednezhed [5] analyzed the impact of suspension of nano-structures on transport of heat energy in convective transport of momentum in fluid immersed in porous medium. Sheikholeslami and Rashid [6] analyzed heat transfer in Ferro fluid exposed to variable magnetic field. Dogonchi et al. [7] performed numerical analysis of thermal performance of nanoparticles on transport of heat transfer in fluid filled in a cavity. Dogonchi et al. [8] discussed natural convection on square enclosure with wavy circular heater exposed to magnetic field. Hashemi-Tilehnoee [9] studied factors affecting entropy generation in fluid exposed to magnetic field. By considering various shapes for nanoparticles, Sheikholeslami [10] investigated the influence of magnetic field on flow in a permeable cavity. MHD flow of \(\mathrm{Al}_{2}\mathrm{O}_{3}\)-water nanofluid inside a permeable medium also studied by Sheikholeslami [11]. Selimefendigil et al. [12] investigated MHD CuO-water flow of nanofluid with forced convection in channel. Selimefendigil and Hakan [13] studied mixed convection corrugation type effects through vented cavity for fluid-solid interaction. Turkyilmazoglu [14] presented a numerical study, in which he discussed laminar (MHD) flow of an electrically conducting fluid on a stretchable disk. Hayat [15] analytically presented heat transfer for two-dimensional MHD flow of Maxwell fluid (with viscosity and relaxation time depending upon the pressure. A comprehensive literature review on exact solutions of Navier–Stokes equations were studied by Aristov et al. [16]. Malik et al. [17] investigated two-dimensional MHD flow of the Carreau fluid over a stretching sheet with a variable thickness. The problem (MHD) steady flow and heat transfer of an incompressible (non-Newtonian fluid) that are macromolecular in nature and their resemblance with an elastic solid were solved numerically by Misra [18].

Many researchers are familiar by the practical applications of the non-Newtonian fluids. In industry, non-Newtonian fluids got much importance due to their usage in modern technology but on the other hand such fluids must be investigated to get the desired results. Due to complexity of these fluids, many models have been anticipated. Among them, micropolar model is the prominent. Blood, polymers and many industrial liquids containing crystals and micro-solid structures are examples of micropolar fluid. For the modeling of heat transfer one additional law, the law of conservation of angular momentum is used along with a usual conservation laws. Micro-rotation in micro-polar fluid is due to couple stress. Further, vortex viscosity and spin gradient viscosities are also significant in such fluid. Due to its diversity from other fluids, many researchers have discussed various aspects of this rheology. For example, Fabula and Hoyt [19] claimed that micropolar fluid cannot be explained and characterized by those fluids that cannot be explained and characterized by Newtonian relationship they could be explained by micro-polar model which was later introduced by Eringen [20] was first to introduce set of balance laws of micropolar fluid. Laminar incompressible flow of a micro-polar fluid between two disks was studied by Kamal [21]. Magnetohydrodynamics (MHD) flow and heat transfer characteristics of a viscous incompressible electrically conducting micropolar fluid in a channel with stretching walls was studied by Ashraf et al. [22]. The characteristics of melting heat transfer in a boundary layer flow of the Jeffrey fluid near the stagnation point on a stretching sheet subject to an applied magnetic field was discussed by Nawaz et al. [23]. Some new strategies for the exact solutions for three-dimensional thermal diffusion equations are introduced, and several cases were discussed in a most recent studies by Aristov and Prosviryakov [24] and new classes of exact solutions of Euler equations derived by Aristov and Polyanin [25].

Despite the fact of importance of exact solution, here numerical method is used; exact solution is not possible to find. Most of the studies on transport mechanism deal with constant viscosity. This assumption is valid to some rare cases. However, in general, viscosity does not remain constant in fluid flowing in the pressure of thermal changes. In view of this, several investigations have been published [26,27,28,29,30,31]. Further, these studies confirmed that the effect on the flow characteristics might change drastically in comparison with the constant viscosity assumption.

Moreover, MHD flow and heat transfer in viscoelastic fluid over a stretching sheet in the presence of variable viscosity and thermal conductivity are studied by Salem [32]. Also, the problem of thermal-diffusion and diffusion thermo effects on mixed free-forced convection and mass transfer boundary layer flow of non-Newtonian fluid with temperature-dependent viscosity was studied numerically by Eldabe and Mohamed [33], using Chebyshev finite difference method. Moreover, Seddeek and Salama [34] studied the effects of variable viscosity and thermal conductivity on an unsteady two-dimensional laminar flow of viscous incompressible conducting fluid past a semi-infinite vertical porous moving plate taking into account the effect of a magnetic field in the presence of variable suction.

Most of the studies on micropolar fluid consider viscosity of fluid to be constant. This assumption is not realistic, and imposition of this assumption of constant viscosity leads to physically unrealistic outcomes as blood and polymers do not posses constant viscosity. In general, such fluids have temperature-dependent viscosity. In view of this strong observation, authors have considered viscosity of micropolar fluid as a function of temperature of fluid itself. Further Ashraf et al. [22] have considered constant viscosity while analyzing heat transfer in a micropolar fluid in a channel. We have extended it the case of temperature-dependent viscosity. Hence, based on above discussion, the present work is an attempt to study the effects of variable viscosity on hydromagnetic flow and heat transfer characteristics of a micropolar non-Newtonian fluid in a channel with stretching walls. The governing equations reduced to similarity boundary layer equations by using suitable transformations. The transformed ordinary differential equations together with the associated boundary conditions are discretized by the central finite differences and solved numerically. Numerical results are shown graphically for the velocity, angular velocity, temperature and concentration distributions.

Mathematical formulations

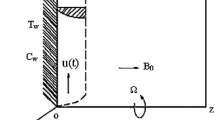
Consider heat transfer in steady two-dimensional hydromagnetic flow of micropolar fluid in a channel with stretching walls in the presence of a transverse applied magnetic field. The induced magnetic field is negligible as compared to the imposed magnetic field under the assumption of small magnetic Reynolds number [35]. Hence, the magnetic field will tend to relax towards a purely diffusive state, for small magnetic Reynolds numbers. Moreover, it is assumed that the electric field vanishes as there is no applied polarization voltage. Microrotation due to solid like structures in the colloidal suspension (called micropolar fluid) is significant. The walls of channel of width 2c are located at \(y = -c\) and \(y = c\) as shown in Fig. 1. The upper and lower walls of channel have constant temperature \(T_{2}\) and \(T_{1}\) respectively. Micropolar fluids exhibit Ohmic dissipation (Joule heating phenomenon) when they move under the influence of applied magnetic field so Joule heating effects are considered.

Fig. 1
figure 1

Flow configuration and coordinates system

Full size image

The unknown flow fields are

$$\begin{aligned} \mathbf{V}=[u(x,y), v(x,y),0],\quad \mathbf{N }=[0,0,\phi (x,y)],\quad T_{\mathrm{{f}}}=T_{\mathrm{{f}}}(x,y) \end{aligned}$$
(1)

where \(\phi\) is the component of the microrotation field normal to the \(xy\)-plane, whereas the microrotation is defined as the rotation of the microscopic particles in the fluid.

Laws of conservation of mass, linear momentum, angular momentum and energy ([36,37,38]) become

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\frac{1}{\rho }\nabla ^2 \left[ (\mu (T_{\mathrm{f}})+\kappa ) u \right] +\frac{\kappa }{\rho }\frac{\partial \phi }{\partial y}-\frac{\sigma B^2_0}{\rho }u, \end{aligned}$$
(3)
$$\begin{aligned}&u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial y}+\frac{1}{\rho }\nabla ^2\left[ (\mu (T_{\mathrm{f}})+\kappa ) v \right] -\frac{\kappa }{\rho }\frac{\partial \phi }{\partial x}, \end{aligned}$$
(4)
$$\begin{aligned}&\rho j\left( u\frac{\partial \phi }{\partial x}+v\frac{\partial \phi }{\partial y}\right) =\gamma \nabla ^2\phi +\kappa \left( \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) -2\kappa \phi , \end{aligned}$$
(5)
$$\begin{aligned}&\rho c_{\mathrm{p}}\left( u\frac{\partial T_{\mathrm{f}}}{\partial x}+v\frac{\partial T_{\mathrm{f}}}{\partial y}\right) = \kappa _0\frac{\partial ^2 T_{\mathrm{f}}}{\partial y^2}+\sigma (B_{0}u)^{2}, \end{aligned}$$
(6)

where \(\kappa\) is the vortex viscosity, \(\rho\) is the density, p is the pressure, \(\gamma\) is the spin gradient viscosity, \(B_0\) is the strength of the magnetic field, j is the microinertia density, \(c_{\mathrm{p}}\) is the specific heat at constant pressure,\(\sigma\) is the electrical conductivity, \(T_{\mathrm{f}}\) is the temperature of the fluid and \(\kappa _0\) is the thermal conductivity. The intensity of the inertial forces due to the microparticles of the fluid is known as microinertia density. Further, it is worth mentioning that for \(\kappa\) (vortex viscosity) is equal to zero the governing PDEs (2)–(6) reduce to governing PDEs for heat transfer in MHD Newtonian fluid.

The boundary conditions for the velocity, microrotation and temperature fields for the present problems are:

$$\begin{aligned} \left. \begin{array}{ccl} &{}&{}u=bx,\quad v=0,\quad \phi =0 \quad \mathrm{at} \quad y=\pm c\\ &{}&{}T_{\mathrm{f}}=T_1 \quad \mathrm{at} \quad y=-c \\ &{}&{}T_{\mathrm{f}}=T_2 \quad \mathrm{at} \quad y=c \end{array}\right\} \end{aligned}$$
(7)

Here, b is the positive constant and has dimension, reciprocal of the dimension of time.

In this stage, the following similarity variables are defined to convert the governing partial differential Eqs. (2)–(6) into the ordinary differential equations:

$$\begin{aligned} \left. \begin{array}{ccl} &{}&{}u=bxf'(\eta ),\quad v=-bcf(\eta ), \quad \eta =\frac{y}{c},\\ &{}&{} \phi = -\frac{b}{c}xg(\eta ),\quad \theta (\eta )=\frac{T_{\mathrm{f}}-T_2}{T_2-T_1}. \end{array}\right\} \end{aligned}$$
(8)

Microrotations are significant in micropolar liquid. Blood and other industrial fluids are examples of such fluids. It is theoretically and experimentally verified that the viscosity of such fluid does not remain constant when thermal changes occurs. Due to this fact, the viscosity of such fluids depends on temperature. There are more than one mathematical model for temperature-dependent viscosity. Most commonly used model Ling and Dybbs [39] is

$$\begin{aligned} \mu (T_{\mathrm{f}})= & {} \frac{\mu _{o}}{1+\delta (T_{\mathrm{f}}-T_{\infty })}=\frac{\mu _{o}}{1+\epsilon \theta } , \nonumber \\&\text {with} \quad \quad \epsilon =\delta (T_2-T_1) \end{aligned}$$
(9)

Here \(\epsilon\) is the viscosity variation parameter, \(\mu _{o}\) is the constant dynamic viscosity, \(\theta\) is the dimensionless temperature and \(\delta\) is the viscosity variation constant.

Using change of variables given in Eq. (8) in conservation laws (2)–(7) and eliminating the pressure, one gets,

$$\begin{aligned}&\left. \begin{array}{ccc} &{}&{}(1+N_1)f''''-N_1g''=2\left( \frac{\epsilon }{1+\epsilon \theta }\right) ^2(\theta ')^2f''-\left( \frac{\epsilon }{1+\epsilon \theta }\right) \theta ''f''+\mathrm{Re}\{f'f''-ff'''\}+Mf'' ,\\ &{}&{}f(1)=0,\quad f'(1)=1 , \quad f(-1)=0 ,\quad f'(-1)=1. \end{array} \right\} \end{aligned}$$
(10)
$$\begin{aligned}&\left. \begin{array}{ccc} &{}&{}N_3g''+N_1N_2(f''-2g)=f'g-fg' ,\\ &{}&{}g(1)=0 ,\quad g(-1)=0. \end{array} \right\} \end{aligned}$$
(11)
$$\begin{aligned}&\left. \begin{array}{ccc} &{}&{}\theta ''+\mathrm{Pr}(\mathrm{Re}f\theta '+M \mathrm{Ec} (f')^{2})=0 ,\\ &{}&{}\theta (1)=0 ,\quad \theta (-1)=1. \end{array} \right\} \end{aligned}$$
(12)

where \(N_1=\frac{\kappa }{\mu _{0}}\) is the vortex viscosity parameter, \(N_2=\frac{\mu _{0}}{\rho j b}\) is the microinertia density parameter, \(N_3=\frac{\gamma }{\rho j c^2 b}\) is the spin gradient viscosity parameter, \(\mathrm{Re}=\frac{\rho c^2 b}{\mu _{0}}>0\) is the stretching Reynolds number, \(\mathrm{Pr}=\frac{\mu _{0} c_{\text{p}}}{\kappa _0}\) is the Prandtl number, \(M=\frac{c^2 \sigma B_0^2}{\mu _{0}}\) is the magnetic parameter and Eckert number \(\mathrm{Ec}=\frac{b^2 x^2 }{c_{\mathrm{p}}(T_{2}-T_{1})}\) defined as Gopal et al. [40]. For \(\epsilon =0\) and \(N_{1}=0\), the boundary value problem given in Eqs. (10)–(12) reduces to Newtonian case and for \(\epsilon =0\) and Ec = 0, reduces to non-Newtonian case, discussed by Ashraf et al. [22].

The skin friction coefficient is defined by

$$\begin{aligned} C_{\mathrm{f}}= & {} \frac{(\mu (T_{\mathrm{f}})+ \kappa ) \frac{\partial u}{\partial y} |_{y=\pm c}}{\frac{1}{2} \rho (bx)^{2}}\nonumber \\= & {} \left( \frac{2 c}{x\mathrm{Re}} \right) \left( \frac{1}{1+\epsilon \theta (\pm 1)}+N_{1}\right) f^{''}(\pm 1) \end{aligned}$$
(13)

Coupled stress coefficient is defined as

$$\begin{aligned} C_{\mathrm{g}}=\frac{ x \gamma \frac{\partial \phi }{\partial y} |_{y=\pm c}}{\frac{1}{2} \rho (bx)^{2}}=2 j N_{3} g^{\prime}(\pm 1) \end{aligned}$$
(14)

Similarly Nusselt number is defined as

$$\begin{aligned} \mathrm{Nu}=\frac{ -x k_{0} \frac{\partial T_{\mathrm{f}}}{\partial y} |_{y=\pm c}}{k_{0} (T_{2}-T_{1})}=-\left( \frac{x}{c} \right) \theta ^{'}(\pm 1) \end{aligned}$$
(15)

Further, it can be noted that for \(\epsilon =0\), problem reduces to the case of constant viscosity, whereas \(N_{1}=0\) is the case of Newtonian fluid. So \(\epsilon =0\), Ec = 0 is the case studied by Ashraf et al. [22] .

Solution procedure

The governing boundary value problems (10)–(12) are solved numerically by employing a computational methodology based on order reduction and finite difference discretization used by Ashraf et al. [22], which is elaborated for the fourth order system as follows:

Let for a function \(G_{\mathrm{f}}\), we write

$$\begin{aligned}&G_{\mathrm{f}}(f,f',f'',f''',f'''')\\&\quad = (1+N_1)f''''-N_1g''-2\left( \frac{\epsilon }{1+\epsilon \theta }\right) ^2(\theta ')^2f'' \\ & \qquad +\,\left( \frac{\epsilon }{1+\epsilon \theta }\right) \theta ''f''-Mf'' -\mathrm{Re}\{f'f''-ff'''\}, \end{aligned}$$

We now suppose that F be the solution of the ODE, then

$$\begin{aligned} G_{\mathrm{f}}(F,F',F'',F''',F'''') = 0. \end{aligned}$$

or can be written in another form as

$$\begin{aligned}&G_{\mathrm{f}}(f+(F-f),\; f'+(F'-f'), f''+(F''-f''), \\&f'''+(F'''-f'''),\; f''''+(F''''-f'''')) = 0. \end{aligned}$$

which on using first-order Taylor series expansion, yields

$$\begin{aligned}&G_{\mathrm{f}}(f,f',f'',f''',f'''')+(F-f)\frac{\partial G}{\partial f} + (F'-f')\frac{\partial G}{\partial f'}\\&\qquad +(F''-f'')\frac{\partial G}{\partial f''}\\&\qquad +(F'''-f''')\frac{\partial G}{\partial f'''} +(F''''-f'''')\frac{\partial G}{\partial f''''}=0, \end{aligned}$$

or

$$\begin{aligned}&(1+N_1)F''''+(\mathrm{Re} f) F'''+-2\left( \frac{\epsilon }{1+\epsilon \theta }\right) ^2(\theta ')^2f''\\&\qquad +\left( \frac{\epsilon }{1+\epsilon \theta }-M-\mathrm{Re} f''\right) F'' (-\mathrm{Re} f'')F'+ (\mathrm{Re} f'') F\\&\quad = N_1g''-\mathrm{Re} f' f''+\mathrm{Re}f f'''. \end{aligned}$$

This equation may be used to set iterative process as

$$\begin{aligned}&(1+N_1)F^{({\text{k}}+1)^{''''}}+(\mathrm{Re} f) F^{({\text{k}}+1)^{'''}}\nonumber \\&\qquad +-2\left( \frac{\epsilon }{1+\epsilon \theta }\right) ^2(\theta ')^2f''\nonumber \\&\qquad +\left( \frac{\epsilon }{1+\epsilon \theta }-M-\mathrm{Re} f''\right) F^{({\text{k}}+1)^{''}}\nonumber \\&\qquad (-\mathrm{Re} f'')F^{({\text{k}}+1)^{''''}}+ (\mathrm{Re} f'') F^{({\text{k}}+1)}\nonumber \\&\quad = N_1g^{({\text{k}}+1)^{''}}-Re f^{({\text{k}}+1)^{'}} f^{({\text{k}}+1)^{''}}+\mathrm{Re}f f^{({\text{k}}+1)^{''}}. \end{aligned}$$
(16)

Similar process may be adopted for the rest of the equations. Finally, the iterative procedure can be summarized as follows:

  • An initial guess satisfying the corresponding boundary conditions is provided for f, g and \(\theta\)

  • A new approximation of f is obtained for solving Eq. (16)

  • The updated f is then used to find the modified g and \(\theta\).

  • Above-mentioned procedure is repeated until no significant iterative improvement is noted for f, g and \(\theta\)

Results and discussion

In order to get physical insight into the problem, velocity fields (linear and angular), shear and couple stresses are examined for various values of physical parameters. Numerical values of shear, couple stresses and heat fluxes at the channel wall for various values of Reynolds number, Prandtl number, viscosity parameter and Eckert number are tabulated in Tables 1–5. As the problem is inherently symmetric, numerical values of shear and couple stresses and heat flux for various values of the parameters are given at one channel wall only. Influence of the external magnetic field on the three physical quantities is also observed from Table 1. It is easy to note that the magnetic parameter M has a significant impact on the shear stress. Heat flux at the walls of channel increases with an increase in the Prandtl number (see Table 3). Effect of the viscosity variation parameter on the physical quantities is evident from Table 4. The shear stress and the couple stress are increased by increasing the viscosity parameter. However, the heat transfer exhibits an opposite trend. Behavior of heat flux with the variation of Eckert number is tabulated in Table 5.

Table 1 Magnetic fields effects on shear, couple stresses and heat transfer rate when \(N_1 = 4\), \(N_2 = 0.3\), \(N_3 = 0.6\), Pr = 21, Re = 1, Ec = 0.01 and \(\epsilon =2\)
Full size table
Table 2 Effects of magnetic field on shear, couple stresses and heat transfer rate with \(N_1\) = 4, \(N_2\) = 0.8, \(N_3\) = 0.2, Pr = 1.5, Re = 40, Ec = 0.01 and \(\epsilon =2\)
Full size table
Table 3 Effects of Prandtl number on heat fluxes at channel walls when \(N_1\) = 4, \(N_2\) = 0.3, \(N_3\) = 0.6, \(M = 1\), \(\epsilon =2\), Ec = 0.01 and Re = 1
Full size table
Table 4 Effects of temperature-dependent viscosity parameter on wall shear and couple stresses and wall heat transfer rate when \(N_1\) = 4, \(N_2\) = 0.3, \(N_3\) = 0.6, Pr = 21, \(M=1\), Ec = 0.01 and Re = 1
Full size table
Table 5 Effects of Eckert number on heat fluxes at channel walls when \(N_1\) = 4, \(N_2\) = 0.3, \(N_3\) = 0.6, \(M = 1\), \(\epsilon =2\), Pr = 5 and Re = 5
Full size table

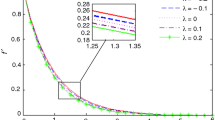
The behavior of streamwise and normal velocities is displayed in Figs. 2–8 when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(M=1\), Ec = 0.01 and Re = 1. Impact of viscosity parameter \(\epsilon\) on the normal velocity of the fluid within the channel for Newtonian (\(N_{1}=0\)) fluid and non-Newtonian (\(N_{1}=1\)) fluid displayed in Fig. 2. It is observed that normal velocity of the fluid is enormously lower in the context of non-Newtonian fluid (\(N_{1}=1\)) then Newtonian fluid (\(N_{1}=0\)) with variation of \(\epsilon\). In addition, normal velocity of both Newtonian and non-Newtonian fluid increases with the increase in viscosity variation parameter. In Fig. 3 , normal velocity increases with the increase in magnetic field due to the presence of temperature-dependent viscosity and Joule heating, while it decreases in the absence of both parameters. Moreover, both Figs. 2 and 3 show the comparison of present result with the existing literature Ashraf et al. [22]. The streamwise velocity decreases when the viscosity parameter is increased (see Fig. 4). The magnitude of streamwise velocity of micropolar fluid with constant viscosity is high as compared to the velocity of micropolar fluid of temperature-dependent viscosity. Therefore, it is concluded that the streamwise velocity of blood in vessels lower when its viscosity varies with respect to the temperature as compared to the case when viscosity of blood is constant. However, monotonic behavior for normal velocity is observed (see Fig. 5).

It can be noted from Fig. 6 that angular motion of blood in vessels is greatly affected by the variation of viscosity of blood. This variation of micro-motion of blood in the vessels is simulated in Fig. 6. The temperature of blood (micropolar liquid) in the vessel increases when the viscosity of the blood is increased by increasing the temperature.

The behavior of temperature of blood for various values of viscosity parameter is shown in Fig. 7. The effect of magnetic field on the normal velocity is shown in Fig. 8. It is obvious from Fig. 8 that normal velocity decreases when the intensity of the magnetic field is increased. This shows that flow of micropolar liquid is decelerated by the opposing Lorentz force. The streamwise velocity profiles are extended to the boundaries (channel walls), and in the central region of the channel, velocity becomes decreases because of damping effects from the magnetic field, shown in Fig. 9. The Reynolds number is the ratio of viscous force to the inertial force. The magnitude of the angular velocity of the micropolar liquid decreases with an increase in the Reynolds number. It means an increase in the viscous force or a decrease in the inertial force results to slow down the micro-motion of the micropolar liquid in the channel (see Fig.10). The effect of the magnetic field on the temperature of the micropolar liquid in the channel is shown in Fig. 11. It can be noted from Fig. 11 that the temperature of micropolar fluid increases near the lower wall of the channel, whereas the opposite trend is noted for upper half of the channel. The magnitude of the normal velocity of the fluid decreases when Reynolds number of the fluid is increased as shown in Fig. 12. An increase in the Reynolds number is due to the decrease in inertial force or an increase in the viscous force. The behavior of streamwise velocity due to an increase in the Reynolds number is depicted in Fig. 13. From this Fig. 13, one can easily notice that the streamwise velocity increase near the channel walls. However, opposite trend can be noted in the center of the channel. From Fig. 14, we observe that Joule heating due to magnetic field has immense effect on the temperatures and consequently increases the temperature with the increase in Eckert number. Figure 15 is the comparison of the present result for temperature profile with Ashraf et al. [22]. Finally, Fig. 16 illustrates the variation in the heat transfer rate within the channel. This figure shows that the rate of heat transfer increases with the increase in magnetic parameter which is exactly because of the fact that, firstly, heat is transmitted from the one end of the wall toward the fluid within the channel, and then, it is transferred from fluid toward the other end of the wall.

The results of special case are compared with already published work. The outcomes related this validation are recorded in Figs. 2, 3 and 15. A good agreement between present results and already published is noted (see Figs. 2, 3, 15).

Fig. 2
figure 2

Comparison of results for normal velocity: Curves with filled circles represent Newtonian fluid for \(N_{1}=0\) and curves without circles represent non-Newtonian fluid for \(N_{1}=1\) when \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(\epsilon =2\), \(R=1\), Ec = 0.01

Full size image
Fig. 3
figure 3

Comparison of results for normal velocity: Curves with filled circles represent results by Ashraf et al. [22] for \(\epsilon =0\), Ec = 0 and curves without circles are present results for \(\epsilon =2\), Ec = 0.01 when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 1.5, \(R=40\), Ec = 0.01

Full size image
Fig. 4
figure 4

Normal velocity profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(M=1\), \(R=1\), Ec = 0.01

Full size image
Fig. 5
figure 5

Streamwise velocity profile for \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(M=1\), \(R=1\), Ec = 0.01

Full size image
Fig. 6
figure 6

Microrotation profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(M=1\), \(R=1\), Ec = 0.01

Full size image
Fig. 7
figure 7

Temperature profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(M=1\), \(R=1\), Ec = 0.01

Full size image
Fig. 8
figure 8

Normal velocity profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(\epsilon =2\), \(R=1\), Ec = 0.01

Full size image
Fig. 9
figure 9

Streamwise velocity profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(\epsilon =2\), \(R=1\) , Ec = 0.01

Full size image
Fig. 10
figure 10

Microrotation profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(\epsilon =2\), \(R=1\), Ec = 0.01

Full size image
Fig. 11
figure 11

Temperature profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 21, \(\epsilon =2\), \(R=1\), Ec = 0.01

Full size image
Fig. 12
figure 12

Normal velocity profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 5, \(\epsilon =2\), \(M=1\), Ec = 0.01

Full size image
Fig. 13
figure 13

Streamwise velocity profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 5, \(\epsilon =2\), \(M=1\), Ec = 0.01

Full size image
Fig. 14
figure 14

Temperature profile when \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 5, \(\epsilon =2\), \(M=1\)

Full size image
Fig. 15
figure 15

Comparison of results for temperature profile: Curves with filled circles represent results by Ashraf et al. [22].) for \(\epsilon =0\), Ec = 0 and curves without circles are present results when \(\epsilon =2\), Ec = 0.01, \(N_{1}=4\), \(N_{2}=0.3\), \(N_{3}=0.6\), Pr = 1, \(M=1\)

Full size image
Fig. 16
figure 16

Nusselt number profile for different values of M

Full size image

Applications and further directions

The constitutive equations of micropolar fluid represents the rheology of blood and other biofluid (synovial fluid). Therefore, micropolar fluid model [8, 9] is frequently used to study the dynamics of blood and other biofluids. The results presented may predict hemodynamic flow of blood in the cardiovascular system when subjected to an external magnetic field. Further, arteries like cardiac vascular artery are channel like structures. Therefore, present analysis is carried out to get insight into the problem in order to give some predictions about blood flow in cardiac vascular. The results of the study are supposed to be of profound importance to medical surgeons in their endeavor to regulate blood flow during surgery. The latest advancement on an enhancement of thermal performance has proved that suspension of nano-sized particles in fluid of temperature viscosity plays a significant role in the improvement of thermal efficiency of working fluid. So, for efficient thermal systems, suspension of hybrid nanoparticles is recommended. Although consideration of such phenomenon leads to complex mathematical problems, such consideration provides information about behavior of thermal system under dispersion of hybrid nanoparticles.

Conclusions

A numerical study is carried out to investigate the effects of temperature-dependent viscosity on heat transfer in flow of magnetohydrodynamic (MHD) micropolar fluid in a channel with stretching walls. The powerful tool of similarity transformation has been employed to convert the governing equations into a set of nonlinear ordinary differential equations. The analysis is summarized as follows:

  • The magnetic parameter has a profound impact on the shear stress as compared to the couple stress and the heat transfer.

  • An increase in Prandtl number causes the heat transfer rate at the channel walls.

  • The viscosity variation parameter enhances the shear stress and the couple stress. However, the heat transfer exhibits an opposite trend.

  • The viscosity variation parameter is the most influential for the thermal distribution.

  • The magnetic field acts as a retarding force which reduces the normal and streamwise velocities as well as the microrotation distribution

  • The Reynolds number affects the velocity and microrotation in the same way as the intensity of magnetic parameter is increased.