Convective heat transfer in a rotating nanofluid cavity with sinusoidal temperature boundary condition

Abstract

Convective heat transfer of alumina–water nanoliquid within a rotating square cavity with left border sinusoidal temperature is studied numerically. The considered region is a rotating square enclosure having constant temperature boundary condition at $\bar{x} = L$, while temperature of the border $\bar{x} = 0$ is changed as a sinusoidal function of coordinate, other walls are adiabatic. Dimensionless control equations formulated using stream function, vorticity and temperature, have been solved by the finite difference method of the second-order accuracy. The effects of Rayleigh number, Taylor number and nanoparticles volume fraction on fluid flow and heat transfer have been analyzed. It has been found that for low values of Ra a growth of nanoparticles concentration leads to the thermal transmission enhancement, while high values of Ta characterize also the intensification of thermal transmission with the nanoparticles concentration. At the same time, convective nanoliquid flow rate decreases with growth of Ta.

Introduction

Rotating flow is very important flow regime for a wide range of scientific and engineering applications, including jet engines, pumps, vacuum cleaners, and so on. Even for applications where rotation is not initially evident, the subject is often fundamental to understanding and modeling the details of the flow physics. Examples include the vorticity produced in flow along a channel, the secondary flow produced for flow around a bend, and the wing-tip vortices produced downstream of a wing (see [1]).

Rotation flow raises Coriolis force and buoyancy force, which can essentially alter the local thermal transmission in a region, owing to the evolution secondary flows. Buoyancy forces in regions are strong due to the high rotational velocities and coolant temperature gradients. Earlier research (e.g., [2]) revealed that there can be substantial differences in the thermal transmission when the buoyancy forces are aligned with or opposite to the forced convection direction. A better understanding of Coriolis and buoyancy influences and the capability to simulate the thermal transmission response to these impacts allow the convective flow in an enclosure to obtain the cooling configurations, which utilize less flow and also decrease thermal stresses in the cavity.

Impacts of buoyancy forces on thermal transmission were reported by Eckert et al. [2], Metais and Eckert [3] and Brundrett and Burroughs [4]. Parallel flow and counter flow configurations were experimentally developed by Eckert et al. [2] and Metais and Eckert [3], who investigated the criteria for forced-, mixed- and free-convection heat transfer. Based on the obtained results, buoyancy forces would be expected to cause significant changes in the heat transfer in turbine blade coolant passages and to be strongly dependent on flow direction. The combined effects of Coriolis and buoyancy forces on heat transfer in rotating models have been studied by a number of investigators, such as Wagner and Velkoff [5], and Wagner et al. [6], Guidez [7], Morris and Ayhan [8], Morris [9], Taslim et al. [10, 11]. Large increases and decreases in local heat transfer were found to occur by some investigators under certain conditions of rotation, while other investigators showed lesser effects. Analysis of these results does not show consistent trends. The inconsistency of the previous results is attributed to differences in the measurement techniques, models and test conditions (see [6]). References on rotating flow can be also found in the book by Greenspan [12] and Childs [1].

Nanofluid is the suspension of nanoparticles in the base fluid. This novel and high performance heat transfer fluid was developed by Choi [13]. Nanofluids, which contain well-dispersed solid nanometer-sized particles, are more stable due to their high surface to volume ratio which is capable of minimizing erosion and clogging (see [14,15,16,17,18,19,20,21,22,23,24], etc.). Experiments proved that with addition of nanoparticles, physical characteristics of ordinary host fluid including density, viscosity, and thermal conductivity have increased [25], [26]. Thus, nanoparticles existence affects the heat transfer rate that is required in practical applications.

Heat transfer is one of the most important processes in many industrial and consumer products. The inherently poor thermal conductivity of conventional fluids puts a fundamental limit on heat transfer [27]. Heat transfer enhancement has considerable importance to build up the compact heat exchangers to get high performance, reasonable cost, moderate weight, and size as narrow as feasible. Thus, energy cost and environmental concerns are encouraging tries to better design for performance over the existing designs. Many engineering applications of nanofluids are within the scientific areas such as cooling system for micro-electronic devices, heat exchangers, solar collectors, and underground cable systems. Challenge of engineers and scientists is to develop a generalization of basic formulation for heat transfer from cavities, channels and tubes in the presence or absence of porous media and nanoparticles [28]. Cooling is one of the most remarkable technical challenges dealing with many diverse industries, consisting of microelectronics, transport, solid-state lighting, and manufacturing [29,30,31]. Convective heat transfer by nanofluids is also one of the present focuses in computational fluid dynamics field in which the rate of nanoparticles and the nanoparticles are the important parameters. Nanofluids can be applied to engineering problems, such as heat exchangers, cooling of electronic equipment and chemical processes. There are two ways for simulation of nanofluid: single-phase and two-phase approaches. In single-phase, researchers treated nanofluids as the common pure fluid and used conventional equations of mass, momentum and energy. In two-phase, researchers assumed that there are slip velocities between nanoparticles and fluid molecules [32, 33]. Moreover, nanofluids can also be applied in evaporators. They have potential to enhance heat transfer coefficient and critical heat flux in pool boiling and flow boiling. The boiling heat transfer coefficient and the critical heat flux enhancement by nanofluids result from a thin porous nanoparticle deposition layer on the heater surface, which serves to improve the wettability and capillarity of the boiling surface. Heat can be extracted from the solar ponds and has been used for industrial process heating, space heating, and power generation. In all these applications, heat is extracted from the bottom of the solar pond which is at a temperature of about 50–60 °C higher than the top surface of the solar pond. A nanofluid flows through a heat exchanger mounted at the bottom of the solar pond to absorb the heat. It expects that nanofluids could enhance the rate of heat removal from the bottom of the solar pond [34].

It is worth mentioning that many references on nanofluids can be found in the books by Das et al. [27], Nield and Bejan [35], Minkowycz et al. [36], Shenoy et al. [28], and in the review papers by Buongiorno et al. [37], Manca et al. [29], Fan and Wang [38], Mahian et al. [34], Sheikholeslami and Ganji [32], Myers et al. [39], etc. Some interesting results can be found also in Addad et al. [40], Bondareva et al. [41] and Mahian et al. [42, 43].

The aim of the present study is a numerical analysis of free convection in a rotating square cavity filled with an alumina–water nanoliquid under the impact of sinusoidal temperature boundary condition using the mathematical nanofluid model proposed by Tiwari and Das [15]. We used experimentally based correlations to calculate the properties of nanofluids (see [44]). To our best of knowledge, there are no any papers published before on rotating cavity with a sinusoidal temperate side wall distribution filled by nanoliquids. Therefore, the present results are new and original can be used in many practical applications of nanoliquids in the modern industry.

Mathematical formulation

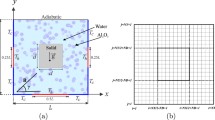
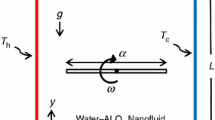
The physical model of free convection in a rotating square Al₂O₃–water nanoliquid cavity and the coordinate system are schematically shown in Fig. 1. The considered region includes the nanoliquid-filled rotating enclosure (see Fig. 1) with a left border sinusoidal temperature distribution. The domain is rotated counterclockwise with a constant angular velocity ζ₀. Horizontal walls are assumed to be thermally insulated, while right vertical boundary is kept at constant low-temperature T_c. Temperature of the left border varies sinusoidally in dependence on the vertical coordinate [45, 46]. It is considered in the research that the thermophysical properties of the liquid are temperature independent, and the flow mode is laminar.

Fig. 1

A scheme of the system

The nanoliquid is Newtonian and the Boussinesq model is used. The host liquid and the nanoparticles are in thermal equilibrium. The thermophysical properties of the host liquid and the nanoparticles are given in Table 1. It is assumed that viscous dissipation and thermal radiation are neglected. Using these assumptions, the control equations of mathematical physics can be written in dimensional Cartesian coordinates as follows [47, 48].

Table 1 Physical properties of base fluid and Al₂O₃ nanoparticles (Oztop and Abu-Nada [16])

$$ \frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{\partial \bar{v}}}{{\partial \bar{y}}} = 0 $$

(1)

$$ \begin{aligned} \rho_{\text{nf}} \left( {\frac{{\partial \bar{u}}}{\partial t} + \bar{u}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \bar{v}\frac{{\partial \bar{u}}}{{\partial \bar{y}}}} \right) = - \frac{{\partial \bar{p}}}{{\partial \bar{x}}} + \mu_{\text{nf}} \left( {\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} \bar{u}}}{{\partial \bar{y}^{2} }}} \right) + \hfill \\ + \left( {\rho \beta } \right)_{\text{nf}} g\left( {T - T_{\text{c}} } \right){ \sin }\left( {\zeta_{0} t} \right) - \left( {\rho \beta } \right)_{\text{nf}} \left( {T - T_{\text{c}} } \right)\zeta_{0}^{2} \bar{x} + 2\rho_{\text{nf}} \bar{v}\zeta_{0} \hfill \\ \end{aligned} $$

(2)

$$ \begin{aligned} \rho_{\text{nf}} \left( {\frac{{\partial \bar{v}}}{\partial t} + \bar{u}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \bar{v}\frac{{\partial \bar{v}}}{{\partial \bar{y}}}} \right) = - \frac{{\partial \bar{p}}}{{\partial \bar{y}}} + \mu_{\text{nf}} \left( {\frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} \bar{v}}}{{\partial \bar{y}^{2} }}} \right) + \hfill \\ + \left( {\rho \beta } \right)_{\text{nf}} g\left( {T - T_{c} } \right){ \cos }\left( {\zeta_{0} t} \right) - \left( {\rho \beta } \right)_{\text{nf}} \left( {T - T_{c} } \right)\zeta_{0}^{2} \bar{y} - 2\rho_{\text{nf}} \bar{u}\zeta_{0} \hfill \\ \end{aligned} $$

(3)

$$ \left( {\rho c_{\text{p}} } \right)_{\text{nf}} \left( {\frac{\partial T}{\partial t} + \bar{u}\frac{\partial T}{{\partial \bar{x}}} + \bar{v}\frac{\partial T}{{\partial \bar{y}}}} \right) = k_{\text{nf}} \left( {\frac{{\partial^{2} T}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }}} \right) $$

(4)

with the following boundary conditions

$$ \begin{aligned} t = 0 : { } & \bar{u} = \bar{v} = 0 , { }T = T_{\text{c}} {\text{ at }}\quad 0 \le \bar{x} \le L ,\quad 0 \le \bar{y} \le L ;\\ t > 0 : { } & \bar{u} = \bar{v} = 0 , { }T = T_{\text{c}} + \left( {T_{h} - T_{\text{c}} } \right){ \sin }\left( {{{\pi \bar{y}} \mathord{\left/ {\vphantom {{\pi \bar{y}} L}} \right. \kern-0pt} L}} \right){\text{ at }}\quad \bar{x} = 0 , { }\quad 0 \le \bar{y} \le L ;\\ & \bar{u} = \bar{v} = 0 , { }T = T_{\text{c}} {\text{ at }}\quad \bar{x} = L , { }\quad 0 \le \bar{y} \le L ;\\ & \bar{u} = \bar{v} = 0 , { }\frac{\partial T}{{\partial \bar{y}}} = 0{\text{ at }}\quad \bar{y} = 0 , { }L , { }\quad 0 \le \bar{x} \le L \\ \end{aligned} $$

(5)

The effective density, specific heat and thermal expansion coefficient of nanoliquid are given by using the following equations (see [16])

$$ \rho_{\text{nf}} = \left( {1 - \phi } \right)\rho_{\text{f}} + \phi \rho_{\text{p}} $$

(6)

$$ \left( {\rho c_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \phi \left( {\rho c_{\text{p}} } \right)_{\text{p}} $$

(7)

$$ \left( {\rho \beta } \right)_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{\text{f}} + \phi \left( {\rho \beta } \right)_{\text{p}} $$

(8)

The effective thermal conductivity of the nanofluid can be defined using the empirical data of Ho et al. [44] in the following way:

$$ k_{\text{nf}} = k_{\text{f}} \left( {1 + 2.944\phi + 19.672\phi^{2} } \right) $$

(9)

for 1% ≤ ϕ ≤ 4%.

The effective viscosity can be defined as follows (see [44]):

$$ \mu_{\text{nf}} = \mu_{\text{f}} \left( {1 + 4.93\phi + 222.4\phi^{2} } \right) $$

(10)

Introducing the following dimensionless variables

$$ \begin{aligned} x = {{\bar{x}} \mathord{\left/ {\vphantom {{\bar{x}} L}} \right. \kern-0pt} L} , { }\quad y = {{\bar{y}} \mathord{\left/ {\vphantom {{\bar{y}} L}} \right. \kern-0pt} L} ,\quad \tau = \zeta_{0} t ,\quad u = {{\bar{u}} \mathord{\left/ {\vphantom {{\bar{u}} {\left( {\zeta_{0} L} \right)}}} \right. \kern-0pt} {\left( {\zeta_{0} L} \right)}} ,\quad v = {{\bar{v}} \mathord{\left/ {\vphantom {{\bar{v}} {\left( {\zeta_{0} L} \right)}}} \right. \kern-0pt} {\left( {\zeta_{0} L} \right)}} ,\\ \theta = {{\left( {T - T_{\text{c}} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{\text{c}} } \right)} {\left( {T_{\text{h}} - T_{\text{c}} } \right)}}} \right. \kern-0pt} {\left( {T_{\text{h}} - T_{\text{c}} } \right)}} ,\quad \psi = {{\bar{\psi }} \mathord{\left/ {\vphantom {{\bar{\psi }} {\left( {\zeta_{0} L^{2} } \right)}}} \right. \kern-0pt} {\left( {\zeta_{0} L^{2} } \right)}} ,\quad \omega = {{\bar{\omega }} \mathord{\left/ {\vphantom {{\bar{\omega }} {\zeta_{0} }}} \right. \kern-0pt} {\zeta_{0} }} \\ \end{aligned} $$

and new dependent functions:

$$ u = \frac{\partial \psi }{\partial y} , { }\quad v = - \frac{\partial \psi }{\partial x} ,\quad \omega = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} $$

the governing Eqs. (1)–(4) are

$$ \frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial y^{2} }} = - \omega $$

(11)

$$ \frac{\partial \omega }{\partial \tau } + u\frac{\partial \omega }{\partial x} + v\frac{\partial \omega }{\partial y} = \frac{{H_{1} }}{{\sqrt {Ta} }}\left( {\frac{{\partial^{2} \omega }}{{\partial x^{2} }} + \frac{{\partial^{2} \omega }}{{\partial y^{2} }}} \right) + \frac{{Ra \cdot H_{2} }}{\Pr \cdot Ta}\left[ {\frac{\partial \theta }{\partial x}{ \cos }\left( \tau \right) - \frac{\partial \theta }{\partial y}{ \sin }\left( \tau \right)} \right] $$

(12)

$$ \frac{\partial \theta }{\partial \tau } + u\frac{\partial \theta }{\partial x} + v\frac{\partial \theta }{\partial y} = \frac{{H_{3} }}{{\Pr \cdot \sqrt {Ta} }}\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) $$

(13)

with boundary conditions

$$ \begin{aligned} \tau = 0 {:} { } & \psi = 0 , { }\omega = 0 , { }\theta = 0.5{\text{ at}}\quad 0 \le x \le 1 ,\quad 0 \le y \le 1 ;\\ \tau > 0 {:} { } & \psi = 0 , { }\frac{\partial \psi }{\partial x} = 0 , { }\theta = { \sin }\left( {\pi y} \right){\text{ at}}\quad x = 0 ,\quad 0 \le y \le 1 ;\\ & \psi = 0 , { }\frac{\partial \psi }{\partial x} = 0 , { }\theta = 0{\text{ at}}\quad x = 1 ,\quad 0 \le y \le 1 ;\\ & \psi = 0 , { }\frac{\partial \psi }{\partial y} = 0 , { }\frac{\partial \theta }{\partial y} = 0{\text{ at}}\quad y = 0 , { 1,}\quad 0 \le x \le 1 \\ \end{aligned} $$

(14)

The dimensionless parameters appearing in Eqs. (11)–(13) are defined as

$$ \begin{aligned} \Pr & = \frac{{\left( {\mu c_{\text{p}} } \right)_{\text{f}} }}{{k_{\text{f}} }} , { }\quad Ra = \frac{{g\left( {\rho \beta } \right)_{\text{f}} \left( {\rho c_{\text{p}} } \right)_{\text{f}} \left( {T_{\text{h}} - T_{\text{c}} } \right)L^{3} }}{{\mu_{\text{f}} k_{\text{f}} }} ,\quad Ta = \frac{{\rho_{\text{f}}^{2} \zeta_{0}^{2} L^{4} }}{{\mu_{\text{f}}^{2} }} ,\\ H_{1} & = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}\frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }} = \frac{{1 + 4.93\phi + 222.4\phi^{2} }}{{1 - \phi + \phi {{\rho_{\text{p}} } \mathord{\left/ {\vphantom {{\rho_{\text{p}} } {\rho_{\text{f}} }}} \right. \kern-0pt} {\rho_{\text{f}} }}}} ,\quad H_{2} = \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\rho_{\text{nf}} \beta_{\text{f}} }} = \frac{{1 - \phi + \phi {{\left( {\rho \beta } \right)_{\text{p}} } \mathord{\left/ {\vphantom {{\left( {\rho \beta } \right)_{\text{p}} } {\left( {\rho \beta } \right)_{\text{f}} }}} \right. \kern-0pt} {\left( {\rho \beta } \right)_{\text{f}} }}}}{{1 - \phi + \phi {{\rho_{\text{p}} } \mathord{\left/ {\vphantom {{\rho_{\text{p}} } {\rho_{\text{f}} }}} \right. \kern-0pt} {\rho_{\text{f}} }}}} ,\\ H_{3} & = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\frac{{\left( {\rho c_{\text{p}} } \right)_{\text{f}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{nf}} }} = \frac{{1 + 2.944\phi + 19.672\phi^{2} }}{{1 - \phi + \phi {{\left( {\rho c_{\text{p}} } \right)_{\text{p}} } \mathord{\left/ {\vphantom {{\left( {\rho c_{\text{p}} } \right)_{\text{p}} } {\left( {\rho c_{\text{p}} } \right)_{\text{f}} }}} \right. \kern-0pt} {\left( {\rho c_{\text{p}} } \right)_{\text{f}} }}}} \\ \end{aligned} $$

(15)

For description of the heat transfer rate, the local Nusselt number is

$$ Nu = - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\left. {\frac{\partial \theta }{\partial x}} \right|_{x = 0} $$

(16)

and the average Nusselt number $\left( {\overline{Nu} } \right)$ is

$$ \overline{Nu} = \int\limits_{0}^{1} {Nu} {\text{ d}}y $$

(17)

Numerical procedure

The control Eqs. (11)–(13) with conditions (14) were solved by the finite difference method [22,23,24, 30, 38,39,40, 45,46,47,48,49,50]. The diffusive terms were approximated by central differences, while the convective terms were discretized by the Samarskii monotonic difference scheme. The parabolic Eqs. (12) and (13) were solved by the Samarskii locally one-dimensional scheme [45,46,47,48,49,50]. The obtained systems of algebraic equations were solved by the Thomas algorithm. The partial differential equation for the stream function (11) was discretized by the five-point difference scheme. The linear discretized equation was solved by the successive over relaxation method.

In order to validate the developed numerical code, the experimental [44] and numerical [51] studies of nanoliquid free convection in a differentially heated square area are considered. Table 2 gives the average Nusselt number for different nanoparticles concentrations. It can be clearly seen that the results obtained by the developed computational code agree well that demonstrates the accuracy of the present code for nanoliquid simulation.

Table 2 Comparison of $\overline{Nu}$ for nanoliquid free convection in a differentially heated square enclosure

For the further validation, the experimental data of Hamady et al. [52] and numerical results of Tso et al. [53] for free convection in a rotating square differentially heated enclosure were used. The calculated temperature isolines at different rotating angles γ compared with experimental and numerical results [52, 53] are shown in Fig. 2 for Ra = 3·10⁵ and Pr = 0.7. This comparison reflects a very good agreement with results of other researchers.

Fig. 2

Temperature isolines at different rotating angles γ for Ra = 3·10⁵ and Pr = 0.7 (a), results of Hamady et al. [50] (b), results of Tso et al. [51] (c)

A grid sensitivity analysis was performed using three different grid sizes (50 × 50, 100 × 100 and 200 × 200) for Ra = 10⁵, Ta = 10⁵, Pr = 6.82, ϕ = 0.02. Figures 3 and 4 demonstrate that the deviations for $\overline{Nu}$ and $\left| \psi \right|_{ \hbox{max} }$ using meshes of 100 × 100 points and 200 × 200 points are insignificant. Hence, a mesh of 100 × 100 nodes was selected for the further numerical analysis.

Fig. 3

Time variations of $\left| \psi \right|_{ \hbox{max} }$ during the first twenty periods (a) and the last twenty periods between 180 and 200 revolutions for Ra = 10⁵, Ta = 10⁵, Pr = 6.82, ϕ = 0.02 and different meshes

Fig. 4

Time variations of $\overline{Nu}$ during the first twenty periods (a) and the last twenty periods between 180 and 200 revolutions for Ra = 10⁵, Ta = 10⁵, Pr = 6.82, ϕ = 0.02 and different meshes

Results and discussion

In the present study, we investigate free convection of an alumina–water nanoliquid in a rotating square area with a sinusoidal left border temperature distribution. The effects of the Rayleigh number (Ra = 10⁴–10⁶), Taylor number (Ta = 10⁴ – 10⁶) and nanoparticles concentration (ϕ = 0.0–0.04) on the liquid flow and thermal transmission are examined for Pr = 6.82. The results are presented in the form of isolines for temperature and stream function, as well as the average Nusselt number and nanoliquid flow rate.

Figures 5 and 6 show streamlines and isotherms plotted by solid and dashed lines for the clear fluid (ϕ = 0.0) and nanofluid (ϕ = 0.03), respectively, at Ra = 10⁵ and Ta = 10⁴. Presented distributions are very complicated due to simultaneous impacts of rotation and sinusoidal temperature distribution. It should be noted that the presented distributions have been obtained during the 200th revolution. Such high number of revolutions is necessary for a formation of periodical behavior of flow structures and heat transfer patterns. Thus, for γ = 0, one can find inside the cavity three convective cells illustrating the formation of ascending flow near the left wall with sinusoidal temperature distribution and descending flow near the right cold wall, while the central vortex reflects a combination of these two vortices taking into account the different motion directions of these vortices in the central part, namely from the left convective cell we have a downstream motion in the center, while from the right vortex we have upstream motion; therefore, the central convective cell allows to combine these vortices. At the same time, the temperature distribution (see Fig. 6) characterizes an appearance of essential heating of the central part of the left wall, while the right wall is cooled and isotherms from this cold wall distribute parallel to this wall. The curvature of the isotherms in central part reflects an effect of rotation. In the case of γ = π/4 the central vortex vanishes, while one can find a formation of global external circulation with the downstream flows near the cold wall and upstream flows near the heated wall. Such flow structure changes lead to a little smoothing of isotherms in the central part.

Fig. 5

Streamlines during complete revolution for Ra = 10⁵, Ta = 10⁴ and ϕ = 0.0 (solid lines), ϕ = 0.03 (dashed lines)

Fig. 6

Isotherms during complete revolution for Ra = 10⁵, Ta = 10⁴ and ϕ = 0.0 (solid lines), ϕ = 0.03 (dashed lines)

Further rotation (γ = π/2) illustrates a combination of two central vortices in one major circulation, while a secondary recirculation is located near the “upper” part of the heated wall, where the wall is cooled under the sinusoidal temperature distribution. For γ = 3π/4, an additional recirculation appears near the “upper” part of the cold wall due to the buoyancy force effect jointly with rotation impact. Temperature distributions characterize a formation of central temperature stratification core where isotherms are parallel to the adiabatic walls, and such distributions reflect a heat conduction mechanism between hot part and cold part. In the case of γ = π, we have the flow structures that are similar to the case of γ = 0 where near the cold wall the downstream flow occurs and near the heated wall the upstream flow develops with a central circulation for combination of these two vortices. For γ = 5π/4, the side circulations rise and the central vortex decreases, while the isotherms begin to curve in the central part. Further rotation characterizes also a vanishing of the central circulation and a formation of external global nanofluid motion, and for γ = 7π/4 one can find an appearance of one major circulation with two weak secondary recirculations near the “upper” part of the cold wall and close to the central part of the heated wall. Isotherms reflect the vanishing of the central temperature stratification core with a following rotation.

In the case of alumina nanoparticles addition (ϕ = 0.03), one can find a modification of some flow structures and heat transfer patterns. For example, for γ = π/4 an inclusion of nanoparticles leads to a combination of two central vortices and the same differences can be found for γ = 3π/2. At the same time, isotherms in the case of nanofluid with ϕ = 0.03 can be found less deflected in the central part in comparison with pure fluid due to a growing role of the heat conduction in comparison with clear water.

Figure 7 demonstrates the behavior of the average Nusselt number and nanofluid flow rate during two complete revolutions between 198 and 200 revolutions for Ra = 10⁵, Ta = 10⁴ and different values of nanoparticles volume fraction. For the considered regime, it is obviously seen that the period of oscillations is 2π and a growth of the nanoparticles volume fraction leads to the heat transfer rate reduction during the whole revolution, while nanofluid flow rate is changed non-monotonic with ϕ during the considered revolution.

Fig. 7

Variations of average Nusselt number (a) and fluid flow rate (b) with rotation angle γ during two complete revolutions for Ra = 10⁵, Ta = 10⁴ and different values of nanoparticles volume fraction

The influence of the Rayleigh number and nanoparticles concentration on $\overline{Nu}$ and $\left| \psi \right|_{ \hbox{max} }$ is presented in Fig. 8. As it was expected, a raise of Ra leads to the heat transfer enhancement and convective flow intensification and more essential intensification occurs for Ra = 10⁶. At the same time, a growth of the Rayleigh number characterizes a rise of the oscillations amplitude and the structure of oscillations is complicated. It should be noted that an increase in Ra illustrates a growth of number of revolutions for reaching the periodical structures and for Ra = 10⁶ a growth of the nanoparticles volume fraction has a non-monotonic impact on heat transfer rate and nanofluid flow rate. While for Ra = 10⁴ and Ra = 10⁵, one can find the heat transfer enhancement with ϕ.

Fig. 8

Variations of average Nusselt number (a) and fluid flow rate (b) with rotation angle γ during two complete revolutions for Ta = 10⁵, different values of Rayleigh number and nanoparticles volume fraction

Figure 9 shows the variations of the average Nusselt number and fluid flow rate for Ra = 10⁵ and different values of Taylor number and nanoparticles volume fraction. A growth of the Taylor number characterizes a diminution of $\overline{Nu}$ and $\left| \psi \right|_{ \hbox{max} }$, while for Ta = 10⁴ a rise of the nanoparticles concentration leads to the heat transfer degradation. In the case of Ta = 10⁵ and Ta = 10⁶ one can find the heat transfer enhancement with ϕ. It is interesting to note that a growth of the Taylor number attenuates the convective flow and the structure of oscillations becomes simpler.

Fig. 9

Variations of average Nusselt number (a) and fluid flow rate (b) with rotation angle γ during two complete revolutions for Ra = 10⁵, different values of Taylor number and nanoparticles volume fraction

Figure 10 demonstrates the influence of the Rayleigh and Taylor numbers on the heat transfer rate and nanofluid flow rate for ϕ = 0.02. As it has been described, a growth of the Rayleigh number characterizes the intensification of convective flow and heat transfer, while a rise of the Taylor number reflects a suppression of these transport mechanisms. It is interesting to note that for Ra = 10⁴, a growth of the Taylor number does not lead to significant variation of the average Nusselt number.

Fig. 10

Variations of average Nusselt number (a) and fluid flow rate (b) with rotation angle γ during two complete revolutions for ϕ = 0.02, different values of Rayleigh and Taylor numbers

Conclusions

Convection heat transfer within a nanofluid rotating square cavity having sinusoidal temperature distribution along one wall, while the opposite wall is isothermally cooled and the rest walls are adiabatic has been studied numerically. Cavity revolves on the z-coordinate line that is perpendicular to the cavity and passes through the central point of the enclosure. The alumina–water nanofluid is located inside the cavity. Governing partial differential equations and corresponding initial and boundary conditions formulated in dimensionless stream function, vorticity and temperature have been solved by finite difference method of the second-order accuracy. Streamlines and isotherms as well as average Nusselt number and nanofluid flow rate illustrate the effects of rotation, Rayleigh and Taylor numbers, and nanoparticles volume fraction on the flow structures and heat transfer patterns. The obtained results have shown that a rotation during one complete revolution includes the double transformation of triple vortex structure to a single vortex, namely, between γ = 0 and γ = 3π/4 and between γ = π and γ = 2π. The temperature field reflects an appearance of the central stratification core in the middle of the rotation process. An increase in the Rayleigh number illustrates the intensification of convective flow and heat transfer, while a growth of the Taylor number reflects a suppression of fluid flow and heat transfer. The heat transfer enhancement with nanoparticles occurs for low Rayleigh numbers (10⁴ and 10⁵) for the considered system and for high Taylor number (10⁵ and 10⁶). Such behavior can be explained by the heat conduction nature of nanoparticles, when intensification is possible for the case of conduction dominated mode or when convection is not significant mechanism. Also an addition of nanoparticles in the considered system characterizes a reduction in time that is needed for formation of periodic oscillations.