Introduction

Azo compounds (azos), materials that easily show unstable performance, are commonly used in radical polymerization in solution. If the temperature of the surrounding environment or process is under improper control, thermal decomposition, generating heat release, may even court a thermal explosion [1].

In the United Nations (UN) classification of dangerous goods, the azos stand as a class 4.1 hazardous category of material. Fire and Disaster Management Agency (FDMA) of Japan defined the azos as the 5th category of dangerous substances, which include diazos, organic peroxides, esters, nitrous, and the mixture containing one of the above substances [1,2,3,4]. Thus, the azo compound has a certain self-reactive trait.

R–N=N–R is a synthesis reaction formula of azo compound, wherein R is an aliphatic hydrocarbon group or an aromatic hydrocarbon group; two R groups may be the same or different. Aliphatic azos are made from the corresponding hydrazine through oxidation or dehydrogenation reaction [3,4,5,6,7]. Aromatic azos, which are generally prepared by the coupling reaction of diazo compound, are mainly used for dyes, and aliphatic azos are used more in the polymerization initiator. The azo initiator, which is selected to research, 2,2′-azobis (2-methylpropionamide) dihydrochloride (AIBA), is widely used in chemical processes. Although there are a series of studies on the individual and multiple thermal hazards of azos [5,6,7,8,9], there is less research on AIBA in the past literature. Most of the research focused on thermal hazard by single calorimetry technique or less on numerical analysis of data under the conditions of processing, storage, or transportation of AIBA.

In essence, azos do not need oxygen in the air or water vapor but can react by themselves, and are often accompanied by an exothermic and gas-product formation. Chemical stability of such self-reactive materials is poor. The slow decomposition will indiscernibly occur even at ambient temperature.

During reaction, storage, or transportation, when the heat production rate (Qg) surpasses the heat removal rate (Qr), the heat released in the reaction process leads to an increment in temperature (T). As the process temperature reaches the apparent exothermic onset temperature (T0), the system may eventually cause the reaction to gradually become unbalanced, and a runaway reaction may even be started. At this instant, if the heat cannot properly be removed, heat accumulation will cause a temperature rise, increasing the progress of reaction and leading the reaction system to combustion, bursting, or even explosion [10,11,12].

We used differential scanning calorimetry (DSC) combined with thermogravimetric analysis (TG) to determine the thermal runaway reaction of AIBA by several heating rates (β). Based on instrument data, numerical methods were the primary technique for further analysis on reaction kinetic of AIBA [13,14,15,16,17]. Mathematical models [18,19,20,21] bring into kinetic assessment operation for quantification and calculation, as well as to establish a specification of assessment for development and preserve the process into stable state. The estimate model was employed to assess thermokinetic parameters, such as apparent exothermic temperature (T0), reaction order (n), temperature at the maximum heat release in reaction (Tp), heat of decomposition (ΔHd), pre-exponential factor (A), and apparent activation energy (Ea). Above-obtained data were applied to classify and construe exothermic mode of AIBA under large scale, and corresponding thermal safety measures can also be analyzed. The mathematical approach combining thermal hazard responses evaluation is a critical basis for the rationality of thermokinetic parameters. To achieve this objective, we used two kinds of isoconversional methods as a preliminary estimate of the thermal hazard parameters and imported two linear fitting methods to calculate the required values that are further required for the process amplification method. Scale-up simulation was implemented by Semenov model [22], which can be applied in real process situation, transportation, or storage conditions.

Experimental and methods

Thermokinetic parameters of AIBA reaction

The basic thermal hazard characteristics of 98 mass% AIBA were determined by DSC temperature screening experiments with a software setting on a Mettler TA8000 system subjoined with a DSC 821e measuring cell [23, 24]. Thermogravimetry, purchased from Hitachi STA 7200RV (simultaneous thermal analysis), was utilized to analyze the alterations of mass loss and thermal degradation behavior for AIBA. Five heating rates of 0.5, 1.0, 2.0, 4.0, and 8.0 °C min−1 were applied in DSC and STA [25].

For acquiring appropriate values for the correctness of the subsequent calculation, we combined the differential isoconversional of Friedman, and Flynn–Wall–Ozawa methods with linear fitting of ASTM E698-11 and Kissinger methods for preliminary determining rudimentary thermokinetic parameters. The calculated data can be used as the basis for the process amplification simulation.

Isoconversional differential method–Friedman method

The Friedman method uses a differential isoconversional model, which is derived from the Arrhenius equation, to determine thermokinetic parameters [26]. The data measured by calorimetry can be determined from natural logarithmic transformation on conversion rate \(({\text{d}}\alpha /{\text{d}}t)\), externalized for formula on reciprocal of corresponding reaction conversion rate (α)t specific absolute temperature [27]:

$$\ln \left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right) = \ln (A(\alpha ) \, f(\alpha ))\exp \left( { - \frac{E(\alpha )}{RT(t)}} \right)$$
(1)
$$t_{\text{a}} = \int\limits_{0}^{t} {{\text{d}}t} = \int\limits_{{\alpha_{0} }}^{\alpha } {\frac{{{\text{d}}\alpha }}{{A^{\prime}(\alpha )\exp \left( { - \frac{E(\alpha )}{RT(t)}} \right)}}}$$
(2)

In Eq. (1), \(E (\alpha )\) and \(A (\alpha )\) are apparent activation energy and frequency factor at conversion \(\alpha\); \(A^{\prime} (\alpha )\) is an amended pre-exponential factor by a product of \(A (\alpha )\) and \(f (\alpha )\). \(f (\alpha )\) is reaction equation. The reaction equation will have different expression patterns depending on the reaction mode of the sample itself, but the method does not need to consider the form of the reaction, so \(f (\alpha )\) can be expressed as a constant. The calculating method of Ea is indicated as relational equation between parameters of − E(α) R−1 in slope and \(\ln (A (\alpha ) { }f (\alpha ) )\) in intercept. The coordinate of x and y axes is characterized by ln (dα/dt) and T(t)−1.

Isoconversional integration–Flynn–Wall–Ozawa method

Flynn–Wall–Ozawa method avoids the possible negligence produced from diverse assumptions concerning kinetic form, which can be expressed as below [28]:

$$\ln \left( \beta \right) = - 1.0516\left( {\frac{{E_{\text{a}} }}{RT}} \right) + {\text{constant}}$$
(3)

If the effects of different heating rates are taken into account, Eq. (3) can be rewritten as Eq. (4):

$$\ln \left( {\beta_{1} } \right) + 1.0516\frac{{E_{\text{ai}} }}{{RT_{\text{a1}} }} = \ln \left( {\beta_{2} } \right) + 1.0516\frac{{E_{\text{ai}} }}{{RT_{\text{a2}} }} = \ln \left( {\beta_{3} } \right) + 1.0516\frac{{E_{\text{ai}} }}{{RT_{\text{a3}} }} = \cdots$$
(4)

The slope Eα can be determined by plotting with ln (β) and T−1. Isoconversional methods have a prominent advantage over non-isoconversional methods. The results, in a wide range of applications actual sample temperatures, may deviate from preset non-isothermal or isothermal methods. This is due to the thermal effect that induces sample self-heating [28]. The method is better suited for a differential type instrument, such as heat-flow data by DSC. The method does not need to consider the models and process of reaction which can be made a preliminary analysis to verify the apparent activation energy [28].

ASTM E698-11 model

The suitability and application of the linear fitting method have been confirmed in several papers for its methodological strength. Compared to the isoconversional method, linear fitting method is applicable for known reaction modes such as nth reaction, or where substances are less complex in the reaction stage. If the reactions are correctly matched, the conditions of the fitting and the result can be relied upon. In this study, the Kissinger method and ASTM E698-11 are deemed suitable for use.

The ASTM E698-11 method can be written in the following form [29]:

$$E_{\text{a}} = \left( { - \frac{2.303R}{D}} \right)\left[ {\frac{{{\text{d}}\left( {\log \beta } \right)}}{{{\text{d}}\left( {\frac{1}{{T_{\text{P}} }}} \right)}}} \right]$$
(5)
$$D = \frac{{{\text{d}}\ln \left[ {p\left( x \right)} \right]}}{{{\text{d}}x}} = \frac{{{\text{d}}\ln \left( {x + 2} \right)x\exp (x)}}{{{\text{d}}x}},\quad {\text{where}}\;x = \frac{{E_{\text{a}} }}{{RT_{\text{P}} }}$$
(6)
$$A = \frac{{E_{\text{a}} \beta }}{{RT_{\text{P}}^{2} }}\exp \left( {\frac{{E_{\text{a}} }}{{RT_{\text{P}} }}} \right)$$
(7)

where α is the conversion of the AIBA groups and A is the rate constant. The values of \(\ln ({\beta \mathord{\left/ {\vphantom {\beta {T^{2} }}} \right. \kern-0pt} {T^{2} }})\) and T−1 in the plot can render the slope = − Eα/(RT).

Kissinger method

The A and Eα can be calculated from drawing the y axes of ln[β/T 2p ] and x axes of 1/Tp [30]:

$$\ln \left( {\frac{\beta }{{T_{\text{p}}^{2} }}} \right) = \ln \left( {\frac{AR}{{E_{\text{a}} }}} \right) - \frac{{E_{\text{a}} }}{{RT_{\text{p}} }}$$
(8)

Calculating relative speed and convenience of the essential parameters are benefits of the linear fitting method, such as ASTM E698-11 and Kissinger methods which were applied in this study. Linear fitting method is usually based on the Arrhenius model, which involves a certain range of heating rates, generally set as 1–10 °C min−1 and assuming a first-order reaction in applied elementary chemical processes, such as decomposition, catalysis, and degradation [30].

Nonlinear fitting method

To clarify the thermokinetics for AIBA, a nonlinear fitting method was applied for DSC thermal curve data treatment [14, 31, 32]. The nonlinear fitting method assumes that the conversion degrees are reflected in variables of systematic status. This approach not only facilitates to establish a more detailed reaction mechanism, but is also consistent with the actual situation and some experimentally obtained overall responses. In addition, the condition occurs when investigating reactions in other self-reactive substances and secondary reactions with more than two stages initiated at elevated temperatures under accidental environments. The nonlinear fitting method can characterize multiple phase reactions that may contain several independent, parallel, and continuous stages. The nth reaction rate models used in this study are demonstrated in Eqs. (9) and (10) [31, 32]:

Simple single-stage reaction A → B:

$$r = \frac{{{\text{d}}\alpha }}{\text{dt}} = k_{\text{o}} e^{{ - \frac{{E_{\text{a}} }}{RT}}} f(\alpha )\left\{ {\begin{array}{*{20}l} {{\text{For}}\;n{\text{th-order}}\;{\text{model}}:\;f(\alpha ) = (1 - \alpha )^{n} } \hfill & {(9)} \hfill \\ {{\text{For}}\;{\text{autocatalysis}}\;{\text{model}}:\;f(\alpha ) = (1 - \alpha )^{{n_{1} }} (\alpha^{{n_{2} }} + \eta \, )} \hfill & {(10)} \hfill \\ \end{array} } \right.$$

where ko denotes the pre-exponential factor of reaction of the nth stage, respectively. R is the gas constant (R = 8.314 J mol−1 K−1), α is the degree of conversion (0–1), and η is the autocatalytic constant.

Process amplification with simulation method and critical condition calculation

Scale-up method is based upon the assumption that (1) the temperature in the system is uniform, (2) there is no temperature gradient, and (3) the temperature of the system is greater than that of the environment. The heat exchange between the system and the environment is concentrated on the surface of the system [33]. This approach not only builds up a more detailed reaction mechanism, but is also in line with the actual situation, and some overall responses, such as heat generation in real process, can be obtained [34]. The fractional conversion of concentration rate XA can be converted to Eqs. (11) and (12) [22, 35]:

$$X_{\text{A}} = \frac{{\Delta H_{\text{t}} }}{{\Delta H_{\text{total}} }} = \frac{{mC_{\text{p}} (T - T_{\text{o}} )}}{{mC_{\text{p}} (T_{\text{p}} - T_{\text{o}} )}} = mC_{\text{p}} \frac{{(T - T_{\text{o}} )}}{{(T_{\text{p}} - T_{\text{o}} )}}$$
(11)
$$C = C_{\text{o}} (1 - X_{\text{A}} ) = C_{\text{o}} \frac{{(T\text{p} - T)}}{{(T\text{p} - T_{\text{o}} )}} = C_{\text{o}} \frac{{(T\text{p} - T)}}{{\Delta T\text{p}}}$$
(12)

where C is concentration of reactants, Co is initial concentration, △Ht is total heat released by decomposition at time, △Htotal is total heat of whole reaction, m is mass of reactants, and CP is specific heat of reactants of interest [35].

The equation of reaction rate (r) can be exemplified as Eq. (13) [36]:

$$- r = \frac{{ - {\text{d}}C}}{{{\text{d}}t}} = kC^{\text{n}}$$
(13)

where k is rate constant, t is a specific period in the chemical process, and n is reaction order.

Substituting and combining Eq. (12) with Eq. (13) and the Arrhenius equation:

$$k = C_{\text{o}}^{{{\text{n}} - 1}} A\exp \left( { - \frac{{E_{\upalpha} }}{RT}} \right) = \left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right)\left[ {\frac{{\Delta T_{{_{\text{p}} }} }}{{(T_{{_{\text{p}} }} - T)}}} \right]^{\text{n}} \Delta T_{{_{\text{p}} }}$$
(14)

Taking the transformation on natural logarithms on Eq. (14) renders Eq. (15) on the following information:

$$\ln k = \ln \left\{ {\left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right)\left[ {\frac{{\Delta T_{{_{\text{p}} }} }}{{(T_{{_{\text{p}} }} - T)}}} \right]\,^{\text{n}} \Delta T_{{_{\text{p}} }} } \right\} = \ln \left( {C_{\text{o}}^{{{\text{n}} - 1}} A} \right) - \frac{{E_{\text{a}} }}{RT}$$
(15)

The dT/dt by adiabatic condition is the magnitude of the temperature rise within the reaction. Amplification model demonstrates heat production rate (qg) composed with volume of reactive material (V), − r, and △Htotal. qg is indicated as Eq. (16):

$$q_{\text{g}} = \Delta H_{\text{total}} V( - r)$$
(16)

Replacing Eq. (13) into Eq. (16), qg can be rewritten as Eq. (17):

$$q_{\text{g}} = \Delta H_{\text{total}} VAC^{\text{n}} \exp \left( { - \frac{{E_{\text{a}} }}{RT}} \right)$$
(17)

The heat reduction rate (qr) caused by cooling system is denoted as Eq. (18):

$$q_{\text{r}} = hS(T - T_{\text{s}} )$$
(18)

where h can be expressed as heat transfer capacity of cooling system, S is total contact surface area for heat exchange, and TS is ambient temperature under current system.

Derived from Eqs. (17) and (18), the thermal balance of system qg − qr can be represented as Eq. (19):

$$\rho VC_{\text{P}} \left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right) = q_{\text{g}} - q_{\text{r}}$$
(19)

where ρ is density of reactants.

From Eqs. (17) to (19), the thermal change in system can be annotated as Eq. (20):

$$\rho VC_{\text{P}} \left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right) = \Delta H_{\text{total}} VAC^{\text{n}} \exp \left( { - \frac{{E_{\text{a}} }}{RT}} \right) - hS(T - T_{\text{s}} )$$
(20)

The reaction order n obtained by this study is 1. Therefore, replacing Eq. (17) into Eq. (20) with n = 1, Eq. (20) can be rewritten as Eq. (21):

$$\rho VC_{\text{P}} \left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right) = \Delta H_{\text{total}} VAC_{\text{o}} \left[ {\frac{{(T_{\text{P}} - T)}}{{(T_{\text{P}} - T_{\text{o}} )}}} \right]\exp \left( { - \frac{{E_{\text{a}} }}{{RT_{\text{c}} }}} \right) = hS(T_{\text{C}} - T_{\text{S}} )$$
(21)

Whether the reaction is in equilibrium under steady state can be obtained by Eqs. (22) and (23) [22]:

$$q_{\text{g}} \left| {_{{T = T_{\text{c}} }} } \right. = q_{\text{r}} \left| {_{{T = T_{\text{c}} }} } \right.$$
(22)
$$\left. {\frac{{{\text{d}}q_{\text{g}} }}{{{\text{d}}T}}\,} \right|_{{T = T_{\text{c}} }} = \left. {\frac{{{\text{d}}q_{\text{r}} }}{{{\text{d}}T}}\,} \right|_{{T = T_{\text{c}} }}$$
(23)

where Tc is the critical temperature.

When the qg subtracted qr is a negative value, (dT/dt) > 0. The cooling system is unable to process the heat generated in the system. As heat continues to accumulate in the system, it is eventually evolving into runaway. With above condition, Eq. (21) can be rewritten as Eq. (24):

$$\Delta H_{\text{total}} VAC_{\text{o}} \left[ {\frac{{(T_{\text{P}} - T_{\text{C}} )}}{{(T_{\text{P}} - T_{\text{o}} )}}} \right]\exp \left( { - \frac{{E_{\text{a}} }}{{RT_{\text{c}} }}} \right) = hS(T_{\text{C}} - T_{\text{S}} )$$
(24)

Combining Eqs. (22) and (23), applicable conditions of heat transfer efficiency hS can be calculated:

$$hS = \frac{{\Delta H_{\text{total}} VAC_{\text{o}} \exp \left( {\frac{{ - E_{\text{a}} }}{{RT_{\text{c}} }}} \right)\left[ { - 1 + \frac{{E_{\text{a}} (T_{\text{p}} - T_{\text{c}} )}}{{RT_{\text{c}}^{2} }}} \right]}}{{(T_{\text{p}} - T_{\text{o}} )}}$$
(25)

Results and discussion

Thermokinetic parameters of AIBA reaction

Thermogravimetry can be used to examine the association between temperature and mass loss for the decomposition or combustion reaction. Therefore, the thermal stability of chemicals can be evaluated in a heating system. Figure 1 shows the mass loss versus time diagram of AIBA in N2 atmosphere at different heating rates, 0.5, 1.0, 2.0, 4.0, and 8.0 °C min−1, by TG test. The time of thermal degradation is lessened with temperature increase, and even the time of thermal degradation of AIBA is less than 8.0 h at low heating rate (0.50 °C min−1), which is defined that the base of AIBA is thermally sensitive material. Moreover, when heating exceeds 4.0 °C min−1, the thermal degradation of AIBA becomes quite violent. Therefore, during the storage or transportation, AIBA should remain at lower temperature to avoid aging or thermal hazard from occurring.

Fig. 1
figure 1

TG thermal curves of AIBA at of 0.5, 1.0, 2.0, 4.0, and 8.0 °C min−1

Full size image

Figure 2 demonstrates the mass loss rate against time diagram of AIBA by TG tests. It can be seen that the AIBA has two mass loss stages and also stands for a severe decomposition reaction. The response amplitude of first stage is a minor effect in the overall reaction, as shown in Fig. 1. We regard the second stage as the main reaction to obtain the thermokinetic parameter under the nonlinear fitting method, and simulation result is well matched with experimental data. It is reasonable to treat the second-stage reaction as the main reaction and the basis for the subsequent process amplification calculation.

Fig. 2
figure 2

dTg thermal curves of AIBA at of 0.5, 1.0, 2.0, 4.0, and 8.0 °C min−1

Full size image

By the arithmetic results of isoconversional method, the conversion of reaction progress α is in the range of values on 0–1 and presented in Figs. 3 and 4. As the reaction proceeds, AIBA has a short prompt reduction of Ea. The value of Eα remains without much change, and then, it is reduced at the end of reaction. The minimum value of Eα occurs at the end of the reaction. The value of Ea varies greatly to the beginning and end of the reaction. The values of Ea provided by reaction process are remaining stable. It can be inferred that AIBA is basically a relatively simple model on decomposition reaction, approximated as an nth order reaction.

Fig. 3
figure 3

Determination of the apparent activation energy of the decomposition of 98 mass% AIBA with the Friedman thermokinetic equation

Full size image
Fig. 4
figure 4

Determination of the apparent activation energy of the decomposition of 98 mass% AIBA with the Flynn–Wall–Ozawa thermokinetic equation

Full size image

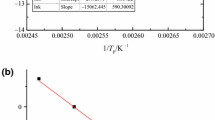
For AIBA, the ranges of Ea from two isoconversional methods are 100.0–112.0 and 99.0–200.0 kJ mol−1, which can be obtained from the data shown in Table 1. Table 2 shows the calculated results from four methods, which can be compared. Among the Ea values, the result from Friedman model is different from the other three models. Even experiments conducted under the same setting conditions cannot be confirmed by the consistency of data retention. A single scanning may cause an offset in instruments. However, the deviation of the calculations and experimentation was greatly reduced by Friedman model, which did not require an accurate understanding of reaction pathway. The results of Flynn–Wall–Ozawa are more suitable for AIBA. Combining the results of ASTM E698 on Fig. 5 and Kissinger methods on Fig. 6, it can be determined that Ea = 125.0 kJ mol−1 instead of a range of values.

Table 1 Non-isothermal data by DSC tests for 98 mass% AIBA at 0.5, 1.0, 2.0, 4.0, and 8.0 °C min−1
Full size table
Table 2 Calculated results of Ea value by four methods
Full size table
Fig. 5
figure 5

Evaluation of Ea by ASTM E698-11 method for 98 mass% AIBA at n = 1.0

Full size image
Fig. 6
figure 6

Evaluation of Ea by Kissinger method for 98 mass% AIBA at n = 1.0

Full size image

Figures 7 and 8 show heat production versus time for the experiments and simulations. The simulation results showed a reasonable fitting of the DSC data under different heating rates. The formal nth model provides a reasonable fit for the entire set of experimental data. The results produced well-fit curves of heat production rates as shown in Fig. 8. The results closely mirrored the same thermokinetic parameters, such as Ea that were obtained by the nonlinear fitting method, and are also similar to data from the four methods given in Table 1. The schemes of heat production and heat production rate against the time of AIBA reaction at the five heating rates demonstrate that AIBA exhibits complex reaction behavior that the obtained thermokinetic parameters can be used to reliably forecast the thermokinetic parameters using the Semenov model. The related thermokinetic parameters are listed in Table 3.

Fig. 7
figure 7

Comparisons of AIBA heat production versus time curves with heating rates of 0.5, 1.0, 2.0, 4.0, and 8.0 °C min−1 by experiments and simulations

Full size image
Fig. 8
figure 8

Comparisons of AIBA heat production rate versus time curves with heating rates of 0.5, 1.0, 2.0, 4.0, and 8.0 °C min−1 by experiments and simulations

Full size image
Table 3 Results of thermokinetic parameters evaluation for the AIBA at 0.5, 1.0, 2.0, 4.0, and 8.0 °C min−1
Full size table

Calculation mode on process amplification calculation mode

For applying experimental scale of thermal hazard data to the actual process operation, such as design of cooling system or storage and transportation characteristic, we simulated heat generation from large-scale system qg and external heat release mode qr based on Eqs. (17) and (18). The parameters to be replaced in the equations are known as fixed values except the TS. TS can be substituted into arbitrary value. In general, azos are commonly used at temperature below 90.0 °C. We chose ambient temperature as 323, 333, and 343 K. Adding the conditions of Eqs. (22) and (23), qg and qr will have intervals of heat balance (qg = qr). From the above situations, the curves formed by qg and qr have two intersection points defined as the stable point of extinguishing temperature (TSE) and the stable point of initiation temperature (TSI) as well as tangent points defined as critical ignition or extinction temperature (TCI) and critical extinguishing temperature (TCE), which are shown in Figs. 9–11 with different surrounding temperatures. The numerical method can be beginning from Eq. (25). The two solutions, TCE and TCI, can be attained, and brought to Eq. (19) to obtain two hS values. Finally, different hS is substituted into Eq. (24) for acquiring other critical parameters.

Fig. 9
figure 9

Balance scheme of heat production rate qg and heat removal rate qr for decomposition reaction of 98 mass% AIBA with TS = 323 K

Full size image
Fig. 10
figure 10

Balance scheme of heat production rate qg and heat removal rate qr for decomposition reaction of 98 mass% AIBA with TS = 333 K

Full size image
Fig. 11
figure 11

Balance scheme of heat production rate qg and heat removal rate qr for decomposition reaction of 98 mass% AIBA with TS = 343 K

Full size image

By the tangent and intersection of qg and qr, it can determine the AIBA in large scale under different cooling system efficiency (qr1, qr2, and qr3). When the heat qr is less than or equal to qr3, which means the cooling system efficiency must at least have reached this value. If the temperature exceeds the value represented by the TCI, qr < qg, the system will tend to be unstable state, or if the temperature exceeds the value of TSI, the qr > qg, and the system will finally move back to steady state. When the cooling efficiency measures up the qr1, substantially the qr ≥ qg, even if the temperature is greater than TSE and TCE, the system will return to steady state.

From the above description, the ideal state of the cooling system is qr ≥ qr1. However, realization of higher cooling efficiency often requires costly designs and equipment. Under the compromise, the real process can select a medium cooling system efficiency qr; there were three intersection points between qr3 and qg, which represents a stable point at lower temperature (TSL), stable point at middle temperature (TM), and stable point at higher temperature (TSH).

The temperature in a normal operating system should always be maintained below TM, but when causing an unexpected situation, such as a disoperation or invalid device, the temperature exceeds TM. If the cooling system does not respond in time, heat accumulation occurs (qr < qg), and resulting system approaches an unstable state or runaway reaction. The reaction progresses to TSH, at which point qr ≥ qg and the system traces back to a steady state.

Conclusions

DSC combined with a mathematical model is a useful method for measuring the thermal hazard of, and avoiding a thermal runaway reaction for, AIBA. Kinetic models can also be integrated with calorimetric data to acquire a variety of thermokinetic parameters. The calculation results can approach more closely to the real situation.

The obtained thermokinetic parameters can be used in the calculation of the process amplification simulation of AIBA under different surrounding temperature during various cooling efficiencies (see Figs. 9–11). When heat discharge rate (hS) is determined by qr1 and qr3, TCI, TSI, TSE, and TCE = 324.78, 437.22, 323.12, and 418.13 K (98 mass% AIBA with TS = 323 K), as the TS increased on 333 K, TCI, TSI, TSE, and TCE = 334.45, 438.22, 333.12, and 422.76 K. The critical temperature increased when the TS value was increased. The range of heat transfer coefficients (hS) was 0.0213–2.8771 kJ min−1 K−1 at 323 K< TS < 353 K for AIBA.

The decomposition reaction of AIBA analyzed by different DSC heating rates and thermokinetic parameters was constructed from four different kinetic theories. These results were used for predicting the exothermic mode of AIBA at the medium scale (25 L). It will decrease the need for large experiments, which are tedious and expensive. The simulation of thermal behavior can assist in evaluation and design basis for an actual process cooling system, transportation, and storage of AIBA.