Introduction

In chemical reaction processes, there are many occurrences of thermal runaway due to the self-reactive material of azo compounds. Azo compounds are typical self-reactive materials. Owing to the functional group, –N = N–, azo compounds are essentially unstable and active. Azobisisobutyronitrile (AIBN), one of the common azo compounds, is focused on various crucial processes contained with the polymerization for common vinyl monomers, blowing agents for the production of vinyl foaming, and some organic reaction processes, and this chemical has been reported as causing many fire and explosion accidents [1].

According to the literature [2], when decomposing, AIBN can release two free nitro radicals at 107 °C, and the decomposition reaction might be terminated immediately by exothermic reaction, which could cause an enormous amount of heat release. AIBN is generally used between 105 and 180 °C in processes. The above-mentioned proved that AIBN processes pose a significant potential hazard. Unfortunately, the critical runaway of AIBN reveals that temperatures and unstable criteria of AIBN are still unknown to date.

In general, as the heat production rate exceeds the rate of heat removed, heat can be accumulated in the reaction system to cause temperature to be increased. When the system temperature reaches the apparent exothermic onset temperature (T 0), this reaction system gradually becomes unstable and a self-reactive reaction is activated. As the temperature attains a specific threshold value, this reactive system will inevitably trigger a runaway reaction or even explosion [3–6].

A literature review was conducted to determine thermal runaway reaction of AIBN by using differential scanning calorimetry (DSC) under various heating rates (β). The reaction kinetics prediction model was employed to evaluate reaction kinetics, apparent exothermic temperature (T 0), reaction order (n), temperature at the maximum heat release in reaction (T p), heat of decomposition (ΔH d), pre-exponential factor (A), and apparent activation energy (E a). Above-mentioned thermokinetic parameters of AIBN were used to determine the critical runaway temperatures and stability criterion of AIBN’s reaction. The calculated kinetic parameters and measured exothermic reaction heat were substituted into the various critical parameters by the formula of thermal explosion [7] to define the critical runaway reaction. The required heat transfer coefficients (hS) in this critical condition could also be estimated.

Experimental and methods

Thermokinetic parameters of AIBN reaction

The reaction thermokinetic parameters of 98 mass% AIBN were determined by Li et al. [8] (see Tables 1, 2).

Table 1 Non-isothermal data by DSC tests for 98 mass% AIBN at 0.5, 2.0, 2.5, 5.0, and 10.0 °C min−1
Full size table
Table 2 Critical conditions for 98 mass% AIBN
Full size table

To calculate the critical conditions in this exothermic reaction of AIBN, thermal hazard parameters of AIBN reaction must be defined, such that E a and A could be used to acquire thermal hazard information using reliable kinetic and Ozawa models. We can compute the thermokinetic parameters through the following equation from Kissinger and Ozawa models, as Eqs. (1) and (2), respectively [9–11]:

$$ \ln \left( {\frac{\beta }{{T_{\text{p}}^{2} }}} \right) = \ln \left( {\frac{AR}{{E_{\text{a}} }}} \right) - \frac{{E_{\text{a}} }}{{RT_{\text{p}} }} $$
(1)
$$ \ln \left( \beta \right) = - 1.0516\frac{{E_{\text{a}} }}{{RT_{\text{p}} }} + C $$
(2)

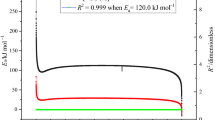
The kinetic parameters A and E a can be determined by plotting the values of ln[β/T 2p ] against 1/T p via Kissinger method. In addition, we also employed the Ozawa method to determine E a by plotting the values of ln[β] against 1/T p and compared the results from Kissinger method [12–14]. The evaluated thermokinetic parameters for the AIBN reaction by Kissinger and Ozawa method are shown in Fig. 1. We observed a large degree of similarity between E a values derived from simulation results of two methods with the values of ca. 125.0 and 124.0 kJ mol−1, respectively. Therefore, the calculation results could be used as reliable information for our study.

Fig. 1
figure 1

Evaluation of E a by (a) Kissinger method and (b) Ozawa method for 98 mass% AIBN at n = 1.0

Full size image

Stability principles and critical runaway parameters for AIBN’s reaction

Reaction concentration can be converted to Eqs. (3) and (4) [15–18]:

$$ X_{\text{A}} = \Delta H_{\text{t}} /\Delta H_{\text{total}} = [mC_{\text{p}} (T - T_{\text{o}} )]/[mC_{\text{p}} (T_{\text{p}} - T_{\text{o}} )] = (T - T_{\text{o}} )/(T_{\text{p}} - T_{\text{o}} ) $$
(3)
$$ C = C_{\text{o}} (1 - X_{\text{A}} ) = C_{\text{o}} (T_{\text{p}} - T)/(T_{\text{p}} - T_{\text{o}} ) = C_{\text{o}} (T_{\text{p}} - T)/\Delta T_{\text{p}} $$
(4)

where C is the concentration of the material, C 0 is the original concentration of the material, X A is the fractional conversion, ΔH t is the heat of decomposition at time, ΔH total is the total heat of decomposition, m is the mass of material, and C P is the specific heat of material.

The reaction rate (r) equation can be represented as Eq. (5):

$$ - r = - {\text{d}}C/{\text{d}}t = kC^{\text{n}} $$
(5)

where k is the reaction rate constant, t is the reaction time, and n is the reaction order.

Substituting and conjoining Eq. (4) into Eq. (5) with the Arrhenius equation:

$$ k = C_{\text{o}}^{{{\text{n}} - 1}} A\exp \left( { - E_{\text{a}} /RT} \right) = ({\text{d}}T/{\text{d}}t)/\left[ {(T_{{_{\text{p}} }} - T)/\Delta T_{{_{\text{p}} }} } \right]\,^{\text{n}} \Delta T_{{_{\text{p}} }} $$
(6)

Taking the natural logarithms on equation renders the following:

$$ \ln k = \ln \left\{ {\;({\text{d}}T/{\text{d}}t)/\left[ {(T_{{_{\text{p}} }} - T)/\Delta T_{{_{\text{p}} }} } \right]\,^{\text{n}} \Delta T_{{_{\text{p}} }} } \right\} = \ln (C_{\text{o}}^{{{\text{n}} - 1}} A) - E_{\text{a}} /RT $$
(7)

Temperature rise rate can be represented as dT/dt by adiabatic measurement mode.

Semenov model indicates that heat production rate (q g) can be expressed by the following parameters: volume of reactant (V), –r, and ΔH total. q g is represented as Eq. (8) [19–21]:

$$ q_{\text{g}} = \Delta H_{\text{total}} V( - r) $$
(8)

Replacing Eq. (5) into Eq. (8), q g can be rewritten as Eq. (9):

$$ q_{\text{g}} = \Delta H_{\text{total}} VAC^{n} \exp ( - E_{\text{a}} /RT) $$
(9)

The heat discharge rate (q r) from the process equipment to the cooling system or cooling medium is denoted as Eq. (10):

$$ q_{\text{r}} = hS(T - T_{\text{a}} ) $$
(10)

where h is the heat exchange capability index of the cooling system, S is the effective heat exchange area, and T a is the surroundings temperature under cooling system.

The energy equilibrium in the reaction can be expressed as Eq. (9) subtracting Eq. (10) and finishing as Eq. (11):

$$ \rho VC_{\text{P}} ({\text{d}}T/{\text{d}}t) = q_{\text{g}} - q_{\text{r}} $$
(11)

where ρ is the density of material.

From Eq. (9) to Eq. (11), the energy balance in the reaction can be expressed as Eq. (12):

$$ \rho VC_{P} ({\text{d}}T/{\text{d}}t) = \Delta H_{\text{total}} VAC^{n} \exp (( - E_{\text{a}} /RT)) - hS(T - T_{\text{a}} ) $$
(12)

As described above, in the computations of thermokinetic parameters of AIBN, we assume that n is a first-order reaction. Thus, replacing Eq. (9) into Eq. (12) with n = 1, Eq. (12) can be rephrased as Eq. (13):

$$ \rho VC_{p} ({\text{d}}T/{\text{d}}t) = \Delta H_{\text{total}} VAC_{\text{o}} [(T_{\text{p}} - T)/(T_{\text{p}} - T_{\text{o}} )]\exp (( - E_{\text{a}} /RT))\, - hS(T - T_{\text{a}} ) $$
(13)

At steady state, Semenov’s reaction state discriminant equations for a “critical situation of the reaction system” can be annotated as Eqs. (14) and (15) [22, 23]:

$$ q_{\text{g}} \left| {_{{T = T_{\text{c}} }} } \right. = q_{\text{r}} \left| {_{{T = T_{\text{c}} }} } \right. $$
(14)
$$ \left. {\frac{{{\text{d}}q_{\text{g}} }}{{{\text{d}}T}}\,} \right|_{{T = T_{\text{c}} }} = \left. {\frac{{{\text{d}}q_{\text{r}} }}{{{\text{d}}T}}\,} \right|_{{T = T_{\text{c}} }} $$
(15)

where T c is the critical temperature.

When the range of q g and q r is negative, (dT/dt) > 0. Heat gathering exceeds the handling capacity of the cooling system. Eventually, the system will produce a thermal runaway reaction. Equation (13) can be rewritten as Eq. (16):

$$ \Delta H_{\text{total}} VAC_{0}[(T_{\text{p}} - T_{\text{c}})/(T_{\text{p}} - T_{0})]\exp (( - E{_\text{a}}/RT_{\text{c}})) = hS(T_{\text{c}} - T_{\text{a}}) $$
(16)

Applying the conditions of Eqs. (14) and (15) gives:

$$ hS = \frac{{\Delta H_{\text{total}} VAC_{\text{o}} \exp (( - E_{\text{a}} /RT_{\text{c}} ))[ - 1 + E_{\text{a}} (T_{\text{p}} - T_{\text{c}} )/RT_{\text{c}}^{2} ]}}{{(T_{\text{p}} - T_{\text{o}} )}} $$
(17)

After dividing Eq. (16) by Eq. (17), the T c can be obtained by Eq. (18):

$$ \frac{{E_{\text{a}} }}{{RT_{\text{c}}^{2} }} = \frac{1}{{(T_{\text{c}} - T_{\text{a}} )}} + \frac{1}{{(T_{{_{\text{p}} }} - T_{\text{c}} )}} $$
(18)

T c can be explained as Eq. (18) [24, 25]:

$$ T_{\text{c}} = \frac{{(T_{\text{p}} + T_{\text{a}} ) \pm \sqrt {(T_{\text{p}} + T_{\text{a}} )^{2} - 4[1 + R(T_{\text{p}} - T_{\text{a}} )/E_{\text{a}} ]\;\,T_{\text{p}} T_{\text{a}} } }}{{2[1 + R(T_{\text{p}} - T_{\text{a}} )/E_{\text{a}} ]}} $$
(19)

Results and discussion

According to Eqs. (14) and (15), Semenov defined the critical conditions of a reaction system; from the above definitions, the critical conditions are not barely the intersection point of trajectory formed by q g and q r; the critical conditions also contain the tangent point of heat production rate curves and heat removal rate curve. These parameters are critical ignition or extinction temperature (T CI) and final stable point of ignition temperature (T FSI) at low performance of cooling treatment, final stable point of extinguish temperature (T FSE), and final critical extinguish temperature (T FCE) at high performance of cooling treatment, stable point at low temperatures (T FSL) and stable point at higher temperatures (T FSH) at medium performance of cooling treatment.

The space containing critical conditions could be applied to decide the stability region of the AIBN reaction system. T a can be substituted into arbitrary value; we chose ambient temperature as 300 K in Figs. 2, 3, 4, 5, 6 and 7. These six figures show the balance of the q g and q r versus the T a. From Eq. (19), the two solutions, T FCE and T CI, can be therefore acquired, and then, the two critical temperatures can be taken into Eq. (17) to obtain two different hS values. These two parameters with Eq. (19) can be used to decide the other critical conditions.

Fig. 2
figure 2

Balance diagram of heat production rate q g and low heat removal rate q r for decomposition reaction of 98 mass% AIBN

Full size image
Fig. 3
figure 3

Balance diagram of heat production rate q g and low heat removal rate q r for decomposition reaction of 98 mass% AIBN with reactor volume = 200.0 L

Full size image
Fig. 4
figure 4

Balance diagram of heat production rate q g and high heat removal rate q r for decomposition reaction of 98 mass% AIBN

Full size image
Fig. 5
figure 5

Balance diagram of heat production rate q g and high heat removal rate q r for decomposition reaction of 98 mass% AIBN with reactor volume = 200.0 L

Full size image
Fig. 6
figure 6

Balance diagram of heat production rate q g and heat removal rate q r for decomposition reaction of 98 mass% AIBN

Full size image
Fig. 7
figure 7

Balance diagram of heat production rate q g and heat removal rate q r for decomposition reaction of 98 mass% AIBN with reactor volume = 200.0 L

Full size image

Low performance of cooling treatment

Figures 2 and 3 show the heat balance between the q g and q r in low performance of cooling treatment. As the temperature T in the reaction system of AIBN at steady state was less than T FCI, at this time, q g was greater than q r, generated heat accumulation in the reaction system, resulted in a temperature rise, and headed for point T FSI. Finally, T reached T FSI and would eventually exceed this point. The opposite situation, q r1, was greater than q g. Consequently, the value of T increased and moved back to point T FSI. Points of T FSI were the final stable point of ignition temperature. These points could be expressed as the temperature of reaction that never ascended and never declined at hS = 0.018 kJ min−1 K−1.

High performance of cooling treatment

Figures 4 and 5 show the heat balance between the heat production rate q g and the heat production rate q r in high performance of cooling treatment. The intersection point and tangent point of q g and q r3 curves were T FSE and T FCE. When the T was less than T FSE, q r3 was less than q g; T increased and recovered to T FSE. When the T was higher than T FSE, q r3 was greater than q g. T dropped to T FSE back again. When the T was greater than T FCE, q r3 was higher than the q g, T moving back to point T FCE. These two points are also described as the temperature that never decreased, and the temperature of no return at hS = 3.495 and 6.988 kJ min−1 K−1 at reactor volume was 100 and 200 L, respectively.

Medium performance of cooling treatment and heat transfer coefficients (hS)

Figures 6 and 7 delineate the heat balance between the heat production rate q g and the heat discharge rate q r in medium performance of cooling treatment. When the range of hS was in 0.032 < hS < 6.988 and 0.000039 < hS < 532.323 kJ min−1 K−1, reactor volume was 100 and 200 L, respectively. There were three intersection points including T FSL, T M, and T FSH at trajectory of q r2 and q g. In particular, T M means that cutoff point between curves q g and q r was at the highest and lowest cooling efficient systems.

Trajectory of q r2 is shown as a dotted line. On former analysis, it was difficult to maintain an equilibrium state at T = T M owing to the variability of this temperature. We supposed that the reaction system began accurately at the T M; as long as the process parameters of any minor alternations would deviate the reaction system from the stable state, they would no longer return to T M but cause T rise or fall to the T FSL or T FSH in a steady state, respectively. Thus, a tiny upsurge in T would encourage q g growth and accelerated the T even higher. In contrast to the situation of the T increase, the minor temperature drop would make the q r greater than q g, which would cause the T to decline again. The medium steady temperature T M was erratic and sensitive. In contrast, T FSL and T FSH would be stable; if the disturbance occurs in any way, reaction would reoccur to unstable state. Table 2 lists critical conditions for 98 mass% AIBN.

Transition point phenomenon

Figure 8 depicts the critical conditions of T CI, T FCE, T FSI, and T FSE against T a by using the above equations for the decomposition reactions of AIBN. These parameters have the following behavior: T FSI > T FCE > T CI > T FSE. Both T FSI and T FCE alleviated, and both T FCI and T FSE heightened progressively with increasing T a. T a rises to a specific value of the transitional point of T a (tr); all of the critical conditions would eventually intersect at a transitional point, T c (tr). The T a (tr) could be inferred from Eqs. (20) and (21):

$$ T_{\text{a}{\text{ (tr)}}} = \frac{1}{{(E_{\text{a}} + 4RT_{\text{p}} )}} $$
(20)
$$ T_{\text{c}{\text{ (tr)}}} = \frac{1}{{(E_{\text{a}} + 2RT_{\text{p}} )}} $$
(21)
Fig. 8
figure 8

Correlation of evaluated temperatures T CI, T FCE, T FSI, and T FSE versus ambient temperature T a for decomposition reaction of 98 mass% AIBN

Full size image

Even as q g < q r in reaction, it is still not enough to express the reaction system as stable. Reaction state also must satisfy the following conditions:

$$ If\;T - T_{\text {s}} > 0,\quad q_{\text {g}} < q_{\text {r}} $$

or

$$ If\;T - T_{\text {s}} < 0,\quad q_{\text {g}} > q_{\text {r}} $$
(22)

Here T S is defined as a stable temperature in a reaction system at the state of q g = q r. Equation (22) indicates that these two discriminant functions are necessary and sufficient conditions for determining and deciding the stability of the reaction. The stable conditions have been predicted and estimated by Lu et al. [24, 25].

By the aforementioned conditions and equations, the stable criteria of AIBN could be decisive. If the T surpassed over the trajectory for T FSI or under the trajectory for T FSE, the system was stable. T would eventually return to these two temperatures. When the T was interposed between the trajectory for T FCI and T FCE, the system was unstable. Additionally, the following range of parameters formed two stable areas: T FSE < T FSL < T CI and T FCE < T FSH < T FSI. As the T a was augmented, T FSI and T FCE temperature trajectories were reduced, where the T CI and T FSE temperature trajectories were expanded and augmented at the same time. These four temperature trajectories moved increasingly. At the time that T a surpassed 400.82 K, these temperature trajectories clustered gathered at the T c (tr) and the value of the T c (tr) was 429.30 K.

Conclusions

After assessing the thermokinetic data, we could mimic the scale-up situation and avoid arriving at the critical temperature. The results are shown in Figs. 2–8. In high performance cooling treatment medium, the critical temperature in high temperature and low temperature was 441.06 and 305.25.15 K, respectively. Through individual low performance cooling treatment medium, the critical temperature in high temperature and low temperature was 458.73 and 304.68 K, respectively. The unstable temperature area was enclosed by the trajectories T CI/T FSI at high performance and T FCE/T FSE in low performance. In exclusion of unstable region, the reaction system of AIBN was stable.

In this study, the reaction and thermal hazard could be effectively evaluated by simulation of required heat removal rate for cooling system during the chemical process. In the future, isothermal kinetic model could be obtained by isothermal calorimeter, TAM III, to calculate SADT or other safety parameters by Semenov model as control temperature for AIBN during transportation and storage.