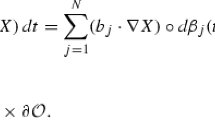Abstract
In this paper, we study the weak differentiability of global strong solution of stochastic differential equations, the strong Feller property of the associated diffusion semigroups and the global stochastic flow property in which the singular drift b and the weak gradient of Sobolev diffusion \(\sigma \) are supposed to satisfy \(\left\| \left| b\right| \cdot \mathbbm {1}_{B(R)}\right\| _{p_1}\le O((\log R)^{{(p_1-d)^2}/{2p^2_1}})\) and \(\left\| \left\| \nabla \sigma \right\| \cdot \mathbbm {1}_{B(R)}\right\| _{p_1}\le O((\log ({R}/{3}))^{{(p_1-d)^2}/{2p^2_1}})\), respectively. The main tools for these results are the decomposition of global two-point motions in Fang et al. (Ann Probab 35(1):180–205, 2007), Krylov’s estimate, Khasminskii’s estimate, Zvonkin’s transformation and the characterization for Sobolev differentiability of random fields in Xie and Zhang (Ann Probab 44(6):3661–3687, 2016).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Main Results
In this paper, we consider the following d-dimension stochastic differential equations (SDEs, for short)
Here, \(\{W_t\}_{t\in [0,T]}\) is a standard Wiener process in \({\mathbb {R}}^m\) which is defined on a complete filtered probability space \((\Omega ,\mathscr {F},{\mathbb {P}},\{\mathscr {F}_t\}_{t\ge 0})\). The coefficients \(b:{\mathbb {R}}^d\rightarrow {\mathbb {R}}^d\) and \(\sigma :{\mathbb {R}}^d\rightarrow {{\mathbb {R}}^{d\times m}}\) are both Borel measurable function. It is well known that stochastic differential equation defines a global stochastic homeomorphism flow if b and \(\sigma \) satisfy global Lipschitz conditions and linear growth conditions. In the past decades, for the non-Lipschitz coefficients SDEs there is increasing interest about their solutions and their properties (for example, the strong completeness property, the weak differentiability, stochastic homeomorphism flow property and so on).
Yamada and Ogura [22] proved the existence of global flow of homeomorphisms for one-dimensional SDEs under local Lipschitz and linear growth conditions. Li [16] proved the strong completeness property of SDEs (1.1) by studying the derivative flow equation of SDEs (1.1). Fang and Zhang [3] used the Gronwall-type estimate to study SDEs under non(local) Lipschitz conditions. Fang et al. [4] proved that Stratonovich equation defines a global stochastic homeomorphism flow if the coefficients are just locally Lipschitz and Lipschitz coefficients with mild growth. Chen and Li [1] studied Sobolev regularity of Eq. (1.1) and strong completeness property when b and \(\sigma \) are Sobolev coefficients.
When \(\sigma =I\) and b is bounded and measurable, Veretennikov [19] first proved existence and uniqueness of the strong solution. When \(\sigma =I\) and b satisfy
Krylov and Röckner [13] used the technique of PDEs to prove the existence and uniqueness of the strong solution. The similar result in time-homogeneous case was obtained by Zhang and Zhao [26], who dropped the assumption \(\int ^t_0\left| b(X_s)\right| ^2\,ds<\infty ,\; \mathrm{a.s.}\). Fedrizzi and Flandoli [5] proved the existence of a stochastic flow of \(\alpha \)-Hölder homeomorphisms for solutions of SDEs as well as weak differentiability of solutions of SDEs under condition (1.2). Zhang [24, 25] extended the results of Krylov and Röckner [13] to the case of multiplicative noises. This extension allowed for the establishment of the well-posedness of solutions and the verification of weak differentiability in solutions. Additionally, it was proven that the solutions form a stochastic flow of homeomorphisms in \({\mathbb {R}}^d\). Key tools employed in this research included Krylov’s estimate and Zvonkin’s transformation. In [21], a characterization for Sobolev differentiability of random field was established. With the characterization, the weak differentiability of solutions was proved under local Sobolev integrability and sup-linear growth assumptions. We refer the reader to [6, 7, 20, 21, 23,24,25, 27] and references therein for applications of Krylov’s estimate, Zvonkin’s transformation and the characterization for Sobolev differentiability of random field. More recently, the critical case, i.e., \(p=d\) in time-homogeneous case, \(\frac{2}{q}+\frac{d}{p}=1\) in time-inhomogeneous have been explored, see [9,10,11,12, 17, 18] and references therein.
In [4], Fang, Imkeller and Zhang obtained a global estimates by employing global decomposition of two-point motions and local estimates. In this paper, we will base on the decomposition, Krylov’s estimate, Khasminskii’s estimate, Zvonkin’s transformation and the characterization of Sobolev differentiability of random fields to obtain the well-posedness and the weak differentiability of solutions, the strong Feller property of associated semigroups and stochastic flow property of SDEs (1.1) under the following assumptions:
- \(\mathbf {(H^b)}\):
-
There exist two positive constants \(\beta \) and \(\tilde{\beta }\) such that for all \(R\ge 1\),
$$\begin{aligned} \left( \int _{B(R)} \left| b(x)\right| ^{p_1} \,dx\right) ^{\frac{1}{p_1}}\le \beta I_b(R)+\tilde{\beta }, \end{aligned}$$where \(B(R):=\{x\in {\mathbb {R}}^d; \left| x\right| \le R\}\) is a ball with center 0 and radius R, \(\left| \cdot \right| \) denote the Euclidean norm, \(p_1>d\) is a constant and \(I_b(R)=(\log R+1)^{{(p_1 -d)^2 }/{(2p^2_1})}\).
- \((\textbf{H}^\sigma _1)\):
-
There exists a constant \(\delta \in (0,1)\) such that for all \(x,\xi \in {\mathbb {R}}^d\),
$$\begin{aligned} \delta ^{\frac{1}{2}}\left| \xi \right| \le \left| \sigma ^\top (x)\xi \right| \le \delta ^{-\frac{1}{2}}\left| \xi \right| , \end{aligned}$$and there exists a constant \(\varpi \in (0,1) \) such that for all \(x,y\in {\mathbb {R}}^d\),
$$\begin{aligned} \left\| \sigma (x)-\sigma (y)\right\| \le \delta ^{-\frac{1}{2}}\left| x-y\right| ^\varpi . \end{aligned}$$Here, we denote \(\sigma ^\top \) the transpose of matrix \(\sigma \), \(\left\| \cdot \right\| \) the Hilbert–Schmidt norm.
- \((\textbf{H}_2^\sigma )\):
-
There exist two positive constants \(\beta \) and \(\tilde{\beta }\) (same with \(\mathbf {(H^b)}\)) such that for all \(R\ge 1\),
$$\begin{aligned} \left( \int _{B(R)}\left\| \nabla \sigma \right\| ^{p_1}\,dx\right) ^{\frac{1}{p_1}}\le \beta I_\sigma (R)+\tilde{\beta }, \end{aligned}$$where \(\nabla \sigma :=[\nabla \sigma ^1,\ldots ,\nabla \sigma ^m]\) and \(I_\sigma (R)=(\log ({R}/{3})+1)^{{(p_1 -d)^2 }/{(2p^2_1})}\).
Our main results are given as the following theorem:
Theorem 1.1
Under the conditions \(\mathbf {(H^b)}\), \(\mathbf {(H^\sigma _1)}\) and \(\mathbf {(H^\sigma _2)}\), there exists a unique global strong solution to (1.1). Moreover, we have the following conclusions:
-
(A)
For all \(t\in [0,T]\) and almost all \(\omega \), the mapping \(x\mapsto X_t(\omega ,x)\) is Sobolev differentiable and for any \(p\ge 2\), there exist constants \(\textbf{C},n>0\) such that for Lebesgue almost all \(x\in {\mathbb {R}}^d\),
$$\begin{aligned} {\mathbb {E}}\left[ \sup _{t\in [0,T]} \left\| \nabla X_t(x)\right\| ^p \right] \le \textbf{C}(1+\left| x\right| ^n), \end{aligned}$$where \(\nabla \) denotes the gradient in the distributional sense.
-
(B)
For any \(t\in [0,T]\) and any bounded measurable function f on \({\mathbb {R}}^d\),
$$\begin{aligned} x\mapsto {\mathbb {E}}[f(X_t(x))]\;\text {is continuous}, \end{aligned}$$i.e., the semigroup \(P_t f(x):= {\mathbb {E}}[f(X_t(x))]\) is strong Feller.
-
(C)
For all \(t\in [0,T]\), \(x\in {\mathbb {R}}^d\) and almost all \(\omega \), the mapping \((t,x)\mapsto X_{t}(\omega ,x)\) is continuous on \([0,T]\times {\mathbb {R}}^d\) and for almost all \(\omega \), \(x\mapsto X_t(\omega ,x)\) is one-to-one on \({\mathbb {R}}^d\).
These results will be proved in Sect. 6.
We would like to compare the work in [21, 24, 26] with the present paper and explain the contributions made in this paper. Following the proof of [26], we generalized [26, Theorem 3.1] to multiplicative noises (cf. Theorem 6.1). In the time-inhomogeneous case, Xie and Zhang [21] proved the weak differentiability of SDEs and the strong Feller property of the associated diffusion semigroup under local Sobolev integrability and sup-linear growth assumptions. In the present paper, we removed the sup-linear growth condition (H2) in [21] by replacing the local Sobolev integrability (H1) in [21] with stronger assumptions \(\mathbf {(H^b)}\), \(\mathbf {(H^\sigma _1)}\) and \((\mathbf {H^\sigma _2})\), proved the weak differentiability of SDEs and the strong Feller property of the associated diffusion semigroup in the time-homogeneous case. In the time-inhomogeneous case, Zhang [24] proved the solution of SDEs forms a stochastic flow of homeomorphisms under conditions:
In the time-homogeneous case, the conditions will be
Our main result Theorem 1.1(C) strengthens the one-to-one property of stochastic flow in [24, Theorem 1.1] by improving the conditions (1.3) with mild growth conditions \((\textbf{H}^b)\) and \((\textbf{H}^\sigma _2)\).
For the proof of Theorem 1.1, there are two main difficulties. The one is finer estimates depend on R is necessary for us to obtain the order of growth in \(\mathbf {(H^b)}\) and \(\mathbf {(H^\sigma _2)}\) by the decomposition of global two-point motions. By our knowledge, all existing results about Krylov’s estimate and Khasminskii’s estimate such as [21, 24,25,26] do not obviously depend on radius R.
Another difficulty is that we need an appropriate truncation for \(\sigma \) due to SDEs (1.1) with multiplicative noises. If we directly truncate \(\sigma \) by characteristic function \(\mathbbm {1}_{\left| x\right| \le R}\), then the truncated \(\sigma \) will be degenerate. Chen and Li [1] provides a truncation method which can guarantee truncated \(\sigma \) is not degenerate, but it seems difficult to estimate the gradient of truncated \(\sigma \) by \((\textbf{H}_2^\sigma )\).
We also give some remarks related to the proof of our main results and conditions posed in it.
-
In Theorem 1.1, we just consider the time-homogeneous case, but by carefully tracking the proof of Theorem 1.1, our idea still work for time-inhomogeneous case.
-
If the condition \((\textbf{H}^\sigma _1)\) of Theorem 1.1 is replaced by
\((\textbf{H}^\sigma _1)_{\textrm{loc}}\) A constant \(\delta _R\in (0,1)\) depends on R such that for all \(x\in B(R),\xi \in {\mathbb {R}}^d\),
$$\begin{aligned} \delta ^{\frac{1}{2}}_R\left| \xi \right| \le \left| \sigma ^\top (x)\xi \right| \le \delta ^{-\frac{1}{2}}_R\left| \xi \right| , \end{aligned}$$and there exist two constants \(L>0\) and \(\varpi \in (0,1) \) such that for all \(x,y\in {\mathbb {R}}^d\),
$$\begin{aligned} \left\| \sigma (x)-\sigma (y)\right\| \le L\left| x-y\right| ^\varpi , \end{aligned}$$where the growth of \(\delta ^{-1}_R\) is mild about R. The techniques in the proof of Theorem 1.1 still can be used. Indeed, if b and \(\sigma \) satisfy \(\left\| \left| b\right| \cdot \mathbbm {1}_{B(R)}\right\| _{p_1}\le O(\tilde{I}_b(R))\), \(\left\| \left\| \nabla \sigma \right\| \cdot \mathbbm {1}_{B(R)}\right\| _{p_1}\le O(\tilde{I}_b(R/3))\) and the assumption \((\textbf{H}^\sigma _1)_{loc}\) holds true, then the following assumptions:
\((\textbf{H}^{\sigma ^R}_1)_{\textrm{loc}}\) A positive constant \(\tilde{\delta }_R^{-{1}/{2}}=\textbf{C}(d,L)\cdot (\delta _R^{-{1}/{2}})>0\) depends on R such that for all \(x,\xi \in {\mathbb {R}}^d\),
$$\begin{aligned} \tilde{\delta }_R^{\frac{1}{2}}\left| \xi \right| \le \left| (\sigma ^R)^\top (x)\xi \right| \le \tilde{\delta }_R^{-\frac{1}{2}}\left| \xi \right| , \end{aligned}$$and for all \(x,y\in {\mathbb {R}}^d\),
$$\begin{aligned} \left\| \sigma ^R(x)-\sigma ^R(y)\right\| \le \tilde{\delta }^{-\frac{1}{2}}_R\left| x-y\right| ^\varpi . \end{aligned}$$\((\textbf{H}_2^{\sigma ^R})_{\textrm{loc}}\) There exist constants \(\textbf{C}(d,L)\) such that for all \(R\ge 1\),
$$\begin{aligned} \left( \int _{{\mathbb {R}}^d} \left\| \nabla \sigma ^R\right\| ^{p_1}\,dx\right) ^\frac{1}{p_1} \le \textbf{C}(d,L)\cdot \tilde{\delta }^{-\frac{1}{2}}_{3R}+O(\tilde{I}_b(R)), \end{aligned}$$hold true, where \(O(\tilde{I}_b(R))\) means there exist two constants \(C>0\) and \(R_0\) such that \(O(\tilde{I}_b(R))\le C\tilde{I}_b(R)\; \,\forall \,R\ge R_0\). On the other hand, by going through carefully the proof of Theorem 4.1 we can find two continuous increasing functions \(G_1:{\mathbb {R}}_{+}\rightarrow {\mathbb {R}}_{+}\) and \(G_2:{\mathbb {R}}_{+}\rightarrow {\mathbb {R}}_{+}\) such that \(C_1\) and \(C_2\) in Theorem 4.1 are equal to \(G_1(\tilde{\delta }_R^{-\frac{1}{2}})\) and \(G_2(\tilde{\delta }_R^{-\frac{1}{2}})\). The \(C_0(\tilde{\delta }_R^{-\frac{1}{2}})\) (the key to obtain \(G_1\)) in the proof of Theorem 4.1 can be obtained by changing of coordinates to reduce \(L^{\sigma ^R(x_0)}\) to \(\Delta \). The \(C_j(\tilde{\delta }_R^{-\frac{1}{2}})\) and \(k_j(\tilde{\delta }_R^{-\frac{1}{2}})\) in (7.6) (the key to obtain \(G_2\)) can be obtained by going through carefully the proof of Page 356 to Page 378 in [15]. Finally, we can take \(\tilde{\delta }^{-\frac{1}{2}}_{3R}\) satisfy \(\textbf{C}(d,L)\cdot \tilde{\delta }^{-\frac{1}{2}}_{3R}\le \textbf{C}\cdot \tilde{I}_b(R)\) and let \(\lambda ^R=(2G_2(\tilde{I}_b(R))\tilde{I}_b(R))^{2p_1/(p_1-d)}\) in Lemma 4.4. Tracking the proof in Theorem 1.1, we can find a concrete \(\tilde{I}_b(R)\) with enough mild growth such that the results in Theorem 1.1 still hold true.
-
In [24], the well-known Bismut–Elworthy–Li’s formula (cf. [2]) was proved. But even if \(\sigma (x)\equiv I_{d\times d}\) (in this case, we do not need to truncate \(\sigma \)), it seems difficult to prove the Bismut–Elworthy–Li’s formula for the solution of SDEs (1.1) under assumptions of this paper due to \({\mathbb {E}}[\left\| \nabla X^R_t(x)\right\| ^2]\le C(R)\) and \(C(R)\rightarrow \infty \) when \(R\rightarrow \infty \).
-
The local estimates (6.23), (6.25) and (6.24) are seemingly not enough to obtain the onto property of the map \(x\mapsto X_t(\omega ,x)\). In fact, if we define
$$\begin{aligned} \mathscr {X}_t(x):={\left\{ \begin{array}{ll} \left( 1+\left| X_t\left( \frac{x}{\left| x\right| ^2}\right) \right| \right) ^{-1},&{}\quad x\ne 0,\\ 0,&{}\quad x=0. \end{array}\right. } \end{aligned}$$We just can obtain for any \(k\in {\mathbb {N}}\), \(x,y\in \{ x: \frac{1}{k}\le \left| x\right| \le 1 \}\cup \{{0}\}\),
$$\begin{aligned} {\mathbb {E}}\left[ \left| \mathscr {X}_t(x)-\mathscr {X}_t(y)\right| ^p \right] \le \textbf{C}(k)\left| x-y\right| ^p. \end{aligned}$$Notice that, the domain \(\{ x: \frac{1}{k}\le \left| x\right| \le 1 \}\cup \{{0}\}\) is not connected, we cannot obtain \(x\mapsto \mathscr {X}_t(x)\) exist a continuous version on \(\{x:\left| x\right| \le 1 \}\).
-
For the critical case, i.e., \(p_1=d\), our idea will not work since Zvonkin’s transformation cannot be used. On the other hand, \(\mathbf {(H^b)}\) and \(\mathbf {(H^\sigma _2)}\) seemingly indicate that the order of growth will be degenerated in the critical case.
The rest of this paper is organized as follows: In Sect. 2, we will present some preliminary knowledge. In Sect. 3, we devote to construct the cutoff functions to truncate SDEs (1.1) and verify assumptions. In Sect. 4, we provide a proof of Krylov’s estimate and Khasminskii’s estimate. In Sect. 5, we use Zvonkin’s transformation to estimate truncated SDEs (3.1). In Sect. 6, we complete the proof of the main Theorem 1.1. Finally, we give a detailed proof of Theorem 4.1 in Appendix.
2 Preliminary
In this section, we introduce some notations, function spaces and well-known theorems which will be used in this paper.
We use \(:=\) as a way of definition. Let \({\mathbb {N}} \) be the collection of all positive integer. For any \(a,b\in {\mathbb {R}}\), set \(a\wedge b:=\min \{a,b\}\) and \(a\vee b:=\max \{a,b\}\). We use \(a\lesssim b\) to denote there is a constant C such that \(a\le Cb\), use \(a\asymp b\) to denote \(a\lesssim b\) and \(b\lesssim a\). For functions f and g, we use \(f*g\) to denote the convolution of f and g.
Let \(L^p({\mathbb {R}}^d)\) be \(L^p\)-space on \({\mathbb {R}}^d\) with norm
Let \(W^{m,p}({\mathbb {R}}^d)\) be Sobolev space on \({\mathbb {R}}^d\) with norm
where \(\nabla ^i\) denotes the i-order gradient operator.
For \(0\le \alpha \in {\mathbb {R}}\) and \(p\in [1,+\infty )\), the Bessel potential space \(H^{\alpha ,p}({\mathbb {R}}^d)\) is defined by
with norm
Let \(C^{\alpha }({\mathbb {R}}^d)\) be Hölder space on \({\mathbb {R}}^d\) with norm
where \(\left\lfloor \alpha \right\rfloor \) denotes the integer part of \(\alpha \). Let \(C^\infty _0({\mathbb {R}}^d)\) be a collection of all smooth function with compact support in \({\mathbb {R}}^d\).
For \(\alpha \in (0,2)\) and \(p\in (1,+\infty )\), we have
where \(\Delta ^{\frac{\alpha }{2}}:=-(-\Delta )^{\frac{\alpha }{2}}\) is the fractional Laplacian.
Let f be a locally integrable function on \({\mathbb {R}}^d\), \({\mathcal {M}}\) be the Hardy–Littlewood maximal operator defined by
here, with a bit of abuse of notations, \(\left| B(R)\right| \) denotes the volume of ball B(R).
Theorem 2.1
(Sobolev embedding theorem) If \(k>l>0,p<d\) and \(1\le p<q<\infty \) satisfy \(k-\frac{d}{p}=l-\frac{d}{q}\), then
If \(\gamma \ge 0\) and \(\gamma <\alpha -\frac{d}{p}\), then
Theorem 2.2
(Hadamard’s theorem) If a function \(\varphi :{\mathbb {R}}^d\rightarrow {\mathbb {R}}^d\) is a k-order smooth function (\(k\ge 1\)) and satisfy:
-
(i)
\(\lim _{\left| x\right| \rightarrow \infty }\left| \varphi (x)\right| =\infty \);
-
(ii)
for all \(x\in {\mathbb {R}}^d\), the Jacobian matrix \(\nabla \varphi (x)\) is an isomorphism of \({\mathbb {R}}^d\);
Then \(\varphi \) is a \(C^k\)-diffeomorphism of \({\mathbb {R}}^d\).
Theorem 2.3
-
(i)
There exists a constant \(C_d\) such that for all \(\varphi \in C^\infty ({\mathbb {R}}^d)\) and \(x,y\in {\mathbb {R}}^d\),
$$\begin{aligned} \left| \varphi (x)-\varphi (y)\right| \le C_d\cdot \left| x-y\right| \cdot \left( {\mathcal {M}}\left| \nabla \varphi \right| (x)+{\mathcal {M}}\left| \nabla \varphi \right| (y) \right) . \end{aligned}$$ -
(ii)
For any \(p>1\), there exists a constant \(C_{d,p}\) such that for all \(\varphi \in L^p({\mathbb {R}}^d)\),
$$\begin{aligned} \left( \int _{{\mathbb {R}}^d} \big ( {\mathcal {M}}\varphi (x) \big )^p\,dx \right) ^{\frac{1}{p}}\le C_{d,p} \left( \int _{{\mathbb {R}}^d} \left| \varphi (x)\right| ^p\,dx \right) ^{\frac{1}{p}}. \end{aligned}$$
3 Truncated SDEs
In this section, we will construct some precise cutoff functions to truncate SDEs (1.1) and verify that the truncated SDEs
satisfy the following assumptions:
- \(\mathbf {(H^{b^R})}\):
-
There exist two positive constants \(\beta \) and \(\tilde{\beta }\) such that for all \(R \ge 1\),
$$\begin{aligned} \left( \int _{{\mathbb {R}}^d} \left| b^R(x)\right| ^{p_1} \,dx\right) ^{\frac{1}{p_1}}\le \beta I_b(R)+\tilde{\beta }, \end{aligned}$$where \(p_1>d\) is a constant.
- \((\textbf{H}^{\sigma ^R}_1)\):
-
There exists a positive constant \(\tilde{\delta }\in (0,1)\) such that for all \(x,\xi \in {\mathbb {R}}^d\),
$$\begin{aligned} \tilde{\delta }^{\frac{1}{2}}\left| \xi \right| \le \left| (\sigma ^R)^\top (x)\xi \right| \le \tilde{\delta }^{-\frac{1}{2}}\left| \xi \right| , \end{aligned}$$and for all \(x,y\in {\mathbb {R}}^d\),
$$\begin{aligned} \left\| \sigma ^R(x)-\sigma ^R(y)\right\| \le \tilde{\delta }^{-\frac{1}{2}}\left| x-y\right| ^\varpi , \end{aligned}$$(3.2)where \(\tilde{\delta }\) is a constant only depend on \(\delta \) and d.
- \((\textbf{H}_2^{\sigma ^R})\):
-
There exist two positive constants \(\beta \) and \(\tilde{\beta }\) such that for all \(R\ge 1\),
$$\begin{aligned} \left( \int _{{\mathbb {R}}^d} \left\| \nabla \sigma ^R\right\| ^{p_1}\,dx\right) ^\frac{1}{p_1}\le \Big (C(d,\delta ,p_1) +(4\beta I_\sigma (3R)+4\tilde{\beta })\Big ), \end{aligned}$$where \(p_1>d\) is a constant and \(C(d,\delta ,p_1)\) is a constant only depend on d, \(\delta \) and \(p_1\).
Let \(\hspace{0.83328pt}\overline{\hspace{-0.83328pt}W\hspace{-0.83328pt}}\hspace{0.83328pt}\) be a d-dimensional standard Wiener process, independent of W and let
We can verify that \(\widetilde{W}\) is a \((d+m)\)-dimensional standard Wiener process. In SDEs (3.1), the coefficients \(b^R\) and \(\sigma ^R\) are defined by
where \(\bar{\sigma }\) is a matrix defined by
The cutoff function \(h_R\) is defined by
It is easy to verify \(h_R\) satisfy
Similarly, we can construct a cutoff function \(\rho _R\) satisfy
Clearly, \(\mathbf {(H^{b^R})}\) hold by the definition of \(b^R\). Notice that
by the definitions of \(\rho _R\), \(h_R\), \(\bar{\sigma }\) and assumption \((\textbf{H}^\sigma _1)\), we have
On the other hand, it is easy to see for all \(x,y\in B(2R)\backslash B(R)\),
and for all \(x,y\notin B(2R)\backslash B(R)\), we have \(\left| h_R(x)-h_R(y)\right| \le \left| x-y\right| ^\varpi ,\ \forall \,R\ge 1\). Hence, for all \(x,y\in {\mathbb {R}}^d\), we obtain
Similarly, we can obtain
Therefore, we have
where the last inequality is due to (3.4) and (3.5). Combining (3.3) with (3.6), we verified the \((\textbf{H}^{\sigma ^R}_1)\).
By the definition \(\sigma ^R=[\rho _R \sigma ,h_R\bar{\sigma }]\) and direct computation, we obtain
Note that \(\left| \nabla \rho _R\right| \le \frac{2}{R}\) in \(B(3R)\backslash B(2R)\), \(\left| \nabla h_R\right| \le \frac{2}{R}\) in \(B(2R)\backslash B(R)\) and \((\textbf{H}_2^\sigma )\), there exists a constant \(C(d,\delta ,p_1)\) only depend on d, \(\delta \) and \(p_1\) such that for all \(R\ge 1\),
Together, \(J_1\), \(J_2\) and \(J_3\) imply \((\textbf{H}_2^{\sigma ^R})\).
4 Krylov’s Estimate and Khasminskii’s Estimate
In this section, we shall prove Krylov’s estimate and Khasminskii’s estimate. We need the following result about elliptic PDEs (4.1).
Theorem 4.1
Suppose \(\sigma ^R\) satisfies \((\textbf{H}_1^{\sigma ^R})\), \(p\in (1,\infty )\), then for any \(f\in L^p({\mathbb {R}}^d)\), there exists a unique \(u\in W^{2,p}({\mathbb {R}}^d)\) such that
where
and \(\lambda >C\) \((C=C(d,\varpi ,\tilde{\delta },p)\ge 2\) is a constant ). Furthermore, for a \(C_1=C_1(d,\varpi ,\tilde{\delta },p)>0\),
Moreover, for any \(\alpha \in [0,2)\) and \(p'\in [1,\infty ]\) with \(\frac{d}{p}<2-\alpha +\frac{d}{p'}\),
where \(C_1(d,\varpi ,\tilde{\delta },p)\) and \(C_2(d,\varpi ,\tilde{\delta },p,\alpha ,p')>0\) are both independent of \(\lambda \).
We believe that Theorem 4.1 is standard although we do not find them in any reference. In [26], authors proved Theorem 4.1 hold true when \(\sigma ^R\equiv I\). For convenience of the reader, we combine [26] with [25] to give a detailed proof in Appendix.
In order to prove Krylov’s estimate and Khasminskii’s estimate, we need to solve the following elliptic equation:
where \(f\in L^p({\mathbb {R}}^d)\) and \(\lambda ^{b^R}>1\) is a constant depend on \(C_2,d,p_1\) and \(\left\| b^R\right\| _{p_1}\).
Lemma 4.2
If \(\left\| b^R\right\| _{p_1}<\infty \) and \((\textbf{H}_1^{\sigma ^R})\) hold, then for any \(p\in (\frac{d}{2}\vee 1,p_1]\), we can find a constant
such that for any \(f\in L^p({\mathbb {R}}^d)\), there exists a unique solution \(u^R\in W^{2,p}({\mathbb {R}}^d)\) to Eq. (4.3) and
where \(C_1\) and \(C_2\) are two constants in Theorem 4.1, \(\alpha \in [0,2)\) and \(p'\in [1,\infty ]\) with \((2-\alpha + \frac{d}{p'}-\frac{d}{p})>0\).
Proof
By Theorem 4.1, for any \(\tilde{f}\in L^p({\mathbb {R}}^d)\), we have
where \(\lambda>C\; (C>2)\), \((2-\alpha + \frac{d}{p'}-\frac{d}{p})>0\) and \(C_1, C_2\) do not depend on \(\lambda \).
Since \(\lambda ^{b^R}=(2C_2\left\| b^R\right\| _{p_1})^{2p_1/(p_1-d)}\), it is easy to see for any \(\lambda \ge \lambda ^{b^R}\),
Let \(u_0=0\) and for \(n\in {\mathbb {N}}\) define
By (4.4) and replacing \((\Delta -\lambda )^{-1}\) with \(( L^{\sigma ^R(x)} -\lambda )^{-1}\) in the proof of [26, Theorem 3.3 (ii)], we completed the proof. \(\square \)
Now, we provide the main result of this section.
Theorem 4.3
If \(\left\| b^R\right\| _{p_1}<\infty \) and \(\mathbf {(H^{\sigma ^R}_1)}\) hold and \(\{X_s^R\}_{s\in [0,T]}\) is a solution of SDE (3.1), then for any \(0\le t_0<t_1\le T\), \(f\in L^p({\mathbb {R}}^d)\) \((p>\frac{d}{2}\vee 1)\), we have
where \(C_2\) is the constant in Theorem 4.1, \(\lambda ^{b^R}=(2C_2\left\| b^R\right\| _{p_1})^{2p_1/(p_1-d)}\). Moreover, for any \(a>0\) we have
Proof
The proof is divided into three steps.
Step (i) We replace \((\Delta -\lambda )^{-1}\) with \(( L^{\sigma ^R(x)} -\lambda )^{-1}\) in the proof of Theorem 3.4 of Zhang and Zhao [26]. Notice that
is enough to ensure \(C_2\lambda ^{(d/p_1-1)/2}\left\| b^R\right\| _{p_1}\le \frac{1}{2}\) for all \(\lambda \ge \lambda ^{b^R}\). Repeating the proof of Theorem 3.4 (ii) of Zhang and Zhao [26], for all \(\tilde{\lambda }\ge \lambda ^{b^R}\), we obtain
Let \(\kappa =T\lambda ^{b^R}\) and \(\tilde{\lambda }=\kappa (t_1-t_0)^{-1}\). Due to \(0\le t_0<t_1\le T\), we have \(\tilde{\lambda }\ge \lambda ^{b^R}\). Taking \(\tilde{\lambda }=\kappa (t_1-t_0)^{-1}\) into (4.6), we proved the Krylov’s estimate (4.5).
Step (ii) Taking \(0\le t_0< t_1<\infty \) satisfy
If \(t_1-t_0\le T\) in (4.7), by the Corollary 3.5 in Zhang and Zhao [26], we have
Since \(e^x=\sum ^\infty _{n=0} \frac{1}{n!} x^n\), we have
Step (iii) Finally, by virtual of the estimate (4.8), we obtain
where \(M=\frac{T}{t_1-t_0}\) and \(0\le t_0<t_1<\cdots <t_{\left\lfloor M\right\rfloor +1}=T\) satisfies \(t_0-0\le t_1-t_0\), \(t_i-t_{i-1}=t_1-t_0\; (i=1,\ldots ,\left\lfloor M\right\rfloor +1)\).
If \(t_1-t_0>T\) in (4.7), it is obvious that
by a similar argument, we have
We completed the proof. \(\square \)
In particular, in the proofs of Lemma 4.4 and Theorem 4.5, replacing \(\lambda ^{b^R}\) with \(\lambda ^R=\big (4C^2_2(\beta I_b(R)+\tilde{\beta })^2\big )^{p_1/(p_1-d)}\), we can obtain the following lemma and theorem:
Lemma 4.4
If \(\mathbf {(H^{b^R})}\) and \((\textbf{H}_1^{\sigma ^R})\) hold, then for any \(p\in (\frac{d}{2}\vee 1,p_1]\), we can find a constant
such that for any \(f\in L^p({\mathbb {R}}^d)\), there exists a unique solution \(u^R\in W^{2,p}({\mathbb {R}}^d)\) to Eq. (4.3) and
where \(C_1\) and \(C_2\) are two constants in Theorem 4.1, \(\alpha \in [0,2)\) and \(p'\in [1,\infty ]\) with \((2-\alpha + \frac{d}{p'}-\frac{d}{p})>0\).
Theorem 4.5
If \((\mathbf {H^{b^R}})\) and \(\mathbf {(H^{\sigma ^R}_1)}\) hold and \(\{X_s^R\}_{s\in [0,T]}\) is a solution of SDE (3.1), then for any \(0\le t_0<t_1\le T\), \(f\in L^p({\mathbb {R}}^d)\) \((p>\frac{d}{2}\vee 1)\), we have
where \(C_2\) is the constant in Theorem 4.1, \(\lambda ^R=\big (4C^2_2(\beta I_b(R)+\tilde{\beta })^2\big )^{p_1/(p_1-d)}\). Moreover, for any \(a>0\) we have
Corollary 4.6
(Generalized Itô’s formula) If \((\mathbf {H^{b^R}})\) and \(\mathbf {(H^{\sigma ^R}_1)}\) hold and \(\{X_s^R\}_{s\in [0,T]}\) is a solution of SDE (3.1), then for any \(f\in W^{2,p}({\mathbb {R}}^d)\) with \(p>\frac{d}{2}\vee 1\), we have
Proof
We just need to consider the case \(p\in (d,p_1]\) since \(W^{2,p}\hookrightarrow W^{2,p_1}\) when \(p>p_1\).
By Hölder’s inequality and Sobolev’s embedding theorem, we have
Let \(\varphi \) be a nonnegative smooth function with compact support in the unit ball of \({\mathbb {R}}^d\) and \(\int _{{\mathbb {R}}^d} \varphi (x)\,dx=1\). Set \(\varphi _n(x):=n^d\varphi (nx)\), \(f_n:=f*\varphi _n\) and applying Itô formula to \(f_n\). By (4.13), we have
Let \(\bar{p}=\frac{dp}{2(d-p)}\), we have
where the second inequality is due to Krylov’s estimate (4.10) and the last inequality is due to Sobolev’s embedding theorem. Together, (4.14) and (4.15) imply (4.12). \(\square \)
5 Zvonkin’s Transformation
Let \(u^R\) solve the following PDE
By Lemma 4.4, we have
Let \(\lambda ^R_H=\gamma \lambda ^R\) and \(\gamma ^{(\frac{d}{2p_1}-\frac{1}{2})}=\frac{1}{2}\), it is easy to check
Define
then
By (5.2), for all \(\lambda \ge \lambda ^R_H\), we have
By the definition of \(\Phi _R(x)\) and (5.3), we have
Therefore, by Theorem 2.2, we obtain \(\Phi _R:{\mathbb {R}}^d\rightarrow {\mathbb {R}}^d\) is a \(C^1\)-diffeomorphism and
Theorem 5.1
Let \(Y^R_t:=\Phi _R(X_t^R)\), then \(X^R_t\) solve equation (3.1) if and only if \(Y^R_t\) solves
where \(\tilde{b}^R(y):=\lambda u^R\circ \Phi _R^{-1}(y)\) and \(\tilde{\sigma }^R(y):={(\nabla \Phi _R(\cdot )\sigma ^R(\cdot ))\circ \Phi _R^{-1}(y)}\).
Proof
Applying Itô formula (4.12) to \(\Phi _R(X^R_t)\), we obtain
Noticing that \(Y^R_t=\Phi _R(X_t^R)\), we obtain \(Y^R_t\) solves (5.5). Similarly, applying Itô formula (4.12) to \(\Phi ^{-1}_R(Y^R_t)\), we completed the proof. \(\square \)
6 The Proof of Theorem 1.1
Proof
In this section, the letters \(\textbf{C}\) and \(\mathbf {\widetilde{C}}\) will denote some unimportant constant whose value is independent of R and may change in different places. Whose dependence on parameters can be traced from the context. We also use \(\textbf{C}(T)\) and \(\textbf{C}(N)\) to emphasize the constant \(\textbf{C}\) depend on T and N, respectively.
Firstly, we prove SDE (3.1) exists a unique strong solution.
Theorem 6.1
Under \((\mathbf {H^{b^R}_1})\), \((\mathbf {H^{\sigma ^R}_1})\) and \((\mathbf {H^{\sigma ^R}_2})\), for all \(x\in {\mathbb {R}}^d\), the SDE (3.1) exists a unique strong solution.
Proof
By Theorem 5.1, we only need to prove SDE (5.5) exists a unique strong solution. By the definition of \(\tilde{b}^R\), \(\tilde{\sigma }^R\) and Lemma 4.4, for all \(\lambda \ge \lambda ^R_H\), we have
Note that \(\tilde{b}^R\) and \(\tilde{\sigma }^R\) are both continuous and bounded. By Yamada–Watanabe’s theorem, we only need to show the pathwise uniqueness. Performing the same procedure in [26, Theorem 3.1], we completed the proof. \(\square \)
Lemma 6.2
Under \((\mathbf {H^{b^R}})\), \((\mathbf {H^{\sigma ^R}_1})\) and \((\mathbf {H^{\sigma ^R}_2})\), let \(\{X^R_s(x)\}_{s\in [0,T]}\) and \(\{X^R_s(y)\}_{s\in [0,T]}\) be two solutions of SDE (3.1) with initial conditions \(X^R_0(x)=x\) and \(X^R_0(y)=y\), respectively, then for any \(\alpha \in {\mathbb {R}}\), we have
and for all \(p\ge 2\),
where \(\widetilde{\textbf{C}}\) is independent of \(\beta \), \(\tilde{\beta }\) and R.
Proof
For \(\Phi _R(x)\ne \Phi _R(y)\), take \( 0<\varepsilon <\left| \Phi _R(x)-\Phi _R(y)\right| \) and set
For convenience, we define \(Z^R_t:= Y^R_t(\Phi _R(x)) -Y^R_t(\Phi _R(y))\) where \(\{Y^R_s(\Phi _R(x))\}_{s\in [0,T]}\) and \(\{Y^R_s(\Phi _R(y))\}_{s\in [0,T]}\) are the solutions of SDE (5.5) with initial conditions \(Y^R_0(\Phi _R(x))=\Phi _R(x)\) and \(Y^R_0(\Phi _R(y))=\Phi _R(y)\), respectively.
By Itô formula, we have
Set
and
By (6.6), we have
By the Doléans–Dade’s exponential, we obtain
By the definitions of \(\tilde{b}^R\) and \(\tilde{\sigma }^R\) in Theorem 5.1 and Lemma 2.3(i), it is easy to see
and
Firstly, we shall prove that for any \(\mu >0\),
and
Combine the definitions of (6.8), (6.7) with (6.10), (6.11), we only need to estimate
and
Take \(f={\mathcal {M}}\left| \nabla ^2u^R\right| ^2\) and \(p=\frac{p_1}{2}\) in (4.11), then we have
We can take \(T\lambda ^R>1\), then \({(T\lambda ^R)}^{\frac{d}{p_1}-1}<{(T\lambda ^R)}^{\frac{d}{p_1}}\). By Theorem 2.3 (ii) and (5.1), we have
Therefore,
where the second inequality is due to \((\mathbf {H^{b^R}})\) and (4.9).
Similarly, taking \(f={\mathcal {M}}\left\| \nabla \sigma ^R\right\| ^2\) and \(p=\frac{p_1}{2}\) in (4.11), we obtain
Taking \(f=\lambda ^R_H \cdot {\mathcal {M}}\left| \nabla u^R\right| \) and \(p=\infty \), we obtain
By Novikov’s criterion, the process
is a continuous exponential martingale. By Hölder’s inequality, we obtain
Let \(\varepsilon \downarrow 0\), we have
Moreover, if \(\alpha >0\), then
Notice that
if \(\alpha <0\), then
Together, (6.12) and (6.13) imply (6.2).
Notice that
we have
Therefore,
By \(X^R_s(x)=\Phi _R^{-1}(Y^R_s(\Phi _R(x)))\), (5.4) and (6.14), we have
Combining the inequality
we can obtain
where \(C(\alpha )=8^\alpha \vee 8^{-\alpha }\). Therefore, we just need to consider the estimate of \({\mathbb {E}}\left[ \left( 1+ \left| Y^R_s(\Phi _R(x))\right| ^2\right) ^\alpha \right] \).
Applying Itô formula to \(\left( 1+\left| Y^R_s(\Phi _R(x))\right| ^2\right) ^\alpha \), we have
By (6.1) and (6.15), we obtain
Using Gronwall’s inequality, we proved (6.3).
It is easy to see
where the last inequality is due to \(\left\| \nabla \Phi _R^{-1}\right\| _{\infty }\le 2\) and \(\Phi _R^{-1}(0)\le 1/2\). So, we only need to estimate \({\mathbb {E}}\left[ \sup _{0\le s\le t} \left| Y^R_s(\Phi _R(x))\right| ^p \right] ,\ p\ge 2\).
By Eq. (5.5), we have
It is not hard to see
So, we obtained (6.4).
Notice that
we only need to estimate \({\mathbb {E}}[\sup _{0\le t\le T}\left| Z^R_t\right| ^p]\). By (6.9), we have
where
We proved (6.5). \(\square \)
Let \(D_t(x):=\sup _{0\le s\le t}\left| X_s(x)\right| \), \(\tau _R(x):=\inf \{t\ge 0, \left| X_t(x)\right| >R\}\) and similarly, let \(D^R_t(x):=\sup _{0\le s\le t}\left| X^R_s(x)\right| \), \(\tau ^R_R(x):=\inf \{ t\ge 0, \left| X^R_t(x)\right| >R \}\). It is easy to see
By the definitions of \(b^R\) and \(\sigma ^R\), it is not hard to obtain
For all \(x\in B(N)\), we have
where the second inequality is due to Markov’s inequality, the last inequality is due to Lemma 6.2. By the definition of \(\lambda ^R\) in (4.9), we can obtain \({(\lambda ^R)^n}/{R^n}\rightarrow 0\) when \(R\rightarrow \infty \). Hence, we have \(\tau _R\rightarrow \infty \) when \(R\rightarrow \infty \). On the other hand, by the definitions of \(b^R\) and \(\sigma ^R\), we observe that if \(D_t(x)<R\), then \(X_t(x)=X^R_t(x)\), i.e., \(X_{t}(x)=X^R_{t}(x)\) for all \(t<\tau _R\). By Theorem 6.1, SDE (3.1) exists a unique strong solution. We can define \(X_t(x)=X^R_t(x)\) for \(t<\tau _R\). It is clear that \(\{X_t(x)\}_{t\in [0,T]}\) is the unique strong solution of SDE (1.1).
By (6.4) and definition of \(\lambda ^R\), for all \(x\in B(N)\), we have
where the last inequality is due to (6.4) and the definition of \(\lambda ^R\).
For all \(x,y\in B(N)\), we consider the following estimate
where the last inequality we used the fact that we can find a constant \({C}(\widetilde{\textbf{C}},p_1,d,n(\beta ))\) such that for all \(\lambda ^R\ge {C}(\widetilde{\textbf{C}},p_1,d,n(\beta ))\),
In fact, if let \(\tilde{\beta }\) satisfy \((2C_2\tilde{\beta })^{2(1-\frac{d}{p_1})^{-1}}= {C}(\widetilde{\textbf{C}},p_1,d,n(\beta ))\), then for all \(R\ge 1\), \(\lambda ^R\) satisfy (6.18), where \(n(\beta )\) be decided by (6.19).
On the other hand, by the definitions of \(\lambda ^R\) and \(I_b(R)\), we have
Therefore, take n satisfy
we obtain
By Lemma 2.1 in [21], (6.16) and (6.20), we proved Theorem 1.1(A).
Following the proof of Zhang [24], it is not hard to prove for any bounded measurable function f and \(t\in [0,T]\),
For any \(x,y\in B(N)\), we have
Together, (6.22), (6.21) and \(\tau _R\rightarrow \infty \) when \(R\rightarrow \infty \) imply Theorem 1.1(B).
Lemma 6.3
Under \(\mathbf {(H^b)}\), \(\mathbf {(H^\sigma _1)}\) and \(\mathbf {(H^\sigma _2)}\), let \(\{X_t(x)\}_{t\in [0,T]}\) and \(\{X_t(y)\}_{t\in [0,T]}\) are two solutions of SDE (1.1) with initial conditions \(X_0(x)=x\) and \(X_0(y)=y\), respectively, then for all \(0\le t\le T\), \(\alpha \in {\mathbb {R}}\) and \(x,y\in B(N)\), we have
and for all \(p\ge 2\),
Proof
Set \(D_t(x):=\sup _{0\le s\le t}\left| X_t(x)\right| \) and \(D_t(y):=\sup _{0\le s\le t}\left| X_t(y)\right| \). It is easy to see if \(D_t(x)< R\) and \(D_t(y)< R\), then \( X_t(x) = X^R_t(x), X_t(y) = X_t^R(y). \) Moreover, by Lemma 6.2, similar to (6.17), for all \(t\in [0,T]\) and \(x,y\in B(N)\), we have
and
On the other hand, it is not hard to obtain
where the last inequality is due to
and
Moreover, for all \(t,s\in [0,T]\) and \(x\in B(N)\), we have
We completed the proof. \(\square \)
By Lemma 6.3, for all \(p\ge 2\), \(t,s\in [0,T]\) and \(x,y\in B(N)\), we have
By Kolmogorov’s lemma, we can obtain for any \(N\in {\mathbb {N}}\), there exists a \({\mathbb {P}}\)-null set \(\Xi _N \) such that for any \(\omega \notin \Xi _N\), \(X_{\cdot }(\omega ,\cdot ):[0,T]\times B(N)\rightarrow {\mathbb {R}}^d\) is continuous. If we set \(\Xi :=\cup _{N=1}^\infty \Xi _N\), then \({\mathbb {P}}(\Xi )=0\) and
Similar to the standard argument (cf. [14]), the proof for any \(t\in [0,T]\), almost all \(\omega \), the maps \(x\mapsto X_{t}(\omega ,x)\) are one-to-one due to (6.23) and (6.25). For the reader’s convenience, we give the details of one-to-one property.
For \(x\ne y \in {\mathbb {R}}^d\), set
then
By Hölder inequality, we have
Moreover, for all \(x,y,x',y'\in B(N)\) and \(\left| x-y\right| \wedge \left| x'-y'\right| >\varepsilon \), we obtain
Choose \(p>4(d+1)\), by Kolmogorov’s lemma, there exists a \({\mathbb {P}}\)-null set \(\Xi _{k,N}\) such that for all \(\omega \notin \Xi _{k,N}\), the mapping \((t,x,y)\mapsto \mathscr {R}(t,x,y)\) is continuous on
Set \(\Xi :=\cup ^\infty _{k,N=1}, \Xi _{k,N}\), then for any \(\omega \notin \Xi \), the mapping \((t,x,y)\mapsto \mathscr {R}(t,x,y)\) is continuous on
We proved one-to-one property. \(\square \)
Data availability
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
References
Chen, X., Li, X.-M.: Strong completeness for a class of stochastic differential equations with irregular coefficients. Electron. J. Probab. 19(91), 34 (2014)
Elworthy, K.D., Li, X.-M.: Formulae for the derivatives of heat semigroups. J. Funct. Anal. 125(1), 252–286 (1994)
Fang, S., Zhang, T.: A study of a class of stochastic differential equations with non-Lipschitzian coefficients. Probab. Theory Related Fields 132(3), 356–390 (2005)
Fang, S., Imkeller, P., Zhang, T.: Global flows for stochastic differential equations without global Lipschitz conditions. Ann. Probab. 35(1), 180–205 (2007)
Fedrizzi, E., Flandoli, F.: Hölder flow and differentiability for SDEs with nonregular drift. Stoch. Anal. Appl. 31(4), 708–736 (2013)
Gyöngy, I., Martínez, T.: On stochastic differential equations with locally unbounded drift. Czechoslov. Math. J. 51(4), 763–783 (2001)
Krylov, N.V.: Controlled Diffusion Processes. Applications of Mathematics, vol. 14. Springer, New York (1980). (Translated from the Russian by A. B. Aries)
Krylov, N.V.: Lectures on Elliptic and Parabolic Equations in Sobolev Spaces. Graduate Studies in Mathematics, vol. 96. American Mathematical Society, Providence (2008)
Krylov, N.V.: On stochastic equations with drift in \(L_d\). Ann. Probab. 49(5), 2371–2398 (2021)
Krylov, N.V.: On stochastic Itô processes with drift in \(L_ d\). Stoch. Process. Appl. 138, 1–25 (2021)
Krylov, N.V.: On strong solutions of Itô’s equations with \(\sigma \in W^1_d\) and \(b\in L_d\). Ann. Probab. 49(6), 3142–3167 (2021)
Krylov, N.V.: On diffusion processes with drift in \(L_d\). Probab. Theory Related Fields 179(1–2), 165–199 (2021)
Krylov, N.V., Röckner, M.: Strong solutions of stochastic equations with singular time dependent drift. Probab. Theory Related Fields 131(2), 154–196 (2005)
Kunita, H.: Stochastic Flows and Stochastic Differential Equations. Cambridge Studies in Advanced Mathematics, vol. 24. Cambridge University Press, Cambridge (1990)
Ladyzhenskaya, O.A., Solonnikov, V.A., Ural’tseva, N.N.: Linear and Quasilinear Equations of Parabolic Type. Translations of Mathematical Monographs, vol. 23. American Mathematical Society, Providence (1968). (Translated from the Russian by S. Smith)
Li, X.-M.: Strong \(p\)-completeness of stochastic differential equations and the existence of smooth flows on noncompact manifolds. Probab. Theory Related Fields 100(4), 485–511 (1994)
Röckner, M., Zhao, G.: SDEs with critical time dependent drifts: weak solutions. arXiv preprint arXiv:2012.04161 (2020)
Röckner, M., Zhao, G.: SDEs with critical time dependent drifts: strong solutions. arXiv preprint arXiv:2103.05803 (2021)
Veretennikov, A.Y.: On the strong solutions of stochastic differential equations. Theory Probab. Appl. 24(2), 354–366 (1979)
Wang, F.-Y., Zhang, X.: Degenerate SDE with Hölder-Dini drift and non-Lipschitz noise coefficient. SIAM J. Math. Anal. 48(3), 2189–2226 (2016)
Xie, L., Zhang, X.: Sobolev differentiable flows of SDEs with local Sobolev and super-linear growth coefficients. Ann. Probab. 44(6), 3661–3687 (2016)
Yamada, T., Ogura, Y.: On the strong comparison theorems for solutions of stochastic differential equations. Z. Wahrsch. Verw. Gebiete 56(1), 3–19 (1981)
Zhang, X.: Strong solutions of SDES with singular drift and Sobolev diffusion coefficients. Stoch. Process. Appl. 115(11), 1805–1818 (2005)
Zhang, X.: Stochastic homeomorphism flows of SDEs with singular drifts and Sobolev diffusion coefficients. Electron. J. Probab. 16(38), 1096–1116 (2011)
Zhang, X.: Stochastic differential equations with Sobolev diffusion and singular drift and applications. Ann. Appl. Probab. 26(5), 2697–2732 (2016)
Zhang, X., Zhao, G.: Singular Brownian diffusion processes. Commun. Math. Stat. 6(4), 533–581 (2018)
Zvonkin, A.K.: A transformation of the phase space of a diffusion process that will remove the drift. Mat. Sb. (N.S.) 93(135), 129–149, 152 (1974)
Acknowledgements
The author is greatly indebted to Professor Xin Chen for many useful discussions and for guidance over the past years. We thank the referees for helpful comments on an earlier version of this paper. Research supported by Project funded by China Postdoctoral Science Foundation (No. 2023M743718), National Key R &D Program of China (No. 2020YFA0712700) and the National Natural Science Foundation of China (Nos. 11931004, 12090014, 12288201) and the key Lab of Random Complex Structures and Data Science, Youth Innovation Promotion Association (2020003), Chinese Academy of Science.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author has no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The Proof of Theorem 4.1:
Step (i) Suppose \(\sigma ^R(x)\) does not depend on x, Krylov proved the estimate (4.2) in [8, Page 109]. Therefore, If \(\sigma ^R(x)\equiv \sigma ^R(x_0)\), then
Step (ii) Suppose for some \(x_0\in {\mathbb {R}}^d\)
we consider the following equation
where \(g:=L^{\sigma ^R(x)}- L^{\sigma ^R(x_0)} + f\). By (7.1) and the definition of \(L^{\sigma ^R(x)}\), we obtain
Hence, by Step (i), we have
i.e.,
Step (iii) Define a smooth cutoff function as follows:
Fix a small constant \(\varepsilon \) which will be determined below.
For fixed \(z\in {\mathbb {R}}^d\), let
It is easy to check that
Multiply both side of (4.1) by \(\zeta ^\varepsilon _z(x)\), we have
where \(g^\varepsilon _z:=(L^{\sigma ^R(x)} u)\zeta ^\varepsilon _z - L^{\sigma ^R(x)}(u\zeta ^\varepsilon _z) - f\zeta ^\varepsilon _z\).
Let
It is easy to obtain
since \(\zeta ^{2\varepsilon }_z(x) = 1 \) for \(\left| x-z\right| \le 2\varepsilon \) and \(\zeta ^\varepsilon _z(x) = 0\) for \(\left| x-z\right| >2\varepsilon \).
By (3.2) and the definition of \(g^\varepsilon _z\), we have
and
By Step (ii), if
then
Now, we consider the following equation:
and take \(\varepsilon \) to be small enough so that
then
According to Fubini’s theorem, (7.2) and (7.3), it is easy to check
Moreover, we have
where the third inequality is due to (7.2) and (7.3) and the last inequality is due to
and Young’s inequality. Therefore, we proved
Since \(\lambda u=L^{\sigma ^R(x)} u -f\), we have
Hence, we obtain
Notice that \(\lambda >(C(d,\varpi ,\tilde{\delta },p)+1)\), we obtain
Combine (7.5) with (7.4), we obtain
Step (iv) Set
where \(\rho (t,x,y)\) is the fundamental solution of the operator \(\partial _t - L^{\sigma ^R(x)}\). It is well known that
By [25, Lemma 3.4], for any \(p,p'\in (1,\infty )\) and \(\alpha \in [0,2)\), there exists a constant \(C=C(d,\varpi ,\tilde{\delta },p,\alpha ,p')\) such that for any \(f\in L^p({\mathbb {R}}^d)\),
Let \(f\in W^{2,p}({\mathbb {R}}^d)\) and
By (7.6) and the definition of \({\mathcal {T}}_{t}\), it is easy to check \(u\in W^{2,p}({\mathbb {R}}^d)\) and u satisfies (4.1). Indeed,
By Jensen’s inequality, we obtain
and
By Fubini’s theorem, we have
and
Moreover, by (2.1), (7.7), (7.8) and (7.9), if \((\frac{d}{p}+\alpha -\frac{d}{p'})/2<\frac{1}{p'}\le 1\), then
where the second inequality is due to Laplace transformation.
Step (v) In this step, we will use weak convergence argument to prove the existence of (4.1). Let \(\varphi \) be a nonnegative smooth function in \({\mathbb {R}}^d\) which satisfies \(\int _{{\mathbb {R}}^d} \varphi (x)\,dx=1\) and support in \(\{ x\in {\mathbb {R}}^d:\left| x\right| \le 1\}\). Let
where \(*\) denotes the convolution.
Denote \(u_n\) be the solution of
By the Step (iii) and Step (iv), we have
and
Since \(W^{2,p}({\mathbb {R}}^d)\) is weakly compact, we can find a subsequence still denoted by \(u_n\) and \(u\in W^{2,p}({\mathbb {R}}^d)\) such that \(u_n\rightharpoonup u\) in \(W^{2,p}({\mathbb {R}}^d)\).
For any test function \(\phi \in C^\infty _0({\mathbb {R}}^d)\), we have
and for fixed m
Hence, we obtain
Notice that
Take \(n\rightarrow \infty \), we obtain
On the other hand, let \(p_*:=\frac{p'}{p'-1}\) and keep in mind \(u_n\rightharpoonup u\) in \(W^{2,p}({\mathbb {R}}^d)\), we have
We completed the proof. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ye, W. Stochastic Differential Equations with Local Growth Singular Drifts. J Theor Probab 37, 2576–2614 (2024). https://doi.org/10.1007/s10959-024-01333-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10959-024-01333-5
Keywords
- Weak differentiability
- Strong Feller property
- Stochastic flow
- Krylov’s estimates
- Zvonkin’s transformation