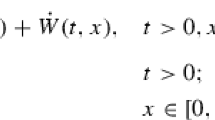Large Time Asymptotic Properties of the Stochastic Heat Equation

Abstract

In this article, we study the large time asymptotic behavior of the stochastic heat equation.

1 Introduction and Main Results

Suppose that $W=\{W(t,x), t\ge 0, x\in {\mathbb {R}}\}$ is a two-parameter Wiener process. That is, W is a zero-mean Gaussian process with covariance function given by

$$\begin{aligned} {\mathbb {E}}(W(t,x) W(s,y) ) = (s\wedge t) ( |x| \wedge |y|)\mathbf {1}_{\{xy >0\}}. \end{aligned}$$

Consider the stochastic heat equation

$$\begin{aligned} \frac{\partial u }{\partial t} = \frac{1}{2} \frac{\partial ^2u }{\partial x^2} +\varphi (W(t,x)) \frac{ \partial ^2 W}{\partial t\partial x}, \quad x\in {\mathbb {R}}, t\ge 0, \end{aligned}$$

(1.1)

where $\varphi : {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a given Borel measurable function such that for each $t \ge 0$ and $x\in {\mathbb {R}}$,

$$\begin{aligned} \int _0^t \int _{{\mathbb {R}}^2} p^2_{t-s} (x-y) \varphi ^2(z) p_{s|y|} (z) dydzds <\infty . \end{aligned}$$

(1.2)

Along the paper, $p_t(x)$ denotes the one-dimensional heat kernel, that is, $p_t(x)= (2\pi t)^{-1/2} e^{ -x^2/2t}$ for $t>0$ and $x\in {\mathbb {R}}$. The mild solution to Eq. (1.1) with initial condition $u(0,x)=0$ is given by

$$\begin{aligned} u(t,x)= \int _0^t \int _{{\mathbb {R}}} p_{t-s} (x-y) \varphi (W(s,y)) W(ds,dy), \end{aligned}$$

where the stochastic integral is well defined in view of condition (1.2).

We are interested in the asymptotic behavior as $t\rightarrow \infty$ of u(t, x) for $x\in {\mathbb {R}}$ fixed. Notice first that in the particular case where $\varphi (x)\equiv c$, then, u(t, x) is a centered Gaussian random variable with variance

$$\begin{aligned} {\mathbb {E}}(u(t,x)^2)= c^2 \int _0^t \int _{{\mathbb {R}}} p^2_{t-s} (x-y) dyds =c^2 \int _0^t p_{2(t-s)} (0) ds = \frac{c^2}{\sqrt{\pi } } \sqrt{t}. \end{aligned}$$

Therefore, $t^{-\frac{1}{4}} u(t,x)$ has the law $N(0, c^2/ \sqrt{\pi })$. In the general case, using the change of variables $s \rightarrow ts$ and $y \rightarrow \sqrt{t }y$, we can write

$$\begin{aligned} u(t,x)&= \int _0^1 \int _{{\mathbb {R}}} p_{t(1-s)} (x-y) \varphi (W(ts,y)) W(tds,dy) \nonumber \\&= \frac{1}{ \sqrt{t}} \int _0^1 \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x-y}{\sqrt{t}}\right) \varphi (W(ts,y)) W(tds,dy) \nonumber \\&= \frac{1}{ \sqrt{t}} \int _0^1 \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y \right) \varphi (W(ts, \sqrt{t} y)) W(tds,\sqrt{t}dy). \end{aligned}$$

(1.3)

By the scaling properties of the two-parameter Wiener process, it follows that u(t, x) has the same law as

$$\begin{aligned} \widetilde{u}(t,x)= t^{1/4}\int _0^1 \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y \right) \varphi ( t^{3/4} W(s, y)) W(ds,dy). \end{aligned}$$

(1.4)

The asymptotic behavior of u(t, x) will depend on the properties of the function $\varphi$. We will consider three classes of functions for which different behaviors appear. We are going to use the following notion of convergence, which is stronger than convergence in distribution (see, for instance, [6, Chapter VIII]).

Definition 1.1

Let $\{F_{n}\}$ be a sequence of X-valued random variables defined on a probability space $(\Omega , {\mathcal {F}}, {\mathbb {P}})$, X being a complete separable metric space. Let F be an X-valued random variable defined on some extended probability space $(\Omega ', {\mathcal {F}}', {\mathbb {P}}')$. We say that $F_{n}$ converges stably to F, written $F_n {\mathop {\longrightarrow }\limits ^\mathrm{stably}} F$, if for every bounded ${\mathcal {F}}$–measurable random variable G, $(G,F_n)$ converges in law to (G, F).

When $X={\mathbb {R}}$, $F_n {\mathop {\longrightarrow }\limits ^\mathrm{stably}} F$ is equivalent to saying that

$$\begin{aligned} \underset{n \rightarrow \infty }{\mathrm{lim}}{\mathbb {E}} \left[ Ge^{i \lambda F_{n}} \right] = {\mathbb {E}}' \left[ Ge^{i \lambda F} \right] , \end{aligned}$$

(1.5)

for every $\lambda \in {\mathbb {R}}$ and every bounded ${\mathcal {F}}$–measurable random variable G.

The first theorem deals with the case where $\varphi$ is an homogeneous-type function.

Theorem 1.2

Suppose that $\varphi :{\mathbb {R}}\rightarrow {\mathbb {R}}$ is a measurable and bounded on compacts function such that¹$\lim _{x \rightarrow \pm \infty } |x|^{-\alpha }\varphi (x) =c_\pm$ for some constants $c_+, c_-$ and $\alpha \ge 0$. Then, as $t\rightarrow \infty$,

$$\begin{aligned}&t^{-\frac{3\alpha +1}{4}} u(t,x) {\mathop {\longrightarrow }\limits ^\mathrm{stably}}c_- \int _0^1 \int _{{\mathbb {R}}} p_{1-s} (y ) | \widehat{W}(s, y)|^\alpha \mathbf {1}_{\{\widehat{W}(s,y) <0\}} \widehat{W}(ds,dy)\\&\qquad +c_+\int _0^1 \int _{{\mathbb {R}}} p_{1-s} (y ) |\widehat{W}(s, y)|^\alpha \mathbf {1}_{\{\widehat{W}(s,y) >0\}} \widehat{W}(ds,dy)=:X. \end{aligned}$$

Here, $\widehat{W}$ is a two-parameter Wiener process independent of W.

Note that in the case that $c_+=c_-$ and $\alpha =0$; then, the limit is Gaussian. Note that one may also consider the case²$\lim _{x \rightarrow \pm \infty } |x|^{-\alpha _\pm }\varphi (x) =c_\pm$ for some constants $c_+, c_-$, $\alpha _+,\alpha _-\ge 0$. In this case, the renormalization factor is $t^{-\frac{3(\alpha _+\vee \alpha _- )+1}{4}}$ and the limit will only have contributions from the largest $\alpha =\alpha _+\vee \alpha _-$.

In the second theorem, we consider the case where $\varphi$ satisfies some integrability properties with respect to the Lebesgue measure on ${\mathbb {R}}$. The limit involves a weighted local time of the two-parameter Wiener process, and the proof has been inspired by the work of Nualart and Xu [7] on the central limit theorem for an additive functional of the fractional Brownian motion.

Theorem 1.3

Suppose that $\varphi \in L^2({\mathbb {R}}) \cap L^p({\mathbb {R}})$ for some $p<2$. Then, as $t\rightarrow \infty$,

$$\begin{aligned} t^{\frac{1}{8}} u(t,x) {\mathop {\longrightarrow }\limits ^\mathrm{stably}}Z \left( \int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} (y ) \delta _0(\widehat{W}(s, y)) dyds \right) ^{\frac{1}{2}} \Vert \varphi \Vert _{L^2({\mathbb {R}})} , \end{aligned}$$

where $\widehat{W}$ is a two-parameter Wiener process, Z is a N(0, 1) random variable and $\widehat{W}$, and W and Z are independent.

In Theorem 1.3, $L_{0,1}:=\int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} (y ) \delta _0(\widehat{W}(s, y)) dyds$ is a weighted local time of the random field $\widehat{W}$ that can be defined (see Lemma 2.1) as the limit in $L^2(\Omega )$ of

$$\begin{aligned} L^\varepsilon _{0,1}:=\int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} (y ) p_\varepsilon (\widehat{W}(s, y)) dyds, \end{aligned}$$

as $\varepsilon$ tends to zero.

The present study originates from a nonlinear stochastic heat equation which is described in Sect. 4. Although we have not been able to obtain explicit results in this general situation, the results presented here provide a range of techniques and results related to this problem.

The paper is organized as follows. Section 2 contains the proofs of the above theorems, and in Sect. 3, we discuss an extension of these results in the case where we consider also space averages on an interval $[-R,R]$ and both R and t tend to infinity. A brief discussion of the case of nonlinear equations is provided in Sect. 4.

2 Proofs

Proof of Theorem 1.2

We know that $t^{-\frac{ 3\alpha +1}{4}} u(t,x)$ has the same law as

$$\begin{aligned} v(t,x ):= t^{-\frac{ 3\alpha }{4}} \int _0^1 \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y \right) \varphi (t^{3/4}W(s,y)) W(ds,dy). \end{aligned}$$

We divide the study of v into two parts according to the boundedness on compacts property for $\varphi$. In fact, for any compact K consider $\varphi _K(x)= \varphi (x)\mathbf {1}_{x\in K}$. Then, we will prove that $v_K(x)\rightarrow 0$ in $L^2(\Omega )$ where

$$\begin{aligned} v_K(t,x ):= t^{-\frac{ 3\alpha }{4}} \int _0^1 \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y \right) \varphi _K(t^{3/4}W(s,y)) W(ds,dy). \end{aligned}$$

In fact, as $\varphi _K$ is bounded by a constant, say M, we have

$$\begin{aligned} {\mathbb {E}}[v^2_K(t,x)]\le M^2t^{-\frac{3\alpha }{2}}\int _0^1 \frac{1}{ \sqrt{2\pi (1-s)}} \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y \right) {\mathbb {P}}(t^{3/4}W(s,y)\in K) dsdy. \end{aligned}$$

The above quantity clearly converges to zero as $t\rightarrow \infty$, if one considers separately the cases $\alpha >0$ and $\alpha =0$.

Given the above result, we can assume without loss of generality that $\varphi (x)=f(x)|x|^\alpha$ with a bounded measurable function f such that $\lim _{x\rightarrow \pm \infty }f(x)=c_\pm$.

For this, we fix $t_0>0$ and compute the conditional characteristic function of $t^{-\frac{ 3\alpha +1}{4}} u(t,x)$ given ${\mathcal {F}}_{t_0}$, where $t>t_0$ and $\{ {\mathcal {F}}_t, t\ge 0\}$ denotes the natural filtration of the two-parameter Wiener process W used in the definition of u³ . For any $\lambda \in {\mathbb {R}}$, we have

$$\begin{aligned} {\mathbb {E}}\left[ e^{i\lambda t^{-\frac{ 3\alpha +1}{4}} u(t,x) } | {\mathcal {F}}_{t_0} \right]&=e^{i\lambda t^{-\frac{ 3\alpha +1}{4}} \int _0 ^{t_0} \int _{{\mathbb {R}}} p_{t-s} (x-y) \varphi (W(s,y)) W(ds,dy) } \\&\quad \times {\mathbb {E}}\left[ e^{i\lambda t^{-\frac{ 3\alpha +1}{4}} \int _{t_0} ^{t} \int _{{\mathbb {R}}} p_{t-s} (x-y) \varphi (W(s,y)) W(ds,dy ) } | {\mathcal {F}}_{t_0} \right] \\&=: e^{i\lambda A_t} \times B_t. \end{aligned}$$

It is easy to show that $\lim _{t\rightarrow \infty } A_t =0$ in $L^2(\Omega )$ as $t\rightarrow \infty$. In fact, using the rescaling properties we obtain that as $t\rightarrow \infty$

$$\begin{aligned}&t^{-\frac{ 3\alpha +1}{2}} {\mathbb {E}}\left[ \int _0 ^{t_0} \int _{{\mathbb {R}}} p_{t-s} (x-y)^2 \varphi (W(s,y))^2dsdy\right] \\&\quad \le \Vert f\Vert _\infty ^2 {\mathbb {E}}\left[ \int _0 ^{t_0/t} \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}}-y\right) ^2 |W(s,y)|^{2\alpha }dsdy\right] \rightarrow 0. \end{aligned}$$

Now, we continue with the term $B_t$ for which we will use the decomposition

$$\begin{aligned} W(s,y)&= W(s,y)- W(t_0,y) + W(t_0,y),\\&=: \widehat{W}(s-t_0,y) + W(t_0,y). \end{aligned}$$

Then, we can write

$$\begin{aligned} B_t=\widehat{{\mathbb {E}}} \left[ \exp \left( i\lambda t^{-\frac{ 3\alpha +1}{4}} \int _{0} ^{t-t_0} \int _{{\mathbb {R}}} p_{t-t_0-s} (x-y) \varphi (\widehat{W}(s,y) + W(t_0,y) ) \widehat{W}(ds,dy ) \right) \right] , \end{aligned}$$

where $\widehat{{\mathbb {E}}}$ denotes the mathematical expectation with respect to the two-parameter Wiener process $\widehat{W}$. By the same renormalization arguments as in (1.3) leading to (1.4), this gives

$$\begin{aligned} B_t&=\widehat{{\mathbb {E}}} \Bigg [ \exp \Bigg (i\lambda \left( \frac{t-t_0}{t} \right) ^{\frac{ 3\alpha +1}{4}} \int _{0} ^{1} \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{ t-t_0}}-y\right) F(t,s,y) \widehat{W}(ds,dy ) \Bigg ) \Bigg ]. \end{aligned}$$

Here,

$$\begin{aligned} F(t,s,y)&:=f((t-t_0)^{3/4}(\widehat{W}(s,y) +(t-t_0) ^{-\frac{3}{4}} W(t_0, \sqrt{ t-t_0}y))) \\&\quad \times |\widehat{W}(s,y) +(t-t_0) ^{-\frac{3}{4}} W(t_0, \sqrt{ t-t_0}y)|^\alpha . \end{aligned}$$

As $t\rightarrow \infty$ and $\lim _{x \rightarrow \pm \infty } |x|^{-\alpha }\varphi (x) =c_\pm$, then $B_t$ converges almost surely to

$$\begin{aligned} \widehat{{\mathbb {E}}} \left[ \exp \left( i\lambda \int _{0} ^{1} \int _{{\mathbb {R}}} p_{1-s} (y) F_\alpha (\widehat{W}(s,y)) \widehat{W}(ds,dy ) \right) \right] , \end{aligned}$$

where $F_\alpha (x)=c_+\mathbf {1}_{x>0}+c_-\mathbf {1}_{x<0}$. Then, the above formula is the characteristic function of X. As a consequence, for every bounded ${\mathcal {F}}_{t_0}$ measurable random variable G, we obtain

$$\begin{aligned} \lim _{t\rightarrow \infty } {\mathbb {E}}\left[ G e^{i\lambda t^{-\frac{ 3\alpha +1}{4}} u(t,x)}\right] = {\mathbb {E}}[G] {\mathbb {E}}[ e^{i\lambda X}]. \end{aligned}$$

This can be extended to any bounded random variable G measurable with respect to the two-parameter Wiener process W, and this provides the desired stable convergence in the sense of Definition 1.1. $\square$

For the proof of Theorem 1.3, we need the following lemma on the existence of the weighted local time $L_{0,r}$.

Lemma 2.1

For any $r\in [0,1]$, the limit in $L^2(\Omega )$, as $\varepsilon$ tends to zero, of

$$\begin{aligned} L_{0,r}^\varepsilon := \int _0^r \int _{{\mathbb {R}}} p^2_{1-s} (y ) p_\varepsilon (W(s, y)) dyds, \end{aligned}$$

exists and the limit random variable will be denoted by $L_{0,r}:=\int _0^r \int _{{\mathbb {R}}} p^2_{1-s} (y ) \delta _0(W(s, y)) dyds$.

Proof

Using the inverse Fourier transform formula for a Gaussian law, we have

$$\begin{aligned} L^\varepsilon _{0,r}=\frac{1}{2\pi } \int _0^r \int _{{\mathbb {R}}^2} p^2_{1-s} (y ) e^{ i\xi W(s,y) - \frac{\varepsilon ^2}{2} \xi ^2} d\xi dyds. \end{aligned}$$

Note that in order to prove the statement in the lemma is enough to prove that ${\mathbb {E}}( L^\varepsilon _{0,r} L^{\varepsilon '}_{0,r})$ converges as $\varepsilon , \varepsilon '\rightarrow 0$. Therefore, consider

$$\begin{aligned} {\mathbb {E}}( L^\varepsilon _{0,r} L^{\varepsilon '}_{0,r})&=(2\pi )^{-2} \int _0^r \int _0^r \int _{{\mathbb {R}}^4} p^2_{1-s} (y ) p^2_{1-s'} (y') \\&\qquad \times {\mathbb {E}}\left( e^{ i\xi W(s,y) - \frac{\varepsilon ^2}{2} \xi '^2 -i\xi ' W(s',y') - \frac{\varepsilon '^2}{2} \xi '^2} \right) d\xi dy d\xi ' dy'\ ds'ds \\&=(2\pi )^{-2} \int _0^r \int _0^r \int _{{\mathbb {R}}^4} p^2_{1-s} (y ) p^2_{1-s'} (y') e^{ - \frac{\varepsilon ^2}{2} \xi ^2 -\frac{\varepsilon '^2}{2} \xi '^2 } \\&\qquad \times e^{ -\frac{1}{2} {\mathbb {E}}( |\xi W(s,y) - \xi 'W(s',y')|^2)} d\xi dy d\xi ' dy'\ ds'ds. \end{aligned}$$

As $\varepsilon$ and $\varepsilon '$ tend to zero, we obtain the limit

$$\begin{aligned} I:= \int _0^1 \int _0^1 \int _{{\mathbb {R}}^2} p^2_{1-s} (y ) p^2_{1-s'} (y') f(s,y,s',y') dy dy'\ ds'ds, \end{aligned}$$

where $f(s,y,s',y')$ is the density at (0, 0) of the random vector $(W(s,y), W(s',y'))$. We claim that $I<\infty$. Indeed, first notice that $f(s,y,s',y')$ is bounded by

$$\begin{aligned}&(2\pi )^{-1} \left( ss' |y| |y'| - (s\wedge s')^2 ( |y| \wedge |y'| )^2 \mathbf {1}_{\{yy'>0\}}\right) ^{-\frac{1}{2}}\\&\quad =(2\pi )^{-1} \left[ (s\wedge s') ( |y| \wedge |y'| ) \left( (s\vee s') (|y|\vee |y'| )- (s\wedge s') ( |y| \wedge |y'|) \mathbf {1}_{\{yy'>0\}}\right) \right] ^{-\frac{1}{2}}. \end{aligned}$$

To show that $I<\infty$, it suffices to consider the integral over the set $\{ yy'>0 \}$, because the integral over $\{ yy' \le 0\}$ is clearly finite. By symmetry, we only need to show that the integral

$$\begin{aligned} J:= \int _{0<s<s'<1} \int _{ 0<y<y'<\infty } (1-s)^{-1} (1-s')^{-1} (sy(s'y'-sy))^{-\frac{1}{2}} e^{-\frac{y^2}{1-s} -\frac{ y'^2}{ 1-s'}} dy dy' ds ds' \end{aligned}$$

is finite. With the change of variables $sy=z$ and $s'y'=z'$, we obtain

$$\begin{aligned} J\le \int _{0<s<s'<1} \int _{ 0<z<z'<\infty } [(1-s) (1-s')ss']^{-1} (z(z'-z))^{-\frac{1}{2}} e^{-\frac{z^2}{s^2(1-s)} -\frac{ z'^2}{ s'^2(1-s')}} dz dz' ds ds'. \end{aligned}$$

Fix $\delta >0$ and let $K_\delta = \sup _{s\in [0,1],z>0} \left( \frac{z^2}{ s^2(1-s)} \right) ^\delta e^{-\frac{z^2}{s^2(1-s)}}$. Then,

$$\begin{aligned} J&\le K_\delta \int _{0<s<s'<1} \int _{ 0<z<z'<\infty } (1-s)^{-1+\delta } (1-s')^{-1} s^{-1+2\delta } (s')^{-1} z^{-\frac{1}{2}-2\delta } (z'-z)^{-\frac{1}{2}}\\&\quad \times e^{-\frac{ z'^2}{ s'^2(1-s')}} dz dz' ds ds'. \end{aligned}$$

Integrating first in z and later in $z'$, it is easy to show that the above integral is finite if $\delta <\frac{1}{4}$. This allows us to conclude the proof of the lemma. $\square$

Proof of Theorem 1.3

Consider the random variable $\widetilde{u}(t,x)$ defined in (1.4). We can put $\widetilde{u}(t,x)= t^{-\frac{3}{8}} M_t(1,x)$, where for $r\in {\mathbb {R}}_+$,

$$\begin{aligned} M_t(r,x) := t^{\frac{3}{8}} \int _0^{r\wedge 1} \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y \right) \varphi ( t^{3/4} W(s, y)) W(ds,dy) +Z_{(r\vee 1)-1} , \end{aligned}$$

where $\{Z_t, t\ge 0\}$ is a standard Brownian motion independent of W, defined, if necessary, on an enlarged probability space. Then, $\{M_t(\cdot , x), t\ge 0 \}$ is a family of continuous martingales in the time interval $[0,\infty )$. We note that the important part of the definition of $M_t(r,x)$ corresponds to $r\in [0,1]$. For this reason, we will concentrate on this interval leaving the calculations and corresponding modifications for $r\in [1,\infty )$ to the reader.

We will find the limit as $t\rightarrow \infty$ of the quadratic variation of these martingales. We have for $r\in [0,1]$

$$\begin{aligned} \langle M_t(\cdot ,x) \rangle _{r}&= t^{\frac{3}{4}} \int _0^r \int _{\mathbb {R}}p^2_{1-s} \left( \frac{x}{\sqrt{t}} -y \right) \varphi ^2( t^{\frac{3}{4}} W(s, y)) dsdy. \end{aligned}$$

The proof of the theorem will be done in several steps.

Step 1    In this step, we prove that $\langle M_t(\cdot ,x) \rangle _{r}$ converges in $L^1(\Omega )$ to the weighted local time $L_{0,r}$, for $r\in [0,1]$. First, we claim that

$$\begin{aligned} \lim _{t\rightarrow \infty } {\mathbb {E}}\left( \left| \langle M_t(\cdot ,x) \rangle _{r} -t^{\frac{3}{4}} \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) \varphi ^2( t^{\frac{3}{4}} W(s, y)) dsdy \right| \right) =0. \end{aligned}$$

(2.1)

This follows from the fact that

$$\begin{aligned} {\mathbb {E}}\left( t^{\frac{3}{4}}\varphi ^2( t^{\frac{3}{4}} W(s, y))\right) \le \Vert \varphi \Vert _{L^2({\mathbb {R}})}^2 (2\pi s |y|)^{-\frac{1}{2}} \end{aligned}$$

(2.2)

and for fixed $r\in [0,1]$

$$\begin{aligned} \lim _{t\rightarrow \infty } \int _0^r \int _{\mathbb {R}}\left| p^2_{1-s} \left( \frac{x}{\sqrt{t}} -y \right) -p^2_{1-s} (y) \right| \frac{1}{ \sqrt{s |y|}} dyds =0. \end{aligned}$$

Note that the bound in (2.2) also shows that the martingale $M_t(\cdot ,x)$ is square integrable. On the other hand, for any fixed t, we have

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} J_{\varepsilon ,t} =0, \end{aligned}$$

(2.3)

where

$$\begin{aligned} J_{\varepsilon ,t}&={\mathbb {E}}\Big ( \Big | t^{\frac{3}{4}} \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) \varphi ^2\left( t^{\frac{3}{4}} W(s, y)\right) dsdy\\&\quad - \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) \int _{{\mathbb {R}}} \varphi ^2(\xi ) p_{\varepsilon t^{-\frac{3}{2}} }\left( W(s, y) -t^{-\frac{3}{4}}\xi \right) d\xi dsdy \Big | \Big ). \end{aligned}$$

To show (2.3), notice first that

$$\begin{aligned}&\int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) \int _{{\mathbb {R}}} \varphi ^2(\xi ) p_{\varepsilon t^{-\frac{3}{2}}}\left( W(s, y) - t^{-\frac{3}{4}}\xi \right) d\xi dsdy \\&\qquad = t^{\frac{3}{4}} \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) \int _{{\mathbb {R}}} \varphi ^2(\xi ) p_\varepsilon \left( t^{\frac{3}{4}} W(s, y) -\xi \right) d\xi dsdy \\&\qquad = t^{\frac{3}{4}} \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) ( \varphi ^2 * p_\varepsilon ) \left( t^{\frac{3}{4}} W(s, y)\right) dsdy. \end{aligned}$$

Therefore,

$$\begin{aligned} J_{\varepsilon ,t}&= {\mathbb {E}}\left( \left| t^{\frac{3}{4}} \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) (\varphi ^2-\varphi ^2 * p_\varepsilon ) \left( t^{\frac{3}{4}} W(s, y)\right) dsdy \right| \right) \\&\le t^{\frac{3}{4}} \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) {\mathbb {E}}\left( | (\varphi ^2-\varphi ^2 * p_\varepsilon ) \left( t^{\frac{3}{4}} W(s, y)\right) |\right) dsdy \\&\le \Vert \varphi ^2 - \varphi ^2 * p_\varepsilon \Vert _{L^1({\mathbb {R}})} \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) (2\pi s |y|) ^{-\frac{1}{2}} dy ds, \end{aligned}$$

which converges to zero as $\varepsilon$ tends to zero because $\int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) (2\pi s |y|) ^{-\frac{1}{2}} dy ds <\infty$ and $\varphi \in L^2({\mathbb {R}})$.

We also claim that

$$\begin{aligned} \lim _{t\rightarrow \infty } \sup _{\varepsilon >0} I_{\varepsilon ,t} =0, \end{aligned}$$

(2.4)

where

$$\begin{aligned} I_{\varepsilon ,t}&= {\mathbb {E}}\Big ( \Big | \int _0^r \int _{{\mathbb {R}}^2} p^2_{1-s} (y) \varphi ^2(\xi ) p_{\varepsilon t^{-\frac{3}{2}}}\left( W(s, y) - t^{-\frac{3}{4}}\xi \right) d\xi dy ds\\&\qquad - \Vert \varphi \Vert _{L^2({\mathbb {R}})}^2 \int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) p_{\varepsilon t^{-3/2} }( W(s, y) ) dy ds \Big |^2 \Big ). \end{aligned}$$

To show (2.4), we write

$$\begin{aligned} I_{\varepsilon ,t}&= (2\pi )^{-2} {\mathbb {E}}\left( \left| \int _0^r \int _{{\mathbb {R}}^2} p^2_{1-s} (y) \varphi ^2(\xi ) \int _{{\mathbb {R}}} e^{i \eta W(s,y) - \frac{\varepsilon ^2 t^{-3}}{2} \eta ^2} \left( e^{i\eta t^{-\frac{3}{4}} \xi } -1\right) d\eta d\xi dyds \right| ^2 \right) \\&= (2\pi )^{-2} \int _{[0,r]^2} \int _{{\mathbb {R}}^4} p^2_{1-s} (y) p^2_{1-s'} (y') \varphi ^2(\xi ) \varphi ^2(\xi ') \\&\qquad \times \int _{{\mathbb {R}}^2} e^ {-\frac{1}{2} {\mathbb {E}}( |\eta W(s,y) -\eta ' W(s',y') |^2)} e^{ - \frac{\varepsilon ^2 t^{-3}}{2}( \eta ^2+ \eta '^2)} \\&\qquad \times ( e^{i\eta t^{-\frac{3}{4}} \xi } -1)( e^{-i\eta ' t^{-\frac{3}{4}} \xi '} -1) d\eta d\eta ' d\xi d\xi ' dy dy'ds ds' , \end{aligned}$$

which leads to the estimate

$$\begin{aligned} \sup _{\varepsilon >0} I_{\varepsilon ,t}&\le (2\pi )^{-2} \int _{[0,r]^2} \int _{{\mathbb {R}}^4} p^2_{1-s} (y) p^2_{1-s'} (y') \varphi ^2(\xi ) \varphi ^2(\xi ') \\&\qquad \times \int _{{\mathbb {R}}^2} e^ {-\frac{1}{2} {\mathbb {E}}( |\eta W(s,y)- \eta ' W(s',y') |^2)} \left( | \eta \xi \eta ' \xi ' | ^\beta t^{-\frac{3}{4} \beta } \wedge 4\right) d\eta d\eta ' d\xi d\xi ' dy dy'ds ds' , \end{aligned}$$

for any $\beta \in [0,1]$. Then, by the dominated convergence theorem, the limit (2.4) follows from

$$\begin{aligned} \int _{[0,r]^2} \int _{{\mathbb {R}}^4} p^2_{1-s} (y) p^2_{1-s'} (y') \int _{{\mathbb {R}}^2} e^ {-\frac{1}{2} {\mathbb {E}}( |\eta W(s,y)- \eta ' W(s',y') |^2)} d\eta d\eta ' dy dy'ds ds' <\infty , \end{aligned}$$

which follows from the fact that $(2\pi )^{-2} \int _{{\mathbb {R}}^2} e^ {-\frac{1}{2} {\mathbb {E}}( |\eta W(s,y)- \eta ' W(s',y') |^2)} d\eta d\eta '$ is the density at (0, 0) of the random vector $(W(s,y), W(s',y'))$ (see the proof of Lemma 2.1).

By Lemma 2.1, $\int _0^r \int _{\mathbb {R}}p^2_{1-s} (y) p_{\varepsilon } (W(s, y) ) dy ds$ converges in $L^2(\Omega )$ as $t\rightarrow \infty$ to the weighted local time $L_{0,r}$. As a consequence, from (2.1), (2.3), (2.4) and Lemma 2.1, we deduce that $\langle M_t(\cdot ,x) \rangle _{r}$ converges as $t\rightarrow \infty$ in $L^1(\Omega )$ to the weighted local time $L_{0,r}=\int _0^r \int _{{\mathbb {R}}} p^2_{1-s} (y ) \delta _0(W(s, y)) dyds$.

Step 2    Fix an orthonormal basis $\{e_i, i\ge 1\}$ of $L^2({\mathbb {R}})$ formed by bounded functions and consider the martingales for $r\in {\mathbb {R}}_+$

$$\begin{aligned} M^i(r)= \int _0^{r} \int _{{\mathbb {R}}} e_i(y) W(ds,dy). \end{aligned}$$

We claim that the total variation of the joint quadratic variation $\langle M_t(\cdot , x), M^i \rangle _r$ converges to zero in $L^1(\Omega )$ as $t\rightarrow \infty$. Indeed,

$$\begin{aligned} \langle M_t(\cdot , x), M^i \rangle _ r= t^{\frac{3}{8}} \int _0^{r\wedge 1} \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) e_i(y) \varphi \left( t^{\frac{3}{4}} W(s,y)\right) dyds. \end{aligned}$$

Then, using the fact that $\varphi \in L^p({\mathbb {R}})$ for some $p<2$, we can write for $r\in [0,1]$

$$\begin{aligned}&{\mathbb {E}}(| \langle M_t(\cdot , x), M^i \rangle |_ r) \le t^{\frac{3}{8}} \int _0^r \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) |e_i(y) | {\mathbb {E}}\left( \left| \varphi \left( t^{\frac{3}{4}} W(s,y)\right) \right| \right) dyds\\&\qquad \le t^{\frac{3}{8}} \int _0^r \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) | e_i(y)| \int _{{\mathbb {R}}} |\varphi (z)| \frac{1}{ \sqrt{ 2\pi t^{\frac{3}{2}} s|y|} } \exp \left( -\frac{z^2}{2 t^{\frac{3}{2}} s|y|}\right) dzdyds\\&\qquad \le t^{\frac{3}{8}- \frac{3}{ 4p}} \Vert e_i \Vert _{\infty } \Vert \varphi \Vert _{L^p({\mathbb {R}})} \int _0^r \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) (s|y|)^{- \frac{1}{2p}} dyds, \end{aligned}$$

where $\frac{1}{p} + \frac{1}{q} =1$. Then, the claim follows because $\frac{3}{8}- \frac{3}{ 4p} <0$ for $p\in (1,2)$ and

$$\begin{aligned} \int _0^r \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) (s|y|)^{-\frac{1}{2p}} dyds <\infty . \end{aligned}$$

Step 3    Given a sequence $t_n \uparrow \infty$, set $M^n_{0,r} = M_{t_n}(r,x)$ and $M^n_{i,r}= M^i(r)$ for $i \ge 1$. These martingales possess Dambis-Dubins-Schwarz Brownian motions $\beta ^n_i$, such that

$$\begin{aligned} M^n_{0,r } = \beta ^n_{0,\langle M^n_0 \rangle _r} \end{aligned}$$

and

$$\begin{aligned} M^n_{i,r} = \beta ^n_{i, r} , \quad i \ge 1. \end{aligned}$$

We have proved in Step 2 that $\sup _{r\in {\mathbb {R}}_+ } |\langle M^n_i, M^n_0 \rangle |_r \rightarrow 0$ in probability as $n\rightarrow \infty$. Moreover, it is clear that for any $1\le i <j$, $\langle M^n_i, M^n_j \rangle _ r =0$. Then, by the asymptotic Ray-Knight theorem (see Theorem 5.1 in Appendix), we conclude that the Brownian motions $\{\beta ^n_{i,y}, y \ge 0\}$, $i\ge 0$, converge in law to a family of independent Brownian motions $\{\beta _{i,y}, y \ge 0\}$, $i\ge 0$. As a consequence, we deduce in particular, the stable convergence in the sense of Definition 1.1, of the sequence of Brownian motions $\beta ^n_0$ to a Brownian motion $\beta _0$ with ${\mathcal {F}}$ being the $\sigma$-field generated by the white noise W on ${\mathbb {R}}_+ \times {\mathbb {R}}$ which is independent of $\beta _0$.

We are going to show using Step 1 that $M_{t_n} (1,x)$ converges stably to $\beta _{0, L_{0,1} \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})} }$ as $n\rightarrow \infty$, where $\beta _0$ is independent of W. Indeed, for any $\lambda \in {\mathbb {R}}$, $\epsilon , K>0$, with the notation $c= \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})}$, and for any W-measurable random variable G such that $|G|\le 1$, we can write

$$\begin{aligned}&\left| {\mathbb {E}}\left( G( e^{ i\lambda M_{t_n} (1,x) } - e^{i\lambda \beta _{0, c L_{0,1} }} )\right) \right| \le \left| {\mathbb {E}}\left( G(e^{ i\lambda \beta ^n_{0, \langle M_0^n \rangle _1} } - e^{ i\lambda \beta ^n_{0, c L_{0,1}} }) \right) \right| \\&\qquad + \left| {\mathbb {E}}\left( G( e^{ i\lambda \beta ^n_{0, c L_{0,1}}} -e^{ i\lambda \beta _{0, c L_{0,1}} }) \right) \right| \\&\quad \le P( | \langle M_0^n \rangle _1- cL_{0,1} |>\epsilon ) + P( c L_{0,1} >K)\\&\qquad +{\mathbb {E}}\left( \sup _{|t-s| <\epsilon , t\le K} | e^{ i\lambda \beta ^n_{0,t} } - e^{ i\lambda \beta ^n_{0,s} } | \right) +\left| {\mathbb {E}}\left( G( e^{ i\lambda \beta ^n_{0, c L_{0,1}} } -e^{ i\lambda \beta _{0, c L_{0,1}} } )\right) \right| \\&\quad := A^1_{n,\epsilon } + A^2_K+ A^3_{n,\epsilon , L}+ A^4_n. \end{aligned}$$

By Step 1, $\lim _{n\rightarrow \infty } A^1_{n,\epsilon } =0$ and the stable convergence of $\beta ^n_0$ to $\beta _0$ implies $\lim _{n\rightarrow \infty } A^4_n =0$. Finally, for fixed K, $A^3_{n,\epsilon ,K}$ does not depend on n and converges to zero as $\epsilon \rightarrow 0$ and, finally, $A^2_K$ tends to zero as $K \uparrow \infty$. Thus, we have proved the stable convergence $t^{\frac{3}{8}} \widetilde{u}(t,x)) {\mathop {\longrightarrow }\limits ^\mathrm{stably}} \beta _{0, L_{0,1} \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})} }$ as $t\rightarrow \infty$, where $L_{0,1}=\int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} (y ) \delta _0(W(s, y)) dyds$ and $\beta _0$ is independent of W.

Step 4    Fix $\lambda \in {\mathbb {R}}$ and $t_0 \ge 0$. To complete the proof, we follow a similar argument as in the proof of Theorem 1.2 based on the method of characteristic functions. In fact, we can write

$$\begin{aligned} {\mathbb {E}}\left[ e^{i\lambda t^{\frac{1}{8}} u(t,x)} |_{{\mathcal {F}}_{t_0}}\right]&=e^{i\lambda t^{\frac{1}{8} } \int _0 ^{t_0} \int _{{\mathbb {R}}} p_{t-s} (x-y) \varphi (W(s,y) ) W(ds,dy) } \\&\quad \times {\mathbb {E}}\left[ e^{i\lambda t^{\frac{1}{8}} \int _{t_0} ^{t} \int _{{\mathbb {R}}} p_{t-s} (x-y) \varphi ( W(s,y)) W(ds,dy) } | {\mathcal {F}}_{t_0} \right] \\&=: e^{i\lambda A_t} \times B_t. \end{aligned}$$

As in the proof of Theorem 1.2, it is easy to show that $\lim _{t\rightarrow \infty } A_t =0$ in $L^2(\Omega )$. On the other hand, with the decomposition

$$\begin{aligned} W(s,y)= W(s,y)- W(t_0,t) + W(t_0,y), \end{aligned}$$

for the term $B_t$, we can write

$$\begin{aligned} B_t=\widehat{{\mathbb {E}}} \left[ \exp \left( i\lambda t^{\frac{1}{8}} \int _{0} ^{t-t_0} \int _{{\mathbb {R}}} p_{t-t_0-s} (x-y) \varphi ( \widehat{W}(s,y) + W(t_0,y) ) \widehat{W}(ds,dy ) \right) \right] , \end{aligned}$$

where $\widehat{{\mathbb {E}}}$ denotes the mathematical expectation with respect to the two-parameter Wiener process $\widehat{W}$ defined by $\widehat{W}(s,y)= W(s+ t_0,y) -W(t_0,y)$. By the same arguments as before, this leads to

$$\begin{aligned} B_t&=\widehat{{\mathbb {E}}} \Bigg [ \exp \Bigg ( (i\lambda { t^{\frac{1}{8}}} (t-t_0)^{\frac{1}{4}} \int _{0} ^{1} \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t-t_0}}-y\right) \\&\qquad \times \varphi ( (t-t_0)^{\frac{3}{4}}\widehat{W}(s,y) + \Phi _{t,y})\widehat{W}(ds,dy ) \Bigg ) \Bigg ]. \end{aligned}$$

Here, we have used the notation $\Phi _{t,y}= (t-t_0) ^{-\frac{3}{4}} W(t_0, \sqrt{t-t_0} y)$. Rather than considering the limit of the above expression, we would like to consider instead the limit of

$$\begin{aligned} B_t^{(1)}&: =\widehat{{\mathbb {E}}} \Bigg [ \exp \Bigg ( (i\lambda { t^{\frac{1}{8}}} (t-t_0)^{\frac{1}{4}} \int _{0} ^{1} \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t-t_0}}-y\right) \\&\qquad \times \varphi ( (t-t_0)^{\frac{3}{4}}\widehat{W}(s,y)) \widehat{W}(ds,dy ) \Bigg ) \Bigg ]. \end{aligned}$$

In order to be able to do this, consider the residual term

$$\begin{aligned} R_t&:= \lambda { t^{\frac{1}{8}}} (t-t_0)^{\frac{1}{4}} \int _{0} ^{1} \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t-t_0}}-y\right) \\&\qquad \times ( \varphi ( (t-t_0)^{\frac{3}{4}}\widehat{W}(s,y) +\Phi _{t,y} )- \varphi ( (t-t_0)^{\frac{3}{4}}\widehat{W}(s,y) ) ) \widehat{W}(ds,dy ) . \end{aligned}$$

We claim that

$$\begin{aligned} \lim _{t\rightarrow \infty } R_t =0 \end{aligned}$$

(2.5)

in $L^2(\Omega )$. Indeed, using bounds for the density of $\hat{W}(s,y)$, we obtain

$$\begin{aligned} {\mathbb {E}}[ R_t^2]&\le \lambda ^2 t^{\frac{1}{4}} (t-t_0)^{\frac{1}{2}} \int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} \left( \frac{x}{\sqrt{t-t_0}} -y\right) \\&\quad \times {\mathbb {E}}\left[ \left| \varphi \left( (t-t_0)^{\frac{3}{4}} \widehat{W}(s,y) + \Phi _{t,y}\right) -\varphi \left( (t-t_0)^{\frac{3}{4}} \widehat{W}(s,y)\right) \right| ^2 \right] dyds\\&\le \lambda ^2 \left( \frac{t}{t-t_0} \right) ^{\frac{1}{4}} \int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} \left( \frac{x}{\sqrt{t-t_0}} -y\right) \frac{1}{\sqrt{2\pi s |y|}}\\&\quad \times {\mathbb {E}}\left[ \int _{{\mathbb {R}}} \left| \varphi (z+ \Phi _{t,y} ) -\varphi (z ) \right| ^2 dz \right] dy ds. \end{aligned}$$

Taking into account that $\int _{{\mathbb {R}}} \left| \varphi (z+ \Phi _{t,y} ) -\varphi (z ) \right| ^2 dz \le 2 \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})}$, and using that

$$\begin{aligned} \lim _{t\rightarrow \infty } \int _{{\mathbb {R}}} \left| \varphi (z+ \Phi _{t,y} ) -\varphi (z ) \right| ^2 dz=0 \end{aligned}$$

almost surely, for any $y\in {\mathbb {R}}$, we conclude the proof of (2.5) by the dominated convergence theorem.

Furthermore, proceeding as in Steps 1–3, we can show that, as $t\rightarrow \infty$, $B^{(1)}_t$ converges to

$$\begin{aligned} \widehat{{\mathbb {E}}} \left[ \exp \left( i\lambda \beta _{0, L_{0,1} \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})} } \right) \right] , \end{aligned}$$

where $L_{0,1}=\int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} (y ) \delta _0(\widehat{W}(s, y)) dyds$ and $\beta _0$ is independent of $\widehat{W}$. As a consequence, for every bounded and ${\mathcal {F}}_{t_0}$-measurable random variable G, we obtain

$$\begin{aligned} \lim _{t\rightarrow \infty } {\mathbb {E}}[ G \exp \left( i\lambda t^{\frac{1}{8}} u(t,x) \right) ] = {\mathbb {E}}[G] {\mathbb {E}}\left[ \exp \left( i\lambda \beta _{0, L_{0,1} \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})} } \right) \right] . \end{aligned}$$

This completes the proof. $\square$

3 Large Times and Space Averages

The asymptotic behavior of the spatial averages $\int _{-R} ^R u(t,x) dx$ as $R\rightarrow \infty$ has been recently studied in References [3,4,5]. In these articles, u(t, x) is the solution to a stochastic partial differential equation with initial condition $u(0,x)=1$ and a Lipschitz nonlinear coefficient function $\sigma (u)$. The solution process is stationary in $x\in {\mathbb {R}}$, and the limit is Gaussian after a proper normalization of the solution process. In the case considered here, the lack of stationarity creates different limit behaviors. In order to achieve a limit, we will consider the case where both R and t tend to infinity.

Set

$$\begin{aligned} u_R(t)= \int _{-R} ^R \int _0^t \int _{{\mathbb {R}}} p_{t-s} (x-y) \varphi (W(s,y))W(ds,dy) dx. \end{aligned}$$

As before, $u_R(t)$ has the same law as

$$\begin{aligned} \widetilde{u}_R(t)= t^{\frac{1}{4}} \int _{-R} ^R \int _0^1 \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}}-y\right) \varphi \left( t^{\frac{3}{4}} W(s,y)\right) W(ds,dy) dx. \end{aligned}$$

Consider first the case where $\varphi$ is an homogeneous function.

Theorem 3.1

Suppose that $\varphi (x) = |x| ^\alpha$ for some $\alpha >0$. Suppose that $t_R \rightarrow \infty$ as $R\rightarrow \infty$. Then, if we let $\widehat{W}$ be a two-parameter Wiener process independent of W, the following stable convergences hold true:

• (i) If $\frac{R}{\sqrt{t_R}} \rightarrow c$, with $c\in (0,\infty )$,

  $$\begin{aligned} t_R^{-\frac{3}{4} (\alpha +1)} u(t_R) {\mathop {\longrightarrow }\limits ^\mathrm{stably}}\int _{-c} ^c \int _0^1 \int _{{\mathbb {R}}} p_{1-s} (x-y) |\widehat{W}(s, y))|^\alpha \widehat{W}(ds,dy)dx. \end{aligned}$$

• (ii) If $\frac{R}{\sqrt{t_R}} \rightarrow 0$,

  $$\begin{aligned} R^{-1} t_R^{-\frac{3\alpha +1}{4}} u(t_R) {\mathop {\longrightarrow }\limits ^\mathrm{stably}}2 \int _0^1 \int _{{\mathbb {R}}} p_{1-s} (y) |\widehat{W} (s, y))|^\alpha \widehat{W}(ds,dy)dx. \end{aligned}$$

• (iii) If $\frac{R}{\sqrt{t_R}} \rightarrow \infty$,

  $$\begin{aligned} R ^{-\frac{ \alpha +1}{2}} t_R^{-\frac{\alpha +1}{2}} u(t_R) {\mathop {\longrightarrow }\limits ^\mathrm{stably}}\int _{-1} ^{ 1} \int _0^1 |\widehat{W}(s,y)| ^{\alpha } \widehat{W}(ds,dy). \end{aligned}$$

Proof

We have, with the change of variable $\frac{x}{\sqrt{t_R}} \rightarrow x$,

$$\begin{aligned} \widetilde{u}_R(t_R)= t_R^{\frac{3\alpha +1}{4}+\frac{1}{2}} \int _{-R/\sqrt{t_R}} ^{ R/\sqrt{t_R}} \int _0^1\int _{{\mathbb {R}}} p_{1-s} (x-y) |W(s,y)| ^\alpha W(ds,dy) dx, \end{aligned}$$

and therefore, (i) follows by letting $R\rightarrow \infty$.

If $\frac{R}{\sqrt{t_R}} \rightarrow 0$, with the change of variable $x \rightarrow Rx$, we can write

$$\begin{aligned} \widetilde{ u}_R(t_R)=R t_R^{\frac{3\alpha +1}{4}} \int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{1-s} \left( x\frac{R}{\sqrt{t_R}}-y\right) |W(s,y)| ^\alpha W(ds,dy) dx, \end{aligned}$$

(3.1)

which implies (ii).

The proof of (iii) is more involved. Making the change of variable $y \rightarrow y \frac{R}{\sqrt{t_R}}$ in (3.1) yields

$$\begin{aligned} \widetilde{ u}_R(t_R)&=R ^{\frac{ \alpha +3}{2}} t_R^{\frac{\alpha }{2}} \int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{1-s} \left( \frac{R}{\sqrt{t_R}}(x-y)\right) |W(s,y)| ^\alpha W(ds,dy) dx \\&=R ^{\frac{ \alpha +1}{2}} t_R^{\frac{ \alpha +1}{2}} \int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{\frac{t_R}{R^2}(1-s)} (x-y) |W(s,y)| ^\alpha W(ds,dy) dx. \end{aligned}$$

Finally, the stochastic integral

$$\begin{aligned} \int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{\frac{t_R}{R^2}(1-s)} (x-y) |W(s,y)| ^{\alpha } W(ds,dy)dx \end{aligned}$$

converges in $L^2(\Omega )$ as $R\rightarrow \infty$ to

$$\begin{aligned} \int _{-1} ^{ 1} \int _0^1 |W(s,y)| ^{\alpha } W(ds,dy). \end{aligned}$$

The stable character of the convergence can be proved by the same arguments, based on the conditional characteristic function, as in the proof of Theorem 1.2. $\square$

For a function which satisfies integrability conditions with respect to the Lebesgue measure, we have the following result.

Theorem 3.2

Suppose that $\varphi \in L^2({\mathbb {R}})$ and that $t_R \rightarrow \infty$ as $R\rightarrow \infty$. Then, with Z a N(0, 1) random variable and $\widehat{W}$ an independent two-parameter Wiener process such that $(Z, \widehat{W})$ are independent of W, the following stable convergences hold true:

• (i) If $\frac{R}{\sqrt{t_R}} \rightarrow c$, with $c\in (0,\infty )$,

  $$\begin{aligned} t_R^{-\frac{3}{8}} u(t_R) {\mathop {\longrightarrow }\limits ^\mathrm{stably}}Z \left( \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})}\int _0^1 \int _{{\mathbb {R}}} \left( \int _{-c} ^c p_{1-s} (x-y) dx \right) ^2 \delta _0(W(s,y)) dyds \right) ^{\frac{1}{2}}. \end{aligned}$$

• (ii) If $\frac{R}{\sqrt{t_R}} \rightarrow 0$,

  $$\begin{aligned} R^{-1} t_R^ {\frac{1}{2}} u(t_R) {\mathop {\longrightarrow }\limits ^\mathrm{stably}}Z \left( 2\Vert \varphi \Vert ^2_{L^2({\mathbb {R}})}\int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} (y) \delta _0(W(s,y)) dyds \right) ^{\frac{1}{2}}. \end{aligned}$$

• (iii) If $\frac{R}{\sqrt{t_R}} \rightarrow \infty$,

  $$\begin{aligned} R ^{-\frac{1}{2}} t_R^{\frac{1}{4}} u(t_R) {\mathop {\longrightarrow }\limits ^\mathrm{stably}}Z \left( 2 \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})}\int _0^1 \int _{-1}^1 p^2_{1-s} (y) \delta _0(W(s,y)) dyds \right) ^{\frac{1}{2}}. \end{aligned}$$

Proof

Let us prove first the case (i). We have, with the change of variable $\frac{x}{\sqrt{t_R}} \rightarrow x$,

$$\begin{aligned} \widetilde{u}_R(t_R)= t_R^{\frac{3}{4}} \int _{-R/\sqrt{t_R}} ^{ R/\sqrt{t_R}} \int _0^1\int _{{\mathbb {R}}} p_{1-s} (x-y) \varphi \left( t_R^{\frac{3}{4}} W(s,y)\right) W(ds,dy) dx. \end{aligned}$$

Consider the family of martingales

$$\begin{aligned} M_R(\cdot , x)= t_R^{\frac{3}{8}} \int _{-R/\sqrt{t_R}} ^{ R/\sqrt{t_R}} \int _0^\cdot \int _{{\mathbb {R}}} p_{1-s} (x-y) \varphi \left( t_R^{\frac{3}{4}} W(s,y)\right) W(ds,dy) dx, \end{aligned}$$

$r\in [0,1]$. We can write

$$\begin{aligned} \langle M_R(\cdot , x )\rangle _r= t_R^{\frac{3}{4}} \int _{ \left[ -\frac{R}{\sqrt{t_R}}, \frac{R}{\sqrt{t_R}} \right] ^2} \int _0^r\int _{{\mathbb {R}}} p_{ 1-s} (x-y) p_{1-s} (x'-y) \varphi ^2\left( t_R^{\frac{3}{4}} W(s,y)\right) dydsdx dx'. \end{aligned}$$

Then, as in the proof of Theorem 1.3, we can show that $\langle M_R(\cdot , x )\rangle _r$ converges in $L^1(\Omega )$ as $R\rightarrow \infty$ to the weighted local time

$$\begin{aligned} \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})}\int _0^r \int _{{\mathbb {R}}} \left( \int _{-c} ^c p_{1-s} (x-y) dx \right) ^2 \delta _0(W(s,y)) dyds. \end{aligned}$$

This completes the proof of (i).

If $\frac{R}{\sqrt{t_R}} \rightarrow 0$, with the change of variable $x \rightarrow Rx$, we can write

$$\begin{aligned} \widetilde{ u}_R(t_R)=R t_R^{\frac{1}{4}} \int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{1-s} \left( x\frac{R}{\sqrt{t_R}}-y\right) \varphi \left( t_R^{\frac{3}{4}} W(s,y)\right) W(ds,dy) dx. \end{aligned}$$

(3.2)

As before, the stochastic integral

$$\begin{aligned} t_R^{\frac{3}{4}} \int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{1-s} \left( x\frac{R}{\sqrt{t_R}}-y\right) \varphi \left( t_R^{\frac{3}{4}} W(s,y)\right) W(ds,dy) dx \end{aligned}$$

converges in law to

$$\begin{aligned} Z \left( 2\Vert \varphi \Vert ^2_{L^2({\mathbb {R}})}\int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} (y) \delta _0(W(s,y)) dyds \right) ^{\frac{1}{2}}, \end{aligned}$$

which implies (ii). To show (iii), we make the change of variable $y \rightarrow y \frac{R}{\sqrt{t_R}}$ in (3.2) to get

$$\begin{aligned} \widetilde{ u}_R(t_R)&=R ^{\frac{3}{2} } \int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{1-s} \left( \frac{R}{\sqrt{t_R}}(x-y)\right) \varphi \left( t_R^{\frac{3}{4}} W(s,y)\right) W(ds,dy) dx \\&=R ^{\frac{1}{2}} t_R^{\frac{1}{2}} \int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{\frac{t_R}{R^2}(1-s)} (x-y) \varphi \left( t_R^{\frac{3}{4}} W(s,y)\right) W(ds,dy) dx. \end{aligned}$$

Finally, the stochastic integral

$$\begin{aligned} t_R^{\frac{3}{4}}\int _{-1} ^{ 1} \int _0^1\int _{{\mathbb {R}}} p_{\frac{t_R}{R^2}(1-s)} (x-y) \varphi \left( t_R^{\frac{3}{4}} W(s,y)\right) W(ds,dy) dx \end{aligned}$$

converges in law as $R\rightarrow \infty$ to

$$\begin{aligned} Z \left( 2 \Vert \varphi \Vert ^2_{L^2({\mathbb {R}})}\int _0^1 \int _{-1}^1 p^2_{1-s} (y) \delta _0(W(s,y)) dyds \right) ^{\frac{1}{2}}. \end{aligned}$$

The stable character of the convergence can be proved by the same arguments, based on the conditional characteristic function, as in the proof of Theorem 1.3. $\square$

4 Case of a Nonlinear Coefficient $\sigma$

In this section, we discuss the case of a nonlinear stochastic heat equation

$$\begin{aligned} \frac{\partial u }{\partial t} = \frac{1}{2} \frac{\partial ^2u }{\partial x^2} +\sigma (u) \frac{ \partial ^2 W}{\partial t\partial x}, \quad x\in {\mathbb {R}}, t\ge 0, \end{aligned}$$

(4.1)

with initial condition $u(0,z)=1$, where $\sigma : {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Lipschitz function. The mild solution to equation (4.1) is given by

$$\begin{aligned} u(t,x)= 1+ \int _0^t \int _{{\mathbb {R}}} p_{t-s} (x-y) \sigma (u(s,y)) W(ds,dy). \end{aligned}$$

We are interested in the asymptotic behavior of u(t, x) as t tends to infinity. As before, we consider different cases:

Case 1.    Suppose that $\sigma (u)=u$. In this case, the solution has a Wiener chaos expansion given by

$$\begin{aligned} u(t,x)&=1+ \sum _{n\ge 1} \int _{{\mathbb {R}}^{n}} \int _{\Delta _n(t) } \prod _{i=0}^{n-1} p_{s_i - s_{i+1}} ( x_i - x_{i+1} ) \, \, W(ds_1, dx_1)\cdots W(ds_n, dx_n) \\&=: 1 + \sum _{n\ge 1} I_n(f_{t,x,n} ) \,, \end{aligned}$$

with

$$\begin{aligned} f_{t,x,n}(s_1, \dots , s_n, x_1, \dots , x_n) = \mathbf{1}_{\Delta _n(t)} (s_1,\dots , s_n) \prod _{i=0}^{n-1} p_{s_i - s_{i+1}}( x_i - x_{i+1} ) \end{aligned}$$

and $\Delta _n(t) =\{ (s_1, \dots , s_n): 0<s_1< \cdots< s_n <t\}$. Here, $I_n$ denotes the multiple stochastic integral of order n with respect to the noise W. If we consider the projection of u(t, x) on a fixed Wiener chaos, we can write with the change of variables $s_i \rightarrow ts_i$ and $x_i \rightarrow \sqrt{t }y_i$,

$$\begin{aligned} I_n(f_{t,x,n} )&= \int _{\Delta _n(1) }\int _{{\mathbb {R}}^n} p_{t(1-s_1)}\left( \frac{x}{\sqrt{t}} -x_1\right) \\&\qquad \times \prod _{i=1}^{n-1} p_{t(s_i-s_{i+1})} (x_i-x_{i+1}) W(tds_1,\sqrt{t}dx_1) \cdots W(tds_n,\sqrt{t}dx_n) \\&=t^{-\frac{n}{2}} \int _{\Delta _n(1) }\int _{{\mathbb {R}}^n} p_{1-s_1} \left( \frac{x}{\sqrt{t}} -x_1\right) \\&\qquad \times \prod _{i=1}^{n-1} p_{s_i-s_{i+1}} (x_i-x_{i+1}) W(tds_1,\sqrt{t}dx_1) \cdots W(tds_n,\sqrt{t}dx_n). \end{aligned}$$

By the scaling properties of the two-parameter Wiener process, it follows that $I_n(f_{t,x,n} )$ has the same law as

$$\begin{aligned} \widetilde{I}_n(f_{t,x,n} )&:=t^{\frac{3n}{4}} \int _{\Delta _n(1) } \int _{{\mathbb {R}}^n} p_{1-s_1}\left( \frac{x}{\sqrt{t}} -x_1\right) \\&\qquad \times \prod _{i=1}^{n-1} p_{s_i-s_{i+1}} (x_i-x_{i+1}) W(ds_1,dx_1) \cdots W(ds_n,dx_n). \end{aligned}$$

As a consequence, $t^{-\frac{3}{4} n} I_n(f_{t,x,n} )$ converges stably to

$$\begin{aligned} \int _{\Delta _n(1) }\int _{{\mathbb {R}}^n} \prod _{i=0}^{n-1} p_{s_i-s_{i+1}} (x_i-x_{i+1}) \widehat{W}(ds_1,dx_1) \cdots \widehat{W}(ds_n,dx_n), \end{aligned}$$

where $\widehat{W}$ is a two-parameter Wiener process independent of W and with the convention $s_0=1$ and $x_0=0$.

Notice that the rate of convergence depends polynomially with respect to the order of the Wiener chaos. This property gives a hint toward a possible exponential type behavior of u(t, x) . This is consistent with the asymptotic behavior of $\log u(t,x)$, when $u(0,x)=\delta _0(x)$, obtained by Amir, Corwin and Quastel in [1].

Case 2.    When $\sigma$ is a Lipschitz function that belongs to $L^2({\mathbb {R}})$, the problem is much more involved and we will give here just some ideas on how to proceed. We can write

$$\begin{aligned} u(t,x)=1+ \frac{1}{\sqrt{t}} \int _0^1 \int _{{\mathbb {R}}} p_{1-s}\left( \frac{x}{\sqrt{t}} -y\right) \sigma (u( ts, \sqrt{t} y)) W(tds ,\sqrt{t}dy). \end{aligned}$$

Furthermore,

$$\begin{aligned} u( ts, \sqrt{t} y)&= 1+ \int _0^{ts} \int _{{\mathbb {R}}} p_{ts-r} (\sqrt{t}y -z) \sigma (u(r,z)) W(dr,dz) \\&=1+ \frac{1}{\sqrt{t}} \int _0^s \int _{{\mathbb {R}}} p_{s-r} (y-z) \sigma (u(tr, \sqrt{t} z)) W(t dr, \sqrt{t} dz). \end{aligned}$$

By the scaling properties of the two-parameter Wiener process, as a function of $\widehat{W}$, $u( ts, \sqrt{t} y)$ has the same law as

$$\begin{aligned} v^t(s,y)= 1+ t^{\frac{1}{4}} \int _0^s \int _{{\mathbb {R}}} p_{s-r} (y-z) \sigma ( v^t(r,z))) \widehat{W}(dr, dz). \end{aligned}$$

Therefore, u(t, x) has the same law as

$$\begin{aligned} \widetilde{u}(t,x)= 1+ t^{\frac{1}{4}} \int _0^1 \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) \sigma (v^t( s, y)) \widehat{W}(ds ,dy). \end{aligned}$$

Then,

$$\begin{aligned} t^{-\frac{1}{6}} \widetilde{u}(t,x)= t^{-\frac{1}{6}} + t^{\frac{1}{12}} \int _0^1 \int _{{\mathbb {R}}} p_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) \sigma (v^t( s,y)) \widehat{W}(ds ,dy). \end{aligned}$$

The quadratic variation of the martingale part of the above stochastic integral is

$$\begin{aligned}&t^{\frac{1}{6}} \int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) \sigma ^2(1+ t^{\frac{1}{6}} Z^t( s, y)) dsdy \\&\quad = \int _0^1 \int _{{\mathbb {R}}} p^2_{1-s} \left( \frac{x}{\sqrt{t}} -y\right) \int _{{\mathbb {R}}} \sigma ^2(\xi ) \delta _0( Z^t( s, y) + t^{-\frac{1}{6}} -\xi t^{-\frac{1}{6}}) d\xi dsdy \end{aligned}$$

where $Z^t(s,y)$ satisfies

$$\begin{aligned} Z^t( s, y)= t^{-\frac{1}{6}} + t^{\frac{1}{12}} \int _0^s \int _{{\mathbb {R}}} p_{s-r} (y-z) \sigma ( 1+ t^{\frac{1}{6}} Z^t(r,z))) \widehat{W}(dr, dz). \end{aligned}$$

From these computations, we conjecture that $t^{-\frac{1}{6}}$ is the right normalization and the limit would satisfy an equation involving a weighted local time of the solution. However, proving these facts is a challenging problem not to be treated in this paper.

Appendix: The Asymptotic Ray–Knight Theorem

The following version has been adapted from [2] (see also [8]). Here, $H^2_{0,\text {loc}}$ denotes the space of locally square integrable martingales.

Theorem 5.1

For $k \ge 2$ and $n \ge 1$, define a sequence $(M_{1,r}^n,M_{2,r}^n, \dots , M_{k,r}^n)$ of k-tuples of continuous local martingales $(M_{j,r}^n)_{r \ge 0} \in H^2_{0,\text {loc}}$ such that for fixed $j=1,\dots ,k$ the limit $\left\langle M_j^n, M_j^n \right\rangle _{\infty }$ is either infinite for all n, or finite for all n. After possibly enlarging the underlying probability space, each $M_j^n$ possesses a Dambis–Dubins–Schwarz Brownian motion $\beta ^n_j$ and an associated time change $T_j^n(y)$, such that

$$\begin{aligned} M_{j,T_j^n(r)}^n = \beta ^n_{j,r} \end{aligned}$$

(5.1)

for $r\ge 0$ and $1 \le j \le k$ (for a proof, see, for example, [9, Ch. V, Thm. 1.7]). If for $a \ge 0$ and $1 \le i,j \le k$ with $i \ne j$

$$\begin{aligned} \sup _{r \in [0,a]} {|\langle {M_i^n},{M_j^n}\rangle _r|} \rightarrow 0, \qquad (n \rightarrow \infty ) \end{aligned}$$

(5.2)

in probability, then the k-dimensional process $\beta ^n_r =(\beta _{1,r}^n,\beta _{2,r}^n, \dots ,\beta _{k,r}^n)_{r \ge 0}$ converges in distribution to a k-dimensional Brownian motion $(\beta _r)_{r\ge 0}$.