Best Finite Approximations of Benford’s Law

Abstract

For arbitrary Borel probability measures with compact support on the real line, characterizations are established of the best finitely supported approximations, relative to three familiar probability metrics (Lévy, Kantorovich, and Kolmogorov), given any number of atoms, and allowing for additional constraints regarding weights or positions of atoms. As an application, best (constrained or unconstrained) approximations are identified for Benford’s Law (logarithmic distribution of significands) and other familiar distributions. The results complement and extend known facts in the literature; they also provide new rigorous benchmarks against which to evaluate empirical observations regarding Benford’s law.

1 Introduction

Given real numbers $b>1$ and $x\ne 0$, denote by $S_b(x)$ the unique number in [1, b[ such that $|x|= S_b(x) b^k$ for some (necessarily unique) integer k; for convenience, let $S_b(0) = 0$. The number $S_b(x)$ often is referred to as the base-bsignificand of x, a terminology particularly well-established in the case of b being an integer. (Unlike in much of the literature [2, 4, 18, 28], the case of integer b does not carry special significance in this article.) A Borel probability measure $\mu$ on $\mathbb {R}$ is Benford baseb, or b-Benford for short, if

$$\begin{aligned} \mu \bigl ( \{ x\in \mathbb {R}: S_b(x) \le s\}\bigr ) = \frac{\log s}{\log b} \quad \forall s \in [1,b[ ; \end{aligned}$$

(1.1)

here and throughout, $\log$ denotes the natural logarithm. Benford probabilities (or random variables) exhibit many interesting properties and have been studied extensively [1, 6, 14, 20, 25, 29]. They provide one major pathway into the study of Benford’s law, an intriguing, multi-faceted phenomenon that attracts interest from a wide range of disciplines; see, e.g., [4] for an introduction, and [21] for a panorama of recent developments. Specifically, denoting by $\beta _b$ the Borel probability measure with

$$\begin{aligned} \beta _b([1,s]) = \frac{\log s}{\log b} \quad \forall s\in [1,b[ , \end{aligned}$$

note that $\mu$ is b-Benford if and only if $\mu \circ S_b^{-1} = \beta _b$.

Historically, the case of decimal (i.e., base-10) significands has been the most prominent, with early empirical studies on the distribution of decimal significands (or significant digits) going back to Newcomb [23] and Benford [2]. If $\mu$ is 10-Benford, note that in particular

$$\begin{aligned} \mu \bigl (\{x\in \mathbb {R}: \text{ leading } \text{ decimal } \text{ digit } \text{ of } x = D \} \bigr ) = \frac{\log (1+D^{-1})}{\log 10 }\quad \forall D =1 , \ldots , 9 . \end{aligned}$$

(1.2)

For theoretical as well as practical reasons, mathematical objects such as random variables or sequences, but also concrete, finite numerical data sets that conform, at least approximately, to (1.1) or (1.2) have attracted much interest [10, 20, 28, 29]. Time and again, Benford’s law has emerged as a perplexingly prevalent phenomenon. One popular approach to understand this prevalence seeks to establish (mild) conditions on a probability measure that make (1.1) or (1.2) hold with good accuracy, perhaps even exactly [7, 12,13,14, 25]. It is the goal of the present article to provide precise quantitative information for this approach.

Concretely, notice that while a finitely supported probability measure, such as, e.g., the empirical measure associated with a finite data set [5], may conform to the first-digit law (1.2), it cannot possibly satisfy (1.1) exactly. For such measures, therefore, it is natural to quantify, as accurately as possible, the failure of equality in (1.1), that is, the discrepancy between $\mu \circ S_b^{-1}$ and $\beta _b$. Utilizing three different familiar metrics $d_{*}$ on probabilities (Lévy, Kantorovich, and Kolmogorov metrics; see Sect. 2 for details), the article does this in a systematic way: For every $n\in \mathbb {N}$, the value of $\min _{\nu } d_{*}(\beta _b, \nu )$ is identified, where $\nu$ is assumed to be supported on no more than n atoms (and may be subject to further restrictions such as, e.g., having only atoms of equal weight, as in the case of empirical measures); the minimizers of $d_{*}(\beta _b, \nu )$ are also characterized explicitly.

The scope of the results presented herein, however, extends far beyond Benford probabilities. In fact, a general theory of best (constrained or unconstrained) $d_{*}$-approximations is developed. As far as the authors can tell, no such theories exist for the Lévy and Kolmogorov metrics—unlike in the case of the Kantorovich metric where it (mostly) suffices to rephrase pertinent known facts [16, 30]. Once the general results are established, the desired quantitative insights for Benford probabilities are but straightforward corollaries. (Even in the context of Kantorovich distance, the study of $\beta _b$ yields a rare new, explicit example of an optimal quantizer [16].) In particular, it turns out that, under all the various constraints considered here, the limit $Q_{*} = \lim _{n\rightarrow \infty } n \min _{\nu } d_{*}(\beta _b, \nu )$ always exists, is finite and positive, and can be computed more or less explicitly. This greatly extends earlier results, notably of [5], and also suggests that $n^{-1}Q_{*}$ may be an appropriate quantity against which to evaluate the many heuristic claims of closeness to Benford’s law for empirical data sets found in the literature [3, 21, 22].

The main results in this article, then, are existence proofs and characterizations for the minimizers of $d_{*}(\mu , \nu )$ for arbitrary (compactly supported) probability measures $\mu$, as provided by Theorems 3.5, 3.6, 4.1, 5.1, and 5.4 (where additional constraints are imposed on the sizes or locations of the atoms of $\nu$), as well as by Theorems 3.9 and 5.6 (where such constraints are absent). As suggested by the title, this work aims primarily at a precise analysis of conformance to Benford’s law (or the lack thereof). Correspondingly, much attention is paid to the special case of $\mu = \beta _b$, leading to explicit descriptions of best (constrained or unconstrained) approximations of the latter (Corollaries 3.10, 4.3, and 5.8) and the exact asymptotics of $d_{*}(\beta _b, \nu )$. As indicated earlier, however, the main results are much more general. To emphasize this fact, two other simple but illustrative examples of $\mu$ are repeatedly considered as well (though in less detail than $\beta _b$), namely the familiar $\text{ Beta }(2,1)$ distribution and the (perhaps less familiar) inverse Cantor distribution. It turns out that while the former is absolutely continuous (w.r.t. Lebesgue measure) and its best approximations behave like those of $\beta _b$ in most respects (Examples 1, 3, 5, and 7), the latter is discrete and the behavior of its best approximations is more delicate (Examples 2, 4, 6, and 8). Even with only a few details mentioned, these examples will help the reader appreciate the versatility of the main results.

The organization of this article is as follows: Sect. 2 reviews relevant basic properties of one-dimensional probabilities and the three main probability metrics used throughout. Each of Sects. 3 to 5 then is devoted specifically to one single metric. In each section, the problem of best (constrained or unconstrained) approximation by finitely supported probability measures is first addressed in complete generality, and then the results are specialized to $\beta _b$ as well as other concrete examples. Section 6 summarizes and discusses the quantitative results obtained, and also mentions a few natural questions for subsequent studies.

2 Probability Metrics

Throughout, let $\mathbb {I}\subset \mathbb {R}$ be a compact interval with Lebesgue measure $\lambda (\mathbb {I})>0$, and $\mathcal {P}$ the set of all Borel probability measures on $\mathbb {I}$. Associate with every $\mu \in \mathcal {P}$ its distribution function$F_{\mu }: \mathbb {R}\rightarrow \mathbb {R},$ given by

$$\begin{aligned} F_{\mu }(x) = \mu (\{ y\in \mathbb {I}: y \le x\}) \quad \forall \ x \in \mathbb {R}, \end{aligned}$$

as well as its (upper) quantile function$F_{\mu }^{-1}:\, [0,1[ \, \rightarrow \mathbb {R},$ given by

$$\begin{aligned} F_{\mu }^{-1} (x) = \left\{ \begin{array}{lcl} \min \mathbb {I}&{} \, &{}\quad \text{ if } 0\le x<\mu (\{\min \mathbb {I}\})\, ,\\ \sup \{y\in \mathbb {I}: F_{\mu }(y) \le x\} &{} \, &{}\quad \text{ if } \mu (\{\min \mathbb {I}\})\le x<1 . \end{array} \right. \end{aligned}$$

(2.1)

Note that $F_{\mu }$ and $F_{\mu }^{-1}$ both are non-decreasing, right-continuous, and bounded. The support of $\mu$, denoted $\text{ supp }\, \mu$, is the smallest closed subset of $\mathbb {I}$ with $\mu$-measure 1. Endowed with the weak topology, the space $\mathcal {P}$ is compact and metrizable.

Three important different metrics on $\mathcal {P}$ are discussed in detail in this article; for a panorama of other metrics, the reader is referred, e.g., to [15, 27] and the references therein. Given probabilities $\mu , \nu \in \mathcal {P}$, their Lévy distance is

$$\begin{aligned} d_\mathsf{L} (\mu , \nu ) = \omega \inf \left\{ y\ge 0: F_{\mu } (\cdot -y) - y \le F_{\nu } \le F_{\mu } (\cdot +y) + y \right\} , \end{aligned}$$

(2.2)

with $\omega =\max \{1,\lambda (\mathbb {I})\}/\lambda (\mathbb {I});$ their $L^r$-Kantorovich (or transport) distance, with $r\ge 1$, is

$$\begin{aligned} d_r (\mu , \nu ) = \lambda (\mathbb {I})^{-1} \left( \int _0^1 \left| F_{\mu }^{-1}(y) - F_{\nu }^{-1}(y)\right| ^r \mathrm{d}y\right) ^{1/r} = \lambda (\mathbb {I})^{-1} \Vert F_{\mu }^{-1} - F_{\nu }^{-1}\Vert _r ; \end{aligned}$$

(2.3)

and their Kolmogorov (or uniform) distance is

$$\begin{aligned} d_\mathsf{K} (\mu , \nu ) = \sup \limits _{x\in \mathbb {R}} \left| F_{\mu } (x) - F_{\nu } (x)\right| = \Vert F_{\mu } - F_{\nu } \Vert _{\infty }. \end{aligned}$$

Henceforth, the symbol $d_{*}$ summarily refers to any of $d_\mathsf{L}, d_r$, and $d_\mathsf{K}$. The (unusual) normalizing factors in (2.2) and (2.3) guarantee that all three metrics are comparable numerically in that $\sup _{\mu , \nu \in \mathcal {P}} d_{*}(\mu , \nu ) =1$ in either case. Note that

$$\begin{aligned} d_1(\mu , \nu ) = \lambda (\mathbb {I})^{-1} \int _{\mathbb {I}} \left| F_{\mu } (x) - F_{\nu } (x)\right| \, \mathrm{d}x \quad \forall \ \mu , \nu \in \mathcal {P}, \end{aligned}$$

by virtue of Fubini’s theorem. The metrics $d_\mathsf{L}$ and $d_r$ are equivalent: They both metrize the weak topology on $\mathcal {P}$, and hence are separable and complete. By contrast, the complete metric $d_\mathsf{K}$ induces a finer topology and is non-separable. However, when restricted to $\mathcal {P}_\mathsf{cts} :=\{\mu \in \mathcal {P}: \mu (\{x\}) = 0 \,\forall \ x \in \mathbb {I}\}$, a dense $G_{\delta }$-set in $\mathcal {P}$, the metric $d_\mathsf{K}$ does metrize the weak topology on $\mathcal {P}_\mathsf{cts}$ and is separable. The values of $d_\mathsf{L}, d_r,$ and $d_\mathsf{K}$ are not completely unrelated since, as is easily checked,

$$\begin{aligned} d_1 \le \frac{1+\lambda (\mathbb {I})}{\omega \lambda (\mathbb {I})} d_\mathsf{L} \, , \quad d_r \le d_s (\text{ if } r\le s) \, , \quad d_1 \le d_\mathsf{K} \, , \quad d_\mathsf{L} \le \omega d_\mathsf{K} , \end{aligned}$$

(2.4)

and all bounds in (2.4) are best possible. Beyond (2.4), however, no relative bounds exist between $d_\mathsf{L}, d_r$, and $d_\mathsf{K}$ in general: If $*\ne 1$, $*\ne \circ$, and $(*, \circ ) \not \in \{ (\mathsf{L}, \mathsf{K}), (r,s) \}$ with $r\le s$ then

$$\begin{aligned} \sup \limits _{\mu , \nu \in \mathcal {P}: \mu \ne \nu } \frac{d_{*} (\mu , \nu )}{d_{\circ } (\mu , \nu )} = +\,\infty . \end{aligned}$$

Each metric $d_{*}$, therefore, captures a different aspect of $\mathcal {P}$ and deserves to be studied independently. To illustrate this further, let $\mathbb {I}= [0,1]$, $\mu =\delta _0 \in \mathcal {P}$, and $\mu _k=(1-k^{-1})\delta _0+k^{-1}\delta _{k^{-2}}$ for $k\in \mathbb {N}$; here and throughout, $\delta _a$ denotes the Dirac (probability) measure concentrated at $a\in \mathbb {R}.$ Then $\lim _{k\rightarrow \infty } d_{*} (\mu , \mu _k) = 0$, but the rate of convergence differs between metrics:

$$\begin{aligned} d_\mathsf{L} (\mu , \mu _k) = k^{-2} \, , \quad d_r (\mu , \mu _k) =k^{-2-1/r}\, , \quad d_\mathsf{K} (\mu , \mu _k) = k^{-1} \, \quad \forall \ k\in \mathbb {N}. \end{aligned}$$

The goal of this article is first to identify, for each metric $d_{*}$ introduced earlier, the best finitely supported $d_{*}$-approximation(s) of any given $\mu \in \mathcal {P}$. The general results are then applied to Benford’s law, as well as other concrete examples. Specifically, if $\mu =\beta _b$ for some $b>1$ then it is automatically assumed that $\mathbb {I}=[1,b].$ The following unified notation and terminology is used throughout: for every $n\in \mathbb {N}$, let $\varXi _n=\{x\in \mathbb {I}^n: x_{,1}\le \cdots \le x_{,n}\}$, $\varPi _n=\{p\in \mathbb {R}^n: p_{,j}\ge 0,\ \sum _{j=1}^np_{,j}=1\}$, and for each $x\in \varXi _n$ and $p\in \varPi _n$ define $\delta _x^p=\sum _{j=1}^np_{,j}\delta _{x_{,j}}$. For convenience, $x_{,0}:=-\,\infty$ and $x_{,n+1}:=+\,\infty$ for every $x\in \varXi _n,$ as well as $P_{,i}=\sum _{j=1}^ip_{,j}$ for $i=0,\ldots ,n$ and $p\in \varPi _n$; note that $P_{,0}=0$ and $P_{,n}=1.$ Henceforth, usage of the symbol $\delta _x^p$ tacitly assumes that $x\in \varXi _n$ and $p\in \varPi _n,$ for some $n\in \mathbb {N}$ either specified explicitly or else clear from the context. Call $\delta _x^p$ a best$d_{*}$-approximation of$\mu \in \mathcal {P}$, given$x\in \varXi _n$ if

$$\begin{aligned} d_{*}\left( \mu ,\delta _x^p\right) \le d_{*}\left( \mu ,\delta _x^q\right) \quad \forall \ q\in \varPi _n . \end{aligned}$$

Similarly, call $\delta _x^p$ a best$d_{*}$-approximation of$\mu$, given$p\in \varPi _n$ if

$$\begin{aligned} d_{*}\left( \mu ,\delta _x^p\right) \le d_{*}\left( \mu ,\delta _y^p\right) \quad \forall \ y\in \varXi _n . \end{aligned}$$

Denote by $\delta _x^{\bullet }$ and $\delta _{\bullet }^p$ any best $d_{*}$-approximation of $\mu$, given x and p, respectively. Best $d_{*}$-approximations, given $p=u_n = (n^{-1}, \ldots , n^{-1})$ are referred to as best uniform$d_{*}$-approximations, and denoted $\delta _{\bullet }^{u_n}$. Finally, $\delta _x^p$ is a best$d_{*}$-approximation of$\mu \in \mathcal {P}$, denoted $\delta _{\bullet }^{\bullet , n}$, if

$$\begin{aligned} d_{*}\left( \mu ,\delta _x^p\right) \le d_{*} \left( \mu ,\delta _y^q\right) \quad \forall \ y\in \varXi _n, q\in \varPi _n . \end{aligned}$$

Notice that usage of the symbols $\delta _x^{\bullet },$$\delta ^p_{\bullet },$ and $\delta _{\bullet }^{\bullet ,n}$ always refers to a specific metric $d_{*}$ and probability measure $\mu \in \mathcal {P}$, both usually clear from the context.

Information theory sometimes refers to $d_{*} (\mu ,\delta _{\bullet }^{\bullet , n})$ as the n-th quantization error, and to $\lim _{n\rightarrow \infty } n d_{*}(\mu ,\delta _{\bullet }^{\bullet , n} )$, if it exists, as the quantization coefficient of $\mu$; see, e.g., [16]. By analogy, $d_{*} (\mu ,\delta _{\bullet }^{u_n})$ and $\lim _{n\rightarrow \infty } n d_{*} (\mu ,\delta _{\bullet }^{u_n})$, if it exists, may be called the n-th uniform quantization error and the uniform quantization coefficient, respectively.

3 Lévy Approximations

This section identifies best finitely supported $d_\mathsf{L}$-approximations (constrained or unconstrained) of a given $\mu \in \mathcal {P}$. To do this in a transparent way, it is helpful to first consider more generally a few elementary properties of non-decreasing functions. These properties are subsequently specialized to either $F_{\mu }$ or $F_{\mu }^{-1}$.

Throughout, let $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ be non-decreasing, and define $f(\pm \, \infty ) = \lim _{x\rightarrow \pm \infty } f(x)\in \overline{\mathbb {R}}$, where $\overline{\mathbb {R}} = \mathbb {R}\cup \{ -\,\infty , +\, \infty \}$ denotes the extended real line with the usual order and topology. Associate with f two non-decreasing functions $f_{\pm }: \mathbb {R}\rightarrow \overline{\mathbb {R}}$, defined as $f_{\pm } (x) = \lim _{\varepsilon \downarrow 0} f(x \pm \varepsilon )$. Clearly, $f_-$ is left-continuous, whereas $f_+$ is right-continuous, with $f_{\pm }(-\,\infty ) = f(-\,\infty )$, $f_{\pm }(+\,\infty ) = f(+\,\infty )$, as well as $f_- \le f \le f_+$, and $f_+(x) \le f_- (y)$ whenever $x<y$; in particular, $f_-(x) = f_+ (x)$ if and only if f is continuous at x. The (upper) inverse function$f^{-1}: \mathbb {R}\rightarrow \overline{\mathbb {R}}$ is given by

$$\begin{aligned} f^{-1} (t) = \sup \{ x\in \mathbb {R}: f(x) \le t\} \quad \forall \ t \in \mathbb {R}; \end{aligned}$$

by convention, $\sup \varnothing := -\,\infty$ (and $\inf \varnothing := +\,\infty$). Note that (2.1) is consistent with this notation. For what follows, it is useful to recall a few basic properties of inverse functions; see, e.g., [30, Sect. 3] for details.

Proposition 3.1

Let $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ be non-decreasing. Then $f^{-1}$ is non-decreasing and right-continuous. Also, $(f_{\pm })^{-1} = f^{-1}$, and $(f^{-1})^{-1} = f_+$.

Given two non-decreasing functions $f,g: \mathbb {R}\rightarrow \overline{\mathbb {R}}$, by a slight abuse of notation, and inspired by (2.2), let

$$\begin{aligned} d_\mathsf{L} (f,g) = \inf \{ y \ge 0 : f(\, \cdot \, - y) - y \le g \le f(\, \cdot \, + y) + y\}\in [0,+\,\infty ] . \end{aligned}$$

For instance, $d_\mathsf{L} (\mu ,\nu ) = \omega d_\mathsf{L} (F_{\mu }, F_{\nu })$ for all $\mu ,\nu \in \mathcal {P}$. It is readily checked that $d_\mathsf{L}$ is symmetric, satisfies the triangle inequality, and $d_\mathsf{L}(f,g)>0$ unless $f_- = g_-$, or equivalently, $f_+ = g_+$. Crucially, the quantity $d_\mathsf{L}$ is invariant under inversion.

Proposition 3.2

Let $f,g:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ be non-decreasing. Then $d_\mathsf{L} (f^{-1}, g^{-1}) = d_\mathsf{L} (f,g)$.

Thus, for instance, $d_\mathsf{L} (\mu , \nu ) = \omega d_\mathsf{L} (F_{\mu }^{-1}, F_{\nu }^{-1})$ for all $\mu , \nu \in \mathcal {P}$. In general, the value of $d_\mathsf{L}(f,g)$ may equal $+\,\infty .$ However, if the set $\{f\ne g\}:=\{x\in \mathbb {R}: f(x)\ne g(x)\}$ is bounded then $d_\mathsf{L}(f,g)<+\,\infty .$ Specifically, notice that $\{ F_{\mu }\ne F_{\nu }\}\subset \mathbb {I}$ and $\{F_{\mu }^{-1}\ne F_{\nu }^{-1}\}\subset [0,1[$ both are bounded for all $\mu ,\nu \in \mathcal {P}$.

Given a non-decreasing function $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$, let $I\subset \overline{\mathbb {R}}$ be any interval with the property that

$$\begin{aligned} f_- (\sup I), -f_+ (\inf I) < +\, \infty , \end{aligned}$$

(3.1)

and define an auxiliary function $\ell _{f,I}:\mathbb {R}\rightarrow \mathbb {R}$ as

$$\begin{aligned} \ell _{f,I} (x) = \inf \{ y\ge 0 : f_- (\sup I - y) - y \le x \le f_+ (\inf I + y) + y\} . \end{aligned}$$

Note that for each $x\in \mathbb {R}$, the set on the right equals $[a,+\infty [$ with the appropriate $a \ge 0$, and hence simply $\ell _{f,I} (x) = a$. Clearly, $\ell _{f,J} \le \ell _{f,I}$ whenever $J\subset I$. Also, for every $a \in \mathbb {R}$, the function $\ell _{f,\{a \}}$ is non-increasing on $]-\,\infty , f_-(a)]$, vanishes on $[f_-(a), f_+(a)]$, and is non-decreasing on $[f_+(a), +\,\infty [$. A few elementary properties of $\ell _{f,I}$ are straightforward to check; they are used below to establish the main results of this section.

Proposition 3.3

Let $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ be non-decreasing, and $I\subset \overline{\mathbb {R}}$ an interval satisfying (3.1). Then $\ell _{f,I}$ is Lipschitz continuous, and

$$\begin{aligned} 0 \le \ell _{f,I} (x) \le |x| + \max \{0, f_-(\sup I), - f_+ (\inf I)\} \quad \forall \ x \in \mathbb {R}. \end{aligned}$$

Moreover, $\ell _{f,I}$ attains a minimal value

which is positive unless $f_-(\sup I) \le f_+ (\inf I)$.

For $\mu \in \mathcal {P}$, note that (3.1) automatically holds if $f= F_{\mu }$, or if $f=F_{\mu }^{-1}$ and $I\subset [0,1]$. In these cases, therefore, $\ell _{f,I}$ has the properties stated in Proposition 3.3, and $\ell _{f,I}^*\le \frac{1}{2}$.

When formulating the main results, the following quantities are useful: Given $\mu \in \mathcal {P}$, $n\in \mathbb {N}$, and $x\in \varXi _n$, let

$$\begin{aligned} \mathsf{L}^{\bullet }(x) = \max \left\{ \ell _{F_{\mu }, [-\infty , x_{,1}]}(0), \ell _{F_{\mu }, [x_{,1}, x_{,2}]}^*, \ldots , \ell _{F_{\mu }, [x_{,n-1}, x_{,n}]}^*, \ell _{F_{\mu }, [x_{,n}, +\infty ]}(1) \right\} ; \end{aligned}$$

similarly, given $p\in \varPi _n$, let

$$\begin{aligned} \mathsf{L}_{\bullet } (p) = \max \nolimits _{j=1}^n \ell _{F_{\mu }^{-1}, [P_{,j-1}, P_{,j}]}^* . \end{aligned}$$

To illustrate these quantities for a concrete example, consider $\mu = \beta _b$, where $\ell _{F_{\mu },[x_{,j}, x_{,j+1}]}^*$ is the unique solution of

$$\begin{aligned} b^{2\ell } = \frac{x_{,j+1} - \ell }{x_{,j} + \ell } \quad j=1, \ldots , n-1 , \end{aligned}$$

whereas $\ell _{F_{\mu }, [-\infty , x_{,1}]}(0)$ and $\ell _{F_{\mu }, [x_{,n}, +\infty ]}(1)$ solve $b^{\ell } = x_{,1} -\ell$ and $b^{\ell } = b/(x_{,n} + \ell )$, respectively. (Recall that $1\le x_{,1} \le \cdots \le x_{,n} \le b$.) Similarly, $\ell _{F_{\mu }^{-1}, [P_{,j-1}, P_{,j}]}^*$ is the unique solution of

$$\begin{aligned} 2\ell = b^{P_{,j} - \ell } - b^{P_{,j-1} + \ell } \quad j = 1, \ldots , n ; \end{aligned}$$

in particular, $j \mapsto \ell _{F_{\mu }^{-1}, [(j-1)/n, j/n]}^*$ is increasing, and hence $\mathsf{L}_{\bullet }(u_n)$ is the unique solution of

$$\begin{aligned} 2L = b^{1 - L} - b^{1 + L - 1/n} . \end{aligned}$$

(3.2)

By using functions of the form $\ell _{f,I}$, the value of $d_\mathsf{L} (\mu , \nu )$ can easily be computed whenever $\nu$ has finite support.

Lemma 3.4

Let $\mu \in \mathcal {P}$ and $n\in \mathbb {N}$. For every $x\in \varXi _n$ and $p\in \varPi _n$,

$$\begin{aligned} d_\mathsf{L} \left( \mu , \delta _x^p\right) = \omega \max \nolimits _{j=0}^n \ell _{F_{\mu } , [x_{,j}, x_{,j+1}]} (P_{,j}) = \omega \max \nolimits _{j=1}^n \ell _{F_{\mu }^{-1}, [P_{,j-1}, P_{,j}]}(x_{,j}) . \end{aligned}$$

(3.3)

Proof

Label $x\in \varXi _n$ uniquely as

$$\begin{aligned} x_{,j_0 + 1}&= \cdots = x_{,j_1}< x_{,j_1+1} = \cdots = x_{,j_2}< x_{,j_2 + 1} = \cdots \\&< \cdots = x_{,j_{m-1}}< x_{,j_{m-1}+1} = \ldots = x_{,j_m} , \end{aligned}$$

with integers $i\le j_i \le n$ for $1\le i\le m$, and $j_0 = 0$, $j_m = n$, and define $y \in \varXi _m$ and $q\in \varPi _m$ as $y_{,i} = x_{,j_i}$ and $q_{,i} = P_{,j_i} - P_{, j_{i-1}}$, respectively, for $i=1, \ldots , m$. For convenience, let $I_j = [x_{,j}, x_{, j+1}]$ for $j=0, \ldots , n$, and $J_i = [y_{,i}, y_{,i+1}]= I_{j_i}$ for $i=0, \ldots , m$. With this, $\delta _{y}^{q} = \delta _x^p$, and

$$\begin{aligned} \omega ^{-1} d_\mathsf{L} \left( \mu , \delta _x^p\right) =\,&d_\mathsf{L} (F_{\mu }, F_{\delta _{y}^{q}}) \\ =&\inf \{ t \ge 0 : F_{\mu -} (y_{,i+1} - t) - t\\&\qquad \qquad \qquad \le Q_{,i} \le F_{\mu } (y_{,i} +t) + t \forall \ i=0, \ldots , m\} \\ =&\max \nolimits _{i=0}^m \ell _{F_{\mu }, J_i} (Q_{,i}) \\ \le&\max \nolimits _{j=0}^n \ell _{F_{\mu }, I_j} (P_{,j}) . \end{aligned}$$

To prove the reverse inequality, pick any $j=0,\ldots , n$. If $x_{,j}< x_{,j+1}$ then $I_j = J_i$ and $P_{,j} = Q_{,i}$, with the appropriate i, and hence $\ell _{F_{\mu }, I_j} (P_{,j}) = \ell _{F_{\mu }, J_i}(Q_{,i})$. If $x_{,j} = x_{,j+1}$ then $I_j = \{y_{,i}\}$ for some i. In this case either $P_{,j} < F_{\mu -} (y_{,i})$ and $Q_{,i-1}\le P_{,j}$, and hence

$$\begin{aligned} \ell _{F_{\mu }, I_j} (P_{,j}) = \ell _{F_{\mu }, \{y_{,i}\}} (P_{,j}) \le \ell _{F_{\mu }, \{y_{,i}\}} (Q_{,i-1}) \le \ell _{F_{\mu }, J_{i-1}} (Q_{,i-1}) ; \end{aligned}$$

or $F_{\mu -} (y_{,i}) \le P_{,j} \le F_{\mu } (y_{,i})$, and hence $\ell _{F_{\mu }, I_j} (P_{,j}) = \ell _{F_{\mu }, \{y_{,i}\}} (P_{,j}) = 0$; or $P_{,j} > F_{\mu }(y_{,i})$ and $Q_{,i} \ge P_{,j}$, and hence

$$\begin{aligned} \ell _{F_{\mu }, I_j} (P_{,j}) = \ell _{F_{\mu }, \{y_{,i}\}} (P_{,j}) \le \ell _{F_{\mu }, \{y_{,i}\}} (Q_{,i}) \le \ell _{F_{\mu }, J_i} (Q_{,i}) . \end{aligned}$$

In all three cases, therefore, $\omega ^{-1} d_\mathsf{L} (\mu ,\delta _x^p) \ge \max _{j=0}^n \ell _{F_{\mu }, I_j} (P_{,j})$, which establishes the first equality in (3.3). The second equality, a consequence of Proposition 3.2, is proved analogously. $\square$

Utilizing Lemma 3.4, it is straightforward to characterize the best finitely supported $d_\mathsf{L}$-approximations of $\mu \in \mathcal {P}$ with prescribed locations.

Theorem 3.5

Let $\mu \in \mathcal {P}$ and $n\in \mathbb {N}$. For every $x\in \varXi _n$, there exists a best $d_\mathsf{L}$-approximation of $\mu$, given x. Moreover, $d_\mathsf{L} (\mu , \delta _x^p) = d_\mathsf{L} (\mu , \delta _x^{\bullet } )$ if and only if, for every $j=0,\ldots , n$,

$$\begin{aligned} x_{,j} < x_{,j+1} \Longrightarrow \ell _{F_{\mu }, [x_{,j}, x_{,j+1}]} (P_{,j}) \le \mathsf{L}^{\bullet } (x) , \end{aligned}$$

(3.4)

and in this case $d_\mathsf{L}(\mu , \delta _x^p )= \omega \mathsf{L}^{\bullet }(x)$.

Proof

Fix $\mu \in \mathcal {P}$, $n\in \mathbb {N}$, and $x\in \varXi _n$. As in the proof of Lemma 3.4, write $I_j=[x_{,j}, x_{,j+1}]$ for convenience. By (3.3), for every $p\in \varPi _n$,

$$\begin{aligned} d_\mathsf{L} \left( \mu , \delta _x^p \right)&= \omega \max \nolimits _{j=0}^n \ell _{F_{\mu }, I_j} (P_{,j}) \\&\ge \omega \max \{ \ell _{F_{\mu }, I_0}(0), \ell _{F_{\mu }, I_1}^* , \ldots , \ell _{F_{\mu }, I_{n-1}}^*, \ell _{F_{\mu }, I_n} (1)\} = \omega \mathsf{L}^{\bullet } (x) . \end{aligned}$$

As seen in the proof of Lemma 3.4, validity of (3.4) implies $\ell _{F_{\mu },[x_{,j},x_{,j+1}]}(P_{,j})$$\le \mathsf{L}^{\bullet }(x)$ for all$j=0,\ldots ,n$. Thus $\delta _x^p$ is a best $d_\mathsf{L}$-approximation of $\mu$, given x, whenever (3.4) holds, i.e., the latter is sufficient for optimality. On the other hand, consider $q\in \varPi _n$ with

$$\begin{aligned} Q_{,j} = \frac{1}{2} \Bigl ( F_{\mu -} \bigl (x_{,j+1} - \mathsf{L}^{\bullet }(x )\bigr ) + F_{\mu } \bigl (x_{,j} + \mathsf{L}^{\bullet }(x) \bigr )\Bigr ) \quad \forall j = 1, \ldots , n-1 . \end{aligned}$$

Note that q is well-defined, since $j\mapsto Q_{,j}$ is non-decreasing, and $0\le Q_{,j}\le 1$ for all $j=1, \ldots , n-1$. Moreover, by the definition of $\mathsf{L}^{\bullet }(x)$,

$$\begin{aligned} \ell _{F_{\mu }, I_j} \left( Q_{,j}\right) \le \mathsf{L}^{\bullet }(x) \quad \forall j=0, \ldots , n , \end{aligned}$$

and hence $d_\mathsf{L} \left( \delta _x^{q}, \mu \right) = \omega \mathsf{L}^{\bullet }(x)$. This shows that best $d_\mathsf{L}$-approximations of $\mu$, given x, do exist, and (3.4) also is necessary for optimality. $\square$

Best finitely supported $d_\mathsf{L}$-approximations of any $\mu \in \mathcal {P}$ with prescribed weights can be characterized in a similar manner. By virtue of (3.3), the proof of the following is completely analogous to the proof of Theorem 3.5.

Proposition 3.6

Let $\mu \in \mathcal {P}$ and $n\in \mathbb {N}$. For every $p\in \varPi _n$, there exists a best $d_\mathsf{L}$-approximation of $\mu$, given p. Moreover, $d_\mathsf{L} (\mu , \delta _x^p ) = d_\mathsf{L} (\mu , \delta _{\bullet }^p )$ if and only if, for every $j=1,\ldots , n$,

$$\begin{aligned} P_{,j-1} < P_{,j} \Longrightarrow \ell _{F_{\mu }^{-1}, \left[ P_{,j-1}, P_{,j}\right] } (x_{,j}) \le \mathsf{L}_{\bullet } (p), \end{aligned}$$

(3.5)

and in this case $d_\mathsf{L} \left( \mu , \delta _x^p\right) = \omega \mathsf{L}_{\bullet }(p)$.

Remark 1

• (i) With f, I as in Proposition 3.3, for every $a \in \mathbb {R}$ the set $\{\ell _{f,I} \le a\}$ is a (possibly empty or one-point) interval. Thus, conditions (3.4) and (3.5) are very similar in spirit to the requirements of [30, Thm. 5.1 and 5.5], restated in Proposition 4.1, though the latter may be quite a bit easier to work with in concrete calculations.

• (ii) Note that if $n=1$ then (3.4) holds automatically, whereas (3.5) shows that $d_\mathsf{L} (\mu , \delta _{a})$ is minimal precisely if the function $\ell _{F_{\mu }^{-1},[0,1]}$ attains its minimal value at a.

As a corollary, Proposition 3.6 identifies all best uniform$d_\mathsf{L}$-approximations of $\beta _b$ with $b>1$. Recall that $\mathbb {I}=[1,b]$, and hence $\omega =\displaystyle \frac{\max \{b,2\}-1}{b-1}=:\omega _b$ in this case.

Corollary 3.7

Let $b>1$ and $n\in \mathbb {N}$. Then $\delta _x^{u_n}$ is a best uniform $d_\mathsf{L}$-approximation of  $\beta _b$ if and only if

$$\begin{aligned} b^{j/n -L} - L \le x_{,j} \le b^{(j-1)/n +L} + L\quad \forall j = 1, \ldots , n , \end{aligned}$$

where L is the unique solution of (3.2); in particular, $\# \text{ supp }\, \delta _{\bullet }^{u_n}= n$. Moreover, $d_\mathsf{L} (\beta _b , \delta _{\bullet }^{u_n})=\omega _b L$, and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } n d_\mathsf{L} \left( \beta _b, \delta _{\bullet }^{u_n}\right) = \frac{\max \{b,2\}-1}{2b-2}\cdot \frac{b \log b}{1+ b \log b} . \end{aligned}$$

Example 1

Consider the $\text{ Beta }(2,1)$ distribution on $\mathbb {I}= [0,1]$, i.e., let $F_{\mu }(x)=x^2$ for all $x\in \mathbb {I}$. Given $n\in \mathbb {N}$, it is straightforward to check that, analogously to (3.2), $\mathsf{L}_{\bullet }(u_n)$ is the unique solution of

$$\begin{aligned} L \sqrt{\frac{2}{n} - 4L^2} = \frac{1}{2n} - L , \end{aligned}$$

(3.6)

and $\delta _x^{u_n}$ with $x\in \varXi _n$ is a best uniform $d_\mathsf{L}$-approximation of $\mu$ if and only if

$$\begin{aligned} \sqrt{\frac{j}{n} - L} - L \le x_{,j} \le \sqrt{\frac{j-1}{n} + L} + L \quad \forall j=1 , \ldots , n . \end{aligned}$$

Moreover, $d_\mathsf{L} (\mu , \delta _{\bullet }^{u_n}) = L$, and (3.6) yields that $\lim _{n\rightarrow \infty } n d_\mathsf{L} (\mu , \delta _{\bullet }^{u_n}) = \frac{1}{2}$. Unlike in the case of $\beta _b$, it is possible to have $\# \text{ supp }\, \delta _{\bullet }^{u_n} <n$ whenever $n\ge 10$.

Example 2

Let again $\mathbb {I}= [0,1]$ and consider $\mu \in \mathcal {P}$ with $\mu (\{ i2^{-m}\}) = 3^{-m}$ for every $m\in \mathbb {N}$ and every odd $1\le i < 2^m$. Thus $\mu$ is a discrete measure with $\text{ supp }\, \mu = \mathbb {I}$. In fact, $\mu$ simply is the inverse Cantor distribution, in the sense that $F_{\mu }^{-1} (x) = F_{\nu }(x)$ for all $x\in \mathbb {I}$, where $\nu$ is the $\log 2/\log 3$-dimensional Hausdorff measure on the classical Cantor middle-thirds set. Given $n\in \mathbb {N}$, Proposition 3.6 guarantees the existence of a best uniform $d_\mathsf{L}$-approximation of $\mu$, though the explicit value of $\mathsf{L}_{\bullet }(u_n)$ is somewhat cumbersome to determine. Still, utilizing the self-similarity of $F_{\mu }^{-1}$, one finds that

$$\begin{aligned} \frac{1}{216}\le \liminf \limits _{n\rightarrow \infty }nd_\mathsf{L}\left( \mu ,\delta _{\bullet }^{u_n}\right) \le \frac{1}{3}\, , \quad \limsup \limits _{n\rightarrow \infty }nd_\mathsf{L}\left( \mu ,\delta _{\bullet }^{u_n}\right) =\frac{1}{2} . \end{aligned}$$

(3.7)

Thus $(n^{-1})$ is the precise rate of decay of $\bigl ( d_\mathsf{L} (\mu , \delta _{\bullet }^{u_n})\bigr )$, just as in the case of $\beta _b$ and $\text{ Beta }(2,1)$, but unlike for the latter, $\lim _{n\rightarrow \infty } n d_\mathsf{L} (\mu , \delta _{\bullet }^{u_n})$ does not exist.

By combining Theorem 3.5 and Proposition 3.6, it is possible to characterize the best $d_\mathsf{L}$-approximations of $\mu \in \mathcal {P}$ as well, that is, to identify the minimizers of $\nu \mapsto d_\mathsf{L}(\mu , \nu )$ subject only to the requirement that $\# \text{ supp }\, \nu \le n$. To this end, associate with every non-decreasing function $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ and every number $a\ge 0$ a map $T_{f,a}:\overline{\mathbb {R}} \rightarrow \overline{\mathbb {R}}$, according to

$$\begin{aligned} T_{f, a} (x) = f_+ (f^{-1}(x+a) + 2a) +a \quad \forall \ x \in \overline{\mathbb {R}} . \end{aligned}$$

For every $n\in \mathbb {N}$, denote by $T_{f,a}^{[n]}$ the n-fold composition of $T_{f,a}$ with itself. The following properties of $T_{f,a}$ are readily verified.

Proposition 3.8

Let $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ be non-decreasing, $a \ge 0$, and $n\in \mathbb {N}$. Then $T_{f,a}^{[n]}$ is non-decreasing and right-continuous. Also, $a \mapsto T_{f,a}^{[n]}(x)$ is increasing and right-continuous for every $x\in \mathbb {R}$, and if $x\le a + f(+\infty )$ then the sequence $( T_{f,a}^{[k]}(x))$ is non-decreasing.

To utilize Proposition 3.8 for the $d_\mathsf{L}$-approximation problem, let $f=F_{\mu }$ with $\mu \in \mathcal {P}$. Then $(T_{F_{\mu }, a}^{[k]}(0))$ is non-decreasing; in fact, $\lim _{k\rightarrow \infty } T_{F_{\mu },a}^{[k]}(0) = a + 1$. On the other hand, given $n\in \mathbb {N}$, clearly $T_{F_{\mu }, a}^{[n]}(0)\ge 1$ for all $a\ge 1$, and hence

$$\begin{aligned} \mathsf{L}_{\bullet }^{\bullet , n} := \min \left\{ a \ge 0 : T_{F_{\mu }, a}^{[n]}(0) \ge 1\right\} < +\infty . \end{aligned}$$

Note that $\mathsf{L}_{\bullet }^{\bullet , n}$ only depends on $\mu$ and n. The sequence $\left( \mathsf{L}_{\bullet }^{\bullet , n}\right)$ is non-increasing, and $n\mathsf{L}_{\bullet }^{\bullet ,n}\le \frac{1}{2}$ for every n. Also, $\mathsf{L}_{\bullet }^{\bullet , n}=0$ if and only if $\# \text{ supp }\, \mu \le n$.

For a concrete example, consider $\mu = \beta _b$ with $a < \frac{1}{2} (b-1)$, where

$$\begin{aligned} T_{F_{\mu }, a}(x) = \left\{ \begin{array}{ll} a &{}\quad \text{ if } x< -\, a \, , \\ a + \log _b (b^{x+a} + 2a) &{}\quad \text{ if } -\,a \le x < -\,a + \log _b(b-2a) \, , \\ a + 1 &{}\quad \text{ if } x\ge -\, a + \log _b (b-2a) , \end{array} \right. \end{aligned}$$

from which it is easily deduced that $\mathsf{L}_{\bullet }^{\bullet , n}$ is the unique solution of

$$\begin{aligned} b^{2n L } = \frac{2L + b (b^L - b^{-L})}{2 L + b^L - b^{- L}} . \end{aligned}$$

(3.8)

As the following result shows, the quantity $\mathsf{L}^{\bullet ,n}_{\bullet }$ always plays a central role in identifying best (unconstrained) $d_\mathsf{L}$-approximations of a given $\mu \in \mathcal {P}$.

Theorem 3.9

Let $\mu \in \mathcal {P}$ and $n\in \mathbb {N}$. There exists a best $d_\mathsf{L}$-approximation of $\mu$, and $d_\mathsf{L} (\mu , \delta _{\bullet }^{\bullet , n}) = \omega \mathsf{L}_{\bullet }^{\bullet , n}$. Moreover, for every $x\in \varXi _n$ and $p\in \varPi _n$, the following are equivalent:

• (i) $d_\mathsf{L} (\mu , \delta _x^p ) = d_\mathsf{L} (\mu , \delta _{\bullet }^{\bullet , n})$;

• (ii) all implications in (3.4) are valid with $\mathsf{L}^{\bullet }(x)$ replaced by $\mathsf{L}^{\bullet , n}_{\bullet }$;

• (iii) all implications in (3.5) are valid with $\mathsf{L}_{\bullet }(p)$ replaced by $\mathsf{L}^{\bullet , n}_{\bullet }$.

Proof

To see that best $d_\mathsf{L}$-approximations of $\mu$ do exist, simply note that the set $\{\nu \in \mathcal {P}: \# \text{ supp }\, \nu \le n\}$ is compact, and the function $\nu \mapsto d_\mathsf{L} (\mu , \nu )$ is continuous, hence attains a minimal value for some $\nu = \delta _x^p$ with $x\in \varXi _n$ and $p\in \varPi _n$. Clearly, any such $\delta _x^p$ also is a best approximation of $\mu$, given p. By Proposition 3.6, therefore, $d_\mathsf{L}(\mu , \delta _x^p) = \omega \mathsf{L}_{\bullet }(p)$, as well as

$$\begin{aligned} F_{\mu -}^{-1} \bigl ( P_{,j} - \mathsf{L}_{\bullet }(p)\bigr ) - \mathsf{L}_{\bullet }(p) \le x_{,j} \le F_{\mu }^{-1} \bigl ( P_{,j-1} + \mathsf{L}_{\bullet }(p)\bigr ) + \mathsf{L}_{\bullet }(p) \end{aligned}$$

whenever $P_{,j-1}<P_{,j}$, and indeed for every $j=1,\ldots , n$. It follows that $P_{,j} \le T_{F_{\mu }, \mathsf{L}_{\bullet }(p)}(P_{,j-1})$ for all j, and hence $1= P_{,n} \le T_{F_{\mu }, \mathsf{L}_{\bullet }(p)}^{[n]}(0)$, that is, $\mathsf{L}_{\bullet }^{\bullet , n} \le \mathsf{L}_{\bullet }(p)$. This shows that $d_\mathsf{L} (\mu , \delta _x^p) \ge \omega \mathsf{L}_{\bullet }^{\bullet , n}$. To establish the reverse inequality, let

$$\begin{aligned} m = \min \left\{ i\ge 1 : T_{F_{\mu }, \mathsf{L}_{\bullet }^{\bullet , n}}^{[i]}(0) \ge 1\right\} . \end{aligned}$$

Clearly, $1\le m \le n$, and $\mathsf{L}_{\bullet }^{\bullet , m} = \mathsf{L}_{\bullet }^{\bullet , n}$. Define $q\in \varPi _m$ via

$$\begin{aligned} Q_{,i} = T_{F_{\mu }, \mathsf{L}_{\bullet }^{\bullet , n}}^{[i]}(0) \quad \forall \ i =1, \ldots , m-1 . \end{aligned}$$

Note that $i\mapsto Q_{,i}$ is non-decreasing, and $0\le Q_{,i}\le 1$, so q is well-defined. Also, consider $y\in \varXi _m$ with

$$\begin{aligned} y_{,i} = \frac{1}{2} \bigl ( F_{\mu -}^{-1} (Q_{,i} -\mathsf{L}_{\bullet }^{\bullet , m} ) + F_{\mu }^{-1} (Q_{,i-1} + \mathsf{L}_{\bullet }^{\bullet , m})\bigr ) \quad \forall \ i=1, \ldots , m . \end{aligned}$$

By the definitions of $\mathsf{L}_{\bullet }^{\bullet , m}$, q, and y,

$$\begin{aligned} \ell _{F_{\mu }^{-1}, [Q_{,i-1}, Q_{,i}]} (y_{,i}) \le \mathsf{L}_{\bullet }^{\bullet , m} \quad \forall i = 1, \ldots , m , \end{aligned}$$

and hence

$$\begin{aligned} d_\mathsf{L} \left( \mu , \delta _x^p\right) \le d_\mathsf{L} \left( \mu , \delta _y^q\right) = \omega \max \nolimits _{i=1}^n \ell _{F_{\mu }^{-1}, [Q_{,i-1}, Q_{,i}]} (y_{,i}) \le \omega \mathsf{L}_{\bullet }^{\bullet , m} = \omega \mathsf{L}_{\bullet }^{\bullet , n} . \end{aligned}$$

This shows that indeed $d_\mathsf{L}(\mu , \delta _x^p) = \omega \mathsf{L}_{\bullet }^{\bullet , n}$ and also proves (i) $\Rightarrow$ (iii). The implication (i) $\Rightarrow$ (ii) follows by a similar argument. That, conversely, either of (ii) and (iii) implies (i) is evident from (3.3), together with the fact that, as seen in the proof of Lemma 3.4, validity of (3.4) and (3.5) implies $\max _{j=0}^n\ell _{F_{\mu }, [x_{,j}, x_{,j+1}]} (P_{,j}) \le \mathsf{L}^{\bullet } (x)$ and $\max _{j=1}^n\ell _{F_{\mu }^{-1}, \left[ P_{,j-1}, P_{,j}\right] } (x_{,j}) \le \mathsf{L}_{\bullet } (p)$, respectively. $\square$

Remark 2

• (i) The proof of Theorem 3.9 shows that in fact

  $$\begin{aligned} \mathsf{L}_{\bullet }^{\bullet , n} = \min \limits _{x\in \varXi _n} \mathsf{L}^{\bullet } (x) = \min \limits _{p\in \varPi _n} \mathsf{L}_{\bullet } (p) . \end{aligned}$$

• (ii) Theorem 3.9 is similar to classical one-dimensional quantization results as presented, e.g., in [16, Sect. 5.2]. What makes the theorem (and its analogue, Theorem 5.6 in Sect. 5) particularly appealing is that its conditions (ii) and (iii) not only are necessary for optimality, but also sufficient. By contrast, it is well known that sufficient conditions for best $d_{*}$-approximations may be hard to come by in general; see, e.g., [16, Sect. 4.1], and also Proposition 4.1(iii), regarding the case of $* =1$.

Fig. 1

The best $d_\mathsf{L}$-approximation (solid red line) of $\beta _{10}$ is unique, whereas best uniform $d_\mathsf{L}$-approximations (broken red lines) are not; see Corollaries 3.10 and 3.7, respectively (Color figure online)

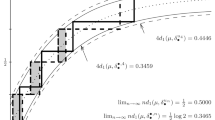
When specialized to $\mu = \beta _b$, Theorem 3.9 yields the best finitely supported $d_\mathsf{L}$-approximations of Benford’s law; see also Fig. 1.

Corollary 3.10

Let $b>1$ and $n\in \mathbb {N}$. Then the best $d_\mathsf{L}$-approximation of  $\beta _b$ is $\delta _x^p$, with

$$\begin{aligned} x_{,j}&= b^{(2j-1)L} + 2L \frac{b^{2jL}-1}{b^{2L} -1} - L = b^{P_{,j} - L} - L \, ,\\ P_{,j}&= \frac{1}{\log b} \log \left( b^{(2j-1) L} + 2L \frac{b^{2jL}-1}{b^{2L} -1} \right) + L = \frac{ \log (x_{,j} + L)}{\log b} + L , \end{aligned}$$

for all $j=1, \ldots , n$, where L is the unique solution of (3.8); in particular, $\#\mathrm{supp}\, \delta _{\bullet }^{\bullet ,n}=n$. Moreover, $d_\mathsf{L}(\beta _b, \delta _{\bullet }^{\bullet , n})=\omega _bL$, and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } n d_\mathsf{L} \left( \beta _b, \delta _{\bullet }^{\bullet , n}\right) = \frac{\max \{b,2\}-1}{2b-2}\cdot \frac{\log (1 + b \log b) -\log (1+\log b)}{\log b} . \end{aligned}$$

To compare this to Corollary 3.7, note that $P_{,j}\not \equiv j/n$ whenever $n\ge 2$, and then the n-th quantization error $d_\mathsf{L} (\beta _b, \delta _{\bullet }^{\bullet , n})$ is smaller than the n-th uniform quantization error $d_\mathsf{L} (\beta _b, \delta _{\bullet }^{u_n})$. The $d_\mathsf{L}$-quantization coefficient of $\beta _b$ also is smaller than its uniform counterpart, since

$$\begin{aligned} \frac{\log (1 + b \log b) -\log (1+\log b)}{\log b} < \frac{b\log b}{1 + b\log b} \quad \forall \ b > 1 . \end{aligned}$$

Example 3

For $\mu = \text{ Beta }(2,1)$, Theorem 3.9 yields a unique best $d_\mathsf{L}$-approximation. Although the equation determining $\mathsf{L}_{\bullet }^{\bullet , n}$ is less transparent than (3.8), it can be shown that $\lim _{n\rightarrow \infty } n d_\mathsf{L} (\mu , \delta _{\bullet }^{\bullet , n}) = \frac{1}{4} (2 - \log 3)< \frac{1}{4}$.

Example 4

For the inverse Cantor distribution, a best $d_\mathsf{L}$-approximation exists by Theorem 3.9, and utilizing the self-similarity of $F_{\mu }^{-1}$, it is possible to derive estimates such as

$$\begin{aligned} \frac{1}{216}\le n^{\log 3/ \log 2}d_\mathsf{L}\left( \mu ,\delta _{\bullet }^{\bullet ,n}\right) \le 3 \quad \forall n \in \mathbb {N}, \end{aligned}$$

(3.9)

which shows that $\bigl ( d_\mathsf{L} (\mu , \delta _{\bullet }^{u_n})\bigr )$ decays like $(n^{-\log 3/ \log 2})$, and hence faster than in the case of $\beta _b$ and $\text{ Beta }(2,1)$.

4 Kantorovich Approximations

This section studies best finitely supported $d_r$-approximations of Benford’s law. Mostly, the results are special cases of more general facts taken from the authors’ comprehensive study on $d_r$-approximations [30].

4.1 $d_1$-Approximations

With $d_\mathsf{L}$ replaced by $d_1$, the main results of the previous section have the following analogues, stated here for the reader’s convenience; see [30, Sect. 5] for details.

Proposition 4.1

Let $\mu \in \mathcal {P}$ and $n\in \mathbb {N}$.

• (i) For every $x\in \varXi _n$, there exists a best $d_1$-approximation of $\mu$, given x. Moreover, $d_1(\mu , \delta _x^p)= d_1(\mu , \delta _x^{\bullet })$ if and only if, for every $j=0,\ldots , n$,

  $$\begin{aligned} x_{,j} < x_{,j+1} \Longrightarrow F_{\mu -} \left( {\textstyle \frac{1}{2}} (x_{,j} + x_{,j+1} )\right) \le P_{,j} \le F_{\mu } \left( {\textstyle \frac{1}{2}} (x_{,j} + x_{,j+1})\right) . \end{aligned}$$

  (4.1)

• (ii) For every $p\in \varPi _n$, there exists a best $d_1$-approximation of $\mu$, given p. Moreover, $d_1(\mu , \delta _x^p)= d_1(\mu , \delta _{\bullet }^p)$ if and only if, for every $j=1,\ldots , n$,

  $$\begin{aligned} P_{,j-1} < P_{,j} \Longrightarrow F^{-1}_{\mu -} \left( {\textstyle \frac{1}{2}} (P_{,j-1} + P_{,j})\right) \le x_{,j} \le F^{-1}_{\mu } \left( {\textstyle \frac{1}{2}} (P_{,j-1} + P_{,j} )\right) . \end{aligned}$$

  (4.2)

• (iii) There exists a best $d_1$-approximation of $\mu$, and if $d_{1}(\mu , \delta _x^p) = d_1(\mu , \delta _{\bullet }^{\bullet ,n})$ then (4.1) and (4.2) are valid for every $j=1,\ldots , n$.

Remark 3

Though the phrasing of Proposition 4.1 emphasizes its analogy to Theorem 3.5 (and also to Theorem 5.1), there nevertheless is a subtle difference: While in (3.4) and (5.1) it can equivalently be stipulated that, respectively, $\ell _{F_{\mu }, [x_{,j}, x_{,j+1}]} (P_{,j}) \le \mathsf{L}^{\bullet } (x)$ and $F_{\mu -}(x_{,j+1})-\mathsf{K}^{\bullet }(x)\le P_{,j}\le F_{\mu }(x_{,j})+\mathsf{K}^{\bullet }(x)$ for all$j=0,\ldots ,n$, simple examples show that the “only if” part of Proposition 4.1(i) may fail, should (4.1) be replaced by

$$\begin{aligned} F_{\mu -} \left( {\textstyle \frac{1}{2}} (x_{,j} + x_{,j+1} )\right) \le P_{,j} \le F_{\mu } \left( {\textstyle \frac{1}{2}} (x_{,j} + x_{,j+1})\right) \quad \forall \ j=0,\ldots ,n. \end{aligned}$$

Similar observations pertain to Proposition 4.1(ii) vis-à-vis Proposition 3.6 and Theorem 5.4.

Proposition 4.1 immediately yields the existence of unique best uniform $d_1$-approximations of $\beta _b$; see also [5, Cor. 2.10].

Corollary 4.2

Let $b>1$ and $n\in \mathbb {N}$. Then the best uniform $d_1$-approximation of  $\beta _b$ is $\delta _x^{u_n}$, with $x_{,j}= b^{(2j-1)/(2n)}$ for all $j=1,\ldots , n$, and $\# \text{ supp }\, \delta _{\bullet }^{u_n}=n$. Moreover, $d_1(\beta _b , \delta _{\bullet }^{u_n}) = \displaystyle {\frac{1}{\log b} \tanh \left( \frac{\log b}{4n}\right) }$, and $\lim _{n\rightarrow \infty } n d_1\left( \beta _b, \delta _{\bullet }^{u_n}\right) = \frac{1}{4}$.

Proof

By Proposition 4.1(ii), $x_{,j}= b^{(2j-1)/(2n)}$ for all $j=1,\ldots , n$, and

$$\begin{aligned} nd_1\left( \beta _b, \delta _{\bullet }^{u_n}\right)&= \frac{n}{b-1} \sum \nolimits _{j=1}^n \int _{(j-1)/n}^{j/n} \left| b^y - b^{(2j-1)/(2n)}\right| \, \mathrm{d}y \\&= \frac{n \left( b^{1/(4n)} - b^{-1/(4n)}\right) ^2}{(b-1)\log b} \sum \nolimits _{j=1}^n b^{(2j-1)/(2n)} \\&= \frac{n}{\log b} \tanh \left( \frac{\log b}{4n}\right) {\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} \frac{1}{4} . \end{aligned}$$

$\square$

Best (unconstrained) $d_1$-approximations of $\beta _b$ exist and are unique, too, by virtue of Proposition 4.1 and a direct calculation.

Corollary 4.3

Let $b>1$ and $n\in \mathbb {N}$. Then the best $d_1$-approximation of  $\beta _b$ is $\delta _{x}^p$, with

$$\begin{aligned} x_{,j}&= \left( 1 + \frac{j-1}{n} \left( b^{1/2} - 1\right) \right) \left( 1 + \frac{j}{n} \left( b^{1/2} - 1\right) \right) \, , \\ \quad P_{,j}&=\frac{2}{\log b} \log \left( 1+ \frac{j}{n} \left( b^{1/2} -1 \right) \right) , \end{aligned}$$

for all $j=1,\ldots , n$; in particular, $\# \text{ supp }\, \delta _{\bullet }^{\bullet ,n}=n$. Moreover, $d_1(\beta _b, \delta _{\bullet }^{\bullet , n}) = \displaystyle { \frac{1}{n\log b} \tanh \left( \frac{\log b}{4}\right) }$.

Proof

Let $\delta _x^p$ be a best $d_1$-approximation. Then, by Proposition 4.1(iii),

$$\begin{aligned} b^{P_{,j}} = \frac{x_{,j} + x_{,j+1}}{2} \quad \forall j = 1, \ldots , n-1 , \end{aligned}$$

but also $x_{,j} = b^{(P_{,j-1} + P_{,j})/2}$ for all $j=1, \ldots , n$, and hence $2b^{P_{,j}/2} = b^{P_{,j-1}/2} + b^{P_{j+1}/2}$. Since $P_0 = 0$, $P_n = 1$, it follows that $b^{P_{,j}/2} = 1 + j (b^{1/2} -1)n^{-1}$ for all $j=0,\ldots , n$. This yields the asserted unique $\delta _x^p$, and

$$\begin{aligned} d_1\left( \beta _b , \delta _{\bullet }^{\bullet , n}\right)&= \frac{1}{b-1} \sum \nolimits _{j=1}^n \int _{P_{,j-1}}^{P_{,j}} |b^y - x_{,j}| \, \mathrm{d}y = \frac{b- x_{,n} - (x_{,1} -1)}{(b-1)\log b} \\&= \frac{1}{n\log b} \tanh \left( \frac{\log b}{4} \right) , \end{aligned}$$

via a straightforward calculation; see also Fig. 2. $\square$

Fig. 2

The best (solid blue line) and best uniform (broken blue line) $d_1$-approximations of $\beta _{10}$ both are unique; see Corollaries 4.3 and 4.2, respectively. Coincidentally, best uniform $d_1$-approximations of $\beta _{10}$ are best $d_\mathsf{K}$-approximations as well; see Corollary 5.8 (Color figure online)

Remark 4

• (i) Due to the highly nonlinear nature of the optimality conditions (4.1) and (4.2), best $d_1$-approximations are rarely given by explicit formulae such as those in Corollary 4.3. Aside from Benford’s law, the authors know of only two other families of continuous distributions that allow for similarly explicit formulae, namely uniform and (one- or two-sided) exponential distributions.

• (ii) A popular family of metrics on $\mathcal {P}$ closely related to $d_1$ are the so-called Fortet–Mourierr-distances ($1\le r<+\,\infty$), given by

  $$\begin{aligned} d_{\mathsf{FM}_{r}} (\mu , \nu ) = \int _{\mathbb {I}} \max \{ 1,|y|\}^{r-1} |F_{\mu }(y) - F_{\nu }(y)|\, \mathrm{d}y . \end{aligned}$$

  Like the Lévy and Kantorovich metrics, the Fortet–Mourier r-distance also metrizes the weak topology on $\mathcal {P}$. The reader is referred to [24, 26] for details on the mathematical background of $d_{\mathsf{FM}_r}$ and its use for stochastic optimization. Note that if $\mathbb {I}\subset [1,+\infty [$ then

  $$\begin{aligned} d_{\mathsf{FM}_r}(\mu , \nu ) = \frac{\lambda \bigl ( T(\mathbb {I})\bigr )}{r} d_1\left( \mu \circ T^{-1}, \nu \circ T^{-1}\right) , \end{aligned}$$

  with the homeomorphism $T: x\mapsto x^r$ of $[1,+\infty [$. For instance, $\beta _b \circ T^{-1} = \beta _{rb}$, and hence best (or best uniform) $d_{\mathsf{FM}_{r}}$-approximations of $\beta _b$ can easily be identified using Corollary 4.3 (or 4.2).

4.2 $d_r$-Approximations ($1<r<+\,\infty$)

Similarly to the case of $r=1$, [30, Thm. 5.5] guarantees that, given any $n\in \mathbb {N}$, there exists a (unique) best uniform $d_r$-approximation $\delta _{\bullet }^{u_n}$ of $\beta _b$. Except for $r=2$, however, no explicit formula seems to be available for $\delta _{\bullet }^{u_n}$. It is desirable, therefore, to at least identify asymptotically best uniform $d_r$-approximations, that is, a sequence $(x_n)$ with $x_n \in \varXi _n$ for all $n\in \mathbb {N}$ such that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } \frac{d_r \left( \beta _b, \delta _{x_n}^{u_n}\right) }{d_r \left( \beta _b, \delta _{\bullet }^{u_n}\right) } = 1 . \end{aligned}$$

Usage of [30, Thm. 5.15] accomplishes this and also yields the uniform $d_r$-quantization coefficient of $\beta _b$. (Notice that, as $r\downarrow 1$, the latter is consistent with Corollary 4.2.)

Proposition 4.4

Let $b,r>1$. Then $\left( \delta _{x_n}^{u_n}\right)$, with $x_{n,j} = b^{(2j-1)/(2n)}$ for all $n\in \mathbb {N}$ and $j=1, \ldots , n$, is a sequence of asymptotically best uniform $d_r$-approximations of  $\beta _b$. Moreover,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } n d_r (\beta _b , \delta _{\bullet }^{u_n}) = \frac{(\log b)^{1-1/r}}{2(b-1)} \left( \frac{b^r - 1}{r(r+1)}\right) ^{1/r} . \end{aligned}$$

The remainder of this section studies best $d_r$-approximations of $\beta _b$. In general, the question of uniqueness of best $d_r$-approximations is a difficult one, for which only partial answers exist; see, e.g., [16, Sec.5]. Specifically, $\beta _b$ does not seem to satisfy any known condition (such as, e.g., log-concavity) that would guarantee uniqueness. However, uniqueness can be established via a direct calculation.

Theorem 4.5

Let $b,r>1$ and $n\in \mathbb {N}$. There exists a unique best $d_r$-approximation $\delta _{\bullet }^{\bullet ,n}$ of  $\beta _b$, and $\#\mathrm{supp}\, \delta _{\bullet }^{\bullet ,n}=n$.

Proof

Existence follows as in Theorem 3.9; alternatively, see [16, Sect. 4.1] or [30, Prop. 5.22]. To avoid trivialities, henceforth assume $n\ge 2$. If $d_r\left( \beta _b, \delta _x^p\right) = d_r \left( \beta _b, \delta _{\bullet }^{\bullet , n}\right)$, then by [30, Thm. 5.23],

$$\begin{aligned} b^{P_{,j}} = \frac{x_{,j} + x_{,j+1}}{2} \quad \forall j = 1, \ldots , n-1 , \end{aligned}$$

but also

$$\begin{aligned} \int _{P_{,j-1}}^{\log _b x_{,j}} \left( x_{,j} - b^y\right) ^{r-1} \, \mathrm{d}y = \int _{\log _b x_{,j}}^{P_{,j}} \left( b^y - x_{,j}\right) ^{r-1} \, \mathrm{d}y \quad \forall j=1, \ldots , n . \end{aligned}$$

(4.3)

Eliminating P and substituting $z = b^y/x_{,j}$ in (4.3) yields n equations for $x_{,1}, \ldots , x_{,n}$, namely

$$\begin{aligned} \int _{1}^{x_{,1}} (z-1)^{r-1} \frac{\mathrm{d}z}{z^r}= & {} 2^{1-r} g_0 \left( \frac{x_{,2}}{x_{,1}}\right) \, , \nonumber \\ g_r\left( \frac{x_{,j}}{x_{,j-1}}\right)= & {} g_0 \left( \frac{x_{,j+1}}{x_{,j}}\right) \, , \quad \forall j=2, \ldots , n-1\, ,\\ g_r\left( \frac{x_{,n}}{x_{,n-1}}\right)= & {} g_0 \left( \frac{2b - x_{,n}}{x_{,n}}\right) ,\nonumber \end{aligned}$$

(4.4)

where the smooth, increasing function $g_a$, with $a\in \mathbb {R}$, is given by

$$\begin{aligned} g_a(x) = \int _1^x \frac{(z-1)^{r-1}}{z^a (z+1)} \, \mathrm{d}z \, , \quad x\ge 1 . \end{aligned}$$

Assume that $\widetilde{x}\in \varXi _n$ also solves (4.4). If $\widetilde{x}_{,1}> x_{,1}$ then $\widetilde{x}_{,j+1}/\widetilde{x}_{,j} > x_{,j+1}/x_{,j}$ and hence $\widetilde{x}_{,j+1} > x_{,j+1}$ for all $j=0,\ldots , n-1$, but by the last equation in (4.4) also $2b/\widetilde{x}_{,n} > 2b /x_{,n}$, an obvious contradiction. Similarly, $\widetilde{x}_{,1}< x_{,1}$ leads to a contradiction. Thus, $\widetilde{x}_{,1} = x_{,1}$, and consequently $\widetilde{x} = x$. (If $n=1$ then (4.4) reduces to

$$\begin{aligned} \int _{1}^{x_{,1}} (z-1)^{r-1} \frac{\mathrm{d}z}{z^r} = 2^{1-r} g_0 \left( \frac{2b - x_{,1}}{x_{,1}}\right) , \end{aligned}$$

which also has a unique solution since, as $x_{,1}$ increases from 1 to b, the left side increases from 0, whereas the right side decreases to 0.) In summary, therefore, $x\in \varXi _n$ and $p\in \varPi _n$ are uniquely determined by $d_r\left( \beta _b, \delta _x^p\right) = d_r \left( \beta _b, \delta _{\bullet }^{\bullet , n}\right)$. $\square$

As in the case of best uniform $d_r$-approximations of $\beta _b$, no explicit formula is available for $\delta _{\bullet }^{\bullet ,n}$, not even when $r=2$. Still, it is possible to identify asymptotically best $d_r$-approximations, that is, a sequence $\left( \delta _{x_n}^{p_n}\right)$ with $x_n \in \varXi _n$ and $p_n \in \varPi _n$ for all $n\in \mathbb {N}$ such that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } \frac{d_r \left( \beta _b, \delta _{x_n}^{p_n}\right) }{d_r \left( \beta _b , \delta _{\bullet }^{\bullet , n}\right) } = 1 . \end{aligned}$$

In addition, the $d_r$-quantization coefficient of $\beta _b$ can be computed explicitly; for details see [30, Prop. 5.26] and the references given there. Notice that, as $r\downarrow 1$, the result is consistent with Corollary 4.3.

Proposition 4.6

Let $b,r>1$. Then $\left( \delta _{x_n}^{p_n}\right)$, with

$$\begin{aligned} x_{n,j} = \left( 1+\frac{j}{n+1}\left( b^{r/(r+1)}-1\right) \right) ^{1 + 1/r}\, , \quad P_{n,j} = \frac{1}{\log b} \log \frac{x_{n,j} + x_{n,j+1}}{2} , \end{aligned}$$

for all $n\in \mathbb {N}$ and $j=1, \ldots , n-1$, and $x_{n,n} = \left( 1 + (b^{r/(r+1)} -1) \frac{n}{n+1} \right) ^{1+1/r}$, is a sequence of asymptotically best $d_r$-approximations of  $\beta _b$. Moreover,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } n d_r (\beta _b , \delta _{\bullet }^{\bullet , n}) = \frac{r+1}{2(b-1)(\log b)^{1/r}} \left( \frac{b^{r/(r+1)} -1 }{r} \right) ^{1+1/r} . \end{aligned}$$

Example 5

For $\mu = \text{ Beta }(2,1)$, given any $n\in \mathbb {N}$, a unique best uniform $d_r$-approximation exists for each $r\ge 1$. The best uniform $d_1$-approximations $\delta _{x}^{u_n}$, where $x_{,j} = \sqrt{\frac{2j-1}{2n}}$ for $j=1, \ldots , n$, also constitute a sequence of asymptotically best uniform $d_r$-approximations for $1<r<2$, with

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } n d_r (\mu , \delta _{\bullet }^{u_n}) = \left( \frac{2^{1-2r}}{(r+1)(2-r)}\right) ^{1/r} , \end{aligned}$$

(4.5)

in analogy to Proposition 4.4. For $r\ge 2$, however, this analogy breaks down, as

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } \frac{n}{\sqrt{\log n}} d_2 (\mu , \delta _{\bullet }^{u_n}) = \frac{1}{4 \sqrt{3}} , \end{aligned}$$

and $\lim _{n\rightarrow \infty } n^{1/2 + 1/r} d_r(\mu , \delta _{\bullet }^{u_n})$ is finite and positive whenever $r>2$.

Since $\mu$ is log-concave, or by an argument similar to the one proving Theorem 4.5, there exists a unique best $d_r$-approximation of $\mu$. While the authors do not know of an explicit formula for $\delta _{\bullet }^{\bullet , n}$, simple asymptotically best $d_r$-approximations in the spirit of Proposition 4.6 exist, and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } n d_r (\mu , \delta _{\bullet }^{\bullet ,n}) = 2^{1/r -1} \frac{r+1}{(r+2)^{1+1/r}} \quad \forall r \ge 1 ; \end{aligned}$$

(4.6)

see [30, Ex. 5.28]. Note that (4.6) is smaller than (4.5) for every $1\le r < 2$.

Example 6

For the inverse Cantor distribution, for every $r\ge 1$ let $\alpha _r = r^{-1} + (1-r^{-1})\log 2/\log 3$, and note that $\log 2/\log 3 < \alpha _r \le 1$. With this, $3^{\alpha _r} d_r (\mu , \delta _{\bullet }^{u_{3n}}) = d_r (\mu , \delta _{\bullet }^{u_n})$ for all $n\in \mathbb {N}$, and it is readily deduced that

$$\begin{aligned} 2^{2/r - 4} 3^{-3/r} \le n^{\alpha _r} d_r (\mu , \delta _{\bullet }^{u_n}) \le 2^{1/r} \quad \forall n \in \mathbb {N}. \end{aligned}$$

Thus $\bigl ( n^{\alpha _r} d_r (\mu , \delta _{\bullet }^{u_n})\bigr )$ is bounded below and above by positive constants. (The authors suspect that this sequence is divergent for every $r\ge 1$.)

Best $d_r$-approximations also exist, and in a similar spirit it can be shown that $\bigl ( n^{\widetilde{\alpha }_r} d_r (\mu , \delta _{\bullet }^{\bullet , n}) \bigr )$ is bounded below and above by positive constants (and again, presumably, divergent), where $\widetilde{\alpha }_r = \alpha _r \log 3 / \log 2$. Note that $1< \widetilde{\alpha }_r \le \log 3/\log 2$, and hence $\bigl ( d_r (\mu , \delta _{\bullet }^{\bullet ,n})\bigr )$ decays faster than $(n^{-1})$ for every $r\ge 1$.

5 Kolmogorov Approximations

This section discusses best finitely supported $d_\mathsf{K}$-approximations. Though ultimately the results are true analogues of their counterparts in Sects. 3 and 4, the underlying arguments are subtly different, which may be seen as a reflection of the fact that $d_\mathsf{K}$ metrizes a topology finer than the weak topology of $\mathcal {P}$. (Recall, however, that $d_\mathsf{K}$ does metrize the weak topology on $\mathcal {P}_\mathsf{cts}$.)

Given $\mu \in \mathcal {P}$ and $n\in \mathbb {N},$ for every $x\in \varXi _n,$ let

$$\begin{aligned} \mathsf{K}^{\bullet }(x)=\max \left\{ F_{\mu -}(x_{,1}),\frac{1}{2}{\max } _{j=1}^{n-1}\ \bigl ( F_{\mu -}(x_{,j+1})-F_{\mu }(x_{,j})\bigr ) , 1-F_{\mu }(x_{,n}) \right\} . \end{aligned}$$

Note that $\mathsf{K}^{\bullet }(x)=d_\mathsf{K}(\mu ,\delta _x^{\pi (x)})$ with $\varPi (x)_{,j}=\frac{1}{2}\bigl (F_{\mu }(x_{,j})+F_{\mu -}(x_{,j+1})\bigr )$ for all $j=1,\ldots ,n-1$. Existence and characterization of best $d_\mathsf{K}$-approximations with prescribed locations are analogous to Theorem 3.5.

Theorem 5.1

Assume that $\mu \in \mathcal {P},$ and $n\in \mathbb {N}.$ For every $x\in \varXi _n,$ there exists a best $d_\mathsf{K}$-approximation of $\mu ,$ given x. Moreover, $d_\mathsf{K}\left( \mu ,\delta _x^p\right) =d_\mathsf{K}\left( \mu ,\delta _x^{\bullet }\right)$ if and only if, for every $j=0,\ldots , n$,

$$\begin{aligned} x_{,j} < x_{,j+1} \Longrightarrow F_{\mu -}\left( x_{,j+1}\right) -\mathsf{K}^{\bullet }(x)\le P_{,j}\le F_{\mu }\left( x_{,j}\right) +\mathsf{K}^{\bullet }(x) \end{aligned}$$

(5.1)

and in this case $d_\mathsf{K}\left( \mu ,\delta _x^{\bullet }\right) =\mathsf{K}^{\bullet }(x)$.

Proof

Given $x\in \varXi _n$ and $p\in \varPi _n$, let $y\in \varXi _m$ and $q\in \varPi _{m}$ as in the proof of Lemma 3.4. Then

$$\begin{aligned} \begin{aligned} d_\mathsf{K} \left( \mu ,\delta _x^p\right)&=\max \nolimits _{i=0}^m\sup \limits _{t\in [y_{,i},y_{ ,i+1}[}\left| F_{\mu }(t)-Q_{,i}\right| \\&\ge \max \left\{ F_{\mu -}(y_{,1}),\frac{1}{2} \max \nolimits _{i=1}^{m-1}\left( F_{\mu -} (y_{,i+1})-F_{\mu }(y_{,i})\right) ,1-F_{\mu }(y_{,m})\right\} \\&= \max \left\{ F_{\mu -}(x_{,1}),\frac{1}{2} \max \nolimits _{j=1}^{n-1}\left( F_{\mu -} (x_{,j+1})-F_{\mu }(x_{,j})\right) ,1-F_{\mu }(x_{,n})\right\} \\&= \mathsf{K}^{\bullet }(x). \end{aligned} \end{aligned}$$

This shows that $\delta _x^{\pi (x)}$ is a best $d_\mathsf{K}$-approximation, given x, and $d_\mathsf{K}\left( \mu ,\delta _x^{\bullet }\right) =\mathsf{K}^{\bullet }(x)$. Moreover, $d_\mathsf{K}\left( \mu ,\delta _x^p\right) =\mathsf{K}^{\bullet }(x)$ if and only if

$$\begin{aligned} \max \left\{ \left| F_{\mu -}(y_{,i+1})-Q_{,i}\right| ,\left| F_{\mu } (y_{,i})-Q_{,i}\right| \right\} \le \mathsf{K}^{\bullet }(x)\,\quad \forall \ i=1,\ldots ,m-1, \end{aligned}$$

that is,

$$\begin{aligned} F_{\mu -}(y_{,i+1})-\mathsf{K}^{\bullet }(x)\le Q_{,i}\le F_{\mu }(y_{,i})+\mathsf{K}^{\bullet }(x)\quad \forall \ i=0,\ldots ,m, \end{aligned}$$

which in turn is equivalent to the validity (5.1) for every j. $\square$

To address the approximation problem with prescribed weights, an auxiliary function analogous to $\ell _{f,I}$ in Sect. 3 is useful. Specifically, given a non-decreasing function $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$, let $I\subset \mathbb {R}$ be any bounded, non-empty interval, and define $\kappa _{f,I}:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ as

$$\begin{aligned} \kappa _{f,I}(x)=\max \left\{ \bigl |f_-(x)-\inf I\bigr |,\bigl |f_+(x)-\sup I\bigr |\right\} . \end{aligned}$$

A few basic properties of $\kappa _{f,I}$ are easily established.

Proposition 5.2

Let $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ be non-decreasing, and $\varnothing \ne I\subset \mathbb {R}$ a bounded interval. Then, with $s:=f^{-1}\left( \frac{1}{2}(\inf I+\sup I)\right)$, the function $\kappa _{f,I}$ is non-increasing on $]-\infty ,s[,$ and non-decreasing on $]s,+\infty [$. Moreover, $\kappa _{f,I}$ attains a minimal value whenever $\inf I\le \frac{1}{2}\bigl (f_-(s)+f_+(s)\bigr )\le \sup I$.

It is worth noting that $\kappa _{f,I}$ may in general not attain its infimum, as the example of $f=15F_{\mu }$, with $\mu =\frac{1}{15}\lambda \left| _{[0,5]}\right. +\frac{2}{3}\delta _5$, and $I=[6,8]$ shows, for which $s=5$, and $\kappa _{f,I}(5-)=3$, $\kappa _{f,I}(5)=7$, $\kappa _{f,I}(5+)=9$; correspondingly, $\frac{1}{2}\bigl (f_-(5)+f_+(5)\bigr )\notin I$.

By using functions of the form $\kappa _{f,I}$, the value of $d_\mathsf{K}(\mu ,\nu )$ can easily be bounded above whenever $\nu$ has finite support. For convenience, for every $n\in \mathbb {N}$ let $\varXi _n^+=\left\{ x\in \varXi _n:\ x_{,1}<\ldots <x_{,n}\right\}$. The proof of the following analogue of Lemma 3.4 is straightforward.

Proposition 5.3

Let $\mu \in \mathcal {P}$ and $n\in \mathbb {N}$. For every $x\in \varXi _n$ and $p\in \varPi _n$,

$$\begin{aligned} d_\mathsf{K}\bigl ( \mu , \delta _x^p \bigr )\le \max \nolimits _{j=1}^n\kappa _{F_{\mu },[P_{,j-1},P_{,j}]}(x_{,j}), \end{aligned}$$

(5.2)

and equality holds in (5.2) whenever $x\in \varXi _n^+$.

Consider for instance $\mu =\frac{1}{6}\lambda \left| _{[0,2]}\right. +\frac{2}{3}\delta _1$, and $x=(1,1)$. Then, for every $p\in \varPi _2$, clearly $d_\mathsf{K}\left( \mu ,\delta _x^p\right) =\frac{1}{6}$, whereas $\max \nolimits _{j=1}^2\kappa _{F_{\mu },[P_{,j-1},P_{,j}]} (x_{,j})=\frac{1}{3}+ \left| p_{,1}-\frac{1}{2}\right| \ge \frac{1}{3}$. Thus the inequality (5.2) may be strict if $x\notin \varXi _n^+$. This, together with the fact that a function $\kappa _{f,I}$ may not attain its infimum, suggests that $d_\mathsf{K}$-approximations with prescribed weights are potentially somewhat fickle. Still, best approximations do exist and can be characterized in a spirit similar to Sects. 3 and 4. To this end, given $\mu \in \mathcal {P}$ and $n\in \mathbb {N}$, for every $p\in \varPi _n$, let

$$\begin{aligned} \mathsf{K}_{\bullet }(p)=d_\mathsf{K}\left( \mu ,\delta _{\xi (p)}^p\right) \,\ \text {with}\ \ \xi (p)_{,j} =F_{\mu }^{-1}\left( \frac{1}{2}\left( P_{,j-1}+P_{,j}\right) \right) \quad \forall \ j=1,\ldots ,n. \end{aligned}$$

Note that $\mathsf{K}_{\bullet }(p)\le \frac{1}{2}\max _{j=1}^np_{,j}$, and in fact $\mathsf{K}_{\bullet }(p)=\frac{1}{2}\max _{j=1}^np_{,j}$ whenever $\mu \in \mathcal {P}_\mathsf{cts}$.

Theorem 5.4

Assume that $\mu \in \mathcal {P}$, and $n\in \mathbb {N}.$ For every $p\in \varPi _n,$ there exists a best $d_\mathsf{K}$-approximation of $\mu ,$ given p. Moreover, $d_\mathsf{K}\left( \mu ,\delta _x^p\right) =d_\mathsf{K}\left( \mu ,\delta ^p_{\bullet }\right)$ if and only if, for every $j=1,\ldots , n$,

$$\begin{aligned} P_{,j-1} < P_{,j} \Longrightarrow F_{\mu -}^{-1}\bigl ( P_{,j}-\mathsf{K}_{\bullet }(p)\bigr ) \le x_{,j}\le F_{\mu }^{-1}\bigl ( P_{,j-1}+\mathsf{K}_{\bullet }(p)\bigr ), \end{aligned}$$

(5.3)

and in this case $d_\mathsf{K}\left( \mu ,\delta _{\bullet }^p\right) =\mathsf{K}_{\bullet }(p).$

Proof

Note first that deleting all zero entries of p does not change the value of $\mathsf{K}_{\bullet }(p)$, and hence does not affect (5.3), nor of course the asserted existence of a best $d_\mathsf{K}$-approximation, given p. Thus assume $\min _{j=1}^np_{,j}>0$ throughout. For convenience, write $\xi (p)$ simply as $\xi$, and for every $x\in \varXi _n$, write $F_{\delta _x^p}$ as G. To prove the existence of a best $d_\mathsf{K}$-approximation of $\mu$, given p, as well as $d_\mathsf{K}\left( \mu ,\delta _{\bullet }^p\right) =\mathsf{K}_{\bullet }(p)$, clearly it suffices to show that

$$\begin{aligned} d_\mathsf{K}\left( \mu ,\delta _x^p\right) \ge d_\mathsf{K}\left( \mu ,\delta _{\xi }^p\right) \quad \, \forall \ x\in \varXi _n. \end{aligned}$$

(5.4)

Similarly to the proof of Lemma 3.4, label $\xi$ uniquely as

$$\begin{aligned} \xi _{,1}&= \cdots = \xi _{,j_1}< \xi _{,j_1+1} = \cdots = \xi _{,j_2}< \xi _{,j_2 + 1} = \cdots \\&< \cdots = \xi _{,j_{m-1}}< \xi _{,j_{m-1}+1} = \cdots = \xi _{,j_m} , \end{aligned}$$

with integers $i\le j_i \le m$ for $1\le i\le m$, and $j_0 = 0$, $j_m = n$, and define $\eta \in \varXi _m$ and $q\in \varPi _m$ as $\eta _{,i} = \xi _{,j_i}$ and $q_{,i} = P_{,j_i} - P_{, j_{i-1}}$, respectively. With this, $\delta _{\xi }^p=\delta _{\eta }^q$, and by Proposition 5.3,

$$\begin{aligned} \mathsf{K}_{\bullet }(p)=d_\mathsf{K}\left( \mu ,\delta _{\eta }^q\right) =\max \nolimits _{i=1}^m\kappa _{F_{\mu },\left[ Q_{,i-1 },Q_{,i}\right] }\left( \eta _{,i}\right) . \end{aligned}$$

Pick i such that $\kappa _{F_{\mu },\left[ Q_{,i-1} ,Q_{,i}\right] }\left( \eta _{,i}\right) =\mathsf{K}_{\bullet }(p)$, that is,

$$\begin{aligned} \max \left\{ \left| F_{\mu -}\left( \eta _{,i}\right) -Q_{,i-1}\right| , \left| F_{\mu }\left( \eta _{,i}\right) -Q_{,i}\right| \right\} = \mathsf{K}_{\bullet }(p). \end{aligned}$$

Clearly, to establish (5.4) it is enough to show that

$$\begin{aligned} \max \left\{ \left| F_{\mu -}\left( \eta _{,i}\right) -G_-\left( \eta _{,i}\right) \right| , \left| F_{\mu }\left( \eta _{,i}\right) -G \left( \eta _{,i}\right) \right| \right\} \ge \mathsf{K}_{\bullet }(p) \end{aligned}$$

(5.5)

and this will now be done. To this end, notice that by the definition of $\eta$,

$$\begin{aligned} \frac{1}{2}\left( P_{,j_{i-1}-1}+P_{,j_{i-1}}\right) \le F_{\mu -}\left( \eta _{,i}\right) \le \frac{1}{2}\left( P_{,j_{i-1}}+P_{, j_{i-1}+1}\right) , \end{aligned}$$

(5.6)

but also

$$\begin{aligned} \frac{1}{2}\left( P_{,j_i-1}+P_{,j_i}\right) \le F_{\mu }\left( \eta _{,i}\right) \le \frac{1}{2}\left( P_{,j_i}+P_{, j_i+1}\right) , \end{aligned}$$

(5.7)

with the convention that $P_{,-1}=0$ and $P_{,n+1}=1$.

Assume first that $\mathsf{K}_{\bullet }(p)=\left| F_{\mu -}(\eta _{,i})-Q_{,i-1}\right|$. If $\eta _{,i}\le x_{,j_{i-1}}$ then $G_-\left( \eta _{,i}\right) \le P_{,j_{i-1}-1}$, and hence $F_{\mu -}(\eta _{,i})-G_-\left( \eta _{,i}\right) \ge F_{\mu -}\left( \eta _{,i}\right) -P_{,j_{i-1}}$, but also, by (5.6),

$$\begin{aligned} F_{\mu -}\left( \eta _{,i}\right) -G_-\left( \eta _{,i}\right)&\ge F_{\mu -}\left( \eta _{,i}\right) -P_{,j_{i-1}} - \left( 2F_{\mu -}\left( \eta _{,i}\right) -P_{,j_{i-1}-1}-P_{,j_{i-1}}\right) \\&=P_{,j_{i-1}}-F_{\mu -}\left( \eta _{,i}\right) , \end{aligned}$$

and consequently

$$\begin{aligned} F_{\mu -}\left( \eta _{,i}\right) -G_-\left( \eta _{,i}\right) \ge \left| F_{\mu -}\left( \eta _{,i}\right) -P_{,j_{i-1}}\right| =\left| F_{\mu -}\left( \eta _{,i}\right) -Q_{,i-1}\right| =\mathsf{K}_{\bullet }(p). \end{aligned}$$

If $x_{,j_{i-1}}<\eta _{,i}\le x_{,j_{i-1}+1}$ then $G_-\left( \eta _{,i}\right) =P_{,j_{i-1}}$ and hence

$$\begin{aligned} \left| F_{\mu -}\left( \eta _{,i}\right) -G_-\left( \eta _{,i}\right) \right| =\mathsf{K}_{\bullet }(p). \end{aligned}$$

Finally, if $\eta _{,i}>x_{,j_{i-1}+1}$ then $G_-\left( \eta _{,i}\right) \ge P_{,j_{i-1}+1}$, and hence $G_-\left( \eta _{,i}\right) -F_{\mu -}\left( \eta _{,i}\right) \ge P_{,j_{i-1}}-F_{\mu -}\left( \eta _{,i}\right)$, but also, again by (5.6),

$$\begin{aligned} G_-\left( \eta _{,i}\right) -F_{\mu -}\left( \eta _{,i}\right)&\ge P_{,j_{i-1}+1}-F_{\mu -}\left( \eta _{,i}\right) -\left( P_{,j_ {i-1}}+P_{,j_{i-1}+1}-2F_{\mu -}\left( \eta _{,i}\right) \right) \\&=F_{\mu -}\left( \eta _{,i}\right) -P_{,j_{i-1}}, \end{aligned}$$

and therefore

$$\begin{aligned} G_-\left( \eta _{,i}\right) -F_{\mu -}\left( \eta _{,i}\right) \ge \left| F_{\mu -}\left( \eta _{,i}\right) -P_{,j_{i-1}}\right| =\mathsf{K}_{\bullet }(p). \end{aligned}$$

Thus (5.5) holds whenever $\mathsf{K}_{\bullet }(p)=\left| F_{\mu -}\left( \eta _{,i}\right) -Q_{,i-1}\right|$.

Next assume that $\mathsf{K}_{\bullet }(p)=\left| F_{\mu }\left( \eta _{,i}\right) -Q_{,i}\right|$. Utilizing (5.7) instead of (5.6), completely analogous arguments show that $\left| F_{\mu }\left( \eta _{,i}\right) -G\left( \eta _{,i}\right) \right| \ge \mathsf{K}_{\bullet }(p)$ in this case as well, which again implies (5.5). The latter therefore holds in either case. As seen earlier, this proves the existence of a best $d_\mathsf{K}$-approximation of $\mu$, given p, and also that $d_\mathsf{K}\left( \mu ,\delta _{\bullet }^p\right) =\mathsf{K}_{\bullet }(p)$.

Finally, with $y\in \varXi _m^+$ and $p\in \varPi _m$ as in the proof of Lemma 3.4, observe that $d_\mathsf{K}\left( \mu ,\delta _x^p\right) = \mathsf{K}_{\bullet }(p)$ if and only if $\max _{i=1}^m\kappa _{F_{\mu },\left[ Q_{,i-1},Q_{,i}\right] }(y_{,i})=\mathsf{K}_{\bullet }(p)$, by Proposition 5.3. As seen in the proof of Theorem 5.1, this means that

$$\begin{aligned} F_{\mu -}(y_{,i+1})-\mathsf{K}_{\bullet }(p)\le Q_{,i}\le F_{\mu }(y_{,i})+\mathsf{K}_{\bullet }(p)\quad \forall \ i=0,\ldots ,m , \end{aligned}$$

or equivalently,

$$\begin{aligned} F_{\mu -}^{-1}\left( Q_{,i}-\mathsf{K}_{\bullet }(p)\right) \le y_{,i}\le F_{\mu }^{-1}\left( Q_{,i-1}+\mathsf{K}_{\bullet }(p)\right) \quad \forall \ i=1,\ldots ,m , \end{aligned}$$

which in turn is equivalent to the validity of (5.3) for every j. $\square$

Corollary 5.5

Assume $\mu \in \mathcal {P}_\mathsf{cts}$, and $n\in \mathbb {N}$. Then $d_\mathsf{K}\left( \mu ,\delta _x^{u_n}\right) \ge \frac{1}{2}n^{-1}$ for all $x\in \varXi _n$, with equality holding if and only if

$$\begin{aligned} F_{\mu -}^{-1}\left( \frac{2j-1}{2n}\right) \le x_{,j}\le F_{\mu }^{-1}\left( \frac{2j-1}{2n}\right) \quad \forall j=1,\ldots ,n. \end{aligned}$$

By combining Theorems 5.1 and 5.4, it is possible to characterize best $d_\mathsf{K}$-approximations of $\mu \in \mathcal {P}$ as well. For this, associate with every non-decreasing function $f:\mathbb {R}\rightarrow \overline{\mathbb {R}}$ and every number $a\ge 0$ a map $S_{f,a}:\overline{\mathbb {R}} \rightarrow \overline{\mathbb {R}}$, given by

$$\begin{aligned} S_{f, a} (x) = f_+ \left( f^{-1}(x+a)\right) +a \quad \forall \ x \in \overline{\mathbb {R}} . \end{aligned}$$

This map is a true analogue of $T_{f,a}$ in Sect. 3, and in fact, Proposition 3.8, with $T_{f,a}$ replaced by $S_{f,a}$, remains fully valid. Identical reasoning then shows that

$$\begin{aligned} \mathsf{K}_{\bullet }^{\bullet , n} := \min \left\{ a \ge 0 : S_{F_{\mu }, a}^{[n]}(0) \ge 1\right\} < +\infty ; \end{aligned}$$

again, $\left( \mathsf{K}_{\bullet }^{\bullet , n}\right)$ is non-increasing, $n\mathsf{K}_{\bullet }^{\bullet ,n}\le \frac{1}{2}$ for every n, and $\mathsf{K}_{\bullet }^{\bullet , n}=0$ if and only if $\# \text{ supp }\, \mu \le n$. Notice that if $\mu \in \mathcal {P}_\mathsf{cts}$ then

$$\begin{aligned} S_{F_{\mu }, a}(x) = \left\{ \begin{array}{ll} a &{}\quad \text{ if } x< - a , \\ 2a + x &{}\quad \text{ if } -a \le x <1 -a , \\ a + 1 &{}\quad \text{ if } x\ge 1 - a , \end{array} \right. \end{aligned}$$

from which it is clear that $\mathsf{K}_{\bullet }^{\bullet , n}=\frac{1}{2}n^{-1}$.

Theorem 5.6

Let $\mu \in \mathcal {P}$ and $n\in \mathbb {N}$. There exists a best $d_\mathsf{K}$-approximation of $\mu$, and $d_\mathsf{K} \left( \mu , \delta _{\bullet }^{\bullet , n}\right) = \mathsf{K}_{\bullet }^{\bullet , n}$. Moreover, for every $x\in \varXi _n$ and $p\in \varPi _n$, the following are equivalent:

• (i) $d_\mathsf{K} \left( \mu , \delta _x^p \right) = d_\mathsf{K} \left( \mu , \delta _{\bullet }^{\bullet , n}\right)$;

• (ii) all implications in (5.1) are valid with $\mathsf{K}^{\bullet }(x)$ replaced by $\mathsf{K}^{\bullet , n}_{\bullet }$;

• (iii) all implications in (5.3) are valid with $\mathsf{K}_{\bullet }(p)$ replaced by $\mathsf{K}^{\bullet , n}_{\bullet }$.

Proof

Note that once the existence of a best $d_\mathsf{K}$-approximation of $\mu$ is established, the proof is virtually identical to that of Theorem 3.9. Thus, only the existence is to be proved here. To this end, let $a=\inf \nolimits _{x\in \varXi _n,p\in \varPi _n}d_\mathsf{K}\left( \mu ,\delta _x^p\right)$, and pick sequences $(x_k)$ and $(p_k)$ in $\varXi _n$ and $\varPi _n$, respectively, with the property that $\lim _{k\rightarrow \infty } d_\mathsf{K}\left( \mu ,\delta _{x_k}^{p_k}\right) = a$. By the compactness of $\varXi _n$, assume w.o.l.g. that $\lim _{k\rightarrow \infty } x_k\ = \eta \in \varXi _n$. Since $a\le \mathsf{K}^{\bullet }(x_k)\le d_\mathsf{K}\left( \mu ,\delta _{x_k}^{p_k}\right)$, it suffices to show that $\mathsf{K}^{\bullet }(\eta )\le a$. To see the latter, assume that $\eta _{,j}<\eta _{,j+1}$ for any $j=1,\ldots ,n-1$. Then $x_{k,j}<x_{k,j+1}$ for all sufficiently large k, and hence by Theorem 5.1, $F_{\mu -}(x_{k,j+1})-F_{\mu }(x_{k,j})\le 2\mathsf{K}^{\bullet }(x_k)$, which in turn implies

$$\begin{aligned} F_{\mu -}(\eta _{,j+1})-F_{\mu }(\eta _{,j})\le \liminf \limits _{k\rightarrow \infty }\left( F_{\mu -}(x_{k,j+1})-F_{\mu }(x_{k,j})\right) \le 2 a . \end{aligned}$$

Since, similarly, $F_{\mu -}\left( \eta _{,1}\right) \le a$ and $1-F_{\mu }\left( \eta _{,n}\right) \le a$, it follows that $\mathsf{K}^{\bullet }(\eta )\le a$, as claimed. $\square$

Corollary 5.7

Assume $\mu \in \mathcal {P}_\mathsf{cts}$, and $n\in \mathbb {N}$. Then $\mathsf{K}_{\bullet }^{\bullet ,n}=\mathsf{K}_{\bullet }(u_n)=\frac{1}{2}n^{-1}$, and $\delta _x^p$ with $x\in \varXi _n$, $p\in \varPi _n$ is a best $d_\mathsf{K}$-approximation of $\mu$ if and only if it is a best uniform $d_\mathsf{K}$-approximation of $\mu$.

Remark 5

• (i) By Theorem 5.6, $\mathsf{K}_{\bullet }^{\bullet ,n}=\min _{x\in \varXi _n}\mathsf{K}^{\bullet }(x)=\min _{p\in \varPi _n}\mathsf{K}_{\bullet }(p)$.

• (ii) If $\mu$ has even a single atom, then $\mathsf{K}_{\bullet }^{\bullet ,n}$ may be smaller than $\mathsf{K}_{\bullet }(u_n)$, and thus a best uniform $d_\mathsf{K}$-approximation may not be a best $d_\mathsf{K}$-approximation. A simple example illustrating this is $\mu =\frac{3}{4}\delta _0+\frac{1}{4}\lambda \left| _{[0,1]}\right.$, where $\mathsf{K}_{\bullet }^{\bullet ,n}= \frac{1}{4}(2n-1)^{-1}$ whereas $\mathsf{K}_{\bullet }(u_n)=\frac{1}{2} \max \{n,2\}^{-1}$, and hence $\mathsf{K}^{\bullet ,n}_{\bullet }<\mathsf{K}_{\bullet }(u_n)$ for every $n\ge 2$.

For Benford’s law, the best $d_\mathsf{K}$-approximations are the same as the best uniform $d_1$-approximations; see also Fig. 1.

Corollary 5.8

Assume $b>1,$ and $n\in \mathbb {N}.$ Then $\delta _{x_n}^{u_n}$ with $x_{n,i}=b^{(2j-1)/(2n)}$ for all $j = 1, \ldots , n$ is the unique best (uniform) $d_\mathsf{K}$-approximation of $\beta _b.$ Moreover, $d_\mathsf{K}\left( \beta _b,\delta _{\bullet }^{\bullet ,n}\right) =\frac{1}{2}n^{-1}$.

Example 7

For $\mu = \text{ Beta }(2,1)$, both $F_{\mu }$ and $F_{\mu }^{-1}$ are continuous. By Corollaries 5.5 and 5.7, the best (or best uniform) $d_\mathsf{K}$-approximation of $\mu$ is $\delta _{x}^{u_n}$, with $x_{,j} = \sqrt{\frac{2j-1}{2n}}$ for $j=1, \ldots , n$, and $d_\mathsf{K} (\mu , \delta _{\bullet }^{u_n}) = d_\mathsf{K} (\mu , \delta _{\bullet }^{\bullet , n}) = \frac{1}{2} n^{-1}$. With Examples 1, 3, and 5, therefore, the sequences $\bigl ( n d_{*} (\mu , \delta _{\bullet }^{\bullet , n})\bigr )$ all converge to a finite, positive limit, and so do $\bigl ( n d_{*} (\mu , \delta _{\bullet }^{u_n})\bigr )$, provided that $r<2$ in case $* = r$.

Example 8

Even though the inverse Cantor distribution is discrete with infinitely many atoms, a best uniform $d_\mathsf{K}$-approximation exists, by Theorem 5.4. Utilizing (2.4), a tedious but elementary analysis of $F_{\mu }$ reveals that (3.7) is valid with $d_\mathsf{K}$ instead of $d_\mathsf{L}$. With Examples 2 and 6, therefore, $\bigl (n d_{*}(\mu , \delta _{\bullet }^{u_n})\bigr )$ is bounded below and above by positive constants for $* = \mathsf{L}, 1 , \mathsf{K}$, but tends to $+\infty$ for $* =r>1$ (Fig. 2).

Very similarly, a best $d_\mathsf{K}$-approximation exists, by Theorem 5.6, and the estimates (3.9) hold with $d_\mathsf{K}$ instead of $d_\mathsf{L}$. Thus, $\bigl ( n^{\log 3 / \log 2} d_{*}(\mu , \delta _{\bullet }^{\bullet , n} ) \bigr )$ is bounded below and above by positive constants for $* = \mathsf{L}, 1, \mathsf{K}$, but tends to $+\infty$ for $* = r>1$.

Fig. 3

The quantization ($Q_{*}$) and uniform quantization ($Q_{*,u}$) coefficients of $\beta _b$ for $d_{*}$; see also Fig. 4

6 Conclusion

As the title of this article suggests, and the introduction explains, the general results have been motivated by a quantitative analysis of Benford’s law, and the precise statements regarding the latter are but simple corollaries of the former. In particular, Sects. 3 to 5 show that the quantization coefficients $Q_{*} = \lim _{n\rightarrow \infty } n d_{*} (\beta _b, \delta _{\bullet }^{\bullet , n})$ and their uniform counterparts $Q_{*,u} = \lim _{n\rightarrow \infty } n d_{*} (\beta _b, \delta _{\bullet }^{u_n})$ all are finite and positive for each metric $d_{*}$ considered. Clearly, $Q_{*} \le Q_{*,u}$ for all $b>1$. Also, note that $\bigl ( n d_{*} (\beta _b, \delta _{\bullet }^{\bullet , n} )\bigr )$ is non-increasing, possibly constant, whereas $\bigl ( n d_{*} (\beta _b, \delta _{\bullet }^{u_n} )\bigr )$ is non-decreasing. Figure 3 summarizes the results obtained earlier.

The dependence of $Q_{*}$ and $Q_{*,u}$ on b is illustrated in Fig. 4. On the one hand, $Q_\mathsf{L}$ and $Q_{\mathsf{L},u}$ tend to $\frac{1}{2}$ as $b\downarrow 1$, but also as $b \rightarrow +\infty$, both attaining their respective minimal value for $b=2$. On the other hand, $Q_r$ and $Q_{r,u}$ both tend to $\frac{1}{2} (r+1)^{-1/r}$ as $b\downarrow 1$, whereas $\lim _{b\rightarrow +\infty } (\log b)^{1/r} Q_r = \frac{1}{2} (r+1) r^{-(r+1)/r}$ and $\lim _{b\rightarrow +\infty } (\log b)^{1/r - 1} Q_{r,u} = \frac{1}{2} r^{-1/r} (r+1)^{-1/r}$. Finally, $Q_\mathsf{K} = Q_{\mathsf{K},u} = \frac{1}{2}$ for all b.

Fig. 4

Comparing the quantization coefficients $Q_{*}$ (solid curves) and uniform quantization coefficients $Q_{*,u}$ (broken curves) of $\beta _b$, for $*= \mathsf{L}$ (red), $*=1,2$ (blue), and $*= \mathsf{K}$ (black), respectively; see also Fig. 3 (Color figure online)

Remark 6

In the context of Benford’s law, $\mathbb {I}= [1,b]$, and since $S_b < b$ always, it may seem more natural to study the approximation problem not on all of $\mathcal {P}$, but rather on the (dense) subset $\widetilde{\mathcal {P}}:= \bigl \{\mu \in \mathcal {P}: \mu (\{b\}) = 0\bigr \}$. Clearly, $d_\mathsf{L}$ and $d_r$ both metrize the weak topology on $\widetilde{\mathcal {P}}$ but are not complete. (By contrast, $d_\mathsf{K}$ is complete but not separable, and induces a finer topology.) Since $\widetilde{\mathcal {P}}$ is a $G_{\delta }$-set in $\mathcal {P}$, a classical theorem [11, Thm. 2.5.4] yields, for instance,

$$\begin{aligned} \widetilde{d}(\mu , \nu ) = \int _0^1 \left| G_{\mu } - G_{\nu }\right| + \sum \limits _{k=1}^{\infty } \frac{2^{-k} \left| \int _{1-k^{-1}}^1 \left( G_{\mu } - G_{\nu } \right) \right| }{ \int _{1-k^{-1}}^1 G_{\mu } \int _{1-k^{-1}}^1 G_{\nu } + \left| \int _{1-k^{-1}}^1 \left( G_{\mu } - G_{\nu } \right) \right| } , \end{aligned}$$

with $G_{\mu } = b - F_{\mu }^{-1}$, $G_{\nu } = b - F_{\nu }^{-1}$, as an equivalent complete, separable metric on $\widetilde{\mathcal {P}}$. However, $\widetilde{d}$ appears to be quite unwieldy, and the authors do not know of an equivalent complete metric on $\widetilde{\mathcal {P}}$ for which explicit results similar to those in Sects. 3 and 4 could be established.

Also, it is readily confirmed that, given any $\mu \in \widetilde{\mathcal {P}}$, there exists a best (or best uniform) $d_{*}$-approximation $\delta _{\bullet }^{\bullet , n}\in \widetilde{\mathcal {P}}$ (or $\delta _{\bullet }^{u_n}\in \widetilde{\mathcal {P}}$), i.e., these approximation problems always have a solution in $\bigl (\widetilde{\mathcal {P}}, d_{*}\bigr )$, notwithstanding the fact that the latter space is not complete (if $* = \mathsf{L}, r$) or not separable (if $* = \mathsf{K}$).

For Benford’s law, as seen above, all best (or best uniform) approximations considered converge at the same rate, namely $(n^{-1})$; the same is true for the $\text{ Beta }(2,1)$ distribution whenever $1\le r < 2$. These are not coincidences. Rather, for many other probability metrics $n^{-1}$ turns out to yield the correct order of magnitude of the n-th quantization error as well. Specifically, consider a metric d on $\mathcal {P}$ for which

(6.1)

with positive constants $a_1, a_2 , s_1, s_2$, and $\epsilon \in \{0, 1 \}$; see, e.g., [8, 26, 27] for examples and properties of such metrics. Note that validity of (6.1) causes d to metrize a topology at least as fine as the weak topology, and clearly (6.1) holds for any $d = d_{*}$. The latter fact, together with [16, Thm. 6.2] yields a simple observation regarding the prevalence of the rate $(n^{-1})$.

Proposition 6.1

Let d be a metric on $\mathcal {P}$ satisfying (6.1). Then, for every $\mu \in \mathcal {P}$,

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty }\,n \inf \nolimits _{x\in \varXi _n , p \in \varPi _n} d\bigl ( \mu , \delta _x^p \bigr ) < + \infty , \end{aligned}$$

and if $\mu$ is non-singular (w.r.t. $\lambda$) then also

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\, n \inf \nolimits _{x\in \varXi _n , p \in \varPi _n} d \bigl ( \mu , \delta _x^p\bigr ) >0 . \end{aligned}$$

Remark 7

• (i) Apart from $d_{*}$, examples of familiar probability metrics that satisfy (6.1) include the discrepancy distance $\sup _{I \subset \mathbb {R}} |\mu (I) - \nu (I)|$ and the $L^r$-distance $\Vert F_{\mu } - F_{\nu }\Vert _r$ between distribution functions [26]. For the important Prokhorov distance, validity of the right-hand inequality in (6.1) appears to be unknown [15], but best approximations are suspected to converge at the rate $\bigl ( n^{-1} \bigr )$ regardless [17, Sec.4]. Also, $(n^{-1})$ is established in [9] as the universal rate of convergence for best approximations under Orlicz norms, which contains $d_r$ as a special case.

• (ii) In [27, Sec.4.2], for any $a\ge 0$, the a-Lévy distance

  $$\begin{aligned} d_{\mathsf{L}_{a}}(\mu ,\nu )= \inf \left\{ y\ge 0: F_{\mu } (\cdot -a y) - y \le F_{\nu } \le F_{\mu } (\cdot + a y) + y \right\} \end{aligned}$$

  is considered. Every $d_{\mathsf{L}_a}$ satisfies (6.1), and $d_{\mathsf{L}_0} = d_\mathsf{K}$, $d_{\mathsf{L}_1} = \omega ^{-1} d_\mathsf{L}$. Usage of a-Lévy distances may enable a unified treatment of the results in Sects. 3 and 5.

• (iii) Under additional assumptions on $\mu$, the value of $n\inf _{x\in \varXi _n} d(\mu , \delta _{x}^{u_n})$ can similarly be bounded above and below by positive constants [30, Thm. 5.15].

Finally, it is worth pointing out that, though motivated here by Benford’s law, compactness of the interval $\mathbb {I}$ was assumed largely for convenience, and can easily be dispensed with for many of the general results in this article. For instance, if $\mathbb {I}$ is (closed but) unbounded then (2.2), with $\omega =1$, still yields $d_\mathsf{L}$ as a complete, separable metric inducing the weak topology on $\mathcal {P}$, though the latter no longer is compact. Clearly, Theorem 3.5 is valid in this situation, as (3.1) holds for $f=F_{\mu }$ and any interval $I \subset \overline{\mathbb {R}}$. Even though (3.1) may fail for $f=F_{\mu }^{-1}$ when $\text{ supp }\, \mu$ is unbounded, it is readily checked that nevertheless the conclusions of Proposition 3.3 remain intact for $\ell _{F_{\mu }^{-1}, I}$, provided that $I \subset [0,1]$ but $I \ne \{0\}$ and $I \ne \{ 1 \}$. With $\ell _{F^{-1}_{\mu }, \{0\}}^* :=\ell _{F^{-1}_{\mu }, \{1\}}^* := 0$, then, Proposition 3.6 holds verbatim, and so does Theorem 3.9. Analogously, Theorems 5.1, 5.4, and 5.6 all can be seen to be correct, with the definition of $\mathsf{K}_{\bullet }(p)$ understood to assume that $p_{,1} p_{,n}>0$. By contrast, the classical $L^1$-Kantorovich distance $d_1 (\mu , \nu ) = \Vert F_{\mu }^{-1} - F_{\nu }^{-1}\Vert _1$ is defined only on the (dense) subset $\mathcal {P}_1 = \left\{ \mu \in \mathcal {P}: \int _{\mathbb {I}} |x| \, \mathrm{d}\mu (x ) < + \infty \right\}$ where it metrizes a topology finer than the weak topology. Still, with $\mathcal {P}$ replaced by $\mathcal {P}_1$, Proposition 4.1 also remains intact; see, e.g., [30, Sec.5]. Note that the sequence $\bigl ( nd_{*} (\mu , \delta _{\bullet }^{u_n})\bigr )$ is bounded when $* = \mathsf{L}, \mathsf{K}$ because $d_\mathsf{L} \le d_\mathsf{K}$, whereas $\bigl ( nd_1 (\mu , \delta _{\bullet }^{\bullet , n})\bigr )$ may decay arbitrarily slowly; see [30, Thm. 5.32]. For a simple application of these results to a probability measure with unbounded support, let $\mu$ be the standard exponential distribution, i.e., $F_{\mu }(x) = \max \{0, 1 - e^{-x}\}$. Calculations quite similar to the ones shown earlier for Benford’s law yield

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }nd_\mathsf{L}\left( \mu ,\delta _{\bullet }^{\bullet ,n}\right) =\frac{\log 2}{2} \, , \quad \lim \limits _{n\rightarrow \infty }nd_\mathsf{L}\left( \mu ,\delta _{\bullet }^{u_n}\right) =\frac{1}{2} , \end{aligned}$$

whereas

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } n d_1\left( \mu ,\delta _{\bullet }^{\bullet , n}\right) =1 \quad \text{ but } \quad \lim \limits _{n\rightarrow \infty }\frac{n}{\log n}d_1 (\mu ,\delta _{\bullet }^{u_n})=\frac{1}{4} , \end{aligned}$$

and clearly $nd_\mathsf{K} (\mu , \delta _{\bullet }^{\bullet , n}) = nd_\mathsf{K} (\mu , \delta _{\bullet }^{u_n})=\frac{1}{2}$ for all n. Even though $\mu$ has finite moments of all orders, there exist probability metrics d for which $\bigl ( nd (\mu , \delta _{\bullet }^{\bullet , n})\bigr )$ is unbounded; see [17, Ex. 5.1(d)].