On the Separating Variables Method for Markov Death-Process Equations

Abstract

We consider a method of obtaining non-closed solutions of the first and second Kolmogorov equations for the exponential (double) generating function of transition probabilities for quadratic death-processes of one, two and three dimensions. We obtain a representation for the generating function of transition probabilities in the form of a Fourier series, using generalized hypergeometric functions and Jacobi polynomials.

1 Introduction

An analytical method for the study of Markov processes with a finite or countable states is based on consideration of the first (backward) and the second (forward) Kolmogorov systems of differential equations for transition probabilities [1, 10]. There are few cases in which an explicit solution can be found: the solutions are known for simple death-process, pure birth-process, birth and death process of linear or Poisson type (see the survey [12], Chap. 2, § 2.1.1), branching processes ([22], Chap. 1, § 8), and some of their modifications.

Different methods have been considered for simple death-process equations, for instance, in [4, 10], etc, operational calculus has been used. The expressions for transition probabilities are cumbersome [10] and of little use for the study of asymptotic properties of the random process.

Under special conditions on the Markov process, the second system of differential equations can be combined into a partial differential equation for generating function of transition probabilities [12]. In the case of a first-order equation, we have the Markov branching process [2, 22].

Researching into Markov death-process of quadric type with the equation of the second order was begun in [19], see also [5, 6]. The method of separating variables was used for the Kolmogorov second equation, and it obtained an expansion for the function of transition probabilities into Fourier series with two separated variables in which eigenfunctions are the Gegenbauer polynomials [19].

By the same method Letessier and Valent (see [16, 24], the survey [17], etc) found solutions for equations of second, third and fourth orders in the form of a Fourier series of special functions. In papers [16, 17], etc, spectrums and eigenfunctions were obtained for some birth and death processes of quadratic, cubic and quartic types. For the second equation of Kolmogorov, the authors build a series with more and more complicated functions, when the equation for eigenfunction belong to the class of hypergeometric equations (the Fuchs equation of second order with three singular points) or is generalized a hypergeometric equation.

In [24] for the birth and death processes of quadratic type, the second equation is solved in the form of a Fourier series with eigenvalues are expressed by elliptic integral, and the equation for eigenfunction belongs to the class of Heun equations (the Fuchs equation of the second order with four singular points, see [8], Chap. 15, § 3).

Numeric coefficients in [16, 19, 24], etc., were expressed by integral formulas, which are standard for the Fourier series theory, and remained uncalculated in many cases. According to the series for transiting probabilities, any opportunity to make some statements about asymptotic properties in considering Markov processes is unclear. A construction of non-closed solutions of Kolmogorov equations is connected with the spectrum-obtaining problem for these equations [15, 17]. Examples of solutions given in [16, 17, 19, 24], etc, have a discrete spectrum; the construction of examples of explicit solutions in the case of continuous spectrum is more challenging [1, 15].

In the present paper, the development of separating variables method owed to Kolmogorov equations is based on the introduction of an exponential generating function for transition probabilities [12] which allow combination of the first system of differential equations into the partial differential equation. At the same time using for first and second equations, the Fourier method gives a series with three separated variables, and coefficients are calculated by comparison with the exponent expansion known in the special functions theory.

We provide examples of the method used for equations of the quadratic death-process on N, $N^2$ and $N^3$. The established series includes the generalized hypergeometric functions and the Jacobi polynomials. In the last part of the paper, we discuss potential transition from the non-closed solution of the first and second equations to the integral represented solution.

2 Generalized Markov Death-Process of Quadratic Type

We consider a time-homogeneous Markov process

$$\begin{aligned} \xi _t,\quad t\in [0,\infty ), \end{aligned}$$

on the set of states

$$\begin{aligned} N=\{0,1,2,\ldots \} \end{aligned}$$

with transition probabilities

$$\begin{aligned} P_{ij}(t)={\mathbb {P}}\{\xi _t=j\mid \xi _0=i\},\quad i,j\in N. \end{aligned}$$

Let us suppose that the transition probabilities have the following form as $t\rightarrow 0+$ ($\lambda \ge 0$, $\mu \ge 0$)

$$\begin{aligned} P_{i,i-2}(t)= & {} p_0i(i-1)\lambda t+o\,(t),\nonumber \\ P_{i,i-1}(t)= & {} (p_1i(i-1)\lambda +i\mu )t+o\,(t),\nonumber \\ P_{ii}(t)= & {} 1-(i(i-1)\lambda +i\mu )t+o\,(t),\nonumber \\ P_{ij}(t)= & {} o\,(t),\quad j\ne i-2,i-1,i, \end{aligned}$$

(1)

where $p_0\ge 0$, $p_1\ge 0$, $p_0+p_1=1$.

Let us introduce the generating functions of the trasition probabilities ($|s|\le 1$)

$$\begin{aligned} F_{i}(t;s)=\sum _{j=0}^{\infty } P_{ij}(t)s^{j},\quad i\in N. \end{aligned}$$

The second system of Kolmogorov differential equations for the transition probabilities of the process $\xi _t$ is equivalent to the partial differential equation [12]

$$\begin{aligned} {{\partial F_{i}(t;s)}\over {\partial t}}= \lambda \big (p_0+p_1s-s^2\big ){{\partial ^2 F_{i}(t;s)}\over {\partial s^2}}+ \mu (1-s){{\partial F_{i}(t;s)}\over {\partial s}}, \end{aligned}$$

(2)

with initial condition $F_{i}(0;s)=s^i$.

Fig. 1

Jumps for the generalized death-process

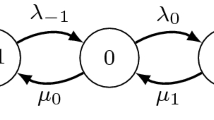
Possible jumps for stochastic process $\xi _t$ are shown in Fig. 1. The Markov process stays at the initial state i during a random time $\tau _i$ with distribution ${\mathbb {P}}\{\tau _i\le t\}=1-e^{-(i(i-1)\lambda +i\mu )t}$. Then the process passes into the state $i-1$ with the probability $(p_1i(i-1)\lambda +i\mu )/(i(i-1)\lambda +i\mu )$ or into the state $i-2$ with the probability $p_0i(i-1)\lambda /(i(i-1)\lambda +i\mu )$, and so on. The state 0 is absorbing. Markov process $\xi _t$ is interpreted as a model of bimolecular chemistry reaction with kinetic scheme $2T\rightarrow 0,T$; $T\rightarrow 0$ [5, 12, 19].

Let $\mathcal{F}(t;z;s)$ be the exponential (double) generating function

$$\begin{aligned} \mathcal{F}(t;z;s)=\sum _{i=0}^{\infty } {{z^i}\over {i!}}F_{i}(t;s)= \sum _{i=0}^{\infty } \sum _{j=0}^{\infty } {{z^i}\over {i!}}P_{ij}(t)s^{j}. \end{aligned}$$

(3)

The function $\mathcal{F}(t;z;s)$ is analytic in the domain $|z|<\infty$, $|s|<1$.

The first (backward) and the second (forward) systems of Kolmogorov differential equations for the transition probabilities for the considered Markov process have the form [12]

$$\begin{aligned} {{\partial \mathcal{F}}\over {\partial t}}&= \lambda z^2\left( p_0\mathcal{F}+p_1{{\partial \mathcal{F}}\over {\partial z}} -{{\partial ^2\mathcal{F}}\over {\partial z^2}}\right) + \mu z\left( \mathcal{F}-{{\partial \mathcal{F}}\over {\partial z}}\right) , \end{aligned}$$

(4)

$$\begin{aligned} {{\partial \mathcal{F}}\over {\partial t}}&= \lambda \big (p_0+p_1s-s^2\big ){{\partial ^2\mathcal{F}}\over {\partial s^2}}+ \mu (1-s){{\partial \mathcal{F}}\over {\partial s}}, \end{aligned}$$

(5)

with initial condition $\mathcal{F}(0;z;s)=e^{zs}$. The linear equations in partial derivatives of the second order (4), (5) are solving by separating variables method.

Furthermore, we need some special functions (see [7, 8, 14, 21], etc). The confluent hypergeometric function is defined by the series ($b\ne 0,-\,1,-\,2,\ldots$)

$$\begin{aligned} {}_1F_1(a;b;z)=1+\sum _{k=1}^\infty {{a(a+1)\ldots (a+k-1)z^k}\over {b(b+1)\ldots (b+k-1)k!}} \end{aligned}$$

(6)

and it satisfies the confluent hypergeometric equation

$$\begin{aligned} zy''+(b-z)y'-a y=0. \end{aligned}$$

(7)

The function (6) is analytic on the complex plane; at some values of the parameters, it can be expressed by the modified Bessel function ([21], Formula 7.11.1.5)

$$\begin{aligned} {}_1F_1(a;2a;z)= \Gamma \Big (a+{1\over 2}\Big )\left( {z\over 4}\right) ^{1/2-a} e^{z/2}I_{a-1/2}\left( {z\over 2}\right) , \end{aligned}$$

where $\Gamma (a)$ is the gamma function.

The Jacobi polynomial of n-th order is defined by the formula ([7], § 10.8)

$$\begin{aligned} P_n^{(\alpha ,\beta )}(x)= & {} \sum _{k=0}^n{{(\alpha +n-k+1)\ldots (\alpha +n) (\beta +k+1)\ldots (\beta +n)} \over {2^n k!(n-k)!}}\\&\quad \times \, (x+1)^k(x-1)^{n-k}, \end{aligned}$$

$n=0,1,\ldots ,$ and it is the unique polynomial solution of the differential (hypergeometric) equation

$$\begin{aligned} (1-x^2)y''+\left( \beta -\alpha -(\alpha +\beta +2)x\right) y'+n(n+\alpha +\beta +1)y=0. \end{aligned}$$

(8)

The following exponent extension is needed for the sequel [7], § 10.20, Formula (4)]

$$\begin{aligned} e^{zx}=\sum _{n=0}^{\infty } {{\Gamma (n+\alpha +\beta +1)}\over {\Gamma (2n+\alpha +\beta +1)}}(2z)^ne^{-z} {}_1F_1(n+\beta +1;2n+\alpha +\beta +2;2z)P_n^{(\alpha ,\beta )}(x). \end{aligned}$$

(9)

Theorem 1

For the Markov process $\xi (t)$ on the set of states N under conditions (1) the double generating function of transition probabilities is as follows $(\lambda >0$, $\mu \ge 0)$

$$\begin{aligned} {\mathcal{F}}(t;z;s)= & {} \sum _{n=0}^{\infty }{{\Gamma (n-1+\mu /\lambda )}\over {\Gamma (2n-1+\mu /\lambda )}}\nonumber \\&\quad \times \, ((1+p_0)z)^{n}e^{-p_0z}{}_1F_1\left( n+\mu /\lambda ;2n+\mu /\lambda ;(1+p_0)z\right) \nonumber \\&\quad \times \, P_n^{(-1,\mu /\lambda -1)}\left( {{2s-1+p_0}\over {1+p_0}}\right) e^{-(n(n-1)\lambda +n\mu )t}, \end{aligned}$$

(10)

where $\Gamma (a)$ is the gamma function, ${}_{1}F_1(a,b;z)$ is the confluent hypergeometric function, $P_n^{(-1,\beta )}(x)$ are the Jacobi polynomials.

Proof

We look for the solution of the system of Eqs. (4), (5) in a form of the series with three separating variables ($|s|<1$)

$$\begin{aligned} \mathcal{F}(t;z;s)=\sum _{n=0}^{\infty }A_n\widetilde{C}_n(z) C_{n}(s)e^{-\lambda _nt}. \end{aligned}$$

(11)

After substitution (11) into (4) and (5), we get the following equations for the functions $\widetilde{C}_n(z)$ and $C_n(s)$:

$$\begin{aligned} \lambda z^2\left( p_0\widetilde{C}_n(z)+p_1\widetilde{C}_n^{\prime }(z)- \widetilde{C}_n^{\prime \prime }(z)\right) + \mu z\left( \widetilde{C}_n(z)-\widetilde{C}_n^{\prime }(z)\right) + \lambda _n\widetilde{C}_n(z)=0;\qquad \end{aligned}$$

(12)

$$\begin{aligned} \lambda \big (p_0+p_1s-s^2\big )C_n^{\prime \prime }(s)+ \mu (1-s)C_n^{\prime }(s)+\lambda _nC_n(s)=0,\quad n=0,1,\ldots .\qquad \end{aligned}$$

(13)

The differential equations (2) and (13) was investigated in [19] under conditions $\mu =0$, and $p_0=0$ or $p_0=1$. Following [19] we can establish that the Eq. (13) gets the additional boundary condition ‘$C_n(s)$ is polynomial’. Then, the sequence of ‘eigenvalues’ $\lambda _n=n(n-1)\lambda +n\mu$, $n=0,1,\ldots$ (cf. [14], Vol. II, Chap. 3, § 9.7). Substituting $x=(2s-1+p_0)/(1+p_0)$ in (13) and denoting $C_n(s)=y(x)$ we obtain the following equation of type (8),

$$\begin{aligned} (1-x^2)y''+\left( {\mu \over \lambda }-{\mu \over \lambda }\,x\right) y'+ n\left( n-1+{\mu \over \lambda }\right) y=0. \end{aligned}$$

Consequently, each $\lambda _n$ has the corresponding ‘eigenfunction’

$$\begin{aligned} C_n(s)=P_n^{(-1,\mu /\lambda -1)}\left( {{2s-1+p_0}\over {1+p_0}}\right) , \end{aligned}$$

where

$$\begin{aligned} P_n^{(-1,\mu /\lambda -1)}(x)= & {} \sum _{k=0}^n{{(n-k)\ldots (n-1)\,(\mu /\lambda +k)\ldots (\mu /\lambda +n-1)} \over {2^n k!(n-k)!}}\nonumber \\&\quad \times \,(x+1)^k(x-1)^{n-k}. \end{aligned}$$

(14)

The Eq. (12) takes the form

$$\begin{aligned}&\lambda z^2\left( p_0\widetilde{C}_n(z)+p_1\widetilde{C}_n^{\prime }(z)- \widetilde{C}_n^{\prime \prime }(z)\right) + \mu z\left( \widetilde{C}_n(z)-\widetilde{C}_n^{\prime }(z)\right) \\&\quad +\,(n(n-1)\lambda +n\mu )\widetilde{C}_n(z)=0, \end{aligned}$$

it is to be the reduced form of the confluent hypergeometric equation (7) ([14], cf. 2.273(6) at $a=-p_1$, $b=\mu /\lambda$, $\alpha =-p_0$, $\beta =-\mu /\lambda$, $\gamma =-n(n-1)-n\mu /\lambda$ ). According to the generation function properties, we are looking an analytic for all $z_1$, $z_2$ solution; following [14], we get

$$\begin{aligned} \widetilde{C}_n(z)=\left( (1+p_0)z\right) ^{n}e^{-p_0z} {}_1F_1(n+\mu /\lambda ;2n+\mu /\lambda ;(1+p_0)z), \end{aligned}$$

where ${}_1F_1(a;b;z)$ is the confluent hypergeometric function.

Hence, the seeking series (11) is

$$\begin{aligned} {\mathcal{F}}(t;z;s)= & {} \sum _{n=0}^{\infty } A_n\left( (1+p_0)z\right) ^{n}e^{-p_0z}{}_1F_1\left( n+\mu /\lambda ;2n+\mu /\lambda ;(1+p_0)z\right) \\&\quad \times \, P_n^{(-1,\mu /\lambda -1)}\left( {{2s-1+p_0}\over {1+p_0}}\right) e^{-(n(n-1)\lambda +n\mu )t}. \end{aligned}$$

The values $A_n$ are obtained by comparing the initial conditions $\mathcal{F}(0;z;s)=e^{zs}$ and the exponent expanding [see (9)]

$$\begin{aligned} e^{zs}= & {} \sum _{n=0}^{\infty } {{\Gamma (n{-}1{+}\mu /\lambda )}\over {\Gamma (2n{-}1{+}\mu /\lambda )}}\left( (1{+}p_0)z\right) ^{n}e^{-p_0z}{}_1F_1(n+\mu /\lambda ;2n+\mu /\lambda ;(1+p_0)z)\nonumber \\&\quad \times \, P_n^{(-1,\mu /\lambda -1)}\left( {{2s-1+p_0}\over {1+p_0}}\right) . \end{aligned}$$

(15)

We get

$$\begin{aligned} A_n=\frac{\Gamma (n-1+\mu /\lambda )}{\Gamma (2n-1+\mu /\lambda )} \end{aligned}$$

and the formula (10). Convergence of the series (10) for all z, s and $t\in [0,\infty )$ follows from the convergence of expansion (15). $\square$

If $t=0$, then the formula (10) is to be the expansion of the exponent $e^{zs}$ into series. If $\mu >0$, $p_0=1$, then we have the expansion into Jacobi polynomial series. If $\mu =0$, $p_0=1$, then we have the Sonine expansion [7], § 7.10.1, Formula (5)].

By (6) we get ${}_1F_1(\mu /\lambda ;\mu /\lambda ;z)=e^z=1+z+z^2/2+\cdots ,$${}_1F_1(1+\mu /\lambda ;2+\mu /\lambda ;z)=1+ ((1+\mu /\lambda )/(2+\mu /\lambda ))z+\cdots ,$${}_1F_1(2+\mu /\lambda ;4+\mu /\lambda ;z)=1+\cdots ,$ by (14) we get $P_0^{(-1,\mu /\lambda -1)}(x)=1$, $P_1^{(-1,\mu /\lambda -1)}(x)=(\mu /(2\lambda ))(x-1)$, $P_2^{(-1,\mu /\lambda -1)}(x)= ((1+\mu /\lambda )/8)[(2+\mu /\lambda )x^2- (2\mu /\lambda )x-2+\mu /\lambda ]$. Substituting this expressions for (10) and equating the coefficients in the equal powers of $1,z,zs,z^2,z^2s,z^2s^2$ to one another with (3), we obtain the transitions probabilities

$$\begin{aligned} P_{00}(t)= & {} 1;\quad P_{10}(t)=1-e^{-\mu t},\quad P_{11}(t)=e^{-\mu t};\\ P_{20}(t)= & {} 1-2\left[ {{1+\mu /\lambda }\over {2+\mu /\lambda }}(1+p_0)-p_0\right] e^{-\mu t}\\&\quad +\,{1\over 4}\left[ {{-2+\mu /\lambda }\over {2+\mu /\lambda }}(1+p_0)^2\right. \\&\left. \quad -\, {{2\mu /\lambda }\over {2+\mu /\lambda }}(-1+p_0^2)+(-1+p_0)^2\right] e^{-(2\lambda +2\mu )t},\\ P_{21}(t)= & {} 2\left[ {{1+\mu /\lambda }\over {2+\mu /\lambda }}(1+p_0)-p_0\right] e^{-\mu t}\\&\quad -\,\left[ {{\mu /\lambda }\over {2+\mu /\lambda }}(1+p_0)+1-p_0\right] e^{-(2\lambda +2\mu )t},\\ P_{22}(t)= & {} e^{-(2\lambda +2\mu )t}. \end{aligned}$$

This formulas for $P_{ij}(t)$ may be obtained by direct solution of the system of Kolmogorov differential equations [10] for the considering generalized death-process.

3 Quadratic Death-Process of Second Dimension

We consider a time-homogeneous Markov process

$$\begin{aligned} \xi (t)=(\xi _1(t),\xi _2(t)),\quad t\in [0,\infty ), \end{aligned}$$

on the set of states

$$\begin{aligned} N^2=\{(\alpha _1,\alpha _2),\ \alpha _1,\alpha _2=0,1,\ldots \}, \end{aligned}$$

with transition probabilities

$$\begin{aligned} P_{(\beta _1,\beta _2)}^{(\alpha _1,\alpha _2)}(t)={\mathbb {P}}\left\{ \xi (t)=(\beta _1,\beta _2)\mid \xi (0)=(\alpha _1,\alpha _2)\right\} \end{aligned}$$

of the following form as $t\rightarrow 0+$ ($\lambda >0$)

$$\begin{aligned} P_{(\alpha _1-1,\alpha _2-1)}^{(\alpha _1,\alpha _2)}(t)= & {} p_{00}\alpha _1\alpha _2\lambda t+o\,(t),\nonumber \\ P_{(\alpha _1,\alpha _2-1)}^{(\alpha _1,\alpha _2)}(t)= & {} p_{10}\alpha _1\alpha _2\lambda t+o\,(t),\nonumber \\ P_{(\alpha _1-1,\alpha _2)}^{(\alpha _1,\alpha _2)}(t)= & {} p_{01}\alpha _1\alpha _2\lambda t+o\,(t),\nonumber \\ P_{(\alpha _1,\alpha _2)}^{(\alpha _1,\alpha _2)}(t)= & {} 1-\alpha _1\alpha _2\lambda t+o\,(t), \end{aligned}$$

(16)

where $p_{00}\ge 0$, $p_{10}\ge 0$, $p_{01}\ge 0$, $p_{00}+p_{10}+p_{01}=1$. Using the generating function ($|s_1|\le 1,|s_2|\le 1$)

$$\begin{aligned} F_{(\alpha _1,\alpha _2)}(t;s_1,s_2)=\sum \limits _{\beta _1,\beta _2=0}^{\infty } P_{(\beta _1,\beta _2)}^{(\alpha _1,\alpha _2)}(t)s_1^{\beta _1}s_2^{\beta _2}, \quad (\alpha _1,\alpha _2)\in N^2, \end{aligned}$$

we can reduce the second system of differential equations for the transition probabilities of the Markov process $(\xi _1(t),\xi _2(t))$ to the partial differential equation [12]

$$\begin{aligned} {{\partial F_{(\alpha _1,\alpha _2)}(t;s_1,s_2)}\over {\partial t}}= \lambda (p_{00}+p_{10}s_1+p_{01}s_2-s_1s_2) {{\partial ^2 F_{(\alpha _1,\alpha _2)}(t;s_1,s_2)}\over {\partial s_1\partial s_2}}, \end{aligned}$$

with initial condition $F_{(\alpha _1,\alpha _2)}(0;s_1,s_2)=s_1^{\alpha _1}s_2^{\alpha _2}$.

Fig. 2

Realization of a two-dimensional death-process

In Fig. 2 we show an example of the realization of a process $(\xi _1(t),\xi _2(t))$. The Markov process stays in its initial state $(\alpha _1,\alpha _2)$ for random time $\tau _{(\alpha _1,\alpha _2)}$ with ${\mathbb {P}}\{\tau _{(\alpha _1,\alpha _2)}\le t\}=1-e^{-\alpha _1\alpha _2\lambda t}$. Then, with the probability $p_{10}$, the process passes to the state $(\alpha _1,\alpha _2-1)$, with the probability $p_{00}$ the process passes to the state $(\alpha _1-1,\alpha _2-1)$ or with the probability $p_{01}$ the process passes to the state $(\alpha _1-1,\alpha _2)$. The further evolution of the process is similar. The states $\{(\gamma _1,0),\ (0,\gamma _2),\ \gamma _1,\gamma _2=0,1,2,\ldots \}$ are absorbing. For the process $(\xi _1(t),\xi _2(t))$ ‘embedded Markov chain’ is a random walk on $N^2$.

The Markov process $(\xi _1(t),\xi _2(t))$ is a model of a population with male individuals and female individuals [11]. The state $(\alpha _1,\alpha _2)$ is interpreted as the existence of a group $\alpha _1$ of particles of type $T_1$ and $\alpha _2$ particles of type $T_2$; in a random time there is an interaction of a pairs of particles, which are transformed into new groups of particles. The main assumptions of the model are as follows: any pair of individuals $T_1+T_2$ in the population generates descendants independently of the others; the frequency of acts of generation of new individuals is proportional both to the number of individuals of type $T_1$ and to the number of individuals of type $T_2$.

Using the exponential generating function

$$\begin{aligned} \mathcal{F}(t;z_1,z_2;s_1,s_2)=\sum \limits _{\alpha _1,\alpha _2=0}^{\infty } {{z_1^{\alpha _1}z_2^{\alpha _2}}\over {\alpha _1!\alpha _2!}} F_{(\alpha _1,\alpha _2)}(t;s_1,s_2) \end{aligned}$$

we can reduce the first and the second system of differential equations for the transition probabilities of the Markov process to the form of partial differential equations [12]

$$\begin{aligned} {{\partial \mathcal{F}}\over {\partial t}}&= \lambda z_1z_2\left( p_{00}\mathcal{F}+ p_{10}{{\partial \mathcal{F}}\over {\partial z_1}}+ p_{01}{{\partial \mathcal{F}}\over {\partial z_2}} -{{\partial ^2\mathcal{F}}\over {\partial z_1\partial z_2}}\right) , \end{aligned}$$

(17)

$$\begin{aligned} {{\partial \mathcal{F}}\over {\partial t}}&= \lambda \left( p_{00}+p_{10}s_1+p_{01}s_2-s_1s_2\right) {{\partial ^2\mathcal{F}}\over {\partial s_1\partial s_2}}, \end{aligned}$$

(18)

with initial condition $\mathcal{F}(0;z_1,z_2;s_1,s_2)=e^{z_1s_1+z_2s_2}$.

The generalized hypergeometric function is defined by the series

$$\begin{aligned} {}_{0}F_1(b;z)=1+\sum _{k=1}^\infty {{z^k}\over {b(b+1)\ldots (b+k-1)k!}}; \end{aligned}$$

(19)

${}_{0}F_1(b;z)$ is a solution of the equation

$$\begin{aligned} zy''+b y'-y=0. \end{aligned}$$

The function (19) can be expressed by the modified Bessel function ([21], Formula 7.13.1.1),

$$\begin{aligned} {}_0F_1(b;z)=\Gamma (b)z^{(1-b)/2}I_{b-1}(2\sqrt{z}). \end{aligned}$$

Theorem 2

Let a Markov process on the state space $N^2$ be given by the densities of transition probabilities (16). The double generating function of the transitions probabilities is $(p_{10}<1,p_{01}<1)$

$$\begin{aligned} \mathcal{F}(t;z_1,z_2;s_1,s_2)= & {} e^{p_{01}z_1+p_{10}z_2}\sum _{\alpha _1,\alpha _2=0}^{\infty } {{\alpha _1+\alpha _2}\over {\mathrm{max}(\alpha _1,\alpha _2)}}{{((1-p_{01})z_1)^{\alpha _1}((1-p_{10})z_2)^{\alpha _2}}\over {(\alpha _1+\alpha _2)!}} \nonumber \\&\times \, {}_0F_1(\alpha _1+\alpha _2+1;(1-p_{01})(1-p_{10})z_1z_2)\nonumber \\&\times \, \left( {{s_\sigma -p_{\sigma }}\over {1-p_{\sigma }}}\right) ^{|\alpha _1-\alpha _2|} P_{\mathrm{min}(\alpha _1,\alpha _2)}^{(-1,|\alpha _1-\alpha _2|)} \left( 2\,{{s_1-p_{01}}\over {1-p_{01}}}\, {{s_2-p_{10}}\over {1-p_{10}}}-1\right) \nonumber \\&\times \, e^{-\alpha _1\alpha _2\lambda t}, \end{aligned}$$

(20)

where ${}_0F_1(b;z)$ is the generalized hypergeometric function, $P_n^{(-1,\beta )}(x)$ are the Jacobi polynomials; if $\alpha _1\ge \alpha _2$, then $s_\sigma =s_1$, $p_{\sigma }=p_{01}$; if $\alpha _1<\alpha _2$, then $s_\sigma =s_2$, $p_{\sigma }=p_{10}$; if $\alpha _1=0$, $\alpha _2=0$ then the expression ${(\alpha _1+\alpha _2)/\max (\alpha _1,\alpha _2)}$ is to be equal to 1.

Proof

Consider the equation in partial derivatives (17), (18). We are looking for the solution in a form of the series ($|s_1|<1$, $|s_2|<1$)

$$\begin{aligned} \mathcal{F}(t;z_1,z_2;s_1,s_2)=\sum _{\alpha _1,\alpha _2=0}^{\infty } A_{\alpha _1\alpha _2}\widetilde{C}_{\alpha _1\alpha _2}(z_1,z_2) C_{\alpha _1\alpha _2}(s_1,s_2)e^{-\lambda _{\alpha _1\alpha _2}t}. \end{aligned}$$

(21)

Substituting (21) in (17) and (18), we get the equations for the functions $\widetilde{C}_{\alpha _1\alpha _2}(z_1,z_2)$ and $C_{\alpha _1\alpha _2}(s_1,s_2)$:

$$\begin{aligned}&\lambda z_1z_2\left( p_{00}\widetilde{C}_{\alpha _1\alpha _2}+ p_{10}{{\partial \widetilde{C}_{\alpha _1\alpha _2}}\over {\partial z_1}}+ p_{01}{{\partial \widetilde{C}_{\alpha _1\alpha _2}}\over {\partial z_2}} -{{\partial ^2 \widetilde{C}_{\alpha _1\alpha _2}}\over {\partial z_1\partial z_2}}\right) +\lambda _{\alpha _1\alpha _2}\widetilde{C}_{\alpha _1\alpha _2}=0;\ \ \ \end{aligned}$$

(22)

$$\begin{aligned}&\lambda (p_{00}+p_{10}s_1+p_{01}s_2-s_1s_2) {{\partial ^2 C_{\alpha _1\alpha _2}}\over {\partial s_1\partial s_2}}+ \lambda _{\alpha _1\alpha _2}C_{\alpha _1\alpha _2}=0;\quad \alpha _1,\alpha _2=0,1,\ldots .\nonumber \\ \end{aligned}$$

(23)

From the assumptions given on the jumps of the process $\xi (t)$, it follows that for the Eq. (23) boundary condition ‘$C_{\alpha _1\alpha _2}(s_1,s_2)$ is polynomial’. Then the sequence ‘eigenvalues’ $\lambda _{\alpha _1\alpha _2}=\alpha _1\alpha _2\lambda$, $\alpha _1,\alpha _2=0,1,\ldots ,$ and from (23) it is not difficult to obtain the corresponding ‘eigenfunction’

$$\begin{aligned} C_{\alpha _1\alpha _2}(s_1,s_2)= \left( {{s_\sigma -p_{\sigma }}\over {1-p_{\sigma }}}\right) ^{|\alpha _1-\alpha _2|} P_{\mathrm{min}(\alpha _1,\alpha _2)}^{(-1,|\alpha _1-\alpha _2|)} \left( 2\,{{s_1-p_{01}}\over {1-p_{01}}}\, {{s_2-p_{10}}\over {1-p_{10}}}-1\right) , \end{aligned}$$

where $P_n^{(-1,\beta )}(x)$ are Jacobi polynomials; $s_\sigma =s_1$, $p_{\sigma }=p_{01}$, if $\alpha _1\ge \alpha _2$ and $s_\sigma =s_2$, $p_{\sigma }=p_{10}$, if $\alpha _1<\alpha _2$.

Hence, the Eq. (22) has the form

$$\begin{aligned} z_1z_2\left( p_{00}\widetilde{C}_{\alpha _1\alpha _2}+ p_{10}{{\partial \widetilde{C}_{\alpha _1\alpha _2}}\over {\partial z_1}}+ p_{01}{{\partial \widetilde{C}_{\alpha _1\alpha _2}}\over {\partial z_2}} -{{\partial ^2 \widetilde{C}_{\alpha _1\alpha _2}}\over {\partial z_1\partial z_2}}\right) +\alpha _1\alpha _2\widetilde{C}_{\alpha _1\alpha _2}=0. \end{aligned}$$

By the definition of the function $\mathcal{F}(t;z_1,z_2;s_1,s_2)$, it follows that the solution must be analytic for all $z_1,z_2$, hence

$$\begin{aligned} \widetilde{C}_{\alpha _1\alpha _2}(z_1,z_2)= & {} ((1-p_{01})z_1)^{\alpha _1}((1-p_{10})z_2)^{\alpha _2} e^{p_{01}z_1+p_{10}z_2}\\&\quad \times \, {}_0F_{1}( \alpha _1 +\,\alpha _2+1;(1-p_{01})(1-p_{10})z_1z_2), \end{aligned}$$

where ${}_0F_1(b;z)$ is generalized hypergeometric function.

Aimed to get the values $A_{\alpha _1\alpha _2}$ let us consider the exponent $e^{z_1s_1+z_2s_2}$ expansion. From generalized hypergeometric function series (19), we obtain the equality

$$\begin{aligned} e^{z_1+z_2}={}_0F_1(1;z_1z_2) +\sum _{k=1}^{\infty }\Big ({{z_1^k}\over {k!}}+{{z_2^k}\over {k!}}\Big ) {}_0F_1(k+1;z_1z_2). \end{aligned}$$

(24)

Considered special functions satisfies the formulas ([21], Formula 6.8.3.13):

$$\begin{aligned} {}_0F_1(1;zs)= & {} {}_0F_1(1;z)+2\sum _{l=1}^{\infty } {{z^l}\over {(2l)!}}{}_0F_1(2l+1;z)P_{l}^{(-1,0)}(2s-1);\ \ \ \ \ \end{aligned}$$

(25)

$$\begin{aligned} {{1}\over {k!}}{}_0F_1(k+1;zs)= & {} \sum _{l=0}^{\infty } {{z^l}\over {(2l+k-1)!(l+k)}} {}_0F_1(2l+k+1;z)P_{l}^{(-1,k)}(2s-1),\nonumber \\ \end{aligned}$$

(26)

$k=1,2,\ldots$ Using (24), (25) and (26), we get the sequence of equalities

$$\begin{aligned} e^{z_1s_1+z_2s_2}= & {} e^{p_{01}z_1+p_{10}z_2}e^{z_1(s_1-p_{01})+z_2(s_2-p_{10})}\nonumber \\= & {} e^{p_{01}z_1+p_{10}z_2}\Big \{{}_0F_1\Big (1;(1-p_{01})(1-p_{10})z_1z_2 \Big ({{s_1-p_{01}}\over {1-p_{01}}}\Big )\Big ({{s_2-p_{10}}\over {1-p_{10}}}\Big )\Big )\nonumber \\&\quad +\,\sum _{k=1}^{\infty } \left[ {{((1-p_{01})z_1)^k}\over {k!}}\Big ({{s_1-p_{01}}\over {1-p_{01}}}\Big )^k+ {{((1-p_{10})z_2)^k}\over {k!}}\Big ({{s_2-p_{10}}\over {1-p_{10}}}\Big )^k\right] \nonumber \\&\quad \, \times \, {}_0 F_1\Big (k+1;(1-p_{01})(1-p_{10})z_1z_2 \Big ({{s_1-p_{01}}\over {1-p_{01}}}\Big )\Big ({{s_2-p_{10}}\over {1-p_{10}}}\Big )\Big )\Big \}\nonumber \\= & {} e^{p_{01}z_1+p_{10}z_2}\Big \{{}_0F_1(1;(1-p_{01})(1-p_{10})z_1z_2)\nonumber \\&\quad +\,2\sum _{\alpha _1=1}^{\infty } {{((1-p_{01})z_1)^{\alpha _1}((1-p_{10})z_2)^{\alpha _1}}\over {(2\alpha _1)!}} \nonumber \\&\quad \times \, {}_0F_{1}(2\alpha _1 +\,1;(1-p_{01})(1-p_{10})z_1z_2)\nonumber \\&\quad \times \,P_{\alpha _1}^{(-1,0)} \left( 2\,{{s_1-p_{01}}\over {1-p_{01}}}\, {{s_2-p_{10}}\over {1-p_{10}}}-1\right) \nonumber \\&\quad +\,\sum _{k=1}^{\infty }\sum _{\alpha _2=0}^{\infty } {{((1-p_{01})z_1)^{\alpha _2+k}((1-p_{10})z_2)^{\alpha _2}}\over {(2\alpha _2+k-1)!(\alpha _2+k)}}\nonumber \\&\quad \times \, {}_0F_{1}(2\alpha _2 +\,\,k+1;(1-p_{01})(1-p_{10})z_1z_2)\nonumber \\&\quad \times \, \Big ({{s_1-p_{01}}\over {1-p_{01}}}\Big )^kP_{\alpha _2}^{(-1,k)} \Big (2\,{{s_1-p_{01}}\over {1-p_{01}}}\, {{s_2-p_{10}}\over {1-p_{10}}}-1\Big )\nonumber \\&\quad +\,\sum _{k=1}^{\infty }\sum _{\alpha _1=0}^{\infty } {{((1-p_{01})z_1)^{\alpha _1}((1-p_{10})z_2)^{\alpha _1+k}}\over {(2\alpha _1+k-1)!(\alpha _1+k)}}\nonumber \\&\quad \times \, {}_0F_{1}(2\alpha _1 + \, k+1;(1-p_{01})(1-p_{10})z_1z_2)\nonumber \\&\quad \times \, \Big ({{s_2-p_{10}}\over {1-p_{10}}}\Big )^kP_{\alpha _1}^{(-1,k)} \Big (2\,{{s_1-p_{01}}\over {1-p_{01}}}\, {{s_2-p_{10}}\over {1-p_{10}}}-1\Big ) \Big \}. \end{aligned}$$

(27)

Comparing the series (21) at $t=0$ with the exponent extension (27), we obtain

$$\begin{aligned} A_{00}= & {} 1,\\ A_{\alpha _1\alpha _2}= & {} \frac{1}{\alpha _1(\alpha _1+\alpha _2-1)!},\quad \alpha _1\ge \alpha _2,\\ A_{\alpha _1\alpha _2}= & {} \frac{1}{\alpha _2(\alpha _1+\alpha _2-1)!},\quad \alpha _1< \alpha _2; \end{aligned}$$

we have the solution (20) of the system (17), (18). Absolute convergence of the series (20) for all $z_1$, $z_2$, $s_1$, $s_2$ and $t\in [0,\infty )$ follows from (27). $\square$

Now we shall give formulas for $P_{(\beta _1,\beta _2)}^{(\alpha _1,\alpha _2)}(t)$ with initial conditions $\alpha _1,\alpha _2,\beta _1,\beta _2$. Using (19), we have ${}_0F_1(1;z)=1+z+\cdots ,$${}_0F_1(2;z)=1+z/2+\cdots ,$${}_0F_1(3;z)=1+\cdots ,$${}_0F_1(4;z)=1+\cdots ,$ by (14) we obtain $P_0^{(-1,0)}(x)=1$, $P_0^{(-1,1)}(x)=1$, $P_1^{(-1,0)}(x)=(1/2)(x-1)$, $P_1^{(-1,1)}(x)=x-1$. Substituting this in (20), using the extension $e^{p_{01}z_1+p_{10}z_2}=1+p_{01}z_1+p_{10}z_2+p_{01}^2z_1^2/2+ p_{01}p_{10}z_1z_2+p_{10}^2z_2^2/2+\cdots ,$ and equaling the coefficients at corresponding degrees $1,z_1,z_1s_1,z_2,z_2s_2,\ldots ,z_1z_2^2s_2^2,z_1z_2^2s_1s_2^2$ in the obtaining series and the double generating function of transitions probabilities, we have

$$\begin{aligned} P^{(0,0)}_{(0,0)}(t)= & {} 1; \\ P^{(1,0)}_{(0,0)}(t)= & {} 0,\quad P^{(1,0)}_{(1,0)}(t)=1,\quad P^{(0,1)}_{(0,0)}(t)=0,\quad P^{(0,1)}_{(0,1)}(t)=1;\\ P^{(1,1)}_{(0,0)}(t)= & {} p_{00}(1-e^{-\lambda t}),\quad P^{(1,1)}_{(1,0)}(t)=p_{10}(1-e^{-\lambda t}),\\ P^{(1,1)}_{(0,1)}(t)= & {} p_{01}(1-e^{-\lambda t}),\quad P^{(1,1)}_{(1,1)}(t)=e^{-\lambda t};\\ P^{(0,2)}_{(0,0)}(t)= & {} 0,\quad P^{(0,2)}_{(0,1)}(t)=0,\quad P^{(0,2)}_{(0,2)}(t)=1;\\ P^{(1,2)}_{(0,0)}(t)= & {} p_{00}p_{10}(1-2e^{-\lambda t}+e^{-2\lambda t}),\quad P^{(1,2)}_{(1,0)}(t)=p_{10}^2(1-2e^{-\lambda t}+e^{-2\lambda t}),\\ P^{(1,2)}_{(0,1)}(t)= & {} p_{00}+p_{10}p_{01}-2p_{10}p_{01}e^{-\lambda t}-(p_{00}-p_{10}p_{01})e^{-2\lambda t},\\ P^{(1,2)}_{(1,1)}(t)= & {} 2p_{10}(e^{-\lambda t}-e^{-2\lambda t}),\quad P^{(1,2)}_{(0,2)}(t)=p_{01}(1-e^{-2\lambda t}),\quad P^{(1,2)}_{(1,2)}(t)=e^{-2\lambda t}. \end{aligned}$$

4 Probabilistic Model of Bimolecular Reaction

We consider a time-homogeneous Markov process

$$\begin{aligned} \xi (t)=(\xi _1(t),\xi _2(t),\xi _3(t)),\quad t\in [0,\infty ), \end{aligned}$$

on the set of states

$$\begin{aligned} N^3=\{(\alpha _1,\alpha _2,\alpha _3),\ \alpha _1,\alpha _2,\alpha _3=0,1,\ldots \}, \end{aligned}$$

Let us suppose that the transition probabilities

$$\begin{aligned} P_{(\beta _1,\beta _2,\beta _3)}^{(\alpha _1,\alpha _2,\alpha _3)}(t) ={\mathbb {P}}\{\xi (t)=(\beta _1,\beta _2,\beta _3)\mid \xi (0)= (\alpha _1,\alpha _2,\alpha _3)\} \end{aligned}$$

have the following form as $t\rightarrow 0+$ ($\lambda >0$)

$$\begin{aligned} P_{(\alpha _1-1,\alpha _2-1,\alpha _3+1)}^{(\alpha _1,\alpha _2,\alpha _3)}(t)= & {} \alpha _1\alpha _2\lambda t+o\,(t),\nonumber \\ P_{(\alpha _1,\alpha _2,\alpha _3)}^{(\alpha _1,\alpha _2,\alpha _3)}(t)= & {} 1-\alpha _1\alpha _2\lambda t+o\,(t). \end{aligned}$$

(28)

The second equation for the generating function of the transition probabilities ($|s_1|\le 1,|s_2|\le 1,|s_3|\le 1$)

$$\begin{aligned} F_{(\alpha _1,\alpha _2,\alpha _3)}(t;s_1,s_2,s_3)= \sum \limits _{\beta _1,\beta _2,\beta _3=0}^{\infty } P_{(\beta _1,\beta _2,\beta _3)}^{(\alpha _1,\alpha _2,\alpha _3)}(t) s_1^{\beta _1}s_2^{\beta _2}s_3^{\beta _3}, \end{aligned}$$

is

$$\begin{aligned} {{\partial F_{(\alpha _1,\alpha _2,\alpha _3)}(t;s_1,s_2,s_3)}\over {\partial t}}= \lambda (s_3-s_1s_2){{\partial ^2 F_{(\alpha _1,\alpha _2,\alpha _3)}(t;s_1,s_2,s_3)} \over {\partial s_1\partial s_2}}, \end{aligned}$$

(29)

with initial condition $F_{(\alpha _1,\alpha _2,\alpha _3)}(0;s_1,s_2,s_3)=s_1^{\alpha _1}s_2^{\alpha _2}s_3^{\alpha _3}$.

Fig. 3

Realization of the process $T_1+T_2 \rightarrow T_3$ in case $\alpha _1>\alpha _2$

The process stays in the state $(\alpha _1,\alpha _2,\alpha _3)$ for a random time $\tau _{(\alpha _1,\alpha _2,\alpha _3)}$, ${\mathbb {P}}\{\tau _{(\alpha _1,\alpha _2,\alpha _3)}\le t\}= 1-e^{-\alpha _1\alpha _2\lambda t}$, and then it passes to the state $(\alpha _1-1,\alpha _2-1,\alpha _3+1)$. Realization of a process $(\xi _1(t),\xi _2(t),\xi _3(t))$ with initial state $(\alpha _1,\alpha _2,0)$, is shown in the Fig. 3. If $\alpha _1\ge \alpha _2$, then the process stops at the absorbing state $(\alpha _1-\alpha _2,0,\alpha _2)$, and if $\alpha _2\ge \alpha _1$, then it stops at $(0,\alpha _2-\alpha _1,\alpha _1)$.

The Markov process $(\xi _1(t),\xi _2(t),\xi _3(t))$ is to be the model for chemical reaction $T_1+T_2\rightarrow T_3$ [19]. The state $(\alpha _1,\alpha _2,\alpha _3)$ of the process is interpreted as the existence of $\alpha _1$ elements of $T_1$ type, $\alpha _2$ elements of $T_2$ type, $\alpha _3$ elements of type $T_3$; at random time moments pair of elements $T_1+T_2$ transformed into the element $T_3$. In [19] the connection between the second Eq. (29) and known in formal kinetics the law of active mass is discussed, see also [20]. In [1] using the method of Laplace transformations the expression for the transition probabilities of the process is obtained, which are, however, not convenient to use.

For the exponential generating function

$$\begin{aligned} \mathcal{F}(t;z_1,z_2;s_1,s_2,s_3)=\sum \limits _{\alpha _1,\alpha _2=0}^{\infty } {{z_1^{\alpha _1}z_2^{\alpha _2}}\over {\alpha _1!\alpha _2!}} F_{(\alpha _1,\alpha _2,0)}(t;s_1,s_2,s_3) \end{aligned}$$

we can write the first and the second system of the Kolmogorov differential equations in the following form [12]

$$\begin{aligned} {{\partial \mathcal{F}}\over {\partial t}}&=\lambda z_1z_2 \left( s_3\mathcal{F}-{{\partial ^2\mathcal{F}}\over {\partial z_1\partial z_2}}\right) , \end{aligned}$$

(30)

$$\begin{aligned} {{\partial \mathcal{F}}\over {\partial t}}&=\lambda (s_3-s_1s_2) {{\partial ^2\mathcal{F}}\over {\partial s_1\partial s_2}},\ \ \ \ \end{aligned}$$

(31)

with initial condition $\mathcal{F}(0;z_1,z_2;s_1,s_2,s_3)=e^{z_1s_1+z_2s_2}$.

Theorem 3

Let a Markov process on the state space $N^3$ be given by the densities of transition probabilities (28). The double generating function of the transitions probabilities is

$$\begin{aligned} \mathcal{F}(t;z_1,z_2;s_1,s_2,s_3)= & {} \sum _{\alpha _1,\alpha _2=0}^{\infty } {{\alpha _1+\alpha _2}\over {\mathrm{max}(\alpha _1,\alpha _2)}} {{z_1^{\alpha _1}z_2^{\alpha _2}}\over {(\alpha _1+\alpha _2)!}}{}_0F_1(\alpha _1+\alpha _2+1;z_1z_2s_3)\nonumber \\&\quad \times \, s_\sigma ^{|\alpha _1-\alpha _2|}s_3^{\mathrm{min}(\alpha _1,\alpha _2)} P_{\mathrm{min}(\alpha _1,\alpha _2)}^{(-1,|\alpha _1-\alpha _2|)} \left( 2{{s_1s_2}\over {s_3}}-1\right) e^{-\alpha _1\alpha _2\lambda t},\nonumber \\ \end{aligned}$$

(32)

where ${}_0F_1(b;z)$ is the generalized hypergeometric function, $P_n^{(-1,\beta )}(x)$ are the Jacobi polynomials; if $\alpha _1\ge \alpha _2$ then $s_\sigma =s_1$; if $\alpha _1<\alpha _2$, then $s_\sigma =s_2$; if $\alpha _1=0$, $\alpha _2=0$, then the expression ${(\alpha _1+\alpha _2)/\max (\alpha _1,\alpha _2)}$ is to be equal to 1.

The proof of the Theorem 3 is similar to the Theorem 2 proof, in the same way the system of Eqs. (30), (31) is solving by the separating variables method. In particular, by putting $p_{10}=p_{01}=0$ (that is $p_{00}=1$) in (20) and $s_3=1$ in (32), we obtain the coincident formulas.

5 Simple Death-Process. Nonlinear Branching Property of the Transition Probabilities for the Death-Process of the Linear Type

We consider Markov process

$$\begin{aligned} \xi _t,\quad t\in [0,\infty ), \end{aligned}$$

on the state space

$$\begin{aligned} N=\{0,1,2,\ldots \}; \end{aligned}$$

transition probabilities $P_{ij}(t)$, $i,j\in N$, can be expressed in the following form [10], as $t\rightarrow 0+$,

$$\begin{aligned} P_{i,i-1}(t)= & {} \varphi _i t+o\,(t),\nonumber \\ P_{ii}(t)= & {} 1-\varphi _i t+o\,(t), \end{aligned}$$

(33)

where $\varphi _0=0$, $\varphi _i>0$ at $i=1,2,\ldots$

Fig. 4

Simple death-process stages

Stages for death-process $\xi _t$ are shown in Fig. 4. The process stays at the initial state i during a random time $\tau _i$ with distribution ${\mathbb {P}}\{\tau _i\le t\}=1-e^{-\varphi _i t}$. At the time $\tau _i$ the process passes to the state $i-1$; and so on.

Using the double generating function ($|s|\le 1$),

$$\begin{aligned} \mathcal{F}(t;z,s)= & {} \sum ^\infty _{i=0}\frac{z^i}{\varphi _1\ldots \varphi _i}F_{i}(t;s),\nonumber \\ F_{i}(t;s)= & {} \sum _{j=0}^{\infty } P_{ij}(t)s^{j},\quad i\in N, \end{aligned}$$

(34)

we may reduce the first and the second systems of differential equations for transition probabilities to [12]

$$\begin{aligned} \frac{\partial \mathcal{F}}{\partial t}&=z(\mathcal{F}-D_z(\mathcal{F})), \end{aligned}$$

(35)

$$\begin{aligned} \frac{\partial \mathcal{F}}{\partial t}&=(1-s)D_{s}(\mathcal{F}), \end{aligned}$$

(36)

with initial condition $\mathcal{F}(0;z;s)=e(zs)$. Here we use the Gel’fond–Leont’ev operator [9] of generalized differentiation

$$\begin{aligned} D_z\Big (\sum _{i=0}^{\infty }a_{i}z^{i}\Big )= \sum _{i=1}^{\infty }a_{i}\varphi _{i}z^{i-1}, \end{aligned}$$

defined for analytic on zero-neighborhood functions. The function

$$\begin{aligned} e(z)=1+\sum ^\infty _{i=1}{z^i\over {\varphi _1\ldots \varphi _i}} \end{aligned}$$

is eigenfunction for the operator $D_z$,

$$\begin{aligned} D_z(e(z))=e(z). \end{aligned}$$

Theorem 4

[12] Let a Markov death-process on the state space N be given by the densities of transposition probabilities (33), $\varphi _{i+1}>\varphi _i$, $i\in N$, and $\lim _{i\rightarrow \infty }\varphi _i=\infty$. The double generating function of the transitions probabilities may be express as the Fourier series

$$\begin{aligned} \mathcal{F}(t;z;s)=\sum _{n=0}^{\infty }{1\over {\varphi _1\ldots \varphi _n}} \,\widetilde{C}_n(z)C_{n}(s)e^{-\varphi _n t}, \end{aligned}$$

(37)

where

$$\begin{aligned} \widetilde{C}_n(z)= & {} z^n+\sum _{k=1}^{\infty }{{z^{n+k}}\over {(\varphi _{n+1}-\varphi _n)\ldots (\varphi _{n+k}-\varphi _n)}},\\ C_{n}(s)= & {} s^n+\sum _{k=0}^{n-1}{{\varphi _{k+1}\ldots \varphi _n}\over {(\varphi _{k}-\varphi _n)\ldots (\varphi _{n-1}-\varphi _n)}}\,s^k. \end{aligned}$$

The series (37) is absolutely convergent for all z, $|s|<1$ and $t\in [0,\infty )$.

Proof

This is the expressions for the simple death-process transition probabilities [10]: $P_{0j}(t)=\delta _j^0,\ j\in N;\ P_{ij}(t)=0$ at $j>i\ge 1;$ at $j\le i$

$$\begin{aligned} P_{ij}(t)=\varphi _{j+1}\ldots \varphi _{i}\!\sum _{n=j}^i\frac{e^{-\varphi _n t}}{(\varphi _i-\varphi _n)\ldots (\varphi _{n+1}-\varphi _n)(\varphi _{n-1}-\varphi _n) \ldots (\varphi _j-\varphi _n)}. \end{aligned}$$

(38)

Following the definition of double generating function (34) and (38), we get

$$\begin{aligned} \mathcal{F}(t;z;s)= & {} \sum ^\infty _{i=0}\sum ^\infty _{j=0} \frac{z^i}{\varphi _1\ldots \varphi _i}P_{ij}(t)s^j\\= & {} \sum ^\infty _{i=0}\sum ^i_{j=0}\sum _{n=j}^i \frac{z^i}{\varphi _1\ldots \varphi _j}\, \frac{e^{-\varphi _n t}}{(\varphi _i-\varphi _n)\ldots (\varphi _{n+1}-\varphi _n)(\varphi _{n-1}-\varphi _n) \ldots (\varphi _j-\varphi _n)}\,s^j\\= & {} \sum _{n=0}^{\infty }{{e^{-\varphi _n t}}\over {\varphi _1\ldots \varphi _n}} \Bigg (z^n+\sum _{i=n+1}^{\infty }{{z^{i}}\over {(\varphi _{n+1}-\varphi _n)\ldots (\varphi _i-\varphi _n)}}\Bigg )\\&\quad \times \,\Bigg (s^n+\sum _{j=0}^{n-1}{{\varphi _{j+1}\ldots \varphi _n}\over {(\varphi _{j}-\varphi _n)\ldots (\varphi _{n-1}-\varphi _n)}}s^j\Bigg ). \end{aligned}$$

Convergence for the series $\mathcal{F}(t;z;s)$ follows from the inequality

$$\begin{aligned} \Big |\sum ^\infty _{i=0}\sum ^\infty _{j=0} \frac{z^i}{\varphi _1\ldots \varphi _i}P_{ij}(t)s^j\Big |\le \sum ^\infty _{i=0}\sum ^\infty _{j=0}\frac{|z|^i}{\varphi _1\ldots \varphi _i}\,|s|^j\le {1\over {1-|s|}}\sum ^\infty _{i=0}\frac{|z|^i}{\varphi _1\ldots \varphi _i}<\infty , \end{aligned}$$

for all z and $|s|<1$. $\square$

Thus, the solution (37) of the system of Kolmogorov equation (35), (36) is the series with three separating variables. For $t=0$ we get an expansion of the function

$$\begin{aligned} e(zs)=\sum _{n=0}^{\infty }{1\over {\varphi _1\ldots \varphi _n}} \widetilde{C}_n(z)C_{n}(s); \end{aligned}$$

the functions $\widetilde{C}_n(z)$ and $C_n(s)$ are connected by an integral transformation.

We have an important particular case at $\varphi _{i}=i\mu$, $i\in N$ ($\mu >0$), this is the death-process of a linear type. Here $D_{z}=\mu \,(d/dz)$ and the generating function of transition probabilities $F_i(t;s)$ satisfies the equation [1, 2, 22] (see Eq. (2) at $\lambda =0$)

$$\begin{aligned} \frac{\partial F_i(t;s)}{\partial t}= \mu (1-s)\frac{\partial F_i(t;s)}{\partial s}, \end{aligned}$$

(39)

with initial condition $F_i(t;s)=s^i$. For the process of linear type, it is easy to sum up the series (37) and for $\mathcal{F}(t;z;s)$ we obtain

$$\begin{aligned} \mathcal{F}(t;z;s)=\sum _{n=0}^{\infty }{{(z/\mu )^n}\over {n!}} e^{z/\mu }(s-1)^n\,e^{-n\mu t} =e^{(z/\mu )(1+(s-1)e^{-\mu t})}. \end{aligned}$$

(40)

From the definition $\mathcal{F}(t;z;s)=\sum ^\infty _{i=0}(z^i/(\mu ^i i!))F_{i}(t;s)$ and the extension (40) with respect to z, equating coefficients of $z^i$, we obtain the branching property for the transition probabilities ([22], Chap. 1)

$$\begin{aligned} F_i(t;s)=(1-e^{-\mu t}+s\,e^{-\mu t})^i=F_1^i(t;s),\quad i\in N. \end{aligned}$$

(41)

The straightforward solution of the linear first order partial equation (39) by a characteristic method give us (41) (see, for instance, [1], § 3.2).

Accepting that the process has the nonlinear property of the transition probabilities (41) then we can consider a death process for particles: at the time moment $t=0$ there is i identical particles, each of them exists during a random time $\tau ^{(k)}$, ${\mathbb {P}}\{\tau ^{(k)}\le t\}=1-e^{-\mu t}$; values $\tau ^{(k)}$, $k=1,\ldots ,i$, are independent (the death of one of them means the passing of Markov process $\xi _t$ from state i to $i-1$; and so on).

6 Concluding Remarks

Powerful analytic methods [2, 22] for the investigation of Markov processes with branching property have been established. Therefore, for simple death-process, the problem of proving the nonlinear property of transition probabilities can be formulated. This problem generalizes the property (41), and it can be reduced to analytic problem of the Fourier series summarized by (37)—under some assumptions concerning the function $\varphi _{i}=\varphi (i)$, $i\in N$.

For the quadratic death-process with $\varphi _{i}=i(i-1)\lambda$ ($D_{z}=\lambda z\,(d^2/dz^2)$), series (37) (i.e., series (10) with $\lambda >0$, $\mu =0$, $p_1=1$) is summing in [12]. Using Gegenbauer’s addition theorem ([7], § 7.6.1), a closed representation of the double generating function of transition probabilities $\mathcal{F}(t;z;s)$ was obtained. For $F_i(t;s)$, an integral representation was obtained which has similar structure (41).

For the generalized quadratic death-process (with $\lambda >0$, $\mu >0$), it is possible to obtain a closed solution of Kolmogorov equations (4), (5) by methods [12]. We consider the series (10) with aim of summing and reducing nonlinear property for transition probabilities

$$\begin{aligned} F_i(t;s)={\mathbb {E}}(X_t+sY_t)^i,\quad i\in N, \end{aligned}$$

(42)

where $X_t,Y_t$ are mutually connected stochastic processes.

For the two-dimensional quadratic death-process, we consider the series (20) with aim of summing up and reducing a closed solution of the system (17), (18) in form similar to nonlinear property (41),

$$\begin{aligned} F_{(\alpha _1,\alpha _2)}(t;s_1,s_2)= {\mathbb {E}}(X_t+s_1Y_t)^{\alpha _1}(Z_t+s_2U_t)^{\alpha _2},\quad (\alpha _1,\alpha _2)\in N^2, \end{aligned}$$

(43)

where $X_t$, $Y_t$, $Z_t$, $U_t$ are mutually connected stochastic processes.

The opportunity for an integral representation in form (42), (43) is discussed in details in Chapter 5 in [12]. Formulas, similar to (42), (43), are established for a epidemic process which is a Markov quadratic death-process on the set of states $N^2$ [13] (see also [18]).

Given the above modification of the separating variables method, which is applicable for the first and the second Kolmogorov equations, it may be useful to use other Markov death-processes. For instance, we indicate the simple death-process of polynomial type with $\varphi _{i}=i(i-1)\ldots (i-k+1)\lambda$ ($k=3,4,\ldots$); equations for double generating function has the following form

$$\begin{aligned} {{\partial \mathcal{F}}\over {\partial t}}= & {} \lambda z^k\left( {{\partial ^{k-1}\mathcal{F}}\over {\partial z^{k-1}}} -{{\partial ^k\mathcal{F}}\over {\partial z^k}}\right) ,\\ {{\partial \mathcal{F}}\over {\partial t}}= & {} \lambda (s^{k-1}-s^k){{\partial ^k\mathcal{F}}\over {\partial s^k}}, \end{aligned}$$

with initial condition $\mathcal{F}(0;z;s)=e^{zs}$.

In the same way by solving the first and second equations for transiting probabilities for the pure birth-process and generalized birth-processes, we get a series with three separated variables [23]. For instance, an interesting application of the quadratic pure birth-process on $N^2$ [1, 3] has the equations for double generating function of the following form

$$\begin{aligned} {{\partial \mathcal{F}}\over {\partial t}}= & {} \lambda z_1z_2\left( {{\partial ^3\mathcal{F}}\over {\partial z_1^2 \partial z_2}} -{{\partial ^2\mathcal{F}}\over {\partial z_1\partial z_2}}\right) + \mu z_2\left( {{\partial ^2\mathcal{F}}\over {\partial z_2^2}} -{{\partial \mathcal{F}}\over {\partial z_2}}\right) ,\\ {{\partial \mathcal{F}}\over {\partial t}}= & {} \lambda (s_1^2s_2-s_1s_2){{\partial ^2\mathcal{F}}\over {\partial s_1\partial s_2}}+ \mu (s_2^2-s_2){{\partial \mathcal{F}}\over {\partial s_2}}, \end{aligned}$$

with initial condition $\mathcal{F}(0;z_1,z_2;s_1,s_2)=e^{z_1s_1+z_2s_2}$.

The problem of developing the discussed method in the case of Markov birth- and death-processes is difficult.