THE DUAL RECIPROCITY BOUNDARY ELEMENT METHOD FOR ONE-DIMENSIONAL NONLINEAR PARABOLIC PARTIAL DIFFERENTIAL EQUATIONS

Abstract

This article describes a numerical method based on the dual reciprocity boundary element method (DRBEM) for solving some well-known nonlinear parabolic partial differential equations (PDEs). The equations include the classic and generalized Fisher’s equations, Allen–Cahn equation, Newell–Whithead equation, FitzHugh–Nagumo equation, and generalized FitzHugh–Nagumo equation with time-dependent coefficients. The concept of the dual reciprocity is used to convert the domain integral to the boundary that leads to an integration-free method. We employ the time stepping scheme to approximate the time derivative, and the linear radial basis functions (RBFs) are used as approximate functions in the presented method. The nonlinear terms are treated iteratively within each time step. The developed formulation is verified in some numerical test examples. The results of numerical experiments are compared with analytical solution to confirm the accuracy and efficiency of the presented scheme.

Introduction

The dual reciprocity boundary element method (DRBEM) is a modern numerical scheme, which has enjoyed increasing popularity and has become one of the most general and effective numerical method for solving different engineering problems [4,5,6,7,8,9, 14, 16, 44]. Generally, the DRBEM is known as a numerical tool for solving two or higher dimensional partial differential equations (PDEs). However, some authors employed this approach for the numerical solution of some one-dimensional PDEs. For example, hyperbolic telegraph equation [19], nonlinear Klein-Gordon equation [20], nonlinear sine–Gordon equation [21], Cahn-Hilliard equation [22], stochastic differential equations [24, 25], and advection–diffusion equation [49] have been solved with the one-dimensional DRBEM approach. Also, some extension of this method is used for numerical solution of some engineering problems  [10, 11].

In this study, a numerical solution based on the DRBEM is applied for solving some well-known one-dimensional nonlinear parabolic PDEs. The idea behind this approach comes from the classic DRBEM introduced by Brebbia and Nardini [15] and Partridge and Brebbia [16] for solving higher-order dimensional problems and expanding the inhomogeneous and nonlinear terms in terms of their values at the nodes which lie in the domain of the problem. The inhomogeneous term is approximated by interpolation in terms of some well-known functions $\phi (r)$, called radial basis functions (RBFs), where r is the distance between a source point and the field point.

Our concern in the current work is to present a numerical method based on the DRBEM for solving the following nonlinear parabolic PDEs

$$\begin{aligned} u_t+\nu (t)u_x-\mu (t)u_{xx}-\eta (t)F(u)=0, \ \ \ \ (x,t) \in [a,b] \times [0,T], \end{aligned}$$

(1)

subject to the initial condition

$$\begin{aligned} u(x,0)=f(x), \ \ \ x \in [a,b], \end{aligned}$$

(2)

and the boundary conditions

$$\begin{aligned} u(a,t)=g_1(t), \ \ \ \ \ \ \ \ u(b,t)=g_2(t), \ \ t \in [0,T], \end{aligned}$$

(3)

where $\nu (t), \mu (t)$, and $\eta (t)$ are arbitrary real-valued functions of t. F(u) in Eq. (1), written as $F_l(u)+F_n(u)$, where $F_l$ and $F_n$ denote the linear and nonlinear parts of F, respectively. Equation (1) for different values of $\nu , \mu , \eta$, and F yields the following well-known problems:

Case 1: the Fitzhugh–Nagumo and real Newell–Whitehead equations

If we set $\nu (t)=\mu (t)=\eta (t)=1$ and $F(u)=u(1-u)(\rho -u)$ where $0 \le \rho \le 1$, Eq. (1) deduces to classic Fitzhugh–Nagumo equation. In addition, if in Fitzhugh–Nagumo equation $\rho$ takes the value $-1$, then the classic Fitzhugh–Nagumo equation deduces to real Newell–Whitehead equation. The Fitzhugh–Nagumo equation has been derived by Fitzhugh [27] and Nagumo et al. [42]. Also, population genetics [12, 53, 54] is another area of application of the Fitzhugh–Nagumo equation. Kawahara and Tanaka [33], Nucci and Clarkson [41], Li and Guo [35], and Abbasbandy [1] have found some new solution of the Fitzhugh–Nagumo equation using the Hirota method, Jacobi elliptic function, first integral method, and homotopy analysis method, respectively. The Haar wavelet method [29], Pseudospectral methods [18], and the homotopy analysis method [53] are some numerical approaches that have been applied to present the approximate solution of the Fitzhugh–Nagumo equation. Meanwhile, the authors of [47] proposed the approximate conditional symmetry method to determine approximate solutions of Fitzhugh–Nagumo equation.

Case 2: the generalized Fitzhugh–Nagumo equation

Let $\nu (t), \mu (t)$, and $\eta (t)$ be an arbitrary function of t and let $F(u)=u(1-u)(\rho -u)$. Then, Eq. (1) deduces to generalized Fitzhugh–Nagumo with time-dependent coefficients and linear dispersion term equation. The authors of [52] derived a new variety of soliton solutions using specific solitary wave ansatz and the tanh method for this equation. Meanwhile, Bhrawy [13] employed Jacobi–Gauss–Lobatto collocation method for the numerical solution of this equation.

Case 3: Fisher’s equation

Fisher’s equation is achieved when $\nu (t)=\mu (t)=\eta (t)=1$ and $F(u)=u(1-u)$. As mentioned in [37, 43, 56], Fisher proposed such equation as a model for the propagation of a mutant gene, with u denoting the density of an advantageous. This equation is encountered in chemical kinetics and population dynamics which include problems such as nonlinear evolution of a population in a one-dimensional habitat, neutron population in a nuclear reaction. Moreover, the same equation occurs in logistic population growth models, flame propagation, neurophysiology, autocatalytic chemical reactions, and branching Brownian motion processes. Sinc collocation method [2], B–spline Galerkin method [30, 40], wavelet Galerkin method [39], moving mesh method [45], finite element methods [46, 51], and finite difference [38] are some numerical techniques that have been applied for the numerical solution of Fisher’s equation. Meanwhile, Wazwaz [56, 57] has found some exact solution for this equation with tanh-coth and Adomian decomposition methods.

Case 4: the Allen–Cahn and generalized Fisher’s equations

If we set $\nu (t)=\mu (t)=\eta (t)=1$ and $F(u)=u(1-u^{\alpha })$ in Eq. (1), the generalized Fisher equation will be obtained. In addition, Eq. (1) for $\alpha =$2 and $\alpha >2$ is called the Allen–Cahn equation and generalized Fisher’s equation. Some useful numerical solutions of this equation are [17, 26, 28, 36]. In addition, [57] provides some exact solutions of these equations.

The organization of the current paper

This article is organized as follows: In "The propose method", the discretized version of equation is obtained, and an iterative scheme based on finite difference scheme is described for the time derivative. In "Numerical simulations", numerical results of some nonlinear parabolic PDEs have been presented, and the obtained results are compared with the exact solutions. "Conclusion" ends this report with a brief conclusion.

The proposed method

Suppose $G_i=G(x,x_i)$ is the fundamental solution of the one-dimensional Laplace operator based on the source point $x_i$, i.e.,

$$\begin{aligned} \frac{\partial ^2 G}{\partial x^2} (x,x_i)=\delta (x,x_i), \end{aligned}$$

(4)

where x is the field point and $\delta$ is Dirac delta function. The fundamental solution and its derivative are given as follows [34]:

$$\begin{aligned} \begin{array}{l} G(x,x_i)=\frac{1}{2}|x-x_i|, \\ \\ G_{,x}(x,x_i)=G'(x,x_i)=\frac{1}{2}sgn(x-x_i), \end{array} \end{aligned}$$

(5)

where the symbol sgn denotes the signum function.

Consider Eq. (1) as follows:

$$\begin{aligned} u_{xx}=\frac{1}{\mu (t)} u_t+\frac{\nu (t)}{\mu (t)} u_x-\frac{\eta (t)}{\mu (t)} \{F(u)\}:=b(x,t). \end{aligned}$$

(6)

Multiplying the above equation by $G_i$, taking integration over [a, b] and applying the integration by parts, we get the following integral form:

$$\begin{aligned}{}[G_iu_x]_a^b-[G_i'u]_a^b+c_iu_i=\int _a^b b(x,t)G_idx, \end{aligned}$$

(7)

where similarly to 2D formulation, $c_i$ takes the values 1 and 1/2 when the source point is located in domain and on the boundary (the points a and b), respectively [16, 32].

The domain integral on the right-hand side of Eq. (7) still remains in the boundary elements formulation. This integral can be evaluated by dividing the domain into cells [31]. The motivation behind DRBEM is to avoid this procedure by transforming the domain integral to an equivalent boundary integral equation. This can be achieved by approximating the function b(x, t) in terms of radial basis functions (RBFs) at some chosen number in [a, b] as

$$\begin{aligned} a=x_1<x_2<\cdots<x_{N-1}<b=x_N. \end{aligned}$$

(8)

So the function b can be expressed as

$$\begin{aligned} b= \sum _{j=1} ^{N} \alpha _j(t) \phi _j, \end{aligned}$$

(9)

where $\alpha _j(t), j=1,...,N$, are the corresponding interpolating coefficients, $\phi _j$ represents the interpolation function, $\phi$, from a field node to source node, i.e.,

$$\begin{aligned} \phi _j:=\phi (|x-x_j|), \ \ x, x_j \in \mathcal {D}, \end{aligned}$$

where $|x-x_j|$ denotes the distance between x and $x_j$. The essential feature in DRBEM is to express $\phi _j$, which is a function of $r_j$, as a Laplacian of another function $\psi _j$. Thus, $\psi _j$ is chosen as the solution to [31]

$$\begin{aligned} \frac{\partial ^2 \psi _j}{\partial x^2} =\phi _j. \end{aligned}$$

(10)

In this paper, we will use linear RBFs as

$$\begin{aligned} \phi _j=1+r_j. \end{aligned}$$

(11)

The function $\psi _j$ is easily determined as

$$\begin{aligned} \psi _j=\frac{1}{2} r_j^2+\frac{1}{6} r_j^3. \end{aligned}$$

(12)

With substitution expansion (9) for b(x, t), applying the integration by part once again, the domain integral in the right-hand side of Eq. (7) reduces to a boundary integral equation

$$\begin{aligned} \int _a^b b(x,t) G_i dx=\sum _{j=1}^{N} \{ [G_i\psi _j']_a^b-[G_i'\psi _j]_a^b+c_i\psi _{ij} \} \alpha _j(t), \end{aligned}$$

(13)

where $\psi _{ij}$ is the value of the function $\psi _j$ at the ith source point. So from Eqs. (7) and (13), the following boundary integral equation can be achieved:

$$\begin{aligned}{}[G_iu_x]_a^b-[G_i'u]_a^b+c_iu_i=\sum _{j=1}^{N} \{ [G_i\psi _j']_a^b-[G_i'\psi _j]_a^b+c_i\psi _{ij} \} \alpha _j(t). \end{aligned}$$

(14)

Imposing all the source points to satisfy Eq. (14) yields the following matrix form:

$$\begin{aligned} \begin{array}{l} \textbf{L}\left[ \begin{array}{c} u_x(a) \\ u_x(b) \\ \end{array} \right] -\textbf{H}\left[ \begin{array}{c} u(a) \\ u(b) \\ \end{array} \right] +\left[ \begin{array}{c} \frac{1}{2}u(a) \\ \textbf{u}_{in} \\ \frac{1}{2}u(b) \\ \end{array} \right] , \\ =\displaystyle \sum _{j=1}^{N} \{ \textbf{L}\left[ \begin{array}{c} \psi _j'(a) \\ \psi _j'(b) \\ \end{array} \right] -\textbf{H}\left[ \begin{array}{c} \psi _j(a) \\ \psi _j(b) \\ \end{array} \right] +\left[ \begin{array}{c} \frac{1}{2}\psi _j(a) \\ \psi _j(x_1) \\ \vdots \\ \psi _j(x_{N-1})\\ \frac{1}{2}\psi _j(b) \\ \end{array} \right] \} \alpha _j(t),\\ \end{array} \end{aligned}$$

(15)

where $\textbf{u}_{in}=[u(x_2),\cdots ,u(x_{N-1})]^T$, $u_x(a)=u_x(a,t), u_x(b)=u_x(b,t), u(x_j)=u(x_j,t), j=1,...,N$ and $\textbf{L}$ and $\textbf{H}$ take the following form:

$$\begin{aligned} \textbf{L}=\left[ \begin{array}{cc} -G_1(a) &{} G_1(b) \\ -G_2(a) &{} G_2(b) \\ \vdots &{} \vdots \\ -G_N(a) &{} G_N(b) \\ \end{array} \right] , \ \ \ \ \ \ \ \textbf{H}=\left[ \begin{array}{cc} -G_1'(a) &{} G_a'(b) \\ -G_2'(a) &{} G_1'(b) \\ \vdots &{} \vdots \\ -G_N'(a) &{} G_N'(b) \\ \end{array} \right] . \end{aligned}$$

If each of the vectors

$$\begin{aligned} \begin{array}{l} \left[ \begin{array}{c} \psi _j'(a) \\ \psi _j'(b) \\ \end{array} \right] , \ \ \ \ \left[ \begin{array}{c} \psi _j(a) \\ \psi _j(b) \\ \end{array} \right] \ \ and \ \ \ \ \left[ \begin{array}{c} \frac{1}{2}\psi _j(a) \\ \psi _j(x_2) \\ \vdots \\ \psi _j(x_{N-1})\\ \frac{1}{2}\psi _j(b) \\ \end{array} \right] , \end{array} \end{aligned}$$

is considered to be one column of the matrices $\Psi _x$, $\Psi$, and $\widetilde{\Psi }$, respectively, Eq. (15) takes the following matrix form:

$$\begin{aligned} \begin{array}{l} \textbf{L}\left[ \begin{array}{c} u_x(a) \\ u_x(b) \\ \end{array} \right] -\textbf{H}\left[ \begin{array}{c} u(a) \\ u(b) \\ \end{array} \right] +\left[ \begin{array}{c} \frac{1}{2}u(a) \\ \textbf{u}_{in} \\ \frac{1}{2}u(b) \\ \end{array} \right] =[\textbf{L} \Psi _x - \textbf{H}\Psi +\widetilde{\Psi }]\alpha . \end{array} \end{aligned}$$

(16)

On the other hand, Eq. (9) can be written in the following matrix form:

$$\begin{aligned} \mathbf {\Phi } \alpha =\textbf{b}, \end{aligned}$$

(17)

where $\Phi _{ij}$ represents the value of the function $\phi _j$ at source point $x_i$ by $\phi _{ij}$ for $i =1, 2,...,N,$ and vector $\textbf{b}$ takes the following form:

$$\begin{aligned} \textbf{b}=\left[ \begin{array}{c} b(x_1,t) \\ \vdots \\ b(x_N,t) \\ \end{array} \right] , \end{aligned}$$

(18)

where

$$\begin{aligned} b(x_j,t)=\frac{1}{\mu (t)} u_t(x_j,t)+\frac{\nu (t)}{\mu (t)} u_x(x_j,t)- \frac{\eta (t)}{\mu (t)}(u(x_j,t)\{ F(u(x_j,t))\}. \end{aligned}$$

(19)

Now, Eq. (16) constitutes a nonlinear system of N equations in N unknown functions of t. This system is solved approximately using the iterative scheme based on the implicit finite difference technique as follows:

$$\begin{aligned} \begin{array}{l} \textbf{L}\left[ \begin{array}{c} u^n_x(a) \\ u^n_x(b) \\ \end{array} \right] -\textbf{H}\left[ \begin{array}{c} u^n(a) \\ u^n(b) \\ \end{array} \right] +\left[ \begin{array}{c} \frac{1}{2}u^n(a) \\ \textbf{u}^n_{in} \\ \frac{1}{2}u^n(b) \\ \end{array} \right] = \textbf{D}\mathbf {\Phi }^{-1} \textbf{b},\\ \end{array} \end{aligned}$$

(20)

where $\textbf{D}=[\textbf{L} \Psi _x - \textbf{H}\Psi +\widetilde{\Psi }]$ and $\textbf{b}$ takes the following form for implicit time discretization:

$$\begin{aligned} \textbf{b}=\frac{\textbf{u}^n-\textbf{u}^{n-1}}{\tau \mu (t_n)}+\frac{\nu (t_n)}{\mu (t_n)} \textbf{u}^n_x- \frac{\eta (t_n)}{\mu (t_n)}\{ F_l(\textbf{u}^n)+F_l(\widetilde{\textbf{u}})\}. \end{aligned}$$

(21)

Also, for Crank-Nicolson, time discretization takes the following form:

$$\begin{aligned} \textbf{b}=\frac{\textbf{u}^n-\textbf{u}^{n-1}}{\tau \mu (t_n)}+ \frac{\nu (t_n)}{2 \mu (t_n)} \textbf{u}^n_x + \frac{\nu (t_{n-1})}{2 \mu (t_{n-1})} \textbf{u}^{n-1}_x - \frac{\eta (t_n)}{2 \mu (t_n)}\{ F_l(\textbf{u}^n)+F_l(\widetilde{\textbf{u}}^n) \} - \frac{\eta (t_{n-1})}{2\mu (t_{n-1})}\{ F_l(\textbf{u}^{n-1})+F_l(\widetilde{\textbf{u}}^{n-1}) \}. \end{aligned}$$

(22)

On the other hand, the solution of Eq. (1) can be approximated as follows [14]:

$$\begin{aligned} u\simeq \sum _{j=1}^N \beta _j \phi _j, \end{aligned}$$

(23)

or in matrix form

$$\begin{aligned} \textbf{u}=\mathbf {\Phi } \beta (t). \end{aligned}$$

(24)

Therefore, from Eqs. (23) and (24), we can write

$$\begin{aligned} \textbf{u}_x=\mathbf {\Phi }_x \beta (t)=\mathbf {\Phi }_x \mathbf {\Phi }^{-1} \textbf{u}. \end{aligned}$$

(25)

So by substituting (25) in (21) and substituting the result in (20) and separating the known quantities from the unknown quantities, the value of $\textbf{u}_{in}^n$ can be obtained by solving a nonlinear system of equation. To avoid solving the nonlinear system of equations, the following iterative algorithm has been proposed [23, 48, 50].

The predictor-corrector scheme

For dealing with the nonlinearity, in time level n at first put

$$\begin{aligned} \widetilde{\textbf{u}}=\textbf{u}^{n-1}. \end{aligned}$$

(26)

With this substitution, Eq. (20) is solved as a system of linear algebraic equations for unknown $\textbf{u}^n=\textbf{u}^{n,0}$. Recompute

$$\begin{aligned} \widetilde{\textbf{u}}=\textbf{u}^{n,0}. \end{aligned}$$

(27)

Now, Eq. (20) is solved using the new $\widetilde{\textbf{u}}$ for unknown $\textbf{u}^{n,l}$. We are at time level n yet and iterate between calculating $\widetilde{\textbf{u}}$ and computing the approximation values of the unknown $\textbf{u}^{n,l}$ and putting

$$\begin{aligned} \widetilde{\textbf{u}}=\textbf{u}^{n,l}, \end{aligned}$$

(28)

until the unknown quantity converges to within a prescribed number of the significant figures. In this paper, we will use the following condition for stopping the iterations in each time level:

$$\begin{aligned} \parallel \textbf{u}^{n,l}-\textbf{u}^{n,l-1} \parallel _{\infty } \le \epsilon , \end{aligned}$$

(29)

where $\epsilon$ is a fixed number. When this condition is satisfied, we put

$$\begin{aligned} \widetilde{\textbf{u}}=\textbf{u}^{n,l}, \end{aligned}$$

(30)

and go on to the next time level. This process is iterated, until reaching the desirable time t.

Numerical simulations

To access both important parameters in numerical solution of problems, the accuracy, and the applicability of the procedure described in the previous section, some test examples are considered. In the following test problems, we will use the $L_{\infty }$ and the root-means-squares (RMS) errors, as defined below, to report the errors

$$\begin{aligned} \begin{array}{l} L_{\infty }-error=\displaystyle {\max _{1 \le j \le N}|e_j|}, \\ RMS-error=\displaystyle {\sqrt{\frac{1}{N} \sum _{j=1}^N |e_j|^2}}, \\ \end{array} \end{aligned}$$

(31)

where

$$\begin{aligned} \begin{array}{l} e=\displaystyle {u_{exact}-u_{approximate}},\\ e_j=\displaystyle {(u_{exact}-u_{approximate})_j}, \ \ \ \ j=2,...,N-1. \\ \end{array} \end{aligned}$$

Also, in this part, we assume $\epsilon =10^{-10}$.

Example 1

Consider the following Fitzhugh–Nagumo equation

$$\begin{aligned} u_t=u_{xx}-u(1-u)(\rho -u), \ \ \ (x,t) \in [a,b] \times [0,T], \end{aligned}$$

(32)

subject to the initial condition

$$\begin{aligned} u(x,0)=\frac{1}{2}+\frac{1}{2} \tanh (\frac{x}{2 \sqrt{2}}), \ \ \ x \in [a,b], \end{aligned}$$

(33)

and the following boundary conditions:

$$\begin{aligned} \begin{array}{l} u(a,t)=\displaystyle (\frac{1}{2}+\frac{1}{2} \tanh (\frac{1}{2 \sqrt{2}}(a-\frac{2\rho -1}{\sqrt{2}}t))), \\ \\ u(b,t)=\displaystyle (\frac{1}{2}+\frac{1}{2} \tanh (\frac{1}{2 \sqrt{2}}(b-\frac{2\rho -1}{\sqrt{2}}t))). \\ \end{array} \end{aligned}$$

(34)

The exact solution of Eq. (32) is given by [13, 57]

$$\begin{aligned} u(x,t)=\displaystyle (\frac{1}{2}+\frac{1}{2} \tanh (\frac{1}{2 \sqrt{2}}(x-\frac{2\rho -1}{\sqrt{2}}t))), \end{aligned}$$

(35)

Table 1 shows the numerical convergence of presented method for different types of time discretization methods. The error norms defined by (31) on grids for different kinds of RBFs (linear, multi-quadrics (MQ), $\phi (r)=\sqrt{c^2 + r^2}$, and thin plate spline (TPS), $\phi (r)= r^2 lnr$) are reported in Table 2. Accordingly, these results with an increasing number of nodes are presented in Table 2. The results reveal that the error decreases when the number of nodes increases.

Table 1 The $L_{\infty }$-error for two kinds of time discretization of Ex. 1

Table 2 The obtained estimate errors for Ex. 1

In addition, the results obtained for approximate solution along with estimate errors for time level $t=1, 5, 10, 20, 40$ and $t=100$ with $h=1/8$ and $t=1/1000$ in $-10 \le x \le 10$ are shown in Fig. 1. The new method can be applied for Eq. (32) with other choices of $\rho$. The space-time graph of approximate solution and related error estimate for $\rho =-1$ (the real Newell–Whitehead equation) in domain $-10 \le x \le 10$ for times $t=0.25, 0.50, 0.75$ and $t=1.0$ are reported in Fig. 2.

Example 2

Consider the following generalized Fitzhugh–Nagumo equation with time-dependent coefficients

$$\begin{aligned} u_t+\cos (t)u_x-\cos (t)u_{xx}-2\cos (t)(u(1-u)(\rho -u))=0,\ \ \ (x,t) \in [a,b] \times [0,t]. \end{aligned}$$

(36)

Also, suppose that the initial and boundary conditions are taken from the exact solution given by [13, 52]

$$\begin{aligned} u(x,t)=\frac{\rho }{2}+\frac{\rho }{2} \tanh (\frac{\rho }{2}(x-(3-\rho )\sin (t))). \end{aligned}$$

(37)

Table 3 lists the errors for this problem using the presented method with constant parameter $a=-b=1$, $\rho =1$, $\tau =0.001$, $t=1$ for different values of h.

Table 3 The estimate errors for Ex. 2 for different values of h

In addition, with the mentioned parameters, the obtained estimate errors for fixed $h=1/128$ and for various $\tau$ are reported in Table 4.

Table 4 The estimate errors for Ex. 2 for different values of $\tau$

We also draw the approximate solutions along with estimate errors for six choices of $\rho =0.25, 0.50, 0.75, 1, 1.25$ and $\rho =1.5$ in $-10 \le x \le 10$ in Fig. 3. This figure shows that by increasing $\rho$, the absolute error increases. In addition, the approximate solution in conjunction with the exact solution for $\tau =0.001$, $\rho =1.5$, and $h=1/4$ at different times $t=0.25, 0.50, 0.75$ and $t=1$ are shown in Fig. 4.

Example 3

Consider the following generalized Fisher’s equation:

$$\begin{aligned} u_t=u_{xx}+u(1-u^{\alpha }), \ \ \ (x,t) \in [-2,2] \times [0,1]. \end{aligned}$$

(38)

The exact solution of the above equation is given by [55, 56]

$$\begin{aligned} u(x,t)=\{\frac{1}{2}\tanh [-\frac{\alpha }{2\sqrt{\alpha +4}}(x-\frac{\alpha +4}{\sqrt{\alpha +4}}t)+ \frac{1}{2}]+\frac{1}{2}\}^{2/\alpha }. \end{aligned}$$

(39)

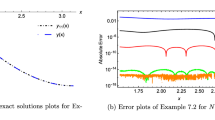
We assume that the initial and the Dirichlet boundary conditions are taken from the above exact solution. The approximate solutions and the estimate errors for this problem when $\alpha =1, 2, 3, 4, 5$ and $\alpha =6$ are shown in Fig. 5. As this figure shows, the estimate errors increase when the value of $\alpha$ increases.

Fig. 1

Graphs of approximated solutions along with estimate errors at times $t=1, 5, 10, 20, 40$ and $t=100$ obtained for Example 1 for constants $t=1/1000$, $h=1/8$, and $\rho =3/4$ in $-10 \le x \le 10$

Fig. 2

Graphs of approximated solutions (left plan) and their estimate errors (right) at times $t=0.25, 0.5, 0.75$ and $t=1.0$ obtained for Example 1 for constants $\tau =1/1000$, $h=1/8$, and $\rho =-1$ in $-10 \le x \le 10$

Fig. 3

Graphs of approximated solutions along with estimate errors at times $t=1$ for various $\rho =0.25, 0.50, 0.75, 1, 1.25$ and $\rho =1.50$ obtained for Example 2 for constants $t=1/1000$ and $h=1/8$ in $-10 \le x \le 10$

Fig. 4

Graphs of approximated solutions along with exact solutions at times $t=0.25, 0.50, 0.75$ and $t=1$ with $\rho =1.50$ for Example 2 for constants $t=1/1000$ and $h=1/8$ in $-10 \le x \le 10$

Fig. 5

Graphs of approximated solutions along with estimate errors for various $\alpha =1, 2, 3, 4, 5$ and $\alpha =6$ at time $t=10$ obtained for generalized Fisher’s equation for constants $t=1/1000$ and $h=1/16$ in $-2 \le x \le 2$

Conclusion

In this article, a numerical method based on the dual reciprocity boundary elements method (DRBEM) is outlined for solving the one-dimensional nonlinear parabolic partial differential equations. The list of equations investigated includes Fisher’s equation, generalized Fisher’s equation, Allen–Cahn equation, Newell–Whithead equation, Fitzhugh–Nagumo equation, and generalized Fitzhugh–Nagumo equation with time variable coefficient. The dual reciprocity idea was applied to eliminate the domain integrals appearing in the boundary integral equation. Linear radial basis functions (RBFs) were used in the presented method as approximate functions. We used the implicit and Crank–Nicolson finite difference method in time and the boundary integral equation technique in space to discretize the main differential equation and convert it to a linear algebraic system of equations. The nonlinear terms are treated iteratively within each time step by using a simple predictor-corrector scheme. Numerical results are presented for some test problems to demonstrate the usefulness and accuracy of the new method.