Stochastic Gradient Methods with Preconditioned Updates

Abstract

This work considers the non-convex finite-sum minimization problem. There are several algorithms for such problems, but existing methods often work poorly when the problem is badly scaled and/or ill-conditioned, and a primary goal of this work is to introduce methods that alleviate this issue. Thus, here we include a preconditioner based on Hutchinson’s approach to approximating the diagonal of the Hessian and couple it with several gradient-based methods to give new ‘scaled’ algorithms: Scaled SARAH and Scaled L-SVRG. Theoretical complexity guarantees under smoothness assumptions are presented. We prove linear convergence when both smoothness and the PL-condition are assumed. Our adaptively scaled methods use approximate partial second-order curvature information and, therefore, can better mitigate the impact of badly scaled problems. This improved practical performance is demonstrated in the numerical experiments also presented in this work.

1 Introduction

This work considers the following, possibly nonconvex, finite-sum optimization problem:

$$\begin{aligned} \min _{w \in \mathbb {R}^d}\left\{ P(w) = \frac{1}{n} \sum \limits ^n_{i = 1} f_i(w)\right\} , \end{aligned}$$

(1)

where $w\in \mathbb {R}^d$ is the model/weight parameter and the loss functions $f_i:\mathbb {R}^d \rightarrow \mathbb {R}$ $\forall i \in [n]:=\{1\dots n\}$ are smooth and twice differentiable. Throughout this work, it is assumed that (1) has an optimal solution, with a corresponding optimal value, denoted by $w^*$, and $P^* = P(w^*)$, respectively. Problems of the form (1) cover a plethora of applications, including empirical risk minimization, deep learning, and supervised learning tasks such as regularized least squares or logistic regression [28]. This minimization problem can be difficult to solve, particularly when the number of training samples n, or problem dimension d, is large, or if the problem is nonconvex.

Stochastic gradient descent (SGD) is one of the most widely known methods for problem (1), and its origins date back to the 1950 s with the work [26]. The explosion of interest in machine learning has led to an immediate need for reliable and efficient algorithms for solving (1). Motivated by, and aiming to improve upon, vanilla SGD, many novel methods have already been developed for convex and/or strongly convex instances of (1), including SAG/SAGA [2, 16], SDCA [29], SVRG [13, 31], S2GD [15] and SARAH [21], to name just a few. In general, these methods are simple, have low per iteration computational costs, and are often able to find an $\varepsilon$-optimal solution to (1) quickly, when $\varepsilon >0$ is not too small. However, they often have several hyper-parameters that can be difficult to tune, they can struggle when applied to ill-conditioned problems, and many iterations may be required to find a high accuracy solution.

Non-convex instances of the optimization problem (1) (for example, arising from deep neural networks (DNNs)) have been diverting the attention of researchers of late, and new algorithms are being developed to fill this gap [7, 8, 17, 19]. Of particular relevance to this work is the PAGE algorithm presented in [18]. The algorithm is conceptually simple, involving only one loop, and a small number of parameters, and can be applied to non-convex problems (1). The main update involves either a minibatch SGD direction, or the previous gradient with a small adjustment (similar to that in SARAH [21]). The Loopless SVRG (L-SVRG) method [9, 24], is also of particular interest here. It is a simpler ‘loopless’ variant of SVRG, which, unlike for PAGE, involves an unbiased estimator of the gradient, and it can be applied to non-convex instances of problem (1).

For problems that are poorly scaled and/or ill-conditioned, second-order methods that incorporate curvature information, such as Newton or quasi-Newton methods [4, 6, 22], can often outperform first-order methods. Unfortunately, they can also be prohibitively expensive, in terms of both computational and storage costs. There are several works that have tried to reduce the potentially high cost of second-order methods by using only approximate, or partial curvature information. Some of these stochastic second-order and quasi-Newton [10, 11] methods have shown good practical performance for some machine learning problems, although, possibly due to the noise in the Hessian approximation, sometimes they perform similarly to first-order variants.

An alternative approach to enhancing search directions is to use a preconditioner. There are several methods for problems of the form (1), which use what we call a ‘first-order preconditioner’—a preconditioner built using gradient information—including Adagrad [5], RMSProp [30], and Adam [14]. Adagrad [5] incorporates a diagonal preconditioner that is built using accumulated gradient information from the previous iterates. The preconditioner allows every component of the current gradient to be scaled adaptively, but it has the disadvantage that the elements of the preconditioner tend to grow rapidly as iterations progress, leading to a quickly decaying learning rate. A method that maintains the ability to adaptively scale elements of the gradient, but overcomes the drawback of a rapidly decreasing learning rate, is RMSProp. It does this by including a momentum parameter, $\beta _2$ in the update for the diagonal preconditioner. In particular, at each iteration the updated diagonal preconditioner is taken to be a convex combination (using a momentum parameter $\beta _2$) of the (square) of the previous preconditioner and the Hadamard product of the current gradient with itself. So, gradient information from all the previous iterates is included in the preconditioner, but there is a preference for more recent information. Adam [14] combines the positive features of Adagrad and RMSProp, but it also uses a first moment estimate of the gradient, providing a kind of additional momentum. Adam preforms well in practice and is among the most popular algorithms for DNN.

Recently, second-order preconditioners that use approximate and/or partial curvature information have been developed and studied. The approach in AdaHessian [32] was to use a diagonal preconditioner that was motivated by Hutchinson’s approximation to the diagonal of the Hessian [1], but that also stayed close to some of the approximations used in existing methods such as Adam [14] and Adagrad [5]. Because of this, the approximation often differed markedly from the true diagonal of the Hessian, and therefore, it did not always capture good enough curvature information to be helpful. The work OASIS [12] proposed a preconditioner that was closely based upon Hutchinson’s approach, provided a more accurate estimation of the diagonal of the Hessian, and correspondingly led to improved numerical behavior in practice. The preconditioner presented in [12] is adopted here.

1.1 Notation and Assumptions

Given a positive definite (PD) matrix $D\in \mathbb {R}^{d\times d}$, the weighted Euclidean norm is defined to be $\Vert x\Vert _D^2 = x^T D x$, where $x\in \mathbb {R}^d$. The symbol $\odot$ denotes the Hadamard product, and diag(x) denotes the $d\times d$ diagonal matrix whose diagonal entries are the components of the vector $x\in \mathbb {R}^d$.

Recall that problem (1) is assumed to have an optimal (probably not a unique) solution $w^*$, with corresponding optimal value $P^* = P(w^*)$. As is standard for stochastic algorithms, the convergence guarantees presented in this work will develop a bound on the number of iterations T, required to push the expected squared norm of the gradient below some error tolerance $\varepsilon >0$, i.e., to find a ${\hat{w}}_T$ satisfying

$$\begin{aligned} {\mathbb {E}}[\Vert \nabla P({\hat{w}}_T)\Vert _2^2] \le \varepsilon ^2. \end{aligned}$$

(2)

A point ${\hat{w}}_T$ satisfying (2) is referred to as an $\varepsilon$-optimal solution. Importantly, ${\hat{w}}_T$ is some iterate generated in the first T iterations of each algorithm, but it is not necessarily the Tth iterate.

Throughout this work, we assume that each $f_i:\mathbb {R}^d \rightarrow \mathbb {R}$ and $P:\mathbb {R}^d \rightarrow \mathbb {R}$ are twice differentiable and also L-smooth. This is formalized in the following assumption.

Assumption 1.1

(L-smoothness) For all $i \in [n]$ $f_i$ and P are assumed to be twice differentiable and L-smooth, i.e., $\forall i \in [n], \forall w,w' \in \text {dom}(f_i)$ we have $\Vert \nabla f_i(w) - \nabla f_i(w') \Vert \le L \Vert w-w'\Vert$, and $\forall w,w' \in \text {dom}(P)$ we have $\Vert \nabla P(w) - \nabla P(w') \Vert \le L \Vert w-w'\Vert .$

For some of the results in this work, it will also be assumed that the function P satisfies the PL-condition. Note that the PL-condition does not imply convexity (see Footnote 1 in [18]).

Assumption 1.2

(Polyak-Łojasiewicz condition) A function $P: \mathbb {R}^d \rightarrow \mathbb {R}$ satisfies the PL-condition if there exists $\mu >0$, such that $\Vert \nabla P(w)\Vert ^2 \ge 2\mu (P(w)-P^{*}),~ \forall w \in \mathbb {R}^d.$

Note that in the case of the PL assumption, we can use the following definition of $\varepsilon$-optimal solution instead of (2):

$$\begin{aligned} {\mathbb {E}}[P({\hat{w}}_T) - P^*] \le \varepsilon . \end{aligned}$$

(3)

Table 1 Comparison of scaled methods for non-convex problems

Table 2 A summary of the main results of this work

1.2 Contributions

The main contributions of this work are stated below and are summarized in Tables 1 and 2.

• Scaled SARAH We present a new algorithm called Scaled SARAH, which is a combination of the SARAH [21] and PAGE [18] algorithms, coupled with the diagonal preconditioner from [12]. The inclusion of the preconditioner results in adaptive scaling of every element of the search direction (negative gradient), which leads to improved practical performance, particularly on ill-conditioned and poorly scaled problems. The algorithm is simple (a single loop) and is easy to tune (Sect. 3).

• Scaled L-SVRG The Scaled L-SVRG algorithm is also presented, which is similar to L-SVRG, but with the addition of the diagonal preconditioner [12]. Again, the preconditioner allows all elements of the gradient to be scaled adaptively, the algorithm uses a single loop structure, and for this algorithm an unbiased estimate of the gradient is used. The inclusion of adaptive local curvature information via the preconditioner leads to improvements in practical performance.

• Convergence Guarantees Theoretical guarantees show that both Scaled SARAH and Scaled L-SVRG converge and we present an explicit bound for the number of iterations required by each algorithm to obtain an iterate that is $\varepsilon$-optimal. Convergence is guaranteed for both Scaled SARAH and Scaled L-SVRG under a smoothness assumption on the functions $f_i$. If both smoothness and the PL-condition hold, then improved iteration complexity results for Scaled SARAH and Scaled L-SVRG are obtained, which show that expected function value gap converges to zero at a linear rate (see Theorems 3.2 and 4.2). Our scaled methods achieve the best known rates of all methods with preconditioning for non-convex deterministic and stochastic problems, and Scaled SARAH and Scaled L-SVRG are the first preconditioned methods that achieve a linear rate of convergence under the PL assumption (see a detailed comparison in Sect. 5).

• Numerical Experiments Extensive numerical experiments were performed (Sect. 6 and Appendix of the full version of the paper [27]) under various parameter settings to investigate the practical behavior of our new scaled algorithms. The inclusion of preconditioning in Scaled SARAH and Scaled L-SVRG led to improvements in performance compared with no preconditioning in several of the experiments, and Scaled SARAH and Scaled L-SVRG were competitive with, and often outperformed, Adam.

Paper Outline This paper is organized as follows. In Sect. 2 we describe the diagonal preconditioner that will be used in this work. In Sect. 3, we describe a new Scaled SARAH algorithm and present theoretical convergence guarantees. In Sect. 5, we discuss our results for the Scaled SARAH method and compare it with other state-of-the-art methods. In Sect. 4, we introduce the Scaled L-SVRG algorithm, which adapts the L-SVRG algorithm to include a preconditioner. We present numerical experiments demonstrating the practical performance of our proposed methods in Sect. 6. Concluding remarks are given in Sect. 7. All proofs, additional numerical experiments, and further details and discussion can be found in the appendix of the full version of the paper [27].

2 Diagonal Preconditioner

In this section, we describe the diagonal preconditioner that is used in this work. The paper [1] described Hutchinson’s approximation to the diagonal of the Hessian, and this provided motivation for the diagonal preconditioner proposed in [12], which is adopted here. In particular, given an initial approximation $D_0$, (to be described soon), and Hessian approximation momentum parameter $\beta \in (0,1)$ (equivalent to the second moment hyperparameter, $\beta _2$ in Adam [14]), for all $t\ge 1$,

$$\begin{aligned} D_{t} = \beta D_{t-1} + (1-\beta )\texttt {diag}\left( z_t\odot \nabla ^2P_{{\mathcal {J}}_t}(w_t)z_t\right) , \end{aligned}$$

(4)

where $z_t$ is a random vector with Rademacher distribution,¹${\mathcal {J}}_t$ is an index set randomly sampled from [n], and

$$\begin{aligned} \nabla ^2P_{{\mathcal {J}}_t}(w_t) = \frac{1}{|{\mathcal {J}}_t|} \sum _{j\in {\mathcal {J}}_t} \nabla ^2 f_{j}(w_t). \end{aligned}$$

(5)

Finally, for $\alpha >0$ (where the parameter $\alpha >0$ is equivalent to the parameter $\varepsilon$ in Adam [14] and AdaHessian [32]), the diagonal preconditioner is:

$$\begin{aligned} \left( {\hat{D}}_{t}\right) _{i,i} = \max \{\alpha , \left| D_t\right| _{i,i}\}. \end{aligned}$$

(6)

The expression (6) ensures that the preconditioner ${\hat{D}}_{t}$ is always PD, so it is well-defined and results in a descent direction. The absolute values are necessary because the objective function is potentially nonconvex, so the batch Hessian approximation could be indefinite. In fact, even if the Hessian is PD, $D_t$ in (4) may still contain negative elements due to the sampling strategy used.

The preconditioner (6) is a good estimate of the diagonal of the (batch) Hessian because Hutchinson’s updating formula (4) is used. Hence, it captures accurate curvature information, which is helpful for poorly scaled and ill-conditioned problems. Because the preconditioner is diagonal it is easy and inexpensive to apply it’s inverse, and the associated storage costs are low.

The preconditioner (4)+(6) depends on the parameter $\beta$: if $\beta = 1$ then the preconditioner is fixed for all iterations, whereas if $\beta = 0$ then the preconditioner is simply a kind of sketched batch Hessian. Taking $0<\beta <1$ gives a convex combination of the previous approximation and the current approximation, thereby ensuring that the entire history is included in the preconditioner, but is damped by $\beta$, and the most recent information is also present.

The main computational cost of the approximation in (4) is the (batch) Hessian vector product $\nabla ^2P_{{\mathcal {J}}_t}(w_t)z_t$. Fortunately, this can be efficiently calculated using two rounds of back propagation. Moreover, the preconditioner is matrix-free, simply needing an oracle to return the Hessian vector product, but it does not need explicit access to the batch Hessian itself; see Appendix B in [12]. Therefore, the costs (both computational and storage) for this preconditioner are not burdensome.

As previously mentioned, the approximation (4) requires an initial estimate $D_0$ of the diagonal of the Hessian, and this is critical to the success of the preconditioner. In particular, one must take

$$\begin{aligned} D_0 = \frac{1}{m} \sum _{j=1}^m \texttt {diag}\left( z_j\odot \nabla ^2P_{{\mathcal {J}}_j}(w_0)z_j\right) , \end{aligned}$$

(7)

where ${\mathcal {J}}_j$ denotes sampled batches and the vectors $z_j$ are generated from a Rademacher distribution. This ensures that ${{\hat{D}}}_t$ does indeed approximate the diagonal of the Hessian; see Section 3.3 in [12].

The following remark confirms that the diagonal preconditioner is both PD and bounded.

Lemma 2.1

(See Remark 4.10 in [12]) For any $t\ge 1$, we have $\alpha I\preccurlyeq {\hat{D}}_t \preccurlyeq \Gamma I$, where $0<\alpha \le \Gamma = \sqrt{\mathrm{{d}}} L$.

Note that Remark 4.10 is proved incorrectly in [12]. The proof is given in Appendix of the full version of the paper. [27]

3 Scaled SARAH

Here we propose a new algorithm, Scaled SARAH, for finite-sum optimization (1). Our algorithm is similar to the SARAH algorithm [21] and the PAGE algorithm [18], but a key difference is that Scaled SARAH includes the option of a preconditioner, ${{\hat{D}}}_t$ for all $t\ge 0$, with a preconditioned approximate gradient step. Scaled SARAH is presented now as Algorithm 1.

Algorithm 1

Scaled SARAH

In each iteration of Algorithm 1, an update is computed in Step 4. The point $w_t$ is adjusted by taking a step in the direction ${{\hat{D}}}_t^{-1}v_t$, of fixed step-size $\eta$. The vector $v_t$ approximates the gradient, and the preconditioner scales that direction. A key difference between Scaled SARAH and PAGE/SARAH is the inclusion of the preconditioner ${{\hat{D}}}_t^{-1}$ in this step.

Step 6 defines the next gradient estimator $v_{t+1}$, for which there are two options. With probability p the full gradient is used. Alternately, with probability $1-p$, the new gradient estimate is the previous gradient approximation $v_t$, with an adjustment term that involves the difference between the gradient of $f_i$ evaluated at $w_{t+1}$ and at $w_t$. The search direction computed in Scaled SARAH contains gradient information, while the preconditioner described in Sect. 2 contains approximate second-order information. When this preconditioner is applied to the gradient estimate, each dimension is scaled adaptively depending on the corresponding curvature. Intuitively, this amplifies dimensions with low curvature (shallow loss surfaces), while damping directions with high curvature (sharper loss surfaces). The aim is for ${{\hat{D}}}_t^{-1} v_t$ to point in a better, adjusted direction, compared with $v_t$.

Scaled SARAH is a single loop algorithm so it is conceptually simple. If $p = 1$, then the algorithm always picks the first option in Step 6, so that Scaled SARAH reduces to a preconditioned GD method. On the other hand, if $p = 0$, then only the second option in Step 6 is used.

Notice that Scaled SARAH is a combination of both the PAGE and SARAH algorithms, coupled with a preconditioner. SARAH [21] is a double loop algorithm, where the inner loop is defined in the same way as update in Step 6. PAGE [18] is based upon SARAH, but PAGE uses a single loop structure, and allows for minibatches to be used in the gradient approximation $v_{t+1}$ (rather than the single component as in Step 6).²Scaled SARAH shares the same single loop structure as PAGE, but also shares the same single component update for the gradient estimator as SARAH (no minibatches). However, different from both PAGE and SARAH, Scaled SARAH uses a preconditioner in Step 4.

In the remainder of this work, we focus on a particular instance of Scaled SARAH, which uses a fixed probability $p_t = p$, and uses the diagonal preconditioner presented in Sect. 2. These choices have been made because a central goal of this work is to understand the impact that a well-chosen preconditioner has on poorly scaled problems. Convergence guarantees and the results of numerical experiments will be presented using this set up.

Theoretical results for Scaled SARAH are presented now. In particular, we present complexity bounds on the number of iterations required by Scaled SARAH to obtain an $\varepsilon$-optimal solution for the non-convex problem (1) (recall Sect. 1.1 with (2) and (3)). The first result holds under Assumption 1.1, while the second theorem holds under both smoothness and PL assumptions. First, we define the following step-size bound:

$$\begin{aligned} {\bar{\eta }} = \frac{\alpha }{L\left( 1 + \sqrt{\tfrac{1-p}{p}}\right) }. \end{aligned}$$

(8)

Theorem 3.1

Suppose that Assumption 1.1 holds, let $\varepsilon >0$, let p denote the probability, and let the step-size satisfy $\eta \le {\bar{\eta }}$ (8). Then, the number of iterations performed by Scaled SARAH, starting from an initial point $w_0\in \mathbb {R}^d$ with $\Delta _0 = P(w_0)-P^*$, required to obtain an $\varepsilon$-approximate solution of the non-convex finite-sum problem (1) can be bounded by

$$\begin{aligned} T ={\mathcal {O}}\left( \frac{\Gamma }{\alpha }\frac{\Delta _0 L}{\varepsilon ^2}\left( 1 + \sqrt{\frac{1-p}{p}}\right) \right) . \end{aligned}$$

Theorem 3.2

Suppose that Assumptions 1.1 and 1.2 hold, let $\varepsilon >0$, and let the step-size satisfy $\eta \le \bar{\eta }$ (8). Then the number of iterations performed by Scaled SARAH sufficient for finding an $\varepsilon$-approximate solution of non-convex finite-sum problem (1) can be bounded by

$$\begin{aligned} T = {\mathcal {O}}\left( \max \left\{ \frac{1}{p}, \frac{L}{\mu }\frac{\Gamma }{\alpha }\left( 1+ \sqrt{\frac{1-p}{p}}\right) \right\} \log \frac{\Delta _0}{\varepsilon }\right) . \end{aligned}$$

Note that this last theorem shows that Scaled SARAH exhibits a linear rate of convergence under both the smoothness assumption and the PL-condition.

We know that Algorithm 1 calls the full gradient at the beginning (Step 2) and then (in expectation) uses $pn + (1-p)$ stochastic gradients for each iteration (Step 6). Thus, the number of stochastic gradient computations (i.e., gradient complexity) is $n + T [pn + (1-p)]$ and the following corollaries of Theorems 3.1 and 3.2 are valid.

Corollary 3.1

Suppose that Assumption 1.1 holds, let $\varepsilon >0$, let $p = \tfrac{1}{n+1}$, and let the step-size satisfy $\eta \le {\bar{\eta }}$ (8). Then, the stochastic gradient complexity performed by Scaled SARAH, starting from an initial point $w_0\in \mathbb {R}^d$ with $\Delta _0 = P(w_0)-P^*$, required to obtain an $\varepsilon$-approximate solution of the non-convex finite-sum problem (1) can be bounded by ${\mathcal {O}}\left( n+ \frac{\Gamma }{\alpha }\frac{\Delta _0 L}{\varepsilon ^2}\sqrt{n} \right) .$

Corollary 3.2

Suppose that Assumptions 1.1 and 1.2 hold, let $\varepsilon >0$, and let the step-size satisfy $\eta \le \bar{\eta }$ (8). Then the stochastic gradient complexity performed by Scaled SARAH sufficient for finding an $\varepsilon$-approximate solution of non-convex finite-sum problem (1) can be bounded by ${\mathcal {O}}\left( \left\{ n + \frac{L}{\mu }\frac{\Gamma }{\alpha } \sqrt{n}\right\} \log \frac{\Delta _0}{\varepsilon }\right) .$

4 Scaled L-SVRG

SVRG [13, 31] is a variance reduced stochastic gradient method that is very popular for finite-sum optimization problems. However, the algorithm has a double loop structure, and careful tuning of hyper-parameters is required for good practical performance.

Recently, in [9], it was proposed a Loopless SVRG (L-SVRG) variant, that has a simpler, single loop structure, which can be applied to problem (1) in the convex and smooth case. This was extended in [24] to cover the composite case with an arbitrary sampling scheme. With its single loop structure, and consequently fewer hyperparameters to tune, coupled with the fact that, unlike for PAGE (recall Sect. 1), L-SVRG uses an unbiased estimate of the gradient, and L-SVRG is a versatile and competitive algorithm for problems of the form (1).

However, as for the other previously mentioned gradient-based methods, L-SVRG can perform poorly when the problem is badly scaled and/or ill-conditioned. This provides the motivation for the Scaled L-SVRG method that we propose in this work. Our Scaled L-SVRG algorithm combines the positive features of L-SVRG, with a preconditioner, to give a method that is loopless, has few hyperparameters to tune, uses an unbiased estimate of the gradient, and adaptively scales the search direction depending upon the local curvature. The Scaled L-SVRG method is presented now as Algorithm 2.

Algorithm 2

Scaled L-SVRG

Scaled L-SVRG can be described, in words, as follows. The algorithm is initialized with an initial main point $w_0$ and an initial reference point $z_0$, a learning rate $\eta$, an initial direction $v_0 = \nabla P(w_0)$, an initial preconditioner ${{\hat{D}}}_0$, and probability p. At each iteration $t\ge 0$ of Scaled L-SVRG (Algorithm 2), the new point $w_{t+1}$ is taken to be a step from $w_t$ in the scaled direction ${\hat{D}}^{-1}_{t}v_t$, of size $\eta$. The new point $z_{t+1}$ is either the (unchanged) previous point $z_t$ with probability p, or the scaled approximate gradient step $w_{t+1}$ with probability $1-p$. Next, we generate the new search direction $v_t$. This is made up of the full gradient plus a small adjustment. Finally, the preconditioner is updated and the next iterate begins. The output denoted by ${{\hat{w}}}_T$ is chosen uniformly from the points $w_t$, for $t=0,\dots , T$, generated by Scaled L-SVRG (Algorithm 2).

Note that a key difference between L-SVRG [9, 24] and our new Scaled L-SVRG is the inclusion of the preconditioner in Step 4; recall that a competitive preconditioner is described in Sect. 2.

The following theorem presents a complexity bound on the number of iterations required by Scaled L-SVRG to obtain an $\varepsilon$-optimal solution for the non-convex problem (1).

Theorem 4.1

Suppose that Assumption 1.1 holds, let $\varepsilon >0$, let p denote the probability, and let the step-size satisfy $\eta \le \min \left\{ \tfrac{\alpha }{4\,L}, \tfrac{\sqrt{p}\alpha }{\sqrt{24}L}, \tfrac{p^{2/3}}{144^{2/3}}\tfrac{\alpha }{L}\right\} .$ Given an initial point $w_0\in \mathbb {R}^d$, let $\Delta _0 = P(w_0)-P^*$. Then the number of iterations performed by Scaled L-SVRG, starting from $w_0$, required to obtain an $\varepsilon$-approximate solution of non-convex finite-sum problem (1) can be bounded by

While the previous theorem held under a smoothness assumption, here we prove a complexity result for Scaled SARAH under both smoothness and PL assumptions.

Theorem 4.2

Suppose that Assumptions 1.1 and 1.2 hold, let $\varepsilon >0$, let p denote the probability, and let the step-size satisfy $\eta \le \min \left\{ \frac{p\Gamma }{6\mu },\frac{1}{4}\frac{\alpha }{L}, \left( \frac{p}{6}\right) ^{1/2}\frac{\alpha }{L}, \left( \frac{p}{6}\right) ^{2/3}\frac{\alpha }{L}\right\} .$ Then the number of iterations performed by Scaled L-SVRG sufficient for finding an $\varepsilon$-approximate solution of non-convex finite-sum problem (1) can be bounded by

Below we provide corollaries on the complexities of stochastic gradient.

Corollary 4.1

Suppose that Assumption 1.1 holds, let $\varepsilon >0$, let $p = \tfrac{1}{n+1}$, and let the step-size satisfy $\eta \le \min \left\{ \tfrac{\alpha }{4\,L}, \tfrac{\sqrt{p}\alpha }{\sqrt{24}L}, \tfrac{p^{2/3}}{144^{2/3}}\tfrac{\alpha }{L}\right\} .$ Given an initial point $w_0\in \mathbb {R}^d$, let $\Delta _0 = P(w_0)-P^*$. Then the stochastic gradient complexity performed by Scaled L-SVRG, starting from $w_0$, required to obtain an $\varepsilon$-approximate solution of non-convex finite-sum problem (1) can be bounded by

Corollary 4.2

Suppose that Assumptions 1.1 and 1.2 hold, let $\varepsilon >0$, let $p = \tfrac{1}{n+1}$, and let the step-size satisfy $\eta \le \min \left\{ \frac{p\Gamma }{6\mu },\frac{1}{4}\frac{\alpha }{L}, \left( \frac{p}{6}\right) ^{1/2}\frac{\alpha }{L}, \left( \frac{p}{6}\right) ^{2/3}\frac{\alpha }{L}\right\} .$ Then the stochastic gradient complexity performed by Scaled L-SVRG sufficient for finding an $\varepsilon$-approximate solution of non-convex finite-sum problem (1) can be bounded by

5 Discussion

In this section, we discuss the theoretical results obtained for Scaled SARAH, Scaled L-SVRG and compare them with other scaled methods, as well as for methods without preconditioning. For convenience, we give Table 3 summarizing all the results.

• In Sect. 2 we consider scaling based on Hutchinson’s approximation, but our analysis can be used to obtain similar estimates for Scaled SARAH and Scaled L-SVRG with Adam preconditioning. In particular, we can prove an analog of Lemma 2.1 (see Appendix of the full version of the paper [27]) by additionally assuming boundedness of the stochastic gradient for all w: $\Vert \nabla f_i (w) \Vert \le M$ (a similar assumption is made in [3] for Adam). We present these results in Table 3 for comparison with the current best results for Adam.

• In the deterministic case, our results are significantly superior to those from [3], in particular, in terms of the accuracy of the solution our estimates give ${\mathcal {O}}(\varepsilon ^{-2})$ dependence, at the same time the guarantees from [3] are ${\mathcal {O}}(\varepsilon ^{-4})$. Compared to OASIS in the deterministic case, we have the same results in terms of $\varepsilon$, but our bounds are much better in terms of d, L, $\alpha$. It is also an interesting detail that our estimates for Scaled SARAH and Scaled L-SVRG with Adam preconditioner are independent of d and with Hutchinson’s preconditioner depend on $\sqrt{d}$, which is important for high-dimensional problems.

• In the stochastic case, our convergence guarantees are also the best among other scaled methods, primarily in terms of $\varepsilon$. This is mainly due to the fact that we use the stochastic finite-sum setting typical for machine learning.

• Unfortunately, our estimates are inferior to the bounds of the unscaled methods: SARAH and L-SVRG (the base methods for our methods) and SGD (the best known method for minimization problems). As one can see in Table 3, all results for methods with preconditioning have the same problem. This is the level of theory development in this field at the moment. It seems that our results are able, in some sense, to reduce this gap between scaled and unscaled methods by decreasing the additional multiplier.

Summary Our theoretical results exceed the estimates already in the literature for scaled methods. If we consider that algorithms with preconditioning are desirable from the point of view of real-world learning problems, it turns out that we prove the best results for the practical class of methods at present. Meanwhile, our estimates are still worse than those for unscaled methods. In Appendix of the full version of the paper [27], one can find a possible explanation for why these estimates cannot be improved. In Sect. 6 we present experiments in which it becomes clear that real problems are not necessarily “the worst”. On the contrary, practical problems are those where our method from Sects. 2 and 3 shows its dominance.

Table 3 Comparison of deterministic and stochastic methods for non-convex problems in the general case and under Polyak-Łojasiewicz condition

6 Numerical Experiments

The purpose of these numerical experiments is to study the practical performance of our new Scaled SARAH and Scaled L-SVRG algorithms, and hence, to understand the advantages of using the proposed diagonal preconditioner on SARAH and L-SVRG. These results will also be compared with SGD, both with and without the preconditioner described in Sect. 2, as well as the state-of-the-art (first-order) preconditioned optimizer Adam.

We test these algorithms on problem (1) with two loss functions: (1) logistic regression loss function, which is convex, and (2) nonlinear least squares loss function, which is nonconvex. The loss functions are described in details below. For further details and experimental results that support the findings of this section, please see Appendix of the full version of the paper [27]. Note that all the experiments were initialized at the point $w_0 = 0$, and each experiment was run for 10 different random seeds.

6.1 Loss Functions

Let P(w) be the empirical risk on a dataset $\{(x_i,y_i)\}_{i=1}^{n}$ where $x_i \in \mathbb {R}^d$ and $y_i \in \{-1,+1\}$. Then, the logistic regression loss is

$$\begin{aligned} P_\text {logistic}(w) = \tfrac{1}{n} \textstyle {\sum }_{i=1}^{n} \log (1 + e^{-y_i x_i^T w}), \end{aligned}$$

(9)

whereas for $y_i \in \{0,1\}$ the nonlinear least squares loss (NLLSQ) is

$$\begin{aligned} P_\text {nllsq}(w) = \tfrac{1}{n} \textstyle {\sum }_{i=1}^{n} (y_i - 1/(1 + e^{-x_i^T w}))^2 \end{aligned}$$

(10)

We consider two different loss functions to test our algorithms on both convex and nonconvex settings.

6.2 Binary Classification on LibSVM Datasets

We train the optimizers on three binary classification LibSVM datasets,³ namely w8a, rcv1, and real-sim. We also consider feature-scaled versions of these datasets, where the scaling is done as follows: we choose a minimum exponent $k_{\min }$ and a maximum exponent $k_{\max }$, and scale the features by values ranging from $10^{k_{\min }}$ to $10^{k_{\max }}$ in equal steps in the exponent according to the number of features and in random order. The setting $(k_{\min }, k_{\max }) = (0,0)$ corresponds to the original, unscaled version of the datasets. We consider combinations of $k_{\min } = 0, -3$ and $k_{\max } = 0, 3$. This scaling is done to check the robustness and overall effectiveness of the diagonal preconditioner in comparison with Adam.

Fig. 1

Best performances of the optimizers, including Adam, on the (unscaled) LibSVM datasets using the logistic loss. The Scaled variants are shown as dashed lines sharing the same color

Fig. 2

Best performances on the unscaled LibSVM datasets using the NLLSQ loss

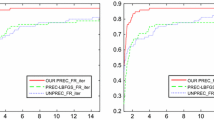
Figure 1 shows the results of the first experiment and presents three types of line plots for each of the datasets of interest where the loss function is the logistic regression loss (9). Figure 2 shows the same for the NLLSQ loss (10). The first row corresponds to the loss, the second is the squared norm of the gradient, and the third is the error. Tuning was performed in order to select the best hyperparameters (that minimize either the loss, gradient norm squared, or the error). The hyperparameter search grid is reported in Appendix of the full version of the paper [27]. We fixed the batch size to be 128, in order to narrow the fine-tuned variables down to $\eta$, $\beta$, and $\alpha$. Figure 1 shows the performances when minimizing the error on the unscaled datasets, $(k_{\min }, k_{\max }) = (0,0)$. Experiments on scaled datasets can be found in Appendix of the full version of the paper [27].

We can see from Figs. 1 and 2 that the scaled versions of SGD, SARAH, and L-SVRG always improve on their non-scaled versions. In fact, they perform better than Adam in most cases. Initial convergence of Adam might be faster, but after enough effective passes, we can see that the scaled algorithms can generalize better.

In order to understand the main factors that affect the preconditioner, we ran comparative studies, including studying the parameters $\beta$, and $\alpha$, as well as studying the initialization of preconditioner $D_0$, including a warm-up period, and studying how the number of samples, z, impacts performance. First, recalling (7), there did not appear to be any significant improvement from averaging across more samples of z per minibatch, neither in the initialization nor in the update step. We also observed that initializing $D_0$ with a batch size of 100 was sufficiently good for non-sparse problems, and consistently resulted in a relative error of within 0.1 from the true diagonal. However, increasing the number of warm-up samples, proportionally to the number of features, led to observable improvements in convergence for sparse datasets.

We also investigated the role that $\beta$ (4) played in algorithm performance. We found that larger values lead to slightly slower but more stable convergence. The best $\beta$ highly depends on the dataset, but the value 0.999 appeared to be a good starting point in general. To ensure a fair comparison, we also optimized Adam’s momentum parameter $\beta _2$ over the same range.

Aside from the batch size and learning rate, we found that, for ill-conditioned problems, the choice of $\alpha$ (recall (6) and Lemma 2.1) played an important role in determining the quality of the solution, convergence speed, and stability (which is not obvious from Fig. 1). For example, if the features were scaled with $k_{\min }=-3$ and $k_{\max }=0$, the best $\alpha$ is often around $10^{-7}$ (very small), whereas if we scaled with $k_{\min }=0$ and $k_{\max }=3$, the best $\alpha$ becomes $10^{-1}$ (relatively large). Therefore, finding the best $\alpha$ might require some additional fine-tuning, depending on the choice of $\eta$ and $\beta$. However, we noticed that once we had tuned the learning rate for one scaled version of the dataset, the same learning rate transferred well to all the other scaled versions. In general, the optimal learning rate in our Scaled algorithms is very robust to feature scaling, given that $\alpha$ is chosen well, whereas Adam’s learning rate depends more heavily upon how ill-conditioned the problem is, so it requires fine-tuning across a potentially much wider range. In our case, tuning $\alpha$ and $\beta$ is straightforward, so we obtained state-of-the-art performance with minimal parameter tuning.

7 Conclusion

This paper investigates optimization methods with scaling for finite sum stochastic problems. The proposed algorithms are based on well-known variance reduction techniques: SARAH/PAGE, SVRG/L-SVRG. In addition to the basic updates, gradient preconditioning matrices are used to allow individually adapting steps for each optimization variable. Rather general assumptions on these matrices (diagonality and positive spectrum) give opportunity to analyze combinations of variance reduction approaches with popular scaling techniques: RMSProp, Adam, and OASIS. Meanwhile, the unification of the assumptions gives the weakness of the result in some sense. The theoretical guarantees of convergence are no better than for the simple unscaled methods. Therefore, while the paper improves the results of methods with scaling for stochastic problems, it does not address the key question of why these methods can be better than the basic algorithms. This is an interesting and important direction for the future research.