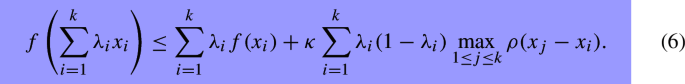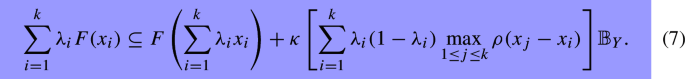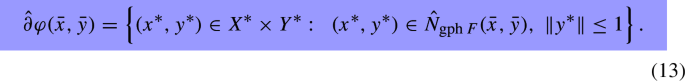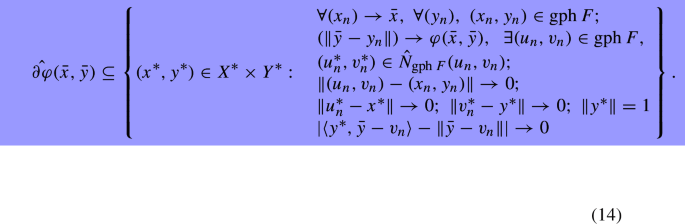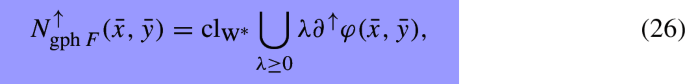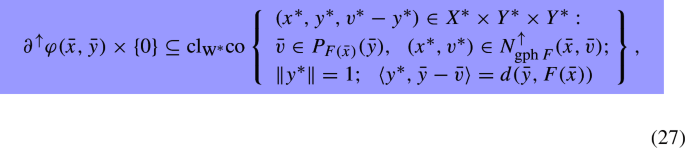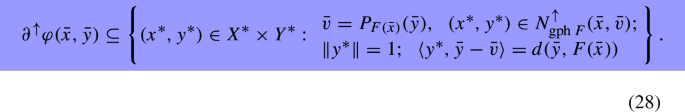Variational Analysis of Paraconvex Multifunctions

Abstract

Our aim in this article is to study the class of so-called $\rho -$paraconvex multifunctions from a Banach space X into the subsets of another Banach space Y. These multifunctions are defined in relation with a modulus function $\rho :X\rightarrow [0,+\infty )$ satisfying some suitable conditions. This class of multifunctions generalizes the class of $\gamma -$paraconvex multifunctions with $\gamma >1$ introduced and studied by Rolewicz, in the eighties and subsequently studied by A. Jourani and some others authors. We establish some regular properties of graphical tangent and normal cones to paraconvex multifunctions between Banach spaces as well as a sum rule for coderivatives for such class of multifunctions. The use of subdifferential properties of the lower semicontinuous envelope function of the distance function associated to a multifunction established in the present paper plays a key role in this study.

1 Introduction and Preliminaries

Because of the importance of convexity, both from a theoretical point of view, but also for the role it plays in certain applications, many efforts have been made in recent decades to extend the notion of convexity. This work dedicated to Franco Giannessi gives us the opportunity to quote one of his remarks concerning generalizations of convexity, a quote given in his book [14, page 127]:

“[...] in the last three decades there has been an impressive growth of definitions of generalized convexity, both for sets and functions. The way of obtaining them is very simple: if we remove one of the many properties enjoyed by convexity, or we extend one of the terms of the definition, then we obtain a generalized concept; now, the same can be done with the concept just obtained, and so on in a practically endless process. Some of such generalizations are of fundamental importance; unfortunately, many generalizations look like mere formal mathematics without any motivation and contribute to drive mathematics away from the real world. Neglecting the fact that definition is the cornerstone of mathematics and hence is the most difficult task, new generalized concepts of convexity sprout like mushrooms (even 30 meaningless generalizations of convexity can be found in a same recent paper! while E. De Giorgi, in his entire mathematical life, gave only one concept: (p,q)-convexity; and G. Stampacchia dealt with coerciveness ; both such extensions of convexity have been introduced and used under strong motivations”.

The problem addressed in this paper belongs to the study of variational properties of paraconvex multifunctions between Banach spaces. The concept of paraconvexity of functions or multifunctions traces back to the work by S. Rolewicz [35,36,37,38,39,40] and later has been the object of contributions by Jourani [18, 19], Ngai and Penot [28] and some others.

Historically, traces of paraconvexity can be found in the notion of $(p,q)-$convexity defined by De Giorgi-Marino-Tosques ( [10], see also [11]) and has been used in the study of evolution equations as well as in some problems related to the calculus of variations. Notions of paraconvexity are also found in Mifflin’s semiconvexity [22], in Cannarsa and Sinestrari [6] (Semi-convex functions ), in Janin [17] (PC functions), in Mazure and Volle [21] (A-convexity), in Spingarn [41] and Rockafellar [33] (lower $C^1$ and lower $C^2$ functions), or in the definition of weak convexity by Vial [45]. A common feature of the above-mentioned classes of functions is that each of them preserves more or less interesting geometrical/analytic properties of convexity. Also, as mentioned, for instance, by Daniidilis and Malick [9], in Hilbert spaces, when f is locally Lipschitz, weakly convexity, lower $C^2$ and $\rho$-paraconvexity (for $\rho (x)=\frac{1}{2}\Vert x\Vert ^2$) are equivalent. This fact is highlighted by the numerous applications of this particular class of functions in optimization, but also in areas such that statistical learning and signal processing. We refer for details to the recent article of Davis and Drusvyatskiy.¹

Another motivation for considering such classes of nonsmooth functions possessing nice variational properties is the point of view of the theory of subdifferentiability. In [4], the authors showed that almost every $1-$Lipschitz function defined on a Banach space has a Clarke subdifferential identically equal to the dual ball. For such functions, the subgradient (Clarke) gives no significant information. Therefore, the task of considering special classes of nonsmooth functions which establish regular properties of subdifferentials plays an important role in variational analysis and applications.

In the works by Rolewicz and the other authors mentioned above, some nice properties on subdifferentials and on generic differentiation of paraconvex functions, as well as some properties of openness, Lipschitzness, metric regularity and error bound of paraconvex multifunctions have been established. This article can be considered as a continuation of these previous works concerning paraconvex multifunctions between Banach spaces. Here, we consider in a unified way paraconvexity with respect to a modulus function satisfying some suitable conditions. Namely, the main results established in this article concern:

• The regularity of graphical tangent and normal cones to paraconvex multifunctions between Banach spaces;

• Some calculus for subgradients of the lower semicontinuous envelope function of the distance function associated to a multifunction. This allows to characterize the paraconvexity via the paramonotonicity;

• A sum rule for coderivatives of paraconvex multifunctions.

We conclude the study by stating some open problems.

1.1 Tools from Variational Analysis

Variational analysis being instrumental in this study, let us briefly gather some of its basics. They can be found for example in [7, 23, 32, 34, 44] and will be used throughout the paper.

Throughout we assume that X is a Banach space with norm $\Vert \cdot \Vert$. We denote by $X^*$ the topological dual of X, and we assume that X and $X^*$ are paired by $\langle \cdot ,\cdot \rangle$. We use $\mathbb {B}_X,$ for the closed unit ball in X and $\mathbb {B}(x,\delta ),\mathbb {B}[x,\delta ]$ for the, respectively, open and closed balls centered at x with radius $\delta >0.$ Given a subset S of X, we note $\text {cl}\, (S)$ and ${{\,\mathrm{Int}\,}}(S)$ the closure and the interior of S, respectively. We use the notation $F:X\rightrightarrows Y$ to mean a multifunction from X to Y, that is, for every $x\in X$, F(x) is a subset (possibly empty) of Y. The graph of F is ${{\,\mathrm{gph}\,}}F:=\{(x,y)\in X\times Y: \; y\in F(x)\}$ and ${{\,\mathrm{Dom}\,}}F= \{x\in X: \; F(x)\ne \emptyset \}$ is the effective domain of F. We say that F is closed-graph (or simply closed) whenever ${{\,\mathrm{gph}\,}}F$ is closed with respect to the product topology on $X\times Y.$

Definition 1.1

(Tangent cones) Let C be a nonempty subset of X and fix $x\in C$.

The contingent (or Bouligand) tangent cone to C at x is the set

$$\begin{aligned} T^-_C(x):=\left\{ u\in X:\;\;\exists \; \text {sequences}\;\; (u_n)\subseteq X,\; u_n\rightarrow u,\; t_n\rightarrow 0^+,\; x+t_nu_n\in C,\;\forall n\in \mathbb {N}\right\} . \end{aligned}$$

The Clarke tangent cone to C at x is the set

$$\begin{aligned} T^\uparrow _C(x):=\left\{ u\in X:\;\; \forall (x_n)\rightarrow x,\;\text {with}\; x_n\in C,\; \forall (t_n)\rightarrow 0^+,\;\; \exists (u_n)\rightarrow u,\; x_n+t_nu_n\in C\right\} . \end{aligned}$$

Definition 1.2

(Normal cones) The Bouligand normal cone to C to $x\in C$ is the set

$$\begin{aligned} N^-_C(x):=\left\{ x^*\in X ^*:\;\; \langle x^*,u\rangle \le 0,\;\forall u\in T^-_C(x)\right\} ; \end{aligned}$$

The Clarke normal cone to C at x is the set

$$\begin{aligned} N_C^\uparrow (x):=\left\{ x^*\in X ^*:\;\; \langle x^*,u\rangle \le 0,\;\forall u\in T^\uparrow _C(x)\right\} . \end{aligned}$$

If $f:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is an extended-real-valued function, its effective domain is the set ${{\,\mathrm{Dom}\,}}f:=\{x\in X: \;f(x)<+\infty \}$. We use the notation $y\xrightarrow [\text {f}]{\text {}}x$ (respectively, $y\xrightarrow [\text {C}]{\text {}}x$ ) to mean $y\rightarrow x$ and $f(y)\rightarrow f(x)$, (respectively, $y\rightarrow x$ and $y \in C$).

Definition 1.3

(Directional derivatives) The (lower) Hadamard directional derivative (or contingent derivative) of f at $x\in {{\,\mathrm{Dom}\,}}f$ in the direction v is

$$\begin{aligned} f^-(x,v):=\liminf _{(t,u)\rightarrow (0^+,v)}\frac{f(x+tv)-f(x)}{t},\;\;v\in X. \end{aligned}$$

The Rockafellar generalized directional derivative of f at $x\in {{\,\mathrm{Dom}\,}}f$ in the direction v is

$$\begin{aligned} f^\uparrow (x,v):=\lim _{\varepsilon \rightarrow 0^+}\limsup _{ y\xrightarrow [\text {f}]{\text {}}x, t\rightarrow 0^+}\inf _{w\in v+\varepsilon \mathbb {B}_X}\frac{f(y+tw)-f(y)}{t}. \end{aligned}$$

Definition 1.4

(Subdifferentials) The Hadamard-subdifferential of f at $x\in {{\,\mathrm{Dom}\,}}f$ is

$$\begin{aligned} \partial ^- f(x):=\{x^*\in X^*:\;\; \langle x^*,v\rangle \le f^-(x,v),\;\;\forall v\in X\}. \end{aligned}$$

The Clarke subdifferential of f at $x\in {{\,\mathrm{Dom}\,}}f$ is

$$\begin{aligned} \partial ^\uparrow f(x):=\{x^*\in X^*:\;\; \langle x^*,v\rangle \le f^\uparrow (x,v),\;\;\forall v\in X\}. \end{aligned}$$

The Fréchet subdifferential $\hat{\partial }f(x)$ of f at $x\in {{\,\mathrm{Dom}\,}}f$ is defined as

$$\begin{aligned} \hat{\partial }f(x):=&\left\{ x^*\in X^*:\;\;\liminf _{h\rightarrow 0}\frac{f(x+h)-f(x)-\langle x^*,h\rangle }{\Vert h\Vert }\ge 0\right\} \\&\text {and}\; \hat{\partial }f(x):=\emptyset \text { if }\; f(x)=+\infty . \end{aligned}$$

Note that the subdifferentials operators $\partial ^\uparrow$ can be represented geometrically as follows:

$$\begin{aligned} \partial ^- f(x)=\{x^*\in X^*:\;\; (x^*,-1)\in N^-_{{{\,\mathrm{epi}\,}}f}(x,f(x))\}, \end{aligned}$$

and

$$\begin{aligned} \partial ^\uparrow f(x)=\{x^*\in X^*:\;\; (x^*,-1)\in N^\uparrow _{{{\,\mathrm{epi}\,}}f}(x,f(x))\}, \end{aligned}$$

where ${{\,\mathrm{epi}\,}}f$ denotes the epigraph of f:

$$\begin{aligned} {{\,\mathrm{epi}\,}}f:=\{(x,\alpha )\in X\times {\mathbb {R}}:\;\; f(x)\le \alpha \}. \end{aligned}$$

Conversely, the Bouligand and Clarke normal cones to a subset $C\subseteq X$ (at $x\in C$) may be represented as the respective subdifferentials of the indicator function $\delta _C$ of C:

$$\begin{aligned} N^-_C(x)=\partial ^- \delta _C(x),\;\;N^\uparrow _C(x)=\partial ^\uparrow \delta _C(x), \end{aligned}$$

where

$$\begin{aligned} \delta _C(x):=\left\{ \begin{array}{ll} 0\quad &{}\text {if}\quad x\in C\\ +\infty \quad &{}\text {otherwise}. \end{array} \right. \end{aligned}$$

The Clarke subdifferential enjoys a sum rule (see [7, Theo. 2.9.8]):

$$\begin{aligned} \partial ^\uparrow (f_1+f_2)(x)\subseteq \partial ^\uparrow f_1(x)+\partial ^\uparrow f_2(x), \end{aligned}$$

(1)

provided $f_1$ is lower semicontinuous and $f_2$ is locally Lipschitz around x.

The Fréchet normal cone to a subset $C\subseteq X$ at some point $x\in C$ is defined as

$$\begin{aligned} {\hat{N}}_C(x):=\hat{\partial }\delta _C(x)=\left\{ x^*\in X^*:\;\; \limsup _{z\rightarrow _C x}\frac{\langle x^*,z-x\rangle }{\Vert z-x\Vert }\le 0\right\} . \end{aligned}$$

The following inclusions hold:

$$\begin{aligned} T^-_C(x)\supseteq T^\uparrow _C(x),\;\;\text { and }\;\;{\hat{N}}_C(x)\subseteq N^-_C(x)\subseteq N^\uparrow _C(x). \end{aligned}$$

When X is Asplund, i.e., when every continuous convex function defined on X is generically Fréchet differentiable, the Fréchet subdifferential enjoys a fuzzy sum rule ( [13], see also [23]): For any $\varepsilon >0,$ for $x\in {{\,\mathrm{Dom}\,}}f_1\cap {{\,\mathrm{Dom}\,}}f_2,$ provided $f_1,f_2$ are lower semicontinuous and one of them is locally Lipschitz around x, one has

$$\begin{aligned}&{\hat{\partial }}(f_1+f_2)(x) \nonumber \\&\quad \subseteq \bigcup \left\{ \hat{\partial }f_1(x_1)+\hat{\partial }f_2(x_2)+\varepsilon \mathbb {B}_{X^*}:\;\; (x_i,f(x_i))\in \mathbb {B}((x,f(x)),\varepsilon ),\;i=1,2\right\} . \end{aligned}$$

(2)

Let X, Y be Banach spaces. Throughout, when considering the cartesian product $X\times Y$, unless otherwise stated, we suppose it endowed with the max-norm:

$$\begin{aligned} \Vert (x,y)\Vert =\max \{\Vert x\Vert ,\Vert y\Vert \},\;\; (x,y)\in X\times Y. \end{aligned}$$

For a multifunction $F:X\rightrightarrows Y$, the naming coderivative of F at a point $(x,y)\in {{\,\mathrm{gph}\,}}F,$ refers to a multifunction $(DF^*)^{!}(x,y): Y^*\rightrightarrows X^*$ and defined as

$$\begin{aligned} (DF^*)^{!}(x,y)(y^*):=\left\{ x^*:\;\;(x^*,-y^*)\in N^!_{{{\,\mathrm{gph}\,}}F}(x,y)\right\} ,\;\;y^*\in Y^*, \end{aligned}$$

for every $(x,y)\in {{\,\mathrm{gph}\,}}F$. The symbol "!" means that the coderivative of F is related either to the lower Hadamard or the Clarke, or the Fréchet normal cone.

2 Paraconvexity of Functions and Multifunctions

We start by introducing a notion of modulus function.

Definition 2.1

(Modulus function) Let X, Y be Banach spaces. We say that a function $\rho : X\rightarrow \mathbb {R}_+:=[0,+\infty )$ is a modulus function if it verifies the following properties:

• (C1) $\rho$ is a continuous convex function on X;

• (C2) $\rho (0)=0,$ and the function $\rho$ is even, i.e., $\rho (-x)=\rho (x),$    for all $x\in X;$

• (C3) $\lim \limits _{\Vert x\Vert \rightarrow 0}\frac{\rho (x)}{\Vert x\Vert }=0.$

Definition 2.2

An extended-real-valued function $f:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is called $\rho -$paraconvex if there exists a nonnegative constant $\kappa$ such that for all $x_1,x_2\in X$, and all $t\in [0,1],$ one has

This definition subsumes known concepts of convexity, depending on the prescribed modulus function:

• When $\rho (x)= \Vert x\Vert ^2$ the notion was introduced by Rolewicz [38] ; it is also known under the name of weakly convex function investigated by [3, 45]

• When $\rho$ in the form $\rho (\cdot )=\Vert \cdot \Vert \eta (\cdot )$ with $\eta (x)\rightarrow 0$ as $x\rightarrow 0$, one retrieves the concept of semiconvexity introduced by Alberti, Ambrosio and Cannarsa [1],

Definition 2.3

A multifunction $F:X\rightrightarrows Y$ between two Banach spaces X and Y is called $\rho$-paraconvex if there exists a nonnegative constant $\kappa$ such that for all $x_1,x_2\in X$, and all $t\in [0,1],$ one has

Taking $\rho (x)= \varepsilon \Vert x\Vert ^\gamma , \; \gamma >1$, we recover the $\gamma$-paraconvexity in the sense of Rolewicz [35]. Obviously if a function $f:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is $\rho$-paraconvex for a modulus function $\rho$ verifying $(C1)-(C3),$ then it is approximately convex at all point $x\in {{\,\mathrm{Dom}\,}}f,$ in the sense introduced and studied by Ngai-Luc-Théra [25], then in [26, 27, 31].

Consider m functions $f_i:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$, $i=1,...,m,$ for some $m\in \mathbb {N}_*.$ Define the multifunction $F:X\rightarrow {\mathbb {R}}^m$ by

$$\begin{aligned} F(x)=\Pi _{i=1}^m[f_i(x),+\infty ),\;\; x\in X. \end{aligned}$$

(5)

The following proposition shows the equivalence between the paraconvexity of the functions $f_i,$ $i=1,...,m,$ and the one of the multifunction F. The proof is straightforward from the definition.

Proposition 2.1

Let X be a Banach space. Let given a modulus function $\rho :X\rightarrow {\mathbb {R}}_+$ and m extended-real-valued functions $f_i:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$, $i=1,...,m,$ and the multifunction F defined by (5). If all $f_i$, $i=1,...,m$ are $\rho$-paraconvex functions, then F is a $\rho$-paraconvex multifunction. The converse holds provided all ${{\,\mathrm{Dom}\,}}f_i$ $(i=1,...,m)$ are equal.

This following folklore lemma is an approximate Jensen inequality (inclusion) for paraconvex functions (resp. multifunctions). Its proof is standard by induction similarly to the convex case that we leave it for the reader.

Lemma 2.1

(Approximate Jensen’s inequality) Let $\rho :X\rightarrow {\mathbb {R}}_+$ be a modulus function verifying $(C1)-(C2).$

• (i) Let $f:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be a $\rho$-paraconvex function with respect to some $\kappa >0$ as in Definition 2.2. Then for any $k\in \mathbb {N}_*,$ $x_1,...,x_k\in X,$ $\lambda _i\ge 0$, $i=1,...,k$ with $\sum _{i=1}^k\lambda _i=1,$ one has

  

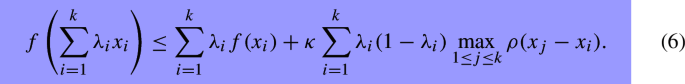
• (ii) Let $F:X\rightrightarrows Y$ be a $\rho$-paraconvex multifunction with respect to some $\kappa >0$ as in Definition 2.3. Then for any $k\in \mathbb {N}_*,$ $x_1,...,x_k\in X,$ $\lambda _i\ge 0$, $i=1,...,k$ with $\sum _{i=1}^k\lambda _i=1,$ one has

  

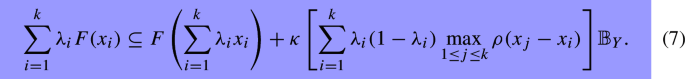
Given a multifunction $F:X\rightrightarrows Y$, we consider the distance function $d_F:X\times Y\rightarrow {\mathbb {R}}\cup \{+\infty \}$ defined by

$$\begin{aligned} d_F(x,y):=d(y,F(x))=\inf \{\Vert y-z\Vert :\;\; z\in F(x)\},\;(x,y)\in X\times Y, \end{aligned}$$

with the convention $d(y,\emptyset )=+\infty .$ This distance function has been studied and used in the literature, e.g., by Thibault [42], Bounkhel-Thibault [5] and Mordukhovich-Nam [24]. Except when Y is finite dimensional, $d_F$ is not lower semicontinuous, even if F is a closed multifunction (i.e., the graph of F is closed in the product space $X\times Y$). We will use the lower semicontinuous envelope $\varphi _F:X\times Y\rightarrow {\mathbb {R}}\cup \{+\infty \}$ of $d_F$ and defined as follows:

This function $\varphi _F$ played a key role in the study of metric regularity and implicit multifunction theorems (e.g., see [20, 29, 30] and the references given therein).

The relationships between the paraconvexity of a multifunction $F:X\rightrightarrows Y$, the associated distance function $d_F$ and its lower semicontinuous envelope $\varphi _F$ are stated in the following proposition. Note that the equivalence between (i) and (ii) for $\gamma -$paraconvex multifunctions for $\gamma >0,$ was given in [18].

Proposition 2.2

Let X and Y be Banach spaces and suppose that $F: X\rightrightarrows Y$ is a multifunction and $\rho :X\rightarrow {\mathbb {R}}$ is a modulus function verifying $(C1)-(C2).$ Let consider the three following statements:

• (i) F is a $\rho$-paraconvex multifunction;

• (ii) $d_F$ is a $\rho$-paraconvex function;

• (iii) $\varphi _F$ is a $\rho$-paraconvex function.

Then, one has $(i)\Leftrightarrow (ii)\Rightarrow (iii).$ Moreover, if Y is a reflexive space, then the three statements are equivalent.

Proof

For $(i)\Rightarrow (ii),$ suppose that the multifunction F is $\rho$-paraconvex with respect to some $\kappa >0$. Given $(x_1,y_1), (x_2,y_2)\in X\times Y,$ $t\in [0,1],$ we need to show that

$$\begin{aligned} d_F(t(x_1,y_1)+(1-t)(x_2,y_2))\le td_F(x_1,y_1)+(1-t)d_F(x_2,y_2)+\kappa t(1-t)\rho (x_1-x_2). \end{aligned}$$

(8)

Obviously, (8) holds trivially when $F(x_1)$ or $F(x_2)$ is an empty set. Hence, we suppose that $F(x_1)\not =\emptyset$, $F(x_2)\not =\emptyset$. Then, picking sequences $(z_k)$ with $z_k\in F(x_1)$ and $(v_k)$ with $v_k\in F(x_2)$ such that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert y_1-z_k\Vert =d_F(x_1,y_1),\;\; \lim _{k\rightarrow \infty }\Vert y_2-v_k\Vert =d_F(x_2,y_2), \end{aligned}$$

and using the $\rho$-paraconvex of F,  for each $k\in \mathbb {N},$ there exists $w_k$ such that

$$\begin{aligned} w_k\in F(tx_1+(1-t)x_2) \quad \text {and}\quad \Vert tz_k+(1-t)v_k-w_k\Vert \le \kappa t(1-t)\rho (x_1-x_2). \end{aligned}$$

Hence,

$$\begin{aligned} d_F(t(x_1,y_1)+(1-t)(x_2,y_2))&\le \Vert ty_1+(1-t)y_2-w_k\Vert \\&\le \Vert ty_1+(1-t)y_2-tz_k-(1-t)v_k\Vert \\&\quad +\Vert tz_k+(1-t)v_k-w_k\Vert \\&\le t\Vert y_1-z_k\Vert +(1-t)\Vert y_2-v_k\Vert +\kappa t(1-t)\rho (x_1-x_2). \end{aligned}$$

By letting $k\rightarrow \infty$ in the preceding relation, we obtain (8).

For $(ii)\Rightarrow (i),$ suppose that $d_F$ is $\rho$-paraconvex with respect to some $\kappa >0.$ Fix $x_1,x_2\in X,$ $t\in [0,1].$ Then for any $y_1\in F(x_1),$ $y_2\in F(x_2),$ observing that $d_F(x_i,y_i)=0$ ($i=1,2$), by taking any real $\mu >\kappa ,$ we may select $w\in F(tx_1+(1-t)x_2)$ such that

$$\begin{aligned} \Vert ty_1+(1-t)y_2-w\Vert \le \mu t(1-t)\rho (x_1-x_2), \end{aligned}$$

establishing that F is $\rho$-paraconvex with respect to any real $\mu >\kappa .$

$(ii)\Rightarrow (iii).$ For $(x_1,y_1), (x_2,y_2)\in {{\,\mathrm{Dom}\,}}\varphi _F,$ for $t\in [0,1],$ picking sequences $(u^1_k)$ and $(u_k^2)$ converging, respectively, to $x_1$ and to $x_2$, such that $d_F(u_k^1,y_1)\rightarrow \varphi _F(x_1,y_1)$ and $d_F(u_k^2,y_2)\rightarrow \varphi _F(x_2,y_2),$ one has

$$\begin{aligned} d_F(t(u^1_k,y_1)+(1-t)(u^2_k,y_2))\le td_F(u^1_k,y_1)+(1-t)d_F(u^2_k,y_2)+\kappa t(1-t)\rho (x_1-x_2). \end{aligned}$$

By letting $k\rightarrow \infty ,$ as

$$\begin{aligned} \varphi _F(t(x_1,y_1)+(1-t)(x_2,y_2))\le \liminf _{k\rightarrow \infty }d_F(t(u^1_k,y_1)+(1-t)(u^2_k,y_2)), \end{aligned}$$

we derive

$$\begin{aligned} \varphi _F(t(x_1,y_1)+(1-t)(x_2,y_2))\le t\varphi _F(x_1,y_1)+(1-t)\varphi _F(x_2,y_2)+\kappa t(1-t)\rho (x_1-x_2), \end{aligned}$$

establishing the $\rho$-paraconvexity of $\varphi _F$.

Suppose now that Y is reflexive and that $\varphi _F$ is $\rho$-paraconvex with respect to some $\kappa >0$. In order to prove $(iii)\Rightarrow (ii),$ it suffices to show that $\varphi _F=d_F,$ i.e., $d_F$ is itself lower semicontinuous on $X\times Y.$ We may assume that $\varphi _F(x,y)<+\infty$, since when $\varphi _F(x,y)=+\infty ,$ then as $\varphi _F\le d_F,$ $d_F(x,y)=+\infty$. Pick sequences $(u_k),(v_k)$ with $u_k\in X,$ $\lim _{k\rightarrow \infty }u_k =x,$ and $v_k\in F(u_k)$ such that $\lim _{k\rightarrow \infty }\Vert y-v_k\Vert =\varphi _F(x,y).$ This yields that $(v_k)$ is a bounded sequence, and consequently, it has a weak convergent subsequence. Without loss of generality, assume that the whole sequence $(v_k)$ converges weakly to $v\in Y.$ By the Mazur Lemma (see [8]), we may find convex combinations

$$\begin{aligned} w_k=\sum _{i=k}^{N(k)}\theta _i^{(k)}v_i,\;\;\text {where}\;\; \theta _i^{(k)}\in [0,1]\;\;\text {and}\;\;\sum _{i=k}^{N(k)}\theta _i^{(k)}=1, \end{aligned}$$

such that $(w_k)$ converges strongly to v. As $\varphi _F$ is $\rho$-paraconvex with respect to $\kappa >0,$ thanks to Lemma 2.1, for $z_k=\sum _{i=k}^{N(k)}\theta _i^{(k)}u_i,$

$$\begin{aligned} \varphi _F(z_k,w_k)\le & {} \sum _{i=k}^{N(k)}\theta _i^{(k)}\varphi _F(u_i,v_i)+\kappa \sum _{i=k}^{N(k)}\theta _i^{(k)}(1-\theta _i^{(k)})\max _{k\le j\le N(k)}\rho (u_j-u_i)\\= & {} \kappa \sum _{i=k}^{N(k)}\theta _i^{(k)}(1-\theta _i^{(k)})\max _{k \le j\le N(k)}\rho (u_j-u_i)\\\le & {} \kappa \max _{k\le i, j\le N(k)}\rho (u_j-u_i). \end{aligned}$$

Reminding that $u_k\rightarrow x,$ and $\rho$ is continuous, the right hand of the preceding relation tends to 0 as $k\rightarrow \infty$ . It follows that

$$\begin{aligned} 0\le \varphi _F(x,v)\le \liminf _{k\rightarrow \infty }\varphi _F(z_k,w_k)=0, \end{aligned}$$

and consequently, $\varphi _F(x,v)=0$. Hence, $v\in F(x),$ since ${{\,\mathrm{gph}\,}}F$ is closed. Finally, since

$$\begin{aligned} d_F(x,y)\le \Vert y-v\Vert \le \lim _{k\rightarrow \infty }\Vert y-v_k\Vert =\varphi _F(x,y)\le d_F(x,y), \end{aligned}$$

one obtains $d_F(x,y)=\varphi _F(x,y).$ $\square$

Open problem 1

Does the equivalence between (i) and (iii) in Proposition 2.2holds when the reflexivity of the image space Y fails?

3 Regularity of Graphical Tangent Cones and Normal Cones of Paraconvex Multifunctions

As mentioned before, every $\rho$-paraconvex function defined on a Banach space X is approximately convex at all points for any modulus function $\rho$ verifying $(C1)-(C3).$ In view of [25, Theo. 3.6], for approximately convex functions, all the usual subdifferentials in the literature coincide. In this section, we shall establish the regularity of graphical tangent cones and normal cones to the graph of paraconvex multifunctions between Banach spaces. The first result concerns the regularity of the Clarke graphical tangent cone.

Proposition 3.1

Let $\rho :X\rightarrow {\mathbb {R}}_+$ be a modulus function satisfying $(C1)-(C3).$ Let $F:X\rightrightarrows Y$ be a $\rho$-paraconvex multifunction. Then Bouligand’s and Clarke’s tangent cones to the graph of F coincide at all $(x,y)\in {{\,\mathrm{gph}\,}}F:$ $T^-_{{{\,\mathrm{gph}\,}}F}(x,y)=T^\uparrow _{{{\,\mathrm{gph}\,}}F}(x,y).$ As a result,

$$\begin{aligned} N^-_{{{\,\mathrm{gph}\,}}F}(x,y)=N^\uparrow _{{{\,\mathrm{gph}\,}}F}(x,y), \,\text { for all} \,(x,y)\in {{\,\mathrm{gph}\,}}F. \end{aligned}$$

Proof

Given $(x,y)\in {{\,\mathrm{gph}\,}}F,$ it always holds $T^\uparrow _{{{\,\mathrm{gph}\,}}F}(x,y)\subseteq T^-_{{{\,\mathrm{gph}\,}}F}(x,y).$ Hence, it suffices to show that $T^-_{{{\,\mathrm{gph}\,}}F}(x,y)\subseteq T^\uparrow _{{{\,\mathrm{gph}\,}}F}(x,y).$ Let $(u,v)\in T^-_{{{\,\mathrm{gph}\,}}F}(x,y)$ be given. Then, there exist sequences $(t_n)\downarrow 0^+, (u_n,v_n)\rightarrow (u,v)$ such that $(x+t_nu_n,y+t_nv_n)\in {{\,\mathrm{gph}\,}}F.$ Pick sequences $((x_n,y_n))\rightarrow _{{{\,\mathrm{gph}\,}}F}(x,y),$ and $(s_n)\downarrow 0^+,$ as well as a sequence of positive reals $(\varepsilon _n)\downarrow 0,$ such that

$$\begin{aligned} \max _{n\in \mathbb {N}}\left\{ s_n,\Vert x_n-x\Vert ,\Vert y_n-y\Vert \right\} \le \varepsilon _1t_1. \end{aligned}$$

For each $n\in \mathbb {N},$ define

$$\begin{aligned} k(n):=\max \left\{ k\in \mathbb {N}:\; \max \{s_i,\Vert x_i-x\Vert ,\Vert y_i-y\Vert :\;i\ge n\}\le \varepsilon _kt_k\right\} . \end{aligned}$$

Then obviously (k(n)) is a non-decreasing sequence. Suppose to contrary that k(n) is bounded above by some $N_0$. Then,

$$\begin{aligned} \max \{s_i,\Vert x_i-x\Vert ,\Vert y_i-y\Vert :\;i\ge n\}> \varepsilon _{N_0+1}t_{N_0+1},\;\;\text {for all}\;\; n\in \mathbb {N}. \end{aligned}$$

This contradicts the convergence of the sequences $(s_n),(\Vert x_n-x\Vert ),$ and $(\Vert y_n-y\Vert )$ to 0. Hence, $\lim \limits _{n\rightarrow \infty }k(n)=+\infty .$ As a result,

$$\begin{aligned} \displaystyle \frac{s_n}{t_{k(n)}}\rightarrow 0,\;\; \displaystyle \displaystyle \frac{x_n-x}{t_{k(n)}}\rightarrow 0,\;\;\text {and}\;\;\displaystyle \displaystyle \frac{y_n-y}{t_{k(n)}}\rightarrow 0. \end{aligned}$$

We may assume that $\displaystyle \displaystyle \frac{s_n}{t_{k(n)}}\in (0,1)$ for all n large. By using the following relations

$$\begin{aligned}&x_n+s_n\left( u_{k(n)}+\displaystyle \frac{x-x_n}{t_{k(n)}}\right) =\left( 1- \displaystyle \frac{s_n}{t_{k(n)}}\right) x_n+\displaystyle \frac{s_n}{t_{k(n)}}(x+t_{k(n)}u_{k(n)});\\&y_n+s_n\left( v_{k(n)}+\displaystyle \frac{y-y_n}{t_{k(n)}}\right) =\left( 1-\displaystyle \frac{s_n}{t_{k(n)}}\right) y_n+\displaystyle \frac{s_n}{t_{k(n)}}(y+t_{k(n)}v_{k(n)}), \end{aligned}$$

and the $\rho$-paraconvexity of F (with respect to $\kappa >0$), we may select

$$\begin{aligned} w_n\in F\left( x_n+s_n\left( u_{k(n)}+\displaystyle \frac{x-x_n}{t_{k(n)}}\right) \right) \end{aligned}$$

such that

$$\begin{aligned} \left\| y_n+s_n\left( v_{k(n)}+\displaystyle \frac{y-y_n}{t_{k(n)}}\right) -w_n\right\| \le \kappa \displaystyle \frac{s_n}{t_{k(n)}}\left( 1-\displaystyle \frac{s_n}{t_{k(n)}}\right) \rho (x_n-x-t_{k(n)}u_{k(n)}). \end{aligned}$$

Thus, by setting

$$\begin{aligned} a_n:=w_n-\left[ y_n+s_n\left( v_{k(n)}+\displaystyle \frac{y-y_n}{t_{k(n)}}\right) \right] , \end{aligned}$$

one obtains $a_n/s_n\rightarrow 0$ as $n\rightarrow \infty ,$ due to $\Vert x_n-x\Vert /t_{k(n)}\rightarrow 0,$ and by (C3), 

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{t_{k(n)}}\rho (x_n-x-t_{k(n)}u_{k(n)})=\lim _{n\rightarrow \infty }\frac{\Vert x_n-x-t_{k(n)}u_{k(n)}\Vert }{t_{k(n)}}\frac{\rho (x_n-x-t_{k(n)}u_{k(n)})}{\Vert x_n-x-t_{k(n)}u_{k(n)}\Vert }=0. \end{aligned}$$

Next, as

$$\begin{aligned} w_n=y_n+s_n\left( v_{k(n)}+\displaystyle \frac{y-y_n}{t_{k(n)}}+\displaystyle \frac{a_n}{s_n}\right) , \end{aligned}$$

one derives that

$$\begin{aligned}&\left( (x_n+s_n\left( u_{k(n)}+\displaystyle \frac{x-x_n}{t_{k(n)}}\right) ,y_n+s_n\left( v_{k(n)}+\displaystyle \frac{y-y_n}{t_{k(n)}}+\displaystyle \frac{a_n}{s_n}\right) \right) \in {{\,\mathrm{gph}\,}}F;\\&\left( u_{k(n)}+\displaystyle \frac{x-x_n}{t_{k(n)}},v_{k(n)}+\displaystyle \frac{y-y_n}{t_{k(n)}}+\displaystyle \frac{a_n}{s_n}\right) \rightarrow (u,v), \end{aligned}$$

which yields $(u,v)\in T^\uparrow _{{{\,\mathrm{gph}\,}}F}(x,y).$ The proof is completed. $\square$

Remark 3.1

By Proposition 8.10.3 of [44], we can establish that the graph of a $\rho$-paraconvex multifunction F is subsmooth in each of its points. Taking into account this fact, one referee pointed out that Proposition 3.1 is a consequence of this subsmoothness. Nevertheless, let us note that the subsmoothness of the graph of a $\rho$-paraconvex multifunction is implied from the next theorem which shows the coincidence of the Clarke, the Bouligand and the Fréchet normal cones to the graph of a $\rho$-paraconvex multifunction.

Theorem 3.1

Let X and Y be Banach spaces, $F: X \rightrightarrows Y$ a $\rho$-paraconvex multifunction with respect to $\kappa >0,$ and $\rho :X\rightarrow {\mathbb {R}}_+$ satisfying $(C1)-(C3).$ Then,

setting

$$\begin{aligned} N^{(\rho ,\kappa )}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}):=\;\left\{ \begin{array}{ll}&{}(x^*,y^*)\in X^*\times Y^*:\\ &{}\langle x^*,x-{\bar{x}}\rangle +\langle y^*,y-{\bar{y}}\rangle \le \kappa \Vert y^*\Vert \rho (x-{\bar{x}}),\;\forall (x,y)\in {{\,\mathrm{gph}\,}}F \end{array}\right\} , \end{aligned}$$

(9)

it holds

for all $({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}F$.

Proof

Obviously, $N^{(\rho ,\kappa )}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},\bar{y})\subseteq {\hat{N}}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}).$ Conversely, take $(x^*,y^*)\in {\hat{N}}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})$. By definition, for each $\varepsilon >0,$ there is $\delta >0,$ such that

$$\begin{aligned} \langle x^*,x-{\bar{x}}\rangle +\langle y^*,y-{\bar{y}}\rangle \le \varepsilon \Vert (x,y)-({\bar{x}},{\bar{y}})\Vert , \end{aligned}$$

for all $(x,y)\in {{\,\mathrm{gph}\,}}F\cap \mathbb {B}(({\bar{x}},{\bar{y}}),\delta ).$ Let $(x,y)\in {{\,\mathrm{gph}\,}}F$ be given. For $t\in (0,1),$ the $\rho$-paraconvexity of F gives the existence of some $w\in F({\bar{x}}+t(x-{\bar{x}}))$ such that

$$\begin{aligned} \Vert {\bar{y}}+t(y-{\bar{y}})-w\Vert \le \kappa t(1-t)\rho (x-{\bar{x}}). \end{aligned}$$

This implies that for $t>0$ sufficiently small,

$$\begin{aligned} ({\bar{x}}+t(x-\bar{x}),w)\in {{\,\mathrm{gph}\,}}F\cap \mathbb {B}(({\bar{x}},{\bar{y}}),\delta ), \end{aligned}$$

and therefore

$$\begin{aligned} \begin{array}{ll} &{}t(\langle x^*,x-{\bar{x}}\rangle +\langle y^*,y-{\bar{y}}\rangle )\\ &{}\quad =\langle x^*,{\bar{x}}+t(x-{\bar{x}})-{\bar{x}}\rangle +\langle y^*,{\bar{y}}+t(y-{\bar{y}})-{\bar{y}}\rangle \\ &{}\quad =\langle x^*,{\bar{x}}+t(x-{\bar{x}})-{\bar{x}}\rangle +\langle y^*,w-{\bar{y}}\rangle +\langle y^*,{\bar{y}}+t(y-{\bar{y}})-w\rangle \\ &{}\quad \le \varepsilon \Vert ({\bar{x}}+t(x-{\bar{x}}),w)-({\bar{x}},{\bar{y}})\Vert +\Vert y^*\Vert \kappa t(1-t)\rho (x-{\bar{x}})\\ &{}\quad \le t\varepsilon (\Vert x-{\bar{x}}\Vert +\Vert y-\bar{y}\Vert +\kappa (1-t)\rho (x-{\bar{x}}))+\Vert y^*\Vert \kappa t(1-t)\rho (x-{\bar{x}}). \end{array}, \end{aligned}$$

Consequently,

$$\begin{aligned} \begin{array}{ll}&{}\langle x^*,x-{\bar{x}}\rangle +\langle y^*,y-{\bar{y}}\rangle \\ &{}\quad \le \varepsilon (\Vert x-{\bar{x}}\Vert +\Vert y-{\bar{y}}\Vert +\kappa (1-t)\rho (x-\bar{x}))+\Vert y^*\Vert \kappa \rho (x-{\bar{x}}). \end{array} \end{aligned}$$

By letting $\varepsilon \downarrow 0,$ one obtains for all $(x,y)\in {{\,\mathrm{gph}\,}}F,$

$$\begin{aligned} \langle x^*,x-{\bar{x}}\rangle +\langle y^*,y-{\bar{y}}\rangle \le \kappa \Vert y^*\Vert \rho (x-{\bar{x}}). \end{aligned}$$

Hence, $(x^*,y^*)\in N^{(\rho ,\kappa )}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}).$ Noticing that ${\hat{N}}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})\subseteq N^-_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})$, by virtue of the previous Proposition 3.1, it suffices to show that $N^{-}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})\subseteq N^{(\rho ,\kappa )}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})$ to complete the proof.

Let $(x,y)\in {{\,\mathrm{gph}\,}}F$ be given. By (C3),  we can pick a sequence of positive reals $(t_n)\downarrow 0$ such that $t_0=1,$ $t_n\in (0,1)$ for all $n\in \mathbb {N}_*,$ and

$$\begin{aligned} \displaystyle \frac{\rho (t_{n+1}(x-{\bar{x}}))}{t_{n+1}} \le \rho (t_n(x-{\bar{x}}))-\rho (t_{n+1}(x-{\bar{x}})),\;\;\text {for all}\;\; n\in \mathbb {N}. \end{aligned}$$

(11)

Set $x_0=x,$ $y_0=w_0,$ $z_{-1}=z_0=0,$ and

$$\begin{aligned} x_1={\bar{x}} +t_1(x-{\bar{x}}),\;\;y_1={\bar{y}} +t_1(y-{\bar{y}}). \end{aligned}$$

As F is $\rho$-paraconvex, choose $w_1\in F(x_1)$ such that $\Vert y_1-w_1\Vert \le \kappa t_1(1-t_1)\rho (x-x_0).$ Setting $z_1:=(w_1-y_1)/t_1,$ one has

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\Vert z_1-z_0\Vert \le \kappa \rho (x-{\bar{x}}),\\ &{}w_1={\bar{y}}+t_1(y-{\bar{y}}+z_1),\\ &{}y_1={\bar{y}}+\displaystyle \frac{t_1}{t_0}(w_1-{\bar{y}})=\bar{y}+t_1(y-{\bar{y}}+z_0). \end{array} \right. \end{aligned}$$

Starting from $x_0,y_0,w_0,z_0$ as above, we shall construct by induction sequences $(x_n),(y_n),(w_n),(z_n)$ with $x_n\in X,$ $y_n,w_n,z_n\in Y,$ such that for all $n\in \mathbb {N},$

$$\begin{aligned} \left\{ \begin{array}{ll} &{}x_n={\bar{x}}+t_n(x-{\bar{x}}),\\ &{}\Vert z_{n+1}-z_n\Vert \le \kappa \displaystyle \frac{\rho (t_n(x-{\bar{x}}))}{t_n},\\ &{}w_n={\bar{y}}+t_n(y-{\bar{y}}+z_n),\;\; (x_n,w_n)\in {{\,\mathrm{gph}\,}}F,\\ \ &{}y_n={\bar{y}}+t_n(y-{\bar{y}}+z_{n-1}). \end{array} \right. \end{aligned}$$

(12)

Indeed, suppose we have constructed $x_n,y_n,w_n,z_n$. Set firstly

$$\begin{aligned} x_{n+1}={\bar{x}}+t_{n+1}(x-{\bar{x}}),\;\; y_{n+1}= {\bar{y}}+t_{n+1}(y-{\bar{y}}+z_n). \end{aligned}$$

Then, one has

$$\begin{aligned} x_{n+1}={\bar{x}}+ \displaystyle \frac{t_{n+1}}{t_n}(x_n-{\bar{x}}),\;\;y_{n+1}={\bar{y}}+ \displaystyle \frac{t_{n+1}}{t_n}(w_n-{\bar{y}}). \end{aligned}$$

Thanks to the $\rho$-paraconvexity of F, we may select $w_{n+1}\in F(x_{n+1})$ such that

$$\begin{aligned} \Vert y_{n+1}-w_{n+1}\Vert \le \kappa \displaystyle \frac{t_{n+1}}{t_n}\left( 1-\displaystyle \frac{t_{n+1}}{t_n}\right) \rho (t_n(x-{\bar{x}})). \end{aligned}$$

So, by setting

$$\begin{aligned} z_{n+1}=\displaystyle \frac{w_{n+1}-{\bar{y}}-t_{n+1}(y-{\bar{y}})}{t_{n+1}}, \end{aligned}$$

we have

$$\begin{aligned} w_{n+1}={\bar{y}}+t_{n+1}(y-{\bar{y}}+z_{n+1}),\;\; z_{n+1}-z_n=(w_{n+1}-y_{n+1})/t_{n+1}. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert z_{n+1}-z_n\Vert =\displaystyle \frac{\Vert w_{n+1}-y_{n+1}\Vert }{t_{n+1}}\le \kappa \displaystyle \frac{\rho (t_n(x-{\bar{x}}))}{t_n}. \end{aligned}$$

Thus, $x_{n+1},y_{n+1},w_{n+1},z_{n+1}$ are well defined and satisfy (12). By (11), for all $n,m\in \mathbb {N},$ with $n<m,$ one has

$$\begin{aligned} \Vert z_n-z_m\Vert \le \sum _{j=n}^{m-1}\Vert z_{j+1}-z_j\Vert \le \rho (t_n(x-{\bar{x}}))- \rho (t_m(x-{\bar{x}})). \end{aligned}$$

From the last inequality, we deduce that $(z_n)$ is a Cauchy sequence which converges to some $z\in Y.$ Then, one has

$$\begin{aligned} \Vert z\Vert \le \sum _{j=0}^{\infty }\Vert z_{j+1}-z_j\Vert \le \sum _{j=0}^\infty \displaystyle \frac{\rho (t_j(x-{\bar{x}}))}{t_j}\le \kappa \rho (x-{\bar{x}}). \end{aligned}$$

By construction, one has $(x-{\bar{x}},y-{\bar{y}}+z)\in T^-_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}).$ Hence, for all $(x^*,y^*)\in N^-_{{{\,\mathrm{gph}\,}}F}(\bar{x},{\bar{y}}),$

$$\begin{aligned} \langle x^*,x-{\bar{x}}\rangle +\langle y^*,y-{\bar{y}}+z\rangle \le 0, \end{aligned}$$

which yields

$$\begin{aligned} \langle x^*,x-{\bar{x}}\rangle +\langle y^*,y-{\bar{y}}\rangle \le \Vert y^*\Vert \kappa \rho (x-{\bar{x}}),\;\;\forall (x,y)\in {{\,\mathrm{gph}\,}}F, \end{aligned}$$

and $(x^*,y^*)\in N^{(\rho ,\kappa )}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}).$ The proof is completed. $\square$

Remark 3.2

One referee pointed out that this theorem can be recovered via the $\rho -$convexity of the function $\varphi _F$ as in Proposition 2.2, by using the descriptions of $N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})$ and ${\hat{N}}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},\bar{y})$ in Theorems Theorems 4.1(i) and 4.2(i).

4 Subdifferentials of the Lower Semicontinuous Envelope of the Distance Function Associated to a Multifunction

Our aim in this section is to establish some calculus rules for Fréchet and Clarke subdifferentials of the lower semicontinuous envelope of the distance function associated to a multifunction in terms of the respective normal cones to their graphs. Consider now a multifunction $F:X\rightrightarrows Y$ between Banach spaces X, Y,  and the lower semicontinuous envelope of the associated distance function:

$$\begin{aligned} \varphi (x,y):=\varphi _F(x,y)= \liminf _{u\rightarrow x}d(y,F(u)),\;\;(x,y)\in X\times Y. \end{aligned}$$

The following observation is immediate from the definition.

Observation 1

Given a multifunction $F:X\rightrightarrows Y,$ let us note by ${\overline{F}}$ the graphical closure of F,  i.e., ${{\,\mathrm{gph}\,}}{\overline{F}}=\text {cl}({{\,\mathrm{gph}\,}}F).$ For $({\bar{x}},{\bar{y}})\in X\times Y,$ one has

• (i) $\varphi ({\bar{x}},{\bar{y}})=0 \iff ({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}{\overline{F}}.$ In particular, when F is closed, then

  $$\begin{aligned} \varphi ({\bar{x}},\bar{y})=0\iff ({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}F; \end{aligned}$$

• (ii) $\varphi _{{\overline{F}}}(x,y)=\varphi _F(x,y),$ for all $(x,y)\in X\times Y;$

• (iii) For $({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}F,$ $\hat{\partial }\varphi ({\bar{x}},{\bar{y}})=\hat{\partial }d_F({\bar{x}},\bar{y}).$

The first theorem concerns the Fréchet subdifferential. Note that the part (i) of Theorem 4.1 could be derived. directly from [43, Prop. 4.1] and Observation 1-(iii). For the reader’s convenience, we give a direct proof.

Theorem 4.1

Let $F:X\rightrightarrows Y$ be a multifunction between Banach spaces X, Y. For $({\bar{x}},{\bar{y}})\in {{\,\mathrm{Dom}\,}}\varphi ,$ one has

• (i) If $({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}F$ then

  

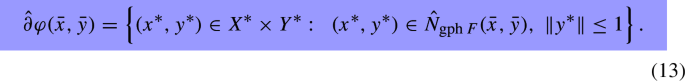
• (ii) Suppose that X and Y are Asplund spaces and F is closed. If $({\bar{x}},{\bar{y}})\notin {{\,\mathrm{gph}\,}}F$ then

  

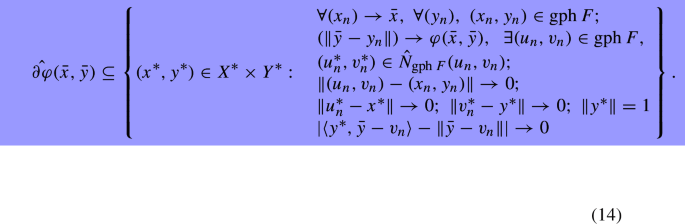
  Moreover, if F is $\rho$-paraconvex for some modulus function $\rho :X\rightarrow {\mathbb {R}}_+$ satisfying $(C1)-(C3),$ then we have equality.

Proof

(i). Assume $({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}F,$ then $\varphi ({\bar{x}},{\bar{y}})=0$. For $(x^*,y^*)\in {\hat{\partial \varphi }}({\bar{x}},{\bar{y}}),$ for any $\varepsilon >0,$ there is $\delta >0$ such that

$$\begin{aligned} \langle (x^*,y^*),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \varphi (x,y)+\varepsilon \Vert (x,y)-({\bar{x}},{\bar{y}})\Vert , \end{aligned}$$

for all $(x,y)\in ({\bar{x}},{\bar{y}})+\delta \mathbb {B}_{X\times Y}.$ Thus

$$\begin{aligned} \langle (x^*,y^ *),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \varepsilon \Vert (x,y)-({\bar{x}},{\bar{y}})\Vert , \end{aligned}$$

for all $(x,y)\in (({\bar{x}},{\bar{y}})+\delta \mathbb {B}_{X\times Y})\cap {{\,\mathrm{gph}\,}}F$. This shows that $(x^*,y ^*)\in {\hat{N}}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}).$ Moreover, since $\langle y^*,y-{\bar{y}}\rangle \le d(y,F(\bar{x}))+\varepsilon \Vert y-{\bar{y}}\Vert \le (1+\varepsilon )\Vert y-{\bar{y}}\Vert$ for all $y\in {\bar{y}}+\delta \mathbb {B}_Y,$ this implies that $\Vert y^*\Vert \le 1.$ Conversely, for $(x^*,y ^*)\in {\hat{N}}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}),$ with $\Vert y^*\Vert \le 1,$ then for any $\varepsilon \in (0,1),$ there is $\delta \in (0,\varepsilon )$ such that

$$\begin{aligned} \langle (x^*,y^ *),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \varepsilon \Vert (x,y)-({\bar{x}},{\bar{y}})\Vert , \end{aligned}$$

(15)

for all $(x,y)\in (({\bar{x}},{\bar{y}})+\delta \mathbb {B}_{X\times Y})\cap {{\,\mathrm{gph}\,}}F.$ Pick $\eta >0$ such that

$$\begin{aligned} \eta \in (0,\delta /4)\quad \text {and}\quad (\Vert x^*\Vert +\Vert y^*\Vert )\eta <\delta /2. \end{aligned}$$

(16)

Let $(x,y)\in B(({\bar{x}},{\bar{y}}),\eta )$ with $(x,y)\not =(\bar{x},{\bar{y}})$ be given arbitrarily. If $\varphi (x,y)\ge \delta /2$ then

$$\begin{aligned} \langle (x^*,y^*),(x,y)-({\bar{x}},{\bar{y}})\rangle \le (\Vert x^*\Vert +\Vert y^*\Vert )\eta <\delta /2\le \varphi (x,y), \end{aligned}$$

(17)

otherwise, pick sequences $(\delta _n)\downarrow 0,$ $\delta _n\in (0,\eta );$ $(u_n)\in \mathbb {B}(x,\delta _n)$ and $(v_n)$ with $(u_n,v_n)\in {{\,\mathrm{gph}\,}}F$ such that

$$\begin{aligned} \Vert y-v_n\Vert \le \varphi (x,y)+\delta _n\Vert (x,y)-({\bar{x}},{\bar{y}})\Vert . \end{aligned}$$

(18)

If $\varphi (x,y)>(\Vert x^*\Vert +\Vert y^*\Vert )\Vert (x,y)-({\bar{x}},{\bar{y}})\Vert ,$ then

$$\begin{aligned} \langle (x^*,y^*),(x,y)-({\bar{x}},\bar{y})\rangle \le \Vert (x^*,y^*)\Vert \Vert (x,y)-({\bar{x}},{\bar{y}})\Vert <\varphi (x,y), \end{aligned}$$

(19)

otherwise, as $\varphi (x,y)<\delta /2,$

$$\begin{aligned} \begin{array}{ll}\Vert v_n-{\bar{y}}\Vert<\Vert y-v_n\Vert +\Vert y-{\bar{y}}\Vert &{}\le \varphi (x,y)+\delta _n\Vert (x,y)-({\bar{x}},{\bar{y}})\Vert +\Vert y-{\bar{y}}\Vert \\ &{}<\delta /2+(\delta _n+1)\eta <\delta .\end{array} \end{aligned}$$

So, $(u_n,v_n)\in \mathbb {B}(({\bar{x}},{\bar{y}}),\delta ),$ and therefore by (15),

$$\begin{aligned} \langle (x^*,y^ *),(u_n,v_n)-({\bar{x}},{\bar{y}})\rangle \le \varepsilon \Vert (u_n,v_n)-({\bar{x}},{\bar{y}})\Vert . \end{aligned}$$

Hence, one obtains the following estimates, by $\Vert y^*\Vert \le 1;$ $u_n\in \mathbb {B}(x,\delta _n);$ relation (18), and $\varphi (x,y)\le (\Vert x^*\Vert +\Vert y^*\Vert )\Vert (x,y)-({\bar{x}},{\bar{y}})\Vert ,$

$$\begin{aligned}&\langle (x^*,y^ *),(x,y)-({\bar{x}},{\bar{y}})\rangle \\&\quad =\langle (x^*,y^ *),(u_n,v_n)-({\bar{x}},{\bar{y}})\rangle +\langle x^*,x-u_n\rangle +\langle y^*,y-v_n\rangle \\&\quad \le \varepsilon \Vert (u_n,v_n)-({\bar{x}},{\bar{y}})\Vert +\Vert x^*\Vert \delta _n+\Vert y-v_n\Vert \\&\quad \le (\varepsilon +\Vert x^ *\Vert )\delta _n+\Vert y-v_n\Vert +\varepsilon (\Vert (x,y)-({\bar{x}},{\bar{y}})\Vert +\Vert y-v_n\Vert )\\&\quad \le (\varepsilon +\Vert x^ *\Vert )\delta _n+\varphi (x,y)+ \delta _n\Vert (x,y)-({\bar{x}},{\bar{y}})\Vert \\&\qquad + \varepsilon (1+\Vert x^*\Vert +\Vert y^*\Vert +\delta _n)\Vert (x,y)-(\bar{x},{\bar{y}})\Vert . \end{aligned}$$

By letting $n\rightarrow \infty ,$ one obtains

$$\begin{aligned} \langle (x^*,y^ *),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \varphi (x,y)+ \varepsilon (1+\Vert x^*\Vert +\Vert y^*\Vert )\Vert (x,y)-({\bar{x}},{\bar{y}})\Vert . \end{aligned}$$

This relation, together with (17) and (19), and the fact that $\varepsilon >0$ is arbitrary, yield $(x^ *,y^*)\in \hat{\partial } \varphi ({\bar{x}},{\bar{y}}),$ which completes the proof of (i).

(ii). Let $({\bar{x}},{\bar{y}})\notin {{\,\mathrm{gph}\,}}F,$ and $(x^*,y^*)\in \hat{\partial }\varphi ({\bar{x}},{\bar{y}})$ be given. Let sequences $(x_n)\rightarrow \bar{x}$, $(y_n),$ such that $(x_n,y_n)\in {{\,\mathrm{gph}\,}}F$ for all $n\in \mathbb {N}$ and $\Vert {\bar{y}}-y_n\Vert \rightarrow \varphi ({\bar{x}},{\bar{y}}).$ Picking a sequence $(\varepsilon _n)\downarrow 0,$ with $\varepsilon _n\in (0,1)$ for all n,  then there is a sequence $(\delta _n)\downarrow 0$, $\delta _n\in (0,1),$ such that

$$\begin{aligned} \langle (x^*,y ^*),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \varphi (x,y)-\varphi ({\bar{x}},{\bar{y}})+\varepsilon _n\Vert (x,y)-(\bar{x},{\bar{y}})\Vert , \end{aligned}$$

(20)

for all $(x,y)\in ({\bar{x}},{\bar{y}})+\delta _n\mathbb {B}_{X\times Y}.$ For each $n\in \mathbb {N},$ set

$$\begin{aligned} k(n):= \max \left\{ k \in \mathbb {N} : \max _{i\ge n} \big \{\Vert x_i-{\bar{x}}\Vert , \Vert {\bar{y}}-y_i\Vert -\varphi ({\bar{x}},{\bar{y}}) \big \}\le \delta _k^2/8 \right\} . \end{aligned}$$

Proceeding similarly to the proof of Proposition 3.1 (k(n)) is a non-decreasing and unbounded sequence. Using (20), one derives that for all $(x,y)\in ({\bar{x}},{\bar{y}})+\delta _{k(n)}\mathbb {B}_{X\times Y}$ and every integer,

$$\begin{aligned} \langle (x^*,y ^*),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \Vert y-v\Vert +\delta _{{{\,\mathrm{gph}\,}}F}(x,v)-\Vert \bar{y}-y_n\Vert +\delta _{k(n)}^2/8+\varepsilon _{k(n)}\delta _{k(n)}. \end{aligned}$$

(21)

Define the function $g:X\times Y\times Y\rightarrow {\mathbb {R}}\cup \{+\infty \}$ by

$$\begin{aligned} g(x,y,v)=\Vert y-v\Vert +\delta _{{{\,\mathrm{gph}\,}}F}(x,v)-\langle (x^*,y^*),(x,y)\rangle ,\;\; (x,y,v)\in X\times Y\times Y. \end{aligned}$$

Relation (21) implies

$$\begin{aligned} g(x_n,{\bar{y}},y_n)\le \inf \{g(x,y,v):\;\;(x,y)\in ({\bar{x}},{\bar{y}})+\delta _{k(n)}\mathbb {B}_{X\times Y},\; (x,v)\in {{\,\mathrm{gph}\,}}F\}+\alpha _n, \end{aligned}$$

where, $\alpha _n=(1+\Vert x^*\Vert )\delta _{k(n)}^2/8+\varepsilon _{k(n)}\delta _{k(n)}.$ Setting $\beta _n:= \;(1+\Vert x^*\Vert )\delta _{k(n)}/2+4\varepsilon _{k(n)}$ and applying the Ekeland Variational Principle [12], take $(a_n, \bar{b}_n,b_n)\in (x_n,{\bar{y}},y_n)+ (\delta _{k(n)}/4)\mathbb {B}_{X\times Y\times Y}$ with $(a_n,b_n)\in {{\,\mathrm{gph}\,}}F,$ such that

$$\begin{aligned} g(a_n,{\bar{b}}_n,b_n)\le g(x,y,v)+\beta _n\Vert (x,y,v)-(a_n,\bar{b}_n,b_n))\Vert , \end{aligned}$$

for all $(x,y)\in ({\bar{x}},\bar{y})+\delta _{k(n)}\mathbb {B}_{X\times Y},$ with $(x,v)\in {{\,\mathrm{gph}\,}}F$. Consequently,

$$\begin{aligned} (0,0,0)\in \hat{\partial }[g+\beta _n\Vert \cdot -(a_n,{\bar{b}}_n,b_n))\Vert ](a_n,{\bar{b}}_n,b_n). \end{aligned}$$

In view of the fuzzy sum rule ( [13]), there exist

$$\begin{aligned}&(u_n,v_n)\in {{\,\mathrm{gph}\,}}F\cap ((a_n,b_n)+(\delta _{k(n)}/4)\mathbb {B}_{X\times Y});\;\; (u_n^*,v_n^*)\in {\hat{N}}_{{{\,\mathrm{gph}\,}}F}(u_n,v_n);\\&(z_n,w_n)\in ({\bar{b}}_n,b_n)+(\delta _{k(n)}/4)\mathbb {B}_{X\times Y};\;\; (z_n^*,w_n^*)\in \hat{\partial } \Vert \cdot -\cdot \Vert (z_n,w_n) \end{aligned}$$

such that

$$\begin{aligned} \Vert (x^*,y^*,0)-(0,z^*_n,w^*_n)-(u^*_n,0,v^*_n)\Vert \le 2\beta _n. \end{aligned}$$

(22)

As,

$$\begin{aligned} \Vert (u_n,v_n)-(a_n,b_n)\Vert \le \delta _{k(n)}/4 \quad \text { and }\quad \Vert (a_n,b_n)-(x_n,y_n)\Vert \le \delta _{k(n)}/4, \end{aligned}$$

one has $\Vert (u_n,v_n)-(x_n,y_n)\Vert \rightarrow 0,$ as $n\rightarrow \infty .$ On one hand, inequality (22), yields

$$\begin{aligned} \Vert u_n^*-x^*\Vert \rightarrow 0, \;\Vert z_n^*-y^*\Vert \rightarrow 0,\; \text {and } \; \Vert w_n^*+v_n^*\Vert \rightarrow 0. \end{aligned}$$

On the other hand, we know that $({\bar{x}},{\bar{y}})\notin {{\,\mathrm{gph}\,}}F$, $(x_n,y_n)\in {{\,\mathrm{gph}\,}}F$, $x_n\rightarrow {\bar{x}},$ $z_n\rightarrow {\bar{y}}.$ Suppose by contradiction that for large n, ($n\ge n_0$), $w_n\equiv z_n$. Then $w_n\rightarrow \bar{y}$ and also $y_n\rightarrow \bar{y}$. Thus, $(x_n,y_n)\in {{\,\mathrm{gph}\,}}F\rightarrow (\bar{x},\bar{y})$. Hence, $({\bar{x}},\bar{y})\in {{\,\mathrm{gph}\,}}F$, a contradiction. Therefore, for $n\ge n_0$, $w_n\ne z_n$. Thus, from the relation $(z_n^*,w_n^*)\in \hat{\partial } \Vert \cdot -\cdot \Vert (z_n,w_n)$, it follows that $\Vert z_n^*\Vert =1$, $w_n^*=-z_n^*,$ and $\langle z_n^*,z_n-w_n\rangle =\Vert z_n-w_n\Vert .$ Thus, as $w_n^*=-z_n^*$, $\Vert w_n^*+v_n^*\Vert \rightarrow 0$ and $z_n^*\rightarrow y^*$, it yields $\Vert v_n^*-y^*\Vert \rightarrow 0.$ Moreover, since $z_n\rightarrow {\bar{y}},$ $\Vert w_n-v_n\Vert \rightarrow 0,$ and $\Vert z_n^*-y^*\Vert \rightarrow 0,$ one obtains

$$\begin{aligned} |\langle y^*,{\bar{y}}-v_n\rangle -\Vert {\bar{y}}-v_n\Vert |\rightarrow 0 \;\text {and} \;\Vert y^*\Vert =1. \end{aligned}$$

Hence, (14) is shown.

Suppose now F is $\rho$-paraconvex with respect to some $\kappa >0,$ for some function $\rho$ verifying $(C1)-(C3).$ Let $(x^*,y^*)$ be in the set of the right side of (14). Since $(u_n^*,v_n^*)\in {\hat{N}}_{{{\,\mathrm{gph}\,}}F}(u_n,v_n),$ thanks to Theorem 3.1, one has

$$\begin{aligned} \langle (u_n^*,v_n^*), (u,v)-(u_n,v_n)\rangle \le \kappa \rho (u-u_n), \end{aligned}$$

(23)

for all $(u,v)\in {{\,\mathrm{gph}\,}}F.$ For $(x,y)\in {{\,\mathrm{Dom}\,}}\varphi ,$ there are sequence $(z_n)\rightarrow x,$ $(w_n)$ with $w_n\in F(z_n),$ such that $\Vert y-w_n\Vert \rightarrow \varphi (x,y).$ One has

$$\begin{aligned}&\langle (x^*,y^ *),(x,y)-({\bar{x}},{\bar{y}})\rangle \\&\quad =\langle x^*,x-z_n+u_n-{\bar{x}}\rangle +\langle (x^*,y^*), (z_n,w_n)-(u_n,v_n)\rangle \\&\qquad +\langle y^*,y-w_n\rangle -\langle y^*,{\bar{y}}-v_n\rangle \\&\quad \le \langle x^*,x-z_n+u_n-\bar{x}\rangle +\kappa \rho (z_n-u_n)+\Vert y-w_n\Vert -\langle y^*,\bar{y}-v_n\rangle . \end{aligned}$$

By letting $n\rightarrow \infty ,$ as $(u_n)\rightarrow {\bar{x}};$ $(z_n)\rightarrow x;$ $\Vert y-w_n\Vert \rightarrow \varphi (x,y),$ and $\langle y^*,\bar{y}-v_n\rangle \rightarrow \varphi ({\bar{x}},{\bar{y}}),$ one obtains

$$\begin{aligned} \langle (x^*,y^ *),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \varphi (x,y)-\varphi ({\bar{x}},{\bar{y}})+\kappa \rho (x-{\bar{x}}), \end{aligned}$$

showing $(x^*,y^*)\in {\hat{\partial \varphi }}({\bar{x}},{\bar{y}}).$ The proof ends. $\square$

The preceding theorem yields the following corollary.

Corollary 4.1

Suppose that X and Y are Asplund spaces and that F is a closed multifunction. Given $({\bar{x}},{\bar{y}})\notin {{\,\mathrm{gph}\,}}F,$ assume that the projection $P_{F({\bar{x}})}({\bar{y}})$ of ${\bar{y}}$ onto $F({\bar{x}})$ is nonempty, and that $\varphi ({\bar{x}},{\bar{y}})=d(\bar{y},F({\bar{x}})).$ Then for any ${\bar{v}}\in P_{F({\bar{x}})}({\bar{y}}),$ one has

[ Moreover, equality holds in (24) if F is $\rho$-paraconvex for some modulus function $\rho :X\rightarrow {\mathbb {R}}_+$ satisfying $(C1)-(C3).$

Proof

Inclusion (24) follows directly from (14) by picking $(x_n)=(u_n):=({\bar{x}}); (y_n)=(v_n):=({\bar{v}}).$ Next, take $(x^*,y^*)$ in the set of the right side of (24). One has

$$\begin{aligned} \langle (x^*,y^*), (u,v)-({\bar{x}},{\bar{v}})\rangle \le \kappa \rho (x-{\bar{x}}), \end{aligned}$$

(25)

for all $(u,v)\in {{\,\mathrm{gph}\,}}F.$ For $(x,y)\in {{\,\mathrm{Dom}\,}}\varphi ,$ pick $(z_n)\rightarrow x,$ $(w_n)$ with $w_n\in F(z_n),$ such that $\Vert y-w_n\Vert \rightarrow \varphi (x,y).$ One has

$$\begin{aligned} \begin{array}{ll} \langle (x^*,y^ *),(x,y)-({\bar{x}},{\bar{y}})\rangle &{}=\langle x^*,x-z_n\rangle +\langle (x^*,y^*), (z_n,w_n)-({\bar{x}},{\bar{v}})\rangle \\ &{}\quad +\langle y^*,y-w_n\rangle -\langle y^*,{\bar{y}}-{\bar{v}}\rangle \\ &{}\le \langle x^*,x-z_n\rangle +\kappa \rho (z_n-\bar{x})+\Vert y-w_n\Vert -\langle y^*,{\bar{y}}-{\bar{v}}\rangle . \end{array} \end{aligned}$$

By letting $n\rightarrow \infty ,$ as $(z_n)\rightarrow x$, $\Vert y-w_n\Vert \rightarrow \varphi (x,y),$ and $\langle y^*,{\bar{y}}-{\bar{v}}\rangle =d({\bar{y}},F(\bar{x}))=\varphi ({\bar{x}},{\bar{y}}),$ one obtains

$$\begin{aligned} \langle (x^*,y^ *),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \varphi (x,y)-\varphi ({\bar{x}},{\bar{y}})+\kappa \rho (x-{\bar{x}}), \end{aligned}$$

showing that $(x^*,y^*)\in {\hat{\partial \varphi }}({\bar{x}},{\bar{y}}).$ $\square$

Remark 4.1

It is important to observe that in the proof of part (ii) of Theorem 4.1, the Asplund property of the spaces under consideration is only needed for using the fuzzy sum rule for Fréchet subdifferentials. When F is $\rho$-paraconvex, according to Theorem 3.1, ${{\,\mathrm{gph}\,}}F$ is Clarke regular, that is $N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})={\hat{N}}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})$ for all $({\bar{x}}, {\bar{y}})\in {{\,\mathrm{gph}\,}}F$. Also, instead of using in the proof of the preceding theorem the fuzzy sum rule for Fréchet subdifferentials in Asplund spaces, we may use the sum rule for Clarke subdifferentials. Hence, we may establish that inclusion (14) in Theorem 4.1, as well as, (24) in Corollary 4.1, are valid for any graphically Clarke regular multifunction F between Banach spaces X and Y. Moreover, when F is $\rho$-paraconvex for $\rho$ verifying $(C1)-(C3),$ equality in (14) and (24) holds in any Banach space.

In general Banach spaces, for establishing an estimate of the Clarke subdifferential $\partial ^\uparrow \varphi ({\bar{x}},{\bar{y}})$ at points $({\bar{x}},{\bar{y}})\in {{\,\mathrm{Dom}\,}}\varphi ,$ outside of the graph of F,  we need the following (graphical) norm-to-weak closedness of F : 

Definition 4.1

A multifunction $F:X\rightrightarrows Y$ is said to be (graphically) norm-to-weak closed at ${\bar{x}}\in {{\,\mathrm{Dom}\,}}F,$ if for any sequences $(u_n)$ and $(v_n)$ with $(u_n,v_n)\in {{\,\mathrm{gph}\,}}F$ such that $(u_n)\rightarrow {\bar{x}} ,$ and $(v_n)$ converges weakly to some ${\bar{v}},$ one has $({\bar{x}},{\bar{v}})\in {{\,\mathrm{gph}\,}}F.$ We shall say that F is norm-to-weak closed if it is norm-to-weak closed at all point $x\in {{\,\mathrm{Dom}\,}}F.$

Obviously, in finite dimension, graphically norm-to-weak closed property coincides with the usual graphical closedness property. As shown in the following Lemma 4.1, when Y is reflexive, graphical norm-to-weak closedness and graphical strong closedness for paraconvex multifunctions agree.

Lemma 4.1

Let Y be a reflexive space, and let $F:X\rightrightarrows Y$ be a $\rho$-paraconvex multifunction for $\rho$ verifying $(C1)-(C2).$ If F is graphically (strongly) closed, then F is graphically norm-to-weak closed.

Proof

Let $x\in {{\,\mathrm{Dom}\,}}F.$ Take sequences $(u_n)\rightarrow x,$ $(v_n)$ with $(u_n,v_n)\in {{\,\mathrm{gph}\,}}F$ and $(v_n)$ converging weakly to $v\in Y.$ By the Mazur Lemma, we may find convex combinations

$$\begin{aligned} w_n=\sum _{k=n}^{N(n)}\theta _k^{(n)}v_k,\;\;\text {where}\;\; \theta _k^{(n)}\in [0,1]\;\;\text {and}\;\;\sum _{k=n}^{N(n)}\theta _k^{(n)}=1, \end{aligned}$$

such that $(w_n)$ converges strongly to v. As F is $\rho$-paraconvex, thanks to Lemma 2.1, for$z_k=\sum _{i=k}^{N(k)}\theta _i^{(k)}u_i,$ there is $y_n\in F(z_n)$ such that

$$\begin{aligned} \begin{array}{ll}\Vert y_n-w_n\Vert &{}\le \kappa \sum _{k=n}^{N(n)}\theta _k^{(n)}(1-\theta _k^{(n)})\max _{n\le j\le N(n)}\rho (u_j-u_k)\\ &{}\le \kappa \max _{n\le i, j\le N(n)}\rho (u_j-u_i). \end{array} \end{aligned}$$

Since $u_n\rightarrow x,$ $(w_n)\rightarrow v,$ $\rho$ is continuous and F is (strongly) closed, then $(y_n)\rightarrow v,$ and one obtains that $v\in F(x).$ $\square$

Lemma 4.2

Let Y be reflexive and $F:X\rightrightarrows Y$ be a norm-to-weak closed multifunction at ${\bar{x}}\in {{\,\mathrm{Dom}\,}}F$. Then, $P_{F({\bar{x}})}(y)\not =\emptyset$ and $\varphi ({\bar{x}},y)=d(y,F(\bar{x}))$ for all $y\in Y.$

Proof

For $y\in Y,$ pick sequences $(u_n)\rightarrow {\bar{x}}$ and $(v_n)$ with $(u_n,v_n)\in {{\,\mathrm{gph}\,}}F$ such that $\Vert y-v_n\Vert \rightarrow \varphi ({\bar{x}},y).$ Then, $(v_n)$ is bounded. So, since Y is reflexive, there is a subsequence $(v_{k(n)})$ converging weakly to some ${\bar{v}}\in F({\bar{x}})$ according to the norm-to weak closedness of F. Hence,

$$\begin{aligned} d(y,F({\bar{x}}))\ge \varphi ({\bar{x}},y)=\lim _n\Vert y-v_n\Vert \ge \Vert y-{\bar{v}}\Vert \ge d(y,F({\bar{x}})). \end{aligned}$$

So, $v\in P_{F({\bar{x}})}(y)$ and $\varphi ({\bar{x}},y)=d(y,F({\bar{x}})).$ $\square$

Recall that a Banach space Y is said to have the Kadec-Klee property if the sequential weak convergence on the unit sphere $\mathbb {S}_Y$ of Y coincides with the norm convergence. Equivalently, whenever a sequence $(x_n)$ in X satisfies $\Vert x_n\Vert \rightarrow \Vert {\bar{x}}\Vert$ and $x_n\ \rightarrow {\bar{x}}$ weakly, then $\lim \limits _{n\rightarrow +\infty } \Vert x_n-{\bar{x}}\Vert = 0.$ It is well known that $L^p$ -spaces ($1< p < +\infty$) have the Kadec-Klee property.

Theorem 4.2

Let $F:X\rightrightarrows Y$ be a closed multifunction between Banach spaces X and Y. Let $({\bar{x}},{\bar{y}})\in {{\,\mathrm{Dom}\,}}\varphi$ be given.

• (i) For $({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}F,$ one has

  

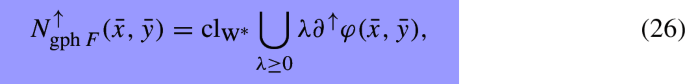
  where the symbol $\text {cl}_{\text {w}^*}$ denotes the $\text {weak} ^*$ closure.

• (ii) For ${\bar{x}}\in {{\,\mathrm{Dom}\,}}F,$ $({\bar{x}},{\bar{y}})\in (X\times Y)\setminus {{\,\mathrm{gph}\,}}F,$ assume that Y is a reflexive space with the norm on Y satisfying the Kadec-Klee property, and that F is (graphically) norm-to-weak closed at ${\bar{x}}.$ Then, one has

  

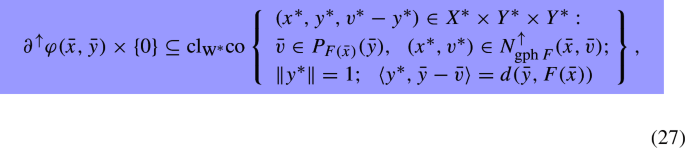
  where the notation $\text {cl}_{\text {w}^*}{\text {co}}$ denotes the $\text {weak}^*$ closed convex hull. As a result, if $P_{F({\bar{x}})}({\bar{y}})$ is singleton (which holds e.g., when the norm on Y is strictly convex and $F({\bar{x}})$ is convex), then

  

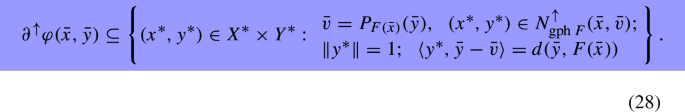
Proof

(i). Define the function $\psi :X\times Y\times Y \rightarrow {\mathbb {R}}\cup \{+\infty \}$ by

$$\begin{aligned} \psi (x,y,v)=\Vert y-v\Vert +\delta _{{{\,\mathrm{gph}\,}}F}(x,v),\;\; (x,y,v)\in X\times Y\times Y. \end{aligned}$$

Given $(u,d)\in X\times Y,$ take sequences $(\varepsilon _n)\downarrow 0,$ $( x_n,y_n)\xrightarrow [ \varphi ]{\text {}}({\bar{x}},{\bar{y}}),$ $(t_n)\downarrow 0$ such that

$$\begin{aligned} \varphi ^\uparrow (({\bar{x}},{\bar{y}}),(u,d))=\lim _{n\rightarrow \infty }\inf _{(u^\prime ,d^\prime )\in (u,d)+\varepsilon _n B_{X\times Y}}\displaystyle \frac{\varphi ((x_n,y_n)+t_n(u^\prime ,d^\prime ))-\varphi (x_n,y_n)}{t_n}. \end{aligned}$$

Pick $(z_n,v_n)\in {{\,\mathrm{gph}\,}}F$ such that $z_n-x_n=t_n\varepsilon _n a_n/2$ with

$$\begin{aligned} \Vert a_n\Vert \le 1 \quad \text {and } \quad \Vert y_n-v_n\Vert \le \varphi (x_n,y_n)+t_n^2. \end{aligned}$$

Note that $(v_n)\rightarrow {\bar{y}}$ since $(\varphi (x_n,y_n))\rightarrow 0$ and $(y_n)\rightarrow {\bar{y}}$, and for any $(u^\prime ,d^\prime ,w^\prime )\in (u,d,w)+(\varepsilon _n/2) \mathbb {B}_{X\times Y\times Y}$, we have

$$\begin{aligned}&\psi (((z_n,y_n,v_n)+t_n(u^\prime ,d^\prime ,w^\prime ))\\&\quad =\Vert (y_n+t_nd')-(v_n+t_nw') \Vert +\delta _{{{\,\mathrm{gph}\,}}F}(z_n+t_nu',v_n+t_nw')\\&\quad \ge \Vert (y_n+t_nd')-(v_n+t_nw')\Vert \;\; \text {with}\;\; v_n+t_nw'\in F(z_n+t_nu')\\&\quad \ge d((y_n+t_nd'),F(z_n+t_nu'))\ge \varphi (z_n+t_nu^\prime ,y_n+t_nd^\prime ). \end{aligned}$$

Combining this inequality with the fact that

$$\begin{aligned} \psi (x_n,y_n,v_n)=\Vert y_n-v_n\Vert \le \varphi (x_n,y_n)+t_n^2, \end{aligned}$$

one has

$$\begin{aligned}&\displaystyle \frac{\psi ((z_n,y_n,v_n)+t_n(u^\prime ,d^\prime ,w^\prime ))-\psi (z_n,y_n,v_n)}{t_n}\nonumber \\&\quad \ge \displaystyle \frac{\varphi (x_n+t_n(u^\prime +\varepsilon _na_n/2),y_n+t_nd^\prime )-\varphi (x_n,y_n)}{t_n}-t_n. \end{aligned}$$

(29)

As $u^\prime \in u+\varepsilon _n/2 B_X,$ $u^\prime +\varepsilon _na_n/2\in u+\varepsilon _n B_X,$ for all $(u,d,w)\in X\times Y\times Y$, (29) yields

$$\begin{aligned} \begin{array}{ll} &{}\psi ^\uparrow (({\bar{x}},{\bar{y}},{\bar{y}}),(u,d,w))\\ &{}\quad \ge \limsup _{n\rightarrow \infty }\inf _{(u^\prime ,d^\prime )\in (u,d)+(\varepsilon _n/2) B_{X\times Y}}\displaystyle \frac{\varphi (x_n+t_n(u^\prime +\varepsilon _na_n/2),y_n+t_nd^\prime )-\varphi (x_n,y_n)}{t_n}\\ &{}\quad \ge \varphi ^\uparrow (({\bar{x}},{\bar{y}}),(u,d)). \end{array} \end{aligned}$$

Hence, $\partial ^\uparrow \varphi ({\bar{x}},{\bar{y}})\times \{0\}\subseteq \partial ^\uparrow \psi ({\bar{x}},{\bar{y}},{\bar{y}}),$ and by the sum rule applied to the Clarke subdifferential of $\psi ,$ one obtains

$$\begin{aligned} \partial ^\uparrow \varphi ({\bar{x}},{\bar{y}})\subseteq \left\{ (x^*,y^*)\in N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}),\; \Vert y^*\Vert \le 1\right\} , \end{aligned}$$

and therefore,

$$\begin{aligned} \text {cl}_{\text {w}^*}\bigcup _{\lambda \ge 0}\lambda \partial ^\uparrow \varphi ({\bar{x}},{\bar{y}})\subseteq N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}). \end{aligned}$$

For the opposite inclusion, consider the distance function $d_{{{\,\mathrm{gph}\,}}F}$ to the graph of F on the product space $X\times Y,$ endowed with the norm

$$\begin{aligned} \Vert (x,y)\Vert =\Vert x\Vert +\Vert y\Vert ,\;\; (x,y)\in X\times Y. \end{aligned}$$

Due to ( [7, Prop. 2.4.2]),

$$\begin{aligned} N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})=\text {cl}_{\text {w}^*}\bigcup _{\lambda \ge 0}\lambda \partial ^\uparrow d_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}}). \end{aligned}$$

Hence, it suffices to show that $\partial ^\uparrow d_{{{\,\mathrm{gph}\,}}F}(\bar{x},{\bar{y}})\subseteq \partial ^\uparrow \varphi ({\bar{x}},{\bar{y}}),$ or equivalently,

$$\begin{aligned} d^\uparrow _{{{\,\mathrm{gph}\,}}F}(({\bar{x}},{\bar{y}}),(u,w))\le \varphi ^\uparrow (({\bar{x}},{\bar{y}}),(u,w)),\;\;\forall (u,w)\in X\times Y. \end{aligned}$$

Indeed, for $(u,w)\in X\times Y,$ pick $(\varepsilon _n)\downarrow 0,$ $(x_n,y_n)\rightarrow ({\bar{x}},{\bar{y}}),$ $(t_n)\downarrow 0$ such that

$$\begin{aligned} d_{{{\,\mathrm{gph}\,}}F}^\uparrow (({\bar{x}},{\bar{y}}),(u,w))\!=\!\lim _{n\rightarrow \infty }\inf _{(u^\prime ,w^\prime )\!\in \! (u,w)+\varepsilon _n B_{X\times Y}}\displaystyle \frac{d_{{{\,\mathrm{gph}\,}}F}((x_n,y_n)\!+\!t_n(u^\prime ,w^\prime ))\!-\!d_{{{\,\mathrm{gph}\,}}F}(x_n,y_n)}{t_n}. \end{aligned}$$

Pick $(u_n,v_n)\in {{\,\mathrm{gph}\,}}F,$ such that

$$\begin{aligned} d((x_n,y_n),(u_n,v_n))= \Vert x_n-u_n\Vert +\Vert y_n-v_n\Vert \le d_{{{\,\mathrm{gph}\,}}F}(x_n,y_n)+t_n^2. \end{aligned}$$

and note that since $(x_n,y_n)\rightarrow ({\bar{x}},{\bar{y}}),$ then $(u_n,v_n)\rightarrow ({\bar{x}},{\bar{y}}).$

For $(u^\prime ,w^\prime )\in (u,w)+\varepsilon _n B_{X\times Y},$ with $\varphi (u_n+t_nu^\prime ,y_n+t_nw^\prime )<+\infty ,$ select a sequence $(z_n,w_n)\in {{\,\mathrm{gph}\,}}F$ such that

$$\begin{aligned}&\Vert z_n-u_n-t_nu^\prime \Vert \le t_n^2;\\&\quad \Vert y_n+t_nw^\prime -w_n\Vert \le \varphi (u_n+t_nu^\prime ,y_n+t_nw^\prime )+t_n^2. \end{aligned}$$

One has

$$\begin{aligned} \begin{array}{ll} &{}\varphi (u_n+t_nu^\prime ,y_n+t_nw^\prime )-\varphi (u_n,y_n)\ge \Vert y_n+t_nw^\prime -w_n\Vert -t_n^2-\Vert y_n-v_n\Vert \\ &{}\ge d_{{{\,\mathrm{gph}\,}}F}(x_n+t_nu^\prime ,y_n+t_nw^\prime )-\Vert x_n+t_nu^\prime -z_n\Vert -\Vert y_n-v_n\Vert -t_n^2\\ &{}\ge d_{{{\,\mathrm{gph}\,}}F}(x_n+t_nu^\prime ,y_n+t_nw^\prime )-\Vert u_n+t_nu^\prime -z_n\Vert -\Vert x_n-u_n\Vert -\Vert y_n-v_n\Vert -t_n^2 \\ &{}\ge d_{{{\,\mathrm{gph}\,}}F}(x_n+t_nu^\prime ,y_n+t_nw^\prime )-d_{{{\,\mathrm{gph}\,}}F}(x_n,y_n)-3t_n^2. \end{array} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned}&\varphi ^\uparrow (({\bar{x}},{\bar{y}}),(u,w))\\&\quad \ge \limsup _{n\rightarrow \infty }\inf _{(u^\prime ,w^\prime )\in (u,w)+\varepsilon _n B_{X\times Y}}\displaystyle \frac{\varphi ((u_n,y_n)+t_n(u^\prime ,w^\prime ))-\varphi (u_n,y_n)}{t_n}\\&\quad \ge \lim _{n\rightarrow \infty }\inf _{(u^\prime ,w^\prime )\in (u,w)+\varepsilon _n B_{X\times Y}}\displaystyle \frac{d_{{{\,\mathrm{gph}\,}}F}((x_n,y_n)+t_n(u^\prime ,w^\prime ))-d_{{{\,\mathrm{gph}\,}}F}(x_n,y_n)}{t_n}\\&\quad =d^\uparrow _{{{\,\mathrm{gph}\,}}F}(({\bar{x}},{\bar{y}}),(u,w)), \end{aligned} \end{aligned}$$

for all $(u,w)\in X\times Y,$ which completes the proof of (i).

(ii). Consider the function $\psi$ as before. Given $(u,d)\in X\times Y,$ take sequences $(\varepsilon _n)\downarrow 0,$ $((x_n,y_n))\xrightarrow [\varphi ]{\text {}}({\bar{x}},{\bar{y}})$, $(t_n)\downarrow 0$ such that

$$\begin{aligned} \varphi ^\uparrow (({\bar{x}},\bar{y}),(u,d))=\lim _{n\rightarrow \infty }\inf _{(z,w)\in (u,d)+\varepsilon _n B_{X\times Y}}\displaystyle \frac{\varphi ((x_n,y_n)+t_n(z,w))-\varphi (x_n,y_n)}{t_n}. \end{aligned}$$

Pick $(z_n)$, $(v_n)$ such that

$$\begin{aligned}&(z_n,v_n)\in {{\,\mathrm{gph}\,}}F;\\&\quad z_n-x_n=t_n\varepsilon _n a_n/2 \;\text {with} \; \Vert a_n\Vert \le 1;\\&\quad \Vert y_n-v_n\Vert \le \varphi (x_n,y_n)+t_n^2. \end{aligned}$$

Observing that

$$\begin{aligned} \Vert v_n\Vert \le \Vert y_n-v_n\Vert +\Vert y_n\Vert \le \varphi (x_n,y_n)+t_n^2+\Vert y_n\Vert , \end{aligned}$$

and combining this estimate along with the convergence of $(\varphi (x_n,y_n))$ to $\varphi (\bar{x}, \bar{y})$ and $(y_n)$ to $\bar{y}$, one concludes that $(v_n)$ is bounded. Moreover, due to the reflexivity of Y and the graphical norm-to-weak closedness of F, relabeling if necessary, we may assume that the whole sequence $(v_n)$ converges weakly to some ${\bar{v}}\in F({\bar{x}}).$ Therefore, one has

$$\begin{aligned} \varphi ({\bar{x}},{\bar{y}})\le \Vert {\bar{y}}-{\bar{v}}\Vert \le \lim _{n\rightarrow \infty }\Vert y_n-v_n\Vert =\lim _{n\rightarrow \infty }\varphi (x_n,y_n)=\varphi ({\bar{x}},{\bar{y}}), \end{aligned}$$

and consequently, $\Vert {\bar{y}}-{\bar{v}}\Vert =\varphi ({\bar{x}},{\bar{y}})$. This yields ${\bar{v}}\in P_{F({\bar{x}})}({\bar{y}}).$ Moreover, as $(v_n)$ converges weakly to ${\bar{v}}$ and $\Vert y_n-v_n\Vert \rightarrow \Vert {\bar{y}}-{\bar{v}}\Vert ,$ due to the Kadec-Klee property, $(v_n)\rightarrow {\bar{v}},$ strongly. Now for any $w\in Y,$ one has

$$\begin{aligned} \begin{aligned}&\psi ^\uparrow (({\bar{x}},{\bar{y}},{\bar{v}}),(u,d,w))\\&\ge \limsup _{n\rightarrow \infty }\inf _{(u^\prime ,d^\prime ,w^\prime )\in (u,d,w)+(\varepsilon _n/2) B_{X\times Y\times Y}}\displaystyle \frac{\psi ((z_n,y_n,v_n)+t_n(u^\prime ,d^\prime ,w^\prime ))-\psi (z_n,y_n,v_n)}{t_n}. \end{aligned} \end{aligned}$$

For any $(u^\prime ,d^\prime ,w^\prime )\in (u,d,w)+(\varepsilon _n/2) B_{X\times Y\times Y},$ let us proceed as in the proof of the first part of (i). Since

$$\begin{aligned} \psi (((z_n,y_n,v_n)\!+\!t_n(u^\prime ,d^\prime ,w^\prime ))\!\ge \! \varphi (z_n\!+\!t_nu^\prime ,y_n\!+\!t_nd^\prime )\!=\!\varphi (x_n+t_n(u^\prime +\varepsilon _na_n/2),y_n+t_nd^\prime ), \end{aligned}$$

and

$$\begin{aligned} \psi (x_n,y_n,v_n)=\Vert y_n-v_n\Vert \le \varphi (x_n,y_n)+t_n^2, \end{aligned}$$

one has

$$\begin{aligned} \begin{aligned}&\displaystyle \frac{\psi ((z_n,y_n,v_n)+t_n(u^\prime ,d^\prime ,w^\prime ))-\psi (z_n,y_n,v_n)}{t_n}\\&\quad \ge \displaystyle \frac{\varphi (x_n+t_n(u^\prime +\varepsilon _na_n/2),y_n+t_nd^\prime )-\varphi (x_n,y_n)}{t_n} -t_n. \end{aligned} \end{aligned}$$

As $u^\prime \in u+\varepsilon /2 B_X,$ $u^\prime +\varepsilon _na_n/2\in u+\varepsilon _n B_X,$ therefore one obtains

$$\begin{aligned} \begin{aligned}&\psi ^\uparrow (({\bar{x}},{\bar{y}},{\bar{v}}),(u,d,w))\\&\quad \ge \limsup _{n\rightarrow \infty }\inf _{(u^\prime ,d^\prime )\in (u,d)+(\varepsilon _n/2) B_{X\times Y}}\displaystyle \frac{\varphi (x_n+t_n(u^\prime +\varepsilon _na_n/2),y_n+t_nd^\prime )-\varphi (x_n,y_n)}{t_n}\\&\quad \ge \varphi ^\uparrow (({\bar{x}},{\bar{y}}),(u,d)). \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \varphi ^\uparrow (({\bar{x}},{\bar{y}}),(u,d))\le \sup \{\psi ^\uparrow (({\bar{x}},{\bar{y}},{\bar{v}}),(u,d,w)):\;\; {\bar{v}}\in P_{F({\bar{x}})}({\bar{y}})\}, \end{aligned}$$

for all $(u,d,w)\in X\times Y\times Y.$ Obviously, for any $\bar{v}\in P_{F({\bar{x}})}({\bar{y}}),$

$$\begin{aligned} \psi ^\uparrow (({\bar{x}},{\bar{y}},{\bar{v}}),(u,d,w))> -\infty ,\;\;\text {for all} \;\;(u,d,w)\in X\times Y\times Y. \end{aligned}$$

Thus, $\psi ^\uparrow (({\bar{x}},{\bar{y}},{\bar{v}}),\cdot ):X\times Y\times Y\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is lower semicontinuous and sublinear. Hence, thanks to (Hörmander [15] or [7, Prop. 2.1.4]), one has

$$\begin{aligned} \partial ^\uparrow \varphi ({\bar{x}},{\bar{y}})\times \{0\}\subseteq \text {cl}_{\text {w}^*}\text {co}\{\partial ^\uparrow \psi ({\bar{x}},{\bar{y}},{\bar{v}}):\;\;v\in P_{F({\bar{x}})}({\bar{y}})\}. \end{aligned}$$

Applying the sum rule to the Clarke subdifferential, for all $\bar{v}\in P_{F({\bar{x}})}({\bar{y}}),$ we have

$$\begin{aligned} \partial ^\uparrow \psi ({\bar{x}},{\bar{y}},{\bar{v}})\subseteq \left\{ (x^*,y^*,w^*+v^*):\;\; (y^*,w^*)\in \partial ^\uparrow \Vert \cdot -\cdot \Vert _Y({\bar{y}},{\bar{v}}),\; (x^*,v^*)\in N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{v}})\right\} . \end{aligned}$$

Consequently,

$$\begin{aligned} \partial ^\uparrow \psi ({\bar{x}},{\bar{y}},{\bar{v}})\!\subseteq \! \left\{ (x^*,y^*,v^*-y^*)\in X^*\!\times \! Y^*\times Y^*:\begin{array}{ll} &{}(x^*,v^*)\!\in \! N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{v}});\\ &{}\Vert y^*\Vert =1;\;\;\langle y^*,{\bar{y}}-{\bar{v}}\rangle =d({\bar{y}},F({\bar{x}})) \end{array}\right\} . \end{aligned}$$

Combining this inclusion with the previous relation shows (27). $\square$

5 $\rho$-Paraconvexity and $\rho$-Paramonotonicity

It is well known that the convexity of a lower semicontinuous function is characterized by the monotonicity of its subdifferential. To characterize some notions of generalized convexity, some corresponding generalized monotonicity has been introduced in the literature. For instance, in this generalized direction of paraconvexity considered in the present paper, $\gamma -$monotonicity for some $\gamma \in [1,2),$ was used in [19], (or more general $\alpha (\cdot )-$paramonotonicity in [37]), and approximate monotonicity in [26]. We introduce a notion of $\rho -$monotonicity associated to a modulus function $\rho$ for a multifunctions $T:X\rightrightarrows X^*,$ which generalizes naturally the one of $\gamma -$monotonicity for some $\gamma >0$ ( [19], see also [28, 37]).

Definition 5.1

Suppose given a Banach space X with continuous dual $X^*$, and a modulus function $\rho :X\rightarrow {\mathbb {R}}_+$. A multifunction $T:X\rightrightarrows X^*$ is called $\rho -$paramonotone with respect to some constant $\kappa >0$ if

If ${{\mathcal {F}}}(X)$ stands for set of all lower semicontinuous extended-real-valued functions $f:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$, recall that (see, e.g., [26]) a subdifferential is a correspondence $\partial :{{\mathcal {F}}}(X)\times X\rightrightarrows X^*$ which assigns to any $f\in {{\mathcal {F}}}(X),$ and $x\in {{\,\mathrm{Dom}\,}}f$ a subset $\partial f(x)\subseteq X^*$ such that $0\in \partial f(x)$ if x is a local minimizer of f.

Definition 5.2

(Fuzzy Mean Value Theorem), [26, Def. 6]) A subdifferential $\partial$ is said to be valuable on X, if for any ${\bar{x}},{\bar{y}}\in X,$ with ${\bar{x}}\not ={\bar{y}}$, and for any (l.s.c.) lower semicontinuous function $f:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$ finite at ${\bar{x}}$ and for any $r\in {\mathbb {R}}$ with $f({\bar{y}})\ge r,$ there exist $u\in [{\bar{x}},{\bar{y}}[:=\{t{\bar{x}}+(1-t){\bar{y}}:\;t\in (0,1]\}$ and sequences $(u_n)\rightarrow u,$ $(u^*_n)$ such that $u^*_n\in \partial f(u_n),$ $(f(u_n))\rightarrow f(u)$,

• (i) $\liminf \limits _{n\rightarrow \infty }\langle u^*_n,{\bar{y}}-{\bar{x}}\rangle \ge r-f({\bar{x}});$

• (ii) $\liminf \limits _{n\rightarrow \infty }\left\langle u^*_n,\displaystyle \frac{{\bar{y}}-u_n}{\Vert {\bar{y}}-u\Vert }\right\rangle \ge \displaystyle \frac{r-f({\bar{x}})}{\Vert {\bar{y}}-{\bar{x}}\Vert };$

• (iii) $\lim \limits _{n\rightarrow \infty }\Vert u^*_n\Vert d_{[{\bar{x}},{\bar{y}}]}(u_n)=0.$

This fuzzy mean value property was firstly established by Zagrodny [46] for the Clarke subdifferential in Banach spaces. Its extensions have been developed in the literature for some classes of subdifferentials (see [2] and the references given therein). For our purpose, we just mention that the Clarke subdifferential is valuable on any Banach space; the Hadamard subdifferential is valuable on any Hadamard smooth Banach space, and the Fréchet subdifferential is valuable on every Asplund space.

Also, let us mention the dag subdifferential associated to the dag derivative and introduced in [31]:

$$\begin{aligned}&f^\dag (x,v):=\limsup _{t\downarrow 0,y\rightarrow _f x}\displaystyle \frac{1}{t}(f(y+t(v+x-y))-f(y))\;\; x\in {{\,\mathrm{Dom}\,}}f,\; v\in X;\\&\partial ^\dag f(x)=\{x^*\in X^*:\;\;\; \langle x^*,v\rangle \le f^\dag (x,v),\;\;\forall v\in X\}, \end{aligned}$$

when $x\in {{\,\mathrm{Dom}\,}}f,$ and $\partial ^\dag f(x)=\emptyset$, otherwise. It seems to be the largest possible subdifferential to be used in our context. In particular, it contains the Clarke subdifferential.

The following subdifferential characterizations generalize the usual convex case, and the one of $\gamma -$convexity for $\gamma \in (1,2]$ in [18]). The proof which is omitted is standard, and similar to the one in [26, Theo. 10] in which the characterizations of approximate convexity have been established.

Theorem 5.1

Let $\rho :X\rightarrow {\mathbb {R}}_+$ be a modulus function verifying $(C1)-(C3)$ on a Banach space X. Let $f:X\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be a lower semicontinuous function. Le $\partial$ be a subdifferential operator such that for any f, $\partial f$ is contained in $\partial ^\dag f.$ Consider the following assertions:

• (i) f is $\rho$-paraconvex;

• (ii) there is some $\kappa >0$ such that for all $x\in {{\,\mathrm{Dom}\,}}f,$ and all $u\in X,$

  $$\begin{aligned} f^\dag (x,u)\le f(x+u)-f(x)+\kappa \rho (u); \end{aligned}$$

• (iii) there is some $\kappa >0$ such that for all $x\in {{\,\mathrm{Dom}\,}}f,$ and all $x^*\in \partial f(x),$

  $$\begin{aligned} \langle x^*,u\rangle \le f(x+u)-f(x)+\kappa \rho (u),\;\;\text {for all}\;\;u\in X; \end{aligned}$$

• (iv) $\partial f$ is $\rho -$paramonotone.

Then, $(i)\Rightarrow (ii)\Rightarrow (iii)\Rightarrow (iv).$ If moreover, $\partial$ is valuable, then all assertions are equivalent.

The preceding theorem subsumes the equivalence between $\rho$-paraconvexity of $\varphi _F$ and $\rho -$paramonotonicity of $\partial \varphi _F$, where $\partial$ is either the Clarke subdifferential on Banach spaces $X\times Y$, or the Fréchet subdifferential when X, Y are Asplund spaces. In the following theorem, we show that $\rho$-paraconvexity of the function $\varphi _F$ can be characterized by the $\rho -$monotonicity of $\partial \varphi _F\cap (X^*\times \mathbb {S}_{Y^*}),$ for the appropriate subdifferential $\partial$, where $\mathbb {S}_{Y^*}$ stands for the unit sphere in $Y^*.$

Here, we adopt the notion of (relative) radial continuity of a function, which means continuity along segments whose extremities belong to the domain of the function. From Proposition 2.2 and ( [25, Cor. 3.3]), one has the following lemma.

Lemma 5.1

If $F:X\rightrightarrows Y$ is $\rho$-paraconvex for a modulus function $\rho$ verifying $(C1)-(C2)$, then $\varphi _F$ is radially continuous.

Theorem 5.2

Let $\rho :X\rightarrow {\mathbb {R}}_+$ be a given modulus function verifying $(C1)-(C3).$ Let $F:X\rightrightarrows Y$ be a closed multifunction between Banach spaces X and Y. Then, the function $\varphi _F$ is $\rho$-paraconvex if and only if $\varphi _F$ is radially continuous, F has convex values and $\partial \varphi _F\cap (X^*\times \mathbb {S}_{Y^*})$ is $\rho -$paramonotone, provided that

• (i) either $\partial ={\hat{\partial }}$ and X, Y being Asplund spaces; moreover, in this case, for the sufficient part, the condition for F to have convex values can be removed,

• (ii) or $\partial =\partial ^\uparrow ,$ Y is reflexive with a strictly convex norm having the Kadec-Klee property, the multifunction F is graphically norm-to-weak closed.

Proof

Due to ( [25, Cor. 3.3]), the $\rho -$paraconvexity of $\varphi _F$ implies immediately the radial continuity of $\varphi _F$. If $\varphi _F$ is $\rho -$paraconvex, then for any $\bar{x}\in X,$ $\varphi _F({\bar{x}},\cdot )$ is convex with respect to the variable y. Therefore, since $\varphi _F(\bar{x},y_1)=\varphi _F({\bar{x}},y_1)=0$, then for any $y_1,y_2\in F(\bar{x}),$ or any $y\in [y_1,y_2],$ $\varphi _F({\bar{x}},y)=0,$ which implies $y\in F({\bar{x}}),$ i.e., F has convex values. So the necessary part is a corollary of the preceding theorem. For the sufficiency part, assume that $\varphi :=\varphi _F$ is radially continuous and there is some $\kappa >0$ such that for $\partial =\partial ^\uparrow ,$ or ${\hat{\partial }},$

$$\begin{aligned} \langle (x^*_1,y^*_1)-(x_2^*,y^*_2),(x_1,y_1)-(x_2,y_2)\rangle \ge -\kappa \rho (x_1-x_2), \end{aligned}$$

(30)

for all $((x_i,y_i),(x_i^*,y_i^*))\in {{\,\mathrm{gph}\,}}\partial \varphi \cap (X \times Y \times X^*\times \mathbb {S}_{Y^*}).$ Let $(x_i,y_i)\in {{\,\mathrm{Dom}\,}}\varphi$ be given with $(x_1,y_1)\not =(x_2,y_2).$ Given $t\in (0,1),$ set $(x,y)=t(x_1,y_1)+(1-t)(x_2,y_2).$ We shall show that

$$\begin{aligned} \varphi (x,y)\le t\varphi (x_1,y_1)+(1-t)\varphi (x_2,y_2)+2\kappa t(1-t)\rho (x_1-x_2). \end{aligned}$$

(31)

If $\varphi (x,y)=0$, then (31) holds trivially. Otherwise, consider the case $\varphi (x,y)>0.$ By the lower semicontinuity of $\varphi ,$ select $({\bar{u}}_i,{\bar{v}}_i)\in [(x_i,y_i),(x,y)[$, $i=1,2,$ such that

$$\begin{aligned} \varphi (u,v)>0,\;\;\text {for all}\;\;(u,v)\in ]({\bar{u}}_1,\bar{v}_1),({\bar{u}}_2,{\bar{v}}_2)[, \end{aligned}$$

(32)

and

$$\begin{aligned} \text {either}\;\; ({\bar{u}}_i,{\bar{v}}_i)=(x_i,y_i)\;\;\text { or}\;\;\varphi ({\bar{u}}_i,{\bar{v}}_i)=0,\;\text {for}\;i=1\; \text {or}\;2. \end{aligned}$$

(33)

Consider ${\bar{s}}\in (0,1)$ such that $(x,y)={\bar{s}}({\bar{u}}_1,\bar{v}_1)+(1-{\bar{s}})({\bar{u}}_2,{\bar{v}}_2),$ along with arbitrary $(u_i,v_i)\in ]({\bar{u}}_i,{\bar{v}}_i),(x,y)[ ,$ $i=1,2$; then there exists $s\in (0,1)$ such that $(x,y)=s(u_1,v_1)+(1-s)(u_2,v_2)$. Applying the fuzzy mean value (Definition 5.2) to $\varphi$ on the segments $[(u_1,v_1),(x,y)],$ with $r<\varphi (x,y),$ we get $(z_1,z_2) \in [(u_1,v_1),(x,y)[$ and sequences $((z_{1,n},z_{2,n}))\rightarrow (z_1,z_2),$ $((z^*_{1,n},z_{2,n}^*))$ such that $(z^*_{1,n},z_{2,n}^*)\in \partial \varphi (z_{1,n},z_{2,n})$ for each n and

$$\begin{aligned} \displaystyle \liminf _{n\rightarrow +\infty }\left\langle (z^*_{1,n},z_{2,n}^*),\displaystyle \frac{(u_2,v_2)-(z_{1,n},z_{2,n})}{\Vert (u_2,v_2)-(z_{1,n},z_{2,n})\Vert } \right\rangle >\displaystyle \frac{r-\varphi (u_1,v_1)}{\Vert (x,y)-(u_1,v_1)\Vert }. \end{aligned}$$

(34)

Let $\beta \in (0,1)$ be such that $(x,y)=\beta (u_2,v_2)+(1-\beta )(z_1,z_2)$ and let $(w_{1,n},w_{2,n})=\beta (u_2,v_2)+(1-\beta )(z_{1,n},z_{2,n}).$ Then, as $\varphi$ is l.s.c., for large n, and using the fact that $(z_{1,n},z_{2,n})\rightarrow (z_1,z_2)$ and $r<\varphi (w_{1,n},w_{2,n})$ we get $((w_{1,n},w_{2,n}))\rightarrow (x,y)$ . Moreover, $\Vert (w_{1,n},w_{2,n})-(u_2,v_2)\Vert =(1-s_n)\Vert (u_1,v_1)-(u_2,v_2)\Vert$ for some sequence $(s_n)\rightarrow s.$ Applying again (Definition 5.2 to $\varphi$ on $[(u_2,v_2),(w_{1,n},w_{2,n})]$, one obtains $(v_{1,n},v_{2,n})\in [(u_2,v_2),(w_{1,n},w_{2,n})[$ a sequence $(v_{1,n,p},v_{2,n,p})\rightarrow (v_{1,n},v_{2,n})$ as $p\rightarrow \infty ,$, $(v^*_{1,n,p},v^*_{2,n,p})$ with $(v^*_{1,n,p},v^*_{2,n,p})\in \partial \varphi (v_{1,n,p},v_{2,n,p})$ for all n, p,  and

$$\begin{aligned}&\displaystyle \liminf _{p}\left\langle (v^*_{1,n,p},v_{2,n,p}^*),\displaystyle \frac{(z_{1,n},z_{2,n})-(v_{1,n,p},v_{2,n,p})}{\Vert (z_{1,n},z_{2,n})-(v_{1,n,p},v_{2,n,p})\Vert } \right\rangle \nonumber \\ {}&\quad >\displaystyle \frac{r-\varphi (u_2,v_2)}{\Vert (w_{1,n},w_{2,n})-(u_2,v_2)\Vert }\nonumber \\&\quad =\displaystyle \displaystyle \frac{r-\varphi (u_2,v_2)}{(1-s_n)\Vert (u_1,v_1)-(u_2,v_2)\Vert }. \end{aligned}$$

(35)

From relation (34), there exists some $m\ge k$ such that for all $n\ge m,$

$$\begin{aligned}&\left\langle (z^*_{1,n},z_{2,n}^*),\displaystyle \frac{(v_{1,n},v_{2,n})-(z_{1,n},z_{2,n})}{\Vert (v_{1,n},v_{2,n})-(z_{1,n},z_{2,n})\Vert } \right\rangle \nonumber \\&\quad =\left\langle (z^*_{1,n},z_{2,n}^*),\displaystyle \frac{(u_2,v_2)-(z_{1,n},z_{2,n})}{\Vert (u_2,v_2)-(z_{1,n},z_{2,n})\Vert } \right\rangle \nonumber \\&\quad > \displaystyle \frac{r-\varphi (u_1,v_1)}{\Vert (x,y)-(u_1,v_1)\Vert }\nonumber \\&\quad =\displaystyle \frac{r-\varphi (u_1,v_1)}{s\Vert (u_1,v_1)-(u_2,v_2)\Vert }. \end{aligned}$$

(36)

On the other hand, since $(v_{1,n,p},v_{2,n,p})\rightarrow (v_{1,n},v_{2,n}),$ for each n and $(s_n)\rightarrow s,$ from (35) and (36), one can find q(n) such that for all $p\ge q(n),$

$$\begin{aligned} \left\langle (v^*_{1,n,p},v_{2,n,p}^*),\frac{(z_{1,n},z_{2,n})-(v_{1,n,p},v_{2,n,p})}{\Vert (z_{1,n},z_{2,n})-(v_{1,n,p},v_{2,n,p})\Vert } \right\rangle >\frac{r-\varphi (u_2,v_2)}{(1-s_n)\Vert (u_1,v_1)-(u_2,v_2)\Vert }, \end{aligned}$$

and

$$\begin{aligned} \left\langle (z^*_{1,n},z_{2,n}^*),\frac{(v_{1,n,p},v_{2,n,p})-(z_{1,n},z_{2,n})}{\Vert (v_{1,n,p},v_{2,n,p})-(z_{1,n},z_{2,n})\Vert } \right\rangle >\frac{r-\varphi (u_1,v_1)}{s_n\Vert (u_1,v_1)-(u_2,v_2)\Vert }. \end{aligned}$$

In view of (33), as $((z_{1,n},z_{2,n}))\rightarrow (z_1,z_2)\in [(u_1,v_2),(x,y)[;$ $((w_{1,n},w_{2,n}))\rightarrow (x,y);$ and $(v_{1,n},v_{2,n})\in [(u_2,v_2),(w_{1,n},w_{2,n})[,$ one can find $M\ge m,$ and $N(n)\ge q(n)$ such that for $n\ge M,$ $p\ge N(n),$ one has $\varphi (z_{1,n},z_{2,n})>0$ and $\varphi (v_{1,n,p},v_{2,n,p})>0,$ as well. Thus, (since ${{\,\mathrm{gph}\,}}F$ is closed), $z_{2,n}\notin F(z_{1,n})$ and $v_{2,n,p}\notin F(v_{1,n,p}),$ and thanks to Theorem 4.1 for the case (i),  and to relation (28) in Theorem 4.1 for the case (ii), $\Vert v_{2,n,p}^*\Vert = \Vert z_{2,n}^*\Vert =1,$ for all $n\ge M,$ $p\ge N(n).$

Adding the corresponding sides of the two inequalities above, and using relation (30), one derives that

$$\begin{aligned} \begin{array}{ll}&{} \kappa s(1-s_{n})\displaystyle \frac{\Vert (u_1,v_1)-(u_2,v_2)\Vert }{\Vert (v_{1,n,p},v_{2,n,p})-(z_{1,n},z_{2,n})\Vert }\rho (v_{1,n,p}-z_{1,n})\\ &{}\quad \ge (1-s_{n})(r-\varphi (u_1,v_1))+s(r-\varphi (u_2,v_2)). \end{array} \end{aligned}$$

(37)

Considering a subsequence if necessary, without loss of generality, we can assume that $((v_{1,n},v_{2,n}))\rightarrow (w_1,w_2)\in [(u_2,v_2),(x,y)].$ Therefore, for each n,  we can find an index $p(n)\ge N(n)$ with $p(n)\rightarrow \infty$ such that $((v_{1,n,p(n)},v_{2,n,p(n)}))\rightarrow (w_1,w_2).$ By taking $p=p(n)$ in (37), and letting $n\rightarrow \infty ,$ one obtains

$$\begin{aligned} \begin{array}{ll}&{} \kappa s(1-s)\frac{\Vert u_1-u_2\Vert }{\Vert w_1-z_1\Vert }\rho (w_1-z_1)= \kappa s(1-s)\displaystyle \frac{\Vert (u_1,v_1)-(u_2,v_2)\Vert }{\Vert (w_1,w_2)-(z_1,z_2)\Vert }\rho (w_1-z_1)\\ &{}\quad \ge (1-s)(r-\varphi (u_1,v_1))+s(r-\varphi (u_2,v_2)). \end{array} \end{aligned}$$

(38)

Note that $\rho$ is convex, $\rho (0)=0,$ and $\rho$ is an even function. As $[z_1,w_1]\subseteq [u_1,u_2],$ one has

$$\begin{aligned} \frac{\Vert u_1-u_2\Vert }{\Vert w_1-z_1\Vert }\rho (w_1-z_1)\le \rho (u_1-u_2). \end{aligned}$$

Hence, since r is arbitrary close to $\varphi (x,y),$ (38) yields

$$\begin{aligned} \varphi (x,y)\le s\varphi (u_1,v_1)+(1-s)\varphi (u_2,v_2)+\kappa s(1-s)\rho (u_1-u_2). \end{aligned}$$

As $(u_i,v_i)$ is, respectively, arbitrary close to $({\bar{u}}_i,\bar{v}_i)$, $i=1,2,$ using the radial continuity of $\varphi ,$ the preceding inequality implies

$$\begin{aligned} \varphi (x,y)\le {\bar{s}}\varphi ({\bar{u}}_1,{\bar{v}}_1)+(1-\bar{s})\varphi ({\bar{u}}_2,{\bar{v}}_2)+\kappa {\bar{s}}(1-{\bar{s}})\rho (\bar{u}_1-{\bar{u}}_2). \end{aligned}$$

(39)

To establish (31) from (39), let $\alpha _1,\alpha _2\in [0,1]$ with $\alpha _1>\alpha _2$ such that

$$\begin{aligned} ({\bar{u}}_i,{\bar{v}}_i)=\alpha _i(x_1,y_1)+(1-\alpha _i)(x_2,y_2),\;\;i=1,2. \end{aligned}$$

Then, $t={\bar{s}}\alpha _1+(1-{\bar{s}})\alpha _2,$ and

$$\begin{aligned} \varphi ({\bar{u}}_1-{\bar{u}}_2)=\varphi ((\alpha _1-\alpha _2)(x_1-x_2))\le (\alpha _1-\alpha _2)\varphi (x_1-x_2). \end{aligned}$$

Therefore, it yields

$$\begin{aligned} {\bar{s}}(1-{\bar{s}})\rho ({\bar{u}}_1-{\bar{u}}_2)\le 2t(1-t)\varphi (x_1-x_2). \end{aligned}$$

(40)

On the other hand, by (33),

$$\begin{aligned} \varphi ({\bar{u}}_i,{\bar{v}}_i)\le \alpha _i\varphi (x_1,y_1)+(1-\alpha _i)\varphi (x_2,y_2),\;\;i=1,2. \end{aligned}$$

Hence,

$$\begin{aligned} \begin{array}{ll} {\bar{s}}\varphi ({\bar{u}}_1,{\bar{v}}_1)+(1-{\bar{s}})\varphi ({\bar{u}}_2,{\bar{v}}_2)&{}\le ({\bar{s}}\alpha _1+(1-{\bar{s}})\alpha _2)\varphi (x_1,y_1)+((1-{\bar{s}})\alpha _1+{\bar{s}}\alpha _2)\varphi (x_2,y_2)\\ &{}=t\varphi (x_1,y_1)+(1-t)\varphi (x_2,y_2).\end{array} \end{aligned}$$

This inequality together with (40) yields (31). $\square$

When Y is a finite dimensional space, using the Bouligand normal cone, Huang [16], gave some characterizations of the $\gamma$-paraconvexity for $\gamma >1$. We present in the next theorems characterizations of the $\rho$-paraconvexity of a multifunction $F:X\rightrightarrows Y$ between a Banach space X and a reflexive Banach space Y.

Theorem 5.3

Let X and Y be Banach spaces with Y reflexive. Let $\rho :X\rightarrow {\mathbb {R}}_+$ be a modulus function verifying $(C1)-(C3)$, and $F:X\rightrightarrows Y$ be a closed multifunction. Consider the following assertions:

• (i) F is $\rho$-paraconvex;

• (ii) F is graphically norm-to-weak closed with convex values and $N^\uparrow _{{{\,\mathrm{gph}\,}}F}(x,y)=N^{(\rho ,\kappa )}(x,y)$ for all $(x,y)\in {{\,\mathrm{gph}\,}}F,$ for some $\kappa >0;$

• (iii) F is graphically norm-to-weak closed with convex values and $N^\uparrow _{{{\,\mathrm{gph}\,}}F}\cap (X^*\times \mathbb {B}_{Y^*})$ is $\rho -$paramonotone;

• (iv) $\varphi _F$ is $\rho$-paraconvex;

• (v) $\partial ^\uparrow \varphi _F$ is $\rho -$paramonotone;

• (vi) $\varphi _F$ is radially continuous, F is graphically norm-to-weak closed with convex values, and $\partial ^\uparrow \varphi _F\cap (X^*\times \mathbb {S}_{Y^*})$ is $\rho -$paramonotone;

• (vii) $\varphi _F$ is radially continuous, F is graphically norm-to-weak closed with convex values, and $N^\uparrow _{{{\,\mathrm{gph}\,}}F}\cap (X^*\times \mathbb {S}_{Y^*})$ is $\rho -$paramonotone.

Then, one has $(i)\Rightarrow (ii)\Leftrightarrow (iii);$ $(i)\Leftrightarrow (iv)\Leftrightarrow (v)\Rightarrow (vi),$ and $(i)\Rightarrow (vii).$ Moreover, if in addition the norm on Y is strictly convex and has the Kadec-Klee property, then all assertions are equivalent.

Proof

$(i)\Rightarrow (ii)$ is due to Lemma 4.1 and Theorem 3.1, while the equivalence of (ii) and (iii) is straightforward from the cone property. The equivalences $(i)\Leftrightarrow (iv)\Leftrightarrow (v)$ is due to Proposition 2.2 and Theorem 5.1, while $(v)\Rightarrow (vi)$ as well as $(i)\Rightarrow (vii)$ are due to $(i)\Leftrightarrow (v);$ $(i)\Rightarrow (iii),$ and Lemma 5.1. Suppose in addition that the norm on Y is strictly convex and has the Kadec-Klee property. The implication $(vii)\Rightarrow (iv)$ follows from Theorem 5.2. [(ii)]. Let us prove $(ii)\Rightarrow (v)$ and $(vii)\Rightarrow (vi)$ to complete the proof. Denote $\varphi :=\varphi _F,$ and let $({\bar{x}},{\bar{y}})\in X\times Y,$ $(x^*,y^*)\in \partial ^\uparrow \varphi ({\bar{x}},{\bar{y}}).$ Then $\Vert y^*\Vert \le 1,$ and by Lemma 4.2, $P_{F({\bar{x}})}({\bar{y}})$ is nonempty and reduces to a singleton since $F({\bar{x}})$ is convex, and $\varphi ({\bar{x}},{\bar{y}})=d({\bar{y}}, F({\bar{x}})).$ From Theorem 4.2, for $\bar{v}:=P_{F({\bar{x}})}({\bar{y}}),$ one has $\langle y^*,{\bar{y}}-\bar{v}\rangle =\Vert {\bar{y}}-{\bar{v}}\Vert =\varphi ({\bar{x}},{\bar{y}}),$ and $(\bar{x}^*,{\bar{y}}^*)\in N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},\bar{v})=N^{(\rho ,\kappa )}(x,y).$ Thus,

$$\begin{aligned} \langle ({\bar{x}}^*,{\bar{y}}^*),(x,v)-({\bar{x}},{\bar{v}})\rangle \le \kappa \rho (x-{\bar{x}}),\;\;\text {for all}\;\; (x,v)\in {{\,\mathrm{gph}\,}}F. \end{aligned}$$

For any $(x,y)\in {{\,\mathrm{Dom}\,}}\varphi ,$ consider sequences $(u_n)\rightarrow x;$ $(v_n)$ with $(u_n,v_n)\in {{\,\mathrm{gph}\,}}F,$ $\Vert y-v_n\Vert \rightarrow \varphi (x,y).$ The relation above implies

$$\begin{aligned} \begin{array}{ll} &{}\langle ({\bar{x}}^*,{\bar{y}}^*),(x,y)-({\bar{x}},{\bar{y}})\rangle \\ &{}\quad =\langle {\bar{x}}^*,x-u_n\rangle +\langle {\bar{y}}^*,y-v_n\rangle -\langle {\bar{y}}^*,{\bar{y}}-{\bar{v}}\rangle +\langle ({\bar{x}}^*,{\bar{y}}^*),(u_n,v_n)-({\bar{x}},{\bar{v}})\rangle \\ &{}\quad \le \langle {\bar{x}}^*,x-u_n\rangle +\Vert y-v_n\Vert -\Vert {\bar{y}}-\bar{v}\Vert +\kappa \rho (u_n-{\bar{x}}), \end{array}. \end{aligned}$$

When $n\rightarrow \infty ,$ we obtain

$$\begin{aligned} \langle ({\bar{x}}^*,{\bar{y}}^*),(x,y)-({\bar{x}},{\bar{y}})\rangle \le \varphi (x,y)-\varphi ({\bar{x}},{\bar{y}})+\kappa \rho (x-{\bar{x}}), \end{aligned}$$

Thus for any $(x,y)\in {{\,\mathrm{Dom}\,}}\varphi$ and $(x^*,y^*)\in \partial ^\uparrow \varphi (x,y),$

$$\begin{aligned} \langle (x^*, y^*),({\bar{x}},{\bar{y}})-(x,y)\rangle \le \varphi ({\bar{x}},{\bar{y}})-\varphi (x,y)+\kappa \rho (x-{\bar{x}}). \end{aligned}$$

Adding side by side the two last inequalities yields,

$$\begin{aligned} \langle ({\bar{x}}^*,{\bar{y}}^*)-(x^*, y^*), ({\bar{x}},{\bar{y}})-(x,y)\rangle \ge - 2\kappa \rho (x-{\bar{x}}), \end{aligned}$$

and the $\rho -$paramonotonicity of $\partial ^\uparrow \varphi .$

For $(vii)\Rightarrow (vi),$ let $({\bar{x}},{\bar{y}}),(x,y)\in X\times Y,$ $({\bar{x}}^*,{\bar{y}}^*)\in \partial ^\uparrow \varphi ({\bar{x}},\bar{y}),$ $(x^*,y^*)\in \partial ^\uparrow \varphi ( x,y)$ with $\Vert \bar{y}^*\Vert =\Vert y^*\Vert =1$ be given. By Theorem 4.2, $({\bar{x}}^*,{\bar{y}}^*)\in N^\uparrow _{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{v}});$ $(x^*,y^*)\in N^\uparrow _{{{\,\mathrm{gph}\,}}F}(x,v);$ $\langle {\bar{y}}^*,\bar{y}-{\bar{v}}\rangle =\Vert {\bar{y}}-{\bar{v}}\Vert$ and $\langle y^*,y-v\rangle =\Vert y-v\Vert ,$ where ${\bar{v}}=P_{F({\bar{x}})}({\bar{y}}),$ $v=P_{F(x)}(y).$ Thus due to the $\rho -$paramonotonicity of $N^\uparrow _{{{\,\mathrm{gph}\,}}F}\cap (X^*\times \mathbb {S}_{Y^*}),$ for some $\kappa >0,$ one has

$$\begin{aligned} \begin{array}{ll} &{}\langle (x^*,y^*)-({\bar{x}}^*,{\bar{y}}^*),(x,y)-({\bar{x}},{\bar{y}})\rangle \\ &{}\quad =\langle y^*,(y-v)-({\bar{y}}-{\bar{v}})\rangle +\langle {\bar{y}}^*,({\bar{y}}-{\bar{v}})-(y-v)\rangle + \langle (x^*,y^*)-({\bar{x}}^*,{\bar{y}}^*), (x,v)-({\bar{x}},{\bar{v}})\rangle \\ &{}\quad \ge (\Vert y-v\Vert -\Vert {\bar{y}}-{\bar{v}}\Vert )+(\Vert {\bar{y}}-\bar{v}\Vert -\Vert y-v\Vert )-\kappa \rho (x-{\bar{x}})=-\kappa \rho (x-{\bar{x}}). \end{array} \end{aligned}$$

That is, $\partial ^\uparrow \varphi _F\cap (X^*\times \mathbb {S}_{Y^*})$ is $\rho -$paramonotone. The proof is complete. $\square$

The next characterizations use Fréchet normal cones and subdifferentials in Asplund spaces.

Theorem 5.4

Let X and Y be Asplund spaces. Let $\rho :X\rightarrow {\mathbb {R}}_+$ be a function verifying $(C1)-(C3).$ For a closed multifunction $F:X\rightrightarrows Y,$ consider the following assertions:

• (i) F is $\rho$-paraconvex;

• (ii) ${\hat{N}}_{{{\,\mathrm{gph}\,}}F}(x,y)=N^{(\rho ,\kappa )}(x,y)$ for all $(x,y)\in {{\,\mathrm{gph}\,}}F,$ for some $\kappa >0,$

• (iii) ${\hat{N}}_{{{\,\mathrm{gph}\,}}F}\cap (X^*\times \mathbb {B}_{Y^*})$ is $\rho -$paramonotone;

• (iv) $\varphi _F$ is $\rho$-paraconvex;

• (v) ${\hat{\partial \varphi _F}}$ is $\rho -$paramonotone;

• (vi) $\varphi _F$ is radially continuous and ${\hat{\partial }}\varphi _F\cap (X^*\times \mathbb {S}_{Y^*})$ is $\rho -$paramonotone;

• (vii) $\varphi _F$ is radially continuous and ${\hat{N}}_{{{\,\mathrm{gph}\,}}F}\cap (X^*\times \mathbb {S}_{Y^*})$ is $\rho -$paramonotone.

Then, one has $(i)\Rightarrow (ii)\Leftrightarrow (iii)\Rightarrow (iv)\Leftrightarrow (v)\Leftrightarrow (vi)\Leftarrow (vii),$ and $(i)\Rightarrow (vii).$ Moreover, if Y is reflexive, then all assertions are equivalent.

Proof

The implications $(i)\Rightarrow (ii)\Leftrightarrow (iii);$ $(i)\Rightarrow (vii)$ and the equivalences $(iv)\Leftrightarrow (v)\Leftrightarrow (vi)$ can be proved as in the preceding theorem. When Y is reflexive, then $(i)\Leftrightarrow (iv).$ It remains to prove $(iii)\Rightarrow (v)$ and $(vii)\Rightarrow (vi).$ Suppose (iii) holds, i.e., ${\hat{N}}_{{{\,\mathrm{gph}\,}}F}\cap (X^*\times \mathbb {B}_{Y^*})$ is $\rho -$monotone with respect to some constant $\kappa >0.$ Let $(x_i,y_i)\in X\times Y,$ $(x_i^*,y_i^*)\in \hat{\partial }\varphi (x_i,y_i),$ $i=1,2$ be given. Thanks to Theorem 4.1, $\Vert y_i^*\Vert \le 1,$ ($i=1,2$), and we can find sequences $((u_i^{(n)},v_i^{(n)}))$ with $(u_i^{(n)},v_i^{(n)})\in {{\,\mathrm{gph}\,}}F$ and $((u_i^{(n)*},v_i^{(n)*})),$ $i=1,2,$ such that

$$\begin{aligned} (u_i^{(n)*},v_i^{(n)*})\in {\hat{N}}_{{{\,\mathrm{gph}\,}}F}(u_i^{(n)},v_i^{(n)});\;\; \Vert u_i^{(n)}-x_i\Vert \rightarrow 0;\;\; \Vert y_i-v_i^{(n)}\Vert \rightarrow \varphi (x_i,y_i), \end{aligned}$$

and

$$\begin{aligned} \Vert ((u_i^{(n)*},v_i^{(n)*})-(x_i^*,y_i^*)\Vert \rightarrow 0;\;\; |\langle v_i^{(n)*},y_i-v_i^{(n)}\rangle -\Vert y_i-v_i^{(n)}\Vert |\rightarrow 0,\;\; i=1,2. \end{aligned}$$

By the $\rho -$paramonotonicity of ${\hat{N}}_{{{\,\mathrm{gph}\,}}F}\cap (X^*\times \mathbb {B}_{Y^*}),$

$$\begin{aligned} \langle (u_1^{(n)*},v_1^{(n)*})-(u_2^{(n)*},v_2^{(n)*}),(u_1^{(n)},v_1^{(n)})-(u_2^{(n)},v_2^{(n)})\rangle \ge -\kappa \rho (u_1^{(n)}-u_2^{(n)}). \end{aligned}$$

Hence,

$$\begin{aligned} \begin{array}{ll} &{}\langle (u_1^{(n)*},v_1^{(n)*})-(u_2^{(n)*},v_2^{(n)*}),(u^{(n)}_1,y_1)-(u^{(n)}_2,y_2)\rangle \\ &{}\quad =\langle (u_1^{(n)*},v_1^{(n)*})-(u_2^{(n)*},v_2^{(n)*}),(u_1^{(n)},v_1^{(n)})-(u_2^{(n)},v_2^{(n)})\rangle \\ &{}\qquad +\langle v_1^{(n)*},(y-v_1^{(n)})-(y_2-v_2^{(n)})\rangle +\langle v_2^{(n)*},(y_2-v_2^{(n)})-(y-v_1^{(n)})\rangle \\ &{}\quad \ge -\kappa \rho (u_1 ^{(n)}-u_2^{(n)})+\langle v_1^{(n)*},(y-v_1^{(n)})\rangle + \langle v_2^{(n)*},(y_2-v_2^{(n)})\rangle \\ &{}\qquad -\Vert v_1^{(n)*}\Vert \Vert y_2-v_2^{(n)}\Vert -\Vert v_2^{(n)*}\Vert \Vert y-v_1^{(n)}\Vert . \end{array} \end{aligned}$$

Noticing that for every $i=1,2,$

$$\begin{aligned}&(u_i^{(n)})\rightarrow x_i; \\&\quad (u_i^{(n)*},v_i^{(n)*})\rightarrow (x^*_i,y_i^*);\\&\quad \Vert y_i^*\Vert \le 1;\\&\quad |\langle v_i^{(n)*},y_i-v_i^{(n)}\rangle -\Vert y_i-v_i^{(n)}\Vert |\rightarrow 0, \end{aligned}$$

and passing to the limit one obtains

$$\begin{aligned} (x_1^{*},y_1^{*})-(x_2^{*},y_2^{*}),(x_1,y_1)-(x_2,y_2)\rangle \ge -\kappa \rho (x_1-x_2), \end{aligned}$$

showing the $\rho -$paramonotonicity of ${\hat{\partial \varphi }}.$ The proof of $(vii)\Rightarrow (vi)$ is completely similar. $\square$

Open problem 2

Does the equivalence of all (or some) of assertions in the two preceding theorems hold without the reflexivity of the image space Y?

6 Coderivatives of the Sum of $\rho$-Paraconvex Multifunctions

Consider two multifunctions $F_1,F_2: X\rightrightarrows Y,$ which are $\rho$-paraconvex for a modulus function verifying $(C1)-(C3).$ Then, the sum multifunction $F_1+F_2$ is $\rho$-paraconvex Hence, the respective coderivatives agree. We denote each of them by $DF^*({\bar{x}},{\bar{y}}),$ for $({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}F.$ Still, due to Theorem 3.1, for some $\kappa >0,$ one has

for all $({\bar{x}},{\bar{y}})\in {{\,\mathrm{gph}\,}}F,$ all $y^*\in Y^*,$ where

$$\begin{aligned} N^{(\rho ,\kappa )}_{{{\,\mathrm{gph}\,}}F}({\bar{x}},{\bar{y}})=\left\{ \begin{array}{ll}&{}(x^*,y^*)\in X^*\times Y^*:\\ &{}\langle x^*,x-{\bar{x}}\rangle +\langle y^*,y-{\bar{y}}\rangle \le \kappa \Vert y^*\Vert \rho (x-{\bar{x}}),\;\forall (x,y)\in {{\,\mathrm{gph}\,}}F \end{array}\right\} . \end{aligned}$$

The paper concludes with a sum rule for the coderivative of $F_1+F_2.$

Theorem 6.1

Let X, Y be Banach spaces. Consider two $\rho$-paraconvex multifunctions $F_1,F_2: X\rightrightarrows Y,$ for a modulus function $\rho$ verifying $(C1)-(C3).$ Then for $({\bar{x}},\bar{y}_1)\in {{\,\mathrm{gph}\,}}F_1$ and $({\bar{x}},{\bar{y}}_2)\in {{\,\mathrm{gph}\,}}F_2,$ one has

Equality in (41) holds provided that the following two conditions are satisfied.

• (i) There are $\delta >0$, $\tau >0$ such that

  $$\begin{aligned} \varphi _{F_1+F_2}(x,y_1+y_2)\le \tau \left( \varphi _{F_1}(x,y_1)+\varphi _{F_ 2}(x,y_2)\right) \end{aligned}$$

  for all $(x,y_1,y_2)\in B(({\bar{x}},{\bar{y}}_1,{\bar{y}}_2),\delta );$

• (ii)
  $$\begin{aligned} \bigcup _{\lambda \ge 0}\lambda \left( {{\,\mathrm{Dom}\,}}\varphi _{F_1}(\cdot ,0)-{{\,\mathrm{Dom}\,}}\varphi _{F_2}(\cdot ,0)\right) \end{aligned}$$

  is a closed subspace of X.

Proof

Let $y^ *\in Y^*,$ $x_i^*\in DF_i^*({\bar{x}},{\bar{y}}_i)(y^*),$ $i=1,2.$ Then for some $\kappa >0,$ $(x_i^*,-y^*)\in N^{(\rho ,\kappa )}_{{{\,\mathrm{gph}\,}}F_i}({\bar{x}},{\bar{y}}_i),$ $i=1,2.$ For any $(x,y)\in {{\,\mathrm{gph}\,}}(F_1+F_2),$ there are $y_i\in F_i(x),$ $i=1,2,$ such that $y_1+y_2= y,$ and therefore

$$\begin{aligned}&\langle x_1^*,x-{\bar{x}}\rangle -\langle y^*,y_1-{\bar{y}}_1\rangle \le \kappa \Vert y^*\Vert \rho (x-{\bar{x}});\\&\quad \langle x_2^*,x-{\bar{x}}\rangle -\langle y^*,y_2-\bar{y}_2\rangle \le \kappa \Vert y^*\Vert \rho (x-{\bar{x}}). \end{aligned}$$

By adding the two inequalities side by side, one obtains

$$\begin{aligned} \langle x_1^*+x_2^*,x-{\bar{x}}\rangle -\langle y^*,y-({\bar{y}}_1+{\bar{y}}_2)\rangle \le 2\kappa \Vert y^*\Vert \rho (x-{\bar{x}}). \end{aligned}$$

The last inequality being verified for all $(x,y)\in {{\,\mathrm{gph}\,}}(F_1+F_2),$ this shows that

$$\begin{aligned} x^*_1+x_2^*\in D(F_1+F_2)^*({\bar{x}},{\bar{y}}_1+\bar{y}_2)(y^*), \end{aligned}$$

proving (41).

Let conditions $(i)-(ii)$ be satisfied. Let $x^*\in D(F_1+F_2)^*({\bar{x}},{\bar{y}}_1+{\bar{y}}_2)(y^*)$ for $y^*\in Y^*.$ Thanks to Theorem 4.1 - part (i),  $(x^*,-y^*)\in \alpha {\hat{\partial }} \varphi _{F_1+F_2}({\bar{x}},\bar{y}_1+{\bar{y}}_2),$ for some $\alpha >0,$ namely $\alpha =1$ if $\Vert y^*\Vert \le 1,$ and $\alpha =\Vert y^*\Vert ,$ otherwise. Thus, as $\varphi _{F_i}({\bar{x}},{\bar{y}}_1+{\bar{y}}_2)=0,$ for any $\varepsilon >0,$ there is $\delta _\varepsilon \in (0,\delta ),$ here $\delta$ is as in (i),  such that

$$\begin{aligned} \langle (x^*,-y^*), (x,y)-({\bar{x}},{\bar{y}}_1+{\bar{y}}_2)\rangle \le \alpha \varphi _{F_1+F_2}(x,y)+\varepsilon \Vert (x,y)-(x,y_1+y_2)\Vert ,\nonumber \\ \end{aligned}$$

(42)

for all $(x,y)\in B(({\bar{x}},{\bar{y}}_1+{\bar{y}}_2),\delta _\varepsilon ).$ Consider the mappings $f_i \;(i=1,2)$ defined on $X\times Y\times Y$ by $f_i(x,y_1,y_2)=\varphi _{F_i}(x,y_i)$. By condition (i),  relation (42) implies that for all $(x,y_1,y_2)\in B((\bar{x},{\bar{y}}_1,{\bar{y}}_2),\delta _\varepsilon /2),$ we have

$$\begin{aligned}&\langle (x^*,-y^*,-y^*),(x,y_1,y_2)-({\bar{x}},{\bar{y}}_1,{\bar{y}}_2)\rangle \nonumber \\&\quad \le \alpha \tau (f_1+f_2)(x,y_1,y_2)+\varepsilon \Vert ((x,y_1,y_2)-(\bar{x},{\bar{y}}_1,{\bar{y}}_2)\Vert . \end{aligned}$$

(43)

This yields

$$\begin{aligned} (x^*,-y^*,-y^*)\in \alpha \tau {\hat{\partial }}(f_1+f_2)({\bar{x}},{\bar{y}}_1,{\bar{y}}_2). \end{aligned}$$

Note that $f_1,f_2$ are lower semicontinuous $\rho$-paraconvex functions, therefore they are approximately convex (at all points). Moreover, ${{\,\mathrm{Dom}\,}}f_i={{\,\mathrm{Dom}\,}}\varphi _{F_i}(\cdot ,0)\times Y\times Y,$ $i=1,2,$ thus by condition (ii), 

$$\begin{aligned} \bigcup _{\lambda \ge 0}\lambda ({{\,\mathrm{Dom}\,}}f_1-{{\,\mathrm{Dom}\,}}f_2) \end{aligned}$$

is a closed space of $X\times Y\times Y.$ So thanks to the sum rule formula for the subdifferential of approximately convex functions [25, Theo. 3.8],

$$\begin{aligned} {\hat{\partial }}(f_1+f_2)({\bar{x}},{\bar{y}}_1,{\bar{y}}_2)=\hat{\partial }f_1({\bar{x}},{\bar{y}}_1,{\bar{y}}_2)+\hat{\partial }f_2({\bar{x}},{\bar{y}}_1,{\bar{y}}_2). \end{aligned}$$

Hence, there exist $(z_i^*,-v_i^*)\in \hat{\partial }\varphi _{F_i}({\bar{x}},{\bar{y}}_i),$ $i=1,2,$ such that

$$\begin{aligned} (x^*,-y^*,-y^*)=\alpha \tau \left( (z_1^*,-v_1^*,0)+(z_2 ^*,0,-v_2^*)\right) . \end{aligned}$$

That is, $\alpha \tau v_i^*=y^*,$ $i=1,2,$ and $x^*=\alpha \tau z^*_1+\alpha \tau z_2^*.$ As $(z_i^*,-v_i^*)\in \hat{\partial }\varphi _{F_i}({\bar{x}},{\bar{y}}_i),$ $i=1,2,$ thanks again to Theorem 4.1 - part (i),  $\alpha \tau z^*_i\in DF_i^*({\bar{x}},{\bar{y}}_i)(y^*),$ $i=1,2$. Thus,

$$\begin{aligned} x^*\in \ DF_1^*({\bar{x}},{\bar{y}}_1)(y^*)+DF_2^*({\bar{x}},{\bar{y}}_2)(y^*), \end{aligned}$$

and accordingly the proof is complete. $\square$

The following lemma gives some verified sufficient conditions to ensure $(i)-(ii).$

Lemma 6.1

Let X, Y be Banach spaces. Consider two $\rho$-paraconvex closed multifunctions $F_1,F_2: X\rightrightarrows Y,$ for a modulus function $\rho$ satisfying $(C1)-(C3).$ Let $({\bar{x}},{\bar{y}}_i)$ be given in ${{\,\mathrm{gph}\,}}F_i,$ $i=1,2.$

• (a) If ${\bar{x}}$ belong either to ${{\,\mathrm{Int}\,}}({{\,\mathrm{Dom}\,}}F_1)$ or to ${{\,\mathrm{Int}\,}}({{\,\mathrm{Dom}\,}}F_2),$ then the both two conditions $(i)-(ii)$ in the preceding theorem are satisfied.

• (b) If Y is reflexive, then condition (i) holds automatically, while (ii) is equivalent to

  $$\begin{aligned} \bigcup _{\lambda \ge 0}\lambda \left( {{\,\mathrm{Dom}\,}}F_1-{{\,\mathrm{Dom}\,}}F_2\right) \end{aligned}$$

  being a closed subspace of X.

Proof

(a). Let e.g., ${\bar{x}}\in {{\,\mathrm{Int}\,}}({{\,\mathrm{Dom}\,}}F_1).$ Then obviously $x\in {{\,\mathrm{Int}\,}}({{\,\mathrm{Dom}\,}}\varphi (\cdot ,0)).$ So as ${\bar{x}}\in {{\,\mathrm{Dom}\,}}F_2,$

$$\begin{aligned} \bigcup _{\lambda \ge 0}\lambda \left( {{\,\mathrm{Dom}\,}}\varphi _{F_1}(\cdot ,0)-{{\,\mathrm{Dom}\,}}\varphi _{F_2}(\cdot ,0)\right) =X, \end{aligned}$$

that is, (ii) is satisfied. In [18, Theo. 2.4], Jourani, established that for a $\gamma$-paraconvex multifunction with $\gamma >1$ between general Banach spaces, the condition $\bar{x}$ belongs to the interior of its domain is equivalent to the locally pseudo-Lipschitzness of the multifunction. Observe that with an almost similar proof (we omit here), this equivalence also holds for $\rho$-paraconvex multifunctions with $\rho$ satisfying $(C1)-(C3).$ That is, if ${\bar{x}}\in {{\,\mathrm{Int}\,}}({{\,\mathrm{Dom}\,}}F_1),$ then for $\bar{y}_1\in F_1({\bar{x}}),$ there are $r,\varepsilon >0$ such that

$$\begin{aligned} F_1(x_1)\cap ({\bar{y}}_1+\varepsilon B_Y)\subseteq F_1(x_2)+r\Vert x_1-x_2\Vert B_Y, \end{aligned}$$

for all $x_i\in {\bar{x}}+\varepsilon B_X,$ $i=1,2.$ Thus, we can say that $d(y_1,F(x))=\varphi _{F_1}(x,y_1)$ for all $(x,y_1)\in B((\bar{x},{\bar{y}}_1),\varepsilon /2),$ and that $\varphi _{F_1}$ is Lipschitz on $B(({\bar{x}},{\bar{y}}_1),\varepsilon /2).$ For any $(x,y_1)\in B((\bar{x},{\bar{y}}_1),\varepsilon /2)$, any $y_2\in Y,$ with $\varphi _{F_2}(x,y_2)<+\infty ,$ taking a sequence $(u_n)\rightarrow x,$ such that $d(y_2,F_2(u_n))\rightarrow \varphi _{F_2} (x,y_2),$ one has

$$\begin{aligned} \begin{array}{ll} \varphi _{F_1+F_2}(x,y_1+y_2)&{}\le \liminf \limits _{n\rightarrow \infty }d(y_1+y_2, F_1(u_n)+F_2(u_n))\\ &{}= \lim \limits _{n\rightarrow \infty }d(y_1, F_1(u_n)) + \liminf \limits _{n\rightarrow \infty }d(y_2,F_2(u_n))\\ &{}= \varphi _{F_1}(x,y_1)+\varphi _{F_2}(x,y_2). \end{array} \end{aligned}$$

Hence, (i) is satisfied with $\tau =1.$

For (b),  when Y is reflexive, due to the proof of $(iii)\Rightarrow (i)$ in Proposition 2.2, $\varphi _{F_i}=d_{F_i}=d(\cdot ,F_i(\cdot )),$ and therefore, ${{\,\mathrm{Dom}\,}}\varphi _{F_i}(\cdot ,0)={{\,\mathrm{Dom}\,}}F_i,$ $i=1,2.$ So (ii) is equivalent to say that

$$\begin{aligned} \bigcup _{\lambda \ge 0}\lambda \left( {{\,\mathrm{Dom}\,}}F_1-{{\,\mathrm{Dom}\,}}F_2\right) \end{aligned}$$

is a closed subspace of X. For any $(x,y_1,y_2)\in X\times Y\times Y,$ one has

$$\begin{aligned} \begin{array}{ll} \varphi _{F_1+F_2}(x,y_1+y_2)&{}\le d(y_1+y_2,F_1(x)+F_2(x))\\ &{}\le d(y_1,F_1(x))+d(y_2,F_2(x))= \varphi _{F_1}(x,y_1)+\varphi _{F_2}(x,y_2), \end{array} \end{aligned}$$

establishing (ii). $\square$

Open problem 3

Is it possible to establish a sum rule for the coderivative of paraconvex multifunctions without the constraint qualifications (i) and (ii) from the previous theorem.

7 Conclusions

We established some regular properties of graphical tangent and normal cones to $\rho$-paraconvex multifunctions between Banach spaces as well as a sum rule for coderivatives for such class of multifunctions. Some characterizations of the $\rho$-paraconvexity via the $\rho$-paramonotonicity of normal cone mappings are presented. This presentation gives rise to three open questions.