1 Introduction

To avoid the onerous demands on power plants at peak, imbalances between electricity generation and consumption, and also costly grid investment, retailers and even grid operators [26] conceive advanced tariffs to encourage the consumer to shift flexible appliances and significantly improve PAR and FI indicators. They are usually nonlinear cost functions that ensure consistent lower bounds and a profit for the designers [8] or related to the contribution of the consumer to the peak/off-peak consumption [20]. Thus, the consumers are motivated to optimize their electricity consumption as long as their savings are substantial. On the one hand, a fixed time-of-use (ToU) tariff that probably does not always follow the load curve is not an efficient tool especially on the mid-run and long run [6], because it does not overlap with the inherent changes in consumers’ behavior. The lack of overlapping between daily load curve and a fixed ToU tariff is frequent as the load curve varies for seasonal reasons. It is even more frequent from region to region because ToU tariff peak and off-peak rates are calculated considering peak and off-peak hours at the national level. However, regional load shape could be different as the peak takes place at different time intervals (hours) than at the national level. On the other hand, a flexible over time or dynamic tariff that is adjusted according to the consumption level has the potential to stimulate consumers to shift the operation of their appliances to the lower tariff rates [29].

Nonetheless, when a high degree of flexibility is available, there are some risks to be encountered such as the swaying of the appliances from peak to off-peak hours. These situations can be handled by providing a constraint matrix or, in its absence, the shifting condition needs to be adapted to avoid the incidence of new peaks. The shifting condition could be true as long as the new peak is lower than daily average consumption. Consequently, massively swaying the appliances from peak to off-peak hours is prevented. Most of the research studies do not address this issue as they usually consider a small number of flexible appliances.

In a classic optimization process, the operation of the flexible appliances is shifted in one iteration only according to a fixed ToU tariff [14,15,16, 21,22,23]. On the other hand, in a game-optimization process, the tariff is created daily based on the total consumption schedule of the community that represents a signal and the consumers optimize the consumption using local computational resources [17, 18] or even mobile phones. Then, they send the schedules to the retailer, who recomputes the tariff according to the new total consumption and so on, until there is no shift that improves the utility functions of both consumers and retailer [2,3,4, 17, 18, 30].

The two approaches have advantages and disadvantages, yet the benefits of the game-optimization process prevail. The main advantages of the first, classic approach, are its simplicity and the low computational requirements, while the advantage of the second, game-optimization approach, consists in being more transparent for consumers and bringing more incentives for shifting and adjusting the tariff to maximize FI. Thus, the second approach is more complex, but the optimization in multiple iterations could be an automatic process that uses machine learning with direct load control (DLC) [7], Internet of Things (IoT) and other mechanisms that ease the process and improve its effectiveness.

In this paper, we propose an optimization algorithm enhanced by an advanced tariff and a Stackelberg-type dynamic nonzero-sum game which emphasizes significant insights into the flexibility degree of the appliances as we use in simulation a large real consumption dataset from 11 complex and modern houses with a high degree of flexibility. The proposed algorithm minimizes the consumers’ cost and avoids the creation of new peaks that could appear as a consequence of the high degree of flexibility.

The current paper is structured in five main sections as follows: the first section is an introduction regarding the goal of our research, and the second section is a literature review briefly describing the current stare-of-art. In the third section, we propose a game theory approach to iteratively optimize the electricity consumption and avoid new peaks. The fourth and fifth sections are organized around simulations, results and conclusion, respectively.

2 Literature Survey

Game theory in the consumption optimization process has previously been approached from various perspectives. Optimization problems using game theory are studied in [1, 3,4,5, 13, 14, 25]. Usually, the privacy of the consumers is assured by a minimal information exchange between consumers and retailer as the retailer does not need to know sensitive information about consumers’ preferences and appliances. The proposed solutions in similar, previous research, decreases the cost, but the results show a lack of validation, as they are not extended for a longer interval (e.g., a one-year period). For instance, one day of simulation with a built scenario including a high energy demand is presented in [4]. In our study, the sensitive information related to consumers’ preferences and detailed consumption of appliances are not revealed as the optimization is performed at the consumers’ level. Furthermore, the proposed algorithm is tested and validated using a large dataset of records and its implementation is performed for one day and also for one year, thus proving the sustainability of the results.

An interesting game-optimization study using a community storage facility is carried out in [8] showing a cost reduction of almost 10% and also a significant PAR reduction with a hybrid combination of a real-time and ToU tariff. Since each consumer is modeled in the laboratory with a small number of appliances and constrained operation hours, the swaying effect discussed in our paper is ignored. The results given for a winter and summer day are chosen as representative. However, aspects related to the flexibility degree of the appliances and the implementation of the solution are not disclosed in similar studies, including [8].

A one-leader, as a virtual supplier, and n followers, as electricity consumers, represent the players of a Stackelberg game to identify the optimal consumption strategy [30]. A real-time price system is implemented to perform simulations. Although the daily payment has been reduced by almost 21%, the results lack validation as the simulations are not repeated for a longer period. Furthermore, the simulation included only a few appliances that are easily handled at the centralized level of the retailer, while an increasing number could lead to significant delays. Also, the swaying effect of appliances from peak to off-peak hours that could occur in real operation is not considered in [5, 30].

Several types of Stackelberg nonzero-sum game, theory and applicability of this game are described in [24], emphasizing their static and dynamic perspectives. This early study highlighted valuable conclusions regarding Stackelberg strategy, conditions for the existence of Stackelberg solution and the relation with Nash solution. Also, for a dynamic game, the conditions for the existence of a Stackelberg solution are identified. A couple of examples are presented to demonstrate the solution concept.

Moreover, the Stackelberg game models the interactions between distributed energy resources (DER) owners and an aggregator [15], comparing two ways of DER owners participation in the wholesale electricity market: direct participation or via an aggregator and quantifying the benefits of using the price of aggregation. The results demonstrated that DER owners are better-off if they cooperate with an aggregator due to its profit-maximizing strategy. By comparison, in our paper, it is shown that the consumers benefit more from interacting with the electricity aggregator or retailer.

A mixed integer linear programming (MILP) problem using a game theory approach is solved in [2], focusing on the communication packet error rate on the optimization process. The results show interesting insights into the impact of the communication issues on the actions of the consumers and retailer. Also, MILP problems with a signaling game integrating local RES are approached in [31]. Its drawback is that it considers a limited number of appliances and a small testing interval of analyses that have not been extended over a longer period.

A game model that includes the EVs charging schedule and the impact on the electricity price are analyzed in [17, 18]. The optimal schedule of EVs using the driving data from the Danish National Travel Surveys considers the battery loading at low-consumption hours leading to a reduced PAR. This research focused more on the randomness of the EV charging schedule [27] and proved to be robust to price forecast errors. To increase the efficiency, DLC managing flexible appliances such as air-conditioning and heating systems could be embedded in DSM [19] using game-optimization algorithms [11, 12]. Such a DLC method, with a multi-objective particle swarm optimization algorithm, calculates multiple local optimization solutions [7] and has been tested at the experimental level using a simulator. With this method, the consumption is not only shifted, but also reduced by means of DLC. A difference between this study and the current research is that non-programmable appliances, for example, refrigerators, freezers (using their cooling inertia) and lighting are considered controllable. We took such appliances as non-controllable since the consumers’ acceptance to control such appliances might be limited; thus, their potential to reduce the costs was not taken into account. Furthermore, another advantage of our study consists in splitting the programmable appliances into interruptible and non-interruptible ones. This approach is realistic as some appliances are shiftable, but they do not support interruption.

With consideration to the points raised above, in this paper, we propose an optimization algorithm enhanced by an advanced flexible tariff and a Stackelberg-type dynamic nonzero-game that increases the optimization potential of the consumers. Our main contributions are:

  • A game-optimization algorithm that maximizes FI that represents the utility function of the retailer using flexible tariff rates that depends on the community hourly consumption;

  • A cost optimization algorithm that minimizes the daily electricity cost considering both interruptible and non-interruptible programmable appliances and calculates the optimal consumption schedules;

  • Involving numerous flexible appliances from real consumption dataset that can have various restricted operation hours that may lead to swaying effect of appliances from peak to off-peak hours depending on the hourly tariff rate. Such effect is discussed and handled with an additional shifting condition to prevent the occurrence of new peaks;

  • The proposed optimization mechanism is transparent to the consumers, provides incentives for shifting programmable appliances and does not disclose sensitive information regarding the consumers’ privacy (preferences and consumption details) as the optimization takes place at the consumers’ level;

  • The algorithm is tested and validated with a large dataset recorded for one year.

3 Game Theory Approach

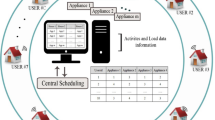
A game is usually characterized by several elements: players—electricity residential consumers, that forms a community, and retailer; actions or decisions or strategies regarding the consumption level and tariffs; rewards or utility functions that can be related to the electricity cost or the peak related indicators. The game equilibrium is found when a set of actions is better than any other set of actions leading to the end of the game. Thus, a Stackelberg-type dynamic nonzero-sum game explains the interaction between a retailer and the electricity consumers as shown in Fig. 1 and in the following paragraphs.

Fig. 1
figure 1

Flows between electricity consumers and retailer

Full size image

Most of the time, the optimization is performed in one iteration: the retailer conceives the tariff and the consumers optimize the consumption accordingly. But the advanced charging system has been created dependent on the total consumption level; thus, it is unlikely to get the minimum electricity cost at the first iteration of the optimization process. Considering that the consumers behave rationally, they will continue to optimize the operating schedule of their appliances as long as the cost declines. Also, using a quadratic cost function, the retailer adjusts the tariff rates at the consumption level in order to flatten the peak.

A Stackelberg-type dynamic nonzero-sum game in which the strategies are announced sequentially describes the iterative interactions between players: the consumers, on the one hand, as followers and electricity retailer as leader, on the other hand. The leader has a tariff structure that is calculated according to the consumption forecast. In this game, considering the initial tariff structure, the consumers send the initial consumption schedules (not optimized) to the retailer, who aggregates the total consumption, calculates the hourly tariff rates based on the community’s hourly consumption and sends them to the consumers. The strategy of the leader consists in a set of messages sent as an array of tariffs: \({\text{ToU}} = \left\{ {t^{{h_{{{\text{rate}}}} }} } \right\}, \forall h = \overline{1,24}\). The consumers will play or act according to the tariff that is sent by the retailer. Then, the consumers will reschedule their programmable appliances (taking actions) according to the tariff rates to lower the electricity cost. The strategy of the consumer consists in the hourly consumption vector, \({\text{DA}}_{i}\) that represents the daily actions of a consumer i. Thus, the utility functions are defined for both leader and followers: \(R_{{{\text{ret}}}} \left( {{\text{TDA}},{\text{ToU}}} \right)\) and \(R_{i} \left( {{\text{DA}}_{i} ,{\text{ToU}}} \right)\), where TDA is the total daily actions. Therefore, the retailer will devise the tariff signal to flatten the peak and encourage the consumers to shift the operation of their appliances to those hours with lower rates.

The optimization problem is formulated for both retailer and consumers to select the optimal strategy in the following paragraphs.

  1. A.

    The strategy of the retailer is to create tariff rates to minimize the peak consumption.

Considering that each consumer has a specific hourly consumption \(A_{i}^{h}\), the array of the hourly consumption for an interval of 24 h represents the \({\text{DA}}_{i}\). Thus, the sum of the hourly actions of all consumers represents the total consumption that a retailer should provide:

$$ {\text{TDA}} = \left\{ {A^{h} |A^{h} \in {\mathbb{R}}, A^{h} \ge 0} \right\}, \;\forall h = \overline{1,24} $$
(1)

where \(A^{h}\) is the total consumption of all consumers at hour h.

$$ A^{h} = A_{1}^{h} + A_{2}^{h} + \ldots + A_{n}^{h} = \mathop \sum \limits_{i = 1}^{n} A_{i}^{h} $$
(2)

Consequently, TDA is obtained by adding up \({\text{DA}}_{i}\) of all consumers; thus, the retailer’s utility function (\(R_{{{\text{ret}}}}\)) is to minimize the peak consumption of the community.

$$ R_{{{\text{ret}}}} \left( {{\text{TDA}},{\text{ToU}}} \right) = \min \left( {\max \left( {A^{h} } \right)} \right){ }, \forall h = \overline{1,24} $$
(3)

A couple of indicators are calculated to measure the retailer’s reward and the performance of the proposed algorithm. FI is the ratio between the average consumption and the consumption at peak, whereas PAR is the ratio between the squared consumption at peak and the squared mean consumption. Thus, the retailer’s utility function can be assimilated with the peak reduction that is described by the two indicators: FI and PAR.

$$ {\text{FI}} = \frac{{{{\left( {\mathop \sum \nolimits_{h = 1}^{24} A^{h} } \right)} \mathord{\left/ {\vphantom {{\left( {\mathop \sum \nolimits_{h = 1}^{24} A^{h} } \right)} {24}}} \right. \kern-\nulldelimiterspace} {24}}}}{{\mathop {\max }\limits_{{h = \overline{1,24} }} A^{h} }} $$
(4)
$$ PAR = \frac{{\left( {\mathop {\max }\limits_{{h = \overline{1,24} }} A^{h} } \right)^{2} }}{{\left( {\left( {\mathop \sum \nolimits_{h = 1}^{24} A^{h} } \right)/24} \right)^{2} }} $$
(5)

The optimization objective for the retailer in case of FI indicator can be expressed as follows:

$$ \max R_{{{\text{ret}}}} \left( {{\text{TDA}},{\text{ToU}}} \right) = \max {\text{FI}} $$
(6)

The peak minimization that is measured by FI is obtained by applying a ToU tariff that influences the hourly consumption of the community \(A^{h}\).

The fixed ToU tariffs have been implemented at the beginning of the DSM strategies [9]. At most, they have performed well in the first months of implementation; then, they have failed to improve the demand response because the shape of the tariff and the load curve differ significantly as a consequence of the consumers changing their behavior. Therefore, a flexible design of ToU tariff is defined as a quadratic cost function depending on the hourly consumption:

$$ t^{h} = f\left( {{ }A^{h} } \right) = a \times \left( {A^{h} } \right)^{2} + b \times A^{h} + c $$
(7)

where a, b, c are coefficients characteristic for the residential consumers. The typical values for these coefficients are: a = 0.00295, b =  − 0.0417 and c = 0.711, but they are slightly adjusted according to the consumption level and market price [10].

Using (7), we have set the rates depending on the hourly consumption of the community at peak, day and off-peak hours. The tariff vector ToU has three components corresponding to peak, off-peak and the remaining hours. The peak tariff rate is calculated as the average of tariff rates \(t^{h}\) for peak hours (between 17 and 21) extracted from the load curve. The off-peak tariff rate is calculated as the average of tariff rates \(t^{h}\) for off-peak hours (between 1 and 4, and 24). The shoulder tariff rate is calculated as the average of tariff rates \(t^{h}\) for the remaining hours.

$${\rm{ToU}} = \left\{ {{t^{{h_{{\rm{rate}}}}}}\left| {{t^{{h_{{\rm{rate}}}}}}} \right. > 0,~{t^{{h_{{\rm{rate}}}}}} \in \left\{ {{t^{{h_{{\rm{peak\_rate}}}}}},{t^{{h_{{\rm{offpeak\_rate}}}}}},{t^{{h_{{\rm{shoulder\_rate}}}}}}} \right\}} \right\},~\forall ~h = \overline {1,24}$$
(8)
$$ t^{{h_{{{\text{offpeak\_rate}}}} }} = {\text{mean}}\left( {{ }t^{h} } \right), \forall h = \overline{1,4} \;{\text{and}}\; h = 24 $$
(9)
$$ t^{{h_{{{\text{shoulder\_rate}}}} }} = {\text{mean}}\left( {{ }t^{h} } \right), \forall h = \overline{5,16} \;{\text{and}} \;h = \overline{22,23} $$
(10)
$$ t^{{h_{{{\text{peak\_rate}}}} }} = {\text{mean}}\left( {{ }t^{h} } \right), \forall h = \overline{17,21} $$
(11)

Thus, the feasible strategy set of the retailer is represented by the vector of ToU tariff calculated according to (7–11).

  1. B.

    The equilibrium strategy of the consumer is to minimize the daily electricity cost by choosing a set of strategies represented by the hourly consumption \(A_{i}^{h}\) given the tariff rates sent by the retailer. Based on the tariff rate \(t^{{h_{{{\text{rate}}}} }}\), the electricity cost for a consumer i is given by the following equation:

    $$ C_{i} = \mathop \sum \limits_{h = 1}^{24} A_{i}^{h} \times t^{{h_{{{\text{rate}}}} }} $$
    (12)

where \(C_{i}\)—the electricity cost for a consumer i;

\(t^{{h_{{{\text{rate}}}} }}\)—the tariff rate for a specific hour of consumption.

Thus, the consumer’s utility function or reward \(R_{i}\):

$$ R_{i} \left( {{\text{DA}}_{i} ,{\text{ToU}}} \right) = C_{i} = \mathop \sum \limits_{h = 1}^{24} A_{i}^{h} \times t^{{h_{{{\text{rate}}}} }} ,\forall i = \overline{1,n} $$
(13)

where n is the number of consumers.

The action (strategy) of a consumer i for hour h, \(A_{i}^{h}\), consists in the consumption of all appliances that operate at a specific hour h.

$$ A_{i}^{h} = {\text{NPA}}_{i}^{h} + {\text{PA}}_{i}^{h} $$
(14)

The appliances are classified into: non-programmable appliances (NPAs) and programmable appliances (PAs). For optimization purposes, PAs are further classified into shiftable interruptible (SI) and shiftable without interruption (SW) appliances. Thus, the operation of SW cannot be split over non-consecutive hours due to their intrinsic characteristics.

$$ {\text{PA}}_{i}^{h} = {\text{PASI}}_{i}^{h} + {\text{PASW}}_{i}^{h} = \mathop \sum \limits_{j = 1}^{m} A_{ij}^{h} $$
(15)
$$ A_{i}^{h} = NPA_{i}^{h} + \mathop \sum \limits_{j = 1}^{m} A_{ij}^{h} $$
(16)

One of SW is the washing machine since once it starts, it has to operate until the washing program finishes; otherwise, the clothing could become stale in the tub or some machines simply do not allow the interruption. Among PAs, SI appliances are usually more numerous and more flexible for shifting. NPAs are usually considered as total. Although NPAs do not shift, they are an important segment of the hourly consumption that must be part of the optimization process.

The electricity consumption optimization process starts with the modeling of the set of constraints. The consumption operating hours of PA are set by the consumers. It forms the programmable appliances constraints matrix \({\text{PACM}}_{i}\), defined by each consumer i.

$$ {\text{PACM}}_{i} = \left\{ {{\text{PACM}}_{ij}^{h} } \right\}, \;\forall i = \overline{1,n} ; \;j = \overline{1,m} ;\; h = \overline{1,24} $$
(17)
$$ {\text{PACM}}_{ij}^{h} \in \left\{ {0,1} \right\} $$

where 1 means that the appliance j can operate at hour h, and 0 otherwise.

Each consumer aims to minimize his daily cost under the constraints imposed by the operating conditions of the appliances defined in the matrix \({\text{PACM}}_{i}\). Therefore, the optimization objective can be expressed as follows:

$$ {\text{min}} R_{i} \left( {{\text{DA}}_{i} ,{\text{ToU}}} \right) = \min C_{i} = \min \mathop \sum \limits_{h = 1}^{24} A_{i}^{h} \times t^{{h_{{{\text{rate}}}} }} ,\forall i = \overline{1,n} $$
(18)

The feasible strategy set of each consumer i is represented by \({\text{DA}}_{i} = \left\{ {A_{i}^{h} |A_{i}^{h} \in {\mathbb{R}},\rm{ }A_{i}^{h} \ge 0} \right\}\), where \(A_{i}^{h}\) is calculated according to (16), each appliance j being restricted by \({\text{PACM}}_{ij}^{h} \in \left\{ {0,1} \right\}\).

To measure the cost reduction at each iteration of the game, relative to the initial unoptimized schedule, the consumer’s gain (\(G_{i} )\) (as the percentage of the cost reduction) can be calculated at the consumer level.

$$ G_{i} = 100 - \frac{{C_{i} \times 100}}{{C_{i}^{0} }} $$
(19)

Furthermore, the cost reduction or the consumers’ gain (G) at the community level is the percentage of the aggregated cost reduction relative to the unoptimized schedule.

$$ G = 100 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} C_{i} \times 100}}{{\mathop \sum \nolimits_{i = 1}^{n} C_{i}^{0} }} $$
(20)

where \(C_{i}^{0}\) is the initial cost and \(C_{i}\) is the cost after the optimization for consumer i.

The community gain is also important for the retailer as it highlights the satisfaction of the consumers.

Stackelberg strategy is the optimal strategy for the retailer (leader) if the consumers schedule their appliances optimally. Thus, the Stackelberg equilibrium is attained in an iterative exchange of messages that stops when the leader finds the best combination of ToU tariff rates that maximizes his utility function and provides the optimal operation solution for programmable appliances. The leader strategy that is to maximize FI is the leader’s equilibrium strategy. Then, the followers minimize their daily costs by choosing the best response to the leader’s equilibrium strategy that is the optimal operation of the programmable appliances. Thus, the Stackelberg equilibrium is characterized by both optimal strategies from which players do not deviate. Let us denote the optimal set of strategies (*) as:

$$ \left( {{\text{ToU}}^{*} ,{\text{TDA}}^{*} } \right) = \arg \max R_{{{\text{ret}}}} \left( {\text{TDA,ToU}} \right), $$
(21)
$$ {\text{TDA}}^{*} = \left\{ {A^{\left( * \right)h} |A^{\left( * \right)h} = \mathop \sum \limits_{i = 1}^{n} A_{i}^{\left( * \right)h} } \right\}, \forall h = \overline{1,24} , $$
(22)
$$ A_{i}^{\left( * \right)h} = \arg {\text{min}} R_{i} \left( {{\text{DA}}_{i} ,{\text{ToU}}} \right) = {\text{arg}}\min \mathop \sum \limits_{h = 1}^{24} A_{i}^{h} \times t^{{{\text{h}}_{{{\text{rate}}}} }} ,\forall i = \overline{1,n} , $$
(23)

To summarize, the consumers send their daily consumption schedule (not optimized) to the retailer that created an initial tariff structure. Considering the aggregated consumers’ schedules, the retailer computes the tariff rates and sends them to the consumers. Each consumer minimizes the cost and obtains the optimal daily consumption schedule. If it is different from the previous schedule, it is sent to the retailer that computes a new tariff until maximum value of FI is obtained in a definite number of iterations established by retailer. This mechanism is explained in detail in Sects. 3.1 and 3.2.

3.1 Cost Minimization Algorithm

The cost optimization algorithm is built upon the community day-ahead optimization algorithms [23]. The significant difference consists in the objective function of the algorithms and the iterative process proposed in the current research. The community day-ahead optimization algorithms in [23] target the flattening of the electricity consumption vector by shifting the consumption of the programmable appliances toward the hours less loaded and, when several fixed ToU tariffs are implemented, the reduction of the electricity cost is also achieved. The newly developed cost minimization algorithm aims to obtain the lowest cost for the consumers by shifting the consumption toward the hours with the cheapest rates. The off-peak \(t^{{h_{{{\text{offpeak\_rate}}}} }}\), shoulder \(t^{{{\text{h}}_{{{\text{shoulder\_rate}}}} }}\) and peak rates \(t^{{h_{{{\text{peak\_rate}}}} }}\) are iteratively calculated with the dynamic ToU tariff described in (7)–(11). The higher the hourly consumption, the higher the rate; thus, the flattening of the consumption vector is a result of the tariff rates.

The cost optimization algorithm is designed to manage the programmable appliances: both the non-interruptible (SW) and the interruptible ones (SI).

3.1.1 Optimization Algorithm for SW

The cost optimization algorithm for SW shifts the consumption to lower rate hours so that the consumer i obtains the lowest cost, by following the next steps:

  1. 1.

    Define the input block. The algorithm extracts for each house (consumer) i the following input:

    • The vector with the total hourly consumption of \({\text{NPA}}\) for consumer i, \({\text{NPA}}_{i}^{h} \in {\text{NPA}}_{i}\), with \(h = \overline{1,24}\) and \(i = \overline{1,n}\). Let us consider \(N_{i}\) a vector with the hourly consumption of the appliances that will not be further rescheduled. Initially, \(N_{i}\) sums the consumption of all NPA because they cannot be shifted. Then, other appliances will be added after their optimal operation schedule is calculated; thus, they will not be further rescheduled.

    • The matrix with the consumption of programmable non-interruptible appliances, \({\text{SW}}_{i}\), with \({\text{SW}}_{ij}^{h} \in {\text{SW}}_{i}\), \(h = \overline{1,24}\), \(i = \overline{1,n}\) and \(j = \overline{{1,m_{{{\text{SW}}}} }}\). The algorithm for SW runs first because they are more restricted (as they have more operation constraints). SW are not allowed to operate at any hour due to constraints imposed by the consumer. Thus, to find the optimal solution, \({\text{PACM}}_{i}\) constraints matrix, with elements \({\text{PACM}}_{ij}^{h} \in \left\{ {0,1} \right\}\), has to be provided by each consumer i depending of their preferences.

  2. 2.

    Generate all possible shifts of an appliance j. The first appliance in \({\text{SW}}\) is selected and all possible shifts are generated through a circular shift function. Therefore, there are 24 possibilities denoted by \(H = \overline{1,24}\), but not all are feasible because of the constraints included into \({\text{PACM}}_{i}\). The combinations that are not feasible are replaced with non-numeric elements. This creates a new matrix, \({\text{SWA}}_{ij}\), with \({\text{SWA}}_{ijH}^{h} \in {\text{SWA}}_{ij}\) with 24 × 24 dimension.

  3. 3.

    Calculate the cost of all possible shifts of an appliance \(j\). For each shift in \({\text{SWA}}_{ij}\), the cost is calculated using the tariff rates. The hourly costs are summed to obtain the daily cost for each possible shift. Thus, a vector \({\text{CW}}_{ijH}\) that has the dimension 1 × 24 is obtained (also without numeric elements for the unfeasible shifts): \({\text{CW}}_{ijH} = \mathop \sum \limits_{h = 1}^{24} {\text{SWA}}_{ijH}^{h} \times t^{{h_{{{\text{rate}}}} }} , \forall h, H = \overline{1,24}\).

  4. 4.

    Calculate the minimum cost. Steps 2 and 3 are repeated until the daily cost of all SW is calculated. By adding a row for each appliance j, we obtain a matrix with \(m_{{{\text{SW}}}} \times 24\) dimension. The lowest cost from \({\text{CW}}_{ijH}\) is calculated as \({\text{mCW}}\) and the appliance with the lowest cost, \(j_{{{\text{mCW}}}}\), is selected for shifting. The best feasible solution is the one with the consumption at the lower rate hours.

  5. 5.

    Update \({\text{SW}}_{i}\) and \(N_{i}\). The appliance that gave the minimum cost at the previous step is added to matrix \(N_{i}\) and removed from the matrix \({\text{SW}}_{i}\). The new \({\text{SW}}_{i}\) matrix has the dimension \(\left( {m_{{{\text{SW}}}} - 1} \right) \times 24\).

  6. 6.

    Return to step 2. The optimization process is repeated until \({\text{SW}}_{i}\) is dimensionless (or has no numerical elements).

To have a better view on its implementation, Fig. 2 shows the flowchart of the cost optimization algorithm for SW.

Fig. 2
figure 2

The flowchart of the cost optimization algorithm for SW

Full size image

3.1.2 Optimization Algorithm for SI

After the consumption of all SW is optimized, SI appliances are processed. The algorithm for SI shifts the electrical consumption at the hours with the lowest rate, by following the next steps for each consumer i:

  1. 1.

    Define the input block—it is the same as described above and can be a common step for both types of PA. Besides the \({\text{NPA}}\) and \({\text{SW}}\), a matrix with the consumption of SI for consumer i, \({\text{SI}}_{i}\), \(\left( {{\text{SI}}_{ij}^{h} \in {\text{SI}}_{i} , j = \overline{{1,m_{{{\text{SI}}}} }} } \right)\) must be extracted.

  2. 2.

    Find the consumption of appliance \(j\) from \({\text{SI}}_{i}\). The algorithm must find the initial scheduled hours for appliance j in order to shift its consumption. To avoid shifting exceptionally low consumptions, a threshold, \({\text{th}}\), can be defined here (\({\text{SI}}_{ij}^{h} > {\text{th}}\)). \(k_{j}\) is the vector that holds the hours from which appliance j will be shifted and \(\alpha_{j}\) is the vector of the consumption of j for the scheduled hours.

  3. 3.

    Sort vector \(N_{i}\) and ToU. The vector with the total hourly consumption of the NPA and the optimal operation schedule of SW (denoted with \(N_{i}\) in Sect. 3.1.1) must be sorted by the lowest rate of ToU. Since there are only three rates (i.e., off-peak, shoulder and peak rates), the vector \(N_{i} \) and ToU can be double sorted in ascending order. This way, the consumption of SI is first shifted at the hour with the lowest consumption of the lowest rate. The sorted vector \(N_{i}\) will be denoted \(sN_{i}\).

  4. 4.

    Shift appliance j according to the matrix \({\text{PACM}}_{i}\). Because not all hours are feasible, the \({\text{PACM}}_{i} \) will be verified before shifting. The consumption of appliance j from \(\alpha_{j}\) will be shifted if \({\text{PACM}}_{ij}^{h} = 1\) where h represents the first available hour in \(sN_{i}\). This step continues for all hours in \(k_{j}\) meaning that it will be repeated \(Lk_{j}\) times, where \(Lk_{j}\) is the length of vector \(k_{j}\). If there is no feasible solution for shifting the appliance j, its consumption remains unshifted. At this step, a temporary matrix \(t{\text{SI}}_{i}\) will hold the shifted consumption.

  5. 5.

    Calculate the cost for appliance j. Based on the same tariff rates, the cost of the newly shifted consumption is calculated. The resulted hourly costs are summed up, and the daily cost for j is obtained as \({\text{CI}}_{ij}\).

  6. 6.

    Find the minimum cost. The cost is calculated for each appliance and concatenated, \({\text{CI}}_{ij}\) becoming a vector of 1 × \(m_{{{\text{SI}}}}\). This is done by repeating the steps 2 to 5 for each appliance. The minimum of \({\text{CI}}_{ij}\) (\({\text{mCI}}\)) can then be found, meaning that the appliance that has the lowest cost will be shifted first.

  7. 7.

    Update \(N_{i}\) and \({\text{SI}}_{i}\). The appliance that has been shifted is added to the matrix \(N_{i}\) and removed from \({\text{SI}}_{i}\).

  8. 8.

    Return to step 2. The optimization process is reiterated until the \({\text{SI}}_{i}\) is dimensionless (or until it has no numerical elements).

For a detailed illustration, Fig. 3 presents the optimization algorithm of SI.

Fig. 3
figure 3

The flowchart of the cost optimization algorithm for the SI

Full size image

3.2 Game-Optimization Algorithm

The results of the cost optimization algorithm are iteratively enhanced by the flexible ToU tariff calculated according to (7)–(11) implemented in a game theory approach. Since the cost optimization algorithm shifts the consumption of the PA toward the hours with the lowest rates, new peaks could be created if the flexibility degree of the PA is high. The search of the optimal solution should be thus constrained, based on the consumers’ preferences or on retailer’s capacity to obtain the flattened consumption vector for which he is willing to offer cost reductions. The cost optimization algorithm is run individually, for each house. Thus, the sensitive consumption data are not disclosed, and the optimization process is more transparent for consumers. Since the tariff is devised as a function of the consumption level of the community, the community cost reduction (G) is monitored. Consequently, the optimization of one house is independent of the optimization of the other houses. The game-optimization algorithm performs the following steps:

  1. 1.

    Define the input block—the game theory algorithm requires the vector of hourly consumption of all consumers, \({\text{TDA}}\), which is the sum of the daily action arrays (\({\text{DA}}_{i}\)) that is initially unoptimized and coefficients, a, b, c for the tariff function. The retailer imposes a maxim number of iterations—niter.

  2. 2.

    Calculate the initial tariff rates, cost, FI and PAR. Based on the \({\text{TDA}}\) previously calculated, the initial tariff rates and cost of the unoptimized dataset, \(C^{0}\), are calculated. The FI and PAR are also calculated on the unoptimized total consumption vector.

  3. 3.

    Optimize the cost of each house (consumer) i. The optimization algorithm for each house in the community performs the optimization individually. The optimization minimizes the electricity costs using the ToU tariff built upon the initial \({\text{TDA}}\) and calculates the individual gains \(G_{i}\), using (19).

  4. 4.

    Calculate the new \({\text{TDA}}\). The retailer aggregates the optimized consumption of each house, obtaining the new vector \({\text{TDA}}\).

  5. 5.

    Calculate FI. The FI and PAR are calculated (using (14) and (15)) on the new optimized \({\text{TDA}}\) to evaluate the degree of flattening obtained after optimization. Also, to measure the community cost reduction and evaluate the consumers’ satisfaction, the community gain, \(G\), is calculated using (20).

  6. 6.

    Return to step 2. The optimization is repeated until the leader equilibrium strategy is obtained meaning that FI is maximized. For this strategy, the followers’ equilibrium strategy is also obtained as their daily consumption is optimized according to the algorithm proposed in Sects. 3.1.1 and 3.1.2. The flowchart of the game-optimization algorithm is presented in Fig. 4.

Fig. 4
figure 4

The flowchart or the game-optimization algorithm

Full size image

The game-optimization algorithm is implemented, and the performance indicators defined in (4), (5), (19), (20) are calculated.

4 Simulations and Results

4.1 Community Input Data

In simulations, we consider a small community that consists of 11 complex houses [28], with more than 300 appliances individually measured. The structure of the appliances for each house is shown in Fig. 5a, whereas the structure of the appliances at the community level is displayed in Fig. 5b. House G is the most flexible followed by houses F, D and K and that have more than 60% flexible load. It also shows a high potential of flexibility. The number of appliances, by type, and the consumption level per month are given in Fig. 6. The highest consumption was recorded in November and January,

Fig. 5
figure 5

The structure of the appliances at house level (a) and community level (b)

Full size image
Fig. 6
figure 6

The number of appliances at house level (a) and monthly community consumption level (b)

Full size image

The typical daily load curve is shown in Fig. 7 as it influences the tariff set by the retailer. It shows the morning and evening peak and the night/afternoon valleys. Also, it shows a high potential for shifting the operation of flexible appliances at the community level.

Fig. 7
figure 7

The typical daily load curve at the community level

Full size image

Starting from peaks, shoulders and valleys of the daily curve, the initial ToU tariff shape can be designed. In this particular case study, the off-peak hours with the lowest rates are 24 and between 1 and 4 in the morning, the average hours (shoulder) are between 5 and 16, and 22 and 23, the peak hours with the highest rates are between 17 and 21. Classifying and timely updating the hours is important as the rates heavily influence the consumers to shift the operation of their appliances from peak to off-peak hours. Also, the level of rates is significant as they reflect the consumption level.

4.2 Simulations and Results

All the algorithms are tested and validated on 24-h and one-year datasets. As stated above, the cost minimization tends to create new peaks by unrestrictedly shifting the consumption of the PA toward the hours with the lowest rates. This is different from other studies as most of them use a small number of appliances. Since the game-optimization algorithm is enhanced by the dynamic ToU tariff, which iteratively calculates the rates based on the total electrical consumption of the community \({\text{TDA}}\), new peaks could be created and the algorithm cannot converge toward an optimal solution. Figure 8 shows the electrical consumption of the community before and after optimization. The 24-h dataset corresponds to a summer day that has the consumption peak at 19:00. Five iterations of the game-optimization algorithm are performed, and the results are displayed in Table 1 in terms of rates, community gain, FI and the individual gains for each house. The dataset in Fig. 8 corresponds to the fifth and last iteration. The FI of the unoptimized data is 0.41 and does not significantly improve as it can be seen in Table 1. The peaks migrate from the day to night hours repeatedly (see the rates in Table 1). Even though the gains can be as high as ~ 32% (e.g., iteration 2 and 4), the Flattening Index is not convenient for the retailer and the constraints must be imposed. Therefore, if the \({\text{PACM}}\) has only ones, that indicates the maximum flexibility of the PA, the swaying effect of the peak will be encountered. Thus, this matrix reflects the consumers’ preferences and should have zeros as well.

Fig. 8
figure 8

The total consumption of the community before (left) and after (right) optimization on 24-h datasets with no constraints on the PA shifting hours

Full size image
Table 1 The gains after the optimization of a 24-h dataset with no constraint
Full size table

The consumer can impose his consumption preferences through the \({\text{PACM}}\) to increase his comfort (e.g., to restrict the functioning of noisy appliances during the night). As there is no real information about the PA constrains and their number is very high, it is assumed that approximately 20% of the operating hours (approximately 5 h per day) are restricted in the \({\text{PACM}}\) randomly. These constraints allow obtaining a considerably better flattening of the consumption vector over the first 5 iterations, as presented in Fig. 9 and Table 2. It can be also observed that no house registers negative gains compared to the unoptimized dataset (compare Table 1 with Table 2). The FI reaches up to 0.7 (and in some other simulations even more) without a substantial loss in gain. Figure 10 shows the individual consumption of the houses in the community for a better insight into the optimization algorithm at the house level.

Fig. 9
figure 9

The total consumption of the community before/after optimization with customers’ preferences

Full size image
Table 2 Community gains after the optimization of a 24-h dataset with consumers’ preferences
Full size table
Fig. 10
figure 10

Individual consumption before (left) and after optimization (right) on a 24-h dataset with consumers’ preferences

Full size image

If restrictions from the customers are not available, or if they are not consistent enough to ensure a desired flattening of the consumption vector, the retailer can create and impose certain constraints in the optimization algorithm or shifting conditions that can be activated when required. Therefore, the retailer can stop the creation of new peaks by imposing a maximum hourly consumption, \({\text{MA}}_{i}\), on the optimized individual \({\text{DA}}_{i}\) vector. This constraint (\(A_{i}^{h} < {\text{MA}}_{i}\)) is more likely to be imposed for SI since they can be easily shifted at the hour with the lowest rate, regardless of consumption. Before shifting, the optimization algorithm verifies if the new total consumption of a certain hour is higher than \({\text{MA}}_{i}\). If \(A_{i}^{h} \ge {\text{MA}}_{i}\), the algorithm restricts the hour in the \({\text{PACM}}_{i} \) and thus, the next position of \(sN_{i}\) is evaluated at step 4 in Sect. 3.1.2. Therefore, \({\text{MA}}_{i}\) could be an optional restriction of the optimization problem. If \({\text{MA}}_{i}\) is too low, the optimization process will be very restricted and only few appliances will be shifted. On the other hand, if \({\text{MA}}_{i}\) is too high, the optimization will remain unconstrained. For the simulations presented below, we consider \({\text{MA}}_{i}\) as twice the average of the hourly consumption of each house. But the shifting condition is at the retailer’s convenience and could be also imposed as long as the new peak is lower than daily average consumption. Figure 11 shows the community consumption before and after optimization with constraints imposed by retailer; the results consist in a particularly good FI of up to 0.8. Table 3 presents the first 5 iterations of the game-optimization algorithm in terms of rates, total gain, FI and individual gains.

Fig. 11
figure 11

The total consumption of the community before/after optimization with retailer’s constraints

Full size image
Table 3 Community gains after the optimization of a 24-h dataset with retailer’s constraints
Full size table

Not all daily consumption profiles look similar, some days have 2 peaks (one in the morning and one in the evening) and others only one peak (in the evening). To investigate the result of the game-optimization algorithm on a bigger time interval, the algorithm is run for a one-year dataset with no constraints. Figure 12 shows the results obtained by displaying the annual hourly averages. The FI of the unoptimized dataset is 0.67 and of the optimized set 0.68 (PAR decreased from 2.25 to 2.18), indicating the need for constraints. Table 4 shows the average annual gains for each house and the total cost after optimization. The different gains between the houses reside in the individual consumption profile and flexibility.

Fig. 12
figure 12

The total consumption of the community before (left) and after (right) optimization on one-year datasets of with no constraints

Full size image
Table 4 Yearly average gains and total cost after optimization with no constraints
Full size table

Figure 13 shows the annual hourly averages after optimization with constraints from the customers (~ 20% restricted hours). In this case, the average FI can be as high as 0.83 (PAR = 1.46), while the gains are similar (as presented in Table 5).

Fig. 13
figure 13

The total consumption of the community before (left) and after (right) optimization on one-year datasets with consumers’ constraints

Full size image
Table 5 Yearly average gains and total cost after optimization with consumers’ constraints
Full size table

Simulations are performed also for the case when the retailer imposes the constraints to prevent the occurrence of the new peaks (see Fig. 14 showing the annual hourly averages for this case). The average FI after optimization is 0.77 (PAR = 1.7).

Fig. 14
figure 14

The total consumption of the community before (left) and after (right) optimization on one-year datasets with retailer’s constraints

Full size image

Tables 5 and 6 present the average gains and the costs after optimization for both cases of constraints. The results are slightly better when the consumers impose their preferences and can be further improved by redesigning the \({\text{PACM}}_{i}\).

Table 6 Yearly average gains and total cost after optimization with retailer’s constraints
Full size table

5 Conclusion

A reliable game-optimization algorithm has been designed to achieve the best reward for a community of 11 houses with numerous appliances, implementing a dynamic ToU tariff. The cost optimization algorithm addresses both types of programmable appliances: non-interruptible and interruptible. The dynamic ToU tariff iteratively calculates the off-peak, shoulder and peak rates based on the total hourly consumption of the community, assigning higher rates at high consumption level, discouraging the peak consumption. The calculated rates are input for the optimization algorithm which provides a solution to minimize the cost by shifting the consumption of the programmable appliances toward hours with lower rates. Because the ToU tariff rates are calculated based on the total hourly consumption array, the algorithm enhances the cost minimization by repetitive optimization, providing, as a result, cost reductions of up to 30%. The simulations without constraints, seen as the highest flexibility degree, lead to new peaks which translates into the need to impose constraints. The simulations have been performed with certain customers’ preferences (~ 20% restricted hours of operation) or with constrains imposed by the retailer (in case the consumers preferences are not available) which limit the shifting flexibility degree of the programmable appliances. The Flattening Index can go as high as 0.83. As future work, as the optimization in multiple iterations is more complex, it could be performed and implemented as an automatic process that uses machine learning with direct load control (DLC), Internet of Things (IoT) and other mechanisms that ease the process and improve its effectiveness.