The Generalized Minimum Branch Vertices Problem: Properties and Polyhedral Analysis

Abstract

This article introduces the Generalized Minimum Branch Vertices problem. Given an undirected graph, where the set of vertices is partitioned into clusters, the Generalized Minimum Branch Vertices problem consists of finding a tree spanning exactly one vertex for each cluster and having the minimum number of branch vertices, namely vertices with degree greater than two. When each cluster is a singleton, the problem reduces to the well-known Minimum Branch Vertices problem, which is NP-hard. We show some properties that any feasible solution to the problem has to satisfy. Some of these properties can be used to determine useless vertices or edges, which can be removed to reduce the size of the instances. We propose an integer linear programming formulation for the problem, we derive the dimension of the polytope, we study the trivial inequalities and introduce two new classes of valid inequalities, that are proved to be facet-defining.

1 Introduction

In this paper, we introduce the Generalized Minimum Branch Vertices (GMBV) problem: given an undirected graph $G=(V,E)$, where V is partitioned into clusters $V_1,\ldots , V_k$, the aim is determining a connected subgraph spanning exactly one vertex for each cluster, and with the minimum number of branch vertices, namely vertices with degree greater than two. The GMBV problem is NP-hard, and indeed when each cluster is a singleton, it reduces to the Minimum Branch Vertices (MBV) problem. The MBV problem was introduced by Gargano et al. [1]. Carrabs et al. [2] proposed four mathematical formulations, while Silvestri et al. [3] derived some valid inequalities and proposed a hybrid formulation with both undirected and directed variables, which was solved through a branch and cut algorithm. Landete et al. [4] investigated decomposition methods for degree dependent spanning tree problems. Merabet et al. [5] proposed a generalization of the MBV problem, introducing the definition of k-branch vertex, a vertex with degree greater than $k+2$. Furthermore, in [6], it is showed that, given a connected graph with n vertices and minimum degree at least equal to $\Big (\frac{1}{s+3}+o(1)\Big )n$, with $s\ge 1$, then there exists in the graph a spanning tree having at most s branch vertices.

The GMBV problem arises in the context of optical networks. When designing Metropolitan Area Network (MAN), we need to interconnect several Local Area Network (LAN), by selecting a hub for each LAN, and then connecting hubs through transmission links. If more than two links entering a hub are chosen, the optical signal has to be split using a dedicated network device, a switch. Then, the minimization of the number of switches in the network is required to minimize the costs. This problem can be modelled as a GMBV problem, where each LAN is a cluster, each hub is a vertex and hubs, where a switch is deployed, are branch vertices. Notice that, in location problems, hubs are facilities, that serve as transhipment and switching point to consolidate flows at certain locations for transportation, airline, and postal systems so they are vital elements of such networks. Here, with the word “hub”, we refer to one of the most simple network devices used as a connection point for devices in a network. Basically, it is a simple repeater because it repeats the signal that comes in one of its ports out all other ports. To the best of our knowledge, the GMBV problem has never been introduced before. However, in the literature, the generalized version of other network design problems have been extensively studied. Feremans et al. [7] provided a definition of the Generalized Network Design Problem, as a problem defined over clustered graph and where the feasibility conditions are expressed in terms of the clusters. Myung et al. [8] introduced the Generalized Minimum Spanning Tree problem, and Feremans et al. [9] proposed several mathematical formulations for it. Moreover in [10], they developed new valid inequalities and designed a Branch and Cut algorithm. Fischetti et al. [11] conducted a polyhedral analysis for the Generalized Travelling Salesman Problem, and in [12], they proposed a Branch and Cut algorithm.

Other applications in the optical networks with clustered graphs arise in the wavelength routing and assignment problem ([13] and [14]), Partition Graph Coloring problem ([15, 16] and [17]), and Bandwidth Allocation problems ([18]).

The remainder of the paper is organized as follows. In Sect. 2, we introduce the definition of the problem and some notations. In Sect. 3, we propose an integer linear programming formulation for the GMBV problem. Section 4 reports some properties about clustered graphs. In Sect. 5, we derive the dimension of the polytope, and we studied the trivial inequalities and introduce two new classes of valid inequalities, that are proved to be facet-defining. Conclusions are given in Sect. 6. Finally, in Appendix, we prove some facetal results regarding the polytope of the MBV problem, that are necessary for the proof of some propositions in Sect. 5.

2 Definition of the Problem and Notation

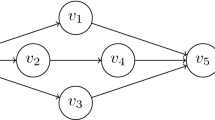
Let $G=(V,E)$ be an undirected graph, where V is the set of vertices, and E is the set of edges. We denote by n the number of vertices, and by m the number of edges in G. Moreover, G is clustered, which means that V is partitioned into k clusters, $V_1,\ldots ,V_k$; see Fig. 1a. A generalized spanning tree (gst) of G is a subgraph $G_T=(V_T,E_T)$ of G, such that $G_T$ is a tree and $|V_T\cap V_i|=1$, for any $i=1,\ldots ,k$. A vertex $v\in V_T$ is a branch vertex if its degree is greater than two in $G_T$. The Generalized Minimum Branch Vertices (GMBV) problem, consists of finding a gst in G, with the minimum number of branch vertices. Since exactly one vertex for each cluster can be selected, from now on we assume that G does not contain any edge within any cluster. Let us consider the graph G shown in Fig. 1a. An optimal solution to the GMBV problem in G is the tree in Fig. 1b, having only one branch vertex.

Fig. 1

a A graph G with five clusters. b A gst of G with one branch vertex

3 Mathematical Formulation

The GMBV problem can be formulated as an integer linear program (ILP) as follows. The binary variables are:

• $x_e$, $\forall e\in E$, is equal to 1 if e is selected, and 0 otherwise;

• $y_v$, $\forall v\in V$, is equal to 1 if v is selected, and 0 otherwise;

• $z_v$, $\forall v\in V$, is equal to 1 if v is a branch vertex, and 0 otherwise.

Given $E'\subseteq E$ and $V'\subseteq V$, we use the notations $x(E')=\sum _{e\in E'} x_e$, and $y(V')=\sum _{v\in V'} y_v$. For $S,T\subseteq V$, we define

$$\begin{aligned} E(S:T)=\{\{u,v\}\in E: u\in S, v\in T\}. \end{aligned}$$

$E(S)=E(S:S)$ is the set of the edges having both extremes in S. We denote by $\delta (S)=E(S:V\setminus S)$ the set of edges incident to vertices in S, and by $N(S)=\{v\in V\setminus S: \exists \{u,v\}\in \delta (S),u\in S\}$. When $S=\{v\}$, $\delta (\{v\})$ and $N(\{v\})$ become $\delta (v)$ and N(v) respectively, and we denote by d(v) the cardinality of $\delta (v)$. Let us denote by ${\mathcal {K}}$ the set of indices of the clusters, ${\mathcal {K}}=\{1,\ldots ,k\}$. Given $S\subseteq V$, we define $\mu (S)=|\{i\in {\mathcal {K}}: V_i\subseteq S\}|$, that is the number of clusters included in S. Given a vertex $v\in V$, we denote by h(v) the index of the cluster containing v, and then by $V_{h(v)}$ the cluster containing v. Finally, given a subset of vertices $V'\subseteq V$, we denote by $G[V']=(V', E(V'))$, the subgraph induced by $V'$. When $V'=\{a_1,\ldots ,a_l\}$, instead of $G[\{a_1,\ldots ,a_l\}]$, we use simply $G[a_1,\ldots ,a_l]$.

The ILP formulation is the following:

$$\begin{aligned} \text{ Minimize } z= \sum _{v\in V} z_v \end{aligned}$$

(1)

subject to

$$\begin{aligned} x(E)&=k-1 \end{aligned}$$

(2)

$$\begin{aligned} y(V_i)&=1 \quad i\in {\mathcal {K}} \end{aligned}$$

(3)

$$\begin{aligned} x(E(S))&\le y(S)-1 \quad S\subset V: |S|\ge 2, \mu (S)>0 \end{aligned}$$

(4)

$$\begin{aligned} x(\delta (v))-2y_v&\le (d(v)-2) z_v \quad v\in V \end{aligned}$$

(5)

$$\begin{aligned} x_e&\in \{0,1\} \quad e\in E \end{aligned}$$

(6)

$$\begin{aligned} y_v&\in \{0,1\} \quad v\in V \end{aligned}$$

(7)

$$\begin{aligned} z_v&\in \{0,1\} \quad v\in V \end{aligned}$$

(8)

The objective function (1) minimizes the number of branch vertices. Constraint (2) requires that the number of selected edges coincides with the number of clusters minus one. Constraints (3) guarantee that exactly a vertex is selected for each cluster. Constraints (4) are the Generalized Subtour Elimination Constraints (GSECs), introduced in [10]. Constraints (5) ensure that a selected vertex v is a branch vertex if at least three edges in $\delta (v)$ are selected. The objective function forces variables $z_v$ to zero when $x(\delta (v))\le 2$ holds.

It is worth noting two particular cases of the GSECs:

$$\begin{aligned} x(E(\{v\}:V_i))&\le y_v \quad i\in {\mathcal {K}},v\in V\setminus (W\cup V_i) \end{aligned}$$

(9)

$$\begin{aligned} x(\delta (v))&\ge y_v \quad v\in V \end{aligned}$$

(10)

Constraints (9) are obtained from constraints (4), when $S=V_i\cup \{v\}$, while (10) are obtained choosing $S=V\setminus \{v\}$. Let us note that constraints (9) ensure that $y_v$ is equal to 1 if at least one edge incident to v is selected, while constraints (10) ensure that $y_v$ is equal to 0 if no edge in $\delta (v)$ is selected.

4 Properties of the Clustered Graphs

In this section, we show some properties that any feasible solution to the GMBV problem satisfies. Some of these properties can be used to determine useless vertices or edges since they do not belong to any feasible solution. These elements could be identified and removed to reduce the size of the graph. Moreover, they will be used in Sect. 5 to obtain some polyhedral results about the GMBV polytope.

4.1 v-Connection

Definition 4.1

Given a vertex $v\in V$, G is v-connected if there exist vertices $a_1\in V_1,\ldots ,a_k\in V_k$, with $a_{h(v)}=v$, such that $G[a_1,\ldots ,a_k]$ is connected.

Given the graph $G=(V,E)$, shown in Fig. 2a, it is easy to see that it is $v_1$-connected since the subgraph $G[v_1,v_4,v_5,v_6]$ is connected (see Fig. 2b). On the contrary, G is not $v_2$-connected, because neither $G[v_2,v_3,v_5,v_6]$ nor $G[v_2,v_4,v_5,v_6]$ is connected. If the subgraph $G[a_1,\ldots ,a_k]$ is not connected, let us denote by $c(a_1,\ldots ,a_k)$ the number of connected components of $G[a_1,\ldots ,a_k]$. Then, we define

$$\begin{aligned} c_v=min\{c(a_1,\ldots ,a_k):&a_1\in V_1,\ldots ,a_k\in V_k, a_{h(v)}=v, \\&G[a_1,\ldots ,a_k] \text{ is } \text{ not } \text{ connected }\}. \end{aligned}$$

For example, in the graph shown in Fig. 2a, it results that $c(v_2,v_3,v_5,v_6)={=c(v_2,v_4,v_5,v_6)=2}$, then $c_{v_2}=2$.

Remark 4.1

If each cluster is a singleton, given a vertex $v\in V$, G is v-connected if and only if G is connected.

Indeed, since each cluster is a singleton, we have that ${V_1=\{a_1\},\ldots ,V_k=\{a_k\}}$, and $G[a_1,\ldots ,a_k]=G$. Therefore, the v-connection is an extension of the connection property to clustered graphs.

Fig. 2

a A graph G, such that G is $v_1$-connected, but not $v_2$-connected. b A connected subgraph $G[v_1,v_4,v_5,v_6]$

Lemma 4.1

Given a vertex $v\in V$, G is v-connected, if and only if there exists a feasible solution to the GMBV problem containing v.

Proof

If G is v-connected, there exist $a_1\in V_1,\ldots ,a_k\in V_k$, with $a_{h(v)}=v$, such that $G[a_1,\dots ,a_k]$ is connected. Therefore, there exists a gst $G_T$ in $G[a_1,\ldots ,a_k]$, that is a feasible solution to the GMBV problem containing v.

On the contrary, let $G_T$ be a gst containing v. The subgraph induced by the vertices in $G_T$ is connected, and then G is v-connected. $\square$

Thanks to Lemma 4.1 it is possible to identify in G vertices that are useless because they do not belong to any feasible solution. To this end, for any $v\in V$, we have to check if G is v-connected and, if this condition does not hold, v can be removed from G. In what follows, we assume that G is v-connected, for any $v\in V$, to guarantee that any vertex may belong to a feasible solution to the GMBV problem. It is worth noting that in G there could be useless edges too. Indeed, given an edge $\{u,v\}\in E$, even if G is both u-connected and v-connected, it may not be contained in any feasible solution, as shown by the following remark:

Remark 4.2

Given an edge $e=\{u,v\}\in E$, even if G is u-connected and v-connected, this does not imply that there exists a feasible solution to the GMBV problem in G, containing e.

Let us consider the graph shown in Fig. 3: it is u-connected and v-connected. It is easy to see that edge $\{u,v\}$ cannot belong to any feasible solution, since the contemporary selection of u and v does not allow to reach cluster $V_3$.

Fig. 3

A v-connected (dotted line) and u-connected (dashed line) graph, such that the edge $\{u,v\}$ does not belong to any feasible solution

Given $1\le l\le k$ and $\{a_1,\ldots ,a_l\}\subseteq V$, with $h(a_1)\ne h(a_2)\ne \ldots \ne h(a_l)$, we denote by $G(a_1,\ldots ,a_l)$ the subgraph of G obtained by removing all vertices in $V_{h(i)}$, except for $a_i$, for $i=1,\ldots ,l$. Thus,

$$\begin{aligned} G(a_1,\ldots ,a_l)=G[V\setminus \{V_{h(a_1)}\setminus \{a_1\}\}\setminus \{V_{h(a_2)}\setminus \{a_2\}\}\setminus \ldots \setminus \{V_{h(a_l)}\setminus \{a_l\}\}]. \end{aligned}$$

Lemma 4.2

Given an edge $e=\{u,v\}\in E$, G(u) is v-connected, if and only if there exists a feasible solution to the GMBV problem in G containing e.

Proof

Since G(u) is v-connected, there exist $a_1\in V_1,\ldots ,a_k\in V_k$, with ${a_{h(v)}=v}$, such that $G[a_1,\ldots ,a_k]$ is connected. Moreover, $V_{h(u)}$ in G(u) is a singleton containing only vertex u, thus $a_{h(u)}=u$. Therefore, in $G[a_1,\ldots ,a_k]$ there exists a gst, $G_T=(V_T,E_T)$, spanning u and v. If edge e belongs to $E_T$, the lemma is proved. Otherwise, we can build a new gst, $G_T'=(V_T, E'_T)$, where $E'_T=E_T\cup \{e\}\setminus \{e'\}$, with $e'$ one of the edges in $E_T$ belonging to the cycle generated by the introduction of e in $G_T$.

On the contrary, if there exists a gst, $G_T=(V_T,E_T)$, in G containing edge e, then $G_T$ is a connected subgraph containing u and v, and this implies that G(u) is v-connected. $\square$

4.2 Generalized Cut Vertex

In this section, we extend the notion of cut vertices to clustered graphs, where a cut vertex is a vertex whose removal disconnects the graph.

Definition 4.2

A vertex $v\in V$ is a generalized cut vertex in G, if there exists a vertex $u\in N(v)$, such that $G[V\setminus V_{h(v)}]$ is not u-connected.

In the graph depicted in Fig. 4, $v_1$ is a generalized cut vertex, and indeed it results that $G[V\setminus V_{h(v_1)}]$ is not u-connected for any $u\in N(v_1)$, with $N(v_1)=\{v_3,v_4,v_6,v_7\}$. If v is a generalized cut vertex, let us denote by $c(v)=min\{c_u: u\in N(v),G[V\setminus V_{h(v)}] \text{ is } \text{ not } u\text{-connected }\}$. In the previous example, we have that $c(v_1)=min\{c_{v_3},c_{v_4},c_{v_6},c_{v_7}\}$, where $c_{v_3}=c_{v_6}=3$, $c_{v_4}=min\{c(v_4,v_5,v_7),c(v_4,v_6,v_7)\}=2$, and $c_{v_7}=2$. Therefore, $c(v_1)=2$.

Fig. 4

A graph G, such that vertex $v_1$ is a generalized cut vertex

Remark 4.3

If each cluster is a singleton, a generalized cut vertex is exactly a cut vertex.

Lemma 4.3

Given a vertex $v\in V$, if $G[V\setminus V_{h(v)}]$ is not u-connected, for any $u\in N(v)$, and $c(v)\ge 3$, then v is a branch vertex in every GMBV feasible solution which contains v.

Proof

Let us suppose that $G[V\setminus V_{h(v)}]$ is not u-connected, for any $u\in N(v)$, and $c(v)\ge 3$. Whenever in cluster $V_{h(v)}$ we select v, to guarantee connectivity, we have to select at least three edges in $\delta (v)$. Therefore, v is a branch vertex in every feasible solution which contains v. $\square$

Lemma 4.4

If a vertex $v\in V$ is not a generalized cut vertex, then there exists a feasible solution to the GMBV problem containing v, and exactly one edge incident on v.

Proof

Since v is not a generalized cut vertex, for any $u\in N(v)$, $G[V\setminus V_{h(v)}]$ is u-connected. W.l.o.g., let us assume $V_{h(v)}=V_1$. According to the definition, there exist $a_2\in V_2,\ldots ,a_k\in V_k$, with $a_{h(u)}=u$, such that $G[a_2,\ldots ,a_k]$ is connected. Therefore, there is a spanning tree $G_{T_u}=(V_{T_u},E_{T_u})$ in $G[a_2,\ldots ,a_k]$, that is a gst in $G[V\setminus V_{h(v)}]$ containing u. Finally, if we consider $G_T=(V_T,E_T)$, where $V_T=V_{T_u}\cup \{v\}$ and $E_T=E_{T_u}\cup \{u,v\}$, it is a feasible solution to the GMBV problem in G, containing v and exactly one edge in $\delta (v)$. $\square$

Notice that, if $v\in V$ is not a generalized cut vertex, we have at least d(v) feasible solutions to the GMBV problem containing v, and exactly one edge incident on it, one for each edge in $\delta (v)$.

Lemma 4.5

If there are no generalized cut vertices in G, then there exists a feasible solution to the GMBV problem containing v, and at least two edges in $\delta (v)$, for any $v\in V$.

Proof

Since G does not contain any generalized cut vertex, $d(v)\ge 2$ for any $v\in V$. Given $v\in V$, let us consider $u\in N(v)$. Since u is not a generalized cut vertex, according to Lemma 4.4, there exists a feasible solution to the GMBV problem, $G_T$, containing u and exactly one edge in $\delta (u)$. In more detail, let us assume that $\{u,v\}$ belongs to $G_T$. Therefore, $G_T$ contains $\{u,v\}$ and at least another edge incident on v, and thus it is a feasible solution to the GMBV problem containing v, and with at least two edges belonging to $\delta (v)$. $\square$

5 Polyhedral Analysis

Let us denote by P(G) the polytope described by the constraints (2)–(8), that is:

$$\begin{aligned} P(G)=conv\{(x,y,z)\in {\mathbb {R}}^{|E|+2|V|}: (x,y,z) \text{ satisfies } (2)-(8)\}. \end{aligned}$$

(11)

In this section, we examine some properties of the polytope P(G). To assure that each vertex could be a branch vertex in a GMBV solution, we assume that $k\ge 4$ and N(v) contains at least three vertices belonging to three different clusters, for any $v\in V$.

Let us consider the set $W=\{v\in V: |V_{h(v)}|=1\}$, containing vertices which belong to clusters that are singletons. We denote by $t=|V\setminus W|$, and by s the number of clusters that are not singletons, namely $s=|\{i\in {\mathcal {K}}:|V_i|>1\}|$. We assume that:

• (A1) G does not contain any generalized cut vertex;

• (A2) if $t>0$, there exist $S_1\subset S_2\subset \ldots \subset S_{t-s}\subset V$, with $\mu (S_i)=0$ and $|S_i|=i$, for any $i=1,\ldots ,t-s$, such that $G[V \setminus S_i]$ does not contain any generalized cut vertex.

Let us consider the graph $G=(V,E)$ shown in Fig. 5. Here we have, $k=4$, $t=6$ and $s=3$. G satisfies assumption (A1). Moreover, it satisfies assumption (A2), with $S_1=\{v_1\}$, $S_2=\{v_1,v_4\}$ and $S_3=\{v_1,v_4,v_7\}$.

Fig. 5

A graph $G=(V,E)$, with $k=4$, $t=6$ and $s=3$, satisfying assumptions (A1) and (A2)

Let us introduce some results, which were proposed by [11] for the Generalized Travelling Salesman problem, and here they are adapted to the GMBV problem.

Definition 5.1

Let $\alpha x\le \beta y+\gamma z+\delta$ be a valid inequality for P(G). We denote by ${\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta )$, the face of P(G) induced by $\alpha x\le \beta y+\gamma z+\delta$. Given a vertex $v\in V\setminus W$, the v-restriction of $\alpha x\le \beta y+\gamma z+\delta$ is the inequality obtained through the deletion of the variables $y_v$, $z_v$ and $x_e$, for all $e\in \delta (v)$.

Lemma 5.1

Given a valid inequality $\alpha x\le \beta y+\gamma z+\delta$, for any $v\in V\setminus W$, the dimension of ${\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta )$ is greater than or equal to the sum of the following quantities:

• (i) the dimension of the face of the polytope $P(G[V\setminus \{v\}])$ induced by the v-restriction of $\alpha x\le \beta y+\gamma z+\delta$;

• (ii) the rank of the matrix containing the coordinates of the extreme points of ${\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta )$ with $y_v=1$, restricted to $y_v$, $z_v$ and $x_e$, for any $e\in \delta (v)$.

Proof

Let us consider the matrix $\mathbf {X}$, where each row is an extreme point of the face ${\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta )$. Let us note that, since the polytope does not contain the origin, the dimension of ${\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta )$ is the rank of $\mathbf {X}$ minus 1. Given $v\in V\setminus W$, matrix $\mathbf {X}$ can be partitioned in this way:

$$\begin{aligned} \mathbf {X}= \begin{bmatrix} {\varvec{X_{11}}} &{} 0 &{} 0 &{} 0 \\ {\varvec{X_{21}}} &{} {\varvec{X_{22}}} &{} 1 &{} 0\\ {\varvec{X_{31}}} &{} {\varvec{X_{32}}} &{} 1 &{} 1 \end{bmatrix} \end{aligned}$$

The last two columns are associated with variables $y_v$ and $z_v$, respectively, while the submatrix $\begin{bmatrix} {\varvec{X_{22}}}\\ {\varvec{X_{32}}} \end{bmatrix}$ contains variables $x_e$, with $e\in \delta (v)$. It results that $rank {\mathbf {X}} \ge rank \mathbf {X_{11}}+rank$ $\begin{bmatrix} {\varvec{X_{22}}} &{} 1 &{} 0\\ {\varvec{X_{32}}} &{} 1 &{} 1 \end{bmatrix}$, where $rank \mathbf {X_{11}}$ minus 1 is exactly the dimension of the face of $P(G[V\setminus \{v\}])$, induced by the v-restriction of $\alpha x\le \beta y+\gamma z+\delta$. $\square$

Given $V'\subseteq V$, we represent $V'$ by its characteristic vector, ${\varvec{\nu }}^{V'}\in {\mathbb {B}}^n$, with ${\varvec{\nu }}_v^{V'}=1$ if $v\in V'$, and ${\varvec{\nu }}_v^{V'}=0$ otherwise. Analogously, given $E'\subseteq E$, let ${\varvec{\pi }}^{E'}\in {\mathbb {B}}^m$ be its characteristic vector, with ${\varvec{\pi }}_e^{E'}=1$ if $e\in E'$, and ${\varvec{\pi }}_e^{E'}=0$ otherwise. Moreover, we denote by $\mathbb {{\mathbf {0}}}$ and $\mathbb {{\mathbf {1}}}$, the vectors of all zeros and all ones, respectively.

Proposition 5.1

If (A1) and (A2) hold, then $dim(P(G))=m+2n-k-1$.

Proof

Inequality $dim(P(G))\le m+2n-k-1$ is trivial, and indeed constraints (2) and (3) are valid for P(G), and they are linearly independent. We show the inverse inequality by induction on t. We recall that $t=|V\setminus W|$, namely t is the number of vertices which belong to clusters that are not singletons. When $t=0$, the GMBV problem reduces to the MBV problem and the claim is true (see [3]). Let us assume that the claim holds for t, we prove it for $t+1$. Since $t>0$, then there exists at least a vertex $v\in V\setminus W$. According to Lemma 5.1, given the valid inequality $0\le 0$, $dim(P(G))\ge rank\; \mathbf {X_{11}}+rank$ $\begin{bmatrix} {\varvec{X_{22}}} &{} 1 &{} 0\\ {\varvec{X_{32}}} &{} 1 &{} 1 \end{bmatrix}$. Furthermore, assumption (A2) implies that we can choose $v\in V\setminus W$ such that $G[V\setminus \{v\}]$ satisfies the same conditions as G. Thus, from the induction hypothesis, it follows that ${rank\; \mathbf {X_{11}}=|E\setminus \delta (v)|+2|V\setminus \{v\}|-k-1}$. Therefore, we need to show that $rank$ $\begin{bmatrix} {\varvec{X_{22}}} &{} 1 &{} 0\\ {\varvec{X_{32}}} &{} 1 &{} 1 \end{bmatrix}$ $=d(v)+2$. This matrix contains the columns associated to $y_v$, $z_v$ and $x_e$, $e\in \delta (v)$, of the incidence vectors of GMBV solutions containing vertex v. We have to exhibit $d(v)+2$ incidence vectors belonging to P(G), such that, when restricted to $y_v$, $z_v$ and $x_e$, ${e\in \delta (v)}$, are linearly independent. Due to assumption (A1) and Lemma 4.4, for any $u\in N(v)$, there exists a gst $G_{T^u}=(V_{T^u},E_{T^u})$, such that $y_v=1$, $x_{\{u,v\}}=1$, and $x(\delta (v))=1$. Therefore, for any $u\in N(v)$, $({\varvec{\pi }}^{E_{T^u}},{\varvec{\nu }}^{V_{T^u}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belongs to P(G), and matrix $\mathbf {X_{22}}$ is the identity matrix $\mathbf {I_{d(v)}}$. Moreover, $({\varvec{\pi }}^{E_{T^u}},{\varvec{\nu }}^{V_{T^u}},{\varvec{1}})$, with $u\in N(v)$, belongs to P(G) too. Due to Lemma 4.5, there exists a gst $G_T=(V_T,E_T)$, with $y_v=1$ and $x(\delta (v))>1$. Thus, $({\varvec{\pi }}^{E_{T}},{\varvec{\nu }}^{V_{T}},{\varvec{1}})$ belongs to P(G). Introducing in the matrix the incidence vectors of these solutions, we have:

$$\begin{aligned} \begin{bmatrix} {\varvec{X_{22}}}&{} 1 &{} 0\\ {\varvec{X_{32}}} &{} 1 &{} 1 \end{bmatrix} = \begin{bmatrix} {\varvec{I_{d(v)}}} &{} 1 &{} 0\\ 1\; 0\; 0\; 0\; \ldots \;0 &{} 1 &{} 1\\ 1\;\ldots 1\; 0\; \ldots \;0&{}1 &{} 1 \end{bmatrix} \end{aligned}$$

The rows of this matrix are linearly independent, and thus its rank is $d(v)+2$. $\square$

Lemma 5.2

Given a valid inequality $\alpha x\le \beta y+\gamma z+\delta$ inducing a proper face of P(G), if there exists a vertex $v\in V\setminus W$ such that:

• (i) $P(G[V\setminus \{v\}])$ satisfies assumptions (A1) and (A2);

• (ii) the v-restriction of this inequality is facet-defining for $P(G[V\setminus \{v\}])$;

• (iii) there are $d(v)+2$ incidence vectors of GMBV solutions containing v and belonging to ${\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta )$, such that their restriction to $x_e$, $e\in \delta (v)$, $y_v$ and $z_v$, are linearly independent;

then, $\alpha x\le \beta y+\gamma z+\delta$ is facet-defining for P(G).

Proof

Inequality $\alpha x\le \beta y+\gamma z+\delta$ induces a proper face of P(G), then $dim({\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta ))\le m+2n-k-2$. Therefore, we have to prove the inverse inequality. From Lemma 5.1 follows that

$$\begin{aligned} dim({\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta ))\ge dim(v-restriction)+rank \begin{bmatrix} {\varvec{X_{22}}} &{} 1 &{} 0\\ {\varvec{X_{32}}} &{} 1 &{} 1 \end{bmatrix}. \end{aligned}$$

Hypothesis (ii) implies that the v-restriction of the inequality is a facet of $P(G[V\setminus \{v\}])$, then, for the Proposition 5.1 it results that $dim(v-restriction)= {=|E\setminus \delta (v)|+2|V\setminus \{v\}|-k-2=m+2n-k-d(v)-4}$. Moreover, Hypothesis 2 implies that $rank$ $\begin{bmatrix} {\varvec{X_{22}}} &{} 1 &{} 0\\ {\varvec{X_{32}}} &{} 1 &{} 1 \end{bmatrix}$ $=d(v)+2$. Therefore, we have that ${dim({\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta ))\ge m+2n-k-d(v)-4+d(v)+2=m+2n-k-2}$. $\square$

Lemma 5.3

Given a valid inequality $\alpha x\le \beta y+\gamma z+\delta$ inducing a proper face of P(G), if there exists a vertex $v\in V\setminus W$ such that:

• (i) $P(G[V\setminus \{v\}])$ satisfies assumptions (A1) and (A2);

• (ii) the v-restriction of this inequality is trivial;

• (iii) there are $d(v)+1$ incidence vectors of GMBV solutions containing v and belonging to ${\mathcal {H}}(\alpha ,\beta ,\gamma ,\delta )$, such that their restriction to $x_e$, $e\in \delta (v)$, $y_v$ and $z_v$, are linearly independent;

then, $\alpha x\le \beta y+\gamma z+\delta$ is facet-defining for P(G).

Proof

The proof of this lemma is almost the same as the one of Lemma 5.2. $\square$

Remark 5.1

Inequality $x_e\ge 0$, $e\in E$, is a facet of P(G) if $G\setminus \{e\}$ satisfies assumptions (A1) and (A2).

Proof

From Proposition 5.1 follows that $dim(P(G\setminus \{e\}))=m-1+2n-k-1$. Thus, in P(G) there exist $m+2n-k-1$ affinely independent incidence vectors which satisfy $x_e\ge 0$ with equality. $\square$

Remark 5.2

Given $e=\{u,v\}\in E$, inequality $x_e\le 1$ is a facet of P(G), if and only if $u,v\in W$.

Proof

It is easy to see that, when u (respectively v) does not belong to W, inequality $x_e\le 1$ is dominated by $x(E(\{u\}:V_{h(v)}))\le y_u$ (respectively, $x(E(\{v\}:V_{h(u)}))\le y_v$). We show the converse by induction on t. If $t=0$, we reduce to the MBV problem and the claim is true. We now assume that the result holds for t, and we show its validity for $t+1$. Given that $t>0$, there exists a vertex $w\in V\setminus W$, such that the graph $G[V\setminus \{w\}]$ satisfies (A1) and (A2). Thanks to the induction hypothesis, the first request of Lemma 5.2 is satisfied, and to complete the proof it remains to exhibit $d(w)+2$ GMBV solutions, such that $y_w=1$, $x_e=1$, and the restrictions of their incidence vectors to $y_w$, $z_w$ and $x_f$, with $f\in \delta (w)$, are linearly independent. Since w is not a generalized cut vertex in G, for any ${\bar{w}}\in N(w)$, there exists a gst $G_{T^{{\bar{w}}}}=(V_{T^{{\bar{w}}}},E_{T^{{\bar{w}}}})$ in G, such that $y_w=1$ and $x(\delta (w))=1$. Furthermore, since both u and v belong to W, it is always possible to choose a subgraph $G_{T^{{\bar{w}}}}$, such that $e\in E_{T^{{\bar{w}}}}$. Therefore, $({\varvec{\pi }}^{E_{T^{{\bar{w}}}}},{\varvec{\nu }}^{V_{T^{{\bar{w}}}}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{w\}})$ belongs to P(G), for any ${\bar{w}}\in N(w)$, and satisfies $x_e\le 1$ to equality. Moreover, $({\varvec{\pi }}^{E_{T^{{\bar{w}}}}},{\varvec{\nu }}^{V_{T^{{\bar{w}}}}},{\varvec{1}})$ belongs to P(G) too. Finally, from Lemma 4.5 follows that there exists a GMBV solution $G_T=(V_T, E_T)$, such that $y_w=1$ and $x(\delta (w))>1$. We can always choose a subgraph $G_T$ such that $e\in E_T$. Thus $({\varvec{\pi }}^{E_{T}},{\varvec{\nu }}^{V_{T}},{\varvec{1}})$ belongs to P(G). Obviously, the restrictions of these GMBV solutions to $y_w$, $z_w$ and $x_f$, with $f\in \delta (w)$, are $d(w)+2$ linearly independent vectors satisfying $y_w=1$ and $x_e=1$. $\square$

Remark 5.3

• 1. Inequality $y_v\ge 0$, $v\in V$, is not facet-defining for P(G).

• 2. Inequality $y_v\le 1$, $v\in V$, is not facet-defining for P(G).

Proof

• 1. Inequality $y_v\ge 0$ is not facet-defining for P(G), and indeed we have that the face $P(G)\cap \{(x,y,z):y_v=0\}$ is properly contained in the proper face $P(G)\cap \{(x,y,z): x(E(\{v\}:V_i))=0\}$, for any $i\ne h(v)$.

• 2. The inequality $y_v\le 1$, $v\in V$, does not define a facet of P(G), because of the constraints (3).

$\square$

Remark 5.4

Inequality $z_v\le 1$, $v\in V$, is a facet of P(G), if assumption (A2) holds for $S_1,\ldots ,S_{t-s}\subset V\setminus \{v\}$.

Proof

We prove the proposition by induction on t. When $t=0$, all clusters are singleton, so the GMBV problem reduces to the MBV problem, and the claim is true. Let us assume that the claim holds for t, we prove it for $t+1$. Since $t>0$, then there is a vertex $u\in V\setminus W$, with $u\ne v$, such that $G[V\setminus \{u\}]$ satisfies assumptions (A1) and (A2). By the induction hypothesis, the first request of Lemma 5.2 is satisfied. If we prove that the second hypothesis of Lemma 5.2 is satisfied too, we are done. To this end, we exhibit $d(u)+2$ GMBV solutions containing u, satisfying $z_v=1$, and such that the restrictions of their incidence vectors to $y_u$, $z_u$ and $x_e$, $e\in \delta (u)$, are linearly independent. By Lemma 4.4, for any $w\in N(u)$, there exists a gst $G_{T^w}=(V_{T^w},E_{T^w})$ in G, with $y_u=1$ and $x(\delta (u))=1$. The vector $({\varvec{\pi }}^{E_{T^w}},{\varvec{\nu }}^{V_{T^w}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{u\}})$ belongs to P(G) and satisfies $z_v=1$, for any $w\in N(u)$. Furthermore, $({\varvec{\pi }}^{E_{T^w}},{\varvec{\nu }}^{V_{T^w}},{\varvec{1}})\in P(G)$ too. By Lemma 4.5, there exists a GMBV solution $G_T=(V_T,E_T)$ having $y_u=1$ and $x(\delta (u))>1$, thus $({\varvec{\pi }}^{E_{T}},{\varvec{\nu }}^{V_{T}},{\varvec{1}})$ belongs to P(G). These are $d(u)+2$ GMBV solutions, which contain u, satisfy $z_v=1$, and such that their restriction to the variables associated to u gives rise to a full rank matrix. $\square$

Remark 5.5

Inequality $z_v\ge 0$, $v\in V$, is a facet of P(G) if

• 1. $G[V\setminus \{v\}]$ satisfies assumptions (A1) and (A2);

• 2. $\mu (N(v))>1$.

Proof

We distinguish two cases:

• $v\in W$: we prove the assert by induction on t. For $t=0$, each cluster is a singleton, and thus the GMBV problem reduces to the MBV problem and the claim is true. Let us assume that the claim is true for t, we prove it for $t+1$. Since $t>0$, there exists $u\in V\setminus W$, such that the graph $G[V\setminus \{u\}]$ satisfies (A1) and (A2). Let us note that $u\ne v$, since $v\in W$. Therefore, by the induction hypothesis, the first request of Lemma 5.2 holds, and to complete the proof, we have to exhibit $d(u)+2$ GMBV solutions, satisfying $y_u=1$ and $z_v=0$, such that the restrictions of their incidence vectors to $y_u$, $z_u$ and $x_e$, with $e\in \delta (u)$, are linearly independent. Given $w\in N(u)$, $w\ne v$, thanks to Hypothesis 1, there exists a gst $G_{{\bar{T}}^w}=(V_{{\bar{T}}^w},E_{{\bar{T}}^w})$ in $G[V\setminus \{v\}]$, such that $y_u=1$, $x_{\{u,w\}}=1$ and $x(\delta (u))=1$. To obtain a gst in G, it is sufficient to add an edge connecting v to a vertex in $V_{{\bar{T}}^w}$, and this can always be done thanks to Hypothesis 2, which ensures that there exists $i\in {\mathcal {K}}\setminus \{h(u)\}$ such that $V_i\subseteq N(v)$. Therefore, $G_{T^w}=(V_{T^w},E_{T^w})$, where $V_{T^w}=V_{{\bar{T}}^w}\cup \{v\}$ and $E_{T^w}=E_{{\bar{T}}^w}\cup \{e\}$, with $e\in \delta (v)\cap \delta (V_i)$, is a gst in G. There are two possibilities:

  • If $v\notin N(u)$, then $({\varvec{\pi }}^{E_{T^w}},{\varvec{\nu }}^{V_{T^w}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{u,v\}})$ belongs to P(G) and satisfies $z_v=0$, for any $w\in N(u)$. Therefore, these are d(u) GMBV solutions containing u.

  • On the contrary, if $v\in N(u)$, $({\varvec{\pi }}^{E_{T^w}},{\varvec{\nu }}^{V_{T^w}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{u,v\}})$, for any $w\ne v$, are $d(u)-1$ GMBV solutions. Furthermore, let us consider the graph ${G_{T^{w'}}=(V_{T^{w'}}, E_{T^{w'}})}$, with $V_{T^{w'}}=V_{{\bar{T}}^{w'}}\cup \{v\}$ and $E_{T^{w'}}=E_{{\bar{T}}^{w'}}\cup \{u,v\}$, where $(V_{{\bar{T}}^{w'}},E_{{\bar{T}}^{w'}})$ is a gst in $G[V\setminus \{v\}]$, for a given $w' \in N(u)\setminus \{v\}$, such that $y_u=1$ and $x(\delta (u))=1$. This is a GMBV solution containing two edges in $\delta (u)$ and satisfying $z_v=0$.

  Thus, in both cases, we have built d(u) GMBV solutions containing u and satisfying $z_v=0$. The remaining two are the followings: one is that represented by $({\varvec{\pi }}^{E_{T^w}},{\varvec{\nu }}^{V_{T^w}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$, for a given $w\in N(u)\setminus \{v\}$; the other one is $({\varvec{\pi }}^{E_{T}},{\varvec{\nu }}^{V_{T}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$, where $V_T=V_{{\bar{T}}}\cup \{v\}$, $E_T=E_{{\bar{T}}}\cup \{e\}$, $e\in \delta (v)\cap \delta (V_i)$, and $(V_{{\bar{T}}},E_{{\bar{T}}})$ is a gst in $G[V\setminus \{v\}]$ having $y_u=1$ and $x(\delta (u))>1$. It is easy to see that these $d(u)+2$ GMBV solutions are such that their restrictions to the variables related to u are linearly independent.

• $v\in V\setminus W$: Since $v\notin W$, then we can apply Lemma 5.3. The v-restriction of $z_v\ge 0$ is the trivial inequality $0\ge 0$. Therefore, to complete the proof it remains to exhibit $d(v)+1$ feasible solutions to the GMBV problem, satisfying $y_v=1$ and $z_v=0$, such that the restrictions of their incidence vectors to $y_v$, $z_v$ and $x_e$, with $e\in \delta (v)$, are linearly independent. For any $u\in N(v)$, there exists a gst $G_{T^u}=(V_{T^u},E_{T^u})$ in G, such that $x(\delta (v))=1$ and $z_v=0$. Therefore, $({\varvec{\pi }}^{E_{T^u}},{\varvec{\nu }}^{V_{T^u}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belongs to P(G) for any $u\in N(v)$. Furthermore, given $u\in N(v)$, let $G_{T^u}=(V_{T^u},E_{T^u})$ be a gst in G having $x(\delta (v))=1=x(\{u,v\})$. Since $\mu (N(v))>1$, then there exist $e\in E_{T^u}$ and $f\in \delta (v)\setminus \{u,v\}$, such that $G_T=(V_T,E_T)$, where $V_T=V_{T^u}$ and $E_T=E_{T^u}\cup \{f\}\setminus \{e\}$, is a gst satisfying $x(\delta (v))=2$. Therefore, $({\varvec{\pi }}^{E_{T}},{\varvec{\nu }}^{V_{T}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belongs to P(G) and satisfies $z_v=0$. It is straightforward to verify that, the restrictions of the incidence vectors of these $d(v)+1$ GMBV solutions to the variables related to v, are linearly independent.

$\square$

Proposition 5.2

Given $k\in K$ and $v\in V\setminus (W\cup V_k)$, $x(E(\{v\}:V_k))\le y_v$ is a facet of P(G) if

• 1. $G[V\setminus \{v\}]$ satisfies assumptions (A1) and (A2);

• 2. $G[V\setminus V_k]$ does not contain any generalized cut vertex.

Proof

We assume that $E(\{v\}:V_k)\ne \emptyset$, otherwise ${x(E(\{v\}:V_k))\le y_v}$ reduces to $y_v\ge 0$.

To prove this proposition we use Lemma 5.3. The v-restriction of the inequality $x(E(\{v\}:V_k))\le y_v$ is the trivial inequality $0\le 0$. Thus, it remains to exhibit $d(v)+1$ feasible solutions to the GMBV problem, satisfying $y_v=1$ and $x(E(\{v\}:V_k))= y_v$, such that the restrictions of their incidence vectors to $y_v$, $z_v$ and $x_e$, with $e\in \delta (v)$, are linearly independent. $G[V\setminus V_k]$ does not contain any generalized cut vertex, then given $u\in N(v)\setminus V_k$, there exists a gst $G_{{\bar{T}}^u}=(V_{{\bar{T}}^u},E_{{\bar{T}}^u})$ in $G[V\setminus V_k]$, such that $x(\delta (v))=1$. Thus, for any $e=\{v,w\}\in E(\{v\}:V_k)$, it results that $G_{T^{u,e}}=(V_{T^{u,e}},E_{T^{u,e}})$, where $V_{T^{u,e}}=V_{{\bar{T}}^u}\cup \{w\}$ and $E_{T^{u,e}}=E_{{\bar{T}}^u}\cup \{e\}$, is a gst in G. It is easy to see that, $({\varvec{\pi }}^{E_{T^{u,e}}},{\varvec{\nu }}^{V_{T^{u,e}}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belongs to P(G) for any $u\in N(v)\setminus V_k$, and for any $e\in E(\{v\}:V_k)$, satisfying $x(E(\{v\}:V_k))=y_v$. These solutions are $(d(v)-|E(\{v\}:V_k)|)|E(\{v\}:V_k)|$, but only $d(v)-1$ of them are such that the restrictions of their incidence vectors to the variables related to v are linearly independent. Furthermore, given $u\in N(v)\setminus V_k$ and $e\in E(\{v\}:V_k)$, $({\varvec{\pi }}^{E_{T^{u,e}}},{\varvec{\nu }}^{V_{T^{u,e}}},{\varvec{1}})$ belongs to P(G) and satisfies $x(E(\{v\}:V_k))= y_v$. Finally, given $u\in N(v)\setminus V_k$, there exists a gst $G_{{\bar{T}}}=(V_{{\bar{T}}},E_{{\bar{T}}})$ in $G[V\setminus V_k]$, such that $x(\delta (v))>1$. Therefore, given $e=\{v,w\}\in E(\{v\}:V_k)$, it results that $G_{T^{e}}=(V_{T^{e}},E_{T^{e}})$, where $V_{T^{e}}=V_{{\bar{T}}}\cup \{w\}$ and $E_{T^{e}}=E_{{\bar{T}}}\cup \{e\}$, is a gst in G, such that $({\varvec{\pi }}^{E_{T^{e}}},{\varvec{\nu }}^{V_{T^{e}}},{\varvec{1}})$ belongs to P(G) and satisfies $x(E(\{v\}:V_k))= y_v$. $\square$

Proposition 5.3

Given $v\in V$, inequality $x(\delta (v))\ge y_v$ is a facet of P(G) if

• 1. $G[V\setminus \{v\}]$ satisfies assumptions (A1) and (A2);

• 2. $\mu (N(v))>1$.

Proof

We distinguish two cases:

• $v\in W$: in this case inequality $x(\delta (v))\ge y_v$ becomes $x(\delta (v))\ge 1$. We prove the proposition in this case by induction on t. For $t=0$, the GMBV problem reduces to the MBV problem and the claim is true (see Proposition A.1 in Appendix). Let us assume that the claim is true for t, we prove it for $t+1$. Since $t>0$, there exists $u\in V\setminus W$, with $u\ne v$, such that the graph $G[V\setminus \{u\}]$ satisfies (A1) and (A2). To complete the proof, we have to exhibit $d(u)+2$ feasible solutions to the GMBV problem, satisfying $y_u=1$ and $x(\delta (v))= 1$, such that the restrictions of their incidence vectors to $y_u$, $z_u$ and $x_e$, with $e\in \delta (u)$, are linearly independent. It is easy to see that the $d(u)+2$ GMBV solutions that we have built in point 5 of the proof of Proposition 5.5, satisfy $x(\delta (v))\ge 1$ with equality, and their restrictions to the variables related to u are linearly independent.

• $v\in V\setminus W$: we can apply Lemma 5.3. The v-restriction of ${x(\delta (v))\ge y_v}$ is the trivial inequality $0\ge 0$. For any $u\in N(v)$, there exists a gst ${G_{T^u}=(V_{T^u}, E_{T^u})}$ in G such that $x(\delta (v))=1$. Therefore, it results that $({\varvec{\pi }}^{E_{T^{u}}},{\varvec{\nu }}^{V_{T^{u}}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belongs to P(G) and satisfies $x(\delta (v))=y_v$, for any $u\in N(v)$. Furthermore, given $u\in N(v)$, $({\varvec{\pi }}^{E_{T^{u}}},{\varvec{\nu }}^{V_{T^{u}}},{\varvec{1}})$ belongs to P(G) too. It is easy to see that, the restrictions of the incidence vectors of these $d(v)+1$ solutions to the variables related to v are linearly independent.

$\square$

We now introduce a new family of valid inequalities, which strengthen constraints (5). Given $v\in V$ and $H\subseteq N(v)$, we introduce the following function ${\alpha _H: K\setminus \{h(v)\} \rightarrow \{0,1\}}$, such that $\alpha _H(i)=1$ if $H\cap V_i\ne \emptyset$, and 0 otherwise. Furthermore, we denote by ${\bar{d}}_H(v)=\sum _{i\in K\setminus \{h(v)\}} \alpha _H(i)$, the number of clusters whose intersection with H is non-empty. When $H=N(v)$, instead of ${\bar{d}}_H(v)$, we use simply ${\bar{d}}(v)$. Obviously, ${\bar{d}}(v)\le d(v)$, and when $V=W$, we have that ${\bar{d}}(v)=d(v)$, for any $v\in V$.

Proposition 5.4

Given $v\in V$, inequality

$$\begin{aligned} x(\delta (v))-2y_v\le ({\bar{d}}(v)-2)z_v \end{aligned}$$

(12)

is valid for P(G).

Proof

Let us note that, given $v\in V$, $x(\delta (v))\le {\bar{d}}(v)$ holds, and indeed it can be selected at most one edge going from v to a vertex in $N(v)\cap V_i$, for any $i\in K\setminus \{h(v)\}$. Therefore, inequality (12) ensures that whenever at least three edges in $\delta (v)$ are selected, then v is a branch vertex. $\square$

It is easy to see that inequalities (12) are stronger than constraints (5).

Proposition 5.5

Given $v\in V$, inequality $x(\delta (v))-2\le ({\bar{d}}(v)-2)z_v$ is a facet of P(G) if

• 1. $G[V\setminus \{v\}]$ satisfies assumptions (A1) and (A2);

• 2. $\mu (N(v))>2$;

• 3. if $v\in V\setminus W$, there exists $u_1,\ldots ,u_{{\bar{d}}(v)}\in N(v)$, with $h(u_1)\ne h(u_2)\ne \ldots \ne \ne h(u_{{\bar{d}}(v)})$, such that $G(u_1,\ldots ,u_{{\bar{d}}(v)})$ is v-connected.

Proof

We need to face two cases:

• $v\in W$: we prove the result by induction on t. For $t=0$, each cluster is a singleton, and thus the GMBV problem reduces to the MBV problem and the claim is true (see Proposition A.2 in Appendix). Let us assume that the claim is true for t, we prove it for $t+1$. Given $t>0$, there exists a vertex $u\in V\setminus W$, with $u\ne v$, such that the graph $G[V\setminus \{u\}]$ satisfies (A1) and (A2). Thus, by the induction hypothesis, the first request of Lemma 5.2 holds. It remains to exhibit $d(u)+2$ feasible solutions to the GMBV problem, such that $y_u=1$ and $x(\delta (v))-2= ({\bar{d}}(v)-2)z_v$ is satisfied, for which the restrictions of their incidence vectors to $y_u$, $z_u$ and $x_e$, with $e\in \delta (u)$, are linearly independent.

  Thanks to Hyphotesis 1, given $w\in N(u)$, $w\ne v$, there exists a gst ${G_{{\bar{T}}^w}=(V_{{\bar{T}}^w},E_{{\bar{T}}^w})}$ in $G[V\setminus \{v\}]$, such that $y_u=1$, $x_{\{u,w\}}=1$ and $x(\delta (u))=1$. To obtain a feasible solution in G satisfying $x(\delta (v))-2= =({\bar{d}}(v)-2)z_v$, it is sufficient to add two edges connecting v to two vertices in $V_{{\bar{T}}^w}$, and this can always be done thanks to Hypothesis 2, which ensures that there exists $i,j\in {\mathcal {K}}\setminus \{h(u)\}$, such that $V_i, V_j\subseteq N(v)$. We distinguish two cases:

  • if $v\notin N(u)$, then for any $w\in N(u)$, $G_{T^w}=(V_{T^w},E_{T^w})$ is a gst in G satisfying $y_u=1$, $x(\delta (u))=1$ and $x(\delta (v))-2= ({\bar{d}}(v)-2)z_v$, where $V_{T^w}=V_{{\bar{T}}^w}\cup \{v\}$, $E_{T^w}=E_{{\bar{T}}^w}\cup \{e,f\}\setminus \{g\}$, $e\in \delta (v)\cap \delta (V_i)$, $f\in \delta (v)\cap \delta (V_j)$ and $g\in E_{{\bar{T}}^w}\setminus \{u,w\}$. Therefore, for any $w\in N(u)$, $({\varvec{\pi }}^{E_{T^w}},{\varvec{\nu }}^{V_{T^w}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{u,v\}})$ belongs to P(G) and satisfies inequality (12) with equality;

  • if $v\in N(u)$, we have that $d(u)-1$ GMBV solutions, one for each ${w\in N(u)\setminus \{v\}}$. Another one GMBV solution is the following: given $w' \in N(u)$ and a gst $(V_{{\bar{T}}^{w'}},E_{{\bar{T}}^{w'}})$ in $G[V\setminus \{v\}]$ for which $x(\delta (u))=1$, let us consider ${G_{T^{w'}}=(V_{T^{w'}}, E_{T^{w'}})}$, where $V_{T^{w'}}=V_{{\bar{T}}^{w'}}\cup \{v\}$ and $E_{T^{w'}}=E_{{\bar{T}}^{w'}}\cup \{\{u,v\},e\}\setminus \{f\}$, with $e\in \delta (v)$ and $f\in E_{{\bar{T}}^{w'}}$. Thus, vector $({\varvec{\pi }}^{E_{T^{w'}}},{\varvec{\nu }}^{V_{T^{w'}}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{u,v\}})$ belongs to P(G) and satisfies inequality (12) with equality;

  Therefore, in both cases, we have d(u) GMBV solutions containing u and satisfying $x(\delta (v))-2= ({\bar{d}}(v)-2)z_v$, and indeed $x(\delta (v))$ is always equal to two. The remaining two solutions are the followings: One is that represented by $({\varvec{\pi }}^{E_{T^w}},{\varvec{\nu }}^{V_{T^w}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$, for a given $w\in N(u)$, and the other one is $({\varvec{\pi }}^{E_{T}},{\varvec{\nu }}^{V_{T}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$, where $G_T=(V_{{\bar{T}}}\cup \{v\},E_{{\bar{T}}}\cup \{e,f\}\setminus \{g\})$, with ${G_{{\bar{T}}}=(V_{{\bar{T}}},E_{{\bar{T}}})}$ a gst in $G[V\setminus \{v\}]$ having $y_u=1$, $x(\delta (u))>1$, $e,f\in \delta (v)$ and $g\in E_{{\bar{T}}}$. These solutions are such that their restrictions to the variables related to u are linearly independent.

• $v\in V\setminus W$: we prove the result by applying Lemma 5.3. The v-restriction of $x(\delta (v))-2y_v\le ({\bar{d}}(v)-2)z_v$ is the trivial inequality $0\le 0$. It remains then to exhibit $d(v)+1$ feasible solutions to the GMBV problem, satisfying $y_v=1$ and $x(\delta (v))-2y_v= ({\bar{d}}(v)-2)z_v$, such that the restrictions of their incidence vectors to $y_v$, $z_v$ and $x_e$, with $e\in \delta (v)$, are linearly independent. For any $u\in N(v)$, there exists a gst $G_{{\bar{T}}^u}=(V_{{\bar{T}}^u},E_{{\bar{T}}^u})$ in G, such that $x(\delta (v))=1$. Since Hypothesis 2 holds, then there exist $e\in \delta (v)\setminus \{u,v\}$ and $f\in E_{{\bar{T}}^u}$, such that $G_{T^u}=(V_{T^u}, E_{T^u})=(V_{{\bar{T}}^u}, E_{{\bar{T}}^u}\cup \{e\}\setminus \{f\})$ is a gst in G, containing v and satisfying $x(\delta (v))=2$. Therefore, for any $u\in N(v)$, $({\varvec{\pi }}^{E_{T^u}},{\varvec{\nu }}^{V_{T^u}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belongs to P(G) and satisfies with equality ${x(\delta (v))-2y_v\le ({\bar{d}}(v)-2)z_v}$. Furthermore, since $\mu (N(v))\ge 3$, it is always possible to choose $e\in \delta (v)$ in such a way that the restrictions of the incidence vectors of these d(v) solutions are linearly independent. Finally, thanks to Hypothesis 3, there exists a gst $G_T=(V_T,E_T)$ in G containing ${\bar{d}}(v)$ edges in $\delta (v)$. Thus, $({\varvec{\pi }}^{E_{T}},{\varvec{\nu }}^{V_{T}},{\varvec{1}})$ belongs to P(G) and satisfies $x(\delta (v))-2y_v= ({\bar{d}}(v)-2)z_v$. It is easy to see that the restriction of this GMBV solution to the variables related to v, is linearly independent of the previous ones.

$\square$

We now present a new family of valid inequalities, which is a generalization of inequalities (12).

Proposition 5.6

Given $v\in V$ and $H\subseteq N(v)$, with ${\bar{d}}_H(v)\ge 3$, inequality

$$\begin{aligned} x(E(\{v\}:H))-2y_v\le ({\bar{d}}_H(v)-2)z_v \end{aligned}$$

(13)

is valid for P(G).

Proof

This inequality is derived from (12) and it ensures that, whenever at least three edges belonging to $E(\{v\}:H)$ are selected, then v is a branch vertex. $\square$

Proposition 5.7

Given $v\in V$ and $H\subseteq N(v)$, with ${\bar{d}}_H(v)\ge 3$, inequality $x(E(\{v\}:H))-2y_v\le ({\bar{d}}_H(v)-2)z_v$ is a facet of P(G) if

• 1. for any $i\in K\setminus \{h(v)\}$ such that $H\cap V_i\ne \emptyset$, then $|H\cap V_i|=|N(v)\cap V_i|$;

• 2. $G[V\setminus \{v\}]$ satisfies assumptions (A1) and (A2);

• 3. $\mu (H)>2$;

• 4. if $v\in V\setminus W$, there exist $u_1,\ldots ,u_{{\bar{d}}_H(v)}\in H$, with $h(u_1)\ne h(u_2)\ne \ldots \ne \ne h(u_{{\bar{d}}_H(v)})$, such that $G(u_1,\ldots ,u_{{\bar{d}}_H(v)})$ is v-connected.

Proof

It is easy to see that, if there exists $j\in K\setminus \{h(v)\}$ such that $H\cap V_j\ne \emptyset$ and $|H\cap V_j|\ne |N(v)\cap V_j|$, then inequality $x(E(\{v\}:H))-2y_v\le ({\bar{d}}_H(v)-2)z_v$ is dominated by inequality $x(E(\{v\}:H\cup H'))-2y_v\le ({\bar{d}}_H(v)-2)z_v$, where $H'=N(v)\cap V_j$.

The proof of this result is almost the same as the one of Proposition 5.5, and indeed inequality (13) is a generalization of (12). $\square$

6 Conclusions

We have provided a formulation for the Generalized Minimum Branch Vertices problem, and we have introduced several properties characterizing any feasible solution to the problem, some of which could be used to reduce the size of the graph. Furthermore, we have derived the dimension of the polytope, studied the trivial inequalities, introduced two new families of valid inequalities, and we have proved that they are facet-defining. Finally, we have proved some facetal results regarding the polytope of the MBV problem too. Future research directions will require the development of a Branch and Cut algorithm, that implements the facets proposed in this paper.

Appendix

In this Appendix, we prove three results about the Minimum Branch Vertices Problem, which are used in the proof of Propositions 5.3, 5.5 and 5.7.

Let $G=(V,E)$ be an undirected connected graph, having $n=|V|$ vertices and $m=|E|$ edges. The Minimum Branch Vertices (MBV) problem consists of finding a spanning tree T of G, with the minimum number of branch vertices. The MBV problem can be formulated as an integer linear program (ILP) as follows. For any $e\in E$, let $x_e$ be a binary variable equal to 1, if e is selected, and 0 otherwise. Moreover, for any $v\in V$, let $z_v$ be a binary variable equal to 1, if v is a branch vertex, and 0 otherwise. The ILP formulation is the following:

$$\begin{aligned} \text{ Minimize } z= \sum _{v\in V} z_v \end{aligned}$$

(14)

subject to

$$\begin{aligned} x(E)&=n-1 \end{aligned}$$

(15)

$$\begin{aligned} x(E(S))&\le |S|-1 \quad S\subset V: |S|\ge 3 \end{aligned}$$

(16)

$$\begin{aligned} x(\delta (v))-2&\le (d(v)-2) z_v \quad v\in V \end{aligned}$$

(17)

$$\begin{aligned} x_e&\in \{0,1\} \quad e\in E \end{aligned}$$

(18)

$$\begin{aligned} z_v&\in \{0,1\} \quad v\in V \end{aligned}$$

(19)

The objective function (14) minimizes the total number of branch vertices. Constraint (15) ensures that the number of selected edges is equal to the number of vertices minus 1. Constraints (16) are the classical Subtour Elimination Constraints. Finally, inequalities (17) ensure that a vertex v is a branch vertex, whenever at least three edges in $\delta (v)$ are selected.

Let us denote by P(G) the polytope described by the constraints (15)–(19), that is:

$$\begin{aligned} P(G)=conv\{(x,z)\in {\mathbb {R}}^{|E|+|V|}: (x,z) \text{ satisfies } (15)-(19)\}. \end{aligned}$$

(20)

Silvestri et al. [3] studied the facial structure of P(G). They showed that, if G is 2-connected, namely it does not contain any cut vertex, then the affine hull of P(G) is the following:

$$\begin{aligned} aff(P(G))=\{(x,z)\in {\mathbb {R}}^{|E|+|V|}:x(E)=n-1\} \end{aligned}$$

As a consequence, if G is 2-connected, then the dimension of P(G) is $n+m-1$. Moreover, they proved that, if G is 2-connected, then $y_v\le 1$, $v\in V$, and $x_e\le 1$, $e\in E$, are facets of P(G). Finally, they showed that, given $v\in V$, if also $G\setminus \{v\}$ is 2-connected, then $y_v\ge 0$ is facet-defining. To prove the polyhedral results we use the following theorem (see Theorem 3.6 of Nemhauser and Wolsey [19]).

Theorem A.1

Let $(A^=,b^=)$ be the equality set of $S\subseteq {\mathbb {R}}^k$, where $A^=$ is a matrix of dimension $m'\times n'$ and $b^=$ has dimension $m'$, and let $F=\{x\in S: \pi x=\pi _0\}$ be a proper face of S. The following two statements are equivalent:

• F is a facet of S.

• If $\lambda x=\lambda _0$ for all $x\in F$, then

  $$\begin{aligned} (\lambda ,\lambda _0)=(\alpha \pi +uA^=,\alpha \pi _0+ub^=) \text{ for } \text{ some } \alpha \in {\mathbb {R}} \text{ and } \text{ some } u\in {\mathbb {R}}^{m'}. \end{aligned}$$

Let us consider the following particular case of constraints (16):

$$\begin{aligned} x(\delta (v))\ge 1, \quad v\in V \end{aligned}$$

(21)

Proposition A.1

Let $G=(V,E)$ be a 2-connected graph. For $v\in V$, if $G\setminus \{v\}$ is 2-connected, then inequality $x(\delta (v))\ge 1$ defines a facet of P(G).

Proof

Let us consider the proper face $F_v=\{(x,z)\in P(G):x(\delta (v))=1\}$, where $v\in V$ such that $G\setminus \{v\}$ is 2-connected. To prove that $F_v$ is a facet of P(G), we show that if $\lambda (x,z)^T=\lambda _0$, for all $(x,z)\in F_v$, then we can express $(\lambda ,\lambda _0)$ as $(\alpha \pi +uA^=,\alpha \pi _0+ub^=)$, with $\alpha ,u \in {\mathbb {R}}$. W.l.o.g., we can assume that $v=v_1$, where $V=\{v_1,\ldots ,v_n\}$, $E=\{e_1,\ldots ,e_m\}$ and $\delta (v)=\{e_1,\ldots ,e_{d(v)}\}$. In this case we have that $(\pi ,\pi _0)=(1,\ldots ,1,0,\ldots ,0,1)$ and $(A^=,b^=)=(1,\ldots ,1,0,\ldots ,0,n-1)$. Let us represent $(\lambda ,\lambda _0)$ as $(s_1,\ldots ,s_m,t_1,\ldots ,t_n,\lambda _0)$, then equality $\lambda (x,z)^T=\lambda _0$ becomes $\sum _{e\in E}s_e x_e+\sum _{v\in V} t_v z_v=\lambda _0$.

Since $G\setminus \{v\}$ is 2-connected, then for any $w\in V\setminus \{v\}$, there exists a spanning tree ${G_{{\bar{T}}_w}=(V\setminus \{v\}, E_{{\bar{T}}_w})}$ of $G\setminus \{v\}$, in which w is not a branch vertex. Given $e\in \delta (v)$, the subgraph $G_{T_w}=(V,E_{T_w})$, with $E_{T_w}=E_{{\bar{T}}_w}\cup \{e\}$, is a spanning tree of G, such that w is not a branch vertex in $G_T$, and the degree of v in $G_T$ is one. Thus, $({\varvec{\pi }}^{E_{T_w}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{w\}})$ and $({\varvec{\pi }}^{E_{T_w}},{\varvec{1}})$ belong to $F_v$. Since $\lambda ({\varvec{\pi }}^{E_{T_w}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{w\}})^T-\lambda ({\varvec{\pi }}^{E_{T_w}},{\varvec{1}})^T=0$, we have that $t_w=0$, for any $w\in V\setminus \{v\}$. Furthermore, since G is 2-connected, there exists a spanning tree $G_{T_v}=(V, E_{T_v})$ of G, such that $x(\delta (v))=1$. Therefore, $({\varvec{\pi }}^{E_{T_v}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ and $({\varvec{\pi }}^{E_{T_v}},{\varvec{1}})$ belong to $F_v$, and $t_v=0$.

$G\setminus \{v\}$ is 2-connected, then there exist two spanning trees of $G\setminus \{v\}$, $G_{\bar{T_1}}=(V\setminus \{v\},E_{\bar{T_1}})$ and $G_{\bar{T_2}}=(V\setminus \{v\},E_{\bar{T_2}})$, such that $E_{\bar{T_2}}=E_{\bar{T_1}}\setminus \{e\}\cup \{f\}$, where $e,f\notin \delta (v)$. Given $e_v\in \delta (v)$, $G_{T_1}=(V,E_{T_1})$ and $G_{T_2}=(V,E_{T_2})$ are two spanning trees of G, where $E_{T_1}=E_{\bar{T_1}}\cup \{e_v\}$ and $E_{T_2}=E_{\bar{T_2}}\cup \{e_v\}$. Since $({\varvec{\pi }}^{E_{T_1}},{\varvec{1}})$ and $({\varvec{\pi }}^{E_{T_2}},{\varvec{1}})$ belong to $F_v$, then $\lambda ({\varvec{\pi }}^{E_{T_1}},{\varvec{1}})^T-\lambda ({\varvec{\pi }}^{E_{T_2}},{\varvec{1}})^T=0$ and $s_e=s_f$. Since $G_{{\bar{T}}_1}$ is a generic spanning tree, we have that $s:=s_e$, for any $e\notin \delta (v)$.

Let $G_{T}=(V\setminus \{v\},E_{T})$ be a spanning tree of $G\setminus \{v\}$. Since $d(v)\ge 2$, there exist $e,f\in \delta (v)$, with $e\ne f$, such that $G_{T_1}=(V,E_{T_1})$ and $G_{T_2}=(V,E_{T_2})$ are two spanning trees of G, where $E_{T_1}=E_T\cup \{e\}$ and $E_{T_2}=E_T\cup \{f\}$. It is easy to see that $({\varvec{\pi }}^{E_{T_1}},{\varvec{1}})$ and $({\varvec{\pi }}^{E_{T_2}},{\varvec{1}})$ belong to $F_v$, then $\lambda ({\varvec{\pi }}^{E_{T_1}},{\varvec{1}})^T-\lambda ({\varvec{\pi }}^{E_{T_2}},{\varvec{1}})^T=0$ and $s_e=s_f$. Since it can be done for any $e,f\in \delta (v)$, it follows that $s':=s_e$, for any $e\in \delta (v)$. Equation $\lambda (x,z)^T=\lambda _0$ reduces to

$$\begin{aligned} s'x(\delta (v))+s\;x(E\setminus \delta (v))=\lambda _0. \end{aligned}$$

Let $G_{{\bar{T}}}=(V\setminus \{v\},E_{{\bar{T}}})$ be a spanning tree of $G\setminus \{v\}$. Given $e\in \delta (v)$, we have that $G_{T}=(V,E_{T})$, where $E_T=E_{{\bar{T}}}\cup \{e\}$, is a spanning tree of G. Since $({\varvec{\pi }}^{E_{T}},{\varvec{1}})$ belong to $F_v$, it results that $\lambda _0=s'+s(n-2)$.

Therefore, $\lambda (x,z)^T=\lambda _0$ becomes

$$\begin{aligned} s'x(\delta (v))+s\;x(E\setminus \delta (v))=s'+s(n-2). \end{aligned}$$

Thus,

$$\begin{aligned} (\lambda ,\lambda _0)=(s',\ldots ,s',s,\ldots ,s,0,\ldots ,0,s'+s(n-2)). \end{aligned}$$

Note that

$$\begin{aligned}&(\alpha \pi +uA^=,\alpha \pi _0+ub^=)\\&\quad =(\alpha +u,\ldots ,\alpha +u,u,\ldots ,u,0,\ldots ,0,\alpha +u(n-1)). \end{aligned}$$

Therefore, we complete the proof by setting $\alpha =s'-s$ and $u=s$. $\square$

Proposition A.2

Let $G=(V,E)$ be a 2-connected graph. For $v\in V$, with $d(v)\ge 3$, if $G\setminus \{v\}$ is 2-connected, then inequality $x(\delta (v))-2\le (d(v)-2) z_v$ defines a facet of P(G).

Proof

We prove the result by using Theorem A.1. Given $v\in V$ such that $G\setminus \{v\}$ is 2-connected, let us consider the proper face $F_v=\{(x,z)\in P(G):x(\delta (v))+(2-d(v)) z_v=2\}$. To show that $F_v$ is a facet of P(G), we need to prove that if $\lambda (x,z)^T=\lambda _0$, for all $(x,z)\in F_v$, then we can express $(\lambda ,\lambda _0)$ as $(\alpha \pi +uA^=,\alpha \pi _0+ub^=)$, with $\alpha ,u \in {\mathbb {R}}$. W.l.o.g., we can assume that $v=v_1$, where $V=\{v_1,\ldots ,v_n\}$, $E=\{e_1,\ldots ,e_m\}$ and $\delta (v)=\{e_1,\ldots ,e_{d(v)}\}$. In this case, we have that $(\pi ,\pi _0)=(1,\ldots ,1,0,\ldots 0,2-d(v),0,\ldots ,0,2)$ and $(A^=,b^=)=(1,\ldots ,1,0,\ldots ,0,n-1)$. Let us represent $(\lambda ,\lambda _0)$ as $(s_1,\ldots ,s_m,t_1,\ldots ,t_n,\lambda _0)$; then equality $\lambda (x,z)^T=\lambda _0$ becomes $\sum _{e\in E}s_e x_e+\sum _{v\in V} t_v z_v=\lambda _0$.

Since $G\setminus \{v\}$ is 2-connected, then for any $w\in V\setminus \{v\}$ there exists a spanning tree ${G_{T_w}=(V\setminus \{v\}, E_{T_w})}$ of $G\setminus \{v\}$, in which w is not a branch vertex. ${G_T=(V,E_T)}$, where $E_T=E_{T_w}\cup \{e,f\} \setminus \{g\}$, with $e,f\in \delta (v)$ and $g\in E_{T_w}$, is a spanning tree of G, such that w is not a branch vertex in $G_T$ and the degree of v in $G_T$ is two. Therefore, it results that $({\varvec{\pi }}^{E_{T}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{w,v\}})$ and $({\varvec{\pi }}^{E_{T}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belong to $F_v$, and satisfy $\lambda (x,z)^T=\lambda _0$. This implies that $\lambda ({\varvec{\pi }}^{E_{T}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{w,v\}})^T-\lambda ({\varvec{\pi }}^{E_{T}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})^T=0$, and then $t_w=0$, for any $w\in V\setminus \{v\}$.

Since $G\setminus \{v\}$ is 2-connected, then there exist two spanning trees $G_{\bar{T_1}}=(V\setminus \{v\},E_{\bar{T_1}})$ and $G_{\bar{T_2}}=(V\setminus \{v\},E_{\bar{T_2}})$ of $G\setminus \{v\}$, such that $E_{\bar{T_2}}=E_{\bar{T_1}}\setminus \{e\}\cup \{f\}$ (see Diestel [20]). Since $d(v)\ge 3$, there exist $e_v,f_v\in \delta (v)$ and $g\in E_{T_1}\cup E_{T_2}\setminus \{e,f\}$, such that ${G_{T_1}=(V,E_{T_1})}$ and ${G_{T_2}=(V,E_{T_2})}$ are two spanning trees of G, where ${E_{T_1}=E_{\bar{T_1}}\cup \{e_v,f_v\}\setminus \{g\}}$ and ${E_{T_2}=E_{\bar{T_2}}\cup \{e_v,f_v\}\setminus \{g\}}$. Moreover, we have that $E_{T_2}=E_{T_1}\setminus \{e\}\cup \{f\}$. It is easy to see that $({\varvec{\pi }}^{E_{T_1}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ and $({\varvec{\pi }}^{E_{T_2}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belong to $F_v$.Then ${\lambda ({\varvec{\pi }}^{E_{T_1}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})^T-\lambda ({\varvec{\pi }}^{E_{T_2}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})^T=0}$ and $s_e=s_f$. Since $G_{{\bar{T}}_1}$ is a generic spanning tree we have that $s:=s_e$, for any $e\notin \delta (v)$.

Let $G_{T}=(V\setminus \{v\},E_{T})$ be a spanning tree of $G\setminus \{v\}$. Since $d(v)\ge 3$, there exist $e,f,g\in \delta (v)$, with $e\ne f\ne g$. There exist $h,h'\in E_T$ such that $G_{T_1}=(V,E_{T_1})$ and $G_{T_2}=(V,E_{T_2})$, where $E_{T_1}=E_T\cup \{e,f\}\setminus \{h\}$ and $E_{T_2}=E_T\cup \{e,g\}\setminus \{h'\}$, are two spanning trees of G. It is easy to see that $({\varvec{\pi }}^{E_{T_1}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ and $({\varvec{\pi }}^{E_{T_2}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belong to $F_v$; then $\lambda ({\varvec{\pi }}^{E_{T_1}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})^T-\lambda ({\varvec{\pi }}^{E_{T_2}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})^T=0$ and $s_f=s_g$. Since it can be done for any $e,f,g\in \delta (v)$, it follows that $s':=s_e$, for any $e\in \delta (v)$. Equation $\lambda (x,z)^T=\lambda _0$ reduces to

$$\begin{aligned} s'x(\delta (v))+s\;x(E\setminus \delta (v))+t_v z_v=\lambda _0. \end{aligned}$$

Let $G_{{\bar{T}}}=(V\setminus \{v\},E_{{\bar{T}}})$ be a spanning tree of $G\setminus \{v\}$. Given $e,f\in \delta (v)$, there exists $g\in E_{{\bar{T}}}$, such that $G_{T}=(V,E_{T})$, where $E_T=E_{{\bar{T}}}\cup \{e,f\}\setminus \{g\}$, is a spanning tree of G. Since $({\varvec{\pi }}^{E_{T}},{\varvec{1}}\setminus {\varvec{\nu }}^{\{v\}})$ belong to $F_v$, it results that $\lambda _0=2s'+s(n-3)$. Finally, given a spanning tree $G_{{\bar{T}}}=(V\setminus \{v\},E_{{\bar{T}}})$ of $G\setminus \{v\}$, there exist $e_1,\ldots ,e_{d(v)-1}\in E_{{\bar{T}}}$, such that $G_{T}=(V,E_{T})$ is a spanning tree of G, where $E_T=E_{{\bar{T}}}\cup \delta (v) \setminus \{e_1,\ldots ,e_{d(v)-1}\}$. It is easy to see that $({\varvec{\pi }}^{E_{T}},{\varvec{1}})$ belongs to $F_v$, then $s'd(v)+s(n-1-d(v))+t_v=2s'+s(n-3)$. It follows that $t_v=(s'-s)(2-d(v))$.

From these observations $\lambda (x,z)^T=\lambda _0$ becomes

$$\begin{aligned} s'x(\delta (v))+s\;x(E\setminus \delta (v))+ (s'-s)(2-d(v)) z_v=2s'+s(n-3). \end{aligned}$$

Therefore, we have that

$$\begin{aligned} (\lambda ,\lambda _0)=(s',\ldots ,s',s,\ldots ,s,(s'-s)(2-d(v)),0,\ldots ,0,2s'+s(n-3)). \end{aligned}$$

Note that

$$\begin{aligned}&(\alpha \pi +uA^=,\alpha \pi _0+ub^=)\\&\quad =(\alpha +u,\ldots ,\alpha +u,u,\ldots ,u,\alpha (2-d(v)),0,\ldots ,0,2\alpha +u(n-1)). \end{aligned}$$

Therefore, we complete the proof by setting $\alpha =s'-s$ and $u=s$. $\square$

Silvestri et al. [3] introduced the following family of valid inequalities:

Proposition A.3

Given $v\in V$ and $H\subseteq \delta (v)$, with $|H|\ge 3$, inequality

$$\begin{aligned} x(H)-2\le (|H|-2)z_v \end{aligned}$$

(22)

is valid for P(G).

The following proposition states that inequalities (22) are facet-defining for P(G).

Proposition A.4

Let $G=(V,E)$ be a 2-connected graph. For $v\in V$ and $H\subseteq \delta (v)$, with $|H|\ge 3$, if $G\setminus \{v\}$ is 2-connected, then inequality $x(H)-2\le (|H|-2) z_v$ defines a facet of P(G).

Proof

Since inequality (22) is a generalization of (17), the proof follows from the one of Proposition A.2. $\square$