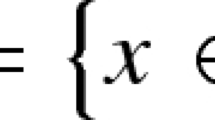1 Introduction

Multiobjective optimization problems (MOPs) are a class of optimization problems involving more than one objective function to be optimized. Many real-life problems can be formulated as MOPs, which include engineering design, economics, financial investment, mechanics, etc. See [1, 2] and references therein. For several theoretical and numerical issues related to MOPs, see [3,4,5,6].

Due to the possible conflicting nature of the objective functions, it is not expected to find a solution that optimizes all of the objective functions simultaneously. Thus, different notions of optimality are developed for MOPs, where one aims at finding best trade-off options (strong/weak Pareto points, see Definition 2.1). As in nonlinear programming, optimality conditions play a crucial role in the development of efficient methods for solving MOPs. Some methods are Newton’s methods [7], SQP methods [8], trust-region methods [9, 10] and scalarization methods such as weighted sum methods [11, 12], \(\varepsilon \)-constraint methods [13], Charnes–Cooper [14, 15], Gerstewitz [16], Pascoletti–Serafini [17] scalarizations, and others.

In scalar optimization problems, the Karush–Kuhn–Tucker (KKT) conditions play a major role in theoretical and numerical optimization. To guarantee the fulfillment of KKT conditions at a minimizer, one needs constraint qualifications (CQs), that is, properties depending only on the functions defining the constraints, which ensure the KKT conditions at local minimizers. For MOPs, the corresponding KKT conditions take into account, simultaneously, multipliers for the constraints and for the objective functions, with the multipliers associated with the objective functions being nonnegative. If there exists at least one positive multiplier corresponding to the objective functions, we say that weak Karush–Kuhn–Tucker (weak KKT) conditions hold, and when all the multipliers corresponding to the objective functions are positive, we say that strong Karush–Kuhn–Tucker (strong KKT) conditions hold. But, differently from the scalar case, usual CQs, in general, do not ensure weak/strong KKT conditions. Thus, additional conditions, which take into account the objective functions, are introduced: the so-called regularity conditions (RC). Such conditions have been used for establishing first-order and second-order optimality conditions for smooth MOPs. For more information, see [18,19,20,21] and references therein.

In this work, we take a new look at CQs for MOPs. We are interested in establishing the weakest possible CQs that guarantee the validity of weak/strong KKT conditions at locally weak Pareto solutions. To develop our new CQs, we rely on a new notion of normal cone adapted to MOPs and some variational analysis tools. For details, see Sect. 4.

The paper is organized as follows: In Sect. 2, we introduce the basic assumptions and concepts useful in our analysis. In Sect. 3, we introduce the multiobjective normal cone and we study its properties and calculus rules. In Sect. 4, we introduce new CQs for MOP and we study their properties. Our concluding remarks are given in Sect. 5.

2 Preliminaries and Basic Assumptions

Our notation is standard in optimization and variational analysis: \({\mathbb {R}}^{n}\) is the n-dimensional real Euclidean space, \(n \in {\mathbb {N}}\). \({\mathbb {R}}_{+}\) is the set of nonnegative numbers and \(a^{+}:=\max \{0,a\}\), \(a \in {\mathbb {R}}\). We denote by \(\Vert \cdot \Vert \) the Euclidean norm in \({\mathbb {R}}^{n}\) and by \(\Vert \cdot \Vert _{1}\) the \(\ell _{1}\)-norm, i.e., \(\Vert z\Vert _{1}:=|z_{1}|+\dots +|z_{n}|\), for \(z \in {\mathbb {R}}^{n}\). Given a differentiable mapping \(F: {\mathbb {R}}^{s} \rightarrow {\mathbb {R}}^{d}\), we use \(\nabla F(x)\) to denote the Jacobian matrix of F at x. For a set-valued mapping \(\varGamma :{\mathbb {R}}^{s} \rightrightarrows {\mathbb {R}}^{d}\), the sequential Painlevé-Kuratowski outer limit of \(\varGamma (z)\) as \(z \rightarrow z^{*}\) is denoted by

$$\begin{aligned} \text {limsup}_{z \rightarrow z^{*}} \varGamma (z):= \{ w^* \in {\mathbb {R}}^{d}: \exists \ \ (z^{k},w^{k})\rightarrow (z^{*},w^{*}) \text { with } w^{k} \in \varGamma (z^{k}) \}. \end{aligned}$$

For a cone \({\mathcal {K}} \subset {\mathbb {R}}^{s}\), its polar is \({\mathcal {K}}^{\circ }:=\{v \in {\mathbb {R}}^{s} : \langle v, k \rangle \le 0 \text { for all } k \in {\mathcal {K}}\}\). It is always the case that \({\mathcal {K}} \subset {\mathcal {K}}^{\circ \circ }\), and when \({\mathcal {K}}\) is a closed convex set, the equality \({\mathcal {K}}^{\circ \circ }={\mathcal {K}}\) holds.

Given \(X \subset {\mathbb {R}}^{n}\) and \({\bar{z}} \in X\), we define the tangent cone to X at \({\bar{z}}\) by

$$\begin{aligned} T({\bar{z}},X):=\{d \in {\mathbb {R}}^{n}: \exists \ \ t_{k} \downarrow 0, d^{k}\rightarrow d \text { with } {\bar{z}}+t_{k}d^{k} \in X \}, \end{aligned}$$

and the regular normal cone to X at \({\bar{z}} \in X\) by

$$\begin{aligned} {\widehat{N}}({\bar{z}},X):=\left\{ w \in {\mathbb {R}}^{n}: \limsup _{z \rightarrow {\bar{z}}, z \in X} \frac{\langle w,z-{\bar{z}} \rangle }{\Vert z-{\bar{z}}\Vert } \le 0\right\} . \end{aligned}$$

The (Mordukhovich) limiting normal cone to X at \({\bar{z}} \in X\) is defined by

$$\begin{aligned} N({\bar{z}},X):=\limsup _{z \rightarrow {\bar{z}}, z \in X} {\widehat{N}}(z,X). \end{aligned}$$

For a function \(\phi : {\mathbb {R}}^n \rightarrow [-\infty ,\infty ]\) and a point \({{\bar{z}}} \in {\mathbb {R}}^n\) where \(\phi ({{\bar{z}}})\) is finite. We write \(z \rightarrow _{\phi }{\bar{z}}\) when \(z \rightarrow {{\bar{z}}}\) and \(\phi (z)\rightarrow \phi ({{\bar{z}}})\). The regular subdifferential of \(\phi \) at \({{\bar{z}}}\) is defined as

$$\begin{aligned} {\widehat{\partial }} \phi ({{\bar{z}}}):= \left\{ v \in {\mathbb {R}}^{n}: \liminf _{z \rightarrow {\bar{z}}, z \in X} \frac{\phi (z)-\phi ({{\bar{z}}})-\langle v,z-{\bar{z}} \rangle }{\Vert z-{\bar{z}}\Vert } \ge 0\right\} . \end{aligned}$$

The limiting subdifferential of \(\phi \) at \({{\bar{z}}}\) is defined as

$$\begin{aligned} \partial \phi ({{\bar{z}}}):=\limsup _{z \rightarrow _{\phi }{\bar{z}}} \ \ {\widehat{\partial }} \phi (z). \end{aligned}$$
(1)

. When X is a nonempty closed set and \(\imath _{X}\) is the indicator function, we see that \({\widehat{N}}({\bar{z}},X)= {\widehat{\partial }} \imath _{X}({{\bar{z}}})\) and \(N({\bar{z}},X)=\partial \imath _{X}({{\bar{z}}})\). For a detailed treatment of variational analysis and optimization, we recommend [22,23,24].

Here, we consider the smooth constrained multiobjective optimization problem (MOP) of the form:

$$\begin{aligned} \begin{array}{ll} \text{ minimize } &{} f(x):=(f_{1}(x), f_2(x), \dots , f_{r}(x)), \\ \text{ subject } \text{ to } &{} h_{i}(x)=0, \ \ i=1,\dots , m; \\ &{} g_{j}(x)\le 0, \ \ j=1, \dots , p, \end{array} \end{aligned}$$
(2)

where \(h(\cdot ):=(h_1(\cdot ),\dots ,h_m(\cdot ))\) and \(g(\cdot ):=(g_1(\cdot ),\dots ,g_p(\cdot ))\) are continuously differentiable on \({\mathbb {R}}^{n}\). We denote by \(\varOmega :=\{ x \in {\mathbb {R}}^{n}: h(x)=0, g(x)\le 0\}\) the feasible set of (2), which is assumed to be a nonempty set.

Due to the possible conflicting nature of the objective functions, it is not expected to find a solution that can locally optimize all of the objective functions simultaneously. Therefore, different notions of optimality are developed for MOPs, where one aims at finding best trade-off options (local Pareto points, see Definition 2.1). We give below some important definitions.

Definition 2.1

Let \({\bar{x}}\) be a feasible point of (2). Then,

  1. 1.

    We say that \({\bar{x}}\) is a local (strongFootnote 1) Pareto optimal point if there is a \(\delta >0\) such that there is no \(x \in \varOmega \cap B({\bar{x}}, \delta )\) with \(f_{\ell }(x)\le f_{\ell }({\bar{x}}), \forall \ell \in \{1,\dots , r\}\) and \(f(x)\ne f({\bar{x}})\);

  2. 2.

    We say that \({\bar{x}}\) is a local weak Pareto optimal point if there is a \(\delta >0\) such that there is no \(x \in \varOmega \cap B({\bar{x}}, \delta )\) with \(f_{\ell }(x)< f_{\ell }({\bar{x}}), \forall \ell \in \{1,\dots , r\}\).

There is a natural way to relate local weak/strong Pareto optimal points with a scalar optimization problem. Indeed, given a set of not all zero scalars (weights) \(\theta _1\ge 0, \dots , \theta _r\ge 0\), all local minimizers of the scalarized problem of minimizing \(\theta _{1}f_{1}(x)+\cdots +\theta _{r}f_{r}(x)\) subject to \(x\in \varOmega \) are local weak Pareto points, while the reverse implication holds under convexity. See [3]. By considering the scalarized problem with positive weights \(\theta _1>0\), \(\dots \), \(\theta _r>0\), all its local minimizers are local Pareto solutions, and, under convexity and compacity assumptions, a dense subset of the local Pareto solutions (so-called proper local Pareto solutions) coincides with the local minimizers of this scalarized problem. See [26]. This suggests the following definitions of Karush–Kuhn–Tucker (KKT) notions associated with local weak and strong Pareto solutions. See [21, 27].

Definition 2.2

Let x be a feasible point of (2) and assume that f is continuously differentiable. Suppose that there exists a vector \(0\ne (\theta , \lambda ,\mu ) \in {\mathbb {R}}_{+}^{r}\times {\mathbb {R}}^{m}\times {\mathbb {R}}_{+}^{p}\) such that \(\mu _{j}g_{j}(x)=0\), for \(j=1,\dots , p\) and

$$\begin{aligned} \sum _{\ell =1}^{r}\theta _{\ell }\nabla f_{\ell }(x)+ \sum _{i=1}^{m}\lambda _{i}\nabla h_{i}(x)+ \sum _{j=1}^{p}\mu _{j}\nabla g_{j}(x)=0. \end{aligned}$$
(3)

Then, we say that:

  1. a)

    x is a weak KKT point, if (3) holds with \(\theta \ne 0\).

  2. b)

    x is a strong KKT point, if (3) holds with \(\theta _{\ell }>0\), \(\forall \ell =1,\dots , r\).

When \(r=1\), both concepts reduce to the classical KKT conditions, which are known to hold at a local minimizer only under a CQ. Among the most known ones, we mention the linear independence CQ (LICQ), which states the linear independence of all the gradients of active constraints, and the Mangasarian-Fromovitz CQ (MFCQ), which states the positive linear independence of such gradients, see [28]. We mention that necessary optimality conditions are not only useful for identifying possible candidate solutions to a problem, but also crucial in designing numerical methods for solving such problems. Also, many CQs (but not all) can be used in the convergence analysis of numerical methods for scalar optimization problems. See [29,30,31] and references therein.

Finally, we recall some basic results on MOPs. In this paper, we use \(V=(v_{\ell })_{\ell =1}^{r}\) to denote a \(n\times r\) matrix whose columns are the vectors \(v_{1}, v_{2}, \dots , v_{r}\) in \({\mathbb {R}}^{n}\). Thus, \(V\theta =\theta _{1} v_{1}+\cdots +\theta _{r} v_{r}\) for \(\theta :=(\theta _{1},\dots , \theta _{r}) \in {\mathbb {R}}^{r}\). From [27, 32], we have the following

Lemma 2.1

Let \({{\bar{x}}}\) be a local weak Pareto point of (2). Consider the scalar optimization problem

$$\begin{aligned} \text {minimize } \varPhi (x):=\max _{\ell =1,\dots , r}(f_{\ell }(x)-f_{\ell }({\bar{x}})), \text { subject to } x \in \varOmega . \end{aligned}$$
(4)

Then, \({{\bar{x}}}\) is a local solution of (4). Furthermore, if f is a \(C^1\) function, \(\max _{\ell =1,\dots , r} \langle \nabla f_{\ell }({\bar{x}}), d \rangle \ge 0\), \( \forall d \in T({\bar{x}}, \varOmega )\).

Remark 2.1

Under the assumptions of Lemma 2.1, it is not difficult to see that there exists \(\delta >0\) such that \({{\bar{x}}}\) is the unique minimizer of

$$\begin{aligned} \text {minimize } \max _{\ell =1,\dots , r}(f_{\ell }(x)-f_{\ell }({\bar{x}}))+\frac{1}{2}\Vert x-{{\bar{x}}}\Vert ^2, \text { s.t.} x \in \varOmega , \Vert x-{{\bar{x}}}\Vert \le \delta . \end{aligned}$$
(5)

From [33], we have the following theorem of alternative

Lemma 2.2

Let A, B, C be given matrices with n columns and \(A \ne 0\). Then, exactly one of the following statements is true:

  1. (s1)

    \(Az>0\), \(Bz \ge 0\), \(Cz=0\) has a solution z;

  2. (s2)

    \(A^{T}y_{1}+B^{T}y_{2}+C^{T}y_{3}=0\), \(y_{1}\ge 0, y_{2}\ge 0\), \(y_{1}\ne 0\) has solution \(y_{1}\), \(y_{2}\), \(y_{3}\).

3 A Multiobjective Normal Cone

In this section, we will introduce a notion of normal cone for multiobjective optimization problems and derive its properties. To the best of our knowledge, this has not been previously considered. We start by taking a closed subset \(\varOmega \) of \({\mathbb {R}}^{n}\) and a point \({\bar{x}} \in \varOmega \).

Definition 3.1

Given \({\bar{x}} \in \varOmega \) and \(r \in {\mathbb {N}}\), the regular r-multiobjective normal cone to \(\varOmega \) at \({{\bar{x}}}\) is the cone defined as

$$\begin{aligned} {\widehat{N}}({\bar{x}},\varOmega ; r):= \left\{ V=(v_\ell )_{\ell =1}^{r} \in {\mathbb {R}}^{n\times r}: \limsup _{x \rightarrow {\bar{x}}, x \in \varOmega } \ \ \min _{\ell =1,\dots , r} \frac{\langle v_{\ell }, x-{\bar{x}} \rangle }{\Vert x-{\bar{x}}\Vert } \le 0 \right\} . \end{aligned}$$
(6)

For a lower semicontinuous mapping f having lower semicontinuous extended real-valued components \(f_{\ell }:{\mathbb {R}}^{n}\rightarrow ]-\infty , \infty ]\), \(\ell =1,\dots , r\), we define the regular r-multiobjective subdifferential of f at \({\bar{x}}\), denoted by \({\widehat{\partial }}f({\bar{x}};r)\), as the set

$$\begin{aligned} \left\{ V=(v_\ell )_{\ell =1}^{r} \in {\mathbb {R}}^{n\times r}: \liminf _{x \rightarrow {\bar{x}}} \ \ \left( \max _{\ell =1,\dots , r} \frac{f_{\ell }(x)-f_{\ell }({\bar{x}})-\langle v_{\ell }, x-{\bar{x}} \rangle }{\Vert x-{\bar{x}}\Vert } \right) \ge 0 \right\} . \end{aligned}$$

Furthermore, we define the limiting r-multiobjective normal cone to \(\varOmega \) at \({{\bar{x}}}\) by

$$\begin{aligned} N({\bar{x}}, \varOmega ;r):= \limsup _{x \rightarrow {\bar{x}}, x\in \varOmega } {\widehat{N}}(x, \varOmega ;r) \end{aligned}$$

and the limiting r-multiobjective subdifferential of f at \({\bar{x}}\)

$$\begin{aligned} \partial f({\bar{x}}; r):= \limsup _{x \rightarrow _f {\bar{x}}} {\widehat{\partial }} f(x ;r). \end{aligned}$$

where \(x \rightarrow _f {\bar{x}}\) means that \(x \rightarrow {\bar{x}}\) with \(f(x) \rightarrow f({\bar{x}})\). Clearly, when \(r=1\), the (limiting/regular) r-multiobjective normal cones and (limiting/regular) r-multiobjective subdifferential coincide with their scalar counterparts which are very well studied in [22, 23]. In the rest of this section, we will analyze the main properties of the multiobjective normal cone. Thus, we start by computing them for some simple cases.

Proposition 3.1

Let \(\varOmega \) be a closed convex set, \({\bar{x}}\in \varOmega \), and \(r\in {\mathbb {N}}\). Then, we have that \(N({\bar{x}}, \varOmega ;r)= {\widehat{N}}({\bar{x}}, \varOmega ;r)\). Furthermore,

$$\begin{aligned} {\widehat{N}}({\bar{x}}, \varOmega ;r)= \{ V=(v_{\ell })_{\ell =1}^{r} \in {\mathbb {R}}^{n\times r} : \min _{\ell =1,\dots , r}\langle v_{\ell }, x-{\bar{x}}\rangle \le 0, \ \ \forall x \in \varOmega \}. \end{aligned}$$
(7)

Proof

First, we will show the equality in (7). Take \(V \in {\widehat{N}}({\bar{x}}, \varOmega ;r)\) and \(x \in \varOmega \). For every \(t \in [0,1]\), set \(x(t):={\bar{x}}+t(x-{\bar{x}}) \in \varOmega \). Thus, since \(x(t)-{\bar{x}}=t(x-{\bar{x}})\), we obtain that

$$\begin{aligned} \min _{\ell =1,\dots , r} \frac{\langle v_{\ell }, x-{\bar{x}}\rangle }{\Vert x-{\bar{x}}\Vert } = \lim _{t\rightarrow 0} \min _{\ell =1,\dots , r} \frac{\langle v_{\ell }, x(t)-{\bar{x}}\rangle }{\Vert x(t)-{\bar{x}}\Vert } \le \limsup _{z \rightarrow {\bar{x}}, z \in \varOmega } \min _{\ell =1,\dots , r} \frac{\langle v_{\ell }, z-{\bar{x}} \rangle }{\Vert z-{\bar{x}}\Vert } \le 0, \end{aligned}$$

which implies that \(\min _{\ell =1,\dots , r}\langle v_{\ell }, x-{\bar{x}}\rangle \le 0\).

Clearly, if \(V=(v_{\ell })_{\ell =1}^{r}\) satisfies \(\min _{\ell =1,\dots , r}\langle v_{\ell }, x-{\bar{x}}\rangle \le 0\) \(\forall x \in \varOmega \), we have that \(V \in {\widehat{N}}({\bar{x}}, \varOmega ;r)\). From (7), we obtain that \(N({\bar{x}}, \varOmega ;r)= {\widehat{N}}({\bar{x}}, \varOmega ;r)\). \(\square \)

When \(\varOmega \) is a polyhedral cone, we can obtain a nice characterization of the r-multiobjective normal cone.

Proposition 3.2

Suppose that \(\varOmega =\{x \in {\mathbb {R}}^{n}: Ax \le 0\}\) for some matrix \(A \in {\mathbb {R}}^{m\times n}\). Then, for every \({\bar{x}} \in \varOmega \), \({\widehat{N}}({\bar{x}}, \varOmega ;r)=N({\bar{x}}, \varOmega ;r)\) holds and

$$\begin{aligned} N({\bar{x}}, \varOmega ;r)= \left\{ V=(v_{\ell })_{\ell =1}^{r} \in {\mathbb {R}}^{n\times r}: \begin{array}{ll} &{} V \theta =A^{T}\lambda ,\text { with } \lambda \in N(A{\bar{x}}, {\mathbb {R}}_{-}^{m}) \\ &{} \text { and } 0\ne \theta \in {\mathbb {R}}^r_+ \end{array} \right\} . \end{aligned}$$
(8)

Proof

This will follow by the more general result proved in Corollary 4.1, for every constraint set satisfying the error bound property. \(\square \)

It is well known that the regular normal cone can be characterized by viscosity subgradients [22, Theorem 6.11]. Here, we have a variational characterization of the regular r-multiobjective normal cone, which extends the viscosity characterization of the classical normal cone when \(r=1\).

Theorem 3.1

Let \({\bar{x}}\) be a feasible point of (2). Then, the following statements are equivalent

  1. (a)

    \(V=(v_\ell )_{\ell =1}^{r} \in {\mathbb {R}}^{n\times r}\) belongs to \({\widehat{N}}({\bar{x}}, \varOmega ; r)\);

  2. (b)

    There is a \(C^{1}\) mapping \(f(x)=(f_{\ell }(x))_{\ell =1}^{r}\) such that \({\bar{x}}\) is a local weak Pareto optimal point relative to \(\varOmega \), and \(v_{\ell }=-\nabla f_{\ell }({\bar{x}})\), for every \(\ell =1,\dots , r\);

  3. (c)

    For every \(d \in T({\bar{x}}, \varOmega )\), we have that \(\min _{\ell =1,\dots , r} \langle v_{\ell }, d \rangle \le 0\).

As a consequence

$$\begin{aligned} {\widehat{N}}({\bar{x}}, \varOmega ; r)= \{ V=(v_\ell )_{\ell =1}^{r} \in {\mathbb {R}}^{n\times r}: \min _{\ell =1,\dots , r} \langle v_{\ell }, d \rangle \le 0, \ \ \forall d \in T({\bar{x}}, \varOmega ) \}. \end{aligned}$$
(9)

Proof

First, we will show that (a) implies (b). Take \(V=(v_\ell )_{\ell =1}^{r} \in {\widehat{N}}({\bar{x}}, \varOmega ; r)\). We will use an argument similar to [22, Theorem 6.11]. We define

$$\begin{aligned} \eta _{0}(r):=\text {Sup }\{\min _{\ell =1,\dots ,r} \langle v_{\ell }, x-{\bar{x}}\rangle : x \in \varOmega , \Vert x-{\bar{x}}\Vert \le r\}. \end{aligned}$$
(10)

Clearly, \(\eta _{0}(r)\le r\min _{\ell =1,\dots ,r}\Vert v_{\ell }\Vert \) and \(0= \eta _{0}(0)\le \eta _{0}(r)\le o(r)\). By using [22, Theorem 6.11], there is \(\eta :{\mathbb {R}}_{+}\rightarrow {\mathbb {R}}\) continuously differentiable on \({\mathbb {R}}_{+}\) with \(\eta _{0}(r)\le \eta (r)\), \(\eta '(r)\rightarrow 0\) and \(\eta (r)/r \rightarrow 0\) as \(r \rightarrow 0\). Thus, for every \(\ell \in \{1,\dots ,r\}\) define \(f_{\ell }(x):=-\langle v_{\ell }, x-{\bar{x}}\rangle +\eta (\Vert x-{\bar{x}}\Vert )\) and \(f(x)=(f_{\ell }(x))_{\ell =1}^{r}\). Clearly, f is a \(C^{1}\) mapping with \(f({\bar{x}})=0\). To show that \({\bar{x}}\) is a local weak Pareto point for f relative to \(\varOmega \), suppose that this is not the case. Then, there is a sequence \(x^{k}\rightarrow {\bar{x}}\) with \(x^{k} \in \varOmega \), \(\forall k \in {\mathbb {N}}\) such that \(f_{\ell }(x^{k})<f_{\ell }({\bar{x}})=0\), \(\forall \ell =1,\dots ,r\). Since \(\eta _{0}(r)\le \eta (r)\) and, by definition of \(f_{\ell }(x)\), we see that \(-\langle v_{\ell }, x^k{}-{\bar{x}}\rangle + \eta _{0}(\Vert x^k-{\bar{x}}\Vert )<0\), \(\forall \ell \) and hence \(\eta _{0}(\Vert x^k-{\bar{x}}\Vert )< \min _{\ell =1,\dots ,r}\langle v_{\ell }, x^k-{\bar{x}}\rangle \) for k large enough, which is a contradiction with (10).

To show that (b) implies (c), suppose that there exists a \(C^{1}\) mapping \(f(x)=(f_{\ell }(x))_{\ell =1}^{r}\) such that \({\bar{x}}\) is a local weak Pareto optimal point relative to \(\varOmega \). From Lemma 2.1, \(\max _{\ell =1,\dots , r} \langle \nabla f_{\ell }({\bar{x}}), d \rangle \ge 0\), \(\forall d \in T({\bar{x}}, \varOmega )\). Thus, if

\(V:=(v_{\ell })_{\ell =1}^{r}\) with \(v_{\ell }:=-\nabla f_{\ell }({\bar{x}})\), \(\forall \ell \), we get that \(\min _{\ell =1,\dots , r} \langle v_{\ell }, d \rangle \le 0\).

Finally, to see that (c) implies (a), assume that V does not belong to \({\widehat{N}}({\bar{x}}, \varOmega ; r)\). Thus, there exist a scalar \(\alpha >0\) and a sequence \(\{x^{k}\} \subset \varOmega \) converging to \({\bar{x}}\) such that

$$\begin{aligned} \lim _{ k \rightarrow \infty } \min _{\ell =1,\dots , r} \frac{\langle v_{\ell }, x^{k}-{\bar{x}} \rangle }{\Vert x^{k}-{\bar{x}}\Vert }>\alpha >0. \end{aligned}$$
(11)

Taking a further subsequence of \(\{x^{k}\}\), we may assume that \((x^{k}-{\bar{x}})/\Vert x^{k}-{\bar{x}}\Vert \) converges to some vector \(d \in {\mathbb {R}}^{n}\). Clearly, \(d \in T({\bar{x}}, \varOmega )\). From (11), we get that \(\min _{\ell =1,\dots , r} \langle v_{\ell }, d \rangle \ge \alpha >0\), a contradiction. Thus, \(V \in {\widehat{N}}({\bar{x}}, \varOmega ; r)\). \(\square \)

Remark 3.1

When \(r=1\), the right-hand side of (9) coincides with \(T({\bar{x}}, \varOmega ) ^{\circ }\). Thus, \({\widehat{N}}({\bar{x}},\varOmega )={\widehat{N}}({\bar{x}},\varOmega ;1)=T({\bar{x}}, \varOmega ) ^{\circ }\).

We have also the following

Lemma 3.1

Consider f and g two lower semicontinuous mappings having lower semicontinuous extended-real-valued components, and \(\varOmega \) a closed subset of \({\mathbb {R}}^{n}\). Then, we always have that

  1. 1.

    \({\widehat{\partial }} {\bar{\imath }}_{\varOmega }(x;r)={\widehat{N}}(x,\varOmega ;r)\) where \({\bar{\imath }}_{\varOmega }\) is the indicator mapping, that is, a mapping defined by \({\bar{\imath }}_{\varOmega }(x)=0\) if \(x \in \varOmega \) and \({\bar{\imath }}_{\varOmega }(x)=\infty \) otherwise.

  2. 2.

    \(V=(v_{\ell })_{\ell =1}^{r} \in {\widehat{\partial }} f(x;r)\) iff there is a \(C^{1}\) mapping h such that x is a local weak Pareto solution of minimizing \(f-h\), and \(v_{\ell }=\nabla h_{\ell }(x)\), \(\forall \ell =1,\dots , r\).

  3. 3.

    If x is a local weak Pareto solution of minimizing f, then \(0 \in {{\widehat{\partial }}} f(x;r)\).

  4. 4.

    If f is a \(C^{1}\) mapping, then

    $$\begin{aligned} {{\widehat{\partial }}} f(x;r)= \{ U \in {\mathbb {R}}^{n\times r}: U \theta =\nabla f(x)^{T}\theta , \ \ \Vert \theta \Vert _{1}=1, \theta \ge 0 \}. \end{aligned}$$
  5. 5.

    If f is a \(C^{1}\) mapping, then

    \({{\widehat{\partial }}}(f+g)(x;r)=\nabla f(x)^T+ {{\widehat{\partial }}} g(x;r)\).

Proof

First, it is straightforward to see that item 1 holds. Also, observe that item 2 is just a modification of Theorem 3.1.

Item 3: Since \({{\bar{x}}}\) is a local weak Pareto solution of minimizing f, we have that \(\max _{\ell =1,\dots ,r}(f_{\ell }(x)-f_{\ell }({{\bar{x}}}))\ge 0\) for every x near \({{\bar{x}}}\), (see Lemma 2.1), and thus, \(0 \in {{\widehat{\partial }}} f({{\bar{x}}};r)\).

Item 4: Take \(V=(v_{\ell })_{\ell =1}^{r} \in {\widehat{\partial }} f({{\bar{x}}};r)\). By item 2, there exists a \(C^{1}\) mapping h such that \({{\bar{x}}}\) is a local weak Pareto solution of minimizing \(f-h\) and \(v_{\ell }=\nabla h_{\ell }({{\bar{x}}})\), \(\forall \ell =1,\dots , r\). Then, \(\max _{\ell =1,\dots ,r}(f_{\ell }(x)-h_{\ell }(x)-(f_{\ell }({{\bar{x}}})-h_{\ell }({{\bar{x}}})))\ge 0\), for every x near \({{\bar{x}}}\). Thus, by Fermat’s rule and computing Clarke’s subdifferential, there exists \(\theta \ge 0\) with \(\Vert \theta \Vert _{1}=1\) such that \(\sum _{\ell =1}^{r} \theta _{\ell }(\nabla f_{\ell }({{\bar{x}}})-\nabla h_{\ell }({{\bar{x}}}))=0\), i.e., \(V \theta =\nabla f({{\bar{x}}})^{T}\theta \).

Now, take \(U=(u_{\ell })_{\ell =1}^{r}\) such that \(U \theta =\nabla f(x)^{T}\theta \) for \(\theta \ge 0\), \(\Vert \theta \Vert _{1}=1\). Observe that

$$\begin{aligned} \max _{\ell =1,\dots , r} \frac{f_{\ell }(x)-f_{\ell }({\bar{x}})-\langle u_{\ell }, x-{\bar{x}} \rangle }{\Vert x-{\bar{x}}\Vert }&\ge \sum _{\ell =1}^{r} \frac{\theta _{\ell }f_{\ell }(x)-\theta _{\ell }f_{\ell }({\bar{x}})-\theta _{\ell }\langle u_{\ell }, x-{\bar{x}} \rangle }{\Vert x-{\bar{x}}\Vert }\\&\ge \sum _{\ell =1}^{r} \frac{\theta _{\ell }f_{\ell }(x)-\theta _{\ell }f_{\ell }({\bar{x}})-\theta _{\ell }\langle \nabla f_{\ell }({{\bar{x}}}), x-{\bar{x}} \rangle }{\Vert x-{\bar{x}}\Vert }\\&\ge \sum _{\ell =1}^{r} \theta _{\ell } \left( \frac{f_{\ell }(x)-f_{\ell }({\bar{x}})-\langle \nabla f_{\ell }({{\bar{x}}}), x-{\bar{x}} \rangle }{\Vert x-{\bar{x}}\Vert } \right) . \end{aligned}$$

Taking limit inferior as \(x \rightarrow {{\bar{x}}}\) in the last expression, we get \(U \in {\widehat{\partial }} f(x;r)\).

Item 5: By item 2 of this Lemma, we see that \(V=(v_{\ell })_{\ell =1}^r \in {{\widehat{\partial }}}(f+g)(x;r)\). iff there is a \(C^{1}\) mapping h such that x is a local weak Pareto solution of \((f+g)-h\) and \(v_{\ell }=\nabla h_{\ell }(x)\), \(\forall \ell \) iff x is also a local weak Pareto solution of \(g-(h-f)\) where \(h-f\) is a \(C^{1}\) mapping iff (using again the item 2) \(V-\nabla f(x)^{T}=(\nabla h_{\ell }(x)-\nabla f_{\ell }(x))_{\ell =1}^{r}\) is in \({{\widehat{\partial }}} g(x;r)\). \(\square \)

We end this section with the following observation: If \({{\bar{x}}}\) is a local Pareto solution of minimizing \(f(x)=(f_{1}(x),\dots , f_{r}(x))\) subject to \(x \in \varOmega \), then \({{\bar{x}}}\) is also a local Pareto solution of the unconstrained MOP of minimizing \(f(x)+{\bar{\imath }}_{\varOmega }(x)\), where \({\bar{\imath }}_{\varOmega }(x)\) is the indicator mapping defined in Lemma 3.1, Item 1. Thus, by Lemma 3.1, Item 3, we obtain that \(0 \in {{\widehat{\partial }}} (f+{\bar{\imath }}_{\varOmega })({{\bar{x}}};r)\). If we assume that f(x) is a \(C^{1}\) mapping, by Lemma 3.1, Item 5, we obtain that \(0 \in (\nabla f_{1}(x),\dots , \nabla f_{r}(x))+{\widehat{N}}({{\bar{x}}}, \varOmega ;r)\).

Corollary 3.1

If \({\bar{x}}\) is a local weak Pareto optimal point of (2), then

$$\begin{aligned} 0 \in (\nabla f_{1}(x),\dots , \nabla f_{r}(x))+ {\widehat{N}}(x, \varOmega ;r). \end{aligned}$$
(12)

Thus, (12) can be interpreted as Fermat’s rule using the r-multiobjective normal cone.

4 On Constraint Qualifications for Multiobjective Optimization

In this section, we will focus on the use of the r-multiobjective normal cone to define CQs to characterize the weak/strong KKT conditions. Later, we will analyze the relations of the r-multiobjective cones with the tangent cone and normal cone of the feasible set.

Let us consider the tangent cone to \(\varOmega \) at \({{\bar{x}}}\), \(T({{\bar{x}}},\varOmega )\), and its first-order approximation, \(L({\bar{x}},\varOmega )\), which is called the linearized tangent cone to \(\varOmega \) at \({{\bar{x}}}\), and is defined by

$$\begin{aligned} L({\bar{x}}, \varOmega ):= \left\{ d \in {\mathbb {R}}^{n}: \begin{array}{ll} &{} \langle \nabla h_{i}({\bar{x}}), d \rangle =0, \ \ i=1,\dots ,m \\ &{} \langle \nabla g_{j}({\bar{x}}), d \rangle \le 0, \ \ j \in A({\bar{x}}) \\ \end{array} \right\} , \end{aligned}$$

where \(A({\bar{x}}):=\{j=1, \dots ,p: g_{j}({{\bar{x}}})=0\}\). Given a feasible point \({{\bar{x}}} \in \varOmega \), Guignard’s CQ is stated as \(T({{\bar{x}}}, \varOmega )^{\circ }=L({{\bar{x}}}, \varOmega )^{\circ }\), while Abadie’s CQ states the stronger equality \(T({{\bar{x}}}, \varOmega )=L({{\bar{x}}}, \varOmega )\).

In this section, we define new CQs for weak/strong KKT conditions based on the multiobjective normal cone, and we analyze their properties.

4.1 Constraint Qualifications for Weak KKT Points

Here, we start by giving the weakest CQ that guarantees that a local weak Pareto minimizer is, in fact, a weak KKT point. This is characterized by the fact that the fulfillment of the CQ is equivalent to the fact that, independently of the objective function, local weak Pareto implies weak KKT.

Theorem 4.1

Let \({\bar{x}}\) be a feasible point of (2). Then, the weakest property under which every local weak Pareto point satisfies the weak KKT conditions, for every continuously differentiable mapping \(f(x)=(f_{1}(x),\dots , f_{r}(x))\), is

$$\begin{aligned} L({\bar{x}}, \varOmega ) \subset \{ d \in {\mathbb {R}}^{n}: \min _{\ell =1,\dots ,r} \langle v_{\ell }, d \rangle \le 0, \text { for all } V=(v_i)_{i=1}^r \in {\widehat{N}}({\bar{x}}, \varOmega ; r) \}.\nonumber \\ \end{aligned}$$
(13)

Proof

Assume that every local weak Pareto point is actually a weak KKT point. We will show that inclusion (13) holds. Indeed, take \(d \in L({\bar{x}},\varOmega )\) and \(V=(v_{\ell })_{\ell =1}^{r} \in {\widehat{N}}({\bar{x}}, \varOmega ; r)\). By Theorem 3.1, there is a \(C^{1}\) mapping f such that \({\bar{x}}\) is a local weak Pareto minimizer of f over \(\varOmega \) and \(v_{\ell }=-\nabla f_{\ell }({\bar{x}})\), for every \(\ell =1,\dots , r\). By hypotheses, we get that \({\bar{x}}\) is a weak KKT point and thus, there exist \(\theta \in {\mathbb {R}}_{+}^{m}\), \(\mu \in {\mathbb {R}}_{+}^{p}\) and \(\lambda \in {\mathbb {R}}^{m}\) such that

$$\begin{aligned} \sum _{\ell =1}^{r} \theta _{\ell }v_{\ell }= \sum _{i=1}^{m} \lambda _{i}\nabla h_{i}({\bar{x}})+ \sum _{j=1}^{p} \mu _{j}\nabla g_{j}({\bar{x}}), \ \ \text { and } \ \ \mu _{j}=0, \ \ \forall j \notin A({\bar{x}}). \end{aligned}$$

Furthermore, we can assume that \(\Vert \theta \Vert _{1}=1\). Since \(d \in L({\bar{x}}, \varOmega )\), we see that

$$\begin{aligned} \min _{\ell =1,\dots ,r} \langle v_{\ell }, d \rangle \le \sum _{\ell =1}^{r} \theta _{\ell }\langle v_{\ell }, d \rangle = \sum _{i=1}^{m} \lambda _{i}\langle \nabla h_{i}({\bar{x}}), d \rangle + \sum _{j=1}^{p} \mu _{j}\langle \nabla g_{j}({\bar{x}}), d \rangle \le 0. \end{aligned}$$

Now, assume that (13) holds. Thus, take \(f(x)=(f_{1}(x),\dots , f_{r}(x))\) a \(C^{1}\) mapping such that \({\bar{x}}\) is a local weak Pareto optimal point over \(\varOmega \). Define \(v_{\ell }:=-\nabla f_{\ell }({\bar{x}})\), \(\forall \ell =1,\dots , r\). By Lemma 2.2, we see that \({\bar{x}}\) is a weak KKT point, if the following system

$$\begin{aligned} \begin{aligned}&\nabla h_{i}({\bar{x}})^{T}d=0, \ \ i=1,\dots , m; \ \ \nabla g_{j}({\bar{x}})^{T}d\le 0, \ \ j \in A({\bar{x}}), \\&\nabla f_{\ell }({\bar{x}})^{T}d<0, \ \ \ell =1,\dots , r \end{aligned} \end{aligned}$$
(14)

has no solution \(d\in {\mathbb {R}}^n\). Now, if we suppose that system (14) admits a solution d, we get that \(d \in L({\bar{x}},\varOmega )\), and by (13), \(\min _{\ell =1,\dots ,r} \langle v_{\ell }, d \rangle \le 0\), which is equivalent to \(\max _{\ell =1,\dots ,r} \langle \nabla f_{\ell }({\bar{x}}), d \rangle \ge 0\), a contradiction with the second line of (14). Thus, (14) has no solution. \(\square \)

Recall that expression (13) is a true CQ, since it only depends on the feasible set, and no information of the objective functions is required. To continue our discussion, define

$$\begin{aligned} {\mathfrak {L}}({\bar{x}},\varOmega ;r)=\left\{ d \in {\mathbb {R}}^{n}: \min _{\ell =1,\dots ,r} \langle v_{\ell }, d\rangle \le 0, \forall V=(v_{\ell })_{\ell =1}^{r} \in {\widehat{N}}({\bar{x}}, \varOmega ; r) \right\} . \end{aligned}$$
(15)

Using (15), Theorem 4.1 states that the weakest CQ guaranteeing that a local weak Pareto minimizer is a weak KKT point is the inclusion \(L({{\bar{x}}}, \varOmega )\subset {\mathfrak {L}}({\bar{x}},\varOmega ;r)\). Note that in the scalar case (\(r=1\)), inclusion (13) reduces to Guignard’s CQ. Indeed, when \(r=1\), we see that \({\mathfrak {L}}({\bar{x}},\varOmega ;1) ={\widehat{N}}({{\bar{x}}}, \varOmega )^{\circ } =T({\bar{x}}, \varOmega )^{\circ \circ }\). Thus, (13) is equivalent to \(L({\bar{x}}, \varOmega )\subset T({\bar{x}}, \varOmega )^{\circ \circ }\), which is equivalent to the classical Guignard’s CQ.

We proceed by analyzing the relation of (13) with Abadie’s and Guignard’s CQs. It is known that Abadie’s CQ is enough to ensure that every local weak Pareto point satisfies the weak KKT conditions, see, for instance, [34], but Guignard’s CQ does not ensure the validity of the weak KKT conditions at local weak Pareto points, [35]. This is the so-called gap in scalar and multiobjective optimization, which has attracted the attention of many researchers. For more details, see also [36,37,38]. Here, we will try to elucidate this “gap” by using the cone \({\mathfrak {L}}({\bar{x}},\varOmega ; r)\). First, consider Proposition 4.1, where some properties about \({\mathfrak {L}}({\bar{x}},\varOmega ; r)\) are stated and another proof of the fact that Abadie’s CQ ensures the validity of weak KKT at local weak Pareto points is provided [see (18)].

Proposition 4.1

Given \({\bar{x}} \in \varOmega \) and \(r \in {\mathbb {N}}\), we always have

$$\begin{aligned}&{\mathfrak {L}}({\bar{x}},\varOmega ; r) \subset {\widehat{N}}({\bar{x}},\varOmega )^{\circ }, \end{aligned}$$
(16)
$$\begin{aligned}&T({\bar{x}}, \varOmega ) \subset {\mathfrak {L}}({\bar{x}},\varOmega ;r), \end{aligned}$$
(17)
$$\begin{aligned}&\hbox {Abadie's CQ at } {{\bar{x}}} \text { implies }L({\bar{x}},\varOmega ) \subset {\mathfrak {L}}({\bar{x}},\varOmega ; r),\end{aligned}$$
(18)
$$\begin{aligned}&L({\bar{x}},\varOmega )\subset {\mathfrak {L}}({\bar{x}},\varOmega ; r) \hbox {implies Guignard's CQ}. \end{aligned}$$
(19)

Proof

To see that (16) holds, take \(d \in {\mathfrak {L}}({\bar{x}},\varOmega ;r)\) and \(w \in {\widehat{N}}({\bar{x}}, \varOmega )\). By Theorem 3.1 in the case that \(r=1\), we see that there exists a \(C^{1}\) function h(x) such that \({\bar{x}}\) is a local minimizer of h(x) over \(\varOmega \) and \(w=-\nabla h({\bar{x}})\). Now, define the \(C^{1}\) mapping \(f(x)=(f_{1}(x),\dots , f_{r}(x))\), where each component \(f_{\ell }(x)=h(x)\), \(\forall x\), \(\forall \ell =1,\dots , r\). It is not difficult to see that \({\bar{x}}\) is a local weak Pareto minimizer for f(x) over \(\varOmega \). Since \(\nabla f_{\ell }({\bar{x}})=\nabla h({\bar{x}})\) for every \(\ell \), we see that \(\langle w, d\rangle =\langle -\nabla h({\bar{x}}), d\rangle =\min _{\ell =1,\dots ,r}\langle -\nabla f_{\ell }({\bar{x}}), d\rangle \le 0\). Thus, we obtain that \(d \in {\widehat{N}}({\bar{x}}, \varOmega )^{\circ }\) and hence (16) holds. Inclusion (17) is a simple consequence of (9). Implication (18) follows directly from inclusion (17), when Abadie’s CQ holds at \({\bar{x}}\) (i.e., \(T({\bar{x}},\varOmega )=L({\bar{x}},\varOmega )\)). To show (19), from (16) and the equality \({\widehat{N}}({\bar{x}}, \varOmega )=T({\bar{x}},\varOmega )^{\circ }\), we see that

$$\begin{aligned} T({\bar{x}},\varOmega )\subset L({\bar{x}}, \varOmega )\subset {\mathfrak {L}}({\bar{x}},\varOmega ; r) \subset {\widehat{N}}({\bar{x}}, \varOmega )^{\circ } = T({\bar{x}},\varOmega )^{\circ \circ }. \end{aligned}$$
(20)

Taking polar in the last sequence of inclusions, we get \(L({\bar{x}}, \varOmega )^{\circ }=T({\bar{x}},\varOmega )^{\circ }\), which is Guignard’s CQ at \({{\bar{x}}}\). \(\square \)

Finally, we show that Abadie’s CQ, Guignard’s CQ and inclusion (13) are independent CQs.

Example 4.1

(Guignard’s CQ is strictly weaker than \(L({{\bar{x}}}, \varOmega )\subset {\mathfrak {L}}({\bar{x}},\varOmega ;r)\)) In \({\mathbb {R}}^2\), take \({{\bar{x}}}=(0,0)\) and the multiobjective problem

$$\begin{aligned} \text { minimize } (f_{1}(x_{1},x_{2}):=x_{1}, \ \ f_{2}(x_1,x_2):=x_2) \text { s.t. } h(x_1,x_2):=x_{1}x_{2}=0. \end{aligned}$$

It is not difficult to see that \({{\bar{x}}}\) is a local weak Pareto point, which is not a weak KKT point. Thus, Theorem 4.1 says that (13) fails. Now, we also observe that \(L({{\bar{x}}}, \varOmega )={\mathbb {R}}^2\) and \(T({{\bar{x}}}, \varOmega )= \{(d_1,d_2) \in {\mathbb {R}}^2: d_1d_2=0\}\), and thus \(L({{\bar{x}}}, \varOmega )^{\circ }=T({{\bar{x}}}, \varOmega )^{\circ }=\{0\}\) holds, that is, Guignard’s CQ is valid at \({{\bar{x}}}\).

Clearly, Abadie’s CQ is strictly stronger than inclusion (13), since in the scalar case, Guignard’s CQ is equivalent to (13).

Fig. 1
figure 1

Gap between Abadie’s and Guignard’s CQ for weak KKT points

Full size image

Finally, we have the following

Proposition 4.2

Let \({\bar{x}}\) be a feasible point of (2) such that \({\mathfrak {L}}({\bar{x}},\varOmega ; r)\) is a closed convex cone. Then, Guignard’s CQ holds at \({{\bar{x}}}\) iff \(L({\bar{x}},\varOmega )\subset {\mathfrak {L}}({\bar{x}},\varOmega ;r)\) holds.

Proof

By Proposition 4.1, inclusion \(L({\bar{x}},\varOmega )\subset {\mathfrak {L}}({\bar{x}},\varOmega ;r)\) implies Guignard’s CQ holds. For the other implication, from (16), (17) and Guignard’s CQ, we get that \( T({\bar{x}},\varOmega )\subset {\mathfrak {L}}({\bar{x}},\varOmega ; r) \subset T({\bar{x}},\varOmega )^{\circ \circ }= L({\bar{x}}, \varOmega )\). Taking the polar and using again Guignard’s CQ, we see that \( L({\bar{x}},\varOmega )^{\circ }\subset {\mathfrak {L}}({\bar{x}},\varOmega ; r)^{\circ } \subset T({\bar{x}},\varOmega )^{\circ }= L({\bar{x}}, \varOmega )^{\circ }\) implies that \(L({\bar{x}},\varOmega )= {\mathfrak {L}}({\bar{x}},\varOmega ;r)^{\circ \circ }={\mathfrak {L}}({\bar{x}},\varOmega ;r)\). \(\square \)

4.2 Constraint Qualifications for Strong KKT Points

Now, we focus on CQs and the fulfillment of the strong KKT conditions. It is well known that Abadie’s CQ is not sufficient to ensure the validity of strong KKT at local weak Pareto minimizers. Using the multiobjective normal cone, similarly to Theorem 4.1, we obtain the weakest CQ needed to guarantee that a local weak Pareto minimizer is a strong KKT point.

Theorem 4.2

Let \({\bar{x}}\) be a feasible point of (2). The weakest property under which every local weak Pareto point is a strong KKT point for every continuously differentiable mapping \(f(x)=(f_{1}(x),\dots , f_{r}(x))\) is

$$\begin{aligned} L({\bar{x}}, \varOmega ) \subset \left\{ d \in {\mathbb {R}}^{n}: \begin{array}{ll} &{} \text { for every } V=(v_i)_{i=1}^r \in {\widehat{N}}({\bar{x}}, \varOmega ; r), \text { we have that } \\ &{} \min _{\ell =1,\dots ,r} \langle v_{\ell }, d \rangle < 0 \text { or } \langle v_{\ell }, d \rangle = 0, \forall \ell =1,\dots ,r \end{array} \right\} .\nonumber \\ \end{aligned}$$
(21)

Proof

To prove inclusion (21), take \(V=(v_{\ell })_{\ell =1}^{r} \in {\widehat{N}}({\bar{x}}, \varOmega ; r)\) and a direction \(d \in L({\bar{x}}, \varOmega )\). By Theorem 3.1, there is a \(C^{1}\) mapping f(x) having \({\bar{x}}\) as a local weak Pareto point over \(\varOmega \), such that \(-\nabla f_{\ell }({\bar{x}})=v_{\ell }\) for every \(\ell =1,\dots , r\). By hypotheses, \({\bar{x}}\) must be a strong KKT point. So, there exist \(\theta \in {\mathbb {R}}_{+}^{r}\), \(\mu \in {\mathbb {R}}_{+}^{p}\) and \(\lambda \in {\mathbb {R}}^{m}\), with \(\theta _{\ell }>0, \ \ \forall \ell =1,\dots ,r\), such that \(\Vert \theta \Vert _{1}=1\) and

$$\begin{aligned} \sum _{\ell =1}^{r} \theta _{\ell }v_{\ell }= \sum _{i=1}^{m} \lambda _{i}\nabla h_{i}({\bar{x}})+ \sum _{j=1}^{p} \mu _{j}\nabla g_{j}({\bar{x}}), \ \ \mu _{j}=0, \ \ \forall j \notin A({\bar{x}}). \ \ \end{aligned}$$
(22)

Now, from (22) and since \(d \in L({\bar{x}},\varOmega )\), we see that

$$\begin{aligned} \sum _{\ell =1}^{r} \theta _{\ell }\langle v_{\ell }, d \rangle = \sum _{i=1}^{m} \lambda _{i}\langle \nabla h_{i}({\bar{x}}), d \rangle + \sum _{j=1}^{p} \mu _{j}\langle \nabla g_{j}({\bar{x}}), d \rangle \le 0. \end{aligned}$$
(23)

From (23), we get that \(\min _{\ell =1,\dots ,r}\langle v_{\ell }, d \rangle <0\) or \(\min _{\ell =1,\dots ,r}\langle v_{\ell }, d \rangle =0\). In the last case, since \(\theta _{\ell }>0\), \(\forall \ell \), we get \(\langle v_{\ell }, d \rangle =0\), for every \(\ell =1,\dots , r\).

Now, let \(f(x)=(f_{1}(x),\dots , f_{r}(x))\) be a \(C^{1}\) mapping such that \({\bar{x}}\) is a local weak Pareto optimal point over \(\varOmega \). Set \(v_{\ell }:=-\nabla f_{\ell }({\bar{x}})\), \(\forall \ell =1,\dots , r\). Using Lemma 2.2, we see that \({\bar{x}}\) is a strong KKT point, if the following system

$$\begin{aligned} \begin{array}{lll} &{} \nabla h_{i}({\bar{x}})^{T}d=0, \ \ i=1,\dots , m; \ \ \ \ &{}\nabla g_{j}({\bar{x}})^{T}d\le 0, \ \ j \in A({\bar{x}}); \\ &{} \nabla f_{\ell }({\bar{x}})^{T}d\le 0, \ \ \ell =1,\dots , r ; \ \ &{}\nabla f_{\ell }({\bar{x}})^{T}d<0, \text { for some } \ell \in \{1,\dots , r\} \end{array} \end{aligned}$$
(24)

has no solution \(d\in {\mathbb {R}}^n\). Indeed, if (24) admits a solution d, then \(d\ne 0\) belongs to \(L({\bar{x}}, \varOmega )\). From (21), we get a contradiction. Thus, \({\bar{x}}\) is a strong KKT point. \(\square \)

When \(r=1\), the right-hand side of (21) collapses to \( {\widehat{N}}({\bar{x}}, \varOmega )^{\circ }\). Thus, (21) coincides with \(L({\bar{x}}, \varOmega )\subset T({\bar{x}}, \varOmega )^{\circ \circ }\) which is Guignard’s CQ.

Observe that inclusion (21) is a true CQ, since it does not require any information of the objective functions for the formulation; moreover, it characterizes the fulfillment of the strong KKT conditions at local weak Pareto points, which coincides with Guignard’s CQ when \(r=1\). Unfortunately, for multiobjective problems (\(r>1\)), inclusion (21) is too strong, in the sense that even in well-behaved constrained system, where LICQ holds, it may fail.

Example 4.2

(Inclusion (21) does not imply LICQ) Consider [39, Example 4.18]: In \({\mathbb {R}}\), take \({{\bar{x}}}=0\) and the constraints \(g_{1}(x):=x\) and \(g_{2}(x):=-\exp (x)+1\). Note that \(\nabla g_{1}(x)=1\) and \(\nabla g_{2}(x)=-\exp (x)\), and thus LICQ fails. Now, from \(L({{\bar{x}}}, \varOmega )=\{0\}\), inclusion (21) holds.

Example 4.3

(LICQ does not imply the inclusion (21)) Indeed, in \({\mathbb {R}}^2\), take \({{\bar{x}}}=(0,0)\), \(a \in {\mathbb {R}}\) and the multiobjective problem

$$\begin{aligned} \text { min } (f_{1}(x_{1},x_{2}):=x_{1}^2, \ \ f_{2}(x_1,x_2):=(x_1-a)^2) \text { s.t. } g(x_1,x_2):=x_{1}^2-x_{2}\le 0. \end{aligned}$$

It is not difficult to see that \({{\bar{x}}}\) is a local weak Pareto point. Straightforward calculations show that \({{\bar{x}}}\) is not a strong KKT point. Thus, Theorem 4.2 says that (21) fails. Now, since \(\nabla g(x_1,x_2):=(2x_1, -1)^T\), LICQ holds at \({{\bar{x}}}\).

From the examples above, we see that usual CQs are not sufficient to obtain strong KKT points at local weak Pareto solutions. Besides this observation, it is still possible to use CQs for obtaining strong KKT, but for a stronger notion of optimality. We focus on the concept of proper Pareto efficiency in the sense of Geoffrion [40].

Definition 4.1

We say that a feasible point \({{\bar{x}}}\) is a local Geoffrion-properly efficient solution, if it is a local strong Pareto solution, within a neighborhood \({\mathcal {N}}\), and there exists a scalar \(M>0\) such that, for each \(\ell \),

$$\begin{aligned} \frac{f_{\ell }(x)-f_{\ell }({{\bar{x}}})}{f_{j}({{\bar{x}}})-f_{j}(x)}\le M, \end{aligned}$$

for some j such that \(f_{j}({{\bar{x}}})<f_{j}(x)\), whenever \(x \in \varOmega \cap {\mathcal {N}}\) and \(f_{\ell }({{\bar{x}}})> f_{\ell }(x)\).

Proposition 4.3

Let \({{\bar{x}}}\) be a feasible point of (2). If \({{\bar{x}}}\) is a Geoffrion-properly efficient point, with Abadie’s CQ holding at \({{\bar{x}}}\), then \({{\bar{x}}}\) is a strong KKT point.

Proof

By Lemma 2.2, \({\bar{x}}\) is a strong KKT point of (2), if the following system

$$\begin{aligned} \begin{array}{lll} &{} \nabla f_{\ell }({\bar{x}})^{T}d\le 0, \ \ \ell =1,\dots , r ; \ \ &{}\nabla f_{\ell }({\bar{x}})^{T}d<0, \text { for some } \ell \in \{1,\dots , r\}; \\ &{} \nabla h_{i}({\bar{x}})^{T}d=0, \ \ i=1,\dots , m; \ \ \ \ &{}\nabla g_{j}({\bar{x}})^{T}d\le 0, \ \ j \in A({\bar{x}}) \end{array} \end{aligned}$$
(25)

has no solution \(d\in {\mathbb {R}}^n\). Thus, suppose that (25) admits a nontrivial solution d. From Abadie’s CQ, there is a sequence \(x^{k}:={{\bar{x}}} + t_{k}d^k \in \varOmega \), with \(t_{k}\rightarrow 0\), \(d^k \rightarrow d \) and \(x^{k}\rightarrow {{\bar{x}}}\). Thus, set \({\mathcal {I}}_{-}:=\{\ell : \nabla f_{\ell }({{\bar{x}}})^{T}d<0\}\) and \({\mathcal {I}}_{0}:=\{\ell : \nabla f_{\ell }({{\bar{x}}})^{T}d=0\}\). Now, consider the set \( {\mathcal {K}}:=\{k \in {\mathbb {N}}: f_{\ell }(x^{k})>f_{\ell }({{\bar{x}}}) \text { for some }\ell \in {\mathcal {I}}_{0}\}\). The set \({\mathcal {K}}\) is infinite; otherwise, we get a contradiction with the fact that \({{\bar{x}}}\) is a local strong Pareto solution. Moreover, taking a further subsequence if necessary, there exists \(\ell _{0}\in {\mathcal {I}}_{0}\) such that \(f_{\ell _{0}}(x^{k})>f_{\ell _{0}}({{\bar{x}}})\), \(\forall k \in {\mathcal {K}}\). Take \(\ell _{1}\in {\mathcal {I}}_{-}\). By using the Taylor expansion, we get

$$\begin{aligned} f_{\ell _{1}}(x^{k})=&f_{\ell _{1}}({{\bar{x}}})+ t_{k} \nabla f_{\ell _{1}}({{\bar{x}}})^{T}d^k+o(\Vert t_{k}d^{k}\Vert ),\\ f_{\ell _{0}}(x^{k})=&f_{\ell _{0}}({{\bar{x}}})+ t_{k} \nabla f_{\ell _{0}}({{\bar{x}}})^{T}d^k+o(\Vert t_{k}d^{k}\Vert ). \end{aligned}$$

From \(f_{\ell _{0}}(x^{k})>f_{\ell _{0}}({{\bar{x}}})\), \(\forall k \in {\mathcal {K}}\), we see that \(\nabla f_{\ell _{0}}({{\bar{x}}})^{T}d^k+o(\Vert t_{k}d^{k}\Vert )t_{k}^{-1}> 0\) and converges to \(\nabla f_{\ell _{0}}({{\bar{x}}})^{T}d=0\) from the right. Thus,

$$\begin{aligned} \frac{f_{\ell _{1}}(x^{k})-f_{\ell _{1}}({{\bar{x}}})}{f_{\ell _{0}}({{\bar{x}}})-f_{\ell _{0}}(x^k)} = \frac{-\nabla f_{\ell _{1}}({{\bar{x}}})^{T}d^k-\frac{o(\Vert t_{k}d^{k}\Vert )}{t_{k}}}{\nabla f_{\ell _{0}}({{\bar{x}}})^{T}d^k+\frac{o(\Vert t_{k}d^{k}\Vert )}{t_{k}}} \rightarrow \infty \text { as } k \rightarrow \infty , \end{aligned}$$

which contradicts the definition of a Geoffrion-properly efficient point. \(\square \)

4.3 Computation of the Multiobjective Normal Cone Under the Error Bound Property

Here, we compute the multiobjective normal cone under the error bound property, see Definition 4.2. The error bound property has a large range of applications, which include convergence analysis of iterative algorithms, stability of inequality systems, to mention a few of them. For more information, see [41, 42] and references therein.

Definition 4.2

We say that the Error Bound Property (EBP) holds for \(\varOmega \) at the feasible point \({\bar{x}}\), if there is a neighborhood \({\mathcal {U}}\) of \({\bar{x}}\) such that

$$\begin{aligned} \text { dist }(x,\varOmega ) \le L \max \{ \Vert h(x)\Vert , \max \{0, g(x)\} \}, \ \ \text { for every } x \in {\mathcal {U}}. \end{aligned}$$

Under EBP, it is possible to get a nice characterization of the multiobjective normal cone. Indeed, we have that

Theorem 4.3

Suppose that EBP holds at \({\bar{x}}\). Then, there is a neighborhood \({\mathcal {U}}\) of \({\bar{x}}\) such that for every feasible point \(x \in {\mathcal {U}}\), we have that:

If \(V=(v_{\ell })_{\ell =1}^{r} \in N(x,\varOmega ;r)\), then there exist \(\theta \in {\mathbb {R}}_{+}^{r}\) with \(\Vert \theta \Vert _{1}=1\) and multipliers \(\lambda \in {\mathbb {R}}^{m}\), \(\mu \in {\mathbb {R}}_{+}^{p}\) with \(\mu _{j}g_{j}(x)=0\), \(\forall j\) such that

$$\begin{aligned} V\theta =\nabla h(x)^{T}\lambda +\nabla g(x)^{T}\mu , \text { and } \ \ \Vert (\lambda , \mu )\Vert \le L \Vert V\theta \Vert . \end{aligned}$$

Proof

First, suppose that \(V \in {\widehat{N}}(x, \varOmega ; r)\). By Theorem 3.1, there exists a \(C^{1}\) mapping f having x as a local weak Pareto solution. Thus, \(v_{\ell }=-\nabla f_{\ell }(x)\), \(\forall \ell \). By Remark 2.1, there exists \(\delta >0\), such that x is the unique solution of

$$\begin{aligned} \text{ Minimize } \max _{\ell =1,\dots , r}(f_{\ell }(z)-f_{\ell }(x))+\frac{1}{2}\Vert z-x\Vert ^2 \text{ s.t. } \Vert z-x\Vert \le \delta , \ \ z \in \varOmega . \end{aligned}$$
(26)

If, in (26), we apply Fermat’s rule at x by using Clarke’s subdifferentials, we obtain an optimality condition based on Clarke’s normal cone, which is usually larger than the limiting normal cone. To avoid the use of Clarke’s subdifferentials, we proceed as follows:

For each \(\eta >0\), consider the smoothing approximation of the max function, \(g_{\eta ,x}(z)\), defined as

$$\begin{aligned} g_{\eta ,x}(z):=\eta \ln \left\{ \sum _{\ell =1}^{r} \exp \left( \frac{f_{\ell }(z)-f_{\ell }(x)}{\eta } \right) \right\} -\eta \ln r, \text { for every } z \in {\mathbb {R}}^{n}. \end{aligned}$$

Note that for each z, \(g_{\mu ,x}(z) \rightarrow \max _{\ell =1,\dots , r}(f_{\ell }(z)-f_{\ell }(x))\) as \(\mu \rightarrow 0\), and

$$\begin{aligned} \nabla g_{\eta ,x}(z)=\sum _{\ell =1}^{r}\theta _{\ell }(z)\nabla f_{\ell }(z), \text { with } \theta _{\ell }(z):= \frac{\exp ((f_{\ell }(z)-f_{\ell }(x))/\eta )}{\sum _{\ell =1}^{r} \exp ((f_{\ell }(z)-f_{\ell }(x))/\eta )}. \end{aligned}$$

Note that \(\Vert \theta _{\ell }(z)\Vert _{1}=1\). Furthermore, we see that

$$\begin{aligned}&\max _{\ell =1,\dots , r}(f_{\ell }(z)-f_{\ell }(x)) \le g_{\eta ,x}(z)+\eta \ln r\le \max _{\ell =1,\dots , r}(f_{\ell }(z)-f_{\ell }(x))+\eta \ln r, \ \ \nonumber \\&\quad \forall z \in {\mathbb {R}}^{n}. \end{aligned}$$
(27)

For applications of the smoothing approximation technique in optimization, we mention [43,44,45] and reference therein.

Now, let \(\{\eta ^{k}\}\) be a sequence of positive parameters converging to 0 and denote by \(x^k \in \varOmega \) the global minimizer of following smooth minimization problem

$$\begin{aligned} \text{ Minimize } g_{\eta ^k,x}(z)+\frac{1}{2}\Vert z-x\Vert ^2 \text{ subject } \text{ to } \Vert z-x\Vert \le \delta , \ \ z \in \varOmega . \end{aligned}$$
(28)

We continue by showing that \(x^k\rightarrow x\).

In fact, using the optimality of \(x^{k}\) and (27), we get that

$$\begin{aligned} g_{\eta ^{k},x}(x^{k})+\frac{1}{2}\Vert x^k-x\Vert ^2 \le g_{\eta ^{k},x}(x) \le \max _{\ell =1,\dots , r}(f_{\ell }(x)-f_{\ell }(x))=0. \end{aligned}$$
(29)

But, from (27), (29) and since x is a weak Pareto point for minimizing f, we see that

$$\begin{aligned} \frac{1}{2}\Vert x^k-x\Vert ^2-\eta ^k \ln r&\le \max _{\ell =1,\dots , r}(f_{\ell }(x^{k})-f_{\ell }(x)) +\frac{1}{2}\Vert x^k-x\Vert ^2-\eta ^{k} \ln r \\&\le g_{\eta ^{k},x}(x^k)+\frac{1}{2}\Vert x^k-x\Vert ^2 \le 0. \end{aligned}$$

Taking limit in the last expression and since \(\eta ^{k}\rightarrow 0\), we get that \(x^{k}\rightarrow x\).

Consider k large enough such that \(\Vert x^k-x\Vert <\delta \). By optimality of \(x^k\) and applying Fermat’s rule for limiting normal cones, we obtain that

$$\begin{aligned} -\nabla g_{\eta ^{k},x}(x^k)-(x^{k}-x)= -\sum _{\ell =1}^{r} \theta _{\ell }(x^k)\nabla f_{\ell }(x^k)-(x^{k}-x) \in N(x^{k},\varOmega ).\nonumber \\ \end{aligned}$$
(30)

Thus, by [46, Theorem 3] applied to \(N(x^{k},\varOmega )\), there are multipliers \(\lambda ^{k} \in {\mathbb {R}}^{m}\), \(\mu ^{k} \in {\mathbb {R}}_{+}^{p}\) with \(\mu _{j}^{k}g_{j}(x^k)=0\), \(\forall j\) such that

$$\begin{aligned}&V^{k}\theta ^{k}-(x^{k}-x)=\nabla h(x^k)^{T}\lambda ^k+\nabla g(x^k)^{T}\mu ^{k}, \end{aligned}$$
(31)
$$\begin{aligned}&\Vert (\lambda ^{k}, \mu ^{k})\Vert \le L \Vert V^{k}\theta ^{k}-(x^{k}-x)\Vert \text { and } \Vert \theta ^{k}\Vert _{1}=1 , \end{aligned}$$
(32)

where \(V^{k}:=(-\nabla f_{\ell }(x^{k}))_{\ell =1}^{r}\). Clearly, \(V^{k}\rightarrow V\). From (31), there is no loss of generality (after possibly taking a further subsequence), if we assume that \(\lambda ^{k}\) and \(\theta ^{k}\) converge to \(\lambda \) and \(\theta \) respectively. Note that \(\Vert \theta \Vert _1=1\) and \(\mu _{j}g_{j}(x)=0\), \(\forall j\). Thus, taking limits in (31), (32), we get the result when V is in \({\widehat{N}}(x, \varOmega ; r)\).

For the general case, take \(V \in N(x, \varOmega ; r)\). Thus, there are sequences \(\{V^{k}\}\subset {\widehat{N}}(x^{k}, \varOmega ; r)\), \(\{x^{k}\} \subset \varOmega \) such that \(V^{k}\rightarrow V\), and \(x^{k}\rightarrow x\). Using the above results for each \(V^{k}\) and after taking a further subsequence, we obtain the desired result for V. \(\square \)

Corollary 4.1

If EBP holds at \({\bar{x}}\), then \(N({\bar{x}},\varOmega ; r)={\widehat{N}}({\bar{x}},\varOmega ; r)\) and

$$\begin{aligned} N({\bar{x}},\varOmega ; r)= \left\{ V \in {\mathbb {R}}^{n\times r}: \begin{array}{ll} &{} V\theta =\nabla h(x)^{T}\lambda +\nabla g(x)^{T}\mu , \text { with } \\ &{} \lambda \in {\mathbb {R}}^{m}, \mu \in {\mathbb {R}}_{+}^{p} \text { and } 0\ne \theta \in {\mathbb {R}}^r_+ \end{array} \right\} . \end{aligned}$$
(33)

Proof

By Theorem 4.3, \(N({\bar{x}},\varOmega ; r)\) is included in the right-hand side set of (33). Now, take \(V=(v_{\ell })_{\ell =1}^{r} \in {\mathbb {R}}^{n\times r}\) such that \( V\theta =\nabla h(x)^{T}\lambda +\nabla g(x)^{T}\mu \), with \(\lambda \in {\mathbb {R}}^{m}\), \(\mu \in {\mathbb {R}}_{+}^{p}\) and \(0\ne \theta \in {\mathbb {R}}^r_+\). Without loss of generality, we assume that \(\Vert \theta \Vert _{1}=1\). Consider \(d \in T({\bar{x}},\varOmega )\), which implies that \(\langle \nabla h_{i}({\bar{x}}), d\rangle =0\), \(i=1,\dots , m\), \(\langle \nabla g_{j}(x), d \rangle \le 0\), \(j \in A({{\bar{x}}})\). Thus,

$$\begin{aligned} \min _{\ell =1,\dots ,r}\langle v_{\ell }, d\rangle \le \sum _{\ell =1}^{r} \theta _{\ell }\langle v_{\ell }, d\rangle&= \langle \sum _{\ell =1}^{r} \theta _{\ell } v_{\ell }, d\rangle = \langle V\theta , d\rangle = \langle \nabla h(x)^{T}\lambda +\nabla g(x)^{T}\mu , d\rangle \\&= \sum _{i=1}^{m}\lambda _{i} \langle \nabla h_{i}({\bar{x}}), d\rangle + \sum _{j=1}^{p}\mu _{j} \langle \nabla g_{j}({\bar{x}}), d \rangle \le 0. \end{aligned}$$

Thus, the last expression shows that item (c) of Theorem 3.1 is satisfied and hence \(V \in {\widehat{N}}({\bar{x}},\varOmega ; r)\subset N({\bar{x}},\varOmega ; r)\), which complete the proof. \(\square \)

5 Conclusions

Constraint qualifications have an important role in nonlinear programming (NLP). These conditions are not only useful for ensuring the validity of the KKT conditions, as they are employed also in stability analysis and convergence of methods for solving NLPs, but their role for MOPs is not so clear, since different notions of solutions and KKT conditions are presented. In this work, we addressed the role of CQs for MOPs. Our main contribution is the use of the concept of multiobjective normal cone to obtain new CQs for MOPs. With this tool, we were able to characterize the weakest CQ possible to guarantee the fulfillment of weak/strong KKT conditions at local weak Pareto minimizers. To analyze the strength of such CQs, we compared them with other CQs stated in the literature. Furthermore, we provided a characterization of the multiobjective normal cone under the error bound property.

As further subject of investigation, we point out the relation of the multiobjective normal cone with the sequential optimality conditions stated in [47], since sequential optimality conditions for NLPs have been widely used for improving and unifying the global convergence analysis of several algorithms. Another interesting sequel to this study is to extend these ideas for multiobjective optimization problems with complementarity constraints, considering similar developments for single-objective problems [48,49,50,51].