1 Introduction

In most real-world applications, optimization problems (OPs) contain uncertain data. The reasons for data uncertainty include, for example, measurement errors (induced by temperature, pressure or material properties), estimation errors (imprecision in evaluating system performance), implementation errors and unknown future developments. Sometimes, solutions to OPs can exhibit remarkable sensitivity to perturbations in the parameters of the problem, thus often rendering a computed solution that is highly infeasible, suboptimal or both (i.e., completely meaningless). Particularly, one cannot ignore this case from the practical point of view.

Nowadays, there have been two prominent approaches to dealing with uncertain OPs, one is robust optimization and the other is stochastic programming. The former is an effective methodology to handle some practical OPs with uncertainties, in which the uncertain parameters belong to a known set. The idea is to minimize the worst possible objective function value, and look for a solution, that is immunized against the effect of data uncertainty. Unlike the former, the latter consists in finding is a better style commonly to find a feasible solution that optimizes the expected value of some objectives or cost function. The uncertain data are assumed to be random and obey a probability distribution known prior. Both methodologies are complementary for handling data uncertainty in optimization, and each has its own advantages and drawbacks.

Robust optimization is becoming more and more popular in solving scalar OPs with uncertain data in last two decades. The first scholar to investigate robust linear OPs under ellipsoidal uncertainty sets was Soyster [1]. Above all, we refer to Ben-Tal and Nemirovski [2], who gave a seminal paper in the early stage of robustness exploration. Specifically, two detailed monographs [3, 4], that provided extensive collections of theoretical results and applications, play a significant role in the development of robust optimization. In the context of computational attractiveness, the modeling power and broad applicability of robust optimization approach, some recent results, both theoretical and applied, were summarized in [5]. Additionally, Goerigk and Schöbel [6] revealed the close connections between algorithm engineering and robust optimization. They also pointed out some open research directions from a new perspective on algorithm engineering. By means of nonlinear scalarization method, Klamroth et al. [7] unified many different concepts of robustness and stochastic programming. Subsequently, they developed a unified characterization of various concepts from vector optimization, set-valued optimization and scalarization points of view in [8], where the uncertain scalar OPs contains infinite scenario sets. Recently, under various constraint qualifications and convexity assumptions, there have been many studies on characterizing robust dual and robust solutions for uncertain convex OPs. For more details, one can refer to [9,10,11,12,13] and reference therein. However, to the best of our knowledge, very few papers concentrate on deriving robust optimality conditions for general uncertain scalar OPs, without any convexity or concavity assumptions. Besides, whether there exists another tool to generate a unified approach to characterizing a variety of robust solutions? These problems facilitate us to make further explorations, as well as contribute the motivation of this paper.

Image space analysis (for short, ISA) was born with [14]. Its gestation has been a long way. A trace was found in C. Charathédory in his book on Calculus of Variations of 1935. Subsequently, several contributions [15,16,17] have been brought, but independently each other. One of them, very important, is due to M. Hestenes in his book [16]. Such an analysis has begun to grow, when separation arguments have been introduced; in this sense, among others, we mention [17]. It has been proven to be a powerful methodology to study, from the geometrical point of view, different kinds of OPs, for example, constrained extremum problems, variational inequalities, nonconvex vector OPs and so on. By constructing the impossibility of a parametric system, the disjunction of two suitable subsets in the image space, one is the image of the functions and the other is a convex cone, can be obtained. Simultaneously, it also can be reached, by showing that the two subsets lie in two disjoint level sets of a linear or nonlinear separation function, which is the main feature of the ISA approach. Thus, separation is vital in the process of implementation. By exploiting separation arguments in the image space, some theoretical aspects, such as optimality conditions, duality, penalty methods, variational principles, gap functions and error bounds, have been developed; see [14, 18,19,20,21,22,23,24,25,26,27,28]. While, the classical image problem of uncertain OP is not equivalent to itself because of the parameters. Then, it seems to be useless to immediately consider the classical image problem, which leads to the failure in investigating this kind of problem by virtue of ISA. Furthermore, if we only consider the image of robust counterpart problem, it may hide the structure of the uncertain problem; see [14, p. 7, lines 9–12]. Therefore, how to introduce an appropriate image problem, such that it is not only equivalent to the corresponding counterpart problem, but also contains some properties of original uncertain problem, is the key to success.

At present, by defining a suitable image, Wei et al. [29] established an equivalence relation between the uncertain OP and its image problem for strictly robustness, as well as achieved some robust optimality conditions. Besides, based on separation, a unified characterization of several multiobjective robustness concepts [30,31,32] for uncertain multiobjective OPs, was presented in [33, 34]. Some characterizations of multiobjective robustness on vectorization counterparts were also provided in [35]. Motivated greatly by the works reported in [7, 8, 14, 29, 33,34,35,36], this paper focuses on a unified approach to characterizing various robust solutions by virtue of ISA. By defining suitable images of original problem, or the images of its counterpart problems appropriately, the corresponding equivalent problems for most known robustness concepts are described, which provide a unified approach to tackling with robustness for uncertain OPs. Meanwhile, ISA has been proven to be an effective and prominent tool for studying scalar robust OPs. It is worthwhile to notice that this paper provides a full answer to the open question (ii) posed in [29]: by virtue of the ISA, it may be interesting to develop a unified approach to dealing with uncertain problems by defining new images for different robustness concepts (such as optimistic robustness, regret robustness, reliable robustness, light robustness, weighted robustness, adjustable robustness and \(\epsilon \)-constraint robustness, as well as Benson robustness and Elastic robustness recently proposed by Wei et al. [36]) to make two suitable subsets of the image space separable.

The remainder of this paper is organized as follows. In Sect. 2, we make some preliminaries and formulate the uncertain problem. By introducing suitable images of the original problem, or the images of its counterpart problems, Sect. 3 characterizes various robust solutions on the unified framework of ISA. Section 4 gives some interpretations for ISA approach, and proposes several open problems. A short conclusion of the paper is provided in Sect. 5.

2 Preliminaries

In this section, we shall recall some notations and definitions, which will be used in the sequel. Let \(\mathbb {R}^{n}\) be the n-dimensional Euclidean space, where n is a positive integer. Let \(\mathcal {X}\subseteq \mathbb {R}^{n}\) be a nonempty subset and Y be a normed linear space. The closure of a set \(M\subseteq Y\) is denoted by \(\text{ cl }\,M\). \(Y{\setminus } M\) implies a set consisting of all elements that belong to Y but not in M. A nonempty subset \(C\subseteq \mathbb {R}^{m}\) is said to be a cone iff \(tC\subseteq C\) for all \(t\ge 0\). A cone \(C\subseteq \mathbb {R}^{m}\) is said to be convex (resp. pointed) iff \(C+C\subseteq C\) (resp. \(C\cap (-C)=\{0_{\mathbb {R}^{m}}\}\)). The set \(\text{ cone }M:=\bigcup _{t\ge 0}tM\) is the cone generated by M.

Now, a general OP with uncertainties both in the objective and constraints is considered. Assume that U is a nonempty subset of a finite dimensional space and an uncertainty set (convex or nonconvex, compact or noncompact, discrete scenarios or continuous interval), where \(\xi \in U\) implies an uncertain parameter, i.e., a real number, a real vector or a scenario. Let \(f{:}\,\mathcal {X}\times U\rightarrow \mathbb {R}\) and \(F_{i}{:}\,\mathcal {X}\times U\rightarrow \mathbb {R},\, i=1,\ldots ,m\). Then, an uncertain scalar OP is defined as a parametric OP

$$\begin{aligned} (Q(\xi ),\; \xi \in U), \end{aligned}$$
(1)

where for a given \(\xi \in U\) the OP (\(Q(\xi )\)) is described by

$$\begin{aligned} \min f(x,\xi )\;\;\text{ s.t. }\;\;F_{i}(x,\xi )\le 0,\,i=1,\ldots ,m,\;\;x\in \mathcal {X}. \end{aligned}$$

We denote by \(\hat{\xi }\in U\) the nominal value, i.e., the value of \(\xi \) that we believe is true today. (\(Q(\hat{\xi })\)) is called the nominal problem.

3 Unified Characterizations of Various Robust Solutions

As far as we know, there is no appropriate methodology to directly solve uncertain problems; thus, it is necessary to replace the uncertain OP by a deterministic version, called the robust counterpart of the uncertain problem. By this means, various robustness concepts, that describe the decision maker’s preferences, have been proposed on the basis of different robust counterparts. With the help of ISA, this section is dedicated to characterizing a variety of robust solutions for different kinds of robustness concepts existing in the literature, which can form a unified approach to tackling with uncertain OPs. In general, the equivalence of problem (1) and its image problem does not hold, due to the effect of parameters; thus, it seems to be meaningless to immediately investigate the image of problem (1). Additionally, if we only consider the image of robust counterpart problem, it may hide the structure of the uncertain problem. Therefore, it is vital to define a proper image problem, such that it can not only be equivalent to the corresponding counterpart problem, but also contain the uncertain parameter on the framework of ISA.

3.1 Strict Robustness

The first classical robustness concept is called strict robustness, which was originally proposed by Soyster [1], for investigating the robust linear OPs under ellipsoidal uncertainty sets. Subsequently, this concept has been extensively researched and developed by Ben-Tal and Nemirovski [2] and Ben-Tal et al. [3]. The idea is to minimize the worst possible objective function value, and search for a solution that is good enough in the worst case. Meanwhile, the constraints should be satisfied for every parameter \(\xi \in U\). Strict robustness is a conservative concept and reveals the pessimistic attitude of a decision maker. Then, the strictly robust counterpart of problem (1) is given by

$$\begin{aligned} \min \,\sup \limits _{\xi \in U}f(x,\xi )\;\;\text{ s.t. }\;\;F_{i}(x,\xi )\le 0,\;\forall \,\xi \in U,\;i=1,\ldots ,m,\;\;x\in \mathcal {X}. \end{aligned}$$
(2)

Set \(D^{1}:=-\mathbb {R}^{m}_{+}\) and \(F(x,\xi ):=(F_{1}(x,\xi ),\ldots ,F_{m}(x,\xi ))\) for a given \(\xi \in U\). It is obvious that \(D^{1}\subseteq \mathbb {R}^{m}\) is a closed and convex cone, and \(F(x,\xi )\in D^{1}\) for feasible points of problem (\(Q(\xi )\)). The set of feasible solutions of problem (2) is denoted as \(X_{1}:=\{x\in \mathcal {X}{:}\,F(x,\xi )\in D^{1},\,\forall \xi \in U\}\). According to [3, pp. 9–10], if a feasible solution \(x\in X_{1}\) is optimal to problem (2), then it is called a strictly robust solution to problem (1). In Sects. 3.1 and 3.3, assume that \(\sup _{\xi \in U}f(x,\xi )<\infty \) and \(\sup _{\xi \in U}F_{i}(x,\xi )<\infty ,i=1,\ldots ,m\) for all \(x\in \mathcal {X}\). Some notations are given to describe the main features of the ISA for problem (1) under the strictly robust counterpart. Let \(\bar{x}\in \mathcal {X}\). Define the map

$$\begin{aligned} A^{1}_{\bar{x}}{:}\,\mathcal {X}\times U\rightarrow \mathbb {R}^{1+m},\quad A^{1}_{\bar{x}}(x,\xi ):=\bigg (f(\bar{x},\xi )-\sup _{\xi \in U}f(x,\xi ),\,F^{1}(x)\bigg ), \end{aligned}$$

where \(F^{1}(x):=(\sup \nolimits _{\xi \in U}F_{1}(x,\xi ),\ldots ,\sup \nolimits _{\xi \in U}F_{m}(x,\xi ))\), and consider the following sets

$$\begin{aligned} \mathcal {K}^{1}_{\bar{x}}:= & {} \left\{ (u,v)\in \mathbb {R}^{1+m}{:}\,(u,v)=A^{1}_{\bar{x}}(x,\xi ),\;x\in \mathcal {X},\,\xi \in U\right\} ,\\ \mathcal {H}^{1}:= & {} \{(u,v)\in \mathbb {R}^{1+m}{:}\,u>0,\,v\in D^{1}\}=\mathbb {R}_{++}\times (-\mathbb {R}^{m}_{+}). \end{aligned}$$

\(\mathcal {K}^{1}_{\bar{x}}\) is called corrected image of problem (1) and \(\mathbb {R}^{1+m}\) is the image space. By means of corrected image, an equivalent characterization of strictly robust solutions for the uncertain OP can be obtained. We should mention that, this separation characterization for the strict robustness has been proposed by authors in [29]. Herein, we make further discussions on it. Particularly, separation characterizations for the weighted robustness and the regret robustness (also known as deviation robustness) will be simultaneously deduced.

Theorem 3.1

A feasible solution \(\bar{x}\in X_{1}\) is a strictly robust solution to problem (1) if and only if

$$\begin{aligned} \mathcal {K}^{1}_{\bar{x}}\cap \mathcal {H}^{1}=\emptyset . \end{aligned}$$
(3)

Proof

Necessity. Suppose that \(\bar{x}\in X_{1}\) is a strictly robust solution to problem (1). Then one can read that

$$\begin{aligned} \sup _{\xi \in U}f(\bar{x},\xi )\le \sup _{\xi \in U}f(x,\xi ),\quad \forall \;x\in X_{1}. \end{aligned}$$
(4)

The inequality (4) is equivalent to

$$\begin{aligned} f(\bar{x},\xi )-\sup _{\xi \in U}f(x,\xi )\le 0,\quad \forall \;x\in X_{1},\;\forall \;\xi \in U. \end{aligned}$$
(5)

In addition, it holds \(F^{1}(x)\not \in D^{1}\) for any \(x\in \mathcal {X}{\setminus } X_{1}\). This, together with inequality (5), one can see that (3) is true.

Sufficiency. Assume (3) holds and \(F^{1}(x)\in D^{1}\) for any \(x\in X_{1}\), then we have inequality (5). It follows from the equivalence of (4) and (5) that \(\bar{x}\in X_{1}\) is a strictly robust solution to problem (1). \(\square \)

Generally, the image of a generalized system is not convex, even when the functions involve some convexity properties. To avoid this drawback, we introduce an extended image \(\mathcal {E}^{1}_{\bar{x}}\), that is a regularization to \(\mathcal {K}^{1}_{\bar{x}}\) with respect to the cone \(\text{ cl }\,\mathcal {H}^{1}\), i.e.,

$$\begin{aligned} \mathcal {E}^{1}_{\bar{x}}:=\mathcal {K}^{1}_{\bar{x}}-\text{ cl }\,\mathcal {H}^{1}= & {} \Big \{(u,v)\in \mathbb {R}^{1+m}{:}\,u\le f(\bar{x},\xi )-\sup _{\xi \in U}f(x,\xi ),v\in F^{1}(x)\\&\quad -\,D^{1},\;x\in \mathcal {X},\,\xi \in U\Big \}. \end{aligned}$$

Similarly as in [14], the following proposition can be derived by virtue of the extended image, and we state it without proof.

Proposition 3.1

A feasible solution \(\bar{x}\in X_{1}\) is a strictly robust solution to problem (1) if and only if

$$\begin{aligned} \mathcal {E}^{1}_{\bar{x}}\cap \mathcal {H}^{1}=\emptyset , \end{aligned}$$
(6)

or equivalently, \(cone \,\mathcal {E}^{1}_{\bar{x}}\cap \mathcal {H}^{1}=\emptyset \), or equivalently, \(\mathcal {E}^{1}_{\bar{x}}\cap \mathcal {H}^{1}_{0}=\emptyset \), where

$$\begin{aligned} \mathcal {H}^{1}_{0}:=\left\{ (u,v)\in \mathbb {R}^{1+m}{:}\,u>0,\,v=0_{\mathbb {R}^{m}}\right\} =\mathbb {R}_{++}\times \{0_{\mathbb {R}^{m}}\}. \end{aligned}$$

Remark 3.1

  1. (i)

    If we consider the classical definition of image set of problem (1), and define the map

    $$\begin{aligned} A_{\bar{x}}{:}\,\mathcal {X}\times U\rightarrow \mathbb {R}^{1+m},\quad A_{\bar{x}}(x,\xi ):=(f(\bar{x},\xi )-f(x,\xi ),\,F(x,\xi )), \end{aligned}$$

    where \(F(x,\xi ):=(F_{1}(x,\xi ),\ldots ,F_{m}(x,\xi ))\), then the image of problem (1) is

    $$\begin{aligned} \mathcal {K}_{\bar{x}}:=\left\{ (u,v)\in \mathbb {R}^{1+m}{:}\,(u,v)=A_{\bar{x}}(x,\xi ),\;x\in \mathcal {X},\,\xi \in U\right\} . \end{aligned}$$

    While, \(\bar{x}\in X_{1}\) being a strictly robust solution to problem (1) cannot ensure the equality \(\mathcal {K}_{\bar{x}}\cap \mathcal {H}^{1}=\emptyset \). This is because the inequality \(\sup _{\xi \in U}f(\bar{x},\xi )\le \sup _{\xi \in U}f(x,\xi )\) usually does not imply the inequality \(f(\bar{x},\xi )\le f(x,\xi )\) for all \(x\in X_{1}\) and \(\xi \in U\). Thus, the equivalence of robust counterpart problem (2) and the classical image problem of (1) are not satisfied.

  2. (ii)

    Another approach, which is from [14, p. 7, lines 9–12] in face of minimax problems, is to discuss directly the image of problem (2). In this circumstance, the strictly robust counterpart can be viewed as a special case of constrained extremum problems. That is, define the map

    $$\begin{aligned} \widetilde{A_{\bar{x}}}{:}\,\mathcal {X}\rightarrow \mathbb {R}^{1+m},\quad \widetilde{A_{\bar{x}}}(x):=\bigg (\sup _{\xi \in U}f(\bar{x},\xi )-\sup _{\xi \in U}f(x,\xi ),\,F^{1}(x)\bigg ), \end{aligned}$$

    and the image of (2) is \(\widetilde{\mathcal {K}_{\bar{x}}}:=\{(u,v)\in \mathbb {R}^{1+m}{:}\,(u,v)=\widetilde{A_{\bar{x}}}(x),\;x\in \mathcal {X}\}\). This method hides the structure of problem (1), although \(\sup _{\xi \in U}f(\bar{x},\xi )\le \sup _{\xi \in U}f(x,\xi )\) is tantamount to \(f(\bar{x},\xi )\le \sup _{\xi \in U}f(x,\xi )\) for all \(x\in X_{1}\) and \(\xi \in U\).

Remark 3.2

Let \(U:=\{\xi _{1},\ldots ,\xi _{q}\}\) be a finite set of scenarios. If some scenarios are more likely to be realized than others, to assign weights \(\mathbf {w}_{j}>0\) to each scenario \(\xi _{j}\in U,j=1,\ldots ,q\), then the weighted robust counterpart of the uncertain OP can be presented, by using \(\sup _{j\in \{1,\ldots ,q\}}\mathbf {w}_{j}f(x,\xi _{j})\) instead of the objective function \(\sup _{\xi \in U}f(x,\xi )\) in (2). If \(\mathbf {w}_{j}=1\) for every \(j=1,\ldots ,q\), the weighted robust counterpart is reduced to (2). The concept of weighted robustness is a generalization of strictly robustness and can be described by the weighted Tschebyscheff scalarization. Additionally, let \(f^{*}{:}\,U\rightarrow \mathbb {R}\) be a function given by \(f^{*}(\xi ):=\min \{f(x,\xi ){:}\,x\in X(\xi )\}\), where \(X(\xi ):=\{x\in \mathcal {X}{:}\,F_{i}(x,\xi )\le 0,\,i=1,\ldots ,m\}\). Here, we assume that an optimal solution exists for every fixed scenario \(\xi \). The optimal value of problem (\(Q(\xi )\)) for a given \(\xi \in U\) is \(f^{*}(\xi )\), and it can be interpreted as an ideal point. If we replace the objective function \(\sup _{\xi \in U}f(x,\xi )\) by \(\sup _{\xi \in U}(f(x,\xi )-f^{*}(\xi ))\) in (2), the regret robust counterpart of the uncertain OP can be addressed. The regret robustness is also known as deviation robustness, in which one evaluates a solution by comparing it with the best possible solution for the realized scenario in the worst case. By making a proper modification of \(A^{1}_{\bar{x}}(x,\xi )\), i.e., let \(A^{\mathbf {w}}_{\bar{x}}(x,\xi _{j})=(\mathbf {w}_{j}f(\bar{x},\xi _{j})-\sup _{j\in \{1,\ldots ,q\}}\mathbf {w}_{j}f(x,\xi _{j}),\,F^{1}(x))\) (or \(A^{r}_{\bar{x}}(x,\xi )=(f(\bar{x},\xi )-f^{*}(\xi )-\sup _{\xi \in U}(f(x,\xi )-f^{*}(\xi )),\,F^{1}(x))\)), the corresponding results of Theorem 3.1 and Proposition 3.1 for weighted (regret) robust counterpart problem would be obtained.

Three examples are employed to emphasize the importance of the theoretical results obtained above for (strictly/weighted/regret) robust counterpart. The uncertainty set contains finite scenario in Examples 3.1 and 3.2, while it is regarded as a closed interval in Example 3.3. In this case, the weighted robustness is invalid in the third example.

Example 3.1

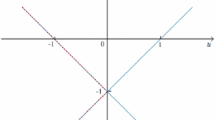
For problem (1), take \(\mathcal {X}=\mathbb {R}\) and \(U=\{\xi _{1},\xi _{2}\}\) be the parameter set. Let \(f(x,\xi _{1})=x\), \(f(x,\xi _{2})=-x\), \(F(x,\xi _{1})=x-1\) and \(F(x,\xi _{2})=x-2\). Thus, \(\max _{\xi \in U}f(x,\xi )=|x|\), \(\max _{\xi \in U}F(x,\xi )=x-1\) and \(X_{1}:=]-\infty ,1]\). For strict robustness, one can reach that \(x^{*}=0\) is the unique strictly robust solution. (i) Set \(\bar{x}=0\). Since \(f(0,\xi _{1})=f(0,\xi _{2})=0\), it holds \(A^{1}_{0}(x,\xi _{1})=A^{1}_{0}(x,\xi _{2})=(-|x|,x-1)\). Let \(u=-|x|\) and \(v=x-1\), we can derive \(v=-u-1,u\le 0\) and \(v=u-1,u<0\). Then, the corrected image set is \(\mathcal {K}^{1}_{0}=\{(u,v)\in \mathbb {R}^{2}{:}\,v=-u-1,\;u\le 0\}\cup \{(u,v)\in \mathbb {R}^{2}{:}\,v=u-1,\;u<0\}\). (ii) Take \(\bar{x}=1\). If \(\xi =\xi _{1}\) or \(\xi =\xi _{2}\), then \(A^{1}_{1}(x,\xi _{1})=(1-|x|,x-1)\) and \(A^{1}_{1}(x,\xi _{2})=(-1-|x|,x-1)\). Two cases are discussed and the corrected image set is

$$\begin{aligned} \mathcal {K}^{1}_{1}&=\{(u,v)\in \mathbb {R}^{2}{:}\,v=u-2,\;u<1\}\cup \{(u,v)\in \mathbb {R}^{2}{:}\,v=-u,\;u\le 1\}\\&\quad \cup \{(u,v)\in \mathbb {R}^{2}{:}\,v=u,\;u<-1\}\cup \{(u,v)\in \mathbb {R}^{2}{:}\,v=-u-2,\;u\le -1\}. \end{aligned}$$

See Fig. 1; the red lines denote \(\mathcal {K}^{1}_{0}\) and the blue ones represent \(\mathcal {K}^{1}_{1}\).

Fig. 1
figure 1

The corrected images for strict robustness in Example 3.1

Full size image

For weighted robustness, let \(\mathbf {w}_{1}=1\) and \(\mathbf {w}_{2}=2\). One can see that

$$\begin{aligned} \max \{\mathbf {w}_{1}f(x,\xi _{1}),\mathbf {w}_{2}f(x,\xi _{2})\}=\max \{x,-2x\}=\left\{ \begin{array}{lll} x,&{}\quad x\ge 0,\\ -\,2x,&{}\quad x<0. \end{array}\right. \end{aligned}$$

It is not difficult to see that \(x^{*}=0\) is the unique weighted robust solution. (i) Taking \(\bar{x}=0\), we obtain \(\mathbf {w}_{1}f(0,\xi _{1})=\mathbf {w}_{2}f(0,\xi _{2})=0\) and \(A^{\mathbf {w}}_{0}(x,\xi _{1})=A^{\mathbf {w}}_{0}(x,\xi _{2})=(-\max \{x,-2x\},x-1)\). Setting \(u=-\max \{x,-2x\}\) and \(v=x-1\), the relation between u and v can be formulated as \(v=-u-1,u\le 0\), \(v=\frac{u}{2}-1,u<0\). The corrected image set is

$$\begin{aligned} \mathcal {K}^{\mathbf {w}}_{0}=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=-u-1,\;u\le 0\}\cup \{(u,v)\in \mathbb {R}^{2}{:}\,v=\frac{u}{2}-1,\;u<0\right\} . \end{aligned}$$

(ii) Set \(\bar{x}=1\), it is obvious that \(\mathbf {w}_{1}f(1,\xi _{1})=1,A^{\mathbf {w}}_{1}(x,\xi _{1})=(1-\max \{x,-2x\},x-1)\), and \(\mathbf {w}_{2}f(1,\xi _{2})=-2\), \(A^{\mathbf {w}}_{1}(x,\xi _{2})=(-2-\max \{x,-2x\},x-1)\). By analyzing two cases, the corresponding corrected image set can be presented by

$$\begin{aligned} \mathcal {K}^{\mathbf {w}}_{1}&=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=-u,\;u\le 1\right\} \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=\frac{u}{2}-\frac{3}{2},\;u<1\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=-u-3,\;u\le -2\right\} \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=\frac{u}{2},\;u<-2\right\} . \end{aligned}$$

In Fig. 2, the red lines and blue ones describe \(\mathcal {K}^{\mathbf {w}}_{0}\) and \(\mathcal {K}^{\mathbf {w}}_{1}\), respectively.

Fig. 2
figure 2

\(\mathcal {K}^{\mathbf {w}}_{0}\) and \(\mathcal {K}^{\mathbf {w}}_{1}\) are corrected images for weighted robustness in Example 3.1

Full size image

For regret robustness, let \(\mathcal {X}=[-\,2,1]\subset \mathbb {R}\), the feasible set of problem (2) is \(X_{1}:=[-\,2,1]\). It follows from Remark 3.2 that \(f^{*}(\xi _{1})=\min _{x\in X(\xi _1)}f(x,\xi _{1})=-2\) and \(f^{*}(\xi _{2})=\min _{x\in X(\xi _2)}f(x,\xi _{2})=-1\). One can read that

$$\begin{aligned}&\max \{f(x,\xi _{1})-f^{*}(\xi _{1}),f(x,\xi _{2})-f^{*}(\xi _{2})\}=\max \{x+2,-x+1\}\\&\quad =\left\{ \begin{array}{lll} x+2,&{}\quad x\in \left[ -\,\,\frac{1}{2},1\right] , \\ -\,x+1,&{}\quad x\in \big [-\,2,-\frac{1}{2}\big [, \end{array}\right. \end{aligned}$$

and \(x^{*}=-\frac{1}{2}\) is the unique regret robust solution. (i) Set \(\bar{x}=-\frac{1}{2}\). For \(\xi =\xi _{1}\) or \(\xi =\xi _{2}\), it holds \(A^{r}_{-\frac{1}{2}}(x,\xi )=\Big (\frac{3}{2}-\max \{x+2,-x+1\},x-1\Big )\). Let \(u=\frac{3}{2}-\max \{x+2,-x+1\}\) and \(v=x-1\), the corrected image set can be given by

$$\begin{aligned} \mathcal {K}^{r}_{-\frac{1}{2}}= & {} \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=-u-\frac{3}{2},\;u\in \left[ -\,\frac{3}{2},0\right] \right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u-\frac{3}{2},\;u\in \Bigg [-\,\frac{3}{2},0\Bigg [\,\right\} . \end{aligned}$$

(ii) Take \(\bar{x}=0\). If \(\xi =\xi _{1}\) (or \(\xi _{2}\)), then \(f(0,\xi _{1})-f^{*}(\xi _{1})-\max \{x+2,-x+1\}=2-\max \{x+2,-x+1\}\) and \(f(0,\xi _{2})-f^{*}(\xi _{2})-\max \{x+2,-x+1\}=1-\max \{x+2,-x+1\}\). The corresponding corrected image set is

$$\begin{aligned} \mathcal {K}^{r}_{0}&=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=-u-1,\;u\in \left[ -\,1,\frac{1}{2}\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u-2,\;u\in \Bigg [-\,1,\,\frac{1}{2}\Bigg [\,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=-u-2,\;u\in \left[ -\,2,-\,\frac{1}{2}\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u-1,\;u\in \Bigg [-\,2,-\,\frac{1}{2}\Bigg [\,\right\} . \end{aligned}$$

See Fig. 3; the red lines and blue ones denote \(\mathcal {K}^{r}_{-\frac{1}{2}}\) and \(\mathcal {K}^{r}_{0}\), respectively.

Fig. 3
figure 3

For regret robustness, the corrected images \(\mathcal {K}^{r}_{-\frac{1}{2}}\) and \(\mathcal {K}^{r}_{0}\) in Example 3.1

Full size image

Example 3.2

For problem (1), let \(\mathcal {X}=[-\,1,1]\), \(U=\{\xi _{1},\xi _{2}\}\), \(f(x,\xi _{1})=\sqrt{1-x^{2}}\), \(f(x,\xi _{2})=1-\frac{1}{2}x\), \(F(x,\xi _{1})=x\) and \(F(x,\xi _{2})=x-1\). It is not difficult to see that

$$\begin{aligned} \max _{\xi \in U}f(x,\xi )=\max \left\{ \sqrt{1-x^{2}},1-\frac{1}{2}x\right\} =\left\{ \begin{array}{lll} 1-\frac{1}{2}x,&{}\quad x\in [-\,1,0]\cup \left[ \frac{4}{5},1\right] ,\\ \sqrt{1-x^{2}},&{}\quad x\in \left[ 0,\frac{4}{5}\right] , \end{array}\right. \end{aligned}$$

and \(\max _{\xi \in U}F(x,\xi )=x\), \(X_{1}=[-\,1,0]\). For strict robustness, by simple calculation, one can read that \(x^{*}=0\) is the unique strictly robust solution. (i) Take \(\bar{x}=0\). Analogous to the process in Example 3.1, the corrected image can be obtained, i.e.,

$$\begin{aligned} \mathcal {K}^{1}_{0}= & {} \left\{ (u,v)\in \mathbb {R}^{2}{:}\,(u-1)^{2}+v^{2}=1,\;u\in \left[ 0,\frac{2}{5}\right] , v\in \left[ 0,\frac{4}{5}\right] \right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=2u,\;u\in \left[ -\,\frac{1}{2},0\right] \cup \left[ \frac{2}{5},\frac{1}{2}\right] \right\} . \end{aligned}$$

(ii) Let \(\bar{x}=-1\). By discussing two cases \(\xi =\xi _{1}\) or \(\xi =\xi _{2}\), we can achieve the corrected image set

$$\begin{aligned} \mathcal {K}^{1}_{-1}&=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=2u+2,\;u\in \left[ -\,\frac{3}{2},-1\right] \cup \left[ -\,\frac{3}{5},-\,\frac{1}{2}\right] \right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,u^{2}+v^{2}=1,\;u\in \left[ -\,1,-\,\frac{3}{5}\right] , v\in \left[ 0,\frac{4}{5}\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=2u-1,\;u\in \left[ 0,\frac{1}{2}\right] \cup \left[ \frac{9}{10},1\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,\left( u-\frac{3}{2}\right) ^{2}+v^{2}=1,\;u\in \left[ \frac{1}{2},\frac{9}{10}\right] ,v\in \left[ 0,\frac{4}{5}\right] \,\right\} . \end{aligned}$$

See Fig. 4; since \(\mathcal {H}^{1}=\{(u,v)\in \mathbb {R}^{2}{:}\,u>0,\,v\le 0\}\), then \(\mathcal {K}^{1}_{0}\cap \mathcal {H}^{1}=\emptyset \).

Fig. 4
figure 4

The red and blue lines denote the corrected images \(\mathcal {K}^{1}_{0}\) and \(\mathcal {K}^{1}_{-1}\), respectively

Full size image

For weighted robustness, let \(f(x,\xi _{2})=1-x,\mathbf {w}_{1}=2\) and \(\mathbf {w}_{2}=1\). Then, we get

$$\begin{aligned}&\max \{\mathbf {w}_{1}f(x,\xi _{1}),\mathbf {w}_{2}f(x,\xi _{2})\}=\max \Big \{2\sqrt{1-x^{2}},1-x\Big \}\\&\quad =\left\{ \begin{array}{lll} 2\sqrt{1-x^{2}},\;&{}\quad x\in \left[ -\,\frac{3}{5},1\right] ,\\ 1-x,\;&{}\quad x\in \left[ -\,1,-\,\frac{3}{5}\right] . \end{array}\right. \end{aligned}$$

Due to \(X_{1}=[-\,1,0]\), one can easily reach that \(x^{*}=-\frac{3}{5}\) is the unique weighted robust solution. (i) Taking \(\bar{x}=-\frac{3}{5}\), it follows from the process in Example 3.1 that the corrected image set is

$$\begin{aligned} \mathcal {K}^{\mathbf {w}}_{-\frac{3}{5}}= & {} \left\{ (u,v)\in \mathbb {R}^{2}{:}\,\frac{\left( u-\frac{8}{5}\right) ^{2}}{4}+v^{2}=1,\;u\in \left[ -\,\frac{2}{5},\frac{8}{5}\right] , v\in \left[ -\,\frac{3}{5},1\right] \right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u-\frac{3}{5},\;u\in \left[ -\,\frac{2}{5},0\right] \right\} . \end{aligned}$$

(ii) Set \(\bar{x}=0\). We consider two cases \(\xi =\xi _{1}\) or \(\xi =\xi _{2}\) and derive the corrected image set

$$\begin{aligned} \mathcal {K}^{\mathbf {w}}_{0}&=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,\frac{(u-2)^{2}}{4}+v^{2}=1,\;u\in [0,2],v\in \left[ -\,\frac{3}{5},1\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u-1,\;u\in \left[ 0,\frac{2}{5}\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,\frac{(u-1)^{2}}{4}+v^{2}=1,\;u\in [-\,1,1],v\in \left[ -\,\frac{3}{5},1\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u,\;u\in \left[ -\,1,-\,\frac{3}{5}\right] \,\right\} . \end{aligned}$$

In Fig. 5, the red lines represent \(\mathcal {K}^{\mathbf {w}}_{-\frac{3}{5}}\), and \(\mathcal {K}^{\mathbf {w}}_{0}\) is presented by blue ones. It is not difficult to see that \(\mathcal {K}^{\mathbf {w}}_{-\frac{3}{5}}\cap \mathcal {H}^{1}=\emptyset \).

Fig. 5
figure 5

The corrected images for weighted robustness: \(\mathcal {K}^{\mathbf {w}}_{-\frac{3}{5}}\) (red lines) and \(\mathcal {K}^{\mathbf {w}}_{0}\) (blue ones)

Full size image

For regret robustness, let \(\mathcal {X}=[-\,1,0]\), and the other conditions are same to weighted robustness. We achieve from Remark 3.2 that \(f^{*}(\xi _{1})=\min _{x\in X(\xi _1)}f(x,\xi _{1})=0\), \(f^{*}(\xi _{2})=\min _{x\in X(\xi _2)}f(x,\xi _{2})=1\) and

$$\begin{aligned}&\max \{f(x,\xi _{1})-f^{*}(\xi _{1}),f(x,\xi _{2})-f^{*}(\xi _{2})\}\\&\quad =\max \Big \{\sqrt{1-x^{2}},-x\Big \}=\left\{ \begin{array}{lll} \sqrt{1-x^{2}},\;&{}\quad x\in \left[ -\,\frac{\sqrt{2}}{2},0\right] ,\\ -x,\;&{}\quad x\in \left[ -\,1,-\,\frac{\sqrt{2}}{2}\right] . \end{array}\right. \end{aligned}$$

It is obvious that \(x^{*}=-\frac{\sqrt{2}}{2}\) is the unique regret robust solution. (i) Let \(\bar{x}=-\frac{\sqrt{2}}{2}\). Similar to the process in Example 3.1, the corrected image set can be given by

$$\begin{aligned} \mathcal {K}^{r}_{-\frac{\sqrt{2}}{2}}&=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,\left( u-\frac{\sqrt{2}}{2}\right) ^{2}+v^{2}=1,\;u\in \left[ -\,1+\frac{\sqrt{2}}{2},0\right] , v\in \left[ -\,\frac{\sqrt{2}}{2},0\right] \right\} \\&\quad \bigcup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u-\frac{\sqrt{2}}{2},\;u\in \left[ -\,1+\frac{\sqrt{2}}{2},0\right] \right\} . \end{aligned}$$

(ii) Set \(\bar{x}=0\). The corresponding corrected image set is

$$\begin{aligned} \mathcal {K}^{r}_{0}&=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,(u-1)^{2}+v^{2}=1,\;u\in \left[ 0,1-\frac{\sqrt{2}}{2}\right] ,v\in \left[ -\,\frac{\sqrt{2}}{2},0\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u-1,\;u\in \left[ 0,1-\frac{\sqrt{2}}{2}\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,u^{2}+v^{2}=1,\;u\in \left[ -\,1,-\,\frac{\sqrt{2}}{2}\right] ,v\in \left[ -\,\frac{\sqrt{2}}{2},0\right] \,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u,\;u\in \left[ -\,1,-\,\frac{\sqrt{2}}{2}\right] \,\right\} . \end{aligned}$$

From Fig. 6, it can be seen that \(\mathcal {K}^{r}_{-\frac{\sqrt{2}}{2}}\cap \mathcal {H}^{1}=\emptyset \).

Fig. 6
figure 6

For regret robustness, the corrected images \(\mathcal {K}^{r}_{-\frac{\sqrt{2}}{2}}\) (red lines) and \(\mathcal {K}^{r}_{0}\) (blue ones)

Full size image

Example 3.3

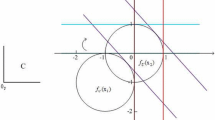
For problem (1), let \(\mathcal {X}=\mathbb {R}\), \(U=[1,2]\), \(f(x,\xi )=x+\xi \) and \(F(x,\xi )=x^{2}-\xi \). Then, we achieve \(\max _{\xi \in U}f(x,\xi )=x+2\), \(\max _{\xi \in U}F(x,\xi )=x^{2}-1\) and \(X_{1}=[-\,1,1]\). One can see that \(x^{*}=-1\) is the unique strictly robust solution. Taking \(\bar{x}=-1\) (resp. \(\bar{x}=1\)), it follows from [29, Example 2.6] that \(\mathcal {K}^{1}_{-1}=\{(u,v)\in \mathbb {R}^{2}{:}\,v=(u+3-\xi )^{2}-1,\xi \in U\}\) and \(\mathcal {K}^{1}_{1}=\{(u,v)\in \mathbb {R}^{2}{:}\,v=(u+1-\xi )^{2}-1,\xi \in U\}\), respectively. Combined with Fig. 7, one can see that \(\mathcal {K}^{1}_{-1}\cap \mathcal {H}^{1}=\emptyset \).

Fig. 7
figure 7

For strict robustness, the corrected images \(\mathcal {K}^{1}_{-1}\) (red parts) and \(\mathcal {K}^{1}_{1}\) (blue ones)

Full size image

For regret robustness, since \(f^{*}(\xi )=\min _{x\in X(\xi )}f(x,\xi )=-\sqrt{\xi }+\xi \), then the objective function is \(\max _{\xi \in U}(f(x,\xi )-f^{*}(\xi ))=x+\sqrt{\xi }\), we can obtain that \(x^{*}=-1\) is the unique regret robust solution. Setting \(\bar{x}=-1\) (resp. \(\bar{x}=0\)), the corrected image sets can be reached by

$$\begin{aligned} \mathcal {K}^{r}_{-1}=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=(u+1+\sqrt{2}-\sqrt{\xi })^{2}-1,\xi \in U\right\} \end{aligned}$$

and \(\mathcal {K}^{r}_{0}=\{(u,v)\in \mathbb {R}^{2}{:}\,v=(u+\sqrt{2}-\sqrt{\xi })^{2}-1,\xi \in U\}\), respectively. Analogous to Fig. 7, it holds \(\mathcal {K}^{r}_{-1}\cap \mathcal {H}^{1}=\emptyset \).

3.2 Optimistic Robustness

While strict robustness concentrates on the worst case, and can be seen as a pessimistic model, optimistic robustness aims at minimizing the best possible objective function value over \(X_{2}\), and shows an optimistic attitude of a decision maker, where \(X_{2}:=\{x\in \mathcal {X}{:}\,F(x,\xi )\in D^{1}\;\text{ for } \text{ some }\;\xi \in U\}\) stands for the set of optimistic feasible solutions. The optimistic counterpart was proposed by Beck and Ben-Tal [12], in the context of studying robust duality theory. Then, we formulate the optimistic counterpart of problem (1) as follows

$$\begin{aligned} \min \,\inf _{\xi \in U}f(x,\xi )\;\;\text{ s.t. }\;\;F_{i}(x,\xi )\le 0,\;\text{ for } \text{ some }\;\xi \in U,\;i=1,\ldots ,m,\;\;x\in \mathcal {X}. \end{aligned}$$
(7)

If a feasible solution \(x\in X_{2}\) is optimal to problem (7), then it is an optimistic robust solution of problem (1). To introduce a suitable corrected image of problem (1) under the optimistic robust counterpart, we assume that the values of \(\inf _{\xi \in U}f(x,\xi )\) and \(\inf _{\xi \in U}F_{i}(x,\xi ),\,i=1,\ldots ,m\) are finite for all \(x\in \mathcal {X}\), and \(\inf _{\xi \in U}F_{i}(x,\xi ),\,i=1,\ldots ,m\) are attained for all \(x\in \mathcal {X}\). Let \(\bar{x}\in \mathcal {X}\) and \(F^{2}(x):=\Big (\min \nolimits _{\xi \in U}F_{1}(x,\xi ),\ldots ,\min \nolimits _{\xi \in U}F_{m}(x,\xi )\Big )\). Define the map

$$\begin{aligned} A^{2}_{\bar{x}}{:}\,\mathcal {X}\times U\rightarrow \mathbb {R}^{1+m},\quad A^{2}_{\bar{x}}(x,\xi ):=\bigg (\inf _{\xi \in U}f(\bar{x},\xi )-f(x,\xi ),\,F^{2}(x)\bigg ), \end{aligned}$$

and consider the following set

$$\begin{aligned}&\mathcal {K}^{2}_{\bar{x}}:=\left\{ (u,v)\in \mathbb {R}^{1+m}{:}\, (u,v)=A^{2}_{\bar{x}}(x,\xi ),\;x\in \mathcal {X},\,\xi \in U\right\} ,\\&\mathcal {H}^{2}:=\mathcal {H}^{1}. \end{aligned}$$

By virtue of the corrected image set \(\mathcal {K}^{2}_{\bar{x}}\), a necessary and sufficient condition of optimistic robust solutions for the uncertain OP can be derived.

Theorem 3.2

A feasible solution \(\bar{x}\in X_{2}\) is an optimistic robust solution to problem (1) if and only if

$$\begin{aligned} \mathcal {K}^{2}_{\bar{x}}\cap \mathcal {H}^{2}=\emptyset . \end{aligned}$$

Proof

Necessity. Suppose that \(\bar{x}\in X_{2}\) is an optimistic robust solution. Then it holds

$$\begin{aligned} \inf _{\xi \in U}f(\bar{x},\xi )\le \inf _{\xi \in U}f(x,\xi ),\quad \forall \;x\in X_{2}. \end{aligned}$$
(8)

Since \(\inf _{\xi \in U}f(x,\xi )\le f(x,\xi )\) for all \(x\in \mathcal {X}\) and \(\xi \in U\), together with inequality (8), it is obvious that

$$\begin{aligned} \inf _{\xi \in U}f(\bar{x},\xi )-f(x,\xi )\le 0,\quad \forall \;x\in X_{2},\,\forall \;\xi \in U. \end{aligned}$$
(9)

When \(x\in \mathcal {X}{\backslash }{X_{2}}\), there is at least one \(j\in \{1,\ldots ,m\}\) such that \(F_{j}(x,\xi )>0\) for all \(\xi \in U\). Then, we have \(\min _{\xi \in U}F_{j}(x,\xi )>0\) for \(x\in \mathcal {X}{\backslash }{X_{2}}\), which implies that \(F^{2}(x)\not \in D^{1}\). From above analysis, one can obtain that \(\mathcal {K}^{2}_{\bar{x}}\cap \mathcal {H}^{2}=\emptyset \).

Sufficiency. Since \(F^{2}(x)\in D^{1}\) for \(x\in X_{2}\), it follows from \(\mathcal {K}^{2}_{\bar{x}}\cap \mathcal {H}^{2}=\emptyset \) that inequality (9) holds. Based on equivalence of (8) and (9), it is not difficult to see that \(\bar{x}\in X_{2}\) is an optimistic robust solution. \(\square \)

Remark 3.3

Another formulation of the corrected image is defined by

$$\begin{aligned} \widetilde{\mathcal {K}^{2}_{\bar{x}}}:=\Big \{(u,v)\in \mathbb {R}^{1+m}{:}\,u=f(\bar{x},\xi )-\inf _{\xi \in U}f(x,\xi ),v=F^{2}(x),\;x\in \mathcal {X},\,\xi \in U\Big \}. \end{aligned}$$

It is not difficult to see that a solution \(\bar{x}\in X_{2}\) is an optimistic robust solution to problem (1) if and only if \(\widetilde{\mathcal {K}^{2}_{\bar{x}}}\cap \mathcal {H}^{2}=\emptyset \). For all \(x\in \mathcal {X}\) and all \(\xi \in U\), since \(f(\bar{x},\xi )-\inf \nolimits _{\xi \in U}f(x,\xi )\le 0\) implies \(\inf \nolimits _{\xi \in U}f(\bar{x},\xi )-f(x,\xi )\le 0\), but the converse is, in general, not true. Then, the conditions of this conclusion seem to be stronger than the ones of Theorem 3.2. Moreover, the corresponding conclusion of Proposition 3.1 for optimistic robust counterpart can be reached, by introducing an extended image of \(\mathcal {K}^{2}_{\bar{x}}\). Three examples are given to emphasize the importance of Theorem 3.2 in the following.

Example 3.4

For problem (1), take \(\mathcal {X}=\mathbb {R}\) and \(U=\{\xi _{1},\xi _{2}\}\) be the parameter set. Consider two cases as follows:

Case 1 The OP with uncertainties only in the objective is introduced. Let \(f(x,\xi _{1})=x\), \(f(x,\xi _{2})=-x\) and \(F(x)=x^{2}-x-2\). It holds \(\min _{\xi \in U}f(x,\xi )=-|x|\) and \(X_{2}:=[-\,1,2]\). It is not difficult to see that \(x^{*}=2\) is the unique optimistic robust solution. Set \(\bar{x}=2\). Since \(\min _{\xi \in U}f(2,\xi )=-2\), then \(\min _{\xi \in U}f(2,\xi )-f(x,\xi _{1})=-2-x\) and \(\min _{\xi \in U}f(2,\xi )-f(x,\xi _{2})=-2+x\). Setting \(u=-2-x\) (or \(u=-2+x\)), \(v=x^{2}-x-2\), one can reach that \(v=u^{2}+5u+4\) (or \(v=u^{2}+3u\)). The corrected image set is \(\mathcal {K}^{2}_{2}=\{(u,v)\in \mathbb {R}^{2}{:}\,v=u^{2}+5u+4\}\cup \{(u,v)\in \mathbb {R}^{2}{:}\,v=u^{2}+3u\}\). It follows from Fig. 8 that \(\mathcal {K}^{2}_{2}\cap \mathcal {H}^{2}=\emptyset \).

Case 2 The OP with uncertainties both in the objective and constraints is discussed. Let \(f(x,\xi _{1})=x\), \(f(x,\xi _{2})=-x\), \(F(x,\xi _{1})=x^{2}+x\) and \(F(x,\xi _{2})=x^{2}-1\). Thus, \(\min _{\xi \in U}f(x,\xi )=-|x|\),

$$\begin{aligned} \min _{\xi \in U}F(x,\xi )=\min \;\{x^{2}+x,x^{2}-1\}=\left\{ \begin{array}{lll} x^{2}+x,&{}\quad x\le -1,\\ x^{2}-1,&{}\quad x\ge -1, \end{array}\right. \end{aligned}$$

and \(X_{2}:=[-\,1,1]\). It is obvious that \(x^{*}=-1\) (resp. 1) is an optimistic robust solution. Taking \(\bar{x}=-1\), analogous to Case 1, the corrected image set can be calculated by

$$\begin{aligned} \mathcal {K}^{2}_{-1}&=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u^{2}+u,\;u\ge 0\right\} \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u^{2}+2u,\;u\le 0\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u^{2}+3u+2,\;u\le -2\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=u^{2}+2u,\;u\ge -2\right\} . \end{aligned}$$

We achieve from Fig. 8 that \(\mathcal {K}^{2}_{-1}\cap \mathcal {H}^{2}=\emptyset \).

Fig. 8
figure 8

The corrected images for optimistic robustness: \(\mathcal {K}^{2}_{2}\) (red lines) and \(\mathcal {K}^{2}_{-1}\) (blue ones)

Full size image

Example 3.5

See Example 3.3, one can conclude that \(\min _{\xi \in U}f(x,\xi )=x+1\), \(\min _{\xi \in U}F(x,\xi )=x^{2}-2\) and \(X_{2}:=[-\,\sqrt{2},\sqrt{2}]\). By simple calculation, it can be seen that \(x^{*}=-\sqrt{2}\) is the unique optimistic robust solution. Setting \(\bar{x}=-\sqrt{2}\) (resp. \(\bar{x}=0\)), we can obtain the corrected image sets

$$\begin{aligned} \mathcal {K}^{2}_{-\sqrt{2}}=\left\{ (u,v)\in \mathbb {R}^{2}{:}\,v=(u+\sqrt{2}-1+\xi )^{2}-2,\,\xi \in U\right\} \end{aligned}$$

and \(\mathcal {K}^{2}_{0}=\{(u,v)\in \mathbb {R}^{2}{:}\,v=(u-1+\xi )^{2}-2,\,\xi \in U\}\), respectively. From Fig. 9, one can reach that \(\mathcal {K}^{2}_{-\sqrt{2}}\cap \mathcal {H}^{2}=\emptyset \).

Fig. 9
figure 9

The corrected images for optimistic robustness: \(\mathcal {K}^{2}_{-\sqrt{2}}\) (red parts) and \(\mathcal {K}^{2}_{0}\) (blue ones)

Full size image

3.3 Reliable Robustness

For some practical problems, it may be hard to find a point \(x\in \mathcal {X}\) that satisfies constraints \(F_{i}(x,\xi )\le 0\), \(i=1,\ldots ,m\) for every realization of the uncertain parameter \(\xi \in U\), i.e., \(X_{1}=\emptyset \). To obtain an OP with feasible solutions, a less conservative approach called the concept of reliable robustness [11] is described. Here, the constraints \(F_{i}(x,\xi )\le 0\) are replaced by \(F_{i}(x,\xi )\le \delta _{i}\) for all \(\xi \in U\), where \(\delta _{i}\in \mathbb {R}\), \(i=1,\ldots ,m\) denote some infeasibility tolerances. But the constraints \(F_{i}(x,\hat{\xi })\le 0,i=1,\ldots ,m\) should be fulfilled for the nominal value \(\hat{\xi }\). Now, the reliable counterpart of problem (1) is given by

$$\begin{aligned} \begin{array}{lll} \min &{}\quad \sup _{\xi \in U}f(x,\xi )\\ \text{ s.t. }&{}\quad F_{i}(x,\hat{\xi })\le 0,\,i=1,\ldots ,m,\\ &{}\quad \forall \xi \in U{:}\,F_{i}(x,\xi )\le \delta _{i},\,i=1,\ldots ,m,\\ &{}\quad x\in \mathcal {X}. \end{array} \end{aligned}$$
(10)

Let \(X_{3}:=\{x\in \mathcal {X}{:}\,F_{i}(x,\xi )\le \delta _{i},\;F_{i}(x,\hat{\xi })\le 0,\;\forall \,\xi \in U,\,i=1,\ldots ,m\}\) be the set of reliable feasible solutions. It is obvious that if a feasible solution \(x\in X_{3}\) is optimal to problem (10), then x is a reliable robust solution of problem (1). We need introduce a proper corrected image of problem (1) under the reliable counterpart, for the sake of achieving an equivalent characterization of reliable robust solutions. Let \(\bar{x}\in \mathcal {X}\) and \(\delta =(\delta _{1},\ldots ,\delta _{m})\in \mathbb {R}^{m}\). Define the map

$$\begin{aligned} A^{3}_{\bar{x}}{:}\,\mathcal {X}\times U\rightarrow \mathbb {R}^{1+2m},\quad A^{3}_{\bar{x}}(x,\xi ):=\bigg (f(\bar{x},\xi )-\sup _{\xi \in U}f(x,\xi ),\,F^{3}(x)\bigg ), \end{aligned}$$

where \(F^{3}(x):=(F_{1}(x,\hat{\xi }),\ldots ,F_{m}(x,\hat{\xi }),\sup \nolimits _{\xi \in U}F_{1}(x,\xi )-\delta _{1},\ldots ,\sup \nolimits _{\xi \in U}F_{m}(x,\xi )-\delta _{m})\), and consider the following sets

$$\begin{aligned}&\mathcal {K}^{3}_{\bar{x}}:=\left\{ (u,v)\in \mathbb {R}^{1+2m}{:}\, (u,v)=A^{3}_{\bar{x}}(x,\xi ),\;x\in \mathcal {X},\,\xi \in U\right\} ,\\&\mathcal {H}^{3}:=\left\{ (u,v)\in \mathbb {R}^{1+2m}{:}\,u>0,\,v\in D^{3}\right\} =\mathbb {R}_{++}\times D^{3}, \end{aligned}$$

where \(D^{3}:=-\mathbb {R}^{2m}_{+}\).

Theorem 3.3

A feasible solution \(\bar{x}\in X_{3}\) is a reliable robust solution to problem (1) if and only if

$$\begin{aligned} \mathcal {K}^{3}_{\bar{x}}\cap \mathcal {H}^{3}=\emptyset . \end{aligned}$$

Proof

Analogous to the proof of Theorem 3.1, this conclusion can be verified easily, so we omit the proof here. \(\square \)

Remark 3.4

If \(\delta _{i}=0,i=1,\ldots ,m\), the reliable robustness is reduced to strict robustness. This concept is described by the Tschebyscheff scalarization with the origin as reference point, and based on a relaxed feasible set. Moreover, by introducing an extended image of \(\mathcal {K}^{3}_{\bar{x}}\), the corresponding conclusion of Proposition 3.1 for reliable robustness can be reached.

Example 3.6

Consider problem (1), take \(\mathcal {X}=\mathbb {R}\), \(U=\{\xi _{1},\xi _{2}\}\) be the parameter set. Let \(f(x,\xi _{1})=x\), \(f(x,\xi _{2})=-x\), \(F(x,\xi _{1})=x^{2}+x\) and \(F(x,\xi _{2})=x^{2}-\frac{3}{2}x+\frac{1}{2}\). Then, we obtain \(\max _{\xi \in U}f(x,\xi )=|x|\) and

$$\begin{aligned} \max _{\xi \in U}F(x,\xi )=\max \Big \{x^{2}+x,x^{2}-\frac{3}{2}x+\frac{1}{2}\Big \}=\left\{ \begin{array}{lll} x^{2}+x,&{}\quad x\ge \frac{1}{5},\\ x^{2}-\frac{3}{2}x+\frac{1}{2},&{}\quad x\le \frac{1}{5}. \end{array}\right. \end{aligned}$$

In this case, the set \(X_{1}=\emptyset \). Setting \(\delta =\frac{3}{2}\) and \(\hat{\xi }=\xi _{1}\), the reliable feasible set \(X_{3}=[-\,\frac{1}{2},0]\). It is obvious that \(x^{*}=0\) is the unique reliable robust solution. (i) Let \(\bar{x}=0\). Analogous to Example 3.1, one can reach that \(\mathcal {K}^{3}_{0}=\{(u,v)\in \mathbb {R}^{1+2}{:}\,u=-|x|,\; v=(x^{2}+x,\max _{\xi \in U}F(x,\xi )-\frac{3}{2}),\; x\in \mathcal {X}\}\) and \(\mathcal {H}^{3}=\mathbb {R}_{++}\times (-\mathbb {R}^{2}_{+})\). Since \(-\,|x|\le 0\) for all \(x\in \mathcal {X}\), it holds \(\mathcal {K}^{3}_{0}\cap \mathcal {H}^{3}=\emptyset \). (ii) Taking \(\bar{x}=-\frac{1}{2}\), by analyzing two cases for \(\xi =\xi _{1}\) or \(\xi =\xi _{2}\), we achieve from part (i) that the corrected image is

$$\begin{aligned} \mathcal {K}^{3}_{-\frac{1}{2}}&=\left\{ (u,v)\in \mathbb {R}^{1+2}{:}\,u=-\frac{1}{2}-|x|,\; v=\left( x^{2}+x,\max _{\xi \in U}F(x,\xi )-\frac{3}{2}\right) ,\; x\in \mathcal {X}\,\right\} \\&\quad \cup \left\{ (u,v)\in \mathbb {R}^{1+2}{:}\,u=\frac{1}{2}-|x|,\; v=\left( x^{2}+x,\max _{\xi \in U}F(x,\xi )-\frac{3}{2}\right) ,\; x\in \mathcal {X}\,\right\} . \end{aligned}$$

If we take \(\tilde{x}=-\frac{1}{3}\), then \(\frac{1}{2}-|\tilde{x}|=\frac{1}{6}>0\) and \((\tilde{x}^{2}+\tilde{x},\max _{\xi \in U}F(\tilde{x},\xi )-\frac{3}{2})=(-\frac{2}{9},-\frac{7}{18})\in -\mathbb {R}^{2}_{+}\), i.e., there exists a \(\tilde{x}=-\frac{1}{3}\) such that \(\mathcal {K}^{3}_{-\frac{1}{2}}\cap \mathcal {H}^{3}\ne \emptyset \). Hence, \(\bar{x}=-\frac{1}{2}\) is not a regret robust solution.

3.4 Light Robustness

It is difficult to determine the upper bounds \(\delta _{i},i=1,\ldots ,m\) for the constraints of reliable robustness. To avoid these inadequacies, the concept of light robustness is described by minimizing these tolerances. Let \(z^{*}>0\) be the optimal value of the nominal problem (\(Q(\hat{\xi })\)), and the nominal value \(f(x,\hat{\xi })\) be bounded by \((1+\gamma )z^{*}\), where \(\gamma \ge 0\). This approach was firstly discussed in [37], and extended to general robust OPs by Schöbel [38], which can be interpreted as a weighted-sum scalarization on upper bounds. The light counterpart of problem (1) is defined by

$$\begin{aligned} \begin{array}{lll} \min \limits _{(\delta ,x)}&{}\quad \sum \limits _{i=1}^{m}\mathbf {w}_{i}\delta _{i}\\ \text{ s.t. }&{}\quad F_{i}(x,\hat{\xi })\le 0,\,i=1,\ldots ,m,\\ &{}\quad f(x,\hat{\xi })\le (1+\gamma )z^{*},\\ &{}\quad \forall \xi \in U{:}\,F_{i}(x,\xi )\le \delta _{i},\,i=1,\ldots ,m,\\ &{}\quad x\in \mathcal {X},\\ &{}\quad \delta _{i}\in \mathbb {R},\,i=1,\ldots ,m, \end{array} \end{aligned}$$
(11)

where \(\mathbf {w}_{i}\ge 0,i=1,\ldots ,m,\sum ^{m}_{i=1}\mathbf {w}_{i}=1\).

Let \(\varXi :=\big \{(\delta ,x)\in \mathbb {R}^{m}\times \mathcal {X}{:}\,F_{i}(x,\hat{\xi })\le 0,\,f(x,\hat{\xi })\le (1+\gamma )z^{*},\, F_{i}(x,\xi )\le \delta _{i},\;\forall \,\xi \in U,\,i=1,\ldots ,m\big \}\ne \emptyset \) be the feasible set of problem (11). An optimal solution \((\delta ^{*},x^{*})\in \varXi \) of the light counterpart problem is called lightly robust. In Sects. 3.4 and 3.5, we assume that \(\sup _{\xi \in U}F_{i}(x,\xi )<\infty ,i=1,\ldots ,m\) for all \(x\in \mathcal {X}\), then an equivalent condition of lightly robust solutions can be captured, by constructing two suitable subsets in the image space of problem (11). Let \(\bar{\delta }=(\bar{\delta }_{1},\ldots ,\bar{\delta }_{m})\in \mathbb {R}^{m},\bar{x}\in \mathcal {X}\). Define the map

$$\begin{aligned} A^{4}_{(\bar{\delta },\bar{x})}{:}\,\mathbb {R}^{m}\times \mathcal {X}\rightarrow \mathbb {R}^{1+(2m+1)},\quad A^{4}_{(\bar{\delta },\bar{x})}(\delta ,x):=\left( \sum ^{m}_{i=1}\mathbf {w}_{i}(\bar{\delta }_{i}-\delta _{i}),\,F^{4}(\delta ,x)\right) , \end{aligned}$$

where \(F^{4}(\delta ,x):=\Big (F_{1}(x,\hat{\xi }),\ldots ,F_{m}(x,\hat{\xi }),f(x,\hat{\xi })-(1+\gamma )z^{*},\sup \nolimits _{\xi \in U}F_{1}(x,\xi )-\delta _{1},\ldots ,\sup \nolimits _{\xi \in U}F_{m}(x,\xi )-\delta _{m}\Big )\), and consider the following sets

$$\begin{aligned}&\mathcal {K}^{4}_{(\bar{\delta },\bar{x})}:=\left\{ (u,v)\in \mathbb {R}^{1+(2m+1)}{:}\,(u,v)=A^{4}_{(\bar{\delta },\bar{x})}(\delta ,x),\;\delta \in \mathbb {R}^{m},\,x\in \mathcal {X}\right\} ,\\&\mathcal {H}^{4}:=\{(u,v)\in \mathbb {R}^{1+(2m+1)}{:}\,u>0,\,v\in D^{4}\}=\mathbb {R}_{++}\times D^{4}, \end{aligned}$$

where \(D^{4}:=-\mathbb {R}_{+}^{2m+1}\).

Theorem 3.4

Let \((\bar{\delta },\bar{x})\in \varXi \). A feasible solution \((\bar{\delta },\bar{x})\) is a lightly robust solution to problem (1) if and only if

$$\begin{aligned} \mathcal {K}^{4}_{(\bar{\delta },\bar{x})}\cap \mathcal {H}^{4}=\emptyset . \end{aligned}$$
(12)

Proof

Necessity. Assume that \((\bar{\delta },\bar{x})\) is a lightly robust solution. For any \((\delta ,x)\in \varXi \), we can achieve \(F^{4}(\delta ,x)\in D^{4}\) and

$$\begin{aligned} \sum ^{m}_{i=1}\mathbf {w}_{i}\bar{\delta }_{i}\le \sum ^{m}_{i=1}\mathbf {w}_{i}\delta _{i}\;\Leftrightarrow \;\sum ^{m}_{i=1}\mathbf {w}_{i}(\bar{\delta }_{i}-\delta _{i})\le 0. \end{aligned}$$
(13)

Additionally, when \((\delta ,x)\in (\mathbb {R}^{m}\times \mathcal {X}){\setminus }\varXi \), it holds \(F^{4}(\delta ,x)\not \in D^{4}\). This, together with inequality (13), the equality (12) can be reached.

Sufficiency. Since \(F^{4}(\delta ,x)\in D^{4}\) for any \((\delta ,x)\in \varXi \) and the equality (12) holds, so inequality (13) can be derived. Combined with \((\bar{\delta },\bar{x})\in \varXi \), one can read that \((\bar{\delta },\bar{x})\) is an optimal solution to problem (11). \(\square \)

Remark 3.5

The feasible set \(\varXi \) can be divided into two parts: one is about variable \(\delta \), and the other is about x. Let

$$\begin{aligned} \Omega&:=\;\left\{ (\delta _{1},\ldots ,\delta _{m})\in \mathbb {R}^{m}{:}\,\exists \,x\in \mathcal {X}\;\text{ s.t. }\;F_{i}(x,\hat{\xi })\le 0,\,f(x,\hat{\xi })\le (1+\gamma )z^{*},\right. \\&\left. \qquad \quad F_{i}(x,\xi )\le \delta _{i},\;\forall \,\xi \in U,\,i=1,\ldots ,m\right\} \end{aligned}$$

and \(X_{\delta }:=\{x\in \mathcal {X}{:}\,F_{i}(x,\hat{\xi })\le 0,\,f(x,\hat{\xi })\le (1+\gamma )z^{*},\, F_{i}(x,\xi )\le \delta _{i},\;\forall \,\xi \in U,\,i=1,\ldots ,m\}\) for a given \(\delta \in \mathbb {R}^{m}\). One can read that \(X_{\delta }\ne \emptyset \) if \(\delta \) belongs to \(\Omega \), otherwise \(X_{\delta }=\emptyset \). By introducing the sets \(\Omega \) and \(X_{\delta }\), and setting \(\delta \in \Omega \), the set \(\varXi \) can be described clearly. Take

$$\begin{aligned} \varPhi :=\left\{ x\in \mathcal {X}{:}\,F_{i}(x,\hat{\xi })\le 0,\,f(x,\hat{\xi })\le (1+\gamma )z^{*},\;i=1,\ldots ,m\right\} . \end{aligned}$$

If \(\varPhi \) is compact and U is finite, then the light counterpart problem (11) admits an optimal solution, even when the set of strictly robust solutions (or the set of reliable robust solutions) is empty; see [38, pp. 167–168].

Remark 3.6

In contrast to the other robustness concepts, \(\mathcal {K}^{4}_{(\bar{\delta },\bar{x})}\) is just the image of problem (11), but not a corrected image of problem (1). This is because the objective function of problem (11) is the tolerances \(\delta _{i}\) with weighed sum. The structures of the images in both problems are completely different. Additionally, when \(U:=\{\xi _{1},\ldots ,\xi _{q}\}\) is a finite set of scenarios, and choose some initial feasible solution \(x^{0}\in X_{1}\), the Benson robustness was introduced in [36, Sect. 3.1]. By using Benson’s method (a scalarization technique to solve MOPs [39, §4.4]), the corresponding robust counterpart of (1) was given by

$$\begin{aligned} \begin{array}{lll} \min \limits _{(l,x)} &{}\quad -\,\sum \limits _{j=1}^q \mathbf {w}_{j}l_{j} &{}\\ \text{ s.t. }&{}\quad f(x^{0},\xi _{j})-l_{j}-f(x,\xi _{j})=0,\quad j=1,\ldots ,q,\\ &{}\quad \forall \,\xi \in U{:}\,F_{i}(x,\xi )\le 0,\quad i=1,\ldots ,m,\\ &{}\quad l\in \mathbb {R}^{q}_{+},\;x\in \mathcal {X},&{} \end{array} \end{aligned}$$
(14)

where \(\mathbf {w}_{j}>0,\,j=1,\ldots ,q,\,\sum _{j=1}^q \mathbf {w}_{j}=1\). Let

$$\begin{aligned} \varPsi&:=\;\big \{(l,x)\in \mathbb {R}^{q}_{+}\times \mathcal {X}{:}\,f(x^{0},\xi _{j})-l_{j}-f(x,\xi _{j})=0,\,j=1,\ldots ,q,\\&\qquad \quad F_{i}(x,\xi )\le 0,\,\forall \,\xi \in U,\,i=1,\ldots ,m\big \}\ne \emptyset \end{aligned}$$

denote the feasible set of problem (14). A feasible solution \((l^{*},x^{*})\in \varPsi \) of (14) is called B-robust. Analogous to the descriptions of light robustness, take \((\bar{l},\bar{x})\in \mathbb {R}^{q}_{+}\times \mathcal {X}\), if we replace \(A^{4}_{(\bar{\delta },\bar{x})}\), \(A^{4}_{(\bar{\delta },\bar{x})}(\delta ,x)\) and \(D^{4}\) by

$$\begin{aligned} A^{B}_{(\bar{l},\bar{x})}{:}\,\mathbb {R}^{q}_{+}\times \mathcal {X}\rightarrow \mathbb {R}^{1+(q+m)},\quad A^{B}_{(\bar{l},\bar{x})}(l,x):=\left( -\sum ^{q}_{j=1}\mathbf {w}_{j}(\bar{l}_{j}-l_{j}),\,F^{B}(l,x)\right) , \end{aligned}$$

and \(D^{B}:=\big \{0_{\mathbb {R}^{q}}\big \}\times D^{1}\), respectively, where

$$\begin{aligned} F^{B}(l,x):= & {} \left( f(x^{0},\xi _{1})-l_{1}-f(x,\xi _{1}),\ldots ,f(x^{0},\xi _{q})\right. \\&\left. \quad -\,l_{q}-f(x,\xi _{q}),\sup _{\xi \in U}F_{1}(x,\xi ),\ldots ,\sup _{\xi \in U}F_{m}(x,\xi )\right) , \end{aligned}$$

an equivalent characterization of B-robust solutions would be achieved.

3.5 \(\epsilon \)-Constraint Robustness

When the preferences of a decision maker have not been represented by other robustness approaches, one can choose to minimize only one objective function for one particular scenario \(\xi _{j}\in U\), while the remaining objectives \(f(x,\xi _{l}),l\in \{1,\ldots ,q\},l\ne j\) bounded by some real values \(\epsilon _{l}\in \mathbb {R}\) are moved to the constraints, which is the description of \(\epsilon \)-constraint robustness. The idea is from the \(\epsilon \)-constraint scalarization method [39] in dealing with multiobjective OPs. The \(\epsilon \)-constraint robustness was initially proposed by Klamroth et al. [7] for a finite uncertainty set, and has been generalized to an infinite compact uncertainty set in [8]. Here, we take \(U:=\{\xi _{1},\ldots ,\xi _{q}\}\) and \(\epsilon =(\epsilon _{1},\ldots ,\epsilon _{q})\) as a finite set of scenarios and a real vector, respectively, the \(\epsilon \)-constraint robust counterpart is thus denoted by

$$\begin{aligned} \begin{array}{lll} \min &{}\quad f(x,\xi _{j})\\ \text{ s.t. }&{}\quad \forall \xi \in U{:}\,\,F_{i}(x,\xi )\le 0,\,i=1,\ldots ,m,\\ &{}\quad x\in \mathcal {X},\\ &{}\quad f(x,\xi _{l})\le \epsilon _{l},\,l\in \{1,\ldots ,q\},\,l\ne j. \end{array} \end{aligned}$$
(15)

Let \(X_{5}:=\{x\in X_{1}{:}\,f(x,\xi _{l})\le \epsilon _{l},\;l\in \{1,\ldots ,q\},\,l\ne j\}\) denote the set of \(\epsilon \)-constraint feasible solutions. If a feasible solution \(x\in X_{5}\) is optimal to problem (15), then x is an \(\epsilon \)-constraint robust solution of problem (1). With the purpose of deriving a necessary and sufficient condition for \(\epsilon \)-constraint robust solutions, some new sets in the image space of problem (15) are considered. Let \(\bar{x}\in \mathcal {X}\), \(\xi _{j}\in U\) and \(\epsilon ^{j}=(\epsilon _{1},\ldots ,\epsilon _{j-1},\epsilon _{j+1},\ldots ,\epsilon _{q})\). Define the map

$$\begin{aligned} A^{5}_{\bar{x}}{:}\,\mathcal {X}\rightarrow \mathbb {R}^{1+(q-1+m)},\quad A^{5}_{\bar{x}}(x):=(f(\bar{x},\xi _{j})-f(x,\xi _{j}),\,F^{5}(x)), \end{aligned}$$

and consider the following sets

$$\begin{aligned}&\mathcal {K}^{5}_{\bar{x}}:=\left\{ (u,v)\in \mathbb {R}^{1+(q-1+m)}{:}\,(u,v)=A^{5}_{\bar{x}}(x),\;x\in \mathcal {X}\right\} ,\\&\mathcal {H}^{5}:=\left\{ (u,v)\in \mathbb {R}^{1+(q-1+m)}{:}\,u>0,\,v\in D^{5}\right\} =\mathbb {R}_{++}\times D^{5}, \end{aligned}$$

where

$$\begin{aligned} F^{5}(x)&:=\Big (f(x,\xi _{1})-\epsilon _{1},\ldots ,f(x,\xi _{j-1})-\epsilon _{j-1},f(x,\xi _{j+1})-\epsilon _{j+1},\ldots ,f(x,\xi _{q})\\&\qquad -\epsilon _{q},\sup \limits _{\xi \in U}F_{1}(x,\xi ),\ldots ,\sup \limits _{\xi \in U}F_{m}(x,\xi )\Big )\;\;\text{ and }\;\;D^{5}:=-\mathbb {R}^{q-1+m}_{+}. \end{aligned}$$

Theorem 3.5

A feasible solution \(\bar{x}\in X_{5}\) is an \(\epsilon \)-constraint robust solution to problem (1) if and only if

$$\begin{aligned} \mathcal {K}^{5}_{\bar{x}}\cap \mathcal {H}^{5}=\emptyset . \end{aligned}$$
(16)

Proof

Necessity. Suppose that \(\bar{x}\in X_{5}\) is an \(\epsilon \)-constraint robust solution. Then, we have

$$\begin{aligned} f(\bar{x},\xi _{j})\le f(x,\xi _{j})\Leftrightarrow f(\bar{x},\xi _{j})-f(x,\xi _{j})\le 0,\quad \forall \;x\in X_{5}, \end{aligned}$$
(17)

where \(\xi _{j}\in U\) is chosen beforehand. Additionally, it is obvious that \(F^{5}(x)\not \in D^{5}\) for any \(x\in \mathcal {X}{\setminus } X_{5}\). This, together with inequality (17), one can reach that the equality (16) holds.

Sufficiency. If the equality (16) holds, we can obtain the inequality (17) because of \(F^{5}(x)\in D^{5}\) for any \(x\in X_{5}\), which implies that \(\bar{x}\in X_{5}\) is an optimal solution to problem (15). \(\square \)

Remark 3.7

The difficulty of \(\epsilon \)-constraint robustness is, how to choose appropriate upper bounds \(\epsilon _{l}\) for the constraints \(f(x,\xi _{l})\le \epsilon _{l}\). If the vector \(\epsilon _{l}\) are chosen too small, the problem (15) may be infeasible (i.e., the feasible set \(X_{5}\) is empty), or the objective function value of \(f(x,\xi _{j})\) may become very bad. In addition, if the bounds \(\epsilon _{j}\) are chosen too big, the quality for the other scenarios decreases, and the objective function values may not attain the expected levels. Meanwhile, the \(\epsilon \)-constraint robust counterpart may be hard to solve in practice, due to the added constraints \(f(x,\xi _{l})\le \epsilon _{l}\). To avoid the drawbacks, the elastic robustness was proposed in [36, Sect. 3.2], by virtue of the elastic constraint scalarization method [39, §4.3], and the elastic robust counterpart of (1) was defined by

$$\begin{aligned} \begin{array}{lll} \min \limits _{(s,x)} &{}\quad \sum \limits _{l\ne j}u_{l}s_{l}+ f(x,\xi _{j}) &{} \\ \text{ s.t. } &{}\quad f(x,\xi _{l})- s_{l}\le \epsilon _{l},\quad l=1,\ldots ,q, \;l\ne j,\\ &{}\quad s_{l}\ge 0,\quad l=1,\ldots ,q,\;l\ne j, \\ &{}\quad \forall \xi \in U{:}\,F_{i}(x,\xi )\le 0,\quad i=1,\ldots ,m,\\ &{}\quad x\in \mathcal {X},&{} \end{array} \end{aligned}$$

where \(u_{l}\ge 0,\,l\ne j\). Combined with the discussions for light robustness and \(\epsilon \)-constraint robustness, an equivalent characterization for elastic robustness can be easily established, when U is a finite set of scenarios.

Remark 3.8

When U contains infinite elements, let \(\epsilon {:}\,U\rightarrow \mathbb {R}\) be a function and \(\bar{\xi }\in U\) be fixed, the \(\epsilon \)-constraint robust counterpart of problem (1) [8, Theorem 23] is given by

$$\begin{aligned} \begin{array}{lll} \min &{}\quad f(x,\bar{\xi })-\epsilon (\bar{\xi })\\ \text{ s.t. }&{}\quad \forall \xi \in U{:}\,F_{i}(x,\xi )\le 0,\,i=1,\ldots ,m,\\ &{}\quad x\in \mathcal {X},\\ &{}\quad \forall \xi \in U{\backslash }\{\bar{\xi }\}{:}\,f(x,\xi )\le \epsilon (\xi ). \end{array} \end{aligned}$$
(18)

In this case, since \(F^{5}(x)\) and \(D^{5}\) are infinitely dimensional, then the sets \(\mathcal {K}^{5}_{\bar{x}}\) and \(\mathcal {H}^{5}\) are not available. It should be interesting and meaningful by introducing suitable sets in the image space of problem (18), such that the equivalent characterization of \(\epsilon \)-constraint robust solutions holds.

3.6 Adjustable Robustness

The concept of adjustable robustness, that has been introduced by Ben-Tal et al. [40] and extensively studied in [3], is significantly less conservative than the usual robustness concepts. It is a two-stage approach in robust optimization, in which there are two types of variables: one type is “here-and-now” variables x, and the other is “wait-and-see” variables \(\zeta \). The former (nonadjustable variables) should get specific numerical values and have to be determined, before the realization of the uncertain parameters; while the latter (adjustable variables) can be decided, after the uncertain parameters becomes known. These variables are chosen, such that the objective function is minimized for given x and realized parameter \(\xi \). Then, an uncertain problem, which contains both “here-and-now” variables \(x\in \mathcal {X}\) and “wait-and-see” variables \(\zeta \in \mathbb {R}^{p}\), is formulated as

$$\begin{aligned} \inf \;f(x,\zeta ,\xi )\;\;\text{ s.t. }\;\;F_{i}(x,\zeta ,\xi )\le 0,\;i=1,\ldots ,m,\;\;x\in \mathcal {X},\;\zeta \in \mathbb {R}^{p}. \end{aligned}$$
(19)

In order to solve the problem (19), the adjustable robust counterpart needs to be provided. Let \(Q(x,\xi )=\inf f(x,\zeta ,\xi )\) be the objective function of the second-stage OP, and

$$\begin{aligned} G(x,\xi ):=\left\{ \zeta \in \mathbb {R}^{p}{:}\,F_{i}(x,\zeta ,\xi )\le 0,\,i=1,\ldots ,m\right\} \end{aligned}$$

denote the set of variables \(\zeta \) for given x and \(\xi \). Thus, the adjustable robust counterpart is defined by

$$\begin{aligned} \min \,\sup _{\xi \in U}Q(x,\xi )\;\;\text{ s.t. }\;\;G(x,\xi )\ne \emptyset ,\;\forall \,\xi \in U,\;\;x\in \mathcal {X}. \end{aligned}$$
(20)

Let \(X_{6}:=\{x\in \mathcal {X}{:}\,\forall \;\xi \in U,\;\exists \;\zeta \in \mathbb {R}^{p}\,\,\text{ s.t. }\,\,F_{i}(x,\zeta ,\xi )\le 0,\;i=1,\ldots ,m\}\) be the adjustable robust feasible set. A feasible solution \(x\in X_{6}\) is called adjustable robust, if it is optimal to problem (20). To obtain an equivalent characterization of adjustable robust solutions, we consider the corrected image of problem (20) and introduce some notations. Assume that \(\sup _{\xi \in U}Q(x,\xi )<\infty \) for all \(x\in \mathcal {X}\). For any given \(\xi _{0}\in U\), we take \(\zeta ^{(x,\xi _{0})}\in \mathbb {R}^{p}\), where the choice of \(\zeta ^{(x,\xi _{0})}\) is connected with variable x and the fixed \(\xi _{0}\). If \(x\in X_{6}\), there exists \(\zeta ^{(x,\xi _{0})}\in \mathbb {R}^{p}\) such that \(F_{i}(x,\zeta ^{(x,\xi _{0})},\xi _{0})\le 0,i=1,\ldots ,m\), then we choose \(\zeta ^{(x,\xi _{0})}\in G(x,\xi _{0})\); otherwise, take \(\zeta ^{(x,\xi _{0})}\not \in G(x,\xi _{0})\). Set \(\bar{x}\in \mathcal {X}\), define the map

$$\begin{aligned} A^{6}_{\bar{x}}{:}\,\mathcal {X}\times U\rightarrow \mathbb {R}^{1+m},\quad A^{6}_{\bar{x}}(x,\xi ):=\bigg (Q(\bar{x},\xi )-\sup _{\xi \in U}Q(x,\xi ),\,F^{6}(x,\xi )\bigg ), \end{aligned}$$

where \(F^{6}(x,\xi ):=\Big (F_{1}\Big (x,\zeta ^{(x,\xi )},\xi \Big ),\ldots ,F_{m}\Big (x,\zeta ^{(x,\xi )},\xi \Big )\Big )\), and consider the following sets

$$\begin{aligned}&\mathcal {K}^{6}_{\bar{x}}:=\left\{ (u,v)\in \mathbb {R}^{1+m}{:}\,(u,v)=A^{6}_{\bar{x}}(x,\xi ),\;x\in \mathcal {X},\,\xi \in U\right\} ,\\&\mathcal {H}^{6}:=\mathcal {H}^{1}. \end{aligned}$$

Theorem 3.6

A feasible solution \(\bar{x}\in X_{6}\) is an adjustable robust solution to problem (1) if and only if

$$\begin{aligned} \mathcal {K}^{6}_{\bar{x}}\cap \mathcal {H}^{6}=\emptyset . \end{aligned}$$

Proof

Analogous to the proof of Theorem 3.1, the verification of this conclusion can be easily reached by a tiny of changes, then we omit it here. \(\square \)

Remark 3.9

It is worthwhile to notice the three following points: (i) For given x and \(\xi \), \(\zeta ^{(x,\xi )}\) can be determined, but \(\zeta ^{(x,\xi )}\) may be variable with the changes of x and \(\xi \). When the parameter \(\xi \) is realized, \(\zeta ^{(x,\xi )}\) only depends on x. Particularly, we have \(F_{i}(x,\zeta ^{(x,\xi )},\xi )\le 0,i=1,\ldots ,m\) for all \(x\in X_{6}\) and all \(\xi \in U\); (ii) Compared with \(F^{i}(x),i=1,\ldots ,5\), \(F^{6}(x,\xi )\) is related to both x and \(\xi \), while the constraints part in the image set is usually independent of other parameters but x, for the sake of ensuring the equivalence relation, which is attributed to the specific constraints (i.e., a family of sets are nonempty) in problem (20); (iii) If we replace \(F^{6}(x,\xi )\) by \(\widetilde{F^{6}}(x):=(\sup _{\xi \in U}F_{1}(x,\zeta _{0},\xi ),\ldots ,\sup _{\xi \in U}F_{m}(x,\zeta _{0},\xi ))\), where \(\zeta _{0}\in \mathbb {R}^{p}\) is given, then the set \(\widetilde{X_{6}}:=\{x\in \mathcal {X}{:}\,\widetilde{F^{6}}(x)\in D^{1}\}\) is just a proper subset of \(X_{6}\), and the conclusion of Theorem 3.6 is not true.

Remark 3.10

In most cases, the adjustable robust counterpart is computationally intractable (NP-hard), and this difficulty is addressed by restricting the adjustable variables to be affine functions of the uncertain data; see [40]. In this subsection, the difficulty is to construct impossibility of a parametric system, when the constraints comprise a series of sets that should be nonempty. As far as we know, it is the first time to deal with OPs with this constraint by using ISA. By this means, it may be convenient to handle some practical problems.

4 Perspectives and Open Problems

As one knows, some equivalent characterizations of various robustness concepts for uncertain OPs have been established in Sect. 3, by introducing appropriate subsets in the image space. In what follows, we make some interpretations for ISA approach used in this paper and provide some further problems worth considering.

There is a commonality of the assumption for different robustness, i.e., the values of the supremum or infimum of functions are finite. It was used to introduce the definition of the robust regularization in [41], and one can also refer to [42, Sect. 4.1] and  [29]. Two reasons are given to explain the validity of the assumption for each robustness concept: For one thing, it is weak and can be satisfied in most of the applications; for another, it ensures that the definitions of \(A^{i}_{\bar{x}},i=1,2,3,5,6,\mathbf {w},r\) and \(A^{4}_{(\bar{\delta },\bar{x})}\) are reasonable, i.e., their corresponding functions would not take the values \(\pm \,\infty \) in their components. Furthermore, strict robustness and optimistic robustness reflect the preferences of a decision maker, from the risk point of view; the former is risk aversion, while the latter is risk appetite. Both of corrected images may be a part of the original image, or a combination of partial initial image and some newly added parts. They contain variable x and parameter \(\xi \) simultaneously. Two less conservative robustness concepts (reliable robustness and light robustness) have been analyzed, and their image sets were defined by different forms. Particularly, the image of light robustness was obtained with the help of an additional variable \(\delta \). It is just the image of its counterpart problem. Analogous to light robustness, \(\xi _{j}\) is any chosen beforehand in \(\epsilon \)-constraint robustness. For the adjustable robustness, it is vital to introduce the notation \(\zeta ^{(x,\xi )}\) that eliminates the parameter \(\zeta \) for every \(\xi \), by this means, the corrected image can be constructed successfully.

ISA, as a new tool to tackle with uncertain problems, plays a significant role in unifying multifarious robustness concepts. It explains clearly the implications of various robust solutions from the geometrical point of view and provides a new method to solve OPs with uncertainties. Even if a unified framework by virtue of ISA has been developed, there are still some problems worth discussing.

  1. 1.

    Referring to Remark 3.8, when U contains infinite elements (i.e., U is an infinite countable set, or is infinite but not countable), the equivalent characterization of \(\epsilon \)-constraint robust solutions is invalid; so how to define suitable subsets is the key to overcoming the difficulties. Furthermore, if U is a subset of infinite dimensional space, the conclusions of this paper may not hold. In this case, it is necessary to develop new theories, according to some researches on infinite-dimensional images; see [26].

  2. 2.

    By means of some known linear and nonlinear (regular) weak separation functions, robust optimality conditions for various robustness concepts, especially saddle point sufficient optimality conditions, can be easily derived. Specifically, one can refer to [29]. However, on the basis of ISA, there have been few works on necessary optimality conditions, and robust duality for scalar robust OPs recently. Thus, it is of value to construct strong separation functions, and use the tools of nonconvex optimization and nonsmooth analysis, to obtain (Lagrangian-type) necessary robust optimality and robust duality results.

  3. 3.

    As we know, unified characterizations of various concepts of robustness and stochastic programming, from vector optimization, set-valued optimization and scalarization points of view, are shown in [7, 8]. Based on ISA, this paper provided another approach to characterizing different kinds of robustness. Then, it would be of interest to explore the relationships between ISA approach and the ones addressed in [8], such as vector optimization, set-valued optimization and scalarization techniques.

5 Conclusions

By using ISA, this paper developed a unifying approach to tackling with scalar robust OPs. Compared with the approaches based on tools from vector optimization, set-valued optimization and scalarization techniques [8], ISA mainly focuses on constructing two subsets in the image space such that they are disjoint, and analyzing the problem from the geometrical point of view. Then, it should have some connections to the existing ones. One possible way is to make use of some notations of ISA presented in Sect. 3, and introduce the corresponding vector OPs and set-valued OPs, and then explore their relations to robustness concepts. To the best of our knowledge, recently very few related papers concentrate on considering robust OPs on the frame of ISA, except for [29, 33,34,35]; it thus provides a good chance to study this kind of problem both in theoretical and practical aspects. What is noteworthy is that this paper gives a full answer to the open question (ii) posed in [29].