1 Introduction

Shape and topology optimization is a broad field of modern research in pure (differential geometry) and applied mathematics, and in structural mechanics. In applied mathematics, it is a branch of the calculus of variations, partial differential equations and numerical methods. In structural mechanics, design and synthesis of metamaterials, fracture and damage modeling and structural optimization are areas of particular interest for shape and topology optimization techniques. Shape and topology optimization is also an efficient mathematical tool for numerical solution of inverse problems, involving defect identification for instance.

The problem of shape optimization is to minimize a shape functional over a family of admissible domains. The shape functional depends directly on geometrical domains and implicitly by means of solutions to the state equation defined in those domains. For example, in structural mechanics, the specific functional depends on solutions to elasticity BVPs defined in the domains of integration. From the mathematical point of view, the questions to address, as usual in the calculus of variations, are:

  1. 1.

    Existence of an optimal domain.

  2. 2.

    Necessary conditions for optimality, which can be obtained for differentiable shape functionals.

  3. 3.

    Convergence of numerical methods of solution of the shape optimization problem under study.

There is a vast literature on the subject; the representative sources are, for example, the monographs [1,2,3,4,5] on the theory and applications in mechanics of solids and fluids.

In general, we cannot expect the existence of a global solution to shape optimization problems, since shape functionals are nonconvex. Therefore, it makes sense to introduce generalized optimal solutions of shape optimization problems, for example, by means of the homogenization technique [6,7,8]. As a result, the optimization procedure leads to optimal microstructures and there appear subdomains of optimal domains filled with metamaterials. These methods are known in structural mechanics as the homogenization method [9] or the SIMP method [10].

In this review, we are interested in applications of asymptotic analysis tools and techniques to shape and topology optimization in singularly perturbed geometrical domains [11] (see also, e.g., [12,13,14]). Regarding the theoretical development of topological asymptotic analysis, see, for instance, [15,16,17,18,19,20,21,22,23,24,25,26,27]. An account of new developments in this branch of shape optimization may be found in the book by Novotny and Sokołowski [28].

2 Classical Shape Optimization and Asymptotic Analysis Related to Topological Derivatives

Topological derivatives of shape functionals were introduced for elliptic BVPs quite recently. Instead of deformations of domains by diffeomorphism [1, 3], asymptotic analysis in singularly perturbed geometrical domains is performed for the purposes of shape sensitivity analysis [11]. However, the approach based on deformations applies to all types of linear PDEs. In addition, the velocity method of shape sensitivity analysis is simpler compared to asymptotic analysis, but it has some drawbacks from the point of view of numerics. In general, there is a close relationship between the two approaches; the results obtained by the second approach can also be derived from the velocity method, under some local regularity assumptions on solutions of elliptic BVPs. In other words, the knowledge of shape gradients and shape Hessians leads to topological derivatives of, for example, energy functionals under additional regularity assumptions. Asymptotic analysis is performed in the original, unperturbed domains. It is worth mentioning that classical shape sensitivity analysis can be derived by using only asymptotic analysis tools. We present a general setting of asymptotic analysis in singularly perturbed geometrical domains in Appendices. In the main body of Part I, for simplicity, we restrict ourselves to the simple case of circular or ball-shaped voids.

As a result of asymptotic analysis, we obtain a function \({\mathcal {T}}(x)\), \(x\in \varOmega \), such that

$$\begin{aligned} J(\varOmega _\varepsilon ) = J(\varOmega ) + f(\varepsilon ) {\mathcal {T}}(x) + o(f(\varepsilon )) \end{aligned}$$

for a given shape functional \(\varOmega \mapsto J(\varOmega )\) and a given domain \(\varOmega \subset {\mathbb {R}}^d\), \(d\ge 2\). Here, \(\varOmega _{\varepsilon } = \varOmega {{\setminus }} \overline{\omega _{\varepsilon }}\), where \(\overline{\omega _{\varepsilon }} \subset \varOmega \) represents a singular domain perturbation of the size governed by a small parameter \(\varepsilon \rightarrow 0\). Finally, \(f(\varepsilon )\) is a positive function such that \(f(\varepsilon ) \rightarrow 0\) as \(\varepsilon \rightarrow 0\). Therefore, the variation of the shape functional associated with the creation of a small singularity around \(x \in \varOmega \) is measured by the function \(x\mapsto {\mathcal {T}}(x)\), which is called the topological derivative of the mapping \(\varOmega \mapsto J(\varOmega )\).

In the first part of the review, we describe some qualitative results for the Laplacian and the elasticity system. In the second and third parts, we present, respectively, the first- and the second-order numerical methods of shape and topology optimization for elliptic BVPs, with many examples and numerical results. In order to fix ideas, let us give a very simple example.

Example 2.1

The notion of topological derivative extends the conventional definition of derivative to functionals depending on a geometrical domain, subjected to singular topology changes. The analogy between \({\mathcal {T}}(x)\) and the corresponding expressions for a conventional derivative should be noted. To illustrate the application of this concept, let us consider the very simple functional

$$\begin{aligned} J(\varOmega ) := |\varOmega | = \int _\varOmega 1, \end{aligned}$$
(1)

with \(\varOmega \subset \mathbb {R}^{2}\) subject to the class of topological perturbations given by the nucleation of circular holes, namely \(\omega _{\varepsilon } = B_{\varepsilon }({\widehat{x}}) := \{ \Vert x-{\widehat{x}}\Vert < \varepsilon \}\), for \({\widehat{x}} \in \varOmega \). For two-dimensional domains \(\varOmega \), the functional \(J(\varOmega )\) represents the area of the domain. The expansion with respect to \(\varepsilon \) in this case is trivial:

$$\begin{aligned} J(\varOmega _{\varepsilon }) = |\varOmega _\varepsilon | = \int _\varOmega 1 - \int _{B_\varepsilon } 1 = J(\varOmega ) - \pi \varepsilon ^2, \end{aligned}$$
(2)

and the topological derivative \({\mathcal {T}}(x)\) and the function \(f(\varepsilon )\) are immediately found to be

$$\begin{aligned} {\mathcal {T}}(x)=-1, \quad f(\varepsilon ) = \pi \varepsilon ^2. \end{aligned}$$
(3)

In this particular case, \({\mathcal {T}}(x)\) is independent of x, and the rightmost term of the topological asymptotic expansion is zero.

A particular case of shape optimization is minimization of a functional over an admissible set of characteristic functions [3]. In Example 2.1, the integral is of this type,

$$\begin{aligned} J(\varOmega ) = \int _{\mathbb {R}^{2}}\chi _{\varOmega }(x) \mathrm{d}x, \end{aligned}$$

where \(\chi _{\varOmega }\) is the characteristic function of \(\varOmega \). We provide an example of a similar problem in the third part of the review.

The main idea of numerical methods based on topological derivatives is the construction of an auxiliary level set function, depending on the topological derivative in the actual domain (see, e.g., [29,30,31,32]). In this method, the shape gradient is simply replaced by the topological derivative. The line search procedure defined by simple rules in terms of the descent direction, given by the current value of the topological derivative, is used to modify the current shape. The shape is determined by the level set function. Therefore, within the topological derivative method, there is no need for the complicated Hamilton–Jacobi equation to control the shape evolution. During the optimization procedure, the shape evolution is governed by a simple updating algorithm based on the current topological derivative. In numerical examples, the procedure converges to a local solution of the topology-shape optimization problem. Therefore, this method belongs to the field of experimental mathematics. To our best knowledge, the convergence of the level set method is still to be shown, except for some particular cases. In contrast to the first-order method presented in the second part of this review, a novel method based on second-order topological derivatives is presented in the third part of the review. The two-term expansion of the functional is exploited, leading to a quadratic and strictly convex form with respect to the parameters under consideration. Therefore, a single optimization step gives the solution, without the need for an iterative algorithm. Second-order methods are discussed in the third part of the review, with details and examples.

In this paper, we are concerned with the ideas for elliptic problems and singular perturbations of the principal part of the elliptic operator. We refer the reader to [28] for the case of penetrable inclusions and associated topological derivatives depending on the contrast parameter \(0<\gamma < \infty \), in particular for isotropic elasticity. There are also many problems where only lower order terms are perturbed, and in such cases asymptotic analysis substantially simplifies.

It is crucial for applications to know the exact form of topological derivatives. Sometimes, the expressions for topological derivatives depend on the unknown polarization tensor for the material, which is used to build geometrical domains.

3 Evaluation of Topological Derivatives

Evaluation of topological derivatives requires approximation of changes to solutions of elliptic BVPs with respect to small singular perturbations of geometrical domains. Such approximations are constructed, for example, in the monographs [33, 34]; see also [35, 36]. We refer the reader to [21] for the comparison of the known methods for evaluation of energy change due to the appearance of cavities in elastic solids. In Appendices, asymptotic analysis of scalar elliptic equations is discussed in a general setting.

We point out that in all methods listed below, for differentiable shape functionals, appropriate adjoint state equations can be introduced. Evaluation methods for topological derivatives depend on specific applications. The computational approaches of particular interest are:

  1. 1.

    The direct method of shape calculus combined with asymptotic expansions of solutions, proposed in the first paper on the topic [37]. In this method, the Taylor expansion of shape functionals, obtained in the framework of the velocity method [3], is used to pass to the limit with the small perturbation parameter, and as a result the topological derivative of the specific shape functional is obtained. The method is improved in [38] and finally uses the first shape derivatives only for a class of shape functionals. The method is difficult to apply for variational inequalities. See, for example, [39] for an application of standard asymptotic analysis to the Signorini problem, performed under the hypothesis of strict complementarity for unknown solutions. In the case of linear elliptic equations, the method can be combined with an adjoint equation approach [18, 40].

  2. 2.

    The direct method of two-scale asymptotic analysis [11] performed for elliptic systems, and leading in particular to self-adjoint extensions of elliptic operators. In this method, appropriate adjoint state equations can be introduced at the end of the procedure, in order to simplify formulas for topological derivatives. In other words, first a two-scale asymptotic approximation of solutions with prescribed precision is constructed, and it is then used to construct an approximation of the functional. Finally, a convenient form of topological derivative is obtained, for the purposes of numerical methods. In [11], complete proofs of the results obtained for linearized elasticity boundary value problems are given.

  3. 3.

    The method using fundamental solutions in truncated domains and the standard two-scale expansion techniques of asymptotic analysis (see [41], for instance). In a sense, this method is substantially improved by the addition of the domain decomposition technique with the Steklov–Poincaré operators; see the last point of this list. In addition, we refer to [15] for compound asymptotic analysis, combined with a modified adjoint sensitivity method.

  4. 4.

    The method using the technique of integral equations in electromagnetism, proposed, for instance, in [42] and [43]. We also refer to the recent book [44] for modeling influence of defects in elastic bodies, using well-established asymptotic formulas, with some applications to imaging.

  5. 5.

    The domain decomposition technique with asymptotic expansions of Steklov–Poincaré operators for small defects [27]. This framework is well adapted to the sensitivity analysis of coupled models in multiphysics, as well as of variational inequalities and contact problems in elasticity. The adjoint state equations are introduced in order to simplify the formulas for topological derivatives. The method has been used in many numerical examples: see, for example, [45, 46].

The evaluation technique depends on the problem under consideration. If there is a state equation, the evaluation process usually includes asymptotic expansions of solutions with respect to a small parameter \(\varepsilon \rightarrow 0\), which governs the size of singular geometrical perturbation. Asymptotic expansions of solutions to scalar equations for a model problem are given in Appendices. The case of the elasticity system is considered in [11].

We restrict ourselves to elliptic BVPs, namely the Laplace or Helmholtz equations, as well as to the BVPs of linear elasticity or for the Stokes system. The expansion depends on the spatial dimensions \(d=2,3\), since we use the fundamental solutions to the associated elliptic equations. Most important for applications are elliptic equations in three spatial dimensions.

The differentiability of energy functionals is the first task of asymptotic analysis for the purposes of topological optimization. This property of functionals is used explicitly in numerical methods and implicitly when using the domain decomposition technique.

The general mathematical theory of solution’s expansions, which applies to the elasticity system, can be found in [11]; see also [47] for the polarization tensors associated with the elasticity system. The results are given for arbitrary shapes of cavities or holes. However, closed formulas are available only for some specific shapes [47]. Usually, the results obtained for the contrast parameter \(0< \gamma < \infty \) lead to the limit cases for rigid inclusions and cavities [28].

Once the result of asymptotic analysis is known, there are some methods available which can be used to identify topological derivatives. We are particularly interested in numerical methods which are used in the framework of topological optimization. Therefore, topological derivatives should be given by robust expressions, which are approximated with the standard finite element techniques. The recommended way of identification is the application of the domain decomposition technique, in particular for topological derivatives of coupled models in multiphysics [27]. See also [41] for an early attempt at the truncated domain approach without Steklov–Poincaré operators.

In order to simplify asymptotic analysis, we are going to explain the application of Steklov–Poincaré operators to evaluation of topological derivatives for elliptic BVPs. Without the state equation, this evaluation is simpler and it becomes a purely geometrical problem; we refer to [48] for recent results in this direction. To be more specific, we are going to explain in detail the asymptotic expansions for the elasticity system in Sects. 4.4.1 and 4.4.2. The Neumann problem on a hole of arbitrary shape is analyzed in Appendices.

To obtain the form of topological derivatives, appropriate asymptotic analysis of solutions to the associated partial differential equation should be performed. There are some monographs on the subject, for example, [33, 34]. We also refer the reader to the related results obtained in collaboration with Nazarov [11, 22, 47, 49,50,51,52,53,54,55]. See also [56] for further developments, using matched asymptotic expansions for the Laplacian. In general, the form of the topological derivative is given in terms of adjoint states and polarization tensors. This is an additional difficulty for numerical methods of topology optimization using topological derivatives, since the polarization tensor is known explicitly only for specific geometries of voids or cavities.

4 Asymptotic Expansions for the Domain Decomposition Technique

The domain decomposition technique seems to be the most important method of evaluation of topological derivatives for numerical methods of topology optimization. In particular, the topological derivatives for BVPs of coupled models in multiphysics can be obtained in the framework of this technique, combined with asymptotic expansions of Steklov–Poincaré operators. In control theory, at least for scalar elliptic problems, the Steklov–Poincaré operator becomes the Dirichlet-to-Neumann map. The domain decomposition method can be applied to linear elliptic problems, as well as to variational inequalities. Numerical applications of the method can be found in [45], for shape–topology optimization in piezo-elasticity, or in [46], for thermo-elasticity.

4.1 Asymptotic Expansions of Steklov–Poincaré Operators

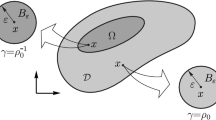
Our goal is to apply the domain decomposition method to evaluate topological derivatives. The first step of such an evaluation for complex models is always the local analysis of singular perturbations of geometrical domains. Thus, for example, in linear elasticity in two or three spatial dimensions, with a traction-free hole or cavity, we consider a ring-shaped domain \(C(R,\varepsilon )\) and obtain an asymptotic expansion of the Steklov–Poincaré operators associated with the elasticity problem, defined in its external boundary \(\varGamma _R\), with respect to the small parameter \(\varepsilon \rightarrow 0\). Let us consider a family of perturbations \(\varOmega _{\varepsilon }\) of the reference domain \(\varOmega \) by small holes or small cavities \(\omega _{\varepsilon }({\widehat{x}})\), with center \({\widehat{x}}\in \varOmega \). The method consists in approximating singular domain perturbations by regular perturbations of the bilinear form \(v\mapsto a(\varOmega ;v,v)\), in the variational formulation of the elliptic boundary value problem. The approximation means that the small domain \(\omega _{\varepsilon }\) is replaced by the correction term to the bilinear form, given by the boundary bilinear form \(v \mapsto \varepsilon ^d b(\varGamma _R;v,v)\) concentrated on the curve or surface \(\varGamma _R\). This bilinear form can be determined from asymptotic expansions of Steklov–Poincaré operators defined at the interface \(\varGamma _R\), i.e., from the topological derivative of the energy functional in \(\varOmega _{\varepsilon }{\setminus }\overline{\varOmega _R}\). In this section, we provide all the necessary details with some examples (Figs. 1, 2).

Remark 4.1

In a sense, our approach is similar, but not equivalent, to self-adjoint extensions of elliptic operators [57] as they are used in physics. See [11, 22, 52, 54] for applications to asymptotic approximations, which lead to equivalent formulas for topological derivatives. In other words, we are able to define an approximate mathematical model in the original domain in such a way that the first-order asymptotic expansion of the energy functional is the same as for the original model in the perturbed domain. For self-adjoint extensions, the domain \(\varOmega _\varepsilon \) is replaced by the punctured domain \(\varOmega {\setminus }\{ {\widehat{x}}\}\), while in our approach the truncated domain is \(\varOmega _R:=\varOmega {\setminus }\overline{B_R({\widehat{x}})}\) for small \(R>\varepsilon >0\). This approximation is sufficient for most of the applications we have in mind. In any case, we need polarization tensors or matrices [47, 49] in order to use topological derivatives in numerical methods applied to shape and topology optimization.

Fig. 1
figure 1

Domain \(\varOmega _{\varepsilon }\) with small void \(\omega _{\varepsilon }\)

Full size image
Fig. 2
figure 2

Truncated domain \(\varOmega _R\) and the ring \(C(R,\varepsilon )\)

Full size image

4.2 From Singular Domain Perturbations to Regular Perturbations of Bilinear Forms

In this section, we present the abstract scheme of asymptotic analysis for solutions of variational problems, posed in singularly perturbed geometrical domains. For simplicity, let us consider linear problems.

A weak solution of a linear elliptic problem with a symmetric, coercive and continuous bilinear form posed in \(\varOmega \subset {\mathbb {R}}^d\),

$$\begin{aligned} u:=u_{\varOmega }\in H \ : \ a(\varOmega ;u,\varphi )=L(\varOmega ;\varphi )\qquad \forall \varphi \in H, \end{aligned}$$
(4)

is given by a unique minimizer of the quadratic functional

$$\begin{aligned} I(\varOmega ;\varphi ):=\dfrac{1}{2}a(\varOmega ;\varphi ,\varphi )-L(\varOmega ;\varphi )=\dfrac{1}{2}a(\varphi ,\varphi )-L(\varphi ) \end{aligned}$$
(5)

over the Sobolev space \(H:=H(\varOmega )\) of functions defined in \(\varOmega \). For simplicity, we write also

$$\begin{aligned} I(\varphi ):=\dfrac{1}{2}a(\varOmega ;\varphi ,\varphi )-L(\varOmega ;\varphi ). \end{aligned}$$

The energy shape functional is defined for \(\varOmega \) as

$$\begin{aligned} \varOmega \mapsto {\mathcal {E}}(\varOmega ):=I(u)=\dfrac{1}{2}a(\varOmega ;u,u)-L(\varOmega ;u). \end{aligned}$$

We consider the singular geometrical perturbation \(\varOmega _{\varepsilon }:=\varOmega {\setminus }\overline{B_{\varepsilon }({\widehat{x}})}\) of the reference domain produced by a small circle or ball.

In order to evaluate the topological derivatives of the energy shape functional, as well as of some other shape functionals, we are going to use the domain decomposition technique. To this end, the reference domain is divided into two subdomains. The complement in \(\varOmega \) of the first subdomain \(\varOmega _R:=\varOmega {\setminus }\overline{B_R({\widehat{x}})}\) is the ball \(B_R({\widehat{x}})\) which includes the singular geometrical perturbation of the reference domain. The energy functional in the perturbed domain is

$$\begin{aligned} {\mathcal {E}}(\varOmega _{\varepsilon })={\mathcal {E}}(\varOmega _R)+{\mathcal {E}}(C(R,{\varepsilon })), \end{aligned}$$

where \(C(R,{\varepsilon })\) is a ring,

$$\begin{aligned} C(R,\varepsilon ):=B_R({\widehat{x}}){\setminus }\overline{B_{\varepsilon }({\widehat{x}})}. \end{aligned}$$

Now, we would like to introduce a bounded perturbation of the bilinear form

$$\begin{aligned} (\varphi ,\varphi )\mapsto b_{\varepsilon }(\varGamma _R;\varphi ,\varphi ), \end{aligned}$$

such that for \({\varepsilon }>0\),

$$\begin{aligned} {\mathcal {E}}(C(R,{\varepsilon }))=b_{\varepsilon }(\varGamma _R;u_{\varepsilon },u_{\varepsilon }). \end{aligned}$$

In fact, we can introduce such a form which is asymptotically exact for the first-order expansion of the solution \(u_{\varepsilon }\), restricted to the truncated domain \(\varOmega _R\), namely

$$\begin{aligned} u^R_{\varepsilon }=u^R+\varepsilon ^dq^R+o(\varepsilon ^d) \end{aligned}$$
(6)

in \(H(\varOmega _R)\) for fixed \(R>\varepsilon >0\). Here, \(f(\varepsilon )=\varepsilon ^d\); thus, we assume implicitly that the homogeneous Neumann boundary conditions are prescribed on the cavity \(B_{\varepsilon }({\widehat{x}})\).

In this way, we could obtain the first-order topological derivatives for shape functionals defined in \(\varOmega _R\), using the expansion of the energy functional in the ring \(C(R,{\varepsilon })\).

Let us fix \({\widehat{x}}\in \varOmega \) and consider again the truncated domain \(\varOmega _R:=\varOmega {\setminus }\overline{B_R({\widehat{x}})}\) and the perturbed domain \(\varOmega _{\varepsilon }:=\varOmega {\setminus }\overline{B_{\varepsilon }({\widehat{x}})}\), where \(R>\varepsilon >0\) are two parameters such that \(\varepsilon \rightarrow 0\) and \(\overline{B_{\varepsilon }({\widehat{x}})}\subset \varOmega \). By definition (5), we associate with the domains the quadratic functionals

$$\begin{aligned} I_R(\varphi ):=\dfrac{1}{2}a(\varOmega _R;\varphi ,\varphi )-L(\varOmega _R;\varphi ) = \dfrac{1}{2}a_R(\varphi ,\varphi )-L_R(\varphi ) \end{aligned}$$

and

$$\begin{aligned} I_{\varepsilon }(\varphi ):=\dfrac{1}{2}a_{\varepsilon }(\varphi ,\varphi )-L_{\varepsilon }(\varphi ), \end{aligned}$$
(7)

obtained by restriction of the test functions \(\varphi \in H(\varOmega )\) to \(\varOmega _R\) (respectively, to \(\varOmega _{\varepsilon }\)). Our goal is to construct an approximation of the quadratic functional for which the minimizer \(u_{\varepsilon }^R\) is given by the restriction to \(\varOmega _R\) of the variational solution \(u_\varepsilon \) in the singularly perturbed domain. The variational solution in \(\varOmega \) is given by (4), and the variational problem in the perturbed domain \(\varOmega _{\varepsilon }\) is given by

$$\begin{aligned} u_{\varepsilon }\in H_{\varepsilon } \ : \ a_{\varepsilon }(u_{\varepsilon },\varphi )=L_{\varepsilon }(\varphi )\qquad \forall \varphi \in H_{\varepsilon }. \end{aligned}$$
(8)

To this end, we introduce the nonlocal Steklov–Poincaré operator \({\mathcal {A}}_{\varepsilon }\) on the interior boundary \(\varGamma _R\) of \(\varOmega _R\). The operator is defined by the nonhomogeneous Dirichlet boundary value problem over \(C(R,\varepsilon )\). We determine the expansion of the Steklov–Poincaré operator

$$\begin{aligned} {\mathcal {A}}_{\varepsilon } = {\mathcal {A}} + \varepsilon ^d {\mathcal {B}} + {\mathcal {R}}_{\varepsilon } \end{aligned}$$

in the space of linear operators and introduce the bilinear form associated with the first term of the expansion,

$$\begin{aligned} b(h,h):=({\mathcal {B}}(h),h)_{\varGamma _R}. \end{aligned}$$

It can be shown that minimization of the first-order approximation of the quadratic functional (9), defined in the original domain, leads to the first-order expansion of the minimizers for the perturbed domain, which holds in the truncated domain \(\varOmega _R\):

Theorem 4.1

Let \( u^R_\varepsilon \) be the minimizer of the approximate quadratic functional

$$\begin{aligned} I^R_\varepsilon (\varphi )=\dfrac{1}{2}a(\varOmega ;\varphi ,\varphi )+ \dfrac{1}{2}\varepsilon ^d({\mathcal {B}}(\varphi ),\varphi )_{\varGamma _R}-L(\varOmega _R;\varphi ). \end{aligned}$$
(9)

Then, the restriction of this minimizer to \(\varOmega _R\) (denoted by the same symbol \(u^R_\varepsilon \)) has in \(H^1(\varOmega _R)\) an expansion

$$\begin{aligned} u^R_\varepsilon =u^R+\varepsilon ^d q^R + o(\varepsilon ^d), \end{aligned}$$
(10)

where \(u^R=u_{|_{\varOmega _R}}\). This expansion coincides with the expansion of the solution to (8) in \(H^1(\varOmega _R)\).

Corollary 4.1

In the case of variational equations resulting from the minimization of (7), we have the same result. Indeed, the first-order expansion of the minimizers \(\varepsilon \mapsto u_{\varepsilon }\), restricted to the truncated domain \(\varOmega _R\), i.e., for \(R>\varepsilon >0\),

$$\begin{aligned} u_{\varepsilon |\varOmega _R}=u_{|\varOmega _R}+\varepsilon ^d q^R + o(\varepsilon ^d) \end{aligned}$$
(11)

is preserved when using the minimization of (9), since, for example, for the second-order elliptic boundary value problems,

$$\begin{aligned} \Vert u_{\varepsilon |\varOmega _R}-u^R_{\varepsilon }\Vert _{H^1(\varOmega _R)}=o(\varepsilon ^d). \end{aligned}$$

Taking into account these estimates, the topological derivatives of shape functionals, defined by integrals in the truncated domain, can be obtained.

Corollary 4.2

The topological derivative of the tracking-type functional,

$$\begin{aligned} J(\varOmega _{\varepsilon }) = \dfrac{1}{2}\int _{\varOmega _R} (u_{\varepsilon }-z_d)^2\mathrm{d}x, \end{aligned}$$
(12)

is given by the expression

$$\begin{aligned} {\mathcal {T}}({\widehat{x}})=\int _{\varOmega _R} (u^R(x)-z_d(x))q^R(x) \mathrm{d}x=\int _{\varOmega _R} (u(x)-z_d(x))q(x) \mathrm{d}x, \end{aligned}$$
(13)

where

$$\begin{aligned} q=\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon ^d}(u_{\varepsilon }-u)\quad \text {in} \;\; \varOmega _R. \end{aligned}$$

Remark 4.2

The topological derivative of the tracking-type functional (12) can be simplified for variational equations by using the adjoint state equation. Then, the full potential of the topological derivative is seen, since it becomes a function of the point \({\widehat{x}}\), obtained at the expense of solving only two sets of state-like systems. The corresponding formulas are given in Parts II [58] and Part III [59] of the paper. However, even if we cannot use adjoint equations, the domain decomposition method based on the asymptotic expansion of the Steklov–Poincaré operator has its advantages. They consist in replacing the influence of the small hole (inclusion) by the small, localized disturbance of the main bilinear form (see (9)), defined in the original domain. In this way, the method facilitates and speeds up numerical approximations, for example, using finite element methods.

4.3 Signorini Problem in Two Spatial Dimensions

Now we shall explain the domain decomposition technique used in approximation of quadratic energy functionals to evaluate topological derivatives for the Laplace operator [27]. We restrict ourselves to the homogeneous Neumann boundary conditions on holes in order to use \(f(\varepsilon )\approx \varepsilon ^2\).

Let us consider the Signorini problem in a domain \(\varOmega \subset {\mathbb {R}}^2\) with smooth boundary \(\partial \varOmega =\varGamma _0\cup \varGamma _s\). The bilinear form

$$\begin{aligned} a(u,v)=a(\varOmega ;u,v)=\int _{\varOmega }\nabla u\cdot \nabla v \mathrm{d}x \end{aligned}$$

is coercive and continuous over the Sobolev space

$$\begin{aligned} H^1_{\varGamma _0}(\varOmega )=\{ v\in H^1(\varOmega ) \ : \ v=0\ \text {on}\ \varGamma _0\}, \end{aligned}$$

and the linear form

$$\begin{aligned} L(v)=L(\varOmega ;v)=\int _{\varOmega } fv \mathrm{d}x \end{aligned}$$

is continuous on \(L^2(\varOmega )\). There is a unique solution to the variational inequality

$$\begin{aligned} u\in K \ : \ a(u,v-u)\ge L(v-u)\qquad \forall v\in K, \end{aligned}$$

where K is the convex and closed cone

$$\begin{aligned} K=K(\varOmega )=\{ v\in H^1_{\varGamma _0}(\varOmega ) \ : \ v \ge 0 \ \text {on}\ \varGamma _s\}. \end{aligned}$$

Let us consider the variational inequality over the singularly perturbed domain \(\varOmega _{\varepsilon }=\varOmega {\setminus } \overline{B}_{\varepsilon }\),

$$\begin{aligned} u_{\varepsilon }\in K_{\varepsilon }=K(\varOmega _{\varepsilon }) \ : \ a_{\varepsilon }(u_{\varepsilon },v-u_{\varepsilon })\ge L_{\varepsilon }(v-u_{\varepsilon })\qquad \forall v\in K_{\varepsilon }, \end{aligned}$$

with the solution given by the unique minimizer of the quadratic functional

$$\begin{aligned} I_{\varepsilon }(v)=\dfrac{1}{2}a_{\varepsilon }(v,v)-L_{\varepsilon }(v) \end{aligned}$$
(14)

over the convex set \(K_{\varepsilon }:=K(\varOmega _{\varepsilon })\). Let us assume that \(L_{\varepsilon }\) is supported in \(\varOmega _R\).

We can show that there is an approximation of (14), denoted by

$$\begin{aligned} I^R_{\varepsilon }(v)=\dfrac{1}{2}a_{\varepsilon }(\varOmega _R;v,v)-L_{\varepsilon }(\varOmega _R;v), \end{aligned}$$

such that the first-order expansion of the minimizers with respect to the small parameter \(\varepsilon ^2\rightarrow 0\) is the same in \(H^1(\varOmega _R)\) as in the perturbed problem. Namely, we can introduce a continuous, symmetric and nonlocal bilinear form on the circle \(\varGamma _R=\{ \Vert x-{\widehat{x}}\Vert = R>\varepsilon >0 \}\),

$$\begin{aligned} H^{1/2}(\varGamma _R)\times H^{1/2}(\varGamma _R)\ni (v,v)\mapsto b(\varGamma _R;v,v)\in {\mathbb {R}}, \end{aligned}$$

such that

$$\begin{aligned} I^R_{\varepsilon }(v)=\dfrac{1}{2}a(\varOmega ;v,v)-L(\varOmega ;v)+\varepsilon ^2b(\varGamma _R;v,v). \end{aligned}$$

Furthermore, if the solution to the perturbed variational inequality has an expansion in \(H^1(\varOmega _R)\),

$$\begin{aligned} u_\varepsilon =u+\varepsilon ^2 q +o(\varepsilon ^2), \end{aligned}$$

then the minimizer \(u^R_{\varepsilon }\) of \(v\mapsto I^R_{\varepsilon }(v)\) over the convex cone \(K(\varOmega )\) has in \(H^1(\varOmega _R)\) the same first-order expansion,

$$\begin{aligned} u^R_{\varepsilon }=u+\varepsilon ^2 q +o(\varepsilon ^2). \end{aligned}$$

Corollary 4.3

The topological derivative of the tracking-type functional for the variational inequality,

$$\begin{aligned} J(\varOmega _{\varepsilon })=\dfrac{1}{2}\int _{\varOmega _R} (u_{\varepsilon }-z_d)^2\mathrm{d}x, \end{aligned}$$
(15)

is given by

$$\begin{aligned} {\mathcal {T}}({\widehat{x}})=\int _{\varOmega _R} (u^R(x)-z_d(x))q^R(x) \mathrm{d}x=\int _{\varOmega _R} (u(x)-z_d(x))q(x) \mathrm{d}x, \end{aligned}$$
(16)

where

$$\begin{aligned} q=\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon ^2}(u_{\varepsilon }-u)\quad \text {in} \;\; \varOmega _R. \end{aligned}$$

For variational inequalities, we cannot introduce adjoint states.

Thus, we are able to replace the singular geometrical domain perturbation \(B_\varepsilon ({\widehat{x}})\) by the regular perturbation \(v\mapsto \varepsilon ^2b(\varGamma _R;v,v)\) of the bilinear form \(v\mapsto a(\varOmega ;v,v)\) and preserve the first-order expansion of minimizers in the truncated domain. The bilinear form is constructed using the expansion of the Steklov–Poincaré operator, defined in \(\varGamma _R\) and given by the expansion of the energy functional in the ring \(C(R,\varepsilon )\):

$$\begin{aligned} a(\varOmega _\varepsilon ;v,v)\cong a(\varOmega ;v,v)+\varepsilon ^2b(\varGamma _R;v,v), \end{aligned}$$

where

$$\begin{aligned} b(\varGamma _R;v,v) = \left( \frac{1}{\pi R^3} \int _{\varGamma _R}v\cdot (x_1-{\widehat{x}}_1)\, \mathrm{d}s \right) ^2 + \left( \frac{1}{\pi R^3} \int _{\varGamma _R}v\cdot (x_2-{\widehat{x}}_2)\, \mathrm{d}s \right) ^2. \end{aligned}$$

For the elasticity system, the relevant formulas are given in Sects. 4.4.1 and 4.4.2.

4.4 Domain Decomposition Method for Elasticity BVPs

The domain decomposition method has been used to evaluate topological derivatives for coupled BVPs [28, 45, 46]. In this section, we shall consider asymptotic corrections to the energy functional corresponding to the elasticity system in \(\mathbb {R}^d\), where \(d=2,3\). The change of energy is caused by creating a small ball-like void of variable radius \(\varepsilon \) in the interior of the domain \(\varOmega \), with the homogeneous Neumann boundary condition on its surface. We assume that the void is centered at the origin \({\mathcal {O}}\). We take \(\varOmega _R = \varOmega {\setminus } \overline{B_R}\), where \(B_R:=B({\mathcal {O}},R)\) is an open ball with fixed radius R. In this way, the void \(B_\varepsilon := B({\mathcal {O}},\varepsilon )\) is surrounded by \(B_R \subset \varOmega \). We also denote the ring or spherical shell as \(C(R,\varepsilon ) = B_R {\setminus } \overline{B_\varepsilon }\), and its boundaries as \(\varGamma _R = \partial B_R\) and \(\varGamma _{\varepsilon }:=\partial B_\varepsilon \).

Using these notations, we define our main tool, the Dirichlet-to-Neumann mapping for linear elasticity, which is called the Steklov–Poincaré operator:

$$\begin{aligned} {\mathcal {A}}_{\varepsilon }\, : \, H^{1/2}(\varGamma _R;\mathbb {R}^d) \rightarrow H^{-1/2}(\varGamma _R;\mathbb {R}^d) \end{aligned}$$

by means of the boundary value problem

$$\begin{aligned}&\mu \varDelta w + (\lambda +\mu )\nabla (\mathrm {div\,}w) = 0,\;\; \text {in} \;\; C(R,\varepsilon ), \nonumber \\&w=v\;\; \text {on}\;\; \varGamma _R, \quad \sigma (u)n = 0\;\; \text {on}\;\; \varGamma _{\varepsilon }, \end{aligned}$$
(17)

so that

$$\begin{aligned} {\mathcal {A}}_{\varepsilon }(v) = \sigma (w)n\;\; \text {on}\;\; \varGamma _R. \end{aligned}$$
(18)

Here, \(\mu ,\lambda \) are the Lamé coefficients, and \(\sigma (w)\) is the Cauchy stress tensor,

$$\begin{aligned} \sigma (w) = 2 \mu (\nabla w)^s + \lambda \, \mathrm {div}(w) \, \mathrm {I}, \quad \text {with} \quad (\nabla w)^s = \frac{1}{2}(\nabla w + (\nabla w)^\top ). \end{aligned}$$

Let \(u^R\) be the restriction of u to \(\varOmega _R\), and \(\gamma ^R(\varphi )\) the trace of \(\varphi \) on \(\varGamma _R\), still denoted by \(\varphi \) for simplicity. We may then define the functional

$$\begin{aligned} I_{\varepsilon }^R(\varphi ) := \frac{1}{2} \int _{\varOmega _R} \sigma (\varphi ) \cdot (\nabla \varphi )^s \, \mathrm{d}x- \int _{\varGamma _N} h \cdot \varphi \, \mathrm{d}s+ \frac{1}{2} \int _{\varGamma _R} {\mathcal {A}}_{\varepsilon }(\varphi ) \cdot \varphi \, \mathrm{d}s\end{aligned}$$
(19)

and the solution \(u_{\varepsilon }^R\) as a minimizer for

$$\begin{aligned} I_{\varepsilon }^R(u_{\varepsilon }^R) := \inf _{\varphi \in K \subset H(\varOmega _R) } I_{\varepsilon }^R(\varphi ), \end{aligned}$$
(20)

We have replaced the variable domain \({\varepsilon }\mapsto \varOmega _{\varepsilon }\) by a fixed truncated domain \(\varOmega _R\), at the price of introducing a variable boundary operator \({\mathcal {A}}_{\varepsilon }\). Thus, the goal is to find an asymptotic expansion

$$\begin{aligned} {\mathcal {A}}_{\varepsilon } = {\mathcal {A}} + \varepsilon ^d {\mathcal {B}} + {\mathcal {R}}_{\varepsilon }, \end{aligned}$$
(21)

where the remainder \({\mathcal {R}}_{\varepsilon }\) is of order \(o(\varepsilon ^d)\) in the operator norm in

$$\begin{aligned} {\mathcal {L}}(H^{1/2}(\varGamma _R;\mathbb {R}^2),H^{-1/2}(\varGamma _R;\mathbb {R}^2)) \end{aligned}$$

and the operator \({\mathcal {B}}\) is regular enough, namely it is bounded and linear:

$$\begin{aligned} {\mathcal {B}} \in {\mathcal {L}} (L^2(\varGamma _R;\mathbb {R}^2), L^2(\varGamma _R;\mathbb {R}^2)). \end{aligned}$$

Under this assumption, the following propositions hold true.

Proposition 4.1

Assume that (21) holds in the operator norm. Then,

$$\begin{aligned} u^R_\varepsilon \rightarrow u^R \end{aligned}$$
(22)

strongly in the \(H^1(\varOmega _R)\)-norm.

Proposition 4.2

The energy functional has a representation

$$\begin{aligned} I_\varepsilon ^R(u^R_\varepsilon )=I(u)+\varepsilon ^d \langle {\mathcal {B}}(u),u\rangle _R + o(\varepsilon ^d)\ , \end{aligned}$$
(23)

where \(o(\varepsilon ^d)/\varepsilon ^d \rightarrow 0\) as \(\varepsilon \rightarrow 0\) in the same energy norm.

Here, \(I^R(u^R)\) denotes the functional \(I_{\varepsilon }^R\) on the original domain, i.e., \(\varepsilon =0\), with \({\mathcal {A}}_{\varepsilon }\) replaced by \({\mathcal {A}}\) applied to truncation of u.

Generally, the energy correction for the elasticity system has the form

$$\begin{aligned} \langle {\mathcal {B}}(u^R),u^R \rangle _R \; =\; -c_d e_u({\mathcal {O}}), \end{aligned}$$

where \(c_d=\mathrm {vol}(B_1)\), with \(B_1\) being the unit ball in \(\mathbb {R}^d\). The energy-like density function \(e_u({\mathcal {O}})\) has the form

$$\begin{aligned} e_u({\mathcal {O}}) = \frac{1}{2} {\mathbb {P}} \sigma (u^R) \cdot (\nabla u^R)^s({\mathcal {O}}), \end{aligned}$$

where for \(d=2\) and the plane stress,

$$\begin{aligned} {\mathbb {P}}\; =\; \frac{1}{1-\nu } (4 {\mathbb {I}} - \mathrm {I} \otimes \mathrm {I} ), \end{aligned}$$

and for \(d=3\),

$$\begin{aligned} {\mathbb {P}} \; = \; \frac{1-\nu }{7-5\nu } (10 {\mathbb {I}} - \frac{1-5\nu }{1-2\nu }\mathrm {I} \otimes \mathrm {I} ). \end{aligned}$$

Here, \({\mathbb {I}}\) is the fourth-order identity tensor, and \( \mathrm {I}\) is the second-order identity tensor.

This approach is important for variational inequalities, since it allows us to derive formulas for topological derivatives which are similar to expressions obtained for the corresponding linear BVPs.

4.4.1 Explicit Form of the Operator \({\mathcal {B}}\) in Two Spatial Dimensions

Let us denote, for the plane stress case,

$$\begin{aligned} k = \frac{\lambda + \mu }{\lambda +3\mu }. \end{aligned}$$

It has been proved in [27] that the following exact formulas hold:

$$\begin{aligned} u_{1,1}({\mathcal {O}})+u_{2,2}({\mathcal {O}})&= \frac{1}{\pi R^3} \int _{\varGamma _R} (u_1 x_1 +u_2 x_2) \, \mathrm{d}s,\\ u_{1,1}({\mathcal {O}})-u_{2,2}({\mathcal {O}})&= \frac{1}{\pi R^3} \int _{\varGamma _R} \Big [ (1-9k)(u_1 x_1 -u_2 x_2) + \frac{12k}{R^2} (u_1 x_1^3 - u_2 x_2^3) \Big ] \, \mathrm{d}s,\\ u_{1,2}({\mathcal {O}})+u_{2,1}({\mathcal {O}})&= \frac{1}{\pi R^3} \int _{\varGamma _R} \Big [(1+9k)(u_1 x_2 +u_2 x_1) - \frac{12k}{R^2} (u_1 x_2^3 + u_2 x_1^3) \Big ] \, \mathrm{d}s. \end{aligned}$$

These expressions contain additional integrals of third powers of \(x_i\). Therefore, strains evaluated at \({\mathcal {O}}\) may be expressed as linear combinations of integrals over the circle of the form

$$\begin{aligned} \int _{\varGamma _R} u_i x_j \, \mathrm{d}s, \qquad \int _{\varGamma _R} u_i x_j^3 \, \mathrm{d}s. \end{aligned}$$

The same is true, due to Hooke’s law, for the stresses \(\sigma _{ij}({\mathcal {O}})\). They may then be inserted into the expression for \({\mathcal {B}}\), yielding

$$\begin{aligned} \langle {\mathcal {B}}(u^R),u^R \rangle _R =-\frac{1}{2} c_2 {\mathbb {P}} \sigma (u) \cdot (\nabla u)^s. \end{aligned}$$

These formulas are quite easy to compute numerically.

4.4.2 Explicit Form of the Operator \({\mathcal {B}}\) in Three Spatial Dimensions

It turns out that a similar situation holds in three spatial dimensions, but obtaining exact formulas is more difficult. Assuming given values of u on \(\varGamma _R\), the solution of the elasticity system in \(B_R\) may be expressed, following partially the derivation from [60] (pp. 285 ff.), as

$$\begin{aligned} u = \sum _{n=0}^{\infty } [U_n + (R^2-r^2)k_n(\nu ) \nabla (\mathrm {div\,}U_n) ], \end{aligned}$$
(24)

where \(k_n(\nu ) = 1/2[(3-2\nu )n-2(1-\nu )]\) and \(r=\Vert x \Vert \), with \(\nu \) denoting the Poisson ratio. In addition,

$$\begin{aligned} U_n = \frac{1}{R^n}[a_{n0} d_n(x) + \sum _{m=1}^n (a_{nm} c_n^m(x) + b_{nm} s_n^m(x))]. \end{aligned}$$
(25)

The vectors

$$\begin{aligned} a_{n0}= & {} (a_{n0}^1,a_{n0}^2,a_{n0}^3)^{\top },\\ a_{nm}= & {} (a_{nm}^1,a_{nm}^2,a_{nm}^3)^{\top },\\ b_{nm}= & {} (b_{nm}^1,b_{nm}^2,b_{nm}^3)^{\top } \end{aligned}$$

are constants, and the set of functions

$$\begin{aligned} \{ d_0;\; d_1, c_1^1, s_1^1;\; d_2, c_2^1,s_2^1,c_2^2,s_2^2;\; d_3,c_3^1,s_3^1,c_3^2,s_3^2,c_3^3,s_3^3;\; \ldots \} \end{aligned}$$

constitutes a complete system of orthonormal harmonic polynomials on \(\varGamma _R\), related to Laplace spherical functions. Specifically,

$$\begin{aligned} c_k^l(x)=\frac{{\hat{P}}_k^{l,c}(x)}{ \Vert {\hat{P}}_k^{l,c} \Vert _R },\quad s_k^l(x)=\frac{{\hat{P}}_k^{l,s}(x)}{ \Vert {\hat{P}}_k^{l,s} \Vert _R },\quad d_k=\frac{P_k(x)}{ \Vert {\hat{P}}_k \Vert _R }. \end{aligned}$$

For example,

$$\begin{aligned} c_3^2({\mathbf {x}}) = \frac{1}{R^4}\sqrt{\frac{7}{240\pi }} (15 x_1^2 x_3 - 15 x_2^2 x_3). \end{aligned}$$

If the value of u on \(\varGamma _R\) is assumed to be given, then, denoting

$$\begin{aligned} \langle \phi ,\psi \rangle _R = \int _{\varGamma _R} \phi \psi \, \mathrm{d}s, \end{aligned}$$

we have for \(n \ge 0\), \(m=1..n\), \(i=1,2,3\):

$$\begin{aligned} a_{n0}^i&= R^n \langle u_i,d_n(x) \rangle _R,\nonumber \\ a_{nm}^i&= R^n \langle u_i,c_n^m(x) \rangle _R,\nonumber \\ b_{nm}^i&= R^n \langle u_i,s_n^m(x) \rangle _R. \end{aligned}$$
(26)

Since we are looking for \(u_{i,j}({\mathcal {O}})\), only the part of u which is linear in x is relevant. It contains two terms:

$$\begin{aligned} {\hat{u}} = U_1 + R^2 k_3(\nu ) \nabla (\mathrm {div\,}U_3). \end{aligned}$$
(27)

For any f(x), \(\nabla \mathrm {div\,}(a f) = H(f) \cdot a\), where a is a constant vector and H(f) is the Hessian matrix of f. Therefore,

$$\begin{aligned} {\hat{u}}= & {} \frac{1}{R} [a_{10} d_1(x) + a_{11} c_1^1(x) + b_{11} s_1^1(x))] \nonumber \\&+\, R^2 k_3(\nu )\frac{1}{R^3} \Big [ H(d_3) (x) a_{30} + \sum _{m=1}^3 \big ( H(c_3^m) (x) a_{3m} + H(s_3^m)(x) b_{3m}\big ) \Big ]. \end{aligned}$$
(28)

From the above, we may single out the coefficients of \(x_1,x_2,x_3\) in \(u_1,u_2,u_3\). For example,

$$\begin{aligned} u_{1,1}({\mathcal {O}}) =&\frac{1}{R^3}\sqrt{\frac{3}{4\pi }} a_{11}^1 + \frac{1}{R^5} k_3(\nu ) \Big [ -3\sqrt{\frac{7}{4\pi }}a_{30}^3 9\sqrt{\frac{7}{24\pi }} a_{31}^1\nonumber \\&-3\sqrt{\frac{7}{24\pi }}b_{31}^2 + 30 \sqrt{\frac{7}{240\pi }} a_{32}^3 + 90 \sqrt{\frac{7}{1440\pi }} a_{33}^1 + 90 \sqrt{\frac{7}{1440\pi }} b_{33}^2\Big ], \nonumber \\ u_{1,2}({\mathcal {O}}) =&\frac{1}{R^3}\sqrt{\frac{3}{4\pi }}( b_{11}^1 + a_{11}^2)+\frac{1}{R^5} k_3(\nu ) \Big [ -3\sqrt{\frac{7}{24\pi }}a_{31}^2- \sqrt{\frac{7}{24\pi }} b_{31}^1\nonumber \\&+15\sqrt{\frac{7}{60\pi }}b_{32}^3 - 90 \sqrt{\frac{7}{1440\pi }} a_{33}^2 + 90 \sqrt{\frac{7}{1440\pi }} b_{33}^1 \Big ]. \end{aligned}$$

Observe that

$$\begin{aligned} u_{1,1}({\mathcal {O}})+u_{2,2}({\mathcal {O}})+u_{3,3}({\mathcal {O}})= \frac{1}{R^3} \sqrt{ \frac{3}{4\pi }} \big ( R\langle u_1,c_1^1 \rangle _R + R\langle u_2,s_1^1 \rangle _R + R \langle u_3,d_1 \rangle _R \big ) \end{aligned}$$

and \(c_1^1=\frac{1}{R^2} \sqrt{ \frac{3}{4\pi } } x_1\), \(s_1^1=\frac{1}{R^2} \sqrt{ \frac{3}{4\pi } } x_2\), \(d_1=\frac{1}{R^2} \sqrt{ \frac{3}{4\pi } } x_3\), which is in agreement with the fact that the trace of the strain tensor is a harmonic function.

As a result, the operator \({\mathcal {B}}\) may be defined by

$$\begin{aligned} \langle {\mathcal {B}} u^R,u^R \rangle _R := -c_3 {\mathbb {P}} \sigma (u) \cdot (\nabla u)^s({\mathcal {O}}), \end{aligned}$$

where the right-hand side consists of integrals of u multiplied by first- and third-order polynomials in \(x_i\) over \(\varGamma _R\) resulting from (26). This is a very similar situation to the case of two spatial dimensions. Thus, the new expressions for strains make it possible to rewrite \({\mathcal {B}}\) in the form of the desired regularity. We refer the reader to [61,62,63] for supplementary material on elasticity models.

5 Perspectives and Open Problems

The topological derivative method in shape and topology optimization introduces the asymptotic analysis of elliptic BVPs, for example, into the field of structural optimization in elasticity. The method requires the local regularity of solutions to elliptic problems. Nowadays, classical shape optimization techniques are not restricted to elliptic problems, but can be applied to evolution problems, including linear parabolic and hyperbolic equations. Extension of the topological derivative method to evolution problems is one of the challenging issues in the field of shape optimization. In particular, for transport equations, the notion of topological derivative is still to be discovered. Let us mention that the transport equations are components of compressible Navier–Stokes equations. The modern theory of shape optimization for compressible Navier–Stokes equations can be found in the monograph [2]. Another domain which is promising for developments of shape optimization is nonlinear elasticity. Evolution of geometrical domains is also used in growth modeling. Shape and topology optimization for nonlinear elasticity is still poorly understood. There is already some numerical evidence that topological derivatives are well adapted to the design of metamaterials in elasticity.

In order to state some open problems for applications of topological sensitivity analysis to numerical solution of shape optimization and inverse problems, we specify the mathematical framework, which combines analysis of weak solutions to elliptic BVPs with the domain decomposition method, as well as with asymptotic approximation of solutions in singularly perturbed geometrical domains.

  1. 1.

    Applications of\(\varGamma \)-convergence to topological differentiability of shape functionals. It is known that the shape derivatives of energy-type functionals can be obtained by the \(\varGamma \)-limit procedure; see the derivation of the elastic energy with respect to crack length [64, 65] or [66,67,68,69,70] for related topics. It is not known whether the same \(\varGamma \)-convergence can be used for topological derivatives.

  2. 2.

    Sensitivity analysis of evolution variational inequalities. Shape optimization for stationary variational inequalities is studied in [3]. The results are based on Hadamard differentiability of the metric projection onto convex sets in Sobolev spaces [71,72,73]. The results are obtained by using potential theory in Dirichlet spaces [74], which leads to Hadamard differentiability of the metric projection. For stationary variational inequalities with local constraints on gradients or on stresses, shape and topological sensitivity analysis is an open problem. For example, for Hencky plasticity, there are no results, either in shape optimization or for topological derivatives. Extension of such results to evolution variational inequalities is a challenging problem, necessary for development of topological derivatives.

  3. 3.

    Asymptotic analysis of evolution variational inequalities. Asymptotic analysis of stationary variational inequalities was studied, for example, by Argatov and Sokolowski [39]. The concept of polyhedral subsets of Sobolev spaces can be used in order to derive topological derivatives for contact problems in solid mechanics. Open problems for stationary variational inequalities include some models of plates and shells and plasticity. This domain of research has stagnated for a long time. The mathematical result required concerns directional differentiability of the metric projection onto a convex set defined by local constraints on the stresses. Extending such results to asymptotic analysis of evolution variational inequalities is another challenging problem.

  4. 4.

    Second-order necessary optimality conditions in topological optimization. First-order necessary optimality conditions are known for linear state equations [26]. Using second-order topological derivatives to derive optimality conditions seems to be an open problem.

  5. 5.

    Exact solutions in singularly perturbed geometrical domains for anisotropic elasticity, transient wave equations and nonlinear transport problems for evaluation of topological derivatives. Exact solutions of elliptic BVPs in a ring are used to evaluate topological derivatives within the domain decomposition technique. Such results are of interest for the PDEs listed below.

    1. (a)

      Elasticity with complex Kolosov potentials and Steklov–Poincaré formalism in domain decomposition. Using complex potentials of Kolosov, one can obtain exact solutions of the elasticity system in two spatial dimensions. These results lead to topological derivatives of arbitrary order. Extending such results to a full range of models in mechanics is an interesting line of research, which is still to be taken up.

    2. (b)

      Wave equations. An important field of applications is electromagnetism and exact solutions, which are not standard from the mathematical point of view for asymptotic analysis. We refer the reader to [75,76,77] for related results in the static case. Open problems in the field of wave equations include all aspects of time-dependent problems, including asymptotic analysis in singularly perturbed geometrical domains. Wave equations with self-adjoint extensions of elliptic operators are used in [78].

    3. (c)

      Transport equations in singularly perturbed domains. The domain decomposition method is also used for transport problems. Open problems in this field involve all aspects of asymptotic analysis. The compressible Navier–Stokes equations can also be considered from the point of view of singular domain perturbations, provided the related results for the transport equation component are established.

6 Conclusions

The proposed approach to evaluation of topological derivatives applies to some classes of variational inequalities and to multiphysics BVPs. From the mathematical point of view, the domain decomposition method of evaluation of topological derivatives uses asymptotic expansions of the energy functional in a small neighborhood of the singular domain perturbation, produced by a hole or a cavity. In our applications, the energy expansions are equivalent to expansions of nonlocal Steklov–Poincaré boundary operators. In the truncated domain, perturbations of boundary conditions with the expansion of Steklov–Poincaré boundary operators lead to regular perturbations of the bilinear form and allow us to avoid self-adjoint extensions of elliptic operators in punctured domains. Topological derivatives are known for linear elliptic BVPs. They remain almost unknown for some nonlinear problems, including nonlinear elasticity and plasticity. See [79] for some recent developments in this direction. Extension of this approach to shape optimization to evolution problems should also be considered for variational inequalities modeling compressible fluids.