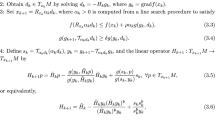Convergence Rate of Descent Method with New Inexact Line-Search on Riemannian Manifolds

Abstract

In this paper, we propose the descent method with new inexact line-search for unconstrained optimization problems on Riemannian manifolds. The global convergence of the proposed method is established under some appropriate assumptions. We further analyze some convergence rates, namely R-linear convergence rate, superlinear convergence rate and quadratic convergence rate, of the proposed descent method.

1 Introduction

Since the non-convex problems can be translated into convex problems with appropriate Riemannian metrics, and constrained optimization problems can be written as unconstrained optimization problems from the Riemannian geometry viewpoint, in recent years, many concepts, techniques, as well as methods of optimization theory have been extended from Euclidean space to Riemannian manifolds; see, for instance, [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. It is an emerging area of research in convex analysis, optimization theory, game theory, etc; see, for example, [12, 14] and the references therein.

The descent method is one of the oldest and widely known methods for solving minimization problems. Many convergence results for descent method have been established in the setting of Euclidean space. For instance, some line-search techniques for the general descent method in $\mathbb {R}^{n}$ are proposed by Nocedal and Wright [16]. They proved the global convergence and studied convergence rate of steepest descent method, Newton’s method and coordinate descent method. Shi and Shen [17] also proved the global convergence and local convergence rate of descent method with new inexact line-search in $\mathbb {R}^{n}$. The new inexact line-search in [17] has many advantages comparing with some other similar line-searches, such as Armijo line-search and Wolfe line-search; see [18, 19]. Based on the results in [17], a new inexact line-search for quasi-Newton method is proposed and some global convergence results are established by Shi [20]. Recently, some authors focused on extending the convergence results for descent methods from Euclidean space to Riemannian manifolds. In particular, the steepest descent method and the Newton method to solve convex optimization problems on Riemannian manifolds have been studied by Udrişte [14], in which the linear convergence result for the steepest descent method is obtained under the assumption of exact line-search. Smith [21] considered the steepest descent, Newton method and conjugate gradient method on Riemannian manifolds and analyzed their convergence properties by employing the Riemannian structure of the manifold. The full convergence result for the steepest descent method with the Armijo line-search on Riemannian manifolds has been studied by da Cruz Neto et al. [4, 5]. A combination of generalized Armijo method and generalized Newton method in the setting of Riemannian manifolds is investigated by Yang [15]. The global convergence results for these methods with less restrictions are obtained. Estimations of linear/quadratic convergence rate for the generalized Armijo–Newton algorithms are also derived in [15]. Moreover, the global and local convergence analysis of the exact and approximate line-search such as the Newton’s method, the gradient descent method and the trust-region method on Riemannian manifolds is studied in [22,23,24,25,26,27].

Motivated by the results described above, in this paper, we propose a new inexact line-search for the descent method on Riemannian manifolds and establish its convergence results. Since the computation of the exponential mapping and parallel transport can be quite expensive in the setting of manifolds, and many convergence results show that the nice properties of some algorithms hold for all suitably defined retractions and isometric vector transports on Riemannian manifolds (see, for example, [6, 13, 28]), we replace the geodesic by retraction and parallel transport by isometric vector transport, respectively. As a result, the global convergence result of the descent method, with new inexact line-search for unconstrained optimization problems on Riemannian manifolds, is proved under some appropriate assumptions. Moreover, we analyze the convergence rate, such as R-linear convergence rate, superlinear convergence rate and quadratic convergence rate, of the descent method on Riemannian manifolds. To the best of our knowledge, these results have not been studied before, and it is very interesting to explore the convergence results for a new inexact line-search algorithm on manifolds by utilizing Riemannian techniques.

The present paper is organized as follows: In Sect. 2, we recall some notions and known results from Riemannian geometry, which will be used throughout the paper. We propose the descent method with new inexact line-search for unconstrained optimization problems on Riemannian manifolds. In Sect. 3, the global convergence result for the descent method on Riemannian manifolds is proved. Section 4 is devoted to analyze the convergence rate of the descent method with new inexact line-search.

2 Preliminaries

In this section, we recall some standard notations, definitions and results from Riemannian manifolds, which can be found in any introductory book on Riemannian geometry; see, for example, [2, 3, 7].

Let M be a finite-dimensional differentiable manifold and $x\in M$. The tangent space of M at x is denoted by $T_{x}M$ and the tangent bundle of M by $TM=\bigcup _{x\in M}T_{x}M$, which is naturally a manifold. We denote by $g_{x}(.,.)$ the inner product on $T_{x}M$ with the associated norm $\Vert \cdot \Vert _{x}$. If there is no confusion, then we omit the subscript x. If M is endowed with a Riemannian metric g, then M is a Riemannian manifold. Throughout the paper, unless otherwise specified, we assume that M is a Riemannian manifold. Given a piecewise smooth curve $\gamma : [t_{0}, t_{1}]\rightarrow M$ joining x to y, that is, $\gamma (t_{0})=x$ and $\gamma (t_{1})=y$, we can define the length of $\gamma$ by $l(\gamma )=\int _{a}^{b}\Vert \gamma '(t)\Vert \hbox {d}t$. Minimizing this length functional over the set of all curves, we obtain a Riemannian distance d(x, y) which induces the original topology on M.

Let $\nabla$ be the Levi-Civita connection associated with M. A vector field $V: M\rightarrow TM$ along $\gamma$ is said to be parallel if $\nabla _{\gamma '} V = 0$. We say that $\gamma$ is a geodesic when $\nabla _{\gamma '} \gamma ' = 0$; in the case $\Vert \gamma '\Vert =1$, $\gamma$ is said to be normalized. Let $\gamma : \mathbb {R}\rightarrow M$ be a geodesic and $P_{\gamma [.,.]}$ denote the parallel transport along $\gamma$, which is defined by $P_{\gamma [\gamma (a),\gamma (b)]}(v)=V(\gamma (b))$ for all $a, b\in \mathbb {R}$ and $v\in T_{\gamma (a)}M$, where V is the unique $C^{\infty }$ vector field such that $\nabla _{\gamma '(t)}V=0$ and $V(\gamma (a))=v$.

A Riemannian manifold is complete if, for any $x\in M$, all geodesic emanating from x are defined for all $t \in \mathbb {R}$. By Hopf–Rinow theorem [29], any pair of points $x,y\in M$ can be joined by a minimal geodesic. The exponential mapping $\exp _{x}: T_{x}M\rightarrow M$ is defined by $\exp _{x}v=\gamma _{v}(1, x)$ for each $v\in T_{x}M$, where $\gamma (\cdot )=\gamma _{v}(\cdot , x)$ is the geodesic starting from x with velocity v, that is, $\gamma (0)=x$ and $\gamma '(0)=v$. It is easy to see that $\exp _{x}tv=\gamma _{v}(t, x)$ for each real number t.

The exponential mapping $\exp _{x}$ provides a local parametrization of M via $T_{x}M$. However, the systematic use of the exponential mapping may not be desirable in all cases. Some local mappings to $T_{x}M$ may reduce the computational cost while preserving the useful convergence properties of the considered method. In this paper, we relax the exponential mapping by a class of mappings called retractions, a concept that can be seen in [1, 6, 13, 30, 31].

Definition 2.1

Given $x\in M$, a retraction is a smooth mapping $R_{x}: T_{x}M\rightarrow M$ such that

• (i) $R_{x}(0_{x})=x$ for all $x\in M$, where $0_{x}$ denotes the zero element of $T_{x}M$;

• (ii) $DR_{x}(0_{x})=\mathrm {id}_{T_{x}M}$, where $DR_{x}$ denotes the derivative of $R_{x}$ and id denotes the identity mapping.

As we know, the exponential mapping is a special retraction, and some retractions can be seen as an approximation of the exponential mapping.

The parallel transport is often too expensive to use in a practical method, so we can consider a more general vector transport (see, for example, [6, 13, 22]), which is built upon the retraction $R_{x}$. A vector transport $\mathscr {\mathscr {\mathscr {T}}}:TM\bigoplus TM\rightarrow TM$, $(\eta _{x},\xi _{x})\mapsto \mathscr {T}_{\eta _{x}}\xi _{x}$ with the associated retraction $R_{x}$ is a smooth mapping such that, for all $\eta _{x}$ in the domain of $R_{x}$ and all $\xi _{x},\zeta _{x}\in T_{x}M$, (i) $\mathscr {T}_{\eta _{x}}\xi _{x}\in T_{R_{x}(\eta _{x})}M$; (ii) $\mathscr {T}_{0_{x}}\xi _{x}=\xi _{x}$; (iii) $\mathscr {T}_{\eta _{x}}$ is a linear mapping. Let $\mathscr {T}_{S}$ denote the isometric vector transport (see, for example, [13, 22, 31]) with $R_{x}$ as the associated retraction. Then it satisfies (i), (ii), (iii) and the following condition (iv):

$$\begin{aligned} g(\mathscr {T}_{S(\eta _{x})}\xi _{x},\mathscr {T}_{S(\eta _{x})}\zeta _{x}) =g(\xi _{x},\zeta _{x}). \end{aligned}$$

(1)

In most of the practical cases, $\mathscr {T}_{S(\eta _{x})}$ exists for all $\eta _{x}\in T_{x}M$, and thus, we make this assumption throughout the paper. Furthermore, let $\mathscr {T}_{R_{x}}$ denote the derivative of the retraction, that is,

$$\begin{aligned} \mathscr {T}_{R_{x}(\eta _{x})}\xi _{x}=\mathrm {D}R_{x}(\eta _{x})[\xi _{x}] = \left. \frac{\mathrm {d}}{\mathrm {d}t}R_{x}(\eta _{x}+t\xi _{x}) \right| _{t=0}. \end{aligned}$$

(2)

Let L(TM, TM) denote the fiber bundle with the base space $M\times M$ such that the fiber bundle over $(x,y)\in M\times M$ is $L(T_{x}M,T_{y}M)$, the set of all linear mappings from $T_{x}M$ to $T_{y}M$. We recall, from Section 4 in [6], that a transporter $\mathscr {L}$ on M to be a smooth section of the bundle L(TM, TM), that is, for all $x,y\in M$, $\mathscr {L}(x,y)\in L(T_{x}M,T_{y}M)$ and $\mathscr {L}(x,x)=\mathrm {id}$, where $\mathrm {id}$ means the identity mapping. Furthermore, $\mathscr {L}(x,y)$ is isometric from $T_{x}M$ to $T_{y}M$, $\mathscr {L}^{-1}(x,y)=\mathscr {L}(y,x)$ and $\mathscr {L}(x,z)=\mathscr {L}(y,z)\mathscr {L}(x,y)$. Given a retraction $R_{x}$, for any $\eta _{x}, \xi _{x}\in T_{x}M$, the isometric vector transport $\mathscr {T}_{S}$ can be defined by

$$\begin{aligned} \mathscr {T}_{S(\eta _{x})}\xi _{x}=\mathscr {L}(x,R_{x}(\eta _{x}))(\xi _{x}). \end{aligned}$$

In this paper, we require

$$\begin{aligned} \mathscr {T}_{R_{x}(\eta _{x})}\xi _{x}=\mathscr {T}_{S(\eta _{x})}\xi _{x}. \end{aligned}$$

In some manifolds, there exist retractions such that the above equality holds, e.g., the Stiefel manifold and the Grassmann manifold [31]. Furthermore, from the above equality and (1), we have

$$\begin{aligned} \Vert \xi _{x}\Vert= & {} \Vert \mathscr {T}_{S(\eta _{x})}\xi _{x}\Vert = \Vert \mathscr {L}(x,R_{x}(\eta _{x}))(\xi _{x})\Vert \\= & {} \Vert \mathscr {T}_{R_{x}(\eta _{x})}\xi _{x}\Vert = \Vert \mathrm {D}R_{x}(\eta _{x})[\xi _{x}]\Vert . \end{aligned}$$

In this paper, we consider the following unconstrained minimization problem

$$\begin{aligned} \min _{x \in M} f(x), \end{aligned}$$

(3)

where $f: M\rightarrow \mathbb {R}$ is a continuously differentiable function with a lower bound and M is a complete Riemannian manifold.

Now, we describe the descent method with new inexact line-search on Riemannian manifolds for finding the solution of the minimization problem (3).

3 New Inexact Line-Search on Riemannian Manifolds

Given $\beta \in \, ]0,1[$ and $\sigma \in \, ]0,1[$, the Hessian approximation $B_{k}$ is symmetric positive definite with respect to the metric g, and $s_{k} = \frac{-g(\mathrm {grad}f(x_{k}),d_{k})}{g(B_{k}[d_{k}],d_{k})}$, where $d_{k}\in T_{x_{k}}M$ is a descent direction with $g(\mathrm {grad}f(x_{k}), d_{k})<0$. The step size $\alpha _{k}$ is the largest one in $\{s_{k}, s_{k}\beta , s_{k}\beta ^{2},\ldots \}$ such that

$$\begin{aligned} f(R_{x_{k}}(\alpha _{k} d_{k}))-f(x_{k})\le \sigma \alpha _{k} \left( g(\mathrm {grad}f(x_{k}), d_{k})+\frac{1}{2} \alpha _{k} g(B_{k}[d_{k}], d_{k}) \right) . \end{aligned}$$

(4)

In comparison with the original Armijo line-search on Riemannian manifolds [4, 5], there are some advantages of the new inexact line-search. For example, let $\alpha _{k}$ denote the step size defined by the original Armijo line-search and $\alpha '_{k}$ denote the step size defined by the new inexact line-search; then, it is easy to see that $\alpha _{k}<\alpha '_{k}$.

Now we present a related descent method with the new inexact line-search on Riemannian manifolds for the minimization problem (3) as follows.

Algorithm 2.1

(Descent Method with New Inexact Line-search)

Step 1. :

Given $x_{0}\in M$, initial Hessian approximation $B_{0}$, which is symmetric positive definite with respect to the metric g, $k:=0$;

Step 2. :

If $\Vert \mathrm {grad}f(x_{k})\Vert =0$, then stop. Else go to step 3;

Step 3. :

Set $x_{k+1}=R_{x_{k}}(\alpha _{k}d_{k})$, where $d_{k}$ is a descent direction with $g(\mathrm {grad}f(x_{k}), d_{k})<0$, $\alpha _{k}$ is defined by the new inexact line-search on Riemannian manifolds;

Step 4. :

Define $p_{k}=\mathrm {grad}f(x_{k+1})-\mathscr {L}(x_{k}, x_{k+1})\mathrm {grad}f(x_{k})$ and modify $B_{k}$ as $B_{k+1}$ by using BFGS quasi-Newton algorithm or other quasi-Newton algorithms (see, for example, [6, 13]);

Step 5. :

Set $k: =k+1$ and go to step 2.

Remark 2.1

If M is a Riemannian manifold with nonnegative curvature, then by Proposition 5.4.1 in [22], the exponential mapping on M induced by $\nabla$ is a retraction R, and the parallel transport is isometric vector transport. Furthermore, if $d_{k}=-\mathrm {grad}f(x_{k})$ and $B_{k}=I$ (I denotes the unit matrix), then from (4), we get

$$\begin{aligned} f(x_{k+1})-f(x_{k})\le \sigma \alpha _{k} \left( \frac{1}{2}\alpha _{k}-1 \right) \Vert \mathrm {grad}f(x_{k})\Vert ^{2}. \end{aligned}$$

In this case, the descent method with new inexact line-search on Riemannian manifolds is a generalization of the steepest descent method with Armijo line-search in [4].

From Lemma 5.2.1 and Lemma 5.2.2 in [31], and the definition of $\mathscr {L}(.,.)$, we obtain the following result.

Lemma 2.1

Suppose that the function $f:M\rightarrow \mathbb {R}$ is twice continuously differentiable on a set $S\subset M$. Then, there exists a constant $L_{0}>0$ such that, for all $x, y\in S$,

$$\begin{aligned} \Vert \mathscr {L}(x,y)\mathrm {grad}f(x)-\mathrm {grad}f(y)\Vert \le L_{0}\Vert R^{-1}_{x}y\Vert . \end{aligned}$$

(5)

4 Global Convergence

In this section, we study the global convergence property of the descent method with new inexact line-search on Riemannian manifolds under some appropriate assumptions.

Definition 3.1

The matrix $B_{k}$ is said to be uniformly positive definite, iff there exist constants $m'$ and $\overline{m}$ such that $0<m'\le \overline{m}$ and for any $k\in \mathbb {N}$,

$$\begin{aligned} m'\Vert d\Vert ^{2}\le g(B_{k}[d],d)\le \overline{m}\Vert d\Vert ^{2}, \quad \forall d\in T_{x_{k}}M. \end{aligned}$$

(6)

Proposition 3.1

Assume that f is twice continuously differentiable on M, $B_{k}$ is uniformly positive definite, $d_{k}$ is a descent direction, and $\{x_{k}\}$ is the sequence generated by Algorithm 2.1. Then, there exists $\tau >0$ such that

$$\begin{aligned} f(x_{k})-f(x_{k+1}) \ge \tau \left( \frac{g(\mathrm {grad}f(x_{k}), d_{k})}{\Vert d_{k}\Vert } \right) ^{2}, \quad \forall k\in \mathbb {N}. \end{aligned}$$

(7)

Proof

Let $K_{1} = \{ k \in \mathbb {N} : \alpha _{k}=s_{k}\}$ and $K_{2} = \{ k \in \mathbb {N} : \alpha _{k}<s_{k}\}$. The proof is divided into two parts.

Part 1. If $k\in K_{1}$, then by (4) and (6), we have

$$\begin{aligned} f(x_{k})-f(x_{k+1})\ge & {} -\alpha _{k}\sigma \left( g(\mathrm {grad}f(x_{k}), d_{k}) +\frac{1}{2}\alpha _{k}g(B_{k}[d_{k}],\alpha _{k}) \right) \\= & {} \frac{\sigma g (\mathrm {grad}f(x_{k}), d_{k})}{g(B_{k}[d_{k}],\alpha _{k})}(g(\mathrm {grad}f(x_{k}),d_{k})\\&-\frac{1}{2}\frac{g(\mathrm {grad}f(x_{k}), d_{k})}{g(B_{k}[d_{k}],\alpha _{k})}g(B_{k}[d_{k}],\alpha _{k}))\\\ge & {} \frac{\sigma }{2\overline{m}} \left( \frac{ g(\mathrm {grad}f(x_{k}), d_{k})}{\Vert d_{k}\Vert } \right) ^{2}, \quad \forall k\in K_{1}. \end{aligned}$$

Thus,

$$\begin{aligned} f(x_{k})-f(x_{k+1})\ge \frac{\sigma }{2\overline{m}} \left( \frac{g(\mathrm {grad}f(x_{k}), d_{k})}{\Vert d_{k}\Vert } \right) ^{2}, \quad \forall k\in K_{1}. \end{aligned}$$

(8)

Part 2. If $k\in K_{2}$, then $\alpha _{k}\beta ^{-1}\in \{s_{k}, s_{k}\beta , s_{k}\beta ^{2},\ldots \}$. This implies that (4) does not hold, and so,

$$\begin{aligned}&f(x_{k})-f(R_{x_{k}}(\alpha _{k}\beta ^{-1}d_{k})) \nonumber \\&\quad < -\,\sigma \alpha _{k}\beta ^{-1}(g(\mathrm {grad}f(x_{k}), d_{k}) +\frac{1}{2}\alpha _{k}\beta ^{-1} g(B_{k}[d_{k}],d_{k})), \quad \forall k\in K_{2}. \end{aligned}$$

(9)

Define $m(t)=f(R_{x_{k}}(td_{k}))$. By using mean value theorem on the left-hand side of the above inequality, there exists $\theta _{k} \in \, ]0,1[$ such that

$$\begin{aligned}&f(x_{k})-f(R_{x_{k}}(\alpha _{k}\beta ^{-1}d_{k}))\\&\quad = m(0)-m(\alpha _{k}\beta ^{-1})\\&\quad =\frac{\mathrm {d}m(\theta _{k}\alpha _{k}\beta ^{-1})}{\mathrm {d}t}(0-\alpha _{k}\beta ^{-1})\\&\quad = -\,\alpha _{k}\beta ^{-1} g \left( \mathrm {grad}f(R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k})), \mathrm {D}R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k})[d_{k}] \right) \\&\quad = -\,\alpha _{k}\beta ^{-1} g \left( \mathrm {grad}f(R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k})), \mathscr {L}({x_{k},R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k})})d_{k} \right) \\&\quad < -\,\sigma \alpha _{k}\beta ^{-1} \left( g(\mathrm {grad}f(x_{k}), d_{k}) +\frac{1}{2}\alpha _{k}\beta ^{-1} g(B_{k}[d_{k}], d_{k}) \right) , \quad \forall k\in K_{2}. \end{aligned}$$

This shows that

$$\begin{aligned}&g \left( \mathrm {grad}f(R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k})), \mathscr {L}({x_{k},R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k})})d_{k} \right) \nonumber \\&\quad > \sigma \left( g(\mathrm {grad}f(x_{k}), d_{k})+\frac{1}{2}\alpha _{k}\beta ^{-1} g(B_{k}[d_{k}], d_{k}) \right) . \end{aligned}$$

(10)

Noting that

$$\begin{aligned} \Vert \mathscr {L}(x_{k},R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k}))d_{k}\Vert =\Vert d_{k}\Vert , \end{aligned}$$

it follows from Lemma 2.1 that there exists $L_{0}>0$ such that

$$\begin{aligned}&g \big ( \mathrm {grad}f(R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k}))\\&\qquad -\mathscr {L}(x_{k},R_{x_{k}}(\theta _{k}\alpha _{k} \beta ^{-1}d_{k}))\mathrm {grad}f(x_{k}), \mathscr {L}(x_{k},R_{x_{k}}(\theta _{k}\alpha _{k} \beta ^{-1}d_{k}))d_{k} \big )\\&\quad \le \Vert \mathrm {grad}f(R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k})) -\mathscr {L}(x_{k},R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k})) \mathrm {grad}f(x_{k})\Vert \Vert d_{k}\Vert \\&\quad \le L_{0}\Vert R^{-1}_{x_{k}}R_{x_{k}}(\theta _{k}\alpha _{k} \beta ^{-1}d_{k})\Vert \Vert d_{k}\Vert \\&\quad \le L_{0}\alpha _{k}\beta ^{-1}\Vert d_{k}\Vert ^{2}. \end{aligned}$$

This together with (10) implies that

$$\begin{aligned}&L_{0}\alpha _{k}\beta ^{-1}\Vert d_{k}\Vert ^{2}\\&\quad \ge g \big ( \mathrm {grad}f(R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k}))\\&\qquad -\,\mathscr {L}(x_{k},R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k}))\mathrm {grad}f(x_{k}), \mathscr {L}(x_{k},R_{x_{k}}(\theta _{k}\alpha _{k}\beta ^{-1}d_{k}))d_{k} \big )\\&\quad>\sigma (g(\mathrm {grad}f(x_{k}), d_{k})+\frac{1}{2}\alpha _{k}\beta ^{-1} g(B_{k}[ d_{k}], d_{k})) -g(\mathrm {grad}f(x_{k}),d_{k})\\&\quad >(\sigma -1)g(\mathrm {grad}f(x_{k}), d_{k}), \quad \forall k\in K_{2}. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \alpha _{k}>\frac{\beta (\sigma -1)}{L_{0}}\cdot \frac{g(\mathrm {grad}f(x_{k}), d_{k})}{\Vert d_{k}\Vert ^{2}}, \quad \forall k\in K_{2}. \end{aligned}$$

Let

$$\begin{aligned} \alpha '_{k}=\frac{\beta (\sigma -1)}{L_{0}}\cdot \frac{g(\mathrm {grad}f(x_{k}), d_{k})}{\Vert d_{k}\Vert ^{2}}. \end{aligned}$$

Then,

$$\begin{aligned} \alpha '_{k}<\alpha _{k}<s_{k}. \end{aligned}$$

(11)

Now, from (4) and (11), one has

$$\begin{aligned} f(x_{k})-f(x_{k+1})\ge & {} -\,\sigma \alpha _{k} \left( g(\mathrm {grad}f(x_{k}), d_{k}) +\frac{1}{2}\alpha _{k}g(B_{k}[d_{k}], d_{k}) \right) \\\ge & {} -\,\sigma \max _{\alpha '_{k}\le \alpha \le s_{k}} \left\{ \alpha \left( g(\mathrm {grad}f(x_{k}), d_{k})+\frac{1}{2}\alpha g(B_{k}[d_{k}],d_{k}) \right) \right\} \\= & {} -\,\sigma \alpha '_{k} \left( g(\mathrm {grad}f(x_{k}), d_{k}) +\frac{1}{2}\alpha _{k}g(B_{k}[d_{k}], d_{k}) \right) \\\ge & {} -\,\sigma \alpha '_{k}g(\mathrm {grad}f(x_{k}), d_{k})-\frac{\sigma }{2}\alpha '_{k}s_{k}g(B_{k}[d_{k}], d_{k})\\= & {} \frac{\beta \sigma (1-\sigma )}{2L_{0}}\left( \frac{g(\mathrm {grad}f(x_{k}), d_{k})}{\Vert d_{k}\Vert }\right) ^{2}, \quad \forall k\in K_{2}. \end{aligned}$$

Thus,

$$\begin{aligned} f(x_{k})-f(x_{k+1}) \ge \frac{\beta \sigma (1-\sigma )}{2L_{0}}\left( \frac{g(\mathrm {grad}f(x_{k}), d_{k})}{\Vert d_{k}\Vert }\right) ^{2}, \quad \forall k\in K_{2}. \end{aligned}$$

(12)

Let

$$\begin{aligned} \tau =\min \left\{ \frac{\sigma }{2\overline{m}}, \frac{\beta \sigma (1-\sigma )}{2L_{0}}\right\} . \end{aligned}$$

By (8) and (12), we obtain

$$\begin{aligned} f(x_{k})-f(x_{k+1})\ge \tau \left( \frac{g(\mathrm {grad}f(x_{k}), d_{k})}{\Vert d_{k}\Vert }\right) ^{2}, \quad \forall k\in \mathbb {N}. \end{aligned}$$

This completes the proof. $\square$

Corollary 3.1

Suppose that all the assumptions of Proposition 3.1 are satisfied and $d_{k}$ satisfies

$$\begin{aligned} \cos \theta _{k}=\frac{-g(\mathrm {grad}f(x_{k}),d_{k})}{\Vert \mathrm {grad}f(x_{k})\Vert \Vert d_{k}\Vert }\ge \mu , \end{aligned}$$

(13)

where $0<\mu \le 1$ is a constant and $\theta _{k}$ denotes the angle between $-\mathrm {grad}f(x_{k})$ and $d_{k}$. Then,

$$\begin{aligned} f(x_{k})-f(x_{k+1})\ge \tau \mu ^{2}\Vert \mathrm {grad}f(x_{k})\Vert ^{2}, \quad \forall k\in \mathbb {N}. \end{aligned}$$

Proof

It follows from (13) that

$$\begin{aligned} g^{2}(\mathrm {grad}f(x_{k}), d_{k})\ge \mu ^{2}\Vert \mathrm {grad}f(x_{k})\Vert ^{2}\Vert d_{k}\Vert ^{2}. \end{aligned}$$

This together with (7) implies that

$$\begin{aligned} f(x_{k})-f(x_{k+1})\ge \tau \mu ^{2}\Vert \mathrm {grad}f(x_{k})\Vert ^{2}, \quad \forall k\in \mathbb {N}. \end{aligned}$$

This completes the proof. $\square$

Theorem 3.1

Suppose that all the assumptions of Corollary 3.1 are satisfied. Then,

$$\begin{aligned} \sum _{k=1}^{+\infty }\Vert \mathrm {grad}f(x_{k})\Vert ^{2}<+\infty , \end{aligned}$$

and thus,

$$\begin{aligned} \lim _{k\rightarrow +\infty }\Vert \mathrm {grad}f(x_{k})\Vert =0. \end{aligned}$$

(14)

Proof

Since f has a lower bound on M, by Corollary 3.1, the result follows. $\square$

Remark 3.1

Theorem 3.1 shows that all accumulation points of the sequence $\{x_{k}\}$ generated by Algorithm 2.1 are stationary points. Moreover, if we consider $M = \mathbb {R}^{n}$ and $R_{x}(\eta ) = x+\eta$, then Theorem 3.1 reduces to Corollary 3.4 in [17].

5 Convergence Rate

In this section, we analyze the convergence rate, such as R-linear convergence rate, superlinear convergence rate and quadratic convergence rate, of the descent method with new inexact line-search on Riemannian manifolds.

Definition 4.1

Let $\{x_{k}\}$ be a sequence converging to $x^*$. The convergence is said to be

• (a) R-linear, iff there exist a constant $0\le \theta <1$ and a positive integer N such that

  $$\begin{aligned}{}[d(x_{k},x^*)]^{\frac{1}{k}}\le \theta , \quad \forall k>N; \end{aligned}$$

• (b) superlinear, iff there exist a sequence $\{\alpha _{k}\}$ converging to 0 and a positive integer N such that

  $$\begin{aligned} d(x_{k+1}, x^*)\le \alpha _{k} d(x_{k},x^*), \quad \forall k>N; \end{aligned}$$

• (c) quadratic, iff there exist a constant $\theta \ge 0$ and a positive integer N such that

  $$\begin{aligned} d(x_{k+1}, x^*)\le \theta d^{2}(x_{k},x^*), \quad \forall k>N. \end{aligned}$$

The convergence rate depends on the property of uniformly retraction-convexity, which is defined as follows.

Definition 4.2

For a function $f:M\rightarrow \mathbb {R}$ on the Riemannian manifold M with the retraction R, define the function $m_{x,\eta }(t)=f(R_{x}(t\eta ))$ for $x\in M$ and $\eta \in T_{x}M$. The function f is said to be uniformly retraction-convex on $S\subset M$, iff $m_{x,\eta }(t)$ is uniformly convex, i.e., there exists a constant $c>0$ such that

$$\begin{aligned} \alpha m_{x,\eta }(t_{1})+(1-\alpha )m_{x,\eta }(t_{2})-m_{x,\eta }(t_{2}+\alpha (t_{1}-t_{2})) \ge c\alpha (1-\alpha )(t_{1}-t_{2})^{2}, \end{aligned}$$

for all $x\in S$, $\eta \in T_{x}M$ with $\Vert \eta \Vert =1$, $\alpha \in \, ]0,1[$ and $t_{1}, t_{2}\ge 0$ such that $R_{x}(\varsigma \eta )\in S$ for all $\varsigma \in [0, \max (t_{1}, t_{2})]$.

Remark 4.1

From Section 3.4 in [32], if there exists a constant $c>0$ such that $\frac{\mathrm {d}^{2}m_{x,\eta }(t)}{\mathrm {d}t^{2}}\ge c$, then $m_{x,\eta }(t)$ is uniformly convex, and so f is uniformly retraction-convex. Next, we provide a sufficient condition to ensure the uniformly retraction-convexity of f. Assume that $x^*$ is a stationary point of f and the Hessian matrix of f at $x^{*}$, denoted by $\mathrm {Hess}f(x^{*})$, is positive definite. Then, from Lemma 3.1 in [6], there exist $c_{1}, c_{2}>0$, $\overline{t}>0$ and a neighborhood N of $x^{*}$ such that $c_{1}\le \frac{\mathrm {d}^{2}m_{x,\eta }(t)}{\mathrm {d}t^{2}}\le c_{2}$ for all $x\in N$ and $t\le \overline{t}$. Thus, f is uniformly retraction-convex on a neighborhood of $x^{*}$.

Lemma 4.1

Assume that f is twice continuously differentiable and uniformly retraction-convex on M, and $x^*$ is a stationary point of f. Moreover, assume that

$$\begin{aligned} \frac{\mathrm {D}}{\mathrm {d}t}\mathrm {D}R_{x}(t\eta )[\eta ]=0, \quad \forall x\in M, \eta \in T_{x}M, \end{aligned}$$

(15)

where $\mathrm {D}/\mathrm {d}t$ denotes the covariant derivative along the curve $t\mapsto R_{x}(t\eta )$ (see Chapter 2 in [33]). Then, there exist constants $m'$ and $\overline{m}$ such that $0<m'\le \overline{m}$ and

$$\begin{aligned} m'\Vert \eta \Vert ^{2}\le g(\mathrm {Hess}f(x)[\eta ],\eta )\le \overline{m}\Vert \eta \Vert ^{2}, \quad \forall x\in M,\eta \in T_{x}M; \end{aligned}$$

(16)

and thus,

$$\begin{aligned}&\frac{1}{2}m'\Vert R_{x^*}^{-1}x\Vert ^{2}\le f(x)-f(x^*)\le \frac{1}{2}\overline{m}\Vert R_{x^*}^{-1}x\Vert ^{2}, \quad \forall x\in M; \end{aligned}$$

(17)

$$\begin{aligned}&m'\Vert R_{x}^{-1}y\Vert ^{2}\le g(\mathscr {L}(y,x)\mathrm {grad}f(y)-\mathrm {grad}f(x),R_{x}^{-1}y) \le \overline{m}\Vert R_{x}^{-1}y\Vert ^{2}, \quad \forall x,y\in M; \nonumber \\\end{aligned}$$

(18)

$$\begin{aligned}&\Vert \mathrm {grad}f(x)\Vert \ge m'\Vert R_{x^*}^{-1}x\Vert , \quad \forall x\in M. \end{aligned}$$

(19)

Proof

Define $m_{x,\eta }(t)=f(R_{x}(t\eta ))$, for all $x\in M, \eta \in T_{x}M$ with $\Vert \eta \Vert =1$ and $t\ge 0$. Let $y=R_{x}(t\eta )$. Then, it is easy to see that $t\eta =R^{-1}_{x}y$. Since f is uniformly retraction-convex on M, there exists a constant $c>0$ such that

$$\begin{aligned} \alpha m_{x,\eta }(0)+(1-\alpha )m_{x,\eta }(t)-m_{x,\eta }(t+\alpha (0-t))\ge c\alpha (1-\alpha )t^{2}, \quad \forall \alpha \in \, ]0,1[. \end{aligned}$$

This implies that

$$\begin{aligned} m_{x,\eta }(0)-m_{x,\eta }(t)\ge & {} \lim _{\alpha \rightarrow 0} \left\{ \frac{m_{x,\eta }(t+\alpha (0-t))-m_{x,\eta }(t)}{\alpha }+c(1-\alpha )t^{2} \right\} \nonumber \\= & {} g(\mathrm {grad}f(R_{x}(t\eta )), (-t)\mathrm {D}R_{x}(t\eta )[\eta ])+ct^{2}\nonumber \\= & {} g(\mathrm {grad}f(R_{x}(t\eta )), \mathscr {L}(x,R_{x}(t\eta ))(-t\eta ))+ct^{2}. \end{aligned}$$

(20)

By the similar argument, we also have

$$\begin{aligned} m_{x,\eta }(t)-m_{x,\eta }(0)\ge g(\mathrm {grad}f(x), t\eta )+ct^{2}. \end{aligned}$$

(21)

Combining (20) and (21), we get

$$\begin{aligned} g(\mathrm {grad}f(R_{x}(t\eta )),-\mathscr {L}(x, R_{x}(t\eta ))t\eta )+g(\mathrm {grad}f(x), t\eta )+2ct^{2}\le 0. \end{aligned}$$

Hence,

$$\begin{aligned} g(\mathscr {L}(y,x)\mathrm {grad}f(y)-\mathrm {grad}f(x),\eta )\ge 2ct\Vert \eta \Vert ^2. \end{aligned}$$

(22)

Clearly,

$$\begin{aligned} \frac{\mathrm {d}m_{x,\eta }(t)}{\mathrm {d}t}= & {} g(\mathrm {grad}f(R_{x}(t\eta )), \mathrm {D}R_{x}(t\eta )[\eta ]) \nonumber \\= & {} g(\mathrm {grad}f(y), \mathscr {L}(x,y)\eta ) \nonumber \\= & {} g(\mathscr {L}(y,x)\mathrm {grad}f(y), \eta ), \end{aligned}$$

(23)

and

$$\begin{aligned} \frac{\mathrm {d}m_{x,\eta }(0)}{\mathrm {d}t}=g(\mathrm {grad}f(x), \eta ). \end{aligned}$$

(24)

Then, it follows from (23) that

$$\begin{aligned} \frac{\mathrm {d}^{2}m_{x,\eta }(t)}{\mathrm {d}t^{2}}= & {} g \left( \mathrm {Hess}f(R_{x}(t\eta ))[\mathrm {D}R_{x}(t\eta )[\eta ]],\mathrm {D}R_{x}(t\eta )[\eta ] \right) \\&+\,g \left( \mathrm {grad}f(R_{x}(t\eta )), \frac{\mathrm {D}}{\mathrm {d}t}\mathrm {D}R_{x}(t\eta )[\eta ] \right) , \end{aligned}$$

Since $\frac{\mathrm {D}}{\mathrm {d}t}\mathrm {D}R_{x}(t\eta )[\eta ]=0$, we have

$$\begin{aligned} \frac{\mathrm {d}^{2}m_{x,\eta }(t)}{\mathrm {d}t^{2}} =g(\mathrm {Hess}f(R_{x}(t\eta ))[\mathrm {D}R_{x}(t\eta )[\eta ]],\mathrm {D}R_{x}(t\eta )[\eta ]). \end{aligned}$$

(25)

Thus, by (22), (23), (24) and (25), we have

$$\begin{aligned} g(\mathrm {Hess}f(x)[\eta ],\eta )= & {} \frac{\mathrm {d}^{2}m_{x,\eta }(0)}{\mathrm {d}t^{2}}\nonumber \\= & {} \lim _{t\rightarrow 0}\frac{g(\mathscr {L}(y,x)\mathrm {grad}f(y),\eta )-g(\mathrm {grad}f(x),\eta )}{t}\nonumber \\= & {} \lim _{t\rightarrow 0}\frac{g(\mathscr {L}(y,x)\mathrm {grad}f(y)-\mathrm {grad}f(x),\eta )}{t} \ge 2c\Vert \eta \Vert ^{2}.\qquad \end{aligned}$$

(26)

Since f is twice continuously differentiable on M, from Lemma 2.1, for $t>0$, we obtain

$$\begin{aligned} \frac{g(\mathscr {L}(y,x)\mathrm {grad}f(y)-\mathrm {grad}f(x),\eta )}{t}\le & {} \frac{\Vert \mathscr {L}(y,x)\mathrm {grad}f(y)-\mathrm {grad}f(x)\Vert \Vert \eta \Vert }{t}\nonumber \\\le & {} \frac{L_{0}\Vert t\eta \Vert \Vert \eta \Vert }{t}=L_{0}\Vert \eta \Vert ^{2}. \end{aligned}$$

(27)

Taking $2c=m'$ and $L_{0}=\overline{m}$, then, it follows from (26) and (27) that

$$\begin{aligned} m'\Vert \eta \Vert ^{2}\le g(\mathrm {Hess}f(x)[\eta ],\eta )\le \overline{m}\Vert \eta \Vert ^{2}, \quad \forall x\in M,\eta \in T_{x}M. \end{aligned}$$

(28)

Thus, (16) holds.

For any $x\in M$ and $x\ne x^*$, let $z=\Vert R^{-1}_{x^*}x\Vert$ and $p=\frac{R^{-1}_{x^*}x}{z}$. Define

$$\begin{aligned} m_{x^*, p}(t)=f(R_{x^*}(tp)). \end{aligned}$$

From Taylor theorem, we have

$$\begin{aligned} m_{x^{*},p}(z)-m_{x^*,p}(0) =\frac{\mathrm {d}m_{x^*,p}(0)}{\mathrm {d}t}(z-0)+\int ^{1}_{0}(1-t) \frac{\mathrm {d}^{2}m_{x^*,p}(tz)}{\mathrm {d}t^{2}}z^{2}\mathrm {d}t . \end{aligned}$$

(29)

Noting that

$$\begin{aligned} \frac{\mathrm {d}^{2}m_{x^*,p}(tz)}{\mathrm {d}t^{2}} =g(\mathrm {Hess}f(R_{x^*}(tzp))[\mathrm {D}R_{x^*}(tzp)[p]],\mathrm {D}R_{x^*}(tzp)[p]), \end{aligned}$$

then, it follows from (29) that

$$\begin{aligned} m_{x^*,p}(z)-m_{x^*,p}(0)= & {} g(\mathrm {grad}f(x^*),R^{-1}_{x^*}x) +\int ^{1}_{0}(1-t)g(\mathrm {Hess}f(R_{x^*}(tR^{-1}_{x^*}x))\nonumber \\&\times [\mathscr {L}(x^*, R_{x^*}(tR^{-1}_{x^*}x))R^{-1}_{x^*}x], \mathscr {L}(x^*, R_{x^*}(tR^{-1}_{x^*}x))R^{-1}_{x^*}x)\mathrm {d}t.\nonumber \\ \end{aligned}$$

(30)

By combining (28) and (30), we obtain

$$\begin{aligned} \frac{1}{2}m'\Vert R^{-1}_{x^*}x\Vert ^{2}= & {} \int ^{1}_{0}(1-t)m'\Vert \mathscr {L}(x^*, R_{x^*} (tR^{-1}_{x^*}x))R^{-1}_{x^*}x\Vert ^2\nonumber \\\le & {} f(x)-f(x^*)\le \int ^{1}_{0}(1-t)\overline{m}\Vert \mathscr {L}(x^*, R_{x^*} (tR^{-1}_{x^*}x))R^{-1}_{x^*}x\Vert ^2\nonumber \\= & {} \frac{1}{2}\overline{m}\Vert R^{-1}_{x^*}x\Vert ^{2}. \end{aligned}$$

(31)

Hence, (17) holds.

For any $x,y\in M$ and $x\ne y$, let $\widetilde{z}=\Vert R^{-1}_{x}y\Vert$ and $\widetilde{p}=\frac{R^{-1}_{x}y}{\widetilde{z}}$. Define $m_{x,p}(t)=f(R_{x}(t\widetilde{p}))$. Then, we have

$$\begin{aligned} \frac{\mathrm {d}m_{x,p}(\widetilde{z})}{\mathrm {d}t} -\frac{\mathrm {d}m_{x,p}(0)}{\mathrm {d}t} =\int ^{\widetilde{z}}_{0}\frac{\mathrm {d}^{2}m_{x,p}(t)}{\mathrm {d}t^{2}}\mathrm {d}t. \end{aligned}$$

Therefore,

$$\begin{aligned}&g(\mathrm {grad}f(y), \mathscr {L}(x,y)\widetilde{p})-g(\mathrm {grad}f(x), \widetilde{p})\nonumber \\&\quad =\int ^{\widetilde{z}}_{0}g(\mathrm {Hess}f(R_{x}(t\widetilde{p})) [\mathrm {D}R_{x}(t\widetilde{p})[\widetilde{p}]], \mathrm {D}R_{x}(t\widetilde{p})[\widetilde{p}])\mathrm {d}t, \end{aligned}$$

(32)

since

$$\begin{aligned} m'\Vert R^{-1}_{x}y\Vert= & {} \int ^{\widetilde{z}}_{0}m'\Vert \widetilde{p}\Vert ^{2}\mathrm {d}t \le \int ^{\widetilde{z}}_{0}g(\mathrm {Hess}f(R_{x}(t\widetilde{p})) [\mathrm {D}R_{x}(t\widetilde{p})[\widetilde{p}]],\mathrm {D}R_{x}(t\widetilde{p})[\widetilde{p}])\mathrm {d}t\\\le & {} \int ^{\widetilde{z}}_{0}\overline{m}\Vert \widetilde{p}\Vert ^{2}\mathrm {d}t =\overline{m}\Vert R^{-1}_{x}y\Vert . \end{aligned}$$

From (32) and the above inequality, we have

$$\begin{aligned} m'\Vert R^{-1}_{x}y\Vert ^{2}\le g(\mathscr {L}(y,x)\mathrm {grad}f(y)-\mathrm {grad}f(x),R_{x}^{-1}y)\le \overline{m}\Vert R^{-1}_{x}y\Vert ^{2}. \end{aligned}$$

Then, inequality (18) holds. Furthermore, we obtain

$$\begin{aligned} m'\Vert R^{-1}_{x}y\Vert \le \Vert \mathrm {grad}f(y)-\mathscr {L}(x,y)\mathrm {grad}f(x)\Vert . \end{aligned}$$

In particular, when $y=x$ and $x=x^*$, one has

$$\begin{aligned} m'\Vert R^{-1}_{x^*}x\Vert \le \Vert \mathrm {grad}f(x)\Vert . \end{aligned}$$

This completes the proof. $\square$

Remark 4.2

If the retraction $R_{x}$ is an exponential mapping, then from [22], assumption (15) holds. We further illustrate assumption (15) by the following example.

We consider the sphere $\mathbb {S}^{n-1} := \{ x \in \mathbb {R}^{n} : x^{\top } x = 1\}$ with its structure of Riemannian submanifold of the Euclidean space $\mathbb {R}^{n}$. The projection retraction $R_{x}$ is defined by

$$\begin{aligned} R_{x}(\eta )=(x+\eta )/\Vert x+\eta \Vert , \quad \forall x\in \mathbb {S}^{n-1}, \, \eta \in T_{x}\mathbb {S}^{n-1}. \end{aligned}$$

The chosen isomeric vector transport $\mathscr {T}$ on $\mathbb {S}^{n-1}$ is

$$\begin{aligned} \mathscr {T}_{R_{x}(\eta )}\xi = \xi -\frac{2y^{\top }\xi }{\Vert x+y\Vert ^{2}}(x+y), \quad \forall x\in M, \, \eta ,\xi \in T_{x}\mathbb {S}^{n-1}, \end{aligned}$$

where $y=R_{x}(\eta )$. For further details, see, for example [22, 31]. From Section 8.1 in [22] and Section 5 in [34], we obtain

$$\begin{aligned} \frac{\mathrm {D}}{\mathrm {d}t}\mathrm {D}R_{x}(t\eta )[\eta ] =\frac{\mathrm {D}}{\mathrm {d}t}\mathscr {T}_{R_{x}(t\eta )}\eta =0, \quad \forall x\in M, \eta \in T_{x}\mathbb {S}^{n-1}. \end{aligned}$$

Thus, assumption (15) holds on $\mathbb {S}^{n-1}$ for the projection retraction.

Lemma 4.2

[13] Let $S\subset M$ be an open set, $x\in S$ and the retraction $R_{x}:T_{x}M\rightarrow M$ has equicontinuous derivatives at x in the sense that

$$\begin{aligned} \forall \epsilon>0, \, \exists \delta >0, \forall x\in S: \Vert v\Vert<\delta \quad \Rightarrow \quad \Vert P_{\gamma [x,R_{x}(v)]}\mathrm {D}R_{x}(0)-\mathrm {D}R_{x}(v)\Vert <\epsilon . \end{aligned}$$

Then, for any $\epsilon >0$, there exists $\epsilon '>0$ such that, for all $x\in S$ and $v,w\in T_{x}M$ with $\Vert v\Vert ,\Vert w\Vert <\epsilon '$,

$$\begin{aligned} (1-\epsilon )\Vert w-v\Vert \le d(R_{x}(v),R_{x}(w))\le (1+\epsilon )\Vert w-v\Vert . \end{aligned}$$

Theorem 4.1

Suppose that all the assumptions of Lemma 4.1 are satisfied, $B_{k}$ is uniformly positive definite, and $d_{k}$ satisfies (13). Furthermore, assume that $\mathrm {D}R_{x_{k}}$ is equicontinuous on a neighborhood U of the stationary point $x^*$. Then, the sequence $\{x_{k}\}$ generated by Algorithm 2.1 converges R-linearly to $x^*$.

Proof

From (14) and (19), we have

$$\begin{aligned} \lim _{k\rightarrow +\infty }x_{k}=x^*. \end{aligned}$$

It follows from Corollary 3.1, (17) and (19) that

$$\begin{aligned} f(x_{k})-f(x_{k+1})\ge & {} \tau \mu ^{2}\Vert \mathrm {grad}f(x_{k})\Vert ^{2}\ge \tau \mu ^{2} m'^{2}\Vert R^{-1}_{x^*}x_{k}\Vert ^{2}\\ {}\ge & {} \frac{2\tau \mu ^{2} m'^{2}}{\overline{m}}(f(x_{k})-f(x^*)). \end{aligned}$$

Set $\theta =\sqrt{2\frac{\tau \mu ^{2}m'^{2}}{\overline{m}}} = m'\sqrt{2\frac{\tau \mu ^{2}}{\overline{m}}}$. Then,

$$\begin{aligned} f(x_{k})-f(x_{k+1})\ge \theta ^{2}(f(x_{k})-f(x^*)). \end{aligned}$$

(33)

We can prove that $\theta <1$. Indeed, since f is twice continuously differentiable on M, it follows from Lemma 2.1 that there exists a constant $L_{0}>0$ such that

$$\begin{aligned} \Vert \mathscr {L}(y,x)\mathrm {grad}f(y)-\mathrm {grad}f(x)\Vert \le L_{0}\Vert R^{-1}_{x}y\Vert , \quad \forall x,y \in M. \end{aligned}$$

Then,

$$\begin{aligned} g(\mathscr {L}(y,x)\mathrm {grad}f(y)\!-\!\mathrm {grad}f(x), R^{-1}_{x}y)\le & {} \Vert \mathscr {L}(y,x)\mathrm {grad}f(y)-\mathrm {grad}f(x)\Vert \Vert R^{-1}_{x}y\Vert \\\le & {} L_{0}\Vert R^{-1}_{x}y\Vert ^{2}, \quad \forall x,y\in M. \end{aligned}$$

Taking $L_{0}= \overline{m}$, then by the definition of $\tau$ in the proof of Proposition 3.1, we obtain

$$\begin{aligned} \theta ^{2}=\frac{2\tau \mu ^{2} m'^{2}}{\overline{m}}\le \frac{2\tau m'^{2}}{\overline{m}} \le \frac{2m'^{2}}{\overline{m}}\cdot \frac{\beta \sigma (1-\sigma )}{2L_{0}}\le \beta \sigma (1-\sigma )<1. \end{aligned}$$

Set $\omega =\sqrt{1-\theta ^{2}}$. Then, $\omega <1$, and from (33), we obtain

$$\begin{aligned}&f(x_{k+1})-f(x^*)\le (1-\theta ^{2})(f(x_{k})-f(x^*))\\&\quad =\omega ^{2}(f(x_{k})-f(x^*))\le \cdots \le \omega ^{2(k+1)}(f(x_{0})-f(x^*)). \end{aligned}$$

From (17), we have

$$\begin{aligned} \Vert R^{-1}_{x^*}x_{k+1}\Vert ^{2}\le \frac{2}{m'}(f(x_{k+1})-f(x^*)) \le \frac{2\omega ^{2(k+1)}}{m'}(f(x_{0})-f(x^*)). \end{aligned}$$

(34)

It follows from Lemma 4.2 that, for k sufficiently large,

$$\begin{aligned} d(x_{k+1}, x^*)= & {} d(R_{x^*}(R^{-1}_{x^*}x_{k+1}), R_{x^*}(0_{x^*}))\\\le & {} \frac{3}{2}\Vert R^{-1}_{x^*}x_{k+1}-0_{x^*}\Vert \\= & {} \frac{3}{2}\Vert R^{-1}_{x^*}x_{k+1}\Vert . \end{aligned}$$

By (34), we get

$$\begin{aligned} \lim _{k\rightarrow +\infty }[d(x_{k+1},x^*)]^{\frac{1}{k+1}}\le & {} \lim _{k\rightarrow +\infty } \left[ \frac{3}{2}\Vert R^{-1}_{x^*}x_{k+1}\Vert \right] ^{\frac{1}{k+1}}\\\le & {} \lim _{k\rightarrow +\infty } \left( \omega ^{k+1}\sqrt{\frac{2\times \frac{9}{4}(f(x_{0})-f(x^*))}{m'}} \right) ^{\frac{1}{k+1}} =\omega <1. \end{aligned}$$

Thus, $x_{k}$ converges R-linearly to $x^*$. This completes the proof. $\square$

In the following, we assume that

• (H) $B_{k}$ and $d_{k}$ generated by Algorithm 2.1 satisfy the following condition

  $$\begin{aligned} \lim _{k\rightarrow +\infty }\frac{\Vert B_{k}[d_{k}]-\mathscr {L}(x^*,x_{k}) (\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}])\Vert }{\Vert d_{k}\Vert }=0. \end{aligned}$$

Lemma 4.3

Suppose that all the assumptions of Lemma 4.1 are satisfied, $B_{k}$ is uniformly positive definite, $d_{k}=-B_{k}^{-1}\mathrm {grad}f(x_{k})$ and the assumption (H) holds. Then, there exists $k'\in \mathbb {N}$ such that

$$\begin{aligned} \alpha _{k}=1, \quad \forall k\ge k'. \end{aligned}$$

Proof

From (14) and (19), we have

$$\begin{aligned} \lim _{k\rightarrow +\infty }x_{k}=x^*. \end{aligned}$$

(35)

Since $B_{k}$ is uniformly positive definite, there exists a constant $q>0$ such that

$$\begin{aligned} \Vert d_{k}\Vert =\Vert -B_{k}^{-1}\mathrm {grad}f(x_{k})\Vert \le \Vert B_{k}^{-1}\Vert \Vert \mathrm {grad}f(x_{k})\Vert \le q\Vert \mathrm {grad}f(x_{k})\Vert . \end{aligned}$$

Then, from (14) and the above inequality, we obtain

$$\begin{aligned} \lim _{k\rightarrow +\infty }\Vert d_{k}\Vert =0, \end{aligned}$$

(36)

and thus,

$$\begin{aligned} \lim _{k\rightarrow +\infty }R_{x_{k}}(td_{k})=x^*. \end{aligned}$$

(37)

Assumption (H) implies that

$$\begin{aligned}&\Vert g(B_{k}[d_{k}], d_{k})-g(\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}]), d_{k})\Vert \\&\quad =\Vert g(B_{k}[d_{k}]-\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}]), d_{k})\Vert \\&\quad \le \Vert B_{k}[d_{k}]-\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}])\Vert \Vert d_{k}\Vert \\&\quad =\Vert d_{k}\Vert o(\Vert d_{k}\Vert ), \end{aligned}$$

and thus,

$$\begin{aligned} g(B_{k}[d_{k}]-\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}]), d_{k}) =o(\Vert d_{k}\Vert ^{2}). \end{aligned}$$

(38)

Clearly,

$$\begin{aligned}&g(\mathrm {Hess}f(R_{x_{k}}(td_{k}))[\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}]\\&\qquad -\,\mathscr {L}(x^*,R_{x_{k}}(td_{k}))(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k}, x^*)d_{k}]),\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k})\\&\quad \le \Vert \mathrm {Hess}f(R_{x_{k}}(td_{k}))[\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}]\\&\qquad -\,\mathscr {L}(x^*,R_{x_{k}}(td_{k}))(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k}, x^*)d_{k}])\Vert \Vert d_{k}\Vert \\&\quad =\Vert \mathrm {Hess}f(R_{x_{k}}(td_{k}))[\mathscr {L}(x^*,R_{x_{k}}(td_{k}))(\mathscr {L}(x_{k},x^*)d_{k})]\\&\qquad -\,\mathscr {L}(x^*,R_{x_{k}}(td_{k}))(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k}, x^*)d_{k}])\Vert \Vert d_{k}\Vert \\&\quad =\Vert (\mathrm {Hess}f(R_{x_{k}}(td_{k}))\mathscr {L}(x^*,R_{x_{k}}(td_{k}))\\&\qquad -\,\mathscr {L}(x^*,R_{x_{k}}(td_{k}))\mathrm {Hess}f(x^*))[\mathscr {L}(x_{k}, x^*)d_{k}]\Vert \Vert d_{k}\Vert \\&\quad \le \Vert \mathrm {Hess}f(R_{x_{k}}(td_{k}))\mathscr {L}(x^*,R_{x_{k}}(td_{k}))\\&\qquad -\,\mathscr {L}(x^*,R_{x_{k}}(td_{k}))\mathrm {Hess}f(x^*)\Vert \Vert \mathscr {L}(x_{k}, x^*)d_{k}\Vert \Vert d_{k}\Vert \\&\quad =\Vert \mathrm {Hess}f(R_{x_{k}}(td_{k}))\mathscr {L}(x^*,R_{x_{k}}(td_{k})) -\mathscr {L}(x^*,R_{x_{k}}(td_{k}))\mathrm {Hess}f(x^*)\Vert \Vert d_{k}\Vert ^2. \end{aligned}$$

This together with (37) implies that, for k sufficiently large,

$$\begin{aligned}&g(\mathrm {Hess}f(R_{x_{k}}(td_{k}))[\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}] -\mathscr {L}(x^*,R_{x_{k}}(td_{k}))\\&\quad (\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k}, x^*)d_{k}]),\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}) =o(\Vert d_{k}\Vert ^2). \end{aligned}$$

Define $m(t)=f(R_{x_{k}}(td_{k}))$. By using Taylor theorem, (38) and the above equality, we obtain for k sufficiently large,

$$\begin{aligned}&m(1)-m(0)= \left. \frac{\mathrm {d}m(t)}{\mathrm {d}t} \right| _{t=0} +\int ^{1}_{0}(1-t) \frac{\mathrm {d}^{2}m}{\mathrm {d}t^{2}}(t)\mathrm {d}t\\&\quad =g(\mathrm {grad}f(x_{k}), d_{k})+\int ^{1}_{0}(1-t)g(\mathrm {Hess}f(R_{x_{k}}(td_{k}))[\mathrm {D}R_{x_{k}}(td_{k})[d_{k}]], \mathrm {D}R_{x_{k}}(td_{k})[d_{k}])\mathrm {d}t\\&\quad =g(\mathrm {grad}f(x_{k}), d_{k})+\frac{1}{2}g(B_{k}[d_{k}],d_{k})\\&\qquad +\int ^{1}_{0}(1-t)\{g(\mathrm {Hess}f(R_{x_{k}}(td_{k})) [\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}],\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k})\\&\qquad -\,g(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k}, x^*)d_{k}], \mathscr {L}(x_{k}, x^*)d_{k})\}\mathrm {d}t-\frac{1}{2}g(B_{k}[d_{k}],d_{k})\\&\qquad +\frac{1}{2}g(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k}, x^*)d_{k}],\mathscr {L}(x_{k}, x^*)d_{k})\\&\quad =g(\mathrm {grad}f(x_{k}), d_{k})+\frac{1}{2}g(B_{k}[d_{k}],d_{k})\\&\qquad +\int ^{1}_{0}(1-t)\{g(\mathrm {Hess}f(R_{x_{k}}(td_{k}))[\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}]\\&\qquad -\,\mathscr {L}(x^*,R_{x_{k}}(td_{k}))(\mathrm {Hess}f(x^*)[L(x_{k}, x^*)d_{k}]), \mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k})\}\mathrm {d}t\\&\qquad +\frac{1}{2}g(\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k}, x^*)d_{k}]) -B_{k}[d_{k}], d_{k})\\&\quad =g(\mathrm {grad}f(x_{k}), d_{k})+\frac{1}{2}g(B_{k}[d_{k}],d_{k})+o(\Vert d_{k}\Vert ^{2})\\&\quad =-\,\frac{1}{2}g(\mathrm {grad}f(x_{k}), B_{k}^{-1}\mathrm {grad}f(x_{k}))+o(\Vert d_{k}\Vert ^{2}). \end{aligned}$$

Thus, for k sufficiently large, we obtain

$$\begin{aligned} f(R_{x_{k}}(d_{k}))-f(x_{k})\le \sigma (g(\mathrm {grad}f(x_{k}),d_{k})+\frac{1}{2}g(B_{k}[d_{k}], d_{k})). \end{aligned}$$

This implies that there exists $k'>0$ such that

$$\begin{aligned} \alpha _{k}=1, \quad \forall k\ge k'. \end{aligned}$$

This completes the proof. $\square$

Theorem 4.2

Suppose that all the assumptions of Lemma 4.3 are satisfied, and $\mathrm {D}R_{x_{k}}$ is equicontinuous on a neighborhood U of the stationary point $x^*$. Then, the sequence $\{x_{k}\}$ generated by Algorithm 2.1 converges superlinearly to $x^*$.

Proof

From Lemma 4.3, we obtain that there exists $k'>0$ such that

$$\begin{aligned} x_{k+1}=R_{x_{k}}(d_{k}), \quad \forall k\ge k', \end{aligned}$$

where $d_{k}=-B^{-1}_{k}\mathrm {grad}f(x_{k})$. Let $\gamma$ be the curve defined by $\gamma (t)=R_{x_{k}}(td_{k})$. Then, we have

$$\begin{aligned}&\Vert P_{\gamma [R_{x_{k}}(td_{k}),x_{k}]}\mathrm {Hess}f(R_{x_{k}}(td_{k})) [\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}]\\&\qquad -\,\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*) [\mathscr {L}(x_{k},x^*)d_{k}])\Vert \\&\quad =\Vert (P_{\gamma [R_{x_{k}}(td_{k}),x_{k}]}\mathrm {Hess}f(R_{x_{k}}(td_{k}))\mathscr {L}(x^*, R_{x_{k}}(td_{k}))\\&\qquad -\,\mathscr {L}(x^*, x_{k})\mathrm {Hess}f(x^*))[\mathscr {L}(x_{k},x^*)d_{k}]\Vert \\&\quad \le \Vert P_{\gamma [R_{x_{k}}(td_{k}),x_{k}]}\mathrm {Hess}f(R_{x_{k}}(td_{k}))\mathscr {L}(x^*, R_{x_{k}}(td_{k}))\\&\qquad -\,\mathscr {L}(x^*, x_{k})\mathrm {Hess}f(x^*)\Vert \Vert d_{k}\Vert . \end{aligned}$$

It follows from (35) and (37) that, for k sufficiently large,

$$\begin{aligned}&\Vert P_{\gamma [R_{x_{k}}(td_{k}),x_{k}]}\mathrm {Hess}f(R_{x_{k}}(td_{k}))[\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}]\nonumber \\&\qquad -\,\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}])\Vert =o(\Vert d_{k}\Vert ). \end{aligned}$$

(39)

Noting that

$$\begin{aligned}&P_{\gamma [x_{k+1},x_{k}]}\mathrm {grad}f(x_{k+1})-\mathrm {grad}f(x_{k})\\&\quad =\int ^{1}_{0}P_{\gamma [R_{x_{k}}(td_{k}),x_{k}]}\mathrm {Hess}f(R_{x_{k}}(td_{k})) [\mathrm {D}R_{x_{k}}(td_{k})[d_{k}]]\mathrm {d}t\\&\quad =\int ^{1}_{0}P_{\gamma [R_{x_{k}}(td_{k}),x_{k}]}\mathrm {Hess}f(R_{x_{k}}(td_{k})) [\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}]\mathrm {d}t\\&\quad =\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}])\\&\qquad +\int ^{1}_{0}\{P_{\gamma [R_{x_{k}}(td_{k}),x_{k}]}\mathrm {Hess}f(R_{x_{k}}(td_{k})) [\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}]\\&\qquad -\,\mathscr {L}(x^*,x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}])\}\mathrm {d}t. \end{aligned}$$

Since $d_{k}=-B_{k}^{-1}\mathrm {grad}f(x_{k})$, we have $\mathrm {grad}f(x_{k})=-B_{k}d_{k}$ and

$$\begin{aligned}&P_{\gamma [x_{k+1},x_{k}]}\mathrm {grad}f(x_{k+1})\\&\quad =\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}])-B_{k}d_{k}\\&\qquad +\int ^{1}_{0}\{P_{\gamma [R_{x_{k}}(td_{k}),x_{k}]}\mathrm {Hess}f(R_{x_{k}}(td_{k})) [\mathscr {L}(x_{k},R_{x_{k}}(td_{k}))d_{k}]\\&\qquad -\,\mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}])\}\mathrm {d}t. \end{aligned}$$

Consequently, for k sufficiently large, it follows from (39) that

$$\begin{aligned}&\Vert P_{\gamma [x_{k+1},x_{k}]}\mathrm {grad}f(x_{k+1})\Vert \\&\quad \le \Vert \mathscr {L}(x^*, x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}])-B_{k}d_{k}\Vert +o(\Vert d_{k}\Vert ). \end{aligned}$$

By assumption (H), we have

$$\begin{aligned}&\lim _{k\rightarrow +\infty }\frac{\Vert \mathrm {grad}f(x_{k+1})\Vert }{\Vert d_{k}\Vert } \nonumber \\&\quad \le \lim _{k\rightarrow +\infty } \frac{\Vert \mathscr {L}(x^*,x_{k})(\mathrm {Hess}f(x^*)[\mathscr {L}(x_{k},x^*)d_{k}]) -B_{k}d_{k}\Vert +o(\Vert d_{k}\Vert )}{\Vert d_{k}\Vert }=0.\nonumber \\ \end{aligned}$$

(40)

From Lemma 4.2, we obtain for k sufficiently large,

$$\begin{aligned} \frac{1}{2}\Vert R^{-1}_{x^*}x_{k+1}\Vert \le d(x_{k+1},x^*) =d(R_{x^*}(R^{-1}_{x^*}x_{k+1}), R_{x^*}(0_{x^*}))\le \frac{3}{2}\Vert R^{-1}_{x^*}x_{k+1}\Vert , \end{aligned}$$

and

$$\begin{aligned} \frac{1}{2}\Vert R^{-1}_{x_{k}}x_{k+1}\Vert \le d(x_{k+1},x_{k}) = d(R_{x_{k}}(R^{-1}_{x_{k}}x_{k+1}), R_{x_{k}}(0_{x_{k}})) \le \frac{3}{2}\Vert R^{-1}_{x_{k}}x_{k+1}\Vert . \end{aligned}$$

This together with (19) implies that

$$\begin{aligned} \frac{\Vert \mathrm {grad}f(x_{k+1})\Vert }{\Vert d_{k}\Vert }\ge & {} \frac{m'\Vert R^{-1}_{x^*}x_{k+1}\Vert }{\Vert R^{-1}_{x_{k}}x_{k+1}\Vert } \ge \frac{m'\times \frac{2}{3}d(x_{k+1},x^*)}{2d(x_{k+1},x_{k})}\\\ge & {} \frac{m'\times \frac{1}{3}d(x_{k+1},x^*)}{d(x_{k+1},x^*)+d(x_{k},x^*)} = \frac{\frac{m'}{3}\frac{d(x_{k+1},x^*)}{d(x_{k},x^*)}}{1+\frac{d(x_{k+1},x^*)}{d(x_{k},x^*)}}. \end{aligned}$$

Consequently, from (40), we obtain

$$\begin{aligned} \lim _{k\rightarrow +\infty }\frac{d(x_{k+1},x^*)}{d(x_{k},x^*)}=0, \end{aligned}$$

which implies that $\{x_{k}\}$ converges superlinearly to $x^*$ . This completes the proof. $\square$

Theorem 4.3

Suppose that all the assumptions of Lemma 4.3 are satisfied, $B_{k}=\mathrm {Hess}f(x_{k})$ for k sufficiently large, and $DR_{x_{k}}$ is equicontinuous on a neighborhood U of the stationary point $x^*$. Moreover, assume there exists a constant $\widetilde{L}>0$ such that

$$\begin{aligned} \Vert \mathrm {Hess}f(y)-P_{\gamma [x,y]}\mathrm {Hess}f(x)\mathscr {L}(y,x)\Vert \le \widetilde{L}d(x,y), \quad \forall x,y\in U. \end{aligned}$$

Then, the sequence $\{x_{k}\}$ generated by Algorithm 2.1 converges quadratically to $x^*$ .

Proof

From Lemma 4.3, there exists $k'>0$ such that

$$\begin{aligned} x_{k+1}=R_{x_{k}}(d_{k}), \quad \forall k\ge k', \end{aligned}$$

where $d_{k}=-(\mathrm {Hess}f(x_{k}))^{-1}\mathrm {grad}f(x_{k})$. Let $\gamma$ be the curve defined by $\gamma (t)=R_{x_{k}}(tR^{-1}_{x_{k}}x^*)$. Then, it follows from Lemma 4.2 that, for k sufficiently large,

$$\begin{aligned}&\Vert \mathrm {Hess}f(x_{k})[d_{k}-R^{-1}_{x_{k}}x^*]\Vert \nonumber \\&\quad = \left\| P_{\gamma [x^*,x_{k}]}\mathrm {grad}f(x^*)-\mathrm {grad}f(x_{k}) -\mathrm {Hess}f(x_{k})[R^{-1}_{x_{k}}x^*] \right\| \nonumber \\&\quad = \left\| \int ^{1}_{0}P_{\gamma [R_{x_{k}}(tR^{-1}_{x_{k}}x^*),x_{k}]} \mathrm {Hess}f(R_{x_{k}}(tR^{-1}_{x_{k}}x^*))[\mathrm {D}R_{x_{k}}(tR^{-1}_{x_{k}}x^*) [R^{-1}_{x_{k}}x^*]]\mathrm {d}t \right. \nonumber \\&\qquad \left. -\,\mathrm {Hess}f(x_{k})[R^{-1}_{x_{k}}x^*] \right\| \nonumber \\&\quad \le \int ^{1}_{0}\Vert (\mathrm {Hess}f(R_{x_{k}}(tR^{-1}_{x_{k}}x^*)) -P_{\gamma [x_{k},R_{x_{k}}(tR^{-1}_{x_{k}}x^*)]}\mathrm {Hess}f(x_{k}) \mathscr {L}( R_{x_{k}}(tR^{-1}_{x_{k}}x^*),x_{k}))\nonumber \\&\qquad [\mathscr {L}(x_{k}, R_{x_{k}}(tR^{-1}_{x_{k}}x^*))R^{-1}_{x_{k}}x^*]\Vert \mathrm {d}t\nonumber \\&\quad \le \int ^{1}_{0}\Vert \mathrm {Hess}f(R_{x_{k}}(tR^{-1}_{x_{k}}x^*)) -P_{\gamma [x_{k},R_{x_{k}}(tR^{-1}_{x_{k}}x^*)]}\mathrm {Hess}f(x_{k}) \mathscr {L}( R_{x_{k}}(tR^{-1}_{x_{k}}x^*),x_{k})\Vert \Vert R^{-1}_{x_{k}}x^*\Vert \mathrm {d}t\nonumber \\&\quad \le \int ^{1}_{0}\widetilde{L}d(x_{k},R_{x_{k}}(tR^{-1}_{x_{k}}x^*))\Vert R^{-1}_{x_{k}}x^*\Vert \mathrm {d}t\nonumber \\&\quad =\widetilde{L}\Vert R^{-1}_{x_{k}}x^*\Vert \int ^{1}_{0}d(x_{k},R_{x_{k}}(tR^{-1}_{x_{k}}x^*))\mathrm {d}t\nonumber \\&\quad =\widetilde{L}\Vert R^{-1}_{x_{k}}x^*\Vert \int ^{1}_{0}d(R_{x_{k}}(0_{x_{k}}),R_{x_{k}} (tR^{-1}_{x_{k}}x^*))\mathrm {d}t\nonumber \\&\quad \le \widetilde{L}\Vert R^{-1}_{x_{k}}x^*\Vert \int ^{1}_{0}\frac{3}{2}\Vert tR^{-1}_{x_{k}}x^*\Vert \mathrm {d}t =\frac{3}{4}\widetilde{L}\Vert R^{-1}_{x_{k}}x^*\Vert ^2. \end{aligned}$$

(41)

Since f is uniformly retraction-convex on M, from (16), there exists $m'>0$ such that

$$\begin{aligned} \Vert \mathrm {Hess}f(x_{k})[d_{k}-R^{-1}_{x_{k}}x^*]\Vert \ge m'\Vert d_{k}-R^{-1}_{x_{k}}x^*\Vert . \end{aligned}$$

(42)

Furthermore, it follows from Lemma 4.2 that, for k sufficiently large,

$$\begin{aligned} d(x_{k+1}, x^*)=d(R_{x_{k}}(d_{k}), R_{x_{k}}(R^{-1}_{x_{k}}x^*))\le \frac{3}{2}\Vert R^{-1}_{x_{k}}x^*-d_{k}\Vert , \end{aligned}$$

(43)

and

$$\begin{aligned} d(x_{k}, x^*)=d(R_{x_{k}}(0_{x_{k}}), R_{x_{k}}(R^{-1}_{x_{k}}x^*))\ge \frac{1}{2}\Vert R^{-1}_{x_{k}}x^*\Vert . \end{aligned}$$

(44)

By (41), (42), (43) and (44), we obtain

$$\begin{aligned} \frac{2}{3}d(x_{k+1},x^*)\le \Vert d_{k}-R^{-1}_{x_{k}}x^*\Vert\le & {} \frac{1}{m'}\Vert \mathrm {Hess}f(x_{k})[d_{k}-R^{-1}_{x_{k}}x^*]\Vert \\\le & {} \frac{3\widetilde{L}}{4m'}\Vert R^{-1}_{x_{k}}x^*\Vert ^2\le \frac{3\widetilde{L}}{m'}d^{2}(x_{k},x^*). \end{aligned}$$

Thus,

$$\begin{aligned} d(x_{k+1},x^*)\le \frac{9\widetilde{L}}{2m'}d^{2}(x_{k},x^*), \end{aligned}$$

which implies that $\{x_{k}\}$ converges quadratically to $x^*$. This completes the proof. $\square$

Remark 4.3

Smith [21, Theorem 4.4] presented Newton’s method on Riemannian manifolds and proved that its convergence is quadratic. If the retraction $R_{x}$ is the exponential mapping, and the isometric vector transport is the parallel transport, then Theorem 4.3 can be seen as a generalization of Theorem 4.4 in [21]. If $M=\mathbb {R}^{n}$ and $R_{x}(\eta )=x+\eta$, then Theorems 4.1, 4.2 and 4.3 reduce to Theorems 4.1, 5.1 and 5.3 in [17].

Example 4.1

Let $\mathrm {St}(p,n) \, (p\le n)$ denote the set of all $n\times p$ orthonormal matrices, that is,

$$\begin{aligned} \mathrm {St}(p,n):=\left\{ X\in \mathbb {R}^{n\times p}:X^{\mathrm {\top }}X=I_{p}\right\} , \end{aligned}$$

where $I_{p}$ denotes the $p\times p$ identity matrix. The set $\mathrm {St}(p,n)$ is called Stiefel manifold. The tangent space of $\mathrm {St}(p,n)$ is given by

$$\begin{aligned} T_{X}\mathrm {St}(p,n)=\left\{ X\varOmega +X_{\bot }K:\varOmega ^{\mathrm {\top }}=-\varOmega , \, K\in \mathbb {R}^{(n-p)\times p}\right\} , \end{aligned}$$

where $X_{\bot }$ is any $n\times (n-p)$ orthonormal matrix such that $(X ~X_{\bot })$ is an orthogonal matrix. The canonical inner product is given by

$$\begin{aligned} g(Z_{1},Z_{2})=\mathrm {trace}(Z_{1}^{\mathrm {\top }}Z_{2}), \quad \forall Z_{1},Z_{2}\in T_{X}\mathrm {St}(p,n). \end{aligned}$$

As in [6], the isometric vector transport from $T_{X_{1}}\mathrm {St}(p,n)$ to $T_{X_{2}}\mathrm {St}(p,n)$ is given by

$$\begin{aligned} \mathscr {L}(X_{1},X_{2})=\mathscr {B}_{X_{2}}\mathscr {B}_{X_{1}}^{\flat }, \end{aligned}$$

where $a^{\flat }$ denotes the flat of $a\in T_{X}\mathrm {St}(p,n)$, i.e., $a^{\flat }:T_{X}\mathrm {St}(p,n)\rightarrow \mathbb {R}:v\rightarrow g(a,v)$. Moreover, a smooth function $\mathscr {B}:U\rightarrow \mathbb {R}^{np\times (\frac{np-p(p+1)}{2})}:X\mapsto \mathscr {B}_{X}$ is defined on an open set U of $\mathrm {St}(p,n)$, and the columns of $\mathscr {B}_{X}$ form an orthonormal basis of $T_{X}\mathrm {St}(p,n)$. Let $X\in \mathrm {St}(p,n)$. Then, from [6, 31], we obtain

$$\begin{aligned} (R_{X}(\eta ) ~ R_{X}(\eta )_{\bot })=(X ~X_{\bot }) \exp \left( \begin{array}{cc}\varOmega &{} \quad -K^{\mathrm {\top }}\\ K &{} \quad 0_{(n-p)\times (n-p)}\\ \end{array} \right) , \end{aligned}$$

where $\varOmega =X^{\mathrm {\top }}\eta$ and $K=X_{\bot }^{\top }\eta$. The function $Y=R_{X}(\eta )$ is the desired retraction by the isometric vector transport $\mathscr {L}(\cdot ,\cdot )$. Consider the cost function

$$\begin{aligned} f(X)=\mathrm {trace}(X^{\mathrm {\top }}AX), \end{aligned}$$

where $A=\mathrm {diag}(\mu _{1},\ldots ,\mu _{p})$ with $0<\mu _{1}<\cdots <\mu _{p}$. From Chapter 11 in [31], the gradient of f is

$$\begin{aligned} \mathrm {grad}f(X)=P_{X}(2AX), \end{aligned}$$

where $\mathrm {sym}(Q)=\frac{Q+Q^{\mathrm {\top }}}{2}$ and $P_{X}(V)=X\mathrm {sym}(X^{\mathrm {\top }}V)$. Moreover, the Hessian of f on $\eta \in T_{X}\mathrm {St}(p,n)$ is given by

$$\begin{aligned} \mathrm {Hess}f(X)\eta =P_{X}\left( 2A\eta -\eta \mathrm {sym}(X^{\mathrm {\top }}(2AX))\right) . \end{aligned}$$

Let $\beta , \sigma \in \, ]0,1[$, $B_{k}=\mathrm {Hess}f(x_{k})$ and $d_{k}=-B_{k}^{-1}\mathrm {grad}f(x_{k})$ for all $k\in \mathbb {N}$. Define $m_{X,\eta }(t)=f(R_{X}(t\eta ))$ for all $X\in \mathrm {St}(p,n)$ and $\eta \in T_{X}\mathrm {St}(p,n)$. From the above equality, it is easy to check that $\frac{\mathrm {d}^{2}m_{X,\eta }(t)}{\mathrm {d}t^{2}}>0$. Thus, by Remark 4.1, f is uniformly retraction-convex. Furthermore, the vector transport $\mathscr {L}(\cdot ,\cdot )$ is parallel translation. From Section 8.1 in [22] and Section 5 in [34], it follows that assumption (15) holds. Thus, all the assumptions of Theorem 4.1 are satisfied. Assume that $X^*$ is a stationary point of f. Then, the sequence $\{X_{k}\}$ generated by Algorithm 2.1 converges R-linearly to the stationary point $X^*$.

Example 4.2

Let $M=\mathbb {H}:=\{(x_{1}, x_{2})\in \mathbb {R}^{2} : x_{2}>0\}$ be the Poincaré plane endowed with the Riemannian metric given by

$$\begin{aligned} g_{ij}=\frac{1}{x_{2}^{2}}\delta _{ij}, \quad i,j=1,2. \end{aligned}$$

Then, $\mathbb {H}$ is a Hadamard manifold with the constant sectional curvature $-\,1$ (see [14]). The geodesics in $\mathbb {H}$ are vertical semilines

$$\begin{aligned} C_{a} \, : \, x=a, \; y=ce^t, \quad t\in ]-\infty , +\infty [, \end{aligned}$$

and semicircles

$$\begin{aligned} C_{b,r} \, : \, x=b-r\tanh t,\; y=\frac{r}{\cosh t}, \quad t\in ]-\infty , +\infty [. \end{aligned}$$

For fixed $(x_{0},y_{0}) \in \mathbb {H}$ and for the vector $p=(p_{1}, p_{2}) \in T_{(x_{0},y_{0})}\mathbb {H}$, we have

$$\begin{aligned}&R_{(x_{0},y_{0})}(tp)=\exp _{(x_{0},y_{0})}(tp)\\&\quad =\left\{ \begin{array}{ll} \left( x_{0}, y_{0}e^{t} \right) , &{} \quad \mathrm {if} \; p_{1}=0, \; p_{2}=y_{0},\\ \left( x_{0}+\frac{p_{2}}{p_{1}}\Vert p\Vert +\frac{\Vert p\Vert ^2}{p_{1}}\tanh t, -y_{0} \frac{\Vert p\Vert }{p_{1}}\frac{1}{\cosh t} \right) , &{} \quad \mathrm {if} \; p_{1}<0, \; t\in [0,+\infty [, \end{array} \right. \end{aligned}$$

where $\Vert p\Vert ^2=\Vert p_{1}\Vert ^2+\Vert p_{2}\Vert ^2$. For further details, see Chapter 1 in [14]. Let $f: \mathbb {H}\rightarrow \mathbb {R}$ be a twice continuously differentiable function. Then, as in [14], the gradient of f and the Hessian of f are given by

$$\begin{aligned} \mathrm {grad}f((x_{1},x_{2})) = \left( x_{2}^2\frac{\partial f}{\partial x_{1}}, \, x_{2}^2\frac{\partial f}{\partial x_{2}} \right) , \end{aligned}$$

and

$$\begin{aligned} \mathrm {Hess}f((x_{1},x_{2})) =\left( \begin{array}{cc}\frac{\partial ^2f}{\partial x_{1}^2}-\frac{1}{x_{2}}\frac{\partial f}{\partial x_{2}} &{} \quad \frac{\partial ^2f}{\partial x_{1}\partial x_{2}}+\frac{1}{x_{2}}\frac{\partial f}{\partial x_{1}}\\ \frac{\partial ^2f}{\partial x_{1}\partial x_{2}}+\frac{1}{x_{2}}\frac{\partial f}{\partial x_{1}} &{} \quad \frac{\partial ^2f}{\partial x_{2}^2}+\frac{1}{x_{2}}\frac{\partial f}{\partial x_{2}}, \end{array} \right) , \end{aligned}$$

respectively. Let $C\subseteq H$ be defined by

$$\begin{aligned} C:=\{(x_{1},x_{2})\in \mathbb {H} : (x_{1}-1)^2+x_{2}^2\le 5, \, x_{1}\ge x_{2}\ge 1\}. \end{aligned}$$

Then, C is geodesic convex in $\mathbb {H}$ (see, [14]). Consider the cost function

$$\begin{aligned} f((x_{1}, x_{2})) = \ln ^{2} \frac{x_{1}}{x_{2}}, \quad \forall (x_{1}, x_{2})\in C. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \mathrm {Hess}f((x_{1},x_{2}))=\left( \begin{array}{cc} \frac{2}{x_{1}^2}(1-\ln \frac{x_{1}}{x_{2}}) +\frac{2}{x_{2}^2}\ln \frac{x_{1}}{x_{2}} &{} \quad \frac{2}{x_{1}x_{2}}(\ln \frac{x_{1}}{x_{2}}-1)\\ \frac{2}{x_{1}x_{2}}(\ln \frac{x_{1}}{x_{2}}-1) &{} \quad \frac{2}{x_{2}^2}\\ \end{array} \right) , \quad \forall (x_{1},x_{2})\in C. \end{aligned}$$

It is easy to check f is uniformly retraction-convex on C. However, f is not uniformly convex on C in Euclidean sense. Suppose that the isometric vector transport is parallel transport. Let $\beta , \sigma \in \, ]0,1[$, $B_{k}=\mathrm {Hess}f(x_{k})$ and $d_{k}=-B_{k}^{-1}\mathrm {grad}f(x_{k})$ for all $k\in \mathbb {N}$. Then, all the assumptions of Theorems 4.1, 4.2 and 4.3 are satisfied. Hence, the sequence $\{x_{k}\}$ generated by Algorithm 2.1 converges R-linearly / superlinearly/quadratically to the stationary point $x^*$.

6 Conclusions

We proposed a descent method with new inexact line-search for unconstrained optimization problems on Riemannian manifolds. By using the retraction and isometric vector transport, the global convergence of the descent method with new inexact line-search on Riemannian manifolds is obtained, under some appropriate assumptions. Moreover, the R-linear / superlinear / quadratic convergence rate of the descent method, with new inexact line-search, is extended from linear spaces to Riemannian manifolds. In the future, we shall explore some other efficiently computable retractions and vector transport, which can be adjusted in the given problems. Moreover, it is interesting to do some numerical experiments and comparisons with other line-search algorithms for practical problems on Riemannian manifolds.