Abstract
This paper concerns optimal control problems for a class of sweeping processes governed by discontinuous unbounded differential inclusions that are described via normal cone mappings to controlled moving sets. Largely motivated by applications to hysteresis, we consider a general setting where moving sets are given as inverse images of closed subsets of finite-dimensional spaces under nonlinear differentiable mappings dependent on both state and control variables. Developing the method of discrete approximations and employing generalized differential tools of first-order and second-order variational analysis allow us to derive nondegenerate necessary optimality conditions for such problems in extended Euler–Lagrange and Hamiltonian forms involving the Hamiltonian maximization. The latter conditions of the Pontryagin Maximum Principle type are the first in the literature for optimal control of sweeping processes with control-dependent moving sets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The original sweeping process (“processus de rafle”) was introduced by Moreau [1] as a differential inclusion governed by the negative normal cone to a nicely moving convex set. The motivation came from problems of elastoplasticity. It has been realized that the Cauchy problem for Moreau’s sweeping process and the like admits a unique solution (see, e.g., [2]), and hence optimization does not make sense in such settings. It was suggested in [3], probably for the first time in the literature, to formulate optimal control problems for the sweeping process by entering control functions into moving sets. In this way, we arrive at new and very challenging classes of optimal control problems on minimizing certain Bolza-type cost functionals over feasible solutions to highly non-Lipschitzian unbounded differential inclusions under irregular pointwise state-control constraints. It occurs that not only results but also methods developed in optimal control theory for controlled differential equations and Lipschitzian differential inclusions (see, e.g., [4,5,6] and the references therein) are not suitable for applications to the new classes of sweeping control systems. Papers [3, 7] present significant extensions to sweeping control systems with controlled polyhedral moving sets of the method of discrete approximations developed in [5, 8] for Lipschitzian differential inclusions. Major new ideas in the obtained extensions consist of marrying the discrete approximation approach to recently established second-order subdifferential calculus and explicit computations of the corresponding second-order constructions of variational analysis. Other developments of the discrete approximation approach to derive necessary conditions for controlled sweeping systems with controls not only in the moving sets but also in additive perturbations are given in [9,10,11], where the reader can find applications of the obtained results to crowd motion models of traffic equilibrium. The method of discrete approximations was also implemented in [12] to study various optimal control issues for evolution inclusions governed by one-sided Lipschitzian mappings and in [13] for those described by maximal monotone operators in Hilbert spaces, but without deriving necessary optimality conditions.
Note that the necessary optimality conditions obtained in the previous papers [7,8,9] do not contain the formalism of the Pontryagin Maximum Principle (PMP) [14] (i.e., the maximization of the corresponding Hamiltonian function) established in classical optimal control and then extended to optimal control problems for Lipschitzian differential inclusions. To the best of our knowledge, necessary optimality conditions involving the maximization of the corresponding Hamiltonian were first obtained for sweeping control systems in [15], where the authors considered a sweeping process with uncontrolled strictly smooth, convex, and solid, and moving sets when control functions entering linearly an adjacent ordinary differential equation. Further results with the maximum condition for global (as in [15]) minimizers were derived in [16, 17] for sweeping control systems with uncontrolled moving sets but with measurable controls entering additive function terms. The assumptions imposed in these papers are pretty strong and involve, in particular, higher-order smoothness requirements on compact moving sets. The penalty-type approximation methods developed in [15,16,17] are different from each other, significantly based on the smoothness of uncontrolled moving sets while being totally distinct from the method of discrete approximations employed in our previous papers and in what follows.
This paper addresses a new class of sweeping control problems where the control-dependent moving sets are given as inverse images of arbitrary closed sets under smooth mappings. Besides being attracted by challenging mathematical issues, our interest to such problems is largely motivated by applications to rate-independent operators that frequently appear, for example, in various plasticity models and in the study of hysteresis; see Sects. 7 and 8. While the underlying approach to derive necessary conditions for local minimizers in the new setting is the usage of the method of discrete approximations and generalized differentiation, similarly to [7] and our other publications on sweeping optimal control, some important elements of our technique here are significantly different from the previous developments. From one side, the new/modified technique allows us to establish nondegenerate necessary optimality conditions for local minimizers in the extended Euler–Lagrange form for more general sweeping systems with relaxing several restrictive technical assumptions of [7] in its polyhedral setting. On the other hand, we obtain optimality conditions of the Hamiltonian/PMP type, which are new even for polyhedral moving sets as in [7] under an additional surjectivity assumption. The optimality conditions in the PMP form are the first results of this type for sweeping process with controlled moving sets.
The rest of the paper is organized as follows. Section 2 contains the problem formulation and presents some background material. In Sect. 3, we formulate and discuss our standing assumptions and present necessary preliminaries from first-order and second-order generalized differentiation that are widely used for deriving the main results of the paper.
Section 4 concerns discrete approximations of feasible and local optimal solutions to the sweeping control problem (P) with the verification of the required strong convergence. In Sect. 5, we derive the extended Euler–Lagrange conditions for local optimal solutions to (P) by passing to the limit from discrete approximations and using the second-order subdifferential calculations.
Section 6 contains necessary optimality conditions of the PMP type involving the maximization of the new Hamiltonian function, discusses relationships with the conventional Hamiltonians, and presents an example showing that the maximum principle in the conventional Hamiltonian form fails in our framework. More examples of some practical meaning in the areas of elastoplasticity and hysteresis are given in Sect. 7. The final Sect. 8 discusses some directions of the future research.
Throughout the paper, we use standard notation of variational analysis and control theory; see, for example, [5, 6, 18]. Recall that \(\mathbb {N}:=\{1,2,\ldots \}\), that \(A^*\) stands for the transposed/adjoint matrix to A, and that \(\mathbb {B}\) denotes the closed unit ball of the space in question.
2 Problem Formulation and Background Material
The basic sweeping process was introduced by Moreau in the form
where \(N(x;\varOmega )\) stands for the normal cone to a convex set \(\varOmega \subset \mathbb {R}^n\) at x defined by
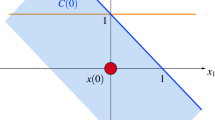
and where the convex variable set C(t) continuously evolves in time. As mentioned in Sect. 1, the Cauchy problem \(x(0)=x_0\in C(0)\) for (1) has a unique solution, and hence there is no room for optimization of (1) in such a framework. This is totally different from the developed optimal control theory for Lipschitzian differential inclusions of the type
which arose from the classical one for controlled differential equations
with \(F(x):=f(x,U)=\{y\in \mathbb {R}^n|\;y=f(x,u)\; \text{ for } \text{ some } \;u\in U\}\) in (3).
It was proposed in [3] to use a control parametrization of the moving set C(t) in the form
This leads us to optimization of non-Lipschitzian differential inclusions with the pointwise constraints
which intrinsically arise from (1) and (5) due to the normal cone construction in (2). Developing the method of discrete approximations, paper [7] establishes necessary optimality conditions for the generalized Bolza problem with the controlled sweeping dynamics in (1), (5), and (6) described by the moving convex polyhedra of the type
where both actions \(u_i(t)\) and \(b_i(t)\) are involved in control. Further developments and applications in this direction are given in [9]–[11] for polyhedral sweeping control problems with control functions acting in both moving sets and additive perturbations.
In this paper, we consider sweeping control systems modeled as
where the controlled moving set is given by
with \(f:[0,T]\times \mathbb {R}^n\rightarrow \mathbb {R}^n\), \(g:\mathbb {R}^n\rightarrow \mathbb {R}^n\), \(\psi :[0,T]\times \mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}^s\), and \(\varTheta \subset \mathbb {R}^s\). Definition (9) amounts to saying that C(t, u) is the inverse image of the set \(\varTheta \) under the mapping \(x\mapsto \psi (t,g(x),u)\) for any ((t, u). Throughout the paper, we assume that the set \(\varTheta \) is locally closed around the reference point. We do not impose any convexity assumption on C(t, u) and use in (8) the (basic, limiting, Mordukhovich) normal cone to an arbitrary locally closed set \(\varOmega \subset \mathbb {R}^n\) at \(\bar{x}\in \mathbb {R}^n\) defined by
where \(\Pi (x;\varOmega )\) stands for the Euclidean projector of x onto \(\varOmega \). When \(\varOmega \) is convex, the normal cone (10) reduces to the one (2) in the sense of convex analysis, but in general the multifunction \(x\rightrightarrows N(x;\varOmega )\) is nonconvex-valued while satisfying a full calculus together with the associated subdifferential of extended real-valued functions and coderivative of set-valued mappings considered below. Such a calculus is due to variational/extremal principles of variational analysis; see [5, 18, 19] for more details.
Our major goal here is to study the optimal control problem (P) of minimizing the cost functional
over absolutely continuous control actions \(u(\cdot )\) and the corresponding absolutely continuous trajectories \(x(\cdot )\) of the sweeping differential inclusion (8) generated by the controlled moving set (9). It follows from (8) and the normal cone definition (10) that the optimal control problem in (8) and (11) intrinsically contains the pointwise constraints on both state and control functions
Observe that the optimal control problem studied in [7] is a particular case of our problem (P) that corresponds to the choice of \(g(x):=x\) (identity operator), of \(\psi (t,x,w):=Ax-b\) with \(w=(A,b)\), and of \(\varTheta :=\mathbb {R}^m_-\) in (8) and (9).
3 Standing Assumptions and Preliminaries
Let us first formulate the major assumptions on the given data of problem (P) that are standing throughout the whole paper. Since our approach to derive necessary optimality conditions for (P) is based on the method of discrete approximations, we impose the a.e. continuity of the functions involved with respect to the time variable, although it is not needed for results dealing with discrete systems before passing to the limit. Note also that the time variable is never included in subdifferentiation. As mentioned above, the constraint set \(\varTheta \) in (9) is assumed to be locally closed unless otherwise stated.
Our standing assumptions are as follows:
(H1) There exits \(L_f>0\) such that \(\Vert f(t,x)-f(t,y)\Vert \le L_f\Vert x-y\Vert \) for all \(x,y\in \mathbb {R}^n,\;t\in [0,T]\) and the mapping \(t\mapsto f(t,x)\) is a.e. continuous on [0, T] for each \(x\in \mathbb {R}^n\).
(H2) There exits \(L_g>0\) such that \(\Vert g(x)-g(y)\Vert \le L_g\Vert x-y\Vert \) for all \(x,y\in \mathbb {R}^n\).
(H3) For each \((t,u)\in [0,T]\times \mathbb {R}^m\), the mapping \(\psi _{t,u}(x):=\psi (t,x,u)\) is \({{\mathcal {C}}}^2\)-smooth around the reference points with the surjective derivative \(\nabla \psi _{t,u}(x)\) satisfying
with the uniform Lipschitz constant \(L_\psi \). Furthermore, the mapping \(t\mapsto \psi (t,x)\) is a.e. continuous on [0, T] for each \(x\in \mathbb {R}^n\) and \(u\in \mathbb {R}^m\).
(H4) There are a number \(\tau >0\) and a mapping \(\vartheta :\times \mathbb {R}^n\times \mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}^m\) locally Lipschitz continuous and uniformly bounded on bounded sets such that for all \(t\in [0,T]\), \(\bar{v}\in N(\psi _{(t,\bar{u})}(\bar{x});\varTheta )\), and \(x\in \psi ^{-1}_{(t,u)}(\varTheta )\) with \(u:=\bar{u}+\vartheta (x,\bar{x},\bar{u})\) there exists \(v\in N(\psi _{(t,u)}(x);\varTheta )\) satisfying \(\Vert v-\bar{v}\Vert \le \tau \Vert x-\bar{x}\Vert \).
(H5) The cost functions \(\varphi :\mathbb {R}^n\rightarrow \overline{\mathbb {R}}:=[-\infty ,\infty [\) and \(\ell (t,\cdot ):\mathbb {R}^{2(n+m)}\rightarrow \overline{\mathbb {R}}\) in (11) are bounded from below and lower semicontinuous (l.s.c.) around a given feasible solution to (P) for a.e. \(t\in [0,T]\), while the integrand \(\ell \) is a.e. continuous in t and is uniformly majorized by a summable function on [0, T].
Assumption (H4) is technical and seems to be the most restrictive. Let us show nevertheless that it holds automatically in the polyhedral setting of [7] and also for nonconvex moving sets.
Proposition 3.1
(Validity of (H4) for controlled polyhedra) For \(x\in \mathbb {R}^n\) and \(w=(A,b)\) where A is a \(m\times n\)-matrix and \(b\in \mathbb {R}^m\), let
in (9). Then condition \(\mathrm{(H4)}\) is satisfied.
Proof
Pick \(\bar{v}\in N({\overline{A}}\bar{x}-\bar{b};\mathbb {R}^m_-)\), \(x\in \mathbb {R}^n\) and denote \(\vartheta (y,z,A):=(0,A(y-z))\). Choose \((A,b):=(\overline{A},\bar{b})+\vartheta (x,\bar{x},{\overline{A}})\) and hence get \(A={\overline{A}}\) and \(b=\bar{b}+{\overline{A}}(x-\bar{x})\), which results in \({\overline{A}}\bar{x}-\bar{b}=A x-b\). Then, \(N(\langle {\overline{A}}\bar{x}-\bar{b};\mathbb {R}^m_-)=N(Ax-b;\mathbb {R}^m_-)\). Thus, condition (H4) is satisfied with \(v:=\bar{v}\) for any \(\tau \ge 1\). \(\square \)
The following simple example illustrates that (H4) is also satisfied in standard nonconvex settings.
Example 3.1
(Validity of (H4) for nonconvex moving sets) Consider the nonconvex set
which corresponds to \(\psi (x,u):=x^2+u-1\) and \(\varTheta :=[0,\infty [\) in (9). To verify (H4) in this setting, denote \(\vartheta (y,z,u):=-(y-z)(y+z)\) and pick any \(\bar{v}\in N(\bar{x}^2+\bar{u}-1;[0,\infty [)\) and \(x\in \mathbb {R}^n\). Choosing now \(u:=\bar{u}-(x-\bar{x})(x+\bar{x})\), we get \(x^2+u-1=\bar{x}^2+\bar{u}-1\) and thus verify (H4) with \(v:=\bar{v}\) for every \(\tau \ge 1\).
Let us next discuss condition (H3), which plays a significant role in deriving some major results of the paper. This condition, which is equivalent in the finite-dimensional setting under consideration to the full rank of the Jacobian matrix \(\nabla \psi _{t,u}(x)\), amounts to metric regularity of the mapping \(x\mapsto \psi _{t,u}(x)\) by the seminal Lyusternik–Graves theorem; see, for example, [5, Theorem 1.57]. The following normal cone calculus rule is a consequence of [5, Theorem 1.17].
Proposition 3.2
(Normal cone representation for inverse images) Under the validity of (H3), the normal cone (10) to the controlled moving set (9) is represented by
To proceed further, we recall some constructions of first-order and second-order generalized differentiation for functions and multifunctions/set-valued mappings needed in what follows; see [5, 19] for detailed expositions. All these constructions are generated geometrically by our basic normal cone (10).
Given a set-valued mapping \(F:\mathbb {R}^n\rightrightarrows \mathbb {R}^q\) and a point \((\bar{x},\bar{y})\in \text{ gph }\,F\) from its graph
the coderivative\(D^*F(\bar{x},\bar{y}):\mathbb {R}^q\rightrightarrows \mathbb {R}^n\) of F at \((\bar{x},\bar{y})\) is defined by
where \(\bar{y}\) is omitted in the notation if \(F:\mathbb {R}^n\rightarrow \mathbb {R}^q\) is single-valued. If furthermore F is \({{\mathcal {C}}}^1\)-smooth around \(\bar{x}\) (or merely strictly differentiable at this point), we have \(D^*F(\bar{x})(v)=\{\nabla F(\bar{x})^*v\}\) via the adjoint Jacobian matrix. In general, the coderivative (12) is a positively homogeneous multifunction satisfying comprehensive calculus rules and providing complete characterizations of major well-posedness properties in variational analysis related to Lipschitzian stability, metric regularity, and linear openness; see [5, 18].
For an extended real-valued function \(\phi :\mathbb {R}^n\rightarrow \overline{\mathbb {R}}\) finite at \(\bar{x}\), i.e., with \(\bar{x}\in \text{ dim }\,\phi \), the (first-order) subdifferential of \(\phi \) at \(\bar{x}\) is defined geometrically by
via the normal cone (10) to the epigraphical set \(\text{ epi }\,\phi :=\{(x,\alpha )\in \mathbb {R}^{n+1}|\;\alpha \ge \phi (x)\}\). If \(\phi (x):=\delta _\varOmega (x)\), the indicator function of a set \(\varOmega \) that is equal to 0 for \(x\in \varOmega \) and to \(\infty \) otherwise, we get \(\partial \phi (\bar{x})=N(\bar{x};\varOmega )\). Given further \(\bar{v}\in \partial \phi (\bar{x})\), the second-order subdifferential (or generalized Hessian) \(\partial ^2\phi (\bar{x},\bar{v}):\mathbb {R}^n\rightrightarrows \mathbb {R}^n\) of \(\phi \) at \(\bar{x}\) relative to \(\bar{v}\) is defined as the coderivative of the first-order subdifferential by
where \(\bar{v}=\nabla \phi (\bar{x})\) is omitted when \(\phi \) is differentiable at \(\bar{x}\). If \(\phi \) is \({{\mathcal {C}}}^2\)-smooth around \(\bar{x}\), then (14) reduces to the classical (symmetric) Hessian matrix
For applications in this paper, we also need partial versions of the above subdifferential constructions for functions of two variables \(\phi :\mathbb {R}^n\times \mathbb {R}^m\rightarrow \overline{\mathbb {R}}\). Consider the partial first-order subdifferential mapping \((x,w)\mapsto \partial _x\phi (x,w)\) for \(\varphi (x,w)\) with respect to x by
and then, picking \((\bar{x},\bar{w})\in \text{ dom }\,\phi \) and \(\bar{v}\in \partial _x\phi (\bar{x},\bar{w})\), define the partial second-order subdifferential of \(\phi \) with respect to x at \((\bar{x},\bar{w})\) relative to \(\bar{v}\) by
If \(\phi \) is \({{\mathcal {C}}}^2\)-smooth around \((\bar{x},\bar{w})\), we have the representation
Taking into account the controlled moving set structure (9), important roles in this paper are played by the parametric constraint system
and the normal cone mapping\(\mathcal{{N}}:\mathbb {R}^n\times \mathbb {R}^m\rightrightarrows \mathbb {R}^n\) associated with (16) by
It is easy to see that the mapping \({{\mathcal {N}}}\) in (17) admits the composite representation
via the \({{\mathcal {C}}}^2\)-smooth mapping \(\psi :\mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}^s\) from (16) and the indicator function \(\delta _\varTheta \) of the closed set \(\varTheta \subset \mathbb {R}^s\). It follows directly from (18) due to the second-order subdifferential construction (15) that
Applying now the second-order chain rule from [20, Theorem 3.1] to the composition in (19) allows us to compute the coderivative of the normal cone mapping (17) via the given data of (16).
Proposition 3.3
(Coderivative of the normal cone mapping for inverse images) Assume that \(\psi \) is \({{\mathcal {C}}}^2\)-smooth around \((\bar{x},\bar{w})\) and that the partial Jacobian matrix \(\nabla _x\psi (\bar{x},\bar{w})\) is of full rank. Then, for each \(\bar{v}\in {{\mathcal {N}}}(\bar{x},\bar{w})\), there is a unique vector \(\bar{p}\in N_{\varTheta }(\psi (\bar{x},\bar{w})):=N(\psi (\bar{x},\bar{w});\varTheta )\) satisfying
and such that the coderivative of the normal cone mapping is computed for all \(u\in \mathbb {R}^n\) by
Thus, Proposition 3.3 reduces the computation of \(D^*\mathcal{N}\) to that of \(D^*N_{\varTheta }\), which has been computed via the given data for broad classes of sets \(\varTheta \); see, for example, [19,20,21,22] for more details and references.
4 Discrete Approximations
In this section, we construct a well-posed sequence of discrete approximations for feasible solutions to the constrained sweeping dynamics in (8), (9) and for local optimal solutions to the sweeping optimal control problem (P). The results obtained here establish the \(W^{1,2}\)-strong convergence of discrete approximations while being free of generalized differentiation. They are certainly of independent interest from just their subsequent applications to deriving necessary optimality conditions for problem (P).
Starting with discrete approximations of the sweeping differential inclusion (8), we replace the time derivative therein by the Euler finite difference \(\dot{x}(t)\approx [x(t+h)-x(t)]/h\) and proceed as follows. For each \(k\in \mathbb {N}\), define \(h_k:=T/k\) and consider the discrete mesh \(T_k:=\{t_j^k:=jh_k|\,j=0,1,\ldots ,k\}\). Then, the sequence of discrete approximations of (8) is given by
The following major result on a strong approximation of feasible solutions to the controlled sweeping process in (8), (9) by feasible solutions to the discretized systems in (21) is essentially different from the related one in [7, Theorem 3.1]. Besides being applied to more general systems, it eliminates or significantly relaxes some restrictive technical assumptions imposed in [7] for the polyhedral controlled sets (7) by using another proof technique under the surjectivity assumption in (H3). Note furthermore that the choices of the reference feasible pair \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in [7] and Theorem 4.1 are also different: Instead of the actual choice of \((\bar{x}(\cdot ),\bar{u}(\cdot ))\in W^{2,\infty }[0,T]\times W^{2,\infty }[0,T]\), we now have the less restrictive pick \((\bar{x}(\cdot ),\bar{u}(\cdot ))\in \mathcal{C}^1[0,T]\times {{\mathcal {C}}}[0,T]\) and establish its strong approximation in the \(W^{1,2}\times {{\mathcal {C}}}\) topology instead of \(W^{1,2}\times W^{1,2}\) in [7]. This actually affects the types of local minimizers for which we derive necessary optimality conditions in the setting of this paper; see Definition 4.1. If, however, the mapping g is linear in (8) and if \(\bar{u}(\cdot )\in W^{1,2}[0,T]\), we obtain the same \(W^{1,2}\)-approximation of the reference control as in the polyhedral framework of [7].
Theorem 4.1
(Strong discrete approximation of feasible sweeping solutions) Let the pair \((\bar{x}(\cdot ),\bar{u}(\cdot ))\in {{\mathcal {C}}}^1[0,T]\times {{\mathcal {C}}}[0,T]\) satisfy (8) with the moving set C(t, u) from (9) under the validity of the standing assumptions in (H1)–(H4). Then, there exists a sequence \(\{(x^k(\cdot ),u^k(\cdot ))\}\) of piecewise linear functions on [0, T] satisfying the discrete inclusions (21) with \((x^k(0),u^k(0))=(\bar{x}_0,\bar{u}(0))\) and such that \(\{(x^k(\cdot ),u^k(\cdot ))\}\) converges to \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in the norm topology of \(W^{1,2}([0,T];\mathbb {R}^{n})\times {{\mathcal {C}}}([0,T];\mathbb {R}^m)\). If in addition the mapping \(g(\cdot )\) in (8) is linear and \(\bar{u}(\cdot )\in W^{1,2}([0,T];\mathbb {R}^m)\), then the sequence \(\{(x^k(\cdot ),u^k(\cdot ))\}\) converges to \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in the norm topology of \(W^{1,2}([0,T];\mathbb {R}^n)\times W^{1,2}([0,T];\mathbb {R}^m)\).
Proof
Fix \(k\in \mathbb {N}\), choose \(x_0^k:=x_0\) and \(u^k_0:=\bar{u}(0)\), and then construct \((x_j^k,u_j^k)\) for \(j=1,\ldots ,k\) by induction. Suppose that \(x_j^k\) is known and satisfies \(\Vert x_j^k-\bar{x}(t_j^k)\Vert \le 1\) without loss of generality. Define
and deduce from the validity of (8) at \(t_j^k\) that \(-{{\dot{\bar{x}}}}(t_j^k)+f(t_j^k,\bar{x}(t_j^k))\in N(g(\bar{x}(t_j^k); C(t_j^k,\bar{u}(t_j^k)))\). Using \(\bar{x}(\cdot )\in \mathcal{C}^1([0,T];\mathbb {R}^n)\) allows us to find \(\eta >0\) such that
The surjectivity of \(\nabla \psi _{t_j^k,\bar{u}(t_j^k)}\) ensures by the open mapping theorem the existence of \(M>0\) for which
Combining it with Proposition 3.2 tells us that
Since \(-{{\dot{\bar{x}}}}(t_j^k)+f(t_j^k,\bar{x}(t_j^k))\in N(g(\bar{x}(t_j^k);C(t_j^k,\bar{u}(t_j^k)))\cap \eta \mathbb {B}\), we find \(w\in N(\psi _{t_j^k,\bar{u}(t_j^k)}(g(\bar{x}(t_j^k)));\varTheta )\) with \(\Vert w\Vert \le \eta M\) satisfying the equality
Using now the mapping \(\vartheta (\cdot )\) from (H4) gives us vectors \(u_j^k\) and \({\widetilde{w}}\in N(\psi _{t_j^k,\bar{u}_j^k}(x_j^k);\varTheta )\) for which
By the assumed uniform boundedness of the mapping \(\vartheta (\cdot )\), it is easy to adjust \(\tau >0\) so that \(\Vert u_j^k-\bar{u}(t_j^k)\Vert \le \tau \Vert g(x_j^k)-g(\bar{x}(t_j^k))\Vert \). Denoting \(v_j^k:=\left( \nabla \psi _{t_j^k,u_j^k}\right) ^*{\widetilde{w}}\), we get \(v_j^k\in N(g(x_j^k);C(t_j^k,u_j^k))\) by employing Proposition 3.2 and then arrive at the following estimates:
Denoting further \(\alpha :=\eta M L_{\psi }\tau L_g+\tau \eta L_g\) and \(\beta :=L_{\psi }\tau ^2 L^2_g\), we get from the above that
Now we are ready to construct the next iterate \(x^k_{j+1}\) by
and thus conclude that inclusion (21) holds at the discrete time j. It follows from the arguments above that for any \(k\in \mathbb {N}\) sufficiently large, we always have \(\Vert x^k_{j+1}-\bar{x}(t_{j+1}^k)\Vert \le 1\). This completes the induction process and gives us therefore a sequence \(\{(x^k(\cdot ),u^k(\cdot ))\}\) defined on the discrete mesh \(T_k\) for large \(k\in \mathbb {N}\) and satisfied therein the discretized sweeping inclusion (21) with the controlled moving set (9).
Next, we prove that piecewise linear extensions \((x^k(t),u^k(t))\), \(0\le t\le T\), of the above sequence to the continuous-time interval [0, T] converge to the reference pair \((\bar{x}(\cdot ),\bar{u}(t))\) in the norm topology of \(W^{1,2}([0,T];\mathbb {R}^n)\times {{\mathcal {C}}}([0,T];\mathbb {R}^m)\). To proceed, fix any \(\epsilon >0\) and recall the definition of \(\epsilon _j\) in (22). Taking into account that \(\bar{x}(\cdot )\in {{\mathcal {C}}}^1([0,T];\mathbb {R}^n)\), we get that \(\epsilon _j\le h_k\epsilon \) for all \(j=0,\ldots ,k-1\) and all \(k\in \mathbb {N}\) sufficiently large. This gives us the relationships
and therefore we arrive at the following estimate:
Define further the quantities \(a_j:=\Vert x_j^k-\bar{x}(t_j^k)\Vert \) for all \(j=0,\ldots ,k\) and \(k\in \mathbb {N}\). Observe that \(a_{j+1}=(1+(\alpha +L_f) h_k+\beta h_k a_j)a_j+h_k \epsilon \) for \(j=0,\ldots ,k-1\), which is equivalent to
Denoting by \(a_{\epsilon }(\cdot )\) the solution of the differential equation
we see that \(a_\epsilon (t)\rightarrow 0\) uniformly on [0, T] as \(\epsilon \downarrow 0\). It readily implies that
This verifies, in particular, that \(\max \{\Vert x_j^k-\bar{x}(t_j^k)\Vert ,\;j=0,\ldots ,k\}\le 1\) for all \(k\in \mathbb {N}\), which was needed to complete the induction process. Since we have
as shown above, the control sequence \(\{u^k(t)\}\) converges to \(\bar{u}(\cdot )\) strongly in \({{\mathcal {C}}}([0,T];\mathbb {R}^m)\).
Let us next justify the strong \(W^{1,2}\)-convergence of the trajectories \(x^k(\cdot )\) to \(\bar{x}(\cdot )\) on [0, T]. We have
where the last term converges to zero due to \(\bar{x}(\cdot )\in \mathcal{C}^1([0,T];\mathbb {R}^n)\). The first term therein also converges to zero by the following estimates valid for all \(j=0,\ldots ,k\):
which is due to (23). Thus, we get \(\int _0^T\Vert \dot{x}^k(t)-{{\dot{\bar{x}}}}(t)\Vert ^2dt\rightarrow 0\) as \(k\rightarrow \infty \). Since \(x_0^k=\bar{x}(0)\), the latter verifies that \(\{x^k(\cdot )\}\) strongly converges to \(\bar{x}(\cdot )\) in \(W^{1,2}([0,T];\mathbb {R}^n)\).
To complete the proof of the theorem, it remains to show that if \(\bar{u}(\cdot )\in W^{1,2}([0,T];\mathbb {R}^m)\) and the mapping \(g(\cdot )\) is linear, then \(u^k(\cdot )\rightarrow \bar{u}(\cdot )\) strongly in \(W^{1,2}([0,T];\mathbb {R}^m)\). Denoting
and using the local Lipschitz continuity of \(d(\cdot )\) with constant \(L_d>0\), we get
where \(M>0\) is sufficiently large. This shows that
and thus verifies the claimed convergence under the assumptions made. \(\square \)
The two approximation results established in Theorem 4.1 allow us to apply the method of discrete approximations to deriving necessary optimality conditions for two types of local minimizers in problem (P). The first type treats the trajectory and control components of the optimal pair \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in the same way and reduces in fact to the intermediate\(W^{1,2}\)-minimizers introduced in [8] in the general framework of differential inclusions and then studied in [7,8,9] for various controlled sweeping processes. The second type seems to be new in control theory; it treats control and trajectory components differently and applies to problems (P) whose running costs do not depend on control velocities.
Definition 4.1
(Local minimizers for controlled sweeping processes) Let the pair \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) be feasible to problem (P) under the standing assumptions made.
(i) We say that \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) be a local\(W^{1,2}\times W^{1,2}\)-minimizer for (P) if \(\bar{x}(\cdot )\in W^{1,2}([0,T];\mathbb {R}^n)\), \(\bar{u}(\cdot )\in W^{1,2}([0,T];\mathbb {R}^m)\), and
sufficiently close to \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in the norm topology of the corresponding spaces in (25).
(ii) Let the running cost \(\ell (\cdot )\) in (11) do not depend on \(\dot{u}\). We say that the pair \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) be a local\(W^{1,2}\times {{\mathcal {C}}}\)-minimizer for (P) if \(\bar{x}(\cdot )\in W^{1,2}([0,T];\mathbb {R}^n)\), \(\bar{u}(\cdot )\in \mathcal{C}([0,T];\mathbb {R}^m)\), and
sufficiently close to \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in the norm topology of the corresponding spaces in (26).
Our main attention in what follows is to derive necessary optimality conditions for both types of local minimizers in Definition 4.1 by developing appropriate versions of the method of discrete approximations. It is clear that any local \(W^{1,2}\times {{\mathcal {C}}}\)-minimizer for (P) is also a local \(W^{1,2}\times W^{1,2}\)-minimizer for this problem, provided that we restrict the class of feasible controls to \(W^{1,2}\)-functions. Thus, necessary optimality conditions for local \(W^{1,2}\times W^{1,2}\)-minimizers are also necessary for local \(W^{1,2}\times \mathcal{C}\)-ones in this framework, while not vice versa. On the other hand, we may deal with local \(W^{1,2}\times {{\mathcal {C}}}\)-minimizers without imposing anything but the continuity assumptions of feasible controls, provided that the running cost in (11) does not depend on control velocities. Note furthermore that considering a \(W^{1,2}\)-neighborhood of the trajectory part \(\bar{x}(\cdot )\) in both settings of Definition 4.1 leads us to potentially more selective necessary optimality conditions for such minimizers than for conventional strong local minimizers and global solutions to (P).
It has been well recognized in the calculus of variations and optimal control, starting with pioneering studies by Bogolyubov and Young, that limiting procedures of dealing with continuous-time dynamical systems involving time derivatives require a certain relaxation stability, which means that the value of cost functionals does not change under the convexification of the dynamics and running cost with respect to velocity variables; see, for example, [6, 19] for more details and references. In sweeping control theory, such issues have been investigated in [23, 24] for controlled sweeping processes somewhat different from (P).
To consider an appropriate relaxation of our problem (P), denote
and formulate the relaxed optimal control problem (R) as a counterpart of (P) with the replacement of the cost functional (11) by the convexified one
where \(\widehat{\ell }(t,x,u,\cdot ,\cdot )\) is defined as the largest l.s.c. convex function majorized by \(\ell (t,x,u,\cdot ,\cdot )\) on the convex closure of the set F in (27) with \(\widehat{\ell }:=\infty \) otherwise. Then, we say that the pair \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) is a relaxed local\(W^{1,2}\times W^{1,2}\)-minimizer for (P) if in addition to the conditions of Definition 4.1(i) we have \(J[\bar{x},\bar{u})=\widehat{J}[\bar{x},\bar{u}]\). Similarly, we define a relaxed local \(W^{1,2}\times \mathcal{C}\)-minimizer for (P) in the setting of Definition 4.1(ii). Note that, in contrast to the original problem (P), the convexified structure of the relaxed problem (R) provides an opportunity to establish the existence of global optimal solutions in the prescribed classes of controls and trajectories. It is not a goal of this paper, but we refer the reader to [11, Theorem 4.1] and [24, Theorem 4.2] for some particular settings of controlled sweeping processes in the classes of \(W^{1,2}\times W^{1,2}\) and \(W^{1,2}\times {{\mathcal {C}}}\) feasible pairs \((\bar{x}(\cdot ),\bar{u}(\cdot ))\), respectively.
There is clearly no difference between the problems (P) and (R) if the normal cone in (27) is convex and the integrand \(\ell \) in (11) is convex with respect to velocity variables. On the other hand, the measure nonatonomicity on [0, T] and the differential inclusion structure of (8) are instrumental to find efficient conditions under which any local minimizer of the types under consideration is also a relaxed one. Without delving into details here, we just mention the possibility to derive such a local relaxation stability from [24, Theorem 4.2] for strong local (in the \(\mathcal{C}\)-norm) minimizers of (P), provided that the controlled moving set C(t, u) in (9) is convex and continuously depends on its variables.
Given now a relaxed local minimizer \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) of the types introduced in Definition 4.1, we construct appropriate sequences of discrete-time optimal control problems corresponding to each type therein separately. For brevity and simplicity, from now on we restrict ourselves to the setting of (P) where \(g(x):=x\), \(f:=0\) while \(\psi \) and \(\ell \) do not depend on t. The reader can easily check that the procedure developed below is applicable to the general version of (P) under the standing assumptions made.
If the pair \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) is a relaxed local \(W^{1,2}\times W^{1,2}\)-minimizer of (P), we fix \(\varepsilon >0\) sufficiently small to accommodate the \(W^{1,2}\times W^{1,2}\)-neighborhood of \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in Definition 4.1(i) and for each \(k\in \mathbb {N}\) define the approximation problem \((P^1_k)\) as follows:
over collections \(z^k:=(x_0^k,\ldots ,x_k^k,u_0^k,\ldots ,u_k^k)\) subject to the constraints
If the pair \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) is a relaxed local \(W^{1,2}\times {{\mathcal {C}}}\)-minimizer of (P), fix \(\varepsilon >0\) sufficiently small to accommodate the \(W^{1,2}\times \mathcal{C}\)-neighborhood of \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in Definition 4.1(ii) and for each \(k\in \mathbb {N}\) define the approximation problem \((P^2_k)\) in the following way corresponding to (26):
over \(z^k=(x_0^k,\ldots ,x_k^k,u_0^k,\ldots ,u_k^k)\) subject to the constraints in (28)–(30) and
To proceed further with the method of discrete approximations, we need to make sure that the approximating problems \((P^i_k)\), \(i=1,2\), admit optimal solutions. This is indeed the case due to Theorem 4.1 and the robustness (closed-graph property) of our basic normal cone (10).
Proposition 4.1
(Existence of discrete optimal solutions) Under the imposed standing assumptions (H1)–(H5), each problem \((P^i_k)\), \(i=1,2\), has an optimal solution for all \(k\in \mathbb {N}\) sufficiently large.
Proof
It follows from Theorem 4.1 and the constructions of \((P^1_k)\), \((P^2_k)\) that the set of feasible solutions to each of these problems is nonempty for all large \(k\in \mathbb {N}\). Applying the classical Weierstrass existence theorem, observe that the boundedness of the feasible sets follows directly from the constraint structures in \((P^1_k)\) and \((P^2_k)\). The remaining closedness of the feasible sets for these problems is a consequence of the robustness property of the normal cone (10) that determines the discrete inclusions (28). \(\square \)
The next theorem establishes the strong convergence in the corresponding spaces of extended discrete optimal solutions for discrete approximation problems to the given relaxed local minimizers for (P).
Theorem 4.2
(Strong convergence of discrete optimal solutions) In addition to the standing assumption (H1)–(H5), suppose that the cost functions \(\varphi \) and \(\ell \) are continuous around the given local minimizer. The following assertions hold:
(i) If \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) is a relaxed local \(W^{1,2}\times W^{1,2}\)-minimizer for (P), then any sequence of piecewise linear extensions on [0, T] of the optimal solutions \((\bar{x}^k(\cdot ),\bar{u}^k(\cdot ))\) to \((P^1_k)\) converges to \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in the norm topology of \(W^{1,2}([0,T];\mathbb {R}^n)\times W^{1,2}([0,T];\mathbb {R}^m)\) as \(k\rightarrow \infty \).
(ii) If \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) is a relaxed local \(W^{1,2}\times {{\mathcal {C}}}\)-minimizer for (P), then any sequence of piecewise linear extensions on [0, T] of the optimal solutions \((\bar{x}^k(\cdot ),\bar{u}^k(\cdot ))\) to \((P^2_k)\) converges to \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) in the norm topology of \(W^{1,2}([0,T];\mathbb {R}^n)\times {{\mathcal {C}}}([0,T];\mathbb {R}^m)\) as \(k\rightarrow \infty \).
Proof
To verify assertion (i), we proceed similarly to the proof of [7, Theorem 3.4] with the usage of the normal cone robustness for (10) instead of Attouch’s theorem in the convex setting of [7]. The proof of assertion (ii) goes in the same lines with observing that the required \({{\mathcal {C}}}\)-compactness of the control sequence follows from the control-state relationship of type (24) valid due to assumption (H4). \(\square \)
5 Extended Euler–Lagrange Conditions for Sweeping Solutions
Having the strong convergence results of Theorem 4.2 as the quintessence of the discrete approximation well-posedness justified in Sect. 4, we now proceed first with deriving necessary optimality conditions in both discrete problems \((P^1_k)\) and \((P^2_k)\) for each \(k\in \mathbb {N}\) and then with the subsequent passage to the limit therein as \(k\rightarrow \infty \). In this way, we arrive at necessary optimality conditions for relaxed local minimizers in (P) of both \(W^{1,2}\times W^{1,2}\) and \(W^{1,2}\times {{\mathcal {C}}}\) types.
Observe that for each fixed \(k\in \mathbb {N}\), both problems \((P^1_k)\) and \((P^2_k)\) belong to the class of finite-dimensional mathematical programming with nonstandard geometric constraints (28) and (29). We can handle them by employing appropriate tools of variational analysis that revolve around the normal cone (10).
Theorem 5.1
(Necessary optimality conditions for \((P^1_k)\)) Fix \(k\in \mathbb {N}\) and consider an optimal solution \(\bar{z}^k:=(x_0,\bar{x}^k_1\ldots ,\bar{x}_k^k,\bar{u}_0^k,\ldots ,\bar{u}_{k}^{k})\) to problem \((P^1_k)\), where F may be a general closed-graph mapping. Suppose that the cost functions \(\varphi \) and \(\ell \) are locally Lipschitzian around the corresponding components of the optimal solution and denote the quantities
Then, there exist dual elements \(\lambda ^k\ge 0\), \(p_j^k=(p^{xk}_j,p^{uk}_j)\in \mathbb {R}^n\times \mathbb {R}^m\) as \(j=0,\ldots ,k\) and subgradient vectors
such that the following conditions are satisfied:
Proof
It follows the lines in the proof of [7, Theorem 5.1] by reducing \((P^1_k)\) to a problem of mathematical programming. The usage of necessary optimality conditions for such problems and calculus rules of generalized differentiation for the basic constructions (10) and (13) available in the books [5, 18, 19] allow us to arrive at (32)–(36) due to the particular structure of the data in \((P^1_k)\). \(\square \)
The same approach holds for verifying the necessary optimality conditions for problem \((P^2_k)\) presented in the next theorem, which also takes into account the specific structure of this problem.
Theorem 5.2
(Necessary optimality conditions for \((P^2_k)\)) Let \(\bar{z}^k:=(x_0,\bar{x}^k_1\ldots ,\bar{x}_k^k,\bar{u}_0^k,\ldots ,\bar{u}_{k}^{k})\) be an optimal solution problem \((P^2_k)\) in the framework of Theorem 5.1. Consider the quantities
Then, there exist dual elements \(\lambda ^k\ge 0\), \(p_j^k=(p^{xk}_j,p^{uk}_j)\in \mathbb {R}^n\times \mathbb {R}^m\) as \(j=0,\ldots ,k\) and subgradient vectors
satisfying the following necessary optimality conditions:
Now we are ready to derive necessary optimality conditions for both types of (relaxed) local minimizers for (P) from Definition 4.1 by passing the limit from those in Theorems 5.1 and 5.2 with taking into account the convergence results from Sect. 4 and calculation results of generalized differentiation presented in Sect. 3. The reader can see that the obtained optimality conditions for both types are local minimizers that are pretty similar under the imposed assumptions. This is largely due to the achieved discrete approximation convergence in Theorem 4.2 and the structures of the discretized problems. Necessary optimality conditions for relaxed local \(W^{1,2}\times W^{1,2}\)-minimizers of (P) were derived in [7, Theorem 6.1] for polyhedral moving sets (7) under significantly more restrictive assumptions, which basically cover the case of \((\bar{x}(\cdot ),\bar{u}(\cdot ))\in W^{2,\infty }([0,T];\mathbb {R}^{n+m})\). Note that the linear independence constraint qualification (LICQ) condition on generating polyhedral vectors imposed therein is a counterpart of our surjectivity assumption (H3) in the polyhedral setting of [7].
Theorem 5.3
(Necessary optimality conditions for the controlled sweeping process) We assume that \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) is a local minimizer for problem (P) of the types specified below. In addition to the standing assumptions, suppose that \(\psi =\psi (x,u)\) is \({{\mathcal {C}}}^2\)-smooth with respect to both variables while \(\varphi \) and \(\ell \) are locally Lipschitzian around the corresponding components of the optimal solution. The following assertions hold:
(i) If \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) is a relaxed local \(W^{1,2}\times W^{1,2}\)-minimizer, then there exist a multiplier \(\lambda \ge 0\), an adjoint arc \(p(\cdot )=(p^x,p^u)\in W^{1,2}([0,T];\mathbb {R}^n\times \mathbb {R}^m)\), a signed vector measure \(\gamma \in C^*([0,T];\mathbb {R}^s)\), as well as pairs \((w^x(\cdot ),w^u(\cdot ))\in L^2([0,T];\mathbb {R}^n\times \mathbb {R}^m)\) and \((v^x(\cdot ),v^u(\cdot ))\in L^\infty ([0,T];\mathbb {R}^n\times \mathbb {R}^m)\) with
satisfying the collection of necessary optimality conditions:
\(\bullet \)Primal-dual dynamic relationships:
where \(\eta (\cdot )\in L^{2}([0,T];\mathbb {R}^s)\) is a uniquely defined vector function determined by the representation
with \(\eta (t)\in N(\psi (\bar{x}(t),\bar{u}(t));\varTheta )\), and where \(q:[0,T]\rightarrow \mathbb {R}^n\times \mathbb {R}^m\) is a function of bounded variation on [0, T] with its left-continuous representative given, for all \(t\in [0,T]\) except at most a countable subset, by
\(\bullet \)Measured coderivative condition: Considering the t-dependent outer limit
over Borel subsets \(B\subset [0,1]\) with the Lebesgue measure |B|, for a.e. \(t\in [0,T]\), we have
\(\bullet \)Transversality condition at the right endpoint:
\(\bullet \)Measure nonatomicity condition: Whenever \(t\in [0,T)\) with \(\psi (\bar{x}(t),\bar{u}(t))\in \mathrm{int}\,\varTheta \), there is a neighborhood \(V_t\) of t in [0, T] such that \(\gamma (V)=0\) for any Borel subset V of \(V_t\).
\(\bullet \)Nontriviality condition:
(ii) If \((\bar{x}(\cdot ),\bar{u}(\cdot ))\) is a relaxed local \(W^{1,2}\times {{\mathcal {C}}}\)-minimizer, then all conditions (38)–(44) in (i) hold with the replacement of the quadruple \((w^x(\cdot ),w^u(\cdot ),v^x(\cdot ),v^u(\cdot ))\) in (37) by the triple \((w^x(\cdot ),w^u(\cdot ),v^x(\cdot ))\in L^2([0,T];\mathbb {R}^n)\times L^2([0,T];\mathbb {R}^m)\times L^\infty ([0,T];\mathbb {R}^n)\) satisfying the inclusion
Proof
We give it only for assertion (i), since the proof of (ii) is similar with taking into account the type of convergence \(\bar{u}^k(\cdot )\rightarrow \bar{u}(\cdot )\) achieved in Theorem 4.2(ii) and that the running cost \(\ell \) in Definition 4.1(ii) does not depend on the control velocity \({\dot{u}}\).
To verify assertion (i), deduce first from (36) and Proposition 3.3 that for each \(k\in \mathbb {N}\) and \(j=0,\ldots ,k-1\) there is a unique vector \(\eta _j^k\in N_{Z}(\psi (\bar{x}_j^k,\bar{u}_j^k))\) satisfying the conditions
with \(u:=p_{j+1}^{xk}-\lambda ^k\Big (v_j^{xk}+\frac{1}{h_k}\theta _j^{xk}\Big )\) and some vectors
Taking this into account, we get from (33) the improved nontriviality condition
with the validity of (35) as well as \(\lambda ^k\ge 0\) and the relationships in (31) and (32) of Theorem 5.1.
Now we proceed with passing to the limit as \(k\rightarrow \infty \) in the obtained optimality conditions for discrete approximations. Since some arguments in this procedure are similar to those used in [7, Theorem 6.1] in a more special setting, we skip them for brevity while focusing on significantly new developments. In particular, the existence of the claimed quadruples \((w^x(\cdot ),w^u(\cdot ),v^x(\cdot ),v^u(\cdot ))\) satisfying (37) is proved as in [13] while the existence of the uniquely defined \(\eta (\cdot )\in L^2([0.T];\varTheta )\) solving the differential equation (40) follows from representation (20) by repeating the limiting procedure of [7, Theorem 6.1].
Next, we define \(q^k(\cdot )=(q^{xk}(\cdot ),q^{uk}(\cdot ))\) by extending \(p_j^k\) piecewise linearly to [0, T] with \(q^{k}(t^k_j):=p^{k}_j\) for \(j=0,\ldots ,k\). Construct \(\gamma ^k(\cdot )\) on [0, T] by
with \(\gamma ^k(T):=0\) and consider the auxiliary functions
so that \(\vartheta ^k(t)\rightarrow t\) uniformly in [0, T] as \(k\rightarrow \infty \). Since \(\vartheta ^{k}(t)=t_{j}^{k}\) for all \(t\in [t_{j}^{k},t_{j+1}^{k})\) and \(j=0,\ldots ,k-1\), the equations in (45) can be rewritten as
where \(u:=q^{xk}(\vartheta ^k_+(t))-\lambda ^k(v^{xk}(t)+\theta ^{xk}(t))\) for every \(t\in (t^k_j,t^k_{j+1})\), \(j=0,\ldots ,k-1\), and \(i=1,\ldots ,m\), and where \(\vartheta ^k_+(t):=t^k_{j+1}\) for \(t\in [t^k_j,t^k_{j+1})\).
Define now we \(p^k(\cdot )=(p^{xk}(\cdot ),p^{uk}(\cdot ))\) on [0, T] by setting
for every \(t\in [0,T]\). This gives us \(p^k(T)=q^k(T)\) with the differential relation
holding for a.e. \(t\in [0,T]\). Substituting the latter into (49), we get
for every \(t\in (t^k_j,t^k_{j+1})\), \(j=0,\ldots ,k-1\), and \(i=1,\ldots ,m\). Define further the vector measures \(\gamma ^k\) by
and observe that, due to the positive homogeneity of all the expressions in the statement of Theorem 5.1 with respect to \((\lambda ^k,p^k,\gamma ^k)\), the nontriviality condition (47) can be rewritten as
which tells us that all the sequential terms in (50) are uniformly bounded. Following the proof of [7, Theorem 6.1], we obtain the relationships in (38), (41), and (43), where the form of the transversality condition (43) benefits from the “full” counterpart of the calculus rule in Proposition 3.2 for normals to inverse images that is valid under the full rank assumption in (H3). The measure nonatomicity condition of this theorem is also verified similarly to [7, Theorem 6.1].
Next, we establish the new measured coderivative condition (42), which was not obtained in [7] even in the particular framework therein. Rewrite first (46) in the form
via the functions \(\vartheta ^k(t)\) from (48). Since \(\gamma ^k(t)\) is a step vector function for each \(k\in N\), taking any \(t\ne t_j^k\) as \(j=0,\ldots ,k\) allows us to choose a number \(\delta _k>0\) sufficiently small so that \(|B|\le \delta _k\) whenever a Borel set B contains t, and thus B does not contain any mesh points. Hence, \(\gamma ^k(t)\) remains constant on B. As a result, we can write the representation
The separability of the space \(C([0,T];\mathbb {R}^s)\) and the boundedness of \(\gamma ^k(\cdot )\) in \(C^*([0,T];\mathbb {R}^s)\) by (50) allow us to select a subsequence of \(\{\gamma ^k(\cdot )\}\) (no relabeling) that weak\(^*\) converges in \(C^*([0,T];\mathbb {R}^s)\) to some \(\gamma (\cdot )\). As a result, we get without loss of generality that
for any Borel set B. To proceed further, choose a sequence \(\{B_k\}\subset B\) such that \(t\in B_k\), \(|B_k|\rightarrow 0\), and \(\frac{1}{|B_k|}\int _{B_k} \gamma (\tau )d\tau \rightarrow \alpha \) as \(k\rightarrow \infty \) for some \(\alpha \in \mathbb {R}^s\). It follows from the constructions above that
Taking into account the coderivative robustness with respect to all of its variables, we arrive at
for a.e. \(t\in [0,T]\), which verifies the measured coderivative condition (42).
To complete the proof of the theorem, it remains to justify the nontriviality condition (44). Arguing by contradiction, suppose that (44) fails and thus find sequences of \(\lambda ^k\rightarrow 0\) and \(\Vert p_j^k\Vert \rightarrow 0\) as \(k\rightarrow \infty \) uniformly in j. It follows from (50) and (39) that \(\int _0^T\Vert \gamma ^{k}(t)\Vert dt\rightarrow 1\) as \(k\rightarrow \infty \). Define now the sequence of measurable vector functions \(\beta ^k:[0,T]\rightarrow \mathbb {R}^s\) by
Using the Jordan decomposition \(\gamma ^k=(\gamma ^k)^+-(\gamma ^k)^-\) gives us a subsequence \(\{\gamma ^k\}\) and a Borel vector measure \(\gamma =\gamma ^+-\gamma ^-\) such that \(\{(\gamma ^{k})^+\}\) weak\(^*\) converges to \(\gamma ^+\) and \(\{(\gamma ^{k})^-\}\) weak\(^*\) converges to \(\gamma ^-\) in \(C^*([0,T];\mathbb {R}^s)\). Taking into account the uniform boundedness of \(\beta ^k(\cdot )\) on [0, T] allows us to apply the convergence result of [6, Proposition 9.2.1] (with \(A=A_i:=\mathbb {B}_{\mathbb {R}^s}\) for all \(i \in \mathbb {N}\) therein) and thus find a Borel measurable vector functions \(\beta ^+,\beta ^-:[0,T]\rightarrow \mathbb {R}^s\) so that, up to a subsequence, \(\{\beta ^k(\gamma ^k)^+\}\) weak\(^*\) converges to \(\beta ^+\gamma ^+\), and \(\{\beta ^k(\gamma ^k)^-\}\) weak\(^*\) converges to \(\beta ^-\gamma ^-\). As a result, we get
This means that \(\Vert \gamma \Vert =\Vert \gamma ^+\Vert +\Vert \gamma ^-\Vert \ne 0\), which contradicts the assumed failure of (44). \(\triangle \)
Note that the nontrivial optimality conditions obtained in Theorem 5.3 do not generally exclude the case of their validity for any feasible solution, although even in this case they may be useful as is shown by examples. The following consequence of Theorem 5.3 presents effective sufficient conditions ensuring nondegenerate optimality conditions for the considered local minimizers of (P). The reader can find more discussions on nondegeneracy in [6, 26, 27] for classical optimal control problems and Lipschitzian differential inclusions and in [7] for sweepings ones over polyhedral controlled sets. \(\square \)
Corollary 5.1
(Nondegeneracy) In the setting of Theorem 5.3, suppose that \(\eta (T)\) is well defined and that \(\theta =0\) is the only vector satisfying the relationships
Then, the necessary optimality conditions of Theorem 5.3 hold with the enhanced nontriviality
Proof
Arguing by contradiction, suppose that (52) fails, which yields \(\lambda =0\), \(q(0)=0\), \(q(T)=0\), and \(q=0\) for a.e. \(t\in [0,T]\). It follows from (38) that \(p\equiv p(T)\) on [0, T]. By using (41) and the fact that \(\nabla \psi (\bar{x}(t),\bar{u}(t))\) has full rank on [0, T], we get \(\gamma :=\theta _1\delta _{\{T\}}+\theta _2\delta _{\{T\}}\) for some \(\theta _1,\theta _2\in \mathbb {R}^s\) via the Dirac measures. Let us now check that \(\theta _1=\theta _2=0\). Since \(\eta (T)\) is well defined and since \(q(T)=0\) and \(\lambda =0\), we conclude that condition (42) holds at \(t=T\) being equivalent to
On the other hand, it follows from \(q(T)=0\) due to (41) that \(p(T)=\nabla \psi (\bar{x}(t),\bar{u}(t))^*\theta \). Using further (43) tells us that \(\nabla \psi (\bar{x}(T),\bar{u}(T))^*\theta _2\in -\nabla \phi (\bar{x}(T),\bar{u}(T))N_\varTheta ((\bar{x}(T),\bar{u}(T))\). Then, it follows from (51) and (53) that \(\theta _2=0\), which yields \(\theta _1=0\) and gives us a contradiction. \(\square \)
Remark 5.1
(Discussions on nondegeneracy) It is easy to see that the imposed assumption (52) excludes the degeneracy case of \(\lambda :=0\), \(p=q\equiv 0\), and \(\gamma :=\delta _{\{T\}}\) in Theorem 5.3. Furthermore, the inferiority assumption \(\psi (\bar{x}(T),\bar{u}(T))\in \mathrm{int}\,\varTheta \) yields (51) while not vice versa. To illustrate it, consider the following example: Minimize the cost
over the dynamics \(-\dot{x}(t)\in N(x(t);]-\infty ,u(t)])\) with \(x(0)=3{/}2\) and \(u(0)=-2\). We can directly check that the only optimal trajectory in this problem is given by \(\bar{x}(t)=3{/}2\) on [0, 1 / 2], \(\bar{x}(t)=2-t\) on [1 / 2, 1], and \(\bar{x}(t)=1\) on [1, 2], It is generated by the optimal control \(\bar{u}(t)=t-2\) on [0, 1] and \(\bar{u}(t)=-1\) on ]1, 2].
To check the nondegeneracy condition (51) in this example with \(\psi (x,u)=x+u\) and \(\varTheta =(-\infty ,0]\), observe that the second inclusion therein reduces to
which is equivalent to \(\alpha \le 0\). The first inclusion reads as
giving us \(\alpha \ge 0\). Thus, \(\alpha =0\), and condition (51) is satisfied. On the other hand, we see that the point \((\bar{x}(2),\bar{u}(2))=(1,-1)\) does not belong to the interior of the set \(\varTheta \).
6 Hamiltonian Formalism and Maximum Principle
The necessary optimality conditions for (P) obtained in Theorem 5.3 and Corollary 5.1 are of the extended Euler–Lagrange type that is pivoting in optimal control of Lipschitzian differential inclusions; see [5, 6]. The result of [5, Theorem 1.34] tells us that the Euler–Lagrange framework involving coderivatives implies the maximum condition of the Weierstrass-Pontryagin type for problems with convex velocities provided that the velocity mapping is inner semicontinuous (e.g., Lipschitzian), which is never the case in our setting (27). Nevertheless, we show in what follows that the Hamiltonian formalism and the maximum condition can be derived from the measured coderivative condition of Theorem 5.3 in rather broad and important situations by using coderivative calculations available in variational analysis.
The first result of this section deals with problem (P) in the case where \(\varTheta :=\mathbb {R}^s_-\). In this case, we consider the set of active constraint indices
It follows from Proposition 3.2 under (H3) that for each \(v\in -N(x;C(u))\), there is a unique collection \(\{\alpha _i\}_{i\in I(x,u)}\) with \(\alpha _i\le 0\) and \(v=\sum _{i\in I(x,u)}\alpha _i[\nabla _x\psi (x,u)]_i\). Given \(\nu \in \mathbb {R}^s\), define the vector \([\nu ,v]\in \mathbb {R}^n\) by
and introduce the modified Hamiltonian function
The following consequence of Theorem 5.3 and Corollary 5.1 shows that the measured coderivative condition (42) yields the maximization of the modified Hamiltonian (56) at the local optimal solutions for (P) with polyhedral constraints corresponding to \(\varTheta =\mathbb {R}^s_-\) in (9).
Corollary 6.1
(Maximum condition for polyhedral sweeping control systems under surjectivity) In the frameworks of Theorem 5.3 and Corollary 5.1 with \(\varTheta =\mathbb {R}^s_-\), we have the corresponding necessary optimality conditions therein together with the following maximum condition: There is a measurable vector function \(\nu :[0,T]\rightarrow \mathbb {R}^s\) such that \(\nu (t)\in \mathop {\mathrm{Lim}\,\mathrm{sup}}_{|B|\rightarrow 0}\frac{\gamma (B)}{|B|}(t)\) and
Proof
Let us show that the maximum condition (57) follows from the measured coderivative condition (42). To proceed, we need to compute the coderivative of the normal cone mapping \(D^*N_{\mathbb {R}^s_-}\), which has been done in variational analysis in several forms; see, for example, [19, 20] for more discussions and references. We use here the one taken from [22]: If \(D^*N_{\mathbb {R}^s_-}(w,\xi )(u)\ne \emptyset \), then
The measured coderivative condition (42) reads in this case as:
with a vector function \(\nu (t)\in \mathop {\mathrm{Lim}\,\mathrm{sup}}_{|B|\rightarrow 0}\frac{\gamma (B)}{|B|}(t)\), which can be selected as (Lebesgue) measurable on [0, T] due to the well-known measurable selection results; see, for example, [6, 18]. It follows from (58) that
which gives us by Eq. (40) that
On the other hand, we get from (54) to (56) with \(I:=I(\bar{x}(t),\bar{u}(t))\) that
for a.e. \(t\in [0,T]\). Applying now (58) gives us the implication
Combining this with (61), we get \(H_{\nu (t)}(\bar{x}(t),\bar{u}(t),q^x(t)-\lambda v^x(t))=0\) for a.e. \(t\in [0,T]\) and thus arrive at the maximum condition (57), where the other equality was established in (60). \(\square \)
Observe that the explicit coderivative computation (58) plays a crucial role in deriving the maximum condition (57) in Corollary 6.1. Available second-order calculus and coderivative evaluations for the normal cone mappings allow us to derive more general results of the maximum principle type in sweeping optimal control. The next theorem addresses the case where the set \(\varTheta \) in (9) is given by
via a smooth mapping \(h:\mathbb {R}^s\rightarrow \mathbb {R}^l\). As mentioned above, the surjectivity condition on the Jacobian \(\nabla h(\bar{z})\) at a fixed point \(\bar{z}\) corresponds to the LICQ condition at \(\bar{z}\). Dealing with linear mappings \(h(z):=Az-b\), we can replace the LICQ condition in the coderivative evaluation by the weaker positive LICQ (PLICQ) condition at \(\bar{x}\) that is discussed and implemented in [7]. It is used in what follows.
Theorem 6.1
(Maximum principle in sweeping optimal control) Consider the control problem (P) in the frameworks of Theorem 5.3 and Corollary 5.1 with the set \(\varTheta \) given by (62), where \(h:\mathbb {R}^s\rightarrow \mathbb {R}^l\) is \({{\mathcal {C}}}^2\)-smooth around the local optimal solution \(\bar{z}(t):=(\bar{x}(t),\bar{u}(t))\) for all \(t\in [0,T]\). Suppose that either \(\nabla h(\bar{z}(t))\) is surjective, or \(h(\cdot )\) is linear and the PLICQ assumption is fulfilled at \(\bar{z}(t)\) on [0, T]. Then, in addition to the corresponding necessary optimality conditions of the statements above, the maximum condition (57) holds with a measurable vector function \(\nu :[0,T]\rightarrow \mathbb {R}^s\) satisfying the inclusions \(\nu (t)\in \mathop {\mathrm{Lim}\,\mathrm{sup}}_{|B|\rightarrow 0}\frac{\gamma (B)}{|B|}(t)\) for a.e. \(t\in [0,T]\) and
where \(\mu :[0,T]\rightarrow \mathbb {R}^l\) is also measurable and such that
Proof
As in the proof of Corollary 6.1, we derive from the measured coderivative condition (42) the existence of a measurable function \({\widetilde{\nu }}:[0,T]\rightarrow \mathbb {R}^l\) satisfying the inclusion
Assuming that \(\nabla h(\bar{z}(t))\) is surjective on [0, T] and applying the second-order chain rule from [5, Theorem 1.127] together with the aforementioned measurable selection results, we find measurable functions \(\nu :[0,T]\rightarrow \mathbb {R}^s\) and \(\mu :[0,T]\rightarrow \mathbb {R}^l\) satisfying the conditions (63) and (64) as well as
which uniquely determines \(\nu (t)\) from \({\widetilde{\nu }}(t)\) for a.e. \(t\in [0,T]\). The validity of the maximum condition follows now from the proof of Corollary 6.1 due to the relationships above.
In the case where h is linear and the PLICQ holds, we proceed similarly by applying the evaluation of \(D^*N_{h^{-1}(\mathbb {R}^l_-)}\) from [7, Lemma 4.2] without claiming that \(\nu (t)\) is uniquely defined by \({\widetilde{\nu }}(t)\). \(\square \)
Remark 6.1
(Discussions on the maximum principle) The necessary optimality conditions of the maximum principle type obtained in Corollary 6.1 and Theorem 6.1 are the first in the literature for sweeping processes with controlled moving sets. Note that our form of the modified Hamiltonian (56) is different from the conventional Hamiltonian form
used in optimal control of Lipschitzian differential inclusions \(\dot{x}\in F(x)\) that extends the Hamiltonian in classical optimal control. We show below in Example 6.1 that the maximum principle via the conventional Hamiltonian (65) fails for our problem (P). The reason is that (65) does not reflect implicit state constraints, which do not appear for Lipschitzian problems while being an essential part of the sweeping dynamics; see the discussions in Sect. 1. Note that the Hamiltonian form (56) is also different from that used in [15,16,17] for deriving maximum principles in sweeping control problems with uncontrolled moving sets that are significantly diverse from our problem (P).
We can see that the new maximum principle form (57) incorporates vector measures that appear through the measured coderivative condition (42). The fact that measures naturally arise in descriptions of necessary optimality conditions in optimal control problems with state constraints has been first realized by Dubovitskii and Milyutin [25] and since that has been fully accepted in the literature; see, for example, [6, 26] and the references therein. There are interesting connections between our form of the maximum principle for controlled sweeping processes and the Hamiltonian formalism in models of contact and nonsmooth mechanics (see, e.g., [28, 29]), which we plan to fully investigate in subsequent publications.
The next example shows that the maximum principle in the conventional form used for Lipschitzian differential inclusions [6, 26] with the standard Hamiltonian (65) fails for the sweeping control problem (P), while our new form obtained in Theorem 6.1 holds.
Example 6.1
(Failure of the conventional maximum principle for sweeping processes) We consider the optimal control problem for the sweeping process taken from [7, Example 7.6], where the controlled moving set is defined by (7) with control actions \(u_j(t)\) and \(b_j(t)\). Specify the initial data as
and fix the u-controls as \(\bar{u}_1\equiv (1,0)\), \(\bar{u}_2\equiv (0,1)\). The necessary optimality conditions of Corollary 5.1 give us in this case the following relationships on [0, 1]:
-
(1)
\(w(\cdot )=0\), \(v^x(\cdot )=0\), \(v^b(\cdot )=\left( {\dot{b}}_1(\cdot ),{\dot{b}}_2(\cdot )\right) \);
-
(2)
\(\;{\dot{\bar{x}}}_i(t)\ne 0\Longrightarrow q^x_i(t)=0\), \(i=1,2\),
-
(3)
\(p^b(\cdot )\) is constant with nonnegative components; \(-p_i^x(\cdot )=\lambda \bar{x}(1)+p_i^b(\cdot )\bar{u}_i\) are constant for \(i=1,2\),
-
(4)
\(q^x(t)=p^x-\gamma ([t,1])\), \(q^b(t)=\lambda {\dot{\bar{b}}}(t)=p^b+\gamma ([t,1])\) for a.e. \(t\in [0,1]\),
-
(5)
\(\lambda +\Vert q(0)\Vert +\Vert p(1)\Vert \ne 0\) with \(\lambda \ge 0\).
Observe first that the pair \(\bar{x}(t)=(1,1)\) and \(\bar{b}(t)=0\) on [0, 1] satisfies the necessary conditions with \(p_1^x=p_2^x=-1\), \(p_1^b=p_2^b=\gamma _1=\gamma _2=0\), and \(\lambda =1\)). The conventional Hamiltonian (65) reads now as
and we get by the direct calculation that
while \(\langle {{\dot{\bar{x}}}}(t),q^x(t)-\lambda v^x(t)\rangle =0\), and thus the conventional maximum principle fails in this example. At the same time, the new maximum condition (57) holds trivially with \(\nu (t)\equiv 0\) on [0, 1].
The following consequence of Theorem 6.1 provides a natural sufficient condition for the validity of the maximum principle in terms of the conventional Hamiltonian (65).
Corollary 6.2
(Maximum principle in the conventional form) Assume that in the setting of Theorem 6.1, we have the condition
where \(\eta (t)\in N(\psi (\bar{x}(t),\bar{u}(t));\varTheta )\) is uniquely defined by (40). Then
Proof
This follows from (59) and its counterpart in the proof of Theorem 6.1 by definitions of the modified and conventional Hamiltonians. \(\square \)
7 Applications to Elastoplasticity and Hysteresis
In this section, we discuss some applications of the obtained necessary optimality conditions to a fairly general class of problems relating to elastoplasticity and hysteresis.
Let us consider the model of this type discussed in [30, Section 3.2], which can be described in our form, where Z is a closed convex subset of the \(\frac{1}{2}n(n+1)\)-dimensional vector space E of symmetric tensors \(n\times n\) with \(\mathrm{int}\,Z\ne \emptyset \). Using the notation of [30], define the strain tensor \(\epsilon =\{\epsilon \}_{i,j}\) by \(\epsilon :=\epsilon ^e+\epsilon ^p\), where \(\epsilon ^e\) is the elastic strain and \(\epsilon ^p\) is the plastic strain. The elastic strain \(\epsilon ^e\) depends on the stress tensor \(\sigma =\{\sigma \}_{i,j}\) linearly, i.e., \(\epsilon ^e=A^2\sigma \), where A is a constant symmetric positive-definite matrix. The principle of maximal dissipation says that
It is shown in [30] that the variational inequality (66) is equivalent to the sweeping processes
where \(\zeta (t):=A\sigma (t)-A^{-1}\epsilon (t)\) and \(C(t):=-A^{-1}\epsilon (t)+AZ\). It can be rewritten in the frame of our problem (P) with \(x:=\zeta \), \(u:=\epsilon \), \(\psi (x,u):=x+A^{-1}u\), and \(\varTheta :=AZ\). Thus, we can apply Theorem 5.3 to this class of hysteresis operators for the general elasticity domain Z. Note that a similar model is considered in [31], only for the von Mises yield criterion. Our results obtained here give us the flexibility of applications to many different elastoplasticity models including those with the Drucker–Prager, Mohr–Coulomb, Tresca, von Mises yield criteria, etc.
In the following example, we summarize applications of Theorem 5.3 to solve a meaningful optimal control problem generated by the elastoplasticity dynamics (67).
Example 7.1
(Optimal control in elastoplasticity) Consider the dynamic optimization problem:
over feasible solutions to the sweeping process (67) with the initial point \(\zeta (0)\in C(0)\). Observe that the linear function \({\bar{\epsilon }}(t):=tz+{\bar{\epsilon }}(0)\) with appropriate adjustments of the starting and terminal points is an optimal control to the corresponding problem (P). Remembering the above notation for \(x,u,\psi \), and \(\varTheta \), we derive from Theorem 5.3 the following necessary optimality conditions:
Assuming that \(\zeta (T)\in \mathrm{int}\,C(T)\) and using the measure nonatomicity condition, we get from (1)–(5) that \(\lambda =1\). It follows from the linearity of \({\bar{\epsilon }}\) that \(\frac{d}{dt}{\bar{\epsilon }}(t)\equiv :a\) and that the choice of \(p\equiv 0\), \(q\equiv (\lambda a,\lambda a)\), and \(\gamma \equiv (-a,-a)\delta _{\{1\}}\) fulfills all conditions (1)–(5). \(\square \)
Note that in the above example we actually guessed the form of optimal solutions and then checked the fulfillment of the obtained necessary optimality conditions. The following example does more by showing how to calculate an optimal solution by using the necessary optimality conditions of Theorem 5.3 together with the maximum condition from Corollary 6.1.
Example 7.2
(Calculation of optimal solutions) Consider here the optimal control problem taken from the example in Remark 5.1. Applying the necessary optimality conditions of Corollary 5.1 with the enhanced nontriviality condition (52), we get the following:
together with the measured coderivative condition telling is that
where \(\nu (t)\in \mathop {\mathrm{Lim}\,\mathrm{sup}}_{|B|\rightarrow 0}\frac{\gamma (B)}{|B|}(t)\). To proceed, take \(\sigma \in ]0,2]\) such that the state constraint is inactive on \([0,\sigma [\) while it is active on \([\sigma ,2]\). It follows from (3) that \((p^x,p^u)\) is constant on [0, 2]. Assuming by contradiction that \(\lambda =0\), we get from (4) that \(q^u\equiv 0\), and so \(q^x\equiv 0\) by (5). It shows that (7) is violated, and thus \(\lambda =1\). Since \(\bar{x}(t)+\bar{u}(t)<0\) on \([0,\sigma [\), it follows from (68) and (58), which gives us the maximum condition (57), that \(\nu (t)=0\) for all \(t\in [0,\sigma [\). Then, \(q^u(t)\) remains constant on \([0,\sigma [\) by (5). Combining this with (4) shows that \(\bar{u}(t)=t-2\) on \([0,\sigma ]\). Using now (2) and the fact that \(\bar{x}(t)+\bar{u}(t)<0\) for \(t\in [0,\sigma [\), we get \(\bar{x}\equiv 3/2\) on \([0,\sigma ]\). Then, \(\bar{x}(\sigma )+\bar{u}(\sigma )=\sigma -2+3/2=0\) and \(\sigma =1/2\). Assuming further that \({{\dot{\bar{x}}}}(t)<0\) on \(]1/2,\sigma _1[\) for some \(\sigma _1\in ]1/2,2]\) and using (68) together with (58) tell us that \(q^x\equiv 0\) on \((1/2,\sigma _1[\). Applying (5) again, we have \(\bar{u}(t)=t-2\) on \([1/2,\sigma _1]\). Since \({{\dot{\bar{x}}}}(t)<0\) on \(]1/2,\sigma _1[\), it follows from (2) that \(\bar{x}(t)=-\bar{u}(t)=2-t\) on \([1/2,\sigma _1]\); thus, we tend to move \(\bar{x}(t)\) toward 1. This means that when \(\bar{x}(\sigma _1)=2-\sigma _1=1\), the object stops moving, i.e., \({{\dot{\bar{x}}}}(t)=0\) on [1, 2]. Note that (5) yields \(\nu (t)=-\dot{q}^u(t)=-\dot{q}^x(t)\) on [0, 2]. If furthermore \(\bar{u}(t)\) is strictly increasing, then \(q^u(t)\) is also strictly increasing. Since \(\nu (t)=-\dot{q}^u(t)\), we get \(\nu (t)<0\). Then, (68) and (58) imply that \({{\dot{\bar{x}}}}(t)<0\), a contradiction. Assuming that \(\bar{u}(t)\) is strictly decreasing tells us by (4) that \(q^u(t)\) is strictly decreasing, and so \(\nu (t)<0\) by \(\nu (t)= -\dot{q}^u(t)\). In this case, conditions (68) and (58) yield \(q^x(t)\ge 0\), and hence we have \(q^x(2)\le 0\) by (6). It shows that \(q^x(t)=0\) on [1, 2] and so \(\nu (t)=-\dot{q}^x(t)=0\), which contradicts the condition \(\nu (t)<0\). Thus, \(\bar{u}(t)\) remains constant on [1, 2], and we find an optimal solution to this problem.
8 Conclusions
This paper presents new results on extended Euler–Lagrange and Hamiltonian optimality conditions for a rather general class of controlled sweeping processes. In our future research in this direction, we plan to focus on optimal control problems governed by rate-independent operators governed by doubly nonlinear evolution inclusions (sometimes referred to as quasi-sweeping processes) in finite-dimensional and Banach spaces. Among our major applications, we plan to consider practical hysteresis models, especially those arising in problems of contact and nonsmooth mechanics; see [28, 29] for more details.
References
Moreau, J.J.: On unilateral constraints, friction and plasticity. In: Capriz, G., Stampacchia, G. (eds.) Proceedings from CIME New Variational Techniques in Mathematical Physics, pp. 173–322. Cremonese, Rome (1974)
Colombo, G., Thibault, L.: Prox-regular sets and applications. In: Gao, D.Y., Motreanu, D. (eds.) Handbook of Nonconvex Analysis, pp. 99–182. International Press, Boston (2010)
Colombo, G., Henrion, R., Hoang, N.D., Mordukhovich, B.S.: Optimal control of the sweeping process. Dyn. Contin. Discrete Impuls. Syst. Ser. B 19, 117–159 (2012)
Clarke, F.H.: Necessary conditions in dynamics optimization. Mem. Am. Math. Soc. 344(816), 299 (2005)
Mordukhovich, B.S.: Variational Analysis and Generalized Differentiation, I: Basic Theory, II: Applications. Springer, Berlin (2006)
Vinter, R.B.: Optimal Control. Birkhaüser, Boston (2000)
Colombo, G., Henrion, R., Hoang, N.D., Mordukhovich, B.S.: Optimal control of the sweeping process over polyhedral controlled sets. J. Differ. Equ. 260, 3397–3447 (2016)
Mordukhovich, B.S.: Discrete approximations and refined Euler–Lagrange conditions for differential inclusions. SIAM J. Control Optim. 33, 882–915 (1995)
Cao, T.H., Mordukhovich, B.S.: Optimal control of a perturbed sweeping process via discrete approximations. Disc. Contin. Dyn. Syst. Ser. B 21, 3331–3358 (2016)
Cao, T.H., Mordukhovich, B.S.: Optimality conditions for a controlled sweeping process with applications to the crowd motion model. Disc. Contin. Dyn. Syst. Ser. B 22, 267–306 (2017)
Cao, T.H., Mordukhovich, B.S.: Optimal control of a nonconvex perturbed sweeping process. J. Differ. Equ. (2018). https://doi.org/10.1016/j.jde.2018.07.066
Donchev, T., Farkhi, E., Mordukhovich, B.S.: Discrete approximations, relaxation, and optimization of one-sided Lipschitzian differential inclusions in Hilbert spaces. J. Differ. Equ. 243, 301–328 (2007)
Briceño-Arias, L.M., Hoang, N.D., Peypouquet, J.: Existence, stability and optimality for optimal control problems governed by maximal monotone operators. J. Differ. Equ. 260, 733–757 (2016)
Pontryagin, L.S., Boltyanskii, V.G., Gamkrelidze, R.V., Mishchenko, E.F.: The Mathematical Theory of Optimal Processes. Wiley, New York (1962)
Brokate, M., Krejčí, P.: Optimal control of ODE systems involving a rate independent variational inequality. Disc. Contin. Dyn. Syst. Ser. B 18, 331–348 (2013)
Arroud, C.E., Colombo, G.: A maximum principle of the controlled sweeping process. Set Valued Var. Anal. 26, 607–629 (2018)
de Pinho, M.D.R., Ferreira, M.M.A., Smirnov, G.V.: Optimal control involving sweeping processes. Set-Valued Var. Anal. (to appear)
Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis. Springer, Berlin (1998)
Mordukhovich, B.S.: Variational Analysis and Applications. Springer, New York (2018)
Mordukhovich, B.S., Rockafellar, R.T.: Second-order subdifferential calculus with applications to tilt stability in optimization. SIAM J. Optim. 22, 953–986 (2012)
Henrion, R., Outrata, J.V., Surowiec, T.: On the coderivative of normal cone mappings to inequality systems. Nonlinear Anal. 71, 1213–1226 (2009)
Mordukhovich, B.S., Outrata, J.V.: Coderivative analysis of quasi-variational inequalities with mapplications to stability and optimization. SIAM J. Optim. 18, 389–412 (2007)
Edmond, J.F., Thibault, L.: Relaxation of an optimal control problem involving a perturbed sweeping process. Math. Program. 104, 347–373 (2005)
Tolstonogov, A.A.: Control sweeping process. J. Convex Anal. 23, 1099–1123 (2016)
Dubovitskii, A.Y., Milyutin, A.A.: Extremum problems in the presence of restrictions. USSR Comput. Math. Math. Phys. 5, 1–80 (1965)
Arutyunov, A.V., Aseev, S.M.: Investigation of the degeneracy phenomenon of the maximum principle for optimal control problems with state constraints. SIAM J. Control Optim. 35, 930–952 (1997)
Arutyunov, A.V., Karamzin, DYu.: Nondegenerate necessary optimality conditions for the optimal control problems with equality-type state constraints. J. Global Optim. 64, 623–647 (2016)
Brogliato, B.: Nonsmooth Mechanics: Models, Dynamics and Control, 3rd edn. Springer, Cham (2016)
Razavy, M.: Classical and Quantum Dissipative Systems. World Scientific, Singapore (2005)
Adly, S., Haddad, T., Thibault, L.: Convex sweeping process in the framework of measure differential inclusions and evolution variational inequalities. Math. Program. 148, 5–47 (2014)
Herzog, R., Meyer, C., Wachsmuth, G.: B-and strong stationarity for optimal control of static plasticity with hardening. SIAM J. Optim. 23, 321–352 (2013)
Acknowledgements
Research of the second author was partly supported by the USA National Science Foundation under grants DMS-1512846 and DMS-1808978, and by the USA Air Force Office of Scientific Research under Grant #15RT0462.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hoang, N.D., Mordukhovich, B.S. Extended Euler–Lagrange and Hamiltonian Conditions in Optimal Control of Sweeping Processes with Controlled Moving Sets. J Optim Theory Appl 180, 256–289 (2019). https://doi.org/10.1007/s10957-018-1384-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-018-1384-4
Keywords
- Optimal control
- Sweeping process
- Variational analysis
- Discrete approximations
- Generalized differentiation
- Euler–Lagrange and Hamiltonian formalisms
- Maximum principle
- Rate-independent operators