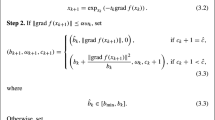An Incremental Subgradient Method on Riemannian Manifolds

Abstract

In this paper, we propose and analyze an incremental subgradient method with a diminishing stepsize rule for a convex optimization problem on a Riemannian manifold, where the object function consisted of the sum of a large number of component functions. This type of function is useful in lots of fields. We establish an important inequality about the sequence generated by the method, provided the sectional curvature of the manifold is nonnegative. Using the inequality, we prove Proposition 3.1, and then we obtain some convergence results of the incremental subgradient method.

1 Introduction

Incremental gradient methods for differentiable unconstrained optimizations have a long tradition, and they are known as backpropagation methods in the training of neural networks. The methods are related to the Widrow–Hoff algorithm [1] and to stochastic gradient/stochastic approximation methods. They are supported by several convergence analyses in [2,3,4,5]. The methods often converge much faster than the steepest descent method when far from the eventual limit. Incremental subgradient methods are motivated by the considerations of convergence rate too. And compared with the incremental gradient methods, incremental subgradient methods do not require object functions be differentiable, which broadens the field of their applications. Incremental subgradient methods were studied first by Kibardin [6], and then by Solodov and Zavriev [7], Nedić and Bertsekas [8], and Ben-Tal et al. [9]. Nedić et al. [10] proposed an asynchronous parallel version of the incremental subgradient method, and a parallel implementation of related methods is proposed by Kiwiel and Lindberg [11]. These methods share the characteristics of computing a subgradient of only one component function per iteration, and using the sum of the (approximate) subgradients of all the component functions as the direction in an iteration. The incremental ways of the incremental subgradient methods are mainly classified by determined or random relay paths. Cyclic and uniform randomized relay modes have been proposed in the seminal paper [12], and their convergence properties of several stepsize rules have been analyzed too. Later, Ram [13] studied the Markov randomized incremental subgradient method. This is a noncyclic version of the incremental algorithm, where the sequence of computing agents is modeled as a time nonhomogeneous Markov chain. Recently, incremental subgradient methods have been used to solve the least square regression problem and SVM classification case in [14], while they can potentially be used to solve any separable optimization problems as indicated in [15]. They can also be used to solve stochastic optimization problem when objective functions are determined in [16], which actually are some incremental stochastic gradient algorithms. A unified framework on distributed estimations in-network using incremental subgradient methods is introduced in [17].

Recently, extensions of optimization problems from Euclidean spaces or Hilbert spaces to Riemannian manifolds has been the subject of many research papers. For instance, some results of convex optimization problem are extended to Riemannian manifolds in [18,19,20]. The proximal point method on Hadamard manifolds and Riemannian manifolds are studied in [21, 22]. Li and Wang have made a lots of research on Newton’s method and its convergence problems on Riemannian manifolds in [23,24,25]. A steepest descent method with Armijo’s rule for multicriteria optimization in the Riemannian context is presented in [26]. The semivectorial bilevel optimization problem in the Riemannian setting is concerned with in [27]. The reason of these extensions is that, as explained in [28], some optimization problems, arising in various applications, cannot be posted in linear spaces and require Riemannian manifold structures for their formalization and study. Besides, such extensions have some other advantage. For example, some constrained optimization problems can be regarded as unconstrained ones from the Riemannian geometry viewpoint. Moreover, when a convexity structure on a Riemannian manifold is considered, some nonconvex optimization problems in the Euclidean setting may become convex by introducing an appropriate Riemannian metric; see, for example, [29,30,31,32]. Also, these extensions give rise to interesting theoretical questions. Due to the increased mathematical technicality of these methods, and the fact that the traditional algorithms have proven to be as successful as they have, it is possible to generalize gradient-based optimization algorithms to curved spaces. The subgradient methods are generalized to the context of Riemannian manifolds first by Ferreira and Oliveira [33], and the convergence properties of the methods have been analyzed too. Later, Ferreira [34] extended the concept of proximal subgradient and some results of proximal analysis from Hilbert spaces to Riemannian manifold setting. Bento and Melo [35], and Bento and Cruz [36] have proposed and analyzed some subgradient-type algorithms for solving convex feasibility problem and multiobjective optimization problems on Riemannian manifolds. Under the assumption that the sectional curvature of the manifold is bounded from below, Wang, Li and Yao [37] established convergence results about the cyclic subgradient projection algorithm for convex feasibility problem on Riemannian manifolds.

In this paper, we propose and analyze an incremental subgradient method with a diminishing stepsize for a convex optimization problems, where the object function consists of the sum of a large number of component functions and defined on a (connected) complete Riemannian manifold. Assuming that the manifold has a nonnegative sectional curvature, we show that, the function values of any sequence generated by the incremental subgradient method converge to the value of some point in the level set. Using the property, we obtain some important convergence results of the incremental subgradient method.

The organization of our paper is as follows. In the next section, we recall some notations and properties of Riemannian geometry, together with some definitions and results of convex analysis on Riemannian manifolds. Some definitions and propositions about quasi-Fejér convergent on Riemannian manifolds are presented too. In Sect. 3, an incremental subgradient method in the Riemannian context is proposed and analyzed, where we employ a diminishing stepsize rule. Assuming that the Riemannian manifold has nonnegative sectional curvature, we establish a useful proposition that will be used in the subsequent convergence analysis. In Sect. 4, we prove our main convergence results of the incremental subgradient method, including a convergence rate result. The last section contains a conclusion.

2 Notations and Preliminaries

In this section, we introduce some basic concepts, properties, and notations on Riemannian geometry. These basic facts can be found in any introductory book on Riemannian geometry; see, for example, [38, 39]. Then we present some definitions and preliminary results of convexity on Riemannian manifolds.

Let M be a connected manifold. We denote by $T_{x}M$ the tangent space of M at x, by $TM=\bigcup _{x\in M}T_xM$ the tangent bundle of M and by $\mathcal {X}(M)$ the spaces of smooth vector fields over M. Recall that a Riemannian metric on a smooth manifold M is a tensor field of type (0,2) that is symmetric and positive definite. Every Riemannian metric thus determines an inner product and a norm on each tangent space $T_x(M)$, which are typically written as $\langle \cdot , \cdot \rangle _x$ and $\Vert \cdot \Vert _x$, where the subscript x may be omitted if no confusion arises. The pair $(M, \langle \cdot , \cdot \rangle )$ is called Riemannian manifold if $\langle \cdot , \cdot \rangle$ is a Riemannian metric on M.

Given x and $y\in M$, the distance from x to y is defined by

$$\begin{aligned} d(x,y):=\inf l(\gamma ), \end{aligned}$$

(1)

where $\gamma : [a,b]\rightarrow M$ is a piecewise smooth curve joining x to y, such that $\gamma (a)=x$ and $\gamma (b)=y$, and

$$\begin{aligned} l(\gamma )=\int _{a}^{b}\Vert \gamma '(t)\Vert \mathrm{d}t, \end{aligned}$$

is the length of $\gamma$.

Let $\nabla$ be the Levi–Civita connection associated with $(M, \langle \cdot , \cdot \rangle )$. A vector field V along $\gamma$ is said to be parallel iff $\nabla _{\gamma '}V=0$. And if $\gamma '$ itself is parallel, then $\gamma$ is a geodesic. Obviously, a geodesic $\gamma$ satisfied a second-order nonlinear ordinary differential equation $\nabla _{\gamma '}\gamma '=0$, which is called the geodesic equation. So the geodesic $\gamma$ is determined by its position and velocity at one point, and given $x\in M$, $\upsilon \in T_xM$, there exists a unique geodesic starting at x such that $\upsilon$ is its tangent vector at x. Such geodesic is denoted by $\gamma _{\upsilon }$, when there is no confusion. It is easy to check that $\Vert \gamma '\Vert$ is constant. We say that $\gamma$ is normalized iff $\Vert \gamma '\Vert =1$. The restriction of a geodesic to a closed bounded interval is called a geodesic segment. A geodesic segment joining x to y in M is said to be minimal if and only if its length is equal to d(x, y), and this geodesic is called a minimizing geodesic.

A Riemannian manifold where all geodesics exist for all time is called complete. According to the Hopf–Rinow theorem [39, Theorem 1.1], if a Riemannian manifold is complete, then any two points $x,x'\in M$ can be joined by a minimal geodesic segment. Moreover, (M, d) is a complete metric space, any bounded and closed subset is compact.

The curvature tensor R is defined by

$$\begin{aligned} R(X, Y)=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X, Y]}Z, \end{aligned}$$

with $X,Y,Z\in \mathcal {X}(M)$, where $[X, Y]=YX-XY$, then the sectional curvature with respect to X and Y is given by

$$\begin{aligned} K(X, Y)=\frac{\langle R(X, Y)Y, X\rangle }{\Vert X\Vert ^{2}\Vert Y\Vert ^{2}-\langle X, Y\rangle ^{2}}, \end{aligned}$$

where $\Vert X\Vert =\langle X, X\rangle ^{1/2}$.

The following result is an immediate consequence of the Toponogov theorem; see, for instance, [33, Corollary 2.1].

Proposition 2.1

Let M be a complete Riemannian manifold with sectional curvature $K \ge 0$. If $\gamma _{\upsilon _{1}}$ and $\gamma _{\upsilon _{2}}$ are normalized geodesics such that $\gamma _{\upsilon _{1}}(0)=\gamma _{\upsilon _{2}}(0)$, then

$$\begin{aligned} d(\gamma _{\upsilon _{1}}(t_{1}), \gamma _{\upsilon _{2}}(t_{2}))\le \Vert t_{2}\upsilon _{2}-t_{1}\upsilon _{1}\Vert . \end{aligned}$$

A real-valued function f defined on a complete Riemannian manifold M is said to be a convex function if and only if for any geodesic segment $\gamma : [-\delta , \delta ]\rightarrow M, \delta >0$, the composition $f\circ \gamma : [-\delta , \delta ]\rightarrow \mathbb {R}$ is convex (in the usual sense). Some definitions and properties related to convex functions on Riemannian manifolds are as follows.

Definition 2.1

Let f be a convex function defined on a Riemannian manifold M. A vector $g\in T_{x}M$ is said to be a subgradient of f at x if for any geodesic $\gamma$ of M with $\gamma (0)=x$,

$$\begin{aligned} (f\circ \gamma )(t)\ge f(x)+t\langle g, \gamma '(0)\rangle , \end{aligned}$$

(2)

for any $t\ge 0$. The set of all the subgradients of f at x, denoted by $\partial f(x)$, is called the subdifferential of f at x.

Proposition 2.2

Let f be a convex function defined on a Riemannian manifold M. Then, for every $x\in M$, $\partial f(x)$ is nonempty, convex, and compact.

Proof

See [29]. $\square$

Proposition 2.3

Let $\{x_k\} \subset M$ a bounded sequence. If the sequence $\{s_k\}$ is such that $s_k\in \partial f(x_k)$ for each $k\in \mathbb {N}$, then $\{s_k\}$ is also bounded.

Proof

See [35]. $\square$

The following definition and property about quasi-Fejér convergent [33] on a Riemannian manifold will be used in the subsequent convergence analysis.

Definition 2.2

A sequence $\{y_k\}$ in the complete metric space (M, d) is quasi-Fejér convergent to a nonempty set $W\subset M$ if, for every $w\in W$, there exists a sequence $\{\delta _k\}\subset \mathbb {R}$ such that $\delta _k\ge 0, \sum _{k=0}^\infty \delta _k<+\infty$, and

$$\begin{aligned} d^2(y_{k+1},w)\le d^2(y_{k},w)+\delta _k, \end{aligned}$$

for all k.

Proposition 2.4

Let $\{y_k\}$ be a sequence in the complete metric space (M, d). If $\{y_k\}$ is quasi-Fejér convergent to a set $W\subset M$, then $\{y_k\}$ is bounded. If furthermore, a cluster point y of $\{y_k\}$ belongs to W, then $\lim _{k\rightarrow \infty }y_k=y$.

The following result is needed in the convergence analysis too.

Proposition 2.5

Let $\{\alpha _k\}, \{\beta _k\}\subset \mathbb {R}$. Assume that $\alpha _k\ge 0$ for all $k\ge 0$, $\sum _{k=0}^{\infty }\alpha _k=\infty$, $\sum _{k=0}^\infty \alpha _k\beta _k<\infty$ and there exists $\widetilde{k}\ge 0$ such that $\beta _k\ge 0$ for $k\ge \widetilde{k}$. Then, there exists a subsequence $\{\beta _{i(k)}\}$ of $\{\beta _k\}$ such that $\lim _{k\rightarrow \infty }\beta _{i(k)}=0$. If there exists $\theta >0$ such that $\beta _{k+1}-\beta _k\le \theta \alpha _k$ for all k, then $\lim _{k\rightarrow \infty }\beta _k=0$.

Proof

See [40]. $\square$

3 Algorithm and Auxiliary Results

In this section, we consider the following problem that consists of the sum of a large number component functions on Riemannian manifolds

$$\begin{aligned} \min _{x\in M} f(x), \end{aligned}$$

(3)

where M is a complete Riemannian manifold, $f(x)=\sum _{i=1}^m f_i(x)$ and $f_i: M\rightarrow \mathbb {R}$, $i=1, 2, \ldots , m$, are convex functions. This kind of problem arise in many contexts, such as dual optimization of separable problems, machine learning (regularized least squares, maximum likelihood estimation, the EM algorithm, neural network training), and others (distributed estimation, the Fermat–Weber problem in location theory). For this problem, incremental methods, consisting of gradient or subgradient iterations applied to single components, have proved very effective. So for problem (3), we give an incremental subgradient method as follows.

Algorithm 3.1

Incremental subgradient method. The sequence {$\alpha _k$} is given with $\alpha _{k}>0$ for $k=1,2,\ldots$.

Step 1: Initialization. Select $x_0\in M$ arbitrarily and obtain $g_0\in \partial f(x_0)$. Set $k=0$.

Step 2: If $g_k=0$, stop. Otherwise, set $\psi _{0,k}=x_k$, $i=1$, and go to Step 3.

Step 3: Obtain $g^{i,i-1}_k\in \partial f_i(\psi _{i-1,k})$. Calculate the geodesics $\gamma _{\upsilon _{i-1,k}}$ with $\gamma _{\upsilon _{i-1,k}}(0)=\psi _{i-1,k}, \gamma '_{\upsilon _{i-1,k}}(0)=\upsilon _{i-1,k}, \upsilon _{i-1,k}=-\frac{g^{i,i-1}_k}{\Vert g^{i,i-1}_k\Vert }$. Set $\psi _{i,k}=\gamma _{\upsilon _{i-1,k}}(t_{i-1, k})$, where $t_{i-1, k}=\alpha _k\Vert g^{i,i-1}_k\Vert$, and go to Step 4.

Step 4: If $i=m$, set $x_{k+1}=\psi _{m,k}$, and go to Step 5. Otherwise, increase i by 1, and go to Step 3.

Step 5: Obtain $g_{k+1}\in \partial f(x_{k+1})$. Set $k=k+1$ and go to Step 2.

The incremental subgradient method is similar to the subgradient method in [33]. The main difference is that at each iteration, x is changed incrementally through a sequence of m step, and each step is a subgradient iteration for a single component function $f_i$. Thus, an iteration can be viewed as a cycle of m subiterations. It follows from Definition 2.1 that if $g_k=0$ for some k, where $g_k\in \partial f(x_k)$, we have $(f\circ \gamma )(t)\ge f(x_k)$ for any $t\ge 0$. It is immediate to know that Algorithm 3.1 stops in some iteration k if and only if $x_k$ is a optimal point of the problem.

Throughout the study process, we use the following notations

$$\begin{aligned} L(x)=\{y\in M: f(y)\le f(x)\}; \end{aligned}$$

(4)

the set is called the level set of f at x.

$$\begin{aligned} f_{\mathrm{inc}}^k= & {} \sum _{i=1}^{m}f_i(\psi _{i-1,k}), \end{aligned}$$

(5)

$$\begin{aligned} C_k= & {} \sup _{1\le i,j\le m}\left\| g_k^{i,j-1}\right\| , \end{aligned}$$

(6)

where $\left\{ g_k^{i,j-1}\right\} \in \partial f_i(\psi _{j-1,k})$ for $i,j=1,2,\ldots ,m$, $k=0, 1, \ldots$. According to Algorithm 3.1, an iteration can be viewed as a cycle of m subiterations. So in the kth iteration, the points $\psi _{i-1,k}, i=1,2,\ldots ,m$ are finite, and $f_i, i=1,2,\ldots ,m$ are convex functions. Combining Proposition 2.3, we know $\left\{ \left\| g_k^{i,j-1}\right\| , i, j=1,2,\ldots ,m\right\}$ of the kth iteration is bounded and denotes the upper bounds by $C_k$.

Assuming that the Riemannian manifold has nonnegative sectional, a useful lemma about the sequence generated by Algorithm 3.1 can be proved.

Lemma 3.1

Let $\{x_k\}$ be a sequence generated by Algorithm 3.1 and take $y\in M$. If M has sectional curvature $K\ge 0$, then

$$\begin{aligned} d^2(x_{k+1},y)\le d^2(x_{k},y)+\alpha _k^2C_k^2m^2+2\alpha _k[f(y)-f(x_k)], \end{aligned}$$

(7)

for all $k\in \mathbb {N}$.

Proof

Take $y\in M$. Let $\gamma _{\upsilon _1}$ be the minimizing geodesics, that is for $\upsilon _1$ such that $\Vert \upsilon _1\Vert =1$, we take $\gamma _{\upsilon _1}(0)=\psi _{i-1,k}$, $\gamma _{\upsilon _1}(t_1)=y$, with $t_1=d(\psi _{i-1,k},y)$. Also, let $\gamma _{\upsilon _2}$ be the geodesics such that $\upsilon _2=\upsilon _{i-1,k}=-\frac{g^{i,i-1}_k}{\Vert g^{i,i-1}_k\Vert }$, $\gamma _{\upsilon _2}(0)=\psi _{i-1,k}$ and $\gamma _{\upsilon _2}(t_2)=\psi _{i,k}$ with $t_2=t_{i-1, k}=\alpha _k\left\| g_k^{i,i-1}\right\|$. Then, it follows from Proposition 2.1 and (6) that

$$\begin{aligned} d^2(\psi _{i,k},y)= & {} d^2(\gamma _{\upsilon _1}(t_1),\gamma _{\upsilon _2}(t_2)) \nonumber \\\le & {} \Vert t_2\upsilon _2-t_1\upsilon _1\Vert ^2\nonumber \\= & {} \left\| -\alpha _k\Vert g_k^{i,i-1}\Vert \left[ \frac{g_k^{i,i-1}}{\left\| g_k^{i,i-1}\right\| }\right] -t_1\upsilon _1\right\| ^2\nonumber \\= & {} t_1^2+\alpha _k^2\left\| g_k^{i,i-1}\right\| ^2+2\frac{\alpha _k\left\| g_k^{i,i-1}\right\| }{\left\| g_k^{i,i-1}\right\| }\left\langle g_k^{i,i-1},t_1\upsilon _1\right\rangle \nonumber \\\le & {} d^2(\psi _{i-1,k},y)+\alpha _k^2C_k^2+2\alpha _k\left\langle g_k^{i,i-1},t_1\upsilon _1\right\rangle . \end{aligned}$$

(8)

Since $g^{i,i-1}_k\in \partial f_i(\psi _{i-1,k})$ and $\gamma _{\upsilon _1}(0)=\psi _{i-1,k}$, it follows from the subgradient inequality (2) that

$$\begin{aligned} f_i(\gamma _{\upsilon _1}(t_1))\ge f_i(\psi _{i-1,k})+t_1\left\langle g^{i,i-1}_k, \gamma _{\upsilon _1}'(0)\right\rangle , \end{aligned}$$

where $\gamma _{\upsilon _1}(t_1)=y$ and $\gamma _{\upsilon _1}'(0)=\upsilon _1$, with the above inequality we have

$$\begin{aligned} \left\langle g_k^{i,i-1},t_1\upsilon _1\right\rangle \le f_i(\gamma _{\upsilon _1}(t_1))-f_i(\psi _{i-1,k})=f_i(y)-f_i(\psi _{i-1,k}). \end{aligned}$$

(9)

By combining the inequalities (8) and (9), we obtain

$$\begin{aligned} d^2(\psi _{i,k},y)\le d^2(\psi _{i-1,k},y)+\alpha _k^2C_k^2+2\alpha _k[f_i(y)-f_i(\psi _{i-1,k})], \end{aligned}$$

and summing up the above inequalities from $i=1$ to $i=m$, with $\psi _{m, k}=x_{k+1}$ and $\psi _{0, k}=x_k$, we have for k

$$\begin{aligned} d^2(x_{k+1},y)\le d^2(x_k,y)+\alpha _k^2C_k^2m+2\alpha _k\left[ f(y)-f_{\mathrm{inc}}^k\right] . \end{aligned}$$

(10)

By the definition of $\psi _{i-1, k}, i=1, 2, \ldots , m$ in Algorithm 3.1, we obtain for k

$$\begin{aligned} f_i(x_k)-f_i(\psi _{i-1,k})=f_i(\psi _{0,k})-f_i(\psi _{i-1,k}) =\sum _{j=1}^{i-1}[f_i(\psi _{j-1,k})-f_i(\psi _{j,k})]. \end{aligned}$$

(11)

From Algorithm 3.1, we have $\gamma _{\upsilon _{j-1, k}}(0)=\psi _{j-1,k}$ and $\gamma _{\upsilon _{j-1, k}}(t_{j-1,k})=\psi _{j,k}$, where $t_{j-1,k}=\alpha _k\Vert g_k^{j,j-1}\Vert$ and $g_k^{j,j-1}\in \partial f_j(\psi _{j-1,k})$, $i,j=1,2,\ldots ,m$. Since $g_k^{i,j-1}\in \partial f_i(\psi _{j-1,k})$, it follows from the subgradient inequality (2) that

$$\begin{aligned} f_i(\psi _{j,k})=f_i(\gamma _{\upsilon _{j-1,k}}(t_{j-1,k}))\ge f_i(\psi _{j-1,k})+t_{j-1,k}\left\langle g^{i,j-1}_k, \gamma _{\upsilon _{j-1,k}}'(0)\right\rangle , \end{aligned}$$

where $\gamma _{\upsilon _{j-1,k}}'(0)=\upsilon _{j-1,k}$ and $\Vert \upsilon _{j-1,k}\Vert =1$, and from the above inequality, we obtain for $i,j=1,2,\ldots ,m$

$$\begin{aligned} f_i(\psi _{j-1,k})-f_i(\psi _{j,k})\le & {} -t_{j-1,k}\left\langle g^{i,j-1}_k, \gamma _{\upsilon _{j-1,k}}'(0)\right\rangle \nonumber \\\le & {} t_{j-1,k}\left\| g^{i,j-1}_k\right\| \Vert \upsilon _{j-1,k}\Vert \nonumber \\= & {} \alpha _k\left\| g_k^{j,j-1}\right\| \left\| g^{i,j-1}_k\right\| . \end{aligned}$$

(12)

By combining the inequalities (11), (12) and (6), we obtain

$$\begin{aligned} f_i(x_k)-f_i(\psi _{i-1,k})\le \sum _{j=1}^{i-1}\alpha _k\left\| g_k^{j,j-1}\right\| \left\| g^{i,j-1}_k\right\| \le \alpha _kC_k^2(i-1), \end{aligned}$$

adding the above inequalities over $i=1,2,\ldots , m$, we have

$$\begin{aligned} f(x_k)-f_{\mathrm{inc}}^k = \sum _{i=1}^m[f_i(x_k)-f_i(\psi _{i-1,k})] \le \sum _{i=1}^m\alpha _kC_k^2(i-1) =\alpha _kC_k^2\frac{m(m-1)}{2}. \end{aligned}$$

Using the above relation and taking f(y) to minus $f(x_k)$ and $f_{\mathrm{inc}}^k$, respectively, we can obtain the follow inequality

$$\begin{aligned} f(y)-f_{\mathrm{inc}}^k\le f(y)-f(x_k)+\alpha _kC_k^2\frac{m(m-1)}{2}. \end{aligned}$$

(13)

Combining (10) and (13), we obtain for k

$$\begin{aligned} d^2(x_{k+1},y)\le & {} d^2(x_k,y)+\alpha _k^2C_k^2m+2\alpha _k\left[ f(y)-f(x_k)+\alpha _kC_k^2\frac{m(m-1)}{2}\right] \\= & {} d^2(x_k,y)+\alpha _k^2C_k^2[m+m(m-1)]+2\alpha _k[f(y)-f(x_k)]\\= & {} d^2(x_k,y)+\alpha _k^2C_k^2m^2+2\alpha _k[f(y)-f(x_k)]. \end{aligned}$$

Now the inequality (7) is proved. $\square$

We consider the convergence result for Algorithm 3.1 with diminishing stepsize rule, that is taking the sequence $\{\alpha _k\}$ in Algorithm 3.1 to satisfy

$$\begin{aligned}&\sum _{k=0}^{\infty }\alpha _k=+\infty , \end{aligned}$$

(14)

$$\begin{aligned}&\sum _{k=0}^{\infty }\alpha _k^2<+\infty . \end{aligned}$$

(15)

With the above lemma, the definition and property of quasi-Fejér convergent, we can obtain a important proposition, which will be used in next section. And we assume that the Riemannian manifolds has nonnegative curvature in the following proof.

Proposition 3.1

If Algorithm 3.1 generates an infinite sequence and there exists $\widetilde{x}\in M$ and $\widetilde{k}\ge 0$ such that $f(\widetilde{x})\le f(x_k)$ for $k\ge \widetilde{k}$, where M be a complete Riemannian manifold and has sectional curvature $K\ge 0$, then

• (1) $\{x_k\}$ is quasi-Fejér convergent to $L(\widetilde{x})$,

• (2) $\{f(x_k)\}$ is convergent sequence with $\lim _{k\rightarrow \infty }f(x_k)=f(\widetilde{x})$,

• (3) the sequence $\{x_k\}$ is convergent to some $\overline{x}\in L(\widetilde{x})$.

Proof

(1) Take $x\in L(\widetilde{x})$ and set $\beta _k=f(x_k)-f(x)$. Based on the definition of $L(\widetilde{x})$, we have that $\beta _k\ge 0$ for $k\ge \widetilde{k}$. And we replace y in Lemma 3.1 with $x\in L(\widetilde{x})$

$$\begin{aligned} d^2(x_{k},x)-d^2(x_{k+1},x)+\alpha _k^2C_k^2m^2\ge 2\alpha _k[f(x_k)-f(x)]=2\alpha _k\beta _k\ge 0. \end{aligned}$$

(16)

Select $\delta _k=\alpha _k^2C_k^2m^2$, it follows from (15), we have $\sum _{k=0}^{\infty }\delta _k=m^2\sum _{k=0}^{\infty }C_k^2\alpha _k^2<+\infty$. Therefore, according to Definition 2.2, $\{x_k\}$ is quasi-Fejér convergent to $L(\widetilde{x})$.

(2) By Proposition 2.4, we know that the sequences $\{x_k\}$ and $\{\psi _{i,k}\}$ are bounded for $i=0,1,\ldots ,m-1$, $k=0,1,\ldots$. And it follows from Proposition 2.3 that the sequences $\{g_k^{i,j-1}\}$ and $\{g_k^i\}$ are also bounded, where $g_k^{i,j-1}\in \partial f_i(\psi _{j-1,k})$, $g_k^i\in \partial f_i(x_k)$ for $i,j=1,2,\ldots ,m$, $k=0,1,\ldots$. So there exists a positive real number C, such that

$$\begin{aligned} C=\sup _{k\ge 0}\{\Vert g\Vert | g\in \partial f_i(x_k)\cup \partial f_i(\psi _{j-1,k}), i,j=1,2,\ldots ,m \}. \end{aligned}$$

(17)

It imply $C_k\le C$ for all k. Therefore, by inequality (16), we obtain for k

$$\begin{aligned} 2\alpha _k\beta _k\le d^2(x_{k},x)-d^2(x_{k+1},x)+\alpha _k^2C^2m^2, \end{aligned}$$

(18)

summing up inequalities (18) from $k=\widetilde{k}$ to n

$$\begin{aligned} 2\sum _{k=\widetilde{k}}^n\alpha _k\beta _k\le & {} d^2(x_{\widetilde{k}},x)-d^2(x_{n+1},x)+C^2m^2\sum _{k=\widetilde{k}}^n\alpha _k^2\\\le & {} d^2(x_{\widetilde{k}},x)+C^2m^2\sum _{k=\widetilde{k}}^n\alpha _k^2. \end{aligned}$$

From the above inequality and (15), we have

$$\begin{aligned} \sum _{k=0}^\infty \alpha _k\beta _k<\infty . \end{aligned}$$

(19)

Select x be any element of $L(\widetilde{x})$. Take $x=\widetilde{x}$, so that $\beta _k=f(x_k)-f(\widetilde{x})$. Then

$$\begin{aligned} \beta _{k+1}-\beta _k=f(x_{k+1})-f(x_k); \end{aligned}$$

(20)

we take $y=x_k$ in inequality (7)

$$\begin{aligned} d^2(x_{k+1},x_k)\le d^2(x_k,x_k)+\alpha ^2_{k}C_{k}^2m^2+2\alpha _k[f(x_k)-f(x_k)] =\alpha ^2_{k}C_{k}^2m^2; \end{aligned}$$

it implies for k

$$\begin{aligned} d(x_{k+1},x_k)\le \alpha _{k}C_{k}m. \end{aligned}$$

(21)

Let $\gamma _{\upsilon _{k+1}}$ be the minimizing geodesics, that is, for $\upsilon _{k+1}$ such that $\Vert \upsilon _{k+1}\Vert =1$, we take $\gamma _{\upsilon _{k+1}}(0)=x_{k+1}$, $\gamma _{\upsilon _{k+1}}(t_k)=x_k$, with $t_k=d(x_{k+1},x_k)$. Since $g_{k+1}^i\in \partial f_i(x_{k+1})$, it follows from the subgradient inequality (2) that for $i=1,2,\ldots ,m$, $k=0,1,\ldots$

$$\begin{aligned} f_i(x_k)=f_i(\gamma _{\upsilon _{k+1}}(t_k))\ge f_i(x_{k+1})+t_{k}\left\langle g_{k+1}^i, \gamma '_{\upsilon _{k+1}}(0)\right\rangle , \end{aligned}$$

where $\gamma '_{\upsilon _{k+1}}(0)=\upsilon _{k+1}$, combining the above inequality, (17) and (21), we obtain

$$\begin{aligned} f_i(x_{k+1})-f_i(x_k)\le & {} -t_k\left\langle g_{k+1}^i, \upsilon _{k+1}\right\rangle \le t_k\left\| g_{k+1}^i\right\| \Vert \upsilon _{k+1}\Vert \\\le & {} d(x_{k+1}, x_k)C \le \alpha _kC^2m. \end{aligned}$$

Adding the above inequalities over $i=1,2,\ldots , m$, we have

$$\begin{aligned} f(x_{k+1})-f(x_k)=\sum _{i=1}^m[f_i(x_{k+1})-f_i(x_k)]\le \alpha _kC^2m^2. \end{aligned}$$

(22)

Set $\theta =C^2m^2$ in inequality (22), and use it in Eq. (20)

$$\begin{aligned} \beta _{k+1}-\beta _k\le \theta \alpha _k. \end{aligned}$$

(23)

Since $\beta _k\ge 0$ for $k\ge \widetilde{k}$, and in view (19) and (23), within the hypotheses of Proposition 2.5, we can conclude that $\lim _{k\rightarrow \infty }\beta _k=0$, that is $\lim _{k\rightarrow \infty }f(x_k)=f(\widetilde{x})$.

(3) Let $\overline{x}$ be a accumulation point of $\{x_k\}$, which exists by (1) and Proposition 2.4. If $\{x_{l_k}\}$ is a subsequence of $\{x_k\}$, whose limit is $\overline{x}$, since convex functions are lower semicontinuous, then we have

$$\begin{aligned} f(\overline{x})\le \liminf _{k\rightarrow \infty }f(x_{l_k})=\lim _{k\rightarrow \infty }f(x_k)=f(\widetilde{x}). \end{aligned}$$

(24)

It follows from (24), that $\overline{x}\in L(\widetilde{x})$ and $\{x_k\}$ is convergent to some $\overline{x}\in L(\widetilde{x})$. $\square$

4 Convergence Analysis

In this section, we prove our main convergence results of the incremental subgradient method, including a convergence rate result. Finally, two examples are presented.

Theorem 4.1

If Algorithm 3.1 generates an infinite sequence, and M be a complete Riemannian manifold and has sectional curvature $K\ge 0$, then

• (1) $\liminf _{k\rightarrow \infty }f(x_k)=\inf _{x\in M}f(x)$,

• (2) If the set $S^*$ of solutions of problem (3) is nonempty, then either Algorithm 3.1 stops at some iteration k, in which case $x_k\in S^*$, or it generates an infinite sequence which converges to some $\overline{x}\in S^*$,

• (3) If $S^*$ is empty, then $\{x_k\}$ is unbounded.

Proof

(1) Let $f^*=\inf _{x\in M}f(x)$, then, we have

$$\begin{aligned} \liminf _{k\rightarrow \infty }f(x_k)\ge f^*. \end{aligned}$$

(25)

And we assume $\liminf _{k\rightarrow \infty }f(x_k)> f^*$. Then, there exists $\widetilde{x}$, such that

$$\begin{aligned} \liminf _{k\rightarrow \infty }f(x_k)>f(\widetilde{x}). \end{aligned}$$

(26)

It follows the above inequality that there exists $\widetilde{k}$ such that $f(x_k)\ge f(\widetilde{x})$ for all $k\ge \widetilde{k}$. By Proposition 3.1, $\lim _{k\rightarrow \infty }f(x_k)=f(\widetilde{x})$, in contradiction with (26). And according to (25), we obtain

$$\begin{aligned} \liminf _{k\rightarrow \infty }f(x_k)= f^*. \end{aligned}$$

(27)

Then the result follows.

(2) Since $S^*\ne \emptyset$, take any $x^*\in S^*$, in which case $L(x^*)=S^*$. By optimality of $x^*$, $f(x_k)\ge f(x^*)$ for all k. By Proposition 3.1(3), which $\widetilde{x}=x^*$, $\widetilde{k}=0$, and conclude that $\{x_k\}$ converge to some $x^*\in S^*$.

(3) Assume that $S^*$ is empty, but $\{x_k\}$ is bounded. Let $\{x_{l_k}\}$ be a subsequence of $\{x_k\}$ such that $\lim _{k\rightarrow \infty }f(x_{l_k})=\liminf _{k\rightarrow \infty }f(x_k)$. Since $\{x_{l_k}\}$ is bounded, without loss of generality, we may assume that $\{x_{l_k}\}$ converges to some $\overline{x}$. By lower semicontinuity of f

$$\begin{aligned} f(\overline{x})\le \liminf _{k\rightarrow \infty }f(x_{l_k}) =\lim _{k\rightarrow \infty }f(x_{l_k})=\liminf _{k\rightarrow \infty }f(x_{k})=f^*, \end{aligned}$$

(28)

using (1) in the equality. By (28), $\overline{x}$ belongs to $S^*$, in contradiction with the hypothesis. It follows that $\{x_k\}$ in unbounded. $\square$

We present a convergence rate result for the sequence of function values $f(x_k)$ as follows.

Theorem 4.2

If the problem (3) has solutions and the sequence $\{x_k\}$ generated by Algorithm 3.1 is infinite, where M be a complete Riemannian manifold and has sectional curvature $K\ge 0$, then there exists a subsequence $\{x_{l_k}\}$ of $\{x_k\}$ such that

$$\begin{aligned} f(x_{l_k})-f(x^*)\le \left( \sum _{j=0}^{l_k}\alpha _j\right) ^{-1}, \end{aligned}$$

(29)

where $x^*$ is any solution of problem (3).

Proof

We replace the $\widetilde{x}$ of Lemma 3.1 with $x^*\in S^*$, where $S^*$ denotes the set of solutions of problem (3). Set $\widetilde{k}=0$, $\beta _k=f(x_k)-f(x^*)$. By inequality (19), we set

$$\begin{aligned} s_k=\sum _{j=0}^k\alpha _j, N_1=\left\{ k: \beta _k\le s_k^{-1}\right\} , N_2=\left\{ k: \beta _k> s_k^{-1}\right\} . \end{aligned}$$

Suppose that $N_1$ is finite, then there exists $\overline{k}$ such that $x_k\in N_2$ for all $k\ge \overline{k}$, so that

$$\begin{aligned} \sum _{k={\overline{k}}}^\infty \frac{\alpha _k}{s_k} \le \sum _{k=\overline{k}}^\infty \alpha _k\beta _k\le \sum _{k=0}^\infty \alpha _k\beta _k<\infty . \end{aligned}$$

It follows that

$$\begin{aligned} \sum _{k=0}^\infty \frac{\alpha _k}{s_k} <\infty . \end{aligned}$$

On the other hand, Abel–Dini’s criterion for divergent series [41] states that if $\sum _{n=0}^\infty \mu _n=\infty$, then $\sum _{n=0}^\infty \left[ \mu _n/\left( \sum _{j=0}^n\mu _j\right) \right] =\infty$. So we conclude, in view of (14), that

$$\begin{aligned} \sum _{k=0}^\infty \frac{\alpha _k}{s_k} =\infty . \end{aligned}$$

This contradiction implies that $N_1$ is infinite, and we can take $\{x_{l_k}\}$ as consisting precisely of those $x_k$ with $k\in N_1$. $\square$

There is a example defined on a complete Riemannian manifolds where the geodesic has an explicit formula.

Example 4.1

The dual of a generalized assignment problem [42]. The problem is to assign m jobs to n machines. If job i is preformed at machine j, it costs $a_{ij}$ and requires $p_{ij}$ time units. Given the total available time $t_j$ at machine j, we want to find the minimum cost assignment of the jobs to the machines. Formally the problem is

$$\begin{aligned} \mathrm{minimize}&\sum _{i=1}^m\sum _{j=1}^na_{ij}y_{ij}\\ \mathrm{subject \ to}&\sum _{j=1}^ny_{ij}=1,\quad i=1,\ldots ,m,\\&\sum _{i=1}^mp_{ij}y_{ij}\le t_j,\quad j=1,\ldots ,n,\\&y_{ij}=0 \ \mathrm{or} \ 1, \quad \mathrm{for \ all} \ i, j, \end{aligned}$$

where $y_{ij}$ is the assignment variable, which is equal to 1 if the ith job is assigned to the jth machine and is equal to 0 otherwise. By relaxing the time constraints for the machines, we obtain the dual problem

$$\begin{aligned} \mathrm{maximize} \quad f(x)=\sum _{i=1}^mf_i(x), \quad \mathrm{subject \ to} \quad x\ge 0, \end{aligned}$$

(30)

where

$$\begin{aligned} f_i(x)=\min _{ \sum _{j=1}^n y_{ij}=1, \ y_{ij}=0 \ \mathrm{or} \ y_{ij}=1 }\sum _{j=1}^n(a_{ij}+x_jp_{ij})y_{ij} -\frac{1}{m}\sum _{j=1}^nt_jx_j, \quad i=1,\ldots ,m. \end{aligned}$$

The problem (30) is solved by using Algorithm 3.1. We will give the reason in the following.

The set

$$\begin{aligned} M'=\mathrm{int}\left( \mathbb {R}_+^n\right) =\{x\in \mathbb {R}^n|x>0\}, \end{aligned}$$

with the affine-scaling metric $g=(g_{ij})$, where $g_{ij}(x)=\delta _{ij}/x_ix_j$ is a complete Riemannian manifold, with $K\equiv 0$ and tangent plane on point $x\in M'$ equal to $T_xM'=\mathbb {R}^n$. The geodesic $\gamma :\mathbb {R}\rightarrow M'$ of $M'$ with initial conditions

$$\begin{aligned} \gamma (0)=a\in M' \quad \mathrm{and} \quad \gamma '=b\in T_aM', \end{aligned}$$

is

$$\begin{aligned} t\rightarrow \gamma (t)=(\gamma _1(t),\ldots , \gamma _n(t)), \end{aligned}$$

with

$$\begin{aligned} \gamma _i=a_i\exp ((a_i/b_i)t),\quad i=1, \ldots , n. \end{aligned}$$

Thus, the following problem is solved by using Algorithm 3.1

$$\begin{aligned} \min _{x\in M'} f(x), \end{aligned}$$

(31)

where $f(x)=\sum _{i=1}^mf_i(x)$ and $f_i:M'\rightarrow \mathbb {R}$ are convex functions. We can see the problem (30) be similar to (31). So the problem (30) is solved by using Algorithm 3.1.

There is another example which problem is defined on a unit sphere in the following.

Example 4.2

The model based on discrete harmonic mappings [43]. A triangle mesh $\mathcal {M}=(V, E)$ is given with a set of vertices $V=(v_1, v_2, \ldots , v_n)$ and a set of edges $E=\{(v_i, v_j)|v_iv_j \ \mathrm {is \ an \ edge \ of \ the \ mesh} \ \mathcal {M}\}$. Suppose that h is any piecewise linear mapping from $\mathcal {M}$ to a unit sphere $\mathbb {S}^2\subset \mathbb {R}^3$ with the restriction conditions

$$\begin{aligned} \Vert h(v_i)\Vert ^2=1,\quad \forall v_i\in V. \end{aligned}$$

(32)

The mapping h is uniquely determined by its value $h(v_i)$ at the vertices of $\mathcal {M}$. Then the discrete harmonic energy of the mapping h associated with the mesh $\mathcal {M}$ is defined as

$$\begin{aligned} f(h, \mathcal {M})=\frac{1}{2}\sum _{(v_i, v_j)\in E}\kappa _{ij}\Vert h(v_i)-h(v_j)\Vert ^2, \end{aligned}$$

(33)

where the spring constants $\kappa _{ij}$ may be computed in many ways. In most cases and the rest of the paper, uniform spring constants are used, i.e., $\kappa _{ij}=1$, for any i and j.

Let $h(v_i)=X_i\in \mathbb {R}^3$; $x=\left( X_1^T, X_2^T, \ldots , X_n^T\right) ^T\in \mathbb {R}^m$, where $m=3n$; $D(i)=\{j|(v_i, v_j)\in E\}$; and d(i) denotes the element number of the set D(i). Then we can setup the parameterization model by minimizing the discrete harmonic energy in (33) with spherical constraints

$$\begin{aligned} \mathrm{min}&f(x)=\frac{1}{2}\sum _{i=1}^n\sum _{j\in D(i)}\kappa _{ij}\Vert X_i-X_j\Vert ^2\nonumber \\ \mathrm{s.t.}&c_i(x)=\Vert X_i\Vert ^2-1=0,\quad i=1, \ldots , n, \end{aligned}$$

(34)

where x is call the vector of optimization variables, f(x) the objective function to be minimized, $c(x)=(c_1(x), c_2(x), \ldots , c_n(x))^T$ the vector of equality constraints.

We consider a special case of the problem (34), that $n-1$ components of the vector x are constant vectors on a positive half unit sphere $\mathbb {S}^2_+\subset \mathbb {R}^3$, where $\mathbb {S}^2_+=\{p=(p_1, p_2, p_3)\in \mathbb {R}^3: \Vert p\Vert =1 \ \mathrm{and} \ p_i\ge 0, i=1, 2, 3\}$. For example, we suppose that $X_2, X_3, \ldots , X_n$ in x are constant vectors on $\mathbb {S}^2_+$, and denote them by $A_1, A_2, \ldots , A_{n-1}$. Moreover we suppose $\kappa _{ij}=1$, for any i and j; $D(1)=\{1, 2, \ldots , k\}$, where $k\le n-1$; $1\in D(l)$, where $l=2, 3, \ldots , n$, and denote $X_1$ in x by X on $\mathbb {S}^2_+$. Then the problem (34) is changed to the following problem

$$\begin{aligned} \min _{X \in \mathbb {S}^2_+} \ F(X)=\sum _{i=1}^{n-1} \ F_i(X), \end{aligned}$$

(35)

when $i\le k$, $F_i(X)=\Vert X-A_i\Vert ^2$, and when $i> k$, $F_i(X)=\frac{1}{2}\Vert X-A_i\Vert ^2$.

The problem (35) is solved by using Algorithm 3.1. The reason is that the problem is defined on a positive half unit sphere $\mathbb {S}^2_+$, which is a complete Riemannian manifold, whose sectional curvature $K=1$; see, for instance, [38, 39]. Furthermore, the Riemannian metric on $\mathbb {S}^2_+$ induced by the Riemannian metric on $\mathbb {R}^3$, the geodesic $\gamma : \mathbb {R}\rightarrow \mathbb {S}^2_+$ with initial conditions

$$\begin{aligned} \gamma (0)=p\in \mathbb {S}^2_+ \quad \mathrm{and} \quad \gamma '(0)=v \in T_{p}\mathbb {S}^2_+, \end{aligned}$$

(36)

then

$$\begin{aligned} \gamma (t)=\cos (t)p + \sin (t)v. \end{aligned}$$

(37)

According to the formula (10) of [32], the gradient on the sphere of the component function $F_i: \mathbb {S}^2_+ \rightarrow \mathbb {R}$, $i=1,2,\ldots ,n-1$ at a point $p\in \mathbb {S}^2_+$ is the vector defined by

$$\begin{aligned} \mathrm{grad} \ F_i(p): =[I-pp^T]DF_i(p)=DF_i(p)-\langle DF_i(p), p\rangle p, \end{aligned}$$

(38)

where $DF_i(p)\in \mathbb {R}^3$ is the usual gradient of $F_i$ at $p\in \mathbb {S}^2_+$.

Moreover, the component functions $F_i(X), i=1,2,\ldots ,n-1$, are convex on $\mathbb {S}^2_+$, because of their Hessian matrices are positive semidefinite on $\mathbb {S}^2_+$. Actually, according to the formula (11) of [32], $\mathrm{Hess} \ F_i(p)$ is given by

$$\begin{aligned} \mathrm{Hess} \ F_i(p): =[I-pp^T][D^2F_i(p)-\langle DF_i(p), p\rangle I], \end{aligned}$$

(39)

where $D^2F_i(p)$ is the usual Hessian of the function F at a point $p\in \mathbb {S}^2_+$. When $i\le k$, we take $F_i(p)=\Vert p-A_i\Vert ^2$ in (39), and then

$$\begin{aligned} \mathrm{Hess} \ F_i(p) =2\langle A_i, p\rangle [I-pp^T], \end{aligned}$$

(40)

where $A_i, p \in \mathbb {S}^2_+$. So $\langle A_i, p\rangle \ge 0$ and $I-pp^T$ is positive semidefinite, then $\mathrm{Hess} \ F_i(p)$ is positive semidefinite. When $i>k$, we can prove $\mathrm{Hess} \ F_i(p)$ is positive semidefinite in the same way.

Then take a initial point $X_0\in \mathbb {S}^2_+$ arbitrarily. According to Algorithm 3.1, we can calculate the iteration sequence of the problem (35) with the formulas in (36)–(38).

5 Conclusions

In this paper, we have studied an incremental subgradient method in the Riemannian context. An algorithm is proposed and analyzed. Assuming that the sectional curvature of the Riemannian manifold be nonnegative, we have proved some convergence results of the algorithm that employ the diminishing stepsize rule. As future work, we intend to use the incremental subgradient methods on the Riemannian manifolds without requiring the sectional curvature nonnegative. Therefore, a different approach is necessary. Some other interesting problems are the convergence properties of the algorithm employing other stepsize rules, e.g., dynamic stepsize rule. In our current work, we focused on the unconstrained optimization on a Riemannian manifold. We intend to propose other more sophisticated and efficient algorithms to solve the constrained optimization on a Riemannian manifold in our future work.