1 Introduction

The alternating direction method of multipliers (ADMM) was initially introduced by Gabay–Mercier [1] and Glowinski–Marrocco [2] for solving convex composite problems. This method has been intensively studied in the past years. One may see for instance a comprehensive review in [3]. The point of main interest is the convergence of ADMM and its convergence rate. Under some assumptions, linear rates can be achieved [4].

The ADMM is linked to another famous algorithm, which is known as the primal–dual hybrid gradient (PDHG) method [5]. This method can be accelerated [6,7,8,9], thanks to an overrelaxation step by Nesterov [10], which leads to the overrelaxed PDHG (OPDHG) method. This algorithm is also shown to converge linearly under some regularity assumptions [7].

Other linear convergence results for variants of the ADMM can be found in the literature. Generally speaking, they differ from our result on the hypotheses made on the problem (both on the regularity of the objective function and on the operators). In [11], the authors propose to add an overrelaxation step in the spirit of Nesterov’s acceleration. They show linear convergence rate for special case requiring strong convexity, Lipschitz continuity of the gradient, invertibility and full column-rank hypotheses. In [12], the authors study the ADMM in a wider framework, by allowing in each partial minimization to add an extra proximal term, which leads to a generalized ADMM. Linear convergence rates are proved for four scenarios, which require both strong convexity and smoothness, but an explicit convergence rate is given for only one scenario [12, Corollary 3.6]. It can be shown that the ADMM iterations are also equivalent to applying the Douglas-Rachford splitting (DRS) to the dual problem [1]. A relaxed version of the DRS, called relaxed Peaceman–Rachford splitting, thus leads to a relaxed version of the ADMM [13]. In [13, Theorem 6.3], the authors prove the linear convergence rate of this variant of the ADMM in various cases (including the one we studied here), which depends on the assumptions made on the problem regularity. However, the study is theoretical and does not provide explicit optimal convergence rates.

The OPDHG has also been subject of numerous studies. A convergence analysis of the method is investigated in [7] under many different assumptions on the problem. A key point is the choice of the method parameters, which can affect the convergence rate [14].

In this paper, we provide a new analysis of the ADMM based on the known equivalence between the ADMM and the OPDHG method. More specifically, we use this analysis to derive convergence rate for the ADMM in a case we refer to be smooth. We indeed made restrictive assumptions on the linear coupling constraint and on the objective function, which is supposed to be strongly convex, with a smooth part. We first establish new linear convergence rates of the OPDHG method, by generalizing the proofs of [7, 9]. This leads to a linear convergence rate for the ADMM and its relaxed variant. The latter is then shown to achieve faster convergence rates.

The present paper is organized as follows. In Sect. 2, we define what we call the smooth case, which will be considered throughout this paper. In Sect. 3, we establish the linear convergence of the OPDHG method, and we provide the best parameter choice. In Sect. 4, we take advantage of the equivalence between the ADMM and the OPDHG to derive new linear convergence rates for the ADMM. We also propose a relaxed variant of the ADMM, which achieves the same asymptotic convergence rate as the OPDHG method, if the parameters are properly chosen. Eventually, in Sect. 5, we applied our relaxed ADMM on two problems, and compared the results with the classical ADMM, the OPDHG and FISTA [15].

2 The Problem and Some Preliminaries

Let X and Y be two finite-dimensional real Hilbert spaces. The inner product is denoted by \(\langle \cdot ,\cdot \rangle \) and \(\Vert \cdot \Vert \) is the induced norm.

2.1 Strong Convexity and Duality

Here are some facts about strong convexity that will be used in this paper.

Definition 2.1

A function \(f:X\rightarrow \mathrm {IR} \cup \{+\infty \}\) is said to be strongly convex of parameter \(\alpha >0\) or \(\alpha -\textit{convex}\) iff for any \((x_1,x_2)\in \mathrm {dom}(f)^2\) and \(p\in \partial f(x_1)\),

$$\begin{aligned} ~ f(x_2)\ge f(x_1) + \langle p,x_2-x_1\rangle + \frac{\alpha }{2}\,\Vert x_2-x_1\Vert ^2. \end{aligned}$$
(1)

where \(\mathrm {dom}(f)\) is the domain of f, i.e., the set of \(x\in X\) for which \(f(x)<+\infty \).

Proposition 2.1

[16] Let \(f:X\rightarrow \mathrm {IR} \cup \{+\infty \}\) be an \(\alpha \)-convex function. Then its convex conjugate \(f^*\), defined for any \(y\in X\) by

$$\begin{aligned} f^*(y) = \sup _{x\in X}\Big \{\langle x,y\rangle - f(x)\Big \} \end{aligned}$$
(2)

is differentiable, and its gradient \(\nabla f^*\) is Lipschitz continuous of constant \(1/\alpha \).

2.2 Smooth Composite Problem

We consider the composite problem

$$\begin{aligned} \min _{x\in X} \Big \{f(x) := g(x)+h(Ax)\Big \}, \end{aligned}$$
(3)

under the following assumptions:

Assumption (S) The convex objective function f in (3) is supposed to satisfy the following smooth case condition:

  1. (a)

    \(g:X\rightarrow \mathrm {IR} \cup \{+\infty \}\) is a proper,Footnote 1 strongly convex of parameter \(\gamma \), and lower semi-continuous (l.s.c.) function.

  2. (b)

    \(h:Y\rightarrow \mathrm {IR} \cup \{+\infty \}\) is a proper, convex, and a continuously differentiable function, and its gradient \(\varvec{\nabla }h\) is Lipschitz continuous of constant \(1/\delta \).

  3. (c)

    \(A:X\rightarrow Y\) is a bounded linear operator, of norm \(L_A\) and of adjoint \(A^*\).

Let us briefly discuss the assumptions made above. Though they may seem to be very restrictive, they can be satisfied in many applications. Assumption (S)-(a) is fulfilled for instance with the least squares error which is widely used as a fidelity term. Assumption (S)-(b) is a typical assumption for many convex optimization algorithms, including the forward–backward algorithm and its variants. When h(Ax) stands for the regularity term, (S)-(b) can be satisfied by considering smooth approximations of classical regularizations (e.g., Huber regularization). Assumption (S)-(c) is also fulfilled in many applications, since it is typically a gradient operator, or a degradation kernel.

Remark 2.1

Problem (3) is a particular instance of the general problem

$$\begin{aligned} \min _{(x,z)\in X\times Z:Ax + Bz = c} g(x) + h(z) \end{aligned}$$
(4)

with \(Z=Y\), \(B=-\mathrm {Id}\) and \(c=0\). For the sake of simplicity, and since problems of standard form (3) arise in many contexts, we focus on problems of this form. However, the interested reader will easily extend our result to the case, when B has full row rank (see Remark 4.3).

Remark 2.2

According to Assumption (S), \(h\circ A\) is Lipschitz continuous, of constant \(L_A^2/\delta \). Hence, one can define \(\kappa _f:=L_A^2/(\delta \gamma )\) the condition number of f as the ratio between the Lipschitz constant of the smooth part and the strong convexity parameter of the nonsmooth part g. When f is both strongly convex and smooth with \(\nabla f\) Lipschitz continuous, this definition recovers the usual definition, and \(\kappa _f\) is always larger than 1 [17]. In the general case, it can be less than 1. When \(\kappa _f\) is large, the function f is said ill-conditioned.

3 New Convergence Analysis for OPDHG in the Smooth Case

As shown in Sect. 4, our convergence analysis of the ADMM and its variants rely on an equivalence with the OPDHG algorithm. Thus, let us introduce this method and state some convergence results.

3.1 Primal–Dual Problem and the OPDHG Algorithm

Let us consider the following saddle-point problem:

$$\begin{aligned} \min _{\xi \in Z}\sup _{y\in Y} \Big \{ \mathcal {L}(\xi ;y):= G(\xi ) + \langle K\xi ,y \rangle - H^*(y) \Big \} \end{aligned}$$
(5)

where the convex–concave function \(\mathcal {L}\) satisfies the following assumption:

Assumption (S2) Let Z and Y be two finite-dimensional real Hilbert spaces.

  1. (a)

    \(G:Z\rightarrow \mathrm {IR} \cup \{+\infty \}\) is a proper, \(\tilde{\gamma }\)-convex, and l.s.c. function.

  2. (b)

    \(H^*:Y\rightarrow \mathrm {IR} \cup \{+\infty \}\) is a proper, \(\tilde{\delta }\)-convex, and l.s.c. function.

  3. (c)

    \(K:Z\rightarrow Y\) is a bounded linear operator of norm \(L_K\).

We recall that, for any convex function \(F:X\mapsto \mathrm {IR}\cup \{+\infty \}\), one can define the proximal operator of F [18] as

$$\begin{aligned} \forall \; x_0\in X,\qquad \mathrm {prox}_{F}(x_0) := \arg \min _{x\in X}\left\{ F(x) + \frac{1}{2}\,\Vert x-x_0\Vert ^2\right\} \end{aligned}$$
(6)

which is uniquely defined for any \(x_0\in X\) as the minimizer of a strongly convex problem. In this section, we establish the convergence proof of the following primal–dual algorithm

figure a

which aims at solving problem (5). The parameters \(\tau ,\sigma >0\) and \(0<\theta \le 1\) are to be specified.

Remark 3.1

When \(\theta =0\), this algorithm is known as the PDHG method [5] or as the Arrow-Hurwicz algorithm [19]. It consists in a proximal gradient ascent step for the dual variable (7), followed by a proximal gradient descent step for the primal variable (8). The overrelaxation step (9) has been added in [6] and studied in [8, 9]. When \(\theta =1\) and \(\tau \sigma \ne 1/L^2_K\), the iterations are equivalent to a preconditioned version of the ADMM [7, 8].

3.2 Convergence Analysis for OPDHG

We set \(\mathcal {G}(\xi ',\xi ;y,y') :=\mathcal {L}(\xi ';y) - \mathcal {L}(\xi ;y')\) for any \((\xi ,\xi ')\in Z^2\) and \((y,y')\in Y^2\). Moreover, if \(0<\omega <1 \), then we denote

$$\begin{aligned} T_N \! := \!\sum _{n=1}^N \frac{1}{\omega ^{n-1}} {=\frac{1-\omega ^N}{\omega ^{N-1}(1-\omega )}}, \quad \Xi _N \!:= \frac{1}{T_N}\!\sum _{n=1}^N\frac{\xi _n}{\omega ^{n-1}},\quad Y_N \!:= \frac{1}{T_N}\!\sum _{n=1}^N\frac{y_n}{\omega ^{n-1}} . \end{aligned}$$
(10)

Let us formulate our main result for the OPDHG algorithm in the smooth case.

Theorem 3.1

Let \(\mathcal {L}\) satisfy Assumption (S2) and \((y_n,\xi _n,\bar{\xi }_n)_{n}\) a sequence generated by Algorithm 1. Assume problem (5) has a solution, which is a saddle point of \(\mathcal {L}\), denoted by \((\xi ^*,y^*)\). Choose \(\tau >0\), \(\sigma >0\) and \(0<\theta \le 1\) such that

$$\begin{aligned} \max \left\{ \frac{1}{\tau \tilde{\gamma }+1},\frac{1}{\sigma \tilde{\delta }+1}\right\} \le \theta \le \frac{1}{L_K^2\tau \sigma }. \end{aligned}$$
(11)

Then, for any \({\omega <1}\) such that

$$\begin{aligned} \max \left\{ \frac{1}{\tau \tilde{\gamma }+1},\frac{\theta +1}{\sigma \tilde{\delta }+2}\right\} \le \omega \le \theta \end{aligned}$$
(12)

we have the following bound for any \((\xi ,y)\in Z\times Y\) and for any \(N\ge 1\):

$$\begin{aligned}&\frac{1-\omega }{\omega (1-\omega ^N)}\left( \frac{\Vert \xi -\xi _N \Vert ^2}{2\tau } +(1-\omega L_K^2\tau \sigma )\frac{\Vert y-y_N\Vert ^2}{2\sigma }\right) +\mathcal {G}(\Xi _N,\xi ;y,Y_N)\nonumber \\&\quad \le \frac{1}{T_N}\left( \frac{\Vert \xi -\xi _0 \Vert ^2}{2\tau } + \frac{\Vert y-y_0 \Vert ^2}{2\sigma }\right) .\quad \end{aligned}$$
(13)

This theorem is an improvement on a result proved in [7, Theorem 3]. The rate we provide here is indeed better, since no restrictive assumptions are made on the parameters values, unless necessary. The proof of Theorem 3.1 is proposed in Appendix A. A consequence of this proof is the linear convergence of the iterates:

Corollary 3.1

Let \(\mathcal {L}\) satisfy Assumption (S2) and \((y_n,\xi _n,\bar{\xi }_n)_{n}\) a sequence generated by Algorithm 1. Assume problem (5) has a solution, which is a saddle point of \(\mathcal {L}\), denoted by \((\xi ^*,y^*)\). Suppose there exist \(\tau \), \(\sigma \), \(\theta \) and \(\omega \) satisfying both conditions (11) and (12). Then, for any \(N\ge 1\),

$$\begin{aligned} \Vert \xi ^*-\xi _N \Vert ^2 \le \omega ^N\left( \Vert \xi ^*-\xi _0 \Vert ^2 + \frac{\tau }{\sigma }\,\Vert y^*-y_0 \Vert ^2\right) . \end{aligned}$$
(14)

Moreover, if \(\omega L_K^2\tau \sigma < 1\), then we also have

$$\begin{aligned} \Vert y^*-y_N\Vert ^2 \le \frac{\omega ^N}{1-\omega L_K^2\tau \sigma }\left( \frac{\sigma }{\tau }\Vert \xi ^*-\xi _0 \Vert ^2 + \Vert y^*-y_0 \Vert ^2\right) . \end{aligned}$$
(15)

3.3 Choice of Parameters and Convergence Rates

Theorem 3.1 holds, provided one can properly choose the steps \(\tau \) and \(\sigma \) and the relaxation parameter \(\theta \). In particular, one can tune \((\tau ,\sigma ,\theta )\), so that the resulting convergence rate \(\omega \) is minimal.

Theorem 3.2

Let \(\kappa _F:=L_K^2/(\tilde{\delta }\tilde{\gamma })\). The best convergence rate in Theorem 3.1 is achieved when the parameters are \((\tau ,\sigma ,\theta ) = (\tau ^*,\sigma ^*,\theta ^*)\), given by

$$\begin{aligned} {\tau ^* = \frac{1+\sqrt{1+4\kappa _F}}{2\tilde{\gamma }\kappa _F},\quad \sigma ^* = \frac{1+\sqrt{1+4\kappa _F}}{2\tilde{\delta }\kappa _F}}\quad \mathrm {and}\quad \theta ^* = \frac{\sqrt{1+4\kappa _F}-1}{\sqrt{1+4\kappa _F}+1}\quad \end{aligned}$$
(16)

which satisfy \(\tau \tilde{\gamma }=\sigma \tilde{\delta }\). The resulting convergence rate is \(\omega = \theta ^*\).

Let us first prove the following lemma, which gives conditions on \(\tau \) and \(\sigma \), so that (11) is well-defined:

Lemma 3.1

For any \(\tau >0\), we define a quantity \(\sigma _{\max }(\tau )>0\) given by

$$\begin{aligned} \sigma _{\max }(\tau ) = \left\{ \begin{array}{ll} (1/\tau +\tilde{\gamma })/L_K^2, &{}\quad \mathrm {if~}0<\tau \le \tau ^*,\\ {1}/{(L_K^2\tau -\tilde{\delta })}, &{}\quad \mathrm {if~}\tau >\tau ^*, \end{array} \right. \end{aligned}$$
(17)

where \(\tau ^*\) is given by (16). Then, for any \((\tau ,\sigma )\in ]0,+\infty [\times ]0,\sigma _{\max }(\tau )]\), there exists \(\theta \) satisfying (11).

Proof

Let \(\tau >0\). The inequality (11) is feasible, if \(1/(\tau \tilde{\gamma }+1) \le 1/(L_K^2\tau \sigma )\) and \(1/(\sigma \tilde{\delta }+1) \le 1/(L_K^2\tau \sigma )\), which, respectively, read

$$\begin{aligned} \sigma \le \frac{1/\tau +\tilde{\gamma }}{L_K^2} \quad \mathrm {and}\quad (L_K^2\tau -\tilde{\delta })\,\sigma \le 1. \end{aligned}$$
(18)

Let us show that these inequalities hold iff \(\sigma \) is less than \(\sigma _{\max }(\tau )\). Because of the second inequality in (18), one should consider two cases.

  1. 1.

    Case \(L_K^2\tau -\tilde{\delta }\le 0\). In this case, the second inequality is always true and (18) reduces to its first inequality, which is \(\sigma \le \sigma _{\max }(\tau )\), since \(\tau \le \tilde{\delta }/L^2_K < \tau ^*\).

  2. 2.

    Case \(L_K^2\tau -\tilde{\delta }>0\). Then one can divide the second inequality by \(L_K^2\tau -\tilde{\delta }\) and (18) reads \( \sigma \le \min \{(1/\tau +\tilde{\gamma })/L_K^2,{1}/({L_K^2\tau -\tilde{\delta }})\}\). One can check that

    $$\begin{aligned} \frac{1/\tau +\tilde{\gamma }}{L_K^2}\le \frac{1}{L_K^2\tau -\tilde{\delta }} \quad \Longleftrightarrow \quad L_K^2\tau ^2-\tilde{\delta }\tau -\frac{\tilde{\delta }}{\tilde{\gamma }}\le 0 \quad \Longleftrightarrow \quad \tau \le \tau ^*. \end{aligned}$$
    (19)

    Thus, \(\sigma \le \sigma _{\max }(\tau )\). \(\square \)

Proof of Theorem 3.2

Let \((\tau ,\sigma )\in ]0,+\infty [\times ]0,\sigma _{\max }(\tau )]\). We denote

$$\begin{aligned} \theta _{\min }(\tau ,\sigma ):=\max \left\{ \frac{1}{\tau \tilde{\gamma }+1},\frac{1}{\sigma \tilde{\delta }+1}\right\} \quad \mathrm {and}\quad \theta _{\max }(\tau ,\sigma ):=\frac{1}{L_K^2\tau \sigma }. \end{aligned}$$
(20)

One has \(\theta _{\min }(\tau ,\sigma )\le \theta _{\max }(\tau ,\sigma )\) (Lemma 3.1). Let \(\theta \in [\theta _{\min }(\tau ,\sigma ), \theta _{\max }(\tau ,\sigma )]\). The best convergence rate that appears in Theorem 3.1 for \((\tau ,\sigma ,\theta )\) is given by the lower bound of (12), namely

$$\begin{aligned} \omega (\tau ,\sigma ,\theta ) = \max \left\{ \frac{1}{\tau \tilde{\gamma }+1},\frac{\theta +1}{\sigma \tilde{\delta }+2}\right\} . \end{aligned}$$
(21)

The aim is thus to find stepsizes \(\tau ^*\in ]0,+\infty [\), \(\sigma ^*\in ]0,\sigma _{\max }(\tau ^*)]\), and parameter \(\theta ^*\in [\theta _{\min }(\tau ^*,\sigma ^*), \theta _{\max }(\tau ^*,\sigma ^*)]\), which minimize \(\omega (\tau ,\sigma ,\theta )\). We first note that, for any feasible \((\tau ,\sigma ,\theta )\), one has

$$\begin{aligned} \omega (\tau ,\sigma ,\theta _{\min }(\tau ,\sigma )) \le \omega (\tau ,\sigma ,\theta ). \end{aligned}$$
(22)

Thus, Problem (21) is equivalent to minimizing \(\omega (\tau ,\sigma ,\theta _{\min }(\tau ,\sigma ))\) subject to \((\tau ,\sigma )\in ]0,+\infty [\times ]0,\sigma _{\max }(\tau )]\). Let \(\sigma _{\min }(\tau ):={\tau \tilde{\gamma }}/{\tilde{\delta }}\). One can verify that

$$\begin{aligned} \theta _{\min }(\tau ,\sigma ) = \left\{ \begin{array}{ll} \displaystyle 1/({\sigma \tilde{\delta }+1}),&{}\quad \mathrm {if~} \tau >\tau ^*,\\ \displaystyle 1/({\sigma \tilde{\delta }+1}),&{} \quad \mathrm {if~} (\tau \le \tau ^* \mathrm {~and~} 0<\sigma \le \sigma _{\min }(\tau )),\\ 1/({\tau \tilde{\gamma }+1}),&{} \quad \mathrm {if~} (\tau \le \tau ^* \mathrm {~and~} \sigma _{\min }(\tau )<\sigma \le \sigma _{\max }(\tau )). \end{array}\right. \end{aligned}$$
(23)

This yields

$$\begin{aligned} \frac{\theta _{\min }(\tau ,\sigma )+1}{\sigma \tilde{\delta }+2} = \left\{ \begin{array}{ll} \displaystyle 1/({\sigma \tilde{\delta }+1}),&{}\quad \mathrm {if~} \tau >\tau ^*,\\ \displaystyle 1/({\sigma \tilde{\delta }+1}),&{}\quad \mathrm {if~} (\tau \le \tau ^* \mathrm {~and~} 0<\sigma \le \sigma _{\min }(\tau )),\\ \displaystyle \frac{\tau \tilde{\gamma }+2}{(\tau \tilde{\gamma }+1)(\sigma \tilde{\delta }+2)}, &{}\quad \mathrm {if\,}(\tau \le \tau ^* \mathrm {~and~} \sigma _{\min }(\tau )<\sigma \le \sigma _{\max }(\tau )). \end{array}\right. \end{aligned}$$
(24)

Obviously, for any feasible \((\tau ,\sigma )\), one has

$$\begin{aligned} \frac{\theta _{\min }(\tau ,\sigma _{\max }(\tau ))+1}{\sigma _{\max }(\tau )\tilde{\delta }+2} \le \frac{\theta _{\min }(\tau ,\sigma )+1}{\sigma \tilde{\delta }+2}. \end{aligned}$$
(25)

As a consequence, \(\omega (\tau ,\sigma _{\max }(\tau ),\theta _{\min }(\tau ,\sigma _{\max }(\tau ))) \le \omega (\tau ,\sigma ,\theta _{\min }(\tau ,\sigma ))\). Thus, Problem (21) reduces to minimize \(\omega ^*(\tau ):=\omega (\tau ,\sigma _{\max }(\tau ),\theta _{\min }(\tau ,\sigma _{\max }(\tau )))\). Let \(\tau >0\). According to (24) and the definition of \(\sigma _{\max }(\tau )\),

$$\begin{aligned} \frac{\theta _{\min }(\tau ,\sigma _{\max }(\tau ))+1}{\sigma _{\max }(\tau )\tilde{\delta }+2} = \left\{ \begin{array}{ll} \displaystyle 1/(\sigma _{\max }(\tau )\tilde{\delta }+1),&{}\quad \mathrm {if~} \tau >\tau ^*,\\ \displaystyle \frac{\tau \tilde{\gamma }+2}{(\tau \tilde{\gamma }+1)(\sigma _{\max }(\tau )\tilde{\delta }+2)}, &{}\quad \mathrm {if\,}\tau \le \tau ^*. \end{array}\right. \end{aligned}$$
(26)

It can be deduced from (23) that \(\tau \tilde{\gamma }>\sigma _{\max }(\tau )\tilde{\delta }\) iff \(\tau >\tau ^*\). This proves that

$$\begin{aligned} \omega ^*(\tau )= \left\{ \begin{array}{ll} \displaystyle 1-{\tilde{\delta }}/{(L_K^2\tau )},&{}\quad \mathrm {if~} \tau >\tau ^*,\\ 1/(\tau \tilde{\gamma }+1),&{}\quad \mathrm {if~} \tau \le \tau ^* , \end{array}\right. \end{aligned}$$
(27)

which is minimal for \(\tau =\tau ^*\). This leads to the rate \(\omega = \omega ^*(\tau ^*)\), which is attained for \(\tau = \tau ^*\), \(\sigma = \sigma _{\max }(\tau ^*) = \sigma ^*\) and \(\theta = \theta _{\min }(\tau ^*,\sigma ^*) = \theta ^*\). \(\square \)

3.4 Overrelaxation on the Dual Variable

Thanks to the symmetry of (5), similar results still hold, if the relaxation is done on the dual variable y, which leads to Algorithm 2.

figure b

As it will be seen later on, such an overrelaxation will be useful for the analysis of the ADMM. Algorithm 2 is obtained by inverting the role of the dual and the primal variables in the saddle-point problem (5). Hence, applying Theorem 3.1 yields the following result:

Theorem 3.3

Let \(\mathcal {L}\) satisfy Assumption (S2) and \((\xi _n,y_n,\bar{y}_n)_{n}\) a sequence generated by Algorithm 2. Assume problem (5) has a solution, which is a saddle point of \(\mathcal {L}\), denoted by \((\xi ^*,y^*)\). Choose \(\tau >0\), \(\sigma >0\) and \(0<\theta \le 1\) such that (11) holds. Then, for any \(\omega <1\) such that

$$\begin{aligned} \max \left\{ \frac{\theta +1}{\tau \tilde{\gamma }+2},\frac{1}{\sigma \tilde{\delta }+1}\right\} \le \omega \le \theta , \end{aligned}$$
(31)

we have the following bound for any \((\xi ,y)\in Z\times Y\) and for any \(N\ge 1\):

$$\begin{aligned}&\frac{1-\omega }{\omega (1-\omega ^N)}\left( (1-\omega L_K^2\tau \sigma )\frac{\Vert \xi -\xi _N \Vert ^2}{2\tau } +\frac{\Vert y-y_N\Vert ^2}{2\sigma }\right) +\mathcal {G}(\Xi _N,\xi ;y,Y_N)\quad \nonumber \\&\quad \le \frac{1}{T_N}\left( \frac{\Vert \xi -\xi _0 \Vert ^2}{2\tau } + \frac{\Vert y-y_0 \Vert ^2}{2\sigma }\right) .\quad \end{aligned}$$
(32)

Note that the conditions on the parameters (31) now slightly differ from the ones in the previous case (see (12)). A variant can be found in [20, Appendix C2]. Similar computations as in the previous section show the linear convergence of the iterates. The parameters, that minimize the convergence rate \(\omega \) appearing in (32), can also be computed as in Sect. 3.3. In particular, the best rate can be shown to be the same as in Theorem 3.2.

4 A Relaxed Variant of the ADMM in the Smooth Case

Let us now consider the initial primal problem (3), which can be interpreted as a constrained problem (see (4) in Remark 2.1). The ADMM aims at solving it by finding a saddle point of the augmented Lagrangian

$$\begin{aligned} \mathop {\min }\limits _{{\mathop {x \in X}\limits _{{z \in Z}} }}\sup _{y\in Y}\left\{ L_{\tau }(x,z;y) := g(x) + h(z) + \langle Ax-z,y \rangle + \frac{1}{2\tau }\,\Vert Ax-z\Vert ^2\right\} \end{aligned}$$
(33)

for \(\tau >0\), by alternating in partial minimizations and gradient ascent:

figure c

Remark 4.1

If A is the identity operator, the minimization steps in Algorithm 3 can be interpreted as proximal gradient descent steps for the ordinary Lagrangian \(L_{\infty }(x,z;y) := g(x) + h(z) + \langle x-z,y \rangle \) associated with Problem (3). We recall that both the Lagrangian \(L_{\infty }\) and the augmented Lagrangian \(L_{\tau },\tau >0\) have same saddle points [1, Theorem 2.2].

4.1 Relaxed Variant of the ADMM

We propose to relax the choice of step \(\tau \) in the updates of z and of y in Algorithm 3. Replacing \(\tau \) by \(\tau '\le \tau \) in these two updates leads to:

figure d

One recovers the ADMM (Algorithm 3), when \(\tau =\tau '\).

4.2 Equivalence Between the Relaxed ADMM and OPDHG

We show in Appendix B that, for \(n\ge 2\), the iterations in Algorithm 4 are equivalent to those of OPDHG with overrelaxation on the dual variable (Algorithm 2), with overrelaxation parameter \(\theta = \tau '/\tau \) and stepsize \((\tau ,\sigma =1/\tau ')\) applied to

$$\begin{aligned} \min _{\xi \in Y}\sup _{y\in Y} \Big \{ \mathcal {L}(\xi ;y):=g_A(\xi ) + \langle \xi ,y \rangle - h^*(y) \Big \}, \end{aligned}$$
(40)

namely

$$\begin{aligned} \begin{array}{ll} \xi _{n+1} = \mathrm {prox}_{\tau g_A}\big (\xi _n - \tau \,\bar{y}^n\big )\\ y_{n+1} = \mathrm {prox}_{h^*/\tau '}(y_n+\xi _{n+1}/\tau ')\\ \bar{y}_{n+1} = y_{n+1}+(\tau '/\tau )\,(y_{n+1}-y_n) \end{array} \end{aligned}$$
(41)

with \(g_A(\xi ):=\inf \{g(x) : Ax=\xi \}\) and \(\xi _{n+1}:=Ax_{n+1}\).

Remark 4.2

The equivalence between the ADMM (\(\tau = \tau '\)) and OPDHG has already been investigated in [8].

Remark 4.3

The equivalence between the relaxed ADMM and the OPDHG iterations as demonstrated in Appendix B still holds, when \(B\ne -\mathrm {Id}\) has full row rank. Indeed, one can check that Appendix B remains true, if \(h^*\circ B^*\) is strongly convex, so that \(h_{-B}:\nu \mapsto \inf \{h(z) : -Bz=\nu \}\) has a Lipschitz continuous gradient, which is the case if B has full row rank, see [21].

Because of the equivalence between the relaxed ADMM and OPDHG recalled above, the convergence analysis of the relaxed ADMM and the classical ADMM may be investigated by applying Theorem 3.3. Let us first check that the equivalent primal–dual problem (40) satisfies Assumption (S2), when the problem (3) satisfies Assumption (S). According to Assumption (S), \(h^*\) is \(\delta \)-convex. Let us prove that, if g is \(\gamma \)-convex, then \(g_A\) is \((\gamma /L_A^2)\)-convex. Indeed,

$$\begin{aligned} g_A^*(y) = \mathop {\sup }\limits _{{\mathop {\xi \in Y}\limits _{{Ax = \xi }} }}\Big \{\langle \xi ,y\rangle -g(x)\Big \} = \sup _{x\in X}\Big \{\langle Ax,y\rangle -g(x)\Big \} = g^*(A^*y) \end{aligned}$$
(42)

where \(\nabla g^*\) is \((1/\gamma )\)-Lipschitz continuous according to Proposition 2.1. By composition, \(g^*_A\) is differentiable and \(\nabla g^*_A\) is \((L^2_A/\gamma )\)-Lipschitz continuous. Thus, \(g_A\) is \((\gamma /L_A^2)\)-convex (Proposition 2.1). Hence, \(\mathcal {L}\) in (40) satisfies Assumption (S2). Then, if we denote for any \(\omega >0\) and for any \(N>1\)

$$\begin{aligned} X_N := \frac{1}{T_N}\sum _{n=1}^N\frac{x_n}{\omega ^{n-1}} \end{aligned}$$
(43)

applying Theorem 3.3 yields

Proposition 4.1

Let f satisfy Assumption (S) and \((x_n,y_n,z_n)_{n}\) a sequence generated by Algorithm 4. Assume problem (3) has a solution denoted by \(x^*\). Choose \(\tau \ge \tau '>0\) such that

$$\begin{aligned} \max \left\{ \frac{1}{\tau \gamma /L_A^2+1},\frac{1}{\delta /\tau '+1}\right\} \le \frac{\tau '}{\tau }\le 1. \end{aligned}$$
(44)

Then, for any \(\omega <1\) such that

$$\begin{aligned} \max \left\{ \frac{\tau '/\tau +1}{\tau \gamma /L_A^2+2},\frac{1}{\delta /\tau '+1}\right\} \le \omega \le \frac{\tau '}{\tau }, \end{aligned}$$
(45)

we have the following bound for any \((x,y)\in X\times Y\) and for any \(N\ge 2\):

$$\begin{aligned}&\frac{1-\omega }{\omega (1-\omega ^N)}\,(1-\omega \tau /\tau ')\frac{\Vert Ax-Ax_N \Vert ^2}{2\tau } +\frac{1-\omega }{\omega (1-\omega ^N)}\,\frac{\Vert y-y_N\Vert ^2}{2/\tau '}\nonumber \\&\quad +\,\mathcal {G}(AX_N,Ax;y,Y_N) \le \frac{1}{T_N}\left( \frac{\Vert Ax-Ax_1 \Vert ^2}{2\tau } + \frac{\Vert y-y_1 \Vert ^2}{2/\tau '}\right) . \end{aligned}$$
(46)

An interesting consequence of this proposition is the ergodic convergence of the relaxed ADMM in terms of objective error and solution error.

Theorem 4.1

Let f satisfy Assumption (S) and \((x_n,y_n,z_n)_{n}\) a sequence generated by Algorithm 4. Assume problem (3) has a solution denoted by \(x^*\). Choose \(\tau \ge \tau '>0\) satisfying (44). Then, for any \(\omega <1\) satisfying (45) and for any \(N\ge 1\), one has

$$\begin{aligned} f(X_N) - f(x^*)\le & {} \frac{1}{T_N}\,\frac{{L_A^2}}{2\tau }\left( 1 + \frac{N}{T_N}\,\frac{2\tau }{\delta ^2/\tau '}\,\frac{\omega }{1-\omega \tau /\tau '}\right) {\Vert x^*-x_1 \Vert ^2}\nonumber \\&\quad +\, \frac{1}{T_N}\,\frac{1}{1/\tau '}\left( 1+ \frac{N}{T_N}\, \frac{\tau }{\delta ^2/\tau '}\,\frac{\omega }{1-\omega \tau /\tau '}\right) \Vert y^*-y_1 \Vert ^2 \end{aligned}$$
(47)

with \(N/T_N\rightarrow 0\) as N goes to infinity. Moreover, one has for any \(N\ge 1\)

$$\begin{aligned} \Vert X_N - x^*\Vert ^2\le & {} \frac{2}{T_N}\,\frac{{L_A^2}}{\gamma \tau }\left( 1 + \frac{N}{T_N}\,\frac{2\tau }{\delta ^2/\tau '}\,\frac{\omega }{1-\omega \tau /\tau '}\right) {\Vert x^*-x_1 \Vert ^2}\nonumber \\&+\, \frac{4}{T_N}\,\frac{1}{\gamma /\tau '}\left( 1+ \frac{N}{T_N}\, \frac{\tau }{\delta ^2/\tau '}\,\frac{\omega }{1-\omega \tau /\tau '}\right) \Vert y^*-y_1 \Vert ^2. \end{aligned}$$
(48)

Proof

For any \((x,y)\in X\times Y\), one has \(\mathcal {L}(Ax;y) = g(x)+\langle Ax,y\rangle -h^*(y)\) and \(f(x) = \sup _{y\in Y}\mathcal {L}(Ax;y)\). Let us apply inequality (46) to \(x=x^*\). Since

$$\begin{aligned} f(x^*) = \mathcal {L}(Ax^*;y^*) = \sup _{y\in Y}\mathcal {L}(Ax^*;y) \ge \mathcal {L}(Ax^*;Y_N) \end{aligned}$$
(49)

we get \(\mathcal {L}(AX_N;y)-f(x^*) \le \mathcal {L}(AX_N;y)-\mathcal {L}(Ax^*;Y_N) = \mathcal {G}(AX_N,Ax^*;y,Y_N)\) for any \(y\in Y\), which implies

$$\begin{aligned} \frac{1-\omega }{\omega (1-\omega ^N)}\,(1-\omega \tau /\tau ')\frac{\Vert Ax^*-Ax_N \Vert ^2}{2\tau } +\frac{1-\omega }{\omega (1-\omega ^N)}\,\frac{\Vert y-y_N\Vert ^2}{2/\tau '}\nonumber \\ +\mathcal {L}(AX_N;y) - f(x^*) \le \frac{1}{T_N}\left( \frac{\Vert Ax^*-Ax_1 \Vert ^2}{2\tau } + \frac{\Vert y-y_1 \Vert ^2}{2/\tau '}\right) . \end{aligned}$$
(50)

Let us define \(y^*_N\in Y\) as the maximizer of \(\mathcal {L}(AX_N;\cdot )\) so that \(\mathcal {L}(AX_N;y^*_N) = f(X_N)\). The left-hand side in (50) is then nonnegative for \(y=y^*_N\) and yields

$$\begin{aligned} 0\le f(X_N) - f(x^*) \le \frac{1}{T_N}\,\frac{1}{2\tau }\,\Vert Ax^*-Ax_1 \Vert ^2 + \frac{1}{T_N}\,\frac{1}{2/\tau '}\,\Vert y^*_N-y_1 \Vert ^2. \end{aligned}$$
(51)

Let us bound that the quantity \(\Vert y^*_N-y_1\Vert \). One can check by first-order optimality condition that \(y^*_N = \nabla h(AX_N)\) and \(y^*=\nabla h(Ax^*)\). Thanks to the Lipschitz continuity of \(\nabla h\) (according to Assumption (S)), this implies that \(\Vert y^*_N-y_1 \Vert \le \Vert Ax^*-AX_N \Vert /\delta +\Vert y^*-y_1 \Vert \). Using that \((a+b)^2\le 2a^2+2b^2\) for any \((a,b)\in \mathrm {IR}^2\), one gets

$$\begin{aligned} \Vert y^*_N-y_1 \Vert ^2\le 2\,\frac{\Vert Ax^*-AX_N \Vert ^2}{\delta ^2}+2\,\Vert y^*-y_1 \Vert ^2 \end{aligned}$$
(52)

However, applying (50) to \(y=y^*\) and \(N=n\) yields after simplification

$$\begin{aligned} \Vert Ax^*-Ax_n \Vert ^2 \le \frac{\omega (1-\omega ^n)}{(1-\omega )(1-\omega \tau /\tau ')}\,\frac{\tau }{T_n}\left( \frac{1}{\tau }\,\Vert Ax^*-Ax_1 \Vert ^2 + \frac{1}{1/\tau '}\,\Vert y^*-y_1 \Vert ^2\right) . \end{aligned}$$
(53)

Using the definition of \(X_N\) and the convexity of the quadratic norm, we get

$$\begin{aligned} \Vert Ax^*-AX_N \Vert ^2 \le \frac{\tau N}{T_N}\,\frac{\omega }{1-\omega \tau /\tau '}\left( \frac{1}{\tau }\,\Vert Ax^*-Ax_1 \Vert ^2 + \frac{1}{1/\tau '}\,\Vert y^*-y_1 \Vert ^2\right) \end{aligned}$$
(54)

since \(T_N=(1-\omega ^N)/(\omega ^{N-1}(1-\omega ))\) according to (10). Injecting (54) in (52), and using the definition of \(L_A\), we get (47). The ergodic convergence of \((X_N)_N\) comes from the strong convexity of f [22, Theorem 9.2.6].\(\square \)

Remark 4.4

The convergence rate for the (relaxed) ADMM slightly differs from the linear rate for OPDHG stated in Corollary 3.1 (and, similarly, in Theorem 3.3). Indeed, for the (relaxed) ADMM, the bounds for the objective error (47) and the solution error (48) are of form

$$\begin{aligned} C\,\omega ^N\,\frac{1}{1-\omega ^N}\left( 1+ C'\frac{N\,\omega ^N}{1-\omega ^N}\right) \qquad C,C'>0\;\mathrm {constant} \end{aligned}$$
(55)

while the bounds for the OPDHG are only of form \(C\,\omega ^N\). The extra multiplicative factor, which appears in (55), decreases to 1. Hence, asymptotically, OPDHG and the (relaxed) ADMM are expected to have same linear convergence rate, provided the same value \(\omega \) can be chosen in both bounds. However, in the first iterations, the decrease in the multiplicative factor can visibly affect the convergence (see Sect. 5.1).

4.3 New Convergence Rate for the Classical ADMM and Acceleration

Let us estimate the best convergence rate, which can be achieved by the ADMM and its relaxed variant in the smooth case.

Theorem 4.2

Let f satisfy Assumption (S). Assume problem (3) has a solution denoted by \(x^*\). Let \(\kappa _f:=L_A^2/(\delta \gamma )\).

  1. (i)

    The best convergence rate in Proposition 4.1 and Theorem 4.1 for the ADMM (Algorithm 3) is reached, when the parameter is \(\tau = \sqrt{2\delta ^2\kappa _f}\). We call this parameter the optimal parameter for the ADMM. The resulting convergence rate is \(\omega = 1/(\sqrt{1/(2\kappa _f)} +1)\).

  2. (ii)

    The best convergence rate in Proposition 4.1 and Theorem 4.1 for the relaxed ADMM (Algorithm 4) is reached, when the parameters are \(\tau = \tau ^*\) and \(\tau ' = 1/\sigma ^*\) given by

    $$\begin{aligned} \tau ^* = \frac{\delta }{2}\left( 1+\sqrt{1+4\kappa _f}\right) \quad \mathrm {and}\quad \sigma ^* = \frac{\gamma }{2L_A^2}\left( 1+\sqrt{1+4\kappa _f}\right) \end{aligned}$$
    (56)

    We call these parameter the optimal parameters for the relaxed ADMM. The resulting rate is \(\omega = (\sqrt{1+4\kappa _f}-1)/(\sqrt{1+4\kappa _f}+1)\), which is the same that the one achieved in Theorem 3.2.

Proof

(i) When \(\tau '=\tau \), the condition (44) is fulfilled for any \(\tau >0\). Then, the convergence rate for any \(\tau >0\) is given by the left-hand side of (45), that is:

$$\begin{aligned} \omega (\tau ) := \max \left\{ \frac{2}{\tau \gamma /L_A^2+2},\frac{1}{\delta /\tau +1}\right\} \end{aligned}$$
(57)

Let us minimize this quantity with respect to \(\tau \). One can first check that

$$\begin{aligned} \omega (\tau ) = \left\{ \begin{array}{ll} \displaystyle 1/(\tau \gamma /(2L_A^2)+1), &{} \mathrm {if~} \tau <\sqrt{2\delta L_A^2/\gamma },\\ \displaystyle 1/(\delta /\tau +1),&{} \mathrm {if~} \tau \ge \sqrt{2\delta L_A^2/\gamma }. \end{array}\right. \end{aligned}$$
(58)

Hence, the minimizer is obviously \(\tau = \sqrt{2\delta L_A^2/\gamma }\).

(ii) To prove this statement, it is sufficient to find \(\tau \ge \tau '\) satisfying both (44) and (45), which minimize

$$\begin{aligned} \omega (\tau ,\tau ') := \max \left\{ \frac{\tau '/\tau +1}{\tau \gamma /L_A^2+2},\frac{1}{\delta /\tau '+1}\right\} \end{aligned}$$
(59)

Set \(\tilde{\gamma }= \gamma /L^2_A\) and \(\tilde{\delta }= \delta \). Then, (59) is exactly the lower bound of (31), applied to \((\tau ,\sigma = 1/\tau ',\theta = \tau '/\tau )\). Because of the link between \(\tau \) and \(\theta \), it follows that

$$\begin{aligned} \mathop {\min }\limits _{{\mathop {(\tau ,\sigma ,\theta )}\limits _{{\mathrm {satisfying}\,(11)}} }}\max \left\{ \frac{\theta +1}{\tau \tilde{\gamma }+2},\frac{1}{\sigma \tilde{\delta }+1}\right\} \le \mathop {\min }\limits _{{\mathop {(\tau ,\sigma ,\theta )}\limits _{{\mathop {{\text {satisfying}}\;11}\limits _{{{\text {and}}\;\theta = 1/(\tau \sigma )}} }} }}\max \left\{ \frac{\theta +1}{\tau \tilde{\gamma }+2},\frac{1}{\sigma \tilde{\delta }+1}\right\} . \end{aligned}$$
(60)

According to Sect. 3.4, the left-hand side equals the rate given by Theorem 3.2. Otherwise said,

$$\begin{aligned} \frac{\sqrt{1+4\kappa _f}-1}{\sqrt{1+4\kappa _f}+1}\le \mathop {\min }\limits _{{\mathop {\tau \ge \tau ^{\prime }}\limits _{{\mathop {{\text {satisfying}}\;(44)}\limits _{{{\text {and}}\;(45)}} }} }}\omega (\tau ,\tau '). \end{aligned}$$
(61)

Hence, it suffices to check that \((\tau ,\tau ') = (\tau ^*,1/\sigma ^*)\) satisfy both (44) and (45), and realize the equality. \(\square \)

5 Numerical Applications

5.1 Denoising with TV-Huber

We apply the relaxed ADMM to a denoising problem. Let \(u\in \mathrm {IR} ^{3N_xN_y}\) be a color (noisy) image. We want to solve the following problem:

$$\begin{aligned} \min _{x\in \mathrm {IR} ^{3N_xN_y}}\left\{ f(x):=\frac{\mu }{2}\,\Vert x-u\Vert _2^2 + h(\nabla x) \right\} , \end{aligned}$$
(62)

where the gradient linear operator \(\nabla =(\delta _x,\delta _y)^{\mathrm T}\) is defined by the forward differences. The TV-Huber regularization term is defined by

$$\begin{aligned} h(\nabla x) = \sum _{i=0}^{N_x-1}\sum _{j=0}^{N_y-1} h_0\big (\Vert (\nabla x)_{i,j}\Vert \big ) \mathrm {~~with~~} h_0(z) = \left\{ \begin{array}{ll} \vert z \vert ^2/2, &{}\quad \mathrm {if } \vert z\vert \le 1,\\ \vert z \vert -1/2, &{}\quad \mathrm {if } \vert z\vert > 1. \end{array}\right. \end{aligned}$$
(63)

Hence, this term acts like a quadratic regularization, when the image variations are small, and like a TV regularization, when they are larger. The quantity \(\mu >0\) is a weight parameter. Let \(g:=\mu \,\Vert \cdot -u\Vert _2^2/2\). Functions \(h^*\) and g are, respectively, 1-convex and \(\mu \)-convex. The gradient operator is bounded of norm \(L\le 2\sqrt{2}\) (this bound being tight when \(N_x\) or \(N_y\) go to \(+\infty \)). Thus, we set \(L=2\sqrt{2}\).

The noisy image u is generated by adding Gaussian white noise of standard variation of 10 to a RGB color image of size \(201\times 201\). The image values are between 0 and 255. The code used in written in MATLAB. We chose \({\mu =0.1}\). Iterations for the ADMM and the relaxed ADMM can be explicitly computed, thanks to the Euler equation. We tested two sets of parameters:

  1. 1.

    the optimal parameter for the ADMM (Algorithm 3) \(\tau = 4/\sqrt{\mu }\); the theoretical rate is \(\omega = 1/(\sqrt{\mu }/4+1)\approx {0.9267}\);

  2. 2.

    the optimal parameters for the relaxed ADMM (Algorithm 4) \(\tau = (\sqrt{1+32/{\mu }}+1)/2\) and \(\tau ' = (\sqrt{1+32/\mu }-1)/2\); the theoretical rate is \(\omega = (\sqrt{1+32/\mu }-1)/(\sqrt{1+32/\mu }+1)\approx {0.8943}\).

For comparison, we also applied OPDHG with the optimal parameters \(\tau = (1+\sqrt{1+32/\mu })/16\), \(\sigma = \mu \tau \), and \(\theta = (\sqrt{1+32/\mu }-1)/(\sqrt{1+32/\mu }+1)\) (as given in Theorem 3.2) and FISTA [15], which solves Problem (62) thanks to an accelerated forward-backward splitting algorithm (with an explicit gradient step for \(h(\nabla \cdot )\) and a proximal step for the quadratic fidelity term g). The optimal parameter for FISTA are chosen according to [20, 23], namely the stepsize is 1 / 8 and the overrelaxation parameter is \((1-\sqrt{\mu /(8+\mu )})^2(1+\mu /8)\) . Note that for OPDHG and FISTA, an initialization of x has to be given, from which \(x_1\) is computed thanks to a gradient descent-like step. This is not the case for the (relaxed) ADMM, where \(x_1\) is defined as a minimizer which depends on \((y_0,z_0)\). Thus, for a fair comparison of the methods, \(x_0\) in OPDHG and FISTA is set to be \(x_1\) generated by the relaxed ADMM, while all the other variables are initialized by zeros.

Fig. 1
figure 1

Empirical convergence of the solution error for TV-Huber denoising. The plain lines stand for the sequence \((x_n)\) while the dashed line stand for \((X_n)\). The y-scale is logarithmic. The x-axis corresponds to the iteration number.

Full size image

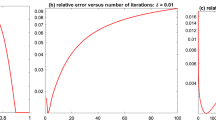
To compare the methods, we compute the solution error (see Fig. 1). This quantity depends on the knowledge of the solution \(x^*\) of Problem (62), which is obviously not available. However, since the OPDHG method has been shown to linearly converge to the solution, we use it to compute an approximation of \(x^*\) by computing a large number of iterations. Note that, even not proved theoretically, the same convergence rates are observed for both the ergodic sequence \((X_n)\) and the iterate sequence \((x_n)\) in the case of the (relaxed) ADMM. The empirical rates, computed by linear regression between iteration 60 and iteration 200, are, respectively, 0.8478 for the ADMM and 0.7826 for the relaxed ADMM. Note that, empirically, we observe that the theoretical rate becomes tight, compared to the observed rate, as the condition number grows to infinity.

Moreover, though the parameters were chosen so that the theoretical rates \(\omega \) are the same for the relaxed ADMM and OPDHG (see Theorems 3.2(ii) and 4.2), the solution error bound for the (relaxed) ADMM has a multiplicative factor (see Remark 4.4) which has an influence on the observed decay. Indeed, if one compares for instance the slope for the ADMM (for which the rate \(\omega \) given in 3.2(i) is greater than that of the OPDHG) and for OPDHG at the 500 first iterations, they look similar, while the slope for the ADMM becomes smaller, as the number of iterations grows. This explains why the ADMM and the relaxed ADMM present a better error decay, at least for the first iterations in the case of the ADMM.

Besides, one should keep in mind that both the ADMM and its relaxed variant require an operator inversion, unlike the OPDHG method and FISTA. Hence, even if comparable numbers of iterations are needed to achieve convergence, the (relaxed) ADMM iterations are more time consuming than the other methods and should be used only when the operator inversion can be implemented efficiently.

5.2 Local Oscillation Behavior

In this section, we consider a simple quadratic problem which reveals oscillating behaviors for OPDHG and FISTA. The ADMM and the relaxed ADMM, as we will see it, are not affected by these artifacts. Let N be a integer. We consider the following constrained problem:

$$\begin{aligned} \min _{x=(x_i)\in \mathrm {IR} ^N : {x_0=1}}\left\{ f(x):=\frac{M-m}{2}\,\Vert K_Nx\Vert _2^2 + \frac{m}{2}\,\Vert x\Vert ^2_2 \right\} , \end{aligned}$$
(64)

where \(K_N: \mathrm {IR} ^N\rightarrow \mathrm {IR} ^{N-1}\) is defined by \((K_Nx)_i=(x_{i+1}-x_{i})/2\). The condition number of this problem is \({\kappa _f=(M-m)/m}\). Hence, the problem is ill-conditioned when m is negligible compared to M. Note that the minimizer of problem (64) can be explicitly computed. We chose \(N=15\), \(m=0.1\) and \(M=10\), so that \(\kappa _f = 99\).

Fig. 2
figure 2

Empirical convergence of the solution error for the toy example. The y-scale is logarithmic. The x-axis corresponds to the iteration number

Full size image

In Fig. 2, we observe oscillations for both the OPDHG method and strongly convex FISTA. Rippling for FISTA has been already observed for quadratic problems of this kind [24]. This phenomena occurs, when the overrelaxation parameter \(\theta \) is chosen too large compared to the eigenvalues of \(m\,\mathrm {I}_N+(M-m)K_N^*K_N\). For the OPDHG method, the reason remains unclear. An investigation of the oscillation behavior for polyhedra objectives can be found in [25]. Note that we do not observe such oscillations for ADMM-like schemes.

6 Conclusions

In this work, we studied the convergence of the OPDHG scheme, in the case where the composite problem is strongly convex with a differentiable with Lipschitz continuous gradient part. Using the equivalence between this algorithm and the ADMM, we provided a new convergence analysis of the latter. This analysis allowed us to design an accelerated variant of the ADMM, by changing the augmented Lagrangian parameter, which is proved to have same convergence rate as the OPDHG method. Hence, we showed that in the smooth case, the choice of the ADMM parameter(s) can be crucial in terms of convergence rate. Experimental results confirmed this theoretical analysis. It has also been observed that the accelerated ADMM does not introduce oscillations in some cases, unlike the OPDHG algorithm and FISTA.