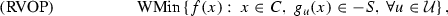Farkas-Type Results for Vector-Valued Functions with Applications

Abstract

The main purpose of this paper consists of providing characterizations of the inclusion of the solution set of a given conic system posed in a real locally convex topological space into a variety of subsets of the same space defined by means of vector-valued functions. These Farkas-type results are used to derive characterizations of the weak solutions of vector optimization problems (including multiobjective and scalar ones), vector variational inequalities, and vector equilibrium problems.

1 Introduction

In this paper, we consider an optimization problem posed in a real locally convex Hausdorff topological vector space (lcHtvs in short), called space of decisions, with a vector-valued objective function f to be minimized on a feasible set A with respect to a given weak partial ordering on a second lcHtvs, called space of criteria, enlarged with a smallest element and a greatest element. The weak ordering on the extended space of criteria is defined from a given pointed, convex cone with non-empty interior and the task “minimize” consists of computing the weak infimum of the set $f\left( A\right)$ in the sense of [1, p. 93] (see also [2, p. 366]).

Different reasons for using a weak ordering in vector optimization are pointed out by many authors. From [3, p. 1421], we quote the following sentence: “The advantages and disadvantages of the different concepts [of solutions] are severely discussed among experts. Efficient solutions are usually motivated by applications and weakly or properly efficient solutions are motivated to be beneficial for the theory and sometimes easier to calculate.” In particular, in multiobjective optimization they are characterized and computed by means of scalarization (assigning weights to the different objectives). Moreover, weak orders are essential in the construction of a complete lattice, giving rise to a conjugate duality approach for set-valued optimization problems, which is considerably close to the conjugate duality for scalar optimization problems (see, for instance, [2, p. 360]). Conjugate maps and Farkas-type results are crucial in any duality theory, and this is why they constitute the main tool and the main objective, respectively, of our research. The state of the art in vector optimization is described, e.g., in [2,3,4,5] and references therein.

The Farkas-type results are well-known basic theoretical tools in scalar optimization. The classical Farkas lemma [6] characterizes the containment of a polyhedral convex cone into a given half-space whose boundary contains the origin. The non-homogeneous version of this famous result [7] characterizes the containment of a polyhedral convex set into a given half-space and was used in the mid-1900s to provide simple proofs of the duality theorem of linear programming and the KKT optimality theorem of nonlinear programming. Since then, many Farkas-type results have been proposed to characterize the inclusion of a give set A,  described by some kind of system, into another set B,  typically the solution set of a single inequality, in order to obtain optimality and duality theorems in different frameworks (see, e.g., the survey papers [8,9,10] and references therein). A Farkas-type result is called asymptotic whenever the characterization of the inclusion involves the closure of certain sets, and it is called $P_{A}$/$P_{B}$ whenever $P_{A}$ and $P_{B}$ are properties satisfied by A and B,  e.g., convexity, non-convexity or being the inverse image by some function of finitely many complements of convex sets (reverse-convexity in brief). In particular, each convex/reverse-convex non-asymptotic Farkas’ lemma provides a different optimality theorem of the KKT-type.

The objective of this paper is to provide Farkas-type results for vector optimization and to show that, like their scalar counterparts in scalar optimization, these results have interesting applications in vector optimization and other fields.

Section 2 contains the necessary preliminaries on epigraphical calculus with scalar functions, calculus rules for the extrema of sets in the sense of [1], and the definitions of conjugate and subdifferential of vector-valued maps. In Sect. 3, we characterize the inclusion of the feasible set A into some reverse-convex set B. Since A is generally non-convex and the characterizations of the inclusion of A in B include closures, Theorems 3.1 and 3.2 are asymptotic non-convex/reverse-convex Farkas’ lemmas. From these two main results, we obtain asymptotic non-convex/linear and convex/reverse-convex Farkas’ lemmas as well as a stable convex/reverse-convex Farkas’ lemma, where the term stability means that the mentioned inclusion is preserved by arbitrary linear perturbations of the convex function defining the reverse-convex set B. Section 4 provides reverse and non-asymptotic Farkas-type results, stable or not, under alternative qualification conditions involving the data. Section 5 is devoted to the characterization of the weak solutions of vector optimization problems, paying attention to some particular types (scalar and multiobjective, constrained, and unconstrained) of optimization problems. Finally, Sect. 6 provides applications to vector variational inequalities and vector equilibrium problems.

2 Preliminaries

Let X be a lcHtvs, whose origin is denoted by $0_{X}$, and with topological dual space represented by $X^{*}$. The only topology we consider on dual spaces is the weak$^{*}$-topology. For a set $U\subset X$, we denote by $\text{ cl }U$, $\text{ conv }U$, and $\text{ cl } \text{ conv }U$ the closure, the convex hull, and the closed convex hull of U, respectively. Note that $\text{ cl } \text{ conv }U=\text{ cl }($ $\text{ conv }$ U). We assume that all the cones under consideration contain the origin of the corresponding space.

Given $f:X\rightarrow {\mathbb {R}}\cup \{\pm \infty \}$, the epigraph of f is the set

$$\begin{aligned} \text{ epi }f:=\{(x,r)\in X\times {\mathbb {R}}:\ x\in \text{ dom }f,\ f(x)\le r\}, \end{aligned}$$

where $\text{ dom }f:=\{x\in X:\ f(x)\ne +\infty \}.$ The function is said to be proper if $\text{ epi }f\ne \emptyset$ and $-\infty \notin f\left( X\right) ,$ it is convex if $\text{ epi }f$ is convex, and it is lower semicontinuous (lsc, in brief) if $\text{ epi } f$ is closed. We denote by ${\varGamma } \left( X\right)$ the class of lsc proper convex functions on X.

The Legendre–Fenchel conjugate of f is the weak$^{*}$-lsc convex function $f^{*}:X^{*}\rightarrow \overline{{\mathbb {R}}}:= \mathbb {R\cup \{-\infty },\mathbb {+\infty \}}$ defined by

$$\begin{aligned} f^{*}\left( x^{*}\right) =\sup _{x\in X}\left( \langle x^{*},x\rangle -f\left( x\right) \right) ,\ \forall x^{*}\in X^{*}. \end{aligned}$$

(1)

Let $f_{1},f_{2}\in {\varGamma } \left( X\right)$ be such that $(\text{ dom } f_{1})\cap (\text{ dom }f_{2})\ne \emptyset .$ Then

$$\begin{aligned} \text{ epi }(f_{1}+f_{2})^{*}=\text{ cl }\left( \text{ epi } f_{1}^{*}+\text{ epi }f_{2}^{*}\right) , \end{aligned}$$

(2)

and, if one of these functions is continuous at a point in the intersection of their domains, we actually have [11, (2.63)]

$$\begin{aligned} \text{ epi }\,(f_{1}+f_{2})^{*}=\text{ epi }\,f_{1}^{*}+ \text{ epi }\,f_{2}^{*}. \end{aligned}$$

(3)

Let $\{f_{i},\,i\in I\}\subset {\varGamma } \left( X\right)$, where I is an arbitrary index set, and suppose that there exists $x_{0}\in X$ such that $\sup \limits _{i\in I}f_{i}(x_{0})<+\infty .$ Then one has [12, Lemma 2.2]

$$\begin{aligned} \text{ epi }\left( \sup _{i\in I}f_{i}\right) ^{*}=\text{ cl } \text{ conv }\left( \bigcup _{i\in I}\text{ epi }\,f_{i}^{*}\right) . \end{aligned}$$

(4)

Now we extend the above concepts to vector-valued functions as it is done in [2] and [1]. Let Y be a second lcHtvs, with origin $0_{Y}$ and topological dual space $Y^{*}$. Let K be a non-empty, closed, pointed, convex cone in Y with non-empty interior, i.e., ${\text{ int } K\ne \emptyset }$. We now define a weak ordering in Y, associated with $\text{ int }K$, in the following way:

$$\begin{aligned} y_{1}<_{K}y_{2}\, \text { if and only if }y_{1}-y_{2}\in -{\text{ int }K}. \end{aligned}$$

Equivalently, $y_{1}\nless _{K}y_{2}$ if and only if $y_{1}-y_{2}\notin -{ \text{ int }K}.$

We enlarge Y by attaching a greatest element $+\infty _{Y}$ and a smallest element $-\infty _{Y}$ with respect to $<_{K}$, which do not belong to Y, and we denote $Y^{\bullet }:=Y\cup \{-\infty _{Y},\ +\infty _{Y}\}$. By convention, $-\infty _{Y}<_{K}y$ and $y<_{K}(+\infty _{Y})$ for any $y\in Y$. We also assume by convention that

$$\begin{aligned} -(+\infty _{Y})= & {} -\infty _{Y},\ -(-\infty _{Y})=+\infty _{Y}, \nonumber \\ (+\infty _{Y})+y= & {} y+(+\infty _{Y})=+\infty _{Y},\ \text {for all }y\in Y\cup \{+\infty _{Y}\}, \nonumber \\ (-\infty _{Y})+y= & {} y+(-\infty _{Y})=-\infty _{Y},\text { for all }y\in Y\cup \{-\infty _{Y}\}. \end{aligned}$$

(5)

The sums $(-\infty _{Y})+(+\infty _{Y})$ and $(+\infty _{Y})+(-\infty _{Y})$ are not considered in this paper.

Given a vector-valued mapping $f:X\rightarrow {Y}^{\bullet }$, the domain of f is defined by

$$\begin{aligned} \text{ dom }f:=\{x\in X:\ f(x)\ne +\infty _{Y}\}, \end{aligned}$$

and f is proper when $\text{ dom }f\not =\emptyset$ and $-\infty _{Y}\notin f(X).$ The $K-$ epigraph of f, denoted by $\text{ epi } _{K}f$, is defined by

$$\begin{aligned} \text{ epi }_{K}\,f=\left\{ (x,y)\in X\times Y:\ y\in f(x)+K\right\} . \end{aligned}$$

Moreover, we say that f is $K-$ epi closed when $\text{ epi } _{K}f$ is a closed set in the product space, and also that f is $K-$ convex, if, $\text{ epi }_{K}\,f$ is a convex set (equivalently, if for any $x_{1}$, $x_{2}\in X$ and $\mu \in [0,1]$ one has $f(\mu x_{1}+(1-\mu )x_{2})-\mu f(x_{1})-(1-\mu )f(x_{2})\in -K$).

Given $M\subset {Y}^{\bullet }$, we shall recall the following definitions (e.g., [2, Definition 7.4.1]):

Definition 2.1

(a) An element ${\bar{v}}\in {Y}^{\bullet }$ is said to be a weakly infimal element of M if for all $v\in M$ we have $v\nless _{K}{\bar{v}}$ and if for any ${\widetilde{v}}\in Y^{\bullet }$ such that $\bar{v }<_{K}{\widetilde{v}}$, then there exists some $v\in M$ satisfying $v<_{K} {\widetilde{v}}$. The set of all weakly infimal elements of M is denoted by $\text{ WInf }M$, and it is called the weak infimum of M.

(b) An element ${\bar{v}}\in {Y}^{\bullet }$ is said to be a weakly supremal element of M if for all $v\in M$ we have ${\bar{v}}\nless _{K}v,$ and if for any ${\widetilde{v}}\in Y^{\bullet }$ such that ${\widetilde{v}}<_{K} {\bar{v}}$, then there exists some $v\in M$ satisfying ${\widetilde{v}}<_{K}v$. The set of all weakly supremal elements of M is denoted by $\text{ WSup } M$, and it is called the weak supremum of M.

Definition 2.2

(a) The weak minimum of M is the set

$$\begin{aligned} \text{ WMin }M=M\cap \text{ WInf }M, \end{aligned}$$

and its elements are the weakly minimal elements of M.

(b) The weak maximum of M is the set

$$\begin{aligned} \text{ WMax }M=M\cap \text{ WSup }M, \end{aligned}$$

and its elements are the weakly maximal elements of M.

Remark 2.1

(a) For any $M\subset Y$, thanks to the conventions $-\infty _{Y}<_{K}y$ and $y<_{K}(+\infty _{Y})$ for any $y\in Y$, it is easy to check that $\text{ WInf }M=\text{ WInf }(M\cup \{+\infty _{Y}\}), \text{ WMin }M=\text{ WMin }(M\cup \{+\infty _{Y}\}), \text{ WSup }M= \text{ WSup }(M\cup \{-\infty _{Y}\})$ and $\text{ WMax }M=\text{ WMax } (M\cup \{-\infty _{Y}\}).$

(b) If $M\ne \emptyset$, since $v<_{K}(+\infty _{Y})$ for all $v\in {M,} +\infty _{Y}\notin \text{ WInf }M$ (similarly, $-\infty _{Y}\notin \text{ WSup }M$). Otherwise, if $M=\emptyset$, and according to the definition, $\text{ WInf }M=\{+\infty _{Y}\}$ and $\text{ WSup } M=\{-\infty _{Y}\}$ [2, Remark 7.4.1].

(c) $(Y^{\bullet },<_{K})$ turns out to be a complete lattice.

(d) If $M\ne \emptyset$, it is easy to see that if $\text{ WSup } M\not =\{+\infty _{Y}\}$, then ${\bar{v}}\in \text{ WSup }M$ if and only if ${\bar{v}}\in Y{\setminus } (M-\text{ int }K)$ and ${\bar{v}}-\text{ int }K\ \subset \ M-\text{ int }K$ (similarly, if $\text{ WInf }M\not =\{-\infty _{Y}\}$  then ${\bar{v}}\in \text{ WInf }M$ if and only if ${\bar{v}}\in Y{\setminus } (M+\text{ int }K)$ and ${\bar{v}}+\text{ int }K\ \subset \ M+ \text{ int }K\mathbf {).}$

Recall (e.g., from [13, Lemma 5.3]) that, given two non-empty sets $N,V\subset Y$ such that V is open, one has

$$\begin{aligned} \text{ cl }N+V=N+V. \end{aligned}$$

(6)

If K is a non-empty, closed, convex cone in Y with non-empty interior, i.e., $\text{ int }K\ne \emptyset ,$ taking in (6) $N=V=\text{ int } K$, we get

$$\begin{aligned} K+\text{ int }K=\text{ int }K, \end{aligned}$$

(7)

and consequently,

$$\begin{aligned} \left. \begin{array}{c} y\in K \\ y+y^{\prime }\notin \text{ int }K \end{array} \right\} \ \Longrightarrow \ y^{\prime }\notin \text{ int }K. \end{aligned}$$

(8)

Definition 2.3

Given $\emptyset \ne M\subset {Y}^{\bullet },$ we define the set ${\mathcal {A}}(M)$ of all points above M,  and the set ${\mathcal {B}}(M)$ of all points below M by

$$\begin{aligned} {\mathcal {A}}(M)=\left\{ {\bar{v}}\in {Y}^{\bullet }:v<_{K}{\bar{v}}\text { for some }v\in M\right\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {B}}(M)=\left\{ {\bar{v}}\in {Y}^{\bullet }:{\bar{v}}<_{K}v\text { for some }v\in M\right\} . \end{aligned}$$

Remark 2.2

$\ (a)$ One has

$$\begin{aligned} {\mathcal {A}}(M)=\left\{ \begin{array}{ll} Y\cup \left\{ +\infty _{Y}\right\} , &{} \text {if}-\infty _{Y}\in M, \\ \emptyset , &{} \text {if }M=\left\{ +\infty _{Y}\right\} , \\ \left\{ +\infty _{Y}\right\} \cup \left( M+\text{ int }K\right) , &{} \text { otherwise,} \end{array} \right. \end{aligned}$$

(9)

and

$$\begin{aligned} {\mathcal {B}}(M)=\left\{ \begin{array}{ll} Y\cup \left\{ -\infty _{Y}\right\} , &{} \text {if}+\infty _{Y}\in M, \\ \emptyset , &{} \text {if }M=\left\{ -\infty _{Y}\right\} , \\ \left\{ -\infty _{Y}\right\} \cup \left( M-\text{ int }K\right) , &{} \text { otherwise.} \end{array} \right. \end{aligned}$$

(10)

(b) In particular,

$$\begin{aligned}&-\infty _{Y}\notin M\ne \left\{ +\infty _{Y}\right\} \ \Longrightarrow \ {\mathcal {A}}(M)=\left\{ +\infty _{Y}\right\} \cup (M+\text{ int }K), \end{aligned}$$

(11)

$$\begin{aligned}&+\infty _{Y}\notin M\ne \left\{ -\infty _{Y}\right\} \ \Longrightarrow \ {\mathcal {B}}(M)=\left\{ -\infty _{Y}\right\} \cup \left( M-\text{ int } K\right) . \end{aligned}$$

(12)

(c) Moreover, it is easy to check that

$$\begin{aligned} \text{ WSup }M=\{+\infty _{Y}\}\Longleftrightarrow & {} \ {\mathcal {B}} (M)=Y\cup \{-\infty _{Y}\} \nonumber \\\Longleftrightarrow & {} \ +\infty _{Y}\in M\text { or }M-\text{ int }K=Y \nonumber \\\Longleftrightarrow & {} \ \forall v\in Y,\ \exists {\widetilde{v}}\in M\ \ \text{ such }\ \text {that}\ v<_{K}{\widetilde{v}}. \end{aligned}$$

(13)

Analogously, we can characterize the case $\text{ WInf }M=\{-\infty _{Y}\}$ . The first equivalence in (13) is Proposition 2.2 (ii) in [1].

Lemma 2.1

Let $\emptyset \not =M\subset Y$ and ${\bar{v}}\in Y$. Then

$$\begin{aligned} \left( {\bar{v}}-\text{ int }K\subset M-\text{ int }K\right) \ \ \Longleftrightarrow \ \ {\bar{v}}\in \text{ cl }(M-\text{ int }K). \end{aligned}$$

Proof

$[\Longrightarrow ]$ Assume that ${\bar{v}}-\text{ int } K\subset M-\text{ int }K$, and let U be a barrelled neighborhood of $0_{Y}$ . We will show that $({\bar{v}}+U)\cap (M-\text{ int }K)\not =\emptyset$. Take $k_{0}\in \text{ int }K$ (remember that $\text{ int } K\not =\emptyset$). Then, there exists $\lambda >0$ such that $-\lambda k_{0}\in U$. Since $\lambda k_{0}\in \text{ int }K$, we get ${\bar{v}} -\lambda k_{0}\in {\bar{v}}-\text{ int }K\subset M-\text{ int }K$, and hence, ${\bar{v}}-\lambda k_{0}\in ({\bar{v}}+U)\cap (M-\text{ int }K)$.

$[\Longleftarrow ]$ Assume that ${\bar{v}}\in \text{ cl }(M-\text{ int }K)$, and let $k\in \text{ int }K$. We will show that ${\bar{v}}-k\in M-\text{ int } K$. Since $0_{Y}\in -k+\text{ int }K$, there is a neighborhood U of $0_{Y}$ such that $U\subset -k+\text{ int }K$, and hence, ${\bar{v}}+U\subset {\bar{v}}-k+\text{ int }K$. Now, as ${\bar{v}}\in \text{ cl }(M-\text{ int } K)$, $({\bar{v}}-k+\text{ int }K)\cap (M-\text{ int }K)\not =\emptyset$. Therefore, ${\bar{v}}-k+k^{\prime }\in M-\text{ int }K$ for some $k^{\prime }\in \text{ int }K$, and so

$$\begin{aligned} {\bar{v}}-k\in M-\text{ int } K-k^{\prime }\subset M-\text{ int } K- \text{ int } K\subset M-\text{ int } K \end{aligned}$$

(as $\text{ int }K$ is a convex cone), and we are done. $\square$

Proposition 2.1

Given $\emptyset \ne M\subset {Y}^{\bullet }$ such that $+\infty _{Y}\notin M\ne \left\{ -\infty _{Y}\right\} ,$ the following statements hold:

• (i) $\mathbf {\emptyset \ne }\text{ WSup }M\subset Y\cup \{+\infty _{Y}\}.$ If $\text{ WSup }M\not =\{+\infty _{Y}\}$, then

  $$\begin{aligned} \text{ WSup }M= & {} \left\{ {\overline{v}}\in {Y}\diagdown \left( M-\text{ int } K\right) :{\overline{v}}-\text{ int }K\subset M-\text{ int }K\right\} \nonumber \\= & {} \text{ cl }\left( M-\text{ int }K\right) \diagdown \left( M-\text{ int } K\right) , \end{aligned}$$

  (14)

  in other words, $\text{ WSup }M$ is the boundary in Y of the set $M- \text{ int } K.$

• (ii) The weak maximum of M is

  $$\begin{aligned} \text{ WMax }M=M\diagdown \left( M-\text{ int }K\right) , \end{aligned}$$

  (15)

  so that $\text{ WMax }M$ is a closed (compact) set whenever M is a closed (compact, respectively) set of Y.

• (iii)

  $$\begin{aligned} {Y}^{\bullet }=\left\{ -\infty _{Y}\right\} \cup \left( M-\text{ int } K\right) \cup (\text{ WSup }M)\cup {\mathcal {A}}\left( \text{ WSup }M\right) . \end{aligned}$$

  Moreover, if $\text{ WSup }M\ne \{+\infty _{Y}\}$, then

  $$\begin{aligned} {Y}=\left( M-\text{ int }K\right) \cup (\text{ WSup }M)\cup (\text{ WSup } M+\text{ int }K), \end{aligned}$$

  (16)

  and the three sets in the right-hand side are disjoint.

• (iv) Let $M\subset Y$ be such that $\text{ cl }M=\text{ cl }(\text{ int } M)$ (e.g., if M is convex and $\text{ int }M\ne \emptyset$), then

  $$\begin{aligned} \text{ WSup }(\text{ int }M)=\text{ WSup }M=\text{ WSup }(\text{ cl }M). \end{aligned}$$

  (17)

Proof

The assumptions on M entail $M\cap Y\ne \emptyset .$

• (i) It is obvious that $\text{ WSup }M\ne \emptyset$ and $-\infty _{Y}\notin \text{ WSup }M$ (see Remark 2.1(b)). Thus, $\emptyset \ne \text{ WSup }M\subset Y\cup \left\{ +\infty _{Y}\right\}$ and the first claim holds.

  Let $\text{ WSup }M\not =\{+\infty _{Y}\}$ or, equivalently (13), ${\mathcal {B}}(M)\not =Y\cup \{-\infty _{Y}\}.$ The first equality in (14) comes from Remark 2.1(d) and the assumption $\text{ WSup } M\not =\{+\infty _{Y}\},$ while the second one comes from the first one and Lemma 2.1.

• (ii) It is a straightforward consequence of $\text{ WMax }M=M\cap \text{ WSup }M.$

• (iii) According to Proposition 7.4.1(b)(d) in [2], and using (12),

  $$\begin{aligned} {Y}^{\bullet }= & {} (\text{ WSup }M)\cup {\mathcal {B}}\left( \text{ WSup } M\right) \cup {\mathcal {A}}\left( \text{ WSup }M\right) \nonumber \\= & {} (\text{ WSup }M)\cup {\mathcal {B}}\left( M\right) \cup {\mathcal {A}}\left( \text{ WSup }M\right) \nonumber \\= & {} \left\{ -\infty _{Y}\right\} \cup \left( M-\text{ int }K\right) \cup ( \text{ WSup }M)\cup {\mathcal {A}}\left( \text{ WSup }M\right) . \end{aligned}$$

  (18)

The first assertion in (iii) holds.

Assume now that $\text{ WSup }M\ne \{+\infty _{Y}\}$. Applying (11) to the set $\text{ WSup }M$ (note that $-\infty _{Y}\notin \text{ WSup }M$), we get

$$\begin{aligned} {\mathcal {A}}\left( \text{ WSup }M\right) =(\text{ WSup }M+\text{ int } K)\cup \left\{ +\infty _{Y}\right\} . \end{aligned}$$

(19)

According to (18) and (19),

$$\begin{aligned} {Y}^{\bullet }=\left\{ -\infty _{Y}\right\} \cup \left( M-\text{ int } K\right) \cup (\text{ WSup }M)\cup \left( \text{ WSup }M+\text{ int } K\right) \cup \left\{ +\infty _{Y}\right\} , \end{aligned}$$

and dropping $-\infty _{Y}$ and $+\infty _{Y}$ in both sides we get (16), together with the conclusion that the three sets in the right-hand side are disjoint (see again Proposition 7.4.1(d) in [2]).

(iv) It is a consequence of (14) and (6), applying the last one to the sets $N:=\text{ int }M$ and $V:=-\text{ int }K.$ $\square$

Observe that (14), (15), and (17) remain true by replacing $\text{ WSup }$, $\text{ WMax }$, and $-\text{ int }K$ with $\text{ WInf }$, $\text{ WMin }$, and $\text{ int }K$, respectively.

We denote by ${\mathcal {L}}(X,Y)$ the space of linear continuous mappings from X to Y, and $0\mathbf {{_{{\mathcal {L}}}}}\in {\mathcal {L}}(X,Y)$ is the zero mapping defined by $0\mathbf {{_{{\mathcal {L}}}}}(x)=0_{Y}$ for all $x\in X$. Obviously, when $Y={\mathbb {R}}$, then ${\mathcal {L}}(X,Y)=X^{*}$.

Definition 2.4

Given $f:X\rightarrow {Y}^{\bullet },$ the set-valued map $f^{*}:{\mathcal {L}}(X,Y)\rightrightarrows {Y}^{\bullet }$ defined by

$$\begin{aligned} f^{*}(L):=\text{ WSup }\{L(x)-f(x):\ x\in X\}\equiv \text{ WSup } \{(L-f)(X)\}, \end{aligned}$$

is called the conjugate map of f. The domain of $f^{*}$ is

$$\begin{aligned} \text{ dom }f^{*}=\left\{ L\in {\mathcal {L}}(X,Y):\ f^{*}(L)\not =\{+\infty _{Y}\}\right\} \end{aligned}$$

and the $K-$ epigraph of $f^{*}$ is

$$\begin{aligned} \text{ epi }_{K}f^{*}=\left\{ (L,y)\in {\mathcal {L}}(X,Y)\times Y:\ y\in f^{*}(L)+K\right\} . \end{aligned}$$

Remark 2.3

• (a) In [1, Definition 3.1] and in [2, Definition 7.4.2], the conjugate map is defined for a set-valued map $F:X\rightrightarrows {Y} ^{\bullet }.$

• (b) In the scalar case, when $Y={\mathbb {R}}$ and $K={\mathbb {R}}_{+},$ the notion of conjugate map introduced in Definition 2.4 collapses to (1) just identifying $y\in \overline{{\mathbb {R}}}$ with $\left\{ y\right\} \in 2^{\overline{{\mathbb {R}}}}.$

• (c) According to Remark 2.1(a), $f^{*}(L)=\text{ WSup } \{(L-f)(\text{ dom }\,f)\}.$ Moreover, by Proposition 2.1 (i), $f^{*}(L)$ is the boundary of $\{(L-f)(\text{ dom }\,f)\}- \text{ int }K$ if f is a proper function and $\text{ WSup }\{(L-f)( \text{ dom }\,f)\}\ne \left\{ +\infty _{Y}\right\} .$ The necessity of the latter assumption can be shown by considering the finite-valued function $f: \mathbb {R\rightarrow R}$ such that $f(x)=-\left| x\right| .$ In fact, given $L=x^{*}\in {\mathbb {R}}$, one has

  $$\begin{aligned} (L-f)(\text{ dom }\,f)=\{x^{*}x+\left| x\right| :\ x\in {\mathbb {R}}\}=\left\{ \begin{array}{c} {\mathbb {R}}_{+},\text { if }x^{*}\in [-1,1], \\ {\mathbb {R}},\text { if }x^{*}\notin [-1,1], \end{array} \right. \end{aligned}$$

  so that

  $$\begin{aligned} \{(L-f)(\text{ dom }\,f)\}-\text{ int }K={\mathbb {R}}, \end{aligned}$$

  with

  $$\begin{aligned} \text{ bd }\left\{ \{(L-f)(\text{ dom }\,f)\}-\text{ int }K\right\} =\emptyset \ne \left\{ +\infty \right\} =f^{*}\left( L\right) . \end{aligned}$$

Proposition 2.2

Let $h:X\rightarrow {Y}^{\bullet }$ be proper and $(L,y)\in {\mathcal {L}}(X,Y)\times Y.$ The following implication holds

$$\begin{aligned} y+h(x)\nless _{K}L(x)\,\forall x\in X\ \Longrightarrow (L,y)\in \text{ epi }_{K}h^{*}, \end{aligned}$$

or equivalently

$$\begin{aligned} y+h(x)-L(x)\notin -{\text{ int }K}\ \forall x\in X\ \Longrightarrow y\in h^{*}(L)+K. \end{aligned}$$

Proof

Let $h:X\rightarrow {Y}^{\bullet }$ be proper and $(L,y)\in {\mathcal {L}}(X,Y)\times Y$ be such that

$$\begin{aligned} y+h(x)-L(x)\notin -{\text{ int }K},\ \text { for all }\ x\in X. \end{aligned}$$

(20)

Observe that (20) is equivalent to

$$\begin{aligned} y\notin \left( L-h\right) (\text{ dom }h)-{\text{ int }K,} \end{aligned}$$

(21)

and then $\text{ WSup }\{\left( L-h\right) (\text{ dom }h)\}\ne \{+\infty _{Y}\}.$ Indeed, assume the contrary, i.e., that

$$\begin{aligned} \text{ WSup }\{\left( L-h\right) (\text{ dom }h)=\{+\infty _{Y}\}. \end{aligned}$$

Then as $y<_{K}+\infty _{Y}$, by the definition of the weak supremum there exists ${\bar{x}}\in \text{ dom }h$ such that

$$\begin{aligned} y<_{K}L({\bar{x}})-h({\bar{x}}), \end{aligned}$$

or equivalently, there is ${\bar{x}}\in X$ satisfying

$$\begin{aligned} y+h({\bar{x}})-L({\bar{x}})\in -{\text{ int }K}, \end{aligned}$$

which contradicts (20).

Now, since $\emptyset \ne \left( L-h\right) (\text{ dom }h)\subset Y$ and $\text{ WSup }\{\left( L-h\right) (\text{ dom }h)\}\ne \{+\infty _{Y}\}$, we get from Proposition 2.1(iii) the following partition of Y : 

$$\begin{aligned} Y= & {} \left\{ \left( L-h\right) (\text{ dom }h)-\text{ int }K\right\} \cup \text{ WSup }\{\left( L-h\right) (\text{ dom }h))\} \\&\cup \left\{ \text{ WSup }\{\left( L-h\right) (\text{ dom }h)\}+ \text{ int }K\right\} . \end{aligned}$$

Then, (21) yields

$$\begin{aligned} \begin{array}{ll} y &{} \in \text{ WSup }\{\left( L-h\right) (\text{ dom }h)\}\cup \left\{ \text{ WSup }\{\left( L-h\right) (\text{ dom }h)\}+\text{ int }K\right\} \\ &{} \subset \text{ WSup }\{\left( L-h\right) (\text{ dom }h)\}+K \\ &{} =h^{*}(L)+K, \end{array} \end{aligned}$$

and we are done. $\square$

The following notion of subdifferential of a vector-valued function particularizes the corresponding one for set-valued maps given in [2, Definition 7.4.2(c)] and in [1, Definition 4.1].

Definition 2.5

Given $f:X\rightarrow {Y}^{\bullet }$ and ${\bar{x}}\in \text{ dom }f$, we say that $L\in {\mathcal {L}}(X,Y)$ is a subgradient of f at ${\bar{x}}$ if

$$\begin{aligned} L({\bar{x}})-f({\bar{x}})\in \text{ WSup }\{(L-f)(X)\}. \end{aligned}$$

The set of all subgradients of f at ${\bar{x}}$ is called subdifferential of f at ${\bar{x}},$ and it is denoted by $\partial f(\bar{x }).$

When $Y={\mathbb {R}}$ and $K={\mathbb {R}}_{+},$ the above definition of subdifferential of f at ${\bar{x}}$ is nothing else but the classical subdifferential of f at ${\bar{x}},$ i.e., $x^{*}\in \partial f({\bar{x}})$ if only if $f(x)-f({\bar{x}})\ge \langle x^{*},x-{\bar{x}}\rangle$ for all $x\in X$.

Proposition 2.3

Given $L\in {\mathcal {L}}(X,Y)$ and ${\bar{x}}\in \text{ dom }f,$ one has

$$\begin{aligned} \begin{array}{ll} L\in \partial f({\bar{x}}) &{} \Longleftrightarrow L({\bar{x}})-f({\bar{x}})\in \text{ WMax }\{(L-f)(X)\} \\ &{} \Longleftrightarrow L({\bar{x}})-f({\bar{x}})\in f^{*}(L) \\ &{} \Longleftrightarrow \left( L,L({\bar{x}})-f({\bar{x}})\right) \in \text{ epi }_{K}\,f^{*}. \end{array} \end{aligned}$$

Proof

From Definitions 2.2, 2.4, and 2.5,

$$\begin{aligned} \begin{array}{ll} L\in \partial f({\bar{x}}) &{} \Longleftrightarrow L({\bar{x}})-f({\bar{x}})\in \text{ WMax }\{L(x)-f(x):\ x\in X\} \\ &{} \Longleftrightarrow L({\bar{x}})-f({\bar{x}})\in f^{*}(L) \\ &{} \Longrightarrow \left( L,L({\bar{x}})-f({\bar{x}})\right) \in \text{ epi }_{K}\,f^{*}. \end{array} \end{aligned}$$

Now we assume that $\left( L,L({\bar{x}})-f({\bar{x}})\right) \in \text{ epi }_{K}\,f^{*}.$ Then $L({\bar{x}})-f({\bar{x}})\in f^{*}(L)+K,$ and there exists $k\in K$ such that

$$\begin{aligned} L({\bar{x}})-f({\bar{x}})-k\in f^{*}(L)=\text{ WSup }\{L(x)-f(x):\ x\in X\}. \end{aligned}$$

From the definition of $\text{ WSup }$

$$\begin{aligned} L({\bar{x}})-L(x)+f(x)-f({\bar{x}})-k\notin -{\text{ int }K},\ \forall x\in X, \end{aligned}$$

and it follows from (8) that

$$\begin{aligned} L({\bar{x}})-L(x)+f(x)-f({\bar{x}})\notin -{\text{ int }K},\ \forall x\in X. \end{aligned}$$

Thus,

$$\begin{aligned} L({\bar{x}})-f({\bar{x}})\in \text{ WSup }\{L(x)-f(x):\ x\in X\}, \end{aligned}$$

i.e., $L\in \partial f({\bar{x}}).$ The proof is complete. $\square$

Strong versions of the above notions of conjugate and subdifferential of a vector-valued function can be found in the recent book [10]. $\square$

3 Reverse and Asymptotic Farkas-Type Results

Let X, Y and Z be lcHtvs, $0_{Z}$ be the zero in Z, S be a non-empty convex cone in Z,  and K be a non-empty, closed, pointed, convex cone in Y with $\text{ int }K\not =\emptyset$. Let $\leqq _{S}$ be the ordering on Z induced by the cone S, i.e.,

$$\begin{aligned} z_{1}\leqq _{S}z_{2}\text { if and only if }z_{1}-z_{2}\in -S. \end{aligned}$$

We also enlarge Z by attaching a greatest element $+\infty _{Z}$ and a smallest element $-\infty _{Z}$ with respect to $\leqq _{S}$, which do not belong to Z, and define $Z^{\bullet }:=Z\cup \{-\infty _{Z},\ +\infty _{Z}\}$. In $Z^{\bullet }$, we adopt the same sign conventions as in (5).

Let $f:X\rightarrow {Y}\cup \left\{ +\infty _{Y}\right\} ,$ $g:X\rightarrow Z\cup \left\{ +\infty _{Z}\right\}$, and consider a non-empty set $C\subset X$.

In this paper, we associate with the data triple $\left( f,g,C\right)$ the constraint system

$$\begin{aligned} \{x\in C,\ g(x)\in -S\}\equiv \{x\in C,\ g(x)\leqq _{S}0_{Z}\}, \end{aligned}$$

with associated feasible set

$$\begin{aligned} A:=C\cap g^{-1}(-S), \end{aligned}$$

and the vector optimization problem

(22)

where $\text{ WMin }$ concerns the weak ordering on ${Y}^{\bullet }$ associated with K. A feasible solution ${\bar{x}}\in A$ is said to be a weak solution to (VOP) if

$$\begin{aligned} f({\bar{x}})\in \text{ WMin }f(A). \end{aligned}$$

We assume from now on that $A\cap \text{ dom }f\not =\emptyset$; in other words, $\mathrm {(VOP)}$ is feasible and non-trivial.

When ${Y}={\mathbb {R}}$ and $K={\mathbb {R}}_{+},$ we say that the data triple $\left( f,g,C\right)$ is scalar. In that case, $\mathrm {(VOP)}$ collapses to the scalar optimization problem

(23)

where $\text{ Min }$ stands for the task consisting of identifying standard optimal solutions to $\mathrm {(SOP)}$. Here $Y^{\bullet }$ is nothing else than the extended real line $\overline{{\mathbb {R}}}$ ordered by $<_{{\mathbb {R}}_{+}}$while $L\in {\mathcal {L}}(X,{\mathbb {R}})$ is usually written as $L=x^{*}\in X^{*}.$

When ${Y}={\mathbb {R}}^{p}$ and $K={\mathbb {R}}_{+}^{p},$ $p\ge 2,$ we say that the data triple $\left( f,g,C\right)$ is componentwise. Then (VOP) becomes the multiobjective optimization problem

$$\begin{aligned} \begin{array}{rrl} \mathrm {(MOP)}&``\text{ Min }''\left\{ f(x):x\in C,\ g(x)\in -S\right\} ,&\end{array} \end{aligned}$$

(24)

where “$\text{ Min }$” stands for the task consisting of computing ${\bar{x}}\in A$ such that $\left( f\left( {\bar{x}} \right) -{\mathbb {R}}_{++}^{p}\right) \cap f\left( A\right) =\emptyset ,$ i.e., weakly efficient solutions to $\mathrm {(MOP),}$ which coincide with the weak solutions to (VOP). Here, given $y=\left( y_{1},...,y_{p}\right)$ and $y^{\prime }=\left( y_{1}^{\prime },...,y_{p}^{\prime }\right) \in {\mathbb {R}}^{p},$

$$\begin{aligned} y<_{{\mathbb {R}}_{+}^{p}}y^{\prime }\Longleftrightarrow y_{j}<y_{j}^{\prime },\ \forall j\in \{1,...,p\}, \end{aligned}$$

and, consequently,

$$\begin{aligned} y\nless _{{\mathbb {R}}_{+}^{p}}y^{\prime }\Longleftrightarrow \exists j_{0}\in \{1,...,p\}\text { such that }\ y_{j_{0}}\ge y_{j_{0}}^{\prime }. \end{aligned}$$

In this paper, we establish Farkas-type results from which we deduce necessary and sufficient conditions for the existence of weak solutions to problem (VOP) and some particular instances as (MOP) and (SOP). With this purpose, we provide next some fundamental results which will be used in the following sections.

For $T\in {\mathcal {L}}(Z,Y)$, we define the composite function $T\circ g:X\rightarrow {Y}^{\bullet }$ as follows:

$$\begin{aligned} (T\circ g)(x)=\left\{ \begin{array}{ll} T(g(x)), &{} \text {if }g(x)\in Z, \\ +\infty _{Y}, &{} \text {if }g(x)=+\infty _{Z}. \end{array} \right. \end{aligned}$$

The indicator map $i_{D}:X\rightarrow {Y}^{\bullet }$ of a set $D\subset X$ is defined by

$$\begin{aligned} i_{D}(x)=\left\{ \begin{array}{ll} 0_{Y}, &{} \text {if }x\in D, \\ +\infty _{Y}, &{} \text {otherwise.} \end{array} \right. \end{aligned}$$

In the case $Y={\mathbb {R}}$, $i_{D}$ is the usual indicator function.

Let us consider

$$\begin{aligned} {\mathcal {L}}_{+}(S,K):=\{T\in {\mathcal {L}}(Z,Y):\ T(S)\subset K\}. \end{aligned}$$

If $Y={\mathbb {R}}$ and $K={\mathbb {R}}_{+}$, then ${\mathcal {L}}_{+}(S,K)=S^{+}$, where $S^{+}$ is the (positive) dual cone of S in the sense of convex analysis, i.e.,

$$\begin{aligned} S^{+}=\{z^{*}\in Z^{*}:\ \langle z^{*},s\rangle \ge 0\ \text { for all}\ s\in S\}. \end{aligned}$$

The sets of the form $(f+i_{C}+T\circ g)^{*}(L),$ with $T\in {\mathcal {L}} _{+}(S,K)$ and $L\in {\mathcal {L}}(X,Y),$ play an important role in this paper. The next example, to be used later, illustrates the way to calculate analytically such sets when the three involved lctHtvs, X,  Y,  and Z,  are finite-dimensional.

Example 3.1

Let $X={\mathbb {R}},$ $Y={\mathbb {R}}^{2},$ $Z={\mathbb {R}} ,$ $K={\mathbb {R}}_{+}^{2},$ $S={\mathbb {R}}_{+},$ and $C=]-1,+\infty [$. Let $f:{\mathbb {R}}\rightarrow {\mathbb {R}}^{2}\cup \left\{ +\infty _{{\mathbb {R}} ^{2}}\right\}$ and $g:{\mathbb {R}}\rightarrow {\mathbb {R}}\cup \left\{ +\infty \right\}$ defined by

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} \left( 0,\frac{1}{x}\right) , &{} \text {if}\ \ x\ne 0, \\ +\infty _{{\mathbb {R}}^{2}}, &{} \text {otherwise,} \end{array} \right. \ \ \ \text { and }\ \ \ \ \ g(x)=\left\{ \begin{array}{ll} -\frac{|x+1|}{x}, &{} \text {if}\ \ x\ne 0, \\ +\infty , &{} \text {otherwise.} \end{array} \right. \end{aligned}$$

The linear mappings $T\in {\mathcal {L}}_{+}({\mathbb {R}}_{+},{\mathbb {R}}_{+}^{2})$ and $L\in {\mathcal {L}}({\mathbb {R}},{\mathbb {R}}^{2})$ can be represented as $T(z)=(az,bz)$ for all $z\in {\mathbb {R}},$ with $a,b\in {\mathbb {R}}_{+},$ and $L(x)=(cx,dx)$ for all $x\in {\mathbb {R}},$ with $c,d\in {\mathbb {R}}.$ We now calculate $(f+i_{C}+T\circ g)^{*}(L)$ for one typical case where $a>0,$ $0<b<1,$ $c=0,$ $d<0,$ and $d<b-1$. One has

$$\begin{aligned}&(f+i_{C}+T\circ g)^{*}(L) \nonumber \\&\quad =\text{ WSup }\left\{ L(x)-f(x)-(T\circ g)(x):\ x\in C\right\} \nonumber \\&\quad =\text{ WSup }\left\{ (0,dx)-\left( 0,\frac{1}{x}\right) +\left( \frac{a|x+1|}{x},\frac{b|x+1|}{x}\right) :x\in C\diagdown \{0\}\right\} \nonumber \\&\quad =\text{ WSup }\left\{ \left( a\left( \frac{x+1}{x}\right) ,dx-\frac{ 1}{x}+b\left( \frac{x+1}{x}\right) \right) :x\in ]-1,+\infty [\diagdown \{0\}\right\} \nonumber \\&\quad =\text{ WSup }\left\{ y\in {\mathbb {R}}^{2}:y_{2}=\left( \frac{b-1}{a} \right) y_{1}+1+\frac{da}{y_{1}-a},\ y_{1}<0\ \ \text {or}\quad y_{1}>a\right\} \nonumber \\&\quad =\bigg \{y\in {\mathbb {R}}^{2}:y_{2}=\frac{\left( b-1\right) y_{1}}{a} +1+\frac{da}{y_{1}-a},\ y_{1}<a+\frac{ad}{1-b} \nonumber \\&\quad =\text {or}\ y_{1}>a+a\frac{ \sqrt{-d}}{\sqrt{1-b}}\bigg \} \nonumber \\&\qquad \bigcup \left( \left[ a+\frac{ad}{1-b},0\right] \times \left\{ 1-d\right\} \right) \cup \left( \{0\}\times \left[ b-2\sqrt{d(b-1)} ,1-d\right] \right) \nonumber \\&\qquad \bigcup \left( \left[ 0,a+a\frac{\sqrt{-d}}{\sqrt{1-b}} \right] \times \left\{ b-2\sqrt{d(b-1)}\right\} \right) . \end{aligned}$$

(25)

The set $(f+i_{C}+T\circ g)^{*}(L)$ in (25),  with $a=1,$ $b= \frac{1}{2},$ $c=0,$ and $d=-1$ is represented in Fig. 1.

Fig. 1

Representation of the set $(f+i_{C}+\left( 1,\frac{1}{2}\right) \circ g)^{*}(0,-1)$

We are now in the position to prove the main results of this section: two versions of reverse Farkas lemma for vector-valued functions. Remember that we are assuming all the time that the triple (f, g, C) satisfies $A\cap \text{ dom }f\not =\emptyset$ with $A=C\cap g^{-1}(-S).$

Theorem 3.1

(Reverse Farkas Lemma I) Let $(L,y)\in {\mathcal {L}}(X,Y)\times Y.$ Then, the following statements are equivalent:

${\mathbf {(a_{1})}}$ :

$g(x)\in -S,\ x\in C\ \ \Longrightarrow \ \ f(x)-L(x)+y\notin -{\text{ int }K},$

${\mathbf {(b_{1})}}$ :

$(L,y)\in \text{ epi }_{K}(f+i_{A})^{*}.$

Proof

Taking $h:=f+i_{A}$, one has $\text{ dom }h=A\cap \text{ dom }f\not =\emptyset .$ Then, by Proposition 2.2, the following implication holds:

$$\begin{aligned} y+(f+i_{A})(x)-L(x)\notin -{\text{ int }K},\ \forall x\in X\ \Longrightarrow y\in (f+i_{A})^{*}(L)+K. \end{aligned}$$

(26)

[${\mathbf {(a_{1})}}$ $\Longrightarrow$ ${\mathbf {(b_{1})}}$] Assume ${\mathbf {(a_{1})}}$ holds, i.e.,

$$\begin{aligned} g(x)\in -S,x\in C\Longrightarrow f(x)-L(x)+y\notin -{\text{ int }K,} \end{aligned}$$

or, equivalently,

$$\begin{aligned} y+(f+i_{A})(x)-L(x)\notin -{\text{ int }K},\forall x\in X. \end{aligned}$$

It then follows from (26) that $(L,y)\in \text{ epi } _{K}(f+i_{A})^{*}.$

[${\mathbf {(b_{1})}}$ $\Longrightarrow$ ${\mathbf {(a_{1})}}$] Assume ${\mathbf {(b_{1})}}$ holds, i.e.,

$$\begin{aligned} y\in (f+i_{A})^{*}(L)+K. \end{aligned}$$

This accounts for the existence of $k\in K$ such that

$$\begin{aligned} y-k\in (f+i_{A})^{*}(L)=\text{ WSup }\{L(x)-(f+i_{A})(x):\ x\in X\}. \end{aligned}$$

By the definition of $\text{ WSup }$, one has

$$\begin{aligned} y-k-(L(x)-(f+i_{A})(x))\notin -{\text{ int }K},\ \forall x\in X. \end{aligned}$$

It follows from this and (8) that

$$\begin{aligned} y+(f+i_{A})(x)-L(x)\notin -{\text{ int }K},\ \forall x\in X, \end{aligned}$$

which is equivalent to

$$\begin{aligned} g(x)\in -S,\ x\in C\Longrightarrow y+f(x)-L(x)\notin -{\text{ int }K}. \end{aligned}$$

The proof is complete. $\square$

Theorem 3.2

(Reverse Farkas Lemma II) Let ${\bar{x}}\in A \cap \text{ dom }\,f.$ The following statements are equivalent:

${\mathbf {(c_{1})}}$ :

$g(x)\in -S,\ x\in C$ $\ \Longrightarrow$ $\ f(x)-f({\bar{x}})\notin -{\text{ int } K},$

${\mathbf {(d_{1})}}$ :

$0\mathbf {{_{{\mathcal {L}}}}}\in \partial (f+i_{A})({\bar{x}}),$

${\mathbf {(e_{1})}}$ :

$(0\mathbf {{_{{\mathcal {L}}}}},-f({\bar{x}}))\in \text{ epi }_{K}\,(f+i_{A})^{*}.$

Proof

$[{\mathbf {(c_{1})\ }}\Longleftrightarrow \ \mathrm { \mathbf {(e_{1})}}]$ follows from Theorem 3.1 with $L=0_{{\mathcal {L}} }$ and ${\overline{y}}=-f({\bar{x}}).$

$[{\mathbf {(d_{1})\ }}\Longleftrightarrow \ {\mathbf {(e_{1})}} ]$ follows from Proposition 2.3 applied to $L=0_{\mathcal { L}}$ and the function $f+i_{A}.$ $\square$

In the absence of the vector-valued function g (or, equivalently, when $g\left( x\right) =0_{Z}$ for all $x\in X$), Theorem 3.2 yields the following immediate corollary:

Corollary 3.1

Let ${\bar{x}}\in C\cap \text{ dom }f$. Then the following statements are equivalent:

${\mathbf {(f_{1})}}$ :

$f(x)-f({\bar{x}})\notin -{\text{ int }K}\ \forall x\in C,$

${\mathbf {(g_{1})}}$ :

$0\mathbf {{_{{\mathcal {L}}}}}\in \partial (f+i_{C})({\bar{x}}),$

${\mathbf {(h_{1})}}$ :

$(0_{{\mathcal {L}}},-f({\bar{x}}))\in \text{ epi }_{K}(f+i_{C})^{*}.$

When we apply Theorem 3.2 to the scalar optimization problem (SOP), we obtain the characterization of optimality given in the following corollary, which does not require the classical closedness and convexity assumptions on C,  $f\in {\varGamma } \left( X\right) ,$ and $S-$epi closedness and $S-$convexity of g. It is worth noting that the first statement (i $_1$) in the next corollary means that ${\overline{x}}$ is an optimal solution of (SOP).

Corollary 3.2

Let $\left( f,g,C\right)$ be a given scalar triple and ${\bar{x}}\in A\cap \text{ dom }\,f$. Then the following statements are equivalent:

${\mathbf {(i_{1})}}$ :

$g(x)\in -S,\ x\in C$ $\ \Longrightarrow$ $\ f(x)-f({\bar{x}})\ge 0,$

${\mathbf {(j_{1})}}$ :

$0_{X^{*}}\in \partial (f+i_{A})({\bar{x}}),$

${\mathbf {(k_{1})}}$ :

$(0_{X^{*}},-f({\bar{x}}))\in \text{ epi } (f+i_{A})^{*}.$

In the rest of this section, we consider some special cases where the results above collapse to several well-known asymptotic Farkas-type results in the literature ([14, 15]). These results have been used to get optimality conditions, duality theorems, and set containment characterizations for (SOP). In particular, Corollary 3.2 leads us back to the following asymptotic Farkas lemma in [16] (see also [8]).

Corollary 3.3

(Asymptotic linear Farkas Lemma) Let $g\in {\mathcal {L}}(X,Z),$ with adjoint operator denoted by $g^{\sharp },$ and assume that the cone S is closed. Given $x^{*}\in X^{*}$, the following statements are equivalent:

${\mathbf {(l_{1})}}$ :

$g(x)\in -S \ \Longrightarrow \ \langle x^{*},x\rangle \ge 0,$

${\mathbf {(m_{1})}}$ :

$-x^{*}\in \text{ cl }(g^{\sharp }(S^{+}))$.

Proof

The conclusion follows from Corollary 3.2. Indeed, let us take $f(\cdot ):=\langle x^{*},\cdot \rangle$, and ${\bar{x}}=0_{X}\in g^{-1}(-S)$. Then $f({\bar{x}})=0$, and it follows from Corollary 3.2 that

$$\begin{aligned} {\mathbf {(l_{1})}}\ \Longleftrightarrow \ (0_{X^{*}},0)\in \text{ epi }(f+i_{A})^{*}, \end{aligned}$$

(27)

where $A=g^{-1}(-S)$. It is a standard fact that $i_{A}=\sup _{z^{*}\in S^{+}}(z^{*}\circ g)$, and hence, by (4), one obtains

$$\begin{aligned} \text{ epi } i_{A}^{*}=\text{ cl }\,\text{ conv }\left( \bigcup _{z^{*}\in S^{+}}{\text{ epi }({z^{*}\circ g})^{*}}\right) . \end{aligned}$$

We now have, by the last equality and the convexity of $S^{+}$:

$$\begin{aligned} \text{ epi }(f+i_{A})^{*}= & {} \text{ epi }f^{*}+\text{ epi } i_{A}^{*}\ \ \ \ \ \ \ \ (\text {by }(3)) \\= & {} \{x^{*}\}\times {\mathbb {R}}_{+}+\text{ cl }\,\text{ conv }\left( \bigcup _{z^{*}\in S^{+}}{\text{ epi }({z^{*}\circ g})^{*}} \right) \ \\= & {} \{x^{*}\}\times {\mathbb {R}}_{+}+\text{ cl }\,\text{ conv }\left( \bigcup _{z^{*}\in S^{+}}\{{z^{*}\circ g}\}\times {\mathbb {R}} _{+}\right) \\= & {} \{x^{*}\}\times {\mathbb {R}}_{+}+\text{ cl }\left( \bigcup _{z^{*}\in S^{+}}\{{z^{*}\circ g}\}\times {\mathbb {R}}_{+}\right) \\= & {} \{x^{*}\}\times {\mathbb {R}}_{+}+\text{ cl }(g^{\sharp }(S^{+}))\times {\mathbb {R}}_{+}. \end{aligned}$$

Therefore,

$$\begin{aligned} (0_{X^{*}},0)\in \text{ epi }(f+i_{A})^{*}\Longleftrightarrow -x^{*}\in \text{ cl }(g^{\sharp }(S^{+})). \end{aligned}$$

The conclusion follows from the last equivalence and (27). $\square$

Next we are approaching scalar asymptotic Farkas-type results for convex systems. Now, $Y={\mathbb {R}},$ $K={\mathbb {R}}_{+},$ $f\in {\varGamma } (X),$ and C is a non-empty, closed, convex set in X. Additionally, we assume that g is $S-$epi closed and $S-$convex. Note that, under these assumptions, $g^{-1}(-S)$ is a closed, convex set and $i_{C}\in {\varGamma } (X).$

As a consequence of Theorem 3.1, we now can provide an asymptotic Farkas lemma for convex systems with linear perturbations which extends some results in the literature ([15, 17]).

Corollary 3.4

(Asymptotic convex Farkas Lemma for linear perturbations) Let $\left( f,g,C\right)$ be a scalar triple such that $f\in {\varGamma } (X)$, C is a closed, convex set, and g is S-convex and S-$\text{ epi }$ closed. Then, for any pair $x^{*}\in X^{*}$ and $\alpha \in {\mathbb {R}}$, the following statements are equivalent:

${\mathbf {(n_{1})}}$ :

$g(x)\in -S,~x\in C$ $\ \Longrightarrow$ $\ f(x)-\langle x^{*},x\rangle +\alpha \ge 0,$

${\mathbf {(o_{1})}}$ :

$(x^{*},\alpha )\in \text{ cl }\left( \bigcup \limits _{\begin{array}{c} z^{*}\in S^{+} \end{array}}\text{ epi }(f+i_{C}+z^{*}\circ g)^{*}\right) ,$

${\mathbf {(p_{1})}}$ :

there exists a net $(z_{i}^{*})_{i\in I}\subset S^{+}$ such that

$$\begin{aligned} f(x)+\liminf \nolimits _{i}(z_{i}^{*}\circ g)(x)-\langle x^{*},x\rangle +\alpha \ge 0,\ \forall x\in C. \end{aligned}$$

Proof

We apply Theorem 3.1 with $Y={\mathbb {R}},$ $K= {\mathbb {R}}_{+},$ $L=x^{*}$ and $y=\alpha .$ Then, ${\mathbf { (n_{1})}}$ is equivalent to $(x^{*},\alpha )\in \text{ epi } \,(f+i_{A})^{*}.$ The equivalence of ${\mathbf {(n_{1})}}$ and ${\mathbf {(o_{1})}}$ follows from the following formula (28) in [18, Theorem 8.2]:

$$\begin{aligned} \text{ epi }(f+i_{A})^{*}=\text{ cl }\left( \bigcup \limits _{\begin{array}{c} z^{*}\in S^{+} \end{array}}\text{ epi }(f+i_{C}+z^{*}\circ g)^{*}\right) . \end{aligned}$$

(28)

[${\mathbf {(o_{1})\ }}$ $\Longrightarrow \$ $\mathrm { \mathbf {(p_{1})}}$] Assume that ${\mathbf {(o_{1})}}$ holds. Then, there exist nets $(z_{i}^{*})_{i\in I}\subset S^{+},$ $(x_{i}^{*},r_{i})_{i\in I}\subset X^{*}\times {\mathbb {R}}$ such that $x_{i}^{*}\rightarrow {x^{*}}$ and $r_{i}\rightarrow \alpha$ and that

$$\begin{aligned} (f+i_{C}+z_{i}^{*}\circ g)^{*}(x_{i}^{*})\le r_{i},\ \forall i\in I, \end{aligned}$$

which leads to

$$\begin{aligned} f(x)+(z_{i}^{*}\circ g)(x)-\langle x_{i}^{*},x\rangle +r_{i}\ge 0,\forall x\in C\text { and }\forall i\in I. \end{aligned}$$

Since $x_{i}^{*}\rightarrow {x^{*}}$ and $r_{i}\rightarrow \alpha$, ${\mathbf {(p_{1})}}$ follows from the last inequality.

[${\mathbf {(p_{1})\ }}$ $\Longrightarrow$ $\ \mathrm { \mathbf {(n_{1})}}$] For any $x\in C$ such that $g(x)\in -S$ one has $(z^{*}\circ g)(x)\le 0$ for all $z^{*}\in S^{+}$. Hence, if ${\mathbf {(p_{1})}}$ holds, one has for such x, $f(x)-\langle x^{*},x\rangle +\alpha \ge 0$ which means that ${\mathbf {(n_{1})} }$ holds. The proof is complete. $\square$

Remark 3.1

Since we also have [19, p. 328]

$$\begin{aligned} \text{ epi }(f+i_{A})^{*}=\text{ cl }\left( \text{ epi }f^{*}+ \text{ epi } i_{C}^{*}+\bigcup \limits _{\begin{array}{c} z^{*}\in S^{+} \end{array}} \text{ epi }\,(z^{*}\circ g)^{*}\right) , \end{aligned}$$

(29)

it follows that ${\mathbf {(n_{1})}}$ is also equivalent to

$$\begin{aligned} (x^{*},\alpha )\in \text{ cl }\left( \text{ epi }f^{*}+\text{ epi } i_{C}^{*}+\bigcup \limits _{\begin{array}{c} z^{*}\in S^{+} \end{array}}\text{ epi } (z^{*}\circ g)^{*}\right) . \end{aligned}$$

The Farkas lemma for linearly perturbed convex systems in Corollary 3.4 extends the sequential Farkas lemma for convex systems given in [17, Proposition 4] and in [15, Theorem 2.1], where $(x^{*},\alpha )=(0_{X^{*}},0)$ (in [15], also $C=X$). When the set in the right-hand side of ${\mathbf {(o_{1})}}$ is closed, Corollary 3.4 leads to the stable Farkas lemma for convex systems ([14, Theorem 3.1], [20, Corollary 4]). Extensions of this result to non-convex systems will be established in the next section. It is worth observing that conditions (28) and (29) have been used in the framework of duality theory (see, e.g., [18, 19]) while some of their generalizations have been used for extensions of Farkas-type results (see, [20, 21]). Moreover, when taking $x^{*}=0_{X^*}$ in Corollary 3.4, the result collapses to an asymptotic Farkas lemma in the next corollary that extends the sequential Farkas lemma established in [15, Theorem 2.1], where $C=X$ and the map g was assumed to be continuous (assumption which is much stronger than the S-epi closedness required below).

Corollary 3.5

(Asymptotic convex Farkas Lemma) Let $\left( f,g,C\right)$ be a scalar triple and $\alpha \in {\mathbb {R}}.$ Assume that $f\in {\varGamma } (X),$ the convex set C is closed and g is S-convex and S-epi closed. Then the following statements are equivalent:

${\mathbf {(q_{1})}}$ :

$g(x)\in -S,\ x\in C\,\ \Longrightarrow \ \ f(x)+\alpha \ge 0,$

${\mathbf {(r_{1})}}$ :

$(0_{X^{*}},\alpha )\in \text{ cl } \left( \bigcup \limits _{\begin{array}{c} z^{*}\in S^{+} \end{array}}\text{ epi } \,(f+i_{C}+z^{*}\circ g)^{*}\right) ,$

${\mathbf {(s_{1})}}$ :

there exists a net $(z_{i}^{*})_{i\in I}\subset S^{+}$ such that

$$\begin{aligned} f(x)+\liminf \nolimits _{i}\ (z_{i}^{*}\circ g)(x)+\alpha \ge 0,\ \forall x\in C. \end{aligned}$$

The next stable Farkas lemma for convex systems under linear perturbations [14] is a direct consequence of the previous results.

Corollary 3.6

(Stable convex Farkas Lemma) [14] Let $\left( f,g,C\right)$ be a scalar triple such that $f\in {\varGamma } (X)$, the convex cone S is closed, and g is S-convex and S-epi closed. Then, the following statements are equivalent:

${\mathbf {(t_{1})}}$ :

The set $\bigcup \limits _{z^{*}\in S^{+}} \text{ epi }\,(f+i_{C}+z^{*}\circ g)^{*}$ is weak$^{*}$-closed,

${\mathbf {(v_{1})}}$ :

For any pair $(x^{*},\alpha )\in X^{*}\times {\mathbb {R}}$, it holds

$$\begin{aligned} \begin{array}{c} \left\{ g(x)\in -S,~x\in C\Longrightarrow f(x)-\langle x^{*},x\rangle +\alpha \ge 0\right\} \\ \Updownarrow \\ \left\{ \exists z^{*}\in S^{+},\forall x\in C:\ f(x)+(z^{*}\circ g)(x)-\langle x^{*},x\rangle +\alpha \ge 0\right\} . \end{array} \end{aligned}$$

Proof

The result is a direct consequence of the equivalences in Corollary 3.4. $\square$

4 Farkas-Type Results for Vector-Valued Functions

In this section, we consider the triple (f, g, C) corresponding to problem (VOP) in (22), with $A=C\cap g^{-1}(-S)$ such that $A\cap \text{ dom }f\not =\emptyset ,$ and we establish a version of Farkas lemma for vector-valued functions corresponding to the mentioned problem (VOP). We firstly give some preliminary lemmas.

Lemma 4.1

It holds

$$\begin{aligned} \bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*}\subset \text{ epi }_{K}(f+i_{A})^{*}. \end{aligned}$$

(30)

Proof

Take arbitrarily $(L,y)\in \bigcup \limits _{T\in {\mathcal {L}} _{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*}$. Then there exists $T_{0}\in {\mathcal {L}}_{+}(S,K)$ such that $y\in (f+i_{C}+T_{0}\circ g)^{*}(L)+K$. Hence, there is $k_{0}\in K$ such that

$$\begin{aligned} y-k_{0}\in (f+i_{C}+T_{0}\circ g)^{*}(L)=\text{ WSup }\left\{ L(x)-f(x)-(T_{0}\circ g)(x):x\in C\right\} . \end{aligned}$$

By the definition of $\text{ WSup }$, one has

$$\begin{aligned} L(x)-f(x)-(T_{0}\circ g)(x)-y+k_{0}\notin \text{ int }K,\ \forall x\in C. \end{aligned}$$

(31)

Observe that if $x\in A$, then $-(T_{0}\circ g)(x)\in K$ (as $T_{0}\in {\mathcal {L}}_{+}(S,K)$). From this, (31) and (8), we get

$$\begin{aligned} L(x)-f(x)-y\notin \text{ int }K,\ \forall x\in A, \end{aligned}$$

or equivalently,

$$\begin{aligned} y+(f+i_{A})(x)-L(x)\notin -\text{ int }K,\ \forall x\in X. \end{aligned}$$

According to Proposition 2.2, we conclude

$$\begin{aligned} (L,y)\in \text{ epi }_{K}(f+i_{A})^{*}, \end{aligned}$$

and so the inclusion (30) has been proved. $\square$

The next example shows that the inclusion (30) can be strict.

Example 4.1

Let X, Y, Z, K, S, C, f, and g,  be as in Example 3.1. Now we shall prove that

$$\begin{aligned} \left( {\overline{L}},(-1,-2)\right) \in \text{ epi }_{K}(f+i_{A})^{ *}\diagdown \bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*}, \end{aligned}$$

for ${\overline{L}}=\left( 0,-1\right) ,$ by showing that

$$\begin{aligned} (-1,-2)\in \left[ (f+i_{A})^{*}({\overline{L}})+{\mathbb {R}}_{+}^{2}\right] \diagdown \bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\left[ (f+i_{C}+T\circ g)^{*}\left( {\overline{L}}\right) +{\mathbb {R}}_{+}^{2}\right] . \end{aligned}$$

On the one hand, since $A=C\cap g^{-1}(-S)=]0,+\infty [,$ we have

$$\begin{aligned} (f+i_{A})^{*}({\overline{L}})= & {} \text{ WSup }\left\{ {\overline{L}} (x)-f(x):\ x\in A\right\} \\= & {} \text{ WSup }\left\{ (0,-x)-\left( 0,\frac{1}{x} \right) :x>0\right\} \\= & {} \text{ WSup }\left\{ \left( 0,-x-\frac{1}{x}\right) :x>0\right\} \\= & {} \left( {\mathbb {R}}_{-}\times \{-2\}\right) \cup \left( \{0\}\times ]-\infty ,-2]\right) , \end{aligned}$$

so that

$$\begin{aligned} (-1,-2)\in (f+i_{A})^{*}({\overline{L}})+{\mathbb {R}}_{+}^{2}=\left( {\mathbb {R}}_{-}\times [ -2,+\infty [ \right) \cup \left( {\mathbb {R}}_{+}\times {\mathbb {R}}\right) . \end{aligned}$$

On the other hand, recalling that $(T\circ g)(0)=T\left( +\infty \right) =+\infty _{{\mathbb {R}}^{2}}$, we can write, for any $T=\left( a,b\right) \in {\mathbb {R}}_{+}^{2},$

$$\begin{aligned}&(f+i_{C}+T\circ g)^{*}({\overline{L}}) =\text{ WSup }\left\{ \overline{L }(x)-f(x)-(T\circ g)(x):\ x\in C\right\} \\&\quad =\text{ WSup }\left\{ (0,-x)-\left( 0,\frac{1}{x}\right) +\left( \frac{ a|x+1|}{x},\frac{b|x+1|}{x}\right) :x\in C\diagdown \{0\}\right\} \\&\quad =\text{ WSup }\left\{ \left( a\left( \frac{x+1}{x}\right) ,-x-\frac{1}{x} +b\left( \frac{x+1}{x}\right) \right) :x\in ]-1,+\infty [\diagdown \{0\}\right\} . \end{aligned}$$

Table 1 describes $\bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\left[ (f+i_{C}+T\circ g)^{*}\left( {\overline{L}}\right) +{\mathbb {R}}_{+}^{2} \right]$ as a union of sets of the form $(f+i_{C}+\left( a,b\right) \circ g)^{*}\left( {\overline{L}}\right) +{\mathbb {R}}_{+}^{2}$ for $\left( a,b\right) \in {\mathcal {L}}_{i},$ where $\left\{ {\mathcal {L}}_{1},...,\mathcal { L}_{8}\right\}$ is the partition of ${\mathbb {R}}_{+}^{2}$ in the second column of Table 1. Observe that (25) allows to express $(f+i_{C}+\left( a,b\right) \circ g)^{*}\left( {\overline{L}}\right) + {\mathbb {R}}_{+}^{2}$ as it appears in row 6, column 3 of Table 1, corresponding to the harder case that $\left( a,b\right) \in {\mathcal {L}} _{6}.$ Similar calculations provide $(f+i_{C}+\left( a,b\right) \circ g)^{*}\left( {\overline{L}}\right) +{\mathbb {R}}_{+}^{2}$ for $i=1,...,8,$ $i\ne 6.$

Table 1 Description of $(f+i_{C}+\left( a,b\right) \circ g)^{*}\left( {\overline{L}}\right) +{\mathbb {R}}_{+}^{2}$

The conclusion follows from the fact that no set in column 3 of Table 1 contains $(-1,-2).$

We shall need the following technical lemmas:

Lemma 4.2

Let $(L,y)\in {\mathcal {L}}(X,Y)\times Y$ and $T\in {\mathcal {L}}(Z,Y)$. The following implication holds:

$$\begin{aligned} y+(f+i_{C}+T\circ g)(x)\nless _{K}L(x)\,\forall x\in X\,\Longrightarrow \,(L,y)\in \text{ epi }_{K}(f+i_{C}+T\circ g)^{*}, \end{aligned}$$

or equivalently,

$$\begin{aligned}&y+(f+i_{C}+T\circ g)(x)-L(x)\notin -{\text{ int }K}\,\forall x\in X\ \\&\quad \Longrightarrow \,y\in (f+i_{C}+T\circ g)^{*}(L)+K, \end{aligned}$$

Proof

It comes from Proposition 2.2 by taking $h:=f+i_{C}+T\circ g$ and observing that $\text{ dom }(T\circ g)=g^{-1}(Z),$ so that

$$\begin{aligned} \text{ dom }(f+i_{C}+T\circ g)=(\text{ dom }f)\cap C\cap g^{-1}(Z)\supset ( \text{ dom }f)\cap A\ne \emptyset . \end{aligned}$$

$\square$

Lemma 4.3

Let $(L,y)\in {\mathcal {L}}(X,Y)\times Y$, and consider the following statements:

${\mathbf {(a_{1})}}$ :

$g(x)\in -S,x\in C\Longrightarrow f(x)-L(x)+y\notin -{\text{ int }K}$,

${\mathbf {(a_{2})}}$ :

$\exists \ T\in {\mathcal {L}}_{+}(S,K)$ such that

$$\begin{aligned} (L,y)\in \text{ epi }_{K}(f+i_{C}+T\circ g)^{*}. \end{aligned}$$

${\mathbf {(b_{2})}}$ :

$\exists \ T\in {\mathcal {L}}_{+}(S,K)\$such that

$$\begin{aligned} \begin{array}{c} f(x)+(T\circ g)(x)-L(x)+y\notin -{\text{ int }K},\ \forall x\in C. \end{array} \end{aligned}$$

We have the following relationships among them:

$$\begin{aligned} {\mathbf {(a_{1})\ \Longleftarrow \ (a_{2})\ \Longleftrightarrow \ (b_{2}).}} \end{aligned}$$

Proof

$[{\mathbf {(a_{1})\ }}$ $\Longleftarrow$ ${\mathbf {\ (a_{2})}}]$ It follows from Lemma 4.1 and Theorem 3.1

(32)

$[{\mathbf {(a_{2})\ }}\Longrightarrow \ {\mathbf {(b_{2})}}]$ Assume that ${\mathbf {(a_{2})}}$ holds; in other words, there exist $T\in {\mathcal {L}}_{+}(S,K)$ and $k\in K$ such that

$$\begin{aligned} y-k\in (f+i_{C}+T\circ g)^{*}(L). \end{aligned}$$

Therefore,

$$\begin{aligned} y-k-L(x)+f(x)+i_{C}(x)+(T\circ g)(x)\ \not \in -\text{ int }{K},\ \forall x\in X. \end{aligned}$$

Now, again by (8), we get

$$\begin{aligned} y-L(x)+f(x)+i_{C}(x)+(T\circ g)(x)\ \not \in -\text{ int }{K},\ \forall x\in X, \end{aligned}$$

(33)

which is nothing else but ${\mathbf {(b_{2})}}$.

$[{\mathbf {(b_{2})\ }}$ $\Longrightarrow$ $\mathrm { \mathbf {\ (a_{2})}}]$ This implication follows from Lemma 4.2. $\square$

Next we present the main result in this section.

Theorem 4.1

(Stable reverse Farkas Lemma)

$$\begin{aligned} \begin{array}{c} \left\{ \text{ epi }_{K}(f+i_{A})^{*}=\bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*}\right\} \\ \Updownarrow \\ \left\{ \forall (L,y)\in {\mathcal {L}}(X,Y)\times Y,\ \ \ {\mathbf { (a_{1})}}\Longleftrightarrow {\mathbf {(a_{2})}}\Longleftrightarrow {\mathbf {(b_{2})}}\right\} . \end{array} \end{aligned}$$

Proof

$\left( \Downarrow \right)$ Now the implication in (32) is an equivalence.

$\left( \Uparrow \right)$ The implication ${\mathbf {(a_{1})}}$ $\Longrightarrow$ ${\mathbf {(a_{2})}}$ yields

$$\begin{aligned} \text{ epi }_{K}(f+i_{A})^{*}\subset \bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*} \mathbf {,} \end{aligned}$$

and we finish the proof by applying (30). $\square$

Remark 4.1

The equivalence ${\mathbf {(a_{1})}}\Longleftrightarrow \mathrm { \mathbf {(a_{2})}}$ in Theorem 4.1 is called stable as it holds for all $(L,y)\in {\mathcal {L}}(X,Y)\times Y.$

Remark 4.2

When we are confined to the convex (SOP) (i.e., $f\in {\varGamma } (X),$ C is a closed, convex set, and g is S-convex and S-epi closed), the equality

$$\begin{aligned} \text{ epi }_{K}(f+i_{A})^{*}=\bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*} \end{aligned}$$

(34)

is equivalent to the weak$^{*}$-closedness of $\bigcup \limits _{\begin{array}{c} z^{*}\in S^{+} \end{array}}\text{ epi }(f+i_{C}+z^{*}\circ g)^{*}$. This condition is necessary and sufficient for the stable Farkas lemma and stable Lagrange duality for (SOP) in [14] (see also [20]). The following example illustrates the fulfillment of (34).

Example 4.2

Let $X={\mathbb {R}},$ $Y={\mathbb {R}}^{2},$ $Z={\mathbb {R}},$ $K={\mathbb {R}} _{+}^{2},$ $S={\mathbb {R}}_{+},$ $C =\, ]0,1[$, $f(x)=(x,x)$, and $g(x)=-x$. We add to $Y={\mathbb {R}}^{2}$ a greatest and smallest elements with respect to the ordering defined by $K={\mathbb {R}}_{+}^{2}$, denoted by $-\infty _{ {\mathbb {R}}^{2}}$ and $+\infty _{{\mathbb {R}}^{2}}$, i.e., $Y^{\bullet }= {\mathbb {R}}^{2}\cup \{-\infty _{{\mathbb {R}}^{2}}\}\cup \{+\infty _{{\mathbb {R}} ^{2}}\}$. Observe first that $A=C\cap g^{-1}(-S) =\, ]0,1[.$ Let $L\in \mathcal {L }(X,Y)={\mathcal {L}}({\mathbb {R}},{\mathbb {R}}^{2})$ be defined by $L(x)=(\alpha x,\beta x)$ for all $x\in X={\mathbb {R}}$ ($\alpha ,\beta \in {\mathbb {R}}$). Then one has

$$\begin{aligned} \begin{array}{ll} (f+i_{A})^{*}(L)&=\text{ WSup }\left\{ ((\alpha -1)x,(\beta -1)x)\in {\mathbb {R}}^{2}:\ x\in A =\, ]0,1[\right\} . \end{array} \end{aligned}$$

On the other hand, for any $T\in {\mathcal {L}}_{+}(S,K)={\mathcal {L}}_{+}( {\mathbb {R}}_{+},{\mathbb {R}}_{+}^{2})$ (it is easy to see that $T(z)=(az,bz)$ for all $z\in Z={\mathbb {R}}$ with $a\ge 0$ and $b\ge 0$), one has

$$\begin{aligned} (f+i_{C}+T\circ g)^{*}(L)=\text{ WSup }\left\{ \left( (\alpha +a-1)x,(\beta +b-1)x\right) :x\in ]0,1[\right\} . \end{aligned}$$

Routine calculations show that condition (34) holds.

Theorem 4.2

(Partially stable reverse Farkas Lemma) The following statements are equivalent:

${\mathbf {(c_{2})}}$ :

$\text{ epi }_{K}(f+i_{A})^{*}\cap (\{0\mathbf {{_{{\mathcal {L}}}}}\}\times Y)=\left( \bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*}\right) \cap (\{0\mathbf {{_{{\mathcal {L}}}}}\}\times Y)$.

${\mathbf {(d_{2})}}$ :

For any $y\in Y,$

$$\begin{aligned} \begin{array}{c} \left\{ g(x)\in -S,x\in C\ \Longrightarrow \ f(x)+y\notin -{\text{ int }K} \right\} \\ \Updownarrow \\ \left\{ \exists \ T\in {\mathcal {L}}_{+}(S,K)\ \text {such that }y+f(x)+(T\circ g)(x)\notin -{\text{ int }K}\ \forall x\in C\right\} . \end{array} \end{aligned}$$

Proof

It is similar to the proofs of Lemma 4.3 and Theorem 4.1, but taking $L=0\mathbf {{_{{\mathcal {L}}}}}.$ $\square$

Remark 4.3

Again for the convex (SOP) (i.e., $f\in {\varGamma } (X),$ C is a closed, convex set, and g is S-convex and S-epi closed), condition ${\mathbf {(c_{2})}}$ accounts for the closedness of $\bigcup \limits _{z^{*}\in S^{+}}\text{ epi }(f+i_{C}+z^{*}\circ g)^{*}$ regarding the set $\{0_{X^{*}}\}\times {\mathbb {R}}$ (recall that a set A is said to be closed regarding to the set B if $B\cap \text{ cl }A=B\cap A,$ see, e.g., [18, p. 56]), and this condition is sufficient for generalized Farkas lemma for systems involving extended real-valued functions (see, e.g., [14, 20, 21]).

The following example illustrates the fulfillment of ${\mathbf {(c_{2})} }$.

Example 4.3

Let $X={\mathbb {R}},$ $Y={\mathbb {R}}^{2},$ $Z={\mathbb {R}},$ $K={\mathbb {R}} _{+}^{2},$ $S={\mathbb {R}}_{+},$ $C =\, ]-1,1[$, $f(x)=(x,x^{2})$, and $g(x)=-x$. We add to $Y={\mathbb {R}}^{2}$ a greatest and smallest elements with respect to the ordering defined by $K={\mathbb {R}}_{+}^{2}$, denoted by $-\infty _{ {\mathbb {R}}^{2}}$ and $+\infty _{{\mathbb {R}}^{2}}$, i.e., $Y^{\bullet }= {\mathbb {R}}^{2}\cup \{-\infty _{{\mathbb {R}}^{2}}\}\cup \{+\infty _{{\mathbb {R}} ^{2}}\}$. Observe firstly that $A=C\cap g^{-1}(-S)=[0,1[$ and

$$\begin{aligned} \begin{array}{ll} (f+i_{A})^{*}(0\mathbf {{_{{\mathcal {L}}}}}) &{} =\text{ WSup }\left\{ (-x,-x^{2}):\ x\in A=[0,1[\right\} \\ &{} =\left( ] -\infty ,0] \times \left\{ 0\right\} \right) \cup \left( \left\{ 0\right\} \times ] -\infty ,0] \right) . \end{array} \end{aligned}$$

Therefore,

$$\begin{aligned} (f+i_{A})^{*}(0\mathbf {{_{{\mathcal {L}}}}})+{\mathbb {R}}_{+}^{2}={\mathbb {R}} ^{2}\diagdown (-{\mathbb {R}}_{++}^{2}). \end{aligned}$$

So,

$$\begin{aligned} \text{ epi }_{K}(f+i_{A})^{*}\cap (\{0\mathbf {{_{{\mathcal {L}}}}} \}\times Y)=\{0\mathbf {{_{{\mathcal {L}}}}}\}\times \left( {\mathbb {R}} ^{2}\diagdown (-{\mathbb {R}}_{++}^{2})\right) . \end{aligned}$$

(35)

On the other hand, given $T=\left( a,b\right) \in {\mathcal {L}}_{+}({\mathbb {R}} _{+},{\mathbb {R}}_{+}^{2})={\mathbb {R}}_{+}^{2},$ one has

$$\begin{aligned} (f+i_{C}+T\circ g)^{*}(0\mathbf {{_{{\mathcal {L}}}}})=\text{ WSup }\left\{ \left( (a-1)x,bx-x^{2}\right) :x\in ]-1,1[\right\} . \end{aligned}$$

New routine calculations, together with (35), show that $\mathrm { \mathbf {(c_{2})}}$ holds.

For problem (SOP), Theorems 4.1 and 4.2 yield, respectively, the following versions of well-known Farkas-type results where we succeeded to eliminate superfluous convexity and lower semicontinuity assumptions. In particular, in [22] the authors require convexity of the involved sets and functions but, in page 1313, they claim that “most results remain valid even if one drops the convexity assumptions.” Of course, for problem (SOP) in (23), we also assume that $A\cap \text{ dom }f\not =\emptyset$.

Corollary 4.1

[22, Theorem 6.7] For problem (SOP) in (23), the following statements are equivalent:

${\mathbf {(e_{2})}}$ :

$\text{ epi }(f+i_{A})^{*}=\bigcup \limits _{z^{*}\in S^{+}}\text{ epi }(f+i_{C}+z^{*}\circ g)^{*}.$

${\mathbf {(f_{2})}}$ :

For any $x^{*}\in X^{*}$ and any $\alpha \in {\mathbb {R}},$

$$\begin{aligned} \begin{array}{c} \left\{ g(x)\in -S,x\in C\ \Longrightarrow \ f(x)-\langle x^{*},x\rangle +\alpha \ge 0\right\} \\ \Updownarrow \\ \left\{ \exists \ z^{*}\in S^{+}\ \text {such that}\ \ f(x)+(z^{*}\circ g)(x)-\langle x^{*},x\rangle +\alpha \ge 0,\ \forall x\in C\right\} . \end{array} \end{aligned}$$

Corollary 4.2

[22, Theorem 6.6] For problem (SOP) in (23), the following statements are equivalent:

${\mathbf {(g_{2})}}$ :

$\text{ epi }(f+i_{A})^{*}\cap \left( \{0_{X^{*}}\}\times {\mathbb {R}}\right) =\left( \bigcup \limits _{z^{*}\in S^{+}}\text{ epi }(f+i_{C}+z^{*}\circ g)^{*}\right) \cap \left( \{0_{X^{*}}\}\times {\mathbb {R}}\right) .$

${\mathbf {(h_{2})}}$ :

For any $\alpha \in {\mathbb {R}},$

$$\begin{aligned} \begin{array}{c} \left\{ g(x)\in -S,x\in C\ \Longrightarrow \ f(x)+\alpha \ge 0\right\} \\ \Updownarrow \\ \left\{ \exists \ z^{*}\in S^{+}\ \text {such that}\ \ f(x)+(z^{*}\circ g)(x)+\alpha \ge 0,\ \forall x\in C\right\} . \end{array} \end{aligned}$$

Condition ${\mathbf {(e_{2})}}$ is called in [22] weak conical epigraph hull property relative to f, whereas $\mathrm { \mathbf {(f_{2})}}$ is called stable Farkas rule with respect to f. The mentioned paper does not assume the lower semicontinuity of the involved functions. In [22], the following condition, similar to $\mathrm { \mathbf {(e_{2})}}$, and called conical epigraph hull property relative to f, is also exploited:

${\mathbf {(e} {\acute{}}\mathbf {_{2})}}$ :

$\text{ epi }(f+i_{A})^{*}=\text{ epi }f^{*}+ \text{ epi } i_{C}^{*}+\bigcup \limits _{z^{*}\in S^{+}}\text{ epi }(z^{*}\circ g)^{*}.$

The conditions in Corollaries 4.1 and 4.2 are the weakest ones (necessary and sufficient conditions) for such Farkas-type results. They are conditions ${\mathbf {(e_{2})}}$ and $\mathrm { \mathbf {(g_{2})}}$, which correspond to the scalar versions of (34) and ${\mathbf {(c_{2})}}$, respectively, but without convexity (see Remark 4.2).

5 Applications to Vector Optimization

This section focuses on the vector optimization problem (VOP) in (22):

assuming once again $A\cap \text{ dom }f\not =\emptyset ,$ where $A=C\cap g^{-1}(-S)$ is the feasible set. Recall that an element ${\bar{x}}\in A$ is said to be a weak solution to (VOP) if

$$\begin{aligned} f({\bar{x}})\in \text{ WMin }f(A). \end{aligned}$$

By Proposition 2.1(ii),

$$\begin{aligned} {\bar{x}}\text { is a weak solution of }\mathrm {(VOP)}\Longleftrightarrow & {} f(x)-f({\bar{x}})\not \in -\text{ int }K,\ \forall x\in A \nonumber \\\Longleftrightarrow & {} \left\{ g(x)\in -S,\ x\in C\Longrightarrow f(x)-f({\bar{x}})\not \in -\text{ int }K\right\} \! .\!\!\nonumber \\ \end{aligned}$$

(36)

The next result is a straightforward consequence of Theorem 3.2.

Proposition 5.1

Let ${\bar{x}}\in A\cap \text{ dom }f.$ The following statements are equivalent:

${\mathbf {(a_{3})}}$ :

${\bar{x}}$ is a weak solution to (VOP),

${\mathbf {(b}}_{\mathrm {3}}{\mathbf {)}}$ :

$0_{{\mathcal {L}}}\in \partial (f+i_{A})({\bar{x}})$,

${\mathbf {(c_{3})}}$ :

$(0_{{\mathcal {L}}},-f({\bar{x}}))\in \text{ epi }_{K}(f+i_{A})^{*}$.

Example 5.1

([23, Example 8.6]) Consider the multiobjective optimization problem $\mathrm {(MOP)}$ in (24), with $C=X=Y={\mathbb {R}} ^{2}$, $Z={\mathbb {R}},$ $K={\mathbb {R}}_{+}^{2},$ $S={\mathbb {R}}_{+},$ $f(x_{1},x_{2})=(x_{1},x_{2}),$ and $g(x_{1},x_{2})=\mathrm {max} \{-x_{1},0\}-x_{2}$. We add to $Y={\mathbb {R}}^{2}$ a greatest and smallest elements with respect to the ordering defined by $K={\mathbb {R}}_{+}^{2}$, denoted by $-\infty _{{\mathbb {R}}^{2}}$ and $+\infty _{{\mathbb {R}}^{2}}$, i.e., $Y^{\bullet }={\mathbb {R}}^{2}\cup \{-\infty _{{\mathbb {R}}^{2}}\}\cup \{+\infty _{{\mathbb {R}}^{2}}\}$. Obviously, the elements of ${\mathcal {L}}(X,Y)$ can be identified with $2\times 2$ matrices and $0_{{\mathcal {L}}}$ with the null matrix. It is clear that $A=\{x\in {\mathbb {R}}^{2}:x_{2}\ge 0,x_{1}+x_{2}\ge 0\},$ and hence

$$\begin{aligned} \begin{array}{ll} (f+i_{A})^{*}(0_{{\mathcal {L}}}) &{} =\text{ WSup }\left\{ -(f+i_{A})(x):x\in {\mathbb {R}}^{2}\right\} =\text{ WSup }\left\{ -A\right\} \\ &{} =\big (] -\infty ,0] \times \{0\}\big )\cup \{x\in {\mathbb {R}} ^{2}:x_{1}\ge 0,x_{1}+x_{2}=0\}. \end{array} \end{aligned}$$

So, given ${\bar{x}}\in A,$ $(0_{{\mathcal {L}}},-f({\bar{x}}))\in \text{ epi }_{K}(f+i_{A})^{*}$ if and only if

$$\begin{aligned} -f({\bar{x}})=-{\bar{x}}\in (f+i_{A})^{*}\left( 0_{{\mathcal {L}}}\right) + {\mathbb {R}}_{+}^{2}=\{x\in {\mathbb {R}}^{2}:x_{2}\ge 0\text { or } x_{1}+x_{2}\ge 0\} \end{aligned}$$

if and only if ${\bar{x}}$ is a boundary point of A. Thus, by Proposition 5.1, we see in this example that the set of weak solutions to (MOP) is nothing else than the boundary of A. Observe that these boundary points satisfy

$$\begin{aligned} 0_{{\mathcal {L}}}({\bar{x}})-f({\bar{x}})=-{\bar{x}}\in \text{ WSup }\left\{ 0_{ {\mathcal {L}}}\left( x\right) -(f+i_{A})(x):x\in {\mathbb {R}}^{2}\right\} , \end{aligned}$$

or equivalently,

$$\begin{aligned} 0_{{\mathcal {L}}}\in \partial (f+i_{A})({\bar{x}}). \end{aligned}$$

Next we establish our main result for $\mathrm {(VOP).}$

Theorem 5.1

(Optimality conditions for (VOP)) Consider the problem $\mathrm {(VOP)}$ in (22), and let ${\bar{x}}\in A\cap \text{ dom }f.$ Then the following statements are equivalent:

${\mathbf {(d_{3})}}$ :

$\text{ epi }_{K}(f+i_{A})^{*}\cap \{(0_{{\mathcal {L}}},-f({\bar{x}}))\}=\left( \bigcup \limits _{T\in \mathcal { L}_{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*}\right) \cap \{(0_{{\mathcal {L}}},-f({\bar{x}}))\}$.

${\mathbf {(e_{3})}}$ :

${\bar{x}}$ is a weak solution of (VOP) if and only if there exists $T\in {\mathcal {L}}_{+}(S,K)$ such that

$$\begin{aligned} -f({\bar{x}})\in (f+i_{C}+T\circ g)^{*}(0\mathbf {{_{{\mathcal {L}}}}})+K. \end{aligned}$$

${\mathbf {(f_{3})}}$ :

${\bar{x}}$ is a weak solution of (VOP) if and only if there exists $T\in {\mathcal {L}}_{+}(S,K)$ such that

$$\begin{aligned} f(x)+(T\circ g)(x)-f({\bar{x}})\notin -{\text{ int }K},\ \forall x\in C. \end{aligned}$$

Moreover, if one of the three statements holds, then the linear operator $T\in {\mathcal {L}}_{+}(S,K)$ whose existence is stated in ${\mathbf { (e_{3})}}$ and ${\mathbf {(f_{3})}}$ can be chosen such that $-(T\circ g)({\bar{x}})\in K{\setminus } \text{ int }K$.

Proof

$[{\mathbf {(d_{3})\ }}\Longleftrightarrow \ \mathrm { \mathbf {(e_{3})}}]$ It follows from Proposition 5.1 that

$$\begin{aligned} {\bar{x}}\text { is a weak solution of (VOP)}\ \Longleftrightarrow \ (0 \mathbf {{_{{\mathcal {L}}}}},-f({\bar{x}}))\in \text{ epi }_{K}(f+i_{A})^{*}. \end{aligned}$$

(37)

On the other hand, it is clear that

$$\begin{aligned} \begin{array}{c} \left( 0\mathbf {{_{{\mathcal {L}}}}},-f({\bar{x}})\right) \in \bigcup \limits _{T\in {\mathcal {L}}_{+}(S,K)}\text{ epi }_{K}(f+i_{C}+T\circ g)^{*} \\ \Updownarrow \\ \exists \ T\in {\mathcal {L}}_{+}(S,K):\ \ -f({\bar{x}})\in (f+i_{C}+T\circ g)^{*}(0\mathbf {{_{{\mathcal {L}}}}})+K, \end{array} \end{aligned}$$

(38)

and hence, the equivalence of ${\mathbf {(d_{3})}}$ and $\mathrm { \mathbf {(e_{3})}}$ follows from (37) and (38).

$[{\mathbf {(e_{3})\ }}\Longrightarrow \ {\mathbf {(f_{3})}}]$ Assume that ${\mathbf {(e_{3})}}$ holds and ${\bar{x}}$ is a weak solution of (VOP). Then there exists $T\in {\mathcal {L}}_{+}(S,K)$ such that $-f({\bar{x}})\in (f+i_{C}+T\circ g)^{*}(0\mathbf {{_{{\mathcal {L}}} }})+K.$ Then, there exists $k\in K$ such that $-f({\bar{x}})-k\in (f+i_{C}+T\circ g)^{*}(0\mathbf {{_{{\mathcal {L}}}}}).$ By the definition of the conjugate function, one has

$$\begin{aligned} (f+i_{C}+T\circ g)(x)-f({\bar{x}})-k\notin -{\text{ int }K},\ \forall x\in X, \end{aligned}$$

so that

$$\begin{aligned} (f+i_{C}+T\circ g)(x)-f({\bar{x}})\notin -{\text{ int }K},\ \forall x\in X, \end{aligned}$$

or equivalently,

$$\begin{aligned} f(x)+(T\circ g)(x)-f({\bar{x}})\notin -{\text{ int }K},\ \forall x\in C. \end{aligned}$$

(39)

Conversely, let us take $T\in {\mathcal {L}}_{+}(S,K)$ such that (39) holds. Now if $x\in C$ and $g(x)\in -S$, then $-(T\circ g)(x)\in K$ (as $T\in {\mathcal {L}}_{+}(S,K)$), and it follows from (8) and (39) that $f(x)-f({\bar{x}})\notin -\text{ int }K$, which shows that ${\bar{x}}$ is a weak solution of (VOP).

$[{\mathbf {(f_{3})\ }}\Longrightarrow \ {\mathbf {(e_{3})}}]$ It follows from Lemma 4.2 with $L=0_{{\mathcal {L}}}$ and $y=-f( {\bar{x}})$.

Lastly, by substituting $x={\bar{x}}$ into (39), we get $-(T\circ g)( {\bar{x}})\not \in {\text{ int }K}$. On the other hand, $g({\bar{x}})\in -S$, $T\in {\mathcal {L}}_{+}(S,K)$ yield $-(T\circ g)({\bar{x}})\in K$, and so, $-(T\circ g)({\bar{x}})\in K{\setminus } \text{ int }K$. The proof is complete. $\square$

Remark 5.1

If we consider the (SOP) problem in (23) with the assumptions that $f\in {\varGamma } (X),$ the convex set C is closed, g is S-convex and S-epi closed, Proposition 5.1 offers an asymptotic optimality condition for (SOP): ${\bar{x}}$ is an optimal solution of (SOP) if and only if

$$\begin{aligned} (0_{X^{*}},-f({\bar{x}}))\in \text{ epi }(f+i_{A})^{*}=\text{ cl } \left( \bigcup \limits _{\begin{array}{c} z^{*}\in S^{+} \end{array}}\text{ epi } (f+i_{C}+z^{*}\circ g)^{*}\right) \end{aligned}$$

(the last equality follows from [18, Theorem 8.2], see also (28)). So in this case, the weak$^{*}$-closedness of the set $\bigcup \nolimits _{\begin{array}{c} z^{*}\in S^{+} \end{array}}\text{ epi } (f+i_{C}+z^{*}\circ g)^{*}$ implies that ${\mathbf {(d_{3})}}$ holds at ${\bar{x}}.$ Moreover, in this specific case, one get a non-asymptotic optimality condition for (SOP): ${\bar{x}}$ is an optimal solution of (SOP) if and only if there is $z^{*}\in S^{+}$ such that $(0_{X^{*}},-f({\bar{x}}))\in \text{ epi } (f+i_{C}+z^{*}\circ g)^{*}$. This simple example illustrates the use and significance of condition ${\mathbf {(d_{3})}}$.

In the case $g\equiv 0_{Z}$ and $C=X$, the problem $\mathrm {(VOP)}$ becomes the unconstrained vector optimization problem

$$\begin{aligned} \begin{array}{rrl} \mathrm {(UVOP)}&\text{ WMin }\,\big \{f(x):x\in X\big \}.&\end{array} \end{aligned}$$

(40)

Corollary 5.1

Let ${\bar{x}}\in \text{ dom }f$. Then ${\bar{x}}$ is a weak solution of the problem $\mathrm {(UVOP)}$, if and only if $0\mathbf {{_{ {\mathcal {L}}}}}\in \partial f({\bar{x}})$.

Proof

The conclusion follows from Proposition 5.1 with $g\equiv 0_{Z}$ and $C=X$. $\square$

If we take $Y={\mathbb {R}}$ and $K={\mathbb {R}}_{+},$ then the problem (UVOP) collapses to the unconstrained scalar optimization problem

Then, according to Corollary 5.1, ${\bar{x}}\in X$ is an optimal solution to $\mathrm {(USOP)}$ if and only if $0_{X^{*}}\in \partial f( {\bar{x}})$.

We now turn back to the (SOP) problem in (23). The optimality conditions above lead us to the corresponding ones for (SOP), which are new and interesting in the sense that they are obtained in the absence of assumptions on convexity, lower semicontinuity of functions/mappings, and closedness of the constraint set.

Corollary 5.2

Let ${\bar{x}}\in A\cap \text{ dom }f.$ The following statements are equivalent:

${\mathbf {(g_{3})}}$ :

$\left( \text{ epi }(f+i_{A})^{*}\right) \cap \{\left( 0_{X^{*}},-f({\bar{x}})\right) \}=\left( \bigcup \limits _{z^{*}\in S^{+}}\text{ epi }\left( f+i_{C}+z^{*}\circ g\right) ^{*}\right) \cap \{\left( 0_{X^{*}},-f({\bar{x}})\right) \}.$

${\mathbf {(h_{3})}}$ :

${\bar{x}}$ is an optimal solution to (SOP) if and only if there exists $z^{*}\in S^{+}$ such that

$$\begin{aligned} 0_{X^{*}}\in \partial (f+i_{C}+z^{*}\circ g)({\bar{x}})\ \text { and }\ (z^{*}\circ g)({\bar{x}})=0. \end{aligned}$$

${\mathbf {(i_{3})}}$ :

${\bar{x}}$ is an optimal solution to (SOP) if and only if there exists $z^{*}\in S^{+}$ such that

$$\begin{aligned} f(x)+(z^{*}\circ g)(x)-f({\bar{x}})\ge 0,\ \forall x\in C. \end{aligned}$$

Proof

The conclusion follows from Theorem 5.1, taking into account the equivalence between ${\mathbf {(h_{3})}}$ and ${\mathbf {(e_{3})}}$ (see, e.g., Proposition 2.4.2(iii) in [11]) since $(z^{*}\circ g)({\bar{x}})=0$ as $K{\setminus } \text{ int }K={\mathbb {R}}_{+}{\setminus } (\text{ int }{\mathbb {R}}_{+})=\{0\}$. $\square$

6 Other Applications

In this last section, we apply the Farkas-type results for vector-valued functions established in Sect. 4 to vector variational inequalities and vector equilibrium problems. We are under the same assumptions of the previous sections, i.e., X, Y are lcHtvs, C is a non-empty subset in X,  and K is a pointed, convex cone in Y such that $\text{ int } K\not =\emptyset .$

6.1 Vector Variational Inequalities

Now we consider the so-called extended vector variational inequality

where $F:X\rightarrow {\mathcal {L}}(X,Y)$ and $H:X\rightarrow Y.$

If $H=0,$ we obtain the vector variational inequality

Remark 6.1

(a) $\mathrm {(EVVI)}$ was introduced in [2, p.356] with the efficient ordering in Y generated by K ($y_{1}\le _{K}y_{2}$ $\Longleftrightarrow$ $y_{2}-y_{1}\in K\diagdown \{0_{Y}\}$) in a more general form (with H being a set-valued mapping).

(b) When $Y={\mathbb {R}}$ and $K={\mathbb {R}}^{+}$, then the problem $\mathrm {(EVVI)}$ becomes the general variational inequality

$$\begin{aligned} \text {Find}\ x\in C\ \text {such that}\ F(x)(z-x)\ge H(x)-H(z)\ \text { for all }z\in C. \end{aligned}$$

Such a model covers the special case when F is a continuous linear operator from X to $X^{*}$, and H is a proper, lsc and convex function considered in [24, 25]. In this case, the problem $\mathrm {(VVI)}$ collapses to the ordinary variational inequality problem

$$\begin{aligned} \text {Find}\ x\in C\ \text {such that }F(x)(z-x)\ge 0\ \ \text {for all}\ z\in C. \end{aligned}$$

For a fixed ${\bar{x}}\in C$, we consider the vector optimization problem

$$\begin{aligned} \begin{array}{rrl} \mathrm {(VOP}(F,H,{\bar{x}})\mathrm {)\ }&\quad \quad \qquad \qquad \qquad \text{ WMin }\left\{ F({\bar{x}})(z-{\bar{x}})+H(z)-H({\bar{x}})\,:\,z\in C\right\} .&\end{array} \end{aligned}$$

It is worth observing that ${\bar{x}}\in C$ is a solution of the problem (EVVI) if only if ${\bar{x}}$ is a weak solution to the vector optimization problem ($\mathrm {VOP}$($F,H,{\bar{x}}$)).

Theorem 6.1

(Characterization of solutions of (EVVI)) Let ${\bar{x}}\in C$. Then the following statements are equivalent:

${\mathbf {(a_{4})}}$ :

${\bar{x}}$ is a solution of $\mathrm {(EVVI)}$,

${\mathbf {(b}}_{\mathrm {4}}{\mathbf {)}}$ :

$-F({\bar{x}})\in \partial (H+i_{C})({\bar{x}})$,

${\mathbf {(c_{4})}}$ :

$-\left( F({\bar{x}}),H({\bar{x}})+F({\bar{x}})(\bar{x })\right) \in \text{ epi }_{K}(H+i_{C})^{*}.$

Proof

Let $f_{{\overline{x}}}:X\rightarrow Y$ be the vector-valued function defined by

$$\begin{aligned} f_{{\overline{x}}}(\cdot ):=F({\bar{x}})(\cdot -{\bar{x}})+H(\cdot )-H({\bar{x}}). \end{aligned}$$

(41)

Obviously,

$$\begin{aligned} {\mathbf {(a_{4})\ \Longleftrightarrow \ }}f_{{\overline{x}}}({\bar{x}})=0_{Y}\in \text{ WMin }f_{{\overline{x}}}(C). \end{aligned}$$

$[{\mathbf {(a_{4})}}$ $\Longleftrightarrow$ $\mathrm { \mathbf {(c_{4})}}]$ In order to apply Proposition 5.1, we need to make some previous calculations. By the definition of conjugate function, we get

$$\begin{aligned} (f_{{\overline{x}}}+i_{C})^{*}(L)= & {} \text{ WSup }\left\{ L(z)-f_{ {\overline{x}}}(z)-i_{C}(z):z\in X\right\} \\= & {} \text{ WSup }\left\{ (L-F({\bar{x}}))(z)-(H+i_{C})(z):z\in X\right\} +H( {\bar{x}})+F({\bar{x}})({\bar{x}}) \\= & {} (H+i_{C})^{*}\left( L-F({\bar{x}})\right) +H({\bar{x}})+F({\bar{x}})({\bar{x}}). \end{aligned}$$

(The second equality above holds by [1, Proposition 3.2(i)]). Hence,

$$\begin{aligned} \text{ epi }_{K}(f_{{\overline{x}}}+i_{C})^{*}=\text{ epi }_{K}(H+i_{C})^{*}+\left( F({\bar{x}}),H({\bar{x}})+F({\bar{x}})(\bar{x })\right) . \end{aligned}$$

(42)

Proposition 5.1 yields the equivalence between ${\mathbf { (a_{4})}}$ and the condition $(0_{{\mathcal {L}}},0_{Y})\in \text{ epi }k(f_{ {\bar{x}}}+i_{C})^{*},$ but from (42)

$$\begin{aligned} (0_{{\mathcal {L}}},0_{Y})\in \text{ epi }k(f_{{\bar{x}}}+i_{C})^{*}\ \Longleftrightarrow \ -\left( F({\bar{x}}),H({\bar{x}})+F({\bar{x}})({\bar{x}})\right) \in \text{ epi }_{K}(H+i_{C})^{*}, \nonumber \\ \end{aligned}$$

(43)

which is ${\mathbf {(c_{4}).}}$

$[{\mathbf {(a_{4})}}$ $\Longleftrightarrow$ $\mathrm { \mathbf {(b_{4})}}]$ It also follows from Proposition 5.1, which establishes

$$\begin{aligned} {\mathbf {(a_{4})\ \Longleftrightarrow \ }}0\mathbf {{_{{\mathcal {L}}}}} \in \partial (f_{{\bar{x}}}+i_{C})({\bar{x}}), \end{aligned}$$

or, equivalently,

$$\begin{aligned} 0_{Y}= & {} 0\mathbf {{_{{\mathcal {L}}}}}({\bar{x}})-(f_{{\bar{x}}}+i_{C})({\bar{x}})\in \left( f_{{\bar{x}}}+i_{C}\right) ^{*}(0\mathbf {{_{{\mathcal {L}}})}} \end{aligned}$$

(44)

$$\begin{aligned}= & {} (H+i_{C})^{*}\left( -F({\bar{x}})\right) +H({\bar{x}})+F({\bar{x}})({\bar{x}}). \end{aligned}$$

(45)

This is also equivalent to

$$\begin{aligned} -F({\bar{x}})({\bar{x}})-H({\bar{x}})-i_{C}({\bar{x}})\in \left( H+i_{C}\right) ^{*}\left( -F({\bar{x}})\right) , \end{aligned}$$

which accounts for (see Proposition 2.3)

$$\begin{aligned} -F({\bar{x}})\in \partial \left( H+i_{C}\right) ({\bar{x}}), \end{aligned}$$

and the equivalence is proved. The proof is complete. $\square$

Example 6.1

Consider the following problem (VVI) with $X=Y={\mathbb {R}}^{2}$, $K= {\mathbb {R}}_{+}^{2}:$

$$\begin{aligned} \text {Find }x\in C\text { such that}\quad \begin{pmatrix} x_{1} &{} x_{1} \\ x_{2} &{} 0 \end{pmatrix} \begin{pmatrix} z_{1}-x_{1} \\ z_{2}-x_{2} \end{pmatrix} \nless _{{\mathbb {R}}_{+}^{2}} \begin{pmatrix} 0 \\ 0 \end{pmatrix} ,\ \ \forall z\in C, \end{aligned}$$

where $C=\{z\in {\mathbb {R}}^{2}:z_{1}+z_{2}\le 2\}$, and again $Y^{\bullet }= {\mathbb {R}}^{2}\cup \{-\infty _{{\mathbb {R}}^{2}}\}\cup \{+\infty _{{\mathbb {R}} ^{2}}\}$. Now we show that ${\bar{x}}=(1,0)$ is a solution of (VVI). Indeed,

$$\begin{aligned} i_{C}^{*}(-F({\bar{x}}))= & {} \text{ WSup }\left\{ -F({\bar{x}} )(z)-i_{C}(z):z\in {\mathbb {R}}^{2}\right\} \\= & {} \text{ WSup }\left\{ - \begin{pmatrix} 1 &{} 1 \\ 0 &{} 0 \end{pmatrix} \begin{pmatrix} z_{1} \\ z_{2} \end{pmatrix} :z_{1}+z_{2}\le 2\right\} \\= & {} \text{ WSup }\left\{ \begin{pmatrix} -z_{1}-z_{2} \\ 0 \end{pmatrix} :z_{1}+z_{2}\le 2\right\} \\= & {} \text{ WSup }\left\{ [-2,+\infty [\times \{0\}\right\} \\= & {} {\mathbb {R}}\times \{0\}. \end{aligned}$$

It is easy to see that $-F({\bar{x}})({\bar{x}})-i_{C}({\bar{x}})=(-1,0)\in i_{C}^{*}(-F({\bar{x}})),$ which is equivalent to $-F({\bar{x}})\in \partial i_{C}({\bar{x}}).$ By Theorem 6.1, ${\bar{x}}=(1,0)$ is a solution of (VVI) (here $H=0$).

6.2 Vector Equilibrium Problem

Let $F:X\times X\rightarrow Y^{\bullet }$ be a bifunction satisfying $F(x,x)=0_{Y}$ for all $x\in C.$ We consider the vector equilibrium problem

Remark 6.2

• (a) $\mathrm {(VEP)}\$ was introduced in [2, p.380] for a set-valued map $F:X\times X\rightrightarrows Y\cup \{+\infty _{Y}\}$.

• (b) When $Y={\mathbb {R}}\$ and $\ K={\mathbb {R}}_{+},$ $\mathrm {(VEP)}$ collapses to the equilibrium problem

  $$\begin{aligned} \text {Find}\ x\in C\ \text {such that}\ F(x,z)\ge 0\ \ \text {for all}\ z\in C. \end{aligned}$$

For a fixed ${\bar{x}}\in C$, we consider the vector optimization problem associated with $\mathrm {(VEP)}$:

Observe that ${\bar{x}}\in C$ is a solution of (VEP) if and only if ${\bar{x}}$ is a weak solution of $\mathrm {(VOEP}(F,{\bar{x}})\mathrm {)}.$ The following result is a straightforward consequence of Proposition 5.1.

Theorem 6.2

(Characterization of solutions of (VEP)) Let ${\bar{x}}\in C$. Then the following statements are equivalent:

${\mathbf {(a_{5})}}$ :

${\bar{x}}$ is a solution of $\mathrm {(VEP)}$,

${\mathbf {(b}}_{\mathrm {5}}{\mathbf {)}}$ :

$0_{{\mathcal {L}}}\in \partial (F({\bar{x}},\cdot )+i_{C})\left( {\bar{x}}\right)$,

${\mathbf {(c_{5})}}$ :

$(0_{{\mathcal {L}}},0_{Y})\in \text{ epi }_{K}(F( {\bar{x}},\cdot )+i_{C})^{*}.$

Example 6.2

Consider the following (VEP) problem, with $X=Y={\mathbb {R}}^{2},$ $K= {\mathbb {R}}_{+}^{2}:$

where $C=\left[ -1,1\right] \times \left[ -1,1\right] .$ Obviously, $F(x,x)= \begin{pmatrix} 0 \\ 0 \end{pmatrix}$ for all $x\in {\mathbb {R}}^{2}.$ We shall show that ${\bar{x}}=(1,0)$ is a solution of (VEP). Indeed, observe that

$$\begin{aligned} \left( F({\bar{x}},\cdot )+i_{C}\right) ^{*}(0\mathbf {{_{{\mathcal {L}}}}})= & {} \text{ WSup }\Big \{-F({\bar{x}},z)-i_{C}(z):z\in {\mathbb {R}}^{2}\Big \} \\= & {} \text{ WSup }\bigg \{ \begin{pmatrix} z_{1}-1 \\ z_{2} \end{pmatrix} :z\in \left[ -1,1\right] \times \left[ -1,1\right] \bigg \} \\= & {} \text{ WSup }\big \{[-2,0]\times [-1,1]\big \} \\= & {} \big (]-\infty ,0]\times \{1\}\big )\cup \big (\{0\}\times ]-\infty ,1]\big ). \end{aligned}$$

It is easy to see that $0\mathbf {{_{{\mathcal {L}}}}}({\bar{x}})-\big (F({\bar{x}}, {\bar{x}})+i_{C}({\bar{x}})\big )=(0,0)\in \big (F({\bar{x}},\cdot )+i_{C}\big ) ^{*}(0\mathbf {{_{{\mathcal {L}}}}}),$ which is equivalent to $0\mathbf {{_{ {\mathcal {L}}}}}\in \partial \big (F({\bar{x}},\cdot )+i_{C}\big )({\bar{x}}).$ It follows from Theorem 6.2 that ${\bar{x}}=(1,0)$ is a solution of the problem $\mathrm {(VEP1)}$.

7 Perspectives

In this paper, we provided Farkas-type results for the vector optimization problem (VOP), which are applied subsequently to derive characterizations of the weak solutions of (VOP) and other specific vector optimization problems.

A key goal was to establish vectorial versions of Farkas Lemma; more precisely, to characterize the implication

$$\begin{aligned} g(x)\in -S,\ x\in C\ \ \Longrightarrow \ \ f(x)-L(x)+y\notin -{\text{ int }K }, \end{aligned}$$

(46)

where $L\in {\mathcal {L}}(X,Y)$ and $y\in Y.$ Let us enunciate three large open problems and guidelines for further research:

• The main applications to (VOP) in this paper, Proposition 5.1 and Theorem 5.3, involve the set $\text{ epi }_{K}(f+i_{A})^{*}$, where $A=\left\{ x\in C:g(x)\in -S\right\}$ denotes the feasible set of (VOP). In the absence of a suitable description of A,  checking the fulfillment of the required properties from $\text{ epi } _{K}(f+i_{A})^{*}$ becomes a hard task. So, it is necessary to get representations of $\text{ epi }_{K}(f+i_{A})^{*}$ which are expressed in terms of the triple data $\left( f,g,C\right)$, leading to verifiable Farkas-type results (i.e., checkable characterizations of (46)) and corresponding optimality conditions. To be more precise, we conjecture that, under suitable assumptions, the inclusion in Lemma 4.1 could become an equation, maybe modifying the left-hand side set by either taking its closure or by eliminating convenient subsets.

• In most real-life applications, the data in (VOP) are uncertain due to estimation errors, prediction errors, or lack of information. When the uncertainty only affects the constraint function g,  the robust approach consists of replacing it with a family of perturbed constraint functions $\left\{ g_{u},u\in {\mathcal {U}}\right\} ,$ where the parameter u (scenario) ranges on some uncertainty set ${\mathcal {U}}.$ Then the robust counterpart is the deterministic problem

  

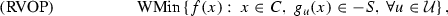
  Getting new robust Farkas-type results for vector-valued functions, and corresponding characterizations of the weak minimum solutions, is a challenging problem.

• For the sake of mathematical simplicity, we have considered up to now exclusively weakly efficient solutions to (VOP) in vector optimization, but most problems considered in this paper (as well as the above open problems) make sense for other types of solutions, some of them (e.g., the Pareto efficient solutions) at least as important in real-life applications as the weakly efficient ones.

8 Conclusions

We resume next the main conclusions that we can extract from the paper:

• Since the Farkas-type results in our setting rely on the set $\text{ epi }_{K}(f+i_{A})^{*},$ the description of this epigraph in terms of the data $\left( f,g,C\right)$ is essential in order to derive results which are crucial in vector optimization.

• In this sense, we exploited this idea and succeeded to derive, from our main Theorem 3.2, optimality conditions for (VOP). In fact, if we take $L=0\mathbf {{_{{\mathcal {L}}}}}$ and $y=-f({\bar{x}})$ where $\bar{ x}\in A\cap \text{ dom }\,f$, the implication (46) is equivalent to the fact ${\bar{x}}$ is a weak solution of $\mathrm {(VOP)}$ (respectively, $\mathrm {(SOP)}$ when $Y={\mathbb {R}}$). If $L\in {\mathcal {L}} (X,Y)$ and $y=-f({\bar{x}})+$ $L({\bar{x}})$ with ${\bar{x}}\in A\cap \text{ dom } \,f$, (46) means that ${\bar{x}}$ is a weak solution of the linearly perturbed $\mathrm {(VOP)}$ with objective function $f-L.$ The fulfillment of (46) for every $(L,y)\in {\mathcal {L}}(X,Y)\times Y$ is a very strong stability property which is characterized in Theorem 4.5 by means of a specific expression of $\text{ epi }_{K}(f+i_{A})^{*}.$

• Most of our results are free of standard assumptions in the literature, as the convexity and closedness of C,  the convexity and lower semicontinuity of f,  and the $S-$convexity and $S-$epi closedness of g.

• A series of important vector optimization problems as the extended vector variational inequality problem (EVVI) and the vector equilibrium problem (VEP) can be reformulated as a (VOP). Hence, the existence of weak solutions for them can be characterized via (46) and its subsequent results in this paper.