New Characterization of Geodesic Convexity on Hadamard Manifolds with Applications

Abstract

In this paper, some new results, concerned with the geodesic convex hull and geodesic convex combination, are given on Hadamard manifolds. An S-KKM theorem on a Hadamard manifold is also given in order to generalize the KKM theorem. As applications, a Fan–Browder-type fixed point theorem and a fixed point theorem for the a new mapping class are proved on Hadamard manifolds.

1 Introduction

In the last few years, several important concepts of nonlinear analysis and optimization problems have been extended from an Euclidean space to a Riemannian manifold setting in order to go further in the study of the convex theory, the fixed point theory, the variational inequality and related topics. In general, a manifold is not a linear space, but the extension of concepts and techniques from linear spaces to Riemannian manifolds is natural by using the geodesic instead of line segment (see [1–3] for more details).

On the other hand, the concept of convexity for sets and functions plays a central role in nonlinear programming with continuous variables and has various applications in the areas of mathematical economics, engineering, operations research, etc. [4]. Therefore, it is important to consider a wider class of generalized convex functions and also to seek practical criteria for convexity or generalized convexity. Udriste [3] and Rapcsák [5] considered a generalization of convexity, called geodesic convexity, and extended many results of convex analysis and optimization theory to Riemannian manifolds. Inspired by the concept of convexity on a linear vector space, the notion of geodesic convexity on some nonlinear metric spaces has become a successful tool on a Riemannian manifold. These ideals have opened a new way to solve other related problems. Actually, in the last decades concepts and techniques, which fit in Euclidean spaces, have extended to the nonlinear framework of Riemannian manifolds. For example, generalized convexity has been introduced and studied by Rapcsák [5], Horvath [6], Mititelu [7], Barani and Pouryayevali [8] and Ferreira [9]. Rapcsák [2] and Ledyaev [10] studied the nonsmooth analysis on manifolds. In 2003, Németh [11] first introduced the variational inequalities on Hadamard manifolds; in 2009, Li et al. [12] generalized it to the Riemannian manifolds. Colao et al. [13], Zhou and Huang [14] researched the equilibrium problems and its applications on the Hadamard manifolds. Moreover, a few researchers have developed several related algorithms on manifolds, see [15–19] and so on.

However, we could not solve some problems such as Knaster, Kuratowski and Mazurkiewicz theorem (in short, KKM theorem) on a manifold, because lack of characterization of a geodesic convex hull. In 2009, Zhou and Huang [20] defined geodesic combination and geodesic convex hull and tried to get a KKM theorem on a Hadamard manifold. Papa Quiroz and Oliver [21] gave a characterization of affinity on a Hadamard manifold in 2009, and this statement is also used in Colao et al [13]. They also gave the analogous to KKM theorem in the setting of a Hadamard manifold (see Lemma 3.1 in [13]). In 2012, Yang and Pu [22] introduced the concept of the geodesic convex hull and claimed that the geodesic convex hull is same as the convex hull. Unfortunately, as pointed out by Kristály et al. [23], there are some conceptual mistakes within the class of Hadamard manifolds, where the authors of these papers used equivalences between convexity notions, which basically reduce the geometric setting to the Euclidean one. Therefore, it is important and interesting to give some new characterization of geodesic convexity with applications on Hadamard manifolds.

Besides, the concept of S-KKM theorem was first introduced by Chang et al. [24–26]. They established an S-KKM theorem whenever S is a single or a set-valued mapping and introduced a new mapping class.

The main purpose of this paper is to give some new results concerned with the geodesic convex hull and geodesic convex combination with applications on Hadamard manifolds. This paper is organized as follows. In Sect. 2, we recall some notations, definitions and basic properties used throughout this paper. In Sect. 3, some new results concerned with the geodesic convex hull and geodesic convex combination on Hadamard manifolds are given. In Sect. 4, we prove an S-KKM theorem on Hadamard manifolds, which can be considered as a generalization and improvement of Theorem 3.2 of [20] and Lemma 3.1 of [13]. Some applications of S-KKM theorem to a Fan–Browder-type fixed point theorem and a fixed point theorem for the mapping class S-KKM(X, Y) on Hadamard manifolds are given in Sect. 5.

2 Preliminaries

In this section, we recall some notations, definitions and basic properties used throughout this paper. It can be found in many introductory books on Riemannian geometry, topology and so on (see, for example, [1–3, 10, 27–29]).

Let M be a simply connected m-dimensional manifold. Given $x \in M$, the tangent space of M at x is denoted by $T_x M$, and the tangent bundle of M by

$$\begin{aligned} \mathrm{TM:}=\bigcup _{x\in M} T_x M, \end{aligned}$$

which is naturally a manifold. A vector field V on M is a mapping of M into TM, which associates to each point $x\in M$ a vector $V(x) \in T_x M$. We always assume that M can be endowed with a Riemannian metric to become a Riemannian manifold. We denote by $\langle \cdot , \cdot \rangle$ the scalar product on $T_x M$ with the associated norm $\Vert \cdot \Vert$, where the subscript x will be omitted. Given a piecewise smooth curve $\gamma : [a, b]\rightarrow M$ joining x to y (i.e. $\gamma (a)=x$ and $\gamma (b)=y$), by using the metric, we can define the length of $\gamma$ as

$$\begin{aligned} L(\gamma ):=\int _a^b \left\| \gamma ^{\prime }(t)\right\| \mathrm{d}t. \end{aligned}$$

Let $\nabla$ be the Levi-Civita connection associated with $(M, \langle \cdot ,\cdot \rangle )$ and $\gamma$ a smooth curve in M. A vector field V is said to be parallel along $\gamma$ iff $\nabla _{\gamma ^{\prime }} V=0$. Iff $\gamma ^{\prime }$ itself is parallel along $\gamma$, we say that $\gamma$ is a geodesic, and in this case $\Vert \gamma ^{\prime }\Vert$ is constant. When $\Vert \gamma ^{\prime }\Vert =1$, $\gamma$ is said to be normalized.

Definition 2.1

([3], p. 22) Let $\varOmega$ be the set of all piecewise $C^\infty$ regular curves joining points x and y in M. The function

$$\begin{aligned} d: M\times M\rightarrow \mathbb {R},\quad d(x,y)=\inf _{\omega \in \varOmega } L(\omega ) \end{aligned}$$

is the distance on M.

Definition 2.2

([28], p. 4) A Hadamard manifold M is a simply connected complete Riemannian manifold of nonpositive sectional curvature.

Definition 2.3

([3], p. 17) The exponential mapping $\mathrm{exp}_p: T_p M\rightarrow {M}$ is defined by $\mathrm{exp}_p \nu :=\gamma _{\nu }(1)$, where $\gamma _{\nu }$ is the geodesic defined by its position p and velocity $\nu$ at p.

Lemma 2.1

([29], p. 149, Theorem 3.1, Cartan-Hadamard theorem) Let M be a Hadamard manifold; then the universal cover of M is a convex geodesic space with respect to the induced length metric d. In particular, any two points of the universal cover are joined by a unique geodesic.

Proposition 2.1

([29], p. 149, Theorem 3.1) Let M be a Hadamard manifold and $p\in M$. Then, $\mathrm{exp}_p: T_p M\rightarrow M$ is a diffeomorphism, and for any two points $p, q\in M$, there exists a unique minimal geodesic

$$\begin{aligned} \gamma _{p, q}(t)=\mathrm{exp}_p (t \mathrm{exp}_p^{-1}q), \end{aligned}$$

for all $t\in [0, 1]$ joining p to q.

Proposition 2.2

([29], p. 150, Lemma 3.2) The exponential mapping and its inverse are continuous on a Hadamard manifold.

Lemma 2.2

([17], Lemma 2.4) Let $x_0\in M$ and $\{x_n\}\subset M$ such that $x_n\rightarrow x_0$. Then, the following assertions hold.

• (i) For any given $y\in M$, $\mathrm{exp}^{-1}_{x_n} y\rightarrow \mathrm{exp}^{-1}_{x_0} y$ and $\mathrm{exp}^{-1}_y x_n \rightarrow \mathrm{exp}^{-1}_y x_0;$

• (ii) If $\{v_n\}$ is a sequence such that $v_n \in T_{x_n} M$ and $v_n\rightarrow v_0$, then $v_0\in T_{x_0} M$;

• (iii) Given the sequences $\{u_n\}$ and $\{v_n\}$ satisfying $u_n, v_n\in T_{x_n} M$, if $u_n\rightarrow u_0$ and $v_n \rightarrow v_0$ with $u_0, v_0\in T_{x_0} M$, then

  $$\begin{aligned} \langle u_n, v_n\rangle \rightarrow \langle u_0, v_0\rangle . \end{aligned}$$

Definition 2.4

([3], p. 58) A subset $C\subset M$ is said to be geodesic convex iff for any two points $x, y\in C$, the geodesic joining x to y is contained in C, that is, if $\gamma : [a, b]\rightarrow M$ is a geodesic such that $x=\gamma (a)$ and $y=\gamma (b)$, then

$$\begin{aligned} \gamma \left( (1-t)a+tb\right) \in C \end{aligned}$$

for all $t\in [0, 1].$

Remark 2.1

By Proposition 2.1, on a Hadamard manifold M, a subset $C\subset M$ is geodesic convex iff

$$\begin{aligned} \mathrm{exp}_x (t \mathrm{exp}_x^{-1}y)\in C \end{aligned}$$

for all $x, y\in C$ and $t \in [0, 1]$.

From now on, let a Hadamard manifold M be endowed by a Riemannian metric $\langle \cdot , \cdot \rangle$ with corresponding norm denoted by $\Vert \cdot \Vert$ and $S\subset M$ be a geodesic convex subset.

Definition 2.5

([28], p. 67, Definition 3.3.1) The geodesic convex hull of a subset $S\subset M$ is the smallest geodesic convex subset of M containing S, and denoted by $\text{ conv }(S)$.

Remark 2.2

The geodesic convex hull defined in Definition 2.5 is equivalent to the intersection of all the geodesic convex sets containing S.

Definition 2.6

([3], p. 61) A real-valued function $f: M\rightarrow \mathbb {R}$, defined on C, is said to be geodesic convex iff, for any geodesic $\gamma$ of C, the composition function is convex, i.e.

for any $a, b\in \mathbb {R}$ and $0\le t\le 1$.

Remark 2.3

By Proposition 2.1, on a Hadamard manifold M, a mapping $f: M\rightarrow \mathbb {R}$ is geodesic convex iff it satisfies

$$\begin{aligned} f\left( \mathrm{exp}_x (t \mathrm{exp}_x^{-1}y)\right) \le (1-t)f(x)+tf(y) \end{aligned}$$

for all $x, y\in M$ and $t\in [0, 1].$

Proposition 2.3

([30] p. 222) If $\varOmega$ is the set of all geodesic joining x and y in M,  the function $d : M \times M \rightarrow \mathbb {R}$ defined by $d(x,y)=\inf _{\omega \in \varOmega } L(\omega )$ is said to be the geodesic distance. Moreover, d is the continuous and geodesic convex function with respect to the product Riemannian metric, that is, for any given pair of geodesics $\gamma _1 : [0, 1]\rightarrow M$ and $\gamma _2 : [0, 1]\rightarrow M$, the following inequality holds for all $t \in [0, 1]:$

$$\begin{aligned} d\left( \gamma _1(t), \gamma _2(t)\right) \le (1-t)d\left( \gamma _1(0), \gamma _2(0)\right) +t d\left( \gamma _1(1), \gamma _2(1)\right) . \end{aligned}$$

In particular, for each $y \in M$, the function $d(\cdot , y) : M\rightarrow \mathbb {R}$ is a geodesic convex function.

Definition 2.7

([13], Lemma 3.1 or [20], Definition 2.8) A set-valued mapping $G:M\rightrightarrows M$ is said to be a KKM mapping on M iff for any point-sets $\{x_1, x_2,\ldots , x_n\}\subset M$,

$$\begin{aligned} \text{ conv }(\{x_1, x_2, \ldots , x_n\})\subset \bigcup _{i=1}^n Gx_i. \end{aligned}$$

Definition 2.8

A topological space X is said to be of fixed point property iff every continuous function $f: X\rightarrow X$ has a fixed point.

Definition 2.9

Let X be a set with $\mathcal {A}=\{A_i\}_{i\in I}$ a family of subsets of X. We say that the collection $\mathcal {A}$ has the finite intersection property iff any finite sub-collection $J\subset I$ has nonempty intersection $\bigcap _{i\in J}A_i.$

Lemma 2.3

([31], p. 17) Let X be a topological space. Then, X is compact iff every collection of closed sets satisfying the finite intersection property has nonempty intersection itself.

Fig. 1

Combination of points on a manifold

3 Convex Analysis on Hadamard Manifolds

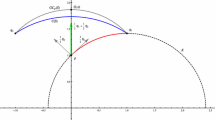
In this section, we give the definition of geodesic convex combination of finite points on a Hadamard manifold. Similar to the Euclidean space, the geodesic convex combination of two points $x_1, x_2\in M$ is the geodesic joining $x_1$ to $x_2$, and denoted by

$$\begin{aligned} \text{ comb }_{(x_1, x_2)}(t_2):=\gamma _{x_1, x_2}(t_2)=\mathrm{exp}_{x_2} \left( t_2 \mathrm{exp}_{x_2}^{-1}x_1\right) , \end{aligned}$$

for all $t_2\in [0, 1]$. Especially,

$$\begin{aligned} \text{ comb }_{(x_1, x_2)}(1)=\gamma _{x_1, x_2}(1)=\mathrm{exp}_{x_2} \left( \mathrm{exp}_{x_2}^{-1}x_1\right) =x_1 \end{aligned}$$

and

$$\begin{aligned} \text{ comb }_{(x_1, x_2)}(0)=\gamma _{x_1, x_2}(0)=\mathrm{exp}_{x_2} 0=x_2. \end{aligned}$$

Furthermore, the geodesic convex combination of three points $x_1, x_2, x_3$ is the geodesic triangle on M, and denoted by

$$\begin{aligned} \mathrm {comb}_{(x_1, x_2, x_3)}(t_2,t_3):=&\mathrm{exp}_{x_3} \left( t_3 \mathrm{exp}_{x_3}^{-1}\left( \text{ comb }_{(x_1, x_2)}(t_2)\right) \right) \\ =&\mathrm{exp}_{x_3} \left( t_3 \mathrm{exp}_{x_3}^{-1}\left( \mathrm{exp}_{x_2} t_2 \mathrm{exp}_{x_2}^{-1}x_1\right) \right) . \end{aligned}$$

for all $t_2,t_3\in [0, 1]$.

Figure  1 provides the geodesic convex combination of two points and three points, respectively.

Definition 3.1

The geodesic convex combination of finite points $x_1, \ldots , x_n$ is the geodesic joining $x_n$ to any geodesic convex combination of $x_1, \ldots , x_{n-1}$, and denoted by

$$\begin{aligned} \text{ comb }_{(x_1, \ldots , x_n)}(t_2, \ldots , t_n):=\mathrm{exp}_{x_n} \left( t_n \mathrm{exp}_{x_n}^{-1}\left( \text{ comb }_{(x_1, \ldots , x_{n-1})}\left( t_2, \ldots , t_{n-1}\right) \right) \right) , \end{aligned}$$

for all $t_i\in [0, 1]$ with $i=2,3,\ldots , n$.

Remark 3.1

Let $x\in M$ be a geodesic convex combination of $x_i\in M$ with $i\in I=\{1, 2, \ldots , n\}$, and denote it by $x=\text{ comb }_{(x_1,x_2,\ldots ,x_n)}(t_2, \ldots ,t_n)$. Take $L:=\{l\in I:t_l=1\}$. Then, x is a geodesic convex combination of $x_k$ with $k\in I\setminus L.$

Next we give two theorems to reveal the relation between the geodesic convex combination and the geodesic convex set and hull.

Theorem 3.1

A subset $C\subset M$ is geodesic convex iff it contains all the geodesic convex combinations of its elements.

Proof

Since C contains all the geodesic convex combinations of its elements, for any $x_1, x_2\in C$ and $t\in [0, 1]$, we have

$$\begin{aligned} \mathrm{exp}_{x_2}(t \mathrm{exp}^{-1}_{x_2} x_1)=\text{ comb }_{(x_1,x_2)}(t)\in C. \end{aligned}$$

By definition of the geodesic convex set, C is a geodesic convex set.

On the other hand, if C is geodesic convex, then

$$\begin{aligned} \text {comb}_{(x_1, x_2)}(t_2)=\mathrm{exp}_{x_2}(t_2 \mathrm{exp}^{-1}_{x_2} x_1)\in C \end{aligned}$$

with any two points $x_1, x_2\in C$ and all $t_2\in [0, 1].$ We must show that any geodesic combination of $x_1, \ldots , x_m\in C$ belongs to C with $m>2.$ Take any $m>2$, and make the induction hypothesis that C contains all the geodesic convex combination of fewer than m points. Set any given geodesic combination

$$\begin{aligned} x:=\text{ comb }_{(x_1, \ldots , x_m)}\left( t_2,\ldots ,t_m\right) \end{aligned}$$

and

$$\begin{aligned} y:=\text{ comb }_{(x_1, \ldots , x_m,x_{m+1})}\left( t_2,\ldots ,t_m,t_{m+1}\right) \end{aligned}$$

with $x_1, \ldots , x_m, x_{m+1}\in C$. It follows from Definition 3.1 that

$$\begin{aligned} y=\mathrm{exp}_{x_{m+1}}\left( t_{m+1}\mathrm{exp}^{-1}_{x_{m+1}}x\right) . \end{aligned}$$

By the induction hypothesis, we know that $x\in C$, and so C is a geodesic convex set. Thus, $y\in C.$ This completes the proof. $\square$

Lemma 3.1

For any given $p,q\in M$, the geodesic $\mathrm{exp}_p (t \mathrm{exp}_p^{-1} q),$ which is joining p to q, and the geodesic $\mathrm{exp}_q (h \mathrm{exp}_q^{-1} p)$ which is joining q to p with any $t,h\in [0, 1]$ are the same geodesic. In other words, for any given point $x=\mathrm{exp}_p (t \mathrm{exp}_p^{-1} q)$ with any $t\in [0, 1]$, there must exists $h\in [0, 1]$ such that $x=\mathrm{exp}_q( h \mathrm{exp}_q^{-1} p).$

Proof

By Lemma 2.1, two points p, q are joined by a unique geodesic, which completes the proof. $\square$

Theorem 3.2

For any $S\subset M$, $\text{ conv } (S)$ consists of all the geodesic convex combinations of elements of S.

Proof

Let $S^*$ consist of all the geodesic convex combination of elements of S. Since $S\subseteq \text {conv}(S)$, all elements of S belong to $\text{ conv } (S).$ Moreover, $\text{ conv } (S)$ is a geodesic convex set, so all the geodesic convex combinations of its elements belong to $\text{ conv } (S)$ by Theorem 3.1. This shows that $S^*\subseteq \text{ conv }(S).$

On the other hand, we should show that $S^*$ is a geodesic convex set. For any given two geodesic combinations $x,y\in S^*$, we have

$$\begin{aligned} x=\text{ comb }_{(x_1, \ldots , x_m)}(t_2,\ldots ,t_m),\; y=\text{ comb }_{(y_1, \ldots , y_n)}(h_2,\ldots ,h_n), \end{aligned}$$

where $x_i, y_j\in S$, $t_i, h_j \in [0,1]$ for all $i=1,\ldots ,m$ and $j=1,\ldots ,n.$ It follows from Lemma 3.1 that there exist $t,h\in [0,1]$ such that

$$\begin{aligned} \text{ comb }_{(y_1, x)}(t)= & {} \mathrm{exp}_x (t \mathrm{exp}_x^{-1} y_1)=\mathrm{exp}_{y_1} (h \mathrm{exp}_{y_1}^{-1} x)\\= & {} \mathrm{exp}_{y_1} \left( h \mathrm{exp}_{y_1}^{-1} \left( \text{ comb }_{(x_1, \ldots , x_m)}(t_2,\ldots ,t_m)\right) \right) \\= & {} \text{ comb }_{(x_1, \ldots , x_m,y_1)}(t_2,\ldots ,t_m,h)\in S^*. \end{aligned}$$

This implies that

$$\begin{aligned} \text{ comb }_{(y_1,y_2,x)}(t,h_2)= & {} \text{ comb }_{(y_2,\text{ comb }_{(x,y_1)})}(h_2)\\= & {} \mathrm{exp}_{y_2}\left( h_2 \mathrm{exp}^{-1}_{y_2}\left( \mathrm{exp}_{y_1}( h \mathrm{exp}_{y_1}^{-1} x)\right) \right) \in S^*. \end{aligned}$$

By the induction, one has $\text{ comb }_{(y_1,\ldots ,y_n,x)}(t,h_2,\ldots ,h_n)\in S^*,$ and so

$$\begin{aligned} \mathrm{exp}_x t \mathrm{exp}_x^{-1}\left( \mathrm{exp}_{y_n} h_n \mathrm{exp}_{y_n}^{-1}\left( \ldots \left( \mathrm{exp}_{y_2} h_2 \mathrm{exp}_{y_2}^{-1}y_1\right) \ldots \right) \right) =\mathrm{exp}_x (t \mathrm{exp}_x^{-1}y)\in S^*, \end{aligned}$$

which means that $S^*$ is a geodesic convex set and $\text{ conv }(S)\subset S^*$. This completes the proof. $\square$

Corollary 3.2

If $A\subset B$, then $\text{ conv }(A)\subset \text{ conv }(B).$

Definition 3.2

The geodesic convex hull of a finite set is said to be a geodesic polytope.

Proposition 3.1

The geodesic polytope of a finite set $\{x_1, \ldots , x_n\}\subset M$ consists of all the elements of the form $\text{ comb }_{(x_1, \ldots , x_n)}(t_2,\ldots ,t_n).$

Proof

Let $S=\{x_1, \ldots , x_n\}$ be a finite set. Setting some $t_i=1$, we know that Theorem 3.2 immediately implies the conclusion. This completes the proof. $\square$

Proposition 3.2

Every geodesic polytope in M is compact.

Proof

Let $P=\text{ conv }(\{x_1, \ldots , x_n\})$ be a geodesic polytope, and define a mapping $T: \mathbb {R}^{n-1}\rightarrow M$ by

$$\begin{aligned} T(t_2,\ldots ,t_n):=\mathrm{exp}_{x_n} t_n \mathrm{exp}_{x_n}^{-1}\left( \mathrm{exp}_{x_{n-1}} t_{n-1} \mathrm{exp}_{x_{n-1}}^{-1}\left( \ldots \left( \mathrm{exp}_{x_2} t_2 \mathrm{exp}_{x_2}^{-1}x_1\right) \ldots \right) \right) . \end{aligned}$$

It follows from Proposition 2.2 and Lemma 2.2, we know that T is continuous. By Proposition 3.1, for any $x\in P$, there exist $\bar{t}_i \in [0,1]$ with $i=2,3,\ldots , n$ such that $x=T(\bar{t}_2,\ldots ,\bar{t}_n).$ Thus, $P=T([0,1]^{n-1})$ and so P is compact by the compactness of $[0,1]^{n-1}$ and the continuity of T. This completes the proof. $\square$

4 S-KKM Theorem on Hadamard Manifolds

In this section, we prove an S-KKM theorem on Hadamard manifolds, which can be considered as a generalization of Theorem 3.2 of [20] and Lemma 3.1 of [13].

Definition 4.1

Let $X \subset M$ be a nonempty subset, $Y\subset M$ a geodesic subset and $S, T: X\rightrightarrows Y$ two set-valued mappings. T is said to be an S-KKM mapping on M iff for any finite subset $\{x_1, x_2, \ldots , x_n\}\subset X$, one has

$$\begin{aligned} \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right) \subset \bigcup _{i=1}^n Tx_i. \end{aligned}$$

Remark 4.1

Every KKM mapping on M, defined in Definition 2.7, is an S-KKM mapping on M. However, the converse does not hold in general.

Example 4.1

Let $M:=\{e^{ix}:0<x<2\pi \}$ and two open subsets

$$\begin{aligned} X:=\left\{ e^{ix}:\frac{1}{4}<x<\frac{1}{3}\right\} ,\; Y:=\left\{ e^{ix}:2<x<2\pi \right\} . \end{aligned}$$

Define two set-valued mappings $S, T: X\rightrightarrows Y$ as follows:

$$\begin{aligned} Se^{ix}:=\left\{ e^{iy}:x+2\le y\le -x+3\right\} ,\; Te^{ix}:=\left\{ e^{iy}:2\le y\le x+3\right\} . \end{aligned}$$

Then, for any $e^{ix_j}\in X$ with $j=1, 2,\ldots , n$ and

$$\begin{aligned} 1/4<x_1\le x_2\le \cdots \le x_n<1/3, \end{aligned}$$

one has

$$\begin{aligned} \text {conv}\left( \{e^{ix_1},\ldots , e^{ix_n}\}\right) =\left\{ e^{iy}:x_1\le y\le x_n\right\} \subset X \end{aligned}$$

and

$$\begin{aligned} \bigcup _{j=1}^n Te^{ix_j}=\left\{ e^{iy}:2\le y\le 3+x_n\right\} \subset \left\{ e^{iy}:2\le y<\frac{10}{3}\right\} =A. \end{aligned}$$

It is easy to see that $X\cap A=\emptyset$, and so

$$\begin{aligned} \text {conv}\left( \{e^{ix_1}, e^{ix_2}, \ldots , e^{ix_n}\}\right) \nsubseteq \bigcup _{j=1}^n Te^{ix_j}, \end{aligned}$$

which shows that T is not a KKM mapping. However, we have

$$\begin{aligned} \bigcup _{j=1}^n Se^{ix_j}=\left\{ e^{iy}:2+x_1<y<3-x_1\right\} , \end{aligned}$$

and so

$$\begin{aligned} \text {conv}\left( \bigcup _{j=1}^n Se^{ix_j}\right) =\left\{ e^{iy}:2+x_1<y<3-x_1\right\} \subset \bigcup _{j=1}^n Te^{ix_j}. \end{aligned}$$

This means that T is an S-KKM mapping on M.

The next lemma is important for establishing the main results of this section.

Lemma 4.1

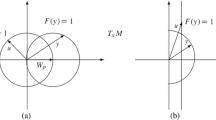
([11], Lemma 1) Let $K\subset M$ be a closed geodesic convex set. If K is compact, then it is of the fixed point property.

Proof

Let $o\in K$ and define a function $t^o_K:K\setminus \{o\}\rightarrow [1,+\infty [$ by

$$\begin{aligned} t^o_K(x):=\max \left\{ t:\mathrm{exp}_o(t \mathrm{exp}_o^{-1}x)\in K\right\} . \end{aligned}$$

Since geodesic ray $\gamma _{o,x}: [0,\infty [\rightarrow M$ from o to x is $\gamma _{o,x}(t)=\mathrm{exp}_o (t \mathrm{exp}^{-1}_o x),$ and the geodesic distance between any two of its points $a=\gamma _{o,x}(t_1)$ and $b=\gamma _{o,x}(t_2)$ is $d(a,b)=d(\gamma _{o,x}(t_1), \gamma _{o,x}(t_2))=|t_1-t_2|$ (see [3], p.23), one has

$$\begin{aligned} \left\{ t:\mathrm{exp}_o(t \mathrm{exp}_o^{-1}x)\in K\right\} =\left\{ t:\gamma _{o,x}(t)\in K\right\} =\left\{ d(o,b):\forall b\in \gamma _{o,x}\cap K\right\} . \end{aligned}$$

Thus,

$$\begin{aligned} t^o_K(x)=\max \left\{ t:\mathrm{exp}_o(t \mathrm{exp}_o^{-1}x)\in K\right\} =\sup _{b\in \gamma _{o,x}\cap K} d(o,b)=d(o, \gamma _{o,x}\cap \partial K), \end{aligned}$$

where $\partial K$ means the boundary of K. Consequently, $t^o_K(x)$ is well defined and continuous because K is closed and bounded and the geodesic distance function is continuous.

Besides, we have

$$\begin{aligned} t_K^o\left( \mathrm{exp}_o(\lambda \mathrm{exp}_o^{-1}(x))\right) =\lambda ^{-1}\max \left\{ t\lambda :\mathrm{exp}_o((t\lambda ) \mathrm{exp}_o^{-1}x)\in K\right\} =\lambda ^{-1}t_K^o(x).\quad \end{aligned}$$

(1)

Denote by $\overline{B}(0,1)$ the closed unit ball in $\mathrm{span}(\mathrm{exp}_o^{-1}K)$, the subspace of $T_o M$ generated by $\mathrm{exp}_o^{-1} K.$ Consider the function $f:K\rightarrow \overline{B}(0,1),$ defined by

$$\begin{aligned} f(x):= \left\{ \begin{aligned} \frac{\mathrm{exp}_o^{-1}x}{t^o_K(x)\Vert \mathrm{exp}_o^{-1}x\Vert },\quad&\text{ if }\quad x\ne o,\\ 0,\quad \quad \quad \quad&\text{ if }\quad x=o.\\ \end{aligned} \right. \end{aligned}$$

By Lemma 2.2, we have that $x\rightarrow o$ implies ${\mathrm{exp}_o^{-1}x}/{(t^o_K(x)\Vert \mathrm{exp}_o^{-1}x\Vert )}\rightarrow 0$. Thus, f is continuous by Proposition 2.2 and the continuity of $t^o_K.$

Now we consider the inverse function $f^{-1}.$ It is easy to see $f^{-1}(0)=o.$ If $x\ne 0,$ letting $\lambda =(t^o_K(x)\Vert \mathrm{exp}_o^{-1}x\Vert )^{-1}$ and $y=f(x)=\lambda \mathrm{exp}_o^{-1}x$, then $x=\mathrm{exp}_o\lambda ^{-1}y$. It follows from relation (1) that

$$\begin{aligned} \lambda ^{-1}&=t^o_K(x)\left\| \mathrm{exp}_o^{-1}x\right\| =\lambda ^{-1} t^o_K(x)\left\| \lambda \mathrm{exp}_o^{-1}x\right\| \\&=t^o_K\left( \mathrm{exp}_o(\lambda \mathrm{exp}^{-1}_o x)\right) \left\| \lambda \mathrm{exp}^{-1}_o x\right\| \\&=t^o_K(\mathrm{exp}_o y)\Vert y\Vert . \end{aligned}$$

Thus, we get

$$\begin{aligned} x=\mathrm{exp}_o(\lambda ^{-1}y)=\mathrm{exp}_o \left( t^o_K(\mathrm{exp}_o y)\Vert y\Vert y\right) , \end{aligned}$$

and the inverse function $f^{-1}:\overline{B}(0,1)\rightarrow K$ is given by

$$\begin{aligned} f^{-1}(x)= \left\{ \begin{aligned} \mathrm{exp}_o(t^o_K(\mathrm{exp}_o x)\Vert x\Vert x),\quad&\text{ if }\quad x\ne 0,\\ o,\quad \quad \quad \quad \quad&\text{ if }\quad x=0.\\ \end{aligned} \right. \end{aligned}$$

Hence $f^{-1}$ is also continuous. Therefore, f is a homeomorphism. By Brower’s fixed point theorem, K is of the fixed point property. $\square$

Theorem 4.1

Let $K\subset M$ be a geodesic convex set and $S, T: K\rightrightarrows K\backslash \{\emptyset \}$ two set-valued mappings on M. If T is an S-KKM mapping and for any $x\in K$, $Tx\subset K$ is closed in K, then for any finite $x_1, x_2, \ldots , x_n\in K$,

$$\begin{aligned} \bigcap _{i=1}^n Tx_i\ne \emptyset . \end{aligned}$$

Proof

Suppose that

$$\begin{aligned} \bigcap _{i=1}^n Tx_i=\emptyset . \end{aligned}$$

Let index set $I:=\{1,2,\ldots , n\}$, and, for each $x\in K$, define $\lambda _i(x)\in [0,1]$ as follows:

$$\begin{aligned} \lambda _i(x):=1-\frac{d_i(x)}{\sum _{j=1}^n d_j(x)}, \end{aligned}$$

where $d_i(x)=d(x,Tx_i)=\inf _{y\in Tx_i} \{d(x, y)\}$ and d(x, y) is the geodesic distance between x and y. Define an index set

$$\begin{aligned} I(x):=\left\{ i\in I:d_i(x)\ne 0\right\} =\left\{ i\in I:x\notin Tx_i\right\} . \end{aligned}$$

Then,

$$\begin{aligned} \lambda _i(x)=1\Leftrightarrow d_i(x)=0\Leftrightarrow x\in Tx_i \end{aligned}$$

and

$$\begin{aligned} \lambda _i(x)<1\Leftrightarrow d_i(x)>0\Leftrightarrow x\notin Tx_i. \end{aligned}$$

Now we prove that, for any $x\in K$, I(x) is not empty. In fact, if there exists $\hat{x}\in K$ such that $I(\hat{x})=\emptyset$ and $d_i(\hat{x})=0$ for all $i\in I$, then the closedness of $Tx_i\subset K$ yields that

$$\begin{aligned} \hat{x}\in \bigcap _{i=1}^n Tx_i, \end{aligned}$$

which implies the absurd statement that $\bigcap _{i=1}^n Tx_i=\emptyset .$ This shows that I(x) is not empty. Thus, $\sum _{j=1}^n d_j(x)\ne 0$ and $\lambda _i:K\rightarrow [0,1]$ is well defined. By Proposition 2.3 and the closedness of $Tx_i$, we know that the mapping $d_i(x)$ is continuous and so is $\lambda _i(x)$. Let $z_i\in Sx_i\subset K$. Since K is a geodesic convex set, the polytope

$$\begin{aligned} Z:=\text{ conv }\left( \{z_i:i\in I\}\right) \subset K. \end{aligned}$$

Define $f: Z\rightarrow Z$ as follows:

$$\begin{aligned} f(x)=f_n(x):=\mathrm{exp}_{z_n}\left( \lambda _n (x)\mathrm{exp}_{z_n}^{-1}(f_{n-1}(x))\right) , \end{aligned}$$

where

$$\begin{aligned} f_k(x)=\mathrm{exp}_{z_k}\left( \lambda _k (x)\mathrm{exp}_{z_k}^{-1}(f_{k-1}(x))\right) \end{aligned}$$

and

$$\begin{aligned} f_2(x)=\mathrm{exp}_{z_2}(\lambda _2 (x)\mathrm{exp}_{z_2}^{-1}x_1). \end{aligned}$$

Since $\lambda _i(x)\in [0,1]$ is continuous, by Proposition 2.2,

$$\begin{aligned} f(x)=\text{ comb }_{(z_1,\ldots ,z_n)}\left( \lambda _2 (x),\ldots ,\lambda _n(x)\right) \end{aligned}$$

is continuous. Besides, by Proposition 3.2, the polytope Z is compact, and so Lemma 4.1 implies that there exists $\overline{x}\in Z$ such that

$$\begin{aligned} \overline{x}=f(\overline{x})=\text{ comb }_{(z_1,\ldots ,z_n)}\left( \lambda _2 (\overline{x}),\ldots ,\lambda _n(\overline{x})\right) . \end{aligned}$$

(2)

Next we consider two situations as follows.

• (a) If $\lambda _2 (\overline{x})=\cdots =\lambda _n (\overline{x})=1$, then $d_2(\overline{x})=\cdots =d_n(\overline{x})=0.$ However, $I(\overline{x})$ is not empty, and so

  $$\begin{aligned} d_1(\overline{x})\ne 0\Rightarrow \overline{x}\notin Tx_1. \end{aligned}$$

  (3)

  It follows from (2) that

  $$\begin{aligned} \overline{x}=f(\overline{x})=\text{ comb }_{(z_1,\ldots ,z_n)}(1,\ldots ,1)=z_1. \end{aligned}$$

  Since T is an S-KKM mapping, we have $\overline{x}=z_1\in Sx_1\subset Tx_1,$ which is a contradiction to (3).

• (b) If there exists $i\in \{2,3,\ldots ,n\}$ such that $\lambda _i(\overline{x})\not =1$, then the index set defined by $I^*:=\{i\in I:\lambda _i(\overline{x})\ne 1\}$ is not empty. It is easy to see that $\lambda _p(\overline{x})\ne 1$ when $p\in I^*$, and $\lambda _q(\overline{x})= 1$ when $q\in I\setminus I^*$. It follows from Remark 3.1 and Theorem 3.2 that

  $$\begin{aligned} \overline{x}=f(\overline{x})=\text{ comb }_{(z_p,p\in I^*)}(\lambda _p(\overline{x}),p\in I^*)\in \text{ conv }(\{z_p:p\in I^*\}). \end{aligned}$$

  Since T is an S-KKM mapping, one has

  $$\begin{aligned} \text{ conv }(\{z_p:p\in I^*\})\subset \text{ conv }(\bigcup _{p\in I^*}Sx_p) \subset \bigcup _{p\in I^*} Tx_p. \end{aligned}$$

  (4)

  On the other hand, for each $p\in I^*$, $\lambda _p(\overline{x})\ne 1$, and so $d_p(\overline{x})> 0$. This implies that

  $$\begin{aligned} \overline{x}\notin \bigcup _{p\in I^*} Tx_p, \end{aligned}$$

  (5)

  which is a contradiction to (4). Therefore, the hypothesis $\bigcap _{i=1}^n Tx_i=\emptyset$ is not true.

This completes the proof. $\square$

Theorem 4.2

Let $K\subset M$ be a geodesic convex subset and $S, T: K\rightrightarrows K\backslash \{\emptyset \}$ be two set-valued mappings on M. If T is an S-KKM mapping, and for any $x\in K$, $Tx\subset K$ is closed in K, and there exists at least one $x_0\in K$ such that $Tx_0$ is compact in K, then

$$\begin{aligned} \bigcap _{x\in K}Tx\ne \emptyset . \end{aligned}$$

Proof

For any $x\in K$, let $\tilde{T}x=Tx\bigcap Tx_0$. Since Hadamard manifold M is a Hausdorff space and $\{\tilde{T}x:x\in K\}$ is closed for all $x\in K$, it follows from Theorem 4.1 that

$$\begin{aligned} \bigcap _{i=1}^n\tilde{T}x_i=\bigcap _{i=1}^n Tx_i\cap Tx_0=\bigcap _{i=0}^n Tx_i\ne \emptyset , \end{aligned}$$

and so $\{\tilde{T}x:x\in K\}$ is of finite intersection property. By Lemma 2.3, one has

$$\begin{aligned} \bigcap _{x\in K}\tilde{T}x\ne \emptyset , \end{aligned}$$

and so

$$\begin{aligned} \bigcap _{x\in K}Tx=\bigcap _{x\in K}\big (Tx\cap Tx_0\big )=\bigcap _{x\in K}\tilde{T}x\ne \emptyset . \end{aligned}$$

This completes the proof. $\square$

Now we give an example to illustrate Theorem 4.2.

Example 4.2

Let $M:=\{e^{ix}:x\in [0, 2\pi ]\}$ and $K:=\left\{ e^{ix}: x\in [1/4,3/4]\right\} .$ Then, K is a geodesic convex subset. Define two set-valued mappings $S, T: K\rightrightarrows K$ as follows:

$$\begin{aligned} Se^{ix}:=\left\{ e^{iy}:y\in \left[ x^{20}+1/4,x^{20}+1/3\right] \cup \left[ x^{20}+2/3,x^{20}+17/24\right] \right\} \end{aligned}$$

and

$$\begin{aligned} Te^{ix}:=\left\{ e^{iy}:y\in \left[ x^{30}+1/4, x^{15}+17/24\right] \right\} . \end{aligned}$$

Then, we know that $Te^{ix}$ is closed and compact for any given $e^{ix}\in K$. Moreover, for any $e^{ix_j}\in K$ with $j=1, 2,\ldots , n$ and $1/4<x_1\le \ldots \le x_n<3/4$, one has

$$\begin{aligned} \bigcup _{j=1}^n Se^{ix_j}=\left\{ e^{iy}:y\in \left[ x_1^{20}+1/4,x_n^{20}+1/3\right] \cup \left[ x_1^{20}+2/3,x_n^{20}+17/24\right] \right\} \end{aligned}$$

and

$$\begin{aligned} \bigcup _{j=1}^n Te^{ix_j}=\left\{ e^{iy}:y\in \left[ x_1^{30}+1/4, x_n^{15}+17/24\right] \right\} . \end{aligned}$$

It is easy to check that

$$\begin{aligned} \text {conv}\left( \bigcup _{j=1}^n Se^{ix_j}\right) =\left\{ e^{iy}:y\in \left[ x_1^{20}+1/4, x_n^{20}+17/24\right] \right\} \subset \bigcup _{j=1}^n Te^{ix_j}, \end{aligned}$$

and so T is an S-KKM mapping on K. Therefore, all conditions of Theorem 4.2 are satisfied, and so $\bigcap _{x\in K}Te^{ix}\ne \emptyset$. In fact, we have

$$\begin{aligned} e^{\frac{1}{2} i}\in \bigcap _{x\in K}Te^{ix}\ne \emptyset . \end{aligned}$$

Corollary 4.2

([13, 20]) Let K be a geodesic convex set and the set-valued mapping $G: K\rightrightarrows K$ be a KKM mapping on K. If for each $x\in K$, Gx is closed in K, and there exists at least one point $x_0\in K$ such that $Gx_0$ is compact in K, then

$$\begin{aligned} \bigcap _{x\in K} Gx\ne \emptyset . \end{aligned}$$

Proof

For each $X\in K$, let $Sx=\{x\}$. Then, all the conditions of Theorem 4.2 are satisfied, and Corollary 4.2 follows immediately from Theorem 4.2. This completes the proof. $\square$

5 Applications to Fixed Point Theorems on Hadamard Manifolds

As applications, in this section, we show a Fan–Browder-type fixed point theorem and a fixed point theorem for the mapping class S-KKM(X, Y) on Hadamard manifolds.

Theorem 5.1

Let $T: K\rightrightarrows K$ be a set-valued mapping satisfying the following conditions:

• (i) for any $x\in K$, Tx is nonempty and geodesic convex in K;

• (ii) for any $y\in K$, $T^{-1}y:=\{x\in K:y\in Tx\}$ is open in K;

• (iii) there exists at least one $y^*\in K$ such that $K\backslash T^{-1}y^*$ is compact in K.

Then, there exists $x_0 \in K$ such that $x_0\in Tx_0$.

Proof

Let

$$\begin{aligned} F(y):=K\backslash T^{-1}y, \quad \forall y\in K. \end{aligned}$$

Then, $F: K\rightrightarrows K$ such that F(y) is closed for each $y\in K$. Now we prove that F is not a KKM mapping. Suppose that $F: K\rightrightarrows K$ is a KKM mapping. Then, it follows from Corollary 4.2 that there exists $y_0 \in K$ such that

$$\begin{aligned} y_0\in \bigcap _{y\in K}Fy=K\backslash \bigcup _{y\in K}\{x\in K:y\in Tx\}. \end{aligned}$$

Thus, we have

$$\begin{aligned} y_0\notin \left\{ x\in K:y\in Tx\right\} , \quad \forall y\in K, \end{aligned}$$

which implies that

$$\begin{aligned} y\notin Ty_0, \quad \forall y\in K, \end{aligned}$$

and so

$$\begin{aligned} Ty_0\cap K=\emptyset , \end{aligned}$$

which implies the absurd statement that for any $x\in K$, Tx is nonempty in K. Therefore, F is not a KKM mapping. Thus, there exists a finite subset $\{y_1, y_2, \ldots , y_n\}\subset K$ and $x_0\in \text{ conv }(\{y_1, y_2, \ldots , y_n\})$ such that

$$\begin{aligned} x_0\notin \bigcup _{i=1}^n Fy_i. \end{aligned}$$

This implies that

$$\begin{aligned} x_0\notin Fy_i=K\backslash T^{-1}y_i, \quad i=1, \ldots , n, \end{aligned}$$

and so

$$\begin{aligned} y_i\in Tx_0, \quad i=1, \ldots , n. \end{aligned}$$

Since $Tx_0$ is geodesic convex, we know that

$$\begin{aligned} x_0\in \text{ conv }(\{y_1, y_2, \ldots , y_n\})\subset Tx_0. \end{aligned}$$

This completes the proof. $\square$

Remark 5.1

Theorem 5.1 can be regarded as a generalization of the Fan–Browder-type fixed point theorem involving a set-valued mapping from an Euclidean space to a Hadamard manifold.

Definition 5.1

Let $X\subset M$ be a nonempty subset and $Y\subset M$ a geodesic convex subset. Assume that $S: X\rightrightarrows Y$, $T: Y\rightrightarrows Y$ and $F: X\rightrightarrows Y$ are three set-valued mappings. F is said to be an S-KKM mapping with respect to T on M iff for any finite subset $\{x_1, x_2, \ldots , x_n\}\subset X$, one has

$$\begin{aligned} T \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right) \subset \bigcup _{i=1}^n Fx_i. \end{aligned}$$

Definition 5.2

A set-valued mapping $T: Y\rightrightarrows Y$ is said to have the S-KKM property iff for any S-KKM mapping F with respect to T, one has

$$\begin{aligned} \bigcap _{x\in X} \overline{Fx}\ne \emptyset . \end{aligned}$$

The class S-KKM(X, Y) is defined to be the set

$$\begin{aligned} \left\{ T:T\; \text{ has } \text{ the } \text{ S-KKM } \text{ property }\right\} . \end{aligned}$$

Remark 5.2

If T satisfies that, for any $A\subset Y$, $A\subseteq TA$, then T has the S-KKM property. In fact,

$$\begin{aligned} \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right) \subseteq T \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right) \subset \bigcup _{i=1}^n Fx_i. \end{aligned}$$

It follows from Theorem 4.2 that the family $\{\overline{Fx}:x\in X\}$ has the finite intersection property. In particular, let T be the identity mapping $1_X$, we have

$$\begin{aligned} \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right) = T \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right) . \end{aligned}$$

Consequently, $1_Y\in S$-KKM$(X, Y)\ne \emptyset .$

Definition 5.3

Let $x\in M$ and $\varepsilon$ be any given positive number. An open $\varepsilon$-neighbourhood of x on M is defined as

$$\begin{aligned} N(x, \varepsilon ):=\left\{ z\in M:d(z, x)<\varepsilon \right\} . \end{aligned}$$

Proposition 5.1

For any $x\in M$ and any $\varepsilon >0$, $\varepsilon$-neighbourhood of x is a geodesic convex set.

Proof

For any $z_1, z_2 \in N(x, \varepsilon )$, we know that $d(z_1, x)< \varepsilon$ and $d(z_2, x)<\varepsilon .$ By Proposition 2.3, the geodesic distance function $d(\cdot , x)$ is a geodesic convex function. For any $t\in [0, 1],$ one has

$$\begin{aligned} d\left( \mathrm{exp}_{z_1} (t \mathrm{exp}^{-1}_{z_1}z_2),\; x\right) \le t d(z_1, x)+(1-t)d(z_2, x)< t\varepsilon +(1-t)\varepsilon =\varepsilon , \end{aligned}$$

and so $\mathrm{exp}_{z_1} (t \mathrm{exp}^{-1}_{z_1}z_2)\in N(x, \varepsilon )$. This completes the proof. $\square$

We now prove the following lemma, which is the key to our main result in this section.

Lemma 5.1

Let X be a nonempty, geodesic convex and compact subset of M and $S, T : X\rightrightarrows X\backslash \{\emptyset \}$ two set-valued mappings satisfying $TX=SX=X$. If $T\in S$-$\mathrm {KKM}(X, X)$, then there exists $x^*\in X$ such that, for any given $0<\varepsilon \le \varepsilon _{\max },$

$$\begin{aligned} N(x^*, \varepsilon )\cap Tx^*\ne \emptyset \end{aligned}$$

where $\varepsilon _{\max }=\sup _{a,b\in X}\{d(a,b)\}.$

Proof

Suppose that, for any $x^*\in X$, $N(x^*, \varepsilon )\cap Tx^*= \emptyset .$ Define a set-valued mapping $F: X\rightrightarrows X$ as follows:

$$\begin{aligned} Fx:=TX\backslash \left\{ z\in X:d(z, Sx)<\varepsilon \right\} , \end{aligned}$$

where $d(z, Sx)=\mathrm {inf}_{y\in Sx} \{d(z, y)\}.$ Then, it is easy to see that

$$\begin{aligned} Fx=X\cap \left\{ z\in X:\varepsilon \le d(z,Sx)\le \varepsilon _{\max }\right\} . \end{aligned}$$

Since X is a compact subset on the m-dimensional manifold and d is continuous, we know that Fx is a nonempty and closed subset of X for any $x\in X$. Moreover, we claim that F is an S-KKM mapping with respect to T. Otherwise, there exists a finite set $\{x_1, \ldots , x_n\}\subset X$, such that

$$\begin{aligned} T\; \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right) \nsubseteq \bigcup _{i=1}^n Fx_i. \end{aligned}$$

This implies that there exist $u\in \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right)$ and $p\in Tu$ such that

$$\begin{aligned} p\notin \bigcup _{i=1}^n Fx_i=TX\backslash \bigcap _{i=1}^n \left\{ z\in X:d(z, Sx_i)<\varepsilon \right\} , \end{aligned}$$

and so

$$\begin{aligned} p\in \bigcap _{i=1}^n\{z\in X:d(z, Sx_i)<\varepsilon \}, \end{aligned}$$

which means that $d(p, Sx_i)<\varepsilon$ for all $i=1, 2, \ldots , n$. By Proposition 2.3, the geodesic distance function $d(p,\cdot )$ is a geodesic convex function. It implies that

$$\begin{aligned} d\left( p, \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right) \right) <\varepsilon . \end{aligned}$$

Therefore, $u\in \text{ conv }\left( \bigcup _{i=1}^n Sx_i\right)$ implies that $p\in N(u, \varepsilon )$. This means that $p\in N(u, \varepsilon )\cap Tu$, which is a contradiction to the hypothesis. Therefore, F is an S-KKM mapping with respect to T. Since Fx is closed and compact in X, we know that $\bigcap _{x\in X}Fx\ne \emptyset .$ Let

$$\begin{aligned} \xi \in \bigcap _{x\in X}Fx=TX\backslash \bigcup _{x\in X}\left\{ z\in X:d(z, Sx)<\varepsilon \right\} . \end{aligned}$$

Then, $\xi \in TX=SX$ implies that there exists $y_0\in X$ such that

$$\begin{aligned} \xi \in Sy_0. \end{aligned}$$

(6)

On the other hand, it is easy to see that

$$\begin{aligned} \xi \notin \bigcup _{x\in X}\left\{ z\in X:d(z, Sx)<\varepsilon \right\} \end{aligned}$$

implies that

$$\begin{aligned} \xi \notin \left\{ z\in X:d(z, Sy_0)<\varepsilon \right\} , \end{aligned}$$

which is a contradiction to (6). This completes the proof. $\square$

Theorem 5.2

Let X be a nonempty, geodesic convex and compact subset of M and $S, T : X\rightrightarrows X\backslash \{\emptyset \}$ two set-valued mappings satisfying $TX=SX=X$. If $T\in S$-$\mathrm {KKM}(X, X)$ is closed in X, then T has a fixed point.

Proof

For any point $x\in X$, let $N(x, \varepsilon _\alpha ), \alpha \in \varLambda$, be a class of open $\varepsilon _\alpha$-neighbourhood of x. By Lemma 5.1, for each $\alpha \in \varLambda$, there exists $x_\alpha \in X$ such that

$$\begin{aligned} N(x_\alpha , \varepsilon _\alpha )\cap Tx_\alpha \ne \emptyset . \end{aligned}$$

Choose $y_\alpha \in N(x_\alpha , \varepsilon _\alpha )\cap Tx_\alpha$. Since T is compact in X, there exists a subsequence $\{y_{\alpha ^{\prime }}\}\subset \{y_\alpha \}$ with $\{y_{\alpha ^{\prime }}\}\rightarrow y_0$ and $y_{\alpha ^{\prime }}\in N(x_{\alpha '}, \varepsilon _{\alpha ^{\prime }})\cap Tx_{\alpha ^{\prime }}.$ It follows from $y_{\alpha ^{\prime }}\in N(x_{\alpha ^{\prime }}, \varepsilon _{\alpha ^{\prime }})$ that $x_{\alpha ^{\prime }}\in N(y_{\alpha ^{\prime }}, \varepsilon _{\alpha ^{\prime }})$, and so the sequence $\{x_{\alpha ^{\prime }}\}$ has a limit denoted by $x_0.$ By the arbitrariness of $\varepsilon _{\alpha ^{\prime }}$, it follows that

$$\begin{aligned} \{x_{\alpha ^{\prime }}\}\rightarrow x_0=y_0. \end{aligned}$$

Furthermore, by the closedness of T, we know that $y_0\in Tx_0=Ty_0.$ This completes the proof. $\square$

6 Conclusions

In the course of this analysis, we give some new characterizations in connection with the geodesic convex hull in Theorems 3.1 and 3.2. We prove the S-KKM theorem on the Hadamard manifolds. Besides, some applications such as fixed point theorems on Hadamard manifolds have also been given in this paper.

In our opinion, there is some additional research which would be interesting. For instance, readers may consider that whether the Carathéodory’s Theorem is true or not on an m-dimensional Hadamard manifold. Moreover, as we have proven in Proposition 3.2 that every geodesic polytope is compact, the question now becomes for which conditions would the infinite geodesic convex set be compact on a manifold. These problems deserve consideration.