1 Introduction

In this paper, we obtain optimality conditions for the problems of approximating a function by linear combinations of fixed knots polynomial splines (whose parameters have to be optimized) and other continuous functions with predefined parameters. This problem is an extension of the theory of polynomial and polynomial spline approximation developed throughout the second half of the twentieth century.

The theory of Chebyshev approximation appeared in the mid-nineteenth century (Chebyshev) and was further developed in the twentieth century [1–8]. Most optimality conditions are based on the notion of alternating extreme deviation point (that is, maximal deviation points with alternating deviation signs). In the first part of this paper, we extend this theory to the approximation by weighted functions to obtain similar alternance conditions.

The objective functions appearing in optimization problems modelling Chebyshev approximation (that is, minimization of the maximal absolute deviation) are typically nonsmooth. In this paper, we propose an approach based on the notion of convex subdifferentials, developed in [9]. Another powerful nonsmooth analysis tool, quasidifferentiability [10, 11], has been successfully applied to improve the existing optimality conditions in the case of free knot polynomial spline approximation [6]. Quasidifferentiability is one of the modern nonsmooth optimization techniques, which can be considered as a generalization of subdifferentials to the case of nonconvex functions (the corresponding objective functions in [6] are nonconvex, and therefore, convex functions subdifferentials are not very efficient). Note also that the problem of best polynomial (and fixed knots polynomial spline) approximation (in its discrete version) can be reduced to a linear programming problem [7] and solved using linear optimization methods.

In general, there are many interesting interconnections between approximation and optimization. It has been pointed out in [12] that the development of powerful optimization techniques is essential for approximation, since it is heavily relying on optimization.

In the second part of this paper, we consider two applications of the theory of approximation by weighted functions, based on two different weighting functions. The first problem arises in the area of signal processing [13–15] and the other in the area of optimal tax modelling.

The paper is organized as follows. In Sect. 2, we introduce necessary definitions and provide existing results from the theory of fixed knot polynomial spline approximation, in particular, alternance-based necessary and sufficient optimality conditions. Then, in Sect. 3, we demonstrate how these conditions can be generalized to the case when polynomial splines combined with other functions. In Sect. 4, we develop alternance-based necessary optimality conditions for the case when more than one spline is involved in approximation. Section 5 provides examples of relevant real-life applications in signal processing and taxation modelling. Finally, in Sect. 6, we give conclusions and further research directions.

2 Preliminaries

2.1 Polynomial Splines

We start with a number of definitions.

Definition 2.1

(Polynomial Spline) A polynomial spline is a piecewise polynomial. Each polynomial piece lies on an interval

$$\begin{aligned}{}[\xi _i,\xi _{i+1}],~i=0,\ldots ,N-1. \end{aligned}$$

The points \(\xi _0\) and \(\xi _N\) are the external knots, and \(\xi _i\), \(i=1,\dots ,N-1\) are the internal knots of the polynomial spline.

Generally, the spline is not infinitely differentiable at its knots; moreover, it can be discontinuous [1]. In this paper, only continuity of the spline is required.

Definition 2.2

A function that is used to approximate (model) the original function or data is called the modelling function.

Polynomials and polynomial splines as well as trigonometric polynomials are very common modelling functions. The choice of modelling functions is based on the nature of the problem and the goals of approximation.

Definition 2.3

The difference between the modelling function and the function to approximate is called the deviation.

Our aim is to minimize the maximal absolute deviation.

Definition 2.4

Points in the interval \([\xi _0,\xi _N]\), where maximal absolute deviation occurs, are called maximal deviation points or extreme points.

Polynomial splines can be constructed in different ways. The most common one is through the truncated power function [1, Appendix, p. 191]:

$$\begin{aligned} {(t-\tau )}^j_+={\left\{ \begin{array}{ll}0, &{} \text {if } t<\tau ; \\ {(t-\tau )}^j, &{} \text {if } t\ge \tau .\end{array}\right. } \end{aligned}$$

Let \(X=(a_{00},x_0,\xi _1,x_1,\ldots ,\xi _{N-1},x_{N-1})\in \mathbb {R}^{(m+1)N}\), where

$$\begin{aligned} x_i=(a_{i1},\ldots ,a_{im})\in \mathbb {R}^m,~i=0,\dots , N-1 \end{aligned}$$

and

$$\begin{aligned} a=\xi _0\le \xi _1\le \dots \le \xi _{N-1}\le \xi _N=b, \end{aligned}$$
(1)

then

$$\begin{aligned} s(t)=s[X](t)=a_{00}+\sum _{i=0}^{N-1} \sum _{j=1}^{m} a_{ij}{(t-\xi _i)}^{m+1-j}_+. \end{aligned}$$
(2)

In this paper, we use an alternative formulation, proposed in [16], which is more flexible and enables one to have different degrees for different intervals:

$$\begin{aligned} s(t)=s[X](t)=a_{00}+\sum _{i=0}^{N-1} \sum _{j=1}^{m_i} a_{ij}{(\min \{t,\xi _{i+1}\}-\xi _i)}^{m_i+1-j}_+, \end{aligned}$$
(3)

where \(m_i\) is the polynomial degree at the ith interval. This formulation also allows one to work with arbitrary knot multiplicities, that is, the difference between the polynomial degree and the order of the highest continuous derivative of the spline at a given knot (see also [8] where a different formulation has been used).

2.2 Fixed Knots Polynomial Spline Approximation

In [1], the authors developed necessary and sufficient optimality conditions for fixed knots polynomial splines with the same degree at every subinterval. Then in [16], these conditions have been generalized to the case when each subinterval can have different degree \(m_i,~i=1,\dots ,N\). This result can be reformulated as follows:

Theorem 2.1

([16]) A polynomial spline s with knots \(\xi _0,\ldots ,\xi _N\) and degree \(m_i\) on the subinterval \([\xi _{i-1} , \xi _{i} ]\) is a best approximation to a function f if and only if there exists a subinterval

$$\begin{aligned}{}[\xi _{p-1},\xi _q],~0\le p\le q\le N \end{aligned}$$

with \(2+\sum _{i=p}^{q}m_i\) maximal deviation points, such that the sign of the deviation function \(\mathrm {sign}(s-f)\) is alternating at these points.

The proof is based on reformulating the necessary condition for a minimum for a convex problem as a linear system involving a matrix whose diagonal blocks are Vandermonde-type matrices and on Cramer’s rules of solving linear systems. Note that in case of free knots spline approximation the corresponding optimization problems are much more complicated. In particular, they are nonconvex [1, 6, 12]. This type of problems are out of scope of this paper.

3 Optimality Conditions

3.1 Objective Function

In this paper, we develop optimality conditions for the following optimization problem:

$$\begin{aligned} \text {min}~f(X)=\max _{t\in [a,b]}\big |y(t)-(w(t)s[X](t)+h(t))\big |, \text {s.t }X\in \mathbb {R}^{\gamma +1}, \end{aligned}$$
(4)

where

  • \(m_i,~i=1,\dots ,N\) is the highest possible degree of the corresponding polynomials at the ith subinterval;

  • N is the number of subintervals (knots are fixed);

  • [a, b] is the approximation interval;

  • \(\gamma \) \(=\sum _{i=1}^{N}m_i\);

  • y(t) is the function to approximate;

  • s[X](t) is a polynomial spline of degree \(M=(m_1,\dots ,m_N)\), whose parameters (X) are subject to optimization and knots \((\xi _i,i=0,\ldots ,N)\) are fixed;

  • w(t) and h(t) are the weighting functions defined on [a, b];

  • \(z(t)=w(t)s[X](t)+h(t))\) is the modelling function.

Definition 3.1

Function s[X](t) whose parameters X are subject to optimization is also called core approximation function, while w(t) and h(t) are given weighting functions.

Note that the additional term h(t) can be omitted by replacing y(t) by \(y(t)-h(t)\), and therefore, it is enough to study a simpler problem:

$$\begin{aligned} \text {minimize}~f(X)=\max _{t\in [a,b]}\big |y(t)-w(t)s[X](t)\big |,\text {s.t } X\in \mathbb {R}^{\gamma +1}. \end{aligned}$$
(5)

Since \(y(t)-(w(t)s[X](t))\) is linear with respect to X, one can conclude that \(q(X)=|y(t)-w(t)s[X](t)|\) is convex in X. Therefore, the objective function (5) is convex as supremum of convex functions.

When the function \(w \equiv 1\), Problem (5) is a classical polynomial spline approximation problem and Theorem 2.1 applies.

Therefore, one can apply convex analysis from [9] to solve this problem or reformulate this problem as a linear programming problem [7, 17, 18] and solve it using a linear optimization method. The linear programming approach may be preferable if the available convex optimization method is not adapted to this problem. In Sect. 3.2, we apply these techniques to develop necessary and sufficient optimality conditions for the optimization problem (5).

Definition 3.2

We denote the deviation function at point t by

$$\begin{aligned} \psi _t(s)=\psi (s,t)=y(t)-w(t)s[X](t). \end{aligned}$$

Definition 3.3

The function \(w(t)\psi (X,t)\) for a chosen X is called the weighted deviation function. The function w is the weighting function.

3.2 Optimality Conditions

Consider a convex function \(f:\mathbb {R}^{\gamma +1}\rightarrow \mathbb {R}\). A point \(x^*\) is a minimizer of f if and only if

$$\begin{aligned} \mathbf {0}_{\gamma +1}\in {\partial } f(x^*), \end{aligned}$$
(6)

where \(\partial f(x^*)\) is the subdifferential of the convex function f at point \(x^*\) [9].

The subdifferential of the objective function (5) at point X can be constructed as follows (using subdifferential calculus, see [9]):

$$\begin{aligned} \mathrm {co}\{w(\tau )\mathrm {sign}(\psi (X,\tau ))T(\tau ),~\tau \in \tau _i~i=1,\dots ,N \}, \end{aligned}$$
(7)

where \(\tau _i\in I_i, ~i=1,\dots ,N\) are the sets of maximal deviation points that belong to the subinterval \([\xi _{i-1},\xi _i]\) and \(T(\tau )\) are as follows:

$$\begin{aligned} \begin{array}{ll} (1,\varDelta (\tau ,m_1,\xi _0),\mathbf {0})^T\in \mathbb {R}^{\gamma +1}, &{}\tau \in [\xi _0,\xi _1];\\ (1,\varDelta (\xi _1,m_1,\xi _0),\varDelta (\tau ,m_2,\xi _1),\mathbf {0})^T\in \mathbb {R}^{\gamma +1}\,&{}\tau \in [\xi _1,\xi _2];\\ \vdots &{} \vdots \\ (1,\varDelta (\xi _{1},m_1,\xi _{0}),\varDelta (\xi _2,m_2,\xi _1),\dots ,\varDelta (\tau ,m_N,\xi _{N-1}))^T\in \mathbb {R}^{\gamma +1}, &{}\tau \in [\xi _{N-1},\xi _N],\\ \end{array} \end{aligned}$$

where

$$\begin{aligned} \varDelta (\alpha ,\beta ,\lambda )=((\alpha -\lambda ),(\alpha -\lambda )^2,\dots (\alpha -\lambda )^\beta )\in \mathbb {R}^{\beta }. \end{aligned}$$

In general, each \(I_i,~i=1,\dots ,n\) can be infinite. However, due to Carathédory’s theorem [19], if (6) holds, it is possible to construct \(\mathbf {0}_{\gamma +1}\) using at most \(\gamma +2\) points from the subdifferential \(\partial f(X^*)\). Therefore, there exists a set of at most \(\gamma +2\) maximal deviation points \(\tau _1,\dots ,\tau _{\sigma }\) and a set of corresponding positive coefficients \(\lambda _1,\dots ,\lambda _{\sigma }\), such that

$$\begin{aligned}{}[w(\tau _1)\mathrm {sign}(\psi (X,\tau _1))T(\tau _1),\dots ,\tau _\sigma \mathrm {sign}(\psi (X,\tau _\sigma ))T(\tau _\sigma )]\varLambda = \mathbf {0}_{\sigma }, \end{aligned}$$
(8)

where \(\varLambda =(\lambda _1,\dots ,\lambda _\sigma )\in \mathbb {R}^{\sigma }\) and \(\sigma \le \gamma +2\).

A similar system has been considered in [16], where \(w(t)\equiv 1\) for any \(t\in [a,b]\) (approximation by spline functions). One additional difficulty here is that w(t) may take zero values at maximal deviation points.

Theorem 3.1

A spline s[X] provides a best weighted approximation to y in (4) if and only if at least one of the following conditions are satisfied.

  1. 1.

    w(t) is zero at one or more maximal deviation points, or

  2. 2.

    there exists a subinterval

    $$\begin{aligned}{}[\xi _{p-1},\xi _q],~0\le p\le q\le N \end{aligned}$$

    with \(2+\sum _{i=p}^{q}m_i\) maximal deviation points, such that the sign of the weighted deviation function

    $$\begin{aligned} w(t)\mathrm {sign}(\psi (X,t)) \end{aligned}$$

    is alternating at these points.

Proof

First assume that

$$\begin{aligned} w(\tau _i)\ne 0,~i=1,\dots ,\sigma . \end{aligned}$$

Follow the same procedure as in [16]. The columns of the system in (8) are the same as in system (11) from  [16]. Therefore, the study of the existence of a strictly positive solution is very similar, since the magnitude of the corresponding components of \(\varLambda \in \mathbb {R}^{\sigma }\) can be changed (providing that they remain nonzero). Similar to [16], obtain that

  • there exists a sequence of \(2+\sum _{i=p}^{q}m_i\) maximal deviation points located at \([\xi _p,\xi _q]\) and

  • the sign of \(w(t)\psi (X,t)\) is alternating at these points.

Now assume that there exists a maximal deviation point \(t^*\) and \(w(t^*)=0\). In this case, the optimality condition (8) is automatically satisfied. Another way to see it is based on the fact that the deviation cannot be changed at the point t where w vanishes, and therefore, it cannot be improved at this points. Hence, the current maximal deviation cannot be improved, and therefore, the current solution is optimal. \(\square \)

Note that

  • the same result can be obtained in the case of discrete (data) approximation, where only discrete values of t from [a, b] are considered;

  • the obtained results resemble the classical alternance-based optimization conditions developed for polynomials and fixed knots polynomial splines.

4 Generalization to Linear Combinations with More Than One Spline

Since the sets of polynomials and polynomial splines are closed under the sum, in classical approximation theory it is not necessary to consider approximating a function by a sum of polynomials or polynomial splines. In our case, however, it makes sense to consider several weighting functions. In this section, we extend the results of Section 3 to the case of linear combinations with more than one spline. We start with the corresponding optimization problem introduction.

$$\begin{aligned} \text {min }f(X)=\max _{t\in [a,b]}\Big |y(t)-\sum _{j=1}^l w_j(t)s_j[X](t)\Big |, \text { s.t. }X\in \mathbb {R}^{\gamma +1} \end{aligned}$$
(9)

where, similar to Sect. 3,

  • \(\gamma \) \(=\sum _{i=1}^{N}m_i\);

  • l is the number of components in the sum of the modelling function;

  • N is the number of subintervals (knots are fixed);

  • \(m_i,~i=1,\dots ,N\) is the highest possible degree of the corresponding polynomials at the ith subinterval;

  • y(t) is the function to approximate;

  • \(z(t)=\sum _{j=1}^{l}w_j(t)s_j[X](t)\) is the modelling function;

  • \(s_j[X](t),~j=1,\dots ,l\) are polynomial spline of degree \(M=(m_1,\dots ,m_N)\), whose parameters are subject to optimization and knots are fixed;

  • [a, b] is approximation interval;

  • \(w_j(t),~j=1,\dots ,l\) are continuous functions defined on [a, b].

The objective function (9) is convex as a supremum of convex functions, and therefore, one can formulate necessary and sufficient conditions for such a function using subdifferential calculus. The coordinates of the points from the corresponding subdifferential consist of l blocks (one block per spline), and each block is similar to the subdifferential in the case of one spline linear combination.

Again, similar to Sect. 3, one can write a necessary and sufficient optimality condition

$$\begin{aligned} \mathbf {0}_{l(\gamma +1)}\in \partial {f(X)}, \end{aligned}$$
(10)

where f(X) is defined in (9). Essentially, this means that now we need to solve l linear systems simultaneously, seeking a nonzero nonnegative solution. Since each system is similar to one spline combination studied in Sect. 3, one can formulate the following necessary optimality condition.

Theorem 4.1

If the splines \(s_1[X],\ldots ,s_l[X]\) provide a best weighted approximation to the function y in (9), then for each \(j=1,\dots ,l\) there exists a subinterval \([\xi _{p-1},\xi _q],~0\le p\le q\le N\) with \(2+\sum _{i=p}^{q}m_i\) maximal deviation points, such that the sign of the deviation function \(w_j(t)\mathrm {sign}(\psi (X,t))\) is alternating at these points.

For sufficiency, one needs to ensure that all the sub-systems are solved simultaneously and, clearly, this is not always the case. The investigation of how this topic can be elaborated is one of our future research directions. The main obstacle for progressing in this direction is the fact that the behaviour of the deviation function depends on the properties of the weighting functions. Therefore, it is very hard to develop any sufficient condition that would hold for any type of weighting function \(w_j~j=1,\dots ,l\). In some cases, however, it is easy to formulate optimality conditions that are necessary and sufficient.

  1. 1.

    Assume that all the weighting functions \(w_j,~j=1,\dots ,l\) vanish at one or more maximal deviation points. In this case, the current spline is optimal, since the current maximal deviation can not be improved.

  2. 2.

    Assume that none of the weighting functions vanishes at the maximal deviation points and

    $$\begin{aligned} w_j(t)/w_1(t),~j=2,\dots ,l \end{aligned}$$
    (11)

    is constant at any maximal deviation point, then the condition of Theorem 4.1 is a necessary and sufficient optimality condition, since it guarantees that the systems are satisfied simultaneously. Note that the condition (11) can be relaxed; namely, it is enough if it is satisfied in the \(2+\sum _{i=p}^{q}m_i\) maximal deviation points, where the sign of the deviation function \(w_j(t)\mathrm {sign}(\psi (X,t))\) is alternating.

  3. 3.

    In general, the number of sequences to consider in Theorem 4.1 is at most the rank of the matrix \(W = (w_j (t_i ))\).

    In general, the choice of core and weighting approximation functions are application driven. Therefore, it is essential to develop optimality conditions to various types of functions.

5 Applications

In this section, we consider two real-life applications where linear combinations of polynomial splines with other functions are used.

5.1 Taxation Modelling

Optimal tax theory [20, 21] is concerned with obtaining a function which represents the optimal average taxation rate for achieving certain goals (typically redistribution of wealth). This function represents the ratio of the total tax to the total (taxable) income. It is not practical, however, to use this function for personal tax calculation, and most systems are based on a tax-free threshold and a number of tax income intervals with the corresponding tax rates (positive numbers between zero and one), while \(a_{00} = 0\). To obtain the taxation system that approximates best the optimal tax function, we can solve the following optimization problem:

$$\begin{aligned} \min _{X}\max _{t\in [a,b]}\big |y(t)-{s[X](t)\over t}\big |, \end{aligned}$$

where variable t is the total taxable income, \(a>0\) is the tax- free threshold and s[X] is a linear spline, whose parameters are the taxation rates (one per subinterval) and the knots are the taxation subintervals borders. This problem is a weighted approximation problem, where the weighting function is

$$\begin{aligned} w(x)={1\over t}. \end{aligned}$$

Definition 5.1

A table that connects the taxation intervals and the corresponding taxation rates is called the taxation table.

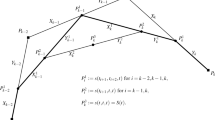
Consider linear splines in detail (see also Fig. 1)

$$\begin{aligned} s[X](t)=a_{00}+\sum _{j=1}^{N}x_{j}(\min \{t,\xi _{j+1}\}-\xi _j)_+, \end{aligned}$$
(12)

where \(a_{00}=0\), \(\xi _0=a\) is the tax-free threshold, \(\xi _N=b\) is the highest possible income considered in this problem, \(\xi _j,j=1,\dots , N, \xi _0=a\) are the borders of the tax intervals and \(x_j\) are the corresponding rates (for simplicity, we remove the index that corresponds to the spline degree, since the degree is always one). Therefore, if \(t<a\), the income is below the tax-free threshold and there is no tax to pay. For an income in the first interval, that is \(a=\xi _0\le t\le \xi _1\), then the first a dollars are untaxed, and the rest of the income (\((t-a)\) dollars) is taxed at the rate \(x_1\). For an income in the second interval, that is \(\xi _1\le t\le \xi _2\), then again the first a dollars of income is untaxed, the next \((\xi _1-\xi _0)\) dollars of income are taxed at the rate \(x_1\), and finally, the rest of the income (\((t-\xi _1)\) dollars) is taxed at the rate  \(x_2\). Continuing this process through all income thresholds, it can be seen that indeed the total tax is calculated using a linear spline whose knots are the borders of the taxation subintervals and the coefficients are the rates. Therefore, if the knots (taxation subintervals) are known, then the total tax amount as a function of income t can be modelled by optimizing the corresponding spline coefficients (taxation rates).

Fig. 1
figure 1

Average taxation rates function with thresholds a (tax-free threshold), \(\xi _1\) and \(\xi _2\)

Full size image

In most taxation systems, there are a number of requirements on spline coefficients. For example, for progressive taxation systems the rates that corresponds to higher income are higher, namely,

$$\begin{aligned} 0<x_1<\dots <x_N. \end{aligned}$$

Nonstrict inequalities are also possible, in this case two or more taxation subintervals are joined together as a single subinterval. Therefore, the optimization problems are constrained optimization problems and require some additional care to solve them. In [22], the author develops an algorithm that can take into account the fact that the corresponding spline coefficients are increasing. However, this algorithm has to be adjusted, since our modelling function is not a polynomial spline (\(w(t)={1\over t}\ne 1\)).

Note also that the following variable substitution:

$$\begin{aligned} \bar{\xi }_1=\xi _1,~\bar{\xi }_2=\xi _2-\xi _1,\dots ,\bar{\xi }_N =\xi _N-\xi _{N-1} \end{aligned}$$

leads to an equivalent constraint optimization problem, where the variables are positive (or nonnegative and some of the intervals can be joined together). This variable substitution is equivalent to spline presentation (2). In this case, the knots are still interpreted as the borders of the taxation subintervals, but the spline coefficients are not interpreted as the taxation rates anymore. Then the optimization problems remain convex and we still can apply convex analysis to deal with this problem. In particular, if a minimum occurs at a point from the interior of the feasible set (that is \(X^*\in \mathbb {R}^{N+}\) for taxation problem, \(\mathbb {R}^{N+}\) is the positive quadrant in \(\mathbb {R}\), where all the coordinates are strictly positive), then a necessary and sufficient optimality conditions is

$$\begin{aligned} \mathbf {0}_{N}\in \partial {f(\bar{X})}, \end{aligned}$$
(13)

where \(f(\bar{X})\) is the maximal deviation function and the corresponding variables are

$$\begin{aligned} \bar{\xi }_1,\dots ,\bar{\xi }_N. \end{aligned}$$

These variables are strictly positive if none of the adjusted subintervals has the same taxation rate. Also note that the dimension of the problem is N, since the value of the corresponding linear spline is fixed at a and equal to zero at this point (tax-free threshold). Such kind of splines is also called fixed tails splines. In the case of fixed tail polynomial spline approximation, similar to the results with free tails, the number of alternance points is \(2+\sum _{j=p}^{q}m_j\) if \(\xi _p>a\) or \(1+\sum _{j=p}^{q}m_j\) if \(\xi _p=a\) (see [16] for details). Therefore, the following theorem holds.

Theorem 5.1

Assume that there exists an optimal taxation table for a given number of taxation subintervals N. Then the corresponding taxation table is optimal if and only if there exists a subinterval

$$\begin{aligned}{}[\xi _p,\xi _q],~a=\xi _0\le \xi _p<\xi _q\le \xi _N=b, \end{aligned}$$

that contains

  • \(q-p+2\) maximal deviation points if \(\xi _p>a\);

  • \(q-p+1\) maximal deviation points if \(\xi _p=a\)

of the modelling function from the approximation function and the signs of deviation are alternating.

Proof

Note that our assumption on the existence of the optimal taxation table implies that the solution lies in the interior of the feasible set of Problem (12), where the same optimality condition on convex functions applies. The weighting approximations function is \({1\over t}>0\), since \(a>0\). Therefore, the sign of the deviation function and the sign of the deviation function multiplied by the weighting function is the same. Then, since it is assumed that global minima achieved in the interior of the feasible region, one can follow the same steps as in Theorem 3.1. To take into account that \(y(a) = 0\), we use fixed tails results from [16]. \(\square \)

5.2 Signal Processing

In these problems, the original signal is modelled as a sine wave and the amplitude is chosen to be a polynomial spline whose parameters are subject to optimization [13–15]. The optimization problem is

$$\begin{aligned} \min _{X}\max _{t\in [a,b]}|y(t)-s[X](t)\sin (\omega t+\tau )|, \end{aligned}$$
(14)

where \(\omega \) (frequency) and \(\tau \) (phase) are known parameters. Therefore, the corresponding weighting approximation function is

$$\begin{aligned} w(x)=\sin (\omega t+\tau ). \end{aligned}$$

In most practical applications, the parameters frequency and phase are not known. One way to obtain them is to include them as additional variables in (14). However, it is not easy to solve such problems, due to its nonconvexity and a high number of local minima. To overcome this problem, there are a number of ways to estimate the frequency and phase. In some applications, where, for example, the frequency is restricted to integers and the phase does not have to be identified very precisely (sleep scoring [14]). In this case, it is possible (and efficient) to establish a fine grid for these two parameters and consider all the possible combinations, selecting the one that gives the smallest maximal deviation to (14).

In some applications, one needs to approximate the original signal by a sum of two or more waves (similar to Sect. 4). In some cases, one of the waves represents the actual signal, while the second one is the noise and has to be removed (or ignored). In this case, the problem remains convex and therefore can be solved relatively inexpensively (providing that frequencies and phases are known and the convex optimization technique can find local minima to nonsmooth functions), but the optimality conditions are not so easy to verify.

Fig. 2
figure 2

Signal processing: brain wave signal (blue) and approximating weighted spline (red)

Full size image

On Fig. 2, the blue curve is the original signal (brain wave, also known as EEG) and the red is the approximation. A K-complex is a special sleep event, characterized by a prominent increase in the amplitude, which then immediately returns back to the original value. The identification of such events is essential for sleep scoring. There is a clear K-complex appearing two seconds after the recording started.

In this application, the computer is attempting to “mimic” doctor’s decision on whether a K-complex occurred or not. This decision is based on a number of rules that the doctor has to apply, in particular, the signal’s frequency and amplitude that describe the “shape” of the wave (phase is not very important, since it does not contribute to the shape of the wave). While the amplitude can be clearly identified through the scales appearing on the computer screen, the frequency identification is much harder: it is based on visual recognition between wave patterns that correspond to different frequencies. These patterns are normally learnt by the scorer at the time of training. Therefore, the frequency identification (when it is done by a medical doctor) is imprecise and limited to just a few possibilities (normally integers, not exceeding 15 Hz).

6 Conclusions

In this paper, we have developed necessary and sufficient optimality conditions for approximation by a model function, that is, constructed as a linear combination of a fixed knot polynomial spline and continuous functions. These conditions are generalizations of alternance type optimality conditions developed for polynomial spline approximation.

In future research, we are planning to extend this study to other types of core approximation functions, in particular, trigonometric functions. Also, it is important to address additional requirements appearing in constrained problems.

Another important research direction is to investigate free knots spline approximation. This additional flexibility will increase the quality of approximation. However, the corresponding optimization problem is much more complicated; in particular, they are nonconvex. This research direction is extremely challenging.

It is also important to develop computational methods for constructing optimal approximations. In particular, it is interesting to see whether the famous Remez algorithm [1, 23], developed for polynomial and polynomial spline approximation, can be extended to the case of linear combinations where the core approximation function is a polynomial spline (or another important class of functions).

Finally, we are planning to elaborate our results for approximating by linear combinations with more than one splines. Currently, we have developed an alternance-based necessary optimality condition and we will work towards developing a necessary and sufficient alternance-based optimality condition.