Robust Optimization for the Loss-Averse Newsvendor Problem

Abstract

In economics and decision theory, loss aversion refers to people’s tendency to strongly prefer avoiding losses to acquiring gains. Many studies have revealed that losses are more powerful, psychologically, than gains. We initially introduce loss aversion into the decision framework of the robust newsvendor model, to provide the theoretical guidance and referential decision for loss-averse decision makers when only the mean and variance of the demand distribution are known. We obtain the explicit expression for the optimal order policy that maximizes the loss-averse newsvendor’s worst-case expected utility. We find that the robust optimal order policy for the loss-averse newsvendor is quite different from that for the risk-neutral newsvendor. Furthermore, the impacts of loss aversion level on the robust optimal order quantity and on the traditional optimal order quantity are roughly the same.

1 Introduction

People are more averse to losses than the same amount of gains they are attracted to. This idea, known as loss aversion, originated from prospect theory proposed by Kahneman and Tversky [1]. Loss aversion is both intuitively appealing and well supported in organizational behavior, marketing, financial markets, labor supply, life savings and consumptions, and real estate (see, e.g., [2–7]). In addition, the empirical study by MacCrimmon and Wehrung [8] revealed that managers’ decision-making behavior is consistent with loss aversion. The experiment designed by Duxbury and Summers [9] also supported people’s loss-averse behavior. As stated by Brooks and Zank [10], “The analysis and consequences of loss aversion have become an important part of economic theories and their applications”.

The newsvendor problem is a popular problem in the operations management literature. The problem is useful for determining ordering policies for relatively short shelf-life products in order to maximize the expected profit for a single period under a stochastic demand environment. Because of its simple but elegant structure, the newsvendor problem has served as a building block for numerous models in inventory management, supply chain management and coordination, yield management, scheduling, option pricing models, and many other areas.

Obviously, coping with loss aversion in newsvendor problem is a problem worthy to study. In contrast with the wide applications and empirical supports of loss aversion in other fields, unfortunately, the development of loss aversion to describe the newsvendor decision bias is still in its early stages. As far as we know, Schweitzer and Cachon [11] and Wang and Webster [12] are among the earliest pioneers who studied the loss-averse newsvendor problem. Schweitzer and Cachon [11] showed that a loss-averse newsvendor would order strictly less than a risk-neutral newsvendor when the shortage cost could be ignorable, and the optimal order quantity was decreasing in loss aversion level. Wang and Webster [12] further found that a loss-averse newsvendor may order more than a risk-neutral newsvendor when the shortage cost is relatively high.

The existing researches have revealed that the effect of the newsvendor’s loss aversion will take substantial impact on the newsvendor’s decision. In general, these works are based on the assumption that the underlying distribution of the demand is precisely known. However, it is often very hard or impossible to figure out the demand distribution, especially in the fast-changing markets in practice. Scarf [13] and Gallego and Moon [14] are the first scholars who introduced the robust optimization approach as a practical extension of the traditional newsvendor model. The robust approach allows us to determine the optimal order quantity for the worst case when only the mean and variance of the demand distribution are available. Scarf [13] derived a closed-form formula for the optimal ordering rule that maximizes the expected profit against the worst possible distribution of the demand with the given mean and variance. He also pointed out that the worst distribution of the demand has positive mass at two points. Gallego and Moon [14] provided a simpler proof of Scarf’s formula and extended Scarf’s ideas to four cases. In the last 20 years since the appearance of Gallego and Moon [14], there have been numerous results in the literature related to extensions of Scarf’s ordering rule to different settings and applications (see, e.g., [15–24]).

So far, one intriguing question still remains:

The newsvendor’s decision-making behavior is unclear if (i) the newsvendor has preference of loss aversion and (ii) only partial information about the demand distribution is available. Is there a similar closed-form expression for the robust newsvendor problem with loss aversion to Scarf’s ordering rule [13]? In particular, whether the loss aversion makes a different effect when some information of the demand distribution is lack?

The main contribution of this work is to answer this long-standing question in an affirmative way. We built a theoretical model to characterize the robust newsvendor problem with loss aversion. We obtain the closed-form expression for the optimal order quantity that maximizes the loss-averse newsvendor’s worst-case expected utility, which is quite different from Scarf’s ordering rule. We find that the worst distribution of the demand has positive mass at three or two points. The robust optimal order quantity for our model is decreasing in loss aversion level under most parameter settings, which is roughly the same but a little different from the result obtained by Schweitzer and Cachon [11] with the complete information of the demand distribution.

The rest of the paper is organized as follows. In Sect. 2, we formulate a robust newsvendor model with loss aversion. In Sect. 3, we obtain the tight lower bound of expected utility over all possible distributions with the given mean and variance, and provide the explicit expression for the optimal order quantity that maximizes the tight lower bound of expected utility. In Sect. 4, we conduct numerical experiments to calculate the optimal order policy under different parameter settings and illustrate the effect of loss aversion level, distribution variation and other parameters on the optimal policies. In Sect. 5, we draw our conclusions and identify opportunities for future research. The proofs of main results are given in the appendices.

2 Robust Newsvendor Model with Loss Aversion

In the newsvendor problem, a decision maker chooses an order quantity q, which arrives before the start of a single selling period. Let D be stochastic demand during this period, $\mu$ be its mean and $\sigma ^2$ be its variance. The decision maker purchases each unit for cost c and sells each unit at price $p>c$. When $q>D$, each unit remaining at the end of the period can be salvaged for $s<c$. Let F be the distribution function of demand and f be the density function. For simplicity, assume F is continuous, differentiable and strictly increasing, but is uncertain. Let $\Gamma (\mu ,\sigma ^{2})$ be the class of all distribution functions with mean $\mu$ and variance $\sigma ^{2}$. Let $\Gamma _{+}(\mu ,\sigma ^{2})\subset \Gamma (\mu ,\sigma ^{2})$ be the subclass of distributions F of nonnegative random variables (i.e., $\int _{0}^{+\infty }{\text {d}}F(x)=1$).

The profit can be written as

$$\begin{aligned} \pi (q,D)= & {} (p-s)\min \{q,D\}-(c-s)q\\= & {} (p-c)q-(p-s)(q-D)_{+}, \end{aligned}$$

where $(y)_{+}:=\max \{y,0\}$.

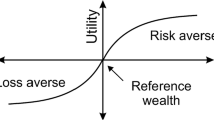
We consider a simple piecewise-linear form of loss aversion utility function

$$\begin{aligned} u(x)=\left\{ \begin{array}{ll} x,&{}\quad x\ge 0; \\ \lambda x,&{}\quad x<0, \end{array} \right. \end{aligned}$$

with $\lambda \ge 1$, where $\lambda$ quantifies the degree of loss aversion. This piecewise-linear form of loss aversion utility function in Fig. 1 has been widely used in the economics, finance, and operations management literature (see, e.g., [11, 12, 25, 26]). The rationale behind such consideration is that typically a decision maker has a reference point in mind, and he/she would feel the loss more acutely than the gain near the reference point.

Fig. 1

A piecewise-linear loss aversion utility function

For a given order quantity q, the decision maker’s break-even sales is $\frac{c-s}{p-s}q$, i.e.,

$$\begin{aligned} \pi \bigg (q,\tfrac{c-s}{p-s}q\bigg )=0. \end{aligned}$$

Hence,

$$\begin{aligned} u(\pi (q,D))=\left\{ \begin{array}{ll} \lambda [(p-s)D-(c-s)q], &{}\quad \hbox {if}\; 0\le D<\tfrac{c-s}{p-s}q;\\ (p-s)D-(c-s)q, &{} \quad \hbox {if}\; \tfrac{c-s}{p-s}q\le D<q;\\ (p-c)q, &{}\quad \hbox {if}\; D\ge q. \end{array} \right. \end{aligned}$$

(1)

We define a product as a high-profit product when $\frac{c-s}{p-s}\le \frac{1}{2}$ and a low-profit product otherwise.

Under the setting that only the mean $\mu$ and variance $\sigma ^{2}$ of demand are known, a loss-averse newsvendor is interested in solving the following robust model:

$$\begin{aligned} \max _{q}\min _{F\in \Gamma _{+}(\mu ,\sigma ^{2})} \text {E}[u(\pi (q,D))], \end{aligned}$$

(M1)

where $F\in \Gamma _{+}(\mu ,\sigma ^{2})$ means that the random variable D conforms to a distribution F which belongs to $\Gamma _{+}(\mu ,\sigma ^{2})$.

Remark 2.1

When loss aversion level $\lambda =1$, i.e., the newsvendor without loss aversion, the above model (M1) reduces to that in [13].

3 Newsvendor’s Optimal Order Policy

In this section, we are interested in solving the robust newsvendor model with loss aversion (M1). To see this, we need a few intermediate steps. Let us first consider

$$\begin{aligned} U(q):=\min _{F\in \Gamma _{+}(\mu ,\sigma ^{2})} \hbox {E}[u(\pi (q,D))] \end{aligned}$$

(P)

the inner problem of the model (M1), where the minimization is over the set of probability distributions, of the nonnegative random variable D satisfying the given mean and variance requirements.

The above problem is equivalent to the following linear programming problem

$$\begin{aligned}&\min _{F}\int _0^{+\infty }u(\pi (q,x)) {\text {d}}F(x) \\&\quad \hbox {s.t. } \int _0^{+\infty } {\text {d}}F(x)=1,\\&\quad \quad \int _0^{+\infty } x {\text {d}}F(x)=\mu ,\\&\quad \quad \int _0^{+\infty } x^2 {\text {d}}F(x)=\mu ^{2}+\sigma ^2,\\&\quad \quad \quad {\text {d}}F(x)\ge 0. \end{aligned}$$

(P)

Motivated by the approaches used in [13] and [27], we use the duality theory to analyze the above primal problem (P). Its dual problem is

$$\begin{aligned}&\qquad \max _{y_{0},y_{1},y_{2}} [y_{0} +\mu y_{1}+ (\mu ^{2}+\sigma ^{2}) y_{2}]\\&\hbox {s.t. }y_{0}+y_{1}x+y_{2}x^{2}\le u(\pi (q,x)),\quad \;\forall x\in \mathbb {R}_{+}, \end{aligned}$$

(D)

where $y_{0}$, $y_{1}$ and $y_{2}$ are the dual variables corresponding to the probability-mass, mean and second-order moment constraints. Our approach to find U(q) is based on constructing a pair of primal-dual feasible solutions $F^{*}(x)$ (a distribution) and $(y_{0}^{*}, y_{1}^{*}, y_{2}^{*})$ for (P) and (D), and make sure that they satisfy the complementary slackness condition. In the case of linear programming, this ensures optimality.

The necessary and sufficient optimality condition, for the primal feasible solution $F^{*}(x)$ to be an optimal solution for (P) and for the dual feasible solution $(y_{0}^{*}, y_{1}^{*}, y_{2}^{*})$ to be an optimal solution for (D), is the complementary slackness condition:

$$\begin{aligned} \int _0^{+\infty }\big (u(\pi (q,x))-y_{0}^{*}-y_{1}^{*}x-y_{2}^{*}x^2\big ){\text {d}}F^{*}(x)=0. \end{aligned}$$

According to the complementary slackness condition, for any point $x\in \mathbb {R}_{+}$ the primal optimal solution $F^{*}(x)$ has nonzero probability if and only if the dual optimal solution $(y_{0}^{*}, y_{1}^{*}, y_{2}^{*})$ satisfies $y_{0}^{*}+y_{1}^{*}x+y_{2}^{*}x^{2}=u(\pi (q,x))$. In other words, the touching points of the smooth curve $g(x):=y_{0}+y_{1}x+y_{2}x^{2}$ and the three-piece line $u(\pi (q,x))$ should be the points where the primal optimal solution places all its masses. As illustrated by Fig. 2, the two functions g(x) and $u(\pi (q,x))$ will have three touch points at most and two at least (a total of seven cases).

Fig. 2

The two functions g(x) and $u(\pi (q,x))$ will have three touch points at most and two at least (a total of seven cases)

On the basis of the above analysis, we provide the closed-form expression for U(q), in the following theorem.

Theorem 3.1

Define

$$\begin{aligned}&x_{0}(q):=\tfrac{\lambda (c-s)-(\lambda -1)(p-c)}{\lambda (p-s)} q, \\&x_{1}(q):=\tfrac{\lambda (c-s)+(\lambda -1)(p-c)}{\lambda (p-s)} q, \\&x_{2}(q):=\tfrac{\lambda (c-s)+(\lambda +1)(p-c)}{\lambda (p-s)} q, \end{aligned}$$

and

$$\begin{aligned}&\hat{x}_{0}(q):=0,\\&\hat{x}_{1}(q):=q\Big [1-\tfrac{\big (\sqrt{(p-c)+\lambda (c-s)}-\sqrt{(\lambda -1)(c-s)}\big )^{2}}{p-s}\Big ], \\&\hat{x}_{2}(q):=q\Big [1+\tfrac{\big (\sqrt{(p-c)+\lambda (c-s)}-\sqrt{(\lambda -1)(c-s)}\big )^{2}}{p-s}\Big ], \end{aligned}$$

and

$$\begin{aligned} \nu (q):=2q \tfrac{(p-c)+\lambda (c-s)}{\lambda (p-s)},\;\;\;\;\omega (q):=2q \tfrac{c-s}{p-s}. \end{aligned}$$

The worst-case expected utility U(q) for all $F\in \Gamma _{+}(\mu ,\sigma ^{2})$ in problem (P) reduces to the following seven cases:

• Case 1: Three-point distribution.

  • (1a) If $\tfrac{c-s}{p-s}\ge \tfrac{\lambda -1}{2\lambda -1}$ and

    $$\begin{aligned} \max \{(x_{1}-\mu )(\mu -x_{0}),(x_{2}-\mu )(\mu -x_{1})\}\le \sigma ^{2}\le (x_{2}-\mu )(\mu -x_{0}), \end{aligned}$$

    then

    $$\begin{aligned}&U(q)=\tfrac{(p-s)[\lambda (p-s)+(p-c)]\mu }{2(p-c)}+\Big [(p-c)-\tfrac{(\lambda (p-s)+(p-c))^{2}}{4\lambda (p-c)}\Big ]q\\&\quad -\tfrac{\lambda (p-s)^{2} \big (\mu ^{2}+\sigma ^{2}\big )}{4(p-c)q}. \end{aligned}$$

  • (1b) If $\frac{c-s}{p-s}< \frac{\lambda -1}{2\lambda -1}$ and

    $$\begin{aligned} \max \{(\hat{x}_{1}-\mu )(\mu -\hat{x}_{0}),(\hat{x}_{2}-\mu )(\mu -\hat{x}_{1})\}\le \sigma ^{2}\le (\hat{x}_{2}-\mu )(\mu -\hat{x}_{0}), \end{aligned}$$

    then

    $$\begin{aligned} U(q)= & {} \tfrac{(p-s)\big [(p-c)+\lambda (c-s)-\sqrt{(\lambda -1)(c-s)((p-c)+\lambda (c-s))}\big ]\mu }{\big [\sqrt{(p-c)+\lambda (c-s)}-\sqrt{(\lambda -1)(c-s)}\big ]^{2}}-\lambda (c-s) q-\\&\tfrac{(p-s)^{2}(\mu ^{2}+\sigma ^{2})}{4\big [\sqrt{(p-c)+\lambda (c-s)}-\sqrt{(\lambda -1)(c-s)}\big ]^{2}q}. \end{aligned}$$

• Case 2: Two-point distribution.

  • (2a) If $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(x_{1}-\mu )(\mu -x_{0})$, or else if $\frac{c-s}{p-s}<\frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(\omega -\mu )(\mu -\hat{x}_{0})$, then

    $$\begin{aligned} U(q)=\tfrac{p-s}{2}\Big [(\lambda +1)(\mu -\tfrac{c-s}{p-s}q)-(\lambda -1)\sqrt{(\mu -\tfrac{c-s}{p-s}q)^{2}+\sigma ^{2}}\Big ]. \end{aligned}$$

  • (2b) If $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(x_{2}-\mu )(\mu -x_{1})$, or else if $\frac{c-s}{p-s}<\frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(\hat{x}_{2}-\mu )(\mu -\hat{x}_{1})$, then

    $$\begin{aligned} U(q)=\tfrac{p-s}{2}\big [(\mu -q)-\sqrt{(\mu -q)^{2}+\sigma ^{2}}\big ]+(p-c)q. \end{aligned}$$

  • (2c) If $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and $(x_{2}-\mu )(\mu -x_{0})<\sigma ^{2}\le (\nu -\mu )(\mu -\hat{x}_{0})$, then

    $$\begin{aligned} U(q)= & {} \tfrac{\lambda (p-s)}{2}\Big [\big (\mu -\tfrac{(p-c)+\lambda (c-s)}{\lambda (p-s)} q\big )-\sqrt{\big (\mu -\tfrac{(p-c)+\lambda (c-s)}{\lambda (p-s)} q\big )^{2}+\sigma ^{2}}\Big ]\\&+(p-c)q. \end{aligned}$$

  • (2d) If $\frac{c-s}{p-s}<\frac{\lambda -1}{2\lambda -1}$ and $(\omega -\mu )(\mu -\hat{x}_{0})\le \sigma ^{2}<(\hat{x}_{1}-\mu )(\mu -\hat{x}_{0})$, then

    $$\begin{aligned} U(q)=(p-s)\mu -(c-s)\tfrac{\mu ^{2}+\lambda \sigma ^{2}}{\mu ^{2}+\sigma ^{2}}q. \end{aligned}$$

  • (2e) If $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}>(\nu -\mu )(\mu -\hat{x}_{0})$, or else if $\frac{c-s}{p-s}< \frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}>(\hat{x}_{2}-\mu )(\mu -\hat{x}_{0})$, then

    $$\begin{aligned} U(q)=\tfrac{(p-c)\mu ^{2}-\lambda (c-s)\sigma ^{2}}{\mu ^{2}+\sigma ^{2}}q. \end{aligned}$$

Furthermore, the worst-case expected utility U(q) is differentiable and concave on $[0,+\infty ]$.

We shall delegate the proof of Theorem 3.1 to Appendix 1.

Fig. 3

Characterization of the different cases in Theorem 3.1

Figure 3 provides a graphical representation of the different cases in Theorem 3.1 in the mean-variance space. We can interpret the result in Theorem 3.1 as follows: If we suppose that $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and the mean $\mu$ in the interval $[x_{0},x_{1}]$, then as we increase the variance $\sigma ^{2}$, the extremal distribution moves from case (2a) to case (1a) to case (2c) to case (2e). These can be interpreted as cases of lowest variance, lower variance, higher variance, and highest variance, respectively, for the particular mean.

Secondly, we will consider $\max \limits _{q} U(q)$. The following theorem provides the explicit expression for the robust optimal order quantity that maximizes the worst-case expected utility U(q).

Theorem 3.2

Define

$$\begin{aligned} q_{1a}= & {} \lambda (p-s)\sqrt{\tfrac{\mu ^{2}+\sigma ^{2}}{(\lambda (c-s)+(\lambda +1)(p-c))^{2}-4\lambda (p-c)^{2}}}, \\ q_{1b}= & {} \tfrac{p-s}{2}\sqrt{\tfrac{\mu ^{2}+\sigma ^{2}}{\lambda (c-s)\big (\sqrt{(p-c)+\lambda (c-s)}-\sqrt{(\lambda -1)(c-s)}\big )^{2}}}, \\ q_{2b}= & {} \mu +\tfrac{\sigma }{2}\Big (\sqrt{\tfrac{p-c}{c-s}}-\sqrt{\tfrac{c-s}{p-c}}\Big ), \\ q_{2c}= & {} \tfrac{\lambda (p-s)}{(p-c)+\lambda (c-s)}\Big [\mu +\tfrac{\sigma }{2}\Big (\sqrt{\tfrac{p-c}{\lambda (c-s)}}-\sqrt{\tfrac{\lambda (c-s)}{p-c}}\Big )\Big ], \\ q_{2e}= & {} 0. \end{aligned}$$

The robust optimal order quantity $q^{*}$ corresponds to the global maximum of the worst-case expected utility U(q) reduces to the following five cases:

• Case 1: The global maximum of U(q) is attained under three-point distribution.

  • (1a) If $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and

    $$\begin{aligned}&\max \{(x_{1}(q_{1a})-\mu )(\mu -x_{0}(q_{1a})),(x_{2}(q_{1a})-\mu ) (\mu -x_{1}(q_{1a}))\}\\&\quad \le \sigma ^{2}\le (x_{2}(q_{1a})-\mu )(\mu -x_{0}(q_{1a})), \end{aligned}$$

    then $q^{*}=q_{1a}.$

  • (1b) If $\frac{c-s}{p-s}< \frac{\lambda -1}{2\lambda -1}$ and

    $$\begin{aligned}&\max \{(\hat{x}_{1}(q_{1b})-\mu )(\mu -\hat{x}_{0}(q_{1b})),(\hat{x}_{2}(q_{1b})-\mu )(\mu -\hat{x}_{1}(q_{1b}))\} \\&\quad \le \sigma ^{2}\le (\hat{x}_{2}(q_{1b})-\mu )(\mu -\hat{x}_{0}(q_{1b})), \end{aligned}$$

    then $q^{*}=q_{1b}.$

• Case 2: The global maximum of U(q) is attained under two-point distribution.

  • (2b) If $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(x_{2}(q_{2b})-\mu )(\mu -x_{1}(q_{2b}))$, or else if $\frac{c-s}{p-s}<\frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(\hat{x}_{2}(q_{2b})-\mu )(\mu -\hat{x}_{1}(q_{2b}))$, then $q^{*}=q_{2b}.$

  • (2c) If $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and

    $$\begin{aligned} (x_{2}(q_{2c})-\mu )(\mu -x_{0}(q_{2c}))<\sigma ^{2}\le (\nu (q_{2c})-\mu )(\mu -\hat{x}_{0}(q_{2c})), \end{aligned}$$

    then $q^{*}=q_{2c}.$

  • (2e) If $\big (\frac{\mu }{\sigma }\big )^{2}\le \frac{\lambda (c-s)}{p-c}$, then $q^{*}=q_{2e}.$

  It is impossible to attain the global maximum of U(q) under the distributions of cases (2a) and (2d).

We shall delegate the proof of Theorem 3.2 to Appendix 2.

The above two theorems and the following corollary are the main results of this paper.

Corollary 3.1

When loss aversion level $\lambda =1$, the result of Theorem 3.2 reduces to that

$$\begin{aligned} {q^{*}=}\left\{ \begin{array}{ll} \mu +\tfrac{\sigma }{2}\Big (\sqrt{\tfrac{p-c}{c-s}}-\sqrt{\tfrac{c-s}{p-c}}\Big ), &{} \hbox {if } \big (\frac{\mu }{\sigma }\big )^{2}>\frac{c-s}{p-c}; \\ 0, &{} \hbox {if }\big (\frac{\mu }{\sigma }\big )^{2}\le \frac{c-s}{p-c},\\ \end{array}\right. \end{aligned}$$

which is consistent with “Scarf’s rule” [13].

We shall delegate the proof of Corollary 3.1 to Appendix 3.

4 Numerical Experiments

In contrast to the existing newsvendor models, the robust newsvendor model with loss aversion (M1) takes both the newsvendor’s distribution-free demand and decision bias into consideration. Therefore, it is expected that the model (M1) may behave differently from the existing models. In the following numerical experiments, we will compare the performance of the model (M1) with that of other two existing models: the loss-averse newsvendor model under the known distribution proposed in [11]

$$\begin{aligned} \max _{q}\text {E}[u(\pi (q,D))], \end{aligned}$$

(M2)

where F is a known distribution belonging to $\Gamma _{+}(\mu ,\sigma ^{2})$; and the robust newsvendor model without loss aversion proposed in [13]

$$\begin{aligned} \max _{q}\min _{F\in \Gamma _{+}(\mu ,\sigma ^{2})} \text {E}[\pi (q,D)]. \end{aligned}$$

(M3)

We denote by $q^{*}$, $q^{F}$, $q^{R}$, respectively, the optimal order quantities for the models (M1), (M2), (M3), and by $U(q^{*})$, $U_{F}(q^{F})$, $U_{R}(q^{R})$, respectively, the optimal expected utilities for the models (M1), (M2), (M3). Especially for the model (M2), when F is the normal distribution, we denote the optimal order quantity by $q^{N}$, and the optimal expected utility by $U_{N}(q^{N})$.

Table 1 The parameter setting of our numerical experiments

Fig. 4

A plot of the worst-case expected utility U(q) with the parameter setting No. I. Loss aversion level $\lambda = 2$

Fig. 5

A plot of the worst-case expected utility U(q) with the parameter setting No. I. Loss aversion level $\lambda = 5$

4.1 Optimal Order Polices

We present numerical experiments to compute the optimal order policies for the model (M1) and illustrate their properties. Our numerical experiments are based on the newsvendor examples introduced in [14] and [28] as shown in Table 1. We plot the optimal order policies for (M1) in Figs.  4, 5, 6, 7 and 8. As indicated in the figures, the worst possible distribution of the demand with the mean $\mu$ and the variance $\sigma ^2$ may be some combination of seven cases, which is consistent with Theorem 3.1. The worst-case expected utility U(q) is differentiable, and is either unimodal or monotone decreasing in q on $[0,+\infty ]$, which is also consistent with Theorem 3.1. The optimal expected utility, i.e., the global maximum of the worst-case expected utility, may be attained under the three-point distribution as Figs. 5, 6 shown, and may be attained under the two-point distribution as Figs. 4, 7, 8 shown, which is consistent with Theorem 3.2.

Fig. 6

A plot of the worst-case expected utility U(q) with the parameter setting No. II. Loss aversion level $\lambda = 1.5$

Fig. 7

A plot of the worst-case expected utility U(q) with the parameter setting No. II. Loss aversion level $\lambda = 5$

Fig. 8

A plot of the worst-case expected utility U(q) as a function of order quantity q with parameters $c=28.0$, $p=32.0$, $s=15.1$, $\mu =1200$ and $\sigma =300$. Loss aversion level $\lambda = 10$

4.2 Relative Expected Value of Additional Information

If we use the order quantity $q^{*}$ instead of $q^{F}$, the ratio of $U_{F}(q^{F})$ and $U_{F}(q^{*})$ is equal to $\frac{U_{F}(q^{F})}{U_{F}(q^{*})}$. This ratio can be regarded as the Relative Expected Value of Additional Information (REVAI).

To ascertain the effectiveness of our approach, we compare the performance of $q^{*}$ with $q^{F}$, in terms of the REVAI for a series of random problems under the normal/uniform distribution. We randomly generate a set of 1000 problems, where each instance of each relevant parameter, including the loss aversion level $\lambda$, is drawn from a uniform distribution, with limits as shown in Table 2. The normal distribution has a mean of 800 units and a standard deviation of 150 units, whereas the uniform distribution has limits of 540 and 1060 units, i.e., a mean of 800 and a standard deviation of 150 units. The minimum, mean, and maximum of these ratios for the 1000 problems under the two distributions examined are reported in Table 3. From this table, it is clear that the expected utilities under the known distribution yielded by $q^{*}$ and $q^{F}$ are quite close. Therefore, we can recommend the use of our robust model in those circumstances when it is almost impossible or very difficult to find the actual distribution of the demand.

Table 2 Distributions for randomly generated parameter values

Table 3 Comparison of the performance of $q^{*}$ with $q^{F}$

Fig. 9

Optimal order quantities and optimal expected utilities with respect to different loss aversion level, with unit cost $c=23$. Under this setting, $\frac{c-s}{p-s}=\frac{1}{10}$

Fig. 10

Optimal order quantities and optimal expected utilities with respect to different loss aversion level, with unit cost $c=30$. Under this setting, $\frac{c-s}{p-s}=\frac{1}{3}$

4.3 The Effect of Loss Aversion Level

Our third numerical study aims to understand the impact of loss aversion level $\lambda$ on the optimal order policy for (M1) in comparison with that for (M2), under different values of $\frac{c-s}{p-s}$ (see Figs. 9, 10, 11 and 12). Set parameters to $p=50$, $s=20$, $\mu =1200$, and $\sigma =300$. It is worthwhile to note that when $\lambda =1$, the optimal order policy for (M1) is just the optimal order policy for (M3), i.e., $q^{*}=q^{R}$ and $U(q^{*})=U_{R}(q^{R})$ in this case. From the figures, we find that:

• (i) The optimal expected utilities for both (M1) and (M2) are decreasing in loss aversion level $\lambda$. Furthermore, when the product profit is higher, the effect of $\lambda$ is stronger. Moreover, the effect of $\lambda$ on the optimal expected utility also depends on the type of model. Indeed, the effect of $\lambda$ for (M1) is more intense than that for (M2).

• (ii) The effect of loss aversion level $\lambda$ on the optimal order quantity depends on the type of model. The optimal order quantity $q^{*}$ for (M1) is decreasing in $\lambda$ under most parameter settings, but under some parameter settings it may increase in $\lambda$ at first and then decrease (see Fig. 11). Such an impact on $q^{*}$ by varying $\lambda$ is a little different from that on $q^{N}$ for (M2). Schweitzer and Cachon [11] found that the optimal order quantity be decreasing in $\lambda$ under a known demand distribution.

Fig. 11

Optimal order quantities and optimal expected utilities with respect to different loss aversion level, with unit cost $c=40$. Under this setting, $\frac{c-s}{p-s}=\frac{2}{3}$

Fig. 12

Optimal order quantities and optimal expected utilities with respect to different loss aversion level, with unit cost $c=47$. Under this setting, $\frac{c-s}{p-s}=\frac{9}{10}$

4.4 The Effect of Distribution Variation

In our fourth numerical experiment, we compare the effect of distribution variation on the optimal order quantities for three types of models. The distribution variation is quantified by mean $\mu$ and standard deviation $\sigma$. We fix $\mu$ and let $\sigma$ vary. We consider both the high-profit product and the low-profit product. Set parameters to $p=50$, $s=20$, $\mu =1000$, and $\lambda =5$.

Figures 13 and 14 show that $q^{*}$ is increasing in $\sigma$ when $\frac{c-s}{p-s}$ is small (high-profit product), and is decreasing in $\sigma$ when $\frac{c-s}{p-s}$ is big (low-profit product). Such an impact on $q^{*}$ for (M1) by varying $\sigma$ is consistent with that on $q^{N}$ for (M2) and $q^{R}$ for (M3).

Fig. 13

Optimal order quantities with respect to different standard deviation, with $c=23$. Under this setting, $\frac{c-s}{p-s}=\frac{1}{10}$

Fig. 14

Optimal order quantities with respect to different standard deviation, with $c=47$. Under this setting, $\frac{c-s}{p-s}=\frac{9}{10}$

Fig. 15

Optimal order quantities with respect to different values of unit cost, with $p=50$ and $s=20$

Fig. 16

Optimal order quantities with respect to different values of unit selling price, with $c=35$ and $s=20$

Moreover, no matter high- or low-profit product, when the deviation of $\sigma$ is 10 %, the deviation of expected utility with respect to $q^{*}$ under the known normal distribution is only 0.2–2.66 %, which is relatively small. The robust optimal ordering policy for variance change has strong adaptability, so the accuracy requirement of variance estimation for the loss-averse newsvendor is not high.

4.5 The Effect of Other Parameters

To gain more insights, in our fifth numerical experiment we study the effect of other parameters (include unit cost, selling price and salvage) on the optimal order quantities for three models. Set the benchmark values of parameters to $\mu =1000$, $\sigma =100$ and $\lambda =5$.

Figures 15, 16 and 17 demonstrate that $q^{*}$ is decreasing in unit cost c and is increasing in unit selling price p and in unit salvage s, respectively. The monotonicity of $q^{*}$ for (M1) with respect to c, p and s, respectively, is consistent with that of $q^{N}$ for (M2) and $q^{R}$ for (M3).

Fig. 17

Optimal order quantities with respect to different values of unit salvage, with $c=35$ and $p=50$

5 Conclusions

Loss aversion is the human tendency to strongly prefer avoiding a loss to receiving a gain. This particular cognitive bias consistently explains why so many of us make the same irrational decisions over and over, in the area of economics and elsewhere. Some scholars have studied the loss-averse newsvendor problem with a known demand distribution and found that the effect of the newsvendor’s loss aversion will take influence on the newsvendor’s decision. Nevertheless, it is often difficult to completely characterize the demand distribution in real life. To fill in this research gap, we initially investigate a newsvendor model that takes both the decision maker’s decision bias and the lack of distributional information of demand into consideration. We use a piecewise-linear loss aversion utility function to describe the decision maker’s decision bias, and apply the robust optimization approach to overcome the lack of information. Our solution is tractable, which makes it attractive for practical application. Our analysis also generates insights into the choice of the demand distribution as an input to the newsvendor model. We summarize our important findings as follows:

• 1. We obtain the closed-form expression for the optimal order quantity that maximizes the loss-averse newsvendor’s worst-case expected utility, which is quite different from Scarf’s ordering rule. The robust optimal order quantity with loss aversion for our model has five different cases, but Scarf’s ordering rule only has two cases. In addition, we find that the worst distribution of the demand has positive mass at three or two points.

• 2. The robust optimal order quantity with loss aversion is decreasing in loss aversion level $\lambda$ under most parameter settings, but may increase in $\lambda$ at first and then decrease under some other parameter settings. This finding is roughly the same, but a little different from the finding by Schweitzer and Cachon [11], which shows that the optimal order quantity with loss aversion is always decreasing in $\lambda$ under a known demand distribution.

• 3. The robust optimal order quantity with loss aversion is increasing in standard deviation $\sigma$ for high-profit product and is decreasing in $\sigma$ for low-profit product. The robust optimal ordering policy for variance change has strong adaptability. Moreover, the robust optimal order quantity is decreasing in unit cost c and is increasing in unit selling price p and in unit salvage s, respectively. Clearly, with respect to $\sigma$, c, p and s, respectively, the tendency of optimal order quantity for our model is consistent with those by Schweitzer and Cachon [11] and Scarf [13].

There are many questions that need to be further explored. For example, other extensions of our model include back ordering, supplying option, lead time, etc. In addition, the robust newsvendor model with other patterns of decision bias by the bounded rationality is worth investigating. Finally, it is hoped that the results obtained in this work will be helpful for both practitioners and researchers and provide some insights for developing related robust newsvendor models.

Appendices

Appendix 1

Proof of Theorem 3.1

Firstly, we prove the closed-form expression for U(q). Our proof is based on constructing a pair of primal-dual feasible solutions for (P) and (D), and make sure that they satisfy the complementary slackness condition. The optimality will then follow.

• Case 1: Three-point distribution. The remaining two bounds correspond to different three-point distribution.

  • (1a): Suppose that the smooth curve g(x) tangents the lines $l_{0}:y=\lambda [(p-s)x-(c-s)q]$, $l_{1}:y=(p-s)x-(c-s)q$ and $l_{2}:y=(p-c)q$. Let us denote these points as $x_{0}$, $x_{1}$ and $x_{2}$, where $0\le x_{0}<\frac{c-s}{p-s}q$, $\frac{c-s}{p-s}q\le x_{1}< q$ and $x_{2}\ge q$. Due to the tangency condition, they must satisfy the following system of equations:

    $$\begin{aligned}&g(x_{0})-u(\pi (q,x_{0}))=0, g'(x_{0})-u'(\pi (q,x_{0}))=0,\\&g(x_{1})-u(\pi (q,x_{1}))=0, g'(x_{1})-u'(\pi (q,x_{1}))=0,\\&g(x_{2})-u(\pi (q,x_{2}))=0, g'(x_{2})-u'(\pi (q,x_{2}))=0. \end{aligned}$$

    From the above system of equations, it is easy to get

    $$\begin{aligned} x_{0}= & {} \tfrac{\lambda (c-s)-(\lambda -1)(p-c)}{\lambda (p-s)} q, \\ x_{1}= & {} \tfrac{\lambda (c-s)+(\lambda -1)(p-c)}{\lambda (p-s)} q, \\ x_{2}= & {} \tfrac{\lambda (c-s)+(\lambda +1)(p-c)}{\lambda (p-s)} q. \end{aligned}$$

    It is easy to see that $x_{0}<\frac{c-s}{p-s}q\le x_{1}<q\le x_{2}$. And $x_{0}\ge 0$ is ensured if $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$. Note that the three-point distribution has to satisfy the mean and variance constraints. This can be obtained using the probabilities of these three points constructed explicitly as:

    $$\begin{aligned} p_{x_{0}}= & {} \tfrac{\sigma ^{2}+(\mu -x_{1})(\mu -x_{2})}{(x_{0}-x_{1})(x_{0}-x_{2})},\\ p_{x_{2}}= & {} \tfrac{\sigma ^{2}+(\mu -x_{0})(\mu -x_{1})}{(x_{2}-x_{0})(x_{2}-x_{1})},\\ p_{x_{1}}= & {} 1-p_{x_{0}}-p_{x_{2}}. \end{aligned}$$

    For the solution $F^{*}(x)$ ($(x_{i},p_{x_{i}}), i=1,2,3$ construct the three-point distribution $F^{*}(x)$) to be primal feasible, we need to ensure that the values of $p_{x_{i}}$ are nonnegative. This is ensured if $\max \{(x_{1}-\mu )(\mu -x_{0}),(x_{2}-\mu )(\mu -x_{1})\}\le \sigma ^{2}\le (x_{2}-\mu )(\mu -x_{0})$. With the values of $x_{0}$, $x_{1}$ and $x_{2}$, it is easy to check that

    $$\begin{aligned} y_{0}^{*}= & {} (p-c)q+y_{2}^{*}x_{2}^{2}=\tfrac{[3(p-c)+\lambda (p-s)][(p-c)-\lambda (p-s)]q}{4(p-c)},\\ y_{1}^{*}= & {} -2y_{2}^{*}x_{2}=\tfrac{(p-s)[(p-c)+\lambda (p-s)]}{2(p-c)},\\ y_{2}^{*}= & {} \tfrac{p-s}{2(x_{1}-x_{2})}=\tfrac{-\lambda (p-s)^{2}}{4(p-c)q}, \end{aligned}$$

    is a dual feasible solution and satisfies the complementarity slackness condition with the primal feasible solution $F^{*}(x)$ that we had identified before. Therefore (P) and (D) have the same optimal objective value, which is equal to

    $$\begin{aligned} U(q)= & {} \lambda [(p-s)x_{0}-(c-s)q]p_{x_{0}}+[(p-s)x_{1}-(c-s)q]p_{x_{1}}\\&+\,(p-c)qp_{x_{2}}\\= & {} y_{0}^{*} +\mu y_{1}^{*}+ (\mu ^{2}+\sigma ^{2}) y_{2}^{*}\\= & {} \tfrac{(p-s)[\lambda (p-s)+(p-c)]\mu }{2(p-c)}+\big [(p-c)-\tfrac{(\lambda (p-s)+(p-c))^{2}}{4\lambda (p-c)}\big ]q\\&-\tfrac{\lambda (p-s)^{2}\big (\mu ^{2}+\sigma ^{2}\big )}{4(p-c)q}. \end{aligned}$$

  • (1b): Suppose that g(x) intersects $l_{0}$ at the origin and tangents $l_{1}$ and $l_{2}$. The following proof is similar to that of (1a).

• Case 2: Two-point distribution. The remaining five bounds correspond to different two-point distributions.

  • (2a): Suppose that g(x) tangents the lines $l_{0}$ and $l_{1}$ only. Let these tangent points be $\bar{x}_{0}$ and $\bar{x}_{1}$, respectively. Due to the tangency condition, we can get

    $$\begin{aligned} \bar{x}_{0}+\bar{x}_{1}= & {} 2\tfrac{c-s}{p-s}q. \end{aligned}$$

    (2)

For the solution to be primal feasible, we need to construct the two-point distribution $F^{*}(x)$ as follows by using a positive variable $\tau$:

$$\begin{aligned} \bar{x}_{0}= & {} \mu -\sigma \tau , \hbox { with probability}\; p_{\bar{x}_{0}}=\frac{1}{\tau ^{2}+1};\nonumber \\ \bar{x}_{1}= & {} \mu +\sigma /\tau , \hbox { with probability}\; p_{\bar{x}_{1}}=\frac{\tau ^{2}}{\tau ^{2}+1}. \end{aligned}$$

(3)

Substituting (3) into the above Eq. (2), we deduce that

$$\begin{aligned} \tau =\tfrac{(\mu -\frac{c-s}{p-s}q)+\sqrt{(\mu -\frac{c-s}{p-s}q)^{2}+\sigma ^{2}}}{\sigma }. \end{aligned}$$

It is easy to see that $\bar{x}_{0}<\frac{c-s}{p-s}q<\bar{x}_{1}$ and prove the following results:

• 1. $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(x_{1}-\mu )(\mu -x_{0})\Rightarrow \sigma ^{2}<(\omega -\mu )(\mu -\hat{x}_{0})$;

• 2. $\frac{c-s}{p-s}< \frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(\omega -\mu )(\mu -\hat{x}_{0})\Rightarrow \sigma ^{2}<(x_{1}-\mu )(\mu -x_{0})$;

• 3. $\sigma ^{2}<(\omega -\mu )(\mu -\hat{x}_{0})\Leftrightarrow \bar{x}_{0}>0$;

• 4. $\sigma ^{2}<(x_{1}-\mu )(\mu -x_{0})\Leftrightarrow \sqrt{(\mu -\frac{c-s}{p-s}q)^{2}+\sigma ^{2}}<\frac{\lambda -1}{\lambda }\cdot \frac{p-c}{p-s}q\Rightarrow \bar{x}_{1}<q$.

The corresponding dual solution which satisfies the complementarity slackness condition with the primal feasible solution $F^{*}(x)$ is

$$\begin{aligned} y_{0}^{*}= & {} -(c-s)q+y_{2}^{*}\bar{x}_{1}^{2}=-(c-s)q-\tfrac{(\lambda -1)(p-s)\big [\frac{c-s}{p-s}q+\sqrt{(\mu -\frac{c-s}{p-s}q)^{2}+\sigma ^{2}}\big ]^{2}}{4\sqrt{(\mu -\frac{c-s}{p-s}q)^{2}+\sigma ^{2}}},\\ y_{1}^{*}= & {} (p-s)-2y_{2}^{*}\bar{x}_{1}=\tfrac{(\lambda +1)(p-s)}{2}+\tfrac{(\lambda -1)(c-s)q}{2\sqrt{(\mu -\frac{c-s}{p-s}q)^{2}+\sigma ^{2}}},\\ y_{2}^{*}= & {} \tfrac{(\lambda -1)(p-s)}{2(\bar{x}_{0}-\bar{x}_{1})}=\tfrac{-(\lambda -1)(p-s)}{4\sqrt{(\mu -\frac{c-s}{p-s}q)^{2}+\sigma ^{2}}}. \end{aligned}$$

In this case, we still need to guarantee that the solution $(y_{0}^{*},y_{1}^{*},y_{2}^{*})$ also satisfies the dual feasibility condition by checking $y_{0}^{*}+y_{1}^{*}x+y_{2}^{*}x^{2}<(p-c)q$ for all $x\ge q$. Let $\varDelta$ be the discriminant of the quadratic function $y_{2}^{*}x^{2}+y_{1}^{*}x+[y_{0}^{*}-(p-c)q]$. If $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(x_{1}-\mu )(\mu -x_{0})$, or else if $\frac{c-s}{p-s}<\frac{\lambda -1}{2\lambda -1}$ and $\sigma ^{2}<(\omega -\mu )(\mu -\hat{x}_{0})$, then we have

$$\begin{aligned} \varDelta= & {} (y_{1}^{*})^{2}-4y_{2}^{*}[y_{0}^{*}-(p-c)q]= \lambda (p-s)^{2}-\tfrac{(\lambda -1)(p-s)(p-c)q}{\sqrt{(\mu -\frac{c-s}{p-s}q)^{2}+\sigma ^{2}}}\\< & {} \lambda (p-s)^{2}-\tfrac{(\lambda -1)(p-s)(p-c)q}{\frac{\lambda -1}{\lambda }\cdot \frac{p-c}{p-s}q}\;\;(\hbox {from the results 2, 4})= 0. \end{aligned}$$

Since $\varDelta <0$ and $y_{2}^{*}<0$, the dual feasibility condition is satisfied. Thus the optimality holds by this pair of solutions.

• (2b): Suppose that g(x) tangents the lines $l_{1}$ and $l_{2}$. The following proof is similar to that of (2a).

• (2c): Suppose that g(x) tangents $l_{0}$ and $l_{2}$. The following proof is similar to that of (2a).

• (2d): Suppose that g(x) intersects $l_{0}$ at the origin and tangents $l_{1}$. The following proof is similar to that of (2a).

• (2e): Suppose that g(x) intersects $l_{0}$ at the origin and g(x) tangents $l_{2}$. The following proof is similar to that of (2a).

Secondly, we prove the differentiability of U(q) on $[0,+\infty ]$. We denote by $U_{1a}(q)$, $U_{1b}(q)$, $U_{2a}(q)$, $U_{2b}(q)$, $U_{2c}(q)$, $U_{2d}(q)$, $U_{2e}(q)$, respectively, the tight lower bound U(q) of cases (1a), (1b), (2a), (2b), (2c), (2d), (2e) in Theorem 3.1.

Since U(q) is a piecewise function made up of seven differentiable cases, we just need to show the differentiability of adjoining points. We indicate the proof for the differentiability of the adjoining point between case (1b) and case (2e) only, and the other proof is similar. From $\sigma ^{2}=(\hat{x}_{2}(q)-\mu )(\mu -\hat{x}_{0}(q))$, we can get that the adjoining point between case (1b) and case (2e) is

$$\begin{aligned} \hat{q}=\tfrac{(p-s)(\mu ^{2}+\sigma ^{2})}{2\mu \big [(p-c)+(\lambda -1)(c-s)-\sqrt{(\lambda -1)(c-s)((p-c)+\lambda (c-s))}\big ]}. \end{aligned}$$

It is easy to verify that

$$\begin{aligned} U_{1b}(\hat{q})=\lim _{q\rightarrow \hat{q}_{-}}U_{2e}(q)=\tfrac{(p-c)\mu ^{2}-\lambda (c-s)\sigma ^{2}}{\mu ^{2}+\sigma ^{2}}\hat{q}, \end{aligned}$$

and

$$\begin{aligned} {U}_{1b}^{'}(\hat{q})=\lim _{q\rightarrow \hat{q}_{-}}U_{2e}^{'}(q)=\tfrac{(p-c)\mu ^{2}-\lambda (c-s)\sigma ^{2}}{\mu ^{2}+\sigma ^{2}}. \end{aligned}$$

Finally, we prove the concavity of U(q) on $[0,+\infty ]$.

• (1a): For any $q\ge 0$, we can calculate that

  $$\begin{aligned} {U}_{1a}^{''}(q)=-\tfrac{\lambda (p-s)^{2}(\mu ^{2}+\sigma ^{2})}{2(p-c)q^{3}}<0. \end{aligned}$$

  So, $U_{1a}(q)$ is concave on $[0,+\infty ]$.

• (1b), (2a), (2b), (2c): These proofs are similar to that of (1a).

• (2d): It is obvious that $U_{2d}(q)$ is a linear function, so $U_{2d}(q)$ is a concave function.

• (2e): This proof is similar to that of (2d). Since the differentiable function U(q) is a piecewise function made up of seven concave cases, U(q) is concave on $[0,+\infty ]$. $\square$

Appendix 2

Proof of Theorem 3.2

• (1a): Setting

  $$\begin{aligned} {U}_{1a}^{'}(q)=(p-c)-\tfrac{[\lambda (c-s)+(\lambda +1)(p-c)]^{2}}{4\lambda (p-c)}+\tfrac{\lambda (p-s)^{2}(\mu ^{2}+\sigma ^{2})}{4(p-c)q^{2}}=0, \end{aligned}$$

  we can get a positive stationary point

  $$\begin{aligned} q_{1a}=\lambda (p-s)\sqrt{\tfrac{\mu ^{2}+\sigma ^{2}}{(\lambda (c-s)+(\lambda +1)(p-c))^{2}-4\lambda (p-c)^{2}}} \end{aligned}$$

  Since $U_{1a}(q)$ is concave, $\hbox {arg}\max \limits _{q}U_{1a}(q)=q_{1a}$. Thus, if $q_{1a}$ satisfies conditions (1a), then $q^{*}=q_{1a}$.

• (1b): This proof is similar to that of (1a).

• (2a): For any $q\ge 0$,

  $$\begin{aligned} {U}_{2a}^{'}(q)=-\tfrac{(\lambda +1)(c-s)}{2}\Big [1-\tfrac{(\lambda -1)(\mu -\frac{c-s}{p-s}q)}{(\lambda +1)\sqrt{(\mu -\frac{c-s}{p-s}q)^{2}+\sigma ^{2}}}\Big ]<0. \end{aligned}$$

  Obviously, $U_{2a}(q)$ is monotone decreasing in q on $[0,+\infty ]$, and $\hbox {arg}\max \limits _{q}U_{2a}(q)=0$. But $q=0$ does not satisfy condition (2a), so $q^{*}$ can not be attained under this case.

• (2b): Setting

  $$\begin{aligned} {U}_{2b}^{'}(q)=\tfrac{(p-c)-(c-s)}{2}+\tfrac{(p-s)(\mu -q)}{2\sqrt{(\mu -q)^{2}+\sigma ^{2}}}=0, \end{aligned}$$

  we can get a unique stationary point

  $$\begin{aligned} q_{2b}=\mu +\tfrac{\sigma }{2}\Big (\sqrt{\tfrac{p-c}{c-s}}-\sqrt{\tfrac{c-s}{p-c}}\Big ). \end{aligned}$$

  If $\tfrac{\mu }{\sigma }<\tfrac{(c-s)-(p-c)}{2(p-c)(c-s)}$, then $q_{2b}<0$. Since $U_{2b}(q)$ is concave, $\hbox {arg}\max \limits _{q}U_{2b}(q)=0$. But $q=0$ does not satisfy condition (2b). If $\tfrac{\mu }{\sigma }\ge \tfrac{(c-s)-(p-c)}{2(p-c)(c-s)}$, then $q_{2b}\ge 0$. Since $U_{2b}(q)$ is concave, $\hbox {arg}\max \limits _{q}U_{2b}(q)=q_{2b}$. To sum up, if $q_{2b}$ satisfies conditions (2b), then $q^{*}=q_{2b}$.

• (2c): This proof is similar to that of (2b).

• (2d): It is easy to verify that if $U_{2d}(q)$ is monotone decreasing in q, $\hbox {arg}\max \limits _{q}U_{2d}(q)=0$. But $q=0$ does not satisfy condition (2d), so $q^{*}$ can not be attained under this case.

• (2e): It is obvious that

  $$\begin{aligned}&U_{2e}(q)\hbox { is monotone increasing in }q,\quad \hbox {if}\; \big (\tfrac{\mu }{\sigma }\big )^{2}>\frac{\lambda (c-s)}{p-c},\\&U_{2e}(q)\hbox { is monotone decreasing in }q, \quad \hbox {if}\; \big (\tfrac{\mu }{\sigma }\big )^{2}\le \frac{\lambda (c-s)}{p-c}. \end{aligned}$$

If $\big (\tfrac{\mu }{\sigma }\big )^{2}>\frac{\lambda (c-s)}{p-c}$, $q^{*}$ can not be attained under this case.

If $\big (\tfrac{\mu }{\sigma }\big )^{2}\le \frac{\lambda (c-s)}{p-c}$, then $\hbox {arg}\max \limits _{q\in [0,+\infty ]}U_{2e}(q)=q_{2e}=0$. It is obvious that $q_{2e}$ satisfies condition (2e), so $q^{*}=q_{2e}$. $\Box$

Appendix 3

Proof of Corollary 3.1

Let $\lambda =1$, then $\frac{c-s}{p-s}\ge \frac{\lambda -1}{2\lambda -1}=0$, $x_{0}(q)=x_{1}(q)=\frac{c-s}{p-s}q$, $x_{2}(q)=\frac{(c-s)+2(p-c)}{p-s}q$ and $q_{2b}=q_{2c}=\mu +\tfrac{\sigma }{2}\Big (\sqrt{\tfrac{p-c}{c-s}}-\sqrt{\tfrac{c-s}{p-c}}\Big )$. Furthermore, the five cases of the robust optimal order quantity $q^{*}$ in Theorem 3.2 can reduce to the following three cases:

• (1a): If $\sigma ^{2}=(x_{2}(q_{1a})-\mu )(\mu -x_{0}(q_{1b}))$, then $q^{*}=q_{1a}$.

• (2b), (2c): If $\sigma ^{2}<(x_{2}(q_{2b})-\mu )(\mu -x_{1}(q_{2b}))$, or else if $(x_{2}(q_{2b})-\mu )(\mu -x_{0}(q_{2b}))<\sigma ^{2}\le (\nu (q_{2b})-\mu )(\mu -\hat{x}_{0}(q_{2b}))$, then $q^{*}=q_{2b}$.

• (2e): If $\big (\tfrac{\mu }{\sigma }\big )^{2}\le \frac{c-s}{p-c}$, then $q^{*}=q_{2e}=0$.

Moreover, it is easy to verify that

• 1. $\big (\tfrac{\mu }{\sigma }\big )^{2}>\frac{c-s}{p-c}\Rightarrow \sigma ^{2}\le (\nu (q_{2b})-\mu )(\mu -\hat{x}_{0}(q_{2b}))$.

• 2. From the result 2 in the proof of Theorem 3.1 (2b), we can get

  $$\begin{aligned} \sigma ^{2}=(x_{2}(q_{2b})-\mu )(\mu -x_{1}(q_{2b}))\Leftrightarrow \mu =\tfrac{[3(p-c)+(c-s)]\sigma }{2(p-c)}\sqrt{\tfrac{c-s}{p-c}}. \end{aligned}$$

• 3. Substitute $\mu =\tfrac{[3(p-c)+(c-s)]\sigma }{2(p-c)}\sqrt{\tfrac{c-s}{p-c}}$ into $q_{1a}$ and $q_{2b}$, we can obtain that

  $$\begin{aligned} q_{1a}=q_{2b}=\tfrac{(p-s)^{2}\sigma }{2(p-c)\sqrt{(p-c)(c-s)}}. \end{aligned}$$

To sum up, from the results 1, 2, 3, we can obtain that

$$\begin{aligned} {q^{*}=}\left\{ \begin{array}{ll} \mu +\tfrac{\sigma }{2}\Big (\sqrt{\tfrac{p-c}{c-s}}-\sqrt{\tfrac{c-s}{p-c}}\Big ), &{} \hbox {if }\big (\frac{\mu }{\sigma }\big )^{2}>\frac{c-s}{p-c};\\ 0, &{} \hbox {if } \big (\frac{\mu }{\sigma }\big )^{2}\le \frac{c-s}{p-c}. \end{array}\right. \end{aligned}$$

$\square$