Phase Transitions for a Class of Time-Inhomogeneous Diffusion Processes

Abstract

In this paper, we study phase transitions of a class of time-inhomogeneous diffusion processes associated with the $\varphi ^4$ model. We prove that when $\gamma <0$, the system has no phase transition and when $\gamma >0$, the system has a phase transition and we study the phase transition of the system through qualitative and quantitative methods. We further show that, as the strength of the mean field tends to 0, the solution and stationary distribution of such system converge locally uniformly in $L^2$ and Wasserstein distance respectively to those of corresponding system without mean field.

1 Introduction

In this paper, we study a class of time-inhomogeneous diffusion processes associated with the $\varphi ^4$ model. These processes are solutions of the following stochastic differential equations defined on a complete filtered probability space $(\Omega ,\mathscr {F},\{\mathscr {F}_{t}\}_{t\ge 0}, \mathbb {P})$:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle dX_t=\sqrt{2}dW_t+\big (\gamma \mathbb {E}X_t-u'(X_t)\big )dt,\\ X_0=\xi , \end{array}\right. \end{aligned}$$

(1)

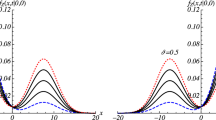
where $\gamma \ne 0$, $\xi$ is a $\mathscr {F}_{0}$-measurable random variable, and $\{W_t\}_{t\ge 0}$ is a Brownian motion defined on $(\Omega ,\mathscr {F},\{\mathscr {F}_{t}\}_{t\ge 0}, \mathbb {P})$, $u(x)=x^4-\beta x^2$, and $\beta \ge 0$ is the inverse temperature. Due to the double-well potential u(x), there is a phase transition in this model. As shown in Fig. , it is difficult for u(x) to get out of a pit at low temperatures.

Fig. 1

The image of $u(x)=x^4-\beta x^2$ with $\beta =100$

Phase transition is a central topic in statistical physics. Many methods have been developed to study phase transitions, including the coupling method [2, 4, 15, 22], the dual method [15, 22], the graph representation and seepage theory [7, 14], the Peirels method and Pirogov–Sinai theory [19], the cluster expansions method [16, 17] and the gap estimation method [3, 13, 15] etc.

In statistical physics, one often studies the mean field models as simplified approximations of the original ones. It is usually a common phenomenon that with the mean field models it is easier to exhibit phase transitions, from which our paper origins. Consider the following operator on $\mathbb {R}$:

$$\begin{aligned} L=a(x)\frac{d^2}{dx^2}+b(x)\frac{d}{dx}+\mathbb {E}X_t\frac{d}{dx}. \end{aligned}$$

The first two terms represent the drift and diffusion terms as given in diffusion process. The new additional drift term $\mathbb {E}X_t$, the mean of the process, represents the exchange of the energy from the outside: a source of energy is provided from the outside according to the mean of the process. Intuitively, this model can be interpreted as follows. Fix a vessel $u\in \mathbb {Z}^d$ in which the reaction is kept. Regard all $v\in \mathbb {Z}^d\backslash \{u\}$ as outside and the diffusions between u and $v\in \mathbb {Z}^d\backslash \{u\}$ are now described simply by the new drift term $\mathbb {E}X_t$. In this sense, the process represents a non-equilibrium model. Clearly, the new term makes the process be time-inhomogeneous. For more information about mean field models, see Dawson and Zheng [8], Feng [9,10,11], Feng and Zheng [12].

In this paper, we restrict ourselves to the time-inhomogeneous $\varphi ^4$ model (1), whose operator is

$$\begin{aligned} L_t=\frac{d^2}{dx^2}+\left( \gamma \mathbb {E}X_t-u'(x)\right) \frac{d}{dx}. \end{aligned}$$

Here, $\gamma$ represents the strength coefficient of the mean field and we are also ready to study its effect on the phase transition. Because $\mathbb {E}X_t$ is a function of the distribution of $X_t$, thus Eq. (1) is a particular type of distribution dependent stochastic differential equation or McKean-Vlasov stochastic differential equation. And the existence and non-uniqueness of invariant probability measures for McKean-Vlasov SDEs was investigated in [23].

The main purpose of this paper is to show that there is a phase transition for the number of invariant probability measures of Eq. (1). In Sect. 2, we give some preliminaries. In Sect. 3, we study the number of invariant probability measures. In the case of $\gamma <0$, the system has no phase transition and in the case of $\gamma >0$, we study the phase transition of the system through qualitative and quantitative methods. More specifically, we prove that there exists a critical value $\beta _{c}$ such that the system admits three invariant probability measures for $\beta >\beta _c$, while the system has a unique invariant probability measure for $\beta \le \beta _c$. We also obtain an expression for $\beta _{c}$ by quantitative analysis and this result is completely new. In the last section, we show that when $\gamma \rightarrow 0$ the solution and invariant probability measure of the system converge to the solution and invariant probability measure in the case of $\gamma =0$.

2 Preliminaries

Consider the following distribution dependent SDE or Mckean–Vlasov SDE on $\mathbb {R}$

$$\begin{aligned} dX_t=b(t,X_t,\mathscr {L}_{X_t})dt+\sigma (t,X_t,\mathscr {L}_{X_t})dW_t, \end{aligned}$$

(2)

where $b:[0,\infty )\times \mathbb {R}\times \mathscr {P}(\mathbb {R})\rightarrow \mathbb {R}$, $\sigma :[0,\infty )\times \mathbb {R}\times \mathscr {P}(\mathbb {R})\rightarrow \mathbb {R}\times \mathbb {R}$ are measurable, and $\mathscr {L}_{X_t}$ is the distribution of $X_t$.

Let $\mathscr {P}(\mathbb {R})$ be the family of all probability measures on $\mathbb {R}$. For $\theta \in [1,\infty )$, we define the following subspace of $\mathscr {P}(\mathbb {R})$:

$$\begin{aligned} \mathscr {P}_\theta := \left\{ \mu \in \mathscr {P}(\mathbb {R}):\int _{\mathbb {R}} {\vert x\vert }^\theta \mu (d x)<\infty \right\} , \end{aligned}$$

which is a Polish space under the Wasserstein distance

$$\begin{aligned} \mathbb {W}_\theta (\mu _1,\mu _2):=\inf _{\pi \in \mathscr {C}(\mu _1,\mu _2)} \left( \int _{\mathbb {R}\times \mathbb {R}}{\vert x-y\vert }^\theta \pi (dx,dy) \right) ^{\frac{1}{\theta }},~~~\mu _1,\mu _2\in \mathscr {P}_\theta , \end{aligned}$$

where $\mathscr {C}(\mu _1,\mu _2)$ is the set of all couplings for$~\mu _1$ and $\mu _2$ (see [2] or [21]).

When Eq. (2) has a unique strong solution (see [21]) in $\mathscr {P}_\theta$, the solution $(X_t)_{t\ge 0}$ is a Markov process in the sense that for any $s\ge 0$, $(X_t)_{t\ge s}$ is determined by solving the equation from time s with initial state $X_s$. More precisely, letting $\{X_{s,t}(\xi )\}_{t\ge s}$ denote the solution of the equation from time s with initial state $X_{s,s}=\xi$, the existence and uniqueness imply

$$\begin{aligned} X_{s,t}(\xi )=X_{r,t}(X_{s,r}(\xi )),~~t\ge r\ge s\ge 0, \end{aligned}$$

(3)

where $\xi$ is $\mathscr {F}_s$-measurable with $\mathbb {E}{\vert \xi \vert }^\theta <\infty$.

When Eq. (2) has $\mathscr {P}_\theta$-weak uniqueness, we may define a semigroup $(P^*_{s,t})_{t\ge s}$ on $\mathscr {P}_\theta$ by letting $P^*_{s,t}\mu :=\mathscr {L}_{X_{s,t}}$ for $\mathscr {L}_{X_{s,s}}=\mu \in \mathscr {P}_\theta$. Indeed, by (3) we have

$$\begin{aligned} P^*_{s,t}=P^*_{r,t}P^*_{s,r},~~ t\ge r\ge s\ge 0. \end{aligned}$$

We can investigate the ergodicity in the time homogeneous case when $\sigma$ and b do not depend on t. In this case we have $P^*_{s,t}=P^*_{t-s}$, for $t\ge s\ge 0$.

We call $\mu \in \mathscr {P}_\theta$ an invariant probability measure of $P^*_t$ if $P^*_t\mu =\mu$ for all $t\ge 0$, and we call the solution ergodic if there exists $\mu \in \mathscr {P}_\theta$ such that $\lim _{t\rightarrow \infty }P^*_t\nu =\mu$ weakly for any $\nu \in \mathscr {P}_\theta .$

Now, we consider the following one-dimensional SDE

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle dX_t=b(X_t)dt+\sigma (X_t)dW_t,\\ X_0=\xi , \end{array}\right. \end{aligned}$$

(4)

where $\sigma (x)\ne 0$ for all $x\in \mathbb {R}$, $\sigma$ and b satisfy the Lipschitz and growth conditions. Thus SDE (4) has a unique strong and non-explosive solution $(X_t)_{t\ge 0}$. The generator of process $(X_t)_{t\ge 0}$ is

$$\begin{aligned} L=a(x)\frac{d^2}{dx^2}+b(x)\frac{d}{dx}, \end{aligned}$$

where $a(x)=\frac{1}{2}\sigma (x)^2$.

Suppose that the function $x\mapsto \frac{1}{a(x)}\exp \big [\int ^x_0\frac{b(y)}{a(y)}dy\big ]$ is Lebesgue integrable for all $x\in \mathbb {R}$. We can verify that L is symmetric with respect to the following measure

$$\begin{aligned} \mu (dx)=\frac{1}{a(x)}\exp \bigg [\int ^x_0\frac{b(y)}{a(y)}dy\bigg ]dx. \end{aligned}$$

(5)

That is,

$$\begin{aligned} \int _\mathbb {R}fLgd\mu =\int _\mathbb {R}gLfd\mu ,\quad \forall f,g\in C_c^2(\mathbb {R}). \end{aligned}$$

(6)

Let $\pi =\mu (\mathbb {R})^{-1}\mu$. Then, (6) implies that $\pi$ is an invariant probability measure of the process $(X_t)_{t\ge 0}$. The detailed proof is provided in Remark 1 at the end of this paper. This assertion also can be seen around Eq. (7.29) on page 172 in [5]. On the other hand, since a(x) is continuous on $\mathbb {R}$ and $a(x)>0$ for all $x\in \mathbb {R}$, it is well known that the process $(X_t)_{t\ge 0}$ is Lebesgue irreducible and has the strong Feller property. Hence, we can get the uniqueness of the invariant measure (see [6]; Theorem 4.2.1). Combining with both conclusions above, we find that the process $(X_t)_{t\ge 0}$ has the unique invariant probability measure $\pi$.

Indeed, due to the Girsanov transform of diffusion process (see [18]), one can see that the transition probability kernel $P_t(x,dy)$ of the SDE (4) is absolutely continuous with respect to each other, which in turn yields the unique invariant probability measure is absolutely continuous with respect to the Lebesgue measure.

3 The Existence of Phase Transitions

In this section, we prove that there exists a phase transition for the number of invariant probability measures of Eq. (1). Equation (1) can be regarded as a Mckean–Vlasov stochastic differential equation, and the existence and uniqueness of the solution can be proved by [21] (for specific verification one can see Remark 2).

In the following, we can refer to [1], which investigated the issue on the phase transition concerning a class of McKean–Vlasov SDEs. Once more, by the algebraic equation, which is based on the fact that the first moment of the solution process coincides with that of the invariant probability measure, the question on phase transition goes back to seek the number of roots.

Assume $(X_t)_{t\ge 0}$ is the unique solution of Eq. (1) and $\mu (t)=\mu (t,dx)$ is a measure on $\mathbb {R}$ with finite first moment $\lambda (t):=\int _\mathbb {R}x\mu (t,dx)$. Recall that a probability measure $\pi \in \mathscr {P}(\mathbb {R})$ is stationary if $\pi (B)=P^*_t\pi (B)=\int _BP^*_t(x,dy)\pi (dx)$ is not dependent on t, where $B\in \mathscr {B}(\mathbb {R})$. If $\pi =\pi (dx)$ is a stationary distribution of $(X_t)_{t\ge 0}$ with finite first moment $m:=\int _\mathbb {R}x\pi (dx)$, then we get $\mathbb {E}X_t=m$. Hence, Eq. (1) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle dX_t=\sqrt{2}dW_t+\big (\gamma m-4X_t^3+2\beta X_t\big )dt,\\ X_0=\xi . \end{array}\right. \end{aligned}$$

(7)

In fact, the stationary distribution $\pi$ can be given by (5):

$$\begin{aligned} \pi (dx)=\mu (dx)/Z, \end{aligned}$$

(8)

where

$$\begin{aligned} \mu (dx)=\exp [-x^4+\beta x^2+\gamma mx]dx,~~ Z=\int _\mathbb {R}\exp [-x^4+\beta x^2+\gamma mx]dx. \end{aligned}$$

Note that Z is well-defined, since it is defined by the integral on the whole real line and the exponent tends to $-\infty$ as x tends to $\infty$ . Then, the finiteness of the first moment gives us a condition

$$\begin{aligned} \int _\mathbb {R}x\exp [-x^4+\beta x^2+\gamma mx]dx=mZ=m\int _\mathbb {R}\exp [-x^4+\beta x^2+\gamma mx]dx<\infty . \end{aligned}$$

We have

$$\begin{aligned} f(m):=\int _\mathbb {R}(x-m)e^{-x^4+\beta x^2+\gamma mx}dx=0. \end{aligned}$$

(9)

Qualitative Analysis

Lemma 1

$$\begin{aligned}{} & {} \vert \mathscr {I}\vert :=\!\!\!\!\sharp \{\pi : \pi ~ \mathrm{{is~a~stationary~distribution\}}}\\{} & {} \quad =\!\!\!\!\sharp \{m\in [0,\infty ): m~\mathrm{{is~a~root~of}}~f(m)\}, \end{aligned}$$

where $\sharp$ represents the number of elements of the set.

Theorem 2

For Eq. (7), we suppose $\beta \ge 0$ and $\gamma \ne 0$.

• (1)  In the case of $\gamma >0$, there exists a critical value $\beta _c>0$ such that

  $$\begin{aligned} \vert \mathscr {I}\vert {\left\{ \begin{array}{ll} \ge 1 &{} in~any~case,\\ =1 &{} for~all~0<\beta \le \beta _c,\\ =3 &{} for~all~\beta>\beta _c>0. \end{array}\right. } \end{aligned}$$

  (10)

  This means that there exists phase transition for the solution of Eq. (7) when $\beta>\beta _c>0$.

• (2)  In the case of $\gamma <0$, there is no phase transition.

Proof

The proof adopts the idea of [20], Theorem 2.1]. Obviously, $f(m)=0$. Using the series expansion of $e^{\gamma mx}$, we have

$$\begin{aligned} f(m)=2\sum ^\infty _{n=0}\frac{I_\beta (2n)}{(2n)!}\gamma ^{2n}m^{2n+1}\Bigg [\frac{\gamma I_\beta (2n+2)}{(2n+1)I_\beta (2n)}-1\Bigg ], \end{aligned}$$

(11)

where

$$\begin{aligned} I_\beta (z):=\int _\mathbb {R_+}x^ze^{-x^4+\beta x^2}dx. \end{aligned}$$

In the case of $\gamma <0$, we have $\frac{\gamma I_\beta (2n+2)}{(2n+1)I_\beta (2n)}-1<0$. From (11) we get that when $m<0$, we have $f(m)>0$; when $m>0$, we have $f(m)<0$. Then f(m) has a unique zero point $m=0$, so there is no phase transition and the result of part (2) is proved.

Now we consider the case of $\gamma >0$. Note that when $\beta =0$, u(x) is not a double-well potential and there is no phase transition.

(a) We will prove that there exists an integer $n_0=n_0(\gamma ,\beta )$ such that for all $n\ge n_0$, $f^{(2n+1)}(0)\le 0$ and for all $n<n_0$, $f^{(2n+1)}(0)>0$. We introduce the quantity

$$\begin{aligned} R_n(\gamma ,\beta ):=\frac{\gamma I_\beta (2n+2)}{(2n+1)I_\beta (2n)}-1,~n\in \mathbb {N}. \end{aligned}$$

Integration by parts gives

$$\begin{aligned} (2n+1)I_\beta (2n)=\!\!\!\!{} & {} (2n+1)\int _{\mathbb {R_+}}x^{2n}e^{-x^4+\beta x^2}dx\\ =\!\!\!\!{} & {} 4I_\beta (2n+4)-2\beta I_\beta (2n+2), \end{aligned}$$

so

$$\begin{aligned} R_n(\gamma ,\beta )=\gamma \left[ \frac{4I_\beta (2n+4)}{I_\beta (2n+2)}-2\beta \right] ^{-1}-1. \end{aligned}$$

First, we will prove that for all $\beta >0$ and $\gamma >0$ the sequence $\{R_n(\gamma ,\beta )\}_{n\in \mathbb {N}}$ is nonincreasing. It is sufficient to prove that sequence $\{I_\beta (2n+4)/I_\beta (2n+2)\}_{n\in \mathbb {N}}$ is nondecreasing. For this, we put $T(x)=(I_\beta (x+2))/(I_\beta (x))$, $x>0$, then

$$\begin{aligned} T'(x)=T(x)\left( \frac{I'_\beta (x+2)}{I_\beta (x+2)}-\frac{I'_\beta (x)}{I_\beta (x)}\right) . \end{aligned}$$

For proving T(x) is nondecreasing, we only need to prove that $\zeta (x):=I'_\beta (x)/I_\beta (x)$ is nondecreasing since $T(x)\ge 0$ for all $x\in \mathbb {R}_+$. By Cauchy–Schwarz inequality, we have

$$\begin{aligned} \zeta '(y)=\!\!\!\!{} & {} \frac{\int _\mathbb {R_+}x^y(\ln x)^2e^{-x^4+\beta x^2}dx\int _\mathbb {R_+}x^ye^{-x^4+\beta x^2}dx}{\big (\int _\mathbb {R_+}x^ye^{-x^4+\beta x^2}dx\big )^2}\\{} & {} -\frac{\big (\int _\mathbb {R_+}x^y(\ln x)e^{-x^4+\beta x^2}dx\big )^2}{\big (\int _\mathbb {R_+}x^ye^{-x^4+\beta x^2}dx\big )^2}\ge 0,~\forall ~y>0. \end{aligned}$$

This means that $\big (R_n(\gamma ,\beta )\big )_{n\in \mathbb {N}}$ is nonincreasing for all $\beta >0$ and $\gamma >0$.

Now we prove that $R_n(\gamma ,\beta )\le 0$ for n large enough. To do this, it is sufficient to find a real a such that $f(a)\le 0$. Put $V(x):=x^4-(\beta +\frac{\gamma }{2})x^2$, take $a=\sqrt{\beta +\frac{\gamma }{2}}$, $y:=x-a$, it is easy to get that $V(y+a)\ge V(y-a)$ for all $y\ge 0$. So we have

$$\begin{aligned} f(a)=\!\!\!\!{} & {} e^{\frac{\gamma a^2}{2}}\int _\mathbb {R}(x-a)e^{-x^4+(\beta +\frac{\gamma }{2})x^2-\frac{\gamma }{2}(x-a)^2}dx\\ =\!\!\!\!{} & {} e^{\frac{\gamma a^2}{2}}\int ^{\infty }_{0}ye^{-\frac{\gamma y^2}{2}}\big [e^{-(y+a)^4+(\beta +\frac{\gamma }{2})(y+a)^2}-e^{-(y-a)^4+(\beta +\frac{\gamma }{2})(y-a)^2}\big ]dy\le 0. \end{aligned}$$

In conclusion, there exists $n\in \mathbb {N}$ such that $R_n(\gamma ,\beta )\le 0$.

Finally, put $n_0:=\min \big \{n:R_n(\gamma ,\beta )\le 0\big \}$. Since $R_n(\gamma ,\beta )$ and $f^{(2n+1)}(0)$ have the same sign, we deduce that $f^{(2n+1)}(0)\le 0$ for all $n\ge n_0$ and $f^{(2n+1)}(0)>0$ for all $n< n_0$.

(b) By the last step, we can write

$$\begin{aligned} f(m)=\sum ^{n_0-1}_{n=0}\frac{f^{(2n+1)}(0)}{(2n+1)!}m^{2n+1}-\sum ^\infty _{n=n_0}\frac{\vert f^{(2n+1)}(0)\vert }{(2n+1)!}m^{2n+1}. \end{aligned}$$

(12)

Taking out a common factor $m^{2n_0+1}$, we get

$$\begin{aligned} f(m)=m^{2n_0+1}\left\{ \sum ^{n_0-1}_{n=0}\frac{f^{(2n+1)}(0)}{(2n+1)!}m^{2(n-n_0)}-\sum ^\infty _{n=n_0}\frac{\vert f^{(2n+1)}(0)\vert }{(2n+1)!}m^{2(n-n_0)}\right\} . \end{aligned}$$

Since the function $m\rightarrow m^{2(n-n_0)}$ (resp. $m\rightarrow -m^{2(n-n_0)}$) is decreasing for all $n\le n_0-1$ (resp. $n\ge n_0$), we deduce that f(m) admits at most one positive zero point. The function f(m) is odd so it admits one or three zero points on $\mathbb {R}$. This means that Eq. (7) admits one or three invariant probability measures.

(c) Here we prove that the uniqueness of the invariant probability measure is directly related to the sign of $f'(0)$. Taking derivative in Eq. (12) and taking out a common factor $m^{2n_0}$, we get

$$\begin{aligned} f'(m)=m^{2n_0}\left\{ \sum ^{n_0-1}_{n=0}\frac{f^{(2n+1)}(0)}{(2n)!}m^{2(n-n_0)}-\sum ^\infty _{n=n_0}\frac{\vert f^{(2n+1)}(0)\vert }{(2n)!}m^{2(n-n_0)}\right\} . \end{aligned}$$

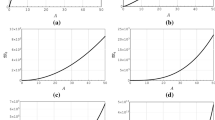
By an argument similar to that in the paragraph above, we deduce that $f'(m)$ vanishes at most one point on $\mathbb {R_+}$. Because $f'(m)$ tends to $-\infty$ when m goes to infinity, this means that $f'(m)$ is either always nonpositive or positive then nonpositive. This means that the behavior of f(m) is related to the sign of $f'(0)$, as is shown in Figs. and .

• For $f'(0)\le 0$, f(m) is nonincreasing on $\mathbb {R_+}$. Since $f(0)=0$, f(m) does not vanish on $\mathbb {R_+}$, so Eq. (7) admits a unique invariant probability measure $\pi (dx)$ such that $\int _{\mathbb {R}}x\pi (dx)=0$.

• For $f'(0)>0$, f(m) is first increasing then nonincreasing on $\mathbb {R_+}$, which admits three zeros 0, $m_0>0$ and $-m_0$. Thus, we have three invariant probability measures $\pi _0(dx),~\pi _+(dx)$, and $\pi _-(dx)$ such that $\int _{\mathbb {R}}x\pi (dx)=0$, $\int _{\mathbb {R}}x\pi _+(dx)=m_0>0$, and $\int _{\mathbb {R}}x\pi _-(dx)=-m_0<0$.

Fig. 2

One zero

Fig. 3

Three zeros

(d) Now we study the sign of $f'(0)$. For all $\beta >0$ and $\gamma >0$, we put

$$\begin{aligned} f'(0)=\int _\mathbb {R}(\gamma x^2-1)e^{-x^4+\beta x^2}dx=0. \end{aligned}$$

(13)

It is easy to see that $\gamma$ is a function of $\beta$,

$$\begin{aligned} \gamma (\beta )=\frac{\int _\mathbb {R}e^{-x^4+\beta x^2}dx}{\int _\mathbb {R}x^2e^{-x^4+\beta x^2}dx}. \end{aligned}$$

By the Cauchy–Schwarz inequality, we get

$$\begin{aligned} \gamma '(\beta )=\frac{\big (\int _\mathbb {R}x^2e^{-x^4+\beta x^2}dx\big )^2}{\big (\int _\mathbb {R}x^2e^{-x^4+\beta x^2}dx\big )^2}-\frac{\big (\int _\mathbb {R}e^{-x^4+\beta x^2}dx\big )\big (\int _\mathbb {R}x^4e^{-x^4+\beta x^2}dx\big )}{\big (\int _\mathbb {R}x^2e^{-x^4+\beta x^2}dx\big )^2}\le 0. \end{aligned}$$

Therefore, $\gamma (\beta )$ is decreasing for all $\beta >0$. Thus, for any fixed $\gamma _c>0$, there exists a unique $\beta _c>0$ such that $f'(0)=0$.

For all $0<\beta \le \beta _c$, we have $\gamma \ge \gamma _c$. This yields

$$\begin{aligned} f'(0)=\int _\mathbb {R}(\gamma _cx^2-1)e^{-x^4+\beta x^2}dx\le \int _\mathbb {R}(\gamma x^2-1)e^{-x^4+\beta x^2}dx=0, \end{aligned}$$

we obtain that the solution of Eq. (7) has a unique invariant probability measure.

For all $\beta >\beta _c$, we have $\gamma <\gamma _c$ then

$$\begin{aligned} f'(0)=\int _\mathbb {R}(\gamma _cx^2-1)e^{-x^4+\beta x^2}dx>\int _\mathbb {R}(\gamma x^2-1)e^{-x^4+\beta x^2}dx=0, \end{aligned}$$

so there are three invariant probability measures. The proof is complete. $\square$

Quantitative Analysis

Theorem 2 implies that when $\gamma <0$, there is no phase transition. So we only consider the case of $\gamma >0$.

Theorem 3

For Eq. (7), we assume $\beta >0$ and $\gamma >0$. Then there exists a critical value $\beta _{c}=\frac{12-\gamma ^2}{2\gamma }>0$ such that

• (i)  For $0<\gamma <2\sqrt{3}$ and $\beta >\beta _c$, or $\gamma \ge 2\sqrt{3}$ and $\beta >0$, there exist three invariant probability measures $\{\pi _s:s=0,\pm \}$. In this case, there exists phase transition for the solution of Eq. (7).

• (ii)  For $0<\gamma <2\sqrt{3}$ and $0<\beta \le \beta _c$, there exists unique invariant probability measure: $\pi _0$. Here,

  $$\begin{aligned} m_0=0,~~m_\pm =\pm \frac{1}{2}\sqrt{(\gamma ^2+2\beta \gamma -12)/\gamma }, \\ \mu _s(dx)=\exp [-x^4+\beta x^2+\gamma m_sx]dx, \\ \pi _s(dx)=\mu _s(dx)/\mu _s(\mathbb {R}),~~s=0,~\pm . \end{aligned}$$

As shown in Fig. , the shaded areas are phase transition areas and others are ergodic ones.

Fig. 4

The image of phase transition areas

Proof

Since

$$\begin{aligned} X_t=X_0-4\int ^t_0X_s^3ds+2\beta \int ^t_0X_sds+\gamma \int ^t_0\mathbb {E}X_sds+\sqrt{2}W_t, \end{aligned}$$

(14)

by Eq. (9) we have

$$\begin{aligned} \int _\mathbb {R}xe^{-x^4+\beta x^2+\gamma mx}dx=\int _\mathbb {R}me^{-x^4+\beta x^2+\gamma mx}dx. \end{aligned}$$

(15)

Taking the derivative of both sides of the above equation with respect to m, we have

$$\begin{aligned} \!\!\!\!\!\!\!\!{} & {} \gamma \int _\mathbb {R}x^2e^{-x^4+\beta x^2+\gamma mx}dx\\ =\!\!\!\!{} & {} \int _\mathbb {R}e^{-x^4+\beta x^2+\gamma mx}dx+\gamma m\int _\mathbb {R} xe^{-x^4+\beta x^2+\gamma mx}dx, \end{aligned}$$

This and Eq. (15) imply

$$\begin{aligned} \gamma \int _\mathbb {R}x^2e^{-x^4+\beta x^2+\gamma mx}dx=(\gamma m^2+1)\int _\mathbb {R}e^{-x^4+\beta x^2+\gamma mx}dx. \end{aligned}$$

Taking the derivative again, we get

$$\begin{aligned} \!\!\!\!\!\!\!\!{} & {} \gamma ^2\int _\mathbb {R}x^3e^{-x^4+\beta x^2+\gamma mx}dx\\ =\!\!\!\!{} & {} 2\gamma m\int _\mathbb {R}e^{-x^4+\beta x^2+\gamma mx}dx+\gamma (\gamma m^2+1)\int _\mathbb {R}xe^{-x^4+\beta x^2+\gamma mx}dx, \end{aligned}$$

and from Eq. (15) we obtain

$$\begin{aligned} \gamma ^2\int _\mathbb {R}x^3e^{-x^4+\beta x^2+\gamma mx}dx=(\gamma ^2m^3+3\gamma m)\int _\mathbb {R}e^{-x^4+\beta x^2+\gamma mx}dx. \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{\int _\mathbb {R}x^3e^{-x^4+\beta x^2+\gamma mx}dx}{\int _\mathbb {R}e^{-x^4+\beta x^2+\gamma mx}dx}=\frac{\gamma m^3+3m}{\gamma }, \end{aligned}$$

that is

$$\begin{aligned} \mathbb {E}X_t^3=\frac{\gamma m^3+3m}{\gamma }. \end{aligned}$$

Taking the expectation of both sides of Eq. (14), we get

$$\begin{aligned} \mathbb {E}X_t=\mathbb {E}X_0-4\int ^t_0\mathbb {E}X_s^3ds+2\beta \int ^t_0\mathbb {E}X_sds+\gamma \int ^t_0\mathbb {E}X_sds. \end{aligned}$$

$\mathbb {E}X_t=m$ and $\mathbb {E}X_t^3=\frac{\gamma m^3+3m}{\gamma }$ imply

$$\begin{aligned} m[4\gamma m^2+12-2\beta \gamma -\gamma ^2]=0. \end{aligned}$$

(16)

By Eq. (16), we have

$$\begin{aligned} m=0~~\textrm{or}~~m^2=\frac{\gamma ^2+2\beta \gamma -12}{4\gamma }. \end{aligned}$$

Put

$$\begin{aligned} g(\gamma ,\beta ):=\frac{\gamma ^2+2\beta \gamma -12}{4\gamma }. \end{aligned}$$

Let $g(\gamma ,\beta )=0$, we have a critical value of $\beta$

$$\begin{aligned} \beta _c=\beta _c(\gamma ):=\frac{12-\gamma ^2}{2\gamma }. \end{aligned}$$

For $g(\gamma ,\beta )>0$, Eq. (16) has three real solutions:

$$\begin{aligned} m_0=0~~m_\pm =\pm \frac{1}{2}\sqrt{(\gamma ^2+2\beta \gamma -12)/\gamma }. \end{aligned}$$

Otherwise Eq. (16) has a unique real solution: $m_0=0$. The specific analysis is as follows.

• For $0<\gamma <2\sqrt{3}$ and $\beta >\beta _c$, or $\gamma \ge 2\sqrt{3}$ and $\beta >0$, we have $g(\gamma ,\beta )>0$.

• For $0<\gamma <2\sqrt{3}$ and $0<\beta \le \beta _c$, we have $g(\gamma ,\beta )\le 0$.

If $g(\gamma ,\beta )>0$, then there exist three invariant probability measures:

$$\begin{aligned} \pi _0(dx)=\frac{\exp [-x^4+\beta x^2]dx}{\int _\mathbb {R}\exp [-y^4+\beta y^2]dy},~~\pi _\pm (dx)=\frac{\exp [-x^4+\beta x^2+\gamma m_\pm x]dx}{\int _\mathbb {R}\exp [-y^4+\beta y^2+\gamma m_\pm y]dx}. \end{aligned}$$

Thus, there exists phase transition for the solution of Eq. (7).

If $g(\gamma ,\beta )\le 0$, then there exists unique invariant probability measure:

$$\begin{aligned} \pi _0(dx)=\frac{\exp [-x^4+\beta x^2]dx}{\int _\mathbb {R}\exp [-y^4+\beta y^2]dy}. \end{aligned}$$

The proof is complete. $\square$

4 Asymptotic Behavior

When $\gamma =0$, Eq. (7) degenerates into the following stochastic differential equation:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle dY_t=\sqrt{2}dW_t+(2\beta Y_t-4Y_t^3)dt,\\ Y_0=\xi . \end{array}\right. \end{aligned}$$

(17)

The existence and uniqueness of the solution $Y_t$ are obvious, and we have the unique invariant probability measure

$$\begin{aligned} \pi _0(dx)=\frac{\exp [-x^4+\beta x^2]dx}{\int _\mathbb {R}\exp [-y^4+\beta y^2]dy}. \end{aligned}$$

For Eq. (7) in order to emphasize $\gamma$, we write $X(t)=X_\gamma (t)$. Let $\pi _\gamma$ denote the invariant probability measure of $X_\gamma (t)$. We shall use the following lemma to study the convergence of $\pi _\gamma$ in Wasserstein distance (see [2]; Theorem 5.6).

Lemma 4

$\pi _\gamma {\mathop {\longrightarrow }\limits ^{W_\theta }}\pi _0$ as $\gamma \rightarrow 0$ iff the following two conditions

• 1. $\pi _\gamma {\mathop {\longrightarrow }\limits ^{w}}\pi _0$ as $\gamma \rightarrow 0$,

• 2. $\int _\mathbb {R}{\vert x-x_0\vert }^\theta \pi _\gamma (dx)\rightarrow \int _\mathbb {R}{\vert x-x_0\vert }^\theta \pi _0(dx)$ for some (or any) $x_0\in \mathbb {R}$ as $\gamma \rightarrow 0$

hold.

Given $\xi \in L^2(\Omega ,\mathscr {F}_0,\mathbb {P};\mathbb {R})$, as $\gamma \rightarrow 0$, we have the following theorem.

Theorem 5

We claim that

• 1. $\lim _{\gamma \rightarrow 0}\mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)-Y(t)\vert }^2=0,~~\forall ~T>0.$

• 2. $\pi _\gamma {\mathop {\longrightarrow }\limits ^{W_\theta }}\pi _0$ as $\gamma \rightarrow 0$.

Proof

(1) By Itô’s formula, we obtain

$$\begin{aligned} {\vert X_\gamma (t)-Y(t)\vert }^2=\!\!{} & {} 2\int ^t_0\langle X_\gamma (s)-Y(s), -4(X^3_\gamma (s)-Y^3(s))\\{} & {} +2\beta (X_\gamma (s)-Y(s))+\gamma \mathbb {E}X_\gamma (s)\rangle dt\\ \le \!\!{} & {} 4\beta \int ^t_0{\vert X_\gamma (s)-Y(s)\vert }^2ds+2\gamma \int ^t_0\vert \mathbb {E}X_\gamma (s)\vert \vert X_\gamma (s)-Y(s)\vert ds\\ \le \!\!{} & {} (4\beta +\gamma )\int ^t_0{\vert X_\gamma (s)-Y(s)\vert }^2ds+\gamma \int ^t_0{\vert \mathbb {E}X_\gamma (s)\vert }^2ds. \end{aligned}$$

For any $T>0$, we have

$$\begin{aligned} \mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)-Y(t)\vert }^2\le \!\!\!\!{} & {} (4\beta +\gamma )\int ^T_0\mathbb {E}\sup _{s\le t}{\vert X_\gamma (s)-Y(s)\vert }^2dt+\gamma \int ^T_0\sup _{s\le t}\mathbb {E}{\vert X_\gamma (s)\vert }^2dt. \end{aligned}$$

Gronwall’s inequality yields

$$\begin{aligned} \mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)-Y(t)\vert }^2 \le \!\!\!\!{} & {} e^{(4\beta +\gamma )T}\gamma \int ^T_0\sup _{s\le t}\mathbb {E}{\vert X_\gamma (s)\vert }^2dt\nonumber \\ \le \!\!\!\!{} & {} e^{(4\beta +\gamma )T}\gamma T\mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)\vert }^2. \end{aligned}$$

(18)

Using the fact $\vert x-y\vert ^2\le 2(\vert x\vert ^2+\vert y\vert ^2)$ and putting $x=X_\gamma -Y$, $y=-Y$, we obtain

$$\begin{aligned} \mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)\vert }^2 \le \!\!\!\!{} & {} 2\left( \mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)-Y(t)\vert }^2+\mathbb {E}\sup _{t\le T}{\vert Y(t)\vert }^2\right) \\ \le \!\!\!\!{} & {} 2\left( e^{(4\beta +\gamma )T}\gamma T\mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)\vert }^2+\mathbb {E}\sup _{t\le T}{\vert Y(t)\vert }^2\right) . \end{aligned}$$

It follows that there exists $\gamma _0>0$ such that we have

$$\begin{aligned} \mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)\vert }^2\le 2(1-2e^{(4\beta +\gamma )T}\gamma T)^{-1}\mathbb {E}\sup _{t\le T}{\vert Y(t)\vert }^2<\infty ,~~~\gamma \le \gamma _0. \end{aligned}$$

Here we used the fact that, due to $\xi \in L^2(\Omega ,\mathscr {F}_0,\mathbb {P};\mathbb {R})$ there exists $\alpha \ge 0$ such that $\mathbb {E}{\vert Y(t)\vert }^2\le \alpha (1+\mathbb {E}\vert \xi \vert ^2)<\infty$ for any $t\in [0,T].$ Thus,

$$\begin{aligned} \sup _{0<\gamma \le \gamma _0}\mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)\vert }^2<\infty . \end{aligned}$$

Finally, by (18) we obtain

$$\begin{aligned} \lim _{\gamma \rightarrow 0}\mathbb {E}\sup _{t\le T}{\vert X_\gamma (t)-Y(t)\vert }^2=0. \end{aligned}$$

(2) (a) For any $f\in C_b(\mathbb {R})$, assume $\vert f(x)\vert \le M$ for all $x\in \mathbb {R}$, then by dominated convergence theorem and

$$\begin{aligned} \lim _{\gamma \rightarrow 0}\pi _\gamma (x)=\!\!\!\!{} & {} \lim _{\gamma \rightarrow 0}\exp [-x^4+\beta x^2+\gamma mx]\left[ \int _\mathbb {R}\exp [-y^4+\beta y^2+\gamma my]dy\right] ^{-1}\\ =\!\!\!\!{} & {} \exp [-x^4+\beta x^2]\left[ \int _\mathbb {R}\exp [-y^4+\beta y^2]dy\right] ^{-1}=\pi _0(x), \end{aligned}$$

we have

$$\begin{aligned} \lim _{\gamma \rightarrow 0}\left| \int _\mathbb {R}f(x)\pi _\gamma (dx)-\int _\mathbb {R}f(x)\pi _0(dx)\right| \!\!\!\!{} & {} \le M\lim _{\gamma \rightarrow 0}\int _\mathbb {R}\vert \pi _\gamma (x)-\pi _0(x)\vert dx\\ \!\!\!\!{} & {} =M\int _\mathbb {R}\lim _{\gamma \rightarrow 0}\vert \pi _\gamma (x)-\pi _0(x)\vert dx=0. \end{aligned}$$

Thus, we have $\pi _\gamma {\mathop {\longrightarrow }\limits ^{w}}\pi _0$.

(b) We still need to prove that $\int _\mathbb {R}{\vert x-x_0\vert }^\theta \pi _\gamma (dx)\rightarrow \int _\mathbb {R}{\vert x-x_0\vert }^\theta \pi _0(dx)$ as $\gamma \rightarrow 0$. Choosing $x_0=0$ and put

$$\begin{aligned} g_\gamma (x)=\frac{{\vert x\vert }^\theta \exp [-x^4+\beta x^2+\gamma mx]}{\int _\mathbb {R}\exp [-y^4+\beta y^2+\gamma my]dy}, \\ g_0(x)=\frac{{\vert x\vert }^\theta \exp [-x^4+\beta x^2]}{\int _\mathbb {R}\exp [-y^4+\beta y^2]dy}. \end{aligned}$$

The dominated convergence theorem yields that

$$\begin{aligned} \lim _{\gamma \rightarrow 0}\int _\mathbb {R}g_\gamma (x)dx=\int _\mathbb {R}g_0(x)dx. \end{aligned}$$

By Lemma 4.1, we have $\pi _\gamma {\mathop {\longrightarrow }\limits ^{W_\theta }}\pi _0$ as $\gamma \rightarrow 0$. The proof is complete. $\square$

Remark 1

In the Eq. (6), for any $f,~g\in C_c^2(\mathbb {R}),$

$$\begin{aligned}{} & {} \int _\mathbb {R}gLfd\mu \\ =\!\!\!\!{} & {} \int _\mathbb {R}\left[ b(x)f'(x)g(x)+a(x)f''(x)g(x)\right] \frac{1}{a(x)}\exp {\left( \int _0^x\frac{b(y)}{b(x)}dy\right) }dx\\ =\!\!\!\!{} & {} \int _\mathbb {R}\frac{b(x)}{a(x)}f'(x)g(x)\exp {\left( \int _0^x\frac{b(y)}{a(y)}dy\right) }dx+\int _\mathbb {R}f''(x)g(x)\exp {\left( \int _0^x\frac{b(y)}{a(y)}dy\right) }dx\\ =:\!\!\!\!{} & {} \mathrm{{I+II}}. \end{aligned}$$

Using integration by parts, we get

$$\begin{aligned} \mathrm{{I}}\!\!\!\!{} & {} =\int _\mathbb {R}\frac{b(x)}{a(x)}g(x)\exp {\left( \int _0^x\frac{b(y)}{a(y)}dy\right) }df(x)\\ \!\!\!\!{} & {} =-\int _\mathbb {R}f(x)\left[ \frac{b'(x)a(x)-a'(x)b(x)+b ^2(x)}{a^2(x)}g(x)+\frac{b(x)}{a(x)}g'(x)\right] \exp {\left( \int _0^x\frac{b(y)}{a(y)}dy\right) }dx, \end{aligned}$$

and

$$\begin{aligned} \mathrm{{II}}\!\!\!\!{} & {} =\int _\mathbb {R}g(x)\exp {\left( \int _0^x\frac{b(y)}{a(y)}dy\right) }df'(x)\\ \!\!\!\!{} & {} =-\int _\mathbb {R}f'(x)\left[ g'(x)+\frac{b(x)}{a(x)}\right] \exp {\left( \int _0^x\frac{b(y)}{a(y)}dy\right) }dx. \end{aligned}$$

Therefore,

$$\begin{aligned} \int _\mathbb {R}gLfd\mu =-\int _\mathbb {R}\left[ \frac{ab'-a'b+b^2}{a^2}fg+\frac{b}{a}fg'+\frac{b}{a}f'g+f'g'\right] (x)\exp {\left( \int _0^x\frac{b(y)}{a(y)}dy\right) }dx. \end{aligned}$$

In the same way, we obtain that the left hand of Eq. (6) is equal to the same formula and Eq. (6) is verified.

Let $(P_t)_{t\ge 0}$ denote the family of transition probability of the process $(X_t)_{t\ge 0}$. Since $(X_t)_{t\ge 0}$ is unique, Eq. (6) is equivalent to

$$\begin{aligned} \int _\mathbb {R}f(x)P_tg(x)\mu (dx)=\int _\mathbb {R}g(x)P_tf(x)\mu (x),\quad \forall f,g\in C_c^2(\mathbb {R}). \end{aligned}$$

Taking $g(x)=\mathrm{{I}}_{\mathbb {R}}(x)$, one can get $P_tg(x)=1$, and then

$$\begin{aligned} \int _\mathbb {R}f(x)\mu (dx)=\int _\mathbb {R}P_tf(x)\mu (x),\quad \forall f\in C_c^2(\mathbb {R}), \end{aligned}$$

which means that $\mu$ is an invariant measure. Thus, we get an invariant probability measure $\pi =\mu (\mathbb {R})^{-1}\mu$.

Remark 2

 At first, for the existence and uniqueness of Eq. (1), we need prove that the coefficients satisfy conditions $({\textbf {H1}})-({\textbf {H3}})$ of Theorem 2.1 in [21]. Note that assumption $({\textbf {H1}})$ holds obviously, thus it is sufficient to prove assumptions $({\textbf {H1}})$ and $({\textbf {H3}})$ hold.

Denote $b(x,\mu )=-4x^3+2\beta x+\gamma \mu (\vert \cdot \vert )$, then for any $x,y\in \mathbb {R},~\mu ,\nu \in \mathscr {P}_1$, we have $({\textbf {H2}})$ (Monotonicity)

$$\begin{aligned} \!\!\!\!{} & {} 2\langle b(x,\mu )-b(y,\nu ),x-y\rangle \\ =\!\!\!\!{} & {} 2\langle -4x^3+2\beta x+\gamma \mu (\vert \cdot \vert )+4y^3-2\beta y-\gamma \nu ({\vert \cdot \vert }),x-y\rangle \\ \le \!\!\!\!{} & {} -8{\vert x-y\vert }^2\cdot {\vert x^2+xy+y^2\vert }+4\beta {\vert x-y\vert }^2\\{} & {} +2\vert \gamma \vert \cdot \left| \int _\mathbb {R}\vert x\vert \mu (dx)-\int _\mathbb {R}\vert y\vert \nu (dy)\right| \cdot {\vert x-y\vert }. \end{aligned}$$

Note that for any coupling $\pi$ of $\mu$ and $\nu$, it is easy to see that

$$\begin{aligned} \left| \int _\mathbb {R}\vert x\vert \mu (dx)-\int _\mathbb {R}\vert y\vert \nu (dy)\right| =\!\!\!\!{} & {} \left| \int _{\mathbb {R}\times \mathbb {R}}\vert x\vert \pi (dx,dy)-\int _{\mathbb {R}\times \mathbb {R}}\vert y\vert \pi (dx,dy)\right| \\ \le \!\!\!\!{} & {} \int _{\mathbb {R}\times \mathbb {R}}\vert x-y\vert \pi (dx,dy). \end{aligned}$$

Since the $\pi$ is arbitrary, taking the infimum over all coupling $\pi$, we obtain that

$$\begin{aligned} 2\langle b(x,\mu )-b(y,\nu ),x-y\rangle \le 4\beta {\vert x-y\vert }^2+2\vert \gamma \vert \mathbb {W}_1(\mu ,\nu )\cdot {\vert x-y\vert }. \end{aligned}$$

$({\textbf {H3}})$ (Growth)

$$\begin{aligned} \vert b(0,\mu )\vert =\vert \gamma \vert \mu ({\vert \cdot \vert })\le \vert \gamma \vert \big [1+\mu ({\vert \cdot \vert })\big ]. \end{aligned}$$

Next, when we say the strong solution, it needs a jointly continuous the spatial and time like Theorem 2.2 in [21]. Thus it is enough to prove that, for any $x,y\in \mathbb {R},~\mu ,\nu \in \mathscr {P}_3$, the following condition holds:

$$\begin{aligned} \left| b(x,\mu )\right| \le \!\!\!\!{} & {} 4\vert x\vert ^3+2\beta \vert x\vert +\vert \gamma \vert \int _\mathbb {R}\vert x\vert \mu (dx)\\ \le \!\!\!\!{} & {} 4\vert x\vert ^3+2\beta \left( \frac{\vert x\vert ^3}{3}+\frac{2}{3}\right) +\vert \gamma \vert \int _\mathbb {R}\left( \frac{\vert x\vert ^3}{3}+\frac{2}{3}\right) \mu (dx)\\ \le \!\!\!\!{} & {} \frac{4\beta +2\vert \gamma \vert }{3}+\left( 4+\frac{2\beta }{3}\right) \vert x\vert ^3+\frac{\vert \gamma \vert }{3}\int _\mathbb {R}\vert x\vert ^3\mu (dx)\\ \le \!\!\!\!{} & {} K\left[ 1+\vert x\vert ^3+\mu (\vert \cdot \vert ^3)\right] , \end{aligned}$$

where $K=\max \{\frac{4\beta +2\vert \gamma \vert }{3}, 4+\frac{2\beta }{3}, \frac{\vert \gamma \vert }{3}\}$, and here we have used the Young-inequality.