1 Introduction

Stochastic processes for the description of finite-velocity random motions have been widely studied during the last decades. Typically, they refer to the motion of a particle moving with finite speed on the real line, or on more general domains, and alternating between various possible velocities or directions at random times. The basic model is pertaining the so-called (integrated) telegraph process, in which the changes of directions of the two possible velocities are governed by the Poisson process (see, for instance, Orsingher [29] and Beghin et al. [2]). Various generalizations of the basic model have been proposed in the past. See, for instance, the one-dimensional random evolution where the new velocity is determined by the outcome of a random trial, cf. Crimaldi et al. [6]. Recent developments in this area are devoted to determining the exact distributions of the maximum of the telegraph process (see Cinque and Orsingher [4]), to analyze telegraph random evolutions on a circle (cf. De Gregorio and Iafrate [8]), to investigate the telegraph process driven by gamma components (cf. Martinucci et al. [28]), and to study the squared telegraph process (see Ratanov et al. [38] and Martinucci and Meoli [27]). Further investigations have been oriented to study generalized telegraph equations and random flights in higher dimensions (cf. Pogorui and Rodríguez-Dagnino [33,34,35] and De Gregorio [7]), telegraph-type reinforced random-walk models leading to superdiffusion (cf. Fedotov et al. [14]), and the Ornstein-Uhlenbeck process of bounded variation with underlying an integrated telegraph process (cf. Ratanov [37]).

Several studies on the telegraph and related processes have been developed in the physics community, since from the very first contributions in the area of finite-velocity random motions due to Goldstein [16] and Kac [19]. Recently, there has been a resurgence of the study of the telegraph process in the physics literature in the context of active matter, where the process is also known as the run-and-tumble particle motion. As a recent contribution in this area we recall the paper by Malakar et al. [26], that is devoted to the determination of the exact probability distribution of a run-and-tumble particle perturbed by Gaussian white noise in one dimension. Here, the authors focus also on the analysis of the relaxation to the steady-state and on certain first-passage-time problems. Moreover, similar problems have been faced in Dhar et al. [9] for a run-and-tumble particle subjected to confining potentials of the type \(V (x) = \alpha \vert x\vert ^p\), with \(p > 0\). An extension of the analysis performed in the previous articles can be found in Santra et al. [40], where a run-and-tumble particle running in two spatial dimensions is considered.

A fruitful research line related to finite-velocity random evolution has been stimulated by applications to insurance and mathematical finance (cf. the books by Rolsky et al. [39], Kolesnik and Ratanov [20], and Swishchuk et al. [42]), since the alternating random behavior of the relevant stochastic processes are especially suitable to describe the floating behaviour of the prices of risky assets observed in financial markets. See, for instance, the model based on the geometric telegraph process by Di Crescenzo and Pellerey [12], the refinement characterized by alternating velocities and jumps introduced in Lopez and Ratanov [25], and the transformed telegraph process for the pricing of European call and put options (cf. Pogorui et al. [36]).

Several real-world applications involve inter-arrival time statistics analogous to those of the counting processes governing the finite-velocity random motions of interest. An example related to the nonhomogeneous Poisson process for the earthquakes occurrences is given in Shcherbakov et al. [41]. Another application in geoscience is related to the Brownian motion process driven by a generalized telegraph process for the description of the vertical motions in the Campi Flegrei volcanic region (see Travaglino et al. [43]).

Moreover, stochastic processes for finite-velocity motions are largely used in biomathematics, motivated by the need of describing a variety of random movements performed by cells, micro-organisms and animals. For instance, Garcia et al. [15] investigate random motions of Daphnia where the animal, while foraging for food, performs a correlated random walk in two dimensions formed by a sequence of straight line hops, each followed by a pause, and a change of direction through a turning angle. See also Hu et al. [17] for a Brownian motion governed by a telegraph process adopted as a moving-resting model for the movements of predators with long inactive periods.

In this area, finite-velocity planar random motions are suitable to model the alternation of particle movements and changes of direction at random times. Then, large efforts have been employed to develop mathematical tools for the determination of the related exact probability laws. For instance, we recall the study of cyclic motions in \({\mathbb {R}}^2\) (cf. Orsingher [30, 31] for the case of exponential times between changes of direction, and Di Crescenzo et al. [10] for the case of Erlang times). Moreover, symmetry properties related to the particle’s motion in \({\mathbb {R}}^2\) are investigated in Kolesnik and Turbin [21]. The probability law of the motion of a particle performing a cyclic random motion in \({\mathbb {R}}^n\) is determined in Lachal [22], while a minimal cyclic random motion is studied in Lachal et al. [23]. The evaluation of the conditional probabilities in terms of order statistics has been successfully applied in the case of planar cyclic random motions with orthogonal directions by Orsingher et al. [32]. A particular case involving orthogonal directions switching at times regulated by a Poisson process is assessed by Leorato et al. [24], whereas a similar model governed by a non-homogeneous Poisson process is treated in Cinque et al. [5].

Several attempts finalized to extend the basic variants of the telegraph process have been performed in the recent years along the generalization or modification of the underlying Poisson process. However, only few instances allow to construct solvable and tractable models of random motions. For instance, see Iacus [18] where the number of velocity switches follows a suitable non-homogeneous Poisson process whose time-varying intensity is the hyperbolic tangent function.

Stimulated by the previous results and motivated by possible applications, in this paper we propose a new paradigm for the underlying point process in suitable instances of the telegraph process. Specifically, we refer to finite-velocity random motions in \({\mathbb {R}}\) and \({\mathbb {R}}^2\), with 2 and 3 velocities alternating cyclically, respectively, where the number of displacements of the motion along each possible direction follows a Geometric Counting Process (GCP) (see, for instance, Cha and Finkelstein [3]).

This new scheme is motivated by the fact that the memoryless property of the times separating successive events in real phenomena represents an exceptional situation, while in many concrete cases their distributions are characterized by heavy tails. Accordingly, the proposed study is finalized to extend the analysis of the classical telegraph process to cases in which the intertimes between velocity changes –instead of the typical exponential distribution– possess an heavy-tailed distribution, such as the modified Pareto distribution concerning the GCP. Moreover, the proposed stochastic processes provide new models for the description of phenomena that are no more governed by hyperbolic PDE’s as the classical telegraph equation. Another point of strength of the present study is the construction of new solvable models of random motion, whose probability laws are obtained in closed and tractable form.

Differently from the classical telegraph process, whose probability density under the Kac’s limiting conditions tends to the Gaussian transition function of Brownian motion, the processes under investigations exhibit a different behaviour. In particular, a noteworthy result of this paper shows that when the parameters of underlying GCP tend to infinity, the probability density of the process tend to (i) a uniform distribution in the one-dimensional case, and (ii) a three-peaked distribution in two-dimensional case.

In detail, we firstly study the process \(\{(X(t),V(t)) \; t\in {\mathbb {R}}_0^+\}\), with state space \({\mathbb {R}} \times \{\vec {v}_1, \vec {v}_2\}\), which represents the motion of a particle on the real line, with alternating velocities \(v_1 > v_2\). As customary, such process has two components: a singular component, corresponding to the case in which there are no velocity switches, and an absolutely continuous component, related to the motion of the particle when the velocity changes at least once. Secondly, we analyze the process \(\{(X(t),Y(t),V(t)), \; t \in {\mathbb {R}}_0^+)\}\), with state-space \({\mathbb {R}}^2 \times \{\vec {v}_1, \vec {v}_2, \vec {v}_3\}\), which describes a particle performing a planar motion with three specific directions. Once defined the region \({\mathcal {R}}(t)\) representing all the possible positions of the particle at a given time, the probability law shows that the distribution of this process is a mixture of two discrete components, describing the situations in which the particle is found on the boundary of the region, and an absolutely continuous part, related to the motion of the particle in the interior of \({\mathcal {R}}(t)\). This type of two-dimensional process well describes the motion of the particle in a turbulent medium, for example, in the presence of a vortex.

This is the plan of the paper. In Sect. 2, we formally describe the process X(t) illustrating some preliminary results on the transition densities in a more general case. In Sect. 3, assuming that the random intertimes between consecutive changes of directions are governed by a geometric counting process (GCP), after the construction of the stochastic model we obtain the formal expression of the probability laws and the moments of the process conditional on the initial velocity \(\vec {v}_1\). In particular, we determine the probability distribution of X(t) and study some limit results when the initial velocity is random. We also show that, when the parameters of the intertimes between velocity changes tend to infinity, the distribution of X(t) tends to be uniform over the relevant diffusion interval. Finally, in Sect. 4, we study a planar random motion determining the exact transition probability density functions of the process when the initial velocity is \(\vec {v}_1\). We investigate the stochastic process and the probability laws of the process with underlying geometric counting process (GCP). As example, we analyze a special case with three fixed cyclic directions. Also in this case we discuss the limiting distribution of the process when the parameters of the intertimes tend to infinity. Differently from the one-dimensional case, the distribution of the planar process tends to a non-uniform distribution characterized by three peaks.

Throughout the paper we assume that \(\sum _{i=1}^0a_i=0\) and \(\prod _{i=1}^0a_i=1\), as customary.

2 A Finite Two-Velocities Random Motion

We consider a particle that starts at the origin of the real line and that proceeds alternately with two velocities \(\vec {v}_1\) and \(\vec {v}_2\). The magnitude of the vector \(\vec {v}_j\) is denoted as \(|\vec {v}_j|=v_j\), with \(j=1,2\) and \(v_1 > v_2\). The direction of the particle motion is determined at each instant by the sign of the velocity, so that it is forward, stationary or backward if \(v_j>0\), \(v_j=0\) or \(v_j<0\), respectively.

Let \(D_{j,k}\), with \(j=1,2\), be the duration of the k-th time intervals during which the motion proceeds with velocity \(\vec {v}_j\). Let \({\mathbb {N}}=\{1,2,\ldots \}\). We assume that \(\{D_{j,k}, \; k\in {\mathbb {N}}\}_{j=1,2}\) are mutually independent sequences of nonnegative and possibly dependent absolutely continuous random variables. With reference to the intertimes \(D_{j,k}\), for all \(x\in {\mathbb {R}}\) we denote the distribution function by \(F_{D_{j,k}}(x)={\mathbb {P}}(D_{j,k}\le x)\), the survival function by \({\overline{F}}_{D_{j,k}}(x)=1-F_{D_{j,k}}(x)\) and the p.d.f. by \(f_{D_{j,k}}(x)\). Let us set

$$\begin{aligned} D_j^{(0)}=0, \qquad D_j^{(k)} =\sum _{i=1}^k D_{j,i}, \qquad k\in {\mathbb {N}}, \end{aligned}$$
(1)

where, for fixed \(j\in \{1,2\}\), the r.v.’s \(D_{j,k}\) are possibly dependent.

We denote by \(T_n\), \(n\in {\mathbb {N}}\), the n-th random instant in which the motion changes velocity. Let \(\{N(t), \; t\in {\mathbb {R}}_0^{+}\}\) be the alternating counting process, with two independent subprocesses, having inter-renewal times \(T_1,T_2,\ldots \), so that N(t) counts the number of velocity reversals of the particle in [0, t], i.e.

$$\begin{aligned} N(0)=0, \qquad N(t)=\sum _{n=1}^{\infty } {\textbf{1}}_{\{T_n\le t\}}, \quad t \in {\mathbb {R}}^+. \end{aligned}$$
(2)

Now we introduce the stochastic process \(\{(X(t),V(t)), \; t\in {\mathbb {R}}_0^{+}\}\), having state-space \({\mathbb {R}}\times \{{v}_1,{v}_2\}\), that describes the motion of the particle, with initial conditions

$$\begin{aligned} X(0)=0, \qquad V(0)\in \{{v}_1,v_2\}. \end{aligned}$$

The position X(t) and the velocity V(t) of the particle at time t are expressed respectively as follows:

$$\begin{aligned} X(t)=\int _{0}^{t} V(s) \text {d}s, \qquad V(t)=\frac{v_1+v_2}{2}+\ell \,\frac{v_1-v_2}{2}(-1)^{N(t)}, \qquad t\in {\mathbb {R}}^+, \end{aligned}$$
(3)

with \(\ell \) defined as

$$\begin{aligned} \ell ={\left\{ \begin{array}{ll} \ \ 1, \quad \textrm{if}\ V(0)=v_1,\\ -1, \quad \textrm{if}\ V(0)=v_2. \\ \end{array}\right. } \end{aligned}$$
(4)

Hence, recalling Eq.  (1), the n-th velocity change satisfies

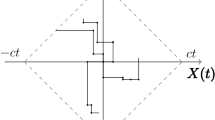
$$\begin{aligned} T_0=0, \qquad T_n={\left\{ \begin{array}{ll} D_j^{(k)}+D_{j+\ell }^{(k-1)}, \quad \text {if}\ n=2k-1, \\ D_j^{(k)}+D_{j+\ell }^{(k)}, \quad \ \ \text {if}\ n=2k,\\ \end{array}\right. } \quad n\in {\mathbb {N}}. \end{aligned}$$
(5)

From Eq.  (3) we have that the particle at every instant \(t \in {\mathbb {R}}^+\) is confined in \([v_2t,v_1t]\). Indeed, if the particle does not change velocity in [0, t], then it occupies one of the extremes of \([v_2t,v_1t]\) according to the initial velocity V(0). Otherwise, if the particle changes velocity at least once in [0, t], then it occupies a state belonging to \((v_2t,v_1t)\). Therefore, the conditional law of \(\{(X(t),V(t));t\ge 0\}\) is characterized by two components, for \(t \in {\mathbb {R}}^+\) and \(v\in \{{v}_1,{v}_2\}\):

  1. (i)

    a discrete component

    $$\begin{aligned} {\mathbb {P}}\{X(t)=vt, V(t)=v\, \vert \,X(0)=0, V(0)=v\}, \end{aligned}$$
    (6)
  2. (ii)

    an absolutely continuous component

    $$\begin{aligned} \begin{aligned} p(x,t\,\vert \,v)&= {\mathbb {P}}\{X(t)\in \textrm{d}x \,\vert \,X(0)=0, V(0)=v\} / \textrm{d}x\\&=p_1(x,t\,\vert \,v)+p_2(x,t\,\vert \,v), \end{aligned} \end{aligned}$$
    (7)

    where, for \(j=1,2\) and \(v_2t<x<v_1t\),

    $$\begin{aligned} p_j(x,t\,\vert \,v)\,\textrm{d}x= {\mathbb {P}}\{X(t)\in \textrm{d}x, V(t)=v_j\, \vert \,X(0)=0, V(0)=v\}. \end{aligned}$$
    (8)

We remark that the case \(v_2<0<v_1\) has been often treated as a typical instance of the (integrated) telegraph process (see [2], for instance), that goes along forward and backward directions alternately. In this case, the functions \(p_1\) and \(p_2\) are respectively the forward and backward p.d.f.’s of the motion given the initial velocity \(V(0)=v\in \{v_1,v_2\}\).

3 Intertimes Distributed as a Geometric Counting Process

The general assumptions considered in Sect. 2 can be specialized to the case in which the alternating counting process defined in Eq.  (2) arises from the alternation of two independent geometric counting processes.

3.1 Background on the Geometric Counting Process

Let us now recall some key results concerning the geometric counting process. We consider a mixed Poisson process \(\{{\tilde{N}}_\lambda (t), \; t\in {\mathbb {R}}_0^{+}\}\), whose marginal distribution is expressed as the following mixture:

$$\begin{aligned} {\mathbb {P}}[{\tilde{N}}_\lambda (t)=k]=\int _0^{\infty }{\mathbb {P}}[N^{(\alpha )}(t)=k] \; \text {d}U_{\lambda }(\alpha ), \qquad t \in {\mathbb {R}}_0^{+}, \; k \in {\mathbb {N}}_0, \end{aligned}$$
(9)

where \(N^{(\alpha )}(t)\) is a Poisson process with intensity \(\alpha \) and where \(U_{\lambda }\) is an exponential distribution with mean \(\lambda \in {\mathbb {R}}^{+}\). According to the terminology adopted in [3], the process \({\tilde{N}}_\lambda (t)\) is said a GCP with intensity \(\lambda \), since its probability distribution is

$$\begin{aligned} {\mathbb {P}}\{{\tilde{N}}_\lambda (t+s)-{\tilde{N}}_\lambda (t)=k\} =\frac{1}{1+\lambda \,s}\bigg (\frac{\lambda \,s}{1+\lambda \,s}\bigg )^k, \quad \forall s,t \in {\mathbb {R}}_0^+, \quad k \in {\mathbb {N}}_0. \end{aligned}$$
(10)

See, for instance, Di Crescenzo and Pellerey [13] for some results and applications of the GCP. We denote by \({\tilde{T}}_{n,\lambda }\), \(n \in {\mathbb {N}}\), the random times denoting the arrival instants of the process \({\tilde{N}}_\lambda (t)\), with \({\tilde{T}}_{0,\lambda } = 0\). Recalling [13], \({\tilde{T}}_{n,\lambda }\) has a modified Pareto (Type I) distribution, with p.d.f.

$$\begin{aligned} f_{{\tilde{T}}_{n,\lambda }}(t)=n \bigg (\frac{\lambda \, t}{1+\lambda \, t}\bigg )^{n-1}\frac{\lambda }{(1+\lambda \, t)^2}, \qquad t \in {\mathbb {R}}^+_0. \end{aligned}$$
(11)

The process \({\tilde{N}}_{\lambda }(t)\) has dependent increments \({\tilde{D}}_{n,\lambda }={\tilde{T}}_{n, \lambda }-{\tilde{T}}_{n-1,\lambda }, \; n \in {\mathbb {N}}\). Moreover, the conditional survival function of \({\tilde{D}}_{n,\lambda }\) conditional on \({\tilde{T}}_{n-1,\lambda }=t\), for \(n \in {\mathbb {N}}\), can be written as (see, e.g. [1])

$$\begin{aligned} {\overline{F}}_{{\tilde{D}}_{n,\lambda }\vert {\tilde{T}}_{n-1,\lambda }}(s\, \vert \,t) ={\mathbb {P}}({\tilde{D}}_{n,\lambda }>s\,\vert \, {\tilde{T}}_{n-1,\lambda }=t) = \bigg (\frac{1+\lambda \, t}{1+\lambda \, (t+s)}\bigg )^n, \quad s,t \in {\mathbb {R}}^+_0. \end{aligned}$$
(12)

The corresponding p.d.f. of \({\tilde{D}}_{n,\lambda }\) conditional on \({\tilde{T}}_{n-1,\lambda }=t\) is:

$$\begin{aligned} f_{{\tilde{D}}_{n,\lambda } \vert {\tilde{T}}_{n-1,\lambda }}(s\,\vert \,t) = \frac{n \lambda (1+\lambda \, t)^n}{[1+\lambda \, (t+s)]^{n+1}}, \qquad s,t \in {\mathbb {R}}^+_0. \end{aligned}$$
(13)

Moreover, the instantaneous jump rate of \({\tilde{N}}(t)\) depends on time and on the number of occurred jumps, being

$$\begin{aligned} \frac{{\mathbb {P}}[{\tilde{N}}_{\lambda }(t + h) - {\tilde{N}}_{\lambda }(t)=1\,\vert \,{\tilde{N}}_{\lambda }(t) = n]}{h} \quad \rightarrow \quad \frac{\lambda \,(n + 1)}{1 + \lambda \, t} \end{aligned}$$
(14)

as \(h \rightarrow 0^{+}\). With reference to the stochastic process \(\{(X(t),V(t)), \; t \in {\mathbb {R}}_0^+\}\) defined in Sect. 2, hereafter we study the random motion in the special case when the alternating phases of the motion are governed by two independent GCP’s with possibly different intensities.

3.2 The Stochastic Process and Its Probability Laws

In this section, we investigate the probability law of the process \(\{(X(t),V(t)), t\in {\mathbb {R}}_0^{+}\}\) when the subprocesses of the alternating counting process (2) are two independent GCP’s. Specifically, we assume that for \(j=1,2\) the sequences of intertimes \(D_{j,k}\), \(k\in {\mathbb {N}}\), during which the motion has velocity \(v_j\), are distributed as the intertimes of a GCP with intensity \(\lambda _j\).

In the remainder of this section, \({\mathbb {P}}_i\) will denote the probability conditional on \(\{X(0)=0, V(0)=v_i\}\), for \(i=1,2\).

Let us now introduce the following conditional sub-densities of the process \(\{(X(t),V(t)), \; t\in {\mathbb {R}}_0^{+}\}\) for \(t>0\), \(v_2 t< x < v_1 t\), \(n \in {\mathbb {N}}\) and \(j=1,2\):

$$\begin{aligned} \begin{aligned} p_{j,n}(x,t\,\vert \, v_1)\,\textrm{d}x = {\mathbb {P}}_1\{X(t) \in \textrm{d}x, V(t)=v_j,\ {}&N(t)= 2n-j+1\} \\ p_{j,n}(x,t\,\vert \, v_2)\,\textrm{d}x = {\mathbb {P}}_2\{X(t) \in \textrm{d}x, V(t)=v_j,\ {}&N(t)= 2(n-1)+j\}, \end{aligned} \end{aligned}$$
(15)

recalling that N(t) gives the number of velocity changes in [0, t]. Hence, from Eqs.  (8) and (15) we have, for \(v\in \{v_1,v_2\}\),

$$\begin{aligned} p_j(x,t\,\vert \,v)= \sum _{n=1}^{+\infty }p_{j,n}(x,t\,\vert \,v). \end{aligned}$$
(16)

For the analysis of finite-velocity random motions one is often led to constructing the PDE’s for the related sub-densities (see, for instance, Di Crescenzo et al. [11] for a finite-velocity damped motion on the real line). In our case, for the p.d.f.’s introduced in (15) a system of hyperbolic PDE’s can be obtained. Details are omitted for brevity. Unfortunately, solving such a system is a very hard task. Thus, in order to obtain the conditional probability law of \(\{(X(t),V(t)), \; t\in {\mathbb {R}}_0^{+}\}\) we develop an approach based on the analysis of the intertimes between consecutive velocity changes. We first consider the case \(V(0)=v_1\).

Theorem 1

Let \(\{(X(t),V(t)), \; t\in {\mathbb {R}}_0^{+}\}\) be the process defined in (3), where N(t) is the alternating counting process determined by two independent GCP’s with intensities \(\lambda _1\) and \(\lambda _2\). Then, for all \(t>0\) we have

$$\begin{aligned} {\mathbb {P}}_1\big \{X(t)=v_1t, V(t)=v_1\big \}=\frac{1}{1+\lambda _1 t}. \end{aligned}$$
(17)

Moreover, for \(v_2t<x<v_1t\) one has

$$\begin{aligned} p_1(x,t\,\vert \,v_1)=\frac{\lambda _1 \lambda _2 \tau }{(v_1-v_2)[1+\lambda _1 \tau +\lambda _2(t-\tau )]^2}, \end{aligned}$$
(18)
$$\begin{aligned} p_2(x,t\,\vert \,v_1)=\frac{\lambda _1[1+\lambda _2(t-\tau )]}{(v_1-v_2)[1+\lambda _1 \tau +\lambda _2(t-\tau )]^2}, \end{aligned}$$
(19)

where

$$\begin{aligned} \tau \equiv \tau (x,t)=\frac{x-v_2t}{v_1-v_2}. \end{aligned}$$
(20)

Proof

Eq. (17) follows from the p.d.f. of \(D_{1,1}\), given in (11) for \(n=1\). To obtain Eq. (18), we first analyze the conditional sub-density \(p_{1,n}(x,t\,\vert \,v_1)\). Recalling the first of (15), and conditioning on the last instant s preceding t in which the particle changes velocity from \(\vec {v}_2\) to \(\vec {v}_1\), we have

$$\begin{aligned}{} & {} p_{1,n}(x,t\,\vert \,v_1)\,\textrm{d}x = {\mathbb {P}}_1\{X(t) \in \textrm{d}x, V(t)=v_1, N(t)= 2n\} \nonumber \\{} & {} \quad = \int _0^t {\mathbb {P}}\Big \{T_{2n}\in \textrm{d}s,X(s)+v_1(t-s) \in \textrm{d}x, D_{1,n+1} > t-s\,\Big \}, \end{aligned}$$
(21)

for \(t>0\), \(v_2t<x<v_1t\) and \(n \in {\mathbb {N}}\). Since \(V(0) = v_1\), one has \(T_{2n}= D_1^{(n)} + D_2^{(n)} = s\) and \(X(s)= v_1D_1^{(n)} + v_2D_2^{(n)}\), so that

$$\begin{aligned} p_{1,n}(x,t\,\vert \,v_1)\,\textrm{d}x= & {} \int _0^t {\mathbb {P}}\Big \{D_1^{(n)}+D_2^{(n)} \in \textrm{d}s, v_1D_1^{(n)}+v_2D_2^{(n)} + v_1(t-s) \in \textrm{d}x, \nonumber \\{} & {} D_{1,n+1} > t-s\,\Big \}. \end{aligned}$$
(22)

Furthermore, the relation \(v_2s< X(s) = x-v_1(t - s)\) yields \(s > t-\tau \), due to (20). Hence, denoting by \(h(\cdot , \cdot )\) the joint p.d.f. of

$$\begin{aligned} \textbf{H}\equiv \Big (D_1^{(n)} + D_2^{(n)}, v_1D_1^{(n)}+v_2D_2^{(n)}\Big ) \end{aligned}$$
(23)

we obtain

$$\begin{aligned} p_{1,n}(x,t\,\vert \,v_1)=\int _{t-\tau }^t h(s,x-v_1(t-s)) \,{\mathbb {P}}\left\{ D_{1,n+1}>t-s \,\vert \, \textbf{H}=(s,x-v_1(t-s))\right\} \textrm{d}s.\nonumber \\ \end{aligned}$$
(24)

Since the sequences \(\{D_{1,n}\}\) and \(\{D_{2,n}\}\) are mutually independent by assumption, making use of Eq. (13) we get

$$\begin{aligned} h\big (s,x-v_1(t-s)\big )= & {} \frac{1}{v_1-v_2}f_{D_1}^{(n)}\big (s-(t-\tau )\big ) f_{D_2}^{(n)}\big (t-\tau \big ) \nonumber \\= & {} \frac{n^2 \lambda _1 \lambda _2}{v_1-v_2} \, \frac{\big \{\lambda _1\big [s-\big (t-\tau \big )\big ]\lambda _2 \big (t-\tau \big )\big \}^{n-1}}{\big \{\big [1+\lambda _1\big (s-(t-\tau )\big )\big ]\big [1+\lambda _2(t-\tau )\big ]\big \}^{n+1}}. \end{aligned}$$
(25)

Moreover, from the conditional survival function given in Eq.  (12) it follows that

$$\begin{aligned}{} & {} {\mathbb {P}} \left\{ D_{1,n+1}>t-s \,\vert \, \textbf{H}=(s,x-v_1(t-s))\right\} \nonumber \\{} & {} \quad = {\mathbb {P}}\{D_{1,n+1}>t-s\,\vert \,D_1^{(n)} = s-(t-\tau )\}=\left[ \frac{1+\lambda _1\left[ s-(t-\tau )\right] }{1+\lambda _1 \tau } \right] ^{n+1}. \end{aligned}$$
(26)

Therefore, from the latter three equations, after some calculations we obtain:

$$\begin{aligned} p_{1,n}(x,t\,\vert \,v_1)=\frac{1}{v_1-v_2} \, \frac{n\, (\lambda _1 \lambda _2)^{n} (t-\tau )^{n-1}\, \tau ^n}{[(1+\lambda _1 \, \tau )\, (1+\lambda _2(t-\tau ))]^{n+1}}, \qquad n \in {\mathbb {N}}. \end{aligned}$$
(27)

Similarly, the first sub-density introduced in (15) for \(j=2\) is given by

$$\begin{aligned} p_{2,n}(x,t\,\vert \,v_1)=\frac{1}{v_1-v_2} \, \frac{n\, \lambda _1^n \lambda _2^{n-1} [\tau (t-\tau )]^{n-1}\,}{(1+\lambda _1 \, \tau )^{n+1}\, [1+\lambda _2(t-\tau )]^{n}}, \qquad n \in {\mathbb {N}}. \end{aligned}$$
(28)

Finally, by making use of Eq.  (16) and

$$\begin{aligned} \sum _{m=0}^{\infty } (m+1)r^m=\frac{1}{(1-r)^2},\quad \textrm{with}\;\; r=\frac{\lambda _1 \lambda _2 \tau (t-\tau )}{(1+\lambda _1 \tau )[1+\lambda _2(t-\tau )]}\in (0,1), \end{aligned}$$
(29)

we obtain the p.d.f.’s (18) and (19). \(\square \)

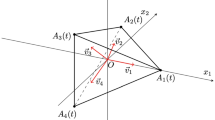
As example, a sample path for the particle motion when \(V(0)=v_1\) is shown in Fig. 1.

Remark 1

It is worth mentioning that the term \(v_1-v_2\) in the right-hand-side of Eqs.  (18) and (19) can be viewed as the measure of the diffusion interval at time \(t=1\).

Fig. 1
figure 1

A sample path of X(t) with \(V(0)=v_1\), where \(S_{2n}=X(s) \equiv v_1D_1^{(n)} +v_2D_2^{(n)}\)

Full size image

Remark 2

Due to symmetry, if \(V(0)=v_2\), the probability law of the process \(\{(X(t),V(t), \; t \in {\mathbb {R}}_0^+\}\) can be obtained from Theorem 1 by interchanging \(p_1\) with \(p_2\), \(\lambda _1\) with \(\lambda _2\), and x with \((v_1+v_2)t-x\). Therefore, we have

$$\begin{aligned} p_j(x,t\,\vert \,v_2)\vert _{\lambda _1,\lambda _2}=p_{3-j}((v_1+v_2)t-x,t\vert v_1)\vert _{\lambda _2,\lambda _1}, \qquad j=1,2. \end{aligned}$$

Moreover, the corresponding p.d.f.’s for \(t>0\) and \(v_2t<x<v_1t\) are given by

$$\begin{aligned} p_1(x,t\vert v_2)=\frac{\lambda _2(1+\lambda _1 \tau )}{(v_1-v_2)[1+\lambda _1\tau +\lambda _2(t-\tau )]^2}, \end{aligned}$$
(30)
$$\begin{aligned} p_2(x,t\vert v_2)=\frac{\lambda _1\lambda _2(t-\tau )}{(v_1-v_2)[1+\lambda _1\tau +\lambda _2(t-\tau )]^2}, \end{aligned}$$
(31)

and analogously to (17) we have

$$\begin{aligned} {\mathbb {P}}_2\big \{X(t)=v_2t, V(t)=v_2\big \}=\frac{1}{1+\lambda _2 t}. \end{aligned}$$
(32)

Remark 3

Under the assumptions of Theorem 1, it is not hard to see that, for \(t\in {\mathbb {R}}^+\) and \(j=1,2\),

$$\begin{aligned} \lim _{x\rightarrow v_j t}p_j(x,t\,\vert \,v_j)= & {} \frac{\lambda _1\lambda _2 t}{(v_1-v_2)(1+\lambda _jt)^2}, \nonumber \\ \lim _{x\rightarrow v_j t}p_j(x,t\,\vert \,v_{3-j})= & {} \frac{\lambda _j}{(v_1-v_2)(1+\lambda _{3-j}t)}, \nonumber \\ \lim _{x\rightarrow v_j t}p_{3-j}(x,t\,\vert \,v_j)= & {} \frac{\lambda _j}{(v_1-v_2)(1+\lambda _jt)^2}, \nonumber \\ \lim _{x\rightarrow v_j t}p_{3-j}(x,t\,\vert \,v_{3-j})= & {} 0. \end{aligned}$$
(33)

Let us now focus on the marginal distribution of \(\{X(t), \; t\in {\mathbb {R}}_0^{+}\}\) conditional on \(\{X(0)=0, V(0)=v_j\}\), \(j=1,2\). In this case, the absolutely continuous components for \(t\in {\mathbb {R}}^+\) and \(x\in (v_2t, v_1t)\) are described by

$$\begin{aligned} p(x,t\vert v_j)\,\textrm{d}x = {\mathbb {P}}_j \big \{ X(t) \in \textrm{d}x\big \}, \qquad j=1,2. \end{aligned}$$
(34)

Since \(p(x,t\vert v_j)=p_1(x,t\vert v_j)+p_2(x,t\vert v_j)\), making use of (18)–(19) and (30)–(31) it is not hard to obtain the following result.

Corollary 1

Under the assumptions of Theorem 1, the probability distribution of \(\{X(t), \; t\in {\mathbb {R}}_0^{+}\}\) conditional on \(\{X(0)=0, V(0)=v_j\}\), \(j=1,2\), is given by a discrete component identical to (17) and (32), respectively, and by

$$\begin{aligned} p(x,t\vert v_j)=\frac{\lambda _j(1+\lambda _{3-j} t)}{(v_1-v_2)[1+\lambda _1 \tau +\lambda _2(\, t-\tau )]^2}, \end{aligned}$$
(35)

for all \(t\in {\mathbb {R}}^+\) and \(v_2t< x < v_1t\), with \(\tau =\tau (x,t)\) given in (20).

3.3 Moments

In this section, let \({\mathbb {E}}_i\) and \(\text {Var}_i\) denote respectively the expectation and the variance conditional on \(\{X(0)=0, V(0)=v_i\}\), \(i=1,2\).

Making use of Eqs. (17) and (35) for \(j=1\), we can now obtain the first and second conditional moments of X(t).

Theorem 2

Under the assumptions of Theorem 1, for all \(t \in {\mathbb {R}}_0^{+}\), we have that, for \(\lambda _1\ne \lambda _2\),

$$\begin{aligned} {\mathbb {E}}_1[X(t)]=\frac{(v_2\lambda _1-v_1\lambda _2)t}{\lambda _1-\lambda _2}+\frac{(v_1-v_2)\lambda _1(1+\lambda _2 t)}{(\lambda _1-\lambda _2)^2}\log {\frac{1+\lambda _1 t}{1+\lambda _2 t}}, \end{aligned}$$
(36)

and

$$\begin{aligned} {\mathbb {E}}_1[X^2(t)]&=\frac{v_1^2t^2}{1+\lambda _1 t}+\frac{\lambda _1 t}{(1+\lambda _1 t)(\lambda _1-\lambda _2)^2} \nonumber \\&\quad \times \left\{ \left[ (1+\lambda _2 t)v_1-(v_1-v_2)^2 v_2 (1+\lambda _1 t) \right] ^2 -(1+\lambda _1 t)(1+\lambda _2 t)\right\} \end{aligned}$$
(37)
$$\begin{aligned}&\quad +\frac{2(v_1-v_2)\lambda _1(1+\lambda _2 t)}{(\lambda _1-\lambda _2)^3}(v_2-v_1+t(\lambda _1 v_2-\lambda _2 v_1))\log {\frac{1+\lambda _1 t}{1+\lambda _2 t}}. \end{aligned}$$
(38)

Moreover, for \(\lambda _1= \lambda _2 \equiv \lambda \) we get

$$\begin{aligned}&{\mathbb {E}}_1[X(t)] =\frac{v_1 t}{1+\lambda t}+\frac{\lambda (v_1+v_2)t^2}{2(1+\lambda t)}, \end{aligned}$$
(39)
$$\begin{aligned}&{\mathbb {E}}_1[X^2(t)] =\frac{v_1^2 t^2}{1+\lambda t}+\frac{\lambda (v_1^2+v_1v_2+v_2^2) t^3}{3(1+\lambda t)}. \end{aligned}$$
(40)

Remark 4

The results from Eqs. (39) and (40) can be generalized in order to obtain the corresponding k-th moment of X(t). Indeed, in the case \(\lambda _1= \lambda _2 \equiv \lambda \), for \(t\in {\mathbb {R}}_0^+\), one has

$$\begin{aligned} {\mathbb {E}}_1[X^k(t)]=\frac{1}{1+\lambda t} \left[ v_1^k t^k + \frac{\lambda \,(v_1^{k+1}-v_2^{k+1})t^{k+1}}{(k+1)(v_1-v_2)} \right] . \end{aligned}$$
(41)

In the case \(\lambda _1\ne \lambda _2\), similarly we have

$$\begin{aligned} {\mathbb {E}}_1[X^k(t)]{} & {} = \frac{v^k t^k}{1+\lambda _1 t} - \frac{k \lambda _1\, (1+\lambda _2\, t)(v_1-v_2)t^{k-1}}{\lambda _1-\lambda _2} \nonumber \\{} & {} \quad \times \; \bigg \{\frac{v_1^{k-1}}{k-1}\,{}_2F_1\bigg [1, 1-k; 2-k; -\frac{v_1(1+\lambda _2\,t)-v_2(1+\lambda _1\,t)}{tv_1(\lambda _1-\lambda _2)}\bigg ] \nonumber \\{} & {} \quad + \; \frac{v_2^{k-1}}{\Gamma (2-k)}\,{}_2F_1\bigg [1, 1-k, 2-k, -\frac{v_1(1+\lambda _2\,t)-v_2(1+\lambda _1\,t)}{tv_1(\lambda _1-\lambda _2)}\bigg ]\bigg \} \nonumber \\{} & {} \quad -\; \frac{\lambda _1 t^k}{1+\lambda _1t}\big [(v_1^k-v_2^k)+(\lambda _2v_1^k-\lambda _1v_2^k)t], \end{aligned}$$
(42)

where \(\Gamma \) and \({}_2F_1\) denote respectively the well-known gamma and Gaussian hypergeometric functions.

Remark 5

Using Eqs. (36)–(38), we can obtain the expression of the variance of X(t) conditional on \(\{X(0)=0,V(0)=v_1\}\). When \(\lambda _1=\lambda _2\), from Eqs. (39)–(40) one has

$$\begin{aligned} \text {Var}_1[X(t)]=\frac{\lambda (v_1-v_2)^2(4+\lambda t)t^3}{12\,(1+\lambda t)^2}. \end{aligned}$$
(43)

In both cases \(\lambda _1 \ne \lambda _2\) and \(\lambda _1=\lambda _2\), we can state that the mean and the variance of X(t) are both linear when t tends to infinity, as shown hereafter.

Corollary 2

Under the assumptions of Theorem 1, the following limits hold:

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{{\mathbb {E}}_1[X(t)]}{t}= & {} {\left\{ \begin{array}{ll} \displaystyle \frac{v_2\lambda _1-v_1\lambda _2}{\lambda _1-\lambda _2}+\ \frac{\lambda _1\lambda _2 (v_1-v_2)}{(\lambda _1-\lambda _2)^2}\log {\frac{\lambda _1}{\lambda _2}},\qquad \lambda _1\ne \lambda _2, \\ \displaystyle \frac{v_1+v_2}{2}, \lambda _1= \lambda _2; \end{array}\right. } \end{aligned}$$
(44)
$$\begin{aligned}{} & {} \lim _{t\rightarrow \infty } \frac{\text {Var}_1[X(t)]}{t^2} = \nonumber \\= & {} {\left\{ \begin{array}{ll} \begin{array}{lll} \displaystyle \frac{\lambda _1\lambda _2(v_1-v_2)^2}{(\lambda _1-\lambda _2)^2} \left\{ 1- 2\left( \frac{\lambda _1\lambda _2}{\lambda _1-\lambda _2}\right) ^2 [\log {(\lambda _1 \lambda _2)}-\log (\lambda _1)\log (\lambda _2)]\right\} , &{} \lambda _1 \ne \lambda _2,\\ \displaystyle \frac{(v_1-v_2)^2}{12}, &{} \lambda _1= \lambda _2. \end{array} \end{array}\right. }\nonumber \\ \end{aligned}$$
(45)

Remark 6

The results obtained in Corollary 2 can be compared with those for the telegraph processes in which the random times between consecutive velocity changes have exponential distribution (i) with constant rates, and (ii) with linearly increasing rates (cf. Di Crescenzo and Martinucci [11]). Indeed, for the process under investigation and for the two above mentioned processes the conditional mean is asymptotically linear as \(t\rightarrow \infty \), so that the following limit holds for all such cases when \(\lambda _1=\lambda _2\):

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{{\mathbb {E}}_1[X(t)]}{t} =\frac{v_1+v_2}{2}. \end{aligned}$$
(46)

This analogy refers to the means of the mentioned processes, and is not extended to other moments. Indeed, for instance, we recall (cf. Section 1 of [13]) that the underling Poisson and geometric processes have the same mean but different variance. Moreover, the Poisson process over time tends to a constant as time tends to \(\infty \), whereas in the same limit the geometric process over time converges in distribution to an exponential random variable.

Remark 7

Under the assumptions of Theorem 1, due to symmetry, for \(t\in {\mathbb {R}}_0^+\) one has:

$$\begin{aligned}{} & {} {\mathbb {E}}_1[X(t)]+{\mathbb {E}}_2[X(t)]= \nonumber \\{} & {} \quad ={\left\{ \begin{array}{ll} \begin{array}{ll} \displaystyle \frac{2(\lambda _1 v_2-\lambda _2 v_1)t}{\lambda _1-\lambda _2}+\frac{(v_1-v_2)(\lambda _1+\lambda _2+2\lambda _1\lambda _2t)}{(\lambda _1-\lambda _2)^2}\log \frac{1+\lambda _1t}{1+\lambda _2t}, &{} \;\;\lambda _1\ne \lambda _2,\\ \displaystyle (v_1+v_2)\,t, &{} \;\;\lambda _1=\lambda _2. \end{array} \end{array}\right. } \end{aligned}$$
(47)

3.4 Random Initial Velocity

Hereafter we analyze the probability distribution of X(t) when the initial velocity is random, according to the following rule, for \(0\le q\le 1\),

$$\begin{aligned} {\mathbb {P}}\{V(0)=v_1\}=q, \qquad {\mathbb {P}}\{V(0)=v_2\}=1-q. \end{aligned}$$
(48)

To this aim, denoting by \({\mathbb {P}}_0\) the probability conditional on \(X(0)=0\) and initial velocity specified as in (48), similarly to Eq. (8) we define

$$\begin{aligned} p_j(x,t)\,\textrm{d}x ={\mathbb {P}}_0\{X(t)\in \textrm{d}x, V(t)=v_j\}, \qquad j=1,2 \end{aligned}$$
(49)

for \(v_2t<x<v_1t\), \(t\in {\mathbb {R}}_0^+\). In analogy with (17), in this case we have

$$\begin{aligned} {\mathbb {P}}_0\big \{X(t)=v_jt, V(t)=v_j\big \} =\left\{ \begin{array}{ll} \displaystyle \frac{q}{1+\lambda _1 t}, &{} \;\; j=1\\ \displaystyle \frac{1-q}{1+\lambda _2 t}, &{} \;\; j=2. \end{array} \right. \end{aligned}$$
(50)

For \(v_2t<x<v_1t\), \(t\in {\mathbb {R}}_0^+\), we now focus on the p.d.f.

$$\begin{aligned} p(x,t)={\mathbb {P}}_0 \big \{ X(t) \in \textrm{d}x\big \}/\textrm{d}x =p_1(x,t)+p_2(x,t), \end{aligned}$$
(51)

and on the so-called flow function

$$\begin{aligned} w(x,t) =p_1(x,t)-p_2(x,t). \end{aligned}$$
(52)

We remark that w(x, t) measures, at each time t, the excess of particles moving with velocity \(v_1\) with respect to the ones moving with velocity \(v_2\) near x in a large ensemble of particles moving according to the stated rules of X(t) (see, e.g. Orsingher [29]). Making use of Eqs. (18), (19), (29), (30) and Corollary 1, now we can state the following results on the distribution and the flow function of X(t) when the initial velocity is random.

Proposition 1

Let the initial velocity of the process \(\{(X(t),V(t)),\; t \in {\mathbb {R}}_{0}^{+}\}\) be distributed as in Eq. (48). Then, for \(t \in {\mathbb {R}}^+\) and \(v_2t< x < v_1t\) we have

$$\begin{aligned} \begin{aligned} p_1(x,t)=\frac{\lambda _2(1+\lambda _1 \tau )-q \lambda _2}{(v_1-v_2)[1+\lambda _1 \tau +\lambda _2(t-\tau )]^2}, \\ p_2(x,t)=\frac{q \lambda _1+\lambda _1\lambda _2(t-\tau ) }{(v_1-v_2)[1+\lambda _1 \tau +\lambda _2(t-\tau )]^2}. \end{aligned}\nonumber \\ \end{aligned}$$
(53)

and therefore, due to Eqs. (51) and (52),

$$\begin{aligned} p(x,t)=\frac{\lambda _2(1+\lambda _1 t)+q(\lambda _1-\lambda _2)}{(v_1-v_2)[1+\lambda _1 \tau +\lambda _2(t-\tau )]^2}, \end{aligned}$$
(54)
$$\begin{aligned} w(x,t)=\frac{\lambda _2[1+\lambda _1(2\tau -t)]-q(\lambda _1+\lambda _2)}{(v_1-v_2)[1+\lambda _1 \tau +\lambda _2(t-\tau )]^2}, \end{aligned}$$
(55)

where \(\tau =\tau (x,t)\) is defined in (20).

Remark 8

Under the assumptions of Proposition 1, from Remark 2 one has the following symmetry relations:

$$\begin{aligned} p(x,t)\vert _{\lambda _1,\lambda _2,q}= & {} p((v_1+v_2)t-x,t)\vert _{\lambda _2,\lambda _1,1-q}, \end{aligned}$$
(56)
$$\begin{aligned} w(x,t)\vert _{\lambda _1,\lambda _2,q}= & {} -w((v_1+v_2)t-x,t)\vert _{\lambda _2,\lambda _1,1-q}, \end{aligned}$$
(57)

valid for \(v_2t<x<v_1 t\), \(t\in {\mathbb {R}}^+\). These properties are confirmed by the plots of the functions (54) and (55) shown in Fig. 2.

Remark 9

Making use of Eq. (55) we are now able to discuss the sign of the flow function of X(t). Under the assumptions of Proposition 1, recalling (20) we have that

$$\begin{aligned} w(x,t)\ge 0 \qquad \hbox {for }\quad x\ge m_t(\textbf{v}) + \beta (q,\textbf{v},{\varvec{\lambda }}), \end{aligned}$$
(58)

where

$$\begin{aligned} m_t(\textbf{v}):=\frac{(v_1+v_2)t}{2}, \qquad \beta (q,\textbf{v},{\varvec{\lambda }}):= \frac{v_1-v_2}{2\lambda _1}\left( q\, \frac{\lambda _1+\lambda _2}{\lambda _2}-1\right) . \end{aligned}$$
(59)

Clearly, \(m_t(\textbf{v})\) is the middle point of the diffusion interval \((v_2t, v_1t)\). Moreover, one has \(\beta (q,\textbf{v},{\varvec{\lambda }})\ge 0\) when \(q\ge \displaystyle \frac{\lambda _2}{\lambda _1+\lambda _2}\).

Fig. 2
figure 2

Plots of p(x, t) and w(x, t) for \(t=1\), \(v_1=2\), \(v_2=-2\), \(q=0.5\), and \((\lambda _1,\lambda _2)=(1, 30), (5, 20), (10, 10), (20, 5), (30, 1)\) from top to bottom near \(x=2\)

Full size image

Remark 10

(i) Under the assumptions of Proposition  1, recalling that \(\tau (x,t)\) is increasing in x, from (54) we immediately have that p(x, t) is strictly increasing (decreasing) in x when \(\lambda _1<\lambda _2\) (\(\lambda _1>\lambda _2\)), for fixed t.

(ii) Moreover, if \(\lambda _1=\lambda _2\equiv \lambda \) then the probability law does not depend on q, and for \(t \in {\mathbb {R}}^+\) it is expressed by

$$\begin{aligned} {\mathbb {P}}_0\big \{X(t)\in \{v_1 t, v_2 t\}\big \}= & {} \frac{1}{1+\lambda t}, \end{aligned}$$
(60)
$$\begin{aligned} p(x,t)= & {} \frac{\lambda }{(v_1-v_2)(1+\lambda t)}, \quad v_2t< x < v_1t. \end{aligned}$$
(61)

In this case, due to (55) the flow function of X(t), \(t \in {\mathbb {R}}^+\), is given by

$$\begin{aligned} w(x,t)= \frac{\lambda [1+\lambda (2\tau -t) -2q]}{(v_1-v_2)\,(1+\lambda t)^2}, \qquad v_2t< x < v_1t. \end{aligned}$$
(62)

Let us now analyze the functions (51) and (52) when x tends to the border of the diffusion interval at a fixed time.

Corollary 3

Let the assumptions of Proposition 1 hold. For fixed \(t\in {\mathbb {R}}^+\) we have

$$\begin{aligned} \lim _{x \rightarrow v_j t} p(x,t)=\frac{\lambda _2(1+\lambda _1 t)+q(\lambda _1-\lambda _2)}{(v_1-v_2)(1+\lambda _j t)^2},\qquad j=1,2 \end{aligned}$$
(63)

and

$$\begin{aligned} \lim _{x \rightarrow v_j t} w(x,t)=\frac{\lambda _2(1- (-1)^j\lambda _1 t)+q(\lambda _1+\lambda _2)}{(v_1-v_2)(1+\lambda _j t)^2}, \qquad j=1,2. \end{aligned}$$
(64)

Making use of Theorem 2 and Remark 7 we can now obtain the mean of X(t) when the initial velocity is random, henceforth denoted by \({\mathbb {E}}_0[X(t)]\).

Corollary 4

Let the initial velocity of the process \(\{(X(t),V(t)),\; t \in {\mathbb {R}}_{0}^{+}\}\) be distributed as in (48). If \(\lambda _1\ne \lambda _2\) then for \(t \in {\mathbb {R}}^+\) one has

$$\begin{aligned} {\mathbb {E}}_0[X(t)] =\frac{t(v_2\lambda _1-v_1\lambda _2)}{\lambda _1-\lambda _2} +\big [q\lambda _1+(1-q)\lambda _2+\lambda _1 \lambda _2 t \big ] \frac{(v_1-v_2)}{(\lambda _1-\lambda _2)^2}\log {\frac{1+\lambda _1 t}{1+\lambda _2 t}},\nonumber \\ \end{aligned}$$
(65)

whereas, if \(\lambda _1=\lambda _2\equiv \lambda \) then for \(t \in {\mathbb {R}}^+\)

$$\begin{aligned} {\mathbb {E}}_0[X(t)] =\frac{\big [q v_1+(1-q)v_2\big ] t}{1+\lambda t}+\frac{\lambda t^2 (v_1+v_2)}{2(1+\lambda t)}. \end{aligned}$$
(66)

Similarly to the classical telegraph process driven by the Poisson process, it is not hard to see that the process X(t) does not admit a stationary state. Indeed, due to Eq. (54), for all \(x\in {\mathbb {R}}\) one has

$$\begin{aligned} \lim _{t\rightarrow +\infty } p(x,t)=0. \end{aligned}$$
(67)

Moreover, for the classical telegraph process driven by the Poisson process it is well known that an asymptotic limit holds under the Kac’s conditions, which involve both intensity and velocity, leading to the Gaussian transition function of Brownian motion (see, e.g., Lemma 2 of Orsingher [29]). We conclude this section with a different result for the stochastic process under investigation. This can be seen in the next corollary, where we let the intensities tend to \(+\infty \) in Eqs. (53) and (54). In this case the limit condition is meaningful even if it does not involve the velocities \(v_i\).

Corollary 5

Let the assumptions of Proposition 1 hold. For \(t\in {\mathbb {R}}^+\) and \(v_2t< x < v_1t\) one has, with \(\tau \) defined in (20),

$$\begin{aligned} \begin{aligned} \mathop {\lim }\limits _{\begin{array}{c} \lambda _1, \lambda _2\rightarrow +\infty \\ \lambda _1/\lambda _2\rightarrow 1 \end{array} } p_1(x,t) =\frac{\tau }{(v_1-v_2)\,t^2}, \qquad \mathop {\lim }\limits _{\begin{array}{c} \lambda _1, \lambda _2\rightarrow +\infty \\ \lambda _1/\lambda _2\rightarrow 1 \end{array} } p_2(x,t) =\frac{t-\tau }{(v_1-v_2)\,t^2}, \end{aligned} \end{aligned}$$
(68)

and

$$\begin{aligned} \mathop {\lim }\limits _{\begin{array}{c} \lambda _1, \lambda _2 \rightarrow +\infty \\ \lambda _1/\lambda _2 \rightarrow 1 \end{array}} p(x,t)=\frac{1}{(v_1-v_2)\,t}. \end{aligned}$$
(69)

The right-hand side of (69) shows that the distribution of the process X(t) tends to be uniform over the diffusion interval \((v_2t,v_1t)\) when the intensities \(\lambda _1\) and \(\lambda _2\) tend to infinity, with \(\lambda _1/\lambda _2\rightarrow 1\), whereas the p.d.f.’s \(p_j(x,t)\) are not asymptotically uniformly distributed.

In the following section we extend the analysis of the finite-velocity motion governed by the GCP to the case when the motion evolves in \({\mathbb {R}}^2\) along three different directions attained cyclically.

4 Planar Random Motion with Underlying Geometric Counting Process

We consider a planar random motion of a particle that moves along three directions. The motion is oriented toward the cyclically alternating directions described by the vector

$$\begin{aligned} \vec {v}_j =\cos \theta _j\vec {h}+\sin \theta _j \vec {k}, \qquad j=1,2,3, \end{aligned}$$
(70)

where \(\vec {h}\) and \(\vec {k}\) are the unit vectors along the Cartesian coordinate axes. Moreover, the angles \(\theta _j\) satisfy the conditions

$$\begin{aligned} 0\le \theta _1< \theta _2< \theta _1+\pi< \theta _3 < \min \{\theta _2+\pi , 2\pi \}. \end{aligned}$$
(71)

The particle moves from the origin at time \(t=0\), running with constant velocity \(c>0\). Initially, it moves along the direction \(\vec {v}_1\). Then, after a random duration denoted \(D_{1,1}\), the particle changes instantaneously the direction, moving along \(\vec {v}_2\) for a random duration \(D_{2,1}\). Subsequently, it moves along \(\vec {v}_3\) for a random duration \(D_{3,1}\), and so on by attaining cyclically the directions \(\vec {v}_1, \vec {v}_2, \vec {v}_3\) for the random periods \(D_{1,2},D_{2,2},D_{3,2},D_{1,3},D_{2,3},D_{3,3},\ldots \). Hence, during the n-th cycle the particle moves along directions \(\vec {v}_1,\vec {v}_2, \vec {v}_3\) in sequence for the random lengths \(D_{1,n},D_{2,n},D_{3,n}\), for \(n \in {\mathbb {N}}\), respectively. Denoting by \(T_{k}\) the k-th random instant in which the motion changes its direction, for \(n \in {\mathbb {N}}_0\) we have

$$\begin{aligned} T_{3n+i+j+1}=D_1^{(n+1)}+D_2^{(n+i)}+D_3^{(n+j)},\qquad i,j=0,1, \quad i\ge j, \end{aligned}$$
(72)

where

$$\begin{aligned} D_j^{(n)}=D_{j,1}+D_{j,2}+ \ldots + D_{j,n}, \qquad j=1,2,3, \quad n \in {\mathbb {N}}, \end{aligned}$$
(73)

is the total duration of the motion along direction \(\vec {v}_j\) until the n-th cycle, with

$$\begin{aligned} D_{1}^{(0)}=D_{2}^{(0)}=D_{3}^{(0)}=0. \end{aligned}$$
(74)

In agreement with (72) we set \(T_0=0\). In the following, we assume that the sequences \(\{ D_{j,k}; \; k \in {\mathbb {N}}\}_{j=1,2,3}\) are mutually independent. Moreover, for \(j=1,2,3\) the durations \(D_{j,1}, D_{j,2}, \ldots \) are nonnegative absolutely continuous possibly dependent random variables.

It is worth mentioning that the conditions (71) ensure that the moving particle can reach any state in \({\mathbb {R}}^2\) in a sufficiently large time t. Moreover, the considered motion provides a simple scheme with the minimal number of possible directions for the description of a vorticity motion with intertimes characterized by heavy tailed distributions.

Hereafter we introduce the stochastic process that describes the planar random motion considered so far.

4.1 The Stochastic Process and Its Probability Laws

Let \(\{(X(t), Y(t), V(t)), t \in {\mathbb {R}}_0^{+}\}\) be a stochastic process with state-space \({\mathbb {R}}^2 \times \{\vec {v}_1, \vec {v}_2, \vec {v}_3\}\), where (X(t), Y(t)) gives the location of the particle and V(t) the direction of the motion at time \(t \in {\mathbb {R}}_0^{+}\), conditional on \(X(0)=0, Y(0)=0, V(0)=\vec {v}_1\). In order to specify the diffusion region of the particle at time \(t\in {\mathbb {R}}^{+}\), let us now define a time-dependent triangle \({\mathcal {R}}(t)\) whose edges are denoted by \(E_{ij}(t)\), with \(i,j=1,2,3\) and \(i < j\), whereas the vertices are given by

$$\begin{aligned} A_j(t)=(ct \cos \theta _j, ct \sin \theta _j), \qquad j=1,2,3 \end{aligned}$$
(75)

for fixed \(c\in {\mathbb {R}}^{+}\). Hence, the angle \(\theta _j\) describes the direction of the vertex corresponding to \(\vec {v}_j\), for \(j=1,2,3\). Therefore, under conditions (71), the equations linking two adjacent vertices are expressed as

$$\begin{aligned} a_{ij}x+b_{ij}y+ctq_{ij}=0, \qquad i,j=1,2,3, \quad i < j, \end{aligned}$$
(76)

where

$$\begin{aligned} a_{ij}=\sin \theta _i-\sin \theta _j, \qquad { b_{ij}=\cos \theta _j-\cos \theta _i,} \qquad q_{ij}=\sin (\theta _j-\theta _i). \end{aligned}$$
(77)

Since the particle moves with velocity \(c\in {\mathbb {R}}^{+}\), and the motion is oriented alternately along the directions determined by vectors (70), the particle at time \(t\in {\mathbb {R}}^{+}\) is located inside the region delimited by the triangle

$$\begin{aligned} {\mathcal {R}}(t)=\left\{ \begin{array}{rl} (x,y) \in {\mathbb {R}}^2: {\left\{ \begin{array}{ll} a_{12}x-b_{12}y+ct q_{12}\ge 0\\ a_{23}x-b_{23}y+ct q_{23}\ge 0\\ a_{13}x-b_{13}y+ct q_{13}\le 0 \end{array}\right. } \end{array} \right\} , \end{aligned}$$
(78)

where the defining conditions arise from Eqs. (76). In particular, the particle motion involves three different, mutually exclusive cases based on the assumption that \(X(0)=0, Y(0)=0,V(0)=\vec {v}_1\):

  1. (i)

    if the direction of the motion does not change in (0, t), then at time \(t\in {\mathbb {R}}^+\) the particle is placed in the vertex \(A_1(t)\);

  2. (ii)

    if the direction of the motion changes once in (0, t), then at time \(t\in {\mathbb {R}}^+\) the particle is situated somewhere on the edge \(E_{12}(t)\);

  3. (iii)

    if more than one direction change occurs in (0, t), then at time \(t\in {\mathbb {R}}^+\) the particle is located in the interior of the region \({\mathcal {R}}(t)\), that will be denoted \(\mathring{{\mathcal {R}}}(t)\).

Let us now denote \(B_1:=\{X(0)=0, Y(0)=0, V_0=\vec {v}_1\}\). To determine the probability laws of the process \(\{(X(t), Y(t), V(t)), t \in {\mathbb {R}}_0^{+}\}\) conditional on \(B_1\), hereafter we express the discrete components concerning events (i) and (ii) considered above. As usual, we denote \({F}_{D}\) and \({\overline{F}}_{D}\) for the distribution function and the survival function of a generic random variable D.

Theorem 3

(Discrete components) Let \(\{(X(t), Y(t), V(t)), t \in {\mathbb {R}}_0^{+}\}\) be the stochastic process defined in Sect. 4.1. For all \(t \in {\mathbb {R}}^+\) we have

$$\begin{aligned} {\mathbb {P}}\{X(t)= ct \cos \theta _1, Y(t)= ct \sin \theta _1, V(t)=\vec {v}_1\,\vert \, B_1\}={\overline{F}}_{D_{1,1}}(t) \end{aligned}$$
(79)

and

$$\begin{aligned} {\mathbb {P}}\{(X(t), Y(t)) \in E_{12}(t), V(t)=\vec {v}_{2}\,\vert \, B_1\}=F_{D_{1,1}+D_{2,1}}(t)-F_{D_{1,1}}(t). \end{aligned}$$
(80)

Proof

Equations (79) and (80) are a consequence of the conditions (i) and (ii) when the initial velocity is \(V(0)=\vec {v}_1\). \(\square \)

Using condition (iii), for \(t\in {\mathbb {R}}^+\) and \(j=1,2,3\) the absolutely continuous component of the probability law can be expressed by

$$\begin{aligned} \begin{aligned} p_{1j}(x,y,t) \textrm{d}x\textrm{d}y= {\mathbb {P}}&\{X(t) \in \textrm{d}x, Y(t) \in \textrm{d}y, V(t)=\vec {v}_j\,\vert \, B_1\}. \end{aligned} \end{aligned}$$
(81)

Clearly, the right-hand-side of Eq. (81) represents the probability that the particle at time \(t\in {\mathbb {R}}^+\) is located in a neighborhood of (x, y) and moves along direction \(\vec {v}_j\), given the initial condition expressed by \(B_1\). Moreover, we can introduce the p.d.f. of the particle location at time \(t \in {\mathbb {R}}^+\), i.e.

$$\begin{aligned} p_{1}(x,y,t) = \frac{{\mathbb {P}}\{X(t)\in \textrm{d}x,Y(t)\in \textrm{d}y \,\vert \,B_1\}}{\textrm{d}x\textrm{d}y}. \end{aligned}$$
(82)

Due to Eqs. (81) and (82), one immediately has

$$\begin{aligned} p_{1}(x,y,t)=\sum _{j=1}^3 p_{1j}(x,y,t). \end{aligned}$$
(83)

In order to determine \(p_{1j}(x,y,t)\), we first introduce the function \(\psi : {\mathbb {R}}^3 \rightarrow {\mathbb {R}}^3\), which is defined as follows:

$$\begin{aligned} \psi (t_1,t_2,t_3)=\left( c \sum _{j=1}^3 x_{\vec {v}_j}t_j, c\sum _{j=1}^3 y_{\vec {v}_j}t_j, \sum _{j=1}^3 t_j \right) . \end{aligned}$$
(84)

Here \(x_{\vec {v}_j}\) and \(y_{\vec {v}_j}\), for \(j=1,2,3\), denote respectively the components of each vector \(\vec {v}_j\) along the x and y axes. For a cycle of the motion with durations \(t_1\), \(t_2\) and \(t_3\), the function introduced in (84) gives a vector containing the displacements performed along x and y axes during the cycle, as well as its whole duration. We also consider the transformation matrix \({\varvec{A}}\) of function \(\psi (t_1,t_2,t_3)\), that is

$$\begin{aligned} {\varvec{A}}=\begin{pmatrix} c \cos \theta _1 &{} c \cos \theta _2 &{} c \cos \theta _3\\ c \sin \theta _1 &{} c \sin \theta _2 &{} c \sin \theta _3\\ 1 &{} 1 &{} 1\\ \end{pmatrix}. \end{aligned}$$
(85)

Remark 11

Recalling the vertices (75), it is easy to see that \(\det (t {\varvec{A}})\) represents the area of the region \({\mathcal {R}}(t)\) defined in (78).

For a given sample path of the process \(\{(X(t), Y(t), V(t)), t \in {\mathbb {R}}_0^{+}\}\) we denote by \(\xi _j=\xi _j(x,y,t)\) the value attained by the residence times of the motion in each direction \(\vec {v}_j\) during [0, t] such that \((X(t), Y(t))=(x,y)\), given by

$$\begin{aligned} \int _0^t \mathbbm {1}_{\{V(s)=\vec {v}_j\}} \textrm{d}s, \qquad j=1,2,3, \end{aligned}$$
(86)

where \(\mathbbm {1}_{\{V(s)=\vec {v}_j\}}\) is the indicator function

$$\begin{aligned} \mathbbm {1}_{\{V(s)=\vec {v}_j\}}= {\left\{ \begin{array}{ll} 1 \qquad \text {if }V(s)=\vec {v}_j \\ 0 \qquad \text {otherwise,} \end{array}\right. } \qquad j=1,2,3, \end{aligned}$$
(87)

so that \(\sum _{j=1}^3\xi _j=t\). It is not hard to see that \(\varvec{\xi }=(\xi _1,\xi _2,\xi _3)^T\) is solution of the system \({\varvec{A}}\, \varvec{\xi }= (x,y,t)^T\). Therefore, recalling (85) and (75), we can express \(\xi _j\) in terms of \(\varvec{\theta }=(\theta _1,\theta _2,\theta _3)\) as follows, for \(j=1,2,3\),

$$\begin{aligned} \xi _j=\frac{1}{\Theta (\varvec{\theta })}\left[ \frac{x}{c}(\sin \theta _{j \hat{+} 1}-\sin \theta _{j \hat{+} 2})-\frac{y}{c}(\cos \theta _{j \hat{+} 1}-\cos \theta _{j \hat{+} 2})+t \sin (\theta _{j \hat{+} 2}-\theta _{j \hat{+} 1}) \right] , \nonumber \\ \end{aligned}$$
(88)

where \(a\hat{+}b\) denotes \((a + b)\mod 3\), and

$$\begin{aligned} \Theta (\varvec{\theta }) =\frac{\det ({\varvec{A}})}{c^2} =\sin (\theta _3-\theta _2)+\sin (\theta _2-\theta _1)+\sin (\theta _1-\theta _3). \end{aligned}$$
(89)

We are now able to formulate the following result about the absolutely continuous component of the process (X(t), Y(t), V(t)), which is concerning the case (iii) considered above. To this aim, we denote by \(f_{D_{j}^{(n)}}\) the p.d.f. of \(D^{(n)}_{j}\), cf. (73). Hence, due to (74), \(f^{(0)}_{D_{j}}\) are delta-Dirac functions, for \(j=1,2,3\). Moreover, we indicate with \({\overline{F}}_{D_{j ,k+1}\vert D_j^{(k)}}\) the conditional survival function of \(D_{j,k+1}\).

Theorem 4

(Absolutely continuous components) For the stochastic process \(\{(X(t), Y(t), V(t)), t \in {\mathbb {R}}_0^{+}\}\) defined in Sect. 4.1, under the initial condition \(B_1\), the absolutely continuous components of the probability law are expressed as follows, for all \((x,y) \in \mathring{{\mathcal {R}}}(t)\) and \(t \in {\mathbb {R}}^+\):

$$\begin{aligned} \begin{aligned} p_{1j}(x,y,t)&=\, \frac{1}{ {\det ({\varvec{A}})} } \sum _{k=0}^{\infty }\Bigg \{\prod _{i=1}^{j-1} f_{D_{i}^{(k+1)}}(\xi _{i})\prod _{i=j+1}^{3} f_{D_{i}^{(k)}}(\xi _i)\\&\times \int _{t-\xi _j}^{t} f_{D_{j}^{(k)}}\big (s-(t-\xi _j)\big ) \, {\overline{F}}_{D_{j ,k+1}\vert D_j^{(k)}}\big (t-s\,\vert \,s-(t-\xi _j)\big )\,\textrm{d}s \Bigg \}, \end{aligned} \end{aligned}$$
(90)

where \(\xi _j=\xi _j(x,y,t)\), for \(j=1,2,3\), is defined as in Eq. (88), and where \(\det ({\varvec{A}})\) can be recovered from (89).

Proof

By conditioning on the number of direction switches in (0, t), say k, and on the last instant s previous to t in which the particle changes its direction to restart a cycle, we can rewrite Eq. (81) as follows (with \(j=1,2,3\))

$$\begin{aligned} \begin{aligned} p_{1j}(x,y,t) \textrm{d}x\textrm{d}y = \sum _{k=0}^{\infty }\int _0^t {\mathbb {P}}\big \{&T_{3k+j-1} \in \textrm{d}s, X(s)+c(t-s) \cos \theta _j \in \textrm{d}x, \\&Y(s)+c(t-s) \sin \theta _j \in \textrm{d}y, D_{j,k+1} > t-s\big \}, \end{aligned} \end{aligned}$$
(91)

where \(T_{3k+j-1}\) is a switching instant occurring at time s such that the particle’s direction becomes \(\vec {v}_j\). Thus, (X(s), Y(s)) is the position of the particle when such direction’s change occurs. Therefore, due to Eq. (72), one has

$$\begin{aligned} T_{3k+j-1}=\sum _{i=1}^{j-1} D_{i}^{(k+1)} +\sum _{i=j+1}^{3} D_{i}^{(k)}+D_{j}^{(k)}. \end{aligned}$$
(92)

Hence, for \(s=T_{3k+j-1}\) it follows that (X(s), Y(s)) can be expressed as suitable combinations of the sums (73) as

$$\begin{aligned} \begin{aligned}&X(s)=c \Bigg [\sum _{i=1}^{j-1} D_{i}^{(k+1)} \cos \theta _i +\sum _{i=j+1}^{3} D_{i}^{(k)} \cos \theta _i+D_{j}^{(k)} \cos \theta _j\Bigg ], \\&Y(s)=c \Bigg [\sum _{i=1}^{j-1} D_{i}^{(k+1)} \sin \theta _i +\sum _{i=j+1}^{3} D_{i}^{(k)} \sin \theta _i+D_{j}^{(k)} \sin \theta _j\Bigg ]. \end{aligned} \end{aligned}$$
(93)

Recalling Eq. (78), the condition \((X(s), Y(s)) \in {\mathcal {R}}(s)\) implies that \(s > t-\xi _j\). Furthermore, using (85) and substituting Eqs. (92) and (93) in Eq. (91), we have

$$\begin{aligned} \begin{aligned} p_{1j}(x,y,t)=&\frac{1}{\det ({\varvec{A}})} \sum _{k=0}^{\infty }\Bigg \{\int _{t-\xi _j}^{t} \phi _{j,k}\Big [s,x-c(t-s)\cos \theta _j,y-c(t-s)\sin \theta _j\Big ]\\&\times {\mathbb {P}}\Big [D_{j ,k+1} > t-s\, \Big \vert \, T_{3k+j-1}=s, X(T_{3k+j-1})= x-x_{\vec {v}_j}(t-s), \\&\quad Y(T_{3k+j-1})=y-y_{\vec {v}_j}(t-s) \Big ] \text {d}s \Bigg \}, \end{aligned} \end{aligned}$$
(94)

where \(\phi _{j,k}\) is the joint p.d.f. of \((T_{3k+j-1}, X(T_{3k+j-1}), Y(T_{3k+j-1}))\), with

$$\begin{aligned}{} & {} T_{3k+j-1}= \sum _{i=1}^{j-1} D_{i}^{(k+1)} +\sum _{i=j+1}^{3} D_{i}^{(k)}+D_{j}^{(k)}, \end{aligned}$$
(95)
$$\begin{aligned}{} & {} X(T_{3k+j-1})= \sum _{i=1}^{j-1} x_{\vec {v}_i} D_{i}^{(k+1)} +\sum _{i=j+1}^{3} x_{\vec {v}_i} D_{i}^{(k)} +x_{\vec {v}_j} D_{j}^{(k)}, \end{aligned}$$
(96)
$$\begin{aligned}{} & {} Y(T_{3k+j-1})= \sum _{i=1}^{j-1} y_{\vec {v}_i} D_{i}^{(k+1)} +\sum _{i=j+1}^{3} y_{\vec {v}_i} D_{i}^{(k)}+y_{\vec {v}_j} D_{j}^{(k)}. \end{aligned}$$
(97)

According to (84), we have

$$\begin{aligned} x_{\vec {v}_i} = v_i\,\cos \theta _i, \qquad y_{\vec {v}_i} = v_i\,\sin \theta _i, \qquad i=1,2,3. \end{aligned}$$
(98)

Due to the mutual independence of the variables \(\{D_{j,k}; \; k \in {\mathbb {N}}\}_{j=1,2,3}\), we get

$$\begin{aligned} \begin{aligned} \phi _{j,k}\Big [s,x-c(t-s)&\cos \theta _j,y-c(t-s)\sin \theta _j\Big ]= \\&=\prod _{i=1}^{j-1} f_{D_{i}^{(k+1)}}(\xi _{i})\prod _{i=j+1}^{3} f_{D_{i}^{(k)}}(t-\xi _i)\, f_{D_{j}^{(k)}}[s-(t-\xi _j)], \end{aligned} \end{aligned}$$
(99)

due to Eq. (88). Therefore, Eq. (90) is directly obtained replacing (99) in Eq. (94). \(\square \)

Remark 12

In analogy with the one-dimensional case, cf. Remark 1, we note that the term \(\det ({\varvec{A}})\) in the right-hand-side of Eq. (90) can be viewed as the measure of the state-space at time \(t=1\), i.e. \(\mathcal{R}(1)\) (cf. Remark 11).

We point out that the cyclic update condition is regulated by the switching times considered in Eq. (92) and by the particle position expressed in Eq. (93). Since the sequence of directions of the motion is fixed by a non-random rule this allows to express those equations in a tractable way. On the contrary, more complex dynamics concerning the random choices of directions would provide for the inclusion of an additional element of randomness in those equations, leading to less tractable expressions. For instance, some results concerning the case when the directions are picked randomly with constant intensities are given in Santra et al. [40].

Clearly, the results given in Theorems 3 and 4 for the discrete and absolutely continuous component of the process can be obtained in a similar way also when the initial velocity is \(V(0)=\vec {v}_2\) and \(V(0)=\vec {v}_3\).

4.2 An Analysis of a Special Case

In this section we analyze an instance of the process considered above, under the initial condition \(B_1\).

Assumptions 1

We consider the following conditions:

  1. (i)

    The motion is characterized by the three directions led by the following angles:

    $$\begin{aligned} \theta _1=\frac{\pi }{3}, \qquad \theta _2=\pi , \qquad \theta _3=\frac{5}{3}\pi . \end{aligned}$$
    (100)
  2. (ii)

    The durations \(D_{j,1}, D_{j,2}, \ldots \) constitute the intertimes of a GCP with intensity \(\lambda _j\in {\mathbb {R}}^+\), where \(D_{j,n}\) is the j-th duration of the motion within the n-th cycle, for \(j=1,2,3\) and \(n\in {\mathbb {N}}\).

In Fig. 3 we show an example of projections onto the state-space of suitable paths of the process \(\{(X(t), Y(t)), t \in {\mathbb {R}}_0^{+}\}\) under the Assumptions 1.

The given assumptions differ from those of similar two-dimensional finite-velocity processes studied in the recent literature. Indeed, apart from the cyclic motions in \({\mathbb {R}}^2\) described in Sect. 1 (see e.g. [10, 30, 31]), Santra et al. [40] considered run-and-tumble particle dynamics regulated by constant switching rates among possible orientations of the particle which can assume a set of discrete values or are governed by a continuous random variable.

According to (78), condition (i) of Assumptions 1 implies that the particle at every instant \(t \in {\mathbb {R}}^+\) is confined in the triangle

$$\begin{aligned} {\mathcal {R}}(t)=\bigg \{(x,y) \in {\mathbb {R}}^2: x \le \frac{1}{2}ct, \; \vert y\vert \le \frac{\sqrt{3}}{3}(x+ct)\bigg \}, \end{aligned}$$
(101)

whose vertices are

$$\begin{aligned} A_1(t)=\Bigg (\frac{1}{2},\frac{\sqrt{3}}{2}\Bigg )ct, \quad A_2(t)=\Bigg (-1,0\Bigg )ct, \quad A_3(t)=\Bigg (\frac{1}{2},-\frac{\sqrt{3}}{2}\Bigg )ct. \end{aligned}$$
(102)

Figure 4 shows a sample of the set \({\mathcal {R}}(t)\) defined in (101), with directions \(\vec {v}_1\), \(\vec {v}_2\) and \(\vec {v}_3\) led by the angles given in (100). Since the angles (100) satisfy conditions (71), it is ensured that the particle can reach any state, i.e. \({\mathcal {R}}(t)\rightarrow {\mathbb {R}}^2\) as \(t\rightarrow \infty \).

Fig. 3
figure 3

Two possible paths depicting the first 10 segments of the planar cyclic motion defined in Sect. 4.1. The initial velocity is \(\vec {v}_1\), and angles are fixed as in (100)

Full size image
Fig. 4
figure 4

A sample of the set \({\mathcal {R}}(t)\) with velocities \(\vec {v}_1\), \(\vec {v}_2\), \(\vec {v}_3\) and fixed angles as in (100)

Full size image

We recall that the sequences \(\{D_{j,k}; \; k \in {\mathbb {N}}\}_{j=1,2,3}\) are mutually independent. Moreover, under condition (ii) of Assumptions 1, for \(j=1,2,3\) the durations \(D_{j,n}\), \(n\in {\mathbb {N}}\), are dependent random variables having marginal p.d.f. (cf. Eq. (11) of [13])

$$\begin{aligned} f_{D_{j,n}}(t)=\frac{\lambda _j}{(1+\lambda _j t)^2}, \qquad t\in {\mathbb {R}}^+. \end{aligned}$$
(103)

Hereafter we determine the explicit probability laws of the process under the assumptions considered so far, i.e. when the random intertimes of the motion along the possible directions follow three independent GCPs with intensities \(\lambda _1\), \(\lambda _2\) and \(\lambda _3\).

Theorem 5

Let \(\{(X(t), Y(t), V(t)), t \in {\mathbb {R}}_0^{+}\}\) be the stochastic process defined in Sect. 4.1, under initial condition \(B_1\). If the Assumptions 1 hold, then for all \(t \in {\mathbb {R}}^+\) we have

$$\begin{aligned} {\mathbb {P}}\bigg \{X(t)=\frac{1}{2} ct, Y(t)=\frac{\sqrt{3}}{2} ct, V(t)=\vec {v}_1\,\Big \vert \, B_1\bigg \}=\frac{1}{1+\lambda _1\,t}, \end{aligned}$$
(104)

and

$$\begin{aligned} \begin{aligned} {\mathbb {P}}\{[X(t), Y(t)]&\in E_{12}(t), V(t)=\vec {v}_{1}\,\vert \, B_1\} \\&=\frac{\lambda _1 \lambda _2 t[\lambda _1^2(1+\lambda _2\,t)+\lambda _2^2(1+\lambda _1\,t)]}{(\lambda _1+\lambda _2+\lambda _1 \lambda _2\, t)^2(1+\lambda _1\,t)(1+\lambda _2\,t)} \\&+\frac{2\lambda _1^2\, \lambda _2^2\log [(1+\lambda _1\,t)(1+\lambda _2\,t)]}{(\lambda _1+\lambda _2+\lambda _1 \lambda _2\, t)^3} -\frac{\lambda _1}{1+\lambda _1\,t}. \end{aligned} \end{aligned}$$
(105)

Moreover, for all \((x,y) \in \mathring{{\mathcal {R}}}(t)\), with reference to the region \({{\mathcal {R}}}(t)\) in (101), we have

$$\begin{aligned} \begin{aligned}&p_{11}(x,y,t)=\lambda _1\lambda _2 \lambda _3 \xi _1\, \frac{1+A(\varvec{\xi })+B(\varvec{\xi })+2C(\varvec{\xi })}{\det ({{\textbf{A}})}\Big [1+A(\varvec{\xi })+B(\varvec{\xi }) \Big ]^3}, \\&p_{12}(x,y,t)=2 \lambda _1^2 \lambda _2 \lambda _3 \xi _1\xi _2 \, \frac{(1+\lambda _2\xi _2)(1+\lambda _3 \xi _3)}{\det ({\textbf{A}})\Big [1+A(\varvec{\xi })+B(\varvec{\xi }) \Big ]^3}, \\&p_{13}(x,y,t) = \lambda _1\lambda _2(1+\lambda _3\xi _3)\, \frac{1+A(\varvec{\xi })+B(\varvec{\xi })+2C(\varvec{\xi })}{\det ({\textbf{A}})\Big [1+A(\varvec{\xi })+B(\varvec{\xi }) \Big ]^3}, \end{aligned} \end{aligned}$$
(106)

with

$$\begin{aligned} \det ({\textbf{A}})= \frac{3\sqrt{3}}{2}\,c^2, \quad A(\varvec{\xi })=\sum _{i=1}^3 \lambda _i \xi _i, \quad B(\varvec{\xi })=\sum _{\begin{array}{c} i,j=1 \\ i <j \end{array}}^{3}\lambda _i\lambda _j \xi _i\xi _j, \quad C(\varvec{\xi })=\prod _{i=1}^3 \lambda _i \xi _i\nonumber \\ \end{aligned}$$
(107)

and where the terms \(\xi _j=\xi _j(x,y,t)\), \(j=1,2,3\), are given by

$$\begin{aligned} \xi _1=\frac{ct+x+\sqrt{3}y}{3c}, \qquad \xi _2=\frac{ct-2x}{3c}, \qquad \xi _3=\frac{ct+x-\sqrt{3}y}{3c}. \end{aligned}$$
(108)

Proof

Recalling Theorem 3, the discrete components of the process are obtained from Eqs. (79) and (80). The absolutely continuous components in Eq. (106) are obtained in closed form as an immediate consequence of Theorem 4 after straightforward but tedious calculations. The right-hand-side of Eq. (90) is made explicit by using the finite sum of the resulting series as seen in Eq. (29) of Theorem 1. \(\square \)

We remark that the values of \(\xi _j\) in (108) are obtained directly from Eq. (88) given the angles in (100). Moreover, due to (83), under the assumptions of Theorem 5 the p.d.f. \(p_{1}(x,y,t)\) can be immediately obtained from Eq. (106). Similarly to the one-dimensional case treated in Corollary 5, we are now able to study the asymptotic behaviour of the p.d.f. of the particle location defined in (82) when the intensities \(\lambda _j\) tend to infinity.

Corollary 6

Under the assumptions of Theorem 5, for \(t\in {\mathbb {R}}^+\) and \((x,y) \in \mathring{{\mathcal {R}}}(t)\) one has

$$\begin{aligned} \mathop {\lim }\limits _{\begin{array}{c} \lambda _1, \lambda _2, \lambda _3 \rightarrow +\infty \\ \lambda _1/\lambda _2\rightarrow 1, \; \lambda _1/\lambda _3\rightarrow 1 \end{array}} p_{1}(x,y,t) = \eta (x,y,t), \end{aligned}$$
(109)

where \(\eta (x,y,t)\) is the following p.d.f.

$$\begin{aligned} \eta (x,y,t) = \frac{2t \,\xi _1\xi _2 \xi _3}{\det ({{\textbf{A}}})\big [(\xi _1 \xi _2)^3+(\xi _1 \xi _3)^3+(\xi _2 \xi _3)^3\big ]}, \end{aligned}$$
(110)

with \(\xi _j\)’s introduced in (108).

Fig. 5
figure 5

Plot of \(\eta (x,y,t)\) for \(c t=1\)

Full size image

Figure 5 shows a plot of the limiting three-peaked density obtained in Corollary 6.

The results expressed so far in this section for \(V(0)=\vec {v}_1\) can be extended to the cases \(V(0)=\vec {v}_2\) and \(V(0)=\vec {v}_3\) by adopting a similar procedure.

5 Conclusions

This paper has been centered on the analysis of telegraph processes in one and two dimensions, with cyclically alternating directions, when the changes of direction follow a GCP. The presence of intertimes possessing Pareto-type distributions yields results that are quite different from those concerning the classical telegraph process with exponential intertimes.

In view of potential applications in engineering, financial and actuarial sciences, we note that possible future developments can be oriented to

  • the study of first-passage-time problems for the considered processes,

  • the extension of the stochastic model to the case of a non-minimal number of directions, along the research line exploited by Lachal [22],

  • the analysis of other dynamics governed by differently distributed inter-arrival times and more general counting processes, even non-homogeneous processes as treated, for instance, in Yakovlev et al. [44].

Further research areas in which the finite-velocity random motions can be used for applications related to (i) mathematical geology, for the description of alternating trends in volcanic areas, to (ii) mathematical biology, for the modelling of the random motions of microorganisms, and to (iii) mathematical physics, for the constructions of simple stochastic models of vorticity motions in two or more dimensions.