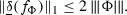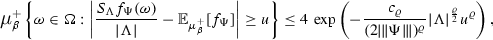On Concentration Inequalities and Their Applications for Gibbs Measures in Lattice Systems

Abstract

We consider Gibbs measures on the configuration space $S^{{\mathbb {Z}}^d}$, where mostly $d\ge 2$ and S is a finite set. We start by a short review on concentration inequalities for Gibbs measures. In the Dobrushin uniqueness regime, we have a Gaussian concentration bound, whereas in the Ising model (and related models) at sufficiently low temperature, we control all moments and have a stretched-exponential concentration bound. We then give several applications of these inequalities whereby we obtain various new results. Amongst these applications, we get bounds on the speed of convergence of the empirical measure in the sense of Kantorovich distance, fluctuation bounds in the Shannon–McMillan–Breiman theorem, fluctuation bounds for the first occurrence of a pattern, as well as almost-sure central limit theorems.

1 Introduction

Concentration inequalities play by now an important role in probability theory and statistics, as well as in various areas such as geometry, functional analysis, discrete mathematics [4, 12, 25]. Remarkably, the scope of these inequalities ranges from the more abstract to the explicit analysis of given models. With a view towards our setting, the elementary manifestation of the concentration of measure phenomenon can be formulated as follows. Consider independent random variables $\{\omega _x, x \in C_n\}$ taking the values $\pm \,1$ with equal probability and indexed by the sites of a large but finite discrete cube $C_n$ of “side length” $2n+1$ in ${\mathbb {Z}}^d$. The partial sum $\sum _{x\in C_n} \omega _x$ has expectation zero. Of course, this sum varies in an interval of size $\mathcal {O}(n^d)$. But, in fact, it sharply concentrates with very high probability in a much narrower range, namely in an interval of size $\mathcal {O}(n^{d/2})$. This statement is quantified by the following “Gaussian bound” or Hoeffding inequality (see [4]):

$$\begin{aligned} \mathbb {P}\left\{ \left| \sum _{x\in C_n} \omega _x\right| \ge u\, (2n+1)^{d/2} \right\} \le 2\, \exp \left( -\frac{u^2}{2}\right) \end{aligned}$$

for all $n\ge 1$ and for all $u>0$. This is a finite-volume quantitative version of the strong law of large numbers, giving the correct scale as in the central limit theorem. This phenomenon is not tied to linear combinations of the $\omega _x$’s, like the above sum, but in fact holds for a broad class of nonlinear functions F of the $\omega _x$’s. Thus, we can get tight bounds for the probability that a complicated or implicitly defined function of the $\omega _x$’s deviates from its expected value. Let us stress that concentration inequalities are valid in every finite volume, and not just asymptotically.

Now, what happens if the $\omega _x$’s are no longer independent? One can expect to still have a Gaussian bound of the same flavour as above provided correlations are weak enough amongst the $\omega _x$’s (see e.g. [8] about Markov chains, and [21] for a survey focused on the martingale method). In the present paper, we are interested in Gibbs measures on a configuration space of the form $\Omega =S^{{\mathbb {Z}}^d}$ where S is a finite set. In the above elementary example, we have $S=\{-1,1\}$ (spins) and the previously considered product measure can be thought as a Gibbs measure at infinite temperature. The first work in this setting is [23] in which it was proved that a Gaussian concentration bound holds in Dobrushin’s uniqueness regime (see below for a precise statement). The constant appearing in the bound is directly related to the “Dobrushin contraction coefficient”. For instance, any finite-range potential at sufficiently high temperature satisfies Dobrushin’s condition, like the Ising model. One of the main motivations of [9] was to figure out what happens for the Ising model at low temperature. One cannot expect that a Gaussian concentration bound holds (see details below), and it was proved in [9] that a stretched-exponential decay of the form $\exp (-c u^\varrho )$ holds, where $0<\varrho <1$ depends on the temperature. Notice that we deal with $d\ge 2$. For $d=1$, the situation is as follows. Finite-range potentials give rise to finite-state Markov chains and thus one has a Gaussian concentration bound. For potentials which are summable in certains sense, one has also a Gausian concentration bound, but the known results are formulated in terms of chains of infinite order (or g-measures) rather than Gibbs measures, see [16]. For long-range potentials, like Dyson models, nothing is known regarding concentration bounds. In that context, let us mention that g-measures can be different from Gibbs measures, see [2] and references therein.

The purpose of the present work is to apply these concentration bounds to various types of functions F of the $\omega _x$’s, both in Dobrushin’s uniqueness regime and in the Ising model at sufficiently low temperature. For example, we obtain quantitative estimates for the speed of convergence of the empirical measure to the underlying Gibbs measure in Kantorovich distance. In the Ising model, this speed depends in particular on the temperature regime. Here the estimation of the expected distance raises an extra problem which requires to adapt methods used to estimate suprema of empirical processes. The problem comes from the fact that our configuration space is topologically a Cantor set. Another application concerns “fattening” finite configurations in the sense of Hamming distance: take, e.g., $S=\{-1,1\}$ and consider the set $\Omega _n=\{\eta _x: x\in C_n\}$. Now, take a subset $\mathcal {B}_n\subset \Omega _n$ of, say, measure 1 / 2, and look at the set $\mathcal {B}_{n,\epsilon }$ of all configurations in $\Omega _n$ obtained from those in $\mathcal {B}_n$ by flipping, say, $\epsilon =5\%$ of the spins. It turns out that, for large but finite n, the set $\mathcal {B}_{n,\epsilon }$ has probability very close to 1. Besides fluctuation bounds, we also obtain an almost-sure central limit theorem, thereby showing how concentration inequalities can also lead to substantial reinforcements of weak limit theorems in great generality.

Concentration inequalities may look weaker than a “large deviation principle” [11]. On one hand, this is true because getting a large deviation principle means that one gets a rate function which gives the correct asymptotic exponential decay to zero of the probability that, e.g., $(2n+1)^{-d}\sum _{x\in C_n} \omega _x$ deviates from its expectation (the magnetization of the system). But, on the other hand, it is hopeless to get a large deviation principle for functions of the $\omega _x$’s which do not have some (approximate) additivity property. This rules out many interesting functions of the $\omega _x$’s. Besides, even in the situation when concentration inequalities and large deviation principles coexist, the former provides simple and useful bounds which are valid in every finite volume.

We also emphasize that concentration inequalities provide upper-bounds which are “permutation invariant”. In particular, for averages of the form $|\Lambda |^{-1}\sum _{x\in \Lambda } f(T_x \omega )$ one obtains bounds in which the dependence on $\Lambda$ is only through its cardinality, and thus insensitive to its shape. In the case of the Gaussian concentration bound, one obtains an upper bound for the logarithm of the exponential moment of $\sum _{x\in \Lambda } f(T_x \omega )$ which is of the order $|\Lambda |$. This provides an order of growth as would be provided by large deviation theory in contexts where the latter is not necessarily available. Indeed, in order to have a large deviation principle, it is necessary that the sets $\Lambda$ grow as a van Hove sequence, see e.g. [15]. An illustrative example is when $\Lambda$ is a subset of $\mathbb {Z}^d$ which is contained in a hyperplane of lower dimension (e.g., a subset of one of the coordinate planes). Indeed, there is a priori no large deviation principle available for projections of Gibbs measures on lower dimensional sets (they might fail to satisfy the variational principle), whereas concentration bounds are still possible.

Before giving the outline of this paper, let us mention the papers [5, 6, 10], and [30, 31], which deal with concentration inequalities for spin models from statistical mechanics. In [10], the author establishes, among other things, a Gaussian concentration bound for partial sums of a random field satisfying a “weak mixing” condition. This includes the Ising model above its critical temperature. In [5, 6], the authors obtain concentration inequalities for mean-field models, like the Curie–Weiss model. These results follow from a method introduced by Chatterjee in [5] (a version of Stein’s method).

The rest of our paper is organized as follows. After some generalities on concentration bounds given in Sect. 3 and tailored for our needs, we gather a number of facts on Gibbs measures which we will use in our applications (Sect. 4). We then review the known concentration properties of Gibbs measures, i.e., the Gaussian concentration bound which is valid in Dobrushin’s uniqueness regime (Sect. 5), and the moment inequalities, as well as a stretched-exponential concentration bound, which hold for the Ising model at sufficiently low temperature (Sect. 6). Then we derive various applications of the concentration bounds in Sects. 7–13.

2 Setting

2.1 Configurations and Shift Action

We work with the configuration space $\Omega =S^{{\mathbb {Z}}^d}$, where S is a finite set, and d an integer greater than or equal to 2. We endow $\Omega$ with the product topology that is generated by cylinder sets. We denote by ${\mathfrak {B}}$ the Borel $\sigma$-algebra which coincides with the $\sigma$-algebra generated by these sets.

An element x of ${\mathbb {Z}}^d$ (hereby called a site) can be written as a vector $(x_1,\ldots ,x_d)$ in the canonical base of the lattice ${\mathbb {Z}}^d$. Let $\Vert x\Vert _\infty =\max _{1\le i\le d} |x_i|$, and denote by $\Vert x\Vert _1$ the Manhattan norm, that is, $\Vert x\Vert _1=|x_1|+\cdots + |x_d|$. More generally, given an integer $p\ge 1$, let $\Vert x\Vert _p=(|x_1|^p+\cdots +|x_d|^p)^{1/p}$. If $\Lambda$ is a finite subset of ${\mathbb {Z}}^d$, denote by $\text {diam}(\Lambda )=\max \{\Vert x\Vert _\infty : x\in \Lambda \}$ its diameter, and by $|\Lambda |$ its cardinality. The collection of finite subsets of ${\mathbb {Z}}^d$ will be denoted by $\mathcal {P}$.

We consider the following distance on $\Omega$ : for $\omega ,\omega '\in \Omega$, let

$$\begin{aligned} d(\omega ,\omega ')=2^{-k}\quad \text {where}\; k=\min \big \{\Vert x\Vert _\infty : \omega _x\ne \omega '_x\big \}. \end{aligned}$$

(1)

This distance induces the product topology, and one can prove that $(\Omega ,d)$ is a compact metric space. Note that $\Omega$ is a Cantor set, so it is totally disconnected.

For $\Lambda \subset {\mathbb {Z}}^d$, we denote by $\Omega _\Lambda$ the projection of $\Omega$ onto $S^\Lambda$. Accordingly, an element of $\Omega _\Lambda$ is denoted by $\omega _\Lambda$ and is viewed as a configuration $\omega \in \Omega$ restricted to $\Lambda$. Another useful notation is the following. For $\sigma ,\eta \in \Omega$ we denote by $\sigma _\Lambda \eta _{\Lambda ^c}$ the configuration which agrees with $\sigma$ on $\Lambda$ and with $\eta$ on $\Lambda ^c$. Finally, we denote by ${\mathfrak {B}}_\Lambda$ the $\sigma$-algebra generated by the coordinate maps $f_x:\omega \mapsto \omega _x$, $x\in \Lambda$.

Subsets of particular interest are cubes centered about the origin of ${\mathbb {Z}}^d$: for every $n\in \mathbb {N}$, define

$$\begin{aligned} C_n=\big \{x\in {\mathbb {Z}}^d: -n\le x_i\le n,\,i=1,2,\ldots ,d\big \}. \end{aligned}$$

For $\omega \in \Omega$ and $n\in \mathbb {N}$, define the cylinder set

$$\begin{aligned} \mathcal {C}_n(\omega )=\big \{\eta \in \Omega : \eta _{C_n}=\omega _{C_n}\big \}. \end{aligned}$$

We simply write $\Omega _n$ for $\Omega _{C_n}$ which is the set of partial configurations supported on $C_n$.

Finally, the shift action $(T_x,x\in {\mathbb {Z}}^d)$ is defined as usual: for each $x\in {\mathbb {Z}}^d$, $T_x:\Omega \rightarrow \Omega$ and $(T_x\omega )_y=\omega _{y-x}$, for all $y\in {\mathbb {Z}}^d$. This corresponds to translating $\omega$ forward by x.

2.2 Functions

Let $F:\Omega \rightarrow \mathbb {R}$ be a continuous function and $x\in {\mathbb {Z}}^d$. We denote by

the oscillation of F at x. It is a natural object because, given a finite subset $\Lambda \subset {\mathbb {Z}}^d$ and two configurations $\omega ,\eta \in \Omega$ such that $\omega _{\Lambda ^c}=\eta _{\Lambda ^c}$, one has

$$\begin{aligned} |F(\omega )-F(\eta )| \le \sum _{x\in \Lambda } \delta _x(F). \end{aligned}$$

We shall say that $F:\Omega \rightarrow \mathbb {R}$ is a local function if there exists a finite subset $\Lambda _F$ of ${\mathbb {Z}}^d$ (the dependence set of F) such that for all $\omega ,{\widetilde{\omega }},{\widehat{\omega }}$, $F(\omega _{\Lambda _F}{\widetilde{\omega }}_{\Lambda ^c_F}) = F(\omega _{\Lambda _F}{\widehat{\omega }}_{\Lambda ^c_F})$. Equivalently, $\delta _x(F)=0$ for all $x\notin \Lambda _F$. It is understood that $\Lambda _F$ is the smallest such set. When $\Lambda _F=C_n$ for some n, F is said to be “cylindrical”.

Let $C^0(\Omega )$ be the Banach space of continuous functions $F:\Omega \rightarrow \mathbb {R}$ equipped with supremum norm $\Vert F\Vert _\infty =\sup _{\omega \in \Omega } |F(\omega )|$. Every local function is continuous and the uniform closure of the set of all local functions is $C^0(\Omega )$. Given F, we write for the infinite array $(\delta _x(F), x\in {\mathbb {Z}}^d)$. For every $p\in \mathbb {N}$, we introduce the semi-norm

Finally, we define the following spaces of functions:

(2)

Each of these spaces obviously contains local functions, and $\Delta _p(\Omega )\subset \Delta _q(\Omega )$ if $1\le p<q\le +\,\infty$. Notice that the space of functions such that for a given $p\in \mathbb {N}$ is neither contained in nor contains $C^0(\Omega )$.

Define the oscillation of a function $F:\Omega \rightarrow \mathbb {R}$ as

$$\begin{aligned} \delta (F)=\sup F -\inf F = \sup _{\omega ,\omega '\in \Omega } |F(\omega )-F(\omega ')|. \end{aligned}$$

If $F\in C^0(\Omega )$, one has

For $p\in \mathbb {N}$, the semi-norm becomes a norm if one considers the quotient space where two functions in $\Delta _p(\Omega )$ are declared to be equivalent if their difference is a constant function. Moreover, this quotient space equipped with the norm is a Banach space.

3 Concentration Bounds for Random Fields: Abstract Definitions and Consequences

We state some abstract definitions and their general consequences that we will use repeatedly in the sequel.

3.1 Gaussian Concentration Bound

Definition 3.1

Let $\nu$ be a probability measure on $(\Omega ,{\mathfrak {B}})$. We say that it satisfies the Gaussian concentration bound with constant $D=D(\nu )>0$ (abbreviated $\mathrm {GCB}\!\left( D\right)$) if, for all functions $F\in \Delta _2(\Omega )$, we have

(3)

A key point in this definition is that D is independent of F. Inequality (3) easily implies Gaussian concentration inequalities that we gather in the following proposition in a convenient form for later use.

Proposition 3.1

If a probability measure $\nu$ on $(\Omega ,{\mathfrak {B}})$ satisfies $\mathrm {GCB}\!\left( D\right)$ then, for all functions $F\in \Delta _2(\Omega )$ and for all $u>0$, one has

(4)

(5)

Proof

If $F\in \Delta _2(\Omega )$, then $\lambda F\in \Delta _2(\Omega )$ for any $\lambda \in \mathbb {R}_+$. We apply Markov’s inequality and (3) to get

We now optimize over $\lambda$ to get (4). Applying this inequality to $-F$ gives the same inequality if ‘$\ge u$’ is replaced by ‘$\le -u$’, whence

which is (5). $\square$

3.2 Moment Concentration Bounds

Definition 3.2

Given $p\in \mathbb {N}$, we say that a probability measure $\nu$ on $(\Omega ,{\mathfrak {B}})$ satisfies the moment concentration bound of order 2p with constant $C_{2p}=C_{2p}(\nu )>0$ [abbreviated $MCB(2p,C_{2p})$] if, for all functions $F\in \Delta _2(\Omega )$, we have

(6)

Again, as for the Gaussian concentration bound, the point is that the involved constant, namely $C_{2p}$, is required to be independent of F. An application of Markov’s inequality immediately gives the following polynomial concentration inequality:

(7)

for all $u>0$.

3.3 Gaussian Tails and Growth of Moments

Let Z be a real-valued random variable with $\mathbb {E}[Z]=0$. If for some positive constant K

$$\begin{aligned} \mathbb {E}[Z^{2p}]\le p! K^p,\;\forall p\in \mathbb {N}, \end{aligned}$$

then $\mathbb {E}[e^{\lambda Z}]\le e^{2K \lambda ^2}$ for all $\lambda \in \mathbb {R}$. Applied to $Z=F-\mathbb {E}_\nu [F]$ for a probability measure $\nu$ satisfying $\mathrm {GCB}\!\left( D\right)$ for all $p\in \mathbb {N}$, this gives a road to establishing that Z satisfies a Gaussian concentration bound.

Conversely, if there exists a constant $K>0$ such that for all $u>0$

$$\begin{aligned} \max \{\mathbb {P}(Z\ge u),\mathbb {P}(-Z\ge u)\}\le \exp \left( -\frac{u^2}{2K}\right) , \end{aligned}$$

then for every integer $p\ge 1$,

$$\begin{aligned} \mathbb {E}[Z^{2p}]\le p!\, (4K)^p. \end{aligned}$$

Applied to $Z=F-\mathbb {E}_\nu [F]$ for a probability measure $\nu$ satisfying $\mathrm {GCB}\!\left( D\right)$, we have (4) and (5) with , thus we get (6) with $C_{2p}=p! (8D)^p$. We refer to [4, Theorem 2.1, p. 25] for a proof of these two general statements.

4 Gibbs Measures

For the sake of convenience, we briefly recall some facts about Gibbs measures which will be used later on. We refer to [17] for details. The largest class of potentials we consider is that of shift-invariant “uniformly summable” potentials.

4.1 Potentials

A potential is a function $\Phi :\mathcal {P}\times \Omega \rightarrow \mathbb {R}$. (Recall that $\mathcal {P}$ is the collection of finite subsets of ${\mathbb {Z}}^d$.) We will assume that $\omega \mapsto \Phi (\Lambda ,\omega )$ is ${\mathfrak {B}}_\Lambda$-measurable for every $\Lambda \in \mathcal {P}$. Shift-invariance is the requirement that $\Phi (\Lambda +x,T_x\omega )=\Phi (\Lambda ,\omega )$ for all $\Lambda \in \mathcal {P}$, $\omega \in \Omega$ and $x\in {\mathbb {Z}}^d$ (where $\Lambda +x=\{y+x: y\in \Lambda \}$). Uniform summability is the property that

(8)

We shall denote by ${\mathscr {B}}_T$ the space of uniformly summable shift-invariant continuous potentials. Equipped with the norm , it is a Banach space.

The most important subclass of uniformly summable shift-invariant potentials is the class of finite-range potentials. A finite-range potential is such that there exists $R>0$ such that $\Phi (\Lambda ,\omega )=0$ if $\text {diam}(\Lambda )>R$. The smallest such R is called the range of the potential. More formally, $R=R(\Phi )=\max _{\Lambda :\Phi (\Lambda ,\cdot )\not \equiv 0}\text {diam}(\Lambda )$. Nearest-neighbor potentials correspond to the case $R=1$. The set of potentials with finite range is dense in ${\mathscr {B}}_T$.

Now define the continuous function

$$\begin{aligned} f_\Phi (\omega )=\sum _{\Lambda \ni 0} \frac{\Phi (\Lambda ,\omega )}{|\Lambda |}. \end{aligned}$$

(9)

The quantity $f_\Phi (\omega )$ can be interpreted as the mean energy per site in the configuration $\omega$.

4.2 Gibbs Measures

Given $\Phi \in {\mathscr {B}}_T$ and $\Lambda \in \mathcal {P}$, the associated Hamiltonian in the finite volume $\Lambda$ with boundary condition $\eta \in \Omega$ is given by

$$\begin{aligned} \mathcal {H}_{\Lambda }(\omega |\eta )= \sum _{\begin{array}{c} \Lambda '\in \mathcal {P}\\ \Lambda '\cap \Lambda \ne \emptyset \end{array}} \Phi (\Lambda ',\omega _{\Lambda }\eta _{{\mathbb {Z}}^d\backslash \Lambda })\,. \end{aligned}$$

The corresponding specification is then defined as

$$\begin{aligned} \varvec{\gamma }^{\Phi }_{\Lambda } (\omega |\eta ) =\frac{\exp \left( -\mathcal {H}_{\Lambda }(\omega |\eta )\right) }{Z_{\Lambda }(\eta )}\, \end{aligned}$$

(10)

where $Z_{\Lambda }(\eta )$ is the partition function in $\Lambda$ (normalizing factor). We say that $\mu$ is a Gibbs measure for the potential $\Phi$ if $\varvec{\gamma }^{\Phi }_{\Lambda } (\omega |\cdot )$ is a version of the conditional probability $\mu (\omega _{\Lambda }| {\mathfrak {B}}\!_{\Lambda ^c})$. Equivalently, this means that for all $A\in {\mathfrak {B}}$, $\Lambda \in \mathcal {P}$, one has the so-called “DLR equations”

$$\begin{aligned} \mu (A)=\int \mathop {}\!\mathrm {d}\mu (\eta ) \sum _{\omega '\in \Lambda } \varvec{\gamma }^{\Phi }_{\Lambda } (\omega '|\eta ) \, \mathbb {1}\!_{A}(\omega '_{\Lambda }\eta _{\Lambda ^c}). \end{aligned}$$

(11)

A consequence of (8) is that for all $\Lambda \supset \Lambda '$ such that $\Lambda \in \mathcal {P}$, for all $\omega ,{{\tilde{\omega }}}$ such that $\omega _x={{\tilde{\omega }}}_x$ $\forall x\notin \Lambda '$, we have

As a further consequence we get

(12)

The set of Gibbs measures for a given potential is never empty but it may be not reduced to a singleton. This set necessarily contains at least one Gibbs measure that is shift invariant.

Finally, let

$$\begin{aligned} P(\Phi )=\lim _{n\rightarrow \infty } \frac{1}{(2n+1)^d} \log Z_{C_n}(\eta ^{(n)}) \end{aligned}$$

(13)

which exists for any sequence $(\eta ^{(n)})_{n\ge 1}$ and depends only on $\Phi$. At certain places in the sequel, we will need a good control on the measure of cylinders in terms of the ergodic sum of $f_\Phi$. To ensure this we will have to assume additionally that $\Phi$ satisfies

$$\begin{aligned} \sum _{n\ge 1} n^{d-1} \sum _{\begin{array}{c} \Lambda \ni 0\\ \Lambda \cap ({\mathbb {Z}}^d\backslash C_n)\ne \emptyset \end{array}} \frac{\Vert \Phi (\Lambda ,\cdot )\Vert _\infty }{|\Lambda |}<\infty . \end{aligned}$$

(14)

This condition is obviously satisfied by any finite-range potential, but also by a class of spin pair potentials (see below). This condition implies

$$\begin{aligned} \sum _{n\ge 1} n^{d-1}\, \text {var}_n(f_\Phi )<\infty \end{aligned}$$

where $\text {var}_n(f_\Phi ):=\sup \{|f_\Phi (\omega )-f_\Phi (\omega ')| : \omega _{C_n}=\omega '_{C_n}\}$. From [19, Theorem 5.2.4, p. 100] it follows that there exists $C_\Phi >0$ such that for all $\omega \in \Omega$ and for all $n\in \mathbb {N}$, one has

$$\begin{aligned} e^{-C_\Phi (2n+1)^{d-1}}\le \frac{\mu _\Phi (\mathcal {C}_n(\omega ))}{e^{-(2n+1)^d P(\Phi )-\sum _{x\in C_n}f_\Phi (T_x \omega )}} \le e^{C_\Phi (2n+1)^{d-1}}. \end{aligned}$$

(15)

The point, which we will need later, is that, under (14), we have surface-order terms in the exponentials on both sides.

4.3 Entropy, Relative Entropy and the Variational Principle

The entropy (per site) of a shift-invariant probability measure $\nu$ is defined as

$$\begin{aligned} h(\nu )=\lim _{n\rightarrow \infty } -\frac{1}{(2n+1)^d} \sum _{\omega \in \Omega _n} \nu _n(\omega )\log \nu _n(\omega ) \;(\in [0,\log |S|]) \end{aligned}$$

where $\nu _n$ is the probability measure induced on $\Omega _n$ by projection, i.e., $\nu _n(\omega )=\nu (\mathcal {C}_n(\omega ))$.

Given two probability measures $\mu$ and $\nu$ on $\Omega$, let

$$\begin{aligned} H_n(\nu _n|\mu _n)= \sum _{\omega \in \Omega _n} \nu _n(\omega ) \log \frac{\nu _n(\omega )}{\mu _n(\omega )}. \end{aligned}$$

It can be proven [17, Chap. 15] that if $\nu$ is a shift-invariant probability measure and $\mu$ a Gibbs measure, we can define the relative entropy density of $\nu$ with respect to $\mu$ as

$$\begin{aligned} h(\nu |\mu )=\lim _{n\rightarrow \infty } \frac{H_n(\nu _n|\mu _n)}{(2n+1)^d}. \end{aligned}$$

(16)

One has $h(\nu |\mu )\in [0,+\infty )$. Moreover, if $\Phi \in {\mathscr {B}}_T$ and $\mu _\Phi$ is a shift-invariant Gibbs measure for $\Phi$ then

$$\begin{aligned} h(\nu |\mu _\Phi )=P(\Phi )+\mathbb {E}_\nu [f_\Phi ]-h(\nu ). \end{aligned}$$

(17)

Finally, the variational principle ( [17, Chap. 15]) states that $h(\nu |\mu _\Phi )=0$ if and only if $\nu$ is a Gibbs measure for $\Phi$. In particular, for such a $\nu$, one has

$$\begin{aligned} P(\Phi )=h(\nu )-\mathbb {E}_{\nu }[f_\Phi ]. \end{aligned}$$

(18)

4.4 Examples

In order to make things more tangible, we will repeatedly illustrate our results with the following concrete examples.

• (Ising) A fundamental example is the (nearest-neighbor) Ising model for which we take $S=\{-1,+1\}$ and that we define via the nearest-neighbor potential

  $$\begin{aligned} \Phi (\Lambda ,\omega )= {\left\{ \begin{array}{ll} - h\omega _x &{} \text {if}\quad \Lambda =\{x\}\\ - J \omega _x\omega _y &{} \text {if}\quad \Lambda =\{x,y\}\;\text {and}\;\Vert x-y\Vert _1=1\\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

  (19)

  where the parameters $J,h\in \mathbb {R}$ are respectively the coupling strength and the external magnetic field (uniform with strength |h|). When $J>0$, this is called the ferromagnetic case, when $J<0$ it is called the antiferromagnetic case. We shall consider the potential $\beta \Phi$, where $\beta \in \mathbb {R}_+$ is the inverse temperature.

• (Long-range Ising) Sticking to the case $S=\{-1,+1\}$, one can define the so-called spin pair potentials that can be of infinite range. Let $J:{\mathbb {Z}}^d\rightarrow \mathbb {R}$ be an even function such that $J(0)=0$ and $0<\sum _{x\in {\mathbb {Z}}^d} |J(x)|<+\infty$. Then define

  $$\begin{aligned} \Phi (\Lambda ,\omega )= {\left\{ \begin{array}{ll} - J(x-y)\, \omega _x\omega _y &{} \text {if}\quad \Lambda =\{x,y\}\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

  (20)

  When J is positive-valued, we have a ferromagnetic spin pair potential, while when J is negative-valued, we have an anti-ferromagnetic spin pair potential. For this class of potentials, the following facts are known [13] in the ferromagnetic case. Let ${\mathscr {J}}_0:=\sum _{x\in {\mathbb {Z}}^d} J(x)$ (which is finite by assumption). Then ${\mathscr {J}}_0^{-1}\le \beta _c:=\sup \{\beta >0 : \mathbb {E}_{\mu _{\beta \Phi }}[s_0]=0\}$, where $s_0(\omega )=\omega _0$. Moreover, if there exist two linearly independent unit vectors $z,z'$ in $\mathbb {Z}^d$ such that J(z) and $J(z')$ are positive, then $\beta _c$ is finite. Of course, this class contains the nearest-neighbor Ising model with zero external magnetic field.

• (The Potts antiferromagnet) Another example of a nearest-neighbor potential is the Potts antiferromagnet for which $S=\{1,2,\ldots ,q\}$ where q is an integer greater than or equal to 2. The elements of S are traditionally viewed as ‘colors’. The potential is defined as

  $$\begin{aligned} \Phi (\Lambda ,\omega )= {\left\{ \begin{array}{ll} J \mathbb {1}_{\{\omega _x=\omega _y\}} &{} \text {if}\quad \Lambda =\{x,y\}\;\text {and}\;\Vert x-y\Vert _1=1\\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

  (21)

  where $J>0$ is the coupling strength. (For $q=2$, this potential is physically equivalent to the Ising potential.) One can add an external magnetic field as in the Ising model.

5 Gaussian Concentration Bound for Gibbs Measures

The Gaussian concentration property holds under the Dobrushin uniqueness condition. In view of the applications to come, we give concrete examples of potentials satisfying this condition.

5.1 Dobrushin Uniqueness Regime

Let $\Phi \in {\mathscr {B}}_T$ and $\varvec{\gamma }^{\Phi }$ be the corresponding specification. The Dobrushin uniqueness condition is based upon the matrix

$$\begin{aligned} C_{x,y}(\varvec{\gamma }^{\Phi })= \sup _{\omega ,\omega '\in \Omega : \, \omega _{{\mathbb {Z}}^d\backslash y}=\, \omega '_{{\mathbb {Z}}^d\backslash y}} \Vert \varvec{\gamma }^{\Phi }_{\{x\}}(\cdot |\omega )-\varvec{\gamma }^{\Phi }_{\{x\}}(\cdot |\omega ')\Vert _\infty . \end{aligned}$$

Because we consider shift-invariant potentials, $C_{x,y}(\varvec{\gamma }^{\Phi })$ depends only on $x-y$. One says that $\varvec{\gamma }^{\Phi }$ satisfies the Dobrushin uniqueness condition if

$$\begin{aligned} {\mathfrak {c}}(\varvec{\gamma }^{\Phi }):=\sum _{x\in {\mathbb {Z}}^d} C_{0,x}(\varvec{\gamma }^{\Phi })<1. \end{aligned}$$

(22)

It is well known (see e.g. [17, Chap. 8]) that if this condition holds, there is a unique Gibbs measure for $\Phi$ which we denote by $\mu _\Phi$. Moreover it is automatically shift invariant.

5.2 Examples

The following list of examples is not exhaustive. All details can be found in [17, Chap. 8].

Let $\Phi \in {\mathscr {B}}_T$. One has the bound

$$\begin{aligned} {\mathfrak {c}}(\varvec{\gamma }^{\Phi }) \le \frac{1}{2}\sum _{\Lambda \ni 0} \, (|\Lambda |-1)\, \delta (\Phi (\Lambda ,\cdot )) \end{aligned}$$

where

$$\begin{aligned} \delta (\Phi (\Lambda ,\cdot ))=\sup _{\omega ,\omega '\in \Omega } |\Phi (\Lambda ,\omega )-\Phi (\Lambda ,\omega ')|. \end{aligned}$$

Hence a sufficient condition for (22) to hold is that

$$\begin{aligned} \sum _{\Lambda \ni 0} \, (|\Lambda |-1)\, \delta (\Phi (\Lambda ,\cdot ))<2. \end{aligned}$$

(23)

Let us come back to the examples introduced above. As a first example, take a potential $\beta \Phi$ where $\beta >0$ and $\Phi$ is a finite-range potential. It is obvious that (23) holds for all $\beta$ small enough. In this case it is customary to say that we are in the “high-temperature regime” of this potential. A second scenario is when we have a sufficiently large external magnetic field. By this we mean that we take any potential $\Phi$ such that $\Phi (\{x\},\omega )=-h\, \omega _x$ for all $x\in {\mathbb {Z}}^d$ and some $h\in \mathbb {R}$. The condition implying (22) reads

$$\begin{aligned} e^{|h|}> \exp \left( \frac{1}{2} \sum _{\Lambda \ni 0 : |\Lambda |>1} \delta (\Phi (\Lambda ,\cdot ))\right) \, \sum _{\Lambda \ni 0} \, (|\Lambda |-1)\, \delta (\Phi (\Lambda ,\cdot )). \end{aligned}$$

A third scenario occurs at low temperatures for potentials with unique ground state, e.g., the Ising model with $h\ne 0$ and for sufficiently large $\beta$, or any $\beta$ and |h| sufficiently large.

• (Ising) For instance, in the Ising model in two dimensions, (22) holds if $|h|>4\beta |J|+\log (8\beta |J|)$. Without external magnetic field ($h=0$) and with $J=1$, (22) holds if $\beta <\frac{1}{2}\ln (\frac{5}{3})\approx 0.255$.

• (Long-range Ising) For a spin pair potential $\beta \Phi$ one has

  $$\begin{aligned} {\mathfrak {c}}(\varvec{\gamma }^{\beta \Phi }) \le \sum _{x\in {\mathbb {Z}}^d}\tanh (\beta |J(x)|), \end{aligned}$$

  hence (22) holds if

  $$\begin{aligned} \sum _{x\in {\mathbb {Z}}^d}\tanh (\beta |J(x)|)< 1. \end{aligned}$$

  (24)

  This holds in particular if $\sum _{x\in {\mathbb {Z}}^d} \beta |J(x)|\le 1$.

• (Potts antiferromagnet) Potts antiferromagnet (21) satisfies Dobrushin’s uniqueness condition as soon as $q>4d$, regardless of the value of J. Indeed, one can check that ${\mathfrak {c}}(\varvec{\gamma }^{\Phi }) \le \frac{2d}{q-2d}$. We refer to [33] for this result which improves the one described in [17]. Moreover, in that regime, for the unique Gibbs $\mu _\Phi$ it holds that $\mathbb {E}_{\mu _\Phi }[\mathbb {1}_{\{\omega _0=i\}}]=1/q$ for $i\in \{1,\ldots ,q\}$.

5.3 Gaussian Concentration Bound

Theorem 5.1

([9, 23]) Let $\Phi \in {\mathscr {B}}_T$ and assume that the associated specification $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin’s uniqueness condition (22). Then $\mu _\Phi$ satisfies $\mathrm {GCB}\!\left( \frac{1}{2(1-{\mathfrak {c}}(\varvec{\gamma }^{\Phi }))^2}\right)$.

Take for instance a spin pair potential satisfying (24). Then, (5) gives

for all functions $F\in \Delta _2(\Omega )$ and for all $u>0$. Observe that when $\beta$ goes to 0, $\mu _{\beta \Phi }$ goes (in weak topology) to a product measure (namely the product of the measures giving equal mass to each element of S), and one gets in the exponential.

Remark 5.1

Theorem 5.1 was first proved in [23] in a more general setting (in particular, without assuming that potentials are shift invariant). Using a different approach, this theorem was also proved in [9, Sect. 3.1] for shift-invariant potentials, although it was not explicitly stated therein. In particular, the constant is not explicit. Moreover, it was proved for local functions. But it is not difficult to show that, if $\mathrm {GCB}\!\left( D\right)$ holds for all local functions, then it holds for all functions in $\Delta _2(\Omega )$ with the same constant D, as shown in the lemma below.

Lemma 5.1

If (3) holds with constant D, then it holds for all $F\in \Delta _2(\Omega )$ with the same constant D. If (6) holds for some $p\ge 1$ with a constant $C_{2p}$, then it extends to this class of functions, with the same constant.

Proof

We treat the case of the Gaussian concentration bound. The case of moment bounds is very similar. Let $F:\Omega \rightarrow \mathbb {R}$ be a continuous function such that . Since $\Omega$ is compact, F is bounded, thus $\mathbb {E}_\nu [\exp (F)]<+\infty$. We now construct a sequence of local functions $(F_n)_n$ defined in the natural way: We fix once for all $\eta \in \Omega$ and for each $n\ge 1$ we let

$$\begin{aligned} F_n(\omega )=F(\omega _{C_n}\eta _{{\mathbb {Z}}^d\backslash C_n}), \end{aligned}$$

that obviously coincides with F inside the cube $C_n$. We now prove that as $n\rightarrow +\infty$. We first prove that, for each $x\in {\mathbb {Z}}^d$, $\delta _x(F_n-F)\xrightarrow []{n\rightarrow \infty }0$. Since x is fixed and n gets arbitrarily large, we can assume that $x\in C_n$. We have

$$\begin{aligned} \delta _x(F_n-F)=\sup \{|F_n(\omega )-F(\omega ')| : \omega _y=\omega '_y,\, \forall y\ne x\}. \end{aligned}$$

By compactness, there exists two configurations $\omega =\omega _{C_n\backslash \{x\}}s_x\omega _{C_n^c}$ and $\omega '=\omega _{C_n\backslash \{x\}}s'_x\omega _{C_n^c}$ such that this supremum is attained. (The notation should be clear: given $\omega \in \Omega$, $\omega _{C_n\backslash \{x\}}s_x\omega _{C_n^c}$ is the configuration coinciding with $\omega$ except at site $x\in C_n$ where $\omega _x$ is replaced by $s\in S$ at site x.) Therefore

$$\begin{aligned} \delta _x(F_n-F)\le & {} |F(\omega _{C_n\backslash \{x\}}s_x\eta _{C_n^c})-F(\omega _{C_n\backslash \{x\}}s_x\omega _{C_n^c})| \\&\quad +\,|F(\omega _{C_n\backslash \{x\}}s'_x\omega _{C_n^c})-F(\omega _{C_n\backslash \{x\}}s'_x\eta _{C_n^c})|. \end{aligned}$$

By continuity, the two terms go to zero as n goes to infinity. Then we obviously have that $(\delta _x(F_n-F))^2\le 4 (\delta _x(F))^2$. Since $\sum _{x\in {\mathbb {Z}}^d} (\delta _x(F))^2<\infty$, we can apply the dominated convergence theorem for sums to get the desired conclusion.

Now (3) follows for F with the same constant, because $\Vert F-F_n\Vert _\infty \rightarrow 0$ and

This result now follows by taking the limit $n\rightarrow \infty$ in the right-hand side. $\square$

6 Concentration Bounds for the Ising Ferromagnet at Low Temperature

6.1 The Ising Ferromagnet

We consider the low-temperature plus-phase of the Ising model on $\mathbb {Z}^d$, $d\ge 2$, corresponding to the potential (19) with $h=0$, $J>0$ (ferromagnetic case) and the boundary condition $\eta _x=+\,1$ for all $x\in {\mathbb {Z}}^d$. Without loss of generality, we can take $J=1$. This is the probability measure $\mu ^+_\beta$ on $\Omega$ defined as the weak limit as $\Lambda \uparrow \mathbb {Z}^d$ of the finite-volume measures

$$\begin{aligned} \mu ^+_{\Lambda ,\beta }(\omega _\Lambda ) =\frac{1}{Z_{\Lambda ,\beta }(+^{{\mathbb {Z}}^d})}\ \exp \Big (-\beta \mathcal {H}_{\Lambda }\big (\omega \, |+^{{\mathbb {Z}}^d}\big )\Big ) \end{aligned}$$

(25)

where

$$\begin{aligned} \mathcal {H}_{\Lambda }\big (\omega |+^{{\mathbb {Z}}^d}\big )= -\sum _{\begin{array}{c} x,y\in \Lambda \\ \Vert x-y\Vert _1=1 \end{array}} \omega _x\omega _y - \sum _{\begin{array}{c} x\in \partial \Lambda , \ y\notin \Lambda \\ \Vert x-y\Vert _1=1 \end{array}}\omega _x \end{aligned}$$

and where $\beta \in \mathbb {R}^+$. We write $+^{{\mathbb {Z}}^d}$ for the configuration $\eta$ such that $\eta _x=+\,1$ for all $x\in {\mathbb {Z}}^d$, and $\partial \Lambda$ denotes the inner boundary of the set $\Lambda$, i.e., the set of those $x\in \Lambda$ having at least one neighbor $y\notin \Lambda$. The existence of the limit $\Lambda \uparrow \mathbb {Z}^d$ of $\mu _{\Lambda ,\beta }^+$ is by a standard and well-known monotonicity argument, see e.g. [17]. In a similar fashion one can define $\mu _\beta ^-$. Both $\mu _\beta ^+$ and $\mu _\beta ^-$ are shift-invariant and ergodic. It is well known that there exists $\beta _c>0$ such that for all $\beta >\beta _c$, $\mu _\beta ^+\ne \mu _\beta ^-$.

6.2 Moment Concentration Bounds of All Orders

It should not be a surprise that, for the Ising model in the phase coexistence region, a Gaussian concentration bound cannot hold. Indeed, this would contradict the surface-order large deviations for the magnetization in that regime (see below for more details). Nevertheless, one can control all moments, as was shown in [9].

Theorem 6.1

([9]) Let $\mu _\beta ^+$ be the plus phase of the low-temperature Ising model defined above. There exists ${\bar{\beta }}>\beta _c$, such that for each $\beta >{\bar{\beta }}$, there exists a positive sequence $(C_{2p}(\beta ))_{p\in \mathbb {N}}$ such that the measure $\mu _\beta ^+$ satifies $\mathrm {MCB}\!\left( 2p,C_{2p}(\beta )\right)$ for all $p\in \mathbb {N}$. In particular one has for each $p\in \mathbb {N}$

for all functions $F\in \Delta _2(\Omega )$ and for all $u>0$.

Remark 6.1

In view of Sect. 3.3, one can ask whether the previous theorem implies in fact a stronger statement, namely a Gaussian concentration bound. The answer turns out to be negative. Indeed, looking at the proof of Theorem 3 in [9], one sees that $C_{2p}$ is of the form $p^{2p} K^p$ for some constant $K>0$ (depending on F but independent of p). Therefore, one cannot infer a Gaussian bound from these moment bounds.

6.3 Stretched-Exponential Concentration Bound

One can deduce from the previous theorem that the measure $\mu _\beta ^+$ satisfies a ‘stretched-exponential’ concentration bound. This was shown in [9]. In order to state it, we need some notations and definitions. For $0<\varrho <1$, let $M\!_\varrho :\mathbb {R}\rightarrow \mathbb {R}^+$ be the Young function defined by $M\!_\varrho (x)=e^{(|x|+h_\varrho )^\varrho }-e^{h_\varrho ^\varrho }$ where $h_\varrho =(\frac{1-\varrho }{\varrho })^{1/\varrho }$. Then, the Luxemburg norm with respect to $M_\varrho$ of a real-valued random variable Z is defined by

$$\begin{aligned} \Vert Z\Vert _{M\!_\varrho }=\inf \left\{ \lambda >0 : \mathbb {E}\left[ M\!_\varrho \left( \frac{Z}{\lambda }\right) \right] \le 1\right\} . \end{aligned}$$

(Note that the choice $M_p(x)=|x|^p$ would give the usual $L^p$ norm).

Theorem 6.2

([9]) Let $\mu _\beta ^+$ be the plus-phase of the low-temperature Ising model and ${\bar{\beta }}$ as in the previous theorem. Then, for each $\beta >{\bar{\beta }}$, there exist $\varrho =\varrho (\beta )\in (0,1)$ and a constant $K_{\!\varrho }>0$ such that, for all functions $F\in \Delta _2(\Omega )$, one has

(26)

Moreover there exists $c_\varrho >0$ such that for all $u>0$

(27)

All the constants appearing in the previous statement may depend on d.

Theorems 6.1 and 6.2 were proved in [9] for local functions, but Lemma 5.1 shows that their extension to functions in $\Delta _2(\Omega )$ is ensured.

Remark 6.2

For any random variable Z and for any $0<\varrho <1$, there is a real number $B_\varrho >1$ such that, if $\Vert Z\Vert _{M_\varrho }<\infty$, then

$$\begin{aligned} B_\varrho ^{-1} \sup _{q\in 2\mathbb {N}} \frac{\Vert Z\Vert _{L^q}}{q^{1/\varrho }} \le \Vert Z\Vert _{M_\varrho } \le B_\varrho \sup _{q\in 2\mathbb {N}} \frac{\Vert Z\Vert _{L^q}}{q^{1/\varrho }}. \end{aligned}$$

(28)

These estimates are proved in [14, p. 86] where the suprema are taken over all the integers greater than 2. Restricting the supremum to even integers gives the same inequalities with slightly different constants.

Remark 6.3

An essential ingredient in the proofs of Theorems 6.1 and 6.2 is a non-trvial coupling constructed in [27]. In fact, this construction was made for Markov random fields for which the Pirogov–Sinai theory applies, such as the low-temperature pure phases of the ferro- and anti-ferromagnetic Potts model. For the sake of simplicity, only the ferromagnetic Ising model was considered in [9]. Therefore we also restrict ourselves to this case in the present work.

7 Application 1: Ergodic Sums and Empirical Pair Correlations

7.1 General Results

Given a nonempty finite subset $\Lambda$ of ${\mathbb {Z}}^d$ (i.e., $\emptyset \ne \Lambda \in \mathcal {P}$), a continuous function $f:\Omega \rightarrow \mathbb {R}$ and $\omega \in \Omega$, define

$$\begin{aligned} S_\Lambda f(\omega )=\sum _{x\in \Lambda } f(T_x \omega ). \end{aligned}$$

A sequence $(\Lambda _n)_n$ of nonempty finite subsets of ${\mathbb {Z}}^d$ is said to tend to infinity in the sense of van Hove if, for each $x\in {\mathbb {Z}}^d$, one has

$$\begin{aligned} \lim _{n\rightarrow +\infty } |\Lambda _n|=+\infty \quad \text {and}\quad \lim _{n\rightarrow +\infty } \frac{|(\Lambda _n+x)\backslash \Lambda _n|}{|\Lambda _n|}=0. \end{aligned}$$

In the language of countable discrete amenable groups, $(\Lambda _n)_n$ is a Følner sequence. A special case of interest is when $\Lambda _n=C_n$:

$$\begin{aligned} S_n f(\omega ):=\sum _{x\in C_n} f(T_x\omega ), \, n\in \mathbb {N}. \end{aligned}$$

By convention we set $S_0 f(\omega )=f(\omega )$. Given an ergodic measure $\nu$, we are interested in the fluctuations of

$$\begin{aligned} \frac{S_\Lambda f(\omega )}{|\Lambda |}. \end{aligned}$$

When one considers

$$\begin{aligned} \frac{S_{\Lambda _n} f(\omega )}{|\Lambda _n|} \end{aligned}$$

where $(\Lambda _n)_n$ tends to infinity in the sense of van Hove, it is well-known that this average converges $\nu$-almost surely to $\mathbb {E}_\nu [f]$ as $n\rightarrow +\infty$. This is the so-called multidimensional ergodic theorem, see e.g. [35].

We first state a simple lemma that will be repeatedly used in this section and later.

Lemma 7.1

Let $f\in \Delta _1(\Omega )$ and $\Lambda \in \mathcal {P}$. Then

Proof

We observe that $\delta _z(S_\Lambda f)\le \sum _{x\in \Lambda }\delta _{z-x}(f)$. We now use Young’s inequality: if and , where $p,q\ge 1$, then where $r\ge 1$ is such that $1+r^{-1}=p^{-1}+q^{-1}$, and

We apply this inequality with $r=2, p=2,q=1$, $\varvec{u}_x=\mathbb {1}_{\Lambda }(x)$, and $\varvec{v}_x=\delta _x(f)$ to get the desired estimate. $\square$

We get immediately the following general result.

Theorem 7.1

Let $\nu$ be a shift-invariant probability measure satisfying $\mathrm {GCB}\!\left( D\right)$. Then for all $\Lambda \in \mathcal {P}$ and for all $f\in \Delta _1(\Omega )$ we have, for all $u>0$,

(29)

Two functions are of particular interest in the context of Gibbs measures:

• (a) Magnetization: For $S=\{-1,+1\}$ let $f=s_0$ where $s_0(\omega )=\omega _0$. Then, for a given $\Lambda \in \mathcal {P}$, define

  $$\begin{aligned} M_\Lambda (\omega )=\sum _{x\in \Lambda }s_0(T_x \omega )\,, \end{aligned}$$

  which is the empirical (total) magnetization in $\Lambda$. We have

  

• (b) Mean energy per site: Take $f=f_\Phi$ where $\Phi \in {\mathscr {B}}_T$. From (9) we get

  $$\begin{aligned} \delta _x(f_\Phi )\le 2\, \sum _{\begin{array}{c} \Lambda \ni 0\\ \Lambda \ni x \end{array}} \frac{\Vert \Phi (\Lambda ,\cdot )\Vert _\infty }{|\Lambda |} \end{aligned}$$

  As a consequence we have

  

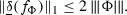
7.2 Empirical Magnetization and Energy in Dobrushin’s Uniqueness Regime

Applying Theorem 7.1 to the previous two functions gives the following two results.

Theorem 7.2

Let $\varvec{\gamma }^{\Phi }$ be the specification of a potential $\Phi \in {\mathscr {B}}_T$ satisfying Dobrushin’s uniqueness condition (22). Then, for all $\Lambda \in \mathcal {P}$, we have

(a):

the concentration bound

$$\begin{aligned} \mu _\Phi \left\{ \omega \in \Omega : \left| \frac{M_\Lambda (\omega )}{|\Lambda |} - \mathbb {E}_{\mu _\Phi }[s_0]\right| \ge u \right\} \le 2 \exp \left( -c\, |\Lambda |\, u^2\right) \end{aligned}$$

for all $u>0$, where

$$\begin{aligned} c=\frac{ (1-{\mathfrak {c}}(\varvec{\gamma }^{\Phi }))^2}{8}, \end{aligned}$$

(b):

and for all $\Psi \in {\mathscr {B}}_T$, the concentration bound

$$\begin{aligned} \mu _\Phi \left\{ \omega \in \Omega : \left| \frac{S_\Lambda f_\Psi (\omega )}{|\Lambda |} - \mathbb {E}_{\mu _\Phi }[f_\Psi ]\right| \ge u \right\} \le 2 \exp \left( -c\, |\Lambda |\, u^2\right) \end{aligned}$$

for all $u>0$, where

We refer back to Sect. 4.4 (which contains our three main examples) if the reader wants to make the previous bounds even more explicit.

7.3 Empirical Magnetization and Energy in the Low-Temperature Ising Model

For the plus-phase of the low-temperature Ising model we can apply Theorem 6.2 to obtain the following analogue of Theorem 7.2.

Theorem 7.3

Let $\mu _\beta ^+$ be the plus phase of the low-temperature Ising model. Then there exists ${\bar{\beta }}>\beta _c$ such that, for each $\beta >{\bar{\beta }}$, there exist $\varrho =\varrho (\beta )\in (0,1)$ and a constant $c_\varrho >0$ such that, for all $\Lambda \in \mathcal {P}$, we have

(a):

the concentration bound

$$\begin{aligned} \mu _\beta ^+\left\{ \omega \in \Omega : \left| \frac{M_\Lambda (\omega )}{|\Lambda |} - \mathbb {E}_{\mu _\beta ^+}[s_0]\right| \ge u\right\} \le 4\, \exp \left( -\frac{c_\varrho }{2^\varrho } |\Lambda |^{\frac{\varrho }{2}} u^{\varrho }\right) , \end{aligned}$$

for all $u>0$,

(b):

and, for all $\Psi \in {\mathscr {B}}_T$, the concentration bound

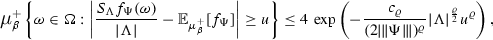
for all $u>0$

It is known that when $d=1$, one has $\mathbb {E}_{\mu _\beta ^+}[s_0]=0$, whereas for $d=2$ (see e.g. [26]) one has

$$\begin{aligned} \mathbb {E}_{\mu _\beta ^+}[s_0]=\left( 1-\big (\sinh (2\beta )\big )^{-4}\right) ^{\frac{1}{8}} \end{aligned}$$

for all $\beta \ge \beta _c=\frac{1}{2}\ln (1+\sqrt{2})$. When $d\ge 3$ no explicit formula is known.

Remark 7.1

Probabilities of large deviations for the magnetization are well known for the Ising model. At low temperature, one has “surface-order” large deviations, see [34] for instance. In particular one has the following estimate. Let a, b such that $-m_{\mu _\beta ^+}<a<b<m_{\mu _\beta ^+}$. Then, the probability (under $\mu _\beta ^+$) that $M_n$ falls into [a, b] is exponentially small in $(2n+1)^{d-1}$, as n goes to infinity. Comparing with Theorem 7.3, we see that we get a weaker result (since $\varrho d/2<d-1$ for all $d\ge 2$) which, however, is valid in any finite volume. Moreover, we get a bound not only for cubes but for all finite volumes.

7.4 Empirical Pair Correlations

Let $f\in C^0(\Omega )$. For $\omega \in \Omega$, $x\in {\mathbb {Z}}^d$ and $n\in \mathbb {N}$, define

$$\begin{aligned} \Gamma _{n,x}(\omega )= \frac{1}{(2n+1)^d} \sum _{y\in C_n} f(T_y\omega )f(T_{y+x}\omega ). \end{aligned}$$

It follows from the multidimensional ergodic theorem (see, e.g. [17, p. 302]) that, given an ergodic probability measure $\nu$, for each $x\in {\mathbb {Z}}^d$,

$$\begin{aligned} \Gamma _{n,x}(\omega )\xrightarrow []{n\rightarrow +\infty }\mathbb {E}_\nu [ f\cdot f\circ T_x] \end{aligned}$$

for $\nu$-almost every $\omega$. Notice that $\mathbb {E}[\Gamma _{n,x}]=\mathbb {E}_\nu [ f\cdot f\circ T_x]$ for all $n\in \mathbb {N}$ and for all $x\in {\mathbb {Z}}^d$. We state a lemma whose proof follows the lines of Lemma 7.1.

Lemma 7.2

Let $f\in \Delta _1(\Omega )$, $x\in {\mathbb {Z}}^d$ and $n\in \mathbb {N}$. We have

Proof

For any $z\in {\mathbb {Z}}^d$ we have

$$\begin{aligned}&\delta _{z}\left( \sum _{y\in C_n} f\circ T_y (\cdot )f\circ T_{y+x}(\cdot )\right) \\&\qquad \qquad =\,\sup _{\begin{array}{c} \omega ,\omega ' \\ \text {differing only at}\, z \end{array}} \left| \sum _{y\in C_n} \big ( f\circ T_y (\omega )- f\circ T_y (\omega ')\big )f\circ T_{y+x}(\omega )\right. \\&\qquad \qquad \quad \left. +\,\sum _{y\in C_n} \big ( f\circ T_{y+x} (\omega )- f\circ T_{y+x} (\omega ')\big )f\circ T_{y}(\omega ') \right| \\&\qquad \qquad \le \,\Vert f\Vert _\infty \, \sum _{y\in C_n} \delta _z \big (f\circ T_y\big ) + \Vert f\Vert _\infty \, \sum _{y\in C_n} \delta _z \big (f\circ T_{y+x}\big )\,. \end{aligned}$$

To finish the proof we use Young’s inequality as in the proof of Lemma 7.1. $\square$

We have the following results.

Theorem 7.4

Let $\varvec{\gamma }^{\Phi }$ be the specification of a potential $\Phi \in {\mathscr {B}}_T$ satisfying Dobrushin’s uniqueness condition (22). Let $f\in \Delta _1(\Omega )$. Then

for all $u>0$, for all $n\in \mathbb {N}$ and for all $x\in {\mathbb {Z}}^d$.

Proof

We apply Theorem 5.1 and Lemma 7.2 and replace u by $(2n+1)^d u$. $\square$

We can apply the previous theorem to $s_0(\omega )=\omega _0$ to get

$$\begin{aligned}&\mu _\Phi \left\{ \omega \in \Omega : \left| \frac{\Gamma _{n,x}(\omega )}{(2n+1)^d} - \mathbb {E}_{\mu _\Phi }[ s_0\cdot s_0\circ T_x] \right| \ge u \right\} \\&\qquad \qquad \le \,2 \exp \left( -\frac{ (1-{\mathfrak {c}}(\varvec{\gamma }^{\Phi }))^2}{16}\, (2n+1)^d\, u^2\right) \end{aligned}$$

for all $u>0$, for all $n\in \mathbb {N}$ and for all $x\in {\mathbb {Z}}^d$.

For the low-temperature Ising model, we have the following estimate.

Theorem 7.5

Let $\mu _\beta ^+$ be the plus phase of the low-temperature ferromagnetic Ising model. Let $f\in \Delta _1(\Omega )$. Then there exists ${\bar{\beta }}>0$ such that, for each $\beta >{\bar{\beta }}$, there exist $\varrho =\varrho (\beta )\in (0,1)$ such that

for all $u>0$, for all $n\in \mathbb {N}$ and for all $x\in {\mathbb {Z}}^d$, where $c_\varrho >0$ is as in Theorem 6.2.

Proof

We apply Theorem 6.2 and Lemma 7.2. $\square$

8 Application 2: Speed of Convergence of the Empirical Measure

8.1 Generalities

For $\Lambda \in \mathcal {P}$ and $\omega \in \Omega$, let

$$\begin{aligned} \mathcal {E}_\Lambda (\omega )=\frac{1}{|\Lambda |} \sum _{x\in \Lambda } \delta _{T_x\omega }. \end{aligned}$$

Let $\nu$ be an ergodic measure on $(\Omega ,{\mathfrak {B}})$. It is a consequence of the multidimensional ergodic theorem that, for any van Hove sequence $(\Lambda _n)_n$, we have

$$\begin{aligned} \mathcal {E}_{\Lambda _n}(\omega )\xrightarrow [\text {weakly}]{n\rightarrow \infty } \nu \end{aligned}$$

for $\nu$-almost every $\omega \in \Omega$ (see [35]). To quantify the speed of this convergence, we endow the set of probability measures on $\Omega$ with the Kantorovich distance $d_{{\scriptscriptstyle K}}$ defined by

$$\begin{aligned} d_{{\scriptscriptstyle K}}(\mu _1,\mu _2)= \sup _{\begin{array}{c} G:\Omega \rightarrow \mathbb {R}\\ G\;1-\text {Lipshitz} \end{array}}\left( \mathbb {E}_{\mu _1}[G] -\mathbb {E}_{\mu _2}[G]\right) . \end{aligned}$$

(30)

A function $G:\Omega \rightarrow \mathbb {R}$ is 1-Lipschitz if $|G(\omega )-G(\eta )|\le d(\omega ,\eta )$ where the distance $d(\cdot ,\cdot )$ is defined in (1). The distance $d_{{\scriptscriptstyle K}}$ metrizes the weak topology on the space of probability measures on $\Omega$.

We are interested in bounding the fluctuations of $d_{{\scriptscriptstyle K}}(\mathcal {E}_\Lambda (\omega ),\mu )$ where $\mu$ will be a Gibbs measure. We start with a lemma.

Lemma 8.1

Let $\nu$ be a probability measure. For each $\Lambda \in \mathcal {P}$, consider the function

$$\begin{aligned} F(\omega )=\sup _{\begin{array}{c} G:\, \Omega \rightarrow \mathbb {R}\\ G\;1-\text {Lipshitz} \end{array}} \left( \sum _{x\in \Lambda } G(T_x\omega )-\mathbb {E}_{\nu }[G]\right) . \end{aligned}$$

Then, we have

(31)

where $c_d>0$ is a constant only depending on d (the dimension of the lattice).

Proof

Let $\omega , \omega '\in \Omega$ and $G:\Omega \rightarrow \mathbb {R}$ be a 1-Lipschitz function. Without loss of generality, we can assume that $\mathbb {E}_{\nu }[G]=0$. We have

$$\begin{aligned} \sum _{x\in \Lambda } G(T_x\omega ) \le \sum _{x\in \Lambda } G(T_x\omega ')+ \sum _{x\in \Lambda } d(T_x \omega ,T_x \omega '). \end{aligned}$$

Taking the supremum over 1-Lipschitz functions thus gives

$$\begin{aligned} F(\omega )-F(\omega ')\le \sum _{x\in \Lambda } d(T_x \omega ,T_x \omega '). \end{aligned}$$

We can interchange $\omega$ and $\omega '$ in this inequality, whence

$$\begin{aligned} |F(\omega )-F(\omega ')|\le \sum _{x\in \Lambda } d(T_x \omega ,T_x \omega '). \end{aligned}$$

Now we assume that there exists $z\in {\mathbb {Z}}^d$ such that $\omega _y=\omega '_y$ for all $y\ne z$. This means that $d(T_x \omega ,T_x \omega ')\le 2^{-\Vert z-x\Vert _\infty }$ for all $x\in {\mathbb {Z}}^d$, whence

$$\begin{aligned} \delta _z(F)\le \sum _{x\in \Lambda } 2^{-\Vert z-x\Vert _\infty }. \end{aligned}$$

Therefore, using Young’s inequality as in the proof of Lemma 7.1,

We thus obtain the desired estimate with $c_d=\Big (\sum _{z\in {\mathbb {Z}}^d} 2^{-\Vert z\Vert _\infty }\Big )^2$. $\square$

8.2 Concentration of the Kantorovich Distance

We can now formulate two results.

Theorem 8.1

Let $\Phi \in {\mathscr {B}}_T$ and assume that the associated specification $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin’s uniqueness condition (22). Denote by $\mu _\Phi$ the corresponding Gibbs measure. Then

$$\begin{aligned}&\mu _\Phi \!\left\{ \omega \in \Omega \! : \!\Big |d_{{\scriptscriptstyle K}}(\mathcal {E}_\Lambda (\omega ),\mu _\Phi )- \mathbb {E}_{\mu _\Phi }\big [ d_{{\scriptscriptstyle K}}(\mathcal {E}_\Lambda (\cdot ),\mu _\Phi )\big ]\Big |\ge u \right\} \\&\qquad \qquad \le \,2\, \exp \big (-c\, |\Lambda | u^2\big ) \end{aligned}$$

for all $\Lambda \in \mathcal {P}$ and for all $u>0$, where

$$\begin{aligned} c=\frac{ (1-{\mathfrak {c}}(\varvec{\gamma }^{\Phi }))^2}{2c_d} \end{aligned}$$

and $c_d$ is the constant appearing in Lemma 8.1.

Proof

We apply Theorem 5.1 and the estimate (31) to get the announced inequality. $\square$

For the plus-phase of the low temperature Ising model we can apply Theorem 6.2 to get immediately the following inequality.

Theorem 8.2

Let $\mu _\beta ^+$ be the plus phase of the low-temperature Ising model. There exists ${\bar{\beta }}$ such that, for each $\beta >{\bar{\beta }}$, there exist $\varrho =\varrho (\beta )\in (0,1)$ and a constant $c_\varrho >0$ such that

$$\begin{aligned}&\mu _\beta ^+\left\{ \omega \in \Omega : \Big |d_{{\scriptscriptstyle K}}(\mathcal {E}_\Lambda (\omega ),\mu _\beta ^+ )- \mathbb {E}_{\mu _\beta ^+}\big [d_{{\scriptscriptstyle K}}(\mathcal {E}_\Lambda (\cdot ),\mu _\beta ^+)\big ]\Big |\ge u\right\} \\&\qquad \qquad \le \,4\, \exp \left( -c_\varrho |\Lambda |^{\frac{\varrho }{2}}u^{\varrho }\right) \end{aligned}$$

for all $\Lambda \in \mathcal {P}$ and for all $u>0$.

Proof

It is a direct application of Theorem 6.2 and estimate (31). $\square$

8.3 Expectation of Kantorovich Distance

At this stage we can only control $d_{{\scriptscriptstyle K}}(\mathcal {E}_\Lambda (\omega ),\mu _\Phi )$ minus its expected value. So we still need to obtain an upper bound for $\mathbb {E}_{\mu _\Phi }\big [ d_{{\scriptscriptstyle K}}(\mathcal {E}_\Lambda (\cdot ),\mu _\Phi )\big ]$. For the sake of simplicity, we will provide an asymptotic upper bound in the cardinality of $\Lambda$. The reader can infer from the proofs that giving a non-asymptotic upper bound for all $\Lambda$ is possible but tedious.

Let $\nu$ be a probability measure on $(\Omega ,{\mathfrak {B}})$, $f:\Omega \rightarrow \mathbb {R}$ a continuous function and $\Lambda$ a finite subset of ${\mathbb {Z}}^d$. Define

$$\begin{aligned} X^\Lambda _f= \frac{1}{|\Lambda |}\sum _{x\in \Lambda } \left( f\circ T_x-\mathbb {E}_\nu [f]\right) \end{aligned}$$

(32)

We have

$$\begin{aligned} \sup _{f\in {\mathscr {F}}} X^\Lambda _f = d_{{\scriptscriptstyle K}}\left( \mathcal {E}_\Lambda (\cdot ),\nu \right) \end{aligned}$$

where ${\mathscr {F}}$ is the collection of all Lipschitz functions $f:\Omega \rightarrow \mathbb {R}$ with Lipschitz constant less than or equal to one. We want to estimate the expected distance

$$\begin{aligned} \mathbb {E}_\nu \left[ d_{{\scriptscriptstyle K}}\left( \mathcal {E}_\Lambda (\cdot ),\nu \right) \right] = \mathbb {E}_\nu \left[ \sup _{f\in {\mathscr {F}}} X^\Lambda _f\right] . \end{aligned}$$

Notice that we can subtract a constant from f without influencing $X^\Lambda _f$, therefore, using that f is Lipschitz and the maximal distance between two configurations in $\Omega$ is equal to 1, we can assume, without loss of generality, that the functions in ${\mathscr {F}}$ take values in [0, 1]. Estimating such a supremum is a classical problem. We adapt the line of thought of [36] to our context where we have to do some extra, non-trivial, work, see Remark 8.1 below for more details.

8.3.1 Case 1: Gaussian Concentration Bound Case

Let $\epsilon >0$ be given. We want to find a finite collection of functions ${\mathscr {F}}_\epsilon$ such that the following two properties are satisfied:

• 1. $\epsilon$ -net property For all $f\in {\mathscr {F}}$ there exists $g\in {\mathscr {F}}\!_\epsilon$ which is uniformly $\epsilon$ close to f, i.e., such that $\Vert f- g\Vert _\infty \le \epsilon$.

• 2. Uniform $\epsilon$ -Gaussian upper bound property There exists $D'>0$ (possibly depending on $\Lambda$) such that for all $f\in {\mathscr {F}}_\epsilon$ and all $\lambda \in \mathbb {R}$ we have

  $$\begin{aligned} \mathbb {E}_\nu \left[ \exp \big (\lambda X^\Lambda _f\big )\right] \le \exp \big (\lambda \epsilon \big ) \exp \left( D' \lambda ^2 \right) . \end{aligned}$$

  (33)

Such a collection ${\mathscr {F}}_\epsilon$ is called a good $\epsilon$-net for ${\mathscr {F}}$. Let us now assume that such a ${\mathscr {F}}_\epsilon$ is given. Then we have

Lemma 8.2

For all ${\mathscr {F}}_\epsilon$ good we have the upper bound

$$\begin{aligned} \mathbb {E}_\nu \left[ \sup _{f\in {\mathscr {F}}}X^\Lambda _f\right] \le 2\left( \epsilon + \sqrt{D'\log |{\mathscr {F}}_\epsilon |}\,\right) . \end{aligned}$$

(34)

Proof

For any $\lambda >0$, we have, using Jensen’s inequality and (33),

$$\begin{aligned} \mathbb {E}_\nu \left[ \sup _{f\in {\mathscr {F}}_\epsilon }X^\Lambda _f\right]&= \frac{1}{\lambda }\mathbb {E}_\nu \left[ \log \exp \left( \lambda \sup _{f\in {\mathscr {F}}_\epsilon }X^\Lambda _f\right) \right] \\&\le \frac{1}{\lambda }\log \mathbb {E}_\nu \left[ \exp \left( \lambda \sup _{f\in {\mathscr {F}}_\epsilon } X^\Lambda _f\right) \right] \\&\le \frac{1}{\lambda }\log \mathbb {E}_\nu \left[ \sum _{f\in {\mathscr {F}}_\epsilon } \exp \left( \lambda X^\Lambda _f\right) \right] \\&\le \frac{1}{\lambda }\left( \log |{\mathscr {F}}_\epsilon | + \lambda ^2 D' +\lambda \epsilon \right) . \end{aligned}$$

Optimizing w.r.t. $\lambda$ gives

$$\begin{aligned} \mathbb {E}_\nu \left[ \, \sup _{f\in {\mathscr {F}}_\epsilon }X^\Lambda _f\right] \le 2\sqrt{D'\log |{\mathscr {F}}_\epsilon |}+\epsilon . \end{aligned}$$

The statement of the lemma now follows from the $\epsilon$-net property of ${\mathscr {F}}_\epsilon$, i.e.,

$$\begin{aligned} \mathbb {E}_\nu \left[ \, \sup _{f\in {\mathscr {F}}}X^\Lambda _f\right] \le \epsilon + \mathbb {E}_\nu \left[ \sup _{f\in {\mathscr {F}}_\epsilon }X^\Lambda _f\right] . \end{aligned}$$

$\square$

We now first show that if ${\mathscr {F}}_\epsilon$ is a finite collection of functions which are all uniformly close to a 1-Lipschitz function f, then (33) holds.

Lemma 8.3

If g is such that there exist a 1-Lipschitz function f such that $\Vert f-g\Vert _\infty \le \epsilon$, and if $\nu$ satisfies $\mathrm {GCB}\!\left( D\right)$, then, for all $\lambda \in \mathbb {R}$, one has

$$\begin{aligned} \mathbb {E}_\nu \left[ \exp \big (\lambda X^\Lambda _g\big )\right] \le \exp (\lambda \epsilon ) \exp \left( D' \lambda ^2\right) . \end{aligned}$$

Proof

It suffices to show that for all f 1-Lipschitz we have

$$\begin{aligned} \mathbb {E}_\nu \left[ \exp \big (\lambda X^\Lambda _f\big )\right] \le \exp \left( D' \lambda ^2\right) , \end{aligned}$$

where $D'$ does not depend on f. This is the consequence of the Gaussian concentration bound and the proof of Lemma 8.1. $\square$

From what precedes, we are left to find a good $\epsilon$-net ${\mathscr {F}}_\epsilon$ in our setting. The first step is to find a $\epsilon$-net for the configuration space $\Omega$. This is defined as a finite set of configurations $\Omega _\epsilon \subset \Omega$ such that for all $\eta \in \Omega$ there exists $\zeta \in \Omega _\epsilon$ with $d(\eta ,\zeta )\le \epsilon$. The following lemma gives such a net.

Lemma 8.4

Let ${\overline{\eta }}$ be a fixed configuration in $\Omega$. We define for $n\in \mathbb {N}$ the set

$$\begin{aligned} \Omega _n^{{\overline{\eta }}}= \{ \eta \in \Omega : \eta _{C_n^c}={{\overline{\eta }}}_{C_n^c}\}. \end{aligned}$$

Then $\Omega _n^{{\overline{\eta }}}$ is a $2^{-n}$ net of cardinality $|S|^{|C_n|}$.

Proof

This follows immediately from the definition of the distance in $\Omega$. $\square$

If f is a 1-Lipschitz function, then we have that if $\eta _{C_n}=\zeta _{C_n}$, $|f(\eta )-f(\zeta )|\le 2^{-n}$. Notice that we can view $\Omega _n^{{\overline{\eta }}}$ in (8.4) as a copy of $S^{C_n}$ via the map

$$\begin{aligned} \psi : S^{C_n}\rightarrow \Omega _n^{{\overline{\eta }}}: \alpha \mapsto \alpha _{C_n}{\overline{\eta }}_{C_n^c}. \end{aligned}$$

This means that ordering the elements of $\Omega _n^{{\overline{\eta }}}$ is the same as ordering the elements of $S^{C_n}$. The aim now is to order the elements of the net $\Omega _n^{{\overline{\eta }}}$ in such a way that the distances between successive elements in the ordering are as small as possible. Because $\Omega$ is a totally disconnected space, we will not be able to avoid that in this order there are distances of $2^{-(n-1)}, 2^{-(n-2)},\ldots , 2^{-1}$. The following lemma explains the hierarchical structure of the ordering.

Lemma 8.5

There exists an ordering of $S^{C_n}$ of the following type

$$\begin{aligned}&\alpha ^0\\&\alpha ^{1,1},\ldots ,\alpha ^{1,P(n,1)}\quad \text {(first list)}\\&\alpha ^{2,1},\ldots ,\alpha ^{2,P(n,2)}\quad \text {(second list)}\\&\qquad \quad \vdots \\&\alpha ^{n,1},\ldots , \alpha ^{n,P(n,n)}\quad \text {(}nth list) \end{aligned}$$

such that for all $k,\ell \in \{0,\ldots , n\}, i\in 1,\ldots , P(n,k), j\in 1,\ldots , P(n,\ell )$, we have

$$\begin{aligned} d(\psi (\alpha ^{k,i}), \psi (\alpha ^{\ell ,j})) = 2^{-(n- k\vee \ell )}, \end{aligned}$$

where d is the distance defined in (1). Here $P(n,1)=|S|^{|C_n\setminus C_{n-1}|}$, $P(n,2)=S^{|C_n\setminus C_{n-1}|+|C_{n-1}\setminus C_{n-2}|}$, etc.

Proof

We choose an arbitrary first element $\alpha ^0$ in $S^{C_n}$. The next elements form an arbitrary enumeration of the configurations which are equal to $\alpha ^0$ in $C_{n-1}$, but different in at least one site $x\in C_{n}\setminus C_{n-1}$. There are at most $P(n,1)=|S|^{|C_n\setminus C_{n-1}|}$ such configurations. They are all at distance $2^{-n}$ from $\alpha ^0$ and from each other. Next are the elements at distance $2^{-(n-1)}$ from $\alpha$. These are at most $|S|^{|C_{n-1}\setminus C_{n-2}|}$ configurations associated to each configuration in the previous list, hence in total this gives $P(n,2)=S^{|C_n\setminus C_{n-1}|+|C_{n-1}\setminus C_{n-2}|}$ configurations in the second list. And so on and so forth. We go on like this, “peeling” off the cube $C_n$ by successive boundary layers $C_n\setminus C_{n-1}, C_{n-1}\setminus C_{n-2},\ldots ,\{0\}$, and end up with the configurations at distance 1 / 2 from $\alpha ^0$, of which there are $P(n,n)=S^{|C_n|-1}$. $\square$

Now we want to make our $\epsilon$ net ${\mathscr {F}}_\epsilon$. We choose n such that $2^{-n}\le \epsilon \le 2^{-(n-1)}$. We will give a function value to each $\psi (\alpha ), \alpha \in S^{C_n}$, which will only depend on $\alpha$, so we identify it with a function $f: S^{C_n}\rightarrow \mathbb {R}$. Because the functions will take values in $\left\{ 0,\frac{1}{2^n},\ldots , \frac{2^n-1}{2^n},1\right\}$, we have $2^n+1$ possibilities for the function value of $\alpha ^0$. Because we will choose the functions in ${\mathscr {F}}_\epsilon$ to be 1-Lipschitz, this restricts the possible values of the functions at $\alpha _1$. Indeed, given the function value of $\alpha ^0$, for the function values of the first list, which contains configurations which are at distance $2^{-n}\le \epsilon$, we have at most three possibilities, namely $f(\alpha ^0)+s$ with $s\in \{-2^{-n},0,2^{-n}\}$. Given the function values in the first list, all the elements of the second list are at distance $2^{-(n-2)}\le 2\epsilon$ from $\alpha ^0$ and from any element of the first list, so we have now $2^2+1$ possible function values, associated to any configuration of the second “layer”, i.e., $|S|^{|C_{n-1}\setminus C_{n-2}|}$ configurations, and so on and so forth. The number of functions we thus obtain is upper bounded by

$$\begin{aligned} |{\mathscr {F}}_\epsilon |=(2^n+1) (2+1)^{P(n,1)} (2^2+1)^{P(n,2)} \cdots (2^n+1)^{P(n,n)}. \end{aligned}$$

Taking the logarithm of this expression gives, using the (crude) upperbound $\log (2^{n}+1)\le n+1$

$$\begin{aligned} \log |{\mathscr {F}}_\epsilon | \le n+1 + P(n,1)2 + P(n,2) 3 +\cdots +(n+1)P(n,n)=:{\mathscr {K}}_\epsilon . \end{aligned}$$

It is clear that the asymptotic behavior of this expression is dominated by the last term, i.e, we have

$$\begin{aligned} {\mathscr {K}}_\epsilon \sim |S|^{(2\log (1/\epsilon )+1)^d} (\log (\tfrac{1}{\epsilon })+1), \end{aligned}$$

where $a_\epsilon \sim b_\epsilon$ means that $a_\epsilon /b_\epsilon \rightarrow 1$ as $\epsilon$ goes to 0.

Remark 8.1

Let us stress that we cannot obtain the previous estimate by a direct application of the standard results on $\epsilon$-entropy. To be more specific, our estimate does not follow from Theorem XV in [22] for the totally disconnected metric space $\Omega$. The problem stems from the fact that we cannot metrically embed $\Omega$ into a finite-dimensional parallelepiped, except in dimension $d=1$.

We now analyse how the bound (34) behaves. By Lemma 8.1 we have that the constant D in this bound is of the form $D'=D_1/|\Lambda |$, where $D_1$ is independent of $|\Lambda |$. Our aim now is to extract the leading order behavior in $|\Lambda |$ of the optimal found in (34), where we replace $\log |{\mathscr {F}}_\epsilon |$ by ${\mathscr {K}}_\epsilon$, i.e., we compute

$$\begin{aligned} B(|\Lambda |)=2 \inf _{\epsilon >0}\left( \epsilon + \sqrt{ \frac{D_1 {\mathscr {K}}_\epsilon }{|\Lambda |}}\, \right) . \end{aligned}$$

(35)

Let us abbreviate $\log (1/\epsilon )=v(\epsilon )$. The optimal $\epsilon =\epsilon ^*$ is the solution of

$$\begin{aligned} \frac{1}{2} \log |\Lambda | +\frac{1}{2}\log (1/D_1) = v(\epsilon ) +\frac{1}{2} \log (|S|) (2 v(\epsilon ))^d+\chi (\epsilon ), \end{aligned}$$

where $\chi (\epsilon )$ is of lower order as $\epsilon$ goes to 0. In order to collect the leading order behavior of $B(|\Lambda |)$ in $|\Lambda |$ on the logarithmic scale, we will therefore omit $\chi (\epsilon )$ in this equation, which will lead to lower order factors in the asymptotic behavior of $B(|\Lambda |)$. We will also omit the term $\frac{1}{2}\log (1/D_1)$ for the same reason.

Let us now introduce two notions of asymptotic comparison. For two strictly positive sequences $(a_n)$ and $(b_n)$, we write $a_n\asymp b_n$ if $\frac{\log a_n}{\log b_n}\rightarrow 1$ as $n\rightarrow \infty$, and $a_n \preceq b_n$ if $\limsup _n \frac{\log a_n}{\log b_n}\le 1$. For instance we have $4n^{-1/2}\log (n)\log (\log (n))\asymp n^{-1/2}$, and $n^{2n} e^{n} \preceq n^{3n}$. Similarly, for two sequences $(a_\Lambda )$ and $(b_\Lambda )$ indexed by finite subsets of ${\mathbb {Z}}^d$ we denote $a_\Lambda \asymp b_\Lambda$ if, for every sequence $(\Lambda _n)$ such that $|\Lambda _n|\rightarrow +\infty$ as $n\rightarrow +\infty$, we have $\frac{\log a_{\Lambda _n}}{\log b_{\Lambda _n}}\rightarrow 1$. Analogously, we define $a_\Lambda \preceq b_\Lambda$.

As a consequence, for $\epsilon =\epsilon ^*$ we find that both terms in the rhs of (35) are of the same order, and hence on this level of roughness, the behavior of $B(|\Lambda |)$ is the same as that of $\epsilon ^*$.

Proceeding like this, we find the following leading order behavior of $B(|\Lambda |)$ as a function of the dimension.

• 1. Dimension $d=1$.

  $$\begin{aligned} \epsilon ^*\asymp |\Lambda |^{-\frac{1}{2}(1+\log |S|)^{-1}}. \end{aligned}$$

• 2. Dimension $d\ge 2$.

  $$\begin{aligned} \epsilon ^*\asymp \exp \left( -\frac{1}{2} \left( \frac{\log |\Lambda |}{\log |S|}\right) ^{1/d}\right) . \end{aligned}$$

  Notice that this does not give the previous bound when we plug in $d=1$ because (only) for $d=1$ the additional tern $v(\epsilon )$ is of the same order as the second term $\frac{1}{2} (\log |S|) (2 v(\epsilon )+1)^d$.

As a conclusion we obtain the following asymptotic estimates.

Theorem 8.3

Let $\nu$ be a probability measure on $\Omega$ satisfying $\mathrm {GCB}\!\left( D\right)$. Then

$$\begin{aligned} \mathbb {E}_\nu \left[ d_{{\scriptscriptstyle K}}\left( \mathcal {E}_\Lambda (\cdot ),\nu \right) \right] \preceq {\left\{ \begin{array}{ll} |\Lambda |^{-\frac{1}{2}(1+\log |S|)^{-1}} &{} \text {if}\quad d=1\\ \exp \left( -\frac{1}{2} \left( \frac{\log |\Lambda |}{\log |S|}\right) ^{1/d}\right) &{} \text {if}\quad d\ge 2. \end{array}\right. } \end{aligned}$$

8.3.2 Case 2: Moment Concentration Bound Case

Let us now see what can be done when exponential moments do not exist, i.e., if we do not have GCB. We call then an $\epsilon$-net ${\mathscr {F}}_\epsilon$ good if we have

• 1. The $\epsilon$ -net property For all $g\in {\mathscr {F}}$ there exists $f\in {\mathscr {F}}_\epsilon$ such that $\Vert f- g\Vert _\infty \le \epsilon$.

• 2. The $\epsilon$ -Moment bound For all $f\in {\mathscr {F}}_\epsilon$

  $$\begin{aligned} \Vert X^\Lambda _f\Vert _{L^{2p}(\nu )}\le \epsilon + \frac{C_{2p}^{1/2p} }{\sqrt{|\Lambda |}}. \end{aligned}$$

  (36)

Then going through the same reasoning, as before (but with the function $x\mapsto e^{\lambda x}$ replaced by $x\mapsto |x|^{2p}$) we obtain the estimate

$$\begin{aligned} \mathbb {E}_\nu \left[ \,\sup _{f\in {\mathscr {F}}} X^\Lambda _f \right] \le \epsilon + |{\mathscr {F}}_\epsilon |^{1/2p} \left( \epsilon + \frac{C_{2p}^{1/2p}}{\sqrt{|\Lambda |}}\right) . \end{aligned}$$

(37)

As in the previous subsection, we have $|{\mathscr {F}}_\epsilon |\asymp \exp (\exp (\alpha (\log (1/\epsilon )^d)))$, with $\alpha =2^d \log |S|$. Let us furthermore assume that we have the bound

$$\begin{aligned} C_{2p}\le p^{\kappa 2p} \end{aligned}$$

(38)

for some $\kappa \ge 1/2$. In particular, for the low-temperature Ising model, we have $\kappa =1$ (see Remark 6.1), whereas we have $\kappa =1/2$ in the case of a Gaussian concentration bound. Then we analyse as before, i.e., on the level of logarithmic equivalence, the bounds we obtain from (37).

• 1. Dimension $d=1$. Then we have $|{\mathscr {F}}_\epsilon |\asymp \exp (\epsilon ^{-\alpha })$. We find the upperbound

  $$\begin{aligned} B(|\Lambda |)\preceq |\Lambda |^{-\frac{1}{2(\alpha \kappa +1)}} \end{aligned}$$

• 2. Dimension $d\ge 2$ we find

  $$\begin{aligned} B(|\Lambda |) \preceq \exp \left( -\left( \frac{\log |\Lambda |}{2\alpha \kappa }\right) ^{1/d}\right) \end{aligned}$$

As a conclusion we obtain the following asymptotic estimates.

Theorem 8.4

Let $\nu$ be a probability measure on $(\Omega ,{\mathfrak {B}})$ satisfying $\mathrm {MCB}\!\left( 2p,C_{2p}\right)$ for all $p\in \mathbb {N}$. Moreover assume that (38) holds. Then

$$\begin{aligned} \mathbb {E}_\nu \left[ d_{{\scriptscriptstyle K}}\left( \mathcal {E}_\Lambda (\cdot ),\nu \right) \right] \preceq {\left\{ \begin{array}{ll} |\Lambda |^{-\frac{1}{2(\alpha \kappa +1)}} &{} \text {if}\quad d=1\\ \exp \left( -\left( \frac{\log |\Lambda |}{2\alpha \kappa }\right) ^{1/d}\right) &{} \text {if}\quad d\ge 2. \end{array}\right. } \end{aligned}$$

Notice that when $\kappa =1/2$, this theorem is exactly the bound we obtained in Theorem 8.3.

9 Application 3: Fluctuations in the Shannon–McMillan–Breiman Theorem and Its Analog for Relative Entropy

If $\nu$ is an ergodic probability measure, the following holds:

$$\begin{aligned} \lim _{n\rightarrow \infty }-\frac{\log \nu (\mathcal {C}_n(\omega ))}{(2n+1)^d}=h(\nu )\quad \text {for}\;\nu \text {-a.e.} \;\omega . \end{aligned}$$

This is usually referred to as the Shannon–Millan–Breiman theorem for random fields and was proved in [20]. If $\Phi \in {\mathscr {B}}_T$ then we have

$$\begin{aligned} \lim _{n\rightarrow \infty }-\frac{1}{(2n+1)^d}\log \frac{\nu (\mathcal {C}_n(\omega ))}{\mu _\Phi (\mathcal {C}_n(\omega ))}=h(\nu |\mu _\Phi )\quad \text {for}\;\nu \text {-a.e.} \;\omega \end{aligned}$$

where $\mu _\Phi$ is any shift-invariant Gibbs measure associated with $\Phi$, and where $h(\nu |\mu _\Phi )$ is the relative entropy (per site) of $\nu$ with respect to $\mu _\Phi$ [cf. (16), (17)]. This result can be deduced using the Shannon–Millan–Breiman theorem (15), and the multidimensional ergodic theorem [35] applied to the measure $\nu$. Our goal is to control the fluctuations of both quantities around their respective limits when $\nu$ is a Gibbs measure. We have the following results.

Theorem 9.1

Let $\Phi \in {\mathscr {B}}_T$ be a potential whose specification $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin’s uniqueness condition (22). Then there exists $u_0>0$ such that

for all $n\in \mathbb {N}$ and for all $u\ge u_0$. Suppose, in addition to Dobrushin’s uniqueness condition, that (14) holds, then there exists $u_0>0$ such that

for all $n\in \mathbb {N}$ and for all $u\ge u_0$, where

$$\begin{aligned} p(d)= {\left\{ \begin{array}{ll} \frac{1}{2} &{} \text {if}\; d=2\\ 1 &{} \text {if}\; d\ge 3. \end{array}\right. } \end{aligned}$$

Proof

For each $n\in \mathbb {N}$, the function $\omega \mapsto F(\omega )=-\log \mu _\Phi (\mathcal {C}_n(\omega ))$ is a local function (with dependence set $C_n$). We apply (11) with $A=\mathcal {C}_n(\omega )$ and $\Lambda =C_n$ which gives

$$\begin{aligned} \mu _\Phi (\mathcal {C}_n(\omega ))=\int \mathop {}\!\mathrm {d}\mu _\Phi (\eta ) \, \varvec{\gamma }^{\Phi }_{C_n}(\omega |\eta ). \end{aligned}$$

(39)

Let $x\in C_n$, and $\omega ,{\tilde{\omega }}\in \Omega$ such that $\omega _y={\tilde{\omega }}_y$ for all $y\ne x$. We want to control

$$\begin{aligned} \log \frac{\mu _\Phi (\mathcal {C}_n(\omega ))}{\mu _\Phi (\mathcal {C}_n({\tilde{\omega }}))} \end{aligned}$$

Using (39), (10) and (12) we obtain

Hence

which immediately implies that

for all $x\in C_n$ ($\delta _x(F)=0$ for all $x\in {\mathbb {Z}}^d\backslash C_n$). The first statement then follows at once by applying Theorem 5.1 and rescaling u. If one can control the measure of cylinders as in (15), we can obtain a good estimate for the expectation of $-\,\log \mu _\Phi (\mathcal {C}_n(\omega ))$ and get the second statement. Since $\Phi$ satisfies (14) we have (15), hence we obtain

$$\begin{aligned} \left| \frac{1}{(2n+1)^d} \, \mathbb {E}_{\mu _\Phi }[-\log \mu _\Phi (\mathcal {C}_n(\omega ))]-h(\mu _\Phi )\right| \le \frac{C_\Phi }{n} \end{aligned}$$

(40)

where we used the variational principle (18). Notice that the bound is independent of d. The announced inequalities follow with $u_0=C_\Phi$. $\square$

Following the same train of thought as in the previous theorem, we obtain the companion result for relative entropy.

Theorem 9.2

Let $\Phi \in {\mathscr {B}}_T$ be a potential whose specification $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin’s uniqueness condition (22), and let $\Psi \in {\mathscr {B}}_T$ satisfying (14). Let $\mu _\Psi$ be any shift-invariant Gibbs measure associated with $\Psi$. Then there exists $u_0>0$ such that

for all $n\in \mathbb {N}$ and for all $u\ge u_0$. Suppose, in addition to Dobrushin’s uniqueness condition, that (14) holds for $\Phi$. Then there exists $u_0>0$ such that

for all $n\in \mathbb {N}$ and for all $u\ge u_0$, where p(d) is defined as in the previous theorem.

We now formulate a companion result on the Ising ferromagnet at low temperature. It is a simple consequence of Theorem 6.2 and inequality (40).

Theorem 9.3

Let $\mu _\beta ^+$ be the plus phase of the low-temperature Ising model on the lattice ${\mathbb {Z}}^d$, $d\ge 2$. There exist two constants, $u_0=u_0(d)>0$ and ${\bar{\beta }}={\bar{\beta }}(d)>0$ such that, for each $\beta >{\bar{\beta }}$, there exist $\varrho =\varrho (\beta )\in (0,1)$ and ${\tilde{c}}_\varrho >0$ such that the following two estimates hold:

(a):

If $d=2$ we have

$$\begin{aligned}&\mu _\beta ^+\left\{ \omega \in \Omega : \left| \frac{-\log \mu _\beta ^+(\mathcal {C}_n(\omega ))}{(2n+1)^2}-h(\mu _\beta ^+)\right| \ge \frac{u}{n^\tau } \right\} \\&\qquad \qquad \le \,4\, \exp \left( -{\tilde{c}}_\varrho (2n+1)^{\varrho (1-\tau )}u^{\varrho }\right) \end{aligned}$$

for all $n\in \mathbb {N}$, for all $u\ge u_0$ and for any $\tau \in (0,1)$, where ${\tilde{c}}_\varrho = c_{\varrho }\, 2^{-\frac{5}{2}\varrho } \beta ^-{\frac{\varrho }{2}}$.

(b):

If $d\ge 3$, we have

$$\begin{aligned}&\mu _\beta ^+\left\{ \omega \in \Omega : \left| \frac{-\log \mu _\beta ^+(\mathcal {C}_n(\omega ))}{(2n+1)^d}-h(\mu _\beta ^+)\right| \ge \frac{u}{n} \right\} \\&\qquad \qquad \le \,4\, \exp \left( -{\tilde{c}}_\varrho (2n+1)^{\varrho (\frac{d}{2}-\tau )}u^{\varrho }\right) \end{aligned}$$

for all $n\in \mathbb {N}$, for all $u\ge u_0$ and for any $1<\tau <\frac{d}{2}$, where ${\tilde{c}}_\varrho = c_{\varrho }\, 2^{-2\varrho }(d\beta )^{-\frac{\varrho }{2}}$.

In both cases, $c_{\varrho }=c_{\varrho }(d)$ is the constant appearing in Theorem 6.2.

The reader can now infer the counterpart of Theorem 9.2 for the low-temperature Ising model.

10 Application 4: First Occurrence of a Pattern of a Configuration in Another Configuration

For a subset $\Lambda$ of ${\mathbb {Z}}^d$, we refer to an element $a=(a_x,x\in \Lambda )\in S^{\Lambda }$ as a pattern supported by $\Lambda$. Given $x\in {\mathbb {Z}}^d$, we say that the patterns $a \in S^{\Lambda }$ and $b\in S^{\Lambda +x}$ are congruent if $a_y=b_{y+x}$ for every $y\in \Lambda$. Now, let $\eta ,\omega \in \Omega$. For each $n\in \mathbb {N}$, we look for the smallest hypercube $C_k$ such that “$\eta _{C_n}$ appears in $\omega _{C_k}$”. This means that there is a pattern a whose support lies inside $C_k$ such that $\eta _{C_n}$ and a are congruent, and that, if we take $k'<k$, there is no pattern whose support lies inside $C_{k'}$ which is congruent to $\eta _{C_n}$. This event can be seen as the first occurrence of the pattern $\eta _{C_n}$ in the configuration $\omega$: imagine that we are increasing at a constant rate the ‘window’ $C_k$ in $\omega$ until we observe the pattern $\eta _{C_n}$ for the first time.

We denote by $W_n(\eta ,\omega )$ the cardinality of the random hypercube $C_k$ we have just defined. It turns out that the natural random variable to consider is $\log W_n(\eta ,\omega )$. Indeed, one can prove (see [1]) that if $\Phi$ of finite range and $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin’s uniqueness condition and $\nu$ is any ergodic measure, then

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{(2n+1)^d} \log W_n(\eta ,\omega )= h(\nu )+h(\nu |\mu _\Phi ),\; \nu \otimes \mu _\Phi -\text {a.e.}. \end{aligned}$$

Now, fix n and $\eta$. It is quite obvious that no a priori control will be possible on $|\log W_n(\eta ,\omega )-\log W_n(\eta ,\omega ')|$ for all configurations $\omega ,\omega '$ which differ only at a site x. Indeed, changing $\omega$ in a single site can cause an arbitrary increase of the size of the hypercube in which we will see $\eta _{C_n}$. This is because we have to consider the worst case changes, not only typical changes for which things would go well. Nevertheless, we will obtain concentration inequalities by making a detour.

Theorem 10.1

Assume that $\Phi$ is of finite range and the associated specification $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin’s uniqueness condition (22). Let $\Psi$ be a potential satisfying (14) and such that its specification satisfies Dobrushin’s uniqueness condition. When $\Phi \ne \Psi$, let

and

Finally, let p(d) defined as in Theorem 9.1. Then there exist positive constants $C,u_0$ such that, for all $n\in \mathbb {N}$ and for all $u\ge u_0$,

$$\begin{aligned}&(\mu _\Psi \!\otimes \! \mu _\Phi )\!\left\{ (\eta ,\omega )\in \Omega \times \Omega : \frac{\log W_n(\eta ,\omega ) }{(2n+1)^d} > h(\mu _\Psi )+h(\mu _\Psi |\mu _\Phi )+\frac{u}{(2n+1)^{p(d)}}\right\} \\&\qquad \qquad \le \,C\, \exp \left( -c_{\Phi ,\Psi }\, (2n+1)\, u^2\right) . \end{aligned}$$

Moreover, we have

$$\begin{aligned}&(\mu _\Psi \! \otimes \! \mu _\Phi )\!\left\{ (\eta ,\omega )\in \Omega \times \Omega : \frac{\log W_n(\eta ,\omega ) }{(2n+1)^d} < h(\mu _\Psi )+h(\mu _\Psi |\mu _\Phi )-\frac{u}{(2n+1)^{p(d)}}\right\} \\&\qquad \qquad \le \,C\, \max \left\{ \exp \left( -c_{\Phi ,\Psi }\, (2n+1)\, u^2\right) , \exp \left( -(2n+1)^{d-p(d)}\, \frac{u}{2}\right) \right\} \end{aligned}$$

for all $n\in \mathbb {N}$ and for all $u\ge u_0$.

Let us make a few comments on this result. The constant $u_0$ is the same as in Theorem 9.1. Notice the dissymmetry between the two bounds when n is fixed: the second bound then becomes exponentially small in u, not in $u^2$ as in the first bound. The second bound is of course useful only if $\frac{u}{(2n+1)^{p(d)}}<h(\mu _\Psi )+h(\mu _\Psi |\mu _\Phi )$. Given $u\ge u_0$, this is always the case if n is large enough.

Proof

We treat the case $\Phi =\Psi$. The other case follows the same lines of proof using Theorem 9.2 instead Theorem 9.1. The idea is to write

$$\begin{aligned} \log W_n(\eta ,\omega )=\log \big [W_n(\eta ,\omega )\mu _\Phi (\mathcal {C}_n(\eta ))\big ] -\log \mu _\Phi (\mathcal {C}_n(\eta )). \end{aligned}$$

Then we have the following obvious inequality.

$$\begin{aligned}&(\mu _\Phi \otimes \mu _\Phi )\left\{ (\eta ,\omega )\in \Omega \times \Omega : \frac{\log W_n(\eta ,\omega )}{(2n+1)^d}> h(\mu _\Phi )+u\right\} \\ \nonumber&\qquad \qquad \le \,(\mu _\Phi \otimes \mu _\Phi )\!\left\{ (\eta ,\omega )\in \Omega \times \Omega : \frac{\log \big [W_n(\eta ,\omega )\mu _\Phi (\mathcal {C}_n(\eta ))\big ]}{(2n+1)^d}> \frac{u}{2}\right\} \\&\qquad \qquad \quad +\,\mu _\Phi \left\{ \eta \in \Omega : -\frac{\log \mu _\Phi (\mathcal {C}_n(\eta ))}{(2n+1)^d} > h(\mu _\Phi )+\frac{u}{2}\right\} . \nonumber \end{aligned}$$

(41)

We now control each term separately. To control the first one, we use Theorem 2.2. in [1] which we formulate here with our notations and under a form suitable for our purposes. Let $a_n$ be any pattern supported on $C_n$. Define $T_{a_n}(\omega )$ as the volume of the smallest hypercube $C_k$ which contains the support of a pattern congruent to $a_n$. Then there exist positive constants $c_1,c_2,\lambda _{a_n},\lambda _1,\lambda _2$ such that $\lambda _{a_n}\in [\lambda _1,\lambda _2]$ and such that, for any $t>0$, one has

$$\begin{aligned} \mu _\Phi \left\{ \omega \in \Omega : T_{a_n}(\omega )>\frac{t}{\lambda _{a_n}\mu _\Phi ([a_n])} \right\} \le c_1\, e^{-c_2 t}. \end{aligned}$$

(42)

By $[a_n]$ we mean the cylinder set made of all configurations $\xi$ such that $\xi _{C_n}=a_n$. The first term in the r.h.s. of (41) is equal to

$$\begin{aligned}&\sum _{a_n\in \Omega _n} \mu _{\Phi }([a_n])\, \mu _{\Phi }\left\{ \omega \in \Omega : T_{a_n}(\omega )\mu _\Phi ([a_n]) > e^{(2n+1)^d\frac{u}{2}} \right\} \nonumber \\&\qquad \qquad \le \,c_1\, \exp \big (-c_2\lambda _1 e^{(2n+1)^d\frac{u}{2}}\big ). \end{aligned}$$

(43)

where the inequality follows by (42). The second term in the r.h.s. of (41) is estimated using Theorem 9.1 from which it follows easily that this term is bounded above by

(44)

for all $n\in \mathbb {N}$ and for all $u\ge u_0$, where $p(d)=1/2$ if $d=2$ and $p(d)=1$ if $d\ge 3$. The bound (44) is much bigger than the bound (43), hence the first inequality of the theorem follows after rescaling u.

We now prove the other inequality of the theorem. We now have

$$\begin{aligned}&(\mu _\Phi \otimes \mu _\Phi )\left\{ (\eta ,\omega )\in \Omega \times \Omega : \frac{1}{(2n+1)^d}\log W_n(\eta ,\omega )< h(\mu _\Phi )-u\right\} \nonumber \\&\qquad \qquad \le \,(\mu _\Phi \otimes \mu _\Phi )\!\left\{ (\eta ,\omega )\in \Omega \times \Omega : \frac{1}{(2n+1)^d}\log \big [W_n(\eta ,\omega )\mu _\Phi (\mathcal {C}_n(\eta ))\big ]< \frac{u}{2}\right\} \nonumber \\&\qquad \qquad \quad +\,\mu _\Phi \left\{ \eta \in \Omega : -\frac{1}{(2n+1)^d}\log \mu _\Phi (\mathcal {C}_n(\eta )) < h(\mu _\Phi )-\frac{u}{2}\right\} . \end{aligned}$$

(45)

The second term in the r.h.s. is also bounded by (44). To get an upper bound for the first term in the r.h.s., we need to use the following result proved in [1, Lemma 4.3]:

$$\begin{aligned} \lambda _1 \le -\frac{\log \mu _\Phi \left\{ \omega \in \Omega : T_{a_n}(\omega )>t\right\} }{t\mu _\Phi ([a_n])}\le \lambda _2 \end{aligned}$$

provided that $t\mu _\Phi ([a_n])\le \frac{1}{2}$, and where $\lambda _1,\lambda _2$ are defined as above in this proof. We get the upper bound

$$\begin{aligned} \lambda _2\, \exp \left( -(2n+1)^d\, \frac{u}{2}\right) . \end{aligned}$$

This ends the proof. $\square$

Combining the results in [7] and Theorem 6.2, one could get the analog of Theorem 10.1 for the low-temperature Ising ferromagnet. But an extra work is needed to make some of the constants involved in the estimates in [7] more explicit and we will not do this.

11 Application 5: Bounding $\bar{d}$-Distance by Relative Entropy

Given $n\in \mathbb {N}$, define the (non normalized) Hamming distance between $\omega$ and $\eta$ that belong to $\Omega _n$ by

$$\begin{aligned} \bar{d}_n(\omega ,\eta )=\sum _{x\in C_n} \mathbb {1}_{\{\omega _x\ne \eta _x\}}. \end{aligned}$$

(46)

Given two shift-invariant probability measures $\mu ,\nu$ on $\Omega$, denote by $\mu _n$ and $\nu _n$ their projections on $\Omega _n$. Next define the $\bar{d}$-distance between $\mu _n$ and $\nu _n$ by

$$\begin{aligned} \bar{d}_n(\mu _n,\nu _n)=\inf _{\mathbb {P}\!_{n}\in \, \mathcal {C}(\mu _n,\nu _n)} \int _{\Omega _n}\int _{\Omega _n} \bar{d}_n(\omega ,\eta )\, \mathop {}\!\mathrm {d}\mathbb {P}_n(\omega ,\eta ) \end{aligned}$$

where $\mathcal {C}(\mu _n,\nu _n)$ denotes the set of all shift-invariant couplings of $\mu _n$ and $\nu _n$, that is, the set of jointly shift-invariant probability measures on $\Omega _n\times \Omega _n$ with marginals $\mu _n$ and $\nu _n$. One can prove (see e.g. [32]) that $\bar{d}_n(\mu _n,\nu _n)$ normalized by $(2n+1)^d$ converges to a limit that we denote by $\bar{d}(\mu ,\nu )$:

$$\begin{aligned} \bar{d}(\mu ,\nu )=\lim _{n\rightarrow \infty } \frac{\bar{d}_n(\mu _n,\nu _n)}{(2n+1)^d}. \end{aligned}$$

This defines a distance on the set of shift-invariant probability measures on $\Omega$. We have the following result.

Theorem 11.1

Let $\Phi \in {\mathscr {B}}_T$ and assume that the associated specification $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin’s uniqueness condition (22). Then, for every shift-invariant probability measure $\nu$

$$\begin{aligned} \bar{d}(\mu _\Phi ,\nu )\le \frac{\sqrt{2}}{1-{\mathfrak {c}}(\varvec{\gamma }^{\Phi })} \, \sqrt{h(\nu |\mu _\Phi )} \end{aligned}$$

where $h(\nu |\mu _\Phi )$ is the relative entropy of $\nu$ with respect to $\mu _\Phi$ (see (16)).

Moreover, if $\nu =\mu _\Psi$ is also a Gibbs measure for a potential $\Psi \in {\mathscr {B}}_T$, then

(47)

Take for instance a finite-range potential $\Phi$ and $\beta _1,\beta _2$ such that $\beta _1<\beta _2$ with $\beta _2$ small enough to be in Dobrushin’s uniqueness regime. Then the previous inequality reads

Before proving the previous theorem, let us introduce a certain set of Lipschitz functions. Given $n\in \mathbb {N}$ and let $F:\Omega \rightarrow \mathbb {R}$ be a cylindrical function with dependence set $C_n$. We have

$$\begin{aligned} |F(\omega )-F(\omega ')|\le \sum _{x\in C_n} \mathbb {1}_{\{\omega _x\ne \omega '_x\}} \delta _x(F). \end{aligned}$$

Assume that $\delta _x(F)=1$ for all $x\in C_n$. In particular We can identify this function with a 1-Lipschitz function on $\Omega _n$ with respect to the distance (46). Denote by $\text {Lip}_{1,\mu _{\Phi ,n}}(\Omega )$ the set of functions F which are 1-Lipschitz and such that $\mathbb {E}_{\mu _{\Phi ,n}}[F]=0$ (Recall that $\mu _{\Phi ,n}$ is the Gibbs measure associated to $\Phi$ induced on $\Omega _n$ by projection).

Proof

We now use a general theorem (see [3, p. 5] or [4, p. 101]). In the present setting, it states that the property that there exists a constant $b>0$ such that

$$\begin{aligned} \mathbb {E}_{\mu _{\Phi ,n}}[\exp (u F)]\le \exp (bu^2),\quad \forall u\in \mathbb {R},\; \forall F\in \text {Lip}_{1,\mu _{\Phi ,n}}(\Omega ) \end{aligned}$$

(48)

is equivalent to the property that, for all probability measures $\nu _n$ on $\Omega _n$, we have

$$\begin{aligned} \bar{d}_n(\mu _{\Phi ,n},\nu _n)\le 2\sqrt{b H_n(\nu _n|\mu _{\Phi ,n})}. \end{aligned}$$

(49)

By Theorem 5.1 we know that $\mu _{\Phi ,n}$ satisfies (48) with

Hence (49) reads

$$\begin{aligned} \bar{d}_n(\mu _{\Phi ,n},\nu _n)\le 2\sqrt{D (2n+1)^d H_n(\nu _n|\mu _{\Phi ,n})}\, . \end{aligned}$$

Dividing both sides by $(2n+1)^d$ and taking the limit $n\rightarrow \infty$ gives the announced inequality.

To prove inequality (47), we use (17) and (18) (applied to $\Psi$) to get

$$\begin{aligned} h(\mu _\Psi |\mu _\Phi )= P(\Phi )+\mathbb {E}_{\mu _\Psi }[f_\Phi ]-h(\mu _\Psi )= P(\Phi )-P(\Psi )+\mathbb {E}_{\mu _\Psi }[f_\Phi ]-\mathbb {E}_{\mu _\Psi }[f_\Psi ]. \end{aligned}$$

The desired inequality follows from the following facts:

and

The theorem is proved. $\square$

12 Application 6: Fattening Patterns

We can naturally generalize the Hamming distance defined in (46) as follows. Let $\Lambda \in \mathcal {P}$ (finite subset of ${\mathbb {Z}}^d$) and define

$$\begin{aligned} \bar{d}_\Lambda (\omega ,\eta )=\sum _{x\in \Lambda } \mathbb {1}_{\{\omega _x\ne \eta _x\}}. \end{aligned}$$

Given a subset $\mathcal {B}_\Lambda \subset \Omega _\Lambda$ define

$$\begin{aligned} \bar{d}_\Lambda (\omega ,\mathcal {B}_\Lambda )=\inf _{\omega '\in \mathcal {B}_\Lambda }\bar{d}_n(\omega ,\omega '). \end{aligned}$$

Given $\epsilon >0$, define the “$\epsilon$-fattening” of $\mathcal {B}_\Lambda$ as

$$\begin{aligned} \mathcal {B}_{\Lambda ,\epsilon }=\big \{\omega \in \Omega _\Lambda : \bar{d}_\Lambda (\omega ,\mathcal {B}_n)\le \epsilon |\Lambda |\big \}. \end{aligned}$$

We have the following abstract result.

Theorem 12.1

Let $\Lambda \in \mathcal {P}$. Suppose that $\nu$ is a probability measure which satisfies $\mathrm {GCB}\!\left( D\right)$ and such that $\nu (\mathcal {B}_\Lambda )=\frac{1}{2}$. Then, we have

$$\begin{aligned} \nu \big (\mathcal {B}_{\Lambda ,\epsilon }\big )\ge 1-\exp \left[ -\frac{|\Lambda |}{4D}\left( \epsilon -\frac{2\sqrt{D\ln 2}}{\sqrt{|\Lambda |}}\,\right) ^2\, \right] \end{aligned}$$

(50)

whenever $\epsilon >\frac{2\sqrt{D \ln 2}}{\sqrt{|\Lambda |}}$.

We take $\nu (\mathcal {B}_\Lambda )=\frac{1}{2}$ for the sake of definiteness. One can take $\nu (\mathcal {B}_\Lambda )=\alpha \in (0,1)$ and replace $\ln 2$ by $\ln \alpha ^{-1}$ in (50). The previous theorem can be loosely phrased as follows: For a probability measure satisfying a Gaussian concentration bound, if we “fatten” a bit a set of patterns which represents, say, half of the mass of $\Omega _\Lambda$, what is left has an extremely small mass.

Proof

Consider the local function $F(\omega )=\bar{d}_\Lambda (\omega ,\mathcal {B}_\Lambda )$. One easily checks that $\delta _x(F)\le 1$ for all $x\in \Lambda$. Applying (4) gives

$$\begin{aligned} \nu \left\{ \omega \in \Omega : F(\omega ) \ge u+\mathbb {E}_\nu [F]\right\} \le \exp \left( -\frac{u^2}{4D|\Lambda |}\right) \end{aligned}$$

(51)

for all $u>0$. We now estimate $\mathbb {E}_\nu [F]$. Applying (3) to $-\lambda F$ ($u\in \mathbb {R}$) we get

$$\begin{aligned} \exp \left( \lambda \mathbb {E}_\nu [F]\right) \mathbb {E}_\nu \big [\exp \left( -\lambda F\right) \big ] \le \exp \left( D\lambda ^2 |\Lambda |\right) . \end{aligned}$$

Observe that by definition of F we have

$$\begin{aligned} \mathbb {E}_\nu \big [\exp \left( -\lambda F\right) \big ]\ge \mathbb {E}_\nu \big [\mathbb {1}_{\mathcal {B}_\Lambda }\exp \left( -\lambda F\right) \big ]=\nu (\mathcal {B}_\Lambda ). \end{aligned}$$

Combining these two inequalities and taking the logarithm gives

$$\begin{aligned} \mathbb {E}_\nu [F]\le \inf _{\lambda >0} \Big \{D \lambda |\Lambda | + \frac{1}{\lambda }\ln \big (\nu (\mathcal {B}_\Lambda )^{-1}\big )\Big \}, \end{aligned}$$

i.e.,

$$\begin{aligned} \mathbb {E}_\nu [F]\le 2\sqrt{D|\Lambda | \ln \big (\nu (\mathcal {B}_\Lambda )^{-1}\big )}:=E. \end{aligned}$$

Therefore inequality (51) implies that

$$\begin{aligned} \nu \left\{ \omega \in \Omega : F(\omega ) \ge u'\right\} \le \exp \left( -\frac{(u'-E)^2}{4D|\Lambda |}\right) \end{aligned}$$

for all $u'>E$. To finish the proof, take $u'=\epsilon |\Lambda |$ and observe that $\nu \left\{ \omega \in \Omega : F(\omega ) \ge u'\right\} =\nu \big (\mathcal {B}_{\Lambda ,\epsilon }^c\big )$. $\square$

Corollary 12.1

Let $\Phi \in {\mathscr {B}}_T$ and assume that the associated specification $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin uniqueness condition (22). Then (50) holds with $D=\frac{1}{2(1-{\mathfrak {c}}(\varvec{\gamma }^{\Phi }))^2}$.

Remark 12.1

Inequality (50) can also be deduced from (49) by an argument due to Marton [29]. But this kind of argument does not work when one has only moment inequalities because there is no analog of (49), to the best of our knowledge.

We now turn to the situation when one has moment inequalities.

Theorem 12.2

Let $\Lambda \in \mathcal {P}$. For $\nu$ satisfying $\mathrm {MCB}\!\left( 2p,C_{2p}\right)$ and such that $\nu (\mathcal {B}_\Lambda )=\frac{1}{2}$, we have

$$\begin{aligned} \nu \big (\mathcal {B}_{\Lambda ,\epsilon }\big )\ge 1-\frac{C_{2p}}{|\Lambda |^{p/d}} \left( \epsilon -\frac{(2C_{2p})^\frac{1}{2p}}{\sqrt{|\Lambda |}} \right) ^{-2p} \end{aligned}$$

whenever $\epsilon >0$ and $n\in \mathbb {N}$ are such that $\epsilon >\frac{(2C_{2p})^\frac{1}{2p}}{\sqrt{|\Lambda |}}$.

Proof

As in the previous proof, consider the local function $F(\omega )=\bar{d}_\Lambda (\omega ,\mathcal {B}_\Lambda )$ which is such that $\delta _x(F)\le 1$ for all $x\in \Lambda$. Applying (7) we get

$$\begin{aligned} \nu \left\{ \omega \in \Omega : F(\omega ) \ge u+\mathbb {E}_\nu [F]\right\} \le \frac{C_{2p}|\Lambda |^{p}}{u^{2p}} \end{aligned}$$

for all $u>0$. We easily obtain an upper bound for $\mathbb {E}_\nu [F]$ by using (6) and the fact that $F\equiv 0$ on $\mathcal {B}_\Lambda$ :

$$\begin{aligned} \nu (\mathcal {B}_\Lambda ) (\mathbb {E}_\nu [F])^{2p}= \mathbb {E}_\nu \left[ \mathbb {1}_{\mathcal {B}_\Lambda }(F-\mathbb {E}_\nu [F])^{2p}\right] \le C_{2p}|\Lambda |^{p}\,. \end{aligned}$$

whence

$$\begin{aligned} \mathbb {E}_\nu [F]\le \frac{C_{2p}^{\frac{1}{2p}}\sqrt{|\Lambda |} }{\nu (\mathcal {B}_\Lambda )^{\frac{1}{2p}}}. \end{aligned}$$

We finish in the same way as in the previous proof to get the desired inequality. $\square$

In view of Theorem 6.1, the previous theorem applies to the plus-phase of the Ising model at sufficiently low temperature. Moreover, we can optimize over p. In fact, applying the stretched-exponential concentration inequality that holds in this case, we have indeed a stronger result.

Theorem 12.3

Let $\mu _\beta ^+$ be the plus-phase of the low-temperature Ising model. Take $\Lambda \in \mathcal {P}$ such that $\mu _\beta ^+(\mathcal {B}_\Lambda )=\frac{1}{2}$. Then there exists ${\bar{\beta }}>\beta _c$ such that, for each $\beta >{\bar{\beta }}$, there exists $\varrho =\varrho (\beta )\in (0,1)$ and two positive constants $c_\varrho$ and $c'_\varrho$ such that

$$\begin{aligned} \mu _\beta ^+\big (\mathcal {B}_{\Lambda ,\epsilon }\big )\ge 1- 4 \exp \left[ -c_\varrho \, |\Lambda |^{\frac{\varrho }{2}} \left( \epsilon -\frac{c'_\varrho }{\sqrt{|\Lambda |}}\right) ^\varrho \, \right] \end{aligned}$$

whenever $\epsilon >0$ and $n\in \mathbb {N}$ are such that $\epsilon >\frac{c'_\varrho }{\sqrt{|\Lambda |}}$.

Proof

Consider the local function $F(\omega )=\bar{d}_\Lambda (\omega ,\mathcal {B}_\Lambda )$ which is such that $\delta _x(F)\le 1$ for all $x\in \Lambda$. We apply Theorem 6.2. Using (27) we get

$$\begin{aligned} \mu _\beta ^+\left\{ \omega \in \Omega : F(\omega )\ge u+\mathbb {E}_{\mu _\beta ^+} [F]\right\} \le 4\, \exp \left( -\frac{c_\varrho u^{\varrho }}{|\Lambda |^\frac{\varrho }{2}}\right) , \end{aligned}$$

for all $u>0$. We now estimate $\mathbb {E}_{\mu _\beta ^+} [F]$ from above by using (28), (26) and the fact that $F\equiv 0$ on $\mathcal {B}_\Lambda$ :

$$\begin{aligned} K\!_\varrho \, \sqrt{|\Lambda |}\ge \Vert F-\mathbb {E}_{\mu _\beta ^+}[F]\Vert _{M\!_\varrho }\ge B\!_\varrho ^{-1}\mathbb {E}_{\mu _\beta ^+} [F] \sup _{q\in 2\mathbb {N}} (2^{-1/q}q^{-1/\varrho }). \end{aligned}$$

(52)

The function $\theta : \mathbb {R}^+\backslash \{0\} \rightarrow \mathbb {R}^+$ defined by $\theta (u)=2^{-1/u}u^{-1/\varrho }$ has a unique maximum at $u=\varrho \ln 2<2$. Hence we take $q=2$ in the right-hand side of (52), which gives

$$\begin{aligned} \mathbb {E}_{\mu _\beta ^+} [F]\le 2^{\frac{1}{\varrho }+\frac{1}{2}}K\!_\varrho \, B\!_\varrho \, (2n+1)^\frac{d}{2}. \end{aligned}$$

The rest of the proof is the same as in the previous proofs and we obtain the announced inequality with $c'_\varrho =2^{\frac{1}{\varrho }+\frac{1}{2}}K\!_\varrho \, B\!_\varrho$. $\square$

13 Application 7: Almost-Sure Central Limit Theorem

In this section we show how to use concentration inequalities to get a limit theorem. We consider limits along cubes but we can generalize without further effort to van Hove sequences.

13.1 Some Preliminary Definitions

Definition 13.1

Let $\nu$ be a shift-invariant probability measure and let $f:\Omega \rightarrow \mathbb {R}$ be a continuous function such that $\int f\mathop {}\!\mathrm {d}\nu =0$. We say that $(f,\nu )$ satisfies the central limit theorem with variance $\sigma _f^2$ if there exists a number $\sigma _f\ge 0$ such that for all $u\in \mathbb {R}$

$$\begin{aligned} \lim _{n\rightarrow \infty }\nu \left\{ \omega \in \Omega : \frac{\sum _{x\in C_n}f(T_x \omega )}{(2n+1)^{\frac{d}{2}}} \le u\right\} = \frac{1}{\sigma \!_f\sqrt{2\pi }}\int _{-\infty }^u \exp \left( -\frac{v^2}{2\sigma \!_f^2}\right) \mathop {}\!\mathrm {d}v. \end{aligned}$$

As a convention, we define the right-hand side to be the Dirac mass at 0 if $\sigma _f=0$. There is of course no loss of generality in considering continuous functions such that $\int f\mathop {}\!\mathrm {d}\nu =0$. In the cases we are going to consider, one has

$$\begin{aligned} \sigma _f^2=\sum _{x\in {\mathbb {Z}}^d} \int f \cdot f\circ T_x \mathop {}\!\mathrm {d}\nu <\infty . \end{aligned}$$

(53)

We need the following convenient definition.

Definition 13.2

(Summable decay of correlations) Given a shift-invariant probability measure $\nu$ and a continuous function f such that $\int f\mathop {}\!\mathrm {d}\nu =0$, we say that we have a summable decay of correlations if

(54)

It follows from (54) that for all $n\in \mathbb {N}$

$$\begin{aligned} \int \Big ( \sum _{x\in C_n} f\circ T_x\Big )^2 \mathop {}\!\mathrm {d}\nu \le C\, (2n+1)^{d} \end{aligned}$$

(55)

where .

The almost-sure central limit theorem is about replacing the convergence in law by the almost-sure convergence (in weak topology) of the following empirical logarithmic average:

(56)

where

$$\begin{aligned} L_N=\sum _{n=1}^N\frac{1}{n}=\ln N + \mathcal {O}(1). \end{aligned}$$

For each $N\in \mathbb {N}$ and $\omega \in \Omega$, (56) defines a probability measure on $\mathbb {R}$. Our goal is to prove that it converges, for $\nu$-almost every $\omega$, to the Gaussian measure $G_{0,\sigma _f^2}$ defined by

$$\begin{aligned} \mathop {}\!\mathrm {d}G_{0,\sigma \!_f^2}(v)=\frac{1}{\sigma _f\sqrt{2\pi }} \, \exp \Big (-\frac{v^2}{2\sigma \!_f^2}\Big )\mathop {}\!\mathrm {d}v, \; v\in \mathbb {R}. \end{aligned}$$

When such a convergence takes place, one says that $(f,\nu )$ satisfies the almost-sure central limit theorem. We shall prove a stronger result: the convergence will be with respect to the Kantorovich distance $d_{{\scriptscriptstyle K}}$ which is defined as follows. Let

$$\begin{aligned} {\mathscr {L}}=\{\rho :\mathbb {R}\rightarrow \mathbb {R}: \rho \;\text {is {1}-Lipschitz}\}. \end{aligned}$$

For two probability measures $\lambda ,\lambda '$ on $\mathbb {R}$, let

$$\begin{aligned} d_{{\scriptscriptstyle K}}(\lambda ,\lambda ') =\sup _{\rho \in {\mathscr {L}}_0} \left( \int \rho \mathop {}\!\mathrm {d}\lambda -\int \rho \mathop {}\!\mathrm {d}\lambda '\right) \end{aligned}$$

where ${\mathscr {L}}_0$ is the set of functions in ${\mathscr {L}}$ vanishing at the origin. We can replace ${\mathscr {L}}$ by ${\mathscr {L}}_0$ in the definition of the distance because we consider probability measures. This distance metrizes the weak topology on the set of probability measures on $\mathbb {R}$ such that $\int _{\mathbb {R}} d(u_0,u) \mathop {}\!\mathrm {d}\lambda (u)<\infty$ (where $u_0\in \mathbb {R}$ is an arbitrary chosen point).

13.2 An Abstract Theorem and Some Applications

The following abstract theorem says that, if the central limit theorem holds and if we have $\mathrm {MCB}\!\left( 2,C_2\right)$, then we have an almost-sure central limit theorem. In fact, the convergence to the Gaussian measure is with respect to the Kantorovich distance, which is stronger than weak convergence.

Theorem 13.1

Let $f\in \Delta _1(\Omega )$ and $\nu$ be a shift-invariant probability measure. Assume that the following conditions hold:

• 1. $(f,\nu )$ satisfies the central limit theorem with variance $\sigma _f^2>0$ (in the sense of Definition 13.1);

• 2. $\nu$ satisfies $\mathrm {MCB}\!\left( 2,C_2\right)$ (in the sense of Definition 3.2);

• 3. the decay of correlations is summable in the sense of (54).

Then, for $\nu$-almost every $\omega \in \Omega$,

$$\begin{aligned} \lim _{N\rightarrow \infty }d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N,\,\omega },G_{0,\sigma _f^2}\big )=0. \end{aligned}$$

We now apply this theorem in two situations, namely under Dobrushin’s uniqueness condition, and for the low-temperature Ising ferromagnet.

Theorem 13.2

Let $\Phi \in {\mathscr {B}}_T$ and assume that the associated specification $\varvec{\gamma }^{\Phi }$ satisfies Dobrushin’s uniqueness condition (22). Moreover, assume that

$$\begin{aligned} \sum _{x\in {\mathbb {Z}}^d} \Vert x\Vert _\infty ^{d+\delta }\, C_{0,x}(\varvec{\gamma }^\Phi ) <+\infty \end{aligned}$$

(57)

for some $\delta >0$, and that $f\in C^0(\Omega )$ satisfies

$$\begin{aligned} \sum _{x\in {\mathbb {Z}}^d} \Vert x\Vert _\infty ^d\, \delta _x(f) <+\infty . \end{aligned}$$

(58)

Without loss of generality, assume that $\int f \mathop {}\!\mathrm {d}\mu _\Phi =0$. Then, for $\mu _\Phi$-almost every $\omega \in \Omega$,

where $\sigma _f^2\in [0,\infty [$ is given by (53).

Proof

The conditions (57) and (58) imply (54). The theorem is a direct consequence of Theorem 13.1 and Theorem 4.1 in [24]. $\square$

The assumptions of the previous theorem are for instance satisfied if $\Phi$ is a finite-range potential with $\beta$ small enough and for any local function f. Let us state a corollary for the empirical magnetization $M_n(\omega )=\sum _{x\in C_n}s_0(T_x \omega )$, where $s_0(\omega )=\omega _0$, in the case of spin pair potentials (20).

Corollary 13.1

Consider a ferromagnetic spin pair potential $\beta \Phi$ such that $\sum _{x\in \mathbb {Z}^d} \tanh (\beta J(x))<1$. Assume that

$$\begin{aligned} \beta \sum _{x\in {\mathbb {Z}}^d} \Vert x\Vert _\infty ^{d+\delta }\, J(x) <+\infty \end{aligned}$$

(59)

for some $\delta >0$. Then, for $\mu _{\beta \Phi }$-almost every $\omega \in \Omega$, we have

where

Recall that in the regime considered in this corollary we have $\mathbb {E}_{\mu _{\beta \Phi }}[s_0]=0$. Observe that, for sufficiently high temperature, condition (59) implies $\sum _{x\in \mathbb {Z}^d} \tanh (\beta J(x))<1$. It is well known (see [18]) that in Dobrushin’s uniqueness regime one has for each $\beta$

$$\begin{aligned} \left| \int s_0\cdot s_0\circ T_x\, \mathop {}\!\mathrm {d}\mu _{\beta \Phi } \right| \le C\, \Vert x\Vert _\infty ^{-(d+\delta )}, \end{aligned}$$

where $C>0$ is independent of x (Recall that $\int s_0 \mathop {}\!\mathrm {d}\mu _{\beta \Phi }=0$ for $\beta <\beta _c$).

The next theorem is an almost-sure central limit theorem for the empirical magnetization in the low-temperature Ising ferromagnet.

Theorem 13.3

Let $\mu _\beta ^+$ be the plus phase of the low-temperature Ising model. Then there exists ${\bar{\beta }}$ such that, for each $\beta >{\bar{\beta }}$ and for $\mu _\beta ^+$-almost every $\omega \in \Omega$, we have

where

Proof

The theorem follows at once from Theorem 6.1, [28] and Theorem 13.1. $\square$

13.3 Proof of the Abstract Theorem

We now prove Theorem 13.1. Throughout the proof, we use the notations

First step We are going to prove that

$$\begin{aligned} \lim _{N\rightarrow \infty } \mathbb {E}_\nu \big [d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N,\cdot },G_{0,\sigma _f^2}\big )\big ]=0. \end{aligned}$$

(60)

Let $B>0$. Since for any $\rho \in {\mathscr {L}}_0$ one has $|\rho (v)|\le |v|$ for all v we have

$$\begin{aligned} d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N,\omega },G_{0,\sigma _f^2}\big )\le & {} \sup _{\rho \, \in {\mathscr {L}}_0} \int _{-B}^B \rho (v) \big (\mathop {}\!\mathrm {d}\mathcal {A}_{N,\omega }(v)-\mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)\big )\nonumber \\&\quad +\,\int _{\{|v|>B\}} |v|\mathop {}\!\mathrm {d}\mathcal {A}_{N,\omega }(v) +\int _{\{|v|>B\}} |v|\mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v). \end{aligned}$$

(61)

The last integral is obviously bounded by $c_1/B$ where $c_1>0$ depends only on f. (It is indeed much smaller but this bound suffices.) We now bound the expectation of the second term in the r.h.s., uniformly in N. Using (55) and the inequality

$$\begin{aligned} \mathbb {E}_\nu \left[ \mathbb {1}_{(B,+\infty )}(Z)\, Z\right] \le \frac{\mathbb {E}_\nu [Z^2]}{B}, \end{aligned}$$

which follows from Cauchy–Schwarz inequality and Bienaymé–Chebyshev inequality, we get

$$\begin{aligned}&\mathbb {E}_\nu \left[ \int _{\{|v|>B\}} |v|\mathop {}\!\mathrm {d}\mathcal {A}_{N,\cdot }(v)\right] \nonumber \\&\qquad \qquad =\,\frac{1}{L_N}\sum _{n=1}^N \frac{1}{n}\, \mathbb {E}_\nu \left[ \mathbb {1}_{(B,+\infty )}\left( \frac{|S_nf|}{(2n+1)^{d/2}}\right) \frac{|S_nf|}{(2n+1)^{d/2}}\right] \nonumber \\&\qquad \qquad \le \,\frac{c_2}{B} \end{aligned}$$

(62)

where $c_2>0$ is independent of N and B. We turn to the first term in the r.h.s. of (61). Since $[-B,B]$ is compact, we can apply Arzelà–Ascoli theorem to conclude that ${\mathscr {L}}_0$ is precompact in the uniform topology. As a consequence, given $\epsilon >0$, there exists a positive integer $r=r(\epsilon )$ and functions ${{\tilde{\rho }}}_j:[-B,B]\rightarrow \mathbb {R}$ in ${\mathscr {L}}_0$, $j=1,\ldots ,r$, such that, for any $\rho \in {\mathscr {L}}_0$, there is at least one integer $1\le j\le r$ such that

$$\begin{aligned} \sup _{|v|\le B}|\rho (v)-{{\tilde{\rho }}}_j(v)|\le \epsilon . \end{aligned}$$

Therefore we have

$$\begin{aligned}&\sup _{\rho \in {\mathscr {L}}_0} \int _{-B}^B \rho (v) \big (\mathop {}\!\mathrm {d}\mathcal {A}_{N,\omega }(v)-\mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)\big ) \nonumber \\&\qquad \qquad \le \,\sup _{1\le j\le r} \int _{-B}^B {{\tilde{\rho }}}_j(v) \big (\mathop {}\!\mathrm {d}\mathcal {A}_{N,\omega }(v)-\mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)\big )+2\epsilon . \end{aligned}$$

(63)

To proceed, we need to define, for each function ${{\tilde{\rho }}}_j$, a function $\rho _j\in {\mathscr {L}}_0$ defined on $\mathbb {R}$ and coinciding with ${{\tilde{\rho }}}_j$ on $[-B,B]$. This is done by setting

$$\begin{aligned} \rho _j(v)= {\left\{ \begin{array}{ll} 0 &{} \text {if} \; v<-B-|{{\tilde{\rho }}}_j(-B)| \\ {{\tilde{\rho }}}_j(-B)+{{\mathrm{sign}}}({{\tilde{\rho }}}_j(-B))(v+B) &{} \text {if}\; -B-|{{\tilde{\rho }}}_j(-B)|\le v<-B\\ {{\tilde{\rho }}}_j(v) &{} \text {if} \; v\in [-B,B]\\ {{\tilde{\rho }}}_j(B)-{{\mathrm{sign}}}({{\tilde{\rho }}}_j(B))(v-B) &{} \text {if}\; B<v\le B+|{{\tilde{\rho }}}_j(B)|\\ 0 &{} \text {if} \quad v>B+|{{\tilde{\rho }}}_j(B)|. \end{array}\right. } \end{aligned}$$

Next, for each $1\le j\le r$ and for each $N\ge 1$, introduce the functions

$$\begin{aligned} {\widetilde{F}}_N^{(j)}(\omega ) =\int _{-B}^B {{\tilde{\rho }}}_j(v) \big (\mathop {}\!\mathrm {d}\mathcal {A}_{N,\omega }(v)-\mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)\big ) \end{aligned}$$

and

$$\begin{aligned} F_N^{(j)}(\omega )&=\int \rho _j(v) \big (\mathop {}\!\mathrm {d}\mathcal {A}_{N,\omega }(v)-\mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)\big )\\&= \frac{1}{L_N}\sum _{n=1}^N \frac{1}{n}\left[ \rho _j\left( \frac{S_nf(\omega )}{(2n+1)^{d/2}} \right) -\int \rho _j \mathop {}\!\mathrm {d}G_{0,\sigma _f^2} \right] . \end{aligned}$$

We have

$$\begin{aligned} {\widetilde{F}}_N^{(j)}(\omega )=F_N^{(j)}(\omega )+R_N^{(j)}(\omega ) \end{aligned}$$

(64)

where

$$\begin{aligned} \mathbb {E}_\nu \left( \sup _{1\le j\le r}|R_N^{(j)}(\omega )|\right) \le \frac{c_3}{B} \end{aligned}$$

(65)

where $c_3>0$ is independent of N, r and B. This estimate is proved as above [see (61) and (62)]. We now estimate the variance of $F_N^{(j)}$. Given $z\in {\mathbb {Z}}^d$ we have

(66)

The r.h.s. term can be rewritten as $\sum _{x\in {\mathbb {Z}}^d}\, \delta _{z-x}(f)\,\varvec{u}^{(N)}_x$ where

We now apply Young’s inequality to get

Since $f\in \Delta _1(\Omega )$ by assumption, , and it remains to estimate . We have

where $c>0$ does not depend on N. Hence, for any $1\le j\le r$, we have

Since we assumed that $\nu$ satisfies $\mathrm {MCB}\!\left( 2,C_2\right)$, we end up with the following estimate for the variance of $F_N^{(j)}$:

(67)

We now use (64), (65), Cauchy–Schwarz inequality and (67) to obtain

By assumption, we have, for each $j=1,\ldots ,r$, $\lim _{N\rightarrow \infty } \mathbb {E}_\nu \big [F_N^{(j)}\big ]=0$ by the central limit theorem. Therefore we obtain

$$\begin{aligned} \limsup _{N\rightarrow \infty }\mathbb {E}_\nu \left[ \sup _{1\le j\le r} \int _{-B}^B \rho _j(v) \big (\mathop {}\!\mathrm {d}\mathcal {A}_{N,\omega }(v)-\mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)\big )\right] \le \frac{c_3}{B}. \end{aligned}$$

It now follows from (61), (62) and (63) we have

$$\begin{aligned} 0\le \limsup _{N\rightarrow \infty } \mathbb {E}_\nu \big [d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N,\cdot },G_{0,\sigma _f^2}\big )\big ] \le 2\epsilon +\frac{c_1+c_2+c_3}{B}. \end{aligned}$$

We now let $\epsilon$ tend to zero, then B to infinity. Therefore we obtain (60).

Second step We are going to estimate the variance of $d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N,\cdot },G_{0,\sigma _f^2}\big )$. We want to apply (6) with $p=1$ to the following function :

since $d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N,\omega },G_{0,\sigma _f^2}\big )=F_N(\omega )$. To this end, define for each $\rho \in {\mathscr {L}}_0$ the function

$$\begin{aligned} F_N^{(\rho )}(\omega )=\frac{1}{L_N}\sum _{n=1}^N \frac{1}{n} \left( \rho \left( \frac{S_nf(\omega )}{(2n+1)^{d/2}} \right) -\int \rho \mathop {}\!\mathrm {d}G_{0,\sigma _f^2}\right) . \end{aligned}$$

Let $z\in {\mathbb {Z}}^d$ and $\omega ,{\tilde{\omega }}\in \Omega$ such that $\omega _y\ne {\tilde{\omega }}_y$ for all $y\ne z$. We have

$$\begin{aligned} F_N^{(\rho )}(\omega ) \le \varvec{v}_z^{(N)} + F_N^{(\rho )}({\tilde{\omega }}) \end{aligned}$$

where $\varvec{v}_z^{(N)}$ is defined in (66). Now take the supremum over $\rho$ on both sides to get

$$\begin{aligned} F_N(\omega ) \le \varvec{v}_z^{(N)} + F_N({\tilde{\omega }}). \end{aligned}$$

The same inequality holds upon interchanging $\omega$ and ${\tilde{\omega }}$, hence

$$\begin{aligned} |F_N(\omega )-F_N({\tilde{\omega }})|\le \varvec{v}_z^{(N)}, \end{aligned}$$

therefore

$$\begin{aligned} \delta _z(F_N)\le \varvec{v}_z^{(N)}. \end{aligned}$$

Proceeding as above, we end up with

where $c'>0$ does not depend on N. Since $\nu$ satisfies $\mathrm {MCB}\!\left( 2,C_2\right)$ we have

Fix $0<\delta <1$ and let $N_k=e^{k^{1+\delta }}$. From the previous inequality we get at once

$$\begin{aligned} \sum _{k} \mathbb {E}_\nu \left[ \left( d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N_k,\cdot },G_{0,\sigma _f^2}\big ) -\mathbb {E}_\nu \left[ d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N_k,\cdot },G_{0,\sigma _f^2}\big )\right] \right) ^2\right] <\infty . \end{aligned}$$

It follows from Beppo Levi’s theorem that for $\nu$-almost every $\omega$

$$\begin{aligned} \lim _{k\rightarrow \infty } \Big ( d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N_k,\omega },G_{0,\sigma _f^2}\big ) -\mathbb {E}_\nu \left[ d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N_k,\omega },G_{0,\sigma _f^2}\big )\right] \Big )=0. \end{aligned}$$

(68)

By (60), the theorem will be proved if we can show that $N_k <N\le N_{k+1}$ implies that

$$\begin{aligned} \big |d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N,\omega },G_{0,\sigma _f^2}\big ) - d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N_k,\omega },G_{0,\sigma _f^2}\big )\big |\xrightarrow []{k\rightarrow \infty } 0 \end{aligned}$$

(69)

for $\nu$-almost every $\omega$. Indeed, if $N_k <N\le N_{k+1}$, one has

$$\begin{aligned}&\big |d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N,\omega },G_{0,\sigma _f^2}\big ) - d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N_k,\omega },G_{0,\sigma _f^2}\big )\big |\\&\qquad \qquad \le \,\frac{L_N-L_{N_k}}{L_N}\, d_{{\scriptscriptstyle K}}\big (\mathcal {A}_{N_k,\omega },G_{0,\sigma _f^2}\big )\\&\qquad \qquad \quad +\,\sup _{\rho \in {\mathscr {L}}_0} \frac{1}{L_N} \sum _{n=N_k+1}^N \frac{1}{n} \left( \rho \left( \frac{S_nf(\omega )}{(2n+1)^{d/2}} \right) -\int \rho \mathop {}\!\mathrm {d}G_{0,\sigma _f^2}\right) . \end{aligned}$$

The first term in the r.h.s goes to zero by (68). We handle the second one. We have

$$\begin{aligned}&\left| \sup _{\rho \in {\mathscr {L}}_0} \frac{1}{L_N} \sum _{n=N_k+1}^N \frac{1}{n} \left( \rho \left( \frac{S_nf(\omega )}{(2n+1)^{d/2}} \right) -\int \rho \mathop {}\!\mathrm {d}G_{0,\sigma _f^2}\right) \right| \\&\qquad \qquad \le \,\frac{1}{L_N} \sum _{n=N_k+1}^N \frac{1}{n} \left( \frac{\left| S_nf(\omega ) \right| }{(2n+1)^{d/2}}+\int |v| \mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)\right) \\&\qquad \qquad \le \,\frac{1}{L_{N_k}} \sum _{n=N_k+1}^{N_{k+1}} \frac{1}{n} \left( \frac{\left| S_nf(\omega ) \right| }{(2n+1)^{d/2}}+\int |v| \mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)\right) . \end{aligned}$$

It follows easily from our choice of $(N_k)$ that

$$\begin{aligned} \lim _{k\rightarrow \infty } \frac{1}{L_{N_k}} \sum _{n=N_k+1}^{N_{k+1}} \frac{1}{n}\, \int |v| \mathop {}\!\mathrm {d}G_{0,\sigma _f^2}(v)=0. \end{aligned}$$

It remains to prove the almost-sure convergence to zero of the sequence $(U_k)$ defined by

$$\begin{aligned} U_k=\frac{1}{L_{N_k}} \sum _{n=N_k+1}^{N_{k+1}} \frac{\left| S_nf(\omega ) \right| }{n(2n+1)^{d/2}}. \end{aligned}$$

For this purpose we estimate the expectation of the square of $U_k$. Using Cauchy–Schwarz inequality and (55) we get

$$\begin{aligned} \mathbb {E}_\nu [U_k^2]&\le \frac{1}{L_{N_k}^2} \sum _{n_1,n_2=N_k+1}^{N_{k+1}} \frac{\left( \mathbb {E}_\nu \left[ \left( S_{n_1}f(\omega ) \right) ^2\right] \right) ^{\frac{1}{2}}}{n_1(2n_1+1)^{d/2}} \, \frac{\left( \mathbb {E}_\nu \left[ \left( S_{n_2}f(\omega ) \right) ^2\right] \right) ^{\frac{1}{2}}}{n_2(2n_2+1)^{d/2}}\\&\le \frac{(\ln N_{k+1}-\ln N_k+\mathcal {O}(1))^2}{L_{N_k}^2}\le \frac{\mathcal {O}(1)}{k^2}. \end{aligned}$$

It follows that $\mathbb {E}_\nu [U_k^2]$ is summable in k and by Beppo Levi’s theorem we have that $U_k$ goes to zero almost surely. Therefore we have proved (69), which finishes the proof the theorem.