Critical Surface of the Hexagonal Polygon Model

Abstract

The hexagonal polygon model arises in a natural way via a transformation of the 1–2 model on the hexagonal lattice, and it is related to the high temperature expansion of the Ising model. There are three types of edge, and three corresponding parameters $\alpha ,\beta ,\gamma >0$. By studying the long-range order of a certain two-edge correlation function, it is shown that the parameter space $(0,\infty )^3$ may be divided into subcritical and supercritical regions, separated by critical surfaces satisfying an explicitly known formula. This result complements earlier work on the Ising model and the 1–2 model. The proof uses the Pfaffian representation of Fisher, Kasteleyn, and Temperley for the counts of dimers on planar graphs.

1 Introduction

The polygon model studied here is a process of statistical mechanics on the space of disjoint unions of closed loops on finite subsets of the hexagonal lattice ${\mathbb H}$ with toroidal boundary conditions. It arises naturally in the study of the 1–2 model, and indeed the main result of the current paper is complementary to the exact calculation of the critical surface of the 1–2 model reported in [5, 6] (to which the reader is referred for background and current theory of the 1–2 model). The polygon model may in addition be viewed as an asymmetric version of the O(n) model with $n=1$ (see [2] for a recent reference to the O(n) model).

Let $G=(V,E)$ be a finite subgraph of ${\mathbb H}$. The configuration space $\Sigma _G$ of the polygon model is the set of all subsets S of E such that every vertex in V is incident to an even number of members of S. The measure of the model is a three-parameter product probability measure conditioned on belonging to $\Sigma _G$, in which the three parameters are associated with the three classes of edge (see Fig. 1).

This model may be regarded as the high temperature expansion of a certain inhomogenous Ising model on the hexagonal lattice. The latter is a special case of the general eight-vertex model of Lin and Wu [16] (see also [25]). Whereas Lin and Wu concentrated on a mapping between their eight-vertex model and a generalized Ising model, the current paper utilizes the additional symmetries of the polymer model to calculate in closed form the equation of the critical surface for a given choice of order parameter. The parameter space of the polymer model extends beyond the set of parameter values corresponding to the classical Ising model, and thus our overall results do not appear to follow from classical facts (see also Remarks 2.2 and 2.4).

The order parameter used in this paper is the one that corresponds to the two-point correlation function of the Ising model, namely, the ratio $Z_{G,e\leftrightarrow f}/Z_G$, where $Z_{G,e\leftrightarrow f}$ is the partition function for configurations that include a path between two edges e, f, and $Z_G$ is the usual partition function.

Here is an overview of the methods used in this paper. The polymer model may be transformed into a dimer model on an associated graph, and the above ratio may be expressed in terms of the ratio of certain counts of dimer configurations. The last may be expressed (by classical results of Kasteleyn [7, 8], Fisher [3], and Temperley and Fisher [19]) as Pfaffians of certain antisymmetric matrices. The squares of these Pfaffians are determinants, and these converge as $G \uparrow {\mathbb H}$ to the determinants of infinite block Toeplitz matrices. Using results of Widom [22, 23] and others, these limits are analytic functions of the parameters except for certain parameter values determined by the spectral curve of the dimer model. This spectral curve has an explicit representation, and this enables a computation of the critical surface of the polygon model upon which the limiting order parameter is non-analytic.

More specifically, the parameter space $(0,\infty )^3$ may be partitioned into two regions, termed the supercritical and subcritical phases. The order parameter displays long-range order in the supercritical phase, but not in the subcritical phase.

The results of the current paper bear resemblance to earlier results of [6], in which the same authors determine the critical surface of the 1–2 model. The outline shape of the main proof (of Theorem 2.5) is similar to that of the corresponding result of [6]. In contrast, neither result seems to imply the other, and the dimer correspondence and associated calculations of the current paper are based on a different dimer representation from that of [6].

The characteristics of the hexagonal lattice that are special for this work include the properties of trivalence, planarity, and support of a ${\mathbb Z}^2$ action. It may be possible to extend the results to other such graphs, such as the Archimedean $(3,12^2)$ lattice, and the square/octagon $(4,8^2)$ lattice.

This article is organized as follows. The polygon model is defined in Sect. 2, and the main Theorem 2.5 is given in Sect. 2.3. The relationship between the polygon model and the 1–2 model, the Ising model, and the dimer model is explained in Sect. 3. The characteristic polynomial of the corresponding dimer model is calculated in Sect. 3.5, and Theorem 2.5 is proved in Sect. 4.

2 The Polygon Model

We begin with a description of the polygon model. Its relationship to the 1–2 model is explained in Sect. 3.1. The main result (Theorem 2.5) is given in Sect. 2.3.

2.1 Definition of the Polygon Model

Let the graph $G=(V,E)$ be a finite connected subgraph of the hexagonal lattice ${\mathbb H}=({\mathbb V},{\mathbb E})$, suitably embedded in ${\mathbb R}^2$ as in Fig. 1. The embedding of ${\mathbb H}$ is chosen in such a way that each edge may be described by one of the three directions: horizontal, NW, or NE. (Later we shall consider a finite box with toroidal boundary conditions.) Horizontal edges are said to be of type $a$, and NW edges (respectively, NE edges) type $b$ (respectively, type $c$), as illustrated in Fig. 1. Note that ${\mathbb H}$ is a bipartite graph, and we call the two classes of vertices black and white.

Let $\Pi$ be the product space $\Pi =\{0,1\}^E$. The sample space of the polygon model is the subset $\Pi ^{\mathrm {poly}}=\Pi ^{\mathrm {poly}}(G)\subseteq \Pi$ containing all $\pi =(\pi _e: e \in E) \in \Pi$ such that

$$\begin{aligned} \sum _{e\ni v} \pi _e \quad \text {is either} \ 0 \text { or } 2,\quad v \in V. \end{aligned}$$

(2.1)

Each $\pi \in \Pi ^{\mathrm {poly}}$ may be considered as a union of vertex-disjoint cycles of G, together with isolated vertices. We identify $\pi \in \Pi$ with the set $\{e\in E:\pi _e=1\}$ of ‘open’ edges under $\pi$. Thus (2.1) requires that every vertex is incident to an even number of open edges.

Fig. 1

An embedding of the hexagonal lattice, with the edge-types marked

Let $\epsilon _a, \epsilon _b, \epsilon _c\ne 0$. To the configuration $\pi \in \Pi ^{\mathrm {poly}}$, we assign the weight

$$\begin{aligned} w(\pi )= \epsilon _a^{2|\pi (a)|}\epsilon _b^{2|\pi (b)|} \epsilon _c^{2|\pi (c)|}, \end{aligned}$$

(2.2)

where $\pi (s)$ is the set of open s-type edges of $\pi$. The weight function w gives rise to the partition function

$$\begin{aligned} Z_G(P)=\sum _{\pi \in \Pi ^{\mathrm {poly}}} w(\pi ). \end{aligned}$$

(2.3)

This, in turn, gives rise to a probability measure on $\Pi ^{\mathrm {poly}}$ given by

$$\begin{aligned} {\mathbb P}_G(\pi ) = \frac{1}{Z_G(P)}w(\pi ),\quad \pi \in \Pi ^{\mathrm {poly}}. \end{aligned}$$

(2.4)

The measure ${\mathbb P}_G$ may be viewed as a product measure conditioned on the outcome lying in $\Pi ^{\mathrm {poly}}$. We concentrate here on an order parameter to be given next.

It is convenient to view the polygon model as a model on half-edges. To this end, let $A G=(A V, A E)$ be the graph derived from $G=(V,E)$ by adding a vertex at the midpoint of each edge in E. Let $M E=\{M e: e \in E\}$ be the set of such midpoints, and $A V = V \cup M V$. The edges A E are precisely the half-edges of E, each being of the form $\langle v, Me\rangle$ for some $v \in V$ and incident edge $e \in E$. A polygon configuration on G induces a polygon configuration on A G, which may be described as a subset of AE with the property that every vertex in AV has even degree. For an a-type edge $e\in E$, the two half-edges of e are assigned weight $\epsilon _a$ (and similarly for b- and c-type edges). The weight function w of (2.2) may now be expressed as

$$\begin{aligned} w(\pi )= \epsilon _a^{|\pi (a)|}\epsilon _b^{|\pi (b)|} \epsilon _c^{|\pi (c)|}, \quad \pi \in \Pi ^{\mathrm {poly}}(AG). \end{aligned}$$

(2.5)

We introduce next the order parameter of the polygon model. Let $e, f\in ME$ be distinct midpoints of AG, and let $\Pi _{e,f}$ be the subset of all $\pi \in \{0,1\}^{AE}$ such that: (i) every $v\in AV$ with $v\ne e,f$ is incident to an even number of open half-edges, and (ii) the midpoints of e and f are incident to exactly one open half-edge. We define the order parameter as

$$\begin{aligned} M_G(e,f)=\frac{Z_{G,e\leftrightarrow f}}{Z_G(P)}, \end{aligned}$$

(2.6)

where

$$\begin{aligned} Z_{G,e\leftrightarrow f} := \sum _{\pi \in \Pi _{e,f}} \epsilon _a^{|\pi (a)|}\epsilon _b^{|\pi (b)|} \epsilon _c^{|\pi (c)|}. \end{aligned}$$

(2.7)

Remark 2.1

(Notation) We write $\epsilon _s$ for the parameter of an s-type edge, and $\epsilon _g$ for that of edge g. For conciseness of notation, we shall later work with the parameters

$$\begin{aligned} \alpha :=\epsilon _a^2, \quad \beta := \epsilon _b^2, \quad \gamma := \epsilon _c^2, \end{aligned}$$

and the main result, Theorem 2.5, is expressed in terms of these new variables. The ‘squared’ variables $\epsilon _s^2$ are introduced to permit use of the ‘unsquared’ signed variables $\epsilon _s$ in the definition of the polymer model on AG.

The weight functions of (2.2) and (2.5) are unchanged under the sign change $\epsilon _s \rightarrow -\epsilon _s$ for $s\in \{a,b,c\}$. Similarly, if the edges e and f have the same type, then, for $\pi \in \Pi _{e,f}$, the weight $w(\pi )$ of (2.7) is unchanged under such sign changes. Therefore, if e and f have the same type, the order parameter $M_G(e,f)$ is independent of the sign of the $\epsilon _g$, and may be considered as a function of the parameters $\alpha$, $\beta$, $\gamma$.

Remark 2.2

(High temperature expansion) If $(\alpha ,\beta ,\gamma ) \in (0,1)^3$, the polygon model with weight function (2.5) is immediately recognized as the high temperature expansion of an inhomogeneous Ising model on AG in which the edge-interaction $J_s$ of an s-type half-edge satisfies $\tanh J_s = |\epsilon _s|$. Under this condition, the order parameter $M_G(e,f)$ of (2.6) is simply a two-point correlation function of the Ising model (see Lemma 3.2). If the $|\epsilon _s|$ are sufficiently small, this Ising model is a high-temperature model, whence $M_G(e,f)$ tends to zero in the double limit as $G \uparrow {\mathbb H}_n$ and $|e-f|\rightarrow \infty$, in that order. It may in fact be shown (by results of [12, 14, 17] or otherwise) that this Ising model has critical surface given by the equation $\alpha \beta +\beta \gamma +\gamma \alpha =1$.

See [1, p. 75] and [17, 21] for accounts of the high temperature expansion, and [4] for a recent related paper. The above Ising model may be viewed as a special case of the eight-vertex model of Lin and Wu [16]. It is studied further in [6, Sect. 4].

2.2 The Toroidal Hexagonal Lattice

We will work mostly with a finite subgraph of ${\mathbb H}$ subject to toroidal boundary conditions. Let $n \ge 1$, and let $\tau _1$, $\tau _2$ be the two shifts of ${\mathbb H}$, illustrated in Fig. 2, that map an elementary hexagon to the next hexagon in the given directions. The pair $(\tau _1,\tau _2)$ generates a ${\mathbb Z}^2$ action on ${\mathbb H}$, and we write ${\mathbb H}_n=(V_n,E_n)$ for the quotient graph of ${\mathbb H}$ under the subgroup of ${\mathbb Z}^2$ generated by the powers $\tau _1^n$ and $\tau _2^n$. The resulting ${\mathbb H}_n$ is illustrated in Fig. 2, and may be viewed as a finite subgraph of ${\mathbb H}$ subject to toroidal boundary conditions. We write $M_n(e,f):= M_{{\mathbb H}_n}(e,f)$.

Fig. 2

The graph ${\mathbb H}_n$ is an $n\times n$ ‘diamond’ wrapped onto a torus, as illustrated here with $n=4$

As in Remark 2.1, let

$$\begin{aligned} \alpha =\epsilon _a^2,\quad \beta =\epsilon _b^2,\quad \gamma =\epsilon _c^2. \end{aligned}$$

(2.8)

Theorem 2.3

Let e, f be distinct edges of ${\mathbb H}_n$. The order parameter $M_n(e,f)=M_n^{\alpha ,\beta ,\gamma }(e,f)$ is invariant under the change of variables $(\alpha ,\beta ,\gamma ) \mapsto (\alpha ,\beta ^{-1},\gamma ^{-1})$, and similarly under the other two changes of variables in which exactly two of the parameters $\alpha$, $\beta$, $\gamma$ are replaced by their reciprocals.

Proof

Let $\pi \in \Pi ^{\mathrm {poly}}$ be a polygon configuration on $A{\mathbb H}_n$, and let $\pi '$ be obtained from $\pi$ by

$$\begin{aligned} \pi '(e) = {\left\{ \begin{array}{ll} \pi (e) &{}\text {if }\quad e \ \text {has type }a,\\ 1-\pi (e) &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(2.9)

Since $\pi '$ is obtained from $\pi$ by adding, modulo 2, a collection of edges that induce an even subgraph of ${\mathbb H}_n$, we have that $\pi '\in \Pi ^{\mathrm {poly}}$. Let $w^{\alpha ,\beta ,\gamma }(\pi )$ be the weight of $\pi$ as in (2.5), with $\alpha$, $\beta$, $\gamma$ given by (2.8). Then

$$\begin{aligned} w^{\alpha ,\beta ,\gamma }(\pi )=(\beta ^{\# b}\gamma ^{\# c}) w^{\alpha ,\beta ^{-1},\gamma ^{-1}}(\pi '), \end{aligned}$$

(2.10)

where $\# s$ is the number of s-type edges in ${\mathbb H}_n$. Similarly, if $e\ne f$, then $\pi '\in \Pi _{e,f}$ and (2.10) holds.

By (2.9)–(2.10), $M_n$ is unchanged under the map $(\alpha ,\beta ,\gamma )\mapsto (\alpha ,\beta ^{-1},\gamma ^{-1})$. The same proof is valid for the other two cases. $\square$

Remark 2.4

Recall Remark 2.2, where it is noted that the polymer model is the high temperature expansion of a solvable Ising model when $(\alpha ,\beta ,\gamma )\in (0,1)^3$. By Theorem 2.3, this results in a fairly complete picture of the behaviour of $\lim _{n\rightarrow \infty } M_n(e,f)$ when either none or exactly two of the three parameters lie in $(1,\infty )$. In contrast, the dimer-based methods of the current work permit an analysis for all triples $(\alpha ,\beta ,\gamma )\in (0,\infty )^3$, but at the price of assuming that e, f satisfy the conditions of the forthcoming Theorem 2.5.

2.3 Main Result

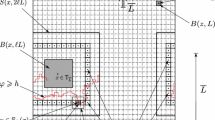
Let $e=\langle x,y\rangle$ denote the edge $e\in {\mathbb E}$ of the hexagonal lattice ${\mathbb H}=({\mathbb V},{\mathbb E})$ with endpoints x, y. We shall make use of a measure of distance $|e-f|$ between edges e and f which, for definiteness, we take to be the Euclidean distance between the midpoints of e and f, with ${\mathbb H}$ embedded in ${\mathbb R}^2$ in the manner of Fig. 2 with unit edge-lengths. Our main theorem is as follows.

Theorem 2.5

Let $e,f \in {\mathbb E}$ be NW edges such that:

$$\begin{aligned} \begin{array}{ll} &{}\text {there exists a path} \ \ell =\ell (e,f) \ \text {of}\ A{\mathbb H}_n \ \,\text {from} \ Me \ \text {to} \ Mf,\\ &{} \text {using only horizontal and NW half-edges}. \end{array} \end{aligned}$$

(2.11)

Let $\epsilon _s \ne 0$ for $s=a,b,c$, so that $\alpha ,\beta ,\gamma >0$, and let

$$\begin{aligned} \gamma _1=\left| \frac{1-\alpha \beta }{\alpha +\beta }\right| , \quad \gamma _2=\left| \frac{1+\alpha \beta }{\alpha -\beta }\right| , \end{aligned}$$

(2.12)

where $\gamma _2$ is interpreted as $\infty$ if $\alpha =\beta$.

• (a) The limit $M(e,f)^2=\lim _{n\rightarrow \infty }M_n(e,f)^2$ exists for $\gamma \ne \gamma _1,\gamma _2$.

• (b) Supercritical case. Let $R_{\text {sup}}$ be the set of all $(\alpha ,\beta ,\gamma )\in (0,\infty )^3$ satisfying

  $$\begin{aligned} \left| \frac{1-\alpha \beta }{\alpha +\beta }\right| <\gamma <\left| \frac{1+\alpha \beta }{\alpha -\beta }\right| . \end{aligned}$$

  The limit $\Lambda (\alpha ,\beta ,\gamma ):=\lim _{|e-f|\rightarrow \infty } M(e,f)^2$ exists on $R_{\text {sup}}$, and satisfies $\Lambda > 0$ except possibly on some nowhere dense subset.

• (c) Subcritical case. Let $R_{\text {sub}}$ be the set of all $(\alpha ,\beta ,\gamma )\in (0,\infty )^3$ satisfying

  $$\begin{aligned} \text {either}\quad \gamma <\left| \frac{1-\alpha \beta }{\alpha +\beta }\right| \quad \text {or}\quad \gamma > \left| \frac{1+\alpha \beta }{\alpha -\beta }\right| . \end{aligned}$$

  The limit $\Lambda (\alpha ,\beta ,\gamma )$ exists on $R_{\text {sub}}$ and satisfies $\Lambda =0$.

The function $\Lambda$ has a singularity when crossing between the subcritical and supercritical regions. A brief explanation of the regions $R_{\text {sub}}$ and $R_{\text {sup}}$ follows. It turns out that the process is ‘critical’ if and only if the spectral curve (see Sect. 3.5) of the corresponding dimer model intersects the unit torus. This occurs if and only the parameter-vector $(\alpha ,\beta ,\gamma )$ is a root of the equation $\alpha \beta +\beta \gamma +\gamma \alpha =1$ or of any one of the three equations obtained from this equation by the changes of variables of Theorem 2.3. See Proposition 3.4.

Assumption (2.11), as illustrated in Fig. 3, is key to the method of proof, and we present no results in the absence of this condition. Thus, Theorem 2.5 is not of itself a complete picture of the location of critical phenomena. For the related 1–2 model, certain further information about the limits corresponding to Theorem 2.5(b, c) may be derived as described in [6] and [17], and we do not explore that here, beyond saying that it includes information on the rates of convergence, and on correlations unconstrained by condition (2.11).

Fig. 3

A path $\ell$ of NW and horizontal edges connecting the midpoints of e and f

By Remark 2.1, it will suffice to prove Theorem 2.5 subject to the assumption that $\epsilon _s>0$ for $s=a,b,c$.

3 The 1–2 and Dimer Models

We summarize next the relations between the polygon and the 1–2 and dimer models.

3.1 The 1–2 Model

A 1–2 configuration on the toroidal graph ${\mathbb H}_n=(V_n,E_n)$ is a subset $F\subseteq E_n$ such that every $v \in V_n$ is incident to either one or two members of F. The subset F may be expressed as a vector in the space $\Sigma _n=\{-1,1\}^{E_n}$ where $-1$ represents an absent edge and 1 a present edge. (It will be convenient later to use the space $\Sigma _n$ rather than the more natural $\Pi _n=\{0,1\}^{E_n}$.) Thus the space of 1–2 configurations may be viewed as the subset of $\Sigma _n$ containing all vectors $\sigma$ such that

$$\begin{aligned} \sum _{e\ni v} \pi _e \in \{1,2\}, \quad v \in V_n, \end{aligned}$$

where $\pi _e=\tfrac{1}{2}(1+\sigma _e)$.

The hexagonal lattice ${\mathbb H}$ is bipartite, and we colour the two vertex-classes black and white. Let $a,b,c \ge 0$ be such that $(a,b,c)\ne (0,0,0)$, and associate these three parameters with the edges as in Fig. 1. For $\sigma \in \Sigma _n$ and $v \in V_n$, let $\sigma |_v$ be the sub-configuration of $\sigma$ on the three edges incident to v, and assign weights $w(\sigma |_v)$ to the $\sigma _v$ as in Fig. 4. We observe the states $\sigma _{e_{v,a}},\sigma _{e_{v,b}}, \sigma _{e_{v,c}}$, where $e_{v,s}$ is the edge of type s incident to v. The corresponding signature is the word $\pi (e_{v,c})\pi (e_{v,b})\pi (e_{v,a})$ of length 3. The signature of v is given as in Fig. 4, together with the local weight $w(\sigma |_v)$ associated with each of the six possible signatures.

Fig. 4

The six possible local configurations $\sigma |_v$ at a vertex v in the two cases of black and white vertices of ${\mathbb H}_n$ (see the upper and lower figures, respectively). The signature of each is given, and also the local weight $w(\sigma |_v)$ associated with each local configuration

Let

$$\begin{aligned} w(\sigma ) = \prod _{v\in V} w(\sigma |_v), \quad \sigma \in \Sigma _n, \end{aligned}$$

(3.1)

and

$$\begin{aligned} Z_n=\sum _{\sigma \in \Sigma _n} w(\sigma ). \end{aligned}$$

(3.2)

This gives rise to the probability measure

$$\begin{aligned} \mu _n(\sigma ) = \frac{1}{Z_n} w(\sigma ), \quad \sigma \in \Sigma _n. \end{aligned}$$

(3.3)

We write $\langle X\rangle _n$ for the expectation of the random variable X with respect to $\mu _n$.

The 1–2 model was introduced by Schwartz and Bruck [18] in a calculation of the capacity of a certain constrained coding system. It has been studied by Li [13, 15], and more recently by Grimmett and Li [6]. See [5] for a review.

3.2 The 1–2 Model as a Polygon Model

By [6, Prop.4.1], the partition function $Z_n$ of the 1–2 model with parameters a, b, c on ${\mathbb H}_n$ satisfies

$$\begin{aligned} Z_n=\bigl (\tfrac{1}{4}(a+b+c)\bigr )^{|V_n|} Z_n', \end{aligned}$$

where

$$\begin{aligned} Z_n'=\sum _{\sigma \in \Sigma }\prod _{v\in V_n} \bigl (1+A\sigma _{v,b}\sigma _{v,c}+B\sigma _{v,a}\sigma _{v,c}+C\sigma _{v,a}\sigma _{v,b}\bigr ), \end{aligned}$$

(3.4)

$\sigma _{v,s}$ denotes the state of the s-type edge incident to $v\in V$, and

$$\begin{aligned} A=\frac{a-b-c}{a+b+c},\quad B=\frac{b-a-c}{a+b+c},\quad C=\frac{c-a-b}{a+b+c}. \end{aligned}$$

(3.5)

Each $e =\langle u,v\rangle \in E_n$ contributes twice to the product in (3.4), in the forms $\sigma _{u,s}$ and $\sigma _{v,s}$ for some $s\in \{a,b,c\}$. We write $\sigma _e$ for this common value, and we expand (3.4) to obtain a polynomial in the variables $\sigma _e$. In summing over $\sigma \in \Sigma _n$, a term disappears if it contains some $\sigma _e$ with odd degree. Therefore, in each monomial $M(\sigma )$ of the resulting polynomial, every $\sigma _e$ has even degree, that is, degree either 0 or 2. With the monomial M we associate the set $\pi _M$ of edges e for which the degree of $\sigma _e$ is 2. By examination of (3.4) or otherwise, we may see that $\pi _M$ is a polygon configuration in ${\mathbb H}_n$, which is to say that the graph $(V_n,\pi _M)$ comprises vertex-disjoint circuits (that is, closed paths that revisit no vertex) and isolated vertices. Indeed, there is a one-to-one correspondence between monomials M and polygon configurations $\pi$. The corresponding polygon partition function is given at (2.3) where the weights $\epsilon _a$, $\epsilon _b$, $\epsilon _c$ satisfy

$$\begin{aligned} \epsilon _b\epsilon _c=A,\quad \epsilon _a\epsilon _c=B, \quad \epsilon _a\epsilon _b= C, \end{aligned}$$

(3.6)

which is to say that

$$\begin{aligned} \epsilon _a^2=\frac{BC}{A},\quad \epsilon _b^2=\frac{AC}{B},\quad \epsilon _c^2=\frac{AB}{C}. \end{aligned}$$

(3.7)

Note that these squares may be negative, whence the corresponding $\epsilon _a$, $\epsilon _b$, $\epsilon _c$ are either real or purely imaginary.

The relationship between $\epsilon _s$ and the parameters a, b, c is given in the following elementary lemma, the proof of which is omitted.

Lemma 3.1

Let $a\ge b\ge c>0$, and let $\epsilon _s$ be given by (3.5)–(3.7).

• (a) Let $a<b+c$. Then $\epsilon _a,\epsilon _b,\epsilon _c$ are purely imaginary, and moreover

  • (i) if $a^2<b^2+c^2$, then $0<|\epsilon _a|<1$, $0<|\epsilon _b|<1$, $0<|\epsilon _c|<1$,

  • (ii) if $a^2=b^2+c^2$, then $|\epsilon _a|=1$, $0<|\epsilon _b|<1$, $0<|\epsilon _c|<1$,

  • (iii) if $a^2>b^2+c^2$, then $|\epsilon _a|>1$, $0<|\epsilon _b|<1$, $0<|\epsilon _c|<1$.

• (b) If $a=b+c$, then $|\epsilon _a|=\infty$, $\epsilon _b=\epsilon _c=0$.

• (c) If $a>b+c$, then $\epsilon _a,\epsilon _b,\epsilon _c$ are real, and moreover $|\epsilon _a|>1$, $0<|\epsilon _b|<1$, $0<|\epsilon _c|<1$.

Equations (3.6)–(3.7) express the $\epsilon _g$ in terms of A, B, C. Conversely, for given real $\epsilon _s\ne 0$, it will be useful later to define A, B, C by (3.6), even when there is no corresponding 1–2 model.

3.3 Two-Edge Correlation in the 1–2 Model

Consider the 1–2 model on ${\mathbb H}_n$ with parameters a, b, c, and specifically the two-edge correlation $\langle \sigma _e\sigma _f\rangle _n$ where $e,f\in E_n$ are distinct.

We multiply through (3.4) by $\sigma _e\sigma _f$ and expand in monomials. This amounts to expanding (3.4) and retaining those monomials M in which every $\sigma _g$ has even degree except $\sigma _e$ and $\sigma _f$, which have degree 1. We may associate with M a set $\pi _M$ of half-edges of $A {\mathbb H}_n$ such that: (i) the midpoints M e and M f have degree 1, and (ii) every other vertex in $A V_n$ has even degree. Such a configuration comprises a set of cycles together with a path between Me and Mf. The next lemma is immediate.

Lemma 3.2

The two-edge correlation function of the 1–2 model satisfies

$$\begin{aligned} \langle \sigma _e\sigma _f\rangle _n=\frac{Z_{n,e\leftrightarrow f}}{Z_n(P)}=M_n(e,f), \end{aligned}$$

(3.8)

where the numerator $Z_{n,e\leftrightarrow f}$ is given in (2.7), and the parameters of the polygon model satisfy (3.7) and (3.5).

3.4 The Polygon Model as a Dimer Model

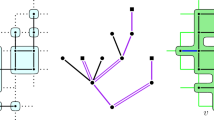
We show next a one-to-one correspondence between polygon configurations on ${\mathbb H}_n$ and dimer configurations on the corresponding Fisher graph of ${\mathbb H}_n$. The Fisher graph ${\mathbb F}_n$ is obtained from ${\mathbb H}_n$ by replacing each vertex by a ‘Fisher triangle’ (comprising three ‘triangular edges’), as illustrated in Fig. 5. A dimer configuration (or perfect matching) is a set D of edges such that each vertex is incident to exactly one edge of D.

Let $\pi$ be a polygon configuration on ${\mathbb H}_n$ (considered as a collection of edges). The local configuration of $\pi$ at a black vertex $v \in V_n$ is one of the four configurations at the top of Fig. 5, and the corresponding local dimer configuration is given in the lower line (a similar correspondence holds at white vertices). The construction may be expressed as follows. Each edge e of ${\mathbb F}_n$ is either triangular or is inherited from ${\mathbb H}_n$ (that is, e is the central third of an edge of ${\mathbb H}_n$). In the latter case, we place a dimer on e if and only if $e \notin \pi$. Having applied this rule on the edges inherited from ${\mathbb H}_n$, there is a unique allocation of dimers to the triangular edges that results in a dimer configuration on ${\mathbb F}_n$. We write $D=D(\pi )$ for the resulting dimer configuration, and note that the correspondence $\pi \leftrightarrow D$ is one-to-one.

Fig. 5

To each local polygon configuration at a black vertex of ${\mathbb H}_n$, there corresponds a dimer configuration on the Fisher graph ${\mathbb F}_n$. The situation at a white vertex is similar. In the leftmost configuration, the local weight of the polygon configuration is $\epsilon _b\epsilon _c$, and in the dimer configuration A

By (2.2), the weight $w(\pi )$ is the product (over $v\in V_n$) of a local weight at v belonging to the set $\{\epsilon _a\epsilon _b, \epsilon _b \epsilon _c, \epsilon _c\epsilon _a, 1\}$, where the particular value depends on the behavior of $\pi$ at v (see Figure 5 for an illustration of the four possibilities at a black vertex). We now assign weights to the edges of the Fisher graph ${\mathbb F}_n$ in such a way that the corresponding dimer configuration has the same weight as $\pi$.

Each edge of a Fisher triangle has one of the types: vertical (denoted ‘${\mathrm {V}}$’), NE, or NW, according to its orientation. To each edge e of ${\mathbb F}_n$ lying in a Fisher triangle, we allocate the weight:

$$\begin{aligned} A\quad&\text {if} \ e \ \text {is vertical},\\ B\quad&\text {if}\ e \ \text {is NE},\\ C\quad&\text {if}\ e \ \text {is NW}, \end{aligned}$$

where A, B, C satisfy (3.6)–(3.7). The dimer partition function is given by

$$\begin{aligned} Z_n(D) := \sum _D A^{|D({\mathrm {V}})|} B^{|D({\mathrm {NE}})|} C^{|D({\mathrm {NW}})|}, \end{aligned}$$

(3.9)

where $D(s)\subseteq D$ is the set of dimers of type s. It is immediate, by inspection of Figure 5, that the correspondence $\pi \leftrightarrow D$ is weight-preserving, and hence

$$\begin{aligned} Z_n(D) = Z_n(P). \end{aligned}$$

3.5 The Spectral Curve of the Dimer Model

We turn now to the spectral curve of the weighted dimer model on ${\mathbb F}_n$, for the background to which the reader is referred to [14]. The fundamental domain of ${\mathbb F}_n$ is drawn in Fig. 6, and the edges of ${\mathbb F}_n$ are oriented as in that figure. It is easily checked that this orientation is ‘clockwise odd’, in the sense that any face of ${\mathbb H}_n$, when traversed clockwise, contains an odd number of edges oriented in the corresponding direction. The fundamental domain has 6 vertices labelled $1, 2, \dots , 6$, and its weighted adjacency matrix (or ‘Kasteleyn matrix’) is the $6\times 6$ matrix $W=(k_{i,j})$ with

$$\begin{aligned} k_{i,j} = {\left\{ \begin{array}{ll} w_{i,j} &{}\text {if} \ \langle i,j\rangle \ \text {is oriented from} \ i \ \text {to} \ j,\\ -w_{i,j} &{}\text {if}\ \langle i,j\rangle \ \text {is oriented from} \ j\ \text {to} \ i,\\ 0 &{}\text {if there is no edge between} \ i \ \text {and}\ j, \end{array}\right. } \end{aligned}$$

where the $w_{i,j}$ are as indicated in Fig. 6. From W we obtain a modified adjacency (or ‘modified Kasteleyn’) matrix K as follows.

Fig. 6

Weighted $1\times 1$ fundamental domain of ${\mathbb F}_n$. The vertices are labelled $1,2,\dots ,6$, and the weights $w_{i,j}$ and orientations are as indicated. The further weights $w^{\pm 1}$, $z^{\pm 1}$ are as indicated

We may consider the graph of Fig. 6 as being embedded in a torus, that is, we identify the upper left boundary and the lower right boundary, and also the upper right boundary and the lower left boundary, as illustrated in the figure by dashed lines.

Let $z,w \in {\mathbb C}$ be non-zero. We orient each of the four boundaries of Fig. 6 (denoted by dashed lines) from their lower endpoint to their upper endpoint. The ‘left’ and ‘right’ of an oriented portion of a boundary are as viewed by a person traversing in the given direction.

Each edge $\langle u,v\rangle$ crossing a boundary corresponds to two entries in the weighted adjacency matrix, indexed (u, v) and (v, u). If the edge starting from u and ending at v crosses an upper-left/lower-right boundary from left to right (respectively, from right to left), we modify the adjacency matrix by multiplying the entry (u, v) by z (respectively, $z^{-1}$). If the edge starting from u and ending at v crosses an upper-right/lower-left boundary from left to right (respectively, from right to left), in the modified adjacency matrix, we multiply the entry by w (respectively, $w^{-1}$). We modify the entry (v, u) in the same way. For a definitive interpretation of Fig. 6, the reader is referred to the matrix following.

The signs of these weights are chosen to reflect the orientations of the edges. The resulting modified adjacency matrix (or ‘modified Kasteleyn matrix’) is

$$\begin{aligned} K = \left( \begin{array}{cccccc} 0&{} -C&{} B&{} -1&{} 0&{} 0\\ C&{} 0&{} -A&{} 0&{} -z^{-1}&{} 0\\ -B&{} A&{} 0&{} 0&{} 0 &{}-w^{-1}\\ 1&{} 0&{} 0&{} 0&{} -C&{} B\\ 0&{} z&{} 0&{} C&{} 0&{} -A\\ 0&{} 0&{} w&{} -B&{} A&{} 0\end{array}\right) . \end{aligned}$$

The characteristic polynomial is given (using Mathematica or otherwise) by

$$\begin{aligned} P(z,w)&:=\det K\nonumber \\&= 1+A^4+B^4+C^4+(A^2C^2-B^2)\left( w+\frac{1}{w}\right) \nonumber \\&\ \quad +(A^2B^2-C^2)\left( z+\frac{1}{z}\right) +(B^2C^2-A^2)\left( \frac{w}{z} + \frac{z}{w}\right) . \end{aligned}$$

(3.10)

By (3.6) and (2.8),

$$\begin{aligned} P(z,w)&=1+\alpha ^2\beta ^2+\alpha ^2\gamma ^2+ \beta ^2\gamma ^2+\alpha \gamma (\beta ^2-1)\left( w+\frac{1}{w}\right) \\&\quad \ +\alpha \beta (\gamma ^2-1)\left( z+\frac{1}{z}\right) +\beta \gamma (\alpha ^2-1)\left( \frac{w}{z}+\frac{z}{w}\right) . \end{aligned}$$

The spectral curve is the zero locus of the characteristic polynomial, that is, the set of roots of $P(z,w)=0$. It will be useful later to identify the intersection of the spectral curve with the unit torus ${\mathbb T}^2=\{(z,w): |z|=|w|=1\}$.

Let

$$\begin{aligned} \begin{array}{ll} U&{}=\alpha \beta +\beta \gamma +\gamma \alpha -1,\\ V&{}=-\alpha \beta +\beta \gamma +\gamma \alpha +1,\\ S&{}=\alpha \beta -\beta \gamma +\gamma \alpha +1,\\ T&{}=\alpha \beta +\beta \gamma -\gamma \alpha +1. \end{array} \end{aligned}$$

(3.11)

Proposition 3.3

Let $\epsilon _a,\epsilon _b,\epsilon _c\ne 0$, so that $\alpha ,\beta ,\gamma >0$. Either the spectral curve does not intersect the unit torus ${\mathbb T}^2$, or the intersection is a single real point of multiplicity 2. Moreover, the spectral curve intersects ${\mathbb T}^2$ at a single real point if and only if $UVST=0$, where U, V, S, T are given by (3.11).

Proof

The proof follows by a computation similar to those of the proofs of [11, Thm. 9] and [13, Lemma 3.2]. A number of details of the proof are very close to those of [11, 13] and are omitted. Instead, we highlight where differences arise.

Let $\epsilon _a,\epsilon _b,\epsilon _c>0$. By (2.8) and (3.6)–(3.7), the map $\psi :(A,B,C)\mapsto (\alpha ,\beta ,\gamma )$ is a bijection between $(0,\infty )^3$ and itself. That $P(z,w)\ge 0$, for $(z,w)\in {\mathbb T}^2$ and $(\alpha ,\beta ,\gamma )\in (0,\infty )^3$, follows by the corresponding argument in the proofs of [11, Thm. 9] and [13, Lemma 3.2]. It holds in the same way that the intersection of $P(z,w)=0$ with ${\mathbb T}^2$ can only be a single point of multiplicity 2.

We turn now to the four points when $z,w=\pm 1$. Note that

$$\begin{aligned} P(1,1)&=(-1+A^2+B^2+C^2)^2=U^2,\\ P(-1,-1)&=(1-A^2+B^2+C^2)^2=S^2,\\ P(-1,1)&=(1+A^2-B^2+C^2)^2=T^2,\\ P(1,-1)&=(1+A^2+B^2-C^2)^2=V^2, \end{aligned}$$

by (3.6). Since $A,B,C\ne 0$, no more than one of the above four quantities can equal zero. $\square$

The condition $UVST\ne 0$ may be understood as follows. Let $\gamma _i$ be given by (2.12), and note that

$$\begin{aligned} \gamma _2(\alpha ^{-1},\beta )=1/\gamma _1(\alpha ,\beta ). \end{aligned}$$

(3.12)

Proposition 3.4

Let $\alpha ,\beta ,\gamma >0$ and let U, V, S, T satisfy (3.11).

• (a) We have that $UVST=0$ if and only if $\gamma \in \{\gamma _1,\gamma _2\}$.

• (b) The region $R_{\text {sup}}$ of Theorem 2.5 is an open, connected subset of $(0,\infty )^3$.

• (c) The region $R_{\text {sub}}$ is the disjoint union of four open, connected subsets of $(0,\infty )^3$, namely,

  $$\begin{aligned} \begin{array}{llllll} R_{\text {sub}}^1&{}=\{\gamma <\gamma _1\}\cap \{\alpha \beta <1\}, \quad &{}&{}R_{\text {sub}}^2=\{\gamma <\gamma _1\}\cap \{\alpha \beta >1\},\\ R_{\text {sub}}^3&{}=\{\gamma >\gamma _2\}\cap \{\alpha <\beta \}, \quad &{}&{}R_{\text {sub}}^4=\{\gamma >\gamma _2\}\cap \{\alpha >\beta \}. \end{array} \end{aligned}$$

  (3.13)

Proof

Part (a) follows by an elementary manipulation of (3.11). Part (b) holds since $\gamma _1<\gamma _2$ for all $\alpha ,\beta >0$. Part (c) is a consequence of the facts that $\gamma _1=0$ when $\alpha +\beta =0$, and $\gamma _2=\infty$ when $\alpha -\beta =0$. $\square$

4 Proof of Theorem 2.5

4.1 Outline of Proof

We begin with an outline of the main steps of the proof. In Sect. 4.2, the two-edge correlation of the polymer model on ${\mathbb H}_n$ is expressed as the ratio of expressions involving Pfaffians of modified adjacency matrices of dimer models on the graph of Sect. 3.4. The squares of such Pfaffian ratios are shown in Sect. 4.4 to converge to a certain determinant. This implies the existence of the limit $M(e,f)^2$ of the two-edge correlation, and completes the proof of part (a) of the theorem. For parts (b) and (c), one considers the square $M(e,f)^2$ as the determinant of a block Toeplitz matrix. By standard facts about Toeplitz matrices, the limit $\Lambda :=\lim _{|e-f|\rightarrow \infty } M(e,f)^2$ exists and is analytic except when the spectral curve intersects the unit torus. The remaining claims follow by Proposition 3.3.

4.2 The Order Parameter in Terms of Pfaffians

By Remark 2.1, we shall assume without loss of generality that $\epsilon _a,\epsilon _b,\epsilon _c>0$. Let $\ell$ be the path of $A{\mathbb H}_n$ connecting Me and Mf as in (2.11). To a configuration $\pi \in \Pi _{e,f}$ we associate the configuration $\pi ':= \pi + \ell \in \Pi ^{\mathrm {poly}}$ (with addition modulo 2). The correspondence $\pi \leftrightarrow \pi '$ is one-to-one between $\Pi _{e,f}$ and $\Pi ^{\mathrm {poly}}$. By considering the configurations contributing to $Z_{n,e\leftrightarrow f}$, we obtain by Lemma 3.2 that

$$\begin{aligned} M_n(e,f) = \frac{Z_{n,e\leftrightarrow f}}{Z_n(P)}= \Biggl (\prod _{g\in \ell }\epsilon _g\Biggr )\frac{Z_{n,\ell }(P)}{Z_n(P)}, \end{aligned}$$

(4.1)

where $Z_{n,\ell }(P)$ is the partition function of polygon configurations on $A{\mathbb H}_n$ with the weights of s-type half-edges along $\ell$ changed from $\epsilon _s$ to $\epsilon _s^{-1}$.

From the Fisher graph ${\mathbb F}_n$, we construct an augmented Fisher graph $A{\mathbb F}_n$ by placing two further vertices on each non-triangular edge of ${\mathbb F}_n$, see Fig. 7. We will construct a weight-preserving correspondence between polygon configurations on $A{\mathbb H}_n$ and dimer configurations on $A{\mathbb F}_n$.

Fig. 7

The fundamental domain of $A{\mathbb F}_n$, which may be compared with Fig. 6

We assign weights to the edges of $A{\mathbb F}_n$ as follows. Each triangular edge of $A{\mathbb F}_n$ is assigned weight 1. Each non-triangular s-type edge of the Fisher graph ${\mathbb F}_n$ is divided into three parts in $A{\mathbb F}_n$ to which we refer as the left edge, the middle edge, and the right edge. The left edge and right edges are assigned weight $\epsilon _s^{-1}$, while the middle edge is assigned weight 1. We shall identify the characteristic polynomial $P^A$ of this dimer model in the forthcoming Lemma 4.3. Let $E_\ell$ be the set of left and right non-triangular edges corresponding to half-edges in $\ell$, and let $V_\ell$ be the set of vertices of edges in $E_\ell$.

There is a one-to-one correspondence between polygon configurations on $A{\mathbb H}_n$ and polygon configurations on ${\mathbb H}_n$. The latter may be placed in one-to-one correspondence with dimer configurations on $A{\mathbb F}_n$ as follows. Consider a polygon configuration $\pi$ on ${\mathbb H}_n$. An edge $e\in E_n$ is present in $\pi$ if and only if the corresponding middle edge of e is present in the corresponding dimer configuration $D=D(\pi )$ on $A{\mathbb F}_n$. Once the states of middle edges of $A{\mathbb F}_n$ are determined, they generate a unique dimer configuration on $A{\mathbb F}_n$.

By consideration of the particular situations that can occur within a given fundamental domain, one obtains that the correspondence is weight-preserving (up to a fixed factor), whence

$$\begin{aligned} Z_n(P)= \Biggl (\prod _{g\in AE_n} \epsilon _g \Biggr )Z_n(AD), \end{aligned}$$

where $Z_n(AD)$ is the partition function of the above dimer model on $A{\mathbb F}_n$, and $\epsilon _g$ is the parameter corresponding to an edge with the type of g. A similar dimer interpretation is valid for $Z_{n,\ell }(P)$, and thus we have

$$\begin{aligned} \frac{Z_{n,e\leftrightarrow f}}{Z_n(P)}= \Biggl (\prod _{g\in \ell }\epsilon _g\Biggr )\frac{Z_{n,\ell }(P)}{Z_n(P)} = \left( \prod _{g\in \ell }\epsilon _g^{-1}\right) \frac{Z'_n(AD)}{Z_n(AD)}, \end{aligned}$$

(4.2)

where $Z'_{n}(AD)$ is the partition function for dimer configurations on $A{\mathbb F}_n$, in which an edge of $E_\ell$ has weight $\epsilon _g$ (where g is the corresponding half-edge), and all the other left/right non-triangular edges have unchanged weights $\epsilon _g^{-1}$.

We assign a clockwise-odd orientation to the edges of $A{\mathbb F}_n$ as indicated in Fig. 7. The above dimer partition functions may be represented in terms of the Pfaffians of the weighted adjacency matrices corresponding to $Z_n(AD)$ and $Z_n'(AD)$. See [7, 8, 12, 20].

Recall that $A{\mathbb F}_n$ is a graph embedded in the $n\times n$ torus. Let $\gamma _x$ and $\gamma _y$ be two non-parallel homology generators of the torus, that is, $\gamma _x$ and $\gamma _y$ are cycles winding around the torus, neither of which may be obtained from the other by continuous movement on the torus. Moreover, we assume that $\gamma _x$ and $\gamma _y$ are paths in the dual graph that meet in a unique face and that cross disjoint edge-sets. For definiteness, we take $\gamma _x$ (respectively, $\gamma _y$) to be the upper left (respectively, upper right) dashed cycles of the dual triangular lattice, as illustrated in Fig. 8. We multiply the weights of all edges crossed by $\gamma _x$ (respectively, $\gamma _y$) by z or $z^{-1}$ (respectively, w or $w^{-1}$), according to their orientations. Note that $\ell$ crosses neither $\gamma _x$ nor $\gamma _y$.

Fig. 8

Two cycles $\gamma _x$ and $\gamma _y$ in the dual triangular graph of the toroidal graph ${\mathbb H}_n$. The upper left and lower right sides of the diamond are identified, and similarly for the other two sides

Let $K_n(z,w)$ be the weighted adjacency matrix of the original dimer model above, and let $K_n'(z,w)$ be that with the weights of s-type edges along $\ell$ changed from $\epsilon _s^{-1}$ to $\epsilon _s$.

If n is even, by (4.2) and results of [7, 12] and [17, Chap. IV],

$$\begin{aligned} \frac{Z_{n,e\leftrightarrow f}}{Z_n(P)}=\Biggl (\prod _{g\in \ell }\epsilon _g^{-1}\Biggr ) \frac{-\mathrm {Pf}\, K_n'(1,1)+\mathrm {Pf}\, K_n'(-1,1)+\mathrm {Pf}\, K_n'(1,-1)+\mathrm {Pf}\, K_n'(-1,-1)}{2Z_n(P)}, \end{aligned}$$

(4.3)

where

$$\begin{aligned} 2Z_n(P) = -\mathrm {Pf}\, K_n(1,1)+\mathrm {Pf}\, K_n(-1,1)+\mathrm {Pf}\, K_n(1,-1)+\mathrm {Pf}\, K_n(-1,-1). \end{aligned}$$

(4.4)

The corresponding formula when n is odd is

$$\begin{aligned} \frac{Z_{n,e\leftrightarrow f}}{Z_n(P)}=\Biggl (\prod _{g\in \ell }\epsilon _g^{-1}\Biggr ) \frac{\mathrm {Pf}\, K_n'(1,1)+\mathrm {Pf}\, K_n'(-1,1)+\mathrm {Pf}\, K_n'(1,-1)-\mathrm {Pf}\, K_n'(-1,-1)}{2Z_n(P)}, \end{aligned}$$

as explained in the discussion of ‘crossing orientations’ of [18, pp. 2192–2193]. The ensuing argument is essentially identical in the two cases, and therefore we may assume without loss of generality that n is even.

4.3 The limit as $n\rightarrow \infty$

In studying the limit of (4.3) as $n \rightarrow \infty$, we shall require some facts about the asymptotic behaviour of the inverse matrix of $K_n(\theta ,\nu )$. We summarise these next.

The graph $A{\mathbb F}_n$ may be regarded as $n\times n$ copies of the fundamental domain of Fig. 7, with vertices labelled as in Figs. 9 and 10. We index these by (p, q) with $p,q = 1,2,\dots ,n$, and let $D_{p,q}$ be the fundamental domain with index (p, q). Let ${\mathcal D}=\{(p,q): D(p,q)\cap \ell \ne \varnothing \}$, so that the cardinality of ${\mathcal D}$ depends only on $|e-f|$. Each $D_{p,q}$ contains 12 vertices. For $v_1,v_2\in D_{1,1}$, we write $K_n^{-1}(D_{p_1,q_1},v_1;D_{p_2,q_2},v_2)$ for the $(u_1,u_2)$ entry of $K_n^{-1}$, where $u_i$ is the translate of $v_i$ lying in $D_{p_i,q_i}$.

Fig. 9

The fundamental domain of $A{\mathbb F}_n$ with vertex-labels

Fig. 10

Part of the path $\ell$ between two NW edges

Proposition 4.1

Let $\theta ,\nu \in \{-1,1\}$. We have that

(4.5)

where $(p_1,q_1),(p_2,q_2)\in {\mathcal D}$, and $r,s \in \{a_i,b_i:i=1,2,3,4\}$, and $K_1^{-1}(z,w)_{v_{s},v_{r}}$ denotes the $(v_s,v_r)$ entry of $K_1^{-1}(z,w)$.

Proof

The limiting entries of $K_n^{-1}(\theta ,\nu )$ as $n \rightarrow \infty$ can be computed explicitly using the arguments of [10, Thm. 4.3] and [9, Sects 4.2–4.4], details of which are omitted here. $\square$

Note that the right side of (4.5) does not depend on the values of $\theta ,\nu \in \{-1,1\}$.

4.4 Representation of the Pfaffian Ratios

We return to the formulae (4.1) and (4.3)–(4.4) for the two-edge correlation. The matrices $K_n(\theta ,\nu )$ and $K_n'(\theta ,\nu )$ are antisymmetric when $\theta ,\nu \in \{-1,1\}$. For $\theta ,\nu \in \{-1,1\}$,

$$\begin{aligned} \frac{\det K_n'(\theta ,\nu )}{\det K_n(\theta ,\nu )}&=\det [K_n'(\theta ,\nu ) K_n^{-1}(\theta ,\nu )] \nonumber \\&=\det \bigl [R_nK_n^{-1}(\theta ,\nu )+I\bigr ], \end{aligned}$$

(4.6)

where

$$\begin{aligned} R_n=K_n'(\theta ,\nu )-K_n(\theta ,\nu ). \end{aligned}$$

(4.7)

The following argument is similar to that of [12, Thm. 4.2]. Let

and define the $4\times 4$ block matrix

$$\begin{aligned} S_s=\begin{pmatrix} Y(\epsilon _s-\epsilon _s^{-1}) &{}0\\ 0 &{}Y(\epsilon _s-\epsilon _s^{-1}) \end{pmatrix}, \quad s=a,b. \end{aligned}$$

Each half-edge of ${\mathbb H}_n$ along $\ell$ corresponds to an edge of $A{\mathbb F}_n$, namely, a left or right non-triangular edge. Moreover, the path $\ell$ has a periodic structure in $A{\mathbb H}_n$, each period of which consists of four edges of $A{\mathbb H}_n$, namely, a NW half-edge, followed by two horizontal half-edges, followed by another NW half-edge. These four edges correspond to four non-triangular edges of $A{\mathbb F}_n$ with endpoints denoted $v_{b_3}$, $v_{b_4}$, $v_{a_1}$, $v_{a_2}$, $v_{a_3}$, $v_{a_4}$, $v_{b_1}$, $v_{b_2}$. See Fig. 10.

Let $(p,q)\in {\mathcal D}$. The $12\times 12$ block of $R_n$ with rows and columns labelled by the vertices in $D_{p,q}$ may be written as

$$\begin{aligned} R_n(D_{p,q},D_{p,q})= \begin{pmatrix} S_a&{}0&{}0\\ 0&{}-S_b&{}0\\ 0&{}0&{}0\end{pmatrix}. \end{aligned}$$

(4.8)

Each entry in (4.8) is a $4\times 4$ block, and the rows and columns are indexed by $v_{a_2},v_{a_1},v_{a_4},v_{a_3},v_{b_2},v_{b_1},v_{b_4},v_{b_3},v_{c_1},\dots ,v_{c_4}$. All other entries of $R_n$ equal 0.

Owing to the special structure of $R_n$, the determinant of $S_n:=R_nK_n^{-1}(\theta ,\nu )+I$ is the same as that of a certain submatrix of $S_n$ given as follows. From $S_n$, we retain all rows and columns indexed by translations (within ${\mathcal D}$) of the $v_{a_i}$ and $v_{b_j}$. Since each fundamental domain contains four such vertices of each type, the resulting submatrix $S_{n,\ell }$ is square with dimension $8|{\mathcal D}|$. By following the corresponding computations of [12, Sect. 4] and [17, Chap. VIII], we find that $\det S_n=\det S_{n,\ell }$.

Let $X_\ell$ be the $V_\ell \times V_\ell$ block diagonal matrix with rows and columns indexed by vertices in $V_\ell$, and defined as follows. Adopting a suitable ordering of $V_\ell$ as above, the diagonal $2\times 2$ blocks of $X_\ell$ are $Y(\epsilon _s-\epsilon _s^{-1})$, where s depends on the type of the corresponding edge, and off-diagonal $2\times 2$ blocks of $X_\ell$ are 0. Note that

$$\begin{aligned} \det X_\ell = \prod _{g\in E_\ell } \left( \epsilon _g-\frac{1}{\epsilon _g}\right) ^2. \end{aligned}$$

(4.9)

Let $K_n^{-1}(\theta ,\nu )_\ell$ be the submatrix of $K_n^{-1}(\theta ,\nu )$ with rows and columns indexed by $V_\ell$. By Proposition 4.1, the limit

$$\begin{aligned} K_\ell := \lim _{n\rightarrow \infty } K_n^{-1}(\theta ,\nu )_\ell \end{aligned}$$

(4.10)

exists and is independent of $\theta ,\nu \in \{-1,1\}$.

Proposition 4.2

The limit $M(e,f)^2=\lim _{n\rightarrow \infty }M_n(e,f)^2$ exists and satisfies

$$\begin{aligned} M(e,f)^2=\lim _{n\rightarrow \infty }\left( \frac{Z_{n,e\leftrightarrow f}}{Z_n(P)}\right) ^2 =\det (X_\ell K_{\ell }^{-1}+I)\Biggl (\prod _{g\in E_{\ell }}\frac{1}{\epsilon _g^2}\Biggr ). \end{aligned}$$

(4.11)

Proof

Let $\theta ,\nu \in \{-1,1\}$, and assume first that $\epsilon _a,\epsilon _b\ne 1$. By (4.6)–(4.9) and the discussion before the proposition,

$$\begin{aligned} \frac{\det K_n'(\theta ,\nu )}{\det K_n(\theta ,\nu )}&=\det [X_\ell K_n^{-1}(\theta ,\nu )_\ell +I]\\&=\det [K_n^{-1}(\theta ,\nu )_\ell +X_\ell ^{-1}]\det X\\&=\det [K_n^{-1}(\theta ,\nu )_\ell +X_\ell ^{-1}] \prod _{g\in E_\ell }\left( \epsilon _g-\frac{1}{\epsilon _g}\right) ^2. \end{aligned}$$

On taking square roots, and noting that $K_n^{-1}(\theta ,\nu )_\ell +X_\ell ^{-1}$ is antisymmetric,

$$\begin{aligned} \frac{\mathrm {Pf}\, K_n'(\theta ,\nu )}{\mathrm {Pf}\, K_n(\theta ,\nu )}= (-1)^j\mathrm {Pf}\, [K_n^{-1}(\theta ,\nu )_\ell +X_\ell ^{-1}] \prod _{g\in E_\ell }\left( \epsilon _g-\frac{1}{\epsilon _g}\right) , \end{aligned}$$

for some j that is independent of $\theta$, $\nu$.

By (4.3),

$$\begin{aligned} 2Z_{n,e\leftrightarrow f}&=(-1)^j \Bigl \{-p(1,1) \mathrm {Pf}\, K_n(1,1) +p(-1,1) \mathrm {Pf}\, K_n(-1,1) \\&\quad \ +p(1,-1)\mathrm {Pf}\, K_n(1,-1)+ p(-1,-1)\mathrm {Pf}\, K_n(-1,-1)\Bigr \}\prod _{g\in E_{\ell }}\left( 1-\frac{1}{\epsilon _g^2}\right) , \end{aligned}$$

where $p(\theta ,\nu )=\mathrm {Pf}\, [K_n^{-1}(\theta ,\nu )_\ell +X_\ell ^{-1}]$. By (4.4) and (4.10),

$$\begin{aligned} \lim _{n\rightarrow \infty }\left( \frac{Z_{n,e\leftrightarrow f}}{Z_n(P)}\right) ^2=\left[ \mathrm {Pf}\, (K_{\ell }^{-1}+X_\ell ^{-1}) \prod _{g\in E_{\ell }}\left( 1-\frac{1}{\epsilon _g^2}\right) \right] ^2, \end{aligned}$$

and (4.11) follows by (4.9) and (4.1).

Assume next that $\epsilon _a=\epsilon _b=1$. We have

$$\begin{aligned} K_n'(\theta ,\nu )=K_n(\theta ,\nu ), \qquad \mathrm {for}\ \theta ,\nu =\pm 1. \end{aligned}$$

Since $X_\ell =0$ in this case, we obtain (4.11) once again. If exactly one of $\epsilon _a$, $\epsilon _b$ equals 1, we obtain (4.11) as above. $\square$

4.5 Proof of Theorem 2.5(a)

As in [10, Thm. 4.3] and [9, Sects 4.2–4.4], by Proposition 4.2, the limit $M(e,f)^2=\lim _{n\rightarrow \infty }M_n(e,f)^2$ exists and equals the determinant of a block Toeplitz matrix with dimension depending on $|e-f|$, and with symbol $\psi$ given by

$$\begin{aligned} \psi (\zeta )=\frac{1}{2\pi }\int _{0}^{2\pi } T(\zeta ,\phi ) \,d\phi , \end{aligned}$$

(4.12)

where $T(\zeta ,\phi )$ is the $8 \times 8$ matrix with rows and columns indexed by $v_{a_1},v_{a_2},v_{a_3},v_{a_4}$, $v_{b_1},v_{b_2},v_{b_3},v_{b_4}$ (with rows and columns ordered differently) given by

$$\begin{aligned} \small \begin{pmatrix} \epsilon _a^{-1}+K_1^{-1}(\zeta ,e^{i\phi })_{v_{a_2},v_{a_1}}\lambda _a&{}K_1^{-1}(\zeta ,e^{i\phi })_{v_{a_2},v_{a_2}}\lambda _a&{}\cdots &{}K_1^{-1}(\zeta ,e^{i\phi })_{v_{a_2},v_{b_4}}\lambda _a\\ -K_1^{-1}(\zeta ,e^{i\phi })_{v_{a_1},v_{a_1}}\lambda _a&{}\epsilon _a^{-1}-K_1^{-1}(\zeta ,e^{i\phi })_{v_{a_1},v_{a_2}}\lambda _a&{}\cdots &{}-K_1^{-1}(\zeta ,e^{i\phi })_{v_{a_1},v_{b_4}}\lambda _a\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ K_1^{-1}(\zeta ,e^{i\phi })_{v_{b_3},v_{a_1}}\lambda _b&{}K_1^{-1}(\zeta ,e^{i\phi })_{v_{b_3},v_{a_2}}\lambda _b&{}\cdots &{}\epsilon _b^{-1}+K_1^{-1}(\zeta ,e^{i\phi })_{v_{b_3},v_{b_4}}\lambda _b \end{pmatrix}, \end{aligned}$$

and $\lambda _g=1-\epsilon _g^{-2}$. See [22–24] and the references therein for accounts of Toeplitz matrices.

One may write

$$\begin{aligned}{}[K_1^{-1}(z,w)]_{i,j}=\frac{Q_{i,j}(z,w)}{P^A(z,w)}, \end{aligned}$$

(4.13)

where $Q_{i,j}(z,w)$ is a Laurent polynomial in z, w derived in terms of certain cofactors of $K_1(z,w)$, and $P^A(z,w)=\det K_1(z,w)$ is the characteristic polynomial of the dimer model.

Lemma 4.3

The characteristic polynomial $P^A$ of the above dimer model on $A{\mathbb F}_n$ satisfies $P^A(z,w)=(\epsilon _a\epsilon _b\epsilon _c)^{-4}P(z,w)$, where P(z, w) is the characteristic polynomial of (3.10).

Proof

The characteristic polynomial $P^A$ satisfies $P^A(z,w)=\det K_1(z,w)$. Each term in the expansion of the determinant corresponds to an oriented loop configuration consisting of oriented cycles and doubled edges, with the property that each vertex has exactly two incident edges. It may be checked that there is a one-to-one correspondence between loop configurations on the two graphs of Figs. 7 and 6, by preserving the track of each cycle and adding doubled edges where necessary. The weights of a pair of corresponding loop configurations differ by a multiplicative factor of $(ABC)^2=(\epsilon _a\epsilon _b\epsilon _c)^4$. $\square$

By the above, the limit $M(e,f)^2$ exists whenever $P^A(z,w)$ has no zeros on the unit torus ${\mathbb T}^2$. By Lemma 4.3 and Proposition 3.3, the last occurs if and only if $UVST \ne 0$. The proof of Theorem 2.5(a) is complete, and we turn towards parts (b) and (c).

4.6 Proofs of Theorem 2.5(b, c)

Consider an infinite block Toeplitz matrix J, viewed as the limit of an increasing sequence of finite truncated block Toeplitz matrices $J_n$. When the corresponding spectral curve does not intersect the unit torus, the existence of $\det J$ as the limit of $\det J_n$ is proved in [22, 23]. By Lemma 4.3 and Proposition 3.3, the spectral curve condition holds if and only if $UVST \ne 0$. We deduce the existence of the limit

$$\begin{aligned} \Lambda (\alpha ,\beta ,\gamma ):= \lim _{|e-f|\rightarrow \infty } M(e,f)^2, \end{aligned}$$

(4.14)

whenever $UVST \ne 0$. By Proposition 3.3, the function $\Lambda$ is defined on the domain $D:= (0,\infty )^3\setminus \{UVST=0\}$.

Lemma 4.4

Assume $\alpha ,\beta ,\gamma >0$. The function $\Lambda$ is an analytic function of the complex variables $\alpha$, $\beta$, $\gamma$ except when $UVST=0$, where U, V, S, T are given by (3.11).

As noted after Theorem 2.5, $\Lambda$ is singular when $UVST=0$.

Proof

This holds as in the proofs of [12, Lemmas 4.4–4.7]. We consider $\Lambda$ as the determinant of a block Toeplitz matrix, and use Widom’s formula (see [22, 23], and also [6, Thm. 8.7]) to evaluate this determinant. As in the proof of [6, Thm. 8.7], $\Lambda$ can be non-analytic only if the spectral curve intersects the unit torus, which is to say (by Lemma 4.3 and Proposition 3.3) if $UVST=0$. $\square$

The equation $UVST=0$ defines a surface in the first octant $(0,\infty )^3$, whose complement is a union of five open, connected components (see Proposition 3.4). By Lemma 4.4, $\Lambda$ is analytic on each such component. It follows that, on any such component: either $\Lambda \equiv 0$, or $\Lambda$ is non-zero except possibly on a nowhere dense set.

Let $\alpha ,\beta ,\gamma >0$. By Proposition 3.4, $UVST\ne 0$ if and only if

$$\begin{aligned} \gamma \in (0,\gamma _1)\cup (\gamma _1,\gamma _2)\cup (\gamma _2,\infty ), \end{aligned}$$

(4.15)

where the $\gamma _i$ are given by (2.12).

Proof of Theorem2.5(b)

By Proposition 3.4, $UVST \ne 0$ on the open, connected region $R_{\text {sup}}$. Therefore, $\Lambda$ is analytic on $R_{\text {sup}}$. Hence, either $\Lambda \equiv 0$ on $R_{\text {sup}}$, or $\Lambda \not \equiv 0$ on $R_{\text {sup}}$ and the zero set $Z:=\{r=(\alpha ,\beta ,\gamma ) \in R_{\text {sup}}: \Lambda (r)=0\}$ is nowhere dense in $R_{\text {sup}}$. It therefore suffices to find $(\alpha ,\beta ,\gamma )\in R_{\text {sup}}$ such that $\Lambda (\alpha ,\beta ,\gamma )\ne 0$.

Consider the 1–2 model of Sects. 3.1–3.3 with $a=b>0$ and $c>4a$. By (2.8), (3.5), and (3.6), the corresponding polygon model has parameters

$$\begin{aligned} \alpha =\beta =\frac{c-2a}{c+2a},\quad \gamma =\frac{c^2}{(c-2a)(c+2a)}. \end{aligned}$$

In this case, $\gamma _2=\infty$ and $\gamma \in (\gamma _1,\gamma _2)$.

By [6, Thm. 3.1], for almost every such c, the 1–2 model has non-zero long-range order. By Lemma 3.2, $\Lambda (\alpha ,\beta ,\gamma )\ne 0$ for such c. $\square$

Proof of Theorem2.5(c)

By Remark 2.2, when $\alpha ,\beta ,\gamma >0$ are sufficiently small, the two-edge correlation function M(e, f) of the polygon model equals the two-spin correlation function $\langle \sigma _e\sigma _f\rangle$ of a ferromagnetic Ising model on $A{\mathbb H}$ at high temperature. Since the latter has zero long-range order, it follows that $\Lambda =0$. Suppose, in addition, that $\alpha \beta <1$ and $\gamma <\gamma _1$. Since $\Lambda$ is analytic on $R_{\text {sub}}^1$ (in the notation of (3.13)), we deduce that $\Lambda \equiv 0$ on $R_{\text {sub}}^1$. We next extend this conclusion to $R_{\text {sub}}^k$ with $k=2,3,4$.

Let $(\alpha ,\beta ,\gamma )\in R_{\text {sub}}^4$. By (3.12), we have that $\alpha ^{-1}\beta <1$ and $\gamma ^{-1}<\gamma _1(\alpha ^{-1},\beta )$, so that $(\alpha ^{-1},\beta ,\gamma ^{-1})\in R_{\text {sub}}^1$. By Theorem 2.3,

$$\begin{aligned} \Lambda (\alpha ,\beta ,\gamma ) = \Lambda (\alpha ^{-1},\beta ,\gamma ^{-1})=0. \end{aligned}$$

Therefore, $\Lambda \equiv 0$ on $R_{\text {sub}}^4$.

Let $(\alpha ,\beta ,\gamma )\in R_{\text {sub}}^2$, whence $(\alpha ^{-1},\beta ^{-1},\gamma )\in R_{\text {sub}}^1$ by (3.12). As above,

$$\begin{aligned} \Lambda (\alpha ,\beta ,\gamma ) = \Lambda (\alpha ^{-1},\beta ^{-1},\gamma )=0, \end{aligned}$$

whence $\Lambda \equiv 0$ on $R_{\text {sub}}^2$. The case of $R_{\text {sub}}^3$ can be deduced as was $R_{\text {sub}}^4$. $\square$