On the Absolute Continuity of the Blackwell Measure

Abstract

In 1957, Blackwell expressed the entropy of hidden Markov chains using a measure which can be characterised as an invariant measure for an iterated function system with place-dependent weights. This measure, called the Blackwell measure, plays a central role in understanding the entropy rate and other important characteristics of fundamental models in information theory. We show that for a suitable set of parameter values the Blackwell measure is absolutely continuous for almost every parameter in the case of binary symmetric channels.

1 Introduction and Statements

Blackwell [1] expressed the entropy for hidden Markov chains using a measure which is called the Blackwell measure and can be characterised as an invariant measure of an iterated function system (IFS). The properties of the Blackwell measure are examined by several papers, for example [7, 8, 11, 15] etc. Blackwell showed some examples, where the support of the measure is at most countable, hence, the measure is singular, see [1, Section 3]. In our paper we focus on the Blackwell measure defined by the binary-symmetric channel with crossover probability $\varepsilon$. Bárány, Pollicott and Simon showed a set of parameters, where the measure is singular, see [4, Theorem 1]. Our goal is to give a set of parameters for which the Blackwell measure is absolutely continuous (a.c.) with respect to the Lebesgue measure. To the best of our knowledge, absolute continuity of the Blackwell measure has not been proved for any example before.

Let us introduce the basic notations for the binary symmetric channel. Let $X:=\left\{ X_i\right\} _{i=-\infty }^{\infty }$ be a binary, symmetric, stationary, ergodic Markov chain source, $X_i\in \left\{ 0,1\right\}$ with probability transition matrix

$$\begin{aligned} \Pi :=\left[ \begin{array}{l@{\quad }l} p &{} 1-p \\ 1-p &{} p \\ \end{array} \right] . \end{aligned}$$

Then it is well known that the entropy $H(X)$ is given by

$$\begin{aligned} H(X)=-p\log p-(1-p)\log (1-p). \end{aligned}$$

By adding to $X$ a binary independent and identically distributed (i.i.d.) noise $E=\left\{ E_i\right\} _{i=-\infty }^{\infty }$ independent of $X$ with

$$\begin{aligned} \mathbb {P}(E_i=0)=1-\varepsilon ,\qquad \mathbb {P}(E_i=1)=\varepsilon , \end{aligned}$$

we get a Markov chain $Y:=\left\{ Y_i\right\} _{i=-\infty }^{\infty }$, $Y_i=(X_i,E_i)$ with states $\{(0,0), (0,1), (1,0), (1,1) \}$ and transition probabilities:

$$\begin{aligned} M:=\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} p(1-\varepsilon ) &{} p\varepsilon &{} (1-p)(1-\varepsilon )&{} (1-p)\varepsilon \\ p(1-\varepsilon ) &{} p\varepsilon &{} (1-p)(1-\varepsilon )&{} (1-p)\varepsilon \\ (1-p)(1-\varepsilon ) &{} (1-p)\varepsilon &{} p(1-\varepsilon ) &{} p\varepsilon \\ (1-p)(1-\varepsilon ) &{} (1-p)\varepsilon &{} p(1-\varepsilon ) &{} p\varepsilon \\ \end{array} \right] . \end{aligned}$$

Let $\Psi :\left\{ (0,0),(0,1),(1,0),(1,1)\right\} \mapsto \{0,1\}$ be a surjective map such that

$$\begin{aligned} \Psi (0,0)=\Psi (1,1)=0\text { and }\Psi (0,1)=\Psi (1,0)=1. \end{aligned}$$

We consider the ergodic stationary process $Z=\left\{ Z_i=\Psi (Y_i)\right\} _{i=-\infty }^{\infty }$, which is the corrupted output of the channel. Equivalently, $Z$ is the stationary stochastic process

$$\begin{aligned} Z_i=X_i\bigoplus E_i, \end{aligned}$$

where $\bigoplus$ denotes the binary addition.

According to [7, Example 4.1] and [4, Sections 3.1, 3.2], the entropy of $Z$ can be characterized as follows. Let us define the three dimensional simplex

$$\begin{aligned} W:=\bigg \{\underline{w}\in \mathbb {R}^4:w_i\ge 0\ \sum _{i=1}^4w_i=1\bigg \} \end{aligned}$$

in $\mathbb {R}^4$ and define $W_0,W_1\subset W$ as

$$\begin{aligned} W_0:=\left\{ \underline{w}\in W:w_2=w_3=0\right\} ,\ W_1:=\left\{ \underline{w}\in W:w_1=w_4=0\right\} . \end{aligned}$$

Let us define two matrices

$$\begin{aligned} M_0&:=\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} p(1-\varepsilon ) &{} 0 &{} 0 &{} (1-p)\varepsilon \\ p(1-\varepsilon ) &{} 0 &{} 0 &{} (1-p)\varepsilon \\ (1-p)(1-\varepsilon ) &{} 0 &{} 0 &{} p\varepsilon \\ (1-p)(1-\varepsilon ) &{} 0 &{} 0 &{} p\varepsilon \\ \end{array} \right] \\ M_1&:=\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 0 &{} p\varepsilon &{} (1-p)(1-\varepsilon ) &{} 0 \\ 0 &{} p\varepsilon &{} (1-p)(1-\varepsilon ) &{} 0 \\ 0 &{} (1-p)\varepsilon &{} p(1-\varepsilon ) &{} 0 \\ 0 &{} (1-p)\varepsilon &{} p(1-\varepsilon ) &{} 0 \\ \end{array} \right] , \end{aligned}$$

and a place-dependent probability vector $(r_0(\underline{w}), r_1(\underline{w}))$, where

$$\begin{aligned} r_i(\underline{w})=\Vert \underline{w}^TM_i\Vert _1, \end{aligned}$$

(1.1)

where $\Vert .\Vert _1$ denotes the $l_1$ norm and $\underline{w}\in W$. Introduce two functions $f_0:W\mapsto W_0$ and $f_1:W\mapsto W_1$ such that

$$\begin{aligned} f_i(\underline{w})=\frac{\underline{w}^TM_i}{\Vert \underline{w}^TM_i\Vert _1}. \end{aligned}$$

(1.2)

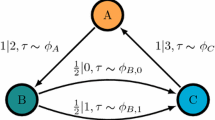
For a visualisation of the system we refer to [4, Figure 2]. Then the entropy of $Z$ can be formulated as follows

$$\begin{aligned} H(Z)=-\int _{W_0\cup W_1} r_0(\underline{w})\log r_0(\underline{w})+r_1(\underline{w})\log r_1(\underline{w})dQ(\underline{w}), \end{aligned}$$

where the Blackwell measure $Q$ is the unique measure with $\mathrm {supp}(Q)\subseteq W_0\cup W_1$ that for every $B\subseteq W_0\cup W_1$ Borel set

$$\begin{aligned} Q(B)=\int _{\left( f_0\right) ^{-1}B}r_0(\underline{w})dQ(\underline{w})+\int _{\left( f_1\right) ^{-1}B}r_1(\underline{w})dQ(\underline{w}). \end{aligned}$$

(1.3)

As we have mentioned before, our main result shows a set of parameters $(\varepsilon ,p)\in (0,1)^2$ such that the Blackwell measure $Q\ll \mathcal {L}$ (shown in Fig. 1), where $\mathcal {L}$ denotes the one dimensional Lebesgue measure restricted to $W_0\cup W_1$ .

Fig. 1

The singularity region (blue region) of the Blackwell measure $Q$ and the absolute continuity region of full measure subset of red region (Color figure online)

Theorem 1.1

The Blackwell measure $Q$ is absolutely continuous w.r.t the Lebesgue measure for every $\varepsilon \ne 1/2$ and Lebesgue almost every $p$ in the red region marked on Fig. 1, but if $\varepsilon =1/2$ then it is singular with $\dim _HQ=0$ for every $p\in (0,1)$.

Remark 1.2

The Blackwell measure is of pure type, i.e. it is either absolute continuous or singular, see [4, Lemma 8]. The measure is singular in the blue region, which was already showed in [4, Theorem 2]. We will precisely characterize the region of absolute continuity in Sects. 3 and 4.

Corollary 1.3

The Blackwell measure $Q$ is equivalent to the measure $\left. \mathcal {L}\right| _{\mathrm {supp}(Q)}$ for every $\varepsilon \ne 1/2$ and Lebesgue almost every $p$ in the red region marked on Fig. 1.

In the study of the properties of an invariant measure of a family of parameterised IFSs the so-called transversality condition is an effective tool (precise definition in Sect. 2). It was introduced by Pollicott and Simon in [14] and has been used to prove absolute continuity or to calculate the Hausdorff dimension of invariant measures in several cases, for example [12, 13, 16–18]. However, the studied invariant measures were not place-dependent probability measures. Until recently, there were no tools for handling this case. In [3] a sufficient condition was given for calculating the Hausdorff-dimension and for proving absolute continuity for place-dependent invariant probability measures, which also used the transversality condition.

In the work of Bahsoun and Góra [2] sufficient conditions are shown for the existence of an absolutely continuous invariant measure for an IFS $\{f_i(x)\}_{i=1}^m$ with place dependent probabilities $\{p_i(x)\}_{i=1}^m$. Their condition

$$\begin{aligned} \sum _{i=1}^m\frac{p_i(x)}{|f'_i(x)|}<1 \;\text { for all }x, \end{aligned}$$

does not hold in our context. In fact for any strictly contractive system this fails, i.e. for systems with $|f'_i(x)|<1$ for all $i$ and every $x$.

The main advantage of the absolute continuity is that there exists a measurable density function $q_{\varepsilon ,p}(\underline{w})$ such that $dQ(\underline{w})=q_{\varepsilon ,p}(\underline{w})d\mathcal {L}(\underline{w})$ for $\underline{w}\in W_0\cup W_1$. Unfortunately, the paper presented here does not give any method to prove properties of $q_{\varepsilon ,p}$. In order to get a better understanding of the entropy rate the next step could be to examine the properties of the density function, which can replace the iterative methods in the calculation by a simple Lebesgue integration.

Structure of the Paper

In Sect. 2 we give a short overview of the main tool of the proof, the transversality condition. A sketch of the proof is also given. Sect. 3 determines the set of parameters $(\varepsilon ,p)\subset (0,1)^2$ for which the transversality condition holds and finally Theorem 1.1 is proved in Sect. 4.

2 Transversality Methods for Place-Dependent Invariant Measures

This section is devoted to introduce the definition of transversality condition and state the results about place-dependent probability measures.

Denote by $\mathcal {S}=\left\{ 1,\dots ,k\right\}$ the set of symbols. Let $X$ be a compact interval on the real line and $U\subset \mathbb {R}^d$ be an open, bounded set. Let us consider a parametrized family of IFSs

$$\begin{aligned} \Psi _{\mathbf {\lambda }}=\big \{f_i^{\mathbf {\lambda }}:X\mapsto X\big \}_{i\in \mathcal {S}},\ \mathbf {\lambda }\in \overline{U}, \end{aligned}$$

such that

(A1) there exists $0<\alpha <\beta <1$ such that $\alpha <\left| (f_i^{\mathbf {\lambda }})'(x)\right| <\beta$ for every $x\in X$, $\mathbf {\lambda }\in \overline{U}$ and $i\in \mathcal {S}$. Let $\Sigma =S^{\mathbb {N}}$ be the symbolic space. The natural projection from the symbolic space to the compact interval $X$ is

$$\begin{aligned} \pi _{\mathbf {\lambda }}(\mathbf {i}):=\lim _{n\rightarrow \infty }f_{i_0}^{\mathbf {\lambda }}\circ \cdots \circ f_{i_n}^{\mathbf {\lambda }}(x)\text { for }\mathbf {i}=(i_0,i_1,\dots )\in \Sigma . \end{aligned}$$

Since the functions $f_i^{\mathbf {\lambda }}$ are uniformly contracting when (A1) is true, the function $\pi :\Sigma \times \overline{U}\mapsto X$ is well defined.

(A2) Let us assume that the functions $\mathbf {\lambda }\mapsto f_i^{\mathbf {\lambda }}$ are uniformly continuous from $\overline{U}$ to $C^{1+\theta }(X)$.

Definition 2.1

We say that $\Psi _{\lambda }$ satisfies the transversality condition on the open, bounded set $U\subset \mathbb {R}^d$, if there exists a constant $C>0$ such that for any $\mathbf {i},\mathbf {j}\in \Sigma$ with $i_0\ne j_0$

$$\begin{aligned} \mathcal {L}_d\left( \lambda \in U:\left| \pi _{\lambda }(\mathbf {i})-\pi _{\lambda }(\mathbf {j})\right| <r\right) <Cr\text { for every }r>0, \end{aligned}$$

(2.1)

where $\mathcal {L}_d$ is the d-dimensional Lebesgue measure.

(A3) Suppose that $\Psi _{\mathbf {\lambda }}$ satisfies the transversality condition on $U$.

Let $P_{\lambda }=\{p_i^{\lambda }:X\mapsto (0,1)\}_{i\in \mathcal {S}}$ be a parameterized family of Hölder continuous place-dependent probabilities, i.e. $\sum _{i\in \mathcal {S}}p_i^{\lambda }(x)\equiv 1$ for every $\lambda \in \overline{U}$.

(A4) Suppose that the functions $\mathbf {\lambda }\mapsto p_i^{\mathbf {\lambda }}$ are uniformly continuous from $\overline{U}$ to $C^{\theta }(X,(0, 1))$.

It follows from [6] that there exists a unique corresponding place-dependent invariant measure $\mu _{\lambda }$ which satisfies

$$\begin{aligned} \mu _{\lambda }(B)=\sum _{i\in \mathcal {S}}\int _{\left( f_i^{\lambda }\right) ^{-1}(B)}p_i^{\lambda }(x)d\mu _{\lambda }(x)\text { for every Borel set B.} \end{aligned}$$

Let us define the entropy $h(\mu _{\lambda })$ and Lyapunov exponent $\chi (\mu _{\lambda })$ of measure $\mu _{\lambda }$ as

$$\begin{aligned} h(\mu _{\lambda }) =-\int \sum _{i\in \mathcal {S}}p_i^{\lambda }(x)\log p_i^{\lambda }(x)d\mu _{\lambda }(x), \end{aligned}$$

(2.2)

$$\begin{aligned} \chi (\mu _{\lambda }) =-\int \sum _{i\in \mathcal {S}}p_i^{\lambda }(x)\log \big |(f_i^{\lambda })'(x)\big |d\mu _{\lambda }(x). \end{aligned}$$

(2.3)

According to the result of Jaroszewska and Rams [10], the quotient $h(\mu _{\lambda })/\chi (\mu _{\lambda })$ is an upper bound for the Hausdorff dimension of the measure $\mu _{\lambda }$ for every $\lambda \in U$. Since an absolute continuous measure w.r.t the Lebesgue measure must have dimension $1$, the inequality $h(\mu _{\lambda })/\chi (\mu _{\lambda })\ge 1$ is a necessary condition for the absolute continuity of $\mu _{\lambda }$. The blue region in Fig. 1 is where the quotient is strictly less than 1.

Theorem 2.2

[3, Theorem 1.1(2)] Suppose that all of the conditions (A1)–(A4) are satisfied. Then $\mu _{\lambda }$ is absolutely continuous w.r.t. the Lebesgue measure for $\mathcal {L}_d$ almost every $\lambda \in \left\{ \lambda \in U: h(\mu _{\lambda })/\chi (\mu _{\lambda })>1\right\}$.

2.1 Sketch of proof of Theorem 1.1

To apply Theorem 2.2 for the Blackwell measure we need to find a region $R_{\mathrm {trans}}\subset (0,1)^2$ of parameters $(\varepsilon ,p)$ where the corresponding IFS satisfies the transversality condition (2.1) and secondly, another region $R_{\mathrm {ratio}}$ where the quotient entropy/Lyapunov exponent is strictly greater than $1$. As a result we can prove absolute continuity in the region $R_{\mathrm {ratio}}\cap R_{\mathrm {trans}}$. Unfortunately, the intersection may be empty in general. However, in the examined case of the Blackwell measure it is not empty, see Sect. 4.

A region for $R_{\mathrm {ratio}}$ can be found using the results of [4, Section 4], see (4.2). It is much harder to find a region $R_{\mathrm {trans}}$, especially in the case of non-linear functions. We show such a method in Sect. 3, similar to [4, Section 7.1]. The key lemma to prove transversality and find $R_{\mathrm {trans}}$ is the following.

Lemma 2.3

[16, Lemma 7.3] Let $U\subset \mathbb {R}^d$ be an open, bounded set. Suppose that $f$ is a $C^1$ real-valued function defined in a neighbourhood of $\overline{U}$ such that there exists an $\eta >0$ satisfying

$$\begin{aligned} \left| f(\lambda )\right| <\eta \Rightarrow \left\| \mathrm {grad}_{\lambda }f(\lambda )\right\| >\eta \text { for every }\lambda \in U. \end{aligned}$$

(2.4)

Then there exists $C = C(\eta )$ such that

$$\begin{aligned} \mathcal {L}_d\left( \lambda \in U:\left| f(\lambda )\right| <r\right) <Cr\text { for every }r>0. \end{aligned}$$

For a visualization of Definition 2.1 and Lemma 2.3 for one parameter see Fig. 2. For every $\mathbf {i},\mathbf {j}$ such that $i_0\ne j_0$, if the graphs of the functions $\lambda \mapsto \pi _{\lambda }(\mathbf {i})$ and $\lambda \mapsto \pi _{\lambda }(\mathbf {j})$ intersect each other then their tangents at the points of intersection are uniformly (in $\mathbf {i}, \mathbf {j}$ and in the point of intersection) separated from each other.

Fig. 2

The transversality condition for one parameter $\lambda \in \mathbb {R}$

3 Transversality Region

For the binary symmetric channel, since the law is determined by the probability of the state being $1$, we consider another measure $\mu _{\varepsilon ,p}$ on $[0,1]$ instead of the measure $Q$ on the simplex $W$ defined in (1.3). Let $\left\{ S_0^{\varepsilon ,p},S_1^{\varepsilon ,p}\right\}$ be an IFS on the interval $[0,1]$,

$$\begin{aligned} S_0^{\varepsilon ,p}(x) :=\dfrac{x\cdot p\cdot (1-\varepsilon )+(1-x)\cdot (1-p)\cdot (1-\varepsilon )}{x\cdot \left[ p(1-\varepsilon )+(1-p)\cdot \varepsilon \right] +(1-x)\cdot \left[ (1-p)(1-\varepsilon )+p\cdot \varepsilon \right] }\end{aligned}$$

(3.1)

$$\begin{aligned} S_1^{\varepsilon ,p}(x) :=\dfrac{x\cdot p\cdot \varepsilon +(1-x)\cdot (1-p)\cdot \varepsilon }{x\cdot \left[ p\varepsilon +(1-p)\cdot (1- \varepsilon ) \right] +(1-x)\cdot \left[ (1-p)\varepsilon +p\cdot (1-\varepsilon ) \right] }. \end{aligned}$$

(3.2)

Further, let us define the place-dependent probability vector $(p_0^{\varepsilon ,p}(x),p_1^{\varepsilon ,p}(x))$ by

$$\begin{aligned} p_0^{\varepsilon ,p}(x) := x\cdot \left[ p(1-\varepsilon )+ (1-p)\cdot \varepsilon \right] +(1-x)\cdot \left[ (1-p)(1-\varepsilon ) +p\cdot \varepsilon \right] ,\end{aligned}$$

(3.3)

$$\begin{aligned} p_1^{\varepsilon ,p}(x) := x\cdot \left[ p\varepsilon + (1-p)\cdot (1- \varepsilon ) \right] +(1-x)\cdot \left[ (1-p)\varepsilon +p\cdot (1-\varepsilon ) \right] . \end{aligned}$$

(3.4)

Indeed, for every $x\in [0,1]$, $p_0^{\varepsilon ,p}(x),p_1^{\varepsilon ,p}(x)>0$ and $p_0^{\varepsilon ,p}(x)+p_1^{\varepsilon ,p}(x)\equiv 1$. Hence, there is a unique probability measure $\mu _{\varepsilon ,p}$ such that for every Borel set $B$

$$\begin{aligned} \mu _{\varepsilon ,p}(B)=\int _{\left( S_0^{\varepsilon ,p}\right) ^{-1}(B)}p_0^{\varepsilon ,p}(x)d\mu _{\varepsilon ,p}(x) +\int _{\left( S_1^{\varepsilon ,p}\right) ^{-1}(B)}p_1^{\varepsilon ,p}(x)d\mu _{\varepsilon ,p}(x), \end{aligned}$$

(3.5)

see [6, Theorem 1.1].

The measures $\mu _{\varepsilon ,p}$ and $Q$ are equivalent. That is, $\dim _H\mu _{\varepsilon ,p}=\dim _HQ$ and $\mu _{\varepsilon ,p}\ll \mathcal {L}$ if and only if $Q\ll \mathcal {L}$, see [4, Section 3.1, 3.2].

To show a region of $(\varepsilon ,p)$ parameters, where the IFS $\left\{ S_0^{\varepsilon ,p},S_1^{\varepsilon ,p}\right\}$ satisfies the transversality condition, we first transform this IFS to an equivalent IFS $\{H_0^{\varepsilon ,q},H_1^{\varepsilon ,q}\}$ for easier handling, where from now on $q:=2p-1$. By symmetrical reasons, without loss of generality, we may suppose $1/2<p<1$.

Lemma 3.1

For every $0<\varepsilon , q<1$, $\varepsilon \ne 1/2$, there exists a linear function $f_{\varepsilon ,q}$ such that $f_{\varepsilon ,q}\circ H_i^{\varepsilon ,q}\circ \left( f_{\varepsilon ,q}\right) ^{-1}\equiv S_i^{\varepsilon ,(q+1)/2}$ for $i=0,1$, i.e. the IFS $\left\{ H_0^{\varepsilon ,q},H_1^{\varepsilon ,q}\right\}$ is equivalent to the IFS $\big \{S_0^{\varepsilon ,(q+1)/2},S_1^{\varepsilon ,(q+1)/2}\big \}$, where

$$\begin{aligned} H_0^{\varepsilon ,q}(x)&= \dfrac{-(2 + (-1 + 3 q + c_{\varepsilon ,q}) x)}{-3 + q + c_{\varepsilon ,q}+2 (-1 + q) (-1 + q + c_{\varepsilon ,q})x},\\ H_1^{\varepsilon ,q}(x)&= \dfrac{(1 + q - c_{\varepsilon ,q}) x}{1 + q + c_{\varepsilon ,q}+2 (-1 + q) (-1 + q + c_{\varepsilon ,q})x}, \end{aligned}$$

and $c_{\varepsilon ,q}=\sqrt{1 + 2 (1 - 8 \varepsilon + 8 \varepsilon ^2) q + q^2}$. Furthermore, $H_0^{\varepsilon ,q}$ and $H_1^{\varepsilon ,q}$

• (1) map the interval $[0,\,\frac{1}{1-q}]$ into itself,

• (2) are strictly monontone increasing on $[0,\,\frac{1}{1-q}]$ for every $0<\varepsilon , q<1$.

Proof

Let

$$\begin{aligned} L_i^{\varepsilon ,q}(x)=S_i^{\varepsilon ,(q+1)/2}(x+1/2)-1/2. \end{aligned}$$

Since $\left\{ S_0,S_1\right\}$ maps [0,1] into itself, $\left\{ L_0,L_1\right\}$ maps $[-1/2,1/2]$ into itself. Moreover, $S_0(x)+S_1(1-x)=1$ implies $L_0(x)=-L_1(-x)$. Let $y_{\varepsilon ,q}$ be the fixed point of $L_0$ in $[-1/2,1/2]$. That is

$$\begin{aligned} y_{\varepsilon ,q}:=-\frac{-1 + q + \sqrt{1 + 2 (1 - 8 \varepsilon + 8 \varepsilon ^2) q + q^2}}{4 (-1 + 2 \varepsilon ) q}. \end{aligned}$$

By the symmetrical properties of $L_0$ and $L_1$, one can show that the fixed point of $L_1$ is $-y_{\varepsilon ,q}$. We define $y_{1/2,q}=0$. So when $\varepsilon \ne 1/2$ the following transformation of the function is valid.

$$\begin{aligned} Q_i^{\varepsilon ,q}(x):=L_i^{\varepsilon ,q}(y_{\varepsilon ,q}x)/y_{\varepsilon ,q}. \end{aligned}$$

Finally, we do the last manipulation:

$$\begin{aligned} H_i^{\varepsilon ,q}(x):=\frac{Q_i^{\varepsilon ,q}(2(1-q)x-1)+1}{2(1-q)}. \end{aligned}$$

By the definition $f_{\varepsilon ,q}(x):=2(1-q)y_{\varepsilon ,q}x+(1-q)y_{\varepsilon ,q}-1$.

It is easy to check that the functions $H_0^{\varepsilon ,q}$ and $H_1^{\varepsilon ,q}$ satisfy property (2). Furthermore, $Q_0^{\varepsilon ,q}(1)=1$ and $Q_1^{\varepsilon ,q}(-1)=-1$, therefore $H_0^{\varepsilon ,q}(\frac{1}{1-q})=\frac{1}{1-q}$ and $H_1^{\varepsilon ,q}(0)=0$. This fact together with (2) implies property (1). $\square$

Remark 3.2

For $\varepsilon =1/2$ the IFS $\big \{H_0^{1/2,q},H_1^{1/2,q}\big \}$ is well defined, but it is not equivalent to the IFS $\big \{S_0^{1/2,(q+1)/2},S_1^{1/2,(q+1)/2}\big \}$. Hence, the properties of any invariant measures are not inherited. However, the importance of the modification of our original IFS comes from the fact that $\lim _{\varepsilon \rightarrow 1/2}H_0^{\varepsilon ,q}(x)=H_0^{1/2,q}(x)=qx+1$ and $\lim _{\varepsilon \rightarrow 1/2}H_1^{\varepsilon ,q}(x)=H_1^{1/2,q}(x)=qx$. Peres and Solomyak [13] proved that the IFS $\left\{ qx+1,qx\right\}$ satisfies (2.4) and hence, the transversality condition for $q\in (0.5,0.65)$. Since the functions $H_0^{\varepsilon ,q},H_1^{\varepsilon ,q},(H_0^{\varepsilon ,q})'$ and $(H_1^{\varepsilon ,q})'$ are smoothly parametrized in $\varepsilon$ (see Lemma 3.1), one can show by using Lemma 2.3 that the IFS $\left\{ H_0^{\varepsilon ,q},H_1^{\varepsilon ,q}\right\}$ satisfies the transversality condition w.r.t the parameter $q$ in a neighbourhood of $\varepsilon =1/2$.

To characterize the transversality region precisely, we will use the technique of [4, Section 7]. First, we restrict ourselves to the set of parameters for which the IFS $\left\{ H_0^{\varepsilon ,q},H_1^{\varepsilon ,q}\right\}$ is strictly contracting. Let $\kappa (\varepsilon ,q)$ denote the contraction ratio of the IFS,

$$\begin{aligned} \kappa (\varepsilon ,q):=\max \Big \{\left( H_0^{\varepsilon ,q}\right) '(0), \left( H_0^{\varepsilon ,q}\right) ' \big (\frac{1}{1-q}\big ), \left( H_1^{\varepsilon ,q}\right) '(0), \left( H_1^{\varepsilon ,q}\right) '\big (\frac{1}{1-q}\big )\Big \}, \end{aligned}$$

and let

$$\begin{aligned} R_{\mathrm {contr}}:=\left\{ (\varepsilon ,q)\in [0,1]^2: \kappa (\varepsilon ,q)<1\right\} . \end{aligned}$$

(3.6)

It is easy to see that the derivatives $(H_0^{\varepsilon ,q})'$ and $(H_1^{\varepsilon ,q})'$ are either strictly monotone increasing or decreasing. Thus, $R_{\mathrm {contr}}$ is exactly the region of parameters, where the IFS is contracting.

Let $\pi _{\varepsilon ,q}$ denote the usual natural projection from the symbolic space $\Sigma =\left\{ 0,1\right\} ^{\mathbb {N}}$ to $[0,\frac{1}{1-q}]$, that is

$$\begin{aligned} \pi _{\varepsilon ,q}(i_0,i_1,i_2,\dots )=\lim _{n\rightarrow \infty }H_{i_0}^{\varepsilon ,q}\circ H_{i_1}^{\varepsilon ,q}\circ \cdots \circ H_{i_n}^{\varepsilon ,q}(0). \end{aligned}$$

Since the functions $H_i^{\varepsilon ,q}$ are contractions for $(\varepsilon ,q)\in R_{\mathrm {contr}}$, the function $\pi _{\varepsilon ,q}$ is well defined.

For every $(\varepsilon ,q)\in R_{\mathrm {contr}}$ there exists a unique non-empty compact set $\Lambda _{\varepsilon ,q}$, the attractor, such that

$$\begin{aligned} \Lambda _{\varepsilon ,q}=\bigcap _{n\ge 0}\bigcup _{i_0,\dots ,i_n=0}^1H_{i_0}^{\varepsilon ,q}\circ H_{i_1}^{\varepsilon ,q}\circ \cdots \circ H_{i_n}^{\varepsilon ,q}([0,\frac{1}{1-q}]). \end{aligned}$$

Hence, the set $\Lambda _{\varepsilon ,q}$ is invariant, i.e. $\Lambda _{\varepsilon ,q}=H_0^{\varepsilon ,q}(\Lambda _{\varepsilon ,q})\cup H_1^{\varepsilon ,q}(\Lambda _{\varepsilon ,q})$, see [5]. The measure $\mu _{\varepsilon ,p}$ is an invariant measure of the IFS $\{H_0^{\varepsilon ,q}, H_1^{\varepsilon ,q}\}$, the support of $\mu _{\varepsilon ,p}$ is $\Lambda _{\varepsilon ,q}$. If $H_0^{\varepsilon ,q}([0,\frac{1}{1-q}])\cap H_1^{\varepsilon ,q}([0,\frac{1}{1-q}])=\emptyset$ then $\Lambda _{\varepsilon ,q}$ is a Cantor set with zero Lebesgue measure, which implies that any measure with support $\Lambda _{\varepsilon ,q}$ is singular. Hence, it is necessary that the two cylinders $H_0^{\varepsilon ,q}([0,\frac{1}{1-q}])$ and $H_1^{\varepsilon ,q}([0,\frac{1}{1-q}])$ overlap (in which case $\Lambda _{\varepsilon ,q}=[0,\frac{1}{1-q}]$).

However, for proving the transversality condition, it is convenient to assume that the overlap between the images of the two cylinder sets is “weak” in the following sense:

$$\begin{aligned} \pi _{\varepsilon ,q}(\mathbf {i})=\pi _{\varepsilon ,q}(\mathbf {j})\text { and }i_0\ne j_0\Rightarrow i_1=1-i_0\ne j_1=1-j_0. \end{aligned}$$

Roughly speaking, only the $[01]$ and $[10]$ cylinders are overlapping. Formally, this defines the set of parameters

$$\begin{aligned} R_{\mathrm {overlap}}:=\Big \{(\varepsilon ,q)\in [0,1]^2: H_0^{\varepsilon ,q}(0)<H_1^{\varepsilon ,q}\big (\frac{1}{1-q}\big ),\nonumber \\ H_0^{\varepsilon ,q}\big (H_0^{\varepsilon ,q}(0)\big )>H_1^{\varepsilon ,q}\big (\frac{1}{1-q}\big ) \,\text { and }\, H_1^{\varepsilon ,q}\big (H_1^{\varepsilon ,q}\big (\frac{1}{1-q}\big )\big )<H_0^{\varepsilon ,q}(0)\Big \}. \end{aligned}$$

(3.7)

Simple calculations show that the functions $\frac{\partial \left( H_i^{\varepsilon ,q}\right) '}{\partial q},\frac{\partial H_i^{\varepsilon ,q}}{\partial q}, H_i^{\varepsilon ,q}:[0,\frac{1}{1-q}]\mapsto \mathbb {R}$ are smooth functions for every $0<\varepsilon ,q<1$. Moreover, the function $\frac{\partial \left( H_i^{\varepsilon ,q}\right) '}{\partial q}$ has the form $\frac{a_{\varepsilon ,q}(x)}{b_{\varepsilon ,q}(x)}$, where $a_{\varepsilon ,q}(x)$ is a first degree and $b_{\varepsilon ,q}(x)$ is a third degree polynomial. Hence, there exists a unique root $x^{\varepsilon ,q}_i$ of the function

$$\begin{aligned} \frac{\partial \left( H_i^{\varepsilon ,q}\right) '}{\partial q}(x^{\varepsilon ,q}_i)=0. \end{aligned}$$

As a technical condition we also need that the functions $\frac{\partial H_0^{\varepsilon ,q}}{\partial q}\text { and }\frac{\partial H_1^{\varepsilon ,q}}{\partial q}$ are monotone increasing. We define

$$\begin{aligned} R_{\mathrm {pos}}:=\Big \{(\varepsilon ,q)\in [0,1]^2:\frac{\partial (H_i^{\varepsilon ,q})'}{\partial q}(0)>0\text { and }x^{\varepsilon ,q}_i\notin \big [0,\frac{1}{1-q}\big ]\text { for }i=0,1\Big \}. \end{aligned}$$

(3.8)

From now we focus our study for the set of parameters $R_{\mathrm {region}}$, where

$$\begin{aligned} R_{\mathrm {region}}:=R_{\mathrm {contr}}\cap R_{\mathrm {overlap}}\cap R_{\mathrm {pos}}, \end{aligned}$$

(3.9)

see Fig. 3. The definition of $R_{\mathrm {region}}$ implies that it is open.

Fig. 3

The regions $R_{\mathrm {contr}}$ (blue region), $R_{\mathrm {overlap}}$ (red) and $R_{\mathrm {pos}}$ (brown). The intersection of the three regions is $R_{\mathrm {region}}$ (Color figure online)

Define $\omega (\varepsilon ,q)$ for $(\varepsilon ,q)\in R_{\mathrm {region}}$ as

$$\begin{aligned} \omega (\varepsilon ,q):=\max \left\{ \frac{\partial H_0^{\varepsilon ,q}}{\partial q}\big (\frac{1}{1-q}\big ), \frac{\partial H_1^{\varepsilon ,q}}{\partial q}\big (\frac{1}{1-q}\big )\right\} . \end{aligned}$$

Lemma 3.3

For every $(\varepsilon ,q)\in R_{\mathrm {region}}$ and $\mathbf {i}\in \Sigma$

$$\begin{aligned} 0\le \frac{\partial }{\partial q}\pi _{\varepsilon ,q}(\mathbf {i})\le \frac{\omega (\varepsilon ,q)}{1-\kappa (\varepsilon ,q)}. \end{aligned}$$

Proof

One can check that for every $(\varepsilon ,q)\in R_{\mathrm {region}}$, $\frac{\partial H_0^{\varepsilon ,q}}{\partial q}(0),\frac{\partial H_1^{\varepsilon ,q}}{\partial q}(0)\ge 0$. Since $H_0^{\varepsilon ,q}, H_1^{\varepsilon ,q}$ and $\frac{\partial H_0^{\varepsilon ,q}}{\partial q},\frac{\partial H_1^{\varepsilon ,q}}{\partial q}$ are monotone increasing, the first inequality holds.

On the other hand,

$$\begin{aligned} \frac{\partial }{\partial q}\pi _{\varepsilon ,q}(\mathbf {i})&= \frac{\partial }{\partial q}( H_{i_0}^{\varepsilon ,q}(\pi _{\varepsilon ,q}(\sigma \mathbf {i}))) \\&=\frac{\partial H_{i_0}^{\varepsilon ,q}}{\partial q}(\pi _{\varepsilon ,q}(\sigma \mathbf {i}))+ (H_{i_0}^{\varepsilon ,q})'(\pi _{\varepsilon ,q}(\sigma \mathbf {i}))\frac{\partial }{\partial q}\pi _{\varepsilon ,q}(\sigma \mathbf {i}) \\&\le \omega (\varepsilon ,q)+\kappa (\varepsilon ,q)\frac{\partial }{\partial q}\pi _{\varepsilon ,q}(\sigma \mathbf {i}). \end{aligned}$$

The second inequality follows by induction. $\square$

Since the functions $H_0^{\varepsilon ,q}, H_1^{\varepsilon ,q}$ are strictly monotone increasing on $[0,\frac{1}{1-q}]$, they are invertible. Denote the inverse functions by

$$\begin{aligned} \mathcal {H}_0^{\varepsilon ,q} :=\left( {H}_0^{\varepsilon ,q}\right) ^{-1} \;\text { and }\; \mathcal {H}_1^{\varepsilon ,q} :=\left( {H}_1^{\varepsilon ,q}\right) ^{-1}. \end{aligned}$$

For simplicity, denote $H_{10}^{\varepsilon ,q}:=H_1^{\varepsilon ,q}\circ H_0^{\varepsilon ,q}$ and $H_{01}^{\varepsilon ,q}:=H_0^{\varepsilon ,q}\circ H_1^{\varepsilon ,q}$. Then easy calculations show that the function

$$\begin{aligned} \mathbb {H}^{\varepsilon ,q}(x):=\frac{\partial H_{10}^{\varepsilon ,q}}{\partial q}\circ \mathcal {H}_0^{\varepsilon ,q}\circ \mathcal {H}_1^{\varepsilon ,q}(x)-\frac{\partial H_{01}^{\varepsilon ,q}}{\partial q}\circ \mathcal {H}_1^{\varepsilon ,q}\circ \mathcal {H}_0^{\varepsilon ,q}(x) \end{aligned}$$

(3.10)

is a convex polynomial of second degree. Denote the value at which the minimum is obtained by $z_{\varepsilon ,q}$.

Lemma 3.4

For every $(\varepsilon _0,q_0)\in R_{\mathrm {trans}}$ and for every $\mathbf {i},\mathbf {j}\in \Sigma$ such that $i_0\ne j_0$ we have

$$\begin{aligned} \pi _{\varepsilon _0,q_0}(\mathbf {i})=\pi _{\varepsilon _0,q_0}(\mathbf {j})\Rightarrow \bigg |\Big .\frac{\partial }{\partial q}\left( \pi _{\varepsilon _0,q}(\mathbf {i})-\pi _{\varepsilon _0,q}(\mathbf {j})\right) \Big |_{q=q_0}\bigg |>0, \end{aligned}$$

where $R_{\mathrm {trans}}$ is a non-empty set defined by

$$\begin{aligned} R_{\mathrm {trans}}:=\Big \{(\varepsilon ,q)\in R_{\mathrm {region}}:\mathbb {H}^{\varepsilon ,q}(z_{\varepsilon ,q})- \frac{\omega (\varepsilon ,q)\kappa (\varepsilon ,q)^2}{1-\kappa (\varepsilon ,q)}>0\Big \}. \end{aligned}$$

(3.11)

One can see the region of parameters $R_{\mathrm {trans}}$ on Fig. 4.

Proof

First, we show that $R_{\mathrm {trans}}\ne \emptyset$, precisely, we show that $(1/2,0.55)\in R_{\mathrm {trans}}$. We note again that $H^{1/2,q}_0(x)=qx+1$ and $H_1^{1/2,q}(x)=qx$. It is easy to check that $(1/2,0.55)\in R_{\mathrm {region}}$. By (3.10) we get $\mathbb {H}^{1/2,0.55}(x)=\frac{2}{0.55}-1$, thus, by (3.11), $\frac{2}{0.55}-1-\frac{0.55^2}{(1-0.55)^2}>0$, which completes the proof of $(1/2,0.55)\in R_{\mathrm {trans}}$. By the definitions, $R_{\mathrm {trans}}$ is open in $\mathbb {R}^2$ thus there exists a point $(\varepsilon ,q)\in R_{\mathrm {trans}}$ such that $\varepsilon \ne 1/2$.

Now, suppose that $\pi _{\varepsilon _0,q_0}(\mathbf {i})=\pi _{\varepsilon _0,q_0}(\mathbf {j})$ and $i_0\ne j_0$ then $(\varepsilon _0,q_0)\in R_{\mathrm {overlap}}$ implies

$$\begin{aligned} 0=\pi _{\varepsilon _0,q_0}(\mathbf {i})-\pi _{\varepsilon _0,q_0}(\mathbf {j})=H_1^{\varepsilon _0,q_0}\circ H_0^{\varepsilon _0,q_0}(\pi _{\varepsilon _0,q_0}(\sigma ^2\mathbf {i}))-H_0^{\varepsilon _0,q_0}\circ H_1^{\varepsilon _0,q_0}(\pi _{\varepsilon _0,q_0}(\sigma ^2\mathbf {j})). \end{aligned}$$

So it is enough to show that the partial derivative by $q$ of the right-hand side is positive. Then from Lemma 3.3 it follows that

$$\begin{aligned}&\frac{\partial }{\partial q} \left( H_{10}^{\varepsilon ,q}(\pi _{\varepsilon ,q}(\sigma ^2\mathbf {i}))-H_{01}^{\varepsilon ,q}(\pi _{\varepsilon ,q}(\sigma ^2\mathbf {j}))\right) \\&\ge \frac{\partial H_{10}^{\varepsilon ,q}}{\partial q}(\pi _{\varepsilon ,q}(\sigma ^2\mathbf {i}))-\frac{\partial H_{01}^{\varepsilon ,q}}{\partial q}(\pi _{\varepsilon ,q}(\sigma ^2\mathbf {j}))-\frac{\kappa (\varepsilon ,q)^2\omega (\varepsilon ,q)}{1-\kappa (\varepsilon ,q)}. \end{aligned}$$

Hence by the definition of $\mathbb {H}^{\varepsilon , q}$

$$\begin{aligned} \frac{\partial H_{10}^{\varepsilon _0,q}}{\partial q}&(\pi _{\varepsilon _0,q}(\sigma ^2\mathbf {i}))-\frac{\partial H_{01}^{\varepsilon _0,q}}{\partial q}(\pi _{\varepsilon _0,q}(\sigma ^2\mathbf {j}))\Big |_{q=q_0} \\&= \frac{\partial H_{10}^{\varepsilon _0,q}}{\partial q} (\mathcal {H}_0^{\varepsilon _0,q}\circ \mathcal {H}_1^{\varepsilon _0,q}(\pi _{\varepsilon _0,q}(\mathbf {i})))-\frac{\partial H_{01}^{\varepsilon _0,q}}{\partial q}(\mathcal {H}_1^{\varepsilon _0,q}\circ \mathcal {H}_0^{\varepsilon _0,q}(\pi _{\varepsilon _0,q}(\mathbf {j})))\Big |_{q=q_0} \\&\ge \mathbb {H}^{\varepsilon _0,q_0}(z_{\varepsilon _0,q_0}), \end{aligned}$$

so the statement follows. $\square$

For the sake of completeness, finally, we give a compactness argument for proving transversality condition.

Proposition 3.5

For every $\varepsilon >0$ the IFS $\left\{ H_0^{\varepsilon ,q},H_1^{\varepsilon ,q}\right\}$ satisfies the transversality condition on any open interval $V\subset \mathbb {R}$ such that $\overline{V}\subset R_{\mathrm {trans}}\cap \left( [0,1]\times \left\{ \varepsilon \right\} \right)$.

Proof

Let $V\subset \mathbb {R}$ an open set such that the closure is contained in $R_{\mathrm {trans}}\cap R_{\mathrm {region}}\cap [0,1]\times \left\{ \varepsilon \right\}$ and let

$$\begin{aligned} \eta _1:=\min _{q\in \overline{V}}\left\{ \mathbb {H}^{\varepsilon ,q}(x)(z_{\varepsilon ,q})-\frac{\omega (\varepsilon ,q)\kappa (\varepsilon ,q)^2}{1-\kappa (\varepsilon ,q)}\right\} , \end{aligned}$$

where $\mathbb {H}^{\varepsilon ,q}$ was defined in (3.10). It is easy to see that the space $\Sigma \times \Sigma \times \overline{V}$ is compact and the function $(\mathbf {i},\mathbf {j},q)\mapsto \frac{\partial }{\partial q}\left( \pi _{\varepsilon ,q}(\mathbf {i})-\pi _{\varepsilon ,q}(\mathbf {j})\right)$ is continuous. The function $(\mathbf {i},\mathbf {j},q)\mapsto \pi _{\varepsilon ,q}(\mathbf {i})-\pi _{\varepsilon ,q}(\mathbf {j})$ is continuous as well. Therefore, for every $\eta \ge 0$, the set $L_{\eta }=\left\{ (\mathbf {i},\mathbf {j},q):\left| \pi _{\varepsilon ,q_0}(\mathbf {i})-\pi _{\varepsilon ,q_0}(\mathbf {j})\right| \le \eta \right\}$ is compact. Since

$$\begin{aligned} \Big |\frac{\partial }{\partial q}\left( \pi _{\varepsilon ,q_0}(\mathbf {i})-\pi _{\varepsilon ,q_0}(\mathbf {j})\right) \Big |\ge \eta _1\text { for every }(\mathbf {i},\mathbf {j},q)\in L_0, \end{aligned}$$

there exists an $\eta _2>0$ depending only on $\varepsilon$ such that for every $q_0\in V$ and any $\mathbf {i},\mathbf {j}\in \Sigma$, $i_0\ne j_0$ we have

$$\begin{aligned} \left| \pi _{\varepsilon ,q_0}(\mathbf {i})-\pi _{\varepsilon ,q_0}(\mathbf {j})\right| <\eta _1\Rightarrow \bigg |\Big .\frac{\partial }{\partial q}\left( \pi _{\varepsilon ,q}(\mathbf {i})-\pi _{\varepsilon ,q}(\mathbf {j})\right) \Big |_{q=q_0}\bigg |>\frac{\eta _2}{2}. \end{aligned}$$

This implies the statement of the proposition by Lemma 2.3. $\square$

4 Proof of Theorem 1.1

The last section of our paper is devoted to prove the absolute continuity of the Blackwell measure. In order to apply Theorem 2.2 we recall a result of [4] to find the region where the quotient entropy over Lyapunov exponent is strictly greater than $1$. Let

$$\begin{aligned} \mathfrak {h}_{\varepsilon ,q}(x)=-\left( p_0^{\varepsilon ,(q+1)/2}(x)\log p_0^{\varepsilon ,(q+1)/2}(x)+ p_1^{\varepsilon ,(q+1)/2}(x)\log p_1^{\varepsilon ,(q+1)/2}(x)\right) . \end{aligned}$$

Define the Perron–Frobenius operator corresponding to measure $\mu _{\varepsilon ,p}$ as follows

$$\begin{aligned} (T_{\varepsilon ,p}f)(x):=p^{\varepsilon ,p}_{0}(x)\cdot f(S^{\varepsilon ,p}_{0}(x))+p^{\varepsilon ,p}_{1}(x)\cdot f(S^{\varepsilon ,p}_{1}(x)), \end{aligned}$$

where the functions and probabilities were defined in (3.1)–(3.4).

Our next step is to find a region on which $\frac{h(\mu _{\varepsilon ,(q+1)/2})}{\chi (\mu _{\varepsilon ,(q+1)/2})}\ge 1$, where $h(\mu _{\varepsilon ,p})$ is the entropy (2.2) and $\chi (\mu _{\varepsilon ,p})$ denotes the Lyapunov exponent (2.3) of the measure $\mu _{\varepsilon ,p}$. According to [4, Corollary 12]

$$\begin{aligned} \chi (\mu _{\varepsilon ,p})=-\log (\varepsilon (1-\varepsilon )q)-2h(\mu _{\varepsilon ,(q+1)/2}) \end{aligned}$$

and hence

$$\begin{aligned} \frac{h(\mu _{\varepsilon ,(q+1)/2})}{\chi (\mu _{\varepsilon ,(q+1)/2})}\ge 1\Leftrightarrow 3h(\mu _{\varepsilon ,(q+1)/2})+\log (\varepsilon (1-\varepsilon )q)\ge 0. \end{aligned}$$

By [4, Proposition 18], $h(\mu _{\varepsilon ,(q+1)/2})\ge (T_{\varepsilon ,(q+1)/2}^{n}\mathfrak {h}_{\varepsilon ,q})(0)$ for every $n\ge 0$, where $T_{\varepsilon ,(q+1)/2}^{n}$ denotes the $n$-th iterate of the operator $T_{\varepsilon ,(q+1)/2}$. Thus,

$$\begin{aligned} 3(T_{\varepsilon ,(q+1)/2}^{10}\mathfrak {h}_{\varepsilon ,q})(0)+\log (\varepsilon (1-\varepsilon )q)>0\Rightarrow \frac{h(\mu _{\varepsilon ,(q+1)/2})}{\chi (\mu _{\varepsilon ,(q+1)/2})}>1. \end{aligned}$$

(4.1)

Define $R_{\mathrm {ratio}}$ as the region where the ratio is strictly greater than $1$

$$\begin{aligned} R_{\mathrm {ratio}}:=\big \{(\varepsilon ,q)\in [0,1]^2: 3(T_{\varepsilon ,(q+1)/2}^{10}\mathfrak {h}_{\varepsilon ,q})(0)+\log (\varepsilon (1-\varepsilon )q)>0\big \}. \end{aligned}$$

(4.2)

Fig. 4

The region $R_{\mathrm {trans}}$

Proof (Proof of Theorem 1.1)

[Proof of Theorem 1.1] During the proof we consider only parameter $q$ as the parameter used for transversality. Therefore, let us fix an $\varepsilon \ne 1/2$. Then the IFS $\big \{S^{\varepsilon ,(q+1)/2}_{0},S^{\varepsilon ,(q+1)/2}_{1}\big \}$ satisfies the transversality condition by Lemma 3.1 and Proposition 3.5 for every open interval $V$ with $\overline{V}\subseteq R_{\mathrm {trans}}\cap ([0,1]\times \{\varepsilon \})$, when $R_{\mathrm {trans}}\cap ([0,1]\times \{\varepsilon \})\ne \emptyset$.

It follows from Theorem 2.2 and (4.1) that for every open interval $V$ and Lebesgue-a.e $q\in V$, where $\overline{V}\subseteq R_{\mathrm {ratio}}\cap R_{\mathrm {trans}}\cap ([0,1]\times \{\varepsilon \})$, the measure $\mu _{\varepsilon ,(q+1)/2}$ is absolutely continuous w.r.t Lebesgue measure. Since the interval $V$ was arbitrary, by using the symmetrical properties of $\mu _{\varepsilon ,p}$, one can finish the proof of absolute continuity.

Now let us assume that $\varepsilon =1/2$. Observe that $S^{1/2,p}_0(x)=S^{1/2,p}_1(x)=xp+(1-x)(1-p)$. By (3.5), the measure $\mu _{\varepsilon ,p}$ is supported on the common fixed point of $S^{1/2,p}_0$ and $S^{1/2,p}_1$, which is $x=1/2$. Thus, it is the Dirac measure supported on $1/2$. $\square$

For the absolute continuity region $R_{\mathrm {ratio}}\cap R_{\mathrm {trans}}$, see Fig. 5. Figure 4 shows us the region of overlap, where transversality condition holds, but it is not guaranteed that the Blackwell measure is absolutely continuous on this region, so we restrict this to the region where it is guaranteed.

Fig. 5

The region $R_{\mathrm {ratio}}\cap R_{\mathrm {trans}}$

Proof of Corollary 1.3

The statement follows immediately from Theorem 1.1 and [9, Theorem 1.1]. $\square$

Remark 4.1

(Concluding remark) In cases where the Blackwell measure, defined by a hidden Markov chain, is equivalent to a place-dependent invariant measure on $\mathbb {R}$, the presented method can be adapted to find a region of absolute continuity (if it exists). Namely, absolute continuity holds almost surely on the set of parameters where the transversality condition holds and the entropy over Lyapunov exponent quotient is strictly greater than one. Unfortunately, this intersection may be empty.