Thermodynamic and Physicochemical Studies of Binary Mixtures of 1-Propoxy-2-Propanol with Amines at Different Temperatures

Abstract

In the present study, intermolecular interactions for binary liquid mixtures of 1-propoxy-2-propanol with amines namely diisopropylamine, dibutylamine and tributylamine have been examined through experimentally measured values of density ($\rho$), speed of sound (u) and viscosity ($\eta$). Measurements were carried out over entire the composition range and temperature range from 298.15 to 308.15 K. Various excess and deviation parameters have been calculated using measured data. These excess and deviation properties have been discussed in terms of intermolecular interactions in the mixtures. The presence of strong intermolecular interactions among unlike molecules in binary mixtures of 1-propoxy-2-propanol with diisopropylamine and dibutylamine while weak interactions in case of tributylamine have been revealed by these properties. Excess and deviation properties have been correlated with composition using Redlich–Kister polynomial. The Jouyban–Acree model was used to correlate the measured data with composition. Further, studies on Fourier-transform infrared spectroscopy were also carried out at room temperature.

1 Introduction

Research on thermodynamic properties of binary liquid mixtures has attained frequent recognition due to their application in various chemical and biochemical industries. Nature and extent of intermolecular interactions among unlike components is also revealed by these properties. Knowledge of thermodynamic properties of non-aqueous mixtures also helps in developing theories or models related to solvent media as well as to test the existing theories or models. Complex natural and chemical phenomena can be understood in simpler way by studying the thermodynamics of binary liquid mixtures. Binary systems of glycol ether, 1-propoxy-2-propanol (1P2P) with amines namely diisopropylamine (DIPA), dibutylamine (DBA) and tributylamine (TBA) have been studied in the present discussion in continuation to our previous study [1,2,3,4]. Glycol ethers are important class of industrial solvents. Because of low vapour pressure, low toxicity, low melting point and high chemical stability, these are used as scrubbing liquids for absorbing gases from industrial production plants for cleaning exhaust air and gas streams [5]. Further, glycol ethers are also used in anionic polymerization, automotive brake fluid, printing ink and paint industries [6]. Amines are self-associated solvents used to study the hydrophobic effects. Amines are also important class of organic solvents because of their applications in many fields such as pharmaceutical industries, gas treatment, in metal ion separations, as corrosion inhibitor etc.

2 Experimental

2.1 Materials Used

Provenance and purity of chemicals used is given in Table 1. 1P2P was used as such because of its high purity content while DIPA, DBA and TBA were doubly distilled prior to measurements. Chemicals were stored with extra care to prevent any further contamination. To ascertain the purity of chemicals, experimentally measured density, speed of sound and viscosity of pure components has been compared with the corresponding literature values in Table 2. Binary mixtures were prepared in culture tubes having Teflon-coated rubber caps. Samples were prepared on the day of measurement.

Table 1 Purity* and provenance of the chemicals used

Table 2 Comparison of experimental values of density (ρ), speed of sound (u) and viscosity ($\eta$) for pure liquids with the corresponding literature values at different temperatures and at pressure, P = 0.10 MPa

2.2 Apparatus and Procedure

Electronic balance Afcoset-ER-120A was used for weighing the appropriate amount of liquid to prepare the binary mixtures. Uncertainty in measurements of electronic balance was found to be 0.05 mg. Density of sample liquids has been measured using single capillary pycnometer with bulb capacity of approximately 8 ml. Pycnometer was hung vertically in an electronic thermostat for temperature maintenance of liquid samples having precision of 0.05 K. Speed of sound (u) of liquid samples was measured using single frequency Ultrasonic interferometer (Model F-81, Mittal Enterprises) operating at 4 MHz. Temperature maintenance of liquid samples was carried out by circulating water from thermostat through water jacketed cell. Pycnometer and interferometer were calibrated at studied temperatures using triply distilled water prior to measurements. Combined uncertainty in density and speed of sound measurement was found to be 0.8 kg⋅m⁻³ and 0.52 m⋅s⁻¹, respectively.

Viscosities of liquid samples were measured using an Ubbelohde suspended level viscometer. Pure solvents, doubly distilled water, hexane and heptane were used to calibrate the viscometer. Flow times of sample liquids were measured using an electronic stop watch of accuracy 0.01 s. Combined uncertainty in viscosity measurement was 0.12 mPa⋅s.

Fourier-transform infrared (FTIR) spectra of pure components and their binary mixtures at mole fractions; x₁ = 0.2, 0.5 and 0.8 were recorded at room temperature using an ABB Horizon (MB 3000) spectrometer. The spectrometer has resolution of the order of 4 cm⁻¹ and maximum signal to noise ratio (root-mean-square, 60 s, 4 cm⁻¹, at peak response) 50,000:1.

3 Results

Experimentally measured $\rho$, u and $\eta$ for the studied binary mixtures have been used to calculate various thermodynamic parameters with the help of different relations. Following expression was used to calculate excess molar volume ($V_{m}^{\text{E}}$) using the density values for pure components and their mixtures:

$$V_{m}^{{\text{E}}} = \sum\limits_{i = 1}^{2} {x_{i} M_{i} \left( {\rho^{ - 1} - (\rho_{i}^{*} )^{ - 1} } \right)}$$

(1)

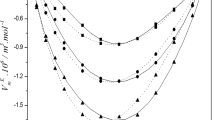
where x_i, ${\text{M}}_{i}$ and $\rho_{i}^{*}$ in this expression are used for mole fraction, molar mass and density of ith component respectively. $\rho$ represents the density of the mixture. Values of $\rho$ and $V_{m}^{\text{E}}$ for studied binary mixtures as a function of mole fraction of 1P2P ($x_{1}$) are reported in Table 3. Values of $V_{m}^{\text{E}}$ for studied binary mixtures have been plotted against mole fraction of 1P2P ($x_{1}$) in Fig. 1 at 298.15 K.

Table 3 Density ($\rho$) and excess molar volume ($V_{m}^{\text{E}}$) for binary liquid mixtures of 1-propoxy-2-propanol ($x_{{1}}$) with studied amines at different temperatures and at pressure, P = 0.10 MPa

Fig. 1

Excess molar volume ($V_{m}^{\text{E}}$) against mole fraction x₁ 1-propoxy-2-propanol + x₂ diisopropylamine (▲); x₂ dibutylamine (●) and x₂ tributylamine (■) at 298.15 K

Acoustic behavior of binary mixtures have been studied by calculating excess molar isentropic compressibility ($K_{S,m}^{\text{E}}$) and excess speed of sound ($u^{\text{E}}$) with the help of experimentally measured data. $K_{S,m}^{\text{E}}$ has been calculated using the following relation:

$$K_{S,m}^{\text{E}} = K_{S} - K_{S,m}^{\text{id}}$$

(2)

where symbols $K_{S}$ and $\it K_{S,m}^{{{\text{id}}}}$ are used for real value of molar isentropic compressibility and value of molar isentropic compressibility if the liquid mixtures behave ideally.

Molar isentropic compressibility ($K_{S}$) for homogeneous non-dissipative fluid is calculated using density and speed of sound data with the help of following relation:

$$K_{S} = - \left( {\frac{\partial V}{{\partial P}}} \right)_{s} = \frac{V}{{\rho \cdot u^{2} }} = V \cdot \kappa_{{\text{S}}}$$

(3)

where term $\left( {{{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial P}}} \right. \kern-0pt} {\partial P}}} \right)_{S}$ is change in molar volume with pressure at constant entropy. Symbols V and $\kappa_{S}$ represent molar volume and isentropic compressibility respectively.

Kiyohara and Benson [7,8,9,10,11] suggested the following equation to calculate $K_{S,m}^{\text{id}}$:

$$ K_{S,m}^{{{\text{id}}}} = \sum {x_{i} \left[ {K_{S,i}^{*} - TA_{P,i}^{*} \left\{ {\left( {{{\sum {x_{i} } A_{P,i}^{*} } \mathord{\left/ {\vphantom {{\sum {x_{i} } A_{P,i}^{*} } {\sum {x_{i} C_{P,i}^{*} } }}} \right. \kern-0pt} {\sum {x_{i} C_{P,i}^{*} } }}} \right) - \left( {{{A_{P,i}^{*} } \mathord{\left/ {\vphantom {{A_{P,i}^{*} } {C_{P,i}^{*} }}} \right. \kern-0pt} {C_{P,i}^{*} }}} \right)} \right\}} \right]}$$

(4)

where $A_{P,i}^{*} ( = V^{*} \times \alpha_{P,i}^{*} )$ is the product of molar volume (V^*) and isobaric expansion coefficient ($\alpha_{P,i}^{*}$), T is the temperature and $C_{P,i}^{*}$ is isobaric molar heat capacity of ith component. The $C_{P,i}^{*}$ value used for 1P2P, DIPA, DBA and TBA at 298.15 K are 283.6 [12], 266 [13], 302 [13] and 392 [13] J⋅mol⁻¹⋅K⁻¹ respectively. Further, $\alpha_{P,i}^{*}$ has been calculated with the help of following relation:

$$\alpha_{P,i}^{*} = - (\rho^{*} )^{ - 1} \cdot \left( {{{\partial \rho^{*} } \mathord{\left/ {\vphantom {{\partial \rho^{*} } {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{P}$$

(5)

Here, $\left( {{{\partial \rho^{*} } \mathord{\left/ {\vphantom {{\partial \rho^{*} } {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{P}$ is the change in density with temperature at constant pressure.

Excess speed of sound ($u^{\text{E}}$) for the studied binary liquid mixtures has been calculated using the following relation:

$$u^{\text{E}} = u - u^{\text{id}}$$

(6)

where $u^{\text{id}}$, speed of sound for the ideal liquid mixture, was calculated using the equation:

$$u^{\text{id}} = ((\sum {\phi_{i} } \rho_{i} )\kappa_{s}^{\text{id}} )^{ - 1/2}$$

(7)

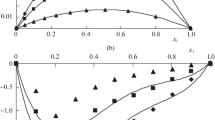
The values of $K_{S,m}^{\text{E}}$ and $u^{\text{E}}$ for the studied binary mixtures are reported as a function of mole fraction of 1P2P ($x_{1}$) in Table 4 over the entire composition range. Values of $K_{S,m}^{\text{E}}$ and $u^{\text{E}}$ for the binary mixtures at 298.15 K are represented graphically against mole fraction of 1P2P in Figs. 2 and 3, respectively.

Table 4 Speed of sound (u), excess molar isentropic compressibility ($K_{S,m}^{\text{E}}$) and excess speed of sound ($u^{\text{E}}$) of the binary liquid mixtures of 1-propoxy-2-propanol with studied amines at different temperatures and at pressure, P = 0.10 MPa

Fig. 2

Excess molar isentropic compressibility ($K_{S,m}^{\text{E}}$) against mole fraction x₁ 1-propoxy-2-propanol + x₂ diisopropylamine (▲); x₂ dibutylamine (●) and x₂ tributylamine (■) at 298.15 K

Fig. 3

Excess speed of sound ($u^{\text{E}}$) against mole fraction x₁ 1-propoxy-2-propanol + x₂ diisopropylamine (▲); x₂ dibutylamine (●) and x₂ tributylamine (■) at 298.15 K

To study the transport behaviour of binary liquid mixtures, the deviation in viscosity ($\Delta \eta$) and excess Gibbs free energy of activation for viscous flow ($\Delta G^{*\text{E}}$) [14] have been computed using the following relations:

$$\Delta \eta = \eta - (x_{1} \eta_{1}^{*} + x_{2} \eta_{2}^{*} )$$

(8)

$$\Delta G^{*\text{E}} = RT\left[ {{\text{ln}}(\eta V_{m} ) - \sum\limits_{i = 1}^{2} {x_{i} \cdot {\text{ln}}(\eta_{i}^{*} V_{i}^{*} )} } \right]$$

(9)

Experimental values of viscosity ($\eta$) along with calculated values of deviation in viscosity ($\Delta \eta$) for studied mixtures are recorded in Table 5. $\Delta \eta$ values are presented graphically against mole fraction of 1P2P at 298.15 K in Fig. 4. Calculated values of Gibbs-free energy ($\Delta G^{*\text{E}}$) are enlisted in Supplementary Table S1 and plotted against mole fraction of 1P2P at 298.15 K in Fig. 5.

Table 5 Experimental viscosity ($\eta$) and deviation in viscosity ($\Delta \eta$) as a function of mole fraction, $x_{{1}}$, of 1-propoxy-2-propanol for binary mixtures with amines at different temperatures and at pressure, P = 0.10 MPa

Fig. 4

Deviation in viscosity ($\Delta \eta$) against mole fraction x₁ 1-propoxy-2-propanol + x₂ diisopropylamine (▲); x₂ dibutylamine (●) and x₂ tributylamine (■) at 298.15 K

Fig. 5

Excess Gibbs free energy of activation of viscous flow ($\Delta G^{\text{*E}}$) against mole fraction x₁ 1-propoxy-2-propanol + x₂ diisopropylamine (▲); x₂ dibutylamine (●) and x₂ tributylamine (■) at 298.15 K

Various excess and deviation properties calculated have been correlated with the composition of mixtures using Redlich–Kister polynomial [15] with the help of relation 10. Density and speed of sound data has also been correlated to composition with the help of Jouyban–Acree model [16, 17] using Eq. 11. For this purpose, data was fitted to corresponding relation using least square method and binary coefficients were computed.

$$Y(x) = x_{{1}} x_{{2}} \sum\limits_{i = 1}^{p} {A_{i} (x_{{1}} - x_{{2}} )^{i - 1} }$$

(10)

$$\ln Y_{m,T} = x_{1} \ln Y_{1,T} + x_{2} \ln Y_{2,T} + x_{1} x_{2} \sum\limits_{i = 0}^{2} {\left[ {{{A_{i} \left( {x_{1} - x_{2} } \right)^{i} } \mathord{\left/ {\vphantom {{A_{i} \left( {x_{1} - x_{2} } \right)^{i} } T}} \right. \kern-0pt} T}} \right]}$$

(11)

Y(x), $Y_{m,T}$, p and A_i are used for the excess or deviation property, measured property at temperature T, number of parameters and binary coefficients respectively. Correlation ability of polynomials was tested by calculating the standard deviation ($\sigma$) using the following relation:

$$\sigma = \left[ {\sum\limits_{i}^{n} {\left\{ {Y\left( x \right)_{{{\text{exp}}}} - Y\left( x \right)_{{{\text{cal}}}} } \right\}^{2} /(n - p)} } \right]^{\frac{1}{2}}$$

(12)

where $Y(x)_{\exp }$ and $Y(x)_{{{\text{cal}}}}$ are used for values of experimental and calculated property respectively. Symbols n and p are used for number of experimental data points and number of estimated parameters respectively. Binary coefficients (A_i) and standard deviation values ($\sigma$) for Redlich–Kister polynomial and Jouyban–Acree model are recorded in Supplementary Tables S2 and S3, respectively.

In addition to this, the apparent molar volume ($V_{\varphi ,i}$) and partial molar volume ($\overline{V}_{m,1}$) have been calculated using the following relations:

$$V_{\varphi ,1} = \frac{{M_{2} (1 - x_{1} )(\rho_{2} - \rho )}}{{x_{1} \rho \rho_{2} }} + \frac{{M_{1} }}{\rho }$$

(13)

$$\overline{V}_{m,1} = V_{m,1} + \left( {\frac{{V_{m}^{\text{E}} }}{{x_{1} }}} \right) + x_{1} (1 - x_{1} )\left[ {\frac{{\partial \left( {V_{m}^{\text{E}} /x_{1} } \right)}}{{\partial x_{1} }}} \right]_{P,T}$$

(14)

Using the Eqs. 10 and 14, partial molar volume for both the components has been calculated as:

$$\overline{V}_{m,1} = V_{m,1} + x_{2}^{2} \sum {A_{k} } (1 - 2x_{2} )^{k - 1} - 2x_{1} (1 - x_{1} )^{2} \sum {A_{k} } (k - 1)(1 - 2x_{1} )^{k - 2}$$

(15)

$$\overline{V}_{m,2} = V_{m,2} + x_{1}^{2} \sum {A_{k} } (1 - 2x_{2} )^{k - 1} + 2x_{1}^{2} (1 - x_{1} )\sum {A_{k} } (k - 1)(1 - 2x_{1} )^{k - 2}$$

(16)

Calculated values of $V_{\varphi ,i}$ and $\overline{V}_{m,i}$ for binary mixtures at different temperatures are listed in Supplementary Tables S4 and S5 respectively. Values of $V_{\varphi ,i}$ are presented graphically in Fig. 6. Excess partial molar volume ($\overline{V}_{m,i}^{\text{E}}$) was calculated using the general equation for calculating the excess properties and corresponding values are recorded in Supplementary Table S6. Values of excess molar volume at x₁ = 0 and x₁ = 1 are the excess partial volume at infinite dilution ($\overline{V}_{m,i}^{{\text{E}},\infty}$) for the component 2 and 1, respectively. Values of $\overline{V}_{m,i}^{\text{E}}$ are plotted graphically against mole fraction of 1P2P in Fig. 7.

Fig. 6

Apparent molar volume ($V_{\varphi ,i}$) against mole fraction x₁ 1-propoxy-2-propanol + x₂ diisopropylamine (▲); x₂ dibutylamine (●) and x₂ tributylamine (■) at 298.15 K

Fig. 7

Excess partial molar volume ($\overline{V}_{m,1}^{\text{E}}$) against mole fraction x₁ 1-propoxy-2-propanol + x₂ diisopropylamine (▲); x₂ dibutylamine (●) and x₂ tributylamine (■) at 298.15 K

Various proposed semi-empirical relations for viscosity have been tested with the help of corresponding relation.

Grunberg and Nissan (GN) proposed the following relation [18] to estimate viscosity of liquid mixtures:

$$\eta = \exp \left[ {\sum\limits_{i} {(x_{i} \ln \eta_{i}^{*} ) + G_{12} \prod\limits_{i} {x_{i} } } } \right]$$

(17)

The magnitude of model parameter G₁₂ is proportional to the extent of interactions among the components of the liquid mixture. This parameter is related to the interchange energy.

Tamura and Kurata (TK) proposed the following relation [19] for the viscosity of binary liquid mixtures:

$$\eta = \sum\limits_{i} {(x_{i} \phi_{i} \eta_{i}^{*} )} + 2T_{12} \prod\limits_{i} {(x_{i} \phi_{i} )^{1/2} }$$

(18)

where T₁₂ is an adjustable parameter and $\phi_{i}$ represents the volume fraction of ith component in the liquid mixture.

Katti and Chaudhri (KC) recommended the following relation [20] for estimation of the viscosity for binary liquid mixtures from those of the pure components:

$$\ln \eta V_{m} = \sum\limits_{i} {x_{i} \ln (\eta_{i}^{*} V_{i}^{*} ) + x_{1} x_{2} \left( {W_{{{\text{vis}}}} /RT} \right)}$$

(19)

where W_vis is an adjustable parameter.

Hind, Mclaughlin and Ubbelohde (HI) derived the following relation [21] for viscosities of binary mixtures:

$$\eta = \sum\limits_{i} {x_{i}^{2} \eta_{i}^{*} + 2H_{12} \prod\limits_{i} {x_{i} } }$$

(20)

where H₁₂ is adjustable model parameter.

McAllister (Mc2) proposed following two parameter relation [22] for kinematic viscosity ($\nu$):

$$\begin{gathered} \ln \nu = x_{1}^{3} \ln \nu_{1}^{*} + x_{2}^{3} \ln \nu_{2}^{*} + 3x_{1}^{2} x_{2} \ln Z_{12} + 3x_{1} x_{2}^{2} \ln Z_{21} - \ln \left( {x_{1} + x_{2} \frac{{M_{2} }}{{M_{1} }}} \right) - \hfill \\ 3x_{1}^{2} x_{2} \ln \left( {\frac{2}{3} + \frac{{M_{2} }}{{3M_{1} }}} \right) + 3x_{1} x_{2}^{2} \ln \left( {\frac{1}{3} + \frac{{2M_{2} }}{{3M_{1} }}} \right) + x_{2}^{3} \ln \left( {\frac{{M_{2} }}{{M_{1} }}} \right) \hfill \\ \end{gathered}$$

(21)

where Z₁₂ and Z₂₁ are adjustable parameters.

Heric–Brewer (HB) three parameter relation for kinematic viscosity ($\nu$) [23] is:

$$\begin{gathered} \ln \nu = x_{1} \ln \nu_{1}^{*} + x_{2} \ln \nu_{2}^{*} + x_{1} \ln M_{1} + x_{2} \ln M_{2} - \ln (x_{1} M_{1} + x{}_{2}M_{2} ) \hfill \\ + x_{1} x_{2} \left[ {a + b(x_{1} - x_{2} ) + c(x_{1} - x_{2} )^{2} } \right] \hfill \\ \end{gathered}$$

(22)

where a, b and c represent the model parameters.

McAllister proposed following three parameter relation (Mc3) for kinematic viscosity ($\nu$) of binary mixture [22]:

$$\begin{gathered} \ln \nu = x_{1}^{4} \ln \nu_{1}^{*} + x_{2}^{4} \ln \nu_{2}^{*} + 4x_{1}^{3} x_{2} Z_{1112} + 6x_{1}^{2} x_{2}^{2} \ln Z_{1122} + 4x_{1} x_{2}^{3} \ln Z_{1222} - \ln \left( {x_{1} + x_{2} \frac{{M_{2} }}{{M_{1} }}} \right) + \hfill \\ 4x_{1}^{3} x_{2} \ln \left( {\frac{3}{4} + \frac{{M_{2} }}{{4M_{1} }}} \right) + 6x_{1}^{2} x_{2}^{2} \ln \left( {\frac{1}{2} + \frac{{M_{2} }}{{2M_{1} }}} \right) + 4x_{1} x_{2}^{3} \ln \left( {\frac{1}{4} + \frac{{3M_{2} }}{{4M_{1} }}} \right) + x_{2}^{4} \ln \left( {\frac{{M_{2} }}{{M_{1} }}} \right) \hfill \\ \end{gathered}$$

(23)

where Z₁₁₁₂, Z₁₁₂₂ and Z₁₂₂₂ are model parameters.

Values of model parameters along with standard deviation ($\sigma$) for studied binary mixtures are tabulated in Supplementary Table S7. Standard deviation ($\sigma$) for semi-empirical relations has been plotted in Fig. 8 at 298.15 K.

Fig. 8

Standard deviation for the binary liquid mixtures for different viscosity correlations models at 298.15 K

4 Discussion

Excess molar volume ($V_{m}^{\text{E}}$) values for studied binary liquid mixtures are enlisted in Table 3. Behavior of $V_{m}^{\text{E}}$ is result of contributions from various effects. Disruptions of 1P2P aggregates on addition of amines result in breaking of hydrogen bonds among 1P2P molecules and make $V_{m}^{\text{E}}$ positive. Molecules of the components with nearly equal molar volumes do not fit well with each other, hence, result in positive $V_{m}^{\text{E}}$ values. On the other hand, factors like strong hydrogen bonding, charge-transfer and dipole–dipole interactions among unlike molecules in the mixture result in negative values of $V_{m}^{\text{E}}$. Favorable interstitial accommodation of unlike molecules among each other also results in negative $V_{m}^{\text{E}}$ values.

$V_{m}^{\text{E}}$ for the studied binary mixtures against mole fraction of 1P2P is presented graphically in Fig. 1. A close perusal of Fig. 1 reveals that values of $V_{m}^{\text{E}}$ are negative for binary mixtures of 1P2P with DIPA and DBA while positive for binary mixture of 1P2P with TBA. Positive values of $V_{m}^{\text{E}}$ for binary mixture of 1P2P with TBA are attributed to breaking of hydrogen bond network of 1P2P upon addition of TBA, which is not compensated by weak interactions among unlike molecules. Negative values of $V_{m}^{\text{E}}$ observed for liquid mixtures of 1P2P with DIPA and DBA could be due to hydrogen bond formation between oxygen atom of 1P2P molecules and hydrogen atom of amine molecules and dominance of packing effect rather than dispersive forces between unlike molecules. Dibutylamine molecules being bulkier in size in comparison to diisopropylamine molecules face little difficulty in approaching towards molecules of 1P2P and hence, interactions in binary mixtures of 1P2P with DBA are less in comparison to mixture of 1P2P with DIPA. With increase in the temperature, magnitude of $V_{m}^{\text{E}}$ for binary mixtures of 1P2P with DIPA and DBA become less negative while that of 1P2P with TBA becomes more positive indicating weakening of interactions. This could be due to systematic volume expansion in binary mixtures resulting from increase in thermal energy with temperature.

A close look of Figs. 2 and 3 reveals that $K_{S,m}^{\text{E}}$ and $u^{\text{E}}$ vary in negative and positive manner respectively for binary mixture of 1P2P with DIPA and DBA. Negative values of $K_{S,m}^{\text{E}}$ and positive values of $u^{\text{E}}$ show that packing of molecules in the mixture is more compact than pure components and hence, specific interactions are present in the mixtures. For binary mixture of 1P2P with TBA, $K_{S,m}^{\text{E}}$ and $u^{\text{E}}$ vary in positive and negative manner respectively. Positive values of $K_{S,m}^{\text{E}}$ and negative values of $u^{\text{E}}$ show that binary mixture is more compressible than ideal one and hence, weak interactions are present among unlike molecules in mixture. Thus, behaviour of $K_{S,m}^{\text{E}}$ and $u^{\text{E}}$ for binary mixtures of 1P2P with amines, is in accordance with behaviour of $V_{m}^{\text{E}}$.

Deviation in viscosity ($\Delta \eta$) and excess Gibbs-free energy of activation for viscous flow ($\Delta G^{*{\text{E}}}$) have been evaluated to study the transport behaviour of binary mixtures. It can be seen from Fig. 4 that $\Delta \eta$ vary in negative manner for binary mixtures of 1P2P with DIPA and TBA and sigmoidal manner in case of binary mixture of 1P2P with DBA. In general, binary mixtures exhibiting negative deviation of $V_{m}^{\text{E}}$ show positive deviation for $\Delta \eta$ and vice-versa [24]. This general trend is followed by binary mixtures of 1P2P with TBA and in amine rich region of 1P2P with DBA mixture. Mixtures of 1P2P with DIPA do not follow this general trend. This difference could be due to dominance of factors like molecular size and shape. Calculated values of excess Gibbs free energy of activation for viscous flow ($\Delta G^{*{\text{E}}}$) are recorded in Supplementary Table S1 and presented graphically in Fig. 5 against mole fraction of 1P2P. Positive deviations are obtained for binary mixtures of 1P2P with DIPA and DBA which indicate strong interactions among unlike molecules in these mixtures. In binary mixture of 1P2P with TBA, negative deviations of $\Delta G^{*{\text{E}}}$ are obtained representing weak interactions among components. With increase in the temperature, values of $\Delta G^{*{\text{E}}}$ become less positive in binary mixtures of 1P2P with DIPA and DBA while more negative in mixture of 1P2P with TBA. This could be due to decrease in interactions for studied binary mixtures with temperature.

In addition to this, change in enthalpy ($\Delta H$) and change in entropy ($\Delta S$) of activation for viscous flow have also been calculated and reported in Supplementary Table S1 along with linear regression (r). Following viscosity equation proposed by Eyring [25, 26] was used to study the thermodynamics of viscous flow:

$$\eta = \left( {{{hN} \mathord{\left/ {\vphantom {{hN} V}} \right. \kern-0pt} V}} \right)\exp \left( {{{\Delta G^{{}} } \mathord{\left/ {\vphantom {{\Delta G^{{}} } {RT}}} \right. \kern-0pt} {RT}}} \right)$$

(24)

where symbols $\eta$, h, N and V are used for viscosity, Planck’s constant, Avogadro’s number and molar volume respectively. Equation 24 was combined with the relation,$\Delta G = \Delta H - T\Delta S$, to calculate thermodynamics parameters like change in enthalpy ($\Delta H$) and change in entropy ($\Delta S$) of activation for viscous flow, which give the following relation:

$$R\ln \left( {{{\eta V} \mathord{\left/ {\vphantom {{\eta V} {hN}}} \right. \kern-0pt} {hN}}} \right) = \left( {{{\Delta H} \mathord{\left/ {\vphantom {{\Delta H} T}} \right. \kern-0pt} T}} \right) - \Delta S$$

(25)

Left hand side of Eq. 25 was plotted against 1/T for studied binary mixtures for each mole fraction, x_i. The plot was found to be linear for each x_i. Slope and intercept from the plot give the value of $\Delta H$ and $\Delta S$ respectively, for each x_i. The increase in the value of $\Delta H$ with x₁ indicate that formation of an activated species, necessary for viscous flow, is easier in amine rich region compared to 1P2P rich region. The values of $\Delta S$ are negative in amine rich region and with increase in x₁ becomes positive. This indicates that there is more structuredness in amine rich region during the viscous flow, as a result of the ease in which the activated species forms as compared to 1P2P rich region where values are comparatively large [27].

Binary coefficients of Redlich–Kister polynomial have been calculated using least square method for studied mixtures and are listed in Supplementary Table S2. Jouyban–Acree model has also been used to correlate the density, speed of sound and viscosity with composition and corresponding binary coefficients are presented in Supplementary Table S3. Small values of standard deviation for both Redlich–Kister polynomial and Jouyban–Acree model justifies the good correlation ability of these equations.

Computed values of apparent molar volumes ($V_{\varphi ,i}$) and partial molar volume ($\overline{V}_{m,i}$) for the binary mixtures are reported in Supplementary Tables S4 and S5, respectively. It is clear from these tables that values of $V_{\varphi ,i}$ and $\overline{V}_{m,i}$ for binary mixtures are less than molar volume of pure components for binary mixture of 1P2P with DIPA and DBA. Lower magnitude of $V_{\varphi ,i}$ and $\overline{V}_{m,i}$ for binary mixture of 1P2P + DIPA compare to 1P2P + DBA indicate stronger interactions in former mixture. Strong intermolecular interaction among unlike molecules lead to availability of less space among molecules and hence, is responsible for lower values of $V_{\varphi ,i}$ and $\overline{V}_{m,i}$. In case of binary mixtures of 1P2P with TBA, $V_{\varphi ,i}$ and $\overline{V}_{m,i}$ values for binary mixtures are more compare to molar volume of pure components. Increase in space among molecules due to weak interactions among components could be possible reason for this. With temperature, magnitude of $V_{\varphi ,i}$ and $\overline{V}_{m,i}$ for studied binary mixtures is found to increase. This indicates weakening of interactions in the studied binary mixtures with temperature.

Excess partial molar volume ($\overline{V}_{m,i}^{\text{E}}$) values for studied binary mixtures have been evaluated using the values of $\overline{V}_{m,i}$ and presented in Supplementary Table S6. Values of $\overline{V}_{m,i}^{\text{E}}$ are plotted against mole fraction of 1P2P in Fig. 7. Values of ($\overline{V}_{m,i}^{\text{E}}$) are found negative for binary mixtures of 1P2P with DIPA and DBA indicating strong interactions among unlike molecules in these mixtures. Values for binary mixture of 1P2P + TBA are found to be positive indicating weak interactions in this mixture. With increase in the temperature, values of ($\overline{V}_{m,i}^{\text{E}}$) for binary mixtures of 1P2P with DIPA and DBA become less negative while for mixture of 1P2P with TBA become more positive. These outcomes indicate weakening of interaction with temperature in studied binary mixtures.

Standard deviation ($\sigma$) of various viscosity models have been evaluated to test their correlation ability. It is clear from Fig. 8 that with increase in the number of adjustable parameters, predicting ability of viscosity model increases. Grunberg–Nissan and Katti–Chaudhri relations are found better in predicting the viscosity of binary mixtures among one parameter models. Sign of parameter, $G_{12}$ in Grunberg–Nissan model gives estimation of type of interaction among the unlike components in binary mixtures [24]. Mixtures exhibiting strong interactions show positive sign of $G_{12}$ while negative sign of $G_{12}$ is possessed by mixtures having weak interactions. Negative sign obtained for binary mixture of 1P2P with TBA and positive sign for binary mixtures of 1P2P with DIPA and DBA confirm the findings obtained from above calculated parameters.

5 Spectral Studies

FTIR spectra for binary mixtures of 1P2P with DIPA, DBA and TBA have been presented in Figs. 9, 10 and 11 respectively at mole fraction x₁ = 0.0, 0.2, 0.5, 0.8 and 1.0. Molecules having hydrogen bonded –OH group possess characteristic peak around 3400 cm⁻¹. Association effects along with hydrogen bonding capability among the molecules with concentration result in change in this characteristic peak. A close perusal of Figs. 9, 10 and 11 reveals that intensity of peak for hydrogen bond in 1P2P diminishes with increase in the concentration of amine. This should lead to expansion in volume of the mixture. In binary mixtures of 1P2P with DIPA and DBA, thermodynamic parameters show that molecules in mixture are in close proximity compare to pure liquid. Therefore, strong intermolecular interaction or better geometrical accommodation must be present in binary mixtures. In case of binary mixtures of 1P2P with TBA, thermodynamic parameters show weak interactions among unlike molecules. This could be due to poor geometrical accommodation of molecules in the mixture.

Fig. 9

FTIR spectra of binary mixture of 1-propoxy-2-propanol (x₁) with diisopropylamine at different mole fraction and at room temperature

Fig. 10

FTIR spectra of binary mixture of 1-propoxy-2-propanol (x₁) with dibutylamine at different mole fraction and at room temperature

Fig. 11

FTIR spectra of binary mixture of 1-propoxy-2-propanol (x₁) with tributylamine at different mole fraction and at room temperature

6 Conclusions

Density ($\rho$), speed of sound (u) and viscosity ($\eta$) for binary mixtures of 1P2P with DIPA, DBA and TBA have been measured for their thermodynamic studies. Interpretation of thermodynamic parameters reveals strong interactions among binary mixtures of 1P2P with DIPA and DBA while weak interactions in mixture of 1P2P with TBA. Interactions have been found to weaken with increase in the temperature. Redlich–Kister polynomial and Jouyban–Acree model were found satisfactory in their correlation ability. Semi-empirical relations for viscosity were used for estimation of viscosity for studied binary mixtures. Results obtained from FTIR studies were found to compliment the outcomes from thermodynamic parameters.