1 Introduction

Chemical reactions in solution are decisively influenced by the surrounding media in the diffusion-controlled regime [1] or in the fluctuation-controlled regime [2, 3]. In the latter case, the viscosity-dependent suppression of ultrafast reactions in the excited states, known as Kramers turnover [4], arises as the retardation of solvent fluctuation adapts to solute reactions in the excited state where the solute–solvent system undergoes a breakdown of chemical equilibrium. Even in the ground states this anomaly can be observed when a reaction proceeds in quite viscous solvents under sufficiently high pressure. Our experimental studies have focused on the Z/E thermally backward isomerization kinetics of azobenzenes and benzylideneailines in solution under a wide range of pressure (up to 1 GPa), where the suppression of isomerization reaction rates is invoked by strong solute–solvent friction [5, 6].

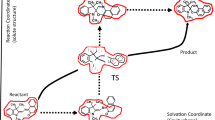
From theoretical viewpoints, condensed phase reaction rate theories have a long history, starting from the landmark Transition State Theory (TST) which supposes that (1) local equilibrium between reactant and transition state (TS) and (2) the point of no return assumption are satisfied. The regime of TST applicability and its extended theories formulated as an activated barrier crossing process or others have been extensively investigated [7,8,9,10]. The solute–solvent coupling scheme for solution reactions has been formulated using two models: the ‘one’ and ‘two’ dimensional ones where the solute coordinate (fast chemical reaction) and the solvent coordinate (slow fluctuation) are coupled synchronously or asynchronously, respectively (Fig. 1). First, the Grote–Hynes (GH) model [11, 12], based on an activated barrier surmounting process governed by the generalized Langevin equation, can be interpreted within the TST framework as a system bilaterally coupled with the surrounding heat bath [13,14,15]. That means that the GH model can be renormalized into the one-dimensional model where the solute and solvent coordinates are coupled synchronously. On the other hand, the two-dimensional model was studied by Agmon and Hopfield [16], which is based on a diffusion–reaction differential equation with a sink term. The model was reformulated by Sumi and Marcus (SM) [17, 18] and Basilevsky and Weinberg (BW) [19]. The models originated from the multidimensional case of GH theory [20, 21] and can be interpreted as a limiting case when the anisotropy between chemical reaction and solvent fluctuation is sufficiently large [22]. There have been arguments over the applicability scope of one- or two-dimensional models in various solution reactions. For example, the GH model combined with the mode coupling theory (MCT) partly reproduced the viscosity dependence of the isomerization rate in a high friction region [23], while the fractional viscosity dependence of the rate failed to be reproduced without the two-dimensionality of ballistic solute reaction and diffusive solvent fluctuation [24,25,26].

Fig. 1
figure 1

Schematic explanation of the reaction (solute–solvent coordinate coupling on a Gibbs energy surface) for two limiting cases. Left panel: equilibrium mechanism. The reaction proceeds while exactly following the intrinsic reaction coordinate through the transition state. Right panel: Non-equilibrium mechanism. The reaction proceeds with solvent pre-organized fluctuation, which is a rate-determining step

Full size image

Qualitatively, features of the Free Energy Surface (FES) play a decisive role in the reaction kinetics. Many computational approaches to evaluating the Gibbs (free) energy have been developed, including thermodynamic integration (TI), free energy perturbation (FEP), Benett’s acceptance ratio (BAR) among others [27]. These approaches can realize the FES prediction at chemical accuracy (within a few kJ·mol−1) but suffer from an explosive computational burden because they have to consider many intermediate states between the reaction starting and end points. To circumvent the huge computational cost in the free energy estimation, a series of enhanced sampling techniques have been developed to mitigate the computational burden [28, 29]. Metadynamics, which herein we employ, is one of the representative methods among the enhanced FES sampling techniques, which can aggressively accelerate the occurrence of rare events by accumulating Gaussian functions (biased potential) on deep basins to surmount the deep FES barrier along Collective Variables (CVs) navigating the reaction [30, 31]. Its original form evolved into several more sophisticated variants: the well-tempered [32], parallel-tempering [33], and bias-exchange [34]. The performance and accuracy of metadynamics have been examined in detail [35, 36].

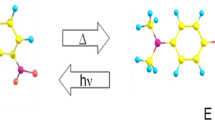
In the present study, the Z/E isomerization kinetics of 4-dimethylamine-4′-nitroazobenzene (DNAB) and three benzylideneailines (N-[4-dimethylamino-benzylidene]-4′-nitroaniline (DBNA), N-[4-dimethylamino-benzylidene]-4′-ethoxyaniline (DBEA), N-[4-(dimethylamino)benzylidene]-4′-bromoamine] (DBBA)), as shown in Fig. 2, were computationally studied by using molecular dynamics (MD) simulations and comparison with the results obtained by the SM and BW models, essentially within the two-dimensional framework.

Fig. 2
figure 2

Nitroazobenzene (DNAB) and benzylideneanilines (DBNA, DBEA, DBBA) examined in this study

Full size image

2 Experimental Insights

In our experimental studies, the Z/E isomerization rate constants of azobenzenes have been measured in non-viscous solvents [37, 38] and in the viscous solvents glycerol triacetate (GTA) and 2-methyl-2,4-pentanediol (MPD) [11, 12]. The corresponding rate constants of benzylideneanilies were also reported [5, 39,40,41]. All of the isomerization rate constants of azobenzenes and benzylideneanilines range within micro- to miliseconds and their behavior is rigorously explained within the TST framework. As high pressure is imposed on the system in viscous solvents, the isothermal rate constant plot shows Kramers turnover. The Z/E isomerization mechanism has been discussed based on switching characteristics that depend on the solvent, rotation or inversion, as shown in Fig. 3. The sign of the activation volumes calculated from the pressure dependence of the rate constants is used to judge the mechanism, positive (rotation) and negative (inversion). Excluding DNAB, all of the compounds undergo the inversion mechanism, where the twist angle (ϕ) around the central (N=N) or (C=N) double bond remains almost unchanged and then the bond angle (θ) gradually changes as was observed for (Z)-azobenzene [37]. Even for DNAB, the isomerization proceeds with the inversion mechanism in non-polar solvents but the mechanism is altered in polar solvents into the rotation mechanism where the heavily intramolecular-polarized TS structure is stabilized by the polar environment and the twist angle (ϕ) gradually changes during the isomerization (electronic contraction) [38, 42]. The inversion mechanism of the C=N double bond for the model compound benzenamines was quantum chemically studied in detail [43], which supports the inversion pathway.

Fig. 3
figure 3

Z/E isomerization mechanism: rotation, inversion (perpendicular), and inversion (planar)

Full size image

3 Computational Procedures

The two independent schemes (the equilibrium and the non-equilibrium schemes explained in the following Sect. 4.1) were adopted to computationally estimate Ccoupled, the coupling magnitude of the solute and solvent coordinates, defined also in the following Sect. 4.1.

First, in the equilibrium scheme, MD simulations were carried out using Amber12 [44]. The TIP3P force field was used for water and the generalized AMBER force field (GAFF) [45] for other molecules, respectively. GAFF for the molecules were constructed using the Antechamber utility [46] and the Restrained Electrostatic Potential (RESP) charges were assigned to the molecules computed at the B3LYP/6-31G(d) level using Gaussian 09 [47]. Metadynamics FES calculations were carried out with a well-tempered scheme using the Plumed 2.2 program [48]. Finally, the solute–solvent coupling magnitudes Ccoupled for the respective solution systems were evaluated by the FES gap between the solute and the solution systems at the reactant and at the TS, respectively.

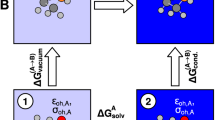
Second, all of the non-equilibrium scheme calculations were done using an in-house shell script. In the scheme, the whole calculations were further decomposed into two procedures for the homogeneous and the heterogeneous systems, respectively. In the heterogeneous systems, as explained in Fig. 4, the solvent cavities were created by extraction of the solute molecule from the trajectory snapshot of NVT MD simulations. The docking of the solvent cavities with the corresponding solute molecule was carried out using the Megadock 4.0 GPU version [49]. The docked droplets were immersed in a solvation box and equilibrated by NVT MD simulations. The solvation Gibbs energies were evaluated by the Energy Representation (ER) method [50] implemented in ERMOD 0.3.2 software [51]. The parameter Ccoupled for the respective solution systems were constructed from the solute Gibbs energies using QM harmonic vibrational frequency calculations and the solvation above Gibbs energies.

Fig. 4
figure 4

Flowchart of non-equilibrium solvation energy calculations: (1) Dock geometrically fixed solute molecule into solvent cavity (using MEGADOCK); (2) immerse the geometrically fixed solvation droplet into the solvent box and equilibrate the whole system (using AMBER); (3) calculate the non-equilibrium solvation energy and the Gibbs energy (using ERMOD)

Full size image

Alternatively, the umbrella sampling simulations with 100 ns NVT-MD duration were carried out to evaluate the FES for DNAB in comparison with the metadynamics FES, as shown in Table 1.

Table 1 Computed solute–solvent coupling magnitude Ccoupled of DNAB by means of the equilibrium scheme
Full size table

The comprehensive details of the computations are described in the Supporting Information.

4 Results and Discussion

4.1 Two Schemes to Evaluate the Solute–Solvent Coupling Magnitude: The Equilibrium and Non-equilibrium Schemes

The two-dimensional FES are described by two parameters (x, y), which represent solvent and solute coordinates, respectively, in line with the pilot solute algorithm reported by Dhaliwal et al. [52]. (x1, y1) and (x2, y2) denote the equilibrated system at the reactant (Z-form) and at the TS, respectively.

The Gibbs energy of whole equilibrated system at (x1, y1) and (x2, y2) can be decomposed into contributions from solute, solvent and solute–solvent interactions (solvation), as expressed in Eqs. 1 and 2, respectively:

$$ U_{\text{all}} (x_{1} ,y_{1} ) = U_{\rm solute} (y_{1} ) + U_{\rm solvent} (x_{1} ) + U_{{\rm solute - {\text{solvent}}}} (x_{1} ,y_{1} ) $$
(1)
$$ U_{\text{all}} (x_{2} ,y_{2} ) = U_{\rm solute} (y_{2} ) + U_{\rm solvent} (x_{2} ) + U_{{\rm solute - {\text{solvent}}}} (x_{2} ,y_{2} ) $$
(2)

Daliwal et al. successfully constructed the two dimensional potential energy surfaces along the solvation and the solute coordinates for DBBA by means of the solute exchange strategy [52]. They subsequently computed the corresponding two-dimensional FESs using the simplified TI scheme where the solvent molecules were approximately expressed as monoatomic particles.

The present study treats a whole system consistently in a realistic way, where the solvent molecules are explicitly dealt with as real molecules, instead of using the monoatomic approximation. Ccoupled, the coupling magnitude of solute and solvent coordinates, is defined by the ratio of the Gibbs energy variation from at (x2, y1) to at (x2, y2) over the isomerization activation Gibbs energy, as expressed by Eq. 3, and schematically explained in Fig. 5. The numerator in Eq. 1 corresponds to the Gibbs energy variation along the solvent fluctuation coordinate between (x1, y1) and (x2, y1), before crossing the Gibbs energy barrier from the point (x2, y1) to the TS (x2, y2):

Fig. 5
figure 5

Schematic explanation of the solute–solvent coupling magnitude Ccoupled. The denominator ∆U is the overall Gibbs energy gap between at the reactant and product at the TS, which corresponds to the activation Gibbs energy of TST in a solution reaction. The numerator ∆Usolvent is the Gibbs energy gap between at the reactant and product in the equilibrated solvation state and at the reactant in the pre-organized solution state into TS. That is, ∆Usolvent corresponds to the pure solvation Gibbs energy variation between the reactant and product at the TS

Full size image
$$ C_{\text{coupled}} \equiv \frac{{U_{\text{all}} (x_{2} ,y_{1} ) - U_{\text{all}} (x_{1} ,y_{1} )}}{{U_{\text{all}} (x_{2} ,y_{2} ) - U_{\text{all}} (x_{1} ,y_{1} )}} $$
(3)

Ccoupled can be qualitatively correlated with the parameter C2 obtained by the BW model [19] and the parameter γ by the SM model [53], respectively.

BW-C2 is defined by Eq. 4, where the numerator ε denotes the effective Gibbs energy variation, purely derived from solvent fluctuations, and is evaluated by numerically solving the reaction–diffusion equation with the sink term at the anisotropic viscosity limit (the BW-equation) in an iteratively optimized way [19]. Within the BW model, the solvent fluctuation is a rate-determining step and drives the solute into the hindered (non-equilibrium solvated) environment along the x-axis (solvent axis) to surmount the Gibbs energy barrier. The solvation-dependent micro rate constant k(x) (x is a solvation coordinate) contributes to the total reaction rate constant in proportion to a Boltzmann distribution in the x-coordinate.

$$ {\text{BW-}}C_{ 2} \equiv \frac{\varepsilon }{{U_{\text{all}} (x_{2} ,y_{2} ) - U_{\text{all}} (x_{1} ,y_{1} )}} $$
(4)

In the present study, the terms in Eq. 3 are approximately evaluated by the two schemes as follows.

4.1.1 Equilibrium Scheme: FES Calculations Using Metadynamics

This approach approximates the solute–solvent interaction term Usolute–solvent (x2, y1) with Usolute–solvent (x2, y2):

$$ C_{\text{coupled}} \simeq 1 - \frac{{U_{\text{solute}} (y_{2} ) - U_{\text{solute}} (y_{1} )}}{{U_{\text{all}} (x_{2} ,y_{2} ) - U_{\text{all}} (x_{1} ,y_{1} )}} $$
(5)

This ‘diagonal’ approximation allows the standard Gibbs energy sampling techniques to be directly applied to evaluate all the terms in Eq. 5. Uall (x1, y1) and Uall (x2, y2) in the denominator were evaluated by using metadynamics at an equilibrated state, (x1, y1) and (x2, y2), respectively. The solute contributions Usolute(y1) and Usolute(y2) in the numerator are also obtained by solute-only metadynamics using the NVT ensemble where the box size is large enough (in a 50 × 50 × 50 Å cubic box) to diminish the solute–solute interactions.

4.1.2 Non-equilibrium Scheme: Solvation Gibbs Energy Calculation for a Frozen Solvation Droplet

This approach introduces an approximation to the solvent term by equating Usolvent(x1) with Usolvent(x2):

$$ C_{{\text{coupled}}} \simeq \frac{{U_{{\rm solute - \text{solvent}}} (x_{2} ,y_{1} ) - U_{{\text{solute} - \text{solvent}}} (x_{1} ,y_{1} )}}{{\{ U_{{\text{solute}}} (x_{2} ,y_{2} ) + U_{{\text{solute} - \text{solvent}}} (x_{2} ,y_{2} )\} - \{ U_{{\text{solute}}} (x_{1} ,y_{1} ) + U_{{\text{solute} - \text{solvent}}} (x_{1} ,y_{1} )\} }} $$
(6)

In Eq. 6, the solvation Gibbs energies Usolute–solvent (x2, y1) at (x2, y1) and Usolute–solvent (x2, y2) at (x2, y2) in the numerator are calculated using the ER method, respectively. That is, the heterogeneous Usolute–solvent (x2, y1) and the homogeneous Usolute–solvent (x2, y2) are computed with the solute geometry at y1 (y2) fixed in the solvent coordinate at x2, which are approximately expressed by the finite size of the solvation droplet immersed in the solvent box, respectively.

Finally, the solute Gibbs energies Usolute (y1) and Usolute (y2) in the denominator are estimated independently by the QM electronic energies combined with harmonic vibrational calculations.

4.2 Equilibrium Approach

The computed Ccoupled for DNAB and DBNA, DBEA, DBBA are shown in Tables 1 and 2, respectively. In the case of the Z/E isomerization process of azobenzene and benzylideneanilines, the coupling between solute and solvent is expected to be weak because drastic change in the solute coordinate, i.e., bond creation/fission, doesn’t occur with the isomerization.

Table 2 Computed solute–solvent coupling magnitude Ccoupled of DBNA, DBEA, DBBA by means of the equilibrium scheme
Full size table

Ccoupled of DNAB exhibits good coincidence between those obtained by umbrella sampling and metadynamics. The agreement indicates the excellent performance of metadynamics, which requires far less computational burden than umbrella sampling. The magnitude of Ccoupled in TIP3P is DNAB > DBEA > DBBA in descending order, which indicates weaker interaction between water and the replaced group in the aniline ring (NO2 > COOEt > Br). Ccoupled and the coupling parameters of the two-dimensional models (BW-C2, Sumi-γ) show opposite relative magnitudes for the two solvents {0.25 (0.42, 0.76) in MPD and 0.39 (0.18, 0.27)} in GTA, respectively. The discrepancies between Ccoupled and (BW-C2, Sumi-γ) in MPD and in GTA were also found for DBNA, DBEA, DBBA.

The qualitative disagreements in Table 2 can be traced back to the two causes. The primary one lies in the inherent error of the solvation energy calculation approximated by Eq. 5, which lacks consideration of the ‘non-equilibrium solvation effect’ between solute and surrounding solvent interactions. The estimations using Eq. 5 correspond to the equilibrated solvation Gibbs energy, not the non-equilibrated one which correctly includes the gap between the activation barrier at (x2, y2) and (x2, y1). That is, the pre-organized solvation structure with the solute coordinate fixed at the reactant (x2, y1) has to be considered in order to compute the non-equilibrium solvation energy at (x2, y1). The second cause lies in the isomerization mechanism falsely predicted by metadynamics. The predicted isomerization undergoes rotation around the N = N bond as shown in Fig. 3, not the inversion which is supported experimentally and computationally at the ab initio QM level. This failure is derived from the GAFF force field parametrization. Highly accurate quantum chemical calculations are required to correctly locate the Z/E reaction path, as shown in the next Sect. 4.3.

4.3 Non-equilibrium Approach

Table 3 shows the components of the potential energy and Gibbs energy of DNAB in TIP3P water. The coupling magnitude Ccoupled of DNAB and DBNA, DBEA, DBBA for the respective solvents are shown in Table 4.

Table 3 Potential energy (E) and Gibbs energy (G) components of reactant and at the transition state of DNAB in TIP3P water
Full size table
Table 4 Computed solute–solvent coupling magnitude Ccoupled of DBNA, DBEA, DBBA by means of the non-equilibrium scheme
Full size table

In contrast to the equilibrium approach, the DFT-optimized structures at the TS were correctly located as an inversion intermediate with the bond angle (θ) of nearly 180°. The non-equilibrium solvation energy can be therefore correctly estimated by the frozen solvation model that adequately treats the asynchronous solvation states.

In Table 3, the non-equilibrium effect between the frozen solvation droplet and the outer region is clearly shown in the case of reactant/TS (the solute with the reactant geometry docked with the TS-equilibrated cavity which is immersed in the outer solvent region). The corresponding positive solvation Gibbs energy (12.26 kJ·mol−1) means that the system is destabilized and reflects the mismatch between the inner (droplet) and outer region.

In Table 4, the relative magnitudes of Ccoupled in MPD and in GTA were corrected for all of the molecules, in contrast to the metadynamics results mentioned in the previous section. The computed Ccoupled were in qualitative agreement with the BW-C2 and Sumi-γ for the all solutes in the respective solvents but absolute agreements were not attained. The present ad-hoc approach, where the electronic energy is computed by DFT and the solvation energy is computed by the classical force field, is not expected to give quantitative agreement between the present results and BW-C2 and Sumi-γ.

The limitation of this approach comes from the inherent error in the estimation of the non-diagonal Usolute–solvent (x2, y1), where the solvent state was approximated by a finite solvation droplet, not by an infinite solvation state at (x2, y1). This error, however, can be expected to smoothly diminish as the solvation droplet size becomes sufficiently large. In the present scheme, the solvation droplet is as large as 30 Å in diameter and the error can be safely ignored.

Conversely, the limitations will lie also in the BW and the SM models where an idealized simple harmonic FES, not a quantitatively accurate FES, is assumed for the numerical evaluations of BW-C2 and Sumi-γ, respectively. Therefore, the pursuit of absolute agreement of the coupling parameters does not seem meaningful between the present study and the two-dimensional models.

5 Conclusions

Our past experimental studies revealed that the Z/E isomerization rate constants of nitroazobenzene and benzylideneanilines show the Kramers turnover in viscous solvents under high pressure, which indicates that the breakdown of the solute–solvent chemical equilibrium arises in the reactions. In the present study aimed to elucidate the non-equilibrium solvation effect, the solute–solvent coupling magnitude was computationally evaluated. The coupling key parameters (Ccoupled), the ratio of solvation Gibbs energy contribution over the corresponding activation Gibbs energy, were estimated by using the two MD-based schemes: (1) the equilibrium scheme (2) the non-equilibrium scheme.

In scheme (1), efficient as well as quantitative metadynamics FES calculations were performed along the two CVs (the dihedral angle between the two aryl rings). The solvation Gibbs energies were evaluated as pure solvation contributions by subtraction of the solute Gibbs energy from the total Gibbs energy. The Gibbs energy contributions from the solute and the solvent coordinate were evaluated in vacuo and in solution, respectively. In scheme (2), the pure solvation Gibbs energies, decoupled contributions to the total Gibbs energies, were calculated independently using the frozen solvation droplet models immersed in an outer solvent box by means of the Energy Representation solvation theory.

The computed Ccoupled by means of the two schemes were compared with the corresponding parameters BW-C2 and Sumi-γ obtained by the BW and the SM models, respectively, which are the solute–solvent two-dimensional models based on the Fokker–Planck equation with a sink term using the hypothetical harmonic FES. The Ccoupled obtained by the scheme (2), using a frozen solvation droplet, showed qualitative agreements with BW-C2 and Sumi-γ, while those by the scheme (1) failed to reach qualitative agreement. This is because the scheme (2) explicitly considers the ‘pre-organized’ solvation droplet that consists of a solute at the reactant geometry immersed in the pre-organized solvent cavity fitted with the solute at the transition state geometry, while the scheme (1) did not consider such a type of non-equilibrium solvation effect.

Final remarks on future prospects. A straightforward extension of the MD-based approach presented here in a fully QM way is blocked by the explosion of computational burden. The continuing efforts to overcome this problem are in progress and will be reported in future.