Tight approximation bounds for the LPT rule applied to identical parallel machines with small jobs

Abstract

We consider a scheduling problem with m identical machines in parallel and the minimum makespan objective. The Longest Processing Time first (LPT) rule is a well-known approximation algorithm for this problem. Although its worst-case approximation ratio has been determined theoretically, it is known that the worst-case approximation ratio of LPT can be smaller with instances of smaller processing times. We assume that each job’s processing time is not longer than 1/k times the optimal makespan for a given integer k. We derive the worst-case approximation ratio of the LPT algorithm in terms of parameters k and m. For that purpose, we divide the whole set of instances of the original problem into classes defined by different values of parameters k and m. On each of those classes, we derive an exact upper bound on the worst-case performance ratio as a function of parameters k and m. We also show that there exist classes of instances for which our worst-case approximation ratio is better than previous bounds. Our bound can complement previous research in terms of the performance analysis of LPT.

1 Introduction

We consider the problem of scheduling n independent jobs on m identical machines in parallel with the minimum makespan objective. This problem is denoted by $P \mid \mid C_{\max }$ in the three-field notation developed by Graham et al. (1979). Since it is a well-known NP-hard problem (see Garey and Johnson 1978), several approximation algorithms have been proposed.

Definition 1

(Williamson and Shmoys 2011) A $\rho$-approximation algorithm for an optimization problem is an algorithm that for all instances of the problem produces a solution whose value is within a factor of $\rho$ of the value of an optimal solution.

Note that $\rho < 1$ for maximization problems and $\rho > 1$ for minimization problems. For example, a 2-approximation algorithm implies that the corresponding problem is a minimization problem and the objective value of the solution generated by the algorithm is at most twice the optimal objective value. In this paper, we refer to $\rho$ as an approximation bound (Ab, for short). Suppose there exists a problem instance in which the approximation bound is met. In that case, the approximation bound is called tight and the problem instance is referred to as a tight example. We denote tight approximation bound as Tab and multiple approximation bounds as Abs (Tabs for multiple tight approximation bounds).

Among those algorithms, the Longest Processing Time (LPT) rule was introduced by Graham (1969). It is an $O(n\log n)$ time algorithm that sorts jobs in decreasing order of their processing times and assigns one job at a time to the machine that has the lowest load so far. The Ab gained by LPT is $(4/3 - 1/3m)$, and this bound is tight (Graham 1969). Although the Tab of LPT is calculated, some researchers argued that this result does not explain the holistic performance of LPT. Several approaches have therefore been proposed for evaluating the performance of LPT. For example, Frenk and Rinnooy Kan (1987) claimed that under a given mild condition on the processing time distribution, LPT is asymptotically optimal. Moreover, Ibarra and Kim (1977) considered a bound on $\omega \doteq p_{\max } / p_{\min }$, which is the ratio of the maximum processing time, to the minimum processing time to strengthen the Ab. They obtained an Ab of $1+2(m-1)/n$ when the number of jobs n satisfies the condition $n \ge 2(m-1)\omega$. Thus, with a larger n LPT gets closer to the optimum.

Several more focused analyses of LPT have been done. Research related to the direction we are following has appeared in the literature. Let the machine determining the makespan of the LPT-schedule be referred to as a critical machine. Coffman and Sethi (1976) proved that when there are N jobs on the critical machine, the Tab is $(N+1)/N - 1/Nm$ for the case $N \ge 3$. Coffman and Sethi (1976) assumed that LPT provides an optimal schedule when $N = 2$, but Chen (1993) corrected the flaw and derived the tight bound of $4/3 - 1/3(m-1)$ for the case $N = 2$. Blocher and Sevastyanov (2015) considered a ‘truncated’ job set that does not contain jobs assigned to machines after the job that determines the makespan of the LPT schedule. They improved the Coffman–Sethi bound using the maximum number of jobs assigned to a machine in the LPT-schedule for the truncated job set. Della Croce and Scatamacchia (2020) introduced a parameter $N''$ as the maximum number of jobs on a non-critical machine in the LPT-schedule for the truncated job set. For the case when $m \ge N'' + 2$ they proved the Ab $(N'' +1)/N''- 1/N''(m-1)$ for LPT. A detailed explanation and a comparison of those Abs is presented in Sect. 4.

Moreover, there are some other approximation algorithms for $P \mid \mid C_{\max }$. For example, Della Croce et al. (2019) applied an extended version of LPT to the $P2 \mid \mid C_{\max }$ problem, and Della Croce and Scatamacchia (2020) used a modified LPT to improve the bound of Graham (1969). Coffman et al. (1978), Lee and Massey (1988), and Gupta and Ruiz-Torres (2001) used bin-packing-based approximation algorithms. Alon et al. (1998), Jansen (2010), and Jansen et al. (2017) used Polynomial Time Approximation Schemes (PTASs). Since we focus on LPT, we do not review these papers in detail.

It is proven that the difference between the LPT makespan and the optimal makespan is no greater than $p_{\max }$ (Graham 1969; Coffman and Sethi 1976). Thus, the smaller the processing times of the jobs are, the better the performance of LPT is. However, the meaning of ‘small’ processing time needs to be defined clearly for all problem instances. Thus, in this paper, we measure the size of the processing times relative to the optimal makespan. For instance, in the tight example of LPT by Graham (1969), the ratios of the processing times to the optimal makespan lie in the range $\left[ 1/3, \ 2/3\right)$ for all jobs, which are relatively large. In our paper, we consider the problem where the processing times of the jobs are less than or equal to 1/k times the optimal makespan for an integer $k \in \{1, 2, \ldots \}$.

Our contribution is as follows. Given an instance I, let $C^*_{\max }[I]$ denote the optimal makespan and $C_{\max }[I]$ denote the makespan obtained with LPT. Furthermore, let $p_{\max }[I] \doteq \max _j p_j$, $K[I] \doteq C^*_{\max }[I]/p_{\max }[I]$, and let ${\mathcal {I}}_m$ denote the set of instances of the m-machine problem $P\mid \mid C_{\max }$. For any given integral $k \ge 1$ and integral $m \ge 2$, we define the class of instances ${\mathcal {I}}_{k,m} \doteq \{ I \in {\mathcal {I}}_m \mid K[I] \ge k \}$. In this paper we investigate the theoretical accuracy of solutions generated using LPT, in terms of parameters k and m. Namely, for any integral values $k \ge 2, m \ge 2$ of parameters k and m, we have found the Tab F(k, m) of LPT when applied to the class of instances ${\mathcal {I}}_{k,m}$. Note that Tab F(1, m) was established by Graham (1969).

Our Tab differs for the cases $m < k$, $k \le m \le k(k+1)/2$ and $m > k(k+1)/2$. For the case $m<k$, we consider two subcases depending on the fulfillment of condition $(k\mod m) \le \left( \left\lfloor {k}/{m}\right\rfloor m + 1\right) / \left( \left\lfloor {k}/{m}\right\rfloor + 1\right)$. For convenience, we consider the case $k = 2$ separately. For each case, we derive the Tab (which is supported by demonstrating a proper worst-case instance). Table 1 summarizes the results for all possible cases and provides references to the sources where those results are obtained. Furthermore, we show that there exist classes of instances with specific parameters where our Tab is better (smaller) than any previous bounds.

Table 1 Tab F(k, m) on different cases

Table 1 shows Tab found for different relations between m and k, including the case $k = 1$ (without any processing time restrictions) analyzed by Graham (1969). Figure 1 shows graphical representations of our Tab. The smaller the processing times are, the lower the Tab is. When $k \ge 3$, the Tab is divided into three different shapes for the range of m. When $2 \le m < k$, the shape of Tab differs depending on the remainder of k divided by m. It approaches to the Tab of $1+(k-1)/k(k+1)$ as m increases. When $k \le m \le k(k+1)/2$, the Tab remains constant. Finally, when $m \ge k(k+1)/2 + 1$ the Tab increases as a hyperbola asymptotically approaching (with $m \rightarrow \infty$) to $1 + 1/(k + 2)$. Moreover, the structures of the tight examples of our Ab show a qualitative change. When $m \le k(k+1)/2$, the total number of jobs is $mk+1$ and $k+1$ jobs are assigned to a critical machine while k jobs are assigned to every other machine. On the other hand, when $m \ge k(k+1)/2 + 1$, the total number of jobs is $m(k+1)+1$ and $k+2$ jobs are assigned to a critical machine while $k+1$ jobs are assigned to every other machine. This phenomenon will be shown through tight examples in Sect. 3.

For each fixed k, the Tab changes smoothly in m, in the sense that at each boundary point of parameter m (namely, $m = k$ and $m = k(k + 1)/2$) both formulas determining the Tab in the neighboring areas have identical values (as can be easily checked).

Fig. 1

Graphical representations of Tab F(k, m)

In Sect. 2, we introduce some necessary notations, discuss essential concepts and present some preliminary results. Sect. 3 presents Tab for different conditions of k and m. Section 4 compares our Tab with that of previous studies. Concluding remarks along with possible extensions are presented in Sect. 5.

2 Preliminaries

In this section, we introduce notations and present some preliminary results that will be used in subsequent sections.

J	The set of jobs $\doteq \{1, \ldots , n\}$
M	The set of machines $\doteq \{1, \ldots , m\}$
$p_j$	The processing time of job j for $j\in J$
$\sigma ^*$	An optimal schedule with the minimum makespan
$\sigma$	A schedule generated by LPT
i(j)	The machine $i \in M$ where job $j \in J$ is assigned by LPT
$S_i^*$	The set of jobs scheduled on machine i in schedule
	$\sigma ^*$ for $i\in M$
$C_{\max }(\sigma ')$	The makespan of an arbitrary schedule $\sigma '$
u(i, t)	The job on machine i in the t-th position in schedule $\sigma$
	for $i \in M$ and $t \in \{1, 2, \ldots \}$

We first define LPT in a more precise way. In what follows we assume that jobs are indexed in a non-increasing order of their processing times: $p_1 \ge p_2 \ge \ldots \ge p_n$. Each job is assigned to the machine among those having the lowest load so far and when there is a tie, the machine with the minimum index is selected. These two procedures directly imply the uniqueness of schedule $\sigma$. When jobs are scheduled one after another according to LPT, we may want to consider in our analysis a partial schedule of the LPT schedule right after job j has been scheduled. Thus, we define $S_i^j$ as the set of jobs scheduled on machine i right after job j has been scheduled by LPT for specific $i\in M$ and $j\in J$. By definition, $S^j_{i(j)} = S^{j-1}_{i(j)} \cup \{j\}$, and $S^j_{i} = S^{j-1}_i$ for all $i \ne i(j).$ We define the function $p(J') \doteq \sum _{j \in J'} p_j$ for $J' \subseteq J$.

The optimal makespan $C_{\max }(\sigma ^*)$ and the makespan $C_{\max }(\sigma )$ of the schedule generated by LPT will be also denoted as (for short) $C^*_{\max }$ and $C_{\max }$, respectively. Using the definition, we denote our problem as $P \mid p_j \le \frac{1}{k}C^*_{\max } \mid C_{\max }$. Moreover, by the definition, we have: $C^*_{\max } = \max _{i\in M} \left\{ p(S_i^*) \right\}$ and $C_{\max } = \max _{i\in M} \left\{ p(S_i^n) \right\}$. The following Proposition is a result by Chen (1993), which describes a particular characteristic of the LPT schedule.

Proposition 1

(Chen 1993) Let $h_i \doteq |S^n_i|$. Then for any $t = 1,\ldots ,h_i$ and $i \in M$, we have:

$$\begin{aligned} p_{u(i,t)} \le C^*_{\max }/t \end{aligned}$$

Next, we define the inequality that will be frequently used concerning the optimal makespan and the total processing time of jobs.

$$\begin{aligned} \sum _{j \in J} p_j \le m C_{\max }^*. \end{aligned}$$

(1)

In the procedures used in the proofs for our Ab, we often use a classical argument leading to a contradiction (an argument first used by Graham 1969). The following is a typical argument that we use. Suppose we want to show that an Ab on LPT for a makespan minimization problem is less than or equal to a certain constant $\rho < \infty$. To do so, we assume that the Ab is not correct and that there exists at least one instance for which the Ab by LPT is strictly larger than $\rho$. We refer to such an instance as a counterexample. Among all possible counterexamples, we consider a counterexample with a minimum number of jobs and refer to it as a minimum counterexample. Any job placed after the makespan determining job could be removed without changing the makespan. Thus, in a minimum counterexample, the last job always determines the makespan. We state, when using this approach in our proofs in subsequent sections, that ‘there exists a minimum counterexample.’

Theorem 1 and Corollary 1 represent the key characteristics of our problem setting and they will be used to derive our Ab.

Theorem 1

For $P \mid \frac{1}{y} C_{\max }^* < p_j \le \frac{1}{k} C_{\max }^* \mid C_{\max }$ with $y \in \{y' \in {\mathbb {R}}^+ \mid k <y' \le 2k\}$, we have

$$\begin{aligned} \max _{i\in M} \{ p(S_i^{\alpha m}) \} - \min _{i\in M} \{ p(S_i^{\alpha m}) \}< & {} \left( \frac{1}{k} - \frac{1}{y}\right) C_{\max }^* \end{aligned}$$

and

$$\begin{aligned} |S_i^{\alpha m}|= & {} \alpha {~~~~} \forall i \in M, \forall \alpha \in \{ 1, \ldots , \left\lfloor \frac{n}{m} \right\rfloor \} \end{aligned}$$

Proof

It can be shown using mathematical induction. First we consider the case $\alpha = 1$. The first m jobs are scheduled on the m machines and $|S_i^{m}| = 1$ for all $i \in M$. We know that

$$\begin{aligned} \max _{i\in M} \{p(S_i^{m})\}= & {} p_1 \ \le \ \frac{1}{k} C_{\max }^* \\ \min _{i\in M} \{p(S_i^{m})\}= & {} p_m \ \ge \ p_n > \frac{1}{y} C_{\max }^* \end{aligned}$$

Thus, the Theorem holds when $\alpha = 1$.

Suppose that the Theorem holds when $\alpha \in \{1, \ldots , \beta -1 \}$ for some $\beta$ such that $\beta \le \left\lfloor n/m \right\rfloor -1$. We consider a partial schedule in which the first $(\beta -1)m$ jobs are scheduled by LPT. By induction hypothesis, we have that

$$\begin{aligned}&\max _{i\in M} \left\{ p(S_i^{(\beta -1) m}) \right\} - \min _{i\in M} \left\{ p(S_i^{\beta -1) m}) \right\} \\&\quad < \left( \frac{1}{k} - \frac{1}{y}\right) C_{\max }^* . \end{aligned}$$

Since

$$\begin{aligned} p_j \ge p_n > \frac{1}{y} C_{\max }^* \ge \left( \frac{1}{k} - \frac{1}{y}\right) C_{\max }^* \end{aligned}$$

for all $j \in \{(\beta -1)m + 1, \ldots , \beta m\}$, the next m jobs will be scheduled by LPT on different machines and, thus, $|S_i^{\beta m}| = \beta$ for all $i \in M$.

Let job $j_i$ in $\{(\beta -1)m + 1, \ldots , \beta m\}$ denote a job scheduled on machine i for some $i\in M$ in schedule $\sigma$. In other words, $S_i^{\beta m} = S_i^{(\beta -1) m} \cup \{j_i\}$. Let h be defined as $\arg \max _{i\in M} \{ p(S_i^{\beta m})\}$. We consider two cases for some machine i, $i\ne h$, based on whether $p(S_i^{(\beta -1)m})$ is greater than $p(S_h^{(\beta -1)m})$ or not.

For the case that $p(S_h^{(\beta -1)m}) - p(S_i^{(\beta -1)m}) > 0$, it follows from the fact that under LPT job $j_i$ must be scheduled before job $j_h$ that $p_{j_h} - p_{j_i} \le 0$. From the induction hypothesis we have that $p(S_h^{(\beta -1)m}) - p(S_i^{(\beta -1)m}) < ({1}/{k} - {1}/{y}) C_{\max }^*$. Thus, we have

$$\begin{aligned}&p(S_h^{\beta m}) - p(S_i^{\beta m}) \\&\quad = \left( p(S_h^{(\beta -1)m}) + p_{j_h}\right) - \left( p(S_i^{(\beta -1)m}) + p_{j_i}\right) \\&\quad = \left( p(S_h^{(\beta -1)m}) - p(S_i^{(\beta -1)m})\right) + \left( p_{j_h} - p_{j_i}\right) \\&\quad < \left( \frac{1}{k} - \frac{1}{y}\right) C_{\max }^*. \end{aligned}$$

For the case when $p(S_h^{(\beta -1)m}) - p(S_i^{(\beta -1)m}) \le 0$ and $i\ne h$, by the assumption of the Theorem, we have $p_{j_h} - p_{j_i} < ({1}/{k} - {1}/{y}) C_{\max }^*$. Thus, we have

$$\begin{aligned}&p(S_h^{\beta m}) - p(S_i^{\beta m}) \\&\quad = \left( p(S_h^{(\beta -1)m}) + p_{j_h}\right) - \left( p(S_i^{(\beta -1)m}) + p_{j_i}\right) \\&\quad = \left( p(S_h^{(\beta -1)m}) - p(S_i^{(\beta -1)m})\right) + \left( p_{j_h} - p_{j_i}\right) \\&\quad < \left( \frac{1}{k} - \frac{1}{y}\right) C_{\max }^*. \end{aligned}$$

Therefore, $p(S_h^{\beta m}) - p(S_i^{\beta m}) < ({1}/{k} - {1}/{y}) C_{\max }^*$ for all $i \in M$. $\square$

Corollary 1

For $P \mid \frac{1}{y}C_{\max }^* < p_j \le \frac{1}{k} C_{\max }^* \mid C_{\max }$ with $y \in \{y' \in {\mathbb {R}}^+ \mid k <y' \le 2k\}$, and $n = \alpha m$ for some $\alpha \in {\mathbb {Z}}^+$, the approximation bound on LPT is less than $1+\frac{1}{2k}\frac{m-1}{m}$.

Proof

Let machine $i^*$ be the machine that determines the makespan under schedule $\sigma$. It follows from Theorem 1 and the definition of machine $i^*$, that

$$\begin{aligned} C_{\max } - p(S_i^n)< & {} \left( \frac{1}{k} - \frac{1}{y}\right) C_{\max }^* \quad \forall i \in M\setminus \{i^* \} \\ C_{\max } - p(S_{i^*}^n)= & {} 0. \end{aligned}$$

By adding the above inequalities along with (1), we have

$$\begin{aligned} C_{\max }< & {} \left( 1+ \left( \frac{1}{k} - \frac{1}{y}\right) \frac{m-1}{m} \right) C_{\max }^*\\\le & {} \left( 1+ \frac{1}{2k} \frac{m-1}{m} \right) C_{\max }^*. \end{aligned}$$

It completes the proof. $\square$

3 Approximation bound results

In this section, we analyze our Tab for problem $P \mid p_j \le \frac{1}{k} C_{\max }^* \mid C_{\max }$. We first consider in Sect. 3.1 the case $k = 2$ and present a Tab. For the case $k \ge 3$ the Tab is determined by the relationship between m and k. For the case $m \ge k$, we consider two subcases based on whether or not $m \le k(k+1)/2$, and they are presented in Sects. 3.2 and 3.3. When $2 \le m < k$, the Tab is determined by the relationship between m, the quotient q, and the remainder $r_1$ when k is divided by m; it is shown in Sect. 3.4.

3.1 The case $k=2$

For the case $k=2$, we consider two subcases $m = 2$ and $m \ge 3$. For the subcase $m = 2$, the tight example of Graham (1969) satisfies the condition of $P \mid p_j \le \frac{1}{2} C_{\max }^* \mid C_{\max }$. Therefore, the Tab is 7/6 which is the same as in Graham (1969). Thus, we need to consider the subcase $m \ge 3$.

Theorem 2

The approximation bound on LPT for $P \mid p_j \le \frac{1}{k} C_{\max }^* \mid C_{\max }$ with $m \ge 3$ and $k=2$ is $\frac{5}{4} - \frac{1}{4m}$ and it is tight.

Proof

Suppose there exists a minimum counterexample. From inequality (1) it follows that

$$\begin{aligned} p(S_i^{n-1}) + p_n> & {} \left( \frac{5}{4} - \frac{1}{4m} \right) C_{\max }^* \quad \forall i\in M \\ m C_{\max }^*\ge & {} \sum _{i=1}^m p(S_i^{n-1}) + p_n. \end{aligned}$$

Adding the two inequalities yields

$$\begin{aligned} p_n > \frac{1}{4}C_{\max }^*. \end{aligned}$$

This implies $|S_i^*| \le 3$ for all $i\in M$ and thus $n \le 3m$. If $n \le 2m$, by Theorem 1, every machine has at most 2 jobs and from the fact that $p_j \le (1/2) C_{\max }^*$, schedule $\sigma$ is optimal.

Thus, we only need to consider $2m+1 \le n \le 3m$. By Theorem 1, $|S_i^{2m}| = 2$ for all $i \in M$ and $2 \le |S_i^n| \le 3$ for all $i \in M$. By Proposition 1, since job n is assigned by LPT to the third position of a machine,

$$\begin{aligned} p_n\le & {} \frac{1}{3}C_{\max }^*. \end{aligned}$$

(2)

By Theorem 1, $|S_i^{\alpha m}| = \alpha$ for all $\alpha \in \{1, 2\}$ and $i\in M$. We can assume without loss of generality that the first m jobs are scheduled on machines 1 to m one after another, and the next m jobs are scheduled on machines m to 1, again one after another. In other words,

$$\begin{aligned} S_i^{2m} = \{ i, \ 2m-i+1 \} {~~~~} \forall i \in M. \end{aligned}$$

Next, we show that the following two inequalities hold:

$$\begin{aligned} p_{2m} + p_n\le & {} \frac{2}{3} C_{\max }^* \end{aligned}$$

(3)

$$\begin{aligned} p_{2m-i(n)+1} + p_n> & {} \frac{2}{3} C_{\max }^*. \end{aligned}$$

(4)

Inequality (3) can be proved as follows. If $p_{2m} + p_n > (2/3) C_{\max }^*$, then by inequality (2), $p_{2m} > (1/3) C_{\max }^*$. This implies that $p_j > (1/3) C_{\max }^*$ for all $j = 1, \ldots , 2m$. Then, in schedule $\sigma ^*$, each machine has exactly two jobs from $\{1, \ldots , 2m\}$. In schedule $\sigma ^*$, job n cannot be added to the scheduled and completed by $C_{\max }^*$, which leads to a contradiction. Thus, we have $p_{2m} + p_n \le (2/3) C_{\max }^*$.

Inequality (4) can be shown as follows. Suppose that

$$\begin{aligned} p_{2m-i(n)+1} + p_n \le \frac{2}{3} C_{\max }^* \end{aligned}$$

is satisfied. Then, since $p_{i(n)} \le ({1}/{2})C_{\max }^*$,

$$\begin{aligned} C_{\max }= & {} p_{i(n)} + p_{2m-i(n)+1} + p_n \\\le & {} \frac{7}{6} C_{\max }^* \ \le \ \left( \frac{5}{4} - \frac{1}{4m}\right) C_{\max }^* \end{aligned}$$

when $m\ge 3$, which leads to a contradiction. Thus, we have

$$\begin{aligned} p_{2m-i(n)+1} + p_n > \frac{2}{3} C_{\max }^*. \end{aligned}$$

Now, we consider the first machine, denoted as machine ${\hat{i}}$, that satisfies the condition.

$$\begin{aligned} p_{2m-{\hat{i}}+2} + p_n\le & {} \frac{2}{3} C_{\max }^* \text {~~and} \\ p_{2m-{\hat{i}}+1} + p_n> & {} \frac{2}{3} C_{\max }^* . \end{aligned}$$

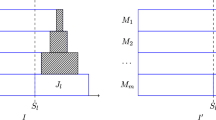
From inequalities (3) and (4) it follows that there must exist a machine ${\hat{i}}$, $2 \le {\hat{i}} \le i(n)$.

See Fig. 2. For all $i \in \{1, \ldots , {\hat{i}} - 1 \}$, we have $|S_i^{n-1}| = 3$. If there is a machine i in $\{1, \ldots , {\hat{i}} - 1 \}$ with $|S_i^{n-1}| = 2$, then job n should have been scheduled on machine i and the makespan would be less than $(7/6) C_{\max }^*$, which is a contradiction.

For all $i\in \{{\hat{i}}, \ldots , m\} \setminus \{i(n)\}$, we do not know whether $|S_i^{n-1}| = 2$ or 3, but we know that $|S_i^{n-1}| \ge 2$. Moreover, we do know that $|S_{i(n)}| = 3$. Thus, we can calculate the following lower bound on the number of jobs:

$$\begin{aligned} n\ge & {} 3({\hat{i}}-1) + 2(m-{\hat{i}}) + 3 = 2m + {\hat{i}}. \end{aligned}$$

(5)

We consider a set of jobs $J' \doteq \{1, \ldots , 2m-{\hat{i}}+1 \}$. See Fig. 2. Since $p_{2m-{\hat{i}}+1 } + p_n > ({2}/{3}) C_{\max }^*$ and $p_n \le ({1}/{3}) C_{\max }^*$ by inequality (2), we know that $p_j > ({1}/{3}) C_{\max }^*$ for all $j \in J'$. It implies that under schedule $\sigma ^*$ there are at most two jobs from $J'$ on each machine.

Fig. 2

A minimum counterexample when $k=2$ and $m \ge 3$

Let $M'$ be the set of machines that have under schedule $\sigma ^*$ exactly two jobs from $J'$ so that $|M'| \ge m-{\hat{i}} + 1$. For some machine $i \in M'$, let $S_i = \{ j_1, j_2 \}$. Then, $p_{j_1} + p_n > ({2}/{3}) C_{\max }^*$ and $p_{j_2} > ({1}/{3}) C_{\max }^*$. It implies that for all $i \in M'$ there are no more additional jobs that can be scheduled on machine i, and it implies $|S^*_i| = 2$ for all $i \in M'$. Since $|S^*_i| \le 3$ for all $i \in M \setminus M'$, we have

$$\begin{aligned} n\le & {} 2(m-{\hat{i}}+1) + 3({\hat{i}}-1) \ = \ 2m + {\hat{i}} - 1. \end{aligned}$$

(6)

Inequalities (5) and (6) contradict one another. Therefore, there is no counterexample with a larger Ab.

The tightness can be shown through an example. Such an example can be obtained by modifying the tight example of LPT in Graham (1969).

We consider a problem instance with $3m+1$ jobs where

$$\begin{aligned} \begin{array}{ll} p_j = 2m-\lceil \frac{j}{2} \rceil &{}\quad \hbox {for }j \in \{ 1, \ldots , 2m\},\hbox { and }\\ p_j = m &{} \quad \hbox {for }j \in \{2m+1, \ldots , 3m + 1 \} . \end{array} \end{aligned}$$

In schedule $\sigma ^*$,

$$\begin{aligned} \begin{array}{ll} S_i^* = \{ i, \ 2m - i - 1\} \cup \{2m+1 + i\} &{}\,\, \hbox {for }i \in \{ 1, \ldots , m-1\} \\ S_m^* = \{2m-1, 2m, 2m+1\} \cup \{3m+1 \}. &{} \end{array} \end{aligned}$$

In schedule $\sigma$,

$$\begin{aligned} \begin{array}{ll} S_1 = \{ 1, \ 2m\} \cup \{2m+1 \} \cup \{3m+1\} &{} \\ S_i = \{i, 2m-i + 1\} \cup \{2m+i \} &{} \quad \hbox {for }i \in \{2, \ldots m\}. \end{array} \end{aligned}$$

Therefore, we have

$$\begin{aligned} \frac{C_{\max }(\sigma )}{C_{\max }(\sigma ^*)} = \frac{5m-1}{4m} = \frac{5}{4} - \frac{1}{4m}. \end{aligned}$$

The proof is complete. $\square$

3.2 The case $3 \le k \le m \le {k(k+1)}/{2}$

Now consider the case $k \ge 3$. Consider the following Lemma that deals with a special problem under the additional restriction that $p_j > ({1}/({k+2})) C_{\max }^*$ for all $j\in J$. The Lemma will be used in the proof of the Ab when $3 \le k \le m$.

Lemma 1

The approximation bound on LPT for $P \mid \frac{1}{k+2} C_{\max }^* < p_j \le \frac{1}{k} C_{\max }^* \mid C_{\max }$ with $3 \le k \le m$ is $1 + \frac{k-1}{k(k+1)}$.

Proof

Suppose there exists a minimum counterexample. If $n \le km$, by Theorem 1, each machine has at most k jobs and then $\sigma$ is optimal since $p_j \le ({1}/{k}) C_{\max }^*$ for all $j \in J$, implying a contradiction.

Thus, $n \ge km+1$. From Proposition 1 and by the fact that job n is put in the $(k+1)$-th position on its machine by LPT, we have $p_n \le ({1}/({k+1})) C_{\max }^*$. Since $p_j > ({1}/({k+2}))C_{\max }^*$ for all $j \in J$, we have $|S_i^*| \le k+1$ for all $i \in M$ and it implies $n \le (k+1)m$. Moreover, when $n = (k+1)m$, by Corollary 1 and the condition $k\ge 3$, we have

$$\begin{aligned} 1+ \frac{1}{2k} \le 1 + \frac{k-1}{k(k+1)}. \end{aligned}$$

Therefore, it is sufficient to consider the case $n=km+r$ for some $r \in \{1,2,\ldots ,m-1\}$. Since $km+1 \le n \le km + (m-1)$ and

$$\begin{aligned} \frac{1}{k+2} C_{\max }^* < p_j \le \frac{1}{k} C_{\max }^*, \end{aligned}$$

the number of jobs assigned to a machine is, either k or $k+1$ by Theorem 1. We consider the following two sets of machines in schedule $\sigma$:

$$\begin{aligned} \begin{aligned} M_k =&\,\text {the set of machines that have { k} jobs under} \text { schedule }\sigma . \\ M_{k+1} =&\,\text {the set of machines that have k+1 jobs under}\\&\text { schedule }\sigma . \end{aligned} \end{aligned}$$

It is clear that $|M_{k+1}| = r$ and $|M_k| = m-r$.

Recall that u(i, t) denotes the job scheduled by LPT under schedule $\sigma$ on machine i in the t-th position, for all $i \in M$ and for all $t \in \{ 1, 2, \ldots \}$. We know $i(n) \in M_{k+1}$ and

$$\begin{aligned} C_{\max }= & {} \sum _{t=1}^{k} p_{u(i(n), t)} + p_n. \end{aligned}$$

Since

$$\begin{aligned} C_{\max } > \left( 1 + \frac{k-1}{k(k+1)}\right) C_{\max }^*, \end{aligned}$$

and

$$\begin{aligned} \sum ^{k-1}_{t=1} p_{u(i(n),t)} \le \frac{k-1}{k}C_{\max }^*, \end{aligned}$$

we have

$$\begin{aligned} p_{u(i(n), k)} + p_n> & {} \left( \frac{2}{k+1}\right) C_{\max }^*. \end{aligned}$$

(7)

Moreover, since job n is scheduled on machine i(n) under schedule $\sigma$,

$$\begin{aligned} \sum ^{k}_{t=1} p_{u(i(n),t)} \le \sum ^{k}_{t=1} p_{u(i, t)}&\quad \forall i \in M_k \end{aligned}$$

and

$$\begin{aligned} \sum ^{k-1}_{t=1} p_{u(i, t)} \le \frac{k-1}{k} C_{\max }^* \quad \forall i \in M_k. \end{aligned}$$

Thus, we have

$$\begin{aligned} p_{u(i, t)} + p_n> & {} \left( \frac{2}{k+1}\right) C_{\max }^* \quad \forall i \in M_k , \forall t \in \{ 1,\ldots , k \}. \end{aligned}$$

Since $p_n \le ({1}/({k+1}))C_{\max }^*$, we have $p_{u(i(n), k)} > ({1}/ ({k+1}))C_{\max }^*$ by inequality (7) and it also implies

$$\begin{aligned} p_{u(i, t)}\ge & {} p_{u(i(n), k)} \\> & {} \frac{1}{k+1}C_{\max }^* \quad \forall i \in M_k, \forall t \in \{ 1, \ldots , k-1\}. \end{aligned}$$

Let the set of jobs $J'$ be defined as follows:

$$\begin{aligned} J' \doteq \left( \bigcup _{i\in M} \bigcup _{t=1}^{k-1}\{ u(i, t)\}\right) \cup \left( \bigcup _{i \in M_k \cup \{i(n)\} } \{u(i, k) \}\right) . \end{aligned}$$

Then, $p_j > ({1}/({k+1})) C_{\max }^*$ and $p_j + p_n > ({2}/({k+1})) C_{\max }^*$ for all $j \in J'$. We know that $|J'| = (k-1)m + (m-r+1) = km-r+1$. Since $p_j > ({1}/({k+1})) C_{\max }^*$ for all $j \in J'$, under schedule $\sigma ^*$ at most k jobs from $J'$ can be scheduled on the same machine.

Let $M'$ be the set of machines that have in schedule $\sigma ^*$ exactly k jobs from $J'$ so that $|M'| \ge m-r+1$. Consider machine $i \in M'$ in schedule $\sigma ^*$. Let $S_i^* \cap J' = \{j_1, j_2, \ldots , j_k\}$ for some $i \in M'$. It is impossible to add the smallest job to this machine i because $p_{j_l} > ({1}/({k+1})) C_{\max }^*$ for all $l \in \{1, \ldots , k-1\}$, and $p_{j_k} + p_n> ({2}/({k+1})) C_{\max }^*$. Thus, no more jobs, in addition to the current k jobs, can be scheduled on machine $i \in M'$ under schedule $\sigma ^*$ and it implies

$$\begin{aligned} |S_i^*| = k \quad \forall i \in M'. \end{aligned}$$

Since $|S_i^*| \le k+1$ for all $i \in M$ and $|M'| \ge m - r + 1$, we have

$$\begin{aligned} n\le & {} k|M'| + (k+1)(m - |M'|) \ = \ (k+1)m - |M'| \\\le & {} (k+1)m - (m-r+1) \ = \ km + r - 1. \end{aligned}$$

This contradicts the fact that $n = km + r$. Therefore, there is no such counterexample with a larger Ab. $\square$

Theorem 3

The approximation bound on LPT for $P \mid p_j \le \frac{1}{k} C_{\max }^* \mid C_{\max }$ with $3\le k \le m \le \frac{k(k+1)}{2}$ is $1 + \frac{k-1}{k(k+1)}$ and it is tight.

Proof

Suppose there exists a minimum counterexample. By inequality (1),

$$\begin{aligned} p(S_i^{n-1}) + p_n> & {} \left( 1 + \frac{k-1}{k(k+1)}\right) C_{\max }^* \quad \forall i \in M\\ m C_{\max }^*\ge & {} \sum _{i \in M} p(S_i^{n-1}) + p_n . \end{aligned}$$

By adding both sides, we have

$$\begin{aligned} p_n> & {} \frac{m}{m-1} \frac{k-1}{k(k+1)} C_{\max }^*. \end{aligned}$$

When $m \le {k(k+1)}/{2}$, we can say that $p_n > ({1}/({k+2})) C_{\max }^*$. By Lemma 1, the Ab should be no more than $1 + ({k-1})/{k(k+1)}$. This results in a contradiction and it implies that there is no counterexample with a greater Ab.

Fig. 3

A tight example of LPT when $3 \le k \le m \le {k(k+1)}/{2}$

The tightness can be shown through the following instance with $km+1$ jobs of two types. See Fig. 3.

Job type	Processing time	The number of jobs
1	1/k	$k(m-1)$
2	$1/(k+1)$	$k+1$

In schedule $\sigma ^*$, there are two types of machines based on the composition of job types and the optimal makespan is 1.

Machine type	The number of machines	The number of jobs of each type
		Job type 1	Job type 2
1	$m-1$	k	0
2	1	0	$k+1$

In schedule $\sigma$, there are three types of machines based on the composition of job types.

Machine type	The number of machines	The number of jobs of each type
		Job type 1	Job type 2
3	$m-k$	k	0
4	1	$k-1$	2
5	$k-1$	$k-1$	1

The makespan of schedule $\sigma$ is determined by the machine of type 4. Therefore, we have

$$\begin{aligned} \frac{C_{\max }(\sigma )}{C_{\max }(\sigma ^*)}= & {} \frac{1}{k} (k-1) + \frac{2}{k+2} = 1 + \frac{k-1}{k(k+1)}. \end{aligned}$$

It completes the proof. $\square$

3.3 The case $m > {k(k+1)}/{2}$ and $k\ge 3$

Theorem 4

The approximation bound on LPT for $P \mid p_j \le \frac{1}{k} C_{\max }^* \mid C_{\max }$ with $m \ge \frac{k(k+1)}{2} + 1$ and $k\ge 3$ is $1+ \frac{1}{k+2} - \frac{1}{(k+2)m}$ and it is tight.

Proof

Suppose there exists a minimum counterexample. By inequality (1),

$$\begin{aligned} p(S_i^{n-1}) + p_n> & {} \left( 1+ \frac{1}{k+2} - \frac{1}{(k+2)m}\right) C_{\max }^* \quad \forall i \in M\\ m C_{\max }^*\ge & {} \sum _{i \in M} p(S_i^{n-1}) + p_n . \end{aligned}$$

By adding both sides, we have

$$\begin{aligned} p_n> & {} \frac{1}{k+2} C_{\max }^*. \end{aligned}$$

By Lemma 1, the Ab should be no more than $1 \!+\! ({k\!-\!1})/{k(k\!+\!1)}$. However, since

$$\begin{aligned} 1 + \frac{k-1}{k(k+1)} < 1+ \frac{1}{k+2} - \frac{1}{(k+2)m} \end{aligned}$$

when $m\ge {k(k+1)}/{2} + 1$, it leads to a contradiction and it implies that there is no such counterexample with a greater Ab.

In order to show the tightness, we present examples. We divide m by k such that $m = \pi k + \gamma$ with nonnegative integers $\pi$ and $\gamma$ satisfying $0 \le \gamma \le k-1$. Because of the condition $m > k(k+1)/2$, we have $\pi \ge \lceil (k+1)/2 - \gamma /k\rceil \ge (k-1)/2.$ To identify the structure of the tight example, we have to consider the following four cases specified by values of $\pi$ and $\gamma$. In all cases, the total number of jobs in the tight example is $m(k+1) + 1$, and the optimal makespan and the makespan by LPT are $m(k+2)$ and $m(k+2)+m-1$, respectively.

• Case 1: $\gamma = 0$

• Case 2: $\gamma = 1$

• Case 3: $\gamma \ge 2$ with $\pi \ge k-\gamma$

• Case 4: $\gamma \ge 2$ with $\pi < k-\gamma$

For Case 1, the following example gives the Tab. See Fig. 4.

Fig. 4

Case 1: A tight example of LPT when $m > {k(k+1)}/{2}$

For Case 2, the following example gives the Tab. See Fig. 5.

Fig. 5

Case 2: A tight example of LPT when $m > {k(k+1)}/{2}$

For Case 3, the following example gives the Tab. See Fig. 6.

Fig. 6

Case 3: A tight example of LPT when $m > {k(k+1)}/{2}$

Fig. 7

Case 4 with $\theta = 1$: A tight example of LPT when $m > {k(k+1)}/{2}$

Finally, for Case 4, we need an additional parameter $\theta \doteq (k-\gamma ) - \pi \ge 1$ to provide a tight example. Even though the example presents one problem instance when $\theta \ge 1$, the optimal schedule and the LPT schedule exhibit different shapes according to the value of $\theta$. Since $(k-2)(m-1)+(2-\theta )(k-2) \ge (k-3)m+ (k-1)$, first $(k-3)$ slots on every machine are filled with only type 4 jobs. However, when $\theta = 1$, even the $(k-2)$th slot on every machine in each schedule is filled with a type 4 job. Thus, the shape in case $\theta = 1$ is different from the one in case $\theta \ge 2$.

Fig. 8

Case 4 with $\theta \ge 2$: A tight example of LPT when $m > {k(k+1)}/{2}$

In conclusion, we show the existence of tight examples for every case when $m > k(k+1)/2$, which completes the proof (Figs. 7, 8).$\square$

3.4 The case $2 \le m < k$

Finally, consider the case $2 \le m < k$. Recall q and $r_1$ be the quotient and the remainder, respectively, when k is divided by m. Thus, $k = q m + r_1$ where $q \in {\mathbb {Z}}^+$ and $0 \le r_1 \le m-1$. In other words, $q = \lfloor {k}/{m} \rfloor$ and $r_1 = k - \lfloor {k}/{m}\rfloor m$.

We will show that the Ab is $B = \max \left( B_1, B_2 \right)$ where the value of $B_1$ and $B_2$ is given in the following table. Moreover, we will show that both $B_1$ and $B_2$ are tight. The conditions on m, q and $r_1$, determines the Ab for each case.

Case	Conditions on m, q and $r_1$	Ab
1	$q(m-r_1) \ge r_1 - 1$	$B_1 \doteq 1+ \frac{m-1}{m}\frac{k-r_1}{k(k-r_1+1)}$
2	$q(m-r_1) < r_1 - 1$	$B_2 \doteq 1 + \frac{k-1}{k(k+1)} - \frac{k-r_1}{mk(k+1)}$

In this section, we consider two cases under the following conditions:

$$\begin{aligned} \text {Case 1:~~} q(m-r_1)\ge & {} r_1 - 1 \end{aligned}$$

(8)

$$\begin{aligned} \text {Case 2:~~}q(m-r_1)< & {} r_1 - 1 \end{aligned}$$

(9)

Lemma 2

If $r_1 = 0$ then the approximation bound on LPT for $2 \le m<k$ is $1+ \frac{m-1}{m}\frac{1}{(k+1)}.$

Proof

The case with $r_1 = 0$ belongs to Case 1 and the target Ab is

$$\begin{aligned} 1+ \frac{m-1}{m}\frac{1}{(k+1)}. \end{aligned}$$

Suppose that the Lemma is not correct. Then there exists a minimum counterexample. By inequality (1),

$$\begin{aligned} p(S_i^{n-1}) + p_n> & {} \left( 1+ \frac{m-1}{m}\frac{1}{(k+1)}\right) C_{\max }^* \quad \forall i \in M\\ m C_{\max }^*\ge & {} \sum _{i \in M} p(S_i^{n-1}) + p_n . \end{aligned}$$

By adding both sides, we have

$$\begin{aligned} p_n> & {} \frac{1}{(k+1)} C_{\max }^*. \end{aligned}$$

It implies that the number of jobs on each machine under schedule $\sigma ^*$ is no more than k. From the assumption that $p_j \le ({1}/{k})C_{\max }^*$ and by Theorem 1, it follows that under schedule $\sigma$ each machine can process at most k jobs, which implies that $\sigma$ is indeed optimal, resulting in a contradiction. Therefore, there is no such counterexample with a greater Ab. $\square$

By the result of Lemma 2, we assume that $r_1 \ge 1$ throughout the remainder of this section.

Lemma 3

If there exists a minimum counterexample for the approximation bound B, then the number of jobs on each machine under schedule $\sigma ^*$ in the minimum counterexample is at most $k+1$. That is, $|S^*_{i}| \le k+1$ for all $i \in M$.

Proof

To prove the Lemma, it suffices to show that $p_n$ is greater than $({1}/({k+2})) C_{\max }^*$ in both cases. In Case 1, the following inequalities hold by inequality (1),

$$\begin{aligned} p(S_i^{n-1}) + p_n> & {} \left( 1+ \frac{m-1}{m}\frac{k-r_1}{k(k-r_1+1)}\right) C_{\max }^* \quad \forall i \in M\\ m C_{\max }^*\ge & {} \sum _{i \in M} p(S_i^{n-1}) + p_n. \end{aligned}$$

By adding both sides, we have

$$\begin{aligned} p_n> & {} \frac{k-r_1}{k(k-r_1+1)} C_{\max }^*. \end{aligned}$$

(10)

In order to compare the coefficient of inequality (10) and ${1}/{(k+2)}$, we calculate the difference

$$\begin{aligned} \frac{k-r_1}{k(k-r_1+1)} - \frac{1}{k+2}= & {} \frac{k-2r_1}{k(k-r_1+1)(k+2)}. \end{aligned}$$

Since $k - 2r_1 = (qm+r_1)- 2r_1 \ge m-r_1 \ge 0$ and $k-r_1+1 \ge (m+r_1)-r_1 +1 >0$, we have $p_n > ({1}/({k+2})) C_{\max }^*$.

In Case 2, the following inequalities hold by inequality (1),

$$\begin{aligned} p(S_i^{n-1})\! +\! p_n> & {} \!\left( \!1 + \frac{k-1}{k(k+1)} \!-\! \frac{k-r_1}{mk(k+1)}\!\right) C_{\max }^* \!\quad \forall i \in M\\ m C_{\max }^*\ge & {} \sum _{i \in M} p(S_i^{n-1}) + p_n. \end{aligned}$$

By adding both sides, we have

$$\begin{aligned} p_n> & {} \frac{m}{m-1}\left( \frac{k-1}{k(k+1)} - \frac{k-r_1}{mk(k+1)}\right) C_{\max }^*. \end{aligned}$$

Using a similar procedure as in Case 1, we calculate the difference

$$\begin{aligned}&\frac{m}{m-1} \left( \frac{k-1}{k(k+1)} - \frac{k-r_1}{mk(k+1)}\right) - \frac{1}{k+2} \\&\quad = \frac{r_{1}k + 2r_{1} - 2m - k }{(m-1)k(k+1)(k+2)}. \end{aligned}$$

Since the denominator is positive, it suffices to check the numerator. By condition (9) of Case 2, $1 \le q(m-r_1) < r_1 -1$. It implies $r_1 > 2$ and since $r_1$ is integer, $r_1 \ge 3$. Recall that $k = qm + r_1$. Thus, the numerator is

$$\begin{aligned} (r_{1}-1)k + 2r_{1} - 2m= & {} (r_1 -1)(qm+r_1) - 2(m-r_1) \\\ge & {} (r_1-3)(m-r_1) \ge 0. \end{aligned}$$

For both cases, we have

$$\begin{aligned} p_n> & {} \frac{1}{k+2}C_{\max }^*. \end{aligned}$$

It implies $|S^*_{i}| \le k+1$ for all $i \in M$, which completes the proof. $\square$

By Lemma 3, $|S^*_{i}| \le k+1$, which implies $n \le m(k+1)$. If $n \le mk$, then schedule $\sigma$ is optimal since every machine has at most k jobs by Theorem 1 and $p_j \le \frac{1}{k}$ for all $j \in J$. Thus, let $n = mk +r_2$, where $1 \le r_2 \le m$. Then Lemma 4 provides a proof that there is no counterexample with Ab greater than B when $r_2 > 1$.

Lemma 4

If there is a minimum counterexample to the approximation bound B for $2 \le m < k$, then $r_2$ cannot be greater than 1.

Proof

Suppose there exists a minimum counterexample with $r_2 > 1$.

First we consider the case $r_2 =m$. By Corollary 1 the Ab is then less than $1 + (({m-1})/{m})({1}/{2k})$. Thus, we calculate the difference between the target Ab and the bound given by Corollary 1 for both cases.

In Case 1, since $k = qm + r_1$, the difference is

$$\begin{aligned}&\left( 1+ \frac{m-1}{m}\frac{k-r_1}{k(k-r_1+1)}\right) - \left( 1 + \frac{m-1}{m}\frac{1}{2k}\right) \\&\quad = \frac{m-1}{m} \frac{k-r_1-1}{2k(k-r_1+1)} \ge 0. \end{aligned}$$

In Case 2, since $k\ge 3$, the difference is

$$\begin{aligned}&\left( 1 + \frac{k-1}{k(k+1)} - \frac{k-r_1}{mk(k+1)} \right) - \left( 1+\frac{m-1}{m}\frac{1}{2k}\right) \\&\quad = \frac{(m-1)(k-3) + 2(r_1- 1)}{2mk(k+1)} \ge 0. \end{aligned}$$

Thus, $r_2$ cannot be m. It suffices to consider the case $1 < r_2 \le m-1$.

In Case 1, suppose $r_2 > 1$. We know that $k \le |S^*_{i}| \le k+1$ for all $i \in M$. Recall that $M_k$ and $M_{k+1}$ denote the sets of machines with k and $k+1$ jobs in schedule $\sigma$, respectively. Then, $|M_{k+1}| = r_2$ and $|M_{k}| = m-r_2$. We know $i(n) \in M_{k+1}$. For some machine $i \in M_k$, if job n is also assigned to it, then the total processing time on the machine exceeds the current makespan. For some machine $i \in M_{k+1}$, it follows from Theorem 1 that the difference between the total processing time and the current makespan is bounded. Thus, by inequality (1), we have

$$\begin{aligned}&p(S_i^{n-1}) + p_n> \left( 1+ \frac{m-1}{m}\frac{k-r_1}{k(k-r_1+1)}\right) C_{\max }^* \\&\quad \forall i \in M_k \cup \{i(n)\} \\&p(S_i^{n-1}) \! > \!\left( \!1\!+\! \frac{m-1}{m}\frac{k-r_1}{k(k-r_1+1)} - \frac{1}{k(k-r_1+1)}\!\right) C_{\max }^* \\&\quad \forall i \in M_{k+1} \setminus \{i(n)\} \\&m C_{\max }^* \ge \sum _{i \in M} p(S_i^{n-1}) + p_n. \end{aligned}$$

Summing these inequalities yields the following inequality.

$$\begin{aligned} p_n> & {} \frac{(m-1)(k-r_1)-r_2+1}{(m-r_2)k(k-r_1+1)} C_{\max }^*. \end{aligned}$$

Suppose the following inequality holds,

$$\begin{aligned} \frac{(m-1)(k-r_1)-r_2+1}{(m-r_2)k(k-r_1+1)} \ge \frac{1}{k+1} \end{aligned}$$

then it leads to a contradiction since schedule $\sigma$ is optimal by the fact that $p_j \le ({1}/{k})C_{\max }^*$ for all $j\in J$ and Theorem 1. Thus, we calculate their difference

$$\begin{aligned}&\frac{(m-1)(k-r_1)-r_2+1}{(m-r_2)k(k-r_1+1)} - \frac{1}{(k+1)} \\&\quad = \frac{(r_2-1) k^2 + (r_1 - r_1 r_2)k + r_1 - r_2 - r_1 m + 1}{(m-r_2)k(k+1)(k-r_1+1)}. \end{aligned}$$

By the definition of k, the denominator is positive. Moreover, the numerator can be written as

$$\begin{aligned} \left\{ (r_2-1)k^2 - r_1 r_2 k\right\} + \left\{ r_1 k - r_1 m\right\} + \left\{ r_1 -r_2 + 1\right\} . \end{aligned}$$

The first part is $k \{ (r_2-1)k - r_1 r_2 \} = k \{ (r_2-1)qm - r_1 \} \ge k(m-r_1) \ge m$ because $k = qm + r_1$, $r_2 \ge 2$ and $k \ge m$. The second part is $r_1(k-1)\ge 1$. The third part is $r_1 -r_2 + 1 \ge -(m-1)$. Thus, the numerator is positive as well, which completes the proof for Case 1.

For Case 2, the same procedure yields:

$$\begin{aligned} p_n> & {} \left( \frac{m(k-1)}{k(k+1)} - \frac{k-r_1}{k(k+1)} - \frac{(2m-r_1-1)(r_2-1)}{(m-1)k(k+1)}\right) \\&\frac{1}{m-r_2} C_{\max }^*. \end{aligned}$$

If

$$\begin{aligned}&\left( \frac{m(k-1)}{k(k+1)} - \frac{k-r_1}{k(k+1)} - \frac{(2m-r_1-1)(r_2-1)}{(m-1)k(k+1)}\right) \\&\quad \frac{1}{m-r_2} \ge \frac{1}{k+1} \end{aligned}$$

holds, then it leads to a contradiction since schedule $\sigma$ is optimal by the same reason with Case 1. Thus, we calculate their difference

$$\begin{aligned}&\left( \frac{m(k-1)}{k(k+1)} - \frac{k-r_1}{k(k+1)} - \frac{(2m-r_1-1)(r_2-1)}{(m-1)k(k+1)}\right) \\&\quad \frac{1}{m-r_2} - \frac{1}{k+1}\\&\quad = \frac{(m-1)(r_2k+r_1-k-m) - (2m-r_1-1)(r_2-1)}{(m-r_2)k(k+1)(m-1)}. \end{aligned}$$

Clearly, the denominator is positive. Since $k = qm + r_1$, the numerator can be written as

$$\begin{aligned}&(m-1)(r_2k+r_1-k-m) - (2m-r_1-1)(r_2-1) \\&\quad = \Big \{((r_2-1)q - 1) m^2 \Big \} + \Big \{(r_1 - q - 2) r_2m\Big \} \\&\qquad + \Big \{(q + 3) m + r_2 - r_1 - 1 \Big \}. \end{aligned}$$

The first part is $((r_2-1)q-1)m^2 \ge 0$ since $r_2 > 1$. For the second part, by condition (9) of Case 2, and $r_1 \le m-1$, we have $q + 1 < r_1$. Since both q and $r_1$ are integer, $r_1 \ge q + 2$. Thus, the second part is $(r_1-q-2)r_2m \ge 0$. The last part is $(q+3)m + r_2 - r_1 - 1 > 0$ since $m > r_1$. Thus, the numerator is positive as well which completes the proof for Case 2.

In conclusion, if $r_2 > 1$ there is no counterexample with an Ab greater than B. Therefore, $r_2$ must be 1. $\square$

Fig. 9

The structure of a minimum counterexample when $r_2 = 1$

By Lemma 4, the only proof remaining is for the case $r_2 = 1$. Figure 9 shows the allocation of jobs to machines under schedule $\sigma$ when $r_2 = 1$. The Ab will be shown via Lemma 5. Job type 1 represents the jobs in schedule $\sigma ^*$ on machine i with $|S^*_{i}| = k$ and job type 2 represents the jobs in schedule $\sigma ^*$ on machine i with $|S^*_{i}| = k+1$. Since $p_j \le ({1}/{k}) C_{\max }^*$, we can always assume that the processing time of a type 1 job is greater than or equal to that of a type 2 job. We can also assume that type 1 jobs are scheduled by LPT earlier than type 2 jobs. Define $J^{(2)}$ as the set of all type 2 jobs. Then, since $r_2 = 1$, under schedule $\sigma ^*$ only one machine has $k+1$ jobs of job type 2. Thus, $P(J^{(2)}) \le C^*_{\max }$.

Lemma 5

If $r_2 = 1$ the approximation bound on LPT cannot be greater than B when $2 \le m < k$.

Proof

Suppose there exists a minimum counterexample.

For convenience, we introduce some additional notation. Let $t' \doteq (m-1)q + r_1$. See Fig. 9. Let set $T_1$ denote the set of machines with $t'$ jobs of type 1 under schedule $\sigma$ and let $T_2 \doteq M \setminus T_1$. In this case, by definition, $|T_1| = m - r_1$ and $|T_2| = r_1$. Let $J_i \doteq \bigcup ^{mq + r_1}_{t = t'} \{ u(i,t) \}$, $i \in T_2$, which represents all type 2 jobs on some machine $i \in T_2$ except job n. Finally, define

$$\begin{aligned} E \doteq \bigcup ^{mq + r_1}_{t = t'+1} \bigcup _{i \in T_1} \{u(i,t)\}, \end{aligned}$$

which represents all type 2 jobs on some machine $i \in T_1$ except job n.

Since $p_j \le ({1}/{k}) C^*_{\max }$ for all $j\in J$,

$$\begin{aligned} \sum ^{t'-1}_{t=1} p_{u(i,t)} \le (t'-1) \frac{1}{k} C^*_{\max } \quad \forall i \in T_2. \end{aligned}$$

Moreover, by the counterexample assumption,

$$\begin{aligned} \sum ^{t'-1}_{t=1} p_{u(i,t)} + p(J_i) + p_n > B C^*_{\max } \quad \forall i \in T_2. \end{aligned}$$

Thus,

$$\begin{aligned}&p(J_i) + p_n \nonumber \\&\quad > \left( B - (t'-1) \frac{1}{k}\right) C^*_{\max } \nonumber \\&\quad = \left( B - ((m-1)q + r_1-1) \frac{1}{k}\right) C^*_{\max } \quad \forall i \in T_2. \end{aligned}$$

(11)

In Case 1, by condition (8), $|E| \ge r_1 - 1$. We consider a set $E'$ such that $E' \subset E$ and $|E'| = r_1 - 1$ and a machine $i'$ such that $i' \in T_2$. Define a bijective function $\psi _1: T_2\setminus \{i'\} \rightarrow E'$. By inequality (11) and $q = ({k-r_1})/{m}$, we have

$$\begin{aligned}&p(J_i) + p_{\psi _1(i)} \nonumber \\&\quad > \left( B_1 - ((m-1)q + r_1-1) \frac{1}{k}\right) C^*_{\max } \quad \forall i \in T_2 \setminus \{i'\} \nonumber \\&\quad = \left( \frac{1}{m} + \frac{2mk-k-r_1k+r^2_{1}-2mr_1 +m}{mk(k-r_1+1)} \right) C_{\max }^*.\nonumber \\ \end{aligned}$$

(12)

Moreover,

$$\begin{aligned}&p(J_{i'}) + p_n \nonumber \\&\quad > \left( \frac{1}{m} + \frac{2mk-k-r_1k+r^2_{1}-2mr_1 +m}{mk(k-r_1+1)} \right) C_{\max }^*.\nonumber \\ \end{aligned}$$

(13)

Define

$$\begin{aligned} \tilde{J} \doteq \left( \bigcup _{i \in T_2}J_i\right) \cup E' \cup \{p_n \}, \end{aligned}$$

which is a set of all type 2 jobs used in inequalities (12) and (13). Thus,

$$\begin{aligned} p\left( \tilde{J}\right)> & {} r_1 \left( \frac{1}{m} + \frac{2mk-k-r_1k+r^2_{1}-2mr_1 +m}{mk(k-r_1+1)} \right) C_{\max }^*. \end{aligned}$$

Moreover, $J^{(2)} \setminus \tilde{J}$ is the set of remaining type 2 jobs which are not used in inequalities (12) and (13). Since $p(J^{(2)}) \le C_{\max }^*$,

$$\begin{aligned}&p\left( J^{(2)}\setminus \tilde{J}\right) \nonumber \\&\quad < \left( 1 - r_1 \left( \frac{1}{m} + \frac{2mk-k-r_1k+r^2_{1}-2mr_1 +m}{mk(k-r_1+1)} \right) \right) C_{\max }^* \nonumber \\&\quad = \left( \frac{m-r_1}{m} - \frac{r_1(2m-r_1-1)}{m(k-r_1+1)} - \frac{r_1(r_1^2-2mr_1+m)}{mk(k-r_1+1)}\right) C_{\max }^*.\nonumber \\ \end{aligned}$$

(14)

From another perspective, $J^{(2)}\setminus \tilde{J} = E\setminus E'$ by definition of $\tilde{J}$. Thus, $|J^{(2)}\setminus \tilde{J}| = |E| - |E'| = q(m-r_1) - r_1 + 1$. Moreover, $p_j> p_n > (k-r_1)/k(k-r_1+1)$ by inequality (10). Hence,

$$\begin{aligned}&p\left( J^{(2)} \setminus \tilde{J}\right) \nonumber \\&\quad > \left( ((m-r_1)q - r_1 + 1)\frac{k-r_1}{k(k-r_1+1)}\right) C_{\max }^* \nonumber \\&\quad = \left( \frac{km-kr_1+2r^2_{1}-3r_1m +m}{m(k-r_1+1)}\right. \nonumber \\&\qquad \left. - \frac{r_1(r^2_{1}-2mr_1+m)}{mk(k-r_1+1)} \right) C_{\max }^* \nonumber \\&\quad = \left( \frac{m-r_1}{m} - \frac{r_1(2m-r_1-1)}{m(k-r_1+1)} \right. \nonumber \\&\qquad \left. - \frac{r_1(r_1^2-2mr_1+m)}{mk(k-r_1+1)}\right) C_{\max }^*. \end{aligned}$$

(15)

Inequalities (14) and (15) contradict one another. Therefore, there is for Case 1 no such counterexample with a greater Ab.

For Case 2, by condition (9), we have $|E| < |T_2| - 1$. We consider $T'_2$ such that $T'_2 \subset T_2$ and $|T'_2| = |E|$. Define a bijective function $\psi _2: T'_2 \rightarrow E$. Then, by inequality (11) and $q = ({k-r_1})/{m}$, the following inequality holds.

$$\begin{aligned}&p(J_i) + p_{\psi _2(i)}\nonumber \\&\quad > \left( B_2 - ((m-1)q + r_1-1) \frac{1}{k}\right) C^*_{\max } \quad \forall i \in T'_2 \nonumber \\&\quad = \left( \frac{1}{m} + \frac{2mk-(r_1+1)k}{mk(k+1)} \right) C_{\max }^*. \end{aligned}$$

(16)

In addition, we consider $i''$ such that $i'' \in T_2 \setminus T'_2$. Then, we have

$$\begin{aligned} p(J_{i''}) + p_n> & {} \left( \frac{1}{m} + \frac{2mk-(r_1+1)k}{mk(k+1)} \right) C_{\max }^*. \end{aligned}$$

(17)

Hence, we have a total of $|E| + 1$ inequalities. Define

$$\begin{aligned} \overset{\approx }{J} \doteq E \cup \left( \bigcup _{i \in T'_2 \cup \{i''\} } J_i \right) \cup \{p_n\}, \end{aligned}$$

which is a set of type 2 jobs used in inequalities (16) and (17). Thus,

$$\begin{aligned} p\left( \overset{\approx }{J}\right) > (|E|+1) \left( \frac{1}{m} + \frac{2mk-(r_1+1)k}{mk(k+1)} \right) C_{\max }^*. \end{aligned}$$

Since $p(J^{(2)}) \le C_{\max }^*$, we have

$$\begin{aligned}&p\left( J^{(2)} \setminus \overset{\approx }{J}\right) \\&\quad < \left( 1 - (|E|+1) \left( \frac{1}{m} + \frac{2mk-(r_1+1)k}{mk(k+1)} \right) \right) C_{\max }^*. \end{aligned}$$

Then, there must exist a machine $i^*$ such that $i^* \in T_2 \setminus (T'_2 \cup \{i''\})$ satisfying the following condition.

$$\begin{aligned} p(J_{i^*})< & {} \left( 1 - (|E| + 1)\left( \frac{1}{m} + \frac{2mk-(r_1+1)k}{mk(k+1)}\right) \right) \\&\frac{1}{r_1-(|E|+1)} C_{\max }^* \\= & {} \left( \frac{-(q^2 + q)m + r_1 + q^2 r_1 - q + 2 q r_1 - 1 }{k+1} \right) \\&\frac{1}{r_1-((m-r_1)q + 1)} C_{\max }^* \\= & {} \frac{q + 1}{k+1}C_{\max }^*. \end{aligned}$$

Whether or not job n is assigned to machine $i^*$ by LPT, the following inequality holds.

$$\begin{aligned} C_{\max }\le & {} p(J_{i^*}) + \frac{(m-1)q+r_1-1}{k}C_{\max }^* + p_n \\< & {} \left( \frac{q + 1}{k+1} + \frac{(m-1)q+r_1-1}{k} + \frac{1}{k+1}\right) C_{\max }^* \\= & {} \left( 1 + \frac{k-1}{k(k+1)} - \frac{k-r_1}{mk(k+1)}\right) C_{\max }^*. \end{aligned}$$

It leads to a contradiction. Thus, there is no counterexample for Case 2. Therefore, there is no instance with a greater Ab than B when $r_2 = 1$ and the proof is complete. $\square$

Theorem 5

The approximation bound on LPT for $P \mid p_j \le \frac{1}{k} C_{\max }^* \mid C_{\max }$ with $2 \le m < k$ is

$$\begin{aligned} B&\doteq \max \left( 1+ \frac{m-1}{m}\frac{k-r_1}{k(k-r_1+1)}, \right. \\&\quad \left. 1 + \frac{k-1}{k(k+1)} - \frac{k-r_1}{mk(k+1)}\right) \end{aligned}$$

and it is tight.

Proof

By Lemma 2, when $r_1 = 0$, the Ab is proved. In addition, Lemma 4 proves the case when $r_2 \ge 2$ and $r_1 \ge 1$. Finally, Lemma 5 proves the case when $r_2 = 1$ and $r_1 \ge 1$. By those Lemmas, we prove that the Ab cannot be greater than B.

Fig. 10

A tight example of LPT when $2 \le m < k$ and $q(m-r_1) \ge r_1 - 1$

Fig. 11

A tight example of LPT when $2 \le m < k$ and $q(m-r_1) < r_1 - 1$

The tightness can be shown for each case. In Case 1, we consider the following problem instance with $km+1$ jobs on m machines. See Fig. 10. From the example, the processing time of a type 2 job is less than the processing time of a type 1 job.

Job type	Processing time	The number of jobs
1	1/k	$(k-\lfloor k/m \rfloor )m$
2	$(1/k) \left( \frac{\lfloor k/m \rfloor m}{\lfloor k/m \rfloor m + 1}\right)$	$\lfloor k/m \rfloor m + 1$

In schedule $\sigma ^*$, there are two types of machines according to the composition of job types and the optimal makespan is 1.

Machine type	The number of machines	The number of jobs of each type
		Job type 1	Job type 2
1	$m-1$	k	0
2	1	$k - \lfloor k/m \rfloor m$	$\lfloor k/m \rfloor m + 1$

In schedule $\sigma$, there are two types of machines according to the composition of job types.

Machine type	Number of machines	Number of jobs of each type
		job type 1	job type 2
3	1	$k-\lfloor k/m \rfloor$	$\lfloor k/m \rfloor + 1$
4	$m-1$	$k-\lfloor k/m \rfloor$	$\lfloor k/m \rfloor$

The makespan of schedule $\sigma$ is determined by machine type 4. Recall that $\lfloor k/m \rfloor = q$ and $k = qm + r_1$. Therefore, the Tab is

$$\begin{aligned} \frac{C_{\max }(\sigma )}{C_{\max }(\sigma ^*)} \!= & {} \!\frac{1}{k} \left( k \!-\! \left\lfloor k/m \right\rfloor \right) \! + \!\frac{1}{k} \left( \!\frac{\lfloor k/m \rfloor m}{\lfloor k/m \rfloor m + 1}\!\right) \left( \left\lfloor k/m \right\rfloor + 1\right) \\= & {} 1 + \frac{q(m-1)}{k(k-r_1+1)} \!=\! 1 + \frac{m-1}{m}\frac{k-r_1}{k(k-r_1+1)}. \end{aligned}$$

In Case 2, we consider the following problem instance with $km+1$ jobs and m machines. See Fig. 11.

Job type	Processing time	The number of jobs
1	1/k	$k(m-1)$
2	$1/(k+1)$	$k+1$

In schedule $\sigma ^*$, there are two types of machines, based on the composition of the job types and the optimal makespan is 1.

Machine type	The number of machines	The number of jobs of each type
		Job type 1	Job type 2
1	$m-1$	k	0
2	1	0	$k + 1$

In schedule $\sigma$, there are three types of machines, based on the composition of job types.

Machine type	Number of machines	Number of jobs of each type
		Job type 1	Job type 2
3	$m-r_1$	$(m-1)\lfloor k/m \rfloor + r_1$	$\lfloor k/m \rfloor$
4	$r_1-1$	$(m-1)\lfloor k/m \rfloor + r_1 - 1$	$\lfloor k/m \rfloor + 1$
5	1	$(m-1)\lfloor k/m \rfloor + r_1-1$	$\lfloor k/m \rfloor + 2$

The makespan of schedule $\sigma$ is determined by machine type 5. Therefore, we have

$$\begin{aligned} \frac{C_{\max }(\sigma )}{C_{\max }(\sigma ^*)}= & {} \frac{1}{k}((m-1)q + r_1 - 1) + \frac{1}{k+1} (q + 2) \\= & {} 1 + \frac{k-1}{k(k+1)} - \frac{k-r_1}{mk(k+1)}. \end{aligned}$$

This proves the tightness for Case 2. Thus, Ab B is tight. $\square$

4 Comparisons of approximation bounds

This section considers Abs in previous research that attempt to improve on the bounds by Graham (1969) as mentioned in Sect. 1; we compare our Tab to these previous bounds. Thus, we present the previous result of Coffman and Sethi (1976), Chen (1993), Blocher and Sevastyanov (2015) and Della Croce and Scatamacchia (2020). The following Theorems provide an overview of the results concerning LPT. Each theorem uses a different parameter as a basis for evaluating LPT.

Theorem 6

(Coffman and Sethi 1976) Let $i'$ be the critical machine, and $N \doteq |S^n_{i'}|$. Then

The bound by Blocher and Sevastyanov (2015) is determined as follows. Given an LPT-schedule $\sigma$, let $n' \in J$ be its terminating job, i.e., the job whose completion time coincides with the makespan. Then, a truncated job instance is defined as $J' \doteq \{1,2,\ldots ,n'\} \subseteq J$. Blocher and Sevastyanov (2015) showed that the Tab on LPT under schedule $\sigma$ is determined by the maximum number of jobs in $J'$ on any machine.

Theorem 7

(Blocher and Sevastyanov 2015) Under schedule $\sigma$, if the makespan is determined by job $n'$ and $N' \doteq \max _{i\in M} |S^{n'}_{i}|$, then

The Ab by Della Croce and Scatamacchia (2020) can be expressed as follows.

Theorem 8

(Della Croce and Scatamacchia 2020) Under schedule $\sigma$, if the makespan is determined by job $n'$ scheduled on machine $i'$ and $N'' \doteq \max _{i \in M\setminus \{i'\}} |S^{n'-1}_{i}|$, then

$$\begin{aligned} \frac{C_{\max }}{C^*_{\max }}&\le \frac{N''+1}{N''} - \frac{1}{N''(m-1)} \quad \text {when} \ N'' \le m- 2 \end{aligned}$$

Each Theorem is based on a different parameter for computing Abs. Theorem 6 uses the number of jobs on the critical machine(N) for the whole job instance (which coincides with that for the truncated instance). In contrast, Theorem 8 uses the maximum number of jobs on a noncritical machine the truncated job instance($N''$). Theorem 7 uses the maximum number of jobs on any machine (regardless of critical or non-critical) in the truncated job instance($N'$). We denote the Abs by Coffman and Sethi (1976), Chen (1993), Blocher and Sevastyanov (2015), and Della Croce and Scatamacchia (2020) as CS-bound, Ch-bound, BS-bound, and DS-bound, respectively.

Table 2 Comparison of our Tab with previous Abs

Before a comparison, we need to compare the features of our Tab to the previous Abs. It should be noted that our Tab (in contrast to previously known a priori and a posteriori bounds) is of a purely theoretical nature. In particular, it enables one to find classes of instances that include cases for which none of the known bounds are exact. However, unlike known a priori and a posteriori bounds, our Tab cannot be applied to estimate the Tab of LPT for any given instance I, since we have no efficient algorithm for answering the question: ‘whether a given instance I belongs to class ${\mathcal {I}}_{k,m}$ for a fixed value of k?’ Thus, comparing previous Abs with our Tab for an arbitrary instance I is not possible.

Instead, we attempt to show the existence of classes where our Tab is better (smaller) or equal to any previous Abs for all instances of the classes. We consider the relationship between the parameters describing each Ab. Previous Abs use parameters N, $N'$, $N''$ and m, and our Tab uses parameters k and m. Since $N' = \max (N,N'')$, we only need to consider four parameters N, $N''$, k and m in the comparison. We compare our Tab with previous Abs for every feasible combination of the parameters and show that there exist classes of instances for which our Tab is better than any other previous Abs.

Table 2 exhibits a comprehensive comparison of our Tab and the previous Abs among different classes of instances. For the main case, we have classes where $N=1,N=2$ and $N\ge 3$. In the first sub-case, we consider the case when LPT is optimal, and then two cases depending on whether the DS-bound is applicable ($N'' \le m-2$) or not ($N'' \ge m-1$). Then, we consider the range of $N''$ as the second sub-case. For the last sub-case condition, we apply a more specific range of m when $N=2$, and we apply a range of k for the classes with $N \ge 3$. A ‘-’ in the Table means that the DS–bound is not applicable for the corresponding class.

For any instance I, the following relationship holds.

$$\begin{aligned} kp_{\max }[I] \le C^*_{\max }[I] \le C_{\max }[I] \le Np_{\max }[I] \end{aligned}$$

and it implies, $N \ge k$. On the other hand, by our problem definition, any truncated instance contains at least $m(k-1) + 1$ jobs, which implies $N'' \ge k-1$. Note that instances with $N'' = k-1$ are included in the class of instances where $N = k$, where the LPT schedule is indeed optimal.

For the instances with $N=1$, the LPT schedule is optimal. For the instances with $N=2$, the LPT schedule is optimal when $m=2$ or $N''=1$ or $k=2$. For the remaining instances with $N = 2$ (satisfying $(k = 1) \& (m \ge 3)$ &$(N'' \ge 2)$), where our Tab is the same as that of Graham (1969), there are eight classes of instances specified by values of $N''$ and m. For all the classes, however, our Tab is dominated by the Ch–bound. Thus, there is no such instance for which our Tab is the best when $N \le 2$.

For the instances with $N \ge 3$, eleven classes of instances are defined. If $N=k$, then LPT is optimal. Otherwise, our bound is the best for instances of three classes satisfying relations $N'' \le N = k+1$. More specifically, our Tab is better than or equal to the previous Abs in class 12, and there exists at least one instance such that our Tab is strictly better than the previous Abs. On the other hand, our Tab is strictly better than the previous Abs in classes 16 and 19 for any instance. Considering conditions for k and m in defining our Tab, our Tab, the previous best Ab, and the comparison between the two are presented in Table 3.

Table 3 Classes where our Tab is the best

5 Conclusion

We investigate the performance of LPT applied to $P \mid p_j \le \frac{1}{k}C_{\max }^* \mid C_{\max }$ when the processing times of the jobs are restricted and we analyze how the restrictions on the processing times affect the Ab. It is to be expected that the Ab in such a setting may be less than or equal to the Ab in more general parallel machine settings. The results show the effectiveness of LPT when there are many small jobs.

We consider the problem for all positive integer values of k and show that the Ab depends on the relationship between m and k. We discover the Abs for all cases and show that all obtained Abs are tight. We also show that our Tabs can be used to complement the performance analysis of LPT that has appeared in previous research.

As an extension, we can consider a problem with only a subset of the jobs being subject to restrictions on their processing times. That is, some jobs may have processing times greater than $({1}/{k}) C^*_{\max }$, but we still have a number of small jobs. With such an extension, we may obtain a more general form of performance guarantee for LPT. As a future research direction, we can consider establishing Abs with k being any real value.

We can also consider an approach utilizing the differences in processing times as proposed by Della Croce and Scatamacchia (2020). They divided jobs into $\lceil n/m \rceil$ sets, namely $\{1,2,\ldots ,m\}, \{m+1,m+2,\ldots ,2m\}$, $\ldots ,$ and calculated the slack for each set, which means the difference between the maximum and the minimum processing time. The jobs in a set are iteratively scheduled on the different machines in decreasing order of the slack of the set. Such a slack-based approach performs very well in practice. However, except for the performance analysis done by Eck and Pinedo (1993) for the two machine case, no subsequent research has appeared in the literature with regard to this type of approach. We expect that with our approach, i.e., imposing restrictions on the job processing times, more results can be obtained in this direction.