A parameterized complexity view on non-preemptively scheduling interval-constrained jobs: few machines, small looseness, and small slack

Abstract

We study the problem of non-preemptively scheduling n jobs, each job j with a release time $t_j$, a deadline $d_j$, and a processing time $p_j$, on m parallel identical machines. Cieliebak et al. (2004) considered the two constraints $|d_j-t_j|\le \lambda {}p_j$ and $|d_j-t_j|\le p_j +\sigma$ and showed the problem to be NP-hard for any $\lambda >1$ and for any $\sigma \ge 2$. We complement their results by parameterized complexity studies: we show that, for any $\lambda >1$, the problem remains weakly NP-hard even for $m=2$ and strongly W[1]-hard parameterized by m. We present a pseudo-polynomial-time algorithm for constant m and $\lambda$ and a fixed-parameter tractability result for the parameter m combined with $\sigma$.

1 Introduction

Non-preemptively scheduling jobs with release times and deadlines on a minimum number of machines is a well-studied problem both in offline and online variants (Chen et al. 2016; Chuzhoy et al. 2004; Cieliebak et al. 2004; Malucelli and Nicoloso 2007; Saha 2013). In its decision version, the problem is formally defined as follows:

For a job $j\in J$, we call the half-open interval $[t_j,d_j)$ its time window. A job may only be executed during its time window. The length of the time window is $d_j-t_j$.

We study Interval-Constrained Scheduling with two additional constraints introduced by Cieliebak et al. (2004). These constraints relate the time window lengths of jobs to their processing times:

Looseness If all jobs $j\in J$ satisfy $|d_j-t_j|\le \lambda p_j$ for some number $\lambda \in \mathbb {R}$, then the instance has looseness $\lambda$. By $\lambda$-Loose Interval-Constrained Scheduling we denote the problem restricted to instances of looseness $\lambda$.

Table 1 Overview of results on Interval-Constrained Scheduling for various parameter combinations. The parameterized complexity with respect to the combined parameter $\lambda + \sigma$ remains open

Slack If all jobs $j\in J$ satisfy $|d_j-t_j|\le p_j + \sigma$ for some number $\sigma \in {\mathbb R}$, then the instance has slack $\sigma$. By $\sigma$-Slack Interval-Constrained Scheduling we denote the problem restricted to instances of slack $\sigma$.

Both constraints on Interval-Constrained Scheduling are very natural: clients may accept some small deviation of at most $\sigma {}$ from the desired start times of their jobs. Moreover, it is conceivable that clients allow for a larger deviation for jobs that take long to process anyway, leading to the case of bounded looseness $\lambda$.

Cieliebak et al. (2004) showed that, even for constant $\lambda >1$ and constant $\sigma \ge 2$, the problems $\lambda$-Loose Interval-Constrained Scheduling and $\sigma$-Slack Interval-Constrained Scheduling are strongly NP-hard.

Instead of giving up on finding optimal solutions and resorting to approximation algorithms (Chuzhoy et al. 2004; Cieliebak et al. 2004), we conduct a more fine-grained complexity analysis of these problems employing the framework of parameterized complexity theory (Cygan et al. 2015; Downey and Fellows 2013; Flum and Grohe 2006; Niedermeier 2006), which so far received comparatively little attention in the field of scheduling with seemingly only a handful of publications (van Bevern et al. 2015a, b; Bodlaender and Fellows 1995; Cieliebak et al. 2004; Fellows and McCartin 2003; Halldórsson and Karlsson 2006; Hermelin et al. 2015; Mnich and Wiese 2015). In particular, we investigate the effect of the parameter m of available machines on the parameterized complexity of interval-constrained scheduling without preemption.

Related work Interval-Constrained Scheduling is a classical scheduling problem and strongly NP-hard already on one machine (Garey and Johnson 1979, problem SS1). Besides the task of scheduling all jobs on a minimum number of machines, the literature contains a wide body of work concerning the maximization of the number of scheduled jobs on a bounded number of machines (Kolen et al. 2007).

For the objective of minimizing the number of machines, Chuzhoy et al. (2004) developed a factor-$O\left( \sqrt{\log n/\log \log n}\right)$-approximation algorithm. Malucelli and Nicoloso (2007) formalized machine minimization and other objectives in terms of optimization problems in shiftable interval graphs. Online algorithms for minimizing the number of machines have been studied as well and we refer to recent work by Chen et al. (2016) for an overview.

Our work refines the following results of Cieliebak et al. (2004), who considered Interval-Constrained Scheduling with bounds on the looseness and the slack. They showed that Interval-Constrained Scheduling is strongly NP-hard for any looseness $\lambda >1$ and any slack $\sigma \ge 2$. Besides giving approximation algorithms for various special cases, they give a polynomial-time algorithm for $\sigma =1$ and a fixed-parameter tractability result for the combined parameter $\sigma$ and $h{}$, where $h{}$ is the maximum number of time windows overlapping in any point in time.

Our contributions We analyze the parameterized complexity of Interval-Constrained Scheduling with respect to three parameters: the number m of machines, the looseness $\lambda$, and the slack $\sigma$. More specifically, we refine known results of Cieliebak et al. (2004) using tools of parameterized complexity analysis. An overview is given in Table 1.

In Sect. 3, we show that, for any $\lambda >1$, $\lambda$-Loose Interval-Constrained Scheduling remains weakly NP-hard even on $m=2$ machines and that it is strongly W[1]-hard when parameterized by the number m of machines. In Sect. 4, we give a pseudo-polynomial-time algorithm for $\lambda$-Loose Interval-Constrained Scheduling for each fixed $\lambda$ and m. Finally, in Sect. 5, we give a fixed-parameter algorithm for $\sigma$-Slack Interval-Constrained Scheduling when parameterized by m and $\sigma$. This is in contrast to our result from Sect. 3 that the parameter combination m and $\lambda$ presumably does not give fixed-parameter tractability results for $\lambda$-Loose Interval-Constrained Scheduling.

2 Preliminaries

Basic notation We assume that $0\in {\mathbb N}$. For two vectors $\mathbf {u}=(u_1,\ldots ,u_k)$ and $\mathbf {v}=(v_1,\ldots ,v_k)$, we write $\mathbf {u}\le \mathbf {v}$ if $u_i\le v_i$ for all $i\in \{1,\ldots ,k\}$. Moreover, we write $\mathbf {u}\lneqq \mathbf {v}$ if $\mathbf {u}\le \mathbf {v}$ and $\mathbf {u}\ne \mathbf {v}$, that is, $\mathbf {u}$ and $\mathbf {v}$ differ in at least one component. Finally, $\mathbf {1}^k$ is the k-dimensional vector consisting of k 1-entries.

Computational complexity We assume familiarity with the basic concepts of NP-hardness and polynomial-time many-one reductions (Garey and Johnson 1979). We say that a problem is (strongly) C-hard for some complexity class C if it is C-hard even if all integers in the input instance are bounded from above by a polynomial in the input size. Otherwise, we call it weakly C-hard.

In the following, we introduce the basic concepts of parameterized complexity theory, which are more detailedly discussed in the corresponding text books (Cygan et al. 2015; Downey and Fellows 2013; Flum and Grohe 2006; Niedermeier 2006).

Fixed-parameter algorithms The idea in fixed-parameter algorithms is to accept exponential running times, which are seemingly inevitable in solving NP-hard problems, but to restrict them to one aspect of the problem, the parameter.

Thus, formally, an instance of a parameterized problem $\varPi$ is a pair (x, k) consisting of the input x and the parameter k. A parameterized problem $\varPi$ is fixed-parameter tractable (FPT) with respect to a parameter k if there is an algorithm solving any instance of $\varPi$ with size n in $f(k) \cdot {{\mathrm{poly}}}(n)$ time for some computable function f. Such an algorithm is called a fixed-parameter algorithm. It is potentially efficient for small values of k, in contrast to an algorithm that is merely running in polynomial time for each fixed k (thus allowing the degree of the polynomial to depend on k). FPT is the complexity class of fixed-parameter tractable parameterized problems.

We refer to the sum of parameters $k_1+k_2$ as the combined parameter $k_1$ and $k_2$.

Parameterized intractability To show that a problem is presumably not fixed-parameter tractable, there is a parameterized analog of NP-hardness theory. The parameterized analog of NP is the complexity class W[1]${}\supseteq {}$FPT, where it is conjectured that FPT${}\ne {}$W[1]. A parameterized problem $\varPi$ with parameter $k$ is called W[1]-hard if $\varPi$ being fixed-parameter tractable implies W[1]${}={}$FPT. W[1]-hardness can be shown using a parameterized reduction from a known W[1]-hard problem: a parameterized reduction from a parameterized problem $\varPi _1$ to a parameterized problem $\varPi _2$ is an algorithm mapping an instance I with parameter k to an instance $I^{\prime }$ with parameter $k^{\prime }$ in time $f(k)\cdot {{\mathrm{poly}}}(|I|)$ such that $k^{\prime }\le g(k)$ and $I^{\prime }$ is a yes-instance for $\varPi _1$ if and only if I is a yes-instance for $\varPi _2$, where $f$ and $g$ are arbitrary computable functions.

3 A strengthened hardness result

In this section, we strengthen a hardness result of Cieliebak et al. (2004), who showed that $\lambda$-Loose Interval-Constrained Scheduling is NP-hard for any $\lambda >1$. This section proves the following theorem:

Theorem 3.1

Let $\lambda {}:{\mathbb N}\rightarrow {\mathbb R}$ be such that $\lambda {}(n)\ge 1+n^{-c}$ for some integer $c\ge 1$ and all $n\ge 2$.

Then $\lambda (n)$-Loose Interval-Constrained Scheduling of n jobs on m machines is

• (i) weakly NP-hard for $m=2$, and

• (ii) strongly W[1]-hard for parameter m.

Note that Theorem 3.1, in particular, holds for any constant function $\lambda (n)>1$.

We remark that Theorem 3.1 cannot be proved using the NP-hardness reduction given by Cieliebak et al. (2004), which reduces 3-Sat instances with $k$ clauses to Interval-Constrained Scheduling instances with $m=3k$ machines. Since 3-Sat is trivially fixed-parameter tractable for the parameter number $k$ of clauses, the reduction of Cieliebak et al. (2004) cannot yield Theorem 3.1.

Fig. 1

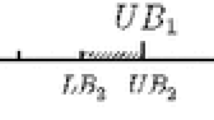
Reduction from Bin Packing with four items $a_1=1,a_2=a_3=2,a_4=3$, bin volume $V=3$, and $m=3$ bins to 3/2-Loose Interval-Constrained Scheduling. That is, Construction 3.2 applies with $c=1$, $A=8$, and $B=3\cdot 4\cdot 8=96$. The top diagram shows (not to scale) the jobs created by Construction 3.2. Herein, the processing time of each job is drawn as a rectangle of corresponding length in an interval being the job’s time window. The bottom diagram shows a feasible schedule for three machines $M_1,M_2$, and $M_3$ that corresponds to putting items $a_1$ and $a_3$ into the first bin, item $a_2$ into the second bin, and $a_4$ into the third bin

Instead, to prove Theorem 3.1, we give a parameterized polynomial-time many-one reduction from Bin Packing with m bins and n items to $\lambda (mn)$-Loose Interval-Constrained Scheduling with m machines and mn jobs.

Since Bin Packing is weakly NP-hard for $m=2$ bins and W[1]-hard parameterized by m even if all input numbers are polynomial in n (Jansen et al. 2013), Theorem 3.1 will follow.

Our reduction, intuitively, works as follows: for each of the $n$ items $a_i$ in a Bin Packing instance with $m$ bins of volume $V$, we create a set $J_i:=\{j^1_i,\ldots ,j^m_i\}$ of $m$ jobs that have to be scheduled on $m$ mutually distinct machines. Each machine represents one of the $m$ bins in the Bin Packing instance. Scheduling job $j_i^1$ on a machine $k$ corresponds to putting item $a_i$ into bin $k$ and will take $B+a_i$ time of machine $k$, where $B$ is some large integer chosen by the reduction. If $j_i^1$ is not scheduled on machine $k$, then a job in $J_i\setminus \{j_i^1\}$ has to be scheduled on machine $k$, which will take only $B$ time of machine $k$. Finally, we choose the latest deadline of any job as $nB+V$. Thus, since all jobs have to be finished by time $nB+V$ and since there are $n$ items, for each machine $k$, the items $a_i$ for which $j_i^1$ is scheduled on machine $k$ must sum up to at most $V$ in a feasible schedule. This corresponds to satisfying the capacity constraint of $V$ of each bin.

Formally, the reduction works as follows and is illustrated in Fig. 1.

Construction 3.2

Given a Bin Packing instance I with $n\ge 2$ items $a_1,\ldots ,a_n$ and $m\le n$ bins, and $\lambda {}:{\mathbb N}\rightarrow {\mathbb R}$ such that $\lambda {}(n)\ge 1+n^{-c}$ for some integer $c\ge 1$ and all $n\ge 2$, we construct an Interval-Constrained Scheduling instance with m machines and mn jobs as follows. First, let

$$\begin{aligned} A:=\sum _{i=1}^n a_i \quad \text {and}\quad B:=(mn)^c\cdot A\ge 2A. \end{aligned}$$

If $V>A$, then I is a yes-instance of Bin Packing and we return a trivial yes-instance of Interval-Constrained Scheduling.

Otherwise, we have $V\le A$ and construct an instance of Interval-Constrained Scheduling as follows: for each $i \in \{1, \ldots , n\}$, we introduce a set $J_i:=\left\{ j^1_i,\ldots ,j^m_i\right\}$ of jobs. For each job $j\in J_i$, we choose the release time

$$\begin{aligned} t_{j}&:=(i-1)B, \end{aligned}$$

the processing time

$$\begin{aligned} \begin{aligned} p_j&:={\left\{ \begin{array}{ll} B+a_i&{}\quad \text {if } j=j_i^1,\\ B&{}\quad \text {if } j\ne j_i^1, \end{array}\right. }\\ \end{aligned} \end{aligned}$$

(3.1)

and the deadline

$$\begin{aligned} d_{j}&:= {\left\{ \begin{array}{ll} iB+A&{}\quad \text {if } i<n,\\ iB+V&{}\quad \text {if } i=n. \end{array}\right. } \end{aligned}$$

This concludes the construction. $\square$

Remark 3.3

Construction 3.2 outputs an Interval-Constrained Scheduling instance with agreeable deadlines, that is, the deadlines of the jobs have the same relative order as their release times. Thus, in the offline scenario, all hardness results of Theorem 3.1 will also hold for instances with agreeable deadlines.

In contrast, agreeable deadlines make the problem significantly easier in the online scenario: Chen et al. (2016) showed an online algorithm with constant competitive ratio for Interval-Constrained Scheduling with agreeable deadlines, whereas there is a lower bound of n on the competitive ratio for general instances (Saha 2013).

In the remainder of this section, we show that Construction 3.2 is correct and satisfies all structural properties that allow us to derive Theorem 3.1.

First, we show that Construction 3.2 indeed creates an Interval-Constrained Scheduling instance with small looseness.

Lemma 3.4

Given a Bin Packing instance with $n\ge 2$ items and m bins, Construction 3.2 outputs an Interval-Constrained Scheduling instance with

• (i) at most m machines and mn jobs and

• (ii) looseness $\lambda (mn)$.

Proof

It is obvious that the output instance has at most mn jobs and m machines and, thus, (i) holds.

Towards (ii), observe that $mn\ge n\ge 2$, and hence, for each $i\in \{1,\ldots ,n\}$ and each job $j\in J_i$, (3.1) yields

$$\begin{aligned} \frac{|d_j-t_j|}{p_j}\le & {} \frac{(iB+A)-(i-1)B}{B} =\frac{B+A}{B} = 1+\frac{A}{B}\\= & {} 1+\frac{A}{(mn)^c\cdot A}= 1+(mn)^{-c}\le \lambda {}(mn). \square \end{aligned}$$

We now show that Construction 3.2 runs in polynomial time and that, if the input Bin Packing instance has polynomially bounded integers, then so has the output Interval-Constrained Scheduling instance.

Lemma 3.5

Let I be a Bin Packing instance with $n\ge 2$ items $a_1,\ldots ,a_n$ and let $a_{\mathrm{max}}:=\max _{1\le i\le n}a_i$. Construction 3.2 applied to I

• (i) runs in time polynomial in |I| and

• (ii) outputs an Interval-Constrained Scheduling instance whose release times and deadlines are bounded by a polynomial in $n+a_{\mathrm{max}}$.

Proof

We first show (ii), thereafter we show (i).

(ii) It is sufficient to show that the numbers A and B in Construction 3.2 are bounded polynomially in $n+a_{\mathrm{max}}$ since all release times and deadlines are computed as sums and products of three numbers not larger than A, B, or n. Clearly, $A=\sum _{i=1}^na_i\le n\cdot \max _{1\le i\le n}a_i$, which is polynomially bounded in $n+a_{\mathrm{max}}$. Since $mn\le n^2$, also $B=(mn)^c\cdot A$ is polynomially bounded in $n+a_{\mathrm{max}}$.

(i) The sum $A=\sum _{1=1}^na_i$ is clearly computable in time polynomial in the input length. It follows that also $B=(mn)^c\cdot A$ is computable in polynomial time. $\square$

It remains to prove that Construction 3.2 maps yes-instances of Bin Packing to yes-instances of Interval-Constrained Scheduling, and no-instances to no-instances.

Lemma 3.6

Given a Bin Packing instance I with m bins and the items $a_1,\ldots ,a_n$, Construction 3.2 outputs an Interval-Constrained Scheduling instance $I^{\prime }$ that is a yes-instance if and only if I is.

Proof

($\Rightarrow$) Assume that I is a yes-instance for Bin Packing. Then, there is a partition $S_1\uplus \ldots \uplus S_m=\{1,\ldots ,n\}$ such that $\sum _{i\in S_k} a_i \le V$ for each $k\in \{1,\ldots ,m\}$. We construct a feasible schedule for $I^{\prime }$ as follows. For each $i \in \{1, \ldots , n\}$ and k such that $i\in S_k$, we schedule $j^1_i$ on machine k in the interval

$$\begin{aligned} \left[ (i-1)B+\sum _{j\in S_k, j < i} a_j\quad , \quad iB+{\sum _{j \in S_k, j < i}} a_j+a_i\right) \end{aligned}$$

and each of the $m-1$ jobs $J_i\setminus \{j_i^1\}$ on a distinct machine $\ell \in \{1,\ldots ,m\}\setminus \{k\}$ in the interval

$$\begin{aligned} \left[ (i-1)B+{\sum _{j\in S_\ell , j < i}} a_j\quad ,\quad iB+{\sum _{j \in S_\ell , j < i}} a_j\right) . \end{aligned}$$

It is easy to verify that this is indeed a feasible schedule.

($\Leftarrow$) Assume that $I^{\prime }$ is a yes-instance for Interval-Constrained Scheduling. Then, there is a feasible schedule for $I^{\prime }$. We define a partition $S_1\uplus \ldots \uplus S_m=\{1,\ldots ,n\}$ for I as follows. For each $k\in \{1,\ldots ,m\}$, let

$$\begin{aligned} S_k&:=\{i\in \{1,\ldots ,n\}\mid j_i^1\, \text { is scheduled on machine }k \}.\quad \end{aligned}$$

(3.2)

Since, for each $i\in \{1,\ldots ,n\}$, the job $j_i^1$ is scheduled on exactly one machine, this is indeed a partition. We show that $\sum _{i\in S_k} a_i \le V$ for each $k\in \{1,\ldots ,m\}$. Assume, towards a contradiction, that there is a k such that

$$\begin{aligned} \sum _{i\in S_k}a_i> V. \end{aligned}$$

(3.3)

By (3.1), for each $i \in \{1, \ldots , n\}$, the jobs in $J_i$ have the same release time, each has processing time at least B, and the length of the time window of each job is at most $B+A\le B+B/2 < 2B$. Thus, in any feasible schedule, the execution times of the m jobs in $J_i$ mutually intersect. Hence, the jobs in $J_i$ are scheduled on m mutually distinct machines. By the pigeonhole principle, for each $i\in \{1,\ldots ,n\}$, exactly one job $j_i^*\in J_i$ is scheduled on machine k. We finish the proof by showing that,

$$\begin{aligned}&\forall i\in \{1,\ldots ,n\},\, \text { job }\, j_i^{*} \text { is not finished before time}\nonumber \\&\quad iB +{\sum _{{j} \in S_k, j \le i}}a_j. \end{aligned}$$

(3.4)

This claim together with (3.3) then yields that job $j_n^*$ is not finished before

$$\begin{aligned} nB+{\sum _{j \in S_k,j \le n}} a_j= nB+{\sum _{j \in S_k}} a_j>nB+V, \end{aligned}$$

which contradicts the schedule being feasible, since jobs in $J_n$ have deadline $nB+V$ by (3.1). It remains to prove (3.4). We proceed by induction.

The earliest possible execution time of $j_1^*$ is, by (3.1), time 0. The processing time of $j_1^*$ is B if $j_1^*\ne j_1^1$, and $B+a_1$ otherwise. By (3.2), $1\in S_k$ if and only if $j_1^1$ is scheduled on machine k, that is, if and only if $j_1^*=j_1^1$. Thus, job $j_1^*$ is not finished before $B+\sum _{j\in S_k,j\le i}a_j$ and (3.4) holds for $i=1$. Now, assume that (3.4) holds for $i-1$. We prove it for i. Since $j_{i-1}^*$ is not finished before $(i-1)B+\sum _{j\in S_k,j\le i-1}a_j$, this is the earliest possible execution time of $j_i^*$. The processing time of $j_i^*$ is B if $j_i^*\ne j_i^1$ and $B+a_i$ otherwise. By (3.2), $i\in S_k$ if and only if $j_i^*=j_i^1$. Thus, job $j_i^*$ is not finished before $iB+\sum _{j\in S_k,j\le i}a_j$ and (3.4) holds. $\square$

We are now ready to finish the proof of Theorem 3.1.

Proof

(of Theorem  3.1) By Lemmas 3.4 to 3.6, Construction 3.2 is a polynomial-time many-one reduction from Bin Packing with $n\ge 2$ items and m bins to $\lambda (mn)$-Loose Interval-Constrained Scheduling, where $\lambda {}:{\mathbb N}\rightarrow {\mathbb R}$ such that $\lambda {}(n)\ge 1+n^{-c}$ for some integer $c\ge 1$ and all $n\ge 2$. We now show the points (i) and (ii) of Theorem 3.1.

(i) follows since Bin Packing is weakly NP-hard for $m=2$ (Jansen et al. 2013) and since, by Lemma 3.4(i), Construction 3.2 outputs instances of $\lambda (mn)$-Loose Interval-Constrained Scheduling with m machines.

(ii) follows since Bin Packing is W[1]-hard parameterized by m even if the sizes of the n items are bounded by a polynomial in n (Jansen et al. 2013). In this case, Construction 3.2 generates $\lambda {}(mn)$ -Loose Interval-Constrained Scheduling instances for which all numbers are bounded polynomially in the number of jobs by Lemma 3.5(ii). Moreover, Construction 3.2 maps the m bins of the Bin Packing instance to the m machines of the output Interval-Constrained Scheduling instance. $\square$

Concluding this section, it is interesting to note that Theorem 3.1 also shows W[1]-hardness of $\lambda$-Loose Interval-Constrained Scheduling with respect to the height parameter considered by Cieliebak et al. (2004):

Definition 3.7

(Height) For an Interval-Constrained Scheduling instance and any time $t\in {\mathbb N}$, let

$$\begin{aligned} S_t:=\{j\in J\mid t\in [t_j,d_j)\} \end{aligned}$$

denote the set of jobs whose time window contains time t. The height of an instance is

$$\begin{aligned} h{}:=\max _{t\in {\mathbb N}}|S_t|. \end{aligned}$$

Proposition 3.8

Let $\lambda {}:{\mathbb N}\rightarrow {\mathbb R}$ be such that $\lambda {}(n)\ge 1+n^{-c}$ for some integer $c\ge 1$ and all $n\ge 2$.

Then $\lambda (n)$-Loose Interval-Constrained Scheduling of n jobs on m machines is W[1]-hard parameterized by the height $h{}$.

Proof

Proposition 3.8 follows in the same way as Theorem 3.1; one additionally has to prove that Construction 3.2 outputs Interval-Constrained Scheduling instances of height at most 2m. To this end, observe that, by (3.1), for each $i\in \{1,\ldots ,n\}$, there are m jobs released at time $(i-1)B$ whose deadline is no later than $iB+A<(i+1)B$ since $A\le B/2$. These are all jobs created by Construction 3.2. Thus, $S_t$ contains only the m jobs released at time $\lfloor t/B\rfloor \cdot B$ and the m jobs released at time $\lfloor t/B-1\rfloor \cdot B$, which are 2m jobs in total. $\square$

Remark 3.9

Proposition 3.8 complements findings of Cieliebak et al. (2004), who provide a fixed-parameter tractability result for Interval-Constrained Scheduling parameterized by $h{}+\sigma$: our result shows that their algorithm presumably cannot be improved towards a fixed-parameter tractability result for Interval-Constrained Scheduling parameterized by $h{}$ alone.

4 An algorithm for bounded looseness

In the previous section, we have seen that $\lambda$-Loose Interval-Constrained Scheduling for any $\lambda >1$ is strongly W[1]-hard parameterized by m and weakly NP-hard for $m=2$. We complement this result by the following theorem, which yields a pseudo-polynomial-time algorithm for each constant m and $\lambda$.

Theorem 4.1

$\lambda$-Loose Interval-Constrained Scheduling is solvable in $\ell ^{O(\lambda m)} \cdot n+O(n\log n)$ time, where $\ell :=\max _{j\in J} |d_j -t_j|$.

The crucial observation for the proof of Theorem 4.1 is the following lemma. It gives a logarithmic upper bound on the height $h{}$ of yes-instances (as defined in Definition 3.7). To prove Theorem 4.1, we will thereafter present an algorithm that has a running time that is single exponential in $h{}$.

Lemma 4.2

Let I be a yes-instance of $\lambda$-Loose Interval-Constrained Scheduling with m machines and $\ell :=\max _{j\in J}|d_j -t_j|$. Then, I has height at most

$$\begin{aligned} 2m \cdot \left( \frac{\log \ell }{\log \lambda {} - \log (\lambda {}-1)}+1\right) . \end{aligned}$$

Proof

Recall from Definition 3.7 that the height of an Interval-Constrained Scheduling instance is $\max _{t\in {\mathbb N}}|S_t|$.

We will show that, in any feasible schedule for I and at any time t, there are at most N jobs in $S_t$ that are active on the first machine at some time $t^{\prime }\ge t$, where

$$\begin{aligned} N\le \frac{\log \ell }{\log \lambda {} - \log (\lambda {}-1)}+1. \end{aligned}$$

(4.1)

By symmetry, there are at most N jobs in $S_t$ that are active on the first machine at some time $t^{\prime }\le t$. Since there are m machines, the total number of jobs in $S_t$ at any time $t$, and therefore the height, is at most 2mN.

It remains to show (4.1). To this end, fix an arbitrary time $t$ and an arbitrary feasible schedule for I. Then, for any $d\ge 0$, let $J(t+d)\subseteq S_t$ be the set of jobs that are active on the first machine at some time $t^{\prime }\ge t$ but finished by time $t+d$. We show by induction on d that

$$\begin{aligned} |J(t+d)|&\le {\left\{ \begin{array}{ll} 0 &{}\quad \text {if }d=0,\\ -\frac{\log d}{ \log (1-{1}/{\lambda {}})}+1&{}\quad \text {if }d \ge 1.\end{array}\right. } \end{aligned}$$

(4.2)

If $d=0$, then $|J(t+0)|= 0$ and (4.2) holds. Now, consider the case $d\ge 1$. If no job in $J(t+d)$ is active at time $t+d-1$, then $J(t+d)=J(t+d-1)$ and (4.2) holds by the induction hypothesis. Now, assume that there is a job $j\in J(t+d)$ that is active at time $t+d-1$. Then, $d_j\ge t+d$ and, since $j\in S_t$, $t_j\le t$. Hence,

$$\begin{aligned} p_j\ge \frac{|d_j-t_j|}{\lambda }\ge \frac{|t+d-t|}{\lambda }= \frac{d}{\lambda }. \end{aligned}$$

It follows that

$$\begin{aligned} |J(t+d)|&\le 1+|J(t+d-\lceil d/\lambda \rceil )|. \end{aligned}$$

(4.3)

Thus, if $d-\lceil d/\lambda \rceil =0$, then $|J(t+d)|\le 1+ |J(t)|\le 1$ and (4.2) holds. If $d-\lceil d/\lambda \rceil >0$, then, by the induction hypothesis, the right-hand side of (4.3) is

$$\begin{aligned}\le & {} 1-\frac{\log (d-\lceil d/\lambda \rceil )}{ \log (1-{1}/{\lambda {}})}+1\\\le & {} 1-\frac{\log ( d(1-{1}/{\lambda {}})) }{ \log (1-{1}/{\lambda {}})}+1\\= & {} 1-\frac{\log d+ \log (1-{1}/{\lambda {}})}{\log (1-{1}/{\lambda {}})}+1\\= & {} -\frac{\log d }{ \log (1-{1}/{\lambda {}})}+1, \end{aligned}$$

and (4.2) holds. Finally, since $\ell =\max _{1\le j\le n} |d_j -t_j|$, no job in $S_t$ is active at time $t+\ell$. Hence, we can now prove (4.1) using (4.2) by means of

$$\begin{aligned} N\le |J(t+\ell )|\le & {} -\frac{\log \ell }{\log (1-{1}/{\lambda {}})}+1\\= & {} -\frac{\log \ell }{\log \left( \frac{\lambda {}-1}{\lambda {}}\right) }+1\\= & {} -\frac{\log \ell }{\log (\lambda {}-1) - \log \lambda {}}+1\\= & {} \frac{\log \ell }{\log \lambda {} - \log (\lambda {}-1)}+1. \square \end{aligned}$$

The following proposition gives some intuition on how the bound behaves for various $\lambda {}$.

Proposition 4.3

For any $\lambda {} \ge 1$ and any $b \in (1,e]$, it holds that

$$\begin{aligned}&\frac{1}{\log _b \lambda {} - \log _b (\lambda {}-1)} \le \lambda {}. \end{aligned}$$

Proof

It is well-known that $(1-1/\lambda {})^{\lambda {}} < 1/e$ for any $\lambda {} \ge 1$. Hence, $\lambda {} \log _b (1 -1/\lambda {}) = \log _b (1 -{1}/{\lambda {}})^{\lambda {}} < \log _b {1}/{e} \le -1$, that is, $-\lambda {} \log _b (1 -{1}/{\lambda {}}) \ge 1$. Thus,

$$\begin{aligned} \frac{1}{-\lambda {} \log _b (1 -{1}/{\lambda {}})}&\le 1 \quad \text {and} \quad \frac{1}{- \log _b (1 -{1}/{\lambda {}})} \le \lambda {}. \end{aligned}$$

Finally,

$$\begin{aligned} \frac{1}{- \log _b (1 -{1}/{\lambda {}})}&= \frac{1}{ -\log _b (\frac{\lambda {}-1}{\lambda {}})}\\&= \frac{1}{-\log _b (\lambda {}-1) + \log _b \lambda {}}. \end{aligned}$$

$\square$

Towards our proof of Theorem 4.1, Lemma 4.2 provides a logarithmic upper bound on the height $h{}$ of yes-instances of Interval-Constrained Scheduling. Our second step towards the proof of Theorem 4.1 is the following algorithm, which runs in time that is single exponential in $h{}$. We first present the algorithm and, thereafter, prove its correctness and running time.

Algorithm 4.4

We solve Interval-Constrained Scheduling using dynamic programing. First, for an Interval-Constrained Scheduling instance, let $\ell :=\max _{j\in J}|d_j-t_j|$, let $S_t$ be as defined in Definition 3.7, and let $S_t^<\subseteq J$ be the set of jobs j with $d_j\le t$, that is, that have to be finished by time t.

We compute a table T that we will show to have the following semantics. For a time $t\in {\mathbb N}$, a subset $S\subseteq S_t$ of jobs and a vector $\mathbf {b}=(b_1,\ldots ,b_m)\in \{-\ell ,\ldots ,\ell \}^m$,

$$\begin{aligned}&T[t,S,\mathbf {b}]\\&= {\left\{ \begin{array}{ll} 1&{}\text {if all jobs in } S\cup S_t^< \text { can be scheduled so that }\\ &{}\quad \text {machine } i\, \text { is idle from time }\, t+b_i \text { for each}\\ &{}\quad i \in \{1, \ldots , m\},\\ 0&{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

To compute T, first, set $T[0,\emptyset ,\mathbf {b}]:=1$ for every vector $\mathbf {b} \in \{-\ell ,\ldots ,\ell \}^m$. Now we compute the other entries of T by increasing t, for each t by increasing $\mathbf {b}$, and for each $\mathbf {b}$ by S with increasing cardinality. Herein, we distinguish two cases.

• (a) If $t \ge 1$ and $S \subseteq S_{t-1}$, then set $T[t,S,\mathbf {b}]:=T[t-1,S^{\prime },\mathbf {b}^{\prime }]$, where

  $$\begin{aligned} S^{\prime }&:=S\cup (S_{t-1} \cap S_t^<)\text { and } \mathbf {b}^{\prime }:=(b^{\prime }_1,\ldots ,b^{\prime }_m)\text { with}\\ b^{\prime }_i&:=\min \{b_i+1,\ell \}\text { for each } i \in \{1, \ldots , m\}. \end{aligned}$$

• (b) Otherwise, set $T[t,S,\mathbf {b}]:=1$ if and only if at least one of the following two cases applies:

  • i) there is a machine $i \in \{1, \ldots , m\}$ such that $b_i> -\ell$ and $T[t,S,\mathbf {b}^{\prime }] =1$, where $\mathbf {b}^{\prime }:=(b^{\prime }_1,\ldots ,b^{\prime }_m)$ with

    $$\begin{aligned} b^{\prime }_{i^{\prime }}&:= {\left\{ \begin{array}{ll} b_i-1&{} \text {if } i^{\prime }=i, \\ b_{i^{\prime }}&{} \text {if } i^{\prime }\ne i, \end{array}\right. } \end{aligned}$$

    or

  • ii) there is a job $j \in S$ and a machine $i \in \{1, \ldots , m\}$ such that $b_i>0$, $t+b_i \le d_j$, $t+b_i-p_j\ge t_j$, and $T[t,S\setminus \{j\},\mathbf {b}^{\prime }]=1$, where $\mathbf {b}^{\prime }:=(b^{\prime }_1,\ldots ,b^{\prime }_m)$ with

    $$\begin{aligned} b^{\prime }_{i^{\prime }}:= {\left\{ \begin{array}{ll} b_i-p_j&{} \text {if } i^{\prime }=i, \\ b_{i^{\prime }}&{} \text {if } i^{\prime }\ne i. \end{array}\right. } \end{aligned}$$

    Note that, since $j\in S_t$, one has $t_j \ge t-\ell$ by definition of $\ell$. Hence, $b^{\prime }_i \ge -\ell$ is within the allowed range $\{-\ell ,\ldots ,\ell \}$.

Finally, we answer yes if and only if $T[t_{\text {max}}, S_{t_{\text {max}}}, \mathbf 1^m\cdot \ell ]=1$, where $t_{\text {max}}:= \max _{j \in J}t_j$. $\square$

Lemma 4.5

Algorithm 4.4 correctly decides Interval-Constrained Scheduling.

Proof

We prove the following two claims: For any time $0\le t\le t_{\max }$, any set $S\subseteq S_t$, and any vector $\mathbf {b}=(b_1,\ldots ,b_m)\in \{-\ell ,\ldots ,\ell \}^m$,

$$\begin{aligned}&\hbox {if } T[t,S,\mathbf {b}]=1, \text {then all jobs in } S\cup S_t^< \text { can be scheduled}\nonumber \\&\quad \text {so that machine } i \text { is idle from time } t +b_i \nonumber \\&\quad \text {for each } i \in \{1, \ldots , m\}, \end{aligned}$$

(4.4)

and

$$\begin{aligned}&\text {if all jobs in } S\cup S_t^< \text { can be scheduled so that machine } i\nonumber \\&\quad \text { is idle from time } t +b_i \text { for each } i \in \{1, \ldots , m\}, \nonumber \\&\quad \text {then } T[t,S,\mathbf {b}]=1. \end{aligned}$$

(4.5)

From (4.4) and (4.5), the correctness of the algorithm easily follows: observe that, in any feasible schedule, all machines are idle from time $t_{\max }+\ell$ and all jobs $J \subseteq S_{t_{\max }}\cup S_{t_{\max }}^<$ are scheduled. Hence, there is a feasible schedule if and only if $T[t_{\max }, S_{t_{\max }}, \mathbf {1}^m\cdot \ell ]=1$. It remains to prove (4.4) and (4.5).

First, we prove (4.4) by induction. For $T[0,\emptyset ,\mathbf {b}]=1$, (4.4) holds since there are no jobs to schedule. We now prove (4.4) for $T[t,S,\mathbf {b}]$ under the assumption that it is true for all $T[t^{\prime },S^{\prime },\mathbf {b}^{\prime }]$ with $t^{\prime } < t$ or $t^{\prime }=t$ and $\mathbf {b}^{\prime } \lneqq \mathbf {b}$.

If $T[t,S,\mathbf {b}]$ is set to 1 in Algorithm 4.4(a), then, for $S^{\prime }$ and $\mathbf {b}^{\prime }$ as defined in Algorithm 4.4(a), $T[t-1,S^{\prime },\mathbf {b}^{\prime }] =1$. By the induction hypothesis, all jobs in $S^{\prime }\cup S_{t-1}^<$ can be scheduled so that machine i is idle from time $t-1+b^{\prime }_i\le t+b_i$. Moreover, $S\cup S_t^< =S^{\prime } \cup S_{t-1}^<$ since $S^{\prime }=S\cup (S_{t-1} \cap S_t^<)$. Hence, (4.4) follows.

If $T[t,S,\mathbf {b}]$ is set to 1 in Algorithm 4.4(bi), then one has $T[t,S,\mathbf {b}^{\prime }] =1$ for $\mathbf {b}^{\prime }$ as defined in Algorithm 4.4(bi). By the induction hypothesis, all jobs in $S\cup S_t^<$ can be scheduled so that machine $i^{\prime }$ is idle from time $t+b^{\prime }_{i^{\prime }}\le t+b_{i^{\prime }}$, and (4.4) follows.

If $T[t,S,\mathbf {b}]$ is set to 1 in Algorithm 4.4(bii), then $T[t,S\setminus \{j\},\mathbf {b}^{\prime }]=1$ for j and $\mathbf {b}^{\prime }$ as defined in Algorithm 4.4(bii). By the induction hypothesis, all jobs in $(S\setminus \{j\})\cup S_t^<$ can be scheduled so that machine $i^{\prime }$ is idle from time $t+b^{\prime }_{i^{\prime }}$. It remains to schedule job j on machine i in the interval $[t+b^{\prime }_i, t+b_i)$, which is of length exactly $p_j$ by the definition of $\mathbf {b}^{\prime }$. Then, machine i is idle from time $t+b_i$ and any machine $i^{\prime }\ne i$ is idle from time $t+b^{\prime }_{i^{\prime }}=t+b_{i^{\prime }}$, and (4.4) follows.

It remains to prove (4.5). We use induction. Claim (4.5) clearly holds for $t=0$, $S=\emptyset$, and any $\mathbf {b}\in \{-\ell ,\ldots ,\ell \}^m$ by the way Algorithm 4.4 initializes T. We now show (4.5) provided that it is true for $t^{\prime } < t$ or $t^{\prime }=t$ and $\mathbf {b}^{\prime } \lneqq \mathbf {b}$.

If $S\subseteq S_{t-1}$, then $S\cup S_t^< =S^{\prime } \cup S_{t-1}^<$ for $S^{\prime }$ as defined in Algorithm 4.4(a). Moreover, since no job in $S^{\prime } \cup S_{t-1}^<$ can be active from time $t-1+\ell$ by definition of $\ell$, each machine i is idle from time $t-1+\min \{b_i+1,\ell \}=t-1+b_i^{\prime }$, for $\mathbf {b}^{\prime }=(b^{\prime }_1,\ldots ,b^{\prime }_m)$ as defined in Algorithm 4.4(a). Hence, $T[t-1,S^{\prime }, \mathbf {b}^{\prime }]=1$ by the induction hypothesis, Algorithm 4.4(a) applies, sets $T[t,S,\mathbf {b}]:=T[t-1,S^{\prime },\mathbf {b}^{\prime }]=1$, and (4.5) holds.

If some machine i is idle from time $t+b_i-1$, then, by the induction hypothesis, $T[t,S,\mathbf {b}^{\prime }]=1$ in Algorithm 4.4(bi), the algorithm sets $T[t,S,\mathbf {b}]:=1$, and (4.5) holds.

In the remaining case, every machine i is busy at time $t+b_i-1$ and $K:=S \setminus S_{t-1}\ne \emptyset$. Thus, there is a machine i executing a job from K. For each job $j^{\prime }\in K$, we have $t_{j^{\prime }} \ge t$. Since machine i is idle from time $t+b_i$ and executes $j^{\prime }$, one has $b_i > 0$. Let j be the last job scheduled on machine i. Then, since machine i is busy at time $t+b_i-1$, we have $d_j \ge t+b_i > t$ and $j \notin S_t^<$. Hence, $j \in S_t$. Since machine i is idle from time $t+b_i$, we also have $t+b_i-p_j\ge t_j$. Now, if we remove j from the schedule, then machine i is idle from time $t+b_i-p_j$ and each machine $i^{\prime }\ne i$ is idle from time $t+b^{\prime }_{i^{\prime }}=t+b_{i^{\prime }}$. Thus, by the induction hypothesis, $T[t,S\setminus \{j\},\mathbf {b}^{\prime }]=1$ in Algorithm 4.4(bii), the algorithm sets $T[t,S,\mathbf {b}]:=1$, and (4.5) holds. $\square$

Lemma 4.6

Algorithm 4.4 can be implemented to run in $O( 2^h{} \cdot (2\ell +1)^m\cdot (h{}^2m+h{}m^2)\cdot n\ell +n\log n)$ time, where $\ell :=\max _{j\in J}|d_j-t_j|$ and h is the height of the input instance.

Proof

Concerning the running time of Algorithm 4.4, we first bound $t_{\max }$. If $t_{\max }>n\ell$, then there is a time $t \in \{0,\ldots ,t_{\max }\}$ such that $S_t = \emptyset$ (cf. Definition 3.7). Then, we can split the instance into one instance with the jobs $S_t^<$ and into one instance with the jobs $J\setminus S_t^<$. We answer “yes” if and only if both of them are yes-instances. Henceforth, we assume that $t_{\max } \le n\ell$.

In a preprocessing step, we compute the sets $S_t$ and $S_{t-1}\cap S_t^<$, which can be done in $O(n\log n+h{}n+t_{\text {max}})$ time by sorting the input jobs by deadlines and scanning over the input time windows once: if no time window starts or ends at time t, then $S_t$ is simply stored as a pointer to the $S_{t^{\prime }}$ for the last time $t^{\prime }$ where a time window starts or ends.

Now, the table T of Algorithm 4.4 has at most $(t_{\max }+1) \cdot 2^h{} \cdot (2\ell +1)^m\le (n\ell +1) \cdot 2^h{} \cdot (2\ell +1)^m$ entries. A table entry $T[t,S,\mathbf {b}]$ can be accessed in $O(m+h)$ time using a carefully initialized trie data structure (van Bevern 2014) since $|S|\le h{}$ and since $\mathbf {b}$ is a vector of length m.

To compute an entry $T[t,S,\mathbf {b}]$, we first check, for each job $j \in S$, whether $j \in S_{t-1}$. If this is the case for each j, then Algorithm 4.4(a) applies. We can prepare $\mathbf {b}^{\prime }$ in O(m) time and $S^{\prime }$ in $O(h{})$ time using the set $S_{t-1} \cap S_t^<$ computed in the preprocessing step. Then, we access the entry $T[t-1,S^{\prime },\mathbf {b}^{\prime }]$ in $O(h{}+m)$ time. Hence, (a) takes $O(h{}+m)$ time.

If Algorithm 4.4(a) does not apply, then we check whether Algorithm 4.4(bi) applies. To this end, for each $i\in \{1,\ldots ,m\}$, we prepare $\mathbf {b}^{\prime }$ in O(m) time and access $T[t,S,\mathbf {b}^{\prime }]$ in $O(h{}+m)$ time. Hence, it takes $O(m^2+h{}m)$ time to check (bi).

To check whether Algorithm 4.4(bii) applies, we try each $j \in S$ and each $i \in \{1, \ldots , m\}$ and, for each, prepare $\mathbf {b}^{\prime }$ in O(m) time and check $T[t,S\setminus \{j\},\mathbf {b}^{\prime }]$ in $O(h{}+m)$ time. Thus (bii) can be checked in $O(h{}^2m + h{}m^2)$ time. $\square$

With the logarithmic upper bound on the height $h{}$ of yes-instances of Interval-Constrained Scheduling given by Lemma 4.2 and using Algorithm 4.4, which, by Lemma 4.6, runs in time that is single exponential in $h{}$ for a fixed number m of machines, we can now prove Theorem 4.1.

Proof

(of Theorem  4.1) We use the following algorithm. Let

$$\begin{aligned} h{}:=2m \cdot \left( \frac{\log \ell }{\log \lambda {} - \log (\lambda {}-1)}+1\right) . \end{aligned}$$

If, for any time $t\in {\mathbb N}$, we have $|S_t|>h{}$, then we are facing a no-instance by Lemma 4.2 and immediately answer “no”. This can be checked in $O(n\log n)$ time: one uses the interval graph coloring problem to check whether we can schedule the time windows of all jobs (as intervals) onto $h{}$ machines.

Otherwise, we conclude that our input instance has height at most h. We now apply Algorithm 4.4, which, by Lemma 4.6, runs in $O( 2^h{} \cdot (2\ell +1)^m\cdot (h{}^2m+h{}m^2)\cdot n\ell +n\log n)$ time. Since, by Proposition 4.3, $h{}\in O(\lambda m \log \ell )$, this running time is $\ell ^{O(\lambda {} m)}h{}\cdot n+O(n\log n)$. $\square$

A natural question is whether Theorem 4.1 can be generalized to $\lambda {}=\infty$, that is, to Interval-Constrained Scheduling without looseness constraint. This question can be easily answered negatively using a known reduction from 3-Partition to Interval-Constrained Scheduling given by Garey and Johnson (1979):

Proposition 4.7

If there is an $\ell ^{O(m)}\cdot {{\mathrm{poly}}}(n)$-time algorithm for Interval-Constrained Scheduling, where $\ell :=\max _{j\in J} |d_j-t_j|$, then P${}={}$NP.

Proof

Garey and Johnson (1979, Theorem 4.5) showed that Interval-Constrained Scheduling is NP-hard even on $m=1$ machine. In their reduction, $\ell \in {{\mathrm{poly}}}(n)$. A supposed $\ell ^{O(m)}\cdot {{\mathrm{poly}}}(n)$-time algorithm would solve such instances in polynomial time. $\square$

5 An algorithm for bounded slack

So far, we considered Interval-Constrained Scheduling with bounded looseness $\lambda {}$. Cieliebak et al. (2004) additionally considered Interval-Constrained Scheduling for any constant slack $\sigma {}$.

Recall that Cieliebak et al. (2004) showed that $\lambda$-Loose Interval-Constrained Scheduling is NP-hard for any constant $\lambda >1$ and that Theorem 3.1 shows that having a small number m of machines does make the problem significantly easier.

Similarly, Cieliebak et al. (2004) showed that $\sigma$-Slack Interval-Constrained Scheduling is NP-hard already for $\sigma =2$. Now we contrast this result by showing that $\sigma$-Slack Interval-Constrained Scheduling is fixed-parameter tractable for parameter $m+\sigma$. More specifically, we show the following:

Theorem 5.1

$\sigma$-Slack Interval-Constrained Scheduling is solvable in time

$$\begin{aligned} O\left( (\sigma +1)^{(2\sigma +1)m}\cdot n\cdot \sigma m\cdot \log \sigma m + n\log n\right) . \end{aligned}$$

Similarly as in the proof of Theorem 4.1, we first give an upper bound on the height of yes-instances of Interval-Constrained Scheduling as defined in Definition 3.7. To this end, we first show that each job $j\in S_t$ has to occupy some of the (bounded) machine resources around time t.

Lemma 5.2

At any time t in any feasible schedule for $\sigma$-Slack Interval-Constrained Scheduling, each job $j\in S_t$ is active at some time in the interval $[t-\sigma ,t+\sigma ]$.

Proof

If the time window of j is entirely contained in $[t-\sigma ,t+\sigma ]$, then, obviously, j is active at some time during the interval $[t-\sigma ,t+\sigma ]$.

Now, assume that the time window of j is not contained in $[t-\sigma ,t+\sigma ]$. Then, since $j\in S_t$, its time window contains t by Definition 3.7 and, therefore, one of $t-\sigma$ or $t+\sigma$. Assume, for the sake of contradiction, that there is a schedule such that j is not active during $[t-\sigma ,t+\sigma ]$. Then j is inactive for at least $\sigma +1$ time units in its time window—a contradiction. $\square$

Now that we know that each job in $S_t$ has to occupy machine resources around time t, we can bound the size of $S_t$ in the amount of resources available around that time.

Lemma 5.3

Any yes-instance of $\sigma$-Slack Interval-Constrained Scheduling has height at most $(2\sigma +1)m$.

Proof

Fix any feasible schedule for an arbitrary yes-instance of $\sigma$-Slack Interval-Constrained Scheduling and any time $t$. By Lemma 5.2, each job in $S_t$ is active at some time in the interval $[t-\sigma ,t+\sigma ]$. This interval has length $2\sigma +1$. Thus, on m machines, there is at most $(2\sigma +1)m$ available processing time in this time interval. Consequently, there can be at most $(2\sigma +1)m$ jobs with time intervals in $S_t$. $\square$

We finally arrive at the algorithm to prove Theorem 5.1.

Proof

(of Theorem  5.1) Let $h{}:=(2\sigma +1)m$. In the same way as for Theorem 4.1, in $O(n\log n)$ time we discover that we face a no-instance due to Lemma 5.3 or, otherwise, that our input instance has height at most h. In the latter case, we apply the $O(n\cdot (\sigma +1)^h{}\cdot h{}\log h{})$-time algorithm due to Cieliebak et al. (2004). $\square$

6 Conclusion

Despite the fact that there are comparatively few studies on the parameterized complexity of scheduling problems, the field of scheduling indeed offers many natural parameterizations and fruitful challenges for future research. Notably, Marx (2011) saw one reason for the lack of results on “parameterized scheduling” in the fact that most scheduling problems remain NP-hard even for a constant number of machines (a very obvious and natural parameter indeed), hence destroying hope for fixed-parameter tractability results with respect to this parameter. In scheduling interval-constrained jobs with small looseness and small slack, we also have been confronted with this fact, facing (weak) NP-hardness even for two machines.

The natural way out of this misery, however, is to consider parameter combinations, for instance combining the parameter number of machines with a second one. In our study, these were combinations with looseness and with slack (see also Table 1). In a more general perspective, this consideration makes scheduling problems a prime candidate for offering a rich set of research challenges in terms of a multivariate complexity analysis (Fellows et al. 2013; Niedermeier 2010). Herein, for obtaining positive algorithmic results, research has to go beyond canonical problem parameters, since basic scheduling problems remain NP-hard even if canonical parameters are simultaneously bounded by small constants, as demonstrated by Kononov et al. (2012).¹ Natural parameters to be studied in future research on Interval-Constrained Scheduling are the combination of slack and looseness—the open field in our Table 1—and the maximum and minimum processing times, which were found to play an important role in the online version of the problem (Saha 2013).

Finally, we point out that our fixed-parameter algorithms for Interval-Constrained Scheduling are easy to implement and may be practically applicable if the looseness, slack, and number of machines are small (about three or four each). Moreover, our algorithms are based on upper bounds on the height of an instance in terms of its number of machines, its looseness, and slack. Obviously, this can also be exploited to give lower bounds on the number of required machines based on the structure of the input instance, namely, on its height, looseness, and slack. These lower bounds may be of independent interest in exact branch and bound or approximation algorithms for the machine minimization problem.