1 Introduction

In a type-I superconducting sample, the magnetic field H is expelled from the bulk of the material below a specific critical magnetic field, called the critical field \(H_{c}\) [1]. However, when the magnetic field exceeds the critical field, the superconductivity is suppressed in the bulk of the material, and a vortex state may form. A vortex is a region within the superconductor where the magnetic field penetrates and is trapped in quantized magnetic flux lines, also known as Shubnikov-Abrikosov vortices [2]. These vortices are arranged in a regular lattice structure within the superconductor, with the magnetic field lines threading through the vortices and circulating them. The formation of a vortex state in a type-I superconducting sample occurs when the magnetic field exceeds the critical field, and the superconducting order parameter, which characterizes the macroscopic pseudo-wave function of the superconducting condensate, is no longer uniform throughout the sample [3,4,5,6,7,8,9,10,11]. The vortices act as “holes" in the superconducting condensate, where the order parameter is suppressed, and the material returns to a normal conducting state within the vortex core. The vortex state in type-I superconductors is typically meta-stable, meaning thermal fluctuations or external perturbations can easily destroy it. The behavior of vortices in type-I superconductors differs from that in type-II superconductors, where vortices are more stable and can form complex structures such as vortex lattices and vortex liquids [12,13,14,15,16].

The dynamics of vortices in type-I superconductors are an active area of research and have important implications for the performance of superconducting devices and applications. The vortices form a disordered and mobile vortex state in a type-I superconductor. As a result, these kinds of materials are used in applications where the formation and stability of a well-defined vortex lattice are required, such as in high-field magnets or superconducting devices that rely on precise control of vortices [12,13,14,15,16]. The term “spike vortex state" in superconductors typically refers to a particular configuration of vortices that can occur in certain superconductors. The spike state is a meta-stable vortex state, like phase-slips and kinematic-vortices, that arises and disappears at a single critical field, the one that sets the transition from the normal to the superconducting state. This state is typically observed in superconducting materials with layered structures or anisotropic properties, where the vortices can be guided along particular crystallographic directions or channels. The formation of the spike vortex state is influenced by factors such as temperature, magnetic field strength, and the properties of the superconducting material (geometry), such as its anisotropy and pinning landscape [17,18,19,20].

In type-I superconducting samples, magnetic flux penetration also can occur in the intermediate state if the thickness of the sample is less than the coherence length \(d < \xi\) [5, 21]. Recently, the intermediate state in type-I superconductors was studied theoretically in the reference [17] and experimentally in the references [22,23,24]. Our study is restricted to constant temperature T and varying the external magnetic field H. We study magnetization curves M(H), magnetic susceptibility \(\chi _{m}(H)\), and density of superconducting electrons \((|\psi |^{2})\) under ascending and descending applied magnetic field. The outline of this paper is as follows. Section 2 is presented the theoretical formalism. In Sect. 3, we report the results and discussions. A conclusion is given in Sect. 4.

2 Theoretical Formalism

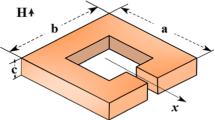
In the present work, we studied the vortex state and the magnetic response in a single-band superconducting irregular octagon in the presence of an external magnetic field H. The studied system exhibits invariance along the z direction (perpendicular to x, y plane), and the external magnetic field is applied in the z-direction. Within this scenario, the problem becomes a bi-dimensional problem for which the physical quantities vary only with the x and y coordinates, and demagnetization effects are absent. We numerically solve the non-lineal time-dependent Ginzburg-Landau (TDGL) equations in a 2D plane [25]. We obtain the hysteresis loop of the magnetization and values of the order parameter as a function of H. The dimensionless form of TDGL for the order parameter \(\psi (x,y)\) and potential vector \({\textbf {A}}(x,y)\), related to magnetic induction as \({\textbf {B}}=\nabla \times {\textbf {A}}\), is [16, 26,27,28,29]:

$$\begin{aligned} \frac{\partial \psi }{\partial t}= & {} -(i \varvec{\nabla } +\textbf{A})^{2}\psi +\psi (1-|\psi |^2)\end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial {\textbf{A}}}{\partial t}= & {} \textrm{Re}\left[ \bar{\psi }{(-i\varvec{\nabla }-\textbf{A})} \psi \right] -\kappa _1\varvec{\nabla }\times \varvec{\nabla }\times \textbf{A}\; \end{aligned}$$
(2)

As usual, the Eqs. 1 and 2 are presented in dimensionless form, with the temperature in units of the critical temperature \(T_{c}\), the order parameter \(\psi\) in units of \(\psi _{\infty }=\sqrt{-\alpha / \beta }\), being \(\alpha , \beta\) experimental parameters, length in units of the coherence length \(\xi (0)\) at zero temperature, and the potential vector \({\textbf {A}}\) in units of \(H_{c2}\xi\), where \(H_{c2}\) is the second critical thermodynamic (which the magnetic field is also measured). So we considered a superconducting octagon of side \(L=20\xi\), immersed in an external applied magnetic field \(H{\textbf {z}}\). In all the studied cases, a superconducting-dielectric boundary is considered \(\textbf{n}\cdot (i\varvec{\nabla }+\textbf{A})\psi =0\), with n an outer vector. The numerical solution of TDGL was done using the link variable method [16, 30, 31] with the size of the computational mesh \(\Delta x=\Delta y=0.1\). With this, we can calculate the magnetic susceptibility \(\chi _{m}=\partial _H M\), (where M is the magnetization \(4\pi {\textbf {M}} = {\textbf {B}} - {\textbf {H}}\) and the dipole moment density \(\mu _0{\textbf {m}}=\chi _{m} {\textbf {B}}\) present in the superconducting sample (\(\mu _{0}\) the magnetic susceptibility of the vacuum) [32,33,34]. The studied sample is an octagon-shaped superconducting sample with horizontal and vertical sides \(a=10\xi\), so the external diagonal has a size \(d=15\sqrt{2}\xi\), and this particular geometry is subscribed in a square of sides \(L=40\xi\) [35,36,37].

3 Results and Discussions

In Fig. 1, we present the magnetization curves for an octagon-shaped superconducting sample immersed in an external magnetic field H. We plot these curves considering three type-I values of the Ginzburg-Landau parameter (GLP) \(\kappa\). We observe that as \(\kappa\) decreases, the magnetic field at which the first vortex entry occurs, \(H_{1}\), decreases. A very interesting situation occurs in the intervals \(1.38<H<1.8\) for \(\kappa =0.65\), \(1.62<H<1.80\) for \(\kappa =0.67\), and \(1.78<H<1.80\) for \(\kappa =0.69\). We see small and atypical jumps in the magnetization curve for a conventional type-I superconducting sample close to the normal superconducting transition field \(H_{2}\). Let us call this field \(H_2*\) because we analyze a type-I superconductor. We also note that for lower \(\kappa\), the field interval in which these jumps occur increases.

Fig. 1
figure 1

Magnetization curve \(-4\pi M\) as a magnetic field function H for a type-I superconducting octagon with \(\kappa =0.69\), \(\kappa =0.67\), and \(\kappa =0.65\)

Full size image

Also, Fig. 1 shows the typical paramagnetic behavior \(M>0\) in the down-branch of the magnetic field, for all \(\kappa\) values, and the magnetization is always negative for any value of the applied field. An interesting result in this figure is the quasi-constant behavior of the magnetization \(4\pi M \approx 0.1\) in the interval \(1.27<H<1.8\) in the down-branch of the magnetic field. That is, the sample remains with a quasi-constant para-magnetization. We think that this fact represents an energetically meta-stable state. Also, as is well known the Gibbs-free energy of the quasi-type-II superconducting sample, it is positive though very close to zero. This small positive value is still sufficient to render it slightly below the normal state of zero-energy [17, 38,39,40,41].

Additionally, in Fig. 2, we present the magnetic susceptibility \(\chi _{m}=\partial _H M\) as a function of the field H applied, for \(\kappa =0.65, 0.67, 0.69\), we can see abrupt jumps in the field where vortices enter very quickly in the superconducting sample. Also, we observe that the first jump in susceptibility occurs for the highest value of the Ginzburg-Landau parameter (GLP) \(\kappa =0.69\), then for \(\kappa =0.67\) and finally \(\kappa =0.65\), it is observed that for the two largest values of \(\kappa\), the oscillations are quasi-periodic with minor susceptibility variations, due to the energy barrier in the superconducting system and the interaction between the vortices inside the octagon (repulsion). Then, we observe a maximum variation in this susceptibility close to \(H=1.8\) for the three values of \(\kappa\), after which it remains with slight variations since the sample is transitioning to a normal state.

Fig. 2
figure 2

Magnetic susceptibility \(\chi _{m}=\partial _H M\), as a magnetic field function H, for a superconducting type-I sample with \(\kappa =0.65, 0.67, 0.69\)

Full size image

The susceptibility \(\chi _{m}\) jumps abruptly; as the field increases, the magnetic susceptibility decreases until another vortex penetrates when its jump occurs. This continues until the superconducting-normal state transitions.

Fig. 3
figure 3

a Cooper pairs density \(|\psi |^{2}\) and b its phase \(\Delta \varphi\) at \(H=1.640\), for \(\kappa =0.65\) (dark (blue) and bright (red) regions represent values of the modulus of the order parameter \(|\psi |\), as well as \(\Delta \varphi /2\pi\), from 0 to 1)

Full size image

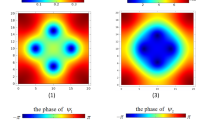
In Fig. 3, we plot the Cooper pairs density \(|\psi |^{2}\) (a) at \(H=1.640\), and its phase \(\Delta \varphi\) (b) for \(\kappa =0.65\). In this figure, we can see that the vorticity N of the sample is equal to \(N=25\) (\(\Delta \varphi =50\pi\)).

Fig. 4
figure 4

a Cooper pairs density \(|\psi |^{2}\) and b its phase \(\Delta \varphi\) at \(H=1.642\) for \(\kappa =0.65\) (dark (blue) and bright (red) regions represent values of the modulus of the order parameter \(|\psi |\), as well as \(\Delta \varphi /2\pi\), from 0 to 1)

Full size image

By increasing the external magnetic field, the surface energy barrier at the borders decreases and allows the entry of more vortices, which we observe in Fig. 4, at \(H=1.642\). Still, although the sample is type-I, there is a very fast entry of transient vortex states for a small variation of the magnetic field, \(\Delta H = 0.002\), which is unconventional. In the intermediate-vortex state, in type-I superconducting samples, the magnetic flux penetration occurs, depending on the thickness of the film. So, the sample may present the presence of quantum fluxoids always that the film thickness is \(d<<< \xi\) [5, 17].

Fig. 5
figure 5

a Cooper pairs density \(|\psi |^{2}\) and b its phase \(\Delta \varphi\) at \(H=1.666\), for \(\kappa =0.65\) (dark (blue) and bright (red) regions represent values of the modulus of the order parameter \(|\psi |\), as well as \(\Delta \varphi /2\pi\) from 0 to 1)

Full size image

In Fig. 5(a), we present the Cooper pairs density for \(\kappa =0.65\), at \(H=1.666\), where we observe a significant change in the magnetic induction in the sample. The separation between the vortices has decreased, generating a very strong repulsion between them, but that finally is not greater than the barrier of energy at the border, with which these are forced to concentrate more and more, and eventually, they will overlap. The mixed state will be lost, leaving the sample in a completely normal state. With this, in Fig. 5(b), we plot the phase of the superconducting condensate, where the large number of vortices in the sample is observed and that the superposition already begins at the borders of these, due to the overlap of the energy barrier and the vortex-vortex interaction.

Fig. 6
figure 6

Logarithm of the modulus of the order parameter \(\ln {|\psi |}\) at a \(H=1.666\), b \(H=1.668\), c \(H=1.670\), d \(H=1.672\), e \(H=1.674\), and f \(H=1.678\), for \(\kappa =0.65\)

Full size image

Together, in Figs. 3, 4, and in Fig. 5, we observe the existence of Abrikosov vortex states in the superconducting sample, which is not the conventional behavior in mesoscopic samples; however, due to the geometry of the confinement of the quantum condensate, the existence of vortices occurs for specific fields, and the vortices enter very quickly, generating transient states (vortex motion), interacting between them and for low variations of these nearby fields between them. The vortex number entering is very high, eventually leading to the normal state in the superconducting sample. In Fig. 6, we plot the logarithm of the order parameter \(\ln {|\psi |}\) at (a) \(H=1.666\), (b) \(H=1.668\); (c) \(H=1.670\); (d) \(H=1.672\); (e) \(H=1.674\); and (f) \(H=1.678\), for \(\kappa =0.65\). We can appreciate the conglomerate (cluster) of vortices at the horizontal and vertical edges of the sample, where we see a higher magnetic fluxoid density than the vortex density inside the sample (and in the diagonal edges). We think that due to the surface energy density (which is negative for a type-I superconductor), the material tends not to allow the formation of the mixed state inside, preventing the magnetic field from entering the sample, but finally, due to confinement effects, the flow quantization is possible and a vortex state occurs.

Fig. 7
figure 7

Logarithm of the modulus of the order parameter \(\ln {|\psi |}\) at \(H=1.780\) for \(\kappa =0.65\)

Full size image

In Fig. 7, we plot the logarithm of the order parameter at \(H=1.780\), for \(\kappa =0.65\). In this graph, we slightly appreciate the center of the vortices at high fields, \(H\sim H_{c2}\). When the magnetic field increases, not is possible appreciate the core of the vortices, and finally, by increasing the magnetic field the centers of the vortices are very close and an impending giant vortex can be predicted before the transition to the normal state. As is well known, the study of type-I superconductors is carried out by increasing and decreasing the magnetic field around a given field in order to study the possible configurations of existing vortices. These works have been widely carried out by various research groups around the world. Our interesting result was to find in this little-studied geometry, Abrikosov vortex states in type-I superconductors when the magnetic field increases. We consider that it may be a novel result with possible technological applications. Ultimately in Fig. 8, we present the vorticity (number of vortices), as a function of the external magnetic field. We observe that in the first entry of vortices, 20 vortices are stabilized in the sample, which coincides with the graph of the order parameter \(|\psi |^{2}\). After this, 100 stable vortices enter, due to the repulsion interaction between them. It is important to note that even with the existence of spike-type vortices, the fluxoid \(\Phi\) continues quantized, which is observed in that the number of vortices is integer, which is a novel result in the analysis of these new type vortices spike.

Fig. 8
figure 8

Vorticity N (number of vortex), as function of the external magnetic field H for \(\kappa =0.65\)

Full size image

4 Conclusions

In this work, we studied the magnetization, magnetic susceptibility, and electronic superconducting density of a superconducting type-I irregular octagon in the presence of an external magnetic field. We solved numerically the time-dependent Ginzburg-Landau equations for a one-band condensate. Our results show the existence of a Abrikosov-Shubnikov-vortex state in the up-branch of the magnetic field when a \(\kappa =0.65\) is considered. Also, we show this behavior in the up-branch of the magnetic field and there is paramagnetic response, in the down-branch of the magnetic field. Finally, we shown the generation of an interesting vortex state into the irregular octagon, for a type-I superconducting sample and we show that even in spike vortices, the fluxoid \(\Phi\) is quantized, allowing the vortices in the superconducting sample to remain at multiples of integers.