On the Critical Temperature of Superconductivity of La$_{2-x}$Sr$_{x}$CuO$_{4}$ Thin Films

Abstract

Superconductivity of the cuprate La$_{2-x}$Sr$_{x}$CuO$_{4}$ thin films is considered within the concept of the preformed pairs (bipolarons). Taking the extended Holstein-Hubbard model as a basis for a strongly interacting hole-lattice system of the cuprate films, a relation between the temperature of Bose-Einstein condensation ($T_{BEC}$) of an ideal gas of the intersite bipolarons and the strains in the thin films is established. In doing that (relation), the chain model of cuprates, proposed by Alexandrov and Kornilovitch in ref. (Phys Rev Lett 82(4):807, 1999), is used. It is shown that the calculated values of the temperature of Bose-Einstein condensation of the bipolarons in the cuprate La$_{2-x}$Sr$_{x}$CuO$_{4}$ thin films grown on LaSrAlO$_4$ and SrTiO$_3$ substrates correlate (and at certain values of doping level x satisfactorily agree) with the experimental values of the critical temperature of superconductivity ($T_c$) of the above systems. The $T_{BEC}$ versus x dependence obtained within the approach is very similar to the dome-shape type $T_{c}$ versus x phase diagram of La$_{2-x}$Sr$_{x}$CuO$_{4}$ thin films. The obtained phase diagram has a feature of “1/8”-anomaly which is a common for both bulk and film samples of La$_{2-x}$Sr$_{x}$CuO$_{4}$.

1 Introduction

Despite the intensive experimental and theoretical studies, for almost four decades now, the mechanism of high-T$_c$ superconductivity of the cuprates remains not entirely clear. Although, a huge amount of experimental data has been accumulated so far on various aspects of the phenomenon, there is no theoretical understanding of these data within the framework of a single concept [2]. The existing theoretical models are unable to explain all aspects of high-T$_c$ superconductivity of cuprates. Even the high-T$_c$ superconductivity of La$_{2-x}$Sr$_{x}$CuO$_{4}$ (LSCO) cuprate with the simplest crystal structure is not fully understood, although there is progress in understanding of some particular aspects of this complex phenomenon. One may say that LSCO cuprate is a testing playground for the models of high-T$_c$ superconductivity. The same is true for thin films of LSCO cuprate whose superconducting properties differ from that of bulk counterparts [3].

Study of superconducting properties of the LSCO thin films was started by the works [4,5,6,7]. Since then, a number of papers have been published on the superconductivity of the LSCO thin films [8,9,10,11,12,13,14,15,16,17,18,19,20,21]. A more detailed information about the recent achievements in the field of superconductivity of the LSCO thin films can be found in the review [3]. The main conclusion of the works [8,9,10,11,12,13,14,15,16,17,18,19,20,21] is that the superconductivity of LSCO thin films depends on several factors. These factors, in addition to the doping level (x), include the growing and annealing conditions of the thin films, the thickness of the thin film itself, and the type of substrate for the thin film. All of the above factors affect the properties of the thin films, determining, in particular, the value of its critical temperature of superconductivity ($T_{c}$). Early studies showed that $T_{c}$ of LSCO thin films depends, at constant doping level and under the same thin film growth conditions, on the strains induced by lattice mismatch between the film and the substrate. It was established that for the (001) oriented thin film of LSCO the compressive strain of the ab-plane lattice constants enhances $T_{c}$ while the compressive strain of the lattice period along c- direction reduces $T_{c}$ [9]. Two substrates are often used for the LSCO thin film growth. They are LaSrAlO$_4$ (LSAO) and SrTiO$_3$ (STO) with the lattice periods of 3.756 Å and 3.905 Å, respectively. It turns out that for the LSCO thin film grown on LSAO (STO) substrate the ab- plane periods are compressed (elongated) and the period in the perpendicular c- direction is elongated (compressed). While a research community has a common view of point of the reasons of enhancement and/or reduction of $T_{c}$ of the thin films which is due to the structural changes of the lattice constants of the film, it is worth to do some notes on the issue. First of all, one must recognize that the study of superconducting properties of the cuprate thin films, in particular LSCO thin films, has become actual due to the possibility of the potential application of the cuprate thin films in the different superconducting devices [22,23,24,25]. Secondly, there are conflicting quantitative reports on the values of $T_c$ of the LSCO thin films obtained at the different doping levels, film thicknesses and other conditions [3, 10, 13]. Thirdly, in the literature, one may come to across to the variety of qualitative approaches (theoretical models) to the strain(pressure)-induced high-$T_{c}$ phenomena in the LSCO thin films [11, 26,27,28,29].

Although these models claim to be able to explain the numerical values of $T_c$ of the LSCO thin films, one cannot say that they take into account all features of the phenomenon under consideration. This concerns the role of the electron-phonon interaction (EPI) in the cuprates which implies a possibility of polaron/bipolaron formation in the strong coupling limit, while quasiparticle tunneling spectra study of La$_{1.84}$Sr$_{0.16}$CuO$_{4}$ films gave clear evidence that the phonons are the relevant bosons involved in quasiparticle-boson interactions [17]. In addition, in the above papers, the phenomenon is considered as a purely two-dimensional one. While the cuprates have a quasi-two-dimensional crystal structure, it is well understood that EPI plays an important role in the cuprates [30, 31], in particular, EPI that involves apical oxygen atoms determines dynamics of charge carrier in copper-oxygen (CuO$_2$) plane [32]. And EPI is strong enough for favouring (bi)polaron formation [33]. The strong EPI manifests itself as polaronic nature of charge carriers in the cuprates [34]. The results of many experiments are also in satisfactory agreement with a (bi)polaronic approach to cuprate superconductivity [35,36,37]. One may conclude that the above theoretical models consider the LSCO thin films totally ignoring the strong electron-phonon interaction, and consequently ignoring the possibility of polaron and/or bipolaron formation. They ignore, in particular, the interaction of in-plane (CuO$_2$) charge carriers with the c- polarized vibrations of the apex oxygen atoms. The latter interaction, which depends mainly on the apical-oxygen displacements, as shows an improved X-ray phase-retrieval method study has a profound effect on the value of $T_{c}$ of LSCO thin films [38]. Therefore, a systematic and comprehensive study of the dependence of the value of $T_{c}$ of LSCO thin films, grown on various families of substrates, on doping level x (or Sr concentration) is of considerable importance for understanding the occurrence of superconductivity not only in these materials but also, in general, in whole family of the cuprates.

In this work, we will try to consider the issue of high-T$_c$ superconductivity of the LSCO thin films, taking into account the polaronic features of the phenomenon. In doing this, we rely on the extended Holstein-Hubbard (or Fröhlich-Coulomb) model of high-T$_c$ superconductivity which assumes formation of intersite bipolarons and their Bose-Einstein condensation (BEC) giving rise the superconductivity. The main idea of our approach was given early in the works [39, 40]. In the work [39], the values of $T_{c}$ of La$_{1.85}$Sr$_{0.15}$CuO$_{4}$ and La$_{1.9}$Sr$_{0.1}$CuO$_{4}$ thin films, grown on LSAO and STO substrates, were satisfactorily explained. The work [40] extends our approach to RBa$_2$Cu$_3$O$_{7-\delta }$ cuprates. Here, we will try to explain the dependence of the value of $T_{c}$ of LSCO thin films, grown on LSAO and STO substrates, on doping level x (or Sr concentration).

2 The Model

Fig. 1

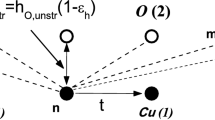
The strained chain model lattice of cuprates. An electron performs hopping motion in a one-dimensional chain of the ions (lower chain — black circles) and interacts with all ions of an upper chain (open circles which is apical oxygen ions O(2)) via a density-displacement type force $f_{\mathbf{m}}(\mathbf{n})$ (dashed lines). The distance between the ions of lower chain a is set equal to CuO$_2$ in-plane lattice period of La$_{2-x}$Sr$_{x}$CuO$_{4}$. The distance between the ions of lower chain and the ions of upper chain are assumed equal to $h_{O}$ which is Cu(1)-O(2) bond length of La$_{2-x}$Sr$_{x}$CuO$_{4}$

The cuprates are characterized as a strongly correlated electron (or hole) and strongly coupled electron-phonon system. Such the system can be described by means of an extended Holstein-Hubbard (or Fröhlich-Coulomb) model [41]. It was shown that within the model, at strong EPI regime and nonadiabatic approximation, intersite bipolaron tunnel in the first order of polaron tunneling and its mass has the same order as polaron mass. For the sake of simplicity, we suppose that the intersite bipolarons form an ideal gas of charged carriers and mass of bipolaron is twice of polaron’s mass, i.e. $m_{bp}=2m_p$. Then, the temperature of Bose-Einstein condensation of the intersite bipolarons defines as [39, 40]

$$\begin{aligned} T_{BEC}=\frac{3.31\hbar ^2n^{2/3}}{2k_{B}m^{*}}e^{-g^2}, \end{aligned}$$

(1)

where $\hbar$ ($k_B$) is Planck’s (Boltzmann’s) constant, $m^{*}=\hbar ^2/2t(a)a^2$ is the bare band mass, n is density of the intersite bipolarons and $g^2$ is the mass renormalization factor of polaronic system. In order to get expression for $g^2$, one uses a chain model lattice (Fig. 1) that was introduced by Alexandrov and Kornilovitch in ref. [1] in order to mimic an interaction of a hole on CuO$_2$ plane with the vibrations of apical oxygen ions in the cuprates. Convincing evidence for a such coupling of in-plane holes with the c- axis polarized vibrations of apical oxygen ions comes from many experiments (for example [42]). Therefore, here we consider only that component of the electron-lattice force which represents an interaction of a hole on CuO$_2$ plane with the c- axis polarized apical oxygen vibrations. In addition, for the sake of simplicity, it is assumed that apical oxygen ions are dispersionless Einstein oscillators with the vibration frequency $\omega$, and we estimate the mass renormalization factor $g^2$ within extended Holstein model (which is consistent with the ideality of Bose gas of intersite bipolarons). In that case, the mass renormalization factor $g^2$ for the given model lattice can be expressed as:

$$\begin{aligned} g^2=\gamma \frac{E_{p}}{\hbar \omega }, \end{aligned}$$

(2)

where

$$\begin{aligned} \gamma =1-\frac{\sum _\mathbf{m} f_{\mathbf{m}}(\mathbf{n}) f_{\mathbf{m}}(\mathbf{n}+\mathbf{a})}{\sum _\mathbf{m} f^2_{\mathbf{m}}(\mathbf{n})} \end{aligned}$$

(3)

is a numerical coefficient,

$$\begin{aligned} E_{p}=\frac{1}{2M\omega ^2}\sum _\mathbf{m} f^2_{\mathbf{m}}(\mathbf{n}) \end{aligned}$$

(4)

is a polaron shift, M is apical oxygen ion’s mass and $f_\mathbf{m}(\mathbf{n})$ is the density-displacement type EPI force defined by analytical formula

$$\begin{aligned} f_\mathbf{m}(\mathbf{n})=\frac{\kappa h_{O}(1-\varepsilon _h)}{[\mid (\mathbf{n}-\mathbf{m})(1-\varepsilon _{a})\mid ^2+(h_{O}(1-\varepsilon _h))^2]^{3/2}}. \end{aligned}$$

(5)

Here $\kappa$ is some coefficient, $\mid \mathbf{n}-\mathbf{m} \mid$ is the distance measured in units of the lattice constant a, $h_{O}$ is Cu(1)-O(2) bond length, $\varepsilon _a$ is the strain of the a- axis lattice period, and $\varepsilon _h$ is the strain of $h_{O}$. The lattice strains are defined as $\varepsilon _a=(a_{unst}-a_{str})/a_{unst}$ and $\varepsilon _h=(h_{O,unst}-h_{O,str})/h_{O,unst}$, where subscripts unstr and str stand for unstrained and strained, respectively. Thus, the positive (negative) value of the variable $\varepsilon _i$ ($i=a,h$) corresponds to the compressive (tensile) strain. Equation (5) is a generalization of the force considered in ref. [1] (see Eq. (9) there). Such an explicit choice of the analytical formula for the force of EPI allows one to interrelate the temperature of Bose-Einstein condensation of the intersite bipolarons with the lattice strains through the mass of intersite bipolaron. The strains contribute to $T_{BEC}$ not only through $g^2$ but also through bipolaron’s concentration n as upon deformation an initial volume $V_{0}$ of the sample changes and becomes $V(\varepsilon _a,\varepsilon _b,\varepsilon _c)=V_{0}(1-\varepsilon _a)(1-\varepsilon _b)(1-\varepsilon _c)$. As a result, the concentration of intersite bipolarons becomes the function of the strains too:

$$\begin{aligned} n=n_0(1+\varepsilon _a)(1+\varepsilon _b)(1+\varepsilon _c). \end{aligned}$$

(6)

In obtaining the last expression, we put $n_0=N/V_{0}$ (N is the total number of intersite bipolarons in the sample) and neglected the terms of the quadratic order of smallness, i.e. $\sim \circ (\varepsilon ^2)$. The above equations are the main analytical results of the model, according to which discussion of the experimental data for LSCO thin films will be done in the next section.

3 Results and Discussion

In the previous section, we expressed the temperature of Bose-Einstein condensation of intersite bipolarons $T_{BEC}$ (Eq. (1)) through two basic parameters of a system: (i) the density of intersite bipolarons n and (ii) the exponent $g^2$ of the polaron mass enhancement. With the help of the above equations, one can study the dependence of the temperature of Bose-Einstein condensation $T_{BEC}$ on the lattices strains $\varepsilon _a$ (or $\varepsilon _b$) and $\varepsilon _c$ through n and $g^2$. The latter dependence, of course, originates from the polaronic effect. Here, we discuss the possibility of application of Eq. (1) to LSCO films with a thickness of 500 Å grown on two types of substrates, namely, on LSAO and STO substrates. A common note to both cases (substrates) is that we consider the influence of the substrate to the superconducting properties of the thin film, in particular, to the value of $T_c$, only through the strains of the lattice constants of the thin films which are originated due to mismatch of lattice constants of the film and substrate. In our formulas, we use the numerical values of physical quantities in natural units, that is, in SI units, in order to easily compare the theoretically calculated results with the available experimental data. As in our study, the essential role is given to the electron-phonon interaction of CuO$_2$ in-plane charge carriers with the c-axis polarized vibrations of apical oxygen ions (i) we put M=16 a.m.u. (2.6565032$\cdot 10^{-26}$ kg); (ii) for the apical oxygen ion’s vibration frequency, we accept $\hbar \omega$=0.075 eV (1.2016324237$\cdot 10^{-20}$ J) which is common for all cuprates. And for the bipolaron concentration, we accept the value $n_{0}=1\cdot 10^{21}$ cm$^{-3}$. Furthermore, we will associate the distance between the ions of lower chain a in Fig. 1 with the CuO$_2$-plane lattice period of tetragonal La$_{2-x}$Sr$_{x}$CuO$_{4}$. And the distance between the ions of lower chain and the ions of upper chain $h_{O}$ in Fig. 1 we will associate with the Cu(1)-O(2) bond length of tetragonal La$_{2-x}$Sr$_{x}$CuO$_{4}$. The distances a and $h_{O}$ for the tetragonal La$_{2-x}$Sr$_{x}$CuO$_{4}$ at different doping levels x (or Sr concentration) can be found in ref. [43]. As for the lattice constants of the LSCO thin films (LSAO and STO substrates), we took them from Fig. 13 and Table 3 of ref. [3]. Concerning the strain $\varepsilon _a$ of the lattice constant a of LSCO thin films grown on LSAO and STO substrates, it is also given in Table 4 of the same ref. [3]. However, these values of the strains, according to our calculations, are more probably related to the state of the films and substrates at T=295 K, while superconductivity of LSCO cuprates occurs at relatively low temperatures of the order of 30 K. Then, it is natural to expect that the lattice strains at low temperatures will differ from those values of Table 4 of the same ref. [3]. Therefore, it would be more adequate to determine and use in our calculations the lattice strains of LSCO thin films corresponding to low temperatures of the order of 30 K. For that reason, we used the data of lattice periods from [43] corresponding to the temperature 10 K. Next, we calculated the numerical values of $T_{BEC}$ of LSCO thin films grown on LSAO and STO substrates. In doing this, we firstly chose the value of polaron shift $E_{p}$ in such a way that the calculated value of $T_{BEC}$ in absence of the strains, i.e. $\varepsilon _a$=0 and $\varepsilon _h$=0, is equal to the experimental value of $T_{c}$ of bulk LSCO. Secondly, since the value of $\varepsilon _c$ is not given in Table 4 of ref. [3] in order to estimate the value of $\varepsilon _c$ for 500 Å thick films, we used the existing correspondences between $\varepsilon _a$ and $\varepsilon _c$ of 2000 Å thick films of LSCO [9]. Thirdly, in calculating $T_{BEC}$ at arbitrary $\varepsilon _a$ and $\varepsilon _h$, for the strain $\varepsilon _h$, we accept a double value of the $\varepsilon _c$, i.e. $\varepsilon _h=2\times \varepsilon _c$, as according to ref. [44] deformation of Cu(1)-O(2) bond length “is roughly twice as large as the cell compression along the same direction (c-axis)”. The calculated values of $T_{BEC}$ of LSCO thin films, with different doping levels x, grown on LSAO and STO substrates are given in Table 1. These values of $T_{BEC}$ are calculated for the doping levels x=0.075, 0.1, 0.1125, 0.1250, 0.1375, 0.15, 0.2 and 0.25. For each doping level, the strains are calculated using the experimental lattice parameters of LSCO both bulk and film. The essential lattice parameters of LSCO both bulk and films are the lattice periods a and c of tetragonal LSCO as well as atomic position parameter z[O(2)]. The latter characterizes a position of O[2] apical oxygen with respect to CuO$_{2}$ plane. Using z[O(2)] and c, one can easily determine the Cu[1]-O[2] distance by a formula $h_{O}=c\times z$[O(2)]. The numerical values of these data as well as the values of polaron shift $E_p$, polaron’s mass $m_p$, in-plane polaron’s mass $m_{ab}$ and $\gamma$ at different levels of Sr concentration x are summarized in the same Table 1. The mass of in-plane polaron $m_{ab}$ is calculated by using the formulas $m_{p}=m_{ab}^{2/3}m_{c}^{1/3}$ and $\gamma _m=m_{c}/m_{ab}$. The latter is taken equal to 160 for LSCO at all doping levels [45]. In the same table, for the purpose of comparison, the experimental values of $T_{c}$ of LSCO thin films are given too. From the table, one can see that there is a good agreement between calculated $T_{BEC}$ of our model and experimental $T_{c}$ of LSCO thin films grown on LSAO and STO substrates. In case of LSCO thin films grown on LSAO substrate, we performed calculations of $T_{BEC}$ for two temperatures, namely, at T=10 K and T=295 K. While for LSCO thin films grown on STO substrate, we could not find measured lattice constants of the films in ref. [3] except the data for the film with doping level x=0.15. Therefore, for doping level x=0.15, we calculated $T_{BEC}$ of LSCO thin films grown on STO films by using the data from Table 4 and Fig. 13 of ref. [3] while for other values of the doping levels we did the same calculations by using $\varepsilon _a$ from Table 4 of ref. [3] and $\varepsilon _c$ estimated from the experimental data of the lattice constants from ref. [43] for the temperature T=10 K. The theoretically obtained results are graphically presented in Fig. 2 too. The experimental values of the temperature of superconductivity $T_{c}$ of LSCO bulk samples are taken from ref. [46] (dashed line). And the same for the films with the thickness of 500 Å grown on LSAO and STO substrates are taken from Fig. 16 of ref. [3]. As one can see from Table 1 as well as from Fig. 2, the theoretically calculated values of $T_{BEC}$ are close to the experimental values of $T_{c}$ of LSCO thin films. This agreement is satisfactorily in a whole region of the doping level. For the LSCO/LSAO system, at some values of the doping levels, namely at x=0.1, 0.1125, 0.2, we found a surprising match between $T_{BEC}$ and $T_{c}$ with the absolute accuracy of less that ${\pm }$ 1 K. In particular, we confirm an early obtained result of $T_{c}$=39 K for 500Å thick La$_{1.9}$Sr$_{0.1}$CuO$_{4}$ film grown on LSAO substrate [3]. Meanwhile, for other values of doping levels of the LSCO/LSAO system, the absolute discrepancies of the calculated values of $T_{BEC}$ from $T_{c}$ are less that ${\pm }$5 K. The absolute discrepancies of the calculated values of $T_{BEC}$ from $T_{c}$ of LSCO/STO system are less that ${\pm }$2.5 K. However, at some values of doping level x, the values of $T_{BEC}$ differ from $T_{c}$ significantly. This discrepancy, as is seen from Fig. 2, is more pronounced in the overdoped regime. The reasons of the discrepancies we will discuss below.

Now, it would be useful to make general remarks on our model and the obtained results:

• (i) Our model takes into account the main features of cuprates, that is, the strong electron-phonon interaction, which determines the state and dynamics of charge carriers (polarons and bipolarons);

• (ii) Our model considers the cuprates as quasi-2D structure in which the dynamics of (bi)polarons is governed not only by the lattice dynamics of CuO$_{2}$-plane (i.e. ab-plane) ions but also by the vibrations of the out of ab-plane ions which are apical oxygen ions;

• (iii) It is able to take also into account the lattice strains in the crystal structure of cuprates, in particularly, the strains in the cuprate thin films which are subjected to the deformation in all direction simultaneously;

• (iv) As it is observed in many experiments our model gives high (low) value of $T_{BEC}$ of thin film compared the bulk value of $T_{BEC}$ when ab-plane of the cuprate film is compressed (stretched). The same is true when c-axis of the cuprate film is stretched (compressed);

In turn, we have to in some way interpret the discrepancies between our $T_{BEC}$ and experimental $T_{c}$ at certain values of doping levels. There might be several reasons of the discrepancies. They are:

• (i) The use of the extended Holstein-Hubbard (or Fröhlich-Coulomb) model at strong coupling regime and nonabiabatic limit while in a real situation the cuprates might be in some doping regimes at moderate values of electron-phonon coupling as well as in intermediate regimes of abiabaticy;

• (ii) The choice of model lattice which is the simplest one. It is one-dimensional. In reality, one should consider the three-dimensional crystal structure of LSCO;

• (iii) The choice of electron-phonon “density-displacement” type force in the form of Eq. (5) that might lead to the underestimation the value of $E_{p}$ in the cuprates like the case with Fröhlich type EPI [47];

• (iv) The estimation the mass of polaron (bipolaron) within the extended Holstein model thus ignoring the correlation effects that is important in the cuprates;

• (v) And the last one is the use of assumption that bipolarons form an ideal gas (their Bose-Einstein condensation temperature is determined by the Eq. (1)). As it is seen from our results, Fig. 2, such the assumption may be valid in underdoped and optimally doped regimes, but in the overdoped regime it underestimates the values of $T_{BEC}$;

All the above points might contribute to the full discrepancy. Apart from the above theoretical reasons, there might be the reasons from the experimental sites that measure $T_{c}$ by various methods. In the literature, one finds the experimental works in which $T_{c}$ reported (measured) as onset temperature, midpoint temperature and the temperature at which the resistivity becomes 90% of the value at the onset temperature as well as the zero-resistivity temperature. In our opinion, these circumstances might also cause some inconsistency between our $T_{BEC}$ and experimental $T_{c}$. Nevertheless, as one can see from our numerical results, in general, our model satisfactorily explains the value of $T_{c}$ of LSCO thin films grown on LSAO and STO substrates. Then, one could conclude that even with such a type of simple assumptions our model captures the essential physics of the LSCO.

It is remarkable that $T_{BEC}$ versus x dependence obtained in our model has a dome-like shape similar to the shape of $T_{c}$ versus x dependence of bulk LSCO, i.e. the phase diagram of bulk LCSO. In such circumstances, Fig. 2 can be interpreted as the phase diagram of the strained LCSO thin films. It is interesting that the phase diagram of LCSO thin films exhibits a feature, near doping level x=1/8, similar to the observed “1/8”-anomaly in the phase diagram of bulk LSCO. Of course, this “1/8”-anomaly (feature) of the phase diagram of LSCO thin films is originated from polaronic-structural effect. And it is one of the conclusions of our model that gives realistic phase diagram for the strained LSCO thin films in ($T_{c}$,x) plane with “1/8”-anomaly feature.

Table 1 The calculated values of $T_{BEC}$, $E_p$, $m_p$, $m_{ab}$ and $\gamma$ at different levels of Sr concentration x for La$_{2-x}$Sr$_{x}$CuO$_{4}$ thin films with a thickness of 500 Å grown on LaSrAlO$_4$ and SrTiO$_{3}$ substrates. The lattice parameters for bulk samples are taken from ref. [43], and the same for the films are taken from [3]. The strains along a-axis of the films as well as the experimental values of $T_{c}$ of the films are also taken from [3]. The value of $\varepsilon _c$ was estimated according to the existing correspondences between $\varepsilon _a$ and $\varepsilon _c$ of 2000 Å thick films of LSCO [9]

Fig. 2

The phase diagram of LSCO films with a thickness of 500 Å in ($T_{BEC},x$) plane. The experimental values of $T_{c}$ of LSCO thin films grown on LSAO (STO) substrate are given by open circles (open triangles). For the LSCO/LSAO system, $T_{BEC}$ is calculated for the temperatures 10 K (filled circles) and 295 K (filled squares). For the LSCO/STO system, $T_{BEC}$ is calculated for the temperature 10 K (filled triangles). The dashed line presents the experimental values of $T_{c}$ of bulk LSCO. The lines are a guide to the eye

4 Conclusion

We studied the thin films of La$_{2-x}$Sr$_{x}$CuO$_{4}$ cuprate within the framework of the extended Holstein-Hubbard (or Fröhlich-Coulomb) model. Namely, we were interested with the values of $T_{c}$ of LSCO thin films grown on LSAO and STO substrates. We accepted the bipolaronic mechanism of superconductivity for cuprates in which $T_{c}$ is associated with the Bose-Einstein condensation temperature $T_{BEC}$ of the ideal gas of the intersite bipolarons. In our model, $T_{BEC}$ we defined from Eq. (1) where both mass of (bi)polaron and concentration of bipolarons depend on the crystal lattice structure through the lattice constants and lattice period’s strains. In turn, the all lattice parameters (periods and strains) of bulk LSCO depend on doping level. In addition, the lattice parameters of the films depend on the type of substrate. Eventually, we were able to interrelate $T_{BEC}$ through the lattice parameters of the films. Then, we calculated the values of Bose-Einstein condensation temperature $T_{BEC}$ of the ideal gas of intersite bipolarons in LSCO thin film grown on LSAO and STO substrates. In doing this, we take into account the real values of lattice constants of the thin films and strains. The calculated values of Bose-Einstein condensation temperature $T_{BEC}$ of the ideal gas of intersite bipolarons in LSCO thin film grown on LSAO and STO substrates are in satisfactory agreement with the values of the temperature of superconductivity $T_{c}$ of the considering thin films. Some discrepancies between our $T_{BEC}$ and experimental $T_{c}$ might be the result of several reasons. We discussed the reasons of the discrepancies too. $T_{BEC}$ versus x dependence obtained in our model has a dome-like shape similar to the shape of $T_{c}$ versus x dependence of bulk LSCO. This dependence has the “1/8”-anomaly feature and can be interpreted as a phase diagram of strained LSCO thin films.