1 Introduction

Double perovskite oxides, A2BB′O6 and AA′BB′O6, where A and A′ are alkaline-earth and/or rare-earth metals and B and B′ are transition metals, have been the subject of intense research in the last few years due to their potential applications and the coexistence of different properties in one material, such as multiferroic compounds which coupled ferromagnetism and ferroelectricity [1]. In addition, these perovskites are also of crystallographic interest [2,3,4].

The B and B′ cations can be distributed in an ordered arrangement or randomly on the 3d-metal (B) sites of the unit cell [5]. Several studies also suggest that the B-site ordering may play a crucial role in determining the physical properties, particularly magnetic properties of double perovskites [6,7,8]. Indeed, in the B-site-ordered structures, only B-O-B′ bonds are possible with a monoclinic symmetry (P21/n space group), while the disordered state of B-site introduces B–O–B, B–O–B′, and B′–O–B′ interactions and, consequently, facilitates different magnetic interactions [9]. For example, LaCoMnO6 (LCMO) with B-site-ordered structure shows a single PM to FM Curie temperature [10] (about 220 K) due to the Co2+-O-Mn4+super exchange interaction [11], while a disordered sublattice of LCMO shows multiple magnetic transitions arising from the Co3+-O-Mn3+ FM and Co3+-O-Co3+ or Mn3+-O- Mn3+ AFM interactions [12]. These competing interactions are responsible for the occurrence of spin glass state. Additionally, the arrangement of B-site (Co/Mn) highly influences the crystal structure of LCMO. It has been found that ordered phase LCMO exhibits a monoclinic symmetry (P21/n space group) [11], while a disordered phase shows an orthorhombic structure (Pbnm space group) [12].

Recently, several compounds based on Mn, Fe, and Ti transition metal such as Sr2TiMnO6, Ca2TiMnO6, Sr2-xGdxMnTiO6 (0 ≤  ×  ≤ 1), Bi2FeMnO6, and CaLaMnFeO6 exhibit intriguing spin-glass behavior and follow various hopping conduction mechanisms [13,14,15,16,17].

In previous work, we have analyzed the physical properties of the La2MnFeO6 sample [18,19,20], finding that these properties are highly sensitive to synthesis conditions and methods. Palakkal et al. [18] reported that La2FeMnO6 (LFMO) prepared via citrate–nitrate gel combustion exhibit an orthorhombic symmetry with the Pbnm space group. In this work, it was shown that the competing magnetic interactions in the sample lead to spin-glass behavior at low temperatures. A strong competing AFM–FIM interaction is found in the cubic crystal structure for LFMO ceramic elaborated by the solid-state method [19]. They [20] also reported the synthesis of LFMO using the sol–gel technique, showing a disordered crystalline orthorhombic structure (Pbnm space group). Two distinct dynamical freezing points above 27 and 92 K of the glassy magnetic state, along with Griffiths-like phase, are proved by dc and ac magnetic measurements in the compound.

For the first time, the sol–gel synthesis of La2MnTiO6 (LMTO) is reported by Shirazi et al. The prepared sample possesses an orthorhombic structure and display high photoactivity properties. In contrast, the magnetic properties of this material are yet to be reported [21].

Recently, the monoclinic phase of the LMTO sample has been studied [22]. The magnetic study shows AFM transitions below 10 K with long-range magnetic ordering.

The properties of this double perovskite can be changed noticeably with the substitution of La3+ by divalent cation with smaller ionic radii like Ca2+. As an example, a partial substitution of La in LFMO by divalent cations to form the compound ALaMnFeO6 (A = Sr, Ba and Ca) leads to a significant increase of the Curie temperature (TC) compared to LFMO from 150 K for LaBaMnFeO6 up to 350 K for LaSrMnFeO6 [23]. In addition, we show a large magnetocaloric effect near room temperature ferromagnetic transition (300 K) for LSMFO.

The observations discussed above imply that the change of the ionic radii and valence La-site ions by incorporation of divalent cations (Ca2+, Sr2+…) has a great effect on the physical properties of La2MnBO6 magnetic properties. On the other hand, as seen the disordered arrangement of the B-site cations is expected to induce new interesting properties like spin-glass behavior, multiple magnetic transition, and room temperature magnetoresistance.

In this work, the usual solid-state reaction technique was used to elaborate new double perovskite oxides of the formula La1.75Ca0.25MnMO6 (with M = Ti and Fe). The structural and magnetic properties of the obtained materials were all studied, and the results were discussed.

2 Experimental Details

Powder compounds with nominal composition La1.75Ca0.25MnMO6 (with M = Ti and Fe) were elaborated using the solid-state method. The stoichiometric quantities of dried oxides and carbonates (La2O3, CaCO3, Fe2O3, TiO2, and MnO2 of high purity > 99.9%) were mixed and first fired at 1000 °C for 18 h. Then, the samples were repeatedly ground and heated for 18 h at 1100 °C and 1200 °C. Finally, they were sintered at 1250 °C for 72 h after grinding and pressing for pellets (of about 2 mm thickness and 12 mm diameter) under an axial pressure of 4 tons. Structural analysis was recorded using a Panalytical Xʹpert PRO3 diffractometer with Cu-Kα radiation (λ = 1.5406 Å). The data are registered in the angular range from 10 to 80° with steps of 0.05°. Fourier transformation infrared spectroscopy (FTIR) spectra in the range of 400 to 4000 cm−1 were carried out in KBr dispersion by FTIR Bruker Tensor 27 spectrometer. Raman spectrums in the range of 100 to 1500 cm−1 were performed using a Jobin Yvon HR 800 (λ = 441.6 nm) Raman spectrometer at room temperature. The magnetic measurements were done by a vibrating sample magnetometer (VSM, Cryogenic – Cryofree) operating between 0 and 350 K with an applied magnetic field up to 2 T. Isothermal magnetization data as a function of the magnetic field was recorded with dc magnetic fields from 0 to 5 T at 5 K and 300 K.

3 Results and Discussion

3.1 X-ray Diffraction

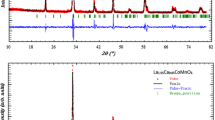
The refinement of typical X-ray diffraction patterns according to the Rietveld method using the Full Prof program [24] is depicted in Fig. 1a, b. The obtained results reveal that both samples crystallize in the orthorhombic structure with the Pbnm space group.

Fig. 1
figure 1

Powder X-ray diffraction patterns for (a) La1.75Ca0.25MnFeO6 and (b) La1.75Ca0.25MnTiO6

Full size image

The estimated values of lattice parameters, atomic coordinates, cell volume, and fit factor values are collected in Table 1. The crystal structure of the compounds has been drawn using the Vesta software [25] and shown in Fig. 2a, b. Figure 2a shows the unit cell of LCMFO, where two octahedra (MnO6 and FeO6) are randomly distributed in corner-shared octahedra environments making the system an antisite-disordered system. The same is observed for the LCMTO compound (Fig. 2b).

Table 1 Unit cell, positional parameters, and discrepancy factors after the refinement of the crystal structure from XRD powder data at RT
Full size table
Fig. 2
figure 2

Overview of the structure of (a) La1.75Ca0.25MnFeO6 and (b) La1.75Ca0.25MnTiO6

Full size image

“Diamond” program was used to determine the interatomic distances and bond angles between all ions in the structure [26]. The selected interatomic distances and bond angles are summarized in Table 2. Therefore, the crystal structure of the LCMFO and LCMTO compounds is characterized by a tilt of the ideal perovskite structure that results in a reduction of the Ti/Mn–O–Mn/Ti and Fe/Mn–O–Mn/Fe angles from the ideal value of 180° to a lower value. Both crystal structures are distorted due to the small size of the La+3 and Ca+2 cations, which force the (Fe/Mn)O6 and (Ti/Mn)O6 octahedra to tilt, to improve the 12-coordinated (La/Ca)–O bond distances. Another important realization is that the octahedra are not regular in the case of the LCMTO compound. They have unequal edge lengths and compression of the octahedra along the c axis. This structural distortion is mainly related to a distortion of the octahedral by the Jahn–Teller effect.

Table 2 Distances and angles of La1.75Ca0.25MnMO6 (M = Ti and Fe)
Full size table

The crystal symmetry of these perovskite structures can be predicted by calculating the Goldschmidt tolerance factor (t) [27]. The value of the t factor for each compound was calculated using the following equation:

$$t=\frac{1.75{r}_{A}+0.25{r}_{A}+2{r}_{O}}{\sqrt{2}({r}_{B}+{r}_{B}+2{r}_{O})}$$

where \({r}_{A}\), \({r}_{A}\), \({r}_{B}\), and \({r}_{O}\) are the ionic radii of La3+, Ca2+, B, B', and O2−, respectively.

The ideal cubic symmetry corresponds to t = 1. The deviation from the tolerance factor t = 1 leads to a distorted perovskite structure in the tetragonal (1.00 > t > 0.97) and orthorhombic or monoclinic (t = 0.96) structures [28]. The obtained values of LCMTO and LCMFO are 0.879 and 0.881, respectively. Therefore, our compounds are orthorhombic symmetry rather than the ideal cubic symmetry, consistent with the XRD results. The lower symmetry is caused by the tilt of the B/B′O6 octahedron.

To determine the average crystallite size, we have used different methods such as the Scherrer relation [29] and Williamson–Hall approach [30]. From XRD patterns, the grain sizes (D) are determined using Scherrer relation given as [29]:

$${D}_{SC}= \frac{0.9\lambda }{\beta\; \mathrm{cos}\;\theta }$$
(1)

In the above equation, λ defines the X-ray wavelength (λ = 1.5405 Å), β is the full width at half maximum (FWHM) of the diffraction peak, and \(\theta\) is the Bragg diffraction angle of the most intense peak.

Williamson–Hall (H–W) analysis is another method to determine the average crystallite size. The Williamson–Hall equation can be expressed as [30]:

$$\beta \;\mathrm{cos}\;\theta =\frac{K\lambda }{{D}_{WH}}+4\varepsilon \;\mathrm{sin}\;\theta$$
(2)

In this relation, \({D}_{\mathrm{WH}}\) represents the average crystallite size, and ɛ is the effective strain.

Representative Williamson–Hall curves of LCMFO and LCMTO compounds are shown in Fig. 3.

Fig. 3
figure 3

Williamson–Hall analysis for La1.75Ca0.25MnMO6 (with M = Ti and Fe) samples

Full size image

The grain size \({D}_{\mathrm{WH}}\) and the strain ɛ was extracted from the intercept and the slope of the linear adjustment of these plots, respectively. The obtained values for \({D}_{\mathrm{SC}}\),\({D}_{\mathrm{WH}}\), and ɛ are regrouped in Table 3; we can confirm the nanometric size of the crystallites of our compounds. It is worth noting that the particle size using the W–H technique was larger than that calculated using the Scherrer relation. This difference can be attributed to the fact that the broadening effect due to the stress is completely excluded in Debye–Scherrer method.

Table 3 Structural parameters as crystallite size determined by Scherer formula (\({D}_{SC}\)) and by Williamson–Hall method (\({\mathrm{D}}_{\mathrm{WH}}\)), the strain (ɛ), X-ray density (\({\uprho }_{\mathrm{x}}\)), the specific surface area (\(\mathrm{S}\)), and the dislocation density (\(\updelta\))
Full size table

On the other hand, we calculated the X-ray density \({d}_{x}\) according to the following expression [31]:

$${\rho }_{x}=\frac{M}{NV}$$
(3)

where M is the molecular mass, N defines the Avogadro number, and V corresponds to the volume determined from the XRD results.

We can also determine the dislocation density δ, which present the amount of defects in the prepared samples. This parameter is defined as the length of the dislocation lines per unit volume of the crystal and is calculated using the following relationship:

$$\delta =\frac{1}{{{D}_{WH}}^{2}}$$
(4)

where \({D}_{\mathrm{WH}}\) is the diameter of the particle in meters (m).

\({\uprho }_{\mathrm{x}}\) and \(\updelta\) values are registered in Table 3.

Electron density ρ (r) calculations, which are scattered from the unit cell of the material, are done using Fourier as a subprogram in Full Prof software. The electron density is calculated using the following relation [32]:

$$\rho (r)=\frac{1}{V}{\sum }_{H}F\left(H\right)exp\left\{-2\pi i\left(Hr\right)\right\}$$
(5)

where r is the position vector inside the unit cell, V is the unit cell volume, H is the reciprocal lattice vector, and F (H) is the coefficient of the complex Fourier.

The two-dimensional Fourier representation of LCMFO and LCMTO is displayed in Fig. 4a, b. To study the atoms and bonding characteristics, we have analyzed the electron density distributions (ED) in three different crystallographic planes. The spherical symmetry of the atoms and the accumulation of the charges towards the charge centre can be seen.

Fig. 4
figure 4

(a) Electron density mapping along (a) (x, y, 0), (b) (0, y, z), and (c) (x, 0, z) direction for La1.75Ca0.25MnFeO6 compound. (b) Electron density mapping along (a) (x, y, 0), (b) (0, y, z), and (c) (x, 0, z) direction for La1.75Ca0.25MnTiO6 compound

Full size image

It is worth noting from these maps that the La/Ca atoms exhibit very high electron densities as compared with Fe/Mn, Ti/Mn, and O elements, which might be ascribed to the high atomic number of La (z = 57). It is further observed that the oxygen elements exhibit a very lower electron density than the others. ED distribution around Fe/Mn elements is found to be 24.64 e/Å3 along with all directions (Fig. 4a). The obtained ED distribution corresponding to Ti/Mn atoms is 8.43 e/Å3 from Fig. 4b.

In the LCMTO and LCMFO materials, we can observe that there is not much charge sharing between La/Ca and O-constituents that confirms the presence of ionic nature along with the La/Ca–O bond. Furthermore, we can show that the charges are shared between Mn/Fe/Ti and O elements along the bonding region between them, which confirms the presence of the strong covalency of the Fe/Mn–O and Ti/Mn–O bonds. This means that the M/MnO6 (M = Fe and Ti) octahedra have a covalent character that might be formed by the overlap of Ti/Mn or Fe/Mn 3d and O 2p electrons.

In the case of LCMFO, it is observed higher and uniform distribution of ED around bond chains Fe/Mn–O–Fe/Mn–O1–Fe/Mn–O1 along z-axes (Fig. 4a), which prove the large overlap of electron clouds around atoms. In contrast, it is observed a non-uniform ED distribution in bond chains Ti/Mn–O1–Ti/Mn–O1–Ti/Mn (Fig. 4b) suggested that the Mn/Fe–O band induced a higher electron density compared to Mn/Ti–O band in the La1.75Ca0.25MnMO6 (with M = Ti and Fe) system. In summary, we can note from the electron density for LCMFO is comparatively higher than the LCMTO sample. The electron density directly affects the electric and magnetic properties in these perovskite systems.

3.2 Fourier Transform Infrared Spectroscopy

Figure 5 represents the FTIR spectra of LCMFO and LCMTO samples. The FTIR spectrum shows two characteristic bands at 403.08 and 632.60 cm−1. According to several studies [33, 34], the bands are assigned to the anti-symmetric stretching mode of the Ti/MnO6 and Fe/MnO6 octahedra. We notice that both FTIR spectra are very similar in position, while the intensity of modes becomes stronger in the case of LFMO. This may be due to the variation of the average B site radius, which produces local stress in Ti/Fe/MnO6 octahedron causing the changes in the bending and tilting of Fe/Mn–O-Mn/Fe and Ti/Mn-OMn/Ti bonds.

Fig. 5
figure 5

FT-IR spectra for La1.75Ca0.25MnMO6 (with M = Ti and Fe) samples

Full size image

3.3 Raman Spectroscopy

According to the group theoretical calculations published in Ref. [35], totally 52 point modes (Γ = 7 Ag + 7 B1g + 5 B2g + 5 B3g + 10 B1u + 8 B2u + 10 B3u) exist in the Pbnm group. Of the total 52 vibrations modes, 24 (Γ = 7 Ag + 7 B1g + 5 B2g + 5 B3g) are Raman active, and the rest are silent. We do not show all the polar phonons allowed in the orthorhombic Pbnm system because of their small strength and/or overlapping. The Raman spectrums of the samples at room temperature are illustrated in Fig. 6. A fit to a combination of Gaussian functions has been performed to evidence all modes. The different peaks are attributed to the symmetry assigned as seen in Table 4. All the Raman modes are related to the orthorhombic crystal structure, and no additional peak corresponding to any other secondary or impurity phases was observed. The Raman active bands showed in the present system are similar to those reported for the Dy2-xLaxFeMnO6 (x = 0.0, 0.2, 0.4, 0.6, and 0.8) [36] and La2CoMnO6 [37] perovskite ceramics. In agreement with the previous systems [36, 37], here also low wavenumber modes below 200 cm−1 are corresponding to La vibration. The stretching of M–O bonds generates the modes located in the mid wavenumber region between 200 and 350 cm−1. The modes observed in the 350–500 cm−1 region arises due to oxygen octahedral bending vibrations, and those between 500 and 900 cm−1 are largely related to O stretching vibrations [38]. Other phonon modes in the high frequency (above 900 cm−1) could originate probably from the combination and overtones of fundamental Ag and/or B1g modes and are a consequence of the displacement of oxygen atoms along the A-O axis in double perovskites [39].

Fig. 6
figure 6

Raman spectra of La1.75Ca0.25MnMO6 (M = Ti and Fe) compounds

Full size image
Table 4 Raman modes of Dy2-xLaxFeMnO6 (x = 0.0, 0.2, 0.4, 0.6, and 0.8) [22] and La1.75Ca0.25MnMO6 (M = Ti and Fe) compounds
Full size table

3.4 Magnetic Properties

The temperature dependence of field-cooled (FC) and zero field-cooled (ZFC) magnetization of LCMFO compound measured under an applied magnetic field of 2000 Oe in the temperature range from 0 to 350 K is shown in Fig. 7. We remark that, at high temperatures, linear behavior of this curve and it is interesting to notice that the magnetization does not go to zero even at room temperature, which proves that the magnetic state is not purely PM. A PM to AFM transition is observed at about 230 K. In addition, strong irreversibility between FC and ZFC curves is seen below TN. In the ZFC process, with decreasing temperature, the magnetic moment increases and shows a cusp at Tcusp = 13.10 K under which the magnetization decreases with a decrease in temperature. The little peak at low temperature is probably due to the presence of antisite-disorder effect in the system. While the FC model shows no such peak, the magnetization goes on increasing with a decrease in temperature. In general, in this type of system, the strong bifurcation between ZFC and FC curves should be attributed to the existence of several magnetic interactions competitively.

Fig. 7
figure 7

Magnetization as a function of the temperature of La1.75Ca0.25MnFeO6 and La1.75Ca0.25MnTiO6 compounds

Full size image

Indeed, doping the disordered LFMO ceramic, in which only Mn3+ and Fe3+ exist, with 25% of the divalent ions Ca2+ causes the conversion of a proportional number of Mn3+ to Mn4+.

Hence, the origin of magnetism in our compound at low temperature can be explained by the random arrangements of the ions Fe3+, Mn3+, and Mn4+ in site B of the perovskite structure, which lead to competing exchange interactions, viz., Mn3+–O–Mn4+ FM interactions, Fe3+-O-Fe3+, and Mn3+–O–Mn3+ AFM interactions and Fe3+-O-Mn3+ FiM interactions.

In the meantime, the ZFC and FC magnetization curves of LCMTO were measured in the temperature range from 0 to 350 K under 2000 Oe (Fig. 7). Similar to LCMFO, the divergence has been observed between ZFC and FC magnetization curves below TN (223 K), but no anomaly is detected in the ZFC curve. The complex magnetic behavior of the LCTMO material can be attributed to the dominant AFM interactions between Mn2+ ions mediated by non-magnetic Ti4+ and oxygen ions with short-range FM interactions.

This divergence has already been reported in similar materials because of the competition of the multi magnetic interactions between the different magnetic cations, which prevents the establishment of a long-range ordered magnetic arrangement [40, 41].

To better understand the magnetic behavior, the temperature dependence of the inverse of the magnetic susceptibility plots χ−1 (defined as H/M) are shown in Fig. 8. The variation of the inverse susceptibility for our compounds is globally similar with a quasi-linear domain at high temperature, which has been modeled by a Curie–Weiss law [42].

$${\upchi }^{-1}=\frac{T \_{\theta }_{C}}{C}$$
(6)

where C represents the Curie constant and θC is the Curie–Weiss temperature. The values of θC and C are extracted from the slope and the intercept of the linear fitting in the PM region.

Fig. 8
figure 8

The temperature dependence of the inverse magnetic susceptibility for La1.75Ca0.25MnMO6 (M = Ti and Fe) samples fitted by Eq. 6

Full size image

The experimental effective moment can be obtained according to the following relation [43]:

$${\mu }_{eff}^{exp}=\sqrt{\frac{3{K}_{B}C}{{N}_{A}}}=\sqrt{8C}{\mu }_{B}$$
(7)

where \({K}_{\mathrm{B}}\) is the Boltzmann constant, \({N}_{A}\) is the Avogadro number, and \({\mu }_{B}\) is the Bohr magneton. The estimated values of θC, C, and \({\mu }_{eff}^{exp}\) are summarized in Table 5. The susceptibility of the materials deviates from Curie–Weiss law above TN. This behavior may be due to the presence of the Griffith phase (GP) described by the presence of magnetic aggregates in the PM phase. However, we remark that the fitting lines cut the negative x-axis, which demonstrates the dominant role of the AFM interactions in the compounds.

Table 5 Magnetic parameters extracted from Figs. 7 and 8
Full size table

To a better understanding of the magnetic properties of our samples, we had study the magnetization vs. magnetic-field isotherms at temperatures of 5 K and 300 K. The field-dependent magnetization at 300 K (Fig. 9) shows a weak hysteresis loop, indicating the appearance of some short-range FM interaction in PM state. Further, the hysteresis loops at 5 K shows an unsaturated magnetization with a value of remnant magnetization, which exhibits FM and/or FiM hysteresis loop superimposed on an AFM signal.

Fig. 9
figure 9

The hysteresis loops of the La1.75Ca0.25MnMO6 (M = Ti and Fe) samples measured at room temperature 300 K

Full size image

At low temperature, the hysteresis loop can be divided into two parts as described by the relation [44]:

$${M \left(T\right)=M}_{FM/FiM }H+{\upchi }_{AFM} H$$
(8)

where the first term refers to the FM and/or FiM component (in our case, it is weak FM and FiM in LCMFO and FM in LCMTO) and the second part χH is a linear component arising due to the AFM contribution. In the expression, MFM/FiM is the magnetization due to FM or/and FiM interactions, χAFM is the AFM susceptibility, and H is the applied magnetic field.

According to the literature [44], the tangent to the demagnetizing curve (upper plot of a hysteresis is loop) at high values of H is taken as the slope of the AFM signal. Indeed, in the first step, we build the AFM response and then extract the FM or/and FiM signal by subtraction of the AFM contribution from the total magnetization (FM + FiM + AFM signals).

The separated components are depicted in Fig. 10, and the relevant parameters are listed in Table 6. For FM/FiM parts, the magnetic properties are typical of interest, such as remanence magnetization (Mr), saturation magnetization (Ms), and coercivity (Hc) can be obtained from the hysteresis loop (Table 6). Accordingly, the AFM contribution at 5 T is 18.3% and 65.5% in LCMFO and LCMTO, respectively.

Fig. 10
figure 10

The hysteresis loops and the extracted FM and AFM parts of the M-H loops of La1.75Ca0.25MnMO6 (M = Ti and Fe) samples measured at 5 K

Full size image
Table 6 Parameters obtained from fitting of magnetization hysteresis loops of La1.75Ca0.25MnFeO6 and La1.75Ca0.25MnTiO6 materials
Full size table

We can see that the hysteresis loops for our compounds at 5 K have double coercivity fields and an asymmetry in the remanence of the decreasing- and the increasing-field branches of the M (H) loops, which proves the presence of the bias effect (EB) in those materials [45]. The coexistence of FM, FiM, and AFM orders is responsible for the observed EB impact. The EB behavior can be due to a coupling between the FM and AFM domains and/or the coupling between FM spin and interfacial. The loop asymmetric along the field axis and magnetization axis can be described by the exchange bias field HE and the exchange bias magnetization ME parameters [46, 47]. The EB field HE and HC are generally defined as \(\left|{Hc}_{1}+{Hc}_{2}\right|/2\) and \(\left|{Hc}_{1}-{Hc}_{2}\right|/2\), respectively, where \({Hc}_{1}\) and \({Hc}_{2}\) are the right and left coercive fields, respectively. The remanence asymmetry (ME) and the magnetic coercivity (MC) are defined as \(-\left({M}_{R1}+{M}_{R2}\right)/2\) and \(-\left({M}_{R1}-{M}_{R2}\right)/2\), where \({M}_{R1}\) and \({M}_{R2}\) are the magnetization at H = 0 for decreasing and increasing branches of the hysteresis loop, respectively [47].

In magnetic systems, the magneto-crystalline anisotropy is proportional to the coercivity phenomena. According to Stoner–Wohlfarth’s equation, the anisotropy constant (\({K}_{a}\)) can be determined from the following expression [48]:

$${H}_{C}=\left(0.98{K}_{a}\right)/{M}_{S}$$
(9)

where \({K}_{\mathrm{a}}\) is the anisotropy constant and \({M}_{\mathrm{S}}\) is the saturation magnetization. The obtained values of the anisotropy constants are listed in Table 6.

4 Conclusions

The structural and magnetic properties of La1.75Ca0.25MnMO6 (M = Ti and Fe) elaborated using the ceramic method have been systematically studied in detail. The room temperature X-ray diffraction data show that the samples crystallize in orthorhombic structure with the Pbnm space group. However, the M = Ti sample shows a special Jahn–Teller deformation of the MnO6 octahedra and significant changes in bond parameters. Raman spectral analysis confirms the phase stabilization of our samples which are in good agreement with group theoretical calculations for the orthorhombic Pbnm symmetry. The temperature dependence of magnetization show PM–AFM transitions at TN \(\sim\) 230 and 223 K for LCMFO and LCMTO compounds, respectively. The non-negligible magnetization and the weak hysteresis cycle at 300 K confirm the presence of ferromagnetism in the PM matrix. The random distribution of B cations introduced inhomogeneous magnetic interactions (FM, FiM, and AFM correlations), leading to a complex magnetic behavior at low temperatures. Consequently, the exchange bias (EB) effect that originates from the interface magnetic exchange interactions between AFM and FM regions was found in both systems.