1 Introduction

Since the successful separation of the single-layer graphene in 2004 [1], the novel physical properties and unique morphology of graphene have been studied intensively. The undoped graphene material is a gapless semimetal because the conduction band and the valence band only contact at the Dirac points [2, 3]. Later, a new concept of spin-gapless semiconductors (SGS) was proposed [4]. For a spin-gapless semiconductor, one spin channel is gapless and exhibits metallicity, while the other is fully gapped. Therefore, the charge carriers, which are excited from the valence band to the conduction band of the SGS, are generally fully spin-polarized. The special energy band structure of a SGS has opened up broad prospects for practical spintronic applications. Therefore, the SGS materials are important for the preparation of spintronic devices. The properties of SGS materials have been a hot topic in the field of the condensed matter physics.

Recently, the nodal-line semimetal materials (NLSM) have attracted broad interest. A three-dimensional NLSM material has one-dimensional loop at the Fermi energy. At the system surface, it has the zero energy flat band. Previously, the NLSM is proposed to be realized in several real materials [5,6,7,8,9,10] and the cold atom system [11]. Many interesting physical properties have been proposed. Particularly, at the system surface, there is a zero energy flat band, leading to the large density of states at the Fermi energy. As a result, the NLSM may be an ideal system to realize the superconductivity with a high transition temperature [12]. And it may provide an ideal platform to realize and study the topological superconductivity [13].

For the superconducting system, one of the most important issues is the pairing symmetry. In the NLSM system, it was proposed experimentally that the s-wave pairing symmetry may be realized [14]. On the other hand, the surface state of an NLSM material is spin polarized. As a result, the surface states do not favor the s-wave pairing; instead, a p-wave pairing symmetry was proposed theoretically [15, 16]. Actually, the competition of the s-wave pairing and the p-wave pairing in the NLSM material always exists and somewhat blocks the realization of superconductivity in the NLSM system.

Very recently, the combination of the spin-gapless feature and a NLSM nature was proposed, namely, the topological nodal-line spin-gapless semimetal (NLSGS) [17]. In an NLSGS material, one spin channel is fully gapped. The other spin channel is gapless with a line-type Fermi surface. The band structure is fully spin polarized and topologically nontrivial with zero energy flat bands. Similar to the usual NLSM material, here the zero energy flat band may favor the superconductivity. Moreover, since one spin channel has been fully gapped; thus, in the superconducting state, now only the p-wave pairing symmetry is possible. Therefore, it is timely and of importance to study the properties and the topological nature of the NLSGS superconductor with the p-wave pairing symmetry.

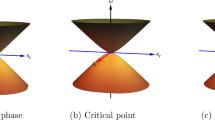
In the past several years, the concept of the higher-order topology was proposed and has been studied intensively [18,19,20,21,22]. For a first-order topological material with the d-dimensional, the band structure is gapless at its d-1 dimensional edges. However, for a higher-order topological system, the band structure is still fully gapped at the d-1 dimensional edges. The gapless edges states appear at the \(d-n\) edges \((n\ge 2)\). In this paper, we study theoretically the physical properties of the NLSGS superconductor with a chiral p-wave pairing symmetry. Our results indicate that the system is a second-order topological superconductor. The second-order topology can be identified through the band structure, the spectral function and the local density of states (LDOS) spectra.

The rest of this article is organized as follows: In Sec. 2, we introduce the model and propose the corresponding formalism. In Sec. 3, we report the numerical calculations and discuss the results obtained. Finally, the full text is briefly summarized in Sec. 4.

2 Model and Hamiltonian

We start from a two-band model describing the NLSGS materials, expressed as,

$$\begin{aligned} H_{NL}(k)= & {} \Big [(\cos k_x+\cos k_y+\cos k_z-r_s)\sigma _1+\sin k_z\sigma _3\Big ]s_3\nonumber \\&+m(1-s_3)\sigma _2-\mu \sigma _0, \end{aligned}$$
(1)

with \(r_s=1+s_3\), where \(s_3=1(-1)\) represents the spin-up (spin-down) electrons, respectively. \(\sigma _{1,2}\) are Pauli matrices representing the orbital channel. \(\sigma _{0}\) is the \(2\times 2\) identity matrix in the momentum space. \(\mu\) is the chemical potential of the system. When the value of m is large, the energy bands for the spin-down electrons are fully gapped, while the spin-up electrons form a nodal-line semimetal with a zero energy flat band at the system surface. In this case, the above model indeed describes the NLSGS materials. Since the system is spin-polarized, we consider the \(p+ip\)-wave superconductivity in the superconducting states. The whole Hamiltonian in the superconducting state is expressed as,

$$\begin{aligned} H=H_{NL}+H^{p+ip}_{sc}. \end{aligned}$$
(2)

The \(p+ip\)-wave pairing term is written as,

$$\begin{aligned} H_{sc}^{p+ip}= \sum _\mathbf{k ,\sigma }\Big [2\Delta _0(\sin k_x+i\sin k_y)C^{\dagger }_\mathbf{k \sigma }C^{\dagger }_{-\mathbf{k} \sigma }+H.c.\Big ]. \end{aligned}$$
(3)

To study the possible topological surface state, we consider the open boundary condition along the z-direction and perform the partial Fourier transformation along the z-dimension for the Hamiltonian. The NLSGS Hamiltonian is then reexpressed as,

$$\begin{aligned} H_{NL}= & {} \pm \sum _{z,\mathbf{k} }(\cos k_x+\cos k_y-r_s)\left[ c^{\dagger }_{zA}(\mathbf{k} )c_{zB}(\mathbf{k} )+H.c.\right] \nonumber \\&\pm \sum _{z,\mathbf{k} }\left[ -\frac{i}{2}c^{\dagger }_{zA}(\mathbf{k} )c_{z+1,A}(\mathbf{k} )-\frac{i}{2}c^{\dagger }_{zB}(\mathbf{k} )c_{z+1,B}(\mathbf{k} )+H.c.\right] \nonumber \\&\pm \sum _{z,\mathbf{k} }\frac{1}{2}\left[ c^{\dagger }_{zA}(\mathbf{k} )c_{z+1,B}(\mathbf{k} )+c^{\dagger }_{zB}(\mathbf{k} )c_{z+1,A}(\mathbf{k} )+H.c.\right] \nonumber \\&+\sum _{z,\mathbf{k} } 2m(1-s_3)i\left[ c^{\dagger }_{zB}(\mathbf{k} )c_{zA}(\mathbf{k} )-c^{\dagger }_{zA}(\mathbf{k} )c_{zB}(\mathbf{k} )\right] \nonumber \\&-\sum _{z,\mathbf{k} ,\sigma }\mu c^{\dagger }_{z\sigma }(\mathbf{k} )c_{z\sigma }(\mathbf{k} ),\nonumber \\ \end{aligned}$$
(4)

in which positive and negative indicate different spin directions. The subscript A, B represents different orbitals. And the momentum \(\mathbf{k}\) is reduced to a two-dimensional parameter with \(\mathbf{k} =(k_x,k_y)\).

Similarly, the Hamiltonian of the superconducting pairing term can be rewritten as,

$$\begin{aligned} H_{sc}^{p_x+ip_y}= \sum _{z,\mathbf{k} ,\sigma }\Big [2\Delta _0(\sin k_x+i\sin k_y)C^{\dagger }_{z\sigma }(\mathbf{k} )C^{\dagger }_{z\sigma }(-\mathbf{k} )+H.c.\Big ]. \end{aligned}$$
(5)

The whole Hamiltonian can be expressed as the \(4N_z\times 4N_z\) matrix form (\(N_z\) is the number of lattice sites along the z-direction). Through diagonalizing the Hamiltonian, we can obtain the spectral functions depending on the reduced momentum \(\mathbf{k}\), expressed as

$$\begin{aligned} A_z(\mathbf{k} ,\omega )= -\frac{1}{\pi }\mathrm{Im}\sum _{\eta ,\sigma }\frac{|u^{\eta }_{i_z\sigma }(\mathbf{k} )|^2}{\omega -E_{\eta }(\mathbf{k} )+i\Gamma }. \end{aligned}$$
(6)

Here, \(u^{\eta }_{i_z\sigma }(\mathbf{k} )\) and \(E_{\eta }(\mathbf{k} )\) are the eigenvectors and eigenvalues. Then, we can obtain the local density of states (LDOS) by summing the momentum \(\mathbf{k}\),

$$\begin{aligned} \rho _z(\omega )= \sum _\mathbf{k }A_z(\mathbf{k} ,\omega ). \end{aligned}$$
(7)

For a second-order topological system, the gapless states emerge at the system hinge. Therefore, to study the second-order topology, we need to consider the open boundary condition along the y and z directions. In this case the Hamiltonian is expressed as,

$$\begin{aligned} H_{NL}= & {} \pm \sum _{z,\mathbf{k} }(\cos k_x-r_s)\left[ c^{\dagger }_{zA}(\mathbf{k} )c_{zB}(\mathbf{k} )+H.c.\right] \nonumber \\&\pm \sum _{z,\mathbf{k} }\left[ -\frac{i}{2}c^{\dagger }_{zA}(\mathbf{k} )c_{z+1,A}(\mathbf{k} )-\frac{i}{2}c^{\dagger }_{zB}(\mathbf{k} )c_{z+1,B}(\mathbf{k} )+H.c.\right] \nonumber \\&\pm \sum _{z,\mathbf{k} }\frac{1}{2}\left[ c^{\dagger }_{zA}(\mathbf{k} )c_{z+1,B}(\mathbf{k} )+c^{\dagger }_{zB}(\mathbf{k} )c_{z+1,A}(\mathbf{k} )+H.c.\right] \nonumber \\&+\sum _{z,\mathbf{k} } 2m(1-s_3)i\left[ c^{\dagger }_{zB}(\mathbf{k} )c_{zA}(\mathbf{k} )-c^{\dagger }_{zA}(\mathbf{k} )c_{zB}(\mathbf{k} )\right] \nonumber \\&\pm \sum _{y,\mathbf{k} }\frac{1}{2}\left[ c^{\dagger }_{yA}(\mathbf{k} )c_{y+1,B}(\mathbf{k} )+c^{\dagger }_{yB}(\mathbf{k} )c_{y+1,A}(\mathbf{k} )+H.c.\right] \nonumber \\&-\sum _{y,z,\mathbf{k} ,\sigma }\mu \left[ c^{\dagger }_{z\sigma }(\mathbf{k} )c_{z\sigma }(\mathbf{k} )+c^{\dagger }_{y\sigma }(\mathbf{k} )c_{y\sigma }(\mathbf{k} )\right] , \end{aligned}$$
(8)

and

$$\begin{aligned} H_{sc}^{p_x+ip_y}= & {} \sum _{z,\mathbf{k} ,\sigma }\Big [2\Delta _0\sin k_x C^{\dagger }_{z\sigma }(\mathbf{k} )C^{\dagger }_{z\sigma }(-\mathbf{k} )+H.c.\Big ]\nonumber \\&+ \sum _{y,\mathbf{k} ,\sigma }\Big [\Delta _0\Big (C_{y\sigma }^{\dagger }(\mathbf{k} )C_{y+1,\sigma }^{\dagger }(-\mathbf{k} )\nonumber \\&\qquad \qquad -C_{y\sigma }^{\dagger }(\mathbf{k} )C_{y-1,\sigma }^{\dagger }(-\mathbf{k} )\Big )+H.c.\Big ].\nonumber \\ \end{aligned}$$
(9)

In addition, we will explore the topology invariants of the model through the winding number to explore the topological nature of the system [23],

$$\begin{aligned} C(\mathbf{k} )= -\frac{i}{\pi }\int ^{\pi }_{\pi }\langle u_n(\mathbf{k} )|\partial k_z|u_n(\mathbf{k} )\rangle dk_z. \end{aligned}$$
(10)

in which \(u_n(\mathbf{k} )\) is the eigenvector of the occupied band.

3 Results and Discussions

We first study the energy bands and possible topological nature in the normal state. The band structures as a function of the in-plane momentum \(\mathbf{k_\parallel }=(k_x,k_y)\) obtained from Eq. (1) in the \(k_z=0\) plane for the undoped sample \((\mu =0)\) with \(m=0\) and \(m=2\) are plotted in Figs. 1(a) and (b), respectively. The corresponding normal state Fermi surfaces are plotted in Figs. 1(c) and (d), respectively. For the case of \(m=0\), both the spin-up energy bands and the spin-down energy bands cross the Fermi energy [Fig. 1(a)], forming two Fermi surface loops, as is shown in Fig. 1(c). As m increases, the energy bands of the spin-up electrons do not change, while the ones of the spin-down electrons depend on the value of m. For the case of \(m=2\), the spin-down electrons are fully gapped [Fig. 1(b)] and in this case only one Fermi surface loop for the spin-up electrons exists [Fig. 1(d)]. Therefore, when exploring the low energy properties, one needs to consider only spin-up electrons. Especially, in the superconducting state, the possibility of the s-wave pairing symmetry can indeed be neglected and only p-wave pairing symmetry is possible. In the following presented results, we focus on the case of \(m=2\) and a \(p+ip\)-wave pairing symmetry is considered for the superconducting state.

Fig. 1
figure 1

(a) The normal state energy bands as a function of the in-plane momentum \(\mathbf{k}_\parallel\) with \(k_z=0\) and \(m=0\).(b) The normal state energy bands as a function of the in-plane momentum \(\mathbf{k}_\parallel\) with \(k_z=0\) and \(m=2\). (c) The normal state Fermi surface with \(k_z=0\) and \(m=0\). (d) The normal state Fermi surface with \(k_z=0\) and \(m=2\)

Full size image

We now discuss the topological features of the normal state energy bands. The energy bands of spin-up electrons with \(m=2\) are similar to those of a NLSM system. One can calculate the topological invariant depending on the in-plane momentum \(\mathbf{k_\parallel }\) according to Eq.(10). We have \(C=1\) when the \(\mathbf{k_\parallel }\) is inside the projection of the nodal loop and \(C=0\) when \(\mathbf{k_\parallel }\) is outside. The non-trivial topological invariants inside the Fermi surface loop generally lead to the topologically protected zero energy flat energy bands at the system surface.

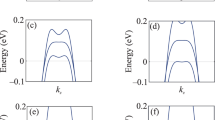
The topological features can be studied further through considering the open boundary condition along the z-direction [Eq.(4)]. The energy bands through diagonalizing the Hamiltonian with \(k_x=0\) are plotted in Fig. 2(a). The LDOS spectra at the system surface (z=1) and in the system bulk (\(z=N_z/2\)) are displayed in Fig. 2(b). The spectral functions at the system surface and in the system bulk are presented in Figs. 2(c) and (d), respectively.

Fig. 2
figure 2

The numerical results of the NLSGS system considering the open boundary condition along the z direction and the periodic boundary condition along the x and z direction. (a) The energy bands in the normal state. (b) The LDOS spectra at the system surface and in the system bulk. (c) The spectral function at the system surface. (d) The spectral function in the system bulk

Full size image

The topological features of the normal state energy bands can be seen clearly in Fig. 2, namely, a zero energy flat band is seen in Fig. 2(a). The LDOS at the system bulk is gapped, due to the nature of the semimetal band structure. At the system surface, the LDOS has a sharp peak at the zero energy due to the existence of the zero energy flat band [Fig. 2(b)]. The surface flat band can be seen further through the spectral function at the system surface, as is shown in Fig. 2(c), while in the system bulk, the spectral function is rather small at the Fermi energy [Fig. 2(d)]. The numerical results for the LDOS spectra and the spectral functions are well consistent, providing useful probe of the topological features of the NLSGS system.

Fig. 3
figure 3

(a) The energy bands in the superconducting state as a function of the in-plane momentum \(\mathbf{k}_\parallel\) with \(k_z=0\). (b) The winding number as a function of the momentum \(k_x\)

Full size image

Let us turn to study the electronic structure and topological features of the superconducting NLSGS system with the chemical potential \(\mu =-0.2\) and the gap magnitude \(\Delta _0=0.2\). Considering the \(p+ip\) pairing symmetry, the energy bands in the momentum space are plotted in Fig. 3(a). As is seen, in the superconducting state, now there are four energy bands for the spin-up electrons. In presence of the superconducting order, the energy bands in the momentum space are fully gapped. We present the numerical results of the winding number from Eq.(10) in Fig. 3(b). Due to the particle–hole symmetry, the winding number increases from 1 to 2 inside the normal state Fermi surface loop. The nonzero winding number indicates that in the superconducting state, the system is still topologically nontrivial.

We now study the energy bands numerically through considering the open boundary condition along the z direction and the periodic boundary condition along the x and y directions. The energy bands from diagonalizing the superconducting state Hamiltonian Eqs. (4-5) as a function of \(k_x\) with \(k_y=0\) are plotted in Fig. 4(a). As is seen, a rather small full gap is opened. The surface states still exist, while in the superconducting state, the surface states are dispersive and the surface states are also fully gapped. These results are significantly different from those shown in the normal state. The fully gapped surface states and no zero energy quasiparticle states indicate that the topological nature of the NLSGS superconductor is different from that of a usual topological superconductor.

Fig. 4
figure 4

The numerical results of the NLSGS superconducting system considering the open boundary condition along the z direction and the periodic boundary condition along the x and z direction, with \(\Delta _0=0.2\) and \(\mu =-0.2\). (a) The energy bands along the \(k_y=0\) line. (b) The LDOS spectra at the system surface and in the system bulk. (c) The spectral function at the system surface. (d) The spectral function in the system bulk

Full size image

We present the numerical results of the LDOS spectra for the NLSGS superconductor at the system surface and system bulk in Fig. 4(b). In the system bulk, the spectra is gapped and no clear superconducting coherent peaks are seen. At the system surface, significant particle–hole asymmetry exists and the LDOS spectrum has a large peak at a certain positive energy. The results are well consistent with the numerical results of the spectral functions shown in Figs. 4(c) and (d). At the system surface, the surface band at the positive energy is seen clearly, leading to the sharp peak of the LDOS spectrum at the positive energy. At the negative energy, the spectral weight of the surface band is rather small. In the system bulk, the most spectral weight appears at the negative energy, as is seen in Fig. 4(d), also consistent with the LDOS spectrum shown in Fig. 4(b).

We consider the open boundary condition along the y and z directions and the periodic boundary condition along the x direction to explore the topological nature of the NLSGS system further. The corresponding energy bands through diagonalizing the Hamiltonian [Eqs.(8) and (9)] are presented in Fig. 5(a). As is seen, for the case of the two open boundaries being considered, the energy gap is closed. Also, the numerical results for the LDOS spectra and the spectral functions at the system hinge and in the system bulk [Figs. 5(b-d)] indicate that the zero energy states indeed exist at the system hinge. There results indicate that the system is indeed a second-order topological superconductor.

Fig. 5
figure 5

The numerical results of the NLSGS superconducting system considering the open boundary condition along the y and z directions and the periodic boundary condition along the x direction, with \(\Delta _0=0.2\) and \(\mu =-0.2\). (a) The energy bands as a function of \(k_x\). (b) The LDOS spectra at the system hinge and in the system bulk. (c) The spectral function at the system hinge. (d) The spectral function in the system bulk

Full size image

The second-order topology in the NLSGS superconductors can be explained qualitatively based on the double band inversion picture [22]. Generally, the nontrivial topological behavior comes from the band inversion effect. Therefore, for a usual NLSM material, the gapless surface state emerges inside the Fermi surface loop due to the band inversion effect. However, as discussed and verified in Ref. [22], for the NLSM system, in the double band inversion region, the system naturally becomes a second-order topological one with the fully gapped surface state and the gapless hinge states. In the present work, in presence of the superconducting pairing term, the wave-vector space in enlarged and the energy bands are doubled naturally due to the particle–hole symmetry, as is seen in Fig. 3. Therefore, inside the Fermi surface loop, the energy bands inverted twice. Our numerical results indicate that the system indeed becomes a second-order topological superconductor, consistent with previous discussions.

4 Summary

In summary, we study theoretically the physical properties and topological behavior of the superconducting nodal-line spin gapless semimetal materials. In the normal state, one spin channel is gapless and topologically nontrivial with a zero energy flat band. Another spin channel is fully gapped and does not contribute to the low energy quasiparticle properties. When a \(p+ip\) superconducting pairing term is considered, the system becomes a second-order topological superconductor. The local density of states and the spectral functions are explored and may be used as a useful probe for the topological nature of the system. The results can be understood well based on the double band inversion picture.