1 Introduction

In the long history of studies of correlated electron systems, superconductivity in repulsively interacting electrons is known to sensitively depend on the underlying band structures. Indeed, this is a first point discerning different classes of superconductors exemplified by the cuprates, iron-based, organic, etc. Then, a question is how we can engineer them for (i) favouring superconductivity (SC) and (ii) controlling the pairing symmetry, with different symmetries possibly coexisting. The thesis of the present paper is that the flat band systems provide an interesting and unique arena for those.

Let us start with a very general question: Which is most favourable for SC, one-band systems or multi-band systems (comprising either multi-orbitals or single-orbital)? As far as the ordinary (dispersive) bands are concerned, Sakakibara et al. have theoretically shown, for the case of multi-orbital multi-band systems, that the farther the second band (with e.g. \(d_{z^{2}}\) orbital character) the higher the TC, and that this trend holds for various compounds in the cuprate family [1,2,3,4]. Namely, the strength of the one-band character dominates the superconductivity within this family.

Given this background, the purpose of the present paper is to compare two cases: a multi-band model in which a flat band coexists with a dispersive one [5], and a single-band case in which a portion of the band dispersion is flat [6]. For the single-orbital multi-band system, the existence of the second band can actually induce the superconductivity especially when the second band is close to, but away from, the Fermi energy. For the single-orbital one-band system with a flat portion in the dispersion, SC can also be induced, in a manner very sensitive to the position of the Fermi energy. We shall compare these to give some hints for various factors dominating the flat band SC.

2 Multi-band Systems Containing Flat Bands

As the simplest possible one-dimensional flat band model that contains a flat band, we take the diamond chain, where diamonds are connected into a chain (Fig. 1a). This model is intimately related with the narrow-wide band model considered by Kuroki and coworkers [7]. If we consider the repulsive Hubbard model on such lattices, the basic idea is this: when the Cooper pairs are formed on the dispersive band, there exist quantum mechanical virtual pair-scattering processes in which pairs are scattered between the dispersive and flat bands. This should especially be important when the flat band is “incipient” (i.e. away from, but close to, the Fermi energy). We have employed DMRG (density-matrix renormalisation group), since the system is quasi-1D, and have shown that: (i) we do have enhanced pairing when the flat band is incipient for intermediate repulsion \(U \simeq 4t\) (t, nearest-neighbour one-electron hopping), where the pair is spin-singlet and formed across the outer sites, and (ii) in that regime we have to take an unusually large number of states, \(m \sim 1500\) in DMRG for convergence, which signifies an anomalously large entanglement [5]. In the phase diagram against band filling (Fig. 2), the superconductivity (SC) sits just below the topological insulator (TI) that occurs when the dispersive band is just completely filled and the flat band is just empty. TI is detected from entanglement spectra and topological edge states, and the situation is similar to the TI in the celebrated Haldane’s S = 1 antiferromagnetic chain.

Fig. 1
figure 1

a Diamond chain, which is a quasi-1D flat band model, and its dispersion. bt-\(t^{\prime }\) model with the second-neighbour hopping (blue lines) \(t^{\prime }\simeq -0.5t\), and its dispersion. Arrows represent typical position of Cooper pairs

Full size image
Fig. 2
figure 2

Schematic phase diagram against the band filling for the diamond chain obtained with DMRG. Bottom panels schematically show the band filling

Full size image

If we actually look at the pair correlation function against real space [8] in Fig. 3, we can see the following: (i) The dominant (longest-tailed) correlation is between the pairs, each of which comprises top and bottom sites in the diamond chain (blue curve in Fig. 3), while the subdominant correlation is between a pair along y (green). In classifying pairing symmetries, it is customary in the ladder physics to call a pair “d-wave” when the correlation between a pair along x direction and another along y has negative values [9]. In this sense, the diamond chain also has a “d-wave”, which is expected to tend to the d-wave in two dimensions. If we look at the pair correlation at distances 1 ≤ r ≤ 6, the functions are seen to oscillate wildly, which should indicate some structure extended in real space. (ii) If we compare the diamond chain with the ordinary ladder system, the pair correlation function in the latter obtained with the quantum Monte Carlo (QMC) shows a long-tailed behaviour, with some wiggles related with the Fermi point effect involving the Fermi wavenumber kF [10]. By contrast, the present result for the diamond chain has a smooth behaviour at large distances, which should be an effect due to the flat band.

Fig. 3
figure 3

DMRG result for the pair correlation function against real-space distance, r, between various spin-singlet pairs as colour-coded

Full size image

Recently, Matsumoto et al. have shown for various flat band models that we do have a general trend for enhanced SC as the Fermi energy EF approaches the flat band energy, with a sharp dip when EF is too close to the flat band [11]. The width of the dip depends on the Hubbard repulsion U, the degree of warping of the flat band due to many-body effects, and also the lattice structure, which is considered to be related with the self-energy effect in the flat band system. Incidentally, while the terminology “incipient” is also used in the community of the iron-based FeSe superconductor for the incipient s± pairing involving the hole band below EF, the concept of the incipient situation was originally introduced by Ref. [7], and we have indeed a drastic effect when we have a flat band instead of dispersive bands. We can also extend the flat band models to two-dimensional lattices, where we can make a flat band pierce a dispersive one [12]. As for candidates for realising the flat band models, they include the mineral azurite [13, 14], and “hidden ladders” in Ruddlesden-Popper compounds such as Sr3Mo2O7 [15] or herbertsmithite.

3 Partially Flat One-Band Superconductivity

Having looked at a multi-band, quasi-1D model, let us move on to partially flat band models that are one band and two-dimensional (2D) [6]. A starting point is that, even within one-band models, we can have a flat portion coexisting with dispersive portions in the band structure (Fig. 1b). An important question then is this: can we still have flat-band superconductivity, and, for 2D systems, how would be the pair-scattering channels in 2D? For such a model, Huang et al. [16] have studied superconductivity for attractive interaction U and Mott insulation for repulsive U in the Hubbard model with the determinantal quantum Monte Carlo (DQMC) method. They have detected an electron correlation effect for less-than-half-filled cases unlike in the ordinary bands.

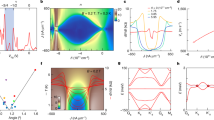
Here, our interest is superconductivity for repulsive interaction. For that we take two models (Fig. 4): one is at-\(t^{\prime }\) model on a square lattice with a second-neighbour hopping \(t^{\prime }\simeq -0.5t\) to have a flat portion along \(k_{x} \simeq 0\) and \(k_{y} \simeq 0\). The other model is a partially flat band (PFB) with a truncated flat bottom. We employ the FLEX+DMFT method, where we combine the fluctuation-exchange approximation and the dynamical mean-field theory [17]. The result for the double occupancy shows that the correlation effect indeed emerges well below half-filling and even for small repulsive U in both models. If we look at the momentum distribution, we can see that electrons are crammed into the flat portion, which should be the reason for the early onset of the double occupancy. The result for the spin susceptibility, χS, exhibits that, for the t-\(t^{\prime }\) model, we have large amplitude of χS along some ridges in k-space that becomes wider as we approach the half-filling, or, for the truncated model, wide plateaux for χS that move from around the Γ point towards the AF points, (±π,±π), as we approach the half-filling. If we turn to the eigenvalue, λ, of the Eliashberg equation in Fig. 4, in the t-\(t^{\prime }\) model, the spin-singlet pairing dominates, where λ exhibits a double-dome structure. We can identify its origin: the peak on the smaller-filling side represents a complicated gap function that have a larger number of nodes than in the usual d-wave, while the peak on the larger filling represents a pairing close to the d-wave. For the truncated model, on the other hand, triplet pairing dominates over an unusually wide filling region with a p-wave-like gap function, which is sharply taken over, as the half-filling is approached, by singlet pairing with a gap function having a larger number of nodes than in the d-wave. If we look at the pairing in real space, the case of large numbers of nodes exhibits unusually extended pairing in real space. We have also detected non-Fermi liquid properties from the frequency dependence of the self energy [6].

Fig. 4
figure 4

For t-\(t^{\prime }\) model (top left inset) and truncated model (right), the eigenvalue, λ, of the Eliashberg equation versus the band filling 〈n〉 is shown for the singlet (filled symbols) and triplet (empty) pairings for t-\(t^{\prime }\) (triangles) and truncated (squares), and cosine-band (circles) models for U = 3,1/(kBT) = 33. A vertical line for the t-\(t^{\prime }\) singlet indicates a change in the pairing symmetry as shown by panels next to it

Full size image

All these are considered to come from the flat portions in the band dispersion. As summarized in Fig. 5 for electron-mechanism superconductivity, usually, we have well-defined nesting vectors that connect “hot spots”, which are the anti-nodal regions in single-orbital, one-band systems as in the d-wave in the cuprates, or the electron and hole pockets in multi-orbital, multi-band systems as in the s±-wave in the iron-based [18]. By contrast, in partially flat band systems we have a bunch of pair-scattering channels, which should be the cause for the peculiar spin structures and the ensuing gap functions there.

Fig. 5
figure 5

We schematically compare ordinary single-orbital, one-band case (here for a d-wave SC; leftmost column) and multi-orbital, multi-band case (here for s±; second column from left), where the nesting vectors (yellow arrows) connecting the specific “hot spots” designate how pairs (blue and orange arrows) hop. These are contrasted with flat band systems for single-orbital, one-band case (second from right) and single-orbital, multi-band case (rightmost), where yellow arrows represent pair-scattering channels. The top row depicts k-space, while the bottom row displays pairs in real space

Full size image

4 Discussions

Can flat bands really favour SC? We can raise several points on this.

  1. (i)

    Dimensionality: Electron-mechanism SC employing spin-fluctuation mediated pairing usually uses well-defined spin structure such as AF fluctuations, and this results in specific and compact regions in k-space in which the pairing interaction is strong. From the phase volume arguments, we can then show that quasi-2D (layered) systems are much more favourable for such SC than in 3D systems [19, 20]. This is also consistent with the empirical fact that most of the new superconductors have layered structures. By contrast, the flat band systems have much wider momentum regions for large spin structure, χS. Another factor in the spin-fluctuation mediated pairing interaction is Green’s function G involved in the Eliashberg equation, and G too exhibits wide regions for the flat bands. How about the structure of the gap function? In a multi-band case of the narrow-wide band model [7], we have an “s± wave” between the flat and dispersive bands, where each band has more or less homogeneous amplitude in k-space, which comes from a featureless χS. The gap function in the diamond lattice also has an extended structure as seen from the pair-pair correlation function (Fig. 3) that is long-tailed and long-ranged structure in real space [5]. So we can expect that 3D systems may be as good as 2D systems in the flat band SC.

  2. (ii)

    Vertex corrections: In general, the size of TC in SC arising from electron-electron repulsion is shown to involve the vertex correction in the pair scattering [21], which is identified as the main reason why TC is two orders of magnitude lower than the electronic energy. Thus, the vertex correction in the flat band systems is an interesting future problem. Incidentally, flat bands have also been discussed where the many-body renormalised mass (which enters in the Fermi liquid theory) is heavy [22], whereas we consider here non-interacting bands that are dispersionless. A heavy renormalised mass (occurring e.g. when the Fermi energy is right at the one-electron flat band that makes the self-energy correction large), which is contrasted with the present case of incipient flat band or portion that can work favourably for superconductivity.

  3. (iii)

    Strong-coupling limit: In the strong-coupling limit, the Hubbard model is converted into a Heisenberg spin model. It has been shown that a kind of Creutz model (with cross-linked interactions) in 2D can accommodate a supersolid phase where superfluid and density wave coexist [23].

  4. (iv)

    Superfluid weight: Törmä and coworkers have shown, for the attractive electron–electron interaction, that superfluidity in topological flat bands has a superfluid weight lower-bounded by the topological number [24,25,26,27]. So the question of what happens for repulsive interactions will be another interesting future problem.

If we summarize the comparison for the flat-band systems between the multi-band and one-band cases, a similarity is that superconductivity can be induced in both cases when the flat band or portion is incipient. The differences are mainly the different gap function structures between the two cases, which is caused by different spin structures as dictated by the band dispersion, and then results in difference in the pairing symmetries. In the multi-band diamond chain, the pairing exploits large entanglement arising from the topological nature of the flat band. Partially flat one-band systems may accommodate something related with topological states.

The group velocity vanishes at van Hove singularities, and there are literatures discussing a possibility of topological superconductivity involving the van Hove singularities [28,29,30]. In the flat band systems, the group velocity vanishes over a finite area rather than at a point. There, we have observed a transition between p-wave and d-wave [6]. It is generally recognized that the boundary regions between different pairing symmetries are a good place for looking for topological superconductivity with broken time-reversal symmetry [31, 32], so there may be a possibility of topological SC in partially flat band systems. Also, partially flat bands remind us of the band structure of the twisted bilayer graphene for which SC was discovered, and first-principles calculations show partial flatness [33,34,35,36]. However, this material involves various complications such as a multi-band character, so the present one-band model will not apply directly. If we go over to three-dimensional systems, Akashi has recently shown that “saddle loops” (an extension of van Hove saddle points) can occur from a general standpoint [37], which may be utilised for band structure engineering.

In a broader context than the flat band physics, studies of superconductivity in two-band systems have a long history, basically starting from Suhl-Kondo mechanism. For repulsively interacting two-band systems, Kuroki and the present author have investigated superconductivity with QMC [38,39,40] and the bosonisation [41]. For the cuprates specifically, effects of hydrostatic and uniaxial pressure for multi-band models [1,2,3,4] or strain control of multigap superconductors [42] have been discussed. For attractively interacting two-band systems, the effects of the second band have been studied with the Nozières-Schmitt-Rink formalism [43], and the multiband Suhl-Matthias-Walker Hamiltonian [44]. The effect of Lifshitz transitions has also been examined [45,46,47,48,49] in terms of the Fano resonance between the flat and dispersive bands in the BCS-BEC crossover regime [50]. Thus, a future problem is how these would apply to different realisations of flat band cases.