Parabolic Scaling in Overdoped Cuprate: a Statistical Field Theory Approach

Abstract

Recently, Bozovic et al. reported that (Nature 536:309–311, 2016) in the overdoped side of the single-crystal La_{2 − x}Sr_xCuO₄ (LSCO) films, the transition temperature T_c and zero-temperature superfluid phase stiffness ρ_s(0) will obey a two-class scaling law: ${T}_c=\gamma \cdotp \sqrt{\rho_s(0)}$ for T_c ≤ T_Q and T_c ∝ ρ_s(0) for T_c ≥ T_M, where γ = (4.2 ± 0.5) K^1/2 , T_Q ≈ 15 K, and T_M ≈ 12 K. They further pointed out that the parabolic scaling observed in the highly overdoped side indicates a quantum phase transition from a superconductor to a normal metal. In this paper, we propose a quantum partition function (QPF) for zero-temperature Cooper pairs, by which one can effectively distinguish between mean-field and quantum critical behaviors. We theoretically show that the two-class scaling law can be exactly derived by using the QPF, and the theoretical values of γ, T_Q, and T_M are well in accordance with experimental measure values. Our analyses indicate that the linear scaling T_c ∝ ρ_s(0) is a mean-field behavior, while the parabolic scaling ${T}_c=\gamma \cdotp \sqrt{\rho_s(0)}$ is a quantum critical behavior.

1 Introduction

Over recent decades, with the great advances in cooling technologies, much attention was focused on investigating the behaviors of Cooper pairs near zero temperature. Among all physical quantities, the zero-temperature superfluid phase stiffness ρ_s(0) is a central parameter for describing zero-temperature Cooper pairs, since it can be exactly obtained by measuring magnetic penetration depths of superconducting materials. For copper oxide materials, there has been much interest for seeking the potential correlations between the transition temperature T_c and ρ_s(0). The earliest pattern was referred to as the Uemura relation [1–2] T_c ∝ ρ_s(0), which works reasonably well for the underdoped materials. Later, a more universal relation, the Homes’ law [3,4,5,6] T_c ∝ ρ_s(0)/σ_dc was found to hold regardless of underdoped, optimally doped, and overdoped materials, where σ_dc denotes the dc conductivity measured at approximately T_c. Theoretically, Homes’ law has been well-known as a mean-field result of the dirty-limit BCS theory [4, 7–8]. Despite these successes, some scholars questioned the validity of Homes’ law in highly underdoped and overdoped sides. For example, the relation between T_c and ρ_s(0) was found to be sub-linear in highly underdoped materials [9,10,11,12]. Recently, by investigating the overdoped side of the single-crystal La_{2 − x}Sr_xCuO₄ films, Bozovic et al. observed a two-class scaling law [13]:

$$ \left\{\begin{array}{cc}{T}_c=\alpha \cdotp {\rho}_s(0)+{T}_0,& {T}_c\ge {T}_M\\ {}{T}_c=\gamma \cdotp \sqrt{\rho_s(0)},& {T}_c\le {T}_Q\end{array}\right., $$

(1)

where T_M ≈ 12 K, T_Q ≈ 15 K, α = 0.37 ± 0.02, T₀ = (7.0 ± 0.1) K, and γ = (4.2 ± 0.5) K^1/2. The difference between T_M and T_Q implies that the two-class scaling law (1) is non-smoothly linked by linear and parabolic parts.

Equation (1) indicates that a parabolic scaling emerges in the highly overdoped side [13]. Since the two-class scaling law (1) differs significantly from Homes’ law, Bozovic et al. concluded that their experimental findings are incompatible with the mean-field description [13,14,15]. The linear part in Eq. (1) can be derived by using the dirty-limit BCS theory [4, 7–8] and therefore is a mean-field result; however, the parabolic part may hint potential new physics [13]. As a possible evidence, Bozovic et al. have observed that with increased doping (T_c → 0), La_{2 − x}Sr_xCuO₄ becomes more metallic, and increased doping induces a quantum phase transition from a superconductor to a normal metal [13,14,15]. This observation indicates that when T_c → 0, quantum fluctuations may play an important role for inducing the parabolic scaling in Eq. (1). In this paper, we propose a quantum partition function for describing quantum critical behaviors of zero-temperature Cooper pairs. Based on such a quantum partition function, we will exactly reproduce the two-class scaling law (1). Here, we adopt the natural units ℏ = c = k_B = 1, where ℏ denotes the reduced Planck constant, c is the light speed, and k_B is the Boltzmann constant.

2 Quantum partition function for zero-temperature Cooper pairs

The free energy density of zero-temperature Cooper pairs can be generally written as [16]:

$$ \mathcal{L}=\sigma \cdotp {\left|{\partial}_{\tau}\phi \left(\boldsymbol{q},\tau \right)\right|}^2+\eta \cdotp {\left|\mathbf{\nabla}\phi \left(\boldsymbol{q},\tau \right)\right|}^2+{\lambda}_2\cdotp {\left|\phi \left(\boldsymbol{q},\tau \right)\right|}^2+{\lambda}_4\cdotp {\left|\phi \left(\boldsymbol{q},\tau \right)\right|}^4, $$

(2)

where ϕ(q, τ) denotes the order parameter of zero-temperature Cooper pairs and it is a function of space q and imaginary time τ. Here, $\tau \in \left[0,\frac{1}{T}\right]$ with the temperature T being 0. σ, η, λ₂, and λ₄ are phenomenological parameters [16].

If one denotes the zero-temperature superfluid phase stiffness by |ϕ(q, τ)|², then, by applying Gor’kov’s Green function method [8] into the BCS theory at T = 0 and T_c ≈ 0, one can obtain [17]:

$$ \eta =1, $$

(3)

$$ {\lambda}_2={\lambda}_2\left({T}_c\right)=-\frac{24{\pi}^2{m}_e}{7\zeta (3)\cdotp {\varepsilon}_F}{T}_c^2, $$

(4)

$$ {\lambda}_4={\lambda}_4\left({T}_c,{\rho}_s(0)\right)=\frac{12{\pi}^2{m}_e}{7\zeta (3)\cdotp {\varepsilon}_F}\cdotp \frac{T_c^2}{\rho_s(0)}, $$

(5)

where ${\rho}_s(0)=\frac{n_s(0)}{4{m}_e}$ and n_s(0) denote zero-temperature superfluid phase stiffness [13] and zero-temperature superfluid density when materials are homogenous, ζ(x) is the Riemann zeta function, ε_F is the Fermi energy, and m_e is the rest mass of an electron. The derivation for Eqs. (3)–(5) can be found in Appendix 1, where we have clarified why Gor’kov’s method holds at T = 0.

Equations (3)–(5) are derived by using the BCS theory, which assumes that quantum fluctuations on all size scales are averaged out. Based on such an assumption of the mean-field, n_s(0) is equal to the total number density of electrons in the normal state [8] and hence can be regarded as a constant. This is the standard explanation of the BCS theory. However, later we will observe that n_s(0) changes with T_c as long as quantum fluctuations cannot be averaged out.

Due to Eqs (3), (4), and (5), σ is the unique phenomenological parameter in Eq. (2). In this paper, we order σ = 1 so that the free energy density (2) yields an exact relativistic form:

$$ \mathcal{L}\left({T}_c\right)={\left|{\partial}_{\tau}\phi \left(\boldsymbol{q},\tau \right)\right|}^2+{\left|\mathbf{\nabla}\phi \left(\boldsymbol{q},\tau \right)\right|}^2+{\lambda}_2\left({T}_c\right)\cdotp {\left|\phi \left(\boldsymbol{q},\tau \right)\right|}^2+{\lambda}_4\left({T}_c,{\rho}_s(0)\right)\cdotp {\left|\phi \left(\boldsymbol{q},\tau \right)\right|}^4. $$

(6)

It is easy to observe that the transition temperature T_c in Eq. (6) plays the role of temperature T in the classical Landau-Ginzburg free energy. Later, we will show that T_c = 0 is a potential critical point. To guarantee the self-consistency of Eq. (6), we need to verify that |ϕ(q, τ)|² is the zero-temperature superfluid phase stiffness. To this end, the free energy density (6) is varied to obtain the field equation of Cooper pairs:

$$ {\partial}_{\tau}^2\phi \left(\boldsymbol{q},\tau \right)+{\nabla}^2\phi \left(\boldsymbol{q},\tau \right)-{\lambda}_2\phi \left(\boldsymbol{q},\tau \right)-2{\lambda}_4\cdotp {\left|\phi \left(\boldsymbol{q},\tau \right)\right|}^2\phi \left(\boldsymbol{q},\tau \right)=0. $$

(7)

For homogenous superconductors, Eq. (7) yields |ϕ(q, τ)|² = − λ₂/2λ₄ = ρ_s(0), where Eqs. (4) and (5) have been used. Because ρ_s(0) denotes the zero-temperature superfluid phase stiffness of homogenous materials, |ϕ(q, τ)|² indeed denotes the zero-temperature superfluid phase stiffness. This verifies the self-consistency of the free energy density (6).

Using the free energy density (6), we propose a quantum partition function (QPF) for zero-temperature Cooper pairs as follows:

$$ Z\left({T}_c,J,{J}^{\ast}\right)=\int {\left[\mathcal{D}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\right]}_{\Lambda}\int {\left[\mathcal{D}\phi \left(\boldsymbol{q},\tau \right)\right]}_{\Lambda}{e}^{-\int d\tau \int {d}^D\boldsymbol{q}\left[\mathcal{L}\left({T}_c\right)-J\left(\boldsymbol{q},\tau \right)\phi \left(\boldsymbol{q},\tau \right)-J{\left(\boldsymbol{q},\tau \right)}^{\ast}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\right]}, $$

(8)

where J(q, τ) denotes the external field, Λ is the momentum cutoff, and D is the dimension of superconducting materials.

From a perspective of effective field theory, a quantum field theory should be defined fundamentally with a cutoff Λ [18,19,20]. For the crystal materials, a rigid renormalization theory can be defined on a cubic lattice of a lattice unit:

$$ a=\frac{1}{\Lambda}, $$

(9)

where a denotes the minimal lattice constant. The physical meaning of Eq. (9) is that quantum fluctuations with wavelengths less than 2πa can be averaged out [19]. Weinberg also pointed out that [21] in solid-state physics, there really is a cutoff, the lattice spacing a, which one must take seriously in dealing with phenomena at similar length scales.

Since the momentum cutoff Λ is determined by a, there is no longer any phenomenological parameter in the QPF (8). Therefore, the validity of the QPF (8) can be justified by the experimental investigation result (1).

3 Parabolic Scaling

We assume that quantum fluctuations with wavelengths larger than 2πa cannot be averaged out. By the theory of critical phenomena, this means that the coefficients λ₂(T_c) and λ₄(T_c, ρ_s(0)) in Eq. (6) should receive the contributions from quantum fluctuations on these size scales. To evaluate the contributions, by applying the renormalization group approach to the QPF (8), one can obtain the renormalization group equations¹ [17]:

$$ \frac{d{\lambda}_2\left({T}_c\right)}{dlnb}={\lambda}_2\left({T}_c\right)\cdotp \left(2-4{\hat{\lambda}}_4\right)+O\left({\hat{\lambda}}_4^2\right), $$

(10)

$$ \frac{d{\hat{\lambda}}_4}{dlnb}=\left(3-D\right)\cdotp {\hat{\lambda}}_4-10{\hat{\lambda}}_4^2+O\left({\hat{\lambda}}_4^3\right), $$

(11)

where the quantum dynamical exponent z is equal to 1 and

$$ {\hat{\lambda}}_4={\lambda}_4\left({T}_c,{\rho}_s(0)\right)\cdotp \frac{{\left(\pi \right)}^{\frac{D}{2}}{\Lambda}^{D-3}}{2{\left(2\pi \right)}^D\Gamma \left(\frac{D}{2}\right)}. $$

(12)

By Eqs. (10)–(12), it is easy to get a nontrivial fixed point:

$$ \left\{\begin{array}{c}{\lambda}_2\left({T}_c\right)\approx 0\\ {}{\lambda}_4\left({T}_c,{\rho}_s(0)\right)\approx \frac{3-D}{10}\cdotp \frac{2{\left(2\pi \right)}^D\Gamma \left(\frac{D}{2}\right)}{{\left(\pi \right)}^{\frac{D}{2}}{\Lambda}^{D-3}}\end{array}\right.. $$

(13)

λ₂(T_c) and λ₄(T_c, ρ_s(0)) are defined by T_c and ρ_s(0) via Eqs. (4) and (5). Substituting Eqs. (4) and (5) into Eq. (13) yields:

$$ \left\{\begin{array}{c}{T}_c\approx 0\\ {}{T}_c\approx \gamma (D)\cdotp \sqrt{\rho_s(0)}\end{array}\right., $$

(14)

where

$$ \gamma (D)=\sqrt{\left(3-D\right)\cdotp {\Lambda}^{3-D}\cdotp \frac{7{\left(2\pi \right)}^D\Gamma \left(\frac{D}{2}\right)\zeta (3)\cdotp {\varepsilon}_F}{60{\left(\pi \right)}^{\frac{D}{2}+2}{m}_e}}. $$

(15)

If we denote T_c ≈ 0 by T_c ≤ T_Q(D), Eq. (14) can be written in the form:

$$ {T}_c=\gamma (D)\cdot \sqrt{\rho_s(0)}\kern0.5em \mathrm{for}\kern0.5em {T}_c\le {T}_Q(D), $$

(16)

where T_Q(D) denotes a sufficiently low temperature. The physical meaning of Eq. (16) is that ρ_s(0) will change with T_c as long as T_c ≤ T_Q(D). Later, we will theoretically show T_Q(2) ≤ γ(2)² and T_Q(3) ≤ 0.

The two-class scaling law (1) was found in the single-crystal La_{2 − x}Sr_xCuO₄ films (D = 2) around x = 0.25 [13]. Therefore, for D = 2, Eq. (16) reproduces the parabolic part in the two-class scaling law (1). To verify this, we show that γ(2) is in accordance with the existing experimental measure value. Plugging Eq. (9) into Eq. (15), one can obtain [21]:

$$ \gamma (2)=\sqrt{\frac{7\cdotp \zeta (3)\cdotp {\varepsilon}_F}{15\cdotp \pi \cdotp a\cdotp {m}_e}}. $$

(17)

For single-crystal La_{2 − x}Sr_xCuO₄ films, substituting the data a ≈ 3.8 × 10⁻¹⁰ m [13] and ε_F(x ≈ 0.2) ≈ 8.75 eV [22] into Eq. (17) yields [21]:

$$ \gamma (2)\approx 4.29\ {K}^{1/2}, $$

(18)

which exactly agrees with the experimental value (4.2 ± 0.5) K^1/2 [13].

The high accordance between theoretical and experimental values thoroughly proves that the parabolic scaling in Eq. (1) is due to quantum fluctuations. From this meaning, the nontrivial fixed point (13) describes the quantum critical behaviors of zero-temperature Cooper pairs when T_c ≤ T_Q(D). However, we do not clarify the range of applicability of the nontrivial fixed point (13), i.e., the value of T_Q(D). According to the renormalization group theory, the nontrivial fixed point (13) is valid if and only if quantum fluctuations cannot be averaged out. Therefore, to evaluate T_Q(D), we need to find a criterion for identifying the validity of the mean-field approximation.

4 Quantum Ginzburg Number

For thermal fluctuations, there exists a clear criterion of the applicability of the mean-field theory, i.e., the classical Ginzburg number G_i [23,24,25], where the mean-field approximation is valid when G_i ≪ 1. To evaluate quantum fluctuations, we extend G_i to a quantum version. To this end, let us first define the correlation function of the order parameter ϕ(q, τ) as [16]:

$$ G\left(\boldsymbol{q}-{\boldsymbol{q}}^{\prime },\tau -{\tau}^{\prime}\right)=\left\langle \left[\phi \left(\boldsymbol{q},\tau \right)-\left\langle \phi \left(\boldsymbol{q},\tau \right)\right\rangle \right]\cdotp \left[\phi {\left({\boldsymbol{q}}^{\prime },{\tau}^{\prime}\right)}^{\ast }-\left\langle \phi {\left({\boldsymbol{q}}^{\prime },{\tau}^{\prime}\right)}^{\ast}\right\rangle \right]\right\rangle, $$

(19)

where the mean value of a physical variable A(q, τ) is defined by

$$ \left\langle A\left(\boldsymbol{q},\tau \right)\right\rangle =\frac{1}{Z\left({T}_c,J,{J}^{\ast}\right)}\int \mathcal{D}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\int \mathcal{D}\phi \left(\boldsymbol{q},\tau \right){e}^{-\int d\tau \int {d}^D\boldsymbol{q}\left[\mathcal{L}\left({T}_c\right)-J\left(\boldsymbol{q},\tau \right)\phi \left(\boldsymbol{q},\tau \right)-J{\left(\boldsymbol{q},\tau \right)}^{\ast}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\right]}\cdotp A\left(\boldsymbol{q},\tau \right). $$

(20)

Using Eqs. (8), (19), and (20), it is easy to obtain:

$$ G\left(\boldsymbol{q}-{\boldsymbol{q}}^{\prime },\tau -{\tau}^{\prime}\right)=\frac{\partial^2 lnZ\left({T}_c,J,{J}^{\ast}\right)}{\partial J\left(\boldsymbol{q},\tau \right)\partial J{\left({\boldsymbol{q}}^{\prime },{\tau}^{\prime}\right)}^{\ast }}=\frac{\partial \left\langle \phi \left(\boldsymbol{q},\tau \right)\right\rangle }{\partial J{\left({\boldsymbol{q}}^{\prime },{\tau}^{\prime}\right)}^{\ast }}. $$

(21)

As a quantum extension of the classical Ginzburg number G_i, by using the correlation function (19) we construct an error function of the order parameter ϕ(q, τ) as follows:

$$ {e}^q(D)=\frac{\left|{\int}_0^{\infty } d\tau \int {d}^D\boldsymbol{q}G\left(\boldsymbol{q},\tau \right)\right|}{\int_0^{\infty } d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right)}, $$

(22)

where e^q(D) returns to the classical Ginzburg number G_i when ϕ(q, τ) is independent of τ, that is, ${e}^q(D)=\frac{\left|\int {d}^D\boldsymbol{q}G\left(\boldsymbol{q}\right)\right|}{\int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q}\right)}^{\ast}\phi \left(\boldsymbol{q}\right)}={G}_i$ if ϕ(q, τ) = ϕ(q). By Eq. (22), the mean-field approximation is valid if and only if

$$ {e}^q(D)\ll 1. $$

(23)

Therefore, when the inequality (23) breaks down, the nontrivial fixed point (13) holds. To rigidly determine the range of applicability of the nontrivial fixed point (13), we need to explore the physical meaning of the inequality (23). To this end, let us order

$$ M\left({T}_c\right)=\left|{\int}_0^{\infty } d\tau \int {d}^D\boldsymbol{q}G\left(\boldsymbol{q},\tau \right)\right|, $$

(24)

$$ W(t)={\int}_0^{\frac{1}{t}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right). $$

(25)

By using Eqs. (24) and (25), Eq. (22) can be written as e^q(D) = M(T_c)/W(0). Obviously, we have W(t) ≤ W(0) and M(T_c) ≤ W(0). Since G(q, τ) is the correlation function, M(T_c) actually denotes the magnitude of quantum fluctuations. Thus, the physical meaning of the inequality (23) is that quantum fluctuations can be omitted if and only if their magnitude is extremely small, that is, M(T_c) ≪ W(0). Based on this observation, there should exist a critical magnitude M₀ so that when M(T_c) ≥ M₀, quantum fluctuations cannot be omitted. This means that the nontrivial fixed point (13) is valid when M(T_c) ≥ M₀. To evaluate the value of M(T_c), we introduce an approximation ϕ(q, τ) ≈ 〈ϕ(q, τ)〉 ≈ 〈ϕ(q, τ)〉_vac. This approximation has been well-known for evaluating the magnitude of thermal fluctuations when T > 0 [23–24].

Proposition 1: If ϕ(q, τ) ≈ 〈ϕ(q, τ)〉 ≈ 〈ϕ(q, τ)〉_vac, then the magnitude of quantum fluctuations, M(T_c), yields:

$$ M\left({T}_c\right)={\xi}^2\propto {T}_c^{-2}, $$

(26)

where ξ = (−λ₂(T_c))^−1/2 denotes the quantum correlation length² and 〈ϕ(q, τ)〉_vac denotes the vacuum expectation value of 〈ϕ(q, τ)〉.

Proof: see Appendix 2. ■

By Eq. (26), the magnitude M(T_c) and the correlation length ξ grow as T_c decreases, and both of them finally diverge at T_c = 0. This implies that T_c = 0 is a critical point. Since M(T_c) increases as T_c declines, there does exist ${T}_Q^{\prime }$ so that when ${T}_c\le {T}_Q^{\prime }$, one has M(T_c) ≥ M₀. This means that the nontrivial fixed point (13) is valid when ${T}_c\le {T}_Q^{\prime }$. To estimate ${T}_Q^{\prime }$, we construct an index as below:

$$ {E}^q\left(D,t\right)=M\left({T}_c\right)/W(t). $$

(27)

It is easy to check E^q(D, 0) = e^q(D) and E^q(D, t) ≥ 0. If we order W(T^∗) = M₀, then E^q(D, T^∗) ≥ 1 is equivalent to M(T_c) ≥ M₀, where W(t) ≤ W(0) and M(T_c) ≤ W(0) have been used. Thus, the following proposition provides a way for estimating ${T}_Q^{\prime }$.

Proposition 2: Let us order ${T}_Q={T}_Q(D)=\mathit{\min}\left\{{T}^{\ast },{T}_Q^{\prime}\right\}$. E^q(D, T_Q) ≥ 1 leads to E^q(D, T^∗) ≥ 1.

Proof: Since T_Q ≤ T^∗, we have W(T_Q) ≥ W(T^∗), which leads to ${E}^q\left(D,{T}_Q\right)=\frac{M\left({T}_c\right)}{W\left({T}_Q\right)}\le \frac{M\left({T}_c\right)}{W\left({T}^{\ast}\right)}={E}^q\left(D,{T}^{\ast}\right)$. That is to say, E^q(D, T_Q) ≥ 1 leads to E^q(D, T^∗) ≥ 1.■

Since E^q(D, T^∗) ≥ 1 is equivalent to M(T_c) ≥ M₀, by the Proposition 2 E^q(D, T_Q) ≥ 1 leads to M(T_c) ≥ M₀. Therefore, we conclude that the nontrivial fixed point (13) is valid when E^q(D, T_Q) ≥ 1. Since T_Q is the lower bound of ${T}_Q^{\prime }$ and the nontrivial fixed point (13) is equivalent to Eq. (16), we have the following criterion:

Criterion A: If E^q(D, T_Q) ≥ 1, the parabolic scaling (16) holds for T_c ≤ T_Q.

To estimate T_Q by using the Criterion A, we need to calculate E^q(D, T_Q). Since M(T_c) has been estimated by Eq. (26), we only calculate the value of W(T_Q). As an approximation, we consider that the integral scope of ∫d^Dqϕ(q, τ)^∗ϕ(q, τ) is up to the correlation length ξ. Thus, by using ϕ(q, τ) ≈ 〈ϕ(q, τ)〉_vac, we have:

$$ W\left({T}_Q\right)\approx \frac{1}{T_Q}{\xi}^D{\left|{\left\langle \phi \left(\boldsymbol{q},\tau \right)\right\rangle}_{vac}\right|}^2=\frac{1}{T_Q}{\xi}^D{\rho}_s(0). $$

(28)

Substituting Eqs. (26) and (28) into E^q(D, T_Q) yields:

$$ {E}^q\left(D,{T}_Q\right)=\frac{T_Q{\xi}^{2-D}}{\rho_s(0)}. $$

(29)

We now estimate T_Q(D) by using Eq. (29). The Criterion A indicates that ${T}_c=\gamma (D)\cdotp \sqrt{\rho_s(0)}$ holds at T_c = T_Q(D), that is, ${T}_Q(D)=\gamma (D)\cdotp \sqrt{\rho_s(0)}$. Substituting it into E^q(D, T_Q) ≥ 1 obtains E^q(D, T_Q) = ξ^{2 − D}γ(D)²/T_Q(D) ≥ 1, which indicates:

$$ {T}_Q(D)\le {\xi}^{2-D}\gamma {(D)}^2. $$

(30)

For D = 2, the inequality (30) yields:

$$ {T}_Q(2)\le \gamma {(2)}^2, $$

(31)

which by using the experimental value γ(2) ≈ 4.2 K^1/2 yields T_Q(2) ≤ 17 K, agreeing with the experimental measure value T_Q(2) ≈ 15 K [13].

For D = 3, substituting γ(3) = 0 into the inequality (30) obtains

$$ {T}_Q(3)\le 0, $$

(32)

which indicates that the parabolic scaling (16) holds for T_c ≤ T_Q(3) = 0. That is to say, the mean-field approximation always holds for D = 3. In fact, Tao has pointed out [17] that D = 3 is the upper critical dimension of quantum critical systems and that the mean-field approximation is valid at the upper critical dimension. Therefore, our result for D = 3 agrees with the previous analysis [17].

5 The Two-Class Scaling

By using Abrikosov-Gor’kov’s mean-field theory for superconducting alloys, for dirty BCS superconductors, the relation between T_c and ρ_s(0) can be derived as [7–8, 17, 27]:

$$ {T}_c=\alpha \cdotp {\rho}_s(0)+{T}_0. $$

(33)

The derivation for Eq. (33) can be found in Appendix 3. In particular, by using the latest experimental data [28], Khodel et al [27] have produced the correct theoretical value of α. This is an evidence for supporting the linear scaling in Eq. (1) as a result of Abrikosov-Gor’kov’s mean-field theory. By Eq. (1), Eq. (33) holds for T_c ≥ T_M. By the Criterion A, if the mean-field approximation is valid, E^q(D, T_Q) ≤ 1 should hold. Using Eq. (27) and T_M ≤ T_Q, it is easy to verify E^q(D, T_M) ≤ E^q(D, T_Q). This implies that one can estimate T_M by using E^q(D, T_M) ≤ 1. The following proposition will rigidly confirm this fact.

Proposition 3: Let us order Ω = ∫ d^Dqϕ(q, τ)^∗ϕ(q, τ). If $\frac{\mathrm{\partial \Omega }}{\partial \tau }=0$ and T_M > 0, then we have:

$$ {e}^q(D)\ll {E}^q\left(D,{T}_M\right). $$

(34)

Proof: see Appendix 4. ■

Corollary 1: If E^q(D, T_M) ≤ 1, then we have e^q(D) ≪ 1.

Regarding the Proposition 3, the condition $\frac{\mathrm{\partial \Omega }}{\partial \tau }=0$ should approximately hold as long as ϕ(q, τ) ≈ 〈ϕ(q, τ)〉_vac is satisfied. Thus, by the Corollary 1, we can replace e^q(D) ≪ 1 by E^q(D, T_M) ≤ 1 to estimate T_M. Since superconducting films imply D = 2, by Eq. (29), we have E^q(2, T_M) = T_M/ρ_s(0). By Eq. (1), T_c = α · ρ_s(0) + T₀ holds at T_c = T_M. Substituting T_M = α · ρ_s(0) + T₀ into E^q(2, T_M) ≤ 1 yields ${E}^q\left(2,{T}_M\right)=\frac{\alpha {T}_M}{T_M-{T}_0}\le 1$, indicating

$$ {T}_M\ge \frac{T_0}{1-\alpha }, $$

(35)

where we have considered 0 < α < 1 [13] and ρ_s(0) ≥ 0.

Substituting experimental data α ≈ 0.37 and T₀ ≈ 7K into the inequality (35) obtains T_M ≥ 11K, which agrees with the experimental value T_M ≈ 12K [13].

Using Eqs. (16), (31), (33), and (35), we exactly produce the two-class scaling law for D = 2 as below:

$$ \left\{\begin{array}{cc}{T}_c=\alpha \cdotp {\rho}_s(0)+{T}_0,& {T}_c\ge {T}_M\approx \frac{T_0}{1-\alpha}\\ {}{T}_c=\gamma (2)\cdotp \sqrt{\rho_s(0)},& {T}_c\le {T}_Q\approx \gamma {(2)}^2\end{array}\right., $$

(36)

where $\gamma (2)=\sqrt{\frac{7\cdotp \zeta (3)\cdotp {\varepsilon}_F}{15\cdotp \pi \cdotp a\cdotp {m}_e}}$.

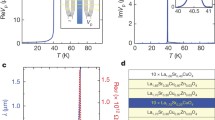
The theoretical values of γ(2), T_Q, and T_M have been listed in Table 1. They agree with experimental measure values. In particular, the difference between T_M ≈ 11 K and T_Q ≈ 17 K implies that the part over [T_M, T_Q] should be a combination of linear and parabolic scaling. Here we have fitted Eq. (36) to experimental data in the Fig. 1. The accordance between theoretical formula and experimental data is pretty well. Equation (36) is the main result of this paper. It can be rigidly tested by investigating other quasi-two-dimensional BCS-like superconductors.

Table 1 Comparison of theoretical results with experimental measure values [13]

Fig. 1

The experimental data from [13] are plotted as black circles, which belong to the T_c interval [5.1 K,  41.6 K]. a The theoretical parabolic scaling (red line) ${T}_c=4.29\ {K}^{1/2}\bullet \sqrt{\rho_s(0)}$ perfectly fits the experimental data in [5.1 K,  T_M], while the linear scaling (blue line) perfectly fits the experimental data in [T_Q,  41.6 K], where T_M ≈ 11 K and T_Q ≈ 17 K, as predicted by Eq. (36). b The theoretical parabolic scaling (red line) ${T}_c=4.29\ {K}^{1/2}\bullet \sqrt{\rho_s(0)}$ is fitted with the experimental data in the T_c interval [0, 15 K] , where T_M ≈ 12 K and T_Q ≈ 15 K are experimentally measured [13]

6 Conclusion

In conclusion, by using the BCS theory, we propose a QPF to describe quantum critical behaviors of zero-temperature Cooper pairs. It was recently found that, in the overdoped side of the single-crystal La_{2 − x}Sr_xCuO₄ films, a two-class scaling law emerges as: ${T}_c=\gamma \cdotp \sqrt{\rho_s(0)}$ for T_c ≤ T_Q and T_c = α · ρ_s(0) + T₀ for T_c ≥ T_M. By using the QPF, we show that the parabolic scaling ${T}_c=\gamma \cdotp \sqrt{\rho_s(0)}$ can be exactly derived when T_c is sufficiently low, where the theoretical value of γ is exactly calculated as 4.29 K^1/2, being in accordance with the experimental measure value γ = (4.2 ± 0.5) K^1/2. Furthermore, we show that the linear scaling T_c = α · ρ_s(0) + T₀ is a mean-field behavior of the dirty-limit BCS theory, which lies far beyond the control of the QPF. To determine the range of applicability of the QPF, we extend the classical Ginzburg number to a quantum version. By using the quantum Ginzburg number, we show that the QPF holds for T_c ≤ T_Q, while the mean-field theory holds for T_c ≥ T_M, where theoretical values of T_Q and T_M are estimated as T_Q ≈ 17 K and T_M ≈ 11 K, respectively, agreeing with experimental measure values 15 K and 12 K. The high accordance of theoretical values of γ, T_Q, and T_M with experimental measure results justifies the validity of the QPF. Finally, the QPF predicts that for 2-dimensional overdoped cuprate films, the transition temperature T_c and the quantum correlation length ξ will obey a scaling $\xi \propto {T}_c^{-\delta }$ with a critical exponent δ being around 1.25. This is a new prediction that can be tested. We propose that one can measure δ by using neutron scattering experiments near T_c = 0, which have been successfully carried out for measuring the critical exponent of the thermal correlation length [26].

Appendices

Appendix 1. Derivation for η, λ₂, and λ₄

By using the BCS Hamiltonian of superconductivity, Gor’kov has shown that when |T − T_c| ≈ 0, the Landau-Ginzburg equation can be written in the form [8]:

$$ \frac{1}{4{m}_e^{\ast }}{\nabla}^2\psi (T)-\frac{1}{\lambda}\cdotp \frac{\left(T-{T}_c\right)}{T_c}\psi (T)-\frac{1}{\lambda \cdotp {n}_s(0)}{\left|\psi (T)\right|}^2\psi (T)=0, $$

(37)

where $\uplambda =\frac{7\zeta (3)\cdotp {\varepsilon}_F}{6{\pi}^2{T}_c^2}$ and |ψ(T)|² denotes the superfluid density at the temperature T. Moreover, n_s(0) denotes the zero-temperature superfluid density when materials are homogenous, ζ(x) is the Riemann zeta function, ε_F is the Fermi energy, and ${m}_e^{\ast }$ is the mass of an electron. Quantitatively, n_s(0) is equal to the total number density of electrons in the normal state [8]. This is the standard description of the BCS theory.

We first verify that Gor’kov’s Eq. (37) holds at T = 0. Since |ψ(T)|² denotes the superfluid density at the temperature T, we should conclude, for homogenous materials, |ψ(0)|² = n_s(0) as long as Gor’kov’s Eq. (37) holds at T = 0. That is to say, when |ψ(0)|² = n_s(0), the self-consistency of Eq. (37) at T = 0 can be justified.

When materials are homogenous, ψ(T) is independent of the space q. Then, Eq. (37) yields:

$$ \frac{1}{\lambda}\cdotp \frac{\left(T-{T}_c\right)}{T_c}\psi (T)+\frac{1}{\lambda \cdotp {n}_s(0)}{\left|\psi (T)\right|}^2\psi (T)=0, $$

(38)

which can be rewritten as

$$ {\left|\psi (T)\right|}^2={n}_s(0)\cdotp \left(\frac{T_c-T}{T_c}\right). $$

(39)

By Eq. (39), we obviously have |ψ(0)|² = n_s(0). This verifies the self-consistency of Eq. (37) at T = 0.

Now we start to derive η, λ₂, and λ₄ in Eq. (2). By rescaling ψ(T) according to $\phi (T)=\frac{1}{\sqrt{4{m}_e^{\ast }}}\psi (T)$, Eq. (37) yields the following Lagrangian function:

$$ \mathcal{L}(T)={\left|\mathbf{\nabla}\phi (T)\right|}^2+\frac{4{m}_e^{\ast }}{\lambda}\cdotp \frac{\left(T-{T}_c\right)}{T_c}\cdotp {\left|\phi (T)\right|}^2+\frac{8{m}_e^{\ast 2}}{\lambda \cdotp {n}_s(0)}\cdotp {\left|\phi (T)\right|}^4. $$

(40)

If we order ρ_s(T) = |ϕ(T)|², then ${\rho}_s(T)=\frac{{\left|\psi (T)\right|}^2}{4{m}_e^{\ast }}$ denotes the superfluid phase stiffness at the temperature T. Thus, by Eq. (39), we have:

$$ {\rho}_s(0)=\frac{n_s(0)}{4{m}_e^{\ast }}. $$

(41)

Substituting Eq. (41) into Eq. (40) yields:

$$ \mathcal{L}(T)={\left|\mathbf{\nabla}\phi (T)\right|}^2+\frac{24{\pi}^2{m}_e^{\ast }}{7\zeta (3)\cdotp {\varepsilon}_F}{T}_c^2\cdotp \frac{\left(T-{T}_c\right)}{T_c}\cdotp {\left|\phi (T)\right|}^2+\frac{12{\pi}^2{m}_e^{\ast }}{7\zeta (3)\cdotp {\varepsilon}_F}\cdotp \frac{T_c^2}{\rho_s(0)}\cdotp {\left|\phi (T)\right|}^4. $$

(42)

If we introduce the imaginary time $\tau \in \left[0,\frac{1}{T}\right]$ with T = 0, then we have ϕ(q, τ) = ϕ(0) [16]. Since Eq. (37) holds at T = 0, we conclude that Eq. (42) holds at T = 0 as well. Therefore, by Eq. (42), we have:

$$ \mathcal{L}(0)={\left|\mathbf{\nabla}\phi \left(\boldsymbol{q},\tau \right)\right|}^2-\frac{24{\pi}^2{m}_e}{7\zeta (3)\cdotp {\varepsilon}_F}{T}_c^2\cdotp {\left|\phi \left(\boldsymbol{q},\tau \right)\right|}^2+\frac{12{\pi}^2{m}_e}{7\zeta (3)\cdotp {\varepsilon}_F}\cdotp \frac{T_c^2}{\rho_s(0)}\cdotp {\left|\phi \left(\boldsymbol{q},\tau \right)\right|}^4, $$

(43)

where we assume ${m}_e^{\ast }={m}_e$ at T = 0 and m_e denotes the rest mass of an electron.

Comparing Eqs. (2) and (43), we have:

$$ \eta =1, $$

(44)

$$ {\lambda}_2={\lambda}_2\left({T}_c\right)=-\frac{24{\pi}^2{m}_e}{7\zeta (3)\cdotp {\varepsilon}_F}{T}_c^2, $$

(45)

$$ {\lambda}_4={\lambda}_4\left({T}_c,{\rho}_s(0)\right)=\frac{12{\pi}^2{m}_e}{7\zeta (3)\cdotp {\varepsilon}_F}\cdotp \frac{T_c^2}{\rho_s(0)}. $$

(46)

Appendix 2. Proof of Proposition 1

Proof: By Eq. (8), it is easy to obtain the field equation of zero-temperature Cooper pairs as below:

$$ \left[{\partial}_{\tau}^2+{\nabla}^2-{\lambda}_2-2{\lambda}_4\cdotp {\left|\phi \left(\boldsymbol{q},\tau \right)\right|}^2\right]\cdotp \phi \left(\boldsymbol{q},\tau \right)=-J{\left(\boldsymbol{q},\tau \right)}^{\ast }. $$

(47)

Substituting ϕ(q, τ) ≈ 〈ϕ(q, τ)〉 into Eq. (47) yields:

$$ \left[{\partial}_{\tau}^2+{\nabla}^2-{\lambda}_2-2{\lambda}_4\cdotp {\left|\left\langle \phi \left(\boldsymbol{q},\tau \right)\right\rangle \right|}^2\right]\cdotp \left\langle \phi \left(\boldsymbol{q},\tau \right)\right\rangle =-J{\left(\boldsymbol{q},\tau \right)}^{\ast }. $$

(48)

Using Eq. (21), Eq. (48) can be written in the form:

$$ \left[{\partial}_{\tau}^2+{\nabla}^2-{\lambda}_2-4{\lambda}_4\cdotp {\left|\left\langle \phi \left(\boldsymbol{q},\tau \right)\right\rangle \right|}^2\right]\cdotp G\left(\boldsymbol{q}-{\boldsymbol{q}}^{\prime },\tau -{\tau}^{\prime}\right)=-\delta \left(\boldsymbol{q}-{\boldsymbol{q}}^{\prime },\tau -{\tau}^{\prime}\right), $$

(49)

where δ(q, τ) denotes the Dirac function.

By using 〈ϕ(q, τ)〉 ≈ 〈ϕ(q, τ)〉_vac and Eq. (6), we have:

$$ {\left|\left\langle \phi \left(\boldsymbol{q},\tau \right)\right\rangle \right|}^2\approx {\left|{\left\langle \phi \left(\boldsymbol{q},\tau \right)\right\rangle}_{vac}\right|}^2=-\frac{\lambda_2}{2{\lambda}_4}. $$

(50)

Substituting Eq. (50) into Eq. (49) obtains

$$ \left[{\partial}_{\tau}^2+{\nabla}^2+{\lambda}_2\right]\cdotp G\left(\boldsymbol{q},\tau \right)=-\delta \left(\boldsymbol{q},\tau \right). $$

(51)

Let us consider the Fourier transforms as follows:

$$ G\left(\boldsymbol{q},\tau \right)={\int}_0^{\infty}\frac{d\omega}{2\pi}\int \frac{d^D\boldsymbol{k}}{{\left(2\pi \right)}^D}\overset{\sim }{G}\left(\boldsymbol{k},\omega \right){e}^{i\boldsymbol{k}\cdotp \boldsymbol{q}+ i\omega \tau}, $$

(52)

$$ \overset{\sim }{G}\left(\boldsymbol{k},\omega \right)={\int}_0^{\infty } d\tau \int {d}^D\boldsymbol{q}G\left(\boldsymbol{q},\tau \right){e}^{-i\boldsymbol{k}\cdotp \boldsymbol{q}- i\omega \tau}, $$

(53)

$$ \delta \left(\boldsymbol{q},\tau \right)={\int}_0^{\infty}\frac{d\omega}{2\pi}\int \frac{d^D\boldsymbol{k}}{{\left(2\pi \right)}^D}{e}^{i\boldsymbol{k}\cdotp \boldsymbol{q}+ i\omega \tau}, $$

(54)

Substituting Eqs. (52)–(54) into Eq.(51) obtains:

$$ \overset{\sim }{G}\left(\boldsymbol{k},\omega \right)=\frac{1}{{\left|\boldsymbol{k}\right|}^2+{\omega}^2-{\lambda}_2}. $$

(55)

Substituting Eq. (55) into Eq. (52) yields:

$$ G\left(\boldsymbol{q},\tau \right)={\int}_0^{\infty}\frac{d\omega}{2\pi}\int \frac{d^D\boldsymbol{q}}{{\left(2\pi \right)}^D}\frac{e^{i\boldsymbol{k}\cdotp \boldsymbol{q}+ i\omega \tau}}{{\left|\boldsymbol{k}\right|}^2+{\omega}^2-{\lambda}_2}\propto {e}^{-\frac{\left|\boldsymbol{q}\right|}{\xi }}, $$

(56)

where ξ = (−λ₂)^−1/2 denotes the correlation length.

Using Eqs. (53) and (55), it is easy to find:

$\overset{\sim }{G}\left(\mathbf{0},0\right)={\int}_0^{\infty } d\tau \int {d}^D\boldsymbol{q}G\left(\boldsymbol{q},\tau \right)={\left(-{\lambda}_2\right)}^{-1}={\xi}^2$.

Appendix 3. Derivation for Eq. (33)

For isotropic BCS superconductors, by using Abrikosov-Gor’kov’s mean-field theory for superconducting alloys, one can obtain [17]:

$$ {\lambda}_p^{-2}(0)=\frac{4{\pi n}_s(0){e}^2}{m_e^{\ast }}\varDelta {(0)}^2{\int}_0^{\infty}\frac{1}{\left({u}^2+\varDelta {(0)}^2\right)\left(\sqrt{u^2+\varDelta {(0)}^2}+\frac{1}{2{\tau}_s}\right)} du, $$

(57)

where λ_p(0) denotes the penetration depth at zero temperature, τ_s denotes the scattering relaxation time, Δ(0) denotes the energy gap at zero temperature, and e denotes the electron charge.

If we order $y=\frac{u}{\varDelta (0)}$, Eq.(57) can be rewritten in the form:

$$ {\lambda}_p^{-2}(0)=\frac{4\pi {n}_s(0){e}^2}{m_e^{\ast }}{\int}_0^{\infty}\frac{1}{\left(1+{y}^2\right)\left(\sqrt{1+{y}^2}+\frac{1}{2{\tau}_s\varDelta (0)}\right)} dy. $$

(58)

We investigate Eq. (58) in terms of two cases, that is, clean and dirty superconductors.

For clean superconductors, we should have τ_s → ∞; thus, Eq. (58) yields:

${\lambda}_p^{-2}(0)=\frac{4\pi {n}_s(0){e}^2}{m_e^{\ast }}{\int}_0^{\infty}\frac{1}{{\left(1+{y}^2\right)}^{\frac{3}{2}}} dy=\frac{4\pi {n}_s(0){e}^2}{m_e^{\ast }}$,that is,

$$ {\lambda}_p(0)=\sqrt{\frac{m_e^{\ast }}{4\pi {n}_s(0){e}^2}}, $$

(59)

which is the famous London penetration depth [8].

For dirty superconductors, we simply consider τ_s → 0; thus, Eq. (58) yields:

$$ {\lambda}_p^{-2}(0)=\frac{8\pi {n}_s(0){e}^2}{m_e^{\ast }}{\tau}_s\varDelta (0){\int}_0^{\infty}\frac{1}{\left(1+{y}^2\right)} dy+o\left({\tau}_s^2\right). $$

(60)

Since ${\rho}_s(0)\propto {\lambda}_p^{-2}(0)$ and Δ(0) ∝ T_c, Eq. (60) implies:

$$ {\rho}_s(0)\propto {T}_c, $$

(61)

which can be generally written as:

$$ {T}_c=\alpha \cdotp {\rho}_s(0)+{T}_0. $$

(62)

Appendix 4. Proof of Proposition 3

Proof: The following equation obviously holds:

$$ {\int}_0^{\frac{1}{T}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right)={\int}_0^{\frac{1}{T_M}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right)+{\int}_{\frac{1}{T_M}}^{\frac{1}{T}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right). $$

(63)

Substituting Ω = ∫ d^Dqϕ(q, τ)^∗ϕ(q, τ) into Eq. (63) and by using $\frac{\mathrm{\partial \Omega }}{\partial \tau }=0$, we obtain:

$$ \underset{T\to 0}{\mathit{\lim}}{\int}_0^{\frac{1}{T}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right)=\frac{1}{T_M}\Omega +\underset{T\to 0}{\mathit{\lim}}\left(\frac{1}{T}-\frac{1}{T_M}\right)\cdotp \Omega . $$

(64)

Since $\frac{1}{T_M}\Omega \ll \underset{T\to 0}{\mathit{\lim}}\left(\frac{1}{T}-\frac{1}{T_M}\right)\cdotp \Omega$, by using Eq. (64), we have:

$$ \frac{1}{T_M}\Omega \ll \underset{T\to 0}{\mathit{\lim}}\left(\frac{1}{T}-\frac{1}{T_M}\right)\cdotp \Omega +\frac{1}{T_M}\Omega =\underset{T\to 0}{\mathit{\lim}}{\int}_0^{\frac{1}{T}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right), $$

(65)

which leads to:

$$ {\int}_0^{\frac{1}{T_M}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right)\ll \underset{T\to 0}{\mathit{\lim}}{\int}_0^{\frac{1}{T}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\tau \right)}^{\ast}\phi \left(\boldsymbol{q},\tau \right). $$

(66)

By using the inequality (66), it is easy to verify:

${e}^q(D)=\underset{T\to 0}{\lim}\frac{\left|{\int}_0^{\frac{1}{T}} d\tau \int {d}^D\boldsymbol{q}G\left(\boldsymbol{q},\boldsymbol{\tau} \right)\right|}{\int_0^{\frac{1}{T}} d\tau \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\boldsymbol{\tau} \right)}^{\ast}\phi \left(\boldsymbol{q},\boldsymbol{\tau} \right)}\ll \underset{T\to 0}{\lim}\frac{\left|{\int}_0^{\frac{1}{T}} d\tau \int {d}^D\boldsymbol{q}G\left(\boldsymbol{q},\boldsymbol{\tau} \right)\right|}{\int_0^{\frac{1}{T_M}}d\boldsymbol{\tau} \int {d}^D\boldsymbol{q}\phi {\left(\boldsymbol{q},\boldsymbol{\tau} \right)}^{\ast}\phi \left(\boldsymbol{q},\boldsymbol{\tau} \right)}={E}^q\left(D,{T}_M\right).$