1 Introduction

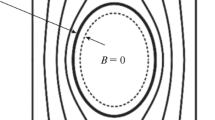
Equilibrium bulk magnetic properties of the mixed state (MS) in type II superconductors are discussed in all superconductivity textbooks and in numerous papers which followed after the discovery of type II superconductivity by Shubnikov with coworkers eight decades ago [1]. References for many of these papers can be found, e.g., in [2,3,4,5]. However, some fundamental magnetic properties of the MS are still not well understood. Examples include, but are not limited to, the magnetization curve M(H), where M is the magnetic moment and H is the external field, and the field strength Hi (also referred to as the magnetic and magnetizing force [7], the thermodynamic field [8], the Maxwell field [9], etc.) in samples of other than cylindrical geometry. Following Abrikosov [9], under “cylindrical geometry,” we imply infinite right cylinders with base of arbitrary shape (e.g., circular cylinders and slabs) in parallel field, that is samples with demagnetizing factor η = 0 [6]. Cross-sectional diagram of the cylindrical geometry is shown in Fig. 1a.

Fig. 1
figure 1

Schematic diagrams showing cross section of samples (painted in gray) for cylindrical (a) and transverse (b) geometries. η is the demagnetizing factor and H is the external field. Dashed lines (not shown in a) depict the lines of the magnetic induction B near and inside the sample

Full size image

Our original interest to equilibrium properties of type II superconductors (that is to properties of pinning-free type II samples) of non-cylindrical geometry and specifically to those with η = 1 (infinite slabs in transverse, i.e., perpendicular field [6]) was due to the fact that the latter do not have a lateral surface by definition. This automatically excludes effects associated with surface current (including the Meissner state) and surface barriers. Hence, properties of sufficiently thick samples of this kind provide access to the pure bulk properties of the MS, i.e., to properties of the vortex assembly. On the other hand, vortices in such samples are evenly distributed due to symmetry and their number density is strictly calculated from the flux conservation. Thus, properties of these samples may also be used for inferring properties of individual vortices. Therefore, knowledge of equilibrium properties of samples of the transverse geometry (this term will be used for samples with η = 1) is of fundamental importance. The sample field configuration for the transverse geometry is shown in Fig. 1b.

It is worth noting that real samples of the cylindrical and the transverse geometries are samples with η → 0 and η → 1, respectively. Correspondingly, effects due to the lateral surface are most significant for the former and practically irrelevant for the latter.

Here, we report on the results of an experimental study of thermodynamically equilibrium (i.e., uniquely determined by parameters of state and hence reversible) bulk magnetic properties of the MS, measured on Nb high-purity film and single-crystal samples [10]. Measurements were performed at the field directed both parallel and perpendicular to the samples’ plane. To the best of our knowledge, such data for the perpendicular field were not reported before. It turned out that none of the existing theories is consistent with these new data. A theoretical model quantitatively accounting for these data is developed and introduced here as well. Similar to the model of Peierls [11] and London [12, 13] for the intermediate state (IS) of type I superconductors, our model describes the MS in thick samples of any ellipsoidal shape (0 ≤ η ≤ 1) in an averaged limit, i.e., without detailing the samples’ magnetic structure and therefore ignoring the surface current and interactions between vortices; in other words, following the terminology of de Gennes [8], it accounts for the properties of the MS in zero-order approximation. At low values of the Ginzburg-Landau (GL) parameter κ, our model converts to the model of Peierls and London. We will show that the description of the vortex matter in terms of a system of non-interacting vortices is the most appropriate for samples of the transverse geometry.

2 Problem Status and Motivation

There are two equilibrium states in which superconductors contain domains of normal (N) phase imbedded into superconducting (S) phase. Those are the IS in type I and the MS in type II materials. In the IS, due to positive energy of the S-N interface, the N domains are multi-flux-quantum laminae, whereas in the MS, due to negative interface energy, these domains are single-flux-quantum vortices. This quantitative difference in the flux magnitude results in drastic qualitative differences between properties of type I and type II superconductors. In particular, the MS takes place in samples of any shape including the cylindrical one (i.e., for 0 ≤ η ≤ 1), whereas the IS occurs only if η≠ 0 [15]. (By “shapes” we imply shapes of ellipsoids, because only ellipsoids allow rigorous theoretical treatment of the magnetic properties [7].)

For this reason, significant attention was paid to measurements of magnetic properties of cylindrical samples of type II superconductors, which, in particular, led to a fairly good knowledge of the M(H) curve for this geometry [1, 3, 16,17,18,19].

For cylinders at H < Hc1, the Meissner condition B = 0 allows one to calculate M(H) in three ways: (i) from thermodynamics, (ii) from magnetostatics (see, e.g., [21]), or (iii) from the Maxwell field Hi, which in this case equals to the applied field H due to continuity of the tangential component of this field [14]. Then, M is calculated from Hi defined (in CGS units) as Hi ≡ B − 4πm, where B is the induction and m is the magnetization, which in superconductors is a macroscopic average M/V, where V is the sample volume [20].

However, in the MS (Hc1 < H < Hc2), complexity of current distribution leaves only one option to calculate M, i.e., through the field Hi via calculation of the average induction \(\bar {B}\). Then, 4πM/V is computed as \(\bar {B}-H_{i}\). For cylinders, where Hi(= H) is known, this was done using the GL theory near Hc1 and Hc2 [15], and also with use of the London equation in the vicinity of Hc1 [9, 22]. In these field regions, approximate analytical expressions for \(\bar {B}\) are available for the extreme type II limit lnκ ≫ 1 [9, 15, 22]. At the same time, it is supposed that the entire M(H) curve for any κ can be calculated via numerical solution of the GL equations [23]. Note, however, that available approximate [15, 24] and high-precision [25] solutions of the GL equations are not quite consistent with this supposition. For instance, theoretical M(H) exhibits an infinite slope at Hc1, whereas the slope of a truly reversible M(H) curve is not infinite [17].

The situation becomes much more complicated for non-cylindrical geometry. For the experiments, this is due to a much larger number of pinning centers in the sample area perpendicular to the field. For that reason, available data on M(H) for type II samples of the transverse geometry (see, e.g., [26,27,28]) are strongly irreversible and therefore inappropriate for judgment on thermodynamic properties.

On the theoretical side, the main complication is due to a demagnetizing field Hd ≡H −Hi. The Maxwell field Hi can be rigorously calculated for uniform (meaning that B is homogeneous throughout the sample) ellipsoids [2, 6, 7]. If H is parallel to the sample axis, relative to which the demagnetizing factor is η, then,

$$\begin{array}{@{}rcl@{}} (1-\eta)H_{i}+\eta B = H. \end{array} $$
(1)

Therefore,

$$\begin{array}{@{}rcl@{}} H_{i} \equiv H - H_{d} = H - \eta(B-H_{i})=H - \eta\, 4\pi M/V. \end{array} $$
(2)

Thus, in uniform samples, Hd = η 4πM/V. In the Meissner state, the sample is (i) uniform and (ii) B(= 0) is known. The former makes it possible to calculate η (see, e.g., [6]) and the latter allows one to use (1) yielding Hi = H/(1 − η). Then, 4πM/V ≡ B − Hi = −H/(1 − η) in full consistency with experiments (see, e.g., [2]). However this is not the case for the MS, where B is not uniform and therefore η is not well defined and neither Hd nor Hi is known.

On the first view, the solution of the problem for η was found long ago by Peierls [11] and London [12] for the IS via replacement of B by \(\bar {B}\), which allows one to use η of the uniform sample. However, (2), which follows from (1), still contains two unknowns (Hi and M) and therefore one more independent relationship is needed to find M. Peierls and London resolve this problem assuming that Hi equals to the thermodynamic critical field Hc in the entire field range of the IS. However, this is not applicable for the MS.

One might object that there is the well-known approach for the MS [8, 29] in which Hi for η≠ 0 is calculated from (1) as \(H_{i}=(H-\eta \bar {B})/(1-\eta )\) [30]. Then, \(\bar {B}\) is calculated using \(\bar {B}(H)\) obtained for the cylindrical geometry (referred to as the constitutive relation Be(H) [29]) replacing H by Hi, and then both Be(Hi) and Hi are used to compute 4πM/V = Be(Hi) − Hi.

Apart from knowing Be(H), the principal condition for using this approach is ability to calculate Hi from (1). However, since no new relationship between Hi and M or B is added (see also [6]), this way to compute Hi is questionable. Indeed, for η = 1, where \(\bar {B}=H\) [9, 31, 32], (1) yields Hi = H(1 − η)/(1 − η) = H and therefore M = 0 regardless of H, implying that Hc2 = ∞. The reason of such a striking inadequacy of this approach is very simple: a uniform sample with η = 1 is just a sample in the N state, where M is indeed zero. In other words, in order to use (1) for inhomogeneous samples, Hi should be found independently, like in the Peierls-London model for the IS (Hi = Hc) or in the cylindrical geometry for the MS (Hi = H) [15].

In [33, 34] M(H) for films with different κ and thickness d in perpendicular field was calculated using the GL theory. Calculated curves strongly depend on κ and d, but contradict the rule of 1/2 [21] (see more about this rule in the Discussion section below) and hence cannot be completely correct.

The approach based on London equation [22] does not work for the transverse geometry either. Specifically, for cylinders the thermodynamic potential \(\tilde {F}\equiv F - BH_{i}/4\pi = F - BH/4\pi \) is minimized at the expense of the second (negative) term, reflecting the work done by the magnet power supply when the flux through the sample changes. Here F is the Helmholtz potential and \(\tilde {F}\) is its Legendre transform, also referred to as the Gibbs free energy [13]. In the transverse geometry the flux is fixed, hence the term BHi/4π is absent [6, 8, 9]. This makes the minimization of \(\tilde {F}=F\) impossible, since all terms and their derivatives in F are positive [22].

After all, inhomogeneities of the field and of the vortex cores near the surface perpendicular to the field should be taken into account. These inhomogeneities, unimportant when η = 0, can be important for films in non-parallel fields, making their properties dependent on the film thickness. For instance, in the IS, they can change the critical field of a few-micrometer-thick film in perpendicular field by more than 50% compared to that in parallel field [21, 35]. An attempt to address this issue for the MS was made by Cody and Miller in experiments with Pb films [28]; however, the results obtained are inconclusive due to strong pinning in their films.

To summarize, (a) available experimental information on the equilibrium magnetic properties of the MS in samples of non-cylindrical geometry is incomplete. In particular, the available M(H) data are strongly irreversible and hence inapplicable for consideration of thermodynamic properties. (b) Available theoretical results and approaches are controversial. In particular, none of the existing theories is capable to address M(H) curve for samples with η = 1. Progress toward solution of this fundamental problem is the goal of our work, which results are presented below.

3 Experimental

Fabrication of pinning-free samples, being very challenging for type I materials [2, 21], is even more difficult for type II superconductors, since most of them are alloys with inevitably significant pinning [1, 8]. A single-crystal sample can be a solution, but since we also need a film for verification of dependencies of the properties on the sample thickness, such a solution is not complete.

Nb is known as a well-verified intrinsic type II superconductor [17, 36,37,38], hence, it is a material from which one can hope to fabricate pinning-free films. On this reason, Nb was chosen for our samples. However, Nb is also a getter [17]. Due to that, our first films, deposited via magnetron sputtering and having residual resistivity ratio RRR up to 70, were still insufficiently clean.

The Nb film sample (Nb-F) used in this work is one of two film samples which were used in [39], where their properties at H ≥ Hc2 are discussed. The film was grown on sapphire via electron cyclotron resonance technique (ECR) [40]; its RRR is 640, the size is 4×6 mm2, and the thickness is 5.7 μ m. This is a record pure Nb film, of the same purity as In films used in IS studies [21, 35]. For comparison, RRR of ultra-pure 2.5-mm thick Nb sheets used for radio-frequency cavities (RFC) in particle accelerators is ≈ 300 [41]. More about ECR-grown Nb films can be found in [42].

Another sample (Nb-SC) was also a sample used in [39]. It is a one-sided polished single-crystal Nb disc Ø7 mm × 1 mm supplied by Surface Preparation Laboratory, The Netherlands. The sample was subjected to a standard treatment used for the RFC fabrication: it was annealed at 800∘C for 3 h and electrochemically polished after that.

However, there is one more issue with Nb. A driving force to achieve thermodynamic equilibrium in inhomogeneous samples is the S-N surface tension [21], whose magnitude in type II Nb is significantly less than that in type I In. This could require even purer Nb samples, but fortunately, pinning weakens with temperature T. Specifically, M(H) data for both our samples are close to reversible at \(T \gtrsim \) 8 K, which means that the samples are nearly pinning free at these temperatures. For this reason, we mostly discuss the data obtained at high temperatures.

The magnetic moment was measured using Quantum Design dc magnetometer (Magnetic Properties Measurement System). Most measurements were performed at constant temperature in the following order. After demagnetizing the magnetometer at T > Tc (Tc is the critical temperature), the sample was cooled down to the chosen temperature in zero applied (i.e., in Earth) field. Then, M was measured vs H up to the field well exceeding the critical field Hc3, where the last traces of superconductivity were absent. After that, the measurements were continued at descending H down to zero applied field.

Data obtained for the Nb-SC sample in parallel field are shown in Fig. 2 and typical data for high temperatures are presented in Fig. 3. As seen from Fig. 2, in the Meissner state, data for all temperatures agree with each other. Hence, the sample was well aligned with H and the flux trapped at the ascending field was low, which allows calculating the thermodynamic critical field Hc(T) from the area above M(H) curves [16]. The sample volume calculated from M(H) at H < Hc1 agrees with that measured directly within 5% error, indicating that η∥≲ 0.05 and therefore η⊥= 1\(-2\eta _{\parallel } \gtrsim 0.9\) [6]. Here, η∥ and η⊥ are the demagnetizing factors in parallel and perpendicular fields, respectively.

Fig. 2
figure 2

Data for the magnetic moment of the Nb-SC sample measured in parallel field at temperatures indicated

Full size image
Fig. 3
figure 3

Data for the magnetic moment of the Nb-SC sample measured in parallel field at T = 8.60 K. Hc1,Hc2 and Hc3 designate the respective critical fields. Dashed arrows indicate either the measurements were conducted at ascending (green arrow) or descending (black arrow) field

Full size image

Data for magnetic moment measured for the Nb-F sample in parallel field are shown in Fig. 4. Typical high-temperature data obtained for this sample are available in [39]. The sample volume was determined from the slope of M(H) curves in the Meissner state; its uncertainty is 10%. η⊥ of this sample is 1− O(10−3) [6].

Fig. 4
figure 4

Data for the magnetic moment of the Nb-F sample measured in parallel field at temperatures indicated

Full size image

The M(H) data measured in parallel field were used to construct the phase diagrams necessary for discussion of experimental results for perpendicular field. These phase diagrams are shown in Figs. 5 and 6 for the Nb-SC and the Nb-F samples, respectively. The inserts show the data for M measured vs temperature at Earth field. For the Nb-SC sample, Tc = 9.20 K and κ calculated as \(H_{c2}/\sqrt {2} H_{c}\) [15] is 1.3 near Tc increasing to 1.6 at 2 K. For the Nb-F sample, Tc = 9.25 K and κ starts from 0.8 near Tc reaching 1.1 at 2 K.

Fig. 5
figure 5

Phase diagram of the single-crystal sample Nb-SC constructed from the M(H) data measured in parallel field. Hc1,Hc2, and Hc3 indicate the graphs for the respective critical fields and Hc is the graph for the thermodynamic critical field. Insert: magnetic moment measured at zero (Earth) field versus temperature

Full size image
Fig. 6
figure 6

Phase diagram of the film sample Nb-F. See captions of Fig. 5 for notations. Insert: magnetic moment measured at zero applied field versus temperature

Full size image

Data for the magnetic moment measured in perpendicular field at high temperatures are shown in Figs. 7 and 8 for the Nb-SC and Nb-F samples, respectively. The data are reversible over more than half of the field range of the MS starting from Hc2. Therefore, in this range, the samples are in the equilibrium state. The equilibrium M(H) are linear, and their extrapolation (represented by the dash-dotted green lines) to H = 0 yields 4πM(0)/V close to − Hc1 (shown by the red star) [43] . The validity of such an extrapolation is supported by the rule of 1/2: the area above the green line equals to the condensation energy \({H_{c}^{2}}V/8\pi \) (= 1/2 in coordinates 4πM/HcV vs H/Hc), where Hc is calculated from the data obtained in parallel field.

Fig. 7
figure 7

Magnetic moment of the Nb-SC sample measured in perpendicular field at the indicated temperatures. The star shows M(0) = −Hc1V/4π or 4πM(0)/V = −Hc1 calculated using Hc1 and V inferred from measurements in parallel field. Left and right vertical scales show M in different units as indicated; horizontal scales give the applied field in Oe (bottom), in units of Hc2∥ (lower top) and in units of Hc (upper top). 1/2 designates the area above the green line representing the condensation energy \({H_{c}^{2}} V/8\pi \) (in coordinates 4πM/HcV vs H/Hc) inferred from the data measured in parallel field

Full size image
Fig. 8
figure 8

Magnetic moment of Nb-F sample measured in perpendicular field at the indicated temperatures. See caption of Fig. 7 for details

Full size image

Comparing Figs. 7 and 8 with Figs. 4 and 5 in [21], one notices a striking similarity in M(H) for the MS and the IS. However, there are also important differences: in the IS, M(0)/V and the critical field strongly depend on the sample thickness, whereas for both our samples, 4πM(0)/V is close to − Hc1 and Hc2⊥ = Hc2∥, where Hc2⊥ and Hc2∥ are the upper critical fields in the perpendicular and the parallel geometries, respectively. Nevertheless, it was important to ensure that our samples are indeed type II superconductors. The most direct way for that is to measure the flux in the N domains.

In the MS \(\bar {B}=n {\Phi }_{0}\) [9], where the planar density n = N/A is the number of flux lines N passing through an area A. In the transverse geometry, \(\bar {B}=H\) and therefore

$$\begin{array}{@{}rcl@{}} n=H/{\Phi}_{0}. \end{array} $$
(3)

Hence, the slope of n(H) curve allows one to determine the flux in the N domains and therefore the type of superconductor.

With this in mind, we probed the film sample with a scanning Hall-probe microscope (SHPM) [44]. The scanned area was 7.6 μm ×7.6 μ m away from the sample edges. The sample was cooled at zero applied field. To achieve better resolution determined by the contrast of the field inside and outside the flux lines, the SHPM images were taken at low H. At low fields, pinning is not small (see Fig. 8, and Fig. 2a in [39]) and therefore the equilibrium hexagonal structure of the vortex ensemble can be mangled. Typical images taken at T = 5.00 and 9.15 K are shown in Fig. 9.

Fig. 9
figure 9

Scanning Hall-probe images of the MS in Nb film taken at 5.00 K (upper row) and 9.15 K (lower row). The colors reflect relative magnitude of the induction with the brightest color corresponding to the strongest B. The bright spots are vortices. The fields in Oe indicated at the top of images are the applied field; the left images are taken at zero applied (Earth) field

Full size image

A graph for n − n0 = (N − N0)/A vs H is shown in Fig. 10. Here, N0 is an adjustable parameter reflecting the occasional number of the lines in the scanned area at Earth field due to pinning and low statistics. As one can see, the experimental points agree with (3), thus confirming that each flux line carries a single flux quantum Φ0. Since κ of our single-crystal sample is larger than that of the film, we conclude that both our samples are classical type II superconductors with Abrikosov vortices [15].

Fig. 10
figure 10

Dependence of the flux line density n on the external field at different temperatures as indicated. Φ0 is the superconducting flux quantum and n0 is an adjustable parameter explained in the text

Full size image

4 Theoretical

The problem of the magnetic properties of inhomogeneous superconductors was for the first time addressed by Peierls [11] and F. London [12, 13] for the IS. As was mentioned above, both authors solved it in an averaged limit, in which the non-uniform induction B is replaced by averaged \(\bar {B}\), and using the demagnetizing factor η of the uniform sample. To supplement (1), Peierls and London assumed that Hi = Hc. This assumption was justified by a paradigm on instability of the N phase when Hi < Hc. Note, however, that this paradigm is valid only for the cylindrical geometry [35].

It is important to stress that the averaged description implies that the real sample structure is neglected and therefore any possible interactions between the structural units are neglected automatically. If, e.g., the sample consists of ℵ unit cells, then the sample free energy \(F=\aleph \bar {F}_{0}\), where \(\bar {F}_{0}\) is the average free energy per unit cell. Therefore, the averaged description does not contain cross terms responsible for interactions, hence excluding them by definition.

The Peierls-London model is valid for thick samples [2, 21, 35], i.e., when the surface-related inhomogeneities can be neglected (condition identical to that for the cylindrical geometry). Since N laminae are screened in the sample interior and interact through the outer field, neglect of the near-surface inhomogeneities means neglect of interaction between the laminae, in full consistency with the averaged approximation. Thus, the Peierls-London model represents a global description of the IS in a zero-order approximation [8], where interaction between the structural units is neglected.

For the MS, such an averaged model is missing, resulting in the absence of a global description of this state and leaving a significant “gap” in understanding the MS magnetic properties. In particular, as shown above, none of the existing theories is capable of addressing the magnetization curve for a slab in perpendicular field. The model, presented below, is targeted to fill this gap.

In Fig. 11, graphs for η = 0 represent the Maxwell field Hi vs H for the cylindrical geometry, where Hi = H. The red (ab) section in Fig. 11b represents this dependence for the MS, meaning that the function Hi(H) is linear and extends from Hc1 to Hc2. On the other hand, the experimental results for the transverse geometry (see Figs. 7 and 8), specifically (a) linear M(H), (b) Hc2⊥ = Hc2∥, and (c) 4πM(0)/V = −Hc1, along with the condition \(\bar {B}=H\), directly indicate [45] that Hi(H) for η = 1 is also a linear function extending in the same range. Therefore, one can assume a linear form of Hi(H) for all η, as it is shown in Fig. 11b. An analytical expression for these functions is

$$ H_{i}= H_{c1}+\frac{H_{c2}-H_{c1}}{H_{c2}-H_{c1}(1-\eta)}[H-H_{c1}(1-\eta)]. $$
(4)

Having Hi, one obtains M from (2):

$$ \frac{4\pi M}{V} = -H_{c1}+\frac{H_{c1}}{H_{c2}-H_{c1}(1-\eta)}[H-H_{c1}(1-\eta)], $$
(5)

then, \(\bar {B}=H_{i}+ 4\pi M/V\) is

$$ \bar{B}= \frac{H_{c2}}{H_{c2}-H_{c1}(1-\eta)}[H-H_{c1}(1-\eta)]. $$
(6)

Graphs of these functions are presented in Fig. 12.

Fig. 11
figure 11

Maxwell field Hi in type I (a) and type II (b) superconductors of different shapes vs external field H. Abbreviations NS, IS, and MS designate the normal, intermediate, and mixed states, respectively. Section ab in (b) represents Hi(H) in the MS for samples with η = 0. The demagnetizing factors η are related to a long cylinder and infinite slab in parallel field (η = 0), to a long circular cylinder in perpendicular field (η = 1/2), and to an infinite slab in perpendicular field (η = 1)

Full size image
Fig. 12
figure 12

a Magnetic moment in terms of 4πM/V and b averaged induction \(\bar {B}\) versus external field H in type II superconductors with different demagnetizing factors η (see caption of Fig. 11 for explanation)

Full size image

In type I materials, where by definition Hc1 = Hc2 = Hc [22], (4) yields Hi = Hc, as in the Peierls-London model. This is easily seen from Fig. 11b: when Hc2 → Hc1, i.e., when a superconductor converts from type II to type I, the graphs in (b) convert to the graphs in (a). Then, (5) and (6) convert to formulas for M and \(\bar {B}\) in the Peierls-London model as well (see [21] for the graphs). Therefore, our model describes the averaged properties of both the MS and the IS in the limit of non-interacting vortices in type II superconductors and laminae in type I superconductors, respectively.

5 Discussion

First, we briefly stop at the rule of 1/2 because, being well known (see, e.g., [2]), it is not always clearly articulated in the textbooks. This rule represents the law of energy conservation in superconductors when M is aligned (antiparallel) to H. Consistency with this rule is a prerequisite for discussion of equilibrium properties.

In the general case, this law reads that, at constant T, the total free energy \(\tilde {F}_{M}\) (for which \(\textbf {M}=-\nabla _{\textbf {H}}\tilde {F}_{M}\) [6]) of any singly connected superconductor of volume V in a dc magnetic field H of any orientation is

$$\begin{array}{@{}rcl@{}} \tilde{F}_{M}(H) &=&\tilde{F}_{M}(0)-\int\textbf{M} d\textbf{H}\\ &=&F_{s0}-\int\textbf{M} d\textbf{H}= F_{n0}-\frac{{H_{c}^{2}} V}{8\pi}-\int\textbf{M} d\textbf{H}, \end{array} $$
(7)

where Fs0 and Fn0 are the Helmholtz free energies of the S and N states in zero field, respectively.

The first two forms of (7) show that the extra total free energy of a sample (above the free energy of the ground state \(\tilde {F}_{M}(0)= F_{s0}\)) is the sample magnetic energy \(E_{M}=-\int \textbf {M} d\textbf {H}\), or the energy of interaction of the external field with the sample magnetic moment induced by this field. Similar as in conventional diamagnetics [14], EM in superconductors is the kinetic energy of the charges (paired electrons) carrying the induced currents [2]. The last form of (7) demonstrates that (i) the total free energy in the N state (= Fn0) is independent of the external field since the magnetic permeability μ of this state is unity, and (ii) the source of EM is the condensation energy \({H_{c}^{2}}V/8\pi \). Finiteness of the latter makes a transition to the N state a mandatory property of any superconductor [6]. At this transition, EM of any sample equals to its condensation energy or area under M(H) curve plotted as 4πM/VHc vs H/Hc, when M is aligned to H, is 1/2. Therefore, the condensation energy density \({H_{c}^{2}}/8\pi \) is the energy per unit volume it takes to destroy superconductivity, i.e., to destroy an electron pairing [47].

As one can see from Fig. 12a, the area under the graphs M(H) for different η is the same, meaning that if the magnetic moment is calculated for different orientations of the applied field, the sample condensation energy is the same, as it should. Therefore, our model meets the rule of 1/2 and we can proceed to the discussion.

Comparing the modeled magnetization curve for η = 1 in Fig. 12a with the experimental data in Figs. 7 and 8, one can see that for the transverse geometry, the model is quantitatively consistent with the experiment.

Next, since the area under the graphs in Fig. 12a equals to \({H_{c}^{2}}/2\), we see that Hc is the geometrical mean of Hc1 and Hc2, which is consistent with the rule known for the extreme type II limit [23]. This suggests that the rule \(H_{c1}H_{c2}\approx {H_{c}^{2}}\) is more general than it looked till now.

Further, as shown by Andreev [46], in the IS, Hi is the Maxwell field and hence the induction in the N domains, where B = μHi = Hi, since μ = 1 in the N phase. Extending this consideration to the MS [22], one can state that Hi is the Maxwell field in the vortex cores. Therefore, our model suggests that B in the vortex cores increases from Hc1 at H = (1 − η)Hc1 to Hc2 at H = Hc2 and the structure of individual vortices (in sufficiently thick samples) does not depend on the sample shape (η).

Also, as seen from Fig. 11b, in the cores B = Hi > H for all η≠ 0. This is consistent with the well-known fact (see, e.g., [48, 49]) that the upper boundary of μ SR measured spectrum of the magnetic induction in type II samples is greater than the external (perpendicularly directed) field.

However, there is an obvious problem. In Fig. 12a, the linear graph M(H) for cylinders (η = 0) differs from the experimental curve, showing a non-linear change near Hc1 (see, e.g., Fig. 3 or [17]). In the standard theory [8, 22, 23], this feature for cylindrical geometry (yielding the unrealistic infinite slope at Hc1) is described assuming overlapping the fields of neighboring vortices, leading to their repulsion. On the other hand, in cylinders, there is the surface current, which is absent in samples of the transverse geometry. The magnitude of this current is determined by the field drop at the surface [6], which is maximal near Hc1 and vanishes upon approaching Hc2. Our model includes neither the vortex-vortex interaction, nor surface current, which explains the difference of the modeled and experimental M(H) curves for η = 0. Note that surface current also is not accounted for in the standard theory [8, 22, 23].

The question then arises whether such a model is needed if vortices interact? The same question can be formulated as: Why for samples of the tranvsverse geometry the experimental M(H) graphs in Figs. 7 and 8 are identical to that in the model of non-interacting vortices in Fig. 12a? The only possible answer we can suggest for both formulations is because vortices in samples of the transverse geometry do not interact.

The field passes through any superconducting sample of the transverse geometry in which currents are optimized so to minimize the sample magnetic energy and therefore the total free energy \(\tilde {F}_{M}\). However, the result of this optimization is different in type I and type II superconductors. Type I samples tune the period of the laminar structure, the fraction of the normal phase, and induction inside it, as well as the currents and the laminae shape near the surfaces, altogether leading to a strong dependence of the magnetic properties on the sample thickness d [21, 35].

No doubt that all these degrees of freedom are also available for type II superconductors, but owing to the gain received from the negative interface energy, in this case, all tunings are performed keeping maximum possible number of vortices and therefore the minimum flux passing through them, i.e., Φ0. Then, the vortex density n is as that in (3) and the parameter of the most effectively packed hexagonal vortex lattice \(b=(2{\Phi }_{0}/\sqrt {3}H)^{1/2}\) [22].

It is important to stress that n and b are as such due to the symmetry and the flux conservation and, hence, do not depend on d.

On the other hand, if vortices in the transverse geometry do not interact, the sample magnetic energy is a simple sum of the free energies of the individual flux lines 𝜖d, where 𝜖 is the energy of the flux line per unit length (line tension). Therefore, considering that \(H=\bar {B}=n{\Phi }_{0}=N{\Phi }_{0}/A\) and using (5) with η = 1 one obtains

$$\begin{array}{@{}rcl@{}} E_{M}&=&-\int\textbf{M}d\textbf{H}=N\epsilon d=\frac{V}{4\pi}H(H_{c1}-\frac{H_{c1}}{2H_{c2}}H)\\ &=&Nd\frac{{\Phi}_{0}}{4\pi}(H_{c1}-\frac{H_{c1}}{2H_{c2}}H), \end{array} $$
(8)

which yields

$$ \epsilon=\frac{{\Phi}_{0} H_{c1}}{4\pi}(1-\frac{H}{2H_{c2}}). $$
(9)

Comparing 𝜖 at Hc1 in the cylinders (= Φ0Hc1/4π [8, 9, 22, 23]) with (9), we see that 𝜖 in the transverse geometry at H→0 when Hi = Hc1 equals to 𝜖 in the cylinders, as it should.

At higher field, 𝜖 decreases becoming Φ0Hc1/8π at H = Hc2, where it yields

$$ E_{M}=N\epsilon d= (\frac{H_{c2}A}{{\Phi}_{0}})(\frac{{\Phi}_{0}H_{c1}}{8\pi})d=\frac{H_{c1}H_{c2}}{8\pi}V=\frac{{H_{c}^{2}}}{8\pi}V, $$
(10)

as it should as well. Note that the latter is consistent with the physical meaning of the condensation energy density \({H_{c}^{2}}/8\pi \) as the energy needed to destroy pairing [47].

This confirms the validity of (9) and, hence, the absence of the interaction between vortices in samples with η = 1.

Therefore, the vortex matter in samples of the transverse geometry can be viewed as a peculiar 2D “gas-like” system of non-interacting vortices where the role of pressure P is taken by the external field H and the equation of state is given by (3) for the entire field range of the MS.

Indeed, similar to the gas, whose density ρ → 0 when pressure P → 0, and isothermal compressibility ρ−1(∂ρ/∂P)T = 1/P, the vortex matter is highly compressible, i.e., its density n → 0 at H → 0 and the “compressibility” n−1(∂n/∂H)T = 1/H. Similar to the gas, where the slope of ρ vs P is determined by the Boltzmann constant, in the vortex matter, the slope of n vs H is determined by the fundamental constant Φ0. But, contrary to the gas, the properties of the vortex matter do not depend on temperature. At constant sample temperature when the field H (“pressure”) changes, the vortex density n changes accordingly. But, when the field has stopped changing, vortices stay motionless, in contrast to the gas, where molecules continue thermal motion. Therefore, vortices in a slab in perpendicular field can be treated as a system at zero temperature. But, zero temperature means zero entropy. Therefore, vortices should be ordered in full consistency with well-known experimental fact [50].

Comparing the gas-like scenario with solid-like pictures [51], one can see that the former is more appropriate for the vortex matter since a primary property of solids, rigidity, is absent in the equilibrium vortex ensemble.

Now, we turn to one more aspect of our experimental results, i.e., the proximity of κ of our film sample to the critical value \(\kappa _{c}= 1/\sqrt {2}\). In recent years, there emerged an active interest in the properties of superconductors with κ ≈ κc (see [52] and references therein). Considering the properties of the critical (κ = κc) superconductors in the framework of classical field theory, Bogomol’nyi showed [53] that vortices with flux exceeding a single flux quantum are unstable against decay to single flux quantum vortices, and that the energy of a system of stable (single-flux-quantum) vortices equals to the sum of the energies of the unit vortex, i.e., vortices do not interact.

The GL parameter of our film sample is 1.1κc, and, as we see, the vortices are indeed single-flux-quantum non-interacting units. The same was found for the Nb-SC sample with κ = 1.8κc. Hence, our experimental results confirm Bogomol’nyi’s predictions for superconductors with \(\kappa \gtrsim 1/\sqrt {2}\).

Finally, we have to address a question inevitably arising when reading this paper: if vortices do not interact when the sample (e.g., a film) is in perpendicular field, why do they interact when the field is parallel, as stated in the standard theory? In view of enormous amount of literature associated with the vortex interaction, a complete answer to this question is hardly feasible in the framework of this paper. Therefore, what follows should be sooner considered as an invitation to discussion than a solid judgment on this matter.

The vortex-vortex interaction in the standard theory follows from the assumption of overlapping of the inductions B of neighboring vortices, which increases the sample free energy thus leading to repulsive interaction between vortices [8, 22, 23]. Note, however, that overlapping of B at some point inside the sample means overlapping of currents at the same point, i.e., overlapping of vortices [55]. The latter is met neither in normal fluids [56] nor in superfluids [57, 58]. In the GL theory, vortices in superconductors also do not overlap [15, 59].

Indeed, in regular matter, overlapping of electron shells of neighboring molecules results in strong molecular repulsion leading to practical incompressibility of liquids and solids. As we have seen, this is not the case for the vortex matter in superconductors. This is because molecules are fixed entities, whereas vortices are self-adjustable units. Recall that currents induced in a singly connected superconductor serve solely to reduce its free energy. Therefore, since the B overlapping increases the free energy, one can expect that the superconductor will tune the currents to avoid that, thus keeping vortices non-interacting regardless of the vortex density. This qualitative scenario is consistent with the reported experimental results for the transverse geometry and, most importantly, with the rule of 1/2, valid for all geometries and indicating that the total free energy of superconductors contains no potential energy.

Coming back to our model of zero-order approximation, we note that it does not include inhomogeneities near the “transverse” (perpendicular to the field) sample surface, as it also takes place in the Peierls-London model for the IS. These inhomogeneities increase the sample magnetic energy and therefore modify the magnetization curve. In particular, as it was mentioned above, in the IS, they can significantly decrease the upper critical field [21]. However, contrary to the IS, where effects of these inhomogeneities were noticed already in 2-mm thick samples [54], such effects were not found in our samples. This can be explained by a finer pattern of these inhomogeneities (compare images in Fig. 9 with those in [35]). Therefore, the surface-related effects in the MS should be expected in thinner samples and they may differ from those in the IS, hence constituting a very interesting problem of fundamental superconductivity.

6 Summary and Outlook

Equilibrium properties of the mixed state in type II superconductors were studied with high-purity film and single-crystalline niobium samples with zero and unity demagnetizing factor η, that is in parallel and perpendicular magnetic fields, respectively. The magnetization curve for the samples with η = 1 was obtained for the first time. It was found that existing theories fail to describe these new data. A theoretical model successfully addressing this problem was developed and experimentally validated.

The new model describes magnetic properties of the mixed state in a zero-order approximation where interactions between vortices and surface current are ignored. The model is applicable to thick samples with any η without limitation for the magnitude of the Ginzburg-Landau parameter κ. The model is quantitatively consistent with the data obtained for the samples with η = 1, where the surface current is absent by definition. This indicates the absence of interaction between vortices in such samples. An expression for the field strength Hi inside superconductors in the mixed state is obtained together with a formula for the line tension of vortices valid in the entire field range of the mixed state. At low κ, our model converts to that of Peierls and London for the intermediate state in type I superconductors, which is valid in the limit of non-interacting laminae. It is shown that visualization of the vortex matter as an ordered 2D gas-like system at zero temperature is more appropriate than the frequently used solid-like scenarios.

The reported model is constructed and verified using experimental results obtained with low-κ Nb type II superconductors. Therefore, it is interesting and important to test the model with materials of higher κ. Single-crystal samples of A15 compounds, e.g., V3Si, can be appropriate candidates for such a verification. Single-crystal samples of unconventional superconductors close to the critical temperature can be also appropriate.