1 Introduction

Second-generation (2G) high-temperature superconducting (HTS) tapes, namely YBCO-coated conductors, are capable of carrying very high transport current due to their high critical current. They become more and more promising for a wide range of applications, such as superconducting cables, superconducting magnetic energy storage, and superconducting electrical machines [1,2,3]. From the application point of view, the critical currents of HTS coils are very important for optimizing design and economical operation. The critical current can help determine the maximum allowable current in a long-term operating HTS coil, which is crucial for operating safety [4]. Therefore, critical current of HTS coils must be analyzed carefully when designing HTS devices. Precisely and quickly calculating the critical current of HTS coils is of vital importance for safe operation and efficiency of designing process.

FEM is a powerful tool for HTS modeling and tremendous efforts have been made to develop efficient models. There are many methods for FEM modeling of HTS, such as A-V [5], T- Ω [6], and H formulations [7]. These three formulations are named by the state variables in the solution process, and are initially derived from Maxwell equations. H formulation was used to calculate critical current of coils by many researchers. In 2013, M. Zhang used H formulation to simulate the critical current and voltage current curve of an HTS pancake coil [8]. In 2015, D. Hu used H formulation to investigate the direct current (DC) characteristics of a triangular epoxy-impregnated HTS coil [9]. Although models based on H formulation can evaluate critical current of some coils, the calculation time is very long. Besides, when the coil becomes very large, it can be very difficult to compute because of the increased computational amount. Moreover, when symmetry cannot be used for dimensional reduction, such as modeling HTS racetrack coils, 3D models have to be built. As a result, the high aspect ratio of 2G HTS tapes results in huge mesh elements and intensive computation requirement. Even when the tape thickness is artificially scaled up, the computation time is still tremendous [10]. To speed up the calculation process, this paper provides a fast algorithm for evaluating critical current of HTS pancake coil. The fast algorithm is realized through a stationary model, which is based on FEM software (i.e., COMSOL 5.0). The stationary model means that the model is solved by stationary study instead of time-dependent study. The major advantage of the stationary model is that it can dramatically reduce the computational amount and speed up the calculating process.

This paper is organized as follows: In Section 2, the theory of the stationary model is presented in details. In Section 3, the stationary model for evaluating critical current of HTS coils is described. In Section 4, the stationary model is validated by comparing the results of calculations and measurements. In Section 5, the stationary model is compared with H formulation model. Finally, a brief summary of this paper is given.

2 Theory

As we know, all electromagnetic phenomena can be described by Maxwell’s equation. Based on this, the following deviations are derived from Maxwell’s equation.

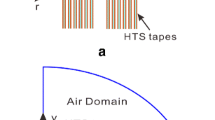
For HTS pancake coil, 2D symmetric model can be applied as shown in Fig. 1. In 2D geometry, the current in the superconducting layer flows in φ direction. Since the electrical field has the same direction with the current, the electrical field is also in φ direction. When substituting E = E φ and B = [ B r , B z ]T into Faraday’s law for cylindrical coordinate, Faraday’s law can be described in (1).

$$ \left[{\begin{array}{l} -\frac{\partial E_{\varphi } }{\partial z} \\ \frac{1}{r}\frac{\partial (rE_{\varphi } )}{\partial r} \\ \end{array}} \right]=-\left[ {\begin{array}{l} \frac{\partial B_{r} }{\partial t} \\ \frac{\partial B_{z} }{\partial t} \\ \end{array}} \right]\quad \quad \quad \quad \quad $$
(1)

When calculating the critical current of an HTS coil, the coil should carry stable direct current (DC). As a result, the surrounding electromagnetic environment is a static field. That is, the magnetic field is constant and it does not change with time. Therefore,

$$ \left\{ {\begin{array}{l} \frac{\partial B_{r} }{\partial t}=0 \\ \frac{\partial B_{z} }{\partial t}=0 \\ \end{array}} \right.\quad \quad \quad \quad \quad \quad \quad \quad \quad $$
(2)

Then, (1) is transformed to

To mathematically satisfy (3) and (4), E φ inside of one YBCO layer can be expressed as:

$$ E_{\varphi } =\frac{k}{r}\quad \quad \quad \quad \quad \quad \quad \quad \quad $$
(5)

where k is a constant inside of one YBCO layer. Let r = R + Δr, where R is the inner radius of this YBCO layer and Δr represents the displacement in r direction in this YBCO layer. As a result, according to (5), E φ can be rewritten in (6).

$$ E_{\varphi } =\frac{k}{r}=\frac{k}{R+{\Delta} r}\quad \quad \quad \quad \quad \quad \quad $$
(6)

The thickness of YBCO layer is 1 μm; hence, Δr ≤ 1 μm. However, the magnitude of R is at centimeter level or higher, so R ≥ Δr. As a result, the E φ in the YBCO layer can be approximated as:

$$ E_{\varphi } =\frac{k}{R+{\Delta} r}\approx \frac{k}{R}\quad \quad \quad \quad \quad \quad \quad \quad $$
(7)

According to (7), it can be concluded that the electrical field in one YBCO layer can be similarly considered uniform. This conclusion is the basic theory of the stationary model. The detailed description is presented in the later section.

Fig. 1
figure 1

Geometry of 2D axial symmetric model (not to scale)

Full size image

3 Stationary Model

When an HTS coil carries stable DC, the surrounding electromagnetic environment is a static field. Therefore, electromagnetic problem of the HTS coil can be solved by stationary study instead of time dependent study. Compared with time-dependent study, stationary study can speed up the computational process tremendously.

According to the deviations in Section 2, the electrical field distribution inside of one YBCO layer is uniform. Based on this conclusion, a stationary model is built to calculate the critical current of HTS coils. The critical current is determined by temperature and magnetic field distribution. Here, since temperature of the whole HTS coil is uniform and fixed, only the magnetic field is considered. In the stationary model, traditional A formulation is used to solve the magnetic distribution. The governing equation is in (8).

$$ \nabla \times \nabla \times \overset{\rightharpoonup}{A} =\mu_{0} \overset{\rightharpoonup}{J} \quad \quad \quad \quad \;\quad \;\quad $$
(8)

where \(\overset {\rightharpoonup }{A} \) is the magnetic vector potential, and \(\overset {\rightharpoonup }{J}\) is the current density.

A pancake coil is modeled by using 2D axis symmetry as shown in Fig. 1. The air domain is assumed to be so large that magnetic field produced by applied current decays to zero on the boundary. Each YBCO layer represents one turn of the coil and the thickness of YBCO layer is 1 μm. Distributed mapped mesh is applied to the HTS domains to control the total mesh size, and the free triangular mesh is applied to the air domain. Finally, the model is solved by stationary study in COMSOL 5.0.

The calculation process of the stationary model is plotted in Fig. 2. Firstly, the currents are applied to each YBCO layer by assuming that the current density inside each layer is uniform. The initial current density is calculated by (9)

$$ J=\frac{I}{W\cdot T} $$
(9)

where J is the current density; I is the applied current; and W and T are the width and thickness of YBCO layer, respectively. Then, the magnetic field (B) distribution is calculated by (8). After calculating magnetic field distribution, the critical current density (J c ) distribution of each YBCO layer can be obtained. Here, an elliptical functional form of J c (B), shown in (10), is used to describe the dependence of critical current density on magnetic field [11].

$$ J_{c} (B_{\vert \vert } ,B_{\bot } )=\frac{J_{c0} }{\left[ {1+\sqrt {(kB_{\vert \vert } )^{2}+B_{\bot }^{2}} /B_{c} } \right]^{b}} $$
(10)

where J c0 is the critical current density at self-field. k, B c , and b are the three parameters used for the curve fitting, and they are related to the type of HTS tapes. Then, the critical current (I c ) of each YBCO layer can be calculated by integrating critical current density in the cross section. According to the E-J power law, the electrical field can be calculated by (11).

$$ E=E_{c} \left( \frac{J}{J_{c} }\right)^{n} $$
(11)

where E c is 10−4 V/m. According to Section 2, final electrical field distribution in one YBCO layer is uniform, which means that the ratio of J to J c is uniform. The uniformity is evaluated by (12).

$$ \left\{ {\begin{array}{l} \text{ratio}=\frac{J}{Jc} \\ \text{unevenness}=\max \left\vert \frac{\text{ratio}}{\text{ratio}_{\text{average}} }-1\right\vert \\ \end{array}} \right. $$
(12)

where ratio average means the average of J/J c in the cross section of the YBCO layer. If the unevenness is not smaller than 1%, the calculation goes to the step of updating the J distribution according to (13).

$$ J=J_{c} \cdot \frac{I}{I_{c} } $$
(13)

After updating J distribution, the iteration continues until that the unevenness is smaller than 1%. When the iteration terminated, the ratio of J to J c in each YBCO layer can be considered uniform. And the final B, J, and J c distribution are obtained. The average voltage can be calculated as (14).

$$ V_{\text{average}} =\frac{V_{\text{total}} }{L_{\text{total}} }=\frac{\sum\limits_{i=1}^{N} {U_{i} } }{L_{\text{total}} }=\frac{\sum\limits_{i=1}^{N} {E_{c} L_{i} \left( \frac{I}{I_{ci} }\right)^{n}} }{L_{\text{total}} } $$
(14)

where V total is the total voltage and L totalis the total length of the coil. N is the total turn number and L i is the length of turn i. According to the 10−4 V/m criterion, if the average voltage equals to 10−4 V/m, the applied current is the critical current of the whole HTS coil.

Fig. 2
figure 2

Schematic diagram of calculation process of stationary model

Full size image

4 Model Validation

In order to validate the model, a single pancake coil was wound. The photograph of the experimental coil is shown in Fig. 3. The detailed information of the coil is listed in Table 1. The HTS tapes used for winding the experimental coil is manufactured by SuNAM. The parameters of J c (B) in (10) are as follows: k = 0.0605, b = 0.7580, and B c = 103 mT. The V-I curve was measured in liquid nitrogen.

Fig. 3
figure 3

Photograph of the experimental single pancake coil

Full size image
Table 1 Specifications of the HTS pancake coil
Full size table

The measured results are plotted in Fig. 4. According to the 10−4 V/m criterion, critical current of the HTS coil is 105 A. We built a stationary model to calculate the critical current of the experimental HTS coil. As a result, the calculated critical current is 100.3 A, which is 4.5% smaller than the measured one. The discrepancy might come from the non-uniformity of the used HTS tape or other reasons. The discrepancy is in the reasonable range, so we conclude that the stationary model can effectively calculate the critical current of HTS pancake coils.

Fig. 4
figure 4

Experimental V-I curve of the HTS pancake coil

Full size image

5 Comparison between Stationary Model and H Formulation Model

In previous investigations, H formulation was successfully applied to evaluate critical current of HTS coils. In order to analyze the stationary model in details, it is compared with H formulation model in this section.

5.1 H Formulation Model

Here, a brief description of the H formulation model is presented. 2D axial symmetrical H formulation is applied to the model. The model contains two variables, defined as H = [ H r , H z ]. Ampere’s law is written as:

$$ J_{\varphi } =\frac{\partial H_{r} }{\partial z}-\frac{\partial H_{z} }{\partial r} $$
(15)

Substitute H = [ H r , H z ] and E = E φ into Faraday’s law for cylindrical coordinate,

$$ \left[ {\begin{array}{l} -\frac{\partial E_{\phi } }{\partial z} \\ \frac{1}{r}\frac{\partial (rE_{\phi } )}{\partial r} \\ \end{array}} \right]=-\mu_{0} \mu_{r} \left[ {\begin{array}{l} \frac{\partial H_{r} }{\partial t} \\ \frac{\partial H_{z} }{\partial t} \\ \end{array}} \right] $$
(16)

Combining (10), (11), (15), and (16), the model can be solved by COMSOL. In (16), there are partial derivatives of H to time. Therefore, the model should use time-dependent solver. When applying direct current I to the coil, the current is ramped to I in 0.1 s and kept constant for 1 s. Then, the coil voltage is calculated by (14).

5.2 Comparison between Stationary Model and H Formulation Model

In order to compare the calculated results by the two models, the same HTS coil, as shown in Fig. 3, is modeled by the two methods. In both models, only the 1-um YBCO layer is modeled. The geometries and meshes of the two models are the same. The same current, which is 100.3 A, is applied to the coil. The current distributions and magnetic distributions are plotted in Figs. 5, 6, and 7, respectively. In order to increase the readability, the thicknesses of YBCO layer are enlarged from 1 to 200 μm.

Fig. 5
figure 5

Current density distribution of the HTS coil. a Stationary model. b H formulation model

Full size image
Fig. 6
figure 6

Vertical magnetic (⊥ ab plane) distribution of the HTS coil. a Stationary model. b H formulation model

Full size image
Fig. 7
figure 7

Parallel magnetic (// ab plane) distribution of the HTS coil. a Stationary model. b H formulation model

Full size image

As shown in Fig. 5, the current density distributions calculated by the two models are very similar, except that the current density in the center of middle turns in stationary model are slightly larger than that in H formulation model. Figure 5 shows that, in each turn, the current density in the center is higher than that in the edge, which means that the critical current density in the center is higher than that in the edge. This phenomenon can be explained by the magnetic distribution plotted in Figs. 6 and 7. As shown, the vertical magnetic (⊥ ab plane) distributions and parallel magnetic (// ab plane) distributions calculated by stationary model and H formulation model are nearly the same. In each turn, the vertical magnetic field in the center is obviously smaller than that in the edge; meanwhile, the parallel magnetic field inside of the layer changes little. According to (10), the critical current density in the center of YBCO layer is larger than that in the edge.

In order to compare the critical currents calculated by the two models in details, the critical currents of each turn is plotted in Fig. 8. The critical currents of each turn calculated by the two models are very close. To be more specific, the maximum relative difference is less than 0.5%. As shown in Fig. 8, the critical currents in middle turns are smaller than that of inner or outer turns. This can be explained by the magnetic distribution plotted in Figs. 6 and 7. As shown, the magnitude of parallel magnetic field in the middle turns are smaller than that in inner or outer turns, but the magnitude of vertical magnetic field in the middle turns are larger than that in inner or outer turns. According to (10), the critical current density is mainly decided by vertical magnetic field. Since larger magnetic means smaller critical current, the critical currents in middle turns are smaller than that of inner or outer turns.

Fig. 8
figure 8

Comparison of critical currents of each turn calculated by stationary and H formulation models

Full size image

According to the description above, stationary model and H formulation model can obtain nearly the same results, including critical current, current density distribution, and magnetic distribution. However, the difference of calculating time used by the two models is very large. Both stationary and H formulation models are solved on the same PC with an Intel i7-7700 CPU and 32 GB of memory. The calculating time used by the two models is plotted in Fig. 9. When we use true thickness of YBCO layer, which is 1 um, the calculating time used by H formulation model is more than 100 h. However, the calculating time used by stationary model is less than 1 min. Even when we artificially scale-up the thickness of YBCO layer from 1 to 100 um, the calculating time used by H formulation is still around 100 h. Therefore, the calculating efficiency of stationary model is dramatically faster than that of H formulation model. This advantage of calculating efficiency is very important for designing HTS devices.

Fig. 9
figure 9

Comparison of calculating time use by stationary and H formulation models

Full size image

6 Conclusion

In this paper, a fast algorithm for evaluating critical current of HTS coils is presented. The fast algorithm is realized through a stationary model, which is based on FEM software. The theory and calculation process is described in details. To validate this stationary model, a pancake coil was wound and the critical current is measured. Meanwhile, a 2D axial symmetric stationary model was built according to the geometry of the experimental coil. By comparing measured and calculated results, the effectiveness of the stationary model was demonstrated. Moreover, the stationary model is compared with H formulation model. The results calculated by the two models, including current distribution, magnetic distribution, and critical current of each turn, are nearly the same. However, by using stationary calculation, the stationary model can remarkably speed up the computational process. For each applied current, calculating time of H formulation model is around 100 h; however, calculating time of stationary model is less than 1 min. Due to the huge advantage of calculating efficiency, the stationary model can be used to characterize and design large-scale HTS applications.