1 Introduction

Magnetic layered structures and nano-films have attracted significant attention recently because of their physical properties and differ dramatically from simple solids. The study of nano-film systems, made from alternating layers, can be a source of magnetization, exchange interlayer, magneto-resistance, and other characteristics [1–3]. The magnetic properties of such systems have been supported by the idea that the properties of the nano-films can be significantly different from those of their constituents. These structures are used in the creation of new semiconductors that exhibit different properties than their included materials. It is believed that one allows build materials with different properties. Consequently, many efforts have been recently devoted to the study of magnetic films, layered structures, and super-lattice models [4–6].

Due to difficulties in experimental studies, the quantum computational methods can be considered as an alternative successful investigation for elaborating interesting materials. Many works dealing with the properties of magnetic multi-layers and nano-films have appeared in the recent years [7–10]. In fact, a special effort has been devoted to the study of the critical phenomena in various magnetic layered and nano-films. Using Monte Carlo simulations [11–14], the behavior and the magnetic properties of such systems have been extensively investigated. In particular, a multi-layer system consisting of spin 1/2 and spin 3/2 ferromagnetic Ising layer and disordered interface is reported in Ref. [15]. The multi-layers for a system with a disordered interface are found to exhibit many characteristic behaviors, especially the dependence of the compensation behavior on the thickness layers [6–10].

The aim of this work is to contribute to the study of the nano-films alternate ferromagnetic/anti-ferromagnetic layers, interacting with alternate crystal fields for the spin 1 system. The ferromagnetic and anti-ferromagnetic properties of the nano-film systems are explored using a Monte Carlo (MC) method.

2 Theoretical Model

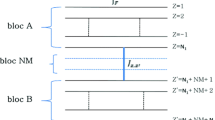
In this work, we examine the alternate nano-film with a simple cubic lattice, with an alternate ferromagnetic and anti-ferromagnetic layers consisting of spins (σ=0,±1) under the effect of alternate crystal fields (see Fig. 1). The nano-film is composed of N layers containing L × L spins in each square layer. In particular, the study will be made in terms of the parity of the layer number. The Hamiltonian dealing with this system takes the following form:

$$ H_{\text{tot}} =H_{\mathrm{F}} +H_{\text{AF}} +H_{\mathrm{p}} +H_{\text{field}} $$
(1)

with

$$ H_{\mathrm{F}} =-J_{\mathrm{F}} \sum\limits_{\begin{array}{l} <i,j>\\ i,j\in (k_{F} ) \end{array}} {\sigma_{i}^{k_{F}} \sigma_{j}^{k_{F}} } $$
(2)
$$ H_{\text{AF}} =-J_{\text{AF}} \sum\limits_{\begin{array}{l} <i,j>\\ i,j\in (k_{AF} ) \end{array}} {\sigma_{i}^{k_{AF}} \sigma_{j}^{k_{AF}} } $$
(3)
$$ H_{\mathrm{P}} =-J_{\mathrm{P}} \sum\limits_{i\in (k_{\mathrm{F}} ),j\in (k_{\text{AF}} )} {\sigma_{i}^{k_{\mathrm{F}}} } S_{j}^{k_{\text{AF}}} $$
(4)
$$ H_{\text{field}} =-{\Delta}_{1} \sum\limits_{i\in (k_{\mathrm{F}} )} {\left( \sigma_{i}^{k_{\mathrm{F}}} \right)^{2}} -{\Delta}_{2} \sum\limits_{i\in (k_{\text{AF}} )} {\left( \sigma_{i}^{k_{\text{AF}}} \right)^{2}} $$
(5)

In these equations, the notation < i,j>stands for the nearest neighbors between the σ i and σ j spins (see Fig. 1). The summations are performed over the ferromagnetic layers (k F) as well as the anti-ferromagnetic layers (k AF). J F and J AF describe the exchange coupling constants between the spins σbelonging to the ferromagnetic (k F) and anti-ferromagnetic (k AF) layers, respectively. The alternate crystal fields Δ1 and Δ2 are acting on the k F and k AF layers, respectively. The general study is beyond the scope of the present work, though we will consider the special case: Δ1=Δ and Δ2=−Δ1. A sketch of the geometry illustrating this system is given in Fig. 1. On the other hand, we will use the reduced parameters T/J, Δ/J, J F/J, and J AF/J, where J = J P (see Fig. 1).

Fig. 1
figure 1

A sketch of the alternating ferromagnetic/anti-ferromagnetic layers. J F and J AF are the exchange coupling between the spins of the ferromagnetic and anti-ferromagnetic layers, respectively. J is the exchange coupling between the layers with alternate crystal fields Δ1=−Δ2

Full size image

3 Monte Carlo Simulations

It is recalled that each layer is constituted with a square made up with L ×L spins σ-layer and N-layers located on a super-lattice. The Monte Carlo Metropolis method has been used to obtain the equilibrium properties of the physical system in contact with a heat bath of temperature (T), in order to simulate the Hamiltonian given by (1). Periodic conditions are taken into account on the super-lattice. The method makes changes in the configuration by sweeping the super-lattice. The algorithm accepts or rejects the new configuration according to some probability based on the Boltzmann statistics. Each iteration of this algorithm is called a MC step. The Metropolis Monte Carlo simulations (MCSs) generate configurations with the system variable values following the Boltzmann distribution, leading to the equilibrium properties from the average of the configurations. Starting from different initial conditions, we perform 10 5 Monte Carlo steps for each spin configuration, discarding the first 10 4 generated configurations. We average over many physical configurations for each initial condition. The nano-films we consider here consists of ferromagnetic (N F) and anti-ferromagnetic (N AF) layers. The total layers of nano-film layers are given by N = N F + N AF.

The internal energy per site is

$$ E_{\text{tot}} =\frac{1}{L\times L\times N}<H_{\text{tot}} > $$
(6)

The corresponding total magnetization is defined as

$$ M_{\text{tot}} =\frac{M_{\mathrm{F}} +M_{\text{AF}}} {2} $$
(7)

The partial magnetizations for each ferromagnetic and anti-ferromagnetic layer is take the forms

$$ M_{\mathrm{F}} =<\frac{1}{L\times L\times N_{\mathrm{F}}} \sum\limits_{i\in (k){\kern 1pt}\,\text{odd}} {\sigma_{i}} > $$
(8)
$$ M_{\text{AF}} =<\frac{1}{L\times L\times N_{\text{AF}}} \sum\limits_{i\in (k)\;\text{even}} {\sigma_{i}} > $$
(9)

The total magnetic susceptibility reads as

$$ \chi_{\text{tot}} =\beta \left( <M_{\text{tot}}^{2} >-<M_{\text{tot}} >^{2} \right) $$
(10)

The partial susceptibilities for each ferromagnetic and anti-ferromagnetic layer are given by:

$$ \chi_{\mathrm{F}} =\beta \left( <M_{\mathrm{F}}^{2} >-<M_{\mathrm{F}} >^{2} \right) $$
(11)

and

$$ \chi_{\text{AF}} =\beta \left( <M_{\text{AF}}^{2} >-<M_{\text{AF}} >^{2} \right) $$
(12)

where \(\beta =\frac {1}{k_{\mathrm {B}} T}\) and k B is the Boltzmann constant which will be fixed at k B=1 in all numerical calculations.

4 Results and Discussion

Now, it would be useful to explore the Monte Carlo simulations to investigate the total effect of the reduced magnetization profiles and reduced crystal field with ferromagnetic and anti-ferromagnetic reduced exchange interactions for different values of reduced temperature and the thicknesses of the nano-films. For this purpose, we present in Fig. 2a–d the variation of the total magnetization versus the reduced exchange interactions for N= 9 and N= 10, respectively. Indeed, Fig. 2a, b corresponds to the reduced anti-ferromagnetic exchange interaction whereas Fig. 2c, d corresponds to the reduced ferromagnetic exchange interaction, respectively. All these figures are plotted for different reduced temperature values: T/ J= 0.5, 1, 1.5, and 3.0 at a fixed value of J F/ J=+1 (in Fig. 2a, b) and J AF/ J=−1 (in Fig. 2c, d). It is found that a critical magnetization (M C) is independent on different temperatures when increasing the exchange interaction (J AF/J in Fig. 2a, b or J F/J in Fig. 2c, d). This critical magnetization (M C) is displaced when increasing the number of layers. The solid line in Fig. 2a, c corresponds to N= 9 layers, and the dashed line corresponds to N= 10 layers. In Fig. 2b, d, the solid line denotes N= 10 layers whereas the dashed line corresponds to N= 9 layers. It is found that for the systems with odd layer numbers, the variation of anti-ferromagnetic reduced exchange interaction is always greater than the corresponding one of systems with even layer numbers. This finding is well illustrated in Fig. 3 for J F/ J=+1. This figure shows also that for large values of N, odd and even corresponding of the reduced exchange interactions become similar.

Fig. 2
figure 2

The total magnetization versus the anti-ferromagnetic and the ferromagnetic reduced exchange interaction for different reduced temperature values: T/ J= 0.5, 1.0, 1.5, and 3.0. a, c N= 9 layers. b, d N= 10 layers. In a, c, the solid lines correspond to N= 9 layers, whereas the dashed lines correspond to N= 10 layers. Conversely, in b, d, the solid lines correspond to N= 10 layers whereas the dashed lines correspond to N= 9 layers

Full size image
Fig. 3
figure 3

The variation of anti-ferromagnetic reduced exchange interaction (J AF/ J)int as a function of the number of layers

Full size image

In order to underline the crystal field effect, we plot in Fig. 4 the total magnetization versus the reduced crystal field for different reduced temperatures, T/ J= 0.5, 1.0, 1.5, and 3.0, at fixed values of J AF/ J=−1 and J F/ J=+1. Figure 4a is plotted for N= 9 layers, whereas Fig. 4b corresponds to N= 10 layers. It is found that, for a fixed number of layer value (N= 9 or N= 10), a fixed value of the total magnetization is not affected by the increasing temperature, when increasing the reduced crystal field. This is due to the competition between thermal fluctuation and increasing crystal field effect. This result is valid for the odd number of layers (N= 9 in Fig. 4a) and for the even number of layers (N= 10 in Fig. 4b).

Fig. 4
figure 4

The total magnetization versus the reduced crystal field for different reduced temperatures, T/ J= 0.5, 1.0, 1.5, and 3.0, at fixed values of J AF/ J=−1 and J F/ J=+1. a N= 9 layers. b N= 10 layers

Full size image

5 Conclusions

In this paper, we have studied the magnetic properties of the Ising model based on a nano-film formed by alternating layers. The effect of the reduced crystal field with the anti-ferromagnetic and ferromagnetic reduced exchange interactions is deduced for N= 9 and N= 10 layers. However, the anti-ferromagnetic reduced exchange interaction (J AF/ J)int increases when the number layers increase, for odd or even values of N. Moreover, the total magnetization increases with increasing of the anti-ferromagnetic and the ferromagnetic reduced exchange interactions. It has been shown that the total magnetization remains almost constant for large values of layer numbers (N). However, it increases rapidly for small values of reduced crystal field.