1 Introduction

The Blume-Capel (BC) model has been the subject of many theoretical studies since its introduction in order to study first-order magnetic phase transitions [1, 2], since then it has been investigated in detail using many approximate methods, namely mean field approximation [3–5], high-temperature series expansion [6–8], constant-coupling approximation [9], and renormalization group techniques [10]; it has also been studied by Monte-Carlo simulation [11]. Later, this model was generalized to the Blume-Emery-Griffiths model [12, 13] to study the He3–He4 mixtures and a variety of other physical systems.

During the last decades, the magnetic materials have become a research domain of special interest, mainly due to their applications in technology. Consequently, the study of magnetic thin films registered an important development, from both theoretical and experimental points of view [14–18]. In this context, many scientific studies (theoretical and experimental) have been dedicated to the magnetic multilayer structures [19–21], considering the interesting interface and surface effect, that can appear in this kind of systems, to the reduced dimensionality and to magnetic interactions. At the same time, the numerical approaches in this domain attract special attention [22, 23], representing a good instrument to test the compatibility of the new proposed physical models and to predict the new potential phenomenon that can appear in certain physical conditions.

The magnetism of ultrathin films, multilayers, and the surface was a new research field [24]. This is due to a range of applications including the possibility of spintronics-based devices, the advances in film preparation and structure characterization at the atomic scale, discovery of new magnetic properties which are different from those of bulk materials, these artificial structures materials, such as perpendicular magnetizations and giant magneto-resistance, where two or more ferromagnetic layers are separated by a very thin non-ferromagnetic space (e.g., Fe/Cr/Fe), and potential applications in high-density magnetic recording. This technological potential has been certainly the driving force in developing research on multilayers [25]. Moreover, when reducing the film thickness down to the atomic monolayer, the space dimensionality decreases leading to reduced Curie temperature (Tc), different temperature dependence of the spontaneous magnetization, and new critical exponents [26–28]. The magnetic multilayers exhibit also two interesting phenomena which are coupling between the ferromagnetic layers through the non-magnetic layers as well as a new magnetoresistance mechanism due to the spin-dependent scattering of the conduction electrons at the interfaces, which can lead to giant magnetoresistance [29]. Leading to a range of applications including the possibility of spintronics-based devices, much interest have been attracted to the magnetic properties of multi-layers due to their novel properties. In addition, different types of multi-layers, such as Pd/Co, Fe/Si, NiFe/Ag, and Fe/Cr, have been studied intensively. In the case of metallic multi-layers, a giant magneto-resistance, where two or more ferromagnetic layers are separated by a very thin non-ferromagnetic space (e.g., Fe/Cr/Fe), is observed after applying a magnetic field which depends on the number of layer thicknesses [30, 31].

In many magnetic materials, long-range exchange interactions play a dominant role, the most familiar being those that stem from the indirect coupling of localized atomic spins arising through the intermediary of the spins, called Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction [32]. It has shown how the pair approximation can be readily extended to treat such long-range interactions in the case of a spin ½ Ising model with RKKY interactions [33]. At certain thicknesses, the RKKY coupling interaction between adjacent ferromagnetic layers with a crystal field becomes anti-ferromagnetic, making it energetically preferable for the magnetizations of adjacent layers to align anti-parallel [34, 35]. Ez-Zahraouy et al. [36] have studied using mean field theory the phase diagrams of a spin-1 Blume-Capel super-lattice model consisting of two different magnetic materials separating by a non-magnetic spacer, and they show that the phase diagrams depend qualitatively and/or quantitatively on the thickness of the magnetic and non-magnetic spacers.

Our aim in this paper is to study, using Monte Carlo simulation in a system formed by two magnetic layers, separated by a number of non-magnetic layers with a spin-3/2 in the Blume-Capel model, the effect of the RKKY interaction, the crystal field, and the exchange couplings ferromagnetic and antiferromagnetic interactions, on the critical temperature and on the magnetic properties of the system.

The paper is organized as follows: In Section 2, we present the theoretical model. In Section 3, we present the Monte Carlo simulation. Results and discussion are given in Section 4, and Section 5 is reserved for the conclusion.

2 Theoretical Model

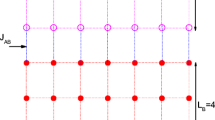
We consider the spin-3/2 in the Blume-Capel model of a simple-cubic lattice formed by N 1and N 2 of alternative ferromagnetic and antiferromagnetic films, separated by a number of non-magnetic films NM (see Fig. 1). The system is finite and symmetric in the x and y directions and of finite thickness in the z direction.

Fig. 1
figure 1

A schematic illustration of the model

Full size image

The Hamiltonian of the system is given by

$$\begin{array}{@{}rcl@{}} H&=&-J_{F}{\sum}_{<i,j>} {{S_{i}^{f}}{S_{j}^{f}}} -J_{AF}{\sum}_{\mathrm{<}i,j>{\prime}} {S_{i}^{af}S}_{j}^{af}\\ &&-{\sum}_{(z,z^{\prime})} J_{z,z^{\prime}} {\sum}_{<i,j>{\prime}{\prime}} {S_{i}S_{j}} -{\Delta}_{1}{\sum}_{i\in \mathrm{bloc~}A} S_{i}^{2} \\ &&-{\Delta}_{2}{\sum}_{i\in \text{bloc}~B} \mathrm{S}_{\mathrm{i}}^{2} \end{array} $$
(1)

where S is the spin random variable which take the values ±3/2,±1/2. First and second sums run over all pairs of nearest-neighbor sites of ferromagnetic and antiferromagnetic films, respectively. J F and J AF are the exchange coupling interactions between the nearest-neighbor pairs on ferromagnetic and antiferromagnetic films, respectively. \({\sum }_{(z,z^{\prime })}\) means the summation over all pairs of layers z(z∈bloc A), and z ′(z ′∈bloc B), \({\sum }_{<i,j>\prime \prime } k \)means the summation over all axially (with the axis being perpendicular to the non-magnetic layers) connected pairs of sites i and jin layers z and z ′, respectively (see Fig. 1). The two sums \({\sum }_{i\in \text {bloc}~A} g \) and \({\sum }_{i\in \text {bloc}~B} f \)mean the summations over all sites of bloc A and bloc B, respectively. \(J_{z,z^{\prime }}\) denotes the “RKKY-like” coupling, across the non-magnetic layers, between the layers z and z ′, given by

$$ J_{z,z^{\prime}}=\frac{a^{2}J_{0}}{{(z-z^{\prime})}^{2}}\cos {(k_{f}\left( z-z^{\prime} \right))} $$
(2)

where k f denotes the Fermi level, a is the lattice constant, J 0 is a magnetic coupling constant [32, 33], and Δ1,Δ2 are the crystal fields applied on bloc A and bloc B, respectively. For simplicity, we assume a = 1 and J 0 = 1.

3 Monte Carlo Simulations

It is recalled that each layer consists of a cubic lattice structure, with the size of each plane being L = 15. The Monte Carlo Metropolis method has been used to obtain the equilibrium properties of the physical system in contact with a heat bath of temperature T, in order to simulate the Hamiltonian given by (1). Periodic conditions are taken into account of the cubic lattice structure. The method makes changes in the configuration by sweeping the cubic lattice. The algorithm accepts or rejects the new configuration according to some probability based on the Boltzmann statistics. This algorithm is called a Monte Carlo (MC) step for each iteration. The Metropolis Monte Carlo simulations (MCS) generate configurations with the system variable values following the Boltzmann distribution, leading to the equilibrium properties from the average of the configurations. Starting from different initial conditions, we perform 105 Monte Carlo steps for each spin configuration and discard the first 104 generated configuration. We average over many physical configurations for each initial condition. The nano-films we consider here consist of N 1 and N 2 layers. The total layers of nano-film layers are given by N = N 1 + N 2.

The internal energy per site is

$$ E_{\text{tot}}=\frac{1}{L\times N}<H_{\text{tot}}> $$
(3)

The corresponding total magnetization is defined as

$$ M_{\text{tot}}=\frac{M_{F}+M_{AF}}{2} $$
(4)

The total magnetic susceptibility reads as

$$ \chi_{\text{tot}} =\beta (<M_{\text{tot}}^{\text{2}} >-<M_{\text{tot}}>^{2} ) $$
(5)

where \(\beta =\frac {1}{k_{B} T}\) and k B denotes the Boltzmann constant which will be fixed at k B = 1 in all the following numerical calculations.

4 Results and Discussion

4.1 Ground State Study (T = 0 K)

We discussed the possible phase diagrams in terms of the variety of different parameters, by computing and comparing all possible configuration energies. Indeed, we can determine the ground state phase diagrams from the Hamiltonian (1). It can produce many stable topologies producing different phase diagrams in terms of adequate parameters. These stable phases are obtained by minimizing the energy values for each parameter and for fixed system size values. The corresponding phase diagrams are presented in Figs. 2a, b and 3a, b, for a fixed number of parameters N = 1, k f = 0.1, and NM = 10.

Fig. 2
figure 2

Ground state phase diagrams of the studied system, for N 1 = N 2 = 5, k f = 0.1, and NM = 10. a In the plane (Δ1,Δ2) for J F = 1 and J AF = −0.1. b In the plane (J AF , J F ) for Δ1 = Δ2 = 1

Full size image
Fig. 3
figure 3

Ground state phase diagrams of the studied system, for N 1 = N 2 = 5, k f = 0.1, and NM = 10. a In the plane (Δ1, J F ) for J AF = 0.1. b In the plane (Δ1, J AF ) for J F = 1

Full size image

In fact, the effect of the crystal field is illustrated in Fig. 2a for fixed values of the parameters J F = 1 and J AF = −0.1. It is found that the only stable configurations are (+ 3/2), (+ 1/2), and (+ 3/2, + 1/2), in three regions of the (Δ1, Δ2) plane. It should be noted that the notation (1/2)10 and (3/2)10 means the configurations where the spins of the sites of all the films are equal to (1/2) and (3/2), and the notation ((1/2)5, (3/2)5) means the configuration where the spins of sites of all films are equal to 1/2 and 3/2, respectively. This is due to the fact that they have the same energy. In addition, we plot in Fig. 2b the corresponding phase diagram in the plane (J AF , J F ), the stable configurations for fixed values of Δ1 = Δ2 = 1. The only stable configuration is (+ 3/2) for the exchange coupling antiferromagnetic interaction values J AF >−25 whereas for values of J AF <−2.5, the stable configuration is (+ 1/2) Due to the fact that each configuration has the same energy, they occupy the same region in the plane (J AF , J F ) (see Fig. 2b).

To complete this ground state study, we illustrate in Fig. 3a, b the corresponding phase diagrams in the two planes (Δ1, J F ) and (Δ1, J AF ). The existence four configurations is shown, namely ((3/2)10), ((3/2)5,(1/2)5), ((1/2)5,(3/2)5), and ((1/2)10), which are stable in Δ1>0 and J F >0, Δ1>2 and J F <0, Δ1<−1 and J F >0.7, and Δ1<2 and J F <0.7 (see Fig. 3a). On the other hand, in the plane, (Δ1 J AF ) shows the existence of four configurations, namely ((3/2)10), ((3/2)5,(1/2)5), ((1/2)5,(3/2)5), and ((1/2)10), which are stable in Δ1>0.5 and J AF >−4, Δ1<0.5 and J AF >−3.5, Δ1>2.2 and J AF <−4, and Δ1<2.2 and J AF <−3.5 (see Fig. 3b). These stable configurations are obtained in precedent figures.

4.2 Study at T>0 K

Now we are studying, using Monte Carlo simulation, the magnetic properties of the Blume-Capel model with RKKY interactions between two blocs, formed by two magnetic layers (N 1 and N 2) separated by a number of non-magnetic layers (NM). We examine the effect of the magnetic films N (N = N 1 + N 2) on the critical temperature of the system, at fixed values of NM = 10, Δ1 = Δ2 = 1 and k f = 0.1 (see Fig. 4). It is found that by increasing the thickness of the magnetic films (N), the critical temperature of two blocs exhibit the same transition (TcA = TcB), and it increases till it reaches the bulk critical temperature Tca = Tcb = 5 (see Fig. 4). These results confirm the results obtained in the case where the system is completely ferromagnetic [3–5].

Fig. 4
figure 4

The behavior of the critical temperature as a function of the magnetic thickness N = N 1 + N 2 for k f = 0.1, NM = 10, Δ1 = Δ2 = 1, JF = 1, and JAF = −0.1

Full size image

Moreover, we plot in Fig. 5 the behavior of the critical temperature as a function of the number of the non-magnetic spacer (NM) and the Fermi level (k f) at fixed values of different parameters of the system. It is found that when increasing the number of non-magnetic spacers, the critical temperatures of the two blocs transit at the same critical temperature (TcA = TcB), and it decreases slightly till it reaches the bulk critical temperature (Tca = Tcb = 4.8). These results are obtained for small values of the non-magnetic spacer (NM < 10) (see Fig. 5a). This is due to the RKKY interaction becoming strongly dominant in comparison to the thermal fluctuations, and then the magnetism in bloc A is reinforced by the magnetism of bloc B via the RKKY interaction. Similarly, the effect of the Fermi level on the critical temperature is plotted in Fig. 5b for a specific value of the non-magnetic spacer NM = 10. It is found that for a lower Fermi level than k f <1.0, the critical temperature remains constant, whereas for 1.0<k f<3.0 this critical value increases, while for k f >3.0 the critical temperature reaches the saturation.

Fig. 5
figure 5

The behavior of the transition temperature as a function of a the non-magnetic thickness NM for k f = 0.1. b The Fermi level for NM = 10. For J F = 1, J AF = −0.1, Δ1 = Δ2 = 1, and N 1 = N 2 = 8

Full size image

The effect of the crystal field on the critical temperature is plotted in Fig. 6. One can see that the effect of increasing the crystal field applied on bloc A is the increasing of the critical temperature of this bloc, but the critical temperature of bloc B remains constant (see Fig. 6a). On the other hand, the critical temperature of bloc B increases with increasing the crystal field applied on this bloc, but in bloc A the critical temperature remains constant. This is due to the effect of the crystal field applied on bloc A (or bloc B), which cannot affect bloc B (or bloc A), because of the distance of the non-magnetic spacer (NM) between two blocs which is very large (NM = 10) (see Fig. 6b).

Fig. 6
figure 6

The behavior of the critical temperature as a function of the crystal field, for J F = 1, J AF = −0.1, NM = 10, N 1 = N 2 = 8, and k f = 0.1. In a for Δ2 = 1 and in b for Δ1 = 1

Full size image

To complete this study, we illustrate in Fig. 7a, b the effect of the exchange coupling ferromagnetic and antiferromagnetic interactions on the critical temperature of the system at fixed values of NM = 10, N 1 = N 2 = 8, k f = 0.1, and Δ1 = Δ2 = 1. In fact, Fig. 7a represents the behavior of the critical temperature as a function of the exchange coupling ferromagnetic interaction. It is found that by increasing the values of the exchange coupling ferromagnetic interaction, the critical temperatures of the two blocs A and B increase (see Fig. 7a) These two critical temperatures of the system are equal (TcF = TcAF) for J F <1.0, but TcF is not equal to TcAF for J F>1.0. Similarly, we plot in Fig. 7b the corresponding behavior of the critical temperature as a function of the exchange coupling antiferromagnetic interaction of the system It is found that by increasing the exchange coupling antiferromagnetic interaction, the critical temperatures of the two blocs are different (TcF and TcAF) as well as by still increasing J AF , they remain constant till they reach a point from where they exhibit the same transition temperature (TcF = TcAF).

Fig. 7
figure 7

The behavior of the transition temperature at fixed values of NM = 10, N 1 = N 2 = 8, k f = 0.1, and Δ1 = Δ2 = 1. a The exchange coupling ferromagnetic interaction (J F ). b The exchange coupling antiferromagnetic interaction (J AF )

Full size image

5 Conclusion

In this work, we have studied, using Monte Carlo simulations, the effect of the RKKY interaction, on the critical temperature of a spin-3/2 Blume-Capel magnetic film formed by two magnetic blocs, separated by non-magnetic spacer layers. We found that the critical temperatures of the two blocs depend strongly on the thickness of the magnetic layers, the thickness of the non-magnetic spacer layers, and the crystal fields of the magnetic blocs, while they depend weakly on the Fermi level.