1 Introduction

In recent years, Heusler and semi-Heusler alloys have been investigated both theoretically and experimentally due to their various interesting physical properties such as half-metallic ferromagnetism, shape memory effect, magneto-caloric effect, etc., which is promising for future technological applications [1, 2]. Nowadays, the interest in Heusler compounds grew enormously due to the discovery of materials with high Curie temperature, high spin polarization and low saturation of magnetization, which may be useful for new devices, related to the magnetic storage of information [3, 4].

Heusler compounds belong to a group of ternary intermetallics with the stoichiometric composition X2YZ ordered in an L21-type structure. X and Y are transition metals and Z is usually a main group element. The L21 structure consists of a primitive fcc lattice with a basis of four atoms. Most of these materials order ferromagnetically which makes them interesting and promising materials for future requirements in the field of technology [5]. Rapid development of modern material science has intensified the research interest in the field of spintronics. One of the most important materials for spintronics is half-metallic materials including half-metallic ferromagnets (HMFs) and half-metallic antiferromagnets [6].

The half-metallic HMF was first proposed by de Groot et al. from the band structure calculations for the semi-Heusler NiMnSb and PtMnSb alloys [7, 8]. Half-metallic materials, in which the majority-spin band is metallic, while the minority-spin band is semiconducting with an energy gap at the Fermi level, have the complete (100 %) spin polarization [8]. Up to now, HM ferromagnets have been widely found in perovskite compounds such as BaCrO3 [9] and Sr2FeMoO6 [10], in Heusler alloys such as Co2MnSi [11] and Mn2ZnCa [12] and in metallic oxides such as CrO2 [13] and Fe3 O 4 [14, 15].

The family of Heusler alloys incorporates more than 1000 members almost all crystallizing in a close-packed cubic structure similar to the binary semiconductors [4]. Most of them are metals exhibiting diverse magnetic phenomena.

The goal of this research work is to study, with ab initio calculation, the structural, electronic, magnetic and half-metallic properties of the Heusler alloys Ti2ZAl (Z = Co, Fe, Mn). The rest of the paper is arranged as follows: Section 2 includes computational details and the method of calculation, Section 3 is devoted to the results and discussion and Section 4 is a summary of our conclusions.

2 Computational Method

Electronic structure calculations were performed using the self-consistent full potential linearized augmented plane wave (FPLAPW) method [16] implemented in WIEN2K code [17] within the density functional theory (DFT). The Perdew–Burke–Ernzerhof generalized gradient approximation (GGA) [18, 19] was used for the exchange correlation correction. In this method, the space is divided into non-overlapping muffin-tin (MT) spheres separated by an interstitial region. The maximum value of angular momentum l m a x = 10 is taken for the wave function expansion inside the atomic spheres. In order to accomplish the energy convergence, the wave function in the interstitial region is expanded with a cutoff parameter K m a x R mt= 8, where K m a x is the maximum value of the reciprocal lattice vector used in the plane wave expansion and R mt is the smallest atomic-sphere radius of all the atomic spheres. The magnitude of the largest vector in charge density Fourier expansion (G m a x ) was 14 (a.u.) -1. A mesh of 64 special k-points was made in the irreducible wedge of the Brillouin zone .The cutoff energy, which defines the separation of valence and core states, was chosen as -6.0 Ry. The self-consistent calculations are considered to be converged only when the total energy of the crystal is converged to less than 10 -4 Ry.

The total energy dependence on the cell volume is fitted to the Murnaghan equation of state [20] to determine the ground state properties.

$$ E(V)=E_{0} (V)+\frac{BV}{B^{\prime} (B^{\prime} -1)}\left[ {B\left( {1-\frac{V_{0}} {V}} \right)+\left( {\frac{V_{0}} {V}} \right)^{B\prime} -1} \right] $$
(1)

where E 0 is the minimum energy at T= 0 K, B is the bulk modulus, B' is the bulk modulus derivative and V 0 is the equilibrium volume. The electronic configurations for the valence states of Ti, Co, Fe and Mn used were [Ar] 3 d 24s 2, [Ar] 3 d 74s 2, [Ar] 3 d 64s 2 and [Ar] 3 d 54s 2, respectively.

3 Results and Discussion

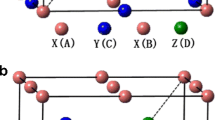
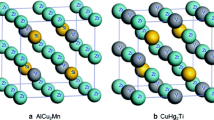
The Heusler compounds have a stoichiometry composition of X2YZ where X and Y are transition metals and Z is a main group element. The full-Heusler compounds crystallizing in the cubic structure have two types: AlCu2Mn and CuHg2Ti. The two structures consist of four interpenetrating fcc sub-lattices and four crystal sites: A (0,0,0), B (1/4,1/4,1/4), C (1/2,1/2,1/2) and D (3/4,3/4,3/4). In the AlCu2Mn type, X atoms occupy the (A, C) site, while in the CuHg2Ti-type structure, the (A, B) sites are occupied by X atoms. The full-Heusler Ti2ZAl (Z = Co, Fe, Mn) with AlCu2Mn and CuHg2Ti structures is shown in Fig. 1. According to Luo et al. [21], site preference of the X and Y atoms is strongly influenced by the number of their 3d electrons. Those elements with more 3d electrons prefer to occupy the A and C sites and those with fewer ones tend to occupy B sites. In the CuHg2Ti-type full-Heusler alloy, X atoms occupy A (0, 0, 0) and B (1/4, 1/4, 1/4) sites, a Y atom occupies the C (1/2, 1/2, 1/2) site and a Z atom occupies the D (3/4, 3/4, 3/4) site. The following discussions about Ti2ZAl (Z = Co, Fe, Mn) are based on the CuHg2Ti-type structure; in this structure, the X atoms entering sites A and B are denoted as X (1) and X (2), respectively. To our knowledge, there is no experimental lattice constant value to compare with our value. The calculated total energies versus volume are fitted to the empirical Murnaghan’s equation of state [20] to determine the ground state properties. The equilibrium lattice constants, bulk modulus and these first derivatives are listed in Table 1. The optimized lattice constants for the Ti2ZAl (Z = Co, Fe, Mn) alloys are 6.08, 6.07 and 6.16 Å which well agree with the previous first-principles calculations 6.14 Å [8], 6.00 Å [22] and 6.24 Å [23].

Fig. 1
figure 1

Crystal structure of Ti2ZAl (Z = Co, Fe, Mn) alloys a CuHg2Ti, b AlCu2Mn

Full size image
Table 1 Calculated lattice constant a (Å), bulk modulus B (GPa) and first derivative \(B\prime \) for Ti2ZAl (Z = Co, Fe, Mn)
Full size table

For Ti2ZAl (Z = Co, Fe, Mn) inverse Heusler alloys, the spin-polarized band structure and atom density of states (DOS) are presented in Figs. 2 and 3, respectively. It is clear from Fig. 2 that the majority-spin band for Ti2CoAl, Ti2FeAl and Ti2MnAl is metallic, while the minority-spin band shows a semiconducting gap around the Fermi level. This energy gap in the minority-spin band leads to 100 % spin polarization at the Fermi level. As shown in `Fig. 3, in minority-spin channel, the total density of states around the Fermi level is predominant due to the d electrons of Co, Ti(X(1)) and Ti(X(2)) transition metals. As can be seen, the presence of the majority-spin states at the Fermi level and a wide band gap in the minority-spin state confirm the HM characteristic of Ti2CoAl and Ti2FeAl alloys (Table 2). The minority-spin band gap is an important factor in HM materials, and the cause of the HM band gap is discussed in the following. The HM band gaps usually take place from three aspects [24]: (1) covalent band gap which exists in the half-Heusler with C1b structure, (2) d–d band gap that is the origin of the HM band gap in the full-Heusler alloys with AlCu2Mn structure and (3) charge transfer band gap [24, 25] which is usually seen in CrO2 and double perovskites [24, 26]. The origin of the band gap in Fe2CrSi for example has been discussed by Galanakis et al. [27], who related the band gap to the covalent hybridization between the lower d bands of the high-valent transition metal (Fe) with the higher d bands of the lower-valent transition metal (Cr). Skaftouros et al. [28] have presented interesting arguments about possible hybridizations between d orbitals of transition metals in the case of the X2YZ inverse Heusler compounds, e.g. Sc-based Heusler compounds. According to their statements, same symmetry of the X (1) and the Y atoms causes their d orbital to hybridize together, creating five bonding d (2 ×eg and 3 ×t2g) and five non-bonding (2 ×eu and 3 ×tu) states. Afterward, the five X (1)–Y bonding d states hybridize with the d orbital of the X (2) atoms and create bonding and anti-bonding states again [29].

Fig. 2
figure 2

The spin-polarized band structure of Ti2ZAl (Z = Co, Fe, Mn) in CuHg2Ti-type structures

Full size image
Fig. 3
figure 3

DOS of Ti2ZAl (Z = Co, Fe, Mn) in CuHg2Ti-type structures

Full size image
Table 2 The calculated HM band gap of Ti2ZAl (Z = Co, Fe, Mn)
Full size table

Slater and Pauling had shown in two pioneering papers that in the case of binary magnetic alloys, when we add one valence electron in the compound, this occupies spin-down states only and the total spin magnetic moment decreases by about 1 µ B [32, 33]. Interestingly, a similar behaviour can be also found in half-metallic Heusler alloys. It was shown that in the case of the semi-Heusler compounds like NiMnSb, the total spin magnetic in the unit cell, M t scales, as a function of the total number of valence electrons, Z t, follows the relation M t=Z t- 18 [34] while in the case of the L21 full Heusler, this relation becomes M t=Z t- 24. [35]. These Slater–Pauling (SP) rules connect the electronic properties (appearance of the half-metallic behaviour) directly to the magnetic properties (total spin magnetic moments) and thus offer a powerful tool to the study of half-metallic Heusler compounds. Recent research reveals that many Ti2-based full-Heusler alloys with the CuHg2Ti-type structure can also belong to the family of half-metallic material, and the total magnetic moments of these alloys follow the M t=Z t- 18 rule instead of the M t=Z t- 24 rule [8, 36]. The Ti2CoAl alloy has 20 valence electrons per unit cell (Z t= 20); thus, the spin magnetic moment is 20 - 18 = 2 µ B for each unit cell, while the atomic magnetic moments are 1.14 µ B for Ti (1), 0.65137 µ B for Ti (2), -0.29248 µ B for Co, 0.00109 µ B for Al and 0.49423 µ B for the interstitial region. It can be clearly seen from Table 3 that the calculated magnetic moments are in excellent agreement with other theoretical values [23]. Hence, the formation of the band gap in the inverse Heusler alloy Ti2CoAl is determined by two mechanisms of covalent hybridization and d–d orbital hybridization between transition metals, but the d–d hybridization plays a dominant role [37, 38]. The total magnetic moment M tot of the Ti2MnAl alloy is integer 0 µ B and is followed by the Slater–Pauling rule M tot=Z tot- 18. The atomic magnetic moments of Ti1, Ti2, Mn and Al atoms are -1.08091, -0.97271, 2.60640 and -0.01920 µ B, respectively. The different local magnetic moments for two Ti atoms in the Ti2MnAl alloy with the CuHg2Ti-type structure are resulted from the different atomic environments, i.e. the Ti1 atom has four nearest Ti2 atoms and four nearest Al atoms as well as six next-nearest Mn atoms, while the Ti2 atom has four nearest Ti1 atoms and four nearest Mn atoms as well as six next-nearest Al atoms [31].

Table 3 The total and partial magnetic moments of Ti2ZAl (Z = Co, Fe, Mn)
Full size table

Ti2FeAl has a total magnetic moment of 1 µ B. As listed in Table 3, the local magnetic moments of Ti1, Ti2 and Fe are 0.86238, 0.56666 and -0.83923 µ B, respectively, although the magnetic moment of the Al atom is small (0.00531) and can be neglectable. It is clear that the alloy has half metallicity because it has an integral total magnetic moment, M tot, which agrees with the Slater–Pauling rule.

4 Conclusion

We investigate the electronic structure and magnetism of Heusler alloys Ti2ZAl (Z = Co, Fe, Mn) using the ab initio density functional theory calculations for alloys with the CuHg2Ti-type structure. The Ti2ZAl (Z = Co, Fe, Mn) alloys are found to be half-metallic ferromagnets. The total magnetic moments of Ti2ZAl (Z = Co, Fe, Mn) are 2, 1 and 0 µ B, respectively, which is in agreement with the Slater–Pauling rule.