Introduction

Crime mapping is a valuable tool: knowing where crime is more frequent leads not only to a more effective and efficient deployment of police forces and other public policies, it can also lead to more accurate models and theories through which the underlying causes can be examined and better understood (Santos 2016; Chainey and Ratcliffe 2013; Wang 2012). The question of where crime takes place, however, implies a definition of “where?” Should crimes be counted and analyzed per police district, or should we use neighborhoods, census tracts, street blocks, or some other unit? Does it really matter? Current scientific consensus is that it does, with issues such as the Modifiable Areal Unit Problem (MAUP, see Openshaw 1979; O’Sullivan and Unwin 2014: 30) and the Ecological Fallacy (O’Sullivan and Unwin 2014: 30) being common examples.

Within this context, there is currently a movement within criminology towards analyzing crime at finer spatial granularities (e.g. street segments, street blocks) as opposed to coarser units such as neighborhoods and census tracts (Gerrel 2017; Groff et al. 2009; Oberwittler and Wikström 2009; Weisburd 2015; Weisburd et al. 2012; Weisburd et al. 2012). There have been two key reasons for this new approach. One stems from theoretical considerations on how routine patterns (Cohen and Felson 1979) and other forms of social dynamics (Weisburd et al. 2014) can be related to micro-geographical units such as single street segments (Weisburd et al. 2012). We will not focus on this aspect for now, but will return to it in the Discussion section later in the article. The second key reason is based on the empirical observation that crime is usually extremely concentrated in only a small percentage of those units, and that aggregating to coarser units would mask this clustering of crime at specific micro-places (Weisburd et al. 2009). The research by Sherman et al. (1989) is considered to have sparked the interest in analyzing crime at the micro-unit level. The authors pointed out that “just over half (50.4%) of all calls to the police for which cars were dispatched went to a mere 3.3% of all addresses and intersections” a pattern known as Zipf’s law or the Pareto distribution (Newman 2005). This phenomenon has also been observed in a range of other social and physical phenomena, such as volunteered geographic information and social media data. Another key driver of the movement towards analyzing crime at the street segment level is the work of Weisburd et al. (2004), and (2012). Their thorough analysis of spatial–temporal crime patterns in Seattle provided solid evidence for the presence of clustering at the street segment level in that city. Their observations have been reproduced by other researchers (Groff et al. 2009; Braga et al. 2011; Curman et al. 2015), culminating with Weisburd (2015) arguing for a law of crime concentration in which “for a defined measure of crime at a specific micro-geographic unit, the concentration of crime will fall within a narrow bandwidth of percentages for a defined cumulative proportion of crime.” While not explicitly specified in the law, this micro-geographic unit has commonly been assumed to be at the scale of street segments (Weisburd et al. 2012). Alternatively, but in a similar line, some authors have proposed that spatial analysis of crime should be conducted at the finest geographical unit available (Oberwittler and Wikström 2009; Gerrel 2017). Empirical evidence of the effectiveness of this paradigm (often known as hot spot policing) for crime prevention has been found (Sherman and Weisburd 1995; Taylor 1998), indicating not only that police presence at the right place and time can reduce crime, but that these places and times correspond to only a small proportion of the total environment, allowing for a more efficient use of resources.

Our present study raises some issues that go against some of these commonly held principles of criminology of place such as “finer is better” (Oberwittler and Wikström 2009; Bernasco 2010; Gerrel 2017), pointing towards a more nuanced approach as to how these micro-geographic locations are defined and the implications for crime prevention. On a theoretical side, we argue that, although finer units reduce the risk of the Ecological Fallacy, the marginal benefit of finer and finer granularities decreases after a certain point, while the robustness of crime counts gets progressively worse. Furthermore, on the empirical side, after analyzing crime patterns in the city of Belo Horizonte, Brazil, we found evidence that contradicts the claim that crime necessarily has a distinctive concentration at the street segment granularity. We argue that a more careful analysis should be conducted with any crime dataset being used before deciding on a specific spatial unit of analysis, and a methodology is proposed to find a granularity that provides a balance between internal uniformity and robustness to error. In addition, we discuss the implications of our study to policing and policy making, as well as to criminological theory such as the law of crime concentration proposed by Weisburd (2015).

This paper is organized as follows. In the Background section, previous work related to the problem of determining an appropriate geographical unit of analysis is discussed, with a focus on the spatial analysis of crime. Metrics for estimating internal uniformity and robustness to error are described in the Methodology section, as well as the criteria for finding a balance between the two. The Data section describes the dataset used for testing the methodology, and the Study Area describes the city of Belo Horizonte, Brazil, from which the data originated. The results of the application of the methodology over the chosen dataset are shown in the Results, and in the Discussion section, practical and theoretical implications are discussed.

Background

The Importance of Granularity

Granularity stands for the level of detail in a dataset (i.e. resolutionFootnote 1), and in a geographical context, to the particular size and shape of the units used for mapping and analysis (Kuhn 2012; Stell and Worboys 1998). Issues involving granularity are a staple in geography and related disciplines. A prime example, the Modifiable Areal Unit Problem (MAUP) refers to models and inferences yielding different results when changing the granularity used to sample a study region (Openshaw 1979; O’Sullivan and Unwin 2014: 30). If the geographical units are arbitrarily chosen, this effect can be problematic, since the results may be partially dependent on the units.

Another difficulty is known as the Ecological Fallacy. If inferences about individuals are to be made based on group characteristics, then a poorly specified granularity can lead to this fallacy, when aggregate indicators do not faithfully represent individual characteristics within the group. Additionally, correlations observed among variables at the aggregated level might not hold at finer granularities (Robinson 1950 is credited for first studying these effects; see also O’Sullivan and Unwin 2014: 32 for relevance in spatial analysis). For instance, if crime incidence is calculated for a whole neighborhood when certain locations have much more crime than others, the aggregated crime incidence will be a poor reflection of actual safety within different parts of the neighborhood (Weisburd et al. 2012). As can be seen, these granularity problems are related to the uniformity of attributes within areal units (and the absence of it), a concept explored in the following subsection.

Uniformity and Regionalization

From a spatial perspective, uniformity (or homogeneity) refers to measurable properties, objects or events (e.g. crimes) being equally distributed across a given area, without any significant clusters. For point sets and processes, then, uniformity is manifested as complete spatial randomness (O’Sullivan and Unwin 2014). In geography, uniformity has been closely related to the concept of region, with Bunge (1966) defining a uniform region as an areal unit identifiable by one or more characteristics that are equally present within the whole area, but not its neighbors. Therefore, a good regionalization map defines regional boundaries so as to minimize variability within each region while maximizing variability between regions; a poor regionalization, on the other hand, would lead to the problems of the Ecological Fallacy. In crime studies and policing, these matters can have very practical consequences, since regionalization maps are sometimes used to define public crime prevention policies (Castro et al. 2004).

Multiple regionalization methods have been proposed, as in Openshaw (1977), Assunção et al. (2006), Duque et al. (2012), as well as more general clustering techniques such as k-means (MacQueen 1967). While these methods may differ, they all build up their regions by aggregating finer areal units into coarser units, according to the contiguity of the finer units and the similarity of their attributes. Therefore, these methods assume: (1) a set of micro-areal units is available; and (2) their attributes are reliable. These assumptions do not hold when aggregating point distributions: even if these points are first aggregated into fine areal units, the estimated counts may lack robustness if these units are too fine, potentially interfering with the regionalization algorithm. The concept of robustness to error is elaborated in the following subsection.

The Importance of Robustness to Error

Robustness to error refers to the relation between error and measurement in a dataset; the smaller the relative amount of error in comparison to the measured quantity, the greater the robustness of the dataset.Footnote 2 While less discussed in the methodology of regionalization, robustness to error has been recognized as an important feature in geographic analysis (Xiao et al. 2007; Zhang and Goodchild 2002), and is an important consideration when choosing a bandwidth in kernel density estimation (KDE).

In KDE (Silverman 1986), a wider bandwidth will lead to smoother density maps, filtering out potential noise but possibly hiding finer interesting details; on the other hand, a shorter range will not hide small variations, but will be more susceptible to random fluctuations. Also, from a probabilistic perspective, if the point density generated by KDE is to be interpreted as an estimate of the underlying probability field for the point distribution, then a smaller bandwidth means a smaller sample, and a greater uncertainty for the estimate.

Choosing the best bandwidth has, therefore, often been approached as striking a good balance between detail and robustness to error. Silverman’s rule of thumbFootnote 3 (Silverman 1986: 43) can be mentioned as one of the most commonly used approaches, minimizing error in cases where the data is normally distributed in space. For crime patterns, however, this assumption is at best simplistic, if not altogether implausible. Nevertheless, the principle that increasing the range leads to greater robustness to error is a valuable one,Footnote 4 suggesting that while there are good reasons to use finer granularities (i.e. improving internal uniformity), there are also valid reasons for adopting a broader one, indicating that multiple factors should be considered for deciding on a particular granularity, including uniformity, robustness and other practical considerations.

Issues of Granularity, Uniformity and Robustness in Spatial Criminology

Interest in studying crime from a geographical perspective has existed for more than a century (Guerry 1833; Quetelet 1842), but it is only fairly recently that granularity, uniformity and robustness started to attract the attention of crime researchers (Weisburd et al. 2009). The effects of granularity over observed crime patterns was studied as early as 1976 by Brantingham et al. (1976); in addition, an interest in analyzing crime at micro-geographic units was sparked by the work of Sherman et al. (1989), who observed that only 3% of all addresses accounted for half of the police calls. However, it is from the year 2000 onwards that a more systematic approach has been taken to data granularity in crime analysis, particularly in the advantages of analyzing crime with micro-geographic units such as street-segments versus other traditional units such as neighborhoods or census units.

The main drivers of this effort can be found in Weisburd et al. (2004), as well as Eck and Weisburd (1995) and Weisburd et al. (2012) and Weisburd (2015). In both Weisburd et al. (2004) and (2012), the authors examined the distribution of crimes per street segment in Seattle from 1989 through 2002, observing a significant concentration on a few segments which persisted through time. Based on this evidence, and other studies that presented similar observations (Groff et al. 2009; Braga et al. 2011; Curman et al. 2015), Weisburd (2015) proposed the existence of a law of crime concentration, stating that “for a defined measure of crime at a specific micro-geographic unit, the concentration of crime will fall within a narrow bandwidth of percentages for a defined cumulative proportion of crime.” While not explicitly stated in this formulation, this bandwidth has usually been identified as having the dimension of street segments; even when alternative definitions are used for a micro-geographic unit. In practice, the unit used is a street segment or a street block (as seen in Oberwittler and Wikström 2009; Gerrel 2017).

Therefore, granularity (and uniformity, albeit less explicitly) have been recognized as key concepts in the geography of crime. Aggregating to coarse units would lead to non-uniform regions, masking internal clusters within each area. One of the practical implications of this insight is on police allocation, in that a great proportion of crime can be tackled by allocation of resources to a few specific locations (a strategy known as hot spot policing). Therefore, looking at crime at micro-locations may have the virtue of not only reducing the complexity of the crime problem but also potentially reducing costs.

In contrast, robustness to error has not been given as much attention in spatial studies of crime. In studies such as Weisburd et al. (2012), a high robustness of spatial patterns was inferred based on their temporal stability and to the large volume of crime data points used. However, not every study may have large enough datasets to automatically guarantee that crime counts taken at very fine granularities will be robust. So far, few studies have attempted to measure robustness of crime counts at different granularities, and its interplay with uniformity in determining an adequate unit of analysis. In particular, we are not aware of a study that has explicitly measured robustness and uniformity at various different granularities in order to determine an adequate unit of analysis.

Oberwittler and Wikström (2009) analyzed the tradeoff between robustness and internal uniformity is the regression study. Their conclusion is that smaller areas are better: not only they are more internally homogeneous but they also allow for more sample units to be used, leading to higher statistical power for regressions. However, their definition of robustness differs from ours, ours being the robustness of crime counts, theirs the robustness of the regression itself. Moreover, only two granularities were tested, and it is worth considering whether “smaller is better” would still be the conclusion had a wider range of granularities been studied. The issue of error in fine units was also brought up by Gerell (2017), mentioning the trade-off between error and uniformity. This tradeoff, however, was not used in the study’s comparison between granularities. Instead, the criterion used was solely the degree of Intra Class Correlation (a metric of internal uniformity). Finally, the study by Malleson et al. (2019) raises similar arguments to this study in favor of a balance between fine and coarse, presenting a multiscale study to determine an adequate unit of analysis. However, their methodology for finding such a balance has significant differences to ours, with their study considering the behavior of a similarity index (see Andresen 2009) at different granularities (see also Andresen and Malleson 2011 for a study testing the influence of scale when comparing different point patterns).

While robustness to error has not been given so much attention compared to uniformity and granularity, it can also have practical implications for policing and policy making. If police forces are intended to concentrate at these crime hot spots, a greater uncertainty associated with these hot spots means a greater proportion of police being potentially misallocated. Thus, for efficient allocation of resources, a compromise between uniformity and robustness must be sought out, along with any other practical considerations. It is the objective of our research to advance the understating of how to attain such balance.

Methodology

To estimate an appropriate micro-unit of analysis for counting and mapping crime, metrics for internal uniformity and robustness to error were calculated for a set of different granularities, and from that a granularity that offers the best balance between the two was determined.

Estimating Internal Uniformity

Internal uniformity is estimated through a series of spatial randomness tests. Given a granularity g, a set of n quadrats of that granularity Sg = {s1g s2g…sng} is generated over the domain of crime points P being tested, and then for each quadrat sig, a spatial randomness test is performed for the points located inside it. The proportion of samples in Sg that fail to reject the complete spatial randomness (CSR) hypothesis at significance \(\alpha\) is attributed as the internal uniformity level ug of the point set P at granularity g. This process is repeated for a range of different granularities. Figures 1 and 2 illustrate this process.

Fig. 1
figure 1

The proportion of samples that failed to reject the CSR hypothesis is assigned as the internal uniformity at granularity g

Full size image
Fig. 2
figure 2

Internal Uniformity is calculated for a range of different granularities

Full size image

To generate the samples, two approaches are proposed: (1) a set of r quadrats of the same granularity (size) is randomly selected inside the bounding rectangle that delimits the point set P, or (2) the bounding rectangle is divided into a set of contiguous quadrats of the same granularity. Figure 3 illustrates these two different approaches. In both cases, any cells with only one point or zero are ignored.

Fig. 3
figure 3

Two approaches for collecting samples to be tested for spatial randomness

Full size image

For assessing spatial randomness, two approaches are considered: (1) Clark-Evans nearest-neighbor distance test (Clark and Evans 1954; O’Sullivan and Unwin 2014, pp 143–145; see Maggi et al. 2017 for an application), and (2) a quadrat count test (Greig-Smith 1952; O’Sullivan and Unwin 2014, pp 142–143; see Maggi et al. 2017 for an application). In the Clark-Evans test, the mean distance between any point in the dataset to its nearest neighbor is calculated: if it significantly differs from what would be obtained by a random Poisson point process, then the null hypothesis of complete spatial randomness can be rejected. In the quadrat count approach, the point pattern is divided in equal bins (quadrats) and the number in each is counted: if that number significantly differs from that expected by a random Poisson point process, then then the null hypothesis of complete spatial randomness can be rejected. While these two tests have their own limitations (O’Sullivan and Unwin 2014, pp 142–145; Clark et al. 2018; Perry et al. 2006), with Clark-Evans being ill-suited for detecting patterns beyond the nearest neighbor scale and the quadrat count test being dependent on the specific quadrat dimensions considered, these are methods of low computational cost—an important feature considering that the test must be repeated multiple times for a given granularity (and then repeated for the multiple granularities being tested). Furthermore, the two tests work well as complements of each other: a quadrat count test is often capable of capturing longer distance patterns that Clark-Evans would be ill-suited to detect, while the quadrat test’s incapability at detecting patterns finer than its quadrats is remedied by Clark-Evan’s performance at closer distances. Therefore, although more sophisticated tests of complete spatial randomness exist and can be used—e.g. using Ripley’s K (Ripley 1977; O’Sullivan and Unwin 2014, pp 146–148) or Monte Carlo simulation approaches (Baddeley et al. 2014; O’Sullivan and Unwin 2014, pp 148–152), see also Clark et al. (2018) for a comparison between methods—we consider that these two tests of low computational cost are complimentary and adequate to perform the check for the purposes of this study.Footnote 5

Estimating Robustness to Error

Robustness of the measured crime counts is evaluated in relation to the expected proportional variation of crime incidence (i.e. the estimated coefficient of variation of the observed crime incidence). For example, a crime rate of 100 crimes per year with a coefficient of variation of 5% is a more stable measure than a rate of 100 crimes per year with a 20% coefficient of variation. As such, in Eq. 1, we define a metric rg for robustness to error at granularity g as a function of the average coefficient of variation of n sample quadrats of granularity g

$$r_{g} = { \exp }\left( { - k \times \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} coef\_var\left( {s_{ig} } \right)} \right)$$
(1)

The exponential transformation is applied to assure that \(r_{g}\) will vary between (0, 1), being comparable to the uniformity metric. For the choiceFootnote 6 of \(k\), we suggest \(k = 3\) since at that value a coefficient of variation of 1 will yield a robustness close to zero (0.05), while a coefficient of variation of 0 will yield a maximum robustness of 1.

To estimate the coefficient of variation for the observed crime distributions, three different methods were compared; additionally, two different approaches for selecting the samples were employed (similar to the calculation of internal uniformity).

The first method for estimating the coefficient of variation (binominal estimation) compares the number of crimes ki within a quadrat of granularity g to the total number k of observed crimes. By assuming pi= ki/k as the likelihood of a crime occurring inside a quadrat sig, the coefficient of variation showed in Eq. 2 follows that of a binomial distribution:

$$\begin{aligned} & coef\_var\left( {s_{ig} } \right) = p_{i} \left( {1 - p_{i} } \right)\frac{1}{\sqrt k } \\ & p_{i} = \frac{{k_{i} }}{k} \\ \end{aligned}$$
(2)

The second method (Poisson estimation), assumes that the crime incidence within a quadrat follows a Poisson distribution and then proceeds to fit the observed sample to that distribution, yielding an estimated coefficient of variation:

$$\begin{aligned} & \lambda_{i} = k_{i} \\ & coef\_var(s_{ig} ) = \frac{1}{{\sqrt {k_{i} } }} \\ \end{aligned}$$
(3)

The third and last method (resampled estimation), effectively combines the first two for estimating the coefficient of variation. In the Poisson distribution, the coefficient of variation is dependent on λi. However, not only is the estimated lambda uncertain, its relation to the coefficient of variation is non-linear. Thus, to estimate the coefficient of variation while taking account the uncertainty in λi, a resampling approach was used: m samples of crime counts are simulated following a binominal distribution with probability pi= ki/k for k events, and for each sample, the coefficient of variation is estimated by fitting it to a Poisson distribution. Finally, the simulated coefficients of variation are averaged to estimate the expected value of the coefficient of variation

$$\begin{aligned} & coef\_var(s_{ig} ) = \frac{1}{m}\mathop \sum \limits_{j = 1}^{m} \frac{1}{{\sqrt {\lambda_{ij} } }} \\ & \lambda_{ij} = Binom\left( {\frac{{k_{i} }}{k},k} \right) \\ \end{aligned}$$
(4)

Balancing Uniformity and Robustness

Having estimated the internal uniformity and robustness to error, the final step is to determine a granularity that offers a compromise between each metric. This can be considered a type of Multi-Criteria Decision Analysis (MCDA) problem (Budiharjo and Muhammad 2017; Melia 2016; Kittur et al. 2015; Tofallis 2014), since there are two metrics that need to be optimized. Drawing in part from MCDA literature, three different approaches are considered here, but it is worthy to remark that other approaches could be considered and may be explored in future work.

One approach considered here is to find the granularity that maximizes the product of internal uniformity and robustness to error (Eq. 5). This approach mirrors the Weighted Product Model from MCDA (Budiharjo and Muhammad 2017; Melia 2016; Kittur et al. 2015; Tofallis 2014), and particularly penalizes cases where one of the criteria is too close to zero. Since uniformity and robustness both vary from zero to one, and are given equivalent importance, the same weight (one) is given to both metrics

$$\hbox{max} u\left( g \right)r\left( g \right)$$
(5)

A second approach is maximizing the sum of the internal uniformity with robustness to error (Eq. 6), essentially a version of Weighted Sum Model from MCDA (Budiharjo and Muhammad 2017; Melia 2016; Kittur et al. 2015; Tofallis 2014). Again, both metrics are given the same weight of one. In contrast to the previous criterion, there is less of a penalty if one of the metrics is relatively low

$$\hbox{max} \left( {u\left( g \right) + r\left( g \right)} \right)$$
(6)

Finally, a third approach considered in this study is to fit a curve for internal uniformity varying as a function of robustness to error, and then find the point where its derivative is equal to minus one (Eq. 7). At this point, the marginal gain in robustness is the same as the marginal loss in uniformity of the same magnitude, and vice versa, meaning that a deviation from that point would be more costly than beneficial for either metric. As far as we are aware, this approach has no direct equivalent in the MCDA literature, but related ideas on the importance of taking account diminishing marginal utility are discussed in Tofallis (2014)

$$\frac{{du\left( {g_{best} } \right)}}{{dr\left( {g_{best} } \right)}} = - 1$$
(7)

Each of these approaches may be suitable to different situations, and they may be used in combination to determine a granularity. However, as will be shown in the Results, they typically yield similar optimal granularities.

Data

The data used in this study is composed of three point sets representing the locations of three types of crime events reported to the police in the city of Belo Horizonte, Brazil: residential burglaries, street robberies, and homicides. For residential burglaries, there is a total of 44,560 events, spanning the period 2008 to 2014; for street robberies, there are 11,626 events, from the year 2012 to 2013; for homicides, the total amount is 1826 cases from 2012 to 2014.

These point sets were generated from boletins de ocorrência, registers created by the police in Brazil to document reported crime incidents. In the case of these particular boletins de ocorrência, they were ceded by the Polícia Militar de Minas Gerais, the branch responsible for police enforcement in the state of Minas Gerais, where the city of Belo Horizonte is located. The street addresses of the reported crimes were geocoded into latitude and longitude coordinates, with an accuracy rate of 95% following the methodology proposed by Chainey and Ratcliffe (2016), Chainey and Ratcliffe (2013).

Study Area

Belo Horizonte, is located in the southern region of Brazil, on the border of São Paulo and Rio de Janeiro states. With an estimated population of 2,523,794 people in 2017, it has a demographic density of about 7167 inhabitants per square kilometer in an area of almost 332 square kilometers. According to the 2010 Census, out of 628,447 households in Belo Horizonte, 66.58% are owner-housing units; 7.23% are in the process of being purchased; and 18.06% are rental housing units. There are 487 neighborhoods in Belo Horizonte including 215 favelas (slums), vilas (improved favelas), and other public housing spread throughout the city. Nearly half a million people live in the more than 130,000 households located in these areas.

Results

The results were obtained by applying our methodology over three datasets: residential burglaries, street robberies and homicides. The set of granularities analyzed for burglaries ranged from quadrats of 25 msFootnote 7 to 1000 meters, with 25 meter intervals (that is, quadrats of 25 meters, 50 meters, etc.); for robberies and homicides, the granularities analyzed ranged from 25 meters to 5025 meters, with intervals of 100 meters. A different set of granularities is shown for burglaries because little variation was found in the metrics beyond 1,000 meters; since a shorter range was used, we decided to also shorten the difference between each individual granularity, so that enough points are generated for the tradeoff analysis.

In short, our findings show that: first, for all three types of crime evaluated, internal uniformity increases with finer granularities, while robustness to error decreases; second, the optimal granularity is different for each type of crime considered, and third, the optimal granularities in most cases do not match those granularities traditionally used in the literature (namely, street segments, census units, and neighborhoods).

These findings for the case of burglaries in Belo Horizonte are illustrated in the next figures. In Fig. 4, the variation of internal uniformity as a function of granularity (i.e. quadrat size) is shown on the left, and the variation of robustness to error as a function of granularity is shown on the right. Notice how internal uniformity increases with smaller quadrat sizes (finer granularities), meaning that a greater proportion of sampled quadrats can be considered uniform (i.e. failed to reject complete spatial randomness), while robustness decreases as quadrats get smaller.

Fig. 4
figure 4

Internal uniformity decreases with granularity, while robustness to error increases

Full size image

In Fig. 5, the tradeoff between uniformity and robustness to error is illustrated for each of the three criteria considered (i.e. balance of gains, product, and sum criteria). On the left, uniformity is plotted as a function of robustness, with the point of balance (derivative equal to minus one) shown in blue. In the middle, the product of uniformity and robustness is shown as a function of granularity (quadrat size), as well as the maximum extracted from the fitted curve. Finally, in the right, the sum of uniformity and robustness is shown as a function of granularity, as well as the corresponding optimal granularity for this criterion. For comparison, the optimal using the balance of gains criterion is also displayed in the middle and right plots (green point).

Fig. 5
figure 5

Optimal granularity for burglary dataset estimated by three different criteria (balance of gains, product and sum criteria)

Full size image

Equivalent graphs for homicides and robberies can be seen in the Appendix; in addition, the Appendix also shows a comparison between the different variants proposed to calculate uniformity, robustness and the optimal granularity (as described in the Methodology). The general pattern of these analyses is similar to those shown here.

The results for estimating optimal granularities for each type of crime are listed in Table 1. As can be seen, the estimated optimal granularities are significantly different for each type of crime. Between the three types of crime the one with the finest optimal granularity is burglary, which is also the one with the greatest number of points; homicide is the type with the least number of points and the coarsest granularity. That was not unexpected, as a greater number of points tends to lead to more stable rates (better robustness at finer granularities).

Table 1 Summary of results for estimating the optimal granularity for each dataset considered
Full size table

For all three types of crimes, the estimated optimal granularities are coarser than the usual scale of street segments or street blocks (100 m on average for Belo Horizonte, see Freitas et al. 2013). Additionally, for two of them (burglary and robbery), the estimated optimal granularities are finer than that of neighborhoods (0.68 km2 on average for Belo Horizonte, see Prefeitura 2017).

Maps of crime incidence using the estimated optimal granularities are shown in Fig. 6. Since robbery is overly concentrated in the downtown area, a log transformation was applied to facilitate visualization, shown alongside the original. As can be seen from these maps, not only are the optimal micro-units different according to each type of crime, so too are their spatial distributions. Burglary has the finest units, at least in part due to the larger quantity of data points available; homicide, having the smallest number of data points, has the coarsest units, with robbery having an optimal unit of an intermediate size when compared to that of burglary and homicide.

Fig. 6
figure 6

Maps of crime counts per areal unit for burglary, homicide, robbery and log(robbery), using their estimated optimal granularities

Full size image

As a whole, the results obtained all indicate the same relationship between uniformity, robustness and granularity: uniformity tends to increase as granularity becomes finer, while robustness tends to decrease. However, the sensitivity of uniformity and robustness to granularity seems to vary across different types of crime, leading to different optimal granularities; furthermore, these estimated optimal granularities do not necessarily match traditionally used units like neighborhoods, census units or street segments. In light of that, we find that choosing a granularity without considering the specifics of the dataset can lead not only to an absence of internal uniformity, such as in the Ecological Fallacy, but also to problems of robustness in the measured crime incidences. Finally, the proportion of units concentrating 50% of crimes when using the estimated optimal granularity also varies according to the dataset examined, which seems to contradict some formulations of the law of crime concentration (this is discussed in more detail in the following section).

Discussion

Choosing a Granularity: Conciliating Multiple Perspectives

One of the goals of this study is to highlight the importance of balancing uniformity and robustness when choosing a granularity. Therefore, our study indicates that “finer is not necessarily better”, in particular for smaller datasets, as shown in Table 1 (notice that uncertainties in geocoding may be an additional reason to use broader units, see Andresen et al. 2020). We do not mean to claim that robustness and uniformity are the only important criteria for choosing a granularity and there are often theoretical and operational reasons for selecting a particular unit. Nevertheless, we believe that these theoretical and operational criteria are also not absolute, and should not justify ignoring spatial considerations.

To illustrate our point, consider the choice of street segments as the preferred granularity. As mentioned in the Introduction, that choice has not solely been based on the observed concentration of crimes, but from an understanding that street segments constitute fundamental units that influence and shape the routine of both potential victims, offenders and guardians (the fundamental triangle of Routine Activities Theories, as in Cohen and Felson 1979). For instance, people within a segment share a visual and physical space and are more likely to know each other, increasing opportunities for interaction; in addition, their movements are shaped by the layout of street segments (Taylor 1998). However, one could also list factors of potential significance that manifest at a different granularity. Neighborhood characteristics encompass a swath of street segments; routine patterns are not solely a function of specific segments, but of a broader activity space (Brantingham and Brantingham 1993); facilities like subway stations, schools and malls often project their influence much further than their own segment (Frank et al. 2011; Groff and Lockwood 2014). Moreover, theories derived from one context (e.g. Western developed countries) might not apply to others. This is particularly important in this case study since clustering patterns of repeat and near-repeat for residential burglaries have been observed to be significantly less intense in the city of Belo Horizonte when compared to cities in the US and the UK (Chainey and Silva 2016). Finally, operational considerations such as police beats matching street segments should also not be considered an absolute criterion, since police organization is not uniform across countries or even regional units, and they can be reorganized (e.g. see Blattman et al. 2017).

As such, our conclusion is that it would be imprudent to decide on a granularity based solely on a specific set of theoretical principles (sometimes subject to their own uncertainties), disregarding the evidence from the spatial data at hand or even other theoretical factors. In light of these considerations, we view this study as offering an additional spatial frame of reference against which theoretical and operational factors can be evaluated and compared, leading to a more grounded choice for a granularity.

Implications to the Law of Crime Concentrations

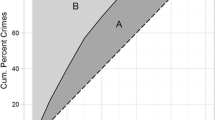
In its most general form, the law of crime concentration states that at a certain micro-geographic unit, a relatively large proportion of crime will be concentrated in a small proportion of units. However, if these proportions are not specified, this statement can in principle be applied not only to crime distributions, but also to random point patterns (see Hipp and Kim 2017; Bernasco and Steenbeek 2017; Mohler et al. 2019). In practice, most studies consider that these proportions are such that 50% of crimes concentrate in less than 10% (typically 5%) of the units (Chainey et al. 2019; Braga et al. 2017; Gill et al. 2017). If that version is considered, then the distribution of crimes observed in our study (using the estimated optimal granularity) is less concentrated than predicted by that law (see Table 1). While higher concentrations could be attained if finer units were used, this would mostly be due to the geometrical properties of aggregating discrete data to areal units, since in our case an average of 90% of the optimal units are already internally uniform, not hiding any finer clusters (as much as the data can tell). These distortions of having too many areal units compared to points is also examined by Bernasco and Steenbeek (2017) and Mohler et al. (2019), albeit with a different methodology (using a Gini-style Lorenz curve to adjust the rates).

Just as there is a diversity of theoretical reasons that justify the use of different granularities, there are multiple reasons that could explain some crime distributions being less concentrated than others: while some types of crime tend to occur close to specific facilities, in other cases the influence small scale places can be manifested at wider areas (Brantingham and Brantingham 1995; Frank et al. 2011, Eck and Weisburd 2015); target selection may manifest in patches (Johnson 2014; Bernasco 2009); and rates of repeat and near-repeat may vary with crime type and region (Chainey & Silva). Although we cannot disregard the fact that the number of points available can also affect the optimal granularity estimated with our method, thus artificially affecting the perceived concentration; nevertheless, in our study, burglary had the lowest spatial concentration of all three types of crime considered, despite having the greatest number of points, suggesting a lower spatial concentration of the underlying phenomena. Moreover, it is worth noting that, at least with our method, a finer granularity does not necessarily mean a greater concentration, as shown in Table 1.

Does our study indicate that the law of criminology should be reformulated? Not by itself, since that would require repeating similar studies in other regions, and it is not in the scope of this article to do so. Although there is a growing body of literature that tends to conform to the current formulation of the law of crime concentration (Gill et al. 2017; Carter et al. 2019; Umar et al. 2020; Chainey et al. 2019), it is unclear how their findings would relate to the issues of uniformity and robustness raised by our study. We hope to examine these questions in future work.

Implications for Policing and Policy Making

Crime maps are useful for efficient allocation of police patrols and other resources (Sherman 1997; Braga 2001; Wang 2012; Chainey and Ratcliffe 2013). This usefulness, however, is dependent on the reliability of the crime frequencies being depicted. There are many aspects influencing this reliability, including underreporting and uncertainties in geocoding of crime events (Chainey and Ratcliffe 2013). Here, we discuss how our methodology for finding an adequate granularity in terms of uniformity and robustness can improve crime map reliability and resource allocation.

Table 2 indicates what would be the expected crime concentrations, uniformities and robustness for our burglary dataset if counted at three different granularities: the estimated optimal, an oversized granularity, and an undersized granularity. We can see that fewer units would need to be covered in order to account for 50% of the burglaries if the optimal granularity (278.25 m) were used instead of the oversized one (1650 m), which could mean more police resources available per targeted unit. Moreover, the uniformity in the oversized granularity is only 0.074, which means that most of the units contain finer clusters that cannot be represented at that granularity, while for the optimal granularity the uniformity is 0.90.

Table 2 Expected crime concentrations, uniformities and robustness when varying the granularity used (for residential burglaries)
Full size table

Why then not use the undersized granularity (100 m), in which 50% of all burglaries are concentrated in only 15% of locations and the uniformity is 1? While that is the case, the estimated robustness value for the undersized granularity is 0.11, indicating that on average the crime rates are expected to have a coefficient of variation of 73% in relation to their estimated value, while for the optimal granularity, this coefficient of variation would be 39% (i.e. robustness equal to 0.31), meaning that the optimal granularity produces more stable rates while still revealing the majority of the crime clusters.

One practical implication for policing is that more stable crime maps decrease the chance that resources will be misallocated to a false hot spot of crime. One of the advantages of looking at crime in micro-units is the more efficient allocation of police and other resources; however, if these rates are unstable, that would impact the efficiency of this allocation. For instance, if police forces are to be allocated in proportion to crime distributions (as in directed patrolling and other forms of hot spot policing, see Braga 2001; Sherman 1997; Wang 2012), a robustness of 0.15 (corresponding to an average coefficient of variation of 0.63) would mean that approximately 63% of the police forces will be misallocated on average. In addition, the production of more reliable maps of crime in general should be useful for Evidence-Based crime prevention programs (Sherman et al. 2002; Wang 2012), both for planning new prevention strategies as well as for evaluating results.

Naturally, this all depends on the specific strategies chosen for policing and crime prevention, which may involve factors that transcend those considered here (e.g. legal and administrative requirements, socio-cultural considerations, political factors). However, should these strategies depend on spatial aspects of crime (as in hot spot policing strategies), crime maps need to be reliable, and these issues of robustness must then be considered. Even if the areal units to be used are predefined by external criteria, the proposed methodology can be used to estimate the robustness to error and the internal uniformity for this predefined granularity, and how much it differs from the optimal, provided that point data for each individual crime event is available.

Moreover, even though hot spot targeting has been shown to be an efficient strategy for policing, its economic viability can still be an issue depending on the quantity of hot spots to be covered and the resources available. For instance, budgetary reasons may force individual patrol units to cover areas broader than the traditional micro-units (e.g. individual street segments or blocks), the other option being some of the hot spots are left uncovered. Although this may be problematic if these areas are large, heterogeneous, and difficult to be effectively covered by a single patrol unit (for instance, the traditional police quadrants referred to in Blattman et al. 2017), areas comprising small groups of blocks or segments may not only feature a uniform crime distribution but may be coverable by individual patrols with significant results (see the study from Chainey et al. 2020). This type of compromise provides an additional reason why finer may not always be better in crime mapping (see Gibson et al. 2017 for a similar idea in the temporal domain). This becomes specifically significant in regions such as Latin America, which not only lack a tradition in data driven approaches (often leading to issues of data limitations and robustness), but also tend to feature both high crime rates and budget constraints (Bergman 2018; Beato et al. 2008).

Lastly, more reliable crime maps can improve the general public’s perception of the nature of crime and its geography,Footnote 8 helping in a better mutual understanding between the police (and other public authorities) and the population. As shown by Alkimim et al. (2013), perceptions of crime and violence by the general public do not necessarily match the actual distribution of crime events, which could lead to misguided impressions by the public on how the police and other public authorities may or may not be doing their work.

Limitations and Future Improvements

One limitation of the proposed methodology is that granularity is required to be the same throughout the whole study area. While this facilitates data manipulation, it may pose problems for point distributions with a sufficiently high degree of clustering. In areas where a cluster is present, the point density is higher, which would not only allow for a finer granularity (i.e. more points, more robustness), but would also probably require a finer granularity to ensure internal uniformity. However, outside of clusters broader granularities would be required. Unsurprisingly, one possible solution for this is to allow granularities to vary across the study area; the problem then becomes one of finding a polygon mesh that provides adequate levels of robustness and uniformity for all its polygons. This approach will be investigated in future work.

Also, an issue of using uniform grids is that these units are abstract, not equivalent to real-world entities such as street segments, neighborhoods, etc., and that environmental data is often available only at these real units. However, while grids may not be equivalent to real-world units, they could be considered adequate approximations in some cases. It is out of the scope of this study to test the quality of such approximations; however, it is worth mentioning that our methodology could be used to calculate robustness and uniformity for these real units (e.g. street blocks, neighborhoods), which can then be compared against each other and against different abstract grids. In addition, resampling schemes may be used to convert data from one set of units to another. While this is an imperfect solution, it is often the case that different environmental indicators are given at different granularities, and the question is then what variable should be given priority in deciding the granularity. For most crime studies, we would argue that crime data should be given priority.

An additional limitation of using square cells (but also of using most areal units, such as census tracts) is that they assume crime events can happen anywhere inside the cell, which is not usually the case. Instead, crime locations will normally follow the shape of streets and roads (pointing to a potential benefit of using street segments). This may create some distortions in the uniformity tests and may also overestimate the concentration of crime, since areas that cannot possibly have any crime might be accounted for in the calculations. This may then indirectly impact evaluations of the law of crime concentration. However, it is worth noting that the observed concentrations in our study were already lower than the ratio predicted by that law; if it is being overestimated, then the real concentration is even lower. It is outside the scope of this paper to evaluate these distortions, but we consider that they probably affect more at the finer granularities, and it is unclear if that would affect the shape of the tradeoff curve and the choice of granularity.

Another limitation in our methodology is that it calculates crime rates at a place by counting how many points are found within each unit of analysis; as such, abrupt variations in crime rates are to be observed across boundaries. A common solution to this type of problem is to use kernel density estimation to generate a smooth field. However, it is not entirely clear how our estimated optimal granularity can be applied to a kernel density approach. On a preliminary assessment, it seems likely that the estimated granularity should influence the bandwidth of the kernel; however, how exactly it should be influenced and whether it should determine the pixel size and the kernel function shape is something yet to be investigated.

There is also a limitation in the specific methods selected for testing complete spatial randomness, as well as the specific methods for balancing uniformity and robustness. The methods employed for testing spatial randomness are two out of many existing in the literature; moreover, different tests have different limitations, encouraging the use and comparison of different tests. The specific tests were selected due to their low computational cost; however, future work should explore the effects of adopting different types of tests. Similarly, the approaches adopted for finding a balance between uniformity and robustness are not necessarily exhaustive, with other methods possibly existing. Nevertheless, it is important to remark that while each of the approaches considered had significant differences from a methodological point of view, they all yielded similar results, giving support to the main conclusion that an adequate granularity is neither the finest nor the coarsest.

Finally, our methodology makes few assumptions about the underlying phenomena, which may or may not be a limitation depending on the context. For instance, our methodology is particularly useful when data is limited and there is a lack of quantitative criminological knowledge about the study area. However, if we do have reasonable assumptions about the crime phenomena, other methodologies could in principle use this additional information to improve the robustness of the estimated crime rates, allowing finer granularities. Examples of these techniques include Empirical Bayes smoothing (Anselin et al. 2004; Filho et al. 2001; Santos et al. 2005) or Markov Chain Monte Carlo (Liu and Zhu 2017; Zhu et al. 2006). The cost, however, is introducing a bias in the case where the assumed prior information does not fit the phenomena being investigated or is unreliable for other reasons. This points to an additional tradeoff dimension of bias versus robustness (often referred to as bias versus variability). It is not the focus of this paper to explore this issue, but we recognize it as an additional important consideration to be made.