Symplectic Hamiltonian Finite Element Methods for Semilinear Wave Propagation

Abstract

This paper presents Hamiltonian finite element methods for approximating semilinear wave propagation problems, including the nonlinear Klein–Gordon and sine-Gordon equations. The aim is to obtain accurate high-order approximations while conserving physical quantities of interest such as energy. To achieve conservation properties at a discrete level, we propose semidiscrete schemes based on two Hamiltonian structures of the equation. These include Mixed finite element methods, discontinuous Galerkin methods, and hybridizable discontinuous Galerkin methods (HDG). In particular, we propose a new class of DG methods using time operators to define the numerical traces, ultimately leading to an energy-conserving scheme. Time discretization uses Symplectic explicit-partitioned and diagonally-implicit Runge–Kutta schemes. Furthermore, the paper showcases several numerical examples that demonstrate the accuracy and energy conservation properties of the approximations, along with the simulation of soliton cloning.

1 Introduction

In this paper, we present several finite element methods for approximating a second-order semilinear wave propagation problem. These include Mixed finite element methods (M), discontinuous Galerkin methods (DG), hybridizable discontinuous Galerkin methods (HDG), and a straightforward example using standard continuous Galerkin methods. Our main objective is to obtain accurate high-order approximations while conserving physical quantities of interest such as energy. In order to describe our results, let us introduce the model second-order semilinear wave equation on a polyhedral and bounded domain $\Omega \subset {\mathbb {R}}^{d}$, with Lipschitz boundary $\Gamma$

$$\begin{aligned} \rho (\varvec{x})\, \ddot{u}(\varvec{x}, t) -\nabla \cdot (\kappa (\varvec{x})\nabla \, u(\varvec{x}, t)) + g(u(\varvec{x},t)) = f(\varvec{x}, t),\quad \varvec{x}\in \Omega ,\,t\in (0,T], \end{aligned}$$

(1a)

where $\kappa =\kappa (\varvec{x})$ is a symmetric and positive definite matrix-valued function, $\rho =\rho (\varvec{x})$ and $f = f(\varvec{x}, t)$ are scalar-valued functions, and g is a real-valued nonlinear functional with notable examples $g(u) = u-u^3$, (cubic Klein–Gordon equation) and $g(u) = \sin (u)$ (sine-Gordon equation) The problem is subject to initial conditions

$$\begin{aligned} u(\varvec{x},0) = u_0(\varvec{x}), \, \dot{u}(\varvec{x},0)&= v_0(\varvec{x}),{} & {} \quad \varvec{x}\in \Omega , \end{aligned}$$

(1b)

and periodic boundary conditions are assumed for the sake of the presentation; however, the methods and their analysis can be adapted to Dirichlet and Neumann boundary conditions.

Perhaps the most notable examples of the semilinear wave model (1) are the sine-Gordon and the nonlinear Klein–Gordon equations. The sine-Gordon equation has many applications in modern physics, such as in sound propagation in crystal lattices, laser and particle physics, and superconductivity, among others. See [4, 12] for more details about the applications. In particular, in superconductivity, the sine-Gordon equation appears in the dynamics of magnetic flux in the Josephson junction where the kinks or antikinks, solitons of the sine-Gordon equations, represent a quantum of magnetic flux (also known as fluxon or Josephson vortex), quantity of interest in several experiments. In Gulevich and Kusmartsev [16] the authors describe an experiment related to the birth of a single Josephson vortex in the Josephson transmission line at a T-shaped junction. In Sect. 6, we replicate the experiment obtaining similar results. The nonlinear Klein–Gordon equation also finds applications in physics, in the fields of general relativity and quantum physics see [15, 20]. In both cases, the soliton interaction has been intensively studied [12].

Finite element methods have been extensively used in linear wave propagation problems, with mixed and discontinuous Galerkin (DG) methods showing advantages over continuous finite element methods. The mixed, first-order velocity-stress [(velocity for the time derivative of the displacement/primal-variable and stress for the flux in (1)] formulation has been widely considered for discretization, mixed methods [13], DG methods [6], symmetric interior penalty methods [14], local DG methods [30], HDG methods [10], HHO methods [5], among others. For the two-dimensional sine-Gordon equation, the first local DG scheme was introduced in [3] and is based on the velocity-stress formulation. This reference also provides a complete list of numerical methods for approximating the sine-Gordon equation, including finite differences and finite element methods. The LDG method in [2, 3] uses alternating fluxes, and it is also energy-conserving. Our analysis in Sect. 4.2 includes this method. Our contribution in this paper builds upon the recently introduced Hamiltonian finite element methods [21] (see also the review article [8]), which combine finite element methods for space discretization with symplectic methods for time discretization. Finite element methods discretize the Hamiltonian system of partial differential equations in a way that results in a system of ODEs that is also Hamiltonian. As a result, when the system is discretized by a symplectic method, the conservation or non-drifting properties of the time integrators apply, making it suitable for long-term simulations. This approach has been used for linear scalar wave [21], elastodynamics [22], and electromagnetism [7, 27], see also the review article [8]. Thus, in this paper, we focus on devising finite element methods for the model problem (1) which preserve the Hamiltonian structure of the system. To do this, we consider two Hamiltonian forms of the equations, namely, the displacement–velocity and displacement–velocity–stress formulation. Note that, in contrast to the linear case, the displacement variable can not be eliminated. In particular, we propose a new class of energy-conserving and Hamiltonian structure-preserving DG schemes for the second formulation. These new methods follow the ideas in [7], introducing time operators in the numerical traces. See Table 1 for a summary of the methods discussed in the paper.

Table 1 HDG and DG methods for the discretization of (1a)

The paper is structured as follows. Section 2 introduces the concept of a Hamiltonian system and the two Hamiltonian formulations of the second-order semilinear wave propagation model problem (1), namely the displacement–velocity and the displacement–velocity–stress formulations. Section 3 proposes several finite element methods for each formulation. Section 4 presents results corresponding to the Hamiltonian form of the method, specifically in Sect. 4.1 the corresponding to the displacement–velocity formulation and in Sect. 4.2 the results for the scheme based on the displacement–velocity–stress formulation. Section 5 discusses the time discretization using symplectic explicit partitioned and diagonally implicit Runge–Kutta schemes of the semidiscrete HDG schemes based on displacement–velocity variables. We present three numerical experiments in Sect. 6, showcasing the optimal convergence and superconvergence of the approximations and the energy-conserving properties of the HDG scheme, including an example of the soliton cloning in a Josephson junction. In addition, we include numerical results regarding the new DG schemes, showcasing their energy-preserving properties. Finally, Sect. 7 provides the conclusions of this work.

2 Hamiltonian Form of the Semilinear Wave Equation

This section presents two Hamiltonian forms of the model problem (1). We will proceed to write the second-order semilinear wave equations as a first-order system of equations. This will result in two equivalent formulations at the continuous level, leading to two different Hamiltonian forms upon which we base the derivation of the numerical schemes in Sect. 3. For this purpose, we begin recalling the definition of a Hamiltonian system of partial differential equations, see [8, 19].

Definition 2.1

A Hamiltonian system of partial differential equations is defined on a phase-space ${\mathcal {M}}$ of smooth functions with suitable boundary conditions in terms of a Hamiltonian functional $\mathcal H:{\mathcal {M}}\rightarrow {\mathbb {R}}$ and a Poisson bracket $\{\cdot , \cdot \}$ by the system of equations

$$\begin{aligned} \dot{u} = \{ u, {\mathcal {H}}\}(u){.} \end{aligned}$$

The Poisson bracket mentioned in the definition above is a general bilinear and skew-adjoint operator acting on a pair of functionals on ${\mathcal {M}}$, and it satisfies the so-called Jacobi identity

$$\begin{aligned} \{{\mathcal {F}}, \{{\mathcal {G}}, {\mathcal {H}}\}\} + \{{\mathcal {G}},\{\mathcal H,{\mathcal {F}}\}\} + \{{\mathcal {H}},\{{\mathcal {F}},{\mathcal {G}}\}\} = 0, \end{aligned}$$

for ${\mathcal {F}}, {\mathcal {G}}, {\mathcal {H}}$ functionals mapping from ${\mathcal {M}}$ to ${\mathbb {R}}$. Poisson brackets are naturally defined through structure skew-adjoint operators $\hbox {J}$ in the following manner,

$$\begin{aligned} \{{\mathcal {F}}, {\mathcal {G}}\} = \int _{\Omega } \delta {\mathcal {F}} \,\text {J}\, \delta {\mathcal {G}}. \end{aligned}$$

Note that, as a consequence of the Poisson bracket’s properties, an autonomous Hamiltonian system will conserve the Hamiltonian (often referred to as the energy) over time.

2.1 Two Hamiltonian Forms of the Wave Equation

Now we can delve into the Hamiltonian forms of the wave Eq. (1). For the sake of presentation, we assume periodic boundary conditions. To derive the first formulation, we transform the second-order model problem into a first-order system by introducing the velocity variable $v=\dot{u}$, obtaining the system

$$\begin{aligned} \rho \,\dot{u}&= \rho \, v,{} & {} \quad \text{ in } \Omega \times (0,T], \end{aligned}$$

(2a)

$$\begin{aligned} \rho \,\dot{v}&= f + \nabla \cdot \, (\kappa \nabla u) - g(u) ,{} & {} \quad \text{ in } \Omega \times (0,T], \end{aligned}$$

(2b)

the Hamiltonian functional $\mathcal {H}=\mathcal {H}[u,v]$ associated with these equations, which is also the energy of the system, is given by

$$\begin{aligned} {\mathcal {H}}[u,v] = \int _{\Omega }\left( \frac{1}{2}\rho v^{2} + \frac{1}{2} \kappa |\nabla u|^{2} + G(u) { -} f u \right) {,} \end{aligned}$$

where the function G is such that $G'(u) = g(u)$, and the corresponding Poisson bracket to the formulation is given, for functionals ${\mathcal {F}} = {\mathcal {F}}[u,v]$ and ${\mathcal {G}}=\mathcal G[u,v]$, by

$$\begin{aligned} \{ {\mathcal {F}}, {\mathcal {G}}\} = \int _{\Omega } \rho ^{-1} \left( \frac{\delta {\mathcal {F}}}{\delta u}\frac{\delta {\mathcal {G}}}{\delta v} - \frac{\delta {\mathcal {F}}}{\delta v}\frac{\delta {\mathcal {G}}}{\delta u} \right) = \int _{\Omega }\delta {\mathcal {F}} \, \text {J} \,\delta {\mathcal {G}}, \end{aligned}$$

where $\text {J}$ is the (canonical) skew-adjoint operator defined by

$$\begin{aligned} \text {J} = \rho ^{-1}\begin{pmatrix} 0 &{} \hbox {Id}\\ Id &{} 0\end{pmatrix}, \end{aligned}$$

and $\hbox {Id}$ denotes the identity operator. A straightforward computation of the variations of the Hamiltonian functional and applying the definition of the Hamiltonian system lead to the first-order system above.

A second Hamiltonian formulation can be derived by introducing the vector-valued (or simply the gradient) variable $\varvec{q} = -\kappa \nabla u$, and adding the equation for its time derivative $\dot{\varvec{q}} = - \kappa \nabla v$ to the dynamics. In the linear case ($g(u) = 0$), this formulation results in a dynamical system that only involves the velocity v and the vector-valued $\varvec{q}$ variables, with the displacement variable u being removed from the equations. However, due to the presence of the nonlinear term g(u) in our model semilinear wave Eq. (1) this is no longer possible. Hence the system including the vector-valued function $\varvec{q}$ will read as follows

$$\begin{aligned} \rho \,\dot{u}&= \rho \, v,{} & {} \quad \text{ in } \Omega \times (0,T], \\ \rho \,\dot{v}&= f + \nabla \cdot \, \varvec{q}- g(u) ,{} & {} \quad \text{ in } \Omega \times (0,T], \\ \kappa ^{-1}\dot{\varvec{q}}&= - \nabla v,{} & {} \quad \text{ in } \Omega \times (0,T]. \end{aligned}$$

Note that in this formulation an element of the phase space ${\mathcal {M}}$ consists of three functions ($u,v,\varvec{q}$), unlike the first formulation where elements of the phase space consist of two functions. The Hamiltonian functional for this formulation also corresponds to the energy and so we need to rewrite it in terms of the three variables $(u,v,\varvec{q})$, i.e.,

$$\begin{aligned} {\mathcal {H}}[u,v, \varvec{q}] = \int _{\Omega }\left( \frac{1}{2}\rho v^{2} + \frac{1}{2} \kappa ^{-1}| \varvec{q}|^{2} + G(u) {-} f u \right) . \end{aligned}$$

The corresponding Poisson bracket now is an operator applying to a pair functionals ${\mathcal {F}} = {\mathcal {F}}[u,v,\varvec{q}]$ and $\mathcal G = {\mathcal {G}}[u,v,\varvec{q}]$, and given by

$$\begin{aligned} \{{\mathcal {F}}, {\mathcal {G}}\} = \int _{\Omega } \rho ^{-1}\left( \frac{\delta {\mathcal {F}}}{\delta u} \frac{\delta {\mathcal {G}}}{\delta v} - \frac{\delta {\mathcal {F}}}{\delta v}\frac{\delta \mathcal G}{\delta u} + \nabla \cdot \kappa \frac{\delta {\mathcal {F}}}{\delta \varvec{q}} \frac{\delta {\mathcal {G}}}{\delta v} - \frac{\delta \mathcal F}{\delta v} \nabla \cdot \kappa \frac{\delta {\mathcal {G}}}{\delta \varvec{q}} \right) = \int _{\Omega } \delta {\mathcal {F}} \,\text {J} \,\delta {\mathcal {G}}{,} \end{aligned}$$

where $\text {J}$ is the skew-adjoint operator defined by

$$\begin{aligned} \text {J} = \rho ^{-1}\begin{pmatrix} 0 &{} \hbox {Id}&{} 0\\ -\hbox {Id}&{} 0 &{} -\nabla \cdot \kappa \\ 0 &{} \nabla \cdot \kappa &{} 0 \end{pmatrix}{.} \end{aligned}$$

2.2 Conservation Laws

We end this section presenting some invariants of the model problem (1). These and other invariants are derived in [25, 29] in a more general context. Here we write them in terms of the three variables of our system $u,v,\varvec{q}$. Table 2 presents four physical quantities of interest, their respective symbol, and their definition. Numerical experiments in Sect. 6 show the behavior over time of their discrete approximations.

Table 2 Conserved quantities for semilinear wave system (when ${f=0}$ and periodic boundary conditions)

3 Semidiscrete Methods

In this section, we introduce several finite element discretizations of the model semilinear wave equation based on the Hamiltonian formulations discussed in the previous section. It turns clear that conforming methods, such as continuous Galerkin and Mixed methods, naturally inherit the Hamiltonian property of the equations, i.e., the corresponding semidiscrete schemes can be interpreted as a generalized Hamiltonian system (or a Poisson system according to [8]). On the other hand, non-conforming methods such as discontinuous Galerkin and hybridizable discontinuous Galerkin methods, need an appropriate definition of the numerical traces, a discrete Hamiltonian, or a discrete Poisson bracket in order to be cast as a generalized Hamiltonian system.

3.1 Notation

Let $\mathcal {T}_h= \{K\}$ be a family of conforming triangulations of the domain $\Omega$ using polyhedral elements K and let $\mathcal {F}_{h}$ be the set of all faces F of the elements $K\in \mathcal {T}_h$. Here the parameter h denotes the mesh size of the triangulation, that is, the maximum inner diameter of the triangulation elements. For a domain $X\subset {\mathbb {R}}^{d}$ we define the volumetric $L^2$ inner product for scalar and vector-valued functions by

$$\begin{aligned} (v, w)_{X} = \int _{X} v \,w\, d\varvec{x},\qquad (\varvec{r}, \varvec{q})_{X} = \int _{X} \varvec{r} \cdot \varvec{q}\, d\varvec{x}, \end{aligned}$$

for $(v, w)\in L^{2}(X)$ and $(\varvec{r}, \varvec{q})\in L^{2}(X)^{d}$. We extend these definitions for a subdomain $Y\subset {\mathbb {R}}^{d-1}$ and denote by $\langle \cdot , \cdot \rangle _{Y}$. For discontinuous Galerkin methods, we define the $L^2$ inner products over the triangulation and the subsets of the set of faces for scalar-valued functions v, w by

$$\begin{aligned} \left( v, w\right) _{\mathcal {T}_h} = \sum _{K\in \mathcal {T}_h} \left( v, w\right) _{K},\quad \left\langle v, w\right\rangle _{\partial \mathcal {T}_{h}} = \sum _{K\in \mathcal {T}_h} \left\langle v, w\right\rangle _{\partial K}, \quad \langle v, \,w\rangle _{Y} = \sum _{F\in Y} \left\langle v, w\right\rangle _{F}, \end{aligned}$$

where Y can denote the set of faces of an element of the triangulation, and the set of all faces, $\partial K, \mathcal {F}_{h}$, respectively. A similar notation is also employed for vector-valued functions.

Standard definitions of jumps and averages of discontinuous Galerkin functions are introduced as follows. For an interior face $F\in \mathcal {F}_{h}^{0}$, such that $F = \partial K^{+}\cap \partial K^{-}$ we define average and normal jumps of scalar and vector-valued functions w and $\varvec{r}$, respectively, by

$$\begin{aligned} \{\!\!\{w\}\!\!\} = \frac{1}{2} (w^{+} + w^{-}),&\quad \llbracket w\rrbracket = w^{+}\varvec{n}^{+} + w^{-}\varvec{n}^{-}{,} \\ \{\!\!\{\varvec{r}\}\!\!\} = \frac{1}{2}(\varvec{r}^{+} + \varvec{r}^{-}),&\quad \llbracket \varvec{r}\rrbracket = \varvec{r}^{+}\cdot \varvec{n}^{+} + \varvec{r}^{-}\cdot \varvec{n}^{-}{,} \end{aligned}$$

where $w^{\pm }$ denotes the trace on F of a function w defined on $K^{\pm }$.

Continuous, mixed, discontinuous, and trace finite element spaces are defined next

$$\begin{aligned} X_h&= \{ w\in H^{1}(\Omega ): w_{K} \in {\mathcal {P}}_{k}(K), \, \forall K\in \mathcal {T}_h\}{,} \\ \varvec{V}_h^{\textrm{M} }&= \{ \varvec{r}\in H({\text {div}}, \Omega ): \varvec{r}|_{K}\in \varvec{V}(K),\ \forall K\in \mathcal {T}_h\}{,}\\ \varvec{V}_h^{\textrm{DG}}&= \{ \varvec{r}\in \left[ L^{2}(\Omega )\right] ^{d}: \varvec{r}|_{K}\in \varvec{V}(K),\ \forall K\in \mathcal {T}_h\}{,} \\ W_h&= \{ w\in L^{2}(\Omega ): w|_{K}\in W(K),\ \forall K\in \mathcal {T}_h\}{,} \\ M_h&= \{ \mu \in L^{2}(\mathcal {F}_{h}): \mu |_{F}\in M(F),\ \forall F\in \mathcal {F}_{h}\}{,} \end{aligned}$$

where ${\mathcal {P}}_{k}$ denotes the space of polynomial of degree k and $\varvec{V}(K),\,W(K), M(F)$ are local polynomial spaces.

We conclude this subsection by stating a well-established property used in DG methods linking the product over $\partial \mathcal {T}_h$ and $\mathcal {F}_{h}$.

Lemma 3.1

Let $w\in W_h$ and $\varvec{r}\in \varvec{V}_h^{\textrm{DG}}$. Then, assuming periodic boundary conditions, we have that

$$\begin{aligned} \left\langle \varvec{r}\cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}} = \left\langle \{\!\!\{\varvec{r} \}\!\!\}, \llbracket w\rrbracket \right\rangle _{\mathcal {F}_{h}} + \left\langle \llbracket \varvec{r}\rrbracket , \{\!\!\{w\}\!\!\}\right\rangle _{\mathcal {F}_{h}}. \end{aligned}$$

3.2 Semi-discrete Methods for the Displacement u and Velocity v Formulation

We shall now proceed to derive the numerical methods based on the formulation (2) for the displacement u and velocity v variables. Let us examine a straightforward example - the $H^1$ conforming discretization of the first order formulation (2) using the piecewise continuous polynomial finite element space $X_h$. We need to find $u_h$ and $v_h$ in $X_h$ such that

$$\begin{aligned} \left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h}&= \left( \rho v_{h}, w\right) _{\mathcal {T}_h},{} & {} \quad \forall w\in X_{h}{,} \\ \left( \rho \,\dot{v}_{h}, w\right) _{\mathcal {T}_h}&= \left( \kappa \nabla u_{h}, \nabla w\right) _{\mathcal {T}_h} -\left( g(u_{h}), w\right) _{\mathcal {T}_h} + \left( f, w\right) _{\mathcal {T}_h},{} & {} \quad \forall w\in X_{h}. \end{aligned}$$

The Hamiltonian nature of the scheme was demonstrated in [8] for the linear case, i.e. $g(u_h) = 0$. The extension to the semilinear case follows a similar approach.

We now explore Mixed formulations of the semilinear wave equations. This involves the addition of a vector-valued stress variable $\varvec{q} = -\kappa \nabla u$ to the system, which can be treated as a steady-state variable or a dynamic variable, that is with or without any time derivative applied to $\varvec{q}$. Thus the first mixed method can be concisely summarized as follows: Find the solution $(u_{h}, v_{h}, \varvec{q}_{h})\in W_{h}\times W_{h} \times \varvec{V}_{h}^{\textrm{M}}$ that satisfies:

$$\begin{aligned} \left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h}&= \left( \rho \,v_h, w\right) _{\mathcal {T}_h} ,{} & {} \quad \forall w\in W_{h}, \end{aligned}$$

(3a)

$$\begin{aligned} \left( \rho \,\dot{v}_h, w\right) _{\mathcal {T}_h}&=-\left( \nabla \cdot \, \varvec{q}_h, w\right) _{\mathcal {T}_h} - \left( g(u_h), w \right) _{\mathcal {T}_h}+ \left( f, w\right) _{\mathcal {T}_h},{} & {} \quad \forall w\in W_h, \end{aligned}$$

(3b)

and where $\varvec{q}_h \in \varvec{V}_h^{\textrm{M}}$ solves for each time t the system

$$\begin{aligned} \left( \kappa ^{-1}\,\varvec{q}_h, \varvec{r}\right) _{\mathcal {T}_h} -\left( u_h, \nabla \cdot \,\varvec{r}\right) _{\mathcal {T}_h}&= -\langle u_{D}, \varvec{r}\cdot \varvec{n}\rangle _{\Gamma },{} & {} \quad \forall \varvec{r}\in \varvec{V}_h^{\textrm{M}}{.} \end{aligned}$$

(3c)

To define the discontinuous Galerkin and hybridizable discontinuous Galerkin methods based on the mixed formulation, we introduce the numerical traces $\widehat{u}_{h}$ and $\widehat{\varvec{q}}_{h}$, approximations of the displacement u and the stress $\varvec{q}$. Their definition specifies a particular choice of DG or HDG method. The general DG formulation is then obtained by relaxing the normal continuity of the vector-valued function and introducing the numerical traces instead: Find $(u_{h}, v_{h}, \varvec{q}_{h})\in W_{h}\times W_{h} \times \varvec{V}_{h}^{\textrm{DG}}$ solution of:

$$\begin{aligned} \left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h}&= \left( \rho \,v_h, w\right) _{\mathcal {T}_h} ,{} & {} \quad \forall w\in W_{h}, \end{aligned}$$

(4a)

$$\begin{aligned} \left( \rho \,\dot{v}_h, w\right) _{\mathcal {T}_h}&=\left( \varvec{q}_h, \nabla w\right) _{\mathcal {T}_h} - \left\langle \widehat{\varvec{q}}_h\cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}} - \left( g(u_h), w \right) _{\mathcal {T}_h}+ \left( f, w\right) _{\mathcal {T}_h},{} & {} \quad \forall w\in W_h, \end{aligned}$$

(4b)

and where $\varvec{q}_h \in \varvec{V}_h^{\textrm{DG}}$ solves for each time t the system

$$\begin{aligned} \left( \kappa ^{-1}\,\varvec{q}_h, \varvec{r}\right) _{\mathcal {T}_h} -\left( u_h, \nabla \cdot \,\varvec{r}\right) _{\mathcal {T}_h}+\left\langle \widehat{u}_h, \varvec{r} \cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}&= 0,{} & {} \quad \forall \varvec{r}\in \varvec{V}_h^{\textrm{DG}}{.} \end{aligned}$$

(4c)

When using HDG methods, a trace approximation space $M_h$ is used, and a new variable, the scalar numerical trace $\widehat{u}_h\in M_h$, is introduced. The vector-valued numerical trace is then defined using a stabilization operator $\tau >0$ and the following definition,

$$\begin{aligned} \widehat{\varvec{q}}_{h} \cdot \varvec{n} = \varvec{q}_{h} \cdot \varvec{n} + \tau (u_{h} - \widehat{u}_{h}), \quad \text {on } \partial \mathcal {T}_h. \end{aligned}$$

The system is completed by weakly enforcing the continuity of the normal component of $\widehat{\varvec{q}}_h$

$$\begin{aligned} \left\langle \widehat{\varvec{q}}_h\cdot \varvec{n}, \mu \right\rangle _{\partial \mathcal {T}_{h}} = 0, \quad \forall \mu \in M_{h}. \end{aligned}$$

On the other hand, discontinuous Galerkin methods use jumps and averages of the approximations of $u_h$ and ${\varvec{q}_h}$ to define numerical traces explicitly,

$$\begin{aligned} \widehat{\varvec{q}}_h = \{\!\!\{\varvec{q}_h\}\!\!\} +C_{11}\llbracket u_h\rrbracket - \varvec{C}_{12}\llbracket \varvec{q}_h\rrbracket , \quad \widehat{u}_h:= \{\!\!\{u_h\}\!\!\} + \varvec{C}_{12} \llbracket u_h\rrbracket + C_{22}\llbracket \varvec{q}_h\rrbracket {,} \end{aligned}$$

on each face $F\in \mathcal {F}_{h}$. Here we assumed periodic boundary conditions.

3.3 Semi-discrete Methods for the Displacement u, Velocity v and Stress $\varvec{q}$ Formulation

We will now discretize the time-dependent formulation for the three variables in the mixed equations. Through a straightforward derivation, we arrive at the mixed method: Find the solution $(u_h, v_h, \varvec{q}_h)\in W_h\times W_h\times \varvec{V}_h^{\textrm{M}}$ that satisfies the equations

$$\begin{aligned} \left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h}&= \left( \rho \,v_h, w\right) _{\mathcal {T}_h}{,}{} & {} \quad \forall w\in W_{h}{,} \end{aligned}$$

(5a)

$$\begin{aligned} \left( \rho \,\dot{v}_h, w\right) _{\mathcal {T}_h}&= - \left( \nabla \cdot \, \varvec{q}_h, w\right) _{\mathcal {T}_h} - \left( g(u_h), w \right) _{\mathcal {T}_h} +\left( f, w\right) _{\mathcal {T}_h},{} & {} \quad \forall w\in W_h, \end{aligned}$$

(5b)

$$\begin{aligned} \left( \kappa ^{-1}\,\dot{\varvec{q}}_h, \varvec{r}\right) _{\mathcal {T}_h}&=\left( v_h, \nabla \cdot \,\varvec{r}\right) _{\mathcal {T}_h} ,{} & {} \quad \forall \varvec{r}\in \varvec{V}_h^\textrm{M}. \end{aligned}$$

(5c)

Note that, in the linear scalar wave equation, the displacement approximation $u_h$ can be eliminated from the system. This results in evolution equations for the velocity $v_h$ and stress $\varvec{q}_h$ variables, which was studied in [18].

Analogously, DG and HDG formulations can be derived by defining suitable numerical traces. The general DG method for the three variables reads as follows: Find $(u_h, v_h, \varvec{q}_h)\in W_h\times W_h\times \varvec{V}_h^{\textrm{DG}}$ satisfying that

$$\begin{aligned} \left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h}&= \left( \rho \,v_h, w\right) _{\mathcal {T}_h} ,{} & {} \quad \forall w\in W_h, \end{aligned}$$

(6a)

$$\begin{aligned} \left( \rho \,\dot{v}_h, w\right) _{\mathcal {T}_h}&= \left( \varvec{q}_h, \nabla \, w\right) _{\mathcal {T}_h} - \left\langle \widehat{\varvec{q}}_h\cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}} - \left( g(u_h), w \right) _{\mathcal {T}_h} +\left( f, w\right) _{\mathcal {T}_h},{} & {} \quad \forall w\in W_h, \end{aligned}$$

(6b)

$$\begin{aligned} \left( \kappa ^{-1}\,\dot{\varvec{q}}_h, \varvec{r} \right) _{\mathcal {T}_h}&= \left( v_h, \nabla \cdot \,\varvec{r}\right) _{\mathcal {T}_h} -\left\langle \widehat{v}_h, \varvec{r}\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}},{} & {} \quad \forall \varvec{r}\in \varvec{V}_h^\mathrm{{DG}}. \end{aligned}$$

(6c)

Similarly to the Mixed method, the displacement approximation $u_h$ can be removed from the equations in the linear case, obtaining a numerical scheme for the velocity $v_h$ and the stress $\varvec{q}_h$. Hence, it is natural to introduce as a new variable to the system the numerical trace approximation of the velocity $\widehat{v}_h\in M_{h}$ for HDG methods and set $\widehat{\varvec{q}}_h$ in terms of the normal traces of $\varvec{q}_h$ and stabilization of the jumps of the velocity, i.e.,

$$\begin{aligned} \left\langle \widehat{\varvec{q}}_h\cdot \varvec{n}, \mu \right\rangle _{\partial \mathcal {T}_{h}} = 0, \quad \text {where}\quad \widehat{\varvec{q}}_h \cdot \varvec{n} = \varvec{q}_h \cdot \varvec{n} + \tau (v_{h} - \widehat{v}_h), \quad \text {on }\partial \mathcal {T}_h, \end{aligned}$$

(7)

for all $\mu \in M_h$. This formulation was the first HDG method for the linear wave equation, and its error analysis is given in [11], where they proved optimal error estimates. As it is observed in [8, 21], this method dissipates energy, and therefore it can not be written in Hamiltonian form. In Theorem 4.2, we assert that the method is not Hamiltonian in the semilinear scenario and then confirm that utilizing stabilization for the trace of the vector-valued function $\varvec{q}_h$ in terms of the jumps of the velocity leads to a dissipative method.

For DG methods the standard definition of the numerical traces $\widehat{\varvec{q}}_h$ and $\widehat{v}_h$, under periodic boundary conditions, is given by

$$\begin{aligned} \widehat{\varvec{q}}_h = \{\!\!\{\varvec{q}_h\}\!\!\} + C_{11}\llbracket v_h\rrbracket - \varvec{C}_{12}\llbracket \varvec{q}_h\rrbracket , \quad \widehat{v}_h = \{\!\!\{v_h\}\!\!\} + \varvec{C}_{12}\llbracket v_h\rrbracket + C_{22} \llbracket \varvec{q}_h\rrbracket {.} \end{aligned}$$

(8)

Unlike the HDG method, DG methods can be Hamiltonian and non-dissipative when using numerical traces for the velocity and the stress. This is proven in Theorem 4.2 ii. An example of such a scheme is the DG method with centered fluxes.

In Chung and Engquist [7] a new class of DG methods that utilize time operators to define the numerical traces were introduced for solving the time-dependent Maxwell equations. We aim to incorporate these ideas to obtain new DG methods for the semilinear wave equation, which possess the energy-conserving property and demonstrate that they are Hamiltonian. Specifically, we introduce novel stabilization functions to define the numerical trace of the vector-valued function ${\widehat{\varvec{q}}_h}$ in terms of the displacement approximation $u_h$ instead of the velocity. Thus, in the case of the DG method, we define the numerical traces $\widehat{v}_h$ and $\widehat{\varvec{q}}_{h}$ appearing in (6) as follows:

$$\begin{aligned} \widehat{\varvec{q}}_h = \{\!\!\{\varvec{q}_h\}\!\!\} + D_{11}\llbracket u_h\rrbracket - \varvec{C}_{12}\llbracket \varvec{q}_h\rrbracket , \quad \widehat{v}_h:= \{\!\!\{v_h\}\!\!\} + \varvec{C}_{12} \llbracket v_h\rrbracket + D_{22}\llbracket \dot{\varvec{q}}_h\rrbracket {.} \end{aligned}$$

(9)

After introducing these definitions into the DG formulation and rearranging the time derivatives on the left-hand side, the following equations are obtained,

$$\begin{aligned}&\left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h} = \left( \rho \,v_h, w\right) _{\mathcal {T}_h} , \end{aligned}$$

(10a)

$$\begin{aligned}&\left( \rho \,\dot{v}_h, w\right) _{\mathcal {T}_h} = \left( \varvec{q}_h, \nabla \, w\right) _{\mathcal {T}_h} - \left( g(u_h), w \right) _{\mathcal {T}_h} +\left( f, w\right) _{\mathcal {T}_h} \end{aligned}$$

(10b)

$$\begin{aligned}&\qquad \qquad \qquad \qquad - \left\langle (\{\!\!\{\varvec{q}_h\}\!\!\} - \varvec{C}_{12}\llbracket \varvec{q}_h\rrbracket )\cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}}- \left\langle D_{11}\llbracket u_h\rrbracket \cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}}, \nonumber \\&\left( \kappa ^{-1}\,\dot{\varvec{q}}_h, \varvec{r} \right) _{\mathcal {T}_h} +D_{22}\left\langle \llbracket \dot{\varvec{q}}_h\rrbracket , \varvec{r}\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}} = \left( v_h, \nabla \cdot \,\varvec{r}\right) _{\mathcal {T}_h} - \left\langle \{\!\!\{v_h\}\!\!\} + \varvec{C}_{12}\llbracket v_h\rrbracket , \varvec{r}\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}, \end{aligned}$$

(10c)

for all $w\in W_h$ and $\varvec{r}\in \varvec{V}_h^{\textrm{DG}}$. The energy-conserving property and the Hamiltonian form of this new DG scheme are presented in Theorems 4.3 and 4.4 in Sect. 4.

Remark 1

In [26] and [28], researchers have previously introduced the use of time operators in the definitions of numerical traces for Discontinuous Galerkin methods. These techniques have been applied to address one-dimensional wave propagation problems within the context of multi-symplectic schemes. As demonstrated in [26], the DG scheme outlined in Eq. (4) adheres to the multi-symplectic structure in one-dimensional scenarios.

3.4 The Initial Conditions

To initialize the semidiscrete methods, we use the initial data $u(t=0) =u_0$ and $v(t=0)=v_0$. For methods written in mixed form, a corresponding discretized version, depending on the method, of the equation ${\varvec{q} = -\kappa \nabla u}$ is used to initialize $\varvec{q}_h$ (and $\widehat{u}_h$ in the case of the HDG methods). This type of initial condition has been used, for instance, in mixed methods for linear elastodynamics by Douglas et al.  [1] and in HDG methods by Cockburn et al. [9], Sanchez et al. [21] for the linear wave equation. In particular, in [21] a short study examines the convergence properties of the method given different types of initial conditions, demonstrating that optimal convergence of the error is achieved under the initial condition described above.

Assuming periodic boundary conditions, the HDG method is initialized by setting $u_h^{0}\in W_h$, $\varvec{q}_h^{0}\in \varvec{V}_h^{\textrm{DG}}$, $\widehat{u}_h^{0}\in M_h$, $\lambda \in \mathbb {R}$ approximations of the displacement, stress, trace of the displacement and the average of the displacement over the domain, at time $t=0$ by solving the following system:

$$\begin{aligned} \left( \kappa ^{-1}\varvec{q}_h^{0}, \varvec{r} \right) _{\mathcal {T}_h} - \left( u_h^{0}, \nabla \cdot \varvec{r} \right) _{\mathcal {T}_h} + \left\langle \widehat{u}_h^{0}, \varvec{r}\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}&= 0 {,} \end{aligned}$$

(11a)

$$\begin{aligned} -\left( \varvec{q}_h^{0}, \nabla w\right) _{\mathcal {T}_h} + \left\langle \widehat{\varvec{q}}_h^{0}\cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}} + \left( \lambda , w\right) _{\mathcal {T}_h}&= \left( -\Delta u_0, w\right) _{\mathcal {T}_h}{,}\end{aligned}$$

(11b)

$$\begin{aligned} \left\langle \widehat{\varvec{q}}_h^{0}\cdot \varvec{n}, \mu \right\rangle _{\partial \mathcal {T}_{h}}&= 0{,}\end{aligned}$$

(11c)

$$\begin{aligned} \left( u_h^{0}, \nu \right) _{\mathcal {T}_h}&= \left( u_0, \nu \right) _{\mathcal {T}_h}{,} \end{aligned}$$

(11d)

for all $(w, {\varvec{r}}, \mu , \nu )\in W_h\times {\varvec{V}_h^{\textrm{DG}}}\times M_h\times \mathbb {R}$. The initial values of the velocity $v_h$ are obtained using the $L^2$ projection onto the finite-dimensional space $W_h$ of the initial data $v_0$, i.e., $v_h^{0} = \Pi v_0$.

4 Hamiltonian Finite Element Methods

The goal of this section is to demonstrate that the numerical schemes presented in Sect. 3 are formulated in Hamiltonian form. As a consequence, the energy of the scheme is conserved in time, and the semidiscrete methods are numerically stable. The analysis assumes periodic boundary conditions, but the findings apply to other boundary conditions with data that do not change over time.

4.1 Analysis of the Mixed, DG, and HDG Methods for Displacement–Velocity Formulation

Let us consider the mixed method (3), and the DG and HDG methods defined in (4), with time evolution for the ${u_h} - {v_h}$ variables and a steady-state equation for ${\varvec{q}_h}$. The following theorem explicitly shows the Hamiltonian form of these equations.

Theorem 4.1

Let $\mathcal {H}_h^{\star }$ be the Hamiltonian functional, for $\star =\mathrm M, \textrm{DG}, \textrm{HDG}$, corresponding to each method, defined by

$$\begin{aligned} \mathcal {H}_h^{\star }[u_h, v_h] = \frac{1}{2}\left( \rho \, v_h, v_h\right) _{\mathcal {T}_h} + \frac{1}{2}\left( \kappa ^{-1}\,\varvec{q}_h, \varvec{q}_h\right) _{\mathcal {T}_h} + \left( G(u_h), 1\right) _{\mathcal {T}_h} - \left( u_h, f\right) _{\mathcal {T}_h} + S_h^{\star }{,} \end{aligned}$$

where $S_{h}^{\star }$ is a stabilization term given by $S_{h}^{\textrm{M}} = 0$ and

$$\begin{aligned} S_{h}^{\star } = {\frac{1}{2}}\left\langle {(\widehat{\varvec{q}}_h - \varvec{q}_h)\cdot \varvec{n}}, {u_h - \widehat{u}_h}\right\rangle _{\partial \mathcal {T}_{h}}, \quad \text {for } \star =\hbox {DG}, \hbox {HDG}{,} \end{aligned}$$

where we use the respective definitions of the numerical traces for mixed, DG, HDG methods. Define the Poisson bracket for functionals ${\mathcal {F}}, {\mathcal {G}}$

$$\begin{aligned} \{ {\mathcal {F}}, {\mathcal {G}}\} = \left( \rho ^{-1} \frac{\delta {\mathcal {F}}}{\delta u_h} , \frac{\delta {\mathcal {G}}}{\delta v_h}\right) _{\mathcal {T}_h} - \left( \rho ^{-1}\frac{\delta {\mathcal {F}}}{\delta v_h}, \frac{\delta {\mathcal {G}}}{\delta u_h} \right) _{\mathcal {T}_h}. \end{aligned}$$

Then, $\mathcal {H}_h^{\star }$, $\{\cdot , \cdot \}$ and the corresponding finite element spaces are Hamiltonian systems, for $\star =\mathrm M, \textrm{DG}, \textrm{HDG}$.

Proof

We start by defining the coordinate functionals associated with each dynamical variable

$$\begin{aligned} {\mathcal {F}}_{u_{h}} = \left( \rho \,u_{h}, w\right) _{\mathcal {T}_h}, \quad \mathcal F_{v_{h}} = \left( \rho \, v_{h}, w\right) _{\mathcal {T}_h}, \end{aligned}$$

for $w\in W_h$. A simple calculation gives us the variations

$$\begin{aligned} \rho ^{-1}\frac{\delta {\mathcal {F}}_{u_h}}{\delta u_h} = w,\quad \rho ^{-1}\frac{\delta {\mathcal {F}}_{u_h}}{\delta v_h} = 0,\quad \rho ^{-1}\frac{\delta {\mathcal {F}}_{v_h}}{\delta u_h} = 0,\quad \rho ^{-1}\frac{\delta {\mathcal {F}}_{v_h}}{\delta v_h} = w. \end{aligned}$$

To prove the Hamiltonian form of systems (3) and (4) with respect to the discrete Hamiltonian $\mathcal {H}^{\star }$, for $\star =\mathrm M, \mathrm DG, \mathrm HDG$ and the Poisson bracket $\{\cdot ,\cdot \}$, we need to verify the following equations

$$\begin{aligned} \left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h}&= \dot{{\mathcal {F}}}_{u_{h}} = \{ {\mathcal {F}}_{u_h}, \mathcal {H}_h^{\star }\} = \left( \rho \, v_{h}, w\right) _{\mathcal {T}_h}{,} \\ \left( \rho \,\dot{v}_h, w\right) _{\mathcal {T}_h}&= \dot{{\mathcal {F}}}_{v_{h}} = \{ {\mathcal {F}}_{v_h}, \mathcal {H}_h^{\star }\} = \left( \varvec{q}_h, \nabla w\right) _{\mathcal {T}_h} - \left\langle \widehat{\varvec{q}}_h\cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}} - \left( g(u_h), w \right) _{\mathcal {T}_h}+ \left( f, w\right) _{\mathcal {T}_h}{,} \end{aligned}$$

and thus by definition of the Poisson bracket and the coordinate functionals, the proof reduces to show that

$$\begin{aligned} \{ {\mathcal {F}}_{u_h}, \mathcal {H}_h^{\star }\}= \left( w, \frac{\delta \mathcal {H}_h^{\star }}{\delta v_{h}} \right) _{\mathcal {T}_h}&= \left( \rho \,v_h, w\right) _{\mathcal {T}_h}, \end{aligned}$$

(12)

$$\begin{aligned} \{ {\mathcal {F}}_{v_h}, \mathcal {H}_h^{\star }\}=-\left( w, \frac{\delta \mathcal {H}_h^{\star }}{\delta u_{h}} \right) _{\mathcal {T}_h}&= \left( \varvec{q}_h, \nabla w\right) _{\mathcal {T}_h} - \left\langle \widehat{\varvec{q}}_h\cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}} - \left( g(u_h), w \right) _{\mathcal {T}_h}+ \left( f, w\right) _{\mathcal {T}_h}{.} \end{aligned}$$

(13)

We compute the variation of $\mathcal {H}_h^\star$ according to the definition

$$\begin{aligned} \delta \mathcal {H}_h^\star := \lim _{\epsilon \rightarrow 0} \frac{\mathcal {H}_h^\star [u_h+\epsilon \delta u_h,v_h+\epsilon \delta v_h] - \mathcal {H}_h^\star [u_h,v_h]}{\epsilon } = \left( \frac{\delta \mathcal {H}_h^\star }{\delta u_h}, \delta u_h\right) _{\mathcal {T}_h} + \left( \frac{\delta \mathcal {H}_h^\star }{\delta v_h}, \delta v_h\right) _{\mathcal {T}_h}. \end{aligned}$$

A simple computation of the variation of $\mathcal {H}_h^\star$ with respect to $v_h$ implies (12). Meanwhile, to derive (13), we need an expression of the variation of $\mathcal {H}_h^\star$ with respect to $u_h$. This variation corresponds to

$$\begin{aligned} \left( \frac{\delta \mathcal {H}_h^{\star }}{\delta u_h}, \delta u_h \right) _{\mathcal {T}_h} = \left( \kappa ^{-1}\,\varvec{q}_h, \delta {\varvec{q}_h}\right) _{\mathcal {T}_h} + \left( g(u_h), \delta u_h\right) _{\mathcal {T}_h} - \left( f, \delta u_h\right) _{\mathcal {T}_h} + \delta S_h^\star . \end{aligned}$$

Observe here that $\varvec{q}_h$ and $\widehat{u}_h$ are interpreted as functions of $u_h$, and then we need to find $\delta \varvec{q}_h$ and $\delta \widehat{u}_h$. For the first term, we use (4c),

$$\begin{aligned} \left( \kappa ^{-1} \delta \varvec{q}_h, \varvec{q}_h\right) _{\mathcal {T}_h}&= \left( \delta u_h, \nabla \cdot \varvec{q}_h\right) _{\mathcal {T}_h}- \left\langle \delta \widehat{u}_h, \varvec{q}_h\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}} \\&= - \left( \nabla \delta u_{h}, \varvec{q}_h\right) _{\mathcal {T}_h} + \left\langle \delta u_h - \delta \widehat{u}_h, \varvec{q}_h\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}\\&= - \left( \nabla \delta u_{h}, \varvec{q}_h\right) _{\mathcal {T}_h} + \left\langle \delta u_h, \widehat{\varvec{q}}_h\cdot \varvec{n} \right\rangle _{\partial \mathcal {T}_{h}} - \left\langle \delta u_h - \delta \widehat{u}_h, (\widehat{\varvec{q}}_h-\varvec{q}_h)\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}. \end{aligned}$$

Moreover, note that the following identity holds

$$\begin{aligned} \left\langle \delta (\widehat{\varvec{q}}_h - \varvec{q}_h)\cdot \varvec{n}, u_h-\widehat{u}_h\right\rangle _{\partial \mathcal {T}_{h}}= \left\langle (\widehat{\varvec{q}}_h - \varvec{q}_h)\cdot \varvec{n}, \delta u_h-\delta \widehat{u}_h\right\rangle _{\partial \mathcal {T}_{h}}. \end{aligned}$$

This identity is straightforward for mixed and HDG methods. For DG method the argument follows Lemma 4.1 in [27]. Thus

$$\begin{aligned} \delta S_h^\star = \left\langle (\widehat{\varvec{q}}_h - \varvec{q}_h)\cdot \varvec{n}, \delta u_h-\delta \widehat{u}_h\right\rangle _{\partial \mathcal {T}_{h}}. \end{aligned}$$

Therefore, by replacing these terms we find that the variation of $\mathcal {H}_h^{\star }$ with respect to $u_h$ is

$$\begin{aligned} \left( \frac{\delta \mathcal {H}_h^{\star }}{\delta u_h}, \delta u_h \right) _{\mathcal {T}_h} = - \left( \nabla \delta u_{h}, \varvec{q}_h\right) _{\mathcal {T}_h}+ \left\langle \delta u_h, \widehat{\varvec{q}}_h\cdot \varvec{n} \right\rangle _{\partial \mathcal {T}_{h}} + \left( g(u_h), \delta u_h\right) _{\mathcal {T}_h} - \left( f, \delta u_h\right) _{\mathcal {T}_h}{.} \end{aligned}$$

and hence it proves (13). $\square$

4.2 Analysis of Methods for Displacement–Velocity–stress Formulation

The following theorem demonstrates that both the mixed and DG methods are equivalent to a Hamiltonian system, provided that the parameters defining the numerical traces satisfy certain conditions. It’s important to note that HDG methods that use the velocity-based numerical flux (7) are not Hamiltonian. To begin with, let’s introduce the Hamiltonian functionals

$$\begin{aligned} \mathcal {H}_h^{\star }[u_h, v_h, \varvec{q}_{h}] = \frac{1}{2}\left( \rho \, v_h, v_h\right) _{\mathcal {T}_h} + \frac{1}{2}\left( \kappa ^{-1}\,\varvec{q}_h, \varvec{q}_h\right) _{\mathcal {T}_h} + \left( G(u_h), 1\right) _{\mathcal {T}_h} - \left( u_h, f\right) _{\mathcal {T}_h}{,} \end{aligned}$$

for $\star = \hbox {M}, \hbox {DG}$. Note that they differ in the finite element spaces in which they are defined, that is, for $\star =M$, the mixed method, $(u_h, v_h, \varvec{q}_{h}) \in W_{h}\times W_{h} \times \varvec{V}_h^\textrm{M}$, whilst for $\star =\hbox {DG}$, the DG method, $(u_h, v_h, \varvec{q}_{h}) \in W_{h}\times W_{h} \times \varvec{V}_h^{\textrm{DG}}$. In addition, we define the discrete Poisson brackets listed below:

$$\begin{aligned} \{{\mathcal {F}}, {\mathcal {G}}\}_{h}^\textrm{M}&= \left( \rho ^{-1}\frac{\delta {\mathcal {F}}}{\delta u_{h}} , \frac{\delta {\mathcal {G}}}{\delta v_{h}}\right) _{\mathcal {T}_h} - \left( \rho ^{-1}\frac{\delta {\mathcal {F}}}{\delta v_{h}} , \frac{\delta {\mathcal {G}}}{\delta u_{h}}\right) _{\mathcal {T}_h} +\left( \rho ^{-1}\nabla \cdot \kappa \frac{\delta {\mathcal {F}}}{\delta \varvec{q}_{h}}, \frac{\delta {\mathcal {G}}}{\delta v_{h}}\right) _{\mathcal {T}_h}\\&\quad -\left( \rho ^{-1}\frac{\delta {\mathcal {F}}}{\delta v_{h}}, \nabla \cdot \kappa \frac{\delta {\mathcal {G}}}{\delta \varvec{q}_{h}}\right) _{\mathcal {T}_h}{,} \end{aligned}$$

for functionals ${\mathcal {F}}, {\mathcal {G}}$ defined for functions in the mixed finite element spaces, and

for functionals ${\mathcal {F}}, {\mathcal {G}}$ defined for functions in the DG spaces. Oberve here that the operator is the numerical flux defined by (assuming periodic boundary conditions). We are now in a position to state the Theorem.

Theorem 4.2

The Mixed, DG, HDG methods defined for the formulations involving the displacement, velocity, and vector-valued variables satisfy:

• i. The Mixed method (5) is Hamiltonian with Hamiltonian functional ${\mathcal {H}}_h^\textrm{M}$, and Poisson bracket $\{\cdot ,\cdot \}_h^\textrm{M}$ and the mixed finite element spaces.

• ii. The DG method (6), with numerical traces (8) and $C_{11} = C_{22} = 0$ is in Hamiltonian form associated to the Hamiltonain functional ${\mathcal {H}}_h^\mathrm{{DG}}$, Poisson bracket $\{\cdot ,\cdot \}_{h}^\mathrm{{DG}}$ and the DG spaces. If $C_{11}\ne 0$ or $C_{22}\ne 0$, then the previous does not hold.

• iii. The HDG method (6) with numerical trace $\widehat{\varvec{q}}_h\cdot \varvec{n} = \varvec{q}_h\cdot \varvec{n} + \tau (v_h-\widehat{v}_h)$ is not Hamiltonian.

Proof

Analogously to the proof of Theorem 4.1 we introduce coordinate functionals corresponding to each dynamic equation of system (6), for $u_h, v_h\in W_h$ and $\varvec{q}_h\in \varvec{V}_h^{\star }, \star =\hbox {M}, \hbox {DG}$

$$\begin{aligned} {\mathcal {F}}_{u_h} = \left( \rho \, u_h, w\right) _{\mathcal {T}_h}, \quad {\mathcal {F}}_{v_h} = \left( \rho \,v_h, w\right) _{\mathcal {T}_h},\quad {\mathcal {F}}_{\varvec{q}_{h}} = \left( \kappa ^{-1} \varvec{q}_h, \varvec{r}\right) _{\mathcal {T}_h}{,} \end{aligned}$$

and compute their variations with respect to the variables $u_h, v_h$, and $\varvec{q}_h$

$$\begin{aligned} \rho ^{-1}\frac{\delta {\mathcal {F}}_{u_h}}{\delta u_h} = w,\quad \rho ^{-1}\frac{\delta {\mathcal {F}}_{v_h}}{\delta v_h} = w,\quad \kappa \frac{\delta {\mathcal {F}}_{\varvec{q}_h}}{\delta \varvec{q}_h} = \varvec{r}, \end{aligned}$$

variations with respect to other variables are zero by definition of the coordinate functional. We first prove i., the Hamiltonian form of the mixed method (5), that is, we want to prove that

$$\begin{aligned} \left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h}&= \dot{{\mathcal {F}}}_{u_{h}} = \{ {\mathcal {F}}_{u_h}, \mathcal {H}_h^\textrm{M}\}_{h}^\textrm{M} = \left( \rho \, v_{h}, w\right) _{\mathcal {T}_h}{,} \\ \left( \rho \,\dot{v}_h, w\right) _{\mathcal {T}_h}&= \dot{{\mathcal {F}}}_{v_{h}} = \{ {\mathcal {F}}_{v_h}, \mathcal {H}_h^\textrm{M}\}_{h}^\textrm{M} = -\left( \nabla \cdot \varvec{q}_h, w\right) _{\mathcal {T}_h} - \left( g(u_h), w \right) _{\mathcal {T}_h}+ \left( f, w\right) _{\mathcal {T}_h}{,} \\ \left( \kappa ^{-1}\dot{\varvec{q}}_h, \varvec{r}\right) _{\mathcal {T}_h}&= \dot{{\mathcal {F}}}_{\varvec{q}_h} = \{ {\mathcal {F}}_{\varvec{q}_h}, \mathcal {H}_h^\textrm{M} \}_{h}^\textrm{M} = \left( v_h, \nabla \cdot \varvec{r}\right) _{\mathcal {T}_h} {.} \end{aligned}$$

Computing the variation of $\mathcal {H}_h^\textrm{M}$ and applying the Poisson bracket we obtain

$$\begin{aligned} \{{\mathcal {F}}_{u_h}, \mathcal {H}_{h}^\textrm{M} \}_{h}^\textrm{M}&= \left( \rho ^{-1}\frac{\delta {\mathcal {F}}_{u_h}}{\delta u_h}, \frac{\delta \mathcal {H}_h^\textrm{M}}{\delta v_{h}} \right) _{\mathcal {T}_h} = \left( \rho \, v_{h}, w\right) _{\mathcal {T}_h}{,} \\ \{{\mathcal {F}}_{v_{h}}, \mathcal {H}_{h}^\textrm{M} \}_{h}^\textrm{M}&= -\left( \rho ^{-1}\frac{\delta {\mathcal {F}}_{v_h}}{\delta v_h}, {\frac{\delta \mathcal {H}_h^\textrm{M}}{\delta u_h}} + \nabla \cdot \kappa \frac{\delta \mathcal {H}_{h}^\textrm{M}}{\delta \varvec{q}_h}\right) _{\mathcal {T}_h}= -\left( \nabla \cdot \varvec{q}_h, w\right) _{\mathcal {T}_h} \\&\qquad - \left( g(u_h), w \right) _{\mathcal {T}_h}+ \left( f, w\right) _{\mathcal {T}_h}{,} \\ \{{\mathcal {F}}_{\varvec{q}_h}, \mathcal {H}_{h}^\textrm{M}\}_{h}^\textrm{M}&= \left( \nabla \cdot \kappa \frac{\delta {\mathcal {F}}_{\varvec{q}_h}}{\delta \varvec{q}_h} , \rho ^{-1} {\frac{\delta \mathcal {H}_h^\textrm{M}}{\delta v_{h}}}\right) _{\mathcal {T}_h} = \left( v_h, \nabla \cdot \varvec{r}\right) _{\mathcal {T}_h}{.} \end{aligned}$$

Now, to prove ii., we need to show that the DG system (6) is Hamiltonian, i.e.

$$\begin{aligned} \left( \rho \,\dot{u}_h, w\right) _{\mathcal {T}_h}&= \dot{{\mathcal {F}}}_{u_{h}} = \{ {\mathcal {F}}_{u_h}, \mathcal {H}_h^\mathrm{{DG}}\}_h^\mathrm{{DG}} = \left( \rho \, v_{h}, w\right) _{\mathcal {T}_h}{,} \\ \left( \rho \,\dot{v}_h, w\right) _{\mathcal {T}_h}&= \dot{{\mathcal {F}}}_{v_{h}} = \{ {\mathcal {F}}_{v_h}, \mathcal {H}_h^\mathrm{{DG}}\}_h^\mathrm{{DG}} = \left( \varvec{q}_h, \nabla w\right) _{\mathcal {T}_h} - \left\langle \widehat{\varvec{q}}_h\cdot \varvec{n}, w\right\rangle _{\partial \mathcal {T}_{h}}\\&- \left( g(u_h), w \right) _{\mathcal {T}_h}+ \left( f, w\right) _{\mathcal {T}_h}{,} \\ \left( \kappa ^{-1}\dot{\varvec{q}}_h, \varvec{r}\right) _{\mathcal {T}_h}&= \dot{{\mathcal {F}}}_{\varvec{q}_h} = \{ {\mathcal {F}}_{\varvec{q}_h}, \mathcal {H}_h^\mathrm{{DG}} \}_h^\mathrm{{DG}} = \left( v_h, \nabla \cdot \varvec{r}\right) _{\mathcal {T}_h} -\left\langle \widehat{v}_h, \varvec{r}\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}{.} \end{aligned}$$

The first identity is simply a direct calculation

$$\begin{aligned} \{{\mathcal {F}}_{u_h}, \mathcal {H}_{h}^\mathrm{{DG}} \}_h^\mathrm{{DG}} = \left( w, \frac{\delta \mathcal {H}_h^\mathrm{{DG}}}{\delta v_{h}} \right) _{\mathcal {T}_h} = \left( \rho v_{h}, w\right) _{\mathcal {T}_h}. \end{aligned}$$

For the second identity, we apply the Poisson bracket and the definition of the variations of ${\mathcal {H}}_h^{DG}$ to obtain

and then the identity follows from rewriting the second term using Lemma 3.1

We observe here that the last step is due to the assumption $C_{11}=C_{22} =0$. Finally, for the third identity, we apply the definition of the Poisson bracket, the variations, and again using that $C_{11}=C_{22} =0$

Finally, we prove iii. Observe that the energy of the HDG method is

$$\begin{aligned} {\mathcal {E}}_h = \frac{1}{2}\left( \rho \, v_h, v_h\right) _{\mathcal {T}_h} + \frac{1}{2}\left( \kappa ^{-1}\,\varvec{q}_h, \varvec{q}_h\right) _{\mathcal {T}_h} + \left( G(u_h), 1\right) _{\mathcal {T}_h} - \left( u_h, f\right) _{\mathcal {T}_h}. \end{aligned}$$

A straightforward computation shows that the energy dissipates in time, and as a result, the method is not Hamiltonian. This completes the proof. $\square$

4.3 Analysis of New DG Methods for Displacement–Velocity–Stress

The Hamiltonian functional associated to the method (6) with numerical traces given by (9) is the following:

$$\begin{aligned} \widetilde{\mathcal {H}}_h^{{\hbox {DG}}}[u_{h}, v_{h}, \varvec{q}_{h}]&= \frac{1}{2}\left( \rho v_{h}, v_{h}\right) _{\mathcal {T}_h} + \frac{1}{2}\left( \kappa ^{-1}\varvec{q}_{h}, \varvec{q}_{h}\right) _{\mathcal {T}_h} +\left( G(u_h), 1\right) _{\mathcal {T}_h} - \left( f, u_{h}\right) _{\mathcal {T}_h}\nonumber \\&\qquad + \frac{1}{2}D_{11}\left\langle \llbracket u_h\rrbracket , \llbracket u_h\rrbracket \right\rangle _{\mathcal {F}_{h}} + \frac{1}{2}D_{22}\left\langle \llbracket \varvec{q}_h\rrbracket , \llbracket \varvec{q}_h\rrbracket \right\rangle _{\mathcal {F}_{h}} {.} \end{aligned}$$

(14)

Theorem 4.3

The semidiscrete DG method (10) with numerical traces $\widehat{\varvec{q}}_h$ and $\widehat{v}_h$ defined in (9) is energy-conserving, i.e., if f is zero in time then the energy defined by ${\mathcal {E}}_h = \widetilde{\mathcal {H}}_h^{{\hbox {DG}}}$, is such that $\dot{\mathcal E}_h = 0$.

Proof

We test the Eqs. (10a), (10b) and (10c) with $w=u_h$, $w=v_h$ and $\varvec{r} = \varvec{q}_h$, respectively, and obtain

$$\begin{aligned}&\left( \rho \,\dot{u}_h, u_h\right) _{\mathcal {T}_h} = \left( \rho \,v_h, u_h\right) _{\mathcal {T}_h} ,\\&\left( \rho \,\dot{v}_h, v_h\right) _{\mathcal {T}_h} = \left( \varvec{q}_h, \nabla \, v_h\right) _{\mathcal {T}_h} - \left( g(u_h), v_h \right) _{\mathcal {T}_h} +\left( f, v_h\right) _{\mathcal {T}_h} \\&\qquad \qquad \qquad \qquad - \left\langle (\{\!\!\{\varvec{q}_h\}\!\!\} - \varvec{C}_{12}\llbracket \varvec{q}_h\rrbracket )\cdot \varvec{n}, v_h\right\rangle _{\partial \mathcal {T}_{h}}- \left\langle D_{11}\llbracket u_h\rrbracket \cdot \varvec{n}, v_h\right\rangle _{\partial \mathcal {T}_{h}}, \nonumber \\&\left( \kappa ^{-1}\dot{\varvec{q}}_h, \varvec{q}_h \right) _{\mathcal {T}_h} + D_{22}\left\langle \llbracket \dot{\varvec{q}}_h\rrbracket , \varvec{q}_h\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}} = \left( v_h, \nabla \cdot \,\varvec{q}_h\right) _{\mathcal {T}_h} - \left\langle \{\!\!\{v_h\}\!\!\} + \varvec{C}_{12}\llbracket v_h\rrbracket , \varvec{q}_h\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}{.} \end{aligned}$$

Adding the last two equations above and observing that $v_h = \dot{u}_{h}$ and that

$$\begin{aligned} D_{11}\left\langle \llbracket u_h\rrbracket , v_h\varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}&= D_{11}\left\langle \llbracket u_h\rrbracket , \llbracket \dot{u}_h\rrbracket \right\rangle _{\mathcal {F}_{h}}{,} \\ D_{22}\left\langle \llbracket \dot{\varvec{q}}_h\rrbracket , \varvec{q}_h\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}}&= D_{22}\left\langle \llbracket \dot{\varvec{q}}_h\rrbracket , \llbracket \varvec{q}_h\rrbracket \right\rangle _{\mathcal {F}_{h}}{,} \end{aligned}$$

we obtain

$$\begin{aligned} \dot{{\mathcal {E}}}_h&= \left( \varvec{q}_h, \nabla v_h\right) _{\mathcal {T}_h}- \left\langle (\{\!\!\{\varvec{q}_h\}\!\!\} - \varvec{C}_{12}\llbracket \varvec{q}_h\rrbracket )\cdot \varvec{n}, v_h\right\rangle _{\partial \mathcal {T}_{h}}\\&\quad + \left( v_h, \nabla \cdot \varvec{q}_h\right) _{\mathcal {T}_h} - \left\langle \{\!\!\{v_h\}\!\!\} + \varvec{C}_{12}\llbracket v_h\rrbracket , \varvec{q}_h\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}} \\&=- \left\langle (\{\!\!\{\varvec{q}_h\}\!\!\} - \varvec{C}_{12}\llbracket \varvec{q}_h\rrbracket )\cdot \varvec{n}, v_h\right\rangle _{\partial \mathcal {T}_{h}} - \left\langle \{\!\!\{v_h\}\!\!\} + \varvec{C}_{12}\cdot \llbracket v_h\rrbracket - v_h , \varvec{q}_h\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}} \\&= 0. \\ \end{aligned}$$

$\square$

Finally, we prove the Hamiltonian form of the new DG scheme (10). For the sake of presentation, we follow the technique presented in [8] to prove the Hamiltonian form using the coefficients of the finite element functions, recasting the semidiscrete method as a Hamiltonian ordinary differential equations system.

Theorem 4.4

The DG method (10) with numerical traces $\widehat{\varvec{q}}_h$ and $\widehat{v}_h$ defined in (9) is Hamiltonian, with Hamiltonian functional $\widetilde{\mathcal {H}}_h^{{\hbox {DG}}}$, i.e., there exists a skew-symmetric matrix J such that the semidiscrete scheme (10) is equivalent to a Hamiltonian ordinary differential equations system in terms of the unknowns ${\textbf {u}}$ as $\dot{{\textbf {u}}} = J (\partial \widetilde{\mathcal {H}}^{\textrm{DG}} / \partial {\textbf {u}})$.

Proof

Let $\{\varphi _i\}$ be an $\rho$-orthonormal basis of $W_h$ and let $\varvec{\xi }_{j}$ be a basis of $\varvec{V}_h^\textrm{DG}$ such that

$$\begin{aligned} \left( \kappa ^{-1}\varvec{\xi }_{j}, \varvec{\xi }_{j}\right) _{\mathcal {T}_h} + D_{22}\left\langle \llbracket \varvec{\xi }_j\rrbracket , \llbracket \varvec{\xi }_i\rrbracket \right\rangle _{\mathcal {F}_{h}} = \delta _{ij}, \quad \text {for }i,j=1,..., \text {dim}(\varvec{V}_{h}^\textrm{DG}){.} \end{aligned}$$

We now denote using sans serif typestyle the coefficients associated with the unknowns, $u_h, v_h, \varvec{q}_{h}$ in these bases, i.e.

$$\begin{aligned} u_{h}(x,t) = \sum _{i} \textsf {u}_i(t)\varphi _i(x), \quad v_{h}(x,t) = \sum _{i} \textsf {v}_i(t)\varphi _i(x), \quad \varvec{q}_h(x,t) = \sum _{j} {\textsf {q}}_{j}(t)\varvec{\xi }_{j}(x). \end{aligned}$$

Linear and nonlinear operators are defined next to express the DG method (6) in terms of the coefficients,

$$\begin{aligned} {\textbf {B}}_{ij}&= \left( \nabla \cdot \varvec{\xi }_{j}, \varphi _i\right) _{\mathcal {T}_h}, \quad{} & {} {\textbf {C}}_{ij} = \left\langle \varvec{\xi }_j\cdot \varvec{n}, \{\!\!\{\varphi _i\}\!\!\} + \varvec{C}_{12}\cdot \llbracket \varphi _i\rrbracket \right\rangle _{\partial \mathcal {T}_{h}}{,}\\ {\textbf {E}}_{ik}&= \left\langle \llbracket \varphi _i\rrbracket , \llbracket \varphi _k\rrbracket \right\rangle _{\mathcal {F}_{h}}, \quad{} & {} \hbox {g}({\textsf {u}})_{i}= \left( g\left( \sum _k \textsf {u}_k\varphi _k\right) , \varphi _i\right) _{\mathcal {T}_h}{,} \end{aligned}$$

for $i=1,...,\hbox {dim}(W_h)$ and $j = 1,...,\hbox {dim}(\varvec{V}_h^{\textrm{DG}})$. The Hamiltonian $\widetilde{\mathcal {H}}_h^{\textrm{DG}}$ can now be formulated in terms of the coefficients as follows

$$\begin{aligned} \widetilde{\mathcal {H}}_h^{\textrm{DG}}[\textsf {u}, \textsf {v}, \textsf {q}] = \frac{1}{2}\textsf {v}^{\top } \textsf {v} + \frac{1}{2} \textsf {q}^\top \textsf {q} + \frac{1}{2} D_{11}\textsf {u}^{\top }{} {\textbf {E}}\textsf {u} + \hbox {G}(\textsf {u}){.} \end{aligned}$$

Variations of the Hamiltonian with respect to the coefficient are now straightforward computations

$$\begin{aligned} \frac{\delta \widetilde{\mathcal {H}}_h^{\textrm{DG}}}{\delta {\textsf {u}}} = \hbox {g}({\textsf {u}}) + D_{11} {\textbf {E}} \textsf {u}, \quad \frac{\delta \widetilde{\mathcal {H}}_h^{\textrm{DG}}}{\delta \textsf {v}} = {\textsf {v}}, \quad \frac{\delta \widetilde{\mathcal {H}}_h^{\textrm{DG}}}{\delta {\textsf {q}}} = {\textsf {q}} {.} \end{aligned}$$

Thus, system (10) is equivalent to

$$\begin{aligned} \begin{bmatrix} \dot{\textsf {u}} \\ \dot{\textsf {v}} \\ \dot{\textsf {q}} \end{bmatrix}&= \begin{bmatrix} 0 &{} {\textrm{Id}} &{} 0 \\ -{\textrm{Id}} &{} 0 &{} -{\textbf {B}} + {\textbf {C}} \\ 0 &{} {\textbf {B}}^{\top } - {\textbf {C}}^{\top } &{} 0 \end{bmatrix} \begin{bmatrix} \hbox {g}({\textsf {u}}) + D_{11} {\textbf {E}} \textsf {u} \\ \textsf {v} \\ \textsf {q} \end{bmatrix}\\&= \begin{bmatrix} 0 &{} {\textrm{Id}} &{} 0 \\ -\hbox {Id} &{} 0 &{} -{\textbf {B}} + {\textbf {C}} \\ 0 &{} {\textbf {B}}^{\top } - {\textbf {C}}^{\top } &{} 0 \end{bmatrix} \begin{bmatrix} {\delta \widetilde{\mathcal {H}}_h^{\textrm{DG}}} / {\delta \textsf {u}} \\ {\delta \widetilde{\mathcal {H}}_h^{\textrm{DG}}} / {\delta \textsf {v}} \\ {\delta \widetilde{\mathcal {H}}_h^{\textrm{DG}}} / {\delta \textsf {q}} \end{bmatrix} \end{aligned}$$

from which we observe that the system is clearly Hamiltonian. $\square$

5 Fully Discrete HDG Methods

This section presents the fully discrete schemes based on the time discretization of the Hamiltonian HDG method (4) by symplectic integrators. The extension to the other presented methods can be extrapolated from the one presented in this section. To represent estimated solutions at different times, we use the notation $\varvec{y}^{n}\approx \varvec{y}(t_n)$, an approximation of $\varvec{y}$ at time $t_n$, where $t_n=t_0+n\Delta t$. For the sake of presentation, we assume that $t_0=0$ and periodic boundary conditions are prescribed. We will display the algorithms in their matrix form by introducing bases of the finite element spaces. Let $\{\phi _i\}$ be a $\rho$-orthonormal basis of $W_h$, let $\{\xi _j\}$ be a $\kappa ^{-1}$-orthonormal basis of $\varvec{V}_h^{\textrm{DG}}$ and $\{\eta _{k}\}$ be a $\tau$-orthonormal basis of $M_h$ (assuming that $\tau$ is constant on each face of $\mathcal {F}_{h}$). Functions in the finite element spaces are represented by their respective basis and employing coefficients, denoted by sans serif typeset. Hence, the solutions of the HDG methods are written as

$$\begin{aligned} u_h(\varvec{x}, t)&= \sum _{i=1}\textsf {u}_i(t)\varphi _i(\varvec{x}){,}&v_h(\varvec{x}, t)&= \sum _{i=1}\textsf {v}_i(t)\varphi _i(\varvec{x}){,} \\ \varvec{q}_h(\varvec{x},t)&= \sum _{j=1}\textsf {q}_j(t)\varvec{\xi }_j(\varvec{x}) {,}&\widehat{u}_h(\varvec{x},t)&= \sum _{m=1}\widehat{\textsf {u}}_m(t)\eta _m(\varvec{x}){,} \end{aligned}$$

for $(\varvec{x}, t)\in \Omega \times [0,T]$. Now we introduce the linear and nonlinear operators associated with the HDG scheme (4),

$$\begin{aligned} {\textbf {B}}_{ij}&= \left( \nabla \cdot \varvec{\xi }_j, \varphi _i\right) _{\mathcal {T}_h},&[{\textbf {S}}_{\tau }]_{i\ell }&= \left\langle \tau \, \varphi _\ell , \varphi _i\right\rangle _{\partial \mathcal {T}_{h}},&\textsf {g}(\textsf {u})_i&= \left( g\left( \sum _{{l}=1}\textsf {u}_{{l}}(t)\varphi _{{l}}(\varvec{x}) \right) , \varphi _i\right) _{\mathcal {T}_h},\\ [{\textbf {E}}_{\tau }]_{ik}&= \left\langle \tau \, \eta _k, \varphi _{i}\right\rangle _{\partial \mathcal {T}_{h}},&{\textbf {C}}_{jk}&= \left\langle \eta _k, \varvec{\xi }_j\cdot \varvec{n}\right\rangle _{\partial \mathcal {T}_{h}},&\textsf {f}_i&= \left( f, \varphi _i\right) _{\mathcal {T}_h}, \end{aligned}$$

for $i,\ell =1,...,\hbox {dim}(W_h)$, $j=1,..., \hbox {dim}(\varvec{V}_h^{\textrm{DG}})$, and $k=1,...,\hbox {dim}(M_h)$. In the next subsections, we introduce two classes of symplectic methods applied to the HDG system.

5.1 ESPRK-HDG

We first consider time-integrators in the class of symplectic partitioned Runge–Kutta methods [17]. These schemes effectively solve separable Hamiltonian such as the semidiscrete HDG scheme (4), obtaining fully time-explicit time-steps. We refer to this class of symplectic methods as explicit symplectic partitioned Runge–Kutta (ESPRK) methods. To define the schemes we introduce two s-stages Runge–Kutta schemes associated with the following Butcher tableaux

(15)

It is important to note that these schemes, by design, satisfy the requirement of being symplectic and are explicit time integrators for separable Hamiltonian systems.

Applying the ESPRK methods, with tableaux given by (15), to the semidiscrete HDG (4) results in fully discrete schemes, with equations written in terms of the unknown coefficients $(\textsf {v}^n, \textsf {u}^n, \textsf {q}^n,\widehat{\textsf {u}}^n)$ as follows

$$\begin{aligned} \textsf {v}^{n,i}&= \textsf {v}^{n,i-1} + \Delta t\,b_{i}\,\textsf {L}^{n}_{i-1}(t_n + C_{i}\Delta t){,} \end{aligned}$$

(16a)

$$\begin{aligned} \textsf {u}^{n,i}&= \textsf {u}^{n,i-1} + \Delta t\,B_i\textsf {v}^{n,i}{,} \end{aligned}$$

(16b)

$$\begin{aligned} \textsf {q}^{n,i} + {\textbf {C}}\widehat{\textsf {u}}^{n,i}&= {\textbf {B}}^{\top }\textsf {u}^{n,i}{,}\end{aligned}$$

(16c)

$$\begin{aligned} {\textbf {C}}^{\top }\textsf {q}^{n,i} -\widehat{\textsf {u}}^{n,i}&= -{\textbf {E}}_{\tau }^{\top }\textsf {u}^{n,i}{,}\end{aligned}$$

(16d)

$$\begin{aligned} \textsf {L}^{n}_{j}(t)&= \textsf {f}(t) -{\textbf {B}}\textsf {q}^{n,j} - {\textbf {S}}_{\tau }\textsf {u}^{n,j} + {\textbf {E}}_{\tau }\widehat{\textsf {u}}^{n,j} - \textsf {g}(\textsf {u}^{n,j}){,} \end{aligned}$$

(16e)

for $i=1,...,s$. We organize the stages of the solver in Algorithm 1.

Algorithm 1

Single iteration of HDG-ESPRK for semilinear wave system

5.2 SDIRK-HDG

Symplectic diagonally implicit Runge–Kutta (SDIRK) schemes are the second class of methods considered in our discretization. Our interest in these methods is justified by the outstanding behavior of the integration over time of quantities of interest, as it is shown in [8, 21, 22, 27]. Symplectic diagonally implicit Runge–Kutta schemes of s-stages have the following Butcher tableau

Note that this structure arises from applying the symplecticity condition on a general diagonally implicit Runge–Kutta method. Now, discretizing using the SDIRK schemes and the HDG semidiscrete method (4) gives the following equations in terms of the vector of coefficients $\textsf {y}^{\top } = (\textsf {u}^{\top },\textsf {v}^{\top },\textsf {q}^{\top },\widehat{\textsf {u}}^{\top })$

$$\begin{aligned} {\textbf {A}}_{i}\textsf {y}^{n,i} + \Delta t\,\frac{b_i}{2}{} {\textbf {G}}(\textsf {y}^{n,i})&= {\textbf {L}}_{i}(t_n + c_{i}\Delta t),&i=1,\dots ,s \end{aligned}$$

(17a)

$$\begin{aligned} \textsf {k}_{i}&= \frac{2}{\Delta t\,b_{i}}(\textsf {y}^{n,i} - \textsf {y}^{n}) - 2\sum _{j=1}^{i-1}\frac{b_{j}}{b_{i}}\textsf {k}_{j},&i=1,\dots ,s\end{aligned}$$

(17b)

$$\begin{aligned} \textsf {y}^{n+1}&= \textsf {y}^{n} + \Delta t\sum _{i=1}^{s}b_i\textsf {k}_i{,}&\end{aligned}$$

(17c)

where the matrix ${\textbf {A}}_i$, the linear form ${\textbf {L}}_{i}$ and the nonlinear term ${\textbf {G}}$ are defined as:

$$\begin{aligned} {\textbf {A}}_i&= \begin{bmatrix} \hbox {Id} &{} -\Delta t\,(b_{i}/2)\hbox {Id} &{} &{}\\ \Delta t\,(b_{i}/2){\textbf {S}}_{\tau } &{} \hbox {Id} &{} \Delta t\,(b_{i}/2){\textbf {B}} &{} -\Delta t\,(b_{i}/2){\textbf {E}}_{\tau }\\ -{\textbf {B}}^{\top } &{} &{} \hbox {Id} &{} {\textbf {C}}\\ {\textbf {E}}_{\tau }^{\top } &{} &{} {\textbf {C}}^{\top } &{} -{\textbf {G}}_{\tau } \end{bmatrix},&{\textbf {G}}(\textsf {y})&= \begin{bmatrix}0\\ \textsf {g}(\textsf {u})\\ 0\\ 0\end{bmatrix}{,} \\ {\textbf {L}}_{i}(t)&= \begin{bmatrix} \textsf {u}^n \\ \textsf {v}^{n} \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ \Delta t\,(b_{i}/2)\textsf {f}(t) \\ 0 \\ 0 \end{bmatrix} + \Delta t\sum _{j=1}^{i-1}b_{j}\textsf {k}_{j}{,} \end{aligned}$$

We solve the resulting nonlinear system (19) using a fixed point iteration based on the inversion of the matrix ${\textbf {A}}_i$ associated with the resulting system of the corresponding linear wave equation. See Algorithm 2.

Algorithm 2

Fixed Point for each SDIRK step

6 Numerical Experiments

This section showcases several numerical examples that illustrate the characteristics of the HDG semidiscrete scheme (4). The scheme uses polynomial local spaces of degree k for all variables and a constant stabilization function $\tau$. For time discretization, we use a ESPRK method and a SDIRK method, both of which exhibit sixth-order accuracy. See Appendix A for the coefficients of the Runge–Kutta methods. We present three examples of our numerical studies. The first example explores the convergence of errors and the number of iterations required by the nonlinear solver in the implicit scheme. The second example provides numerical evidence of the energy-conserving property of the HDG scheme when using periodic boundary conditions, as well of the new DG scheme. Lastly, in the third example, we solve a cloning soliton experiment called the Josephson transmission line, using the HDG scheme and providing evidence of its energy conservation. All experiments in this section were implemented using the open-source finite element software NETGEN/NGSolve [23, 24].

6.1 Example 1: Convergence Properties on Periodic Boundary

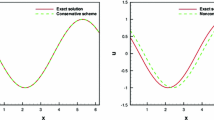
This example examines the convergence properties of the HDG methods (4) with the sixth-order symplectic schemes HDG$_{k}$-ESPRK$_{6}$ and HDG$_{k}$-SDIRK$_6$, and with initial approximation obtained as described in Sect. 3.4. Structured diagonal triangulations were used in the computations. We solve the semilinear wave problem (1) on the domain $\Omega =(0,1)^{2}$ with data $\rho =\kappa =1$, $g(u) = u^2$ and periodic boundary conditions. The source term and the initial conditions are obtained from the manufactured exact solution

$$\begin{aligned} u(\varvec{x}, t) = \sin (2\pi (x_1+x_2-\sqrt{2}t)),\quad \Omega =(0,1)^2,\ 0\le t\le T. \end{aligned}$$

Tables 3 and 4 present the $L^2$ errors and estimated orders of convergence for the approximate solutions $u_h$, $v_h$, and $\varvec{q}_h$, as well as the post-processed approximations $u_h^{*}$ for the HDG$_{k}$-ESPRK$_{6}$ and HDG$_{k}$-SDIRK$_6$ methods. The results show that the approximation $u_h$, $v_h$, and $\varvec{q}_h$ have optimal convergence rates of order $k+1$, while the post-processed approximation $u_h^{*}$ has order $k+2$ for $k>0$. These findings match the results of the linear wave.

The post-processed approximation of the displacement $u_{h}^{*}|_{K}\in \mathcal {P}_{k+1}(K)$ is computed, following the linear case [21], solving the local system (20) for all $w\in \mathcal {P}_{k+1}(K)$, given approximations $u_h^{n}$ and $\varvec{q}_h^{n}$ at each time step.

$$\begin{aligned} \left( \nabla u_h^{*}, \nabla w\right) _{K} + \left( \lambda , w\right) _{K}&= -\left( \varvec{q}_h^{n}, \nabla w\right) _{K}{,} \end{aligned}$$

(18a)

$$\begin{aligned} \left( u_h^{*}, 1\right) _{K}&= \left( u_h^{n}, 1\right) _{K}{.} \end{aligned}$$

(18b)

Table 5 reports the number of iteration steps done by the nonlinear solver Algorithm 2 used in the HDG$_{k}$-SDIRK$_6$ scheme, using a time step of $\Delta t = h/10$ and stabilization parameter $\tau =10$. We display the minimum, mean, and maximum number of iterations taken by fixed point iteration over 150 timesteps for each mesh parameter h and each polynomial degree k, and the corresponding average CPU time. These results were obtained in simulations running on a 2.9GHz Dual-Core Intel Core i5 processor.

Table 3 Convergence results regarding the $L^2$-norm for $\hbox {HDG}_k\hbox {-ESPRK}_6$ method in Example 1

Table 4 Convergence results regarding the $L^2$-norm for $\hbox {HDG}_k\hbox {-SDIRK}_6$ method in Example 1

Table 5 Performance report on fixed point algorithm for the solution of the HDG-semilinear wave system with periodic boundary from Example 1

6.2 Example 2: Conservation of Physical Quantities

In this example, we aim to showcase the conservation properties of the HDG scheme (4), by analyzing the cubic nonlinear Klein–Gordon equation ($g(u) = u-u^{3}$) with zero source $f=0$ over the two-dimensional domain $\Omega =(0,1)^{2}$. The computations are carried out until a final time $T=50$ and employ periodic boundary conditions. The initial conditions are calculated using the initial data.

$$\begin{aligned} u_0(\varvec{x})&= 2^{19}(x_1^{10}(1-x_1)^{10} + x_2^{10}(1-x_2)^{10}){,}\\ v_0(\varvec{x})&= -10\cdot 2^{19}(x_1^{9}(1-x_1)^{9}(1-2x_1) + x_2^{9}(1-x_2)^{9}(1-2x_2)). \end{aligned}$$

We focus on studying the long-term evolution of physical quantities related to the semilinear wave Eq. (1). The quantities approximated here are energy and momentum. We compute the two approximations of the energy; the first ${\mathcal {E}}_h$ corresponds to the continuous energy functional in terms of the approximate variables and the second one the correct Hamiltonian ${\mathcal {H}}_h$ associated with the HDG methods (4).

$$\begin{aligned} \mathcal {H}_h&{:}{=}\mathcal {H}_h^{\textrm{HDG}}{,}\\ \mathcal {E}_h&{:}{=}\frac{1}{2}\left( \rho \, v_h, v_h\right) _{\mathcal {T}_h} + \frac{1}{2}\left( \kappa ^{-1}\,\varvec{q}_h, \varvec{q}_h\right) _{\mathcal {T}_h} + \left( G(u_h), 1\right) _{\mathcal {T}_h}{,}\\ \Vert \mathcal {M}_h\Vert _2&{:}{=}\left\| \int _{\Omega }\rho \,v_h\varvec{q}_h\,d\varvec{x}\right\| _2{.} \end{aligned}$$

The approximate solution is computed at each time step using the HDG scheme with piecewise polynomials of degree 3 with a fixed stabilization parameter $\tau =10$ and ESPRK and SDIRK time stepping schemes of sixth order. In our computations, we use a uniform triangulation with mesh size parameter $h=0.125$ and a fixed time step $\Delta t = h/10$. For each quantity, we compute the relative error for the difference between the approximation at time and the initial approximation.

Figure 1 shows similar behavior in the approximations by scheme HDG-ESPRK and scheme HDG-SDIRK. In the first figure on the left, the energy is approximated up to 5 digits and exhibits non-drifting behavior over time with respect to the initial approximation. The discrete Hamiltonian ${\mathcal {H}}_h$ provides an almost constant approximation of the energy, as shown in the second figure in the middle. In both cases, the approximation does not drift over time. Observe that, in the semilinear case, oscillations of the quantities occur due to the time integration errors of the discrete Hamiltonian induced by the time-stepping schemes. Finally, the third figure on the right shows an error of order $10^{-3}$ over time, indicating a small dissipation compared to the initial approximation.

Fig. 1

Example 2. Plot of the evolution of the relative errors for the approximations of the energy $\mathcal {E}_h$(left) and ${\mathcal {H}}_h$(middle), and the momentum (right). In each of the figures, blue line denotes the approximation by the HDG$_3$-ESPRK$_6$ method, and the red line the approximations by HDG$_3$-SDIRK$_6$

Additionally, we test the new DG methods (10). The election of numerical traces $\widehat{\varvec{q}}_h$ and $\widehat{v}_h$ is given by the coefficients: $D_{11}=1$, $\varvec{C}_{12}=(1/2, 1/2)$ and $D_{22}=1$. Note that these satisfy the assumptions of Theorem 4.3. In particular, note that a non-zero coefficient $D_{22}$ changes the time-stepping procedure by adding to the mass matrix a term that involves the jump across the faces of the elements.

The Hamiltonian quantity in this case corresponds to $\mathcal {H}_h {:}{=}\widetilde{\mathcal {H}}_h^{\textrm{DG}}[u_h, v_h, \varvec{q}_h]$ in (14). We use the same method as before to compute the physical quantities $\mathcal {E}_h$ and $\mathcal {M}_h$.

To obtain our approximations, we utilize piecewise polynomials of degree 3 and employ a sixth-order accurate SDIRK method on a structured triangular mesh with $h=0.125$ and a fixed time step of $\Delta t = h/10$. Figure 2 illustrates the relative error evolution of the physical quantities. We observe that the Hamiltonian $\widetilde{\mathcal {H}}_{h}^{\textrm{DG}}$ is accurately conserved, with oscillations of up to 9 digits of precision. However, the quantity $\mathcal {E}_h$ exhibits a slight drift in contrast to the HDG method shown in Fig. 1. Additionally, we provide a plot of the momentum approximation obtained using the new DG methods, which exhibits a similar behavior to the HDG method’s approximation.

Fig. 2

Example 2. A plot of the evolution of the relative errors for the approximations of the energy $\mathcal {E}_h$(left) and ${\mathcal {H}}_h$(middle), and the momentum (right) for the DG$_3$-SDIRK$_6$ method

6.3 Example 3: Josephson Transmission Line

In this example, we follow the cloning soliton experiment from [16]. The experiment considers the sine-Gordon equation ($g(u) = \sin (u)$) with zero source term $f=0$ on the T-shaped domain illustrated in Fig. 3. Homogeneous Neumann boundary conditions are set on $\partial \Omega$ modeling zero current on the boundary.

Fig. 3

Example 3. Illustration and dimension of T-shaped domain for propagating a cloning soliton

The initial conditions for this system are set to:

$$\begin{aligned} u_0(\varvec{x})&= 4\arctan \left( \exp \left( \frac{x_1 - z}{\sqrt{1-c^2}}\right) \right) {,}\\ v_0(\varvec{x})&= -\frac{2c}{\sqrt{1-c^2}}{{\,\textrm{sech}\,}}\left( \frac{x_1 - z}{\sqrt{1-c^2}}\right) {,} \end{aligned}$$

where z and c are the first components of the initial position and velocity of the solution, respectively. We compute two simulations with $c=0.7$, associated with the non-cloning effect, and $c=0.8$, resulting in the cloning effect of the soliton. The HDG scheme’s initial approximation is computed similarly to the system derived in Sect. 3.4, now imposing the zero Neumann boundary condition.

We approximate the solution of the problem by the HDG$_3$-ESPRK$_6$ method (18) on an unstructured triangulation with mesh parameter $h=0.1$. The stabilization of the HDG method is set to $\tau =10$, and a fixed time step of $\Delta t= h/10$ is taken. The evolution of both examples can be seen in Figs. 4a and b and the relative errors regarding their physical quantities can be seen in Fig. 5.

Our results replicate those obtained in [16], showing the cloning effect of the soliton along the domain given a specific initial velocity. Figure 4a shows the evolution over time of the kink soliton for $t=0,15,20,25$ with $c=0.7$. For this given velocity, the soliton cannot replicate itself through the channels and move backward. On the other hand, Fig. 4b shows the evolution of the kink soliton for $c=0.8$. In this case, the soliton moves forward through both channels proceeding to the right and upwards.

Furthermore, we present in Fig. 5 the evolution relative errors of the two approximations of the energy discussed in the previous example and the approximation of the momentum for each case $c=0.7$ and $c=0.8$ starting at $z=-10$. The discrete Hamiltonian gives an accurate approximation of the energy up to 13 digits of precision in both cases, with non-drifting behaviors as predicted by the Hamiltonian structure of the scheme.

Fig. 4

Example 3. Evolution of Kink soliton on T-shaped domain with velocity $c=0.7$ (a) and $c=0.8$ (b). We observe in (a) the non-cloning effect and in (b) the cloning effect of the kink soliton

Fig. 5

Example 3. Plots of the relative errors evolution for the approximations ${\mathcal {E}}_h$ (blue) and ${\mathcal {H}}_h$ (red) of the energy and ${\mathcal {M}}_h$ (black) of the momentum

7 Conclusions

We present Hamiltonian Mixed, DG, and HDG methods specifically devised to preserve the Hamiltonian structure of the semilinear wave Eq. (1). Our results extend several numerical schemes introduced for the linear wave equation to the nonlinear case. Moreover, we present a new class of discontinuous Galerkin methods with time operators defining their numerical traces. We prove in Theorem 4.3 that the scheme is energy-conserving and that the semidiscrete method is in Hamiltonian form. Numerical experiments demonstrate that the approximate solution converges optimally with an order of $k+1$ when using piecewise polynomial spaces of degree k. Also, a post-processed approximation of the displacement converges with an order $k+2$ consequence of the superconvergence properties. The experiments showcase the energy-conserving property of the approximations as a consequence of the Hamiltonian form of the scheme. We also replicate a soliton cloning effect over a Josephson Transmission line, frequently discussed in applications where computations over a long term are crucial. Additionally, we showcase the energy-preserving properties of the new DG method (10), proving its Hamiltonian structure numerically.

Finally, the error analysis of the new discontinuous Galerkin methods and methods for the nonlinear Schrödinger equation are subjects of ongoing investigation. Possible extensions to other nonlinear wave propagation problems using the Hamiltonian finite element methods could prove essential to devised energy-conserving methods suitable for computation over long periods.

Appendix A. Runge–Kutta Methods

Table 6 Order 6 SDIRK coefficients. Obtained from [21]

Table 7 Order 6 ESPRK coefficients. Obtained from [21]