Abstract
We study the non-Newtonian Stokes–Darcy–Forchheimer system modeling the free fluid coupled with the porous medium flow with shear/velocity-dependent viscosities. The unique existence is proved by using the theory of nonlinear monotone operator and a coupled inf-sup condition. Moreover, we apply the discontinuous Galerkin (DG) method with \(P^k/P^{k-1}\)-DG element for numerical discretization and obtain the well-posedness, stability, and error estimate. For both the continuous and the discrete problem, we explore the convergence of the Picard iteration (or called Kacǎnov method). The theoretical results are confirmed by the numerical examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Stokes–Darcy system modeling the interaction between the free Newtonian fluid and porous medium flow finds a wide application in engineering simulations. The mathematical and numerical analysis of this model has been extensively studied in recent years. However, many real-world fluid problems involve the non-Newtonian fluid (e.g., molten plastics, biological fluids, and engine oils with polymeric additives), and the Newtonian models are not suitable to apply. Several models exist for non-Newtonian free fluids, as discussed in [26]. These models include the Stokes/Navier–Stokes equations with varying types of shear-dependent viscosity (commonly referred to as the generalized Newtonian flow), the Oldroyd-B model, and the Peterlin viscoelastic model, among others. When dealing with non-Newtonian flow in a porous medium, it is generally agreed that the Darcy-Forchheimer model [13], which takes into account viscosity that varies with velocity, is a more suitable approach than the Darcy system. In this paper, we focus on the Stokes–Darcy–Forchheimer system with shear/velocity-dependent viscosities for the non-Newtonian fluid flow passing through the coupled porous medium region, which has massive applications in real-world simulation [17, 24], such as industrial filtering, plasma separation from blood, and so on.
There exist numerous works on numerical methods for coupled fluid models. We only select a few to introduce in the following, which we think are closely related to our model. For the non-Newtonian Stokes–Darcy equations with Beavers–Joseph–Saffman(BJS) interface condition, the finite element method (FEM) is proposed and analyzed [10], as well as the mortar FEM [11] and domain decomposition approach [19]. For the Newtonian (Navier–)Stokes–Darcy–Forchheimer model, the well-posedness and numerical discretization have been studied in [1, 2, 6, 7, 9], including the FEM, the fully-Mixed FEM, and a study on the residual-based a posteriori error estimates. The discontinuous Galerkin (DG) method satisfying the local conservation law is popular for coupled fluid computation. For the Stokes–Darcy system, [27, 29, 33] employs the DG method and mixed FEM for discretization, while [35, 36] adopts the DG scheme combined with the penalty and Nitsche’s approaches to treating the interface condition. In the present work, we apply the DG method for the non-Newtonian Stokes–Darcy–Forchheimer model with shear/velocity-dependent viscosities. To our knowledge, the well-posedness and numerical analysis have not been investigated for this nonlinear system.
It is important to note that various non-Newtonian fluids exhibit varying types of viscosity that are dependent on shear. In this article, we will provide some models for viscosity commonly utilized in describing biological fluids, paints, and similar substances [8, 10]. We denote by \({\varvec{D}}({\varvec{u}}):=(\nabla {\varvec{u}} + \nabla ^\top {\varvec{u}})/2\) the deformation tensor of fluids, and by \(g_1(|{\varvec{D}}({\varvec{u}})|)\) the dynamic viscosity [31] as a function of \({\varvec{D}}({\varvec{u}})\) expressed as
The effective viscosity \(g_2(\cdot )\) [10, 25] for the non-Newtonian porous media flow is determined by
We listed some choices of G(s) in Table 1.
The strong nonlinearity of \(g_1(\cdot )\) and \(g_2(\cdot )\) (see the above models), together with the Forchheimer term \(C_F|{\varvec{u_2}}|{\varvec{u_2}}\) (see (2.2a)), lead to analytical difficulties. The motivation of the present paper is to develop the well-posedness and numerical analysis for the Stokes–Darcy–Forchheimer model with shear/velocity-dependent viscosities. For the PDE model, we utilize the monotone theory [15, 23] to show the well-posedness. And we demonstrate a coupled inf-sup condition (see Lemma 2.4) to show the existence of pressure. The Picard iteration (or called Kacǎnov method) is applied to solve the nonlinear coupled system, and we develop the convergence theorems under different assumptions on \(g_1(\cdot )\) and \(g_2(\cdot )\).
For numerical approximation, we adopt the DG method with \(P^k/P^{k-1}\)-DG element \((k=1,2)\) for the velocity and pressure in both the Stokes and Darcy–Forchheimer regions. We show the well-posedness and a-priori estimates, and also investigate the convergence of the Picard iteration for the nonlinear discrete problem. For error analysis, we introduce the Lagrange multiplier formulation (cf. [21]) using \(P^k\)-DG element for the Lagrange multiplier, and obtain the error estimate \(O(h^k)\) for both velocity and pressure. Several numerical experiments are provided to confirm the theoretical results.
The rest of this article is arranged as follows. In Sect. 2, we derive the variational form of the coupled system and show the well-posedness. Moreover, we prove two convergence theorems for the Picard iteration. The DG scheme is presented in Sect. 3. We demonstrate the well-posedness, the convergence of Picard iteration, and the error estimates. Section 4 is devoted to numerical experiments.
2 The PDE Model and the Well-Posedness
2.1 The PDE Model and Notations
Let \(\Omega \) be an open smooth bounded domain in \({\mathbb {R}}^d\) (\(d = 2,3\)) consisting of the free fluid region \(\Omega _1\) and porous medium region \(\Omega _2\) separated by the interface \(\Gamma \). We denote by \({\varvec{n}}\) the unit outward normal vector to \(\partial \Omega \), and by \({\varvec{n_{12}}}\) the unit normal vector to \(\Gamma \) outward \(\Omega _2\), and set \(\Gamma _i:= \partial \Omega _i\backslash \Gamma \) (\(i = 1,2\)) and \({\varvec{n_{21}}}:= -{\varvec{n_{12}}}\). The velocities and pressures of the fluids in \((\Omega _1,\Omega _2)\) are denoted by \({\varvec{u}} =({\varvec{u_1}},{\varvec{u_2}})\) and \(p =(p_1,p_2)\). The model below represents the coupled non-Newtonian flow in \(\Omega _1\) and \(\Omega _2\).
The free flow in \(\Omega _1\) is governed by the non-Newtonian Stokes equations with shear-dependent viscosity and no-slip boundary condition on \(\Gamma _1\):
The flow in the porous medium domain \(\Omega _2\) is described by the Darcy–Forchheimer system with the velocity-dependent viscosity \(g_2(|{\varvec{u_2}}|)\):
where \(C_F\) is the Forchheimer coefficient and \({\varvec{K}}\) is a symmetric positive definite matrix representing the permeability of the porous medium satisfying
We will make assumptions on the boundedness and continuity of \(g_1(\cdot )\) and \(g_2(\cdot )\) (see (2.4) and (2.5)).
On interface \(\Gamma \), we enforce the conservation law, force balance, and the BJS condition, stated as follows:
where \(r_l\) denote frictional constants and \({\varvec{t_l}}\) denote the tangent vector on \(\Gamma \) (\(l = 1,\ldots ,d-1\)).
Remark 2.1
Beavers and Joseph proposed an experimental condition (called the BJ condition) that states the connection between the slip velocity and the shear stress along the interface, i.e.,
where \(c_l\) is the frictional constant, \(\mu \) is the viscosity. In view of the fact that the tangent velocity of the porous medium is much smaller than the other terms, Saffman proposed simplified interface condition [20, 30], also known as the BJS condition:
In this work, we use the same BJS condition as [10, 21] with dynamic viscosity and demonstrate the well-posedness of the coupling model. It is worth mentioning that the well-posedness of the BJ condition is unclear.
We assume that \(g_1(\cdot )\) is positive, bounded and Lipschitz continuous, and \(g_1(|{\varvec{A}}|){\varvec{A}}\) is strongly monotone, i.e., there exist positive constants \(\nu _{1\infty }\), \(\nu _{10}\), \(C_{g_1}\) and C such that, for any symmetric matrices \({\varvec{A}}, {\varvec{B}} \in {\mathbb {R}}^{d\times d}\):
Likewise, we suppose \(g_2(\cdot )\) satisfies the positivity, boundedness and Lipschitz continuous, and \(g_2(|{\varvec{a}}|){\varvec{a}}\) is strongly monotone, saying for all \({\varvec{a}}, {\varvec{b}} \in {\mathbb {R}}^d\),
where \(\nu _{2\infty }\), \(\nu _{20}\), \(C_{g_2}\), and C are all positive constants.
Remark 2.2
Suppose \(g_1(s), g_2(s) \in C^1({\mathbb {R}})\). We see that
Since we have assumed \(g_1(\cdot ) \ge \nu _{1\infty } > 0\) and \(g_2(\cdot ) \ge \nu _{2\infty } > 0\), the monotonicity (2.4c) and (2.5c) follow if \(g_1(s)\) and \(g_2(s)\) are nondecreasing, i.e., \(g_1^\prime (\cdot )\), \(g_2^\prime (\cdot ) \ge 0\). Otherwise, we have to assume that \(g'_1(|{\varvec{A}}|){\varvec{A}}\) and \(g'_2(|{\varvec{a}}|){\varvec{a}}\) are bounded such that
Remark 2.3
Note that the viscosity of the non-Newtonian fluid model we present in Table 1 displays shear-thinning behavior, which means that viscosity monotonically decreases as the shear rate increases, i.e., \(G^\prime (s)\le 0\). Most fluids show the shear thinning behavior in real life, such as blood, food, and beverages modeled by the famous Carreau fluid, and the flow in the porous medium, the Cross model, is generally considered [14, 18]. It is easy to observe that that G(s) presented in Table 1 satisfies
We see that \(g_1(\cdot )\) (resp. \(g_2(\cdot )\)) given by (1.1) (resp. (1.2)) allows a wide range of shear rate values, where the zero shear-rate (resp. velocity) corresponds to viscosity \(\nu _0\), and infinite shear-rate (resp. velocity) corresponds to \(\nu _\infty \), indicating the above assumptions (2.4a) (resp. (2.5a)). In addition, it is not difficult to validate that the assumptions (2.4b) and (2.4c) (resp. (2.5b) and (2.5c)) also hold for the models listed in Table 1.
To state the weak formulation, we introduce the function spaces:
where \((\cdot ,\cdot )_\omega \) represents the \(L^2(\omega )\) inner product. We endow the above spaces with the following norms:
Noting that \({\varvec{v_2}} \cdot {\varvec{n_{12}}} \in (W^{\frac{1}{3},\frac{3}{2}}_{00}(\Gamma ))^*\) for all \({\varvec{v_2}} \in X_2\), we set the space
which weakly enforces the interface condition (2.3a), i.e., the continuity of normal velocities on \(\Gamma \).
For any \({\varvec{u}} = ({\varvec{u_1}},{\varvec{u_2}})\), \({\varvec{v}} = ({\varvec{v_1}},{\varvec{v_2}}) \in X\) and \(q = (q_1,q_2) \in M\), we set
2.2 Weak Formulation
Testing (2.1a) and (2.2a) by \({\varvec{v_1}}\in X_1\) and \({\varvec{v_2}}\in X_2\) respectively, applying the integration by parts, and using the interface conditions (2.3), we obtain the weak formulation:
Find \(({\varvec{u}},p) \in V \times M \) such that
We introduce the space \( \Lambda :=W^{\frac{1}{3},\frac{3}{2}}_{00}(\Gamma ) \) with the norm \( \Vert \mu \Vert _\Lambda :=\Vert \mu \Vert _{W_{00}^{\frac{1}{3},\frac{3}{2}}(\Gamma )}, \) and the bilinear form
which satisfies the inf-sup condition [10, Lemma 3.2]: there is a constant \(\beta _I\) > 0 such that
It follows from (2.7) that (2.6) is equivalent to the Lagrange multiplier form:
Find \(({\varvec{u}},p,\lambda ) \in X \times M \times \Lambda \) such that
In fact, for sufficiently smooth \(({\varvec{u}}, p)\), one can verify that
2.3 The Unique Existence of Weak Solution
We now turn to the well-posedness of (2.6) (also (2.8)). To this end, we first prove that (2.11) admits a unique solution \({\varvec{u}}\). Then, we derive a coupled inf-sup condition, which implies the unique existence of p such that \(({\varvec{u}},p)\) solves (2.6). The well-posedness of (2.8) is a direct result from (2.7) and the unique existence of (2.6).
Setting
and \(\mathring{V}^*\) the dual of \(\mathring{V}\), we define a nonlinear operator \(A:\mathring{V}\rightarrow \mathring{V}^*\),
and consider the weak formulation:
Find \({\varvec{u}} \in \mathring{V}\) such that
Let us consider the existence and uniqueness of the (2.11). According to [23], we need to verify the hemicontinuity, coercivity, and monotonicity of A, which are illustrated by the following lemmas.
Lemma 2.1
The operator \(A:\mathring{V}\rightarrow \mathring{V}^*\) is continuous and bounded with the estimate
Proof
For any \({\varvec{u}} = ({\varvec{u_1}},{\varvec{u_2}})\in \mathring{V}\), we have \({\varvec{D}}({\varvec{u_1}})\in L^2(\Omega _1)^{d\times d}\) and \({\varvec{u_2}}\in L^3(\Omega _2)^d\) by the definition of space X. And the continuity condition of \(g_1(\cdot )\) and \(g_2(\cdot )\) (see (2.4b) and (2.5b)) implies \(g_1(|{\varvec{D}}({\varvec{u_1}}(x))|)\) and \(g_2(|{\varvec{u_2}}(x)|)\) are measurable on \(\Omega _1\) and \(\Omega _2\) respectively. We begin by proving the boundedness of A. Recalling the definition of operator norm and applying (2.10), we get
By using (2.4a), (2.5a) and \({\textrm{H}}{\ddot{{\textrm{o}}}}{\textrm{lder}}\)’s inequality [12],
Combining (2.13) with these inequalities, we get (2.12).
We proceed to show the continuity of A. Let \(\{{\varvec{u}}^{(n)}\}\) be a sequence in \(\mathring{V}\) satisfying \(\Vert {\varvec{u}}^{(n)} - {\varvec{u}}\Vert _{X}\rightarrow 0\). Then there exists a subsequence \(\{{\varvec{u}}^{(n^\prime )}\}\) and a function \({\varvec{h}} = ({\varvec{h_1}},{\varvec{h_2}})\in \mathring{V}\) such that
For any \({\varvec{w}}\in \mathring{V}\),
where
According to (2.15),
By (2.14) and the continuity of \(g_1(\cdot )\) and \(g_2(\cdot )\), we obtain
which implies
Then, we conclude by the dominated convergence theorem [5] that
It follows from (2.16) and (2.17) that
The proof is completed. \(\square \)
Remark 2.4
The continuity implies A is hemicontinuous, i.e., \(\forall {\varvec{u}}, {\varvec{v}},{\varvec{w}}\in \mathring{V}\),
Lemma 2.2
The operator A is coercive, i.e.,
In particular,
Proof
For all \({\varvec{v}} = ({\varvec{v_1}},{\varvec{v_2}})\in \mathring{V}\), by the Korn inequality [12], Poincaré inequality [5] and \(\nabla \cdot {\varvec{v_2}} = 0\),
Hence, we obtain (2.19), which implies (2.18). \(\square \)
Lemma 2.3
The operator A is strongly monotone, i.e., for all \({\varvec{u}}, {\varvec{v}}\in \mathring{V}\),
Proof
Let \({\varvec{u}}=({\varvec{u_1}},{\varvec{u_2}})\), \({\varvec{v}}=({\varvec{v_1}},{\varvec{v_2}})\in \mathring{V}\). We make the decomposition
By the monotonicity (2.4c) of \(g_1(\cdot )\), Korn inequality and Poincaré inequality, we have
For \(I_2\), (2.5c) implies
For \(I_3\), we calculate as follows
Hence, we conclude (2.20). \(\square \)
Theorem 2.1
There exists a unique solution \(u \in \mathring{V}\) to (2.11) satisfying
Proof
Since \(A:\mathring{V}\rightarrow \mathring{V}^*\) is hemicontinuous, coercive, and monotone (by Lemmas 2.1 to 2.3), the unique existence of \(A{\varvec{u}}={\varvec{f}}\) follows from [23, Theorem 2.1]. To obtain the a-priori estimate, we substitute \({\varvec{v}} = {\varvec{u}}\) into (2.11) and apply (2.19)
where we have used Young’s inequality and \(\Vert {\varvec{u_2}}\Vert _{X_2}=\Vert {\varvec{u_2}}\Vert _{L^3(\Omega _2)}\) (by \(\nabla \cdot {\varvec{u_2}}=0\)) in the last inequality. Hence, we conclude (2.24). \(\square \)
We have obtained the existence of \({\varvec{u}}\). Now let us prove an inf-sup condition which implies the unique existence of \(p\in M\) to (2.6).
Lemma 2.4
There is a constant \(\beta \) > 0 such that
Remark 2.5
A different inf-sup condition for the linear Stokes–Darcy equations is established in [21, Lemma 3.2]:
We modify this inf-sup condition and prove (2.25) to handle the case with \({\varvec{v_2}}\in L^{3}(\Omega _2)\), \(\nabla \cdot {\varvec{v_2}}\in L^{3}(\Omega _2)\) and \(p_2\in L^{\frac{3}{2}}(\Omega _2)\).
Proof
We make decomposition \(p_1 = \mathring{p}_1+\xi _1\), \(p_2 = \mathring{p}_2+\xi _2\), where
Since \(\int _{\Omega _1}q_1dx +\int _{\Omega _2}q_2dx = 0 \), we discover
There exists a \(\mathring{{\varvec{v}}}_\textbf{1}\in W^{1,2}_0(\Omega _1)\) such that
We select \({\hat{p}}_2 = \frac{|p_2|^{-\frac{1}{2}}p_2}{\Vert p_2\Vert _{L^{\frac{3}{2}}(\Omega _2)}^{\frac{1}{2}}} \in L^{\frac{3}{2}}(\Omega _2)\) (note that \(\Vert {\hat{p}}_2\Vert _{L^3(\Omega _2)}=1\)), and set \({\hat{\xi }}_2:=\frac{1}{|\Omega _2|}({\hat{p}}_2,1)_{\Omega _2}\), \(\mathring{\hat{p}}_2:={\hat{p}}_2 -{\hat{\xi }}_2\). By Hölder’s inequality, we have
Note that
For \(\mathring{\hat{p}}_2\), there exists a \(\mathring{\hat{{\varvec{v}}}}_\textbf{2}\in W^{1,3}_0(\Omega _2)\) satisfying
For arbitrary constant \(C^*>0\), there exist \(\tilde{{\varvec{v}}}_{{\varvec{1}}}\), \(\tilde{{\varvec{v}}}_{{\varvec{2}}}\) such that
Now, we set \({\varvec{v_1}}:=\mathring{{\varvec{v}}}_\textbf{1}+\tilde{{\varvec{v}}}_{{\varvec{1}}}\), \({\varvec{v_2}}:=\mathring{\hat{{\varvec{v}}}}_\textbf{2}+\tilde{{\varvec{v}}}_{{\varvec{2}}}\). In view of (2.27), (2.31) and the definition of \(p_1\), we find
It follows from (2.30) and (2.32) that,
Combining (2.34) and (2.35), and applying (2.26) and (2.28), we get
Taking sufficiently large \(\gamma \) and \(C^*=\gamma \frac{\xi _1}{|\xi _1|}\), we obtain
Next, by the triangle inequality, (2.27) and (2.33), we have
Similarly,
Therefore,
In summary, for any \(p\in M\), we have found \(({\varvec{v_1}}, {\varvec{v_2}})\) satisfying
which implies (2.25). \(\square \)
Remark 2.6
In view of the first inequality of (2.37), we can replace \(\Vert {\varvec{v_2}}\Vert _{X_2}\) of the above two inequalities by \(\Vert {\varvec{v_2}}\Vert _{W^{1,3}(\Omega _2)}\), which results
where
Theorem 2.2
There exists a unique \(p\in M\) and \(\lambda \in \Lambda \) such that \(({\varvec{u}}, p)\) solves (2.6) and \(({\varvec{u}},p,\lambda )\) solves (2.8). Moreover, we have
Proof
It follows from Theorem 2.1 and Lemma 2.4 that there exists a unique \(({\varvec{u}}, p)\in V\times M\) of (2.6). Furthermore, by (2.25)
In view of
together with \(L^3(\Omega _2)\subset L^2(\Omega _2)\) and Theorem 2.1, we obtain
Moreover, applying (2.7), we have the unique existence of (2.8), and the boundedness of \(\lambda \):
we get
Together with (2.41) we conclude (2.39). \(\square \)
2.4 Picard Iteration
To solve the nonlinear coupled problem (2.11), we utilize the Picard iterative method (also called Kačanov method) [3, 34]. For any \({\varvec{w}}, {\varvec{u}}, {\varvec{v}}\in \mathring{V}\), we define
Note that \(\hat{a}_1({\varvec{u_1}};{\varvec{u_1}},{\varvec{v_1}}) = a_1({\varvec{u_1}},{\varvec{v_1}})\) and \(\hat{a}_2({\varvec{u_2}};{\varvec{u_2}},{\varvec{v_2}}) = a_2({\varvec{u_2}},{\varvec{v_2}})\). (2.11) is equivalently expressed as:
Find \({\varvec{u}}\in \mathring{V}\) such that
The Kačanov method is stated as follows.
Given \({\varvec{u^{\text {(0)}}}} = ({\varvec{u_1^{\text {(0)}}}},{\varvec{u_2^{\text {(0)}}}})\), for \(l = 1, 2, \ldots ,\) find \({\varvec{u^{\text {(l )}}}}\in \mathring{V}\) such that
(2.43) is a linear elliptic problem admitting a unique solution. We turn to the convergence of Kačanov method. For briefness, we set
Theorem 2.3
Set the constants \(C_1:=\frac{C_{g_1}^2}{\nu _{1\infty }^2}\) and \(C_2:=(\frac{k_{\max }}{\nu _{2\infty }})^2(\frac{C_{g2}}{k_{\min }}+C_F)^2\). Under the assumption that
The unique solution \({\varvec{u}}^{(l)}\) of Picard iteration (2.43) converges to \({\varvec{u}}\). In particular,
Proof
Subtracting (2.43) from (2.42) and taking \({\varvec{v}} = {\varvec{\varepsilon ^{\text {(l )}}}}\), we have
which yields
Applying the Schwarz inequality to the above inequality, we achieve (2.45), which implies that \(\Vert {\varvec{D}}({\varvec{\varepsilon _1^{\text {(l )}}}})\Vert _{L^{2}(\Omega _1)}^2 + \Vert {\varvec{\varepsilon _2^{\text {(l )}}}}\Vert _{L^{2}(\Omega _2)} \le C C_I^l \downarrow 0\) as \(l \rightarrow \infty \) if \(C_I < 1\). \(\square \)
Remark 2.7
If \(\Vert {\varvec{D}}({\varvec{u_1}})\Vert _{L^{\infty }(\Omega _1)}^2\) and \(\Vert {\varvec{u_2}}\Vert _{L^{\infty }(\Omega _2)}\) are sufficiently small, then the assumption (2.44) is satisfied and the convergence is guaranteed. However, since the boundedness of \(\Vert {\varvec{D}}({\varvec{u_1}})\Vert _{L^{\infty }(\Omega _1)}^2\) and \(\Vert {\varvec{u_2}}\Vert _{L^{\infty }(\Omega _2)}\) is unprescribed, the assumption (2.44) is nontrivial to verify. Nevertheless, our numerical examples show the Picard iteration is quite applicable (see Sect. 4).
Next we consider the case that \(C_F = 0\) (i.e., the absence of the Forchheimer term \(C_F|{\varvec{u_2}}|{\varvec{u_2}}\)) and \(g_1(\cdot )\), \(g_2(\cdot )\) are non-increasing functions. We show that the Picard iteration converges without the assumption (2.44). In this case, the model becomes the non-Newtonian Stokes–Darcy system, and we introduce the function spaces:
Given \({\varvec{w}} \in \mathring{{\tilde{V}}}\), we define the bilinear form: for any \({\varvec{u}}, {\varvec{v}}\in \mathring{{\tilde{V}}}\),
The variational form and the Picard iteration are presented as follows.
Find \({\varvec{u}} \in \mathring{{\tilde{V}}}\) such that
Given \({\varvec{u^{\text {(0)}}}} = ({\varvec{u_1^{\text {(0)}}}},{\varvec{u_2^{\text {(0)}}}})\), for \(l = 1, 2, \ldots ,\) find \({\varvec{u^{\text {(l )}}}}\in \mathring{{\tilde{V}}}\) such that
It is apparent that, under (2.4) and (2.5), (2.47) admits a unique solution.
Proposition 2.1
If \(g_1(\cdot )^\prime \le 0\) and \(g_2(\cdot )^\prime \le 0\), then the Picard iteration (2.47) converges, i.e.,
Proof
We define a functional \(F:\mathring{{\tilde{V}}}\rightarrow {\mathbb {R}}\):
It is easy to check that
Since \(g_1(\cdot )^\prime \le 0\) and \(g_2(\cdot )^\prime \le 0\),
which implies
Moreover, \(B({\varvec{w}}; \cdot , \cdot )\) satisfies the continuity and coercivity (by (2.4a), (2.5a), Korn inequality and \(\nabla \cdot {\varvec{u}} =\nabla \cdot {\varvec{v}}=0\)): for all \({\varvec{u}}, {\varvec{v}} \in \mathring{{\tilde{V}}}\),
It follows from (2.48), (2.49) and [34, Theorem 25.L] that \({\varvec{u^{\text {(l )}}}} \rightarrow {\varvec{u}}\) in \(\mathring{{\tilde{V}}}\). \(\square \)
3 Discretization Scheme
We adopt the discontinuous Galerkin method to discretize the coupled system (2.1)–(2.3). In this section, we first prove the unique existence of the discrete solution and investigate the convergence of the Picard iteration, and then show the error estimates.
3.1 The Discontinuous Galerkin Approximation
We denote by \({\mathcal {T}}_i^h\) a regular and quasi-uniform triangulation of \(\Omega _i\), by \(\Gamma _i^h\) the set of interior facets, by \(h_E:= \textrm{diam}(E)\) the diameter of the element E, and by \(h:= \max _{E \in {\mathcal {T}}_1^h\cap {\mathcal {T}}_2^h} h_E\) the mesh size. We introduce the discontinuous finite element spaces:
where the \(P^k(E)\) is the space of polynomials of degree k on the element E (\(k = 1\) or 2).
Let \(\xi \) be a scalar or vector-valued function. We now introduce the average  and jump \([\![\xi ]\!]\) on each interior facet \(e\in \partial E_1\cup \partial E_2\),
and jump \([\![\xi ]\!]\) on each interior facet \(e\in \partial E_1\cup \partial E_2\),

If \(e\in \partial \Omega \) and \(e\in E_1\), then \(.\) The norms of the above spaces are given as follows
where the parameters \(\sigma _{1e}\) and \(\sigma _{2e}\) are positive constants, |e| is the length of edge e, and for \(i = 1,2,\)
The following trace inequalities (cf. [28]) will be used for analysis.
Assume that \({\mathcal {T}}_1^h\) and \({\mathcal {T}}_2^h\) match each other at interface \(\Gamma \). We denote by \({\mathcal {E}}^h\) the partition of the interface \(\Gamma \) inherited from \({\mathcal {T}}_1^h\) (also \({\mathcal {T}}_1^h\)), and set
For any \({\varvec{u^h}} = ({\varvec{u^h_1}},{\varvec{u^h_2}})\), \({\varvec{v^h}} = ({\varvec{v^h_1}},{\varvec{v^h_2}})\in X^h\) and \(q^h = (q^h_1,q^h_2)\in M^h\), we set

Multiplying the equations with the test function \({\varvec{v^h_1}}\in X_1^h\) and \({\varvec{v^h_2}}\in X_2^{h}\), integrating by parts over element E and summing over all element, we obtain the discrete scheme:
Find \(({\varvec{u^h}},p^h) \in V^h \times M^h\) such that
We introduce the quasi-local interpolation [29, 33] \(\Pi :=(\Pi _1,\Pi _2): X \rightarrow X_h\) satisfying
and the stability and error estimates
and, for any \(E\in {\mathcal {T}}_2^h\),
By the definition of \(\Pi _2\) ( [29, 33]), we have \(b_2(\Pi _2{\varvec{v_2}} -{\varvec{v_2}},q^h_2)=0\) \((\forall q_2^h\in M^h_2)\) and \(\int _e(\Pi _2{\varvec{v_2}} -{\varvec{v_2}})\cdot {\varvec{n_e}}{\varvec{w_2^h}}\cdot {\varvec{n_e}}~ds=0\) \((\forall {\varvec{w_2^h}}\in X^h_2)\), which also implies that
Together with
we see that
is valid. Noting that \(\Pi {\varvec{v}}\in V^h\) (\(\forall {\varvec{v}}\in V\)), we have (by (2.38)): for all \(p^h\in M^h\),
The following inf-sup condition can be proved analogously:
Moreover, we set the bilinear form
which satisfies (see [36, Lemma 4.6] for the definition of the discrete \(H^{-\frac{1}{2}}\) norm \(\Vert \cdot \Vert _{-\frac{1}{2}, \Lambda ^h}\)):
It follows from (3.8) that (3.2) is equivalent to the discrete Lagrange multiplier problem:
Find \(({\varvec{u^h}},p^h,\lambda ^h) \in V^h \times M^h \times \Lambda ^h\) such that
For pressure p and Lagrange multiplier \(\lambda \), we introduce the \(L^2\)-projection. Define \(P_M: L^2(\Omega _i) \rightarrow M^h_i\), \(P_\Lambda : L^2(\Gamma ) \rightarrow \Lambda _h\),
The following error estimates are valid:
3.2 Existence and Uniqueness of the Discrete Problem
We consider the well-posedness of (3.9) (also (3.13)) in this subsection. Set
and denote by \((\mathring{V}^h)^*\) the dual of \(\mathring{V}^h\). Define the nonlinear operator \(A^h:\mathring{V}^h\rightarrow (\mathring{V}^h)^*\),
We consider the discrete problem:
Find \({\varvec{u^h}} \in \mathring{V}^h\) such that
As with Sect. 2.3, we will verify the hemicontinuity, coercivity, and monotonicity of \(A^h\), which are presented by the following lemmas.
Lemma 3.1
The operator \(A^h\) is continuous and bounded, satisfying: for any \({\varvec{u^h}},{\varvec{v^h}}\in V^h\),
Proof
In the following, we only prove the boundedness (3.14). The continuity can be proved in the same way as Lemma 2.1. For any \({\varvec{u^h}}=({\varvec{u^h_1}},\ {\varvec{u^h_2}})\), \({\varvec{v^h}}=({\varvec{v_1^h}},{\varvec{v_2^h}})\in \mathring{V}^h\), using (3.1b) and Schwarz inequality, we calculate as

where \(E^+\) and \(E^-\) represent the two elements to which the edge e belongs. It follows from \(\mathrm H\ddot{o}lder\)’s inequality that,
Hence, combining the above inequalities, we deduce (3.14). \(\square \)
Lemma 3.2
If \(\sigma _{1e}\) is sufficiently large, then \(A^h\) is coercive, i.e.,
In particular,
Proof
For all \({\varvec{v^h}}=({\varvec{v_1^h}},{\varvec{v_2^h}})\in \mathring{V}^h\), by the discrete Korn’s inequality [4, 28] and (2.4a)
Applying (2.4a), (3.1b) and Young’s inequalities,

By taking sufficiently large \(\sigma _{1e}\) such that \(\sigma _{1e}- \nu _{1\infty } - C_3 > 0\),
Moreover, by (2.5a), we have
Hence, we obtain (3.16), which implies (3.15). \(\square \)
Lemma 3.3
We assume the boundedness of \(g_1^{\prime } ( |{\varvec{A}}| ){\varvec{A}}\), i.e.,
For sufficiently large \(\sigma _{1e}\), \(A^h\) is monotone, i.e., there is positive constant \(c_\alpha \) such that, for all \({\varvec{u^h}},{\varvec{v^h}}\in \mathring{V}^h\),
Proof
Let \({\varvec{u^h}}=({\varvec{u^h_1}},\ {\varvec{u^h_2}})\), \({\varvec{v^h}}=({\varvec{v_1^h}},{\varvec{v_2^h}})\in \mathring{V}^h\). By \(\big | g_1^{\prime } ( |{\varvec{A}}| ) \big | |{\varvec{A}}|\le C\) and (3.1b), we calculate as

Taking \(\sigma _{1e}>C_4+C\), together with (2.4c) and Korn’s inequality, we obtain
It follows from (2.22) and (2.23) that
Hence, we conclude (3.18). \(\square \)
Theorem 3.1
Under the assumptions (2.4), (2.5), (3.17), \({\varvec{f_1}}\in L^2(\Omega _1)\) and \({\varvec{f_2}}\in L^\frac{3}{2}(\Omega _2)\), there exists a unique solution \({\varvec{u^h}}\in \mathring{V}^h\) of (3.13). Moreover, there is a unique \(p^h\in M^h\) such that \(({\varvec{u^h}},p^h)\) solves (3.2), and exists a unique \(\lambda ^h\in \Lambda ^h\) such that \(({\varvec{u^h}},p^h,\lambda ^h)\) satisfies (3.9). Moreover,
Proof
Since \(A^h:\mathring{V}^h\rightarrow (\mathring{V}^h)^*\) is continuous (so that hemicontinuous), coercive, and monotone, there exists a unique \({\varvec{u^h}}\in \mathring{V}^h\) of (3.13). Substituting \({\varvec{v^h}}={\varvec{u^h}}\) into (3.13) and using (3.16)
which implies (3.19a). By the discrete inf-sup condition (3.6), there is a unique \(p^h\in M^h\) such that \(({\varvec{u^h}},p^h)\) solves (3.2), and we have the boundedness of \(p^h\):
In view of
and together with (3.20), we obtain the boundedness of \(p^h\) of (3.19b). The unique existence of \(\lambda ^h\in \Lambda ^h\) and (3.19b) follows from (3.8). \(\square \)
3.3 Picard Iteration for the Discrete Problem
As with Sect. 2.4, we apply the Picard iteration to solve the nonlinear discrete problem (3.13). We set
where

Note that \(\hat{a}_1^h({\varvec{u_1^h}};{\varvec{u_1^h}},{\varvec{v_1^h}}) = a_1^h({\varvec{u_1^h}},{\varvec{v_1^h}})\) and \(\hat{a}_2^h({\varvec{u_2^h}};{\varvec{u_2^h}},{\varvec{v_2^h}}) = a_2^h({\varvec{u_2^h}},{\varvec{v_2^h}})\). (3.13) is equivalently expressed by:
Find \({\varvec{u^h}}\in \mathring{V}^h\) such that
The Picard iteration is stated as follows.
Given \({\varvec{u}}^{{\varvec{h}},\text {(0)}} = ({\varvec{u_1^{{\varvec{h}},{({0})}}}},{\varvec{u_2^{{\varvec{h}},{({0})}}}})\), for \(l = 1, 2, \ldots ,\) find \({\varvec{u}}^{{\varvec{h}},\text {(l )}}\in \mathring{V}^h\) such that
Setting \({\varvec{\varepsilon }}^{{\varvec{h}},(l)} = ({\varvec{\varepsilon _1^{{\varvec{h}},\text {(l )}}}},{\varvec{\varepsilon _2^{{\varvec{h}},\text {(l )}}}}):= ({\varvec{u_1^h}} - {\varvec{u_1^{{\varvec{h}},\text {(l )}}}},{\varvec{u_2^h}} - {\varvec{u_2^{{\varvec{h}},\text {(l )}}}})\), we turn to the convergence of the iteration.
Theorem 3.2
We set the constants \(C_1:=C_{g_1}^2\frac{C_t^2\nu _{1\infty }+4}{2\nu _{1\infty }^2}\) and \(C_2:=\left( \frac{k_{\max }}{\nu _{2\infty }}\right) ^2\left( \frac{C_{g2}}{k_{\min }}+C_F\right) ^2\). If \(\sigma _{1e}\) is sufficient large and
then the Picard iteration (3.22) converges. In particular,
Proof
Same with the proof of Theorem 2.3, we subtract (3.22) from (3.21), and choose \({\varvec{v^h}} = {\varvec{\varepsilon }}^{{\varvec{h}},(l)}\),
Applying (2.4b), (3.1b) and Young’s inequalities, we have

and

where \(C= \frac{\nu _{10}^2C_t^2}{\nu _{1\infty }}\). Therefore (3.25) yields
Summing up the above two inequalities and taking sufficiently large \(\sigma _{1e}\) such that \(\sigma _{1e}-1-C > 0\), we conclude (3.24). \(\square \)
3.4 The Error Estimates
Theorem 3.3
Let \(({\varvec{u}},p,\lambda )\) and \(({\varvec{u^h}},p^h,\lambda ^h)\) be the solutions of (2.8) and (3.9), respectively. For \(k=1,2\), suppose we have the regularity \({\varvec{u}}_1 \in (H^{k+1}(\Omega _1)) \cap W^{1,\infty }(\Omega _1)\) and \({\varvec{u}}_2 \in (H^k(\Omega _2)) \cap W^{1,r}(\Omega _2)\) \((r \ge d)\) and \(p_i \in H^{k}(\Omega _i)\) \((i = 1,2)\). Then, under the assumptions (2.4), (2.5) and (3.17), we have
Proof
For briefness, we set the notations:
By the triangle inequality and interpolation/projection errors (3.4), (3.5) and (3.11), it suffices to evaluate \(\Vert \tilde{{\varvec{u}}}^{{\varvec{h}}} -{\varvec{u^h}}\Vert _{X^h}\) and \(\Vert {\tilde{p}}^{h}_i - p^h_i\Vert _{L^2(\Omega _i)}\).
It follows from (3.18) that
The task is to bound \({\textrm{I}}\) and \({\textrm{II}}\). To this end, we decompose \({\textrm{I}}\) into three parts \(\{ {\textrm{I}}_i \}_{i=1}^3\) and estimates them as follows. By (2.4a), (2.4b) and (3.4),
where \(C_{\infty 1}=(\nu _{10}+C_{g1}\Vert {\varvec{D}}({\varvec{u_1}})\Vert _{L^{\infty }(\Omega _1)})\), and \(\eta \) is an arbitrary positive constant. Let \(I_h{\varvec{v_1}}\in X_1^h\) be the Lagrange interpolation of \({\varvec{v_1}}\) satisfying
By using (3.1b) and (3.1a), noting that  ,
,  , we calculate as (the last inequality follows from (3.4) and (3.28))
, we calculate as (the last inequality follows from (3.4) and (3.28))

In view of
we derive (by (2.5a), (2.5b) and (3.5a))
Summing up the above estimates of \(\{ {\textrm{I}}_i \}_{i=1}^3\), we achieve
Now we turn to the estimates of \({\textrm{II}}\). Subtracting (3.9) from (2.8), we obtain
Substituting \({\varvec{v^h}} = \tilde{{\varvec{u}}}^h-{\varvec{u}}^h\) into (3.30), we have
which yields
It follows from (3.10a), (3.10b) and (3.11a) that

Together with (3.29), we get
By (3.27), the triangle inequality and taking \(c_\alpha -\eta > 0\), we conclude (3.26a).
It remains to estimate the error of pressure. Applying the inf-sup condition (3.7), (3.30) and (3.10b),
The numerator is bounded as follows.
where \(\Vert {\varvec{u_2^h}}\Vert _{L^3(\Omega _2)}\) is bounded by Theorem 3.1. By the discrete Sobolev embedding \( \Vert {\varvec{v_2^h}}\Vert _{L^6(\Omega _2)}\le C \Vert {\varvec{v_2^h}}\Vert _{X^h_2,W^{1,2}}, \) we obtain
Together with the triangle inequality and the projection error (3.11a), we conclude (3.26b). \(\square \)
4 Numerical Experiments
We first carry out the numerical experiments using \(P^k/P^{k-1}\)-DG element with \(k=1,2\) respectively, and investigate the experimental convergence rates and the performance of the Picard iteration. Secondly, we present a simulation of the industrial filtration system (cf. [17, 22]) with curved interface \(\Gamma \). Then the non-constant permeability [16, 32, 33] is considered with a curved interface in the porous medium.
4.1 Example 1: The Experimental Convergence Rates
We set \(\Omega _1 = \{(x,y):\; 0<x<1,\;1<y<2\}\) and \(\Omega _2 = \{(x,y):\; 0<x<1,\;0<y<1\}\) with the interface \(\Gamma = \{(x,1): 0<x<1\}\) and the boundaries \(\Gamma _1 = \partial \Omega _1\backslash \Gamma \), \(\Gamma _2 = \partial \Omega _2\backslash \Gamma \). Choose the parameters \(C_F=1\), \({\varvec{K}}=I\), and the viscosity functions \(g_1(|{\varvec{D}}({\varvec{u_1}})|)\) and \(g_2(|{\varvec{u_2}}|)\) of the Carreau model with \(\nu _{1\infty }=\nu _{2\infty } = 0.001\), \(\nu _{10} = \nu _{20} = 0.5\), \(G_1(|{\varvec{D}}({\varvec{u_1}})|) = (1+0.5|{\varvec{D}}({\varvec{u_1}})|^2)^{-0.25}\) and \(G_2(|{\varvec{u_2}}|) = (1+0.5|{\varvec{u_2}}|^2)^{-0.25}\). The exact solution is stated as follows.
where \({\varvec{n_{12}}} = (0,-1)^t\). We replace the homogeneous Dirichlet boundary condition (2.1c) with the inhomogeneous one. The solutions \({\varvec{u_1}}\) and \({\varvec{u_2}}\) are divergence-free in \(\Omega _1\) and \(\Omega _2\), respectively. In particular, the BJS condition (2.3c) is satisfied with \(r_l=1\).
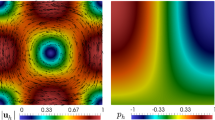
Taking \(\sigma _{1e} = 0.5\) and \(\sigma _{2e} = 1\), we carry out the simulation using \(P^1/P^{0}\)-DG element and \(P^2/P^{1}\)-DG element, respectively. The numerical solutions with \(P^2/P^{1}\)-DG element and \(h=\frac{1}{64}\) are plotted in Fig. 1. The experimental errors and convergence rates are presented in Tables 2 and 3, where we observe the \(O(h^k)\)-convergence of the errors for both the velocity and pressure in two subregions. The experimental results confirm the theoretical error estimates obtained by Theorem 3.3. We also compute the experimental \(L^2\)-error of the Lagrange multiplier \(\lambda _h\) on the interface (see Tables 2 and 3), where the exact \(\lambda \) is obtained by using the formula (2.9).
Furthermore, at l-th iteration step (\(l = 1,2,\ldots \)), we compute the errors \(Eu_i^{(l)}:= \Vert {\varvec{u_i}}^{{\varvec{h}},\text {(l )}} - {\varvec{u_i}}^{{\varvec{h}},(l-1)}\Vert _{X^h_i}\) and \(Ep_i^{(l)}:= \Vert p_i^{h,(l)}-p_i^{h,(l-1)}\Vert _{L^2(\Omega _i)}\) (\(i=1,2\)), and plot them in Fig. 2(1) in log-scale. We see the iteration error decreases exponentially fast, indicating the Picard iteration’s good applicability.
4.2 Example 2: The Dead-end Filter Domain
We consider the region of a concentric quarter circular. The entire domain is divided into the Stokes region \(\Omega _1=\{(x,y):2<x^2+y^2<3, x>0, y>0\}\) and the Darcy region \(\Omega _2=\{(x,y):1< x^2+y^2<2, x>0, y>0\}\) with the interface \(\Gamma =\{(x,y):x^2+y^2=2\}\), and the boundaries \(\Gamma _1=\partial \Omega _1\backslash \Gamma \), \(\Gamma _2=\partial \Omega _2\backslash \Gamma \), \(\Gamma _{21}=\{(x,y):x^2+y^2=1\}\) and \(\Gamma _{22}=\Gamma _2\backslash \Gamma _{21}\). The following boundary conditions are imposed.
We take \(g_1(|{\varvec{D}}({\varvec{u_1}})|)\) and \(g_2(|{\varvec{u_2}}|)\) of the Carreau model with \(G_1(|{\varvec{D}}({\varvec{u_1}})|) = (1+0.5|{\varvec{D}}({\varvec{u_1}})|^2)^{-0.425}\), \(G_2(|{\varvec{u_2}}|) = (1+0.5|{\varvec{u_2}}|^2)^{-0.425}\), \(\nu _{1\infty } = 0.001\), \(\nu _{10} = 0.1\), \(\nu _{2\infty } = 1\) and \(\nu _{20} = 10\). We adopt \(P^2/P^{1}\)-DG element with \(\sigma _{1e} = 10\) and \(\sigma _{2e} = 10\), and plot the numerical solutions with different permeability \({\varvec{K}}\) and Forchheimer coefficient \(C_F\) in Figs. 3, 4, 5, 6, 7. The velocity fields of these four cases are almost the same. In contrast, the magnitude of the pressure behaves differently, which depends on the permeability \({\varvec{K}}\) and the Forchheimer coefficient \(C_F\). The filtration pressure increases dramatically when \({\varvec{K}} \ll 1\) or \(C_F \gg 1\). In this example, we also observe exponentially fast decreasing errors of the Picard iteration (see Fig. 2(2) with \({\varvec{K}} = 10^{-5}I\) and \(C_F = 1\)).
4.3 Example 3: The Varying Permeability Models
In the previous example, the permeability is chosen as a constant. To be more realistic, in this subsection, we explore the velocity and pressure behavior in the coupled domain for non-constant permeability. Particularly, we use the same Stokes and Darcy region, boundary conditions and the non-Newtonian models configuration as in Example 2.
First, we carry out the simulation with a periodic permeability \(K = k_{per}I\) with
\(k_{per}^{-1}\) is plotted in Fig. 8(1). We utilize the \(P^2/P^{1}\)-DG element to calculate \({\varvec{u^h}}\) and \(p_h\), and observe that the velocity and pressure behave periodically as permeability (see Fig. 9).
Next, we randomly selecte a value for \(k_{per}^{-1}\) between 500 and 2000 in a coarse mesh (see Fig. 8(2)). Note that to ensure the accuracy of the calculation, we compute the solution on a refined mesh (see Fig. 8(3)). Figure 10 displays the simulation results, which show that the fluid tends to flow towards with higher permeability in the porous medium region.
In addition, the iteration errors for both the periodic and random permeability cases are plotted in Fig. 2(3)(4), indicating the good applicability of the Picard iteration.
4.4 Concluding Remark
In this remark, we summarize the assumptions made during our theoretical analysis. To establish the well-posedness of the non-Newtonian Stokes-Darcy-Forchheimer model (see Theorems 2.1), we assume the positivity, boundedness, Lipschitz continuity, and strong monotonicity of \(g_1(\cdot )\) and \(g_2(\cdot )\) (as described in (2.4) and (2.5)). We have discussed these assumptions in Remark 2.3, and can confirm that they are satisfied for various non-Newtonian models, such as the Carreau model, Cross model, Powell-Eyring model, and so on, which are listed in Table 1. In order to establish the well-posedness of the \(P^k/P^{k-1}\)-DG approximation problem (3.2) (as stated in Theorem 3.1), it is necessary to take sufficiently large coefficients \(\sigma _{1e}\) and \(\sigma _{2e}\) for the stabilization terms (as explained in Lemmas 3.2 and 3.3). Additionally, we assume that \(g_1^{\prime } ( |{\varvec{A}}| ){\varvec{A}}\) is bounded (see Lemma 3.3), which is true for the models with parameters listed in Table 1.
Furthermore, to obtain the error analysis of the DG method (see Theorem 3.3), we make the regularity assumption \({\varvec{u}}_1 \in (H^{k+1}(\Omega _1)) \cap W^{1,\infty }(\Omega _1)\) and \({\varvec{u}}_2 \in (H^k(\Omega _2)) \cap W^{1,r}(\Omega _2)\) \((r \ge d)\) and \(p_i \in H^{k}(\Omega _i)\) \((i = 1,2)\). To guarantee the convergence of the Picard iteration of the continuous (resp. discrete) problem (see Theorem (2.3) (resp. 3.2)), we introduce a sufficient condition (2.44) (resp. (3.23)), which takes into account the \((W^{1,\infty }, L^\infty )\)-norm of \(({\varvec{u_1}}, {\varvec{u_2}})\) (or \(({\varvec{u_1^h}}, {\varvec{u_2^h}})\)). However, validating this condition can be challenging. Despite this, we find that the Picard iteration is effective in simulating various types of permeability, as demonstrated in our numerical examples.
Data availibility
The authors confirm that the data supporting the findings of this study are available within the article.
References
Almonacid, J.A., Díaz, H.S., Gatica, G.N., Márquez, A.: A fully mixed finite element method for the coupling of the Stokes and Darcy–Forchheimer problems. IMA J. Numer. Anal. 40(2), 1454–1502 (2020). https://doi.org/10.1093/imanum/dry099
Amara, M., Capatina, D., Lizaik, L.: Coupling of Darcy–Forchheimer and compressible Navier–Stokes equations with heat transfer. SIAM J. Sci. Comput. 31(2), 1470–1499 (2009)
Badea, L., Discacciati, M., Quarteroni, A.: Numerical analysis of the Navier–Stokes/Darcy coupling. Numerische Mathematik 115(2), 195–227 (2010)
Brenner, S.C.: Korn’s inequalities for piecewise \({H}^1\) vector fields. Math. Comput. 73(247), 1067–1087 (2003)
Brezis, H.: Functional Analysis. Sobolev spaces and Partial Differential Equations. Springer, New York, NY (2011)
Caucao, S., Gatica, G.N., Oyarzúa, R., Sandoval, F.: Residual-based a posteriori error analysis for the coupling of the Navier–Stokes and Darcy–Forchheimer equations. ESAIM M2AN 55, 659–687 (2021)
Caucao, S., Gatica, G.N., Sandoval, F.: A fully mixed finite element method for the coupling of the Navier–Stokes and Darcy–Forchheimer equations. Numer. Methods Partial Differ. Eq. 37, 2550–2587 (2021)
Chow, S.S., Carey, G.F.: Numerical approximation of generalized Newtonian fluids using Powell–Sabin–Heindl elements. I. Theoretical estimates. Int. J. Numer. Meth. Fluids 41(10), 1085–1118 (2003). https://doi.org/10.1002/fld.480
Cimolin, F., Discacciati, M.: Navier–Stokes/Forchheimer models for filtration through porous media. Appl. Numer. Math. 72(2), 205–224 (2013)
Ervin, V.J., Jenkins, E.W., Sun, S.: Coupled generalized nonlinear Stokes flow with flow through a porous medium. SIAM J. Numer. Anal. 47(2), 929–952 (2009). https://doi.org/10.1137/070708354
Ervin, V.J., Jenkins, E.W., Sun, S.: Coupling nonlinear Stokes and Darcy flow using mortar finite elements. Appl. Numer. Math. 61(11), 1198–1222 (2011)
Evans., L.C.: Partial differential equations, Graduate Studies in Mathematics, vol. 19. Amer. Math. Soc., Providence, RI (2010)
Forchheimer, P.: Wasserbewegung durch boden. Z. Ver. Deutsh. Ing. 45, 1782–1788 (1901)
Galdi, G.P.: Mathematical Problems in Classical and Non-Newtonian Fluid Mechanics, pp. 121–273. Birkhäuser Basel, Basel (2008). https://doi.org/10.1007/978-3-7643-7806-6_3
Girault, V., Raviart., P.A.: Finite Element Methods for Navier–Stokes equations: theory and algorithms. Springer-Verlag, Berlin (1986). https://doi.org/10.1007/978-3-642-61623-5
Girault, V., Rivière, B.: DG approximation of Coupled Navier–Stokes and Darcy Equations by Beaver–Joseph–Saffman interface condition. SIAM J. Numer. Anal. 47(3), 2052–2089 (2009)
Hanspal, N.S., Waghode, A.N., Nassehi, V., Wakeman, R.J.: Numerical analysis of coupled Stokes/Darcy flows in industrial filtrations. Transp. Porous Med. 64, 73–101 (2006)
Hauswirth, S.C., Bowers, C.A., Fowler, C.P., Schultz, P.B., Hauswirth, A.D.W.T., Miller, C.T.: Modeling cross model non-Newtonian fluid flow in porous media. J. Contam. Hydrol. 235, 103708 (2020). https://doi.org/10.1016/j.jconhyd.2020.103708
Hoang, T.T.P., Lee, H.: A global-in-time domain decomposition method for the coupled nonlinear Stokes and Darcy flows. J. Sci. Comput. 87, 22 (2021)
Jäger, W., Mikelić, A.: On the interface boundary condition of Beavers, Joseph, and Saffman. SIAM J. Appl. Math. 60(4), 1111–1127 (2000). https://doi.org/10.1137/S003613999833678X
Layton, W.J., Schieweck, F., Yotov, I.: Coupling fluid flow with porous media flow. SIAM J. Numer. Anal. 40(6), 2195–2218 (2003)
Li, R., Li, J., He, X., Chen, Z.: A stabilized finite volume element method for a coupled Stokes–Darcy problem. Appl. Numer. Math. 133, 2–24 (2018)
Lions., P.L.: Quelques Méthodes de Résolution des Problèmes aux Limites Non Linéaires. Dunod (1969)
Pan, H., Rui, H.: Mixed element method for two-dimensional Darcy–Forchheimer model. J. Sci. Comput. 52(3), 563–587 (2012). https://doi.org/10.1007/s10915-011-9558-3
Pearson, J.R.A., Tardy, P.M.J.: Models for flow of non-Newtonian and complex fluids through porous media. J. Non-Newtonian Fluid Mech. 102, 447–473 (2002)
Renardy, M.: Mathematical Analysis of Viscoelastic Flows. SIAM (2000)
Rivière, B.: Analysis of a discontinuous finite element method for the coupled Stokes and Darcy problems. J. Sci. Comput. 22, 479–500 (2005). https://doi.org/10.1007/s10915-004-4147-3
Rivière., B.: Discontinuous Galerkin methods for Solving Elliptic and Parabolic Equations: Theory and Implementation. SIAM, Philadelphia (2008). https://doi.org/10.1137/1.9780898717440
Rivière, B., Yotov, I.: Locally conservative coupling of Stokes and Darcy flows. SIAM J. Numer. Anal. 42(5), 1959–1977 (2005). https://doi.org/10.1137/S0036142903427640
Saffman, P.: On the boundary condition at the surface of a porous medium. Stud. Appl. Math. 50, 93–101 (1971)
Sequeira, A.: Hemorheology: non-Nsewtonian constitutive models for blood flow simulations. In: Farina, A., Mikelić, A., Rosso, F. (eds.) Non-Newtonian Fluid Mechanics and Complex Flows, Lecture Notes in Mathematics, vol. 2212, pp. 1–44. Springer (2016)
Vassilev, D., Yotov, I.: Coupling Stokes–Darcy flow with transport. J. Sci. Comput. 31(5), 3661–3684 (2009). https://doi.org/10.1137/080732146
Wen, J., Su, J., He, Y., Chen, H.: A discontinuous Galerkin method for the coupled Stokes and Darcy problem. J. Sci. Comput. 85, 26 (2020). https://doi.org/10.1007/s10915-020-01342-6
Zeidler., E.: Nonlinear functional analysis and its applications II/B: Nonlinear monotone operators. Springer-Verlag (1990)
Zhou, G., Kashiwabara, T., Oikawa, I., Chung, E., Shiue, M.C.: Some DG schemes for the Stokes–Darcy problem using P1/P1 element. Japan J. Indust. Appl. Math. 36, 1101–1128 (2019)
Zhou, G., Kashiwabara, T., Oikawa, I., Chung, E., Shiue, M.C.: An analysis on the penalty and Nitsche’s methods for the Stokes-Darcy system with a curved interface. Appl. Numer. Math. 165, 83–118 (2021)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare. All co-authors have seen and agree with the contents of the manuscript, and there is no financial interest to report.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research was partially supported by NSFC General Projects No. 12171071,and the Natural Science Foundation of Sichuan Province (No. 2023NSFSC0055). All data generated or analysed during this study are included in this published article.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Hu, J., Zhou, G. The Well-Posedness and Discontinuous Galerkin Approximation for the Non-Newtonian Stokes–Darcy–Forchheimer Coupling System. J Sci Comput 97, 24 (2023). https://doi.org/10.1007/s10915-023-02344-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02344-w