An Improved Arrow–Hurwicz Method for the Steady-State Navier–Stokes Equations

Abstract

This paper presents a novel Arrow–Hurwicz type method for approximating the steady-state Navier Stokes equations using the finite element method. The novel method is inspired from artificial compressibility regularization of unsteady incompressible flows and allows one to circumvent solving saddle-point equations. We derive uniform boundedness and convergence to the exact solution whenever the small data condition for uniqueness of the solution is satisfied. A two-grid version of the scheme is also discussed. Numerical schemes show that the novel scheme significantly accelerates the convergence, without any additional computational cost or decreased accuracy.

1 Introduction

In this paper we consider an improved Arrow–Hurwicz (AH) method for solving the steady-state Navier Stokes equations (NSE) in a domain $\Omega \subset \mathbb {R}^d, d\in \{2,3\},$ with Lipschitz boundary $\partial \Omega$ given by

$$\begin{aligned} \textbf{u}\cdot \nabla \textbf{u}-\nu \Delta \textbf{u}+\nabla p&=\textbf{f}\,\, \text {in} \, \Omega \text {,} \, \end{aligned}$$

(1.1)

$$\begin{aligned} \nabla \cdot \textbf{u}&=0\,\, \text {in} \, \Omega , \end{aligned}$$

(1.2)

$$\begin{aligned} \textbf{u}&=0 \,\, \text {on}\ \partial \Omega , \end{aligned}$$

(1.3)

where $\textbf{u}$ is the fluid velocity, p the pressure, $\nu >0$ the kinematic viscosity and $\textbf{f}$ represents the prescribed external body force. A well-known result states that (1.1)–(1.3) always has a solution and its uniqueness is guaranteed under a small data condition [34]:

$$\begin{aligned} \Lambda = \nu ^{-2}\mathcal {M}\Vert \textbf{f}\Vert _{-1}\le 1 , \end{aligned}$$

(1.4)

where

$$\begin{aligned} \mathcal {M} = \sup \limits _{\textbf{u}, \textbf{v}, \textbf{w}\in H^1_0(\Omega )} \dfrac{(\textbf{u}\cdot \nabla \textbf{v}, \textbf{w})}{\Vert \nabla \textbf{u}\Vert \Vert \nabla \textbf{v}\Vert \Vert \nabla \textbf{u}\Vert }. \end{aligned}$$

(1.5)

The need to solve stationary NSE, (1.1)–(1.3) arises in many applications. For instance, certain hemodynamic flows occur at steady regimes [35]. More commonly, numerical benchmarking of high Reynolds number flows such the Taylor-Coutte flow [15, 29, 30] or the high Rayleigh number natural convection problems [32, 33] is performed by continuation method, where the simulations are usually initiated at smaller values of the physical parameters and are gradually increased. In such circumstances, pseudo-time stepping with unsteady flow codes usually takes a very large number of iterations or demands prohibitively fine mesh and there is a need for alternative and more efficient ways of finding the stationary solutions. One could accelerate the convergence to steady-state by adopting the pseudo-time stepping algorithm based on relaxation/penalty approach of [23], but we shall not pursue this approach here.

Numerical solution of (1.1)–(1.3) requires the linearization of the nonlinear term, commonly performed via Newton or Picard fixed point iterations [20], resulting in Oseen-type equation. The spacial discretization of (1.1)–(1.3) then requires solution of large saddle point problems [4], which are often solved by the preconditioned GMRES method [5, 31]. On the other hand, numerical schemes decoupling the equations for velocity and pressure variables are usually preferred due to their numerical efficiency. Usually such schemes are developed for unsteady flows, the most well-known of them being the projection [18] and artifical compressibility [16, 17] schemes. For steady Navier–Stokes Eqs. (1.1)–(1.3), classical methods are the Uzawa methods [4], the iterated penalty Picard method [7] and the Arrow–Hurwicz (AH) method [3].

The iterative AH scheme for solving the incompressible flow system (1.1)–(1.3) was first introduced by Temam [34]:

$$\begin{aligned} -\frac{1}{\rho }\Delta \left( \textbf{u}^{n+1}-\textbf{u}^{n} \right) + \textbf{u}^n \cdot \nabla \textbf{u}^{n+1} - \nu \Delta \textbf{u}^{n} + \nabla p^{n}&=\textbf{f}\, \text {in} \, \Omega \text {,} \, \end{aligned}$$

(1.6)

$$\begin{aligned} \alpha (p^{n+1}-p^n ) + \rho \nabla \cdot \textbf{u}^{n+1}&=0\, \text {in} \, \Omega , \end{aligned}$$

(1.7)

and it was shown to be weakly convergent to the unique solution $(\textbf{u},p)$ of (1.1)–(1.3) under some restrictions on the value of $\rho$ and the condition (1.4). The classical AH method is an inexact version of Uzawa algorithm and it has been applied for solving various saddle point problems, cf. [19]. The finite element analysis of the AH algorithm (1.6)–(1.7) was considered in [6], where it shown to be a contractive algorithm under certain choices of parameters. Even though the convergence rate was shown to be less than one, it was observed to require a very large number of iterations even for small Reynolds number $(\textrm{Re})$ flow problems (e.g., more than 700 iterations for $\textrm{Re}=100$ two-dimensional cavity flow). A grad-div enhanced AH algorithm (1.6)–(1.7) was recently investigated in [11]. It was shown that, under a certain choice of parameters, the additional grad-div operator improves the convergence. However, the contractivity was shown to hold if $\Lambda < \frac{2}{3}$, which is more restrictive condition than (1.4). The authors also considered an AH scheme synthesized with the Anderson accelaration extrapolation technique and obtained much improved method at the cost of an additional computational complexity.

The AH Algorithm has also been studied with two-grid schemes. The general idea of two-grid methods consist of solving the computationally “cheap” iterations on a coarser mesh and then performing a few “expensive” runs on a fine mesh, thereby saving a large amount of CPU time without sacrificing the accuracy. Some notable studies in the literature are made by Ammi et al. [2], Layton et al. [26, 27], Girault et al. [13], and Li et al. [28]. For the steady state NSE, He et al. developed the two-level stabilized finite element techniques in [21] and a simplified two-level finite element method in [20]. Another related notable work is due to Du et. al. [9], where the authors extended the two-grid AH methods that were originally proposed by Xu et. al. [36, 37].

In the current study, we present novel and improved AH schemes inspired by the first order in time artificial compressibility method. When this idea is adapted to the classical AH system, the only change is observed in one term of the momentum equation. However, the acceleration on convergence speed is notable in terms of CPU time. We utilize the same idea for both single grid and two grid AH algorithms and the results obtained by various numerical examples are quite promising.

The plan of the paper is as follows: Some well-known mathematical foundations and notations used throughout the entire study are given in Sect. 2. Section 3 is devoted for introduction and mathematical analysis for improved AH scheme in single grid considerations and Sect. 4 presents similar concepts for the two grid case. Section 5 demonstrates several numerical examples which support theoretical findings and demonstrate the effectiveness of the schemes introduced. The paper is finalized with some concluding remarks.

2 Notations and Preliminaries

Standard notations for Sobolev spaces and corresponding norms will be used throughout the paper, see e.g., [1]. In particular, $(\cdot ,\cdot )$ and $\Vert \cdot \Vert$ denote $L^2(\Omega )$ inner product and the corresponding norm, respectively. $\textbf{H}^{k}$, where k is an integer greater than zero, will denote the space of vector valued functions each of whose n components belong to $H^k$, the Sobolev space of real-valued functions with square integrable derivates of order up to k equipped with the usuual norm $\Vert \cdot \Vert _k$. The dual space of $\textbf{H}^{k}$ will be denoted by $\textbf{H}^{-k}$.

The equivalent weak formulation of (1.1)–(1.3) reads as follows: $\forall (\textbf{v},q)\in (\textbf{X},Q)$, find $(\textbf{u},p)\in (\textbf{X},Q)$ satisfying

$$\begin{aligned} \nu (\nabla \textbf{u}, \nabla \textbf{v})+b^*(\textbf{u},\textbf{u},\textbf{v})-(p,\nabla \cdot \textbf{v})&= (\textbf{f},\textbf{v}), \end{aligned}$$

(2.1)

$$\begin{aligned} (\nabla \cdot \textbf{u},q)&= 0, \end{aligned}$$

(2.2)

where $\textbf{X}:=(H_0^1(\Omega ))^d$, $Q:=L_0^2(\Omega )$ and

$$\begin{aligned} b^* (\textbf{u},\textbf{v},\textbf{w})&= ((\textbf{u}\cdot \nabla )\textbf{v},\textbf{w})+\frac{1}{2}\left( {(\nabla \cdot \textbf{u})}\textbf{v}, \textbf{w}\right) , \quad { \forall \textbf{u},\textbf{v},\textbf{w}\in X.} \end{aligned}$$

The following basic inequalities holds for all $\textbf{u},\textbf{v},\textbf{w}\in \textbf{X}$, see [14, 34]:

$$\begin{aligned} b^*(\textbf{u},\textbf{v},\textbf{w})\le \mathcal {M} \Vert \nabla \textbf{u}\Vert \Vert \nabla \textbf{v}\Vert \Vert \nabla \textbf{w}\Vert , \end{aligned}$$

(2.3)

where $\mathcal {M}$ is defined in (1.5).

Let $\mathcal {T}_h$ be a conforming triangulation of the domain $\Omega$ and let $h=\max \limits _{K \in \mathcal {T}_h}{h_K}$ denote the diameter of mesh. Then the numerical approximation of NSE reads as follows: for all $(\textbf{v}_h,q_h)\in (\textbf{X}_h,Q_h)$, find $(\textbf{u}_h,p_h)\in (\textbf{X}_h,Q_h)$ satisfying

$$\begin{aligned} \nu (\nabla \textbf{u}_h, \nabla \textbf{v}_h)+b^*(\textbf{u}_h,\textbf{u}_h,\textbf{v}_h)-(p_h,\nabla \cdot \textbf{v}_h)&= (\textbf{f},\textbf{v}_h), \end{aligned}$$

(2.4)

$$\begin{aligned} (\nabla \cdot \textbf{u}_h,q_h)&= 0. \end{aligned}$$

(2.5)

Herein $\textbf{X}_h\subset \textbf{X}$ and $Q_h\subset Q$ are assumed to be conforming finite dimensional subspaces satisfying inf-sup condition, i.e., there is a constant $\beta >0$ independent of h such that

$$\begin{aligned} \inf _{q_h\in {Q}_h}\sup _{\textbf{v}_h\in {X}_h}\frac{(q_h,\,\nabla \cdot \textbf{v}_h)}{||\,\nabla \textbf{v}_h\,||\,||\,q_h\,||}\ge \beta > 0. \end{aligned}$$

(2.6)

The error analysis in Sect. 4 uses the following estimations for trilinear term in 2d and 3d, respectively:

$$\begin{aligned} b^*(\textbf{u}_h,\textbf{v}_h,\textbf{w}_h)&\le \mathcal {M} \sqrt{|\ln h|}\Vert \nabla \textbf{v}_h\Vert \Vert \nabla \textbf{w}_h\Vert \Vert \textbf{u}_h\Vert , \end{aligned}$$

(2.7)

$$\begin{aligned} b^*(\textbf{u}_h,\textbf{v}_h,\textbf{w}_h)&\le \mathcal {M} h^{-1/2}\Vert \nabla \textbf{v}_h\Vert \Vert \nabla \textbf{w}_h\Vert \Vert \textbf{u}_h\Vert , \end{aligned}$$

(2.8)

we refer the reader to [14, 24] for a more detailed derivation of these results.

Similar to the continuous case, the discrete inf-sup condition (2.6) and (1.4) implies the existence and uniqueness of a solution of discrete problem (2.4) –(2.5). The stability estimate of the finite element solution is well known and the details of the proof can be found in [24, 34]: Let $\textbf{u}_h \in \textbf{X}_h$, then we get

$$\begin{aligned} \Vert \nabla \textbf{u}_h\Vert&\le {\nu ^{-1}} \Vert \textbf{f}\Vert _{-1}. \end{aligned}$$

(2.9)

We also recall the following finite element error estimate for the solution of (2.4)–(2.5):

Theorem 1

Assume $(\textbf{u}, p)$ be the exact solution of (2.1)–(2.2) and $(\textbf{u}_h, p_h)$ be the finite element solution of (2.4)–(2.5) with $(\textbf{X}_h,Q_h) =$ $(P_k,P_{k-1}),\, k\ge 1$ polynomials. Then we get

$$\begin{aligned} \Vert \textbf{u}-\textbf{u}_h\Vert +h\Big (\nu \Vert \nabla (\textbf{u}-\textbf{u}_h)\Vert +\Vert p-p_h\Vert \Big )\le C h^2 \Vert \textbf{f}\Vert . \end{aligned}$$

(2.10)

3 Improved AH Scheme

We first describe the derivation of our novel Algorithm. To this end, consider the classical temporally first-order artificial compressibility approximation of unsteady Navier–Stokes:

$$\begin{aligned} \frac{\textbf{u}^{n+1}-\textbf{u}^{n}}{\tau } + \textbf{u}^n \cdot \nabla \textbf{u}^{n+1} - \nu \Delta \textbf{u}^{n} + \nabla p^{n+1}&=\textbf{f}\,\, \text {in} \, \Omega \text {,} \, \end{aligned}$$

(3.1)

$$\begin{aligned} \beta (p^{n+1}-p^n ) + \nabla \cdot \textbf{u}^{n+1}&=0\,\, \text {in} \, \Omega , \end{aligned}$$

(3.2)

where $\tau \ll 1$ is a time-step and $\beta = {{\mathcal {O}}}(1)$. Comparing the above system to the classical AH algorithm (1.6)–(1.7), we see that $\beta = \dfrac{\alpha }{\rho }$ and the main difference between the two systems is in the first term of the momentum equation. Replacing the time derivative approximation $\dfrac{\textbf{u}^{n+1}-\textbf{u}^{n}}{\tau }$ by $-\dfrac{1}{\rho }\Delta \left( \textbf{u}^{n+1}-\textbf{u}^{n} \right)$, we obtain a novel AH scheme:

Algorithm 1

(Improved AH method) Let $\rho$ and $\alpha$ be positive parameters.

Step 1 For all $(\textbf{v}_h,q_h)\in (\textbf{X}_h,Q_h)$, let $(\textbf{u}_h^0,p_h^0)\in (\textbf{X}_h,Q_h)$ be obtained from Stokes equation satisfying

$$\begin{aligned} \nu (\nabla \textbf{u}_h^0,\nabla \textbf{v}_h)-(p_h^0,\nabla \cdot \textbf{v}_h)&=(\textbf{f},\textbf{v}_h), \end{aligned}$$

(3.3)

$$\begin{aligned} (q_h,\nabla \cdot \textbf{u}_h^0)&= 0 . \end{aligned}$$

(3.4)

Step 2 For $n\ge 0$ and for all $(\textbf{v}_h,q_h)\in (\textbf{X}_h,Q_h)$, find $(\textbf{u}_h^{n+1},p_h^{n+1})\in (\textbf{X}_h,Q_h)$ such that

(3.5)

(3.6)

Next we discuss the uniform boundedness of the solutions to the Algorithm 1.

Theorem 2

(Uniform boundedness) Let $(\textbf{u}_h, p_h) \in (\textbf{X}_h,Q_h)$ be the solution of (2.4)–(2.5) and $\{\textbf{u}_h^n, p_h^n\}$ be the function sequence generated by (3.5)–(3.6). If $\Lambda <1$ and

$$\begin{aligned} \rho \le \dfrac{2(1-\Lambda )}{\nu \Lambda ^2}, \end{aligned}$$

(3.7)

then $\{\textbf{u}_h^n,p_h^n\}$ are uniformly bounded with respect to h and n.

Proof

The first step of the proof consists of subtracting (3.5)–(3.6) from (2.4)–(2.5) to get:

$$\begin{aligned} \dfrac{1}{\rho }(\nabla \textbf{e}_h^{n+1}-\nabla \textbf{e}_h^n,\nabla \textbf{v}_h )+\nu (\nabla \textbf{e}_h^{n+1},\nabla v_h)+b^*(\textbf{e}_h^n,\textbf{u}_h,\textbf{v}_h)+b^*(\textbf{u}_h^n,\textbf{e}_h^{n+1},\textbf{v}_h)&\nonumber \\ +\dfrac{\rho }{\alpha } (\nabla \cdot \textbf{e}_h^{n+1}, \nabla \cdot \textbf{v}_h) -(\delta _h^n, \nabla \cdot \textbf{v}_h)&=0, \end{aligned}$$

(3.8)

$$\begin{aligned} \alpha (\delta _h^{n+1}-\delta _h^n,q_h)+\rho (\nabla \cdot \textbf{e}_h^{n+1},q_h)&=0, \end{aligned}$$

(3.9)

where $\textbf{e}_h^n=\textbf{u}_h-\textbf{u}_h^n$, $\delta _h^n=p_h-p_h^n$. Letting $\textbf{v}_h=\textbf{e}_h^{n+1}$, $q_h=\delta _h^n$ in (3.8)–(3.9) and using $b^*(\textbf{u}_h^n,\textbf{e}_h^{n+1},\textbf{e}_h^{n+1})=0$, we have

$$\begin{aligned} \frac{1}{2\rho }\Big (\Vert \nabla \textbf{e}_h^{n+1}\Vert ^2-\Vert \nabla \textbf{e}_h^n\Vert ^2+\Vert \nabla (\textbf{e}_h^{n+1}-\textbf{e}_h^n)\Vert ^2\Big )+\nu \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2&+\dfrac{\rho }{\alpha }\Vert \nabla \cdot \textbf{e}_h^{n+1}\Vert ^2 \nonumber \\ - (\delta _h^{n},\nabla \cdot \textbf{e}_h^{n+1})&=-b^*\left( \textbf{e}_h^n,\textbf{u}_h,\textbf{e}_h^{n+1} \right) \end{aligned}$$

(3.10)

$$\begin{aligned} \dfrac{\alpha }{2\rho }(\Vert \delta _h^{n+1}\Vert ^2-\Vert \delta _h^n\Vert ^2-\Vert \delta _h^{n+1} -\delta _h^n\Vert ^2)+(\nabla \cdot \textbf{e}_h^{n+1},\delta _h^n)&=0. \end{aligned}$$

(3.11)

Also, setting $q_h=\delta _h^{n+1}-\delta _h^n$ in (3.9) produces

$$\begin{aligned} \dfrac{\alpha }{\rho }\Vert \delta _h^{n+1}-\delta _h^n\Vert ^2=-(\nabla \cdot \textbf{e}_h^{n+1},\delta _h^{n+1}-\delta _h^n). \end{aligned}$$

(3.12)

Applying Cauchy–Schwarz inequality to (3.12) yields

$$\begin{aligned} \Vert \delta _h^{n+1}-\delta _h^n\Vert \le \dfrac{\rho }{\alpha }\Vert \nabla \cdot \textbf{e}_h^{n+1}\Vert . \end{aligned}$$

(3.13)

Adding (3.10) to (3.11) yields

$$\begin{aligned}{} & {} \frac{1}{2\rho }\Big (\Vert \nabla \textbf{e}_h^{n+1}\Vert ^2-\Vert \nabla \textbf{e}_h^n\Vert ^2+\Vert \nabla (\textbf{e}_h^{n+1}-\textbf{e}_h^n)\Vert ^2\Big )\nonumber \\{} & {} \quad +\nu \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\rho }{\alpha }\Big (\Vert \nabla \cdot \textbf{e}_h^{n+1}\Vert ^2-\dfrac{\alpha ^2}{2\rho ^2}\Vert \delta _h^{n+1}-\delta _h^n\Vert ^2\Big )\nonumber \\{} & {} \quad +\dfrac{\alpha }{2\rho }(\Vert \delta _h^{n+1}\Vert ^2-\Vert \delta _h^n\Vert ^2) \le |b^*(\textbf{e}_h^n,\textbf{u}_h,\textbf{e}_h^{n+1})|. \end{aligned}$$

(3.14)

On the other hand, the right hand side of the Eq. (3.14) can be bounded by (2.3), (2.9) and (1.4)

$$\begin{aligned} |b^*(\textbf{e}_h^n,\textbf{u}_h,\textbf{e}_h^{n+1})|&\le \Lambda \nu \Vert \nabla \textbf{e}_h^n\Vert \Vert \nabla \textbf{e}_h^{n+1}\Vert \nonumber \\&\le \Lambda \nu (\Vert \nabla (\textbf{e}_h^{n+1}-\textbf{e}_h^n)\Vert +\Vert \nabla \textbf{e}_h^{n+1}\Vert )\Vert \nabla \textbf{e}_h^{n+1}\Vert \nonumber \\&\le \dfrac{1}{2 \rho }\Vert \nabla (\textbf{e}_h^{n+1}-\textbf{e}_h^n)\Vert ^2+\left( \Lambda \nu + \dfrac{\rho \Lambda ^2\nu ^2}{2} \right) \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2. \end{aligned}$$

(3.15)

Inserting the estimation (3.15) into (3.14) yields

$$\begin{aligned}{} & {} \left( \dfrac{1}{2\rho }+\nu -\Lambda \nu -\dfrac{\rho \Lambda ^2\nu ^2}{2} \right) \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\rho }{\alpha }\Big (\Vert \nabla \cdot \textbf{e}_h^{n+1}\Vert ^2-\dfrac{\alpha ^2}{2\rho ^2}\Vert \delta _h^{n+1}-\delta _h^n\Vert ^2\Big )\nonumber \\{} & {} \quad +\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2 \le \dfrac{1}{2\rho }\Vert \nabla \textbf{e}_h^n\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^n\Vert ^2. \end{aligned}$$

(3.16)

Under the assumption (3.7), since $\nu -\Lambda \nu -\dfrac{\rho \Lambda ^2\nu ^2}{2} \ge 0$, using (3.13), dropping the nonnegative term in (3.16) gives

$$\begin{aligned} \dfrac{1}{2\rho }\Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2&\le \dfrac{1}{2\rho } \Vert \nabla \textbf{e}_h^{n}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n}\Vert ^2. \end{aligned}$$

(3.17)

Therefore, one has

$$\begin{aligned} \dfrac{1}{2\rho } \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2&\le \dfrac{1}{2\rho } \Vert \nabla \textbf{e}_h^{0}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{0}\Vert ^2. \end{aligned}$$

(3.18)

It is clear that $\{\textbf{u}_h^n,p_h^n\}$ is uniformly bounded if $\textbf{e}_h^0$ and $\delta _h^0$ are. To show uniform boundness of $\textbf{e}_h^0$ and $\delta _h^0$, subtract (3.3)–(3.4) from (2.4)–(2.5), which results

$$\begin{aligned} \nu (\nabla \textbf{e}_h^0,\nabla \textbf{v}_h)-(\delta _h^0,\nabla \cdot \textbf{v}_h)&=-b(\textbf{u}_h,\textbf{u}_h,\textbf{v}_h), \end{aligned}$$

(3.19)

$$\begin{aligned} (q_h,\nabla \cdot \textbf{e}_h^0)&=0. \end{aligned}$$

(3.20)

Choosing $\textbf{v}_h=\textbf{u}_h-\textbf{u}_h^0 =\textbf{e}_h^0$, $q_h=p_h-p_h^0=\delta _h^0$ in (3.19)–(3.20) and adding (3.19) to (3.20) and applying (2.3) yields

$$\begin{aligned} \nu \Vert \nabla \textbf{e}_h^0\Vert ^2&\le \mathcal {M}\Vert \nabla \textbf{u}_h\Vert ^2\Vert \nabla \textbf{e}_h^0\Vert . \end{aligned}$$

(3.21)

Finally, using (1.4) and (2.9) gives

$$\begin{aligned} \nu \Vert \nabla \textbf{e}_h^0\Vert&\le \mathcal {M}\Vert \nabla \textbf{u}_h\Vert ^2 \le \Lambda \Vert f\Vert _{-1}. \end{aligned}$$

(3.22)

By inf-sup condition, it follows that

$$\begin{aligned} \Vert \delta _h^0\Vert \le 2 \Lambda \beta ^{-1}\Vert f\Vert _{-1}. \end{aligned}$$

(3.23)

Hence (3.18) becomes

$$\begin{aligned} \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\alpha \Vert \delta _h^{n+1}\Vert ^2&\le (\nu ^{-2}+4\alpha \beta ^{-2})\Lambda ^2 \Vert f\Vert _{-1}^2. \end{aligned}$$

(3.24)

proving that $\{\textbf{u}_h^n,p_h^n\}$ are uniformly bounded, independent of n and h. $\square$

Remark 1

Note that the presence of the $\dfrac{1}{\rho }(\nabla (\textbf{u}_h^{n+1}-\textbf{u}_h^n),\nabla \textbf{v}_h)$ term in (3.5) is crucial in being able to control the term $\dfrac{1}{2 \rho }\Vert \nabla (\textbf{e}_h^{n+1}-\textbf{e}_h^n)\Vert ^2$ in (3.15). This would not be possible with the artificial compressibility scheme (3.1).

Remark 2

Note that since we are proving standard uniform boundedness and convergence results, the theoretical analysis is also a standard one. But the results are much improved from those in [6] in a sense that, we have no additional restriction on $\Lambda$ besides $\Lambda <1$. In addition, improved AH scheme requires much simpler inequality for $\rho$ compared with $\rho$ of [6].

Next, we establish the contraction property of the Algorithm 1.

Theorem 3

Let $(\textbf{u}_h, p_h) \in (\textbf{X}_h, Q_h)$ be the solution of (2.4)–(2.5) and $\{\textbf{u}_h^n, p_h^n\}$ be the function sequence generated by (3.5)–(3.6). Under the assumption that $\Lambda <1$, the error estimate satisfies

$$\begin{aligned} \tau \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2&\le \kappa \Big (\tau \Vert \nabla \textbf{e}_h^{n}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n}\Vert ^2 \Big ), \end{aligned}$$

(3.25)

where $\tau , \kappa \in (0,1)$ are independent of h and n.

Proof

According to the Lemma 2, there exist a real number ${C}_1$ such that $\Vert \nabla \textbf{u}_h^n\Vert \le {C}_1$. Utilizing inf-sup condition, (2.3), (1.4), and the inequality $\Vert \nabla \cdot \textbf{e}_h^{n+1}\Vert \le \Vert \nabla \textbf{e}_h^{n+1}\Vert$ one gets

$$\begin{aligned} \beta \Vert \delta _h^n\Vert&\le \sup \limits _{\textbf{v}_h\in \textbf{V}_h} \dfrac{(\delta _h^n, \nabla \cdot \textbf{v}_h)}{\Vert \nabla \textbf{v}_h\Vert }\nonumber \\&\le \rho ^{-1}\Vert \nabla \textbf{e}_h^{n+1}-\nabla \textbf{e}_h^n\Vert +\nu \Vert \nabla \textbf{e}_h^{n+1}\Vert +\mathcal {M} \Vert \nabla \textbf{e}_h^n\Vert \Vert \nabla \textbf{u}_h\Vert \nonumber \\&\quad +\mathcal {M}\Vert \nabla \textbf{u}_h^n\Vert \Vert \nabla \textbf{e}_h^{n+1}\Vert +\rho \alpha ^{-1}\Vert \nabla \cdot \textbf{e}_h^{n+1}\Vert \nonumber \\&\le \rho ^{-1}\Vert \nabla \textbf{e}_h^{n+1}\Vert +\rho ^{-1}\Vert \nabla \textbf{e}_h^n\Vert +\nu \Vert \nabla \textbf{e}_h^{n+1}\Vert +\nu \Lambda \Vert \nabla \textbf{e}_h^n\Vert +\mathcal {M} {C}_1\Vert \nabla \textbf{e}_h^{n+1} \Vert \nonumber \\&\quad +\rho \alpha ^{-1}\Vert \nabla \textbf{e}_h^{n+1}\Vert \nonumber \\&= (\rho ^{-1}+\nu \Lambda )\Vert \nabla \textbf{e}_h^n\Vert +(\rho ^{-1}+\nu +\mathcal {M}{C}_1+\rho \alpha ^{-1})\Vert \nabla \textbf{e}_h^{n+1}\Vert . \end{aligned}$$

(3.26)

Taking the square of both sides of the Eq. (3.26) and using the fact that $(a+b)^2\le 2a^2+2b^2$ for any real numbers a and b, we have

$$\begin{aligned} \beta ^2 \Vert \delta _h^n\Vert ^2&\le 2(\rho ^{-1}+\nu \Lambda )^2\Vert \nabla \textbf{e}_h^n\Vert ^2+2(\rho ^{-1}+\nu +\mathcal {M}{C}_1+\rho \alpha ^{-1})^2\Vert \nabla \textbf{e}_h^{n+1}\Vert ^2. \end{aligned}$$

(3.27)

Hence,

$$\begin{aligned} \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2&\ge {C}_2\Vert \delta _h^n\Vert ^2 - {C}_3\Vert \nabla \textbf{e}_h^n\Vert ^2, \end{aligned}$$

(3.28)

where ${C}_2=\dfrac{1}{2}\Big (\dfrac{\beta }{\rho ^{-1}+\nu +\mathcal {M}{C}_1+\rho \alpha ^{-1}}\Big )^2$ and ${C}_3=\Big (\dfrac{\rho ^{-1}+\nu \Lambda }{\rho ^{-1}+\nu +\mathcal {M}{C}_1+\rho \alpha ^{-1}}\Big )^2 < 1$.

Using (3.13) and dropping the second term on the left hand side of (3.16), we get

$$\begin{aligned} \left( \dfrac{1}{2\rho }+ D\right) \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2 +\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2 \le \dfrac{1}{2\rho }\Vert \nabla \textbf{e}_h^n\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^n\Vert ^2. \end{aligned}$$

(3.29)

where $D=\nu -\Lambda \nu -\dfrac{\rho \Lambda ^2\nu ^2}{2}$. Adding and subtracting the term $\xi \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2$ to (3.29) and using (3.28) gives

$$\begin{aligned}{} & {} \left( \dfrac{1}{2\rho }+ D-\xi \right) \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2\nonumber \\ {}{} & {} \quad \le \left( \dfrac{1}{2\rho }+\xi {C}_3 \right) \Vert \nabla \textbf{e}_h^{n}\Vert ^2+\left( \dfrac{\alpha }{2\rho }-\xi {C}_2 \right) \Vert \delta _h^{n}\Vert ^2, \end{aligned}$$

(3.30)

where $\xi > 0$ is to be determined. Suppose $\dfrac{1}{2\rho }+ D-\xi > 0$ and $\dfrac{\alpha }{2\rho }-\xi {C}_2>0$, then one can calculate the parameter $\xi >0$ such that

$$\begin{aligned} \dfrac{\dfrac{1}{2\rho }+\xi {C}_3}{\dfrac{1}{2\rho }+ D-\xi } = \dfrac{\dfrac{\alpha }{2\rho }-\xi {C}_2}{\dfrac{\alpha }{2\rho }}. \end{aligned}$$

(3.31)

Reorganizing (3.31) gives

$$\begin{aligned} \xi ^2{C}_2-\left( {C}_2 D+\dfrac{\alpha }{2\rho }+\dfrac{1}{2\rho }({C}_2+\alpha {C}_3) \right) \xi +\dfrac{\alpha }{2\rho } D=0. \end{aligned}$$

(3.32)

The discriminant of the quadratic Eq. (3.32) is

$$\begin{aligned} b^2-4ac&=\Big ({C}_2 D+\dfrac{\alpha }{2\rho }+\dfrac{1}{2\rho }({C}_2+\alpha {C}_3) \Big )^2-\dfrac{2{C}_2{\alpha } D}{\rho }\nonumber \\&>\Big ({C}_2 D+\dfrac{\alpha }{2\rho } \Big )^2-\dfrac{2{C}_2{\alpha } D}{\rho }\nonumber \\&=\Big ({C}_2 D-\dfrac{\alpha }{2\rho } \Big )^2\ge 0. \end{aligned}$$

(3.33)

Under the assumption

$$\begin{aligned} \max \left\{ 2\rho C_2D, \dfrac{C_2 (4\rho D+1)}{2-C_3}\right\}<\alpha < \dfrac{C_2}{C_3}, \end{aligned}$$

(3.34)

(3.32) has two real, distinct roots $\xi _{1,2}=\Big (\mathcal {S}\pm \sqrt{\mathcal {S}^2-\dfrac{2{C}_2{\alpha } D}{\rho }}\Big )/{2{C}_2}$, where $\mathcal {S}= {C}_2 D+\dfrac{1}{2\rho }(\alpha +{C}_2+\alpha {C}_3)$. We select

$$\begin{aligned} \xi =\dfrac{\mathcal {S}-\sqrt{\mathcal {S}^2-\dfrac{2{C}_2{\alpha } D}{\rho }}}{2{C}_2}. \end{aligned}$$

(3.35)

Inserting (3.35) into (3.30) produces

$$\begin{aligned} \tau \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2 \le \kappa \Big (\tau \Vert \nabla \textbf{e}_h^{n}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n}\Vert ^2 \Big ), \end{aligned}$$

(3.36)

where $\tau =\dfrac{1}{2\rho }+ D-\xi$ and $\kappa =1-\dfrac{2\rho \xi {C}_2}{\alpha }$. This completes the proof. $\square$

One can deduce an error estimate of $\textbf{u}-\textbf{u}_h$ and $p-p_h$ by applying Theorem 3 and the triangle inequality.

Corollary 1

Let $(\textbf{u}_h, p_h)$ and $(\textbf{u}_h^n, p_h^n)$ be the solutions of (2.4)–(2.5) and Algorithm 1, respectively. For $\Lambda <1$, the error estimate satisfies the following bound

$$\begin{aligned} \Vert \nabla (\textbf{u}_h-\textbf{u}_h^{n+1})\Vert ^2&\le \kappa ^{n+1} \left( \nu ^{-2} +{2\alpha } (\rho \tau )^{-1}\beta ^{-2} \right) \Lambda ^2\Vert \textbf{f}\Vert _{-1}^2, \end{aligned}$$

(3.37)

$$\begin{aligned} \Vert p_h-p_h^{n+1}\Vert ^2&\le \kappa ^{n+1} \left( 2\rho \tau \alpha ^{-1} \nu ^{-2} +4 \beta ^{-2} \right) \Lambda ^2\Vert \textbf{f}\Vert _{-1}^2, \end{aligned}$$

(3.38)

where $\tau , \kappa \in (0,1)$ are independent of h and n.

Proof

From Theorem 3, we get

$$\begin{aligned} \tau \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2&\le \kappa \Big (\tau \Vert \nabla \textbf{e}_h^{n}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n}\Vert ^2 \Big ), \end{aligned}$$

(3.39)

where $\textbf{e}_h^n=\textbf{u}_h-\textbf{u}_h^n$, $\delta _h^n=p_h-p_h^n$. This yields

$$\begin{aligned} \tau \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2&\le \kappa ^{n+1} \Big (\tau \Vert \nabla \textbf{e}_h^{0}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{0}\Vert ^2 \Big ). \end{aligned}$$

(3.40)

We now use (3.22) and (3.23) to get

$$\begin{aligned} \tau \Vert \nabla \textbf{e}_h^{n+1}\Vert ^2+\dfrac{\alpha }{2\rho }\Vert \delta _h^{n+1}\Vert ^2&\le \kappa ^{n+1} \left( \tau \nu ^{-2} +{2\alpha } \rho ^{-1}\beta ^{-2} \right) \Lambda ^2\Vert \textbf{f}\Vert _{-1}^2, \end{aligned}$$

(3.41)

which produces (3.37)–(3.38). $\square$

Theorem 4

Assume $(\textbf{u}, p)$ and $(\textbf{u}_h^{n+1}, p_h^{n+1} )$ solve (2.1)–(2.2) and Algorithm 1, respectively. Then, we have

$$\begin{aligned}&\nu \Vert \nabla (\textbf{u}-\textbf{u}_h^{n+1})\Vert + \Vert p-p_h^{n+1}\Vert \nonumber \\ {}&\quad \le Ch+\Big ( \dfrac{\nu }{\sqrt{\tau }}+\sqrt{{2\rho }\alpha ^{-1}}\Big ) \sqrt{\kappa ^{n+1}(\tau \nu ^{-2} +{2\alpha } \rho ^{-1}\beta ^{-2} )}\Lambda \Vert \textbf{f}\Vert _{-1}. \end{aligned}$$

(3.42)

Proof

Applying triangle inequality produces

$$\begin{aligned}&\nu \Vert \nabla (\textbf{u}-\textbf{u}_h^{n+1})\Vert + \Vert p-p_h^{n+1}\Vert \nonumber \\ {}&\quad \le \nu \Vert \nabla (\textbf{u}-\textbf{u}_h)\Vert + \Vert p-p_h\Vert + \nu \Vert \nabla (\textbf{u}_h-\textbf{u}_h^{n+1})\Vert + \Vert p_h-p_h^{n+1}\Vert . \end{aligned}$$

Combining Theorem 1 and Corollary 1, yields the stated result. $\square$

3.1 Extension to Nonhomogeneous and Open Boundary Conditions Case

The analysis we presented in the preceding section uses homogeneous Dirichlet boundary conditions. We now briefly comment on the extension of our AH Algorithm 1 to a more general boundary conditions case:

$$\begin{aligned} \textbf{u}\cdot \nabla \textbf{u}-\nu \Delta \textbf{u}+\nabla p&=\textbf{f}\,\, \text {in} \, \Omega \text {,} \, \end{aligned}$$

(3.43)

$$\begin{aligned} \nabla \cdot \textbf{u}&=0\,\, \text {in} \, \Omega , \end{aligned}$$

(3.44)

$$\begin{aligned} \textbf{u}&= \textbf{g}\,\, \text {on}\ \partial \Omega _D, \end{aligned}$$

(3.45)

$$\begin{aligned} -\nu \nabla \textbf{u}\cdot \textbf{n}+ p \textbf{n}&= 0 \,\, \text {on}\ \partial \Omega _N. \end{aligned}$$

(3.46)

In the above, we assume that $\Omega$ is bounded, locally Lipschitz domain and $\textbf{g}\in \textbf{H}^{1/2}\left( \Omega _D \right)$, which is crucial for the existence of the appropriate solenoidal extension of $\textbf{g}$ (still denoted by $\textbf{g}$) to $\Omega$ [10, Lemma IX.4.2]. , we look for the solution as

$$\begin{aligned} \textbf{u}= \widehat{\textbf{u}}+ \textbf{g}, \end{aligned}$$

where $(\widehat{\textbf{u}},p)$ now solve:

$$\begin{aligned} \widehat{\textbf{u}}\cdot \nabla \widehat{\textbf{u}}+ \widehat{\textbf{u}}\cdot \nabla \textbf{g}+ \textbf{g}\cdot \nabla \widehat{\textbf{u}}-\nu \Delta \widehat{\textbf{u}}+\nabla p&= \textbf{f}+ \nu \Delta \textbf{g}- \textbf{g}\cdot \nabla \textbf{g}\,\, \text {in} \, \Omega \text {,} \, \end{aligned}$$

(3.47)

$$\begin{aligned} \nabla \cdot \widehat{\textbf{u}}&=0\,\, \text {in} \, \Omega , \end{aligned}$$

(3.48)

$$\begin{aligned} \widehat{\textbf{u}}&= \textbf{0} \,\, \text {on}\ \partial \Omega _D, \end{aligned}$$

(3.49)

$$\begin{aligned} -\nu \nabla \widehat{\textbf{u}}\cdot \textbf{n}+ p \textbf{n}&= \nu \nabla \textbf{g}\cdot \textbf{n}\,\, \text {on}\ \partial \Omega _N. \end{aligned}$$

(3.50)

The derivation of the weak formulation and the extension of our Algorithm 1 to the above system is immediate: After appropriate initialization, for $n\ge 0$ and for all $(\textbf{v}_h,q_h)\in (\textbf{X}_h,Q_h)$, find $(\widehat{\textbf{u}}_h^{n+1},p_h^{n+1})\in (\textbf{X}_h,Q_h)$ such that

$$\begin{aligned}&\dfrac{1}{\rho }(\nabla (\widehat{\textbf{u}}_h^{n+1}-\widehat{\textbf{u}}_h^n),\nabla \textbf{v}_h)+\nu (\nabla \widehat{\textbf{u}}_h^{n+1}, \nabla \textbf{v}_h) + b^*(\widehat{\textbf{u}}_h^{n}, \widehat{\textbf{u}}_h^{n+1},\textbf{v}_h) \nonumber \\ {}&\quad + b^*(\textbf{g},\widehat{\textbf{u}}_h^{n+1},\textbf{v}_h) + b^*(\widehat{\textbf{u}}_h^{n+1},\textbf{g},\textbf{v}_h) \nonumber \\&\quad + \dfrac{\rho }{\alpha }(\nabla \cdot \widehat{\textbf{u}}_h^{n+1}, \nabla \cdot \textbf{v}_h) = \textbf{F}(\textbf{v}_h) \end{aligned}$$

(3.51)

$$\begin{aligned}&\quad \alpha (p_h^{n+1}-p_h^n,q_h)+\rho (\nabla \cdot \widehat{\textbf{u}}_h^{n+1},q_h) = 0, \end{aligned}$$

(3.52)

where $\textbf{F}(\textbf{v}_h)$ represents all the terms on the right-hand side. Thus, using the crucial bound

$$\begin{aligned} |b^*(\textbf{v},\textbf{g},\textbf{v})| \le \varepsilon \Vert \nabla \textbf{v}\Vert ^2, \end{aligned}$$

for all $\varepsilon >0$, one can extend the earlier results to this case as well.

4 Improved Two-Grid AH Method

For two-grid algorithm, consider conforming triangulation $\mathcal {T}_H$ of the domain $\Omega$ such that $\mathcal {T}_h$ is refinement of $\mathcal {T}_H$ with $\textbf{X}_H\subset \textbf{X}_h$ and $Q_H\subset Q_h$. Let $(\textbf{X}_H,Q_H)$ be inf-sup stable spaces such that (2.6) is fulfilled. Three kinds of two grid methods are introduced by in [9]. We modify Algorithm 3 of [9] to present improvement of our method for that two grid approach.

Algorithm 2

(Improved Two-Grid AH method) Let $\rho$ and $\alpha$ be positive parameters satisfying (3.7) and (3.34), respectively.

Step 1 (Initialize on coarse grid) For all $(\textbf{v}_H,q_H)\in (\textbf{X}_H,Q_H)$, let $(\textbf{u}_H^0,p_H^0)\in (\textbf{X}_H,Q_H)$ be obtained from Stokes equation satisfying

$$\begin{aligned} \nu (\nabla \textbf{u}_H^0,\nabla \textbf{v}_H)-(p_H^0,\nabla \cdot \textbf{v}_H)&=(\textbf{f},\textbf{v}_H), \end{aligned}$$

(4.1)

$$\begin{aligned} (q_H,\nabla \cdot \textbf{u}_H^0)&= 0. \end{aligned}$$

(4.2)

Step 2 (Coarse grid AH) For $n = \overline{0,m-1}$ and for all $(\textbf{v}_H,q_H)\in (\textbf{X}_H,Q_H)$, find $(\textbf{u}_H^{n+1},p_H^{n+1})\in (X_H,Q_H)$ such that

$$\begin{aligned}{} & {} \dfrac{1}{\rho } (\nabla (\textbf{u}_H^{n+1}-\textbf{u}_H^n),\nabla \textbf{v}_H)+\nu (\nabla \textbf{u}_H^{n+1}, \nabla \textbf{v}_H)+b^*(\textbf{u}_H^{n},\textbf{u}_H^{n+1},\textbf{v}_H)\nonumber \\{} & {} +\dfrac{\rho }{\alpha }(\nabla \cdot \textbf{u}_H^{n+1}, \nabla \textbf{v}_H)=(p_H^n,\nabla \cdot \textbf{v}_H)+(\textbf{f},\textbf{v}_H), \end{aligned}$$

(4.3)

$$\begin{aligned}{} & {} \alpha (p_H^{n+1}-p_H^n,q_H)+\rho (\nabla \cdot \textbf{u}_H^{n+1},q_H) =0. \end{aligned}$$

(4.4)

Step 3 (Fine grid mixed problem) For all $(\textbf{v}_h,q_h)\in (\textbf{X}_h,Q_h)$, let $(\textbf{u}_{mh},p_{mh})\in (X_h,Q_h)$ be the solution of

$$\begin{aligned} \nu (\nabla \textbf{u}_{mh}, \nabla \textbf{v}_h) -(p_{mh},\nabla \cdot \textbf{v}_h)+b^*(\textbf{u}_H^{m},\textbf{u}_{mh}, \textbf{v}_h)&= (\textbf{f},\textbf{v}_h), \end{aligned}$$

(4.5)

$$\begin{aligned} (\nabla \cdot \textbf{u}_{mh},q_h)&= 0. \end{aligned}$$

(4.6)

The well-posedness of the two-grid Algorithm 2 is easily established.

Theorem 5

Assume $\textbf{u}_{mh}$ solves Algorithm 2, then one gets

$$\begin{aligned} \Vert \nabla \textbf{u}_{mh}\Vert \le \nu ^{-1}\Vert \textbf{f}\Vert _{-1}. \end{aligned}$$

(4.7)

Proof

Letting $\textbf{v}_h=\textbf{u}_{mh}$ and $q_h=p_{mh}$ in (4.5), and using the skew symmetry property we have

$$\begin{aligned} \nu \Vert \nabla \textbf{u}_{mh}\Vert ^2 =(\textbf{f},\textbf{u}_{mh}). \end{aligned}$$

(4.8)

Applying Cauchy–Schwarz yields the stated result. $\square$

Next we shall establish the error bounds for Algorithm 2.

Theorem 6

Assume $(\textbf{u}_{mh}, p_{mh})$ solves Algorithm 2, then the following bounds hold in 2d and 3d, respectively:

$$\begin{aligned} \Vert \nabla (\textbf{u}_h-\textbf{u}_{mh})\Vert +\Vert p_h-p_{mh}\Vert&\le C\Lambda \sqrt{|\ln h|}\Big (H^2+ \sqrt{\kappa ^{n+1}( \nu ^{-2} +{2\alpha } (\rho \tau )^{-1}\beta ^{-2} )}\Lambda \Vert \textbf{f}\Vert _{-1}\Big ), \end{aligned}$$

(4.9)

$$\begin{aligned} \Vert \nabla (\textbf{u}_h-\textbf{u}_{mh})\Vert +\Vert p_h-p_{mh}\Vert&\le C\Lambda h^{-1/2}\Big (H^2+ \sqrt{\kappa ^{n+1}( \nu ^{-2} +{2\alpha } (\rho \tau )^{-1}\beta ^{-2} )}\Lambda \Vert \textbf{f}\Vert _{-1}\Big ). \end{aligned}$$

(4.10)

Proof

We begin the proof by subtracting (4.5)–(4.6) from (2.4)–(2.5):

$$\begin{aligned} \nu (\nabla \textbf{e}_{mh}, \nabla \textbf{v}_h) -(\delta _{h}^m,\nabla \cdot \textbf{v}_h)+b^*(\textbf{u}_h-\textbf{u}_H^{m}, \textbf{u}_h,\textbf{v}_h)+b^*(\textbf{u}_H^{m},\textbf{e}_{mh},\textbf{v}_h)&= 0, \end{aligned}$$

(4.11)

$$\begin{aligned} (\nabla \cdot \textbf{e}_{mh},q_h)&= 0. \end{aligned}$$

(4.12)

where $\textbf{e}_{mh}=\textbf{u}_h-\textbf{u}_{mh}$, $\delta _{h}^m=p_h-p_{mh}$. Setting $\textbf{v}_h=\textbf{e}_{mh}$, $q_h=\delta _{h}^m$ in (4.11)–(4.12), using $b^*(\textbf{u}_H^m,\textbf{e}_{mh},\textbf{e}_{mh})=0$, and adding (4.11) to (4.12), we get

$$\begin{aligned} \nu \Vert \nabla \textbf{e}_{mh}\Vert ^2 \le |b^*(\textbf{u}_h-\textbf{u}_H^m,\textbf{u}_h,\textbf{e}_{mh})|. \end{aligned}$$

(4.13)

Utilizing (1.4), (2.7), (2.8), (2.9), and applying Corollary 1 and Theorem 1, Poincaré’s inequality, the nonlinear term in (4.13) can be bounded as

$$\begin{aligned} |b^*(\textbf{u}_h-\textbf{u}_H^m,\textbf{u}_h,\textbf{e}_{mh})|&\le \Lambda \nu \sqrt{|\ln h|}\Vert \nabla \textbf{e}_{mh}\Vert \Vert \textbf{u}_h-\textbf{u}_H^m\Vert \nonumber \\&\le \Lambda \nu \sqrt{|\ln h|}\Vert \nabla \textbf{e}_{mh}\Vert (\Vert \textbf{u}_h-\textbf{u}\Vert +\Vert \textbf{u}-\textbf{u}_H\Vert +\Vert \textbf{u}_H-\textbf{u}_H^m\Vert )\nonumber \\&\le \Lambda \nu \sqrt{|\ln h|}\Vert \nabla \textbf{e}_{mh}\Vert \Big (H^2+ C_p\sqrt{\kappa ^{n+1}( \nu ^{-2} +{2\alpha } (\rho \tau )^{-1}\beta ^{-2} )}\Lambda \Vert \textbf{f}\Vert _{-1}\Big ) \end{aligned}$$

(4.14)

in 2d and as

$$\begin{aligned} |b^*(\textbf{u}_h-\textbf{u}_H^m,\textbf{u}_h,\textbf{e}_{mh})| \le \Lambda \nu h^{-1/2} \Vert \nabla \textbf{e}_{mh}\Vert \Big (H^2+ C_p\sqrt{\kappa ^{n+1}( \nu ^{-2} +{2\alpha } (\rho \tau )^{-1}\beta ^{-2} )}\Lambda \Vert \textbf{f}\Vert _{-1}\Big ) \nonumber \\ \end{aligned}$$

(4.15)

in 3d.

Inserting (4.14), (4.15) into (4.13), we have

$$\begin{aligned} \Vert \nabla \textbf{e}_{mh}\Vert \le C\Lambda \sqrt{|\ln h|}\Big (H^2+ \sqrt{\kappa ^{n+1}( \nu ^{-2} +{2\alpha } (\rho \tau )^{-1}\beta ^{-2} )}\Lambda \Vert \textbf{f}\Vert _{-1}\Big ) \text { in 2d,} \end{aligned}$$

(4.16)

and

$$\begin{aligned} \Vert \nabla \textbf{e}_{mh}\Vert \le C \Lambda h^{-1/2}\Big (H^2+ \sqrt{\kappa ^{n+1}( \nu ^{-2} +{2\alpha } (\rho \tau )^{-1}\beta ^{-2} )}\Lambda \Vert \textbf{f}\Vert _{-1}\Big ) \text { in 3d.} \end{aligned}$$

(4.17)

Moreover, using inf-sup condition (2.6) yields following bound for pressure error:

$$\begin{aligned} \Vert \delta _{h}^m\Vert \le \beta ^{-1}\sup _{\textbf{v}_h\in {X}_h}\frac{(\delta _{h}^m,\,\nabla \cdot \textbf{v}_h)}{||\,\nabla \textbf{v}_h\,||}. \end{aligned}$$

(4.18)

Under the assumption (1.4), utilizing (2.7), (2.9), (4.16) produces

$$\begin{aligned} \Vert \delta _{h}^m\Vert&\le \beta ^{-1} \Big (\nu \Vert \nabla \textbf{e}_{mh}\Vert + \mathcal {M}\sqrt{|\ln h|}\Vert \nabla \textbf{u}_h\Vert \Vert \textbf{u}_h-\textbf{u}_H^{m}\Vert +\mathcal {M}\Vert \nabla \textbf{u}_H^m\Vert \Vert \nabla \textbf{e}_h^m\Vert \Big )\nonumber \\&\le \beta ^{-1} \Big (\nu (1+\Lambda )\Vert \nabla \textbf{e}_{mh}\Vert + \Lambda \nu \sqrt{|\ln h|}\Vert \textbf{u}_h-\textbf{u}_H^{m}\Vert \Big )\nonumber \\&\le C\Lambda \sqrt{|\ln h|}\Big (H^2+ \sqrt{\kappa ^{n+1} (\nu ^{-2} +{2\alpha } (\rho \tau )^{-1}\beta ^{-2} )}\Lambda \Vert \textbf{f}\Vert _{-1}\Big ) \end{aligned}$$

(4.19)

in 2d. Analogous bound is easily obtained in 3d. Combining (4.16) with (4.19) yields the stated result. $\square$

5 Numerical Experiments

In this part of the paper, we present some numerical tests to verify the theoretical findings and to demonstrate the effectiveness of the proposed Algorithms 1 and 2. We first perform a convergence test with a manufactured solution. Then, we carry out a detailed comparison between the Algorithm 1 and the classical AH scheme for Kovasznay flow [25] problem. Next we extensively test our schemes on a classical lid driven cavity flow problem at different Reynolds numbers. The last numerical test will be on flow around a step problem. We consider the Taylor-Hood finite element pair throughout all computations and direct solvers for all linear systems. The finite element software FreeFem++ [22] is used for implementation along entire study.

5.1 Convergence Test

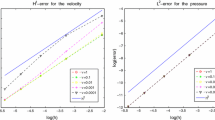
To measure the error and define the convergence rates, we first consider a manufactured solution of (1.1)–(1.2) in the unit square as:

$$\begin{aligned} \textbf{u}=\left( \begin{array}{c} 2 \theta (x^2 - x)^2 (y^2 - y)(2y - 1) \\ -2 \theta (y^2 - y)^2 (x^2 - x)(2x - 1) \end{array} \right) ,\quad p=\theta (2x-1)(2y-1), \end{aligned}$$

(5.1)

where $\theta$ is used to adjust the value of $\Lambda$. The right-hand side $\textbf{f}$ corresponding to (5.1) is promptly computed. We choose $\nu =1$, $\rho = \dfrac{2(1-\Lambda )}{\nu \Lambda ^2}$ and $\alpha =1$ for varying spatial mesh sizes h. The initial velocity and pressure fields are obtained from the Stokes system. The stopping criteria is taken as

$$\begin{aligned} \max \left\{ \dfrac{\Vert \textbf{u}_{h}^{n+1}-\textbf{u}_{h}^{n}\Vert _\infty }{\Vert \textbf{u}_{h}^{n}\Vert _\infty }, \dfrac{\Vert p_{h}^{n+1}-p_{h}^{n}\Vert _\infty }{\Vert p_{h}^{n}\Vert _\infty } \right\} \le 10^{-6}. \end{aligned}$$

Corresponding errors in various norms and convergence rates for the Algorithm 1 are presented in Tables 1 and 2. As could clearly be deduced from the table, expected rates of convergence are achieved for all quantities and the number of iterations is nearly uniform.

Table 1 Errors and rates for $\theta = 2$, $\alpha =1$ and $\rho = 543.1$ with a single grid Algorithm 1

Table 2 Errors and rates for $\theta = 1$, $\alpha =1$ and $\rho = 2240.4$ with a single grid Algorithm 1

Next we test the two-grid the Algorithm 2 and compare the results with the single grid Algorithm 1. In this part of the experiment, we only consider the case of $\rho =2240.4$ and always take $H=\frac{h}{2}$. Firstly, the CPU times comparison for various runs are listed in Table 3. As expected, the two-grid Algorithm needs considerably less execution time.

Table 3 CPU times (in seconds) for $\theta = 1$, $\alpha =1$ and $\rho =2240.4$

The errors for both grids are reported in Table 4. Interestingly enough, in this particular test, not only the two grid algorithm is more faster, but it also yields more accurate solutions.

Table 4 Comparison of velocity and pressure errors between two the Algorithms

5.2 Kovasznay Flow

Herein we use the well-known Kovasznay flow problem [25] to test the stability and convergence of our scheme against the classical Arrow–Hurwicz scheme of [6] and the grad-div stabilized algorithm studied in [11]. The exact solution is

$$\begin{aligned} u_1 = 1 - \textrm{e}^{\lambda x} \cos (2\pi y), \ u_2 = \dfrac{\lambda }{2\pi }\textrm{e}^{\lambda x} \sin (2\pi y), \ p = -\dfrac{\textrm{e}^{2 \lambda x}}{2} + p_0, \end{aligned}$$

where

$$\begin{aligned} \lambda = \dfrac{1}{2\nu } - \sqrt{\dfrac{1}{4\nu ^2} + 4 \pi ^2 } \end{aligned}$$

and $p_0 \in R^1$ is chosen so that p has a mean value zero. The flow domain is taken to be $\Omega = (-0.5,1) \times (-0.5,0.5)$, triangulated with a uniform $100 \times 80$ mesh.

Recall that our scheme is uniformly bounded and convergent under condition (3.7):

$$\begin{aligned} \rho \le \dfrac{2 (1-\Lambda )}{\nu \Lambda ^2} \text { and } \forall \ \alpha > 0, \end{aligned}$$

while the classical scheme [6] has more complex condition for both $\rho$ and $\alpha$:

$$\begin{aligned} \text { if } \rho \le \frac{1}{\nu }, \text { then } \alpha> \dfrac{\rho }{2\nu (1-\Lambda )},\\ \text { and if } \frac{1}{\nu }< \rho < \dfrac{\rho }{2\nu (1+\Lambda )}, \text { then } \alpha > \dfrac{\rho ^2}{2(2-\rho \nu (1+\Lambda ))}. \end{aligned}$$

Thus, for all schemes, $\rho$ should not be too large, and $\alpha$ should be chosen large for the classical scheme and the grad-div stabilized scheme [11].

We tested all the schemes for $\nu =0.01$ and $\nu =0.001$ cases for range of values of $\rho$ and $\alpha$. The findings are summarized in the Tables 5 and 8. For brevity, we shall refer to our results as “AH3”, to the results of the classical scheme as “AH1” and to those of the [11] as “AH2”.

Table 5 Number of iterations needed for convergence for $\nu =0.01$

Table 6 $\rho =500$ and $\nu = 0.01$

Table 7 Number of iterations needed for convergence for $\nu =0.001$

Table 8 $\rho =500$ and $\nu = 0.001$

As the Tables 5, 6, 7 and 8 reveal, our scheme was observed to be always stable and convergent. However, the classical scheme either experienced numerical instability or did not converge at all in any of our simulations. The grad-div stabilized scheme converged only in some cases. Interestingly, optimal parameter values for the AH3 scheme is large $\rho$ and small $\alpha$, while the other schemes tend to perform better for large values of both $\alpha$ and $\rho$.

5.3 Lid Driven Cavity Flow

In this subsection we test our Algorithms on a well known lid driven cavity flow problem. The computational domain is $\Omega = (0,1)^2$, where the top lid is moving in the positive x direction with a unit speed. The boundary conditions are taken to be no-slip along other the walls. In order to avoid the irregularity of the solution at the upper corners, we consider a regularized initial data at the upper boundary as was proposed in [8]:

$$\begin{aligned} \textbf{u}(x,1)&= (u_1(x),0)^T \\ u_1(x)&= {\left\{ \begin{array}{ll} 1 - \dfrac{1}{4}\left( 1-\cos \left( \dfrac{0.1-x}{0.1}\pi \right) \right) ^2 &{} 0 \le x \le 0.1, \\ 1 &{} 0.1< x < 0.9, \\ 1 - \dfrac{1}{4}\left( 1-\cos \left( \dfrac{x-0.9}{0.1}\pi \right) \right) ^2 &{} 0.9 \le x \le 1. \end{array}\right. } \end{aligned}$$

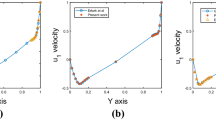
We run the code for four different values of Reynolds number, $\textrm{Re} = 1000, 3200, 5000$ and 10, 000. In all runs, we set $\rho = 100$ and $\alpha =1$. Meshes with various resolutions were tested, and we only report the results done on two finest meshes $96 \times 96$ and $128 \times 128$. All runs are again initiated by solving a steady Stokes equation. For a quantative comparison, we use the reference values of the velocity components at the centerlines through the domain given in Ghia et. al. [12]. In Table 9, we have the values obtained with the Algorithm 1 for $\textrm{Re}=1000$. As it can be seen, the results are quite accurate and in both cases, our scheme converged in 145 iterations. Next in Table 10, we report the results obtained on the finest mesh with the two-grid Algorithm 2 at $\textrm{Re}=10000$. The results are again satisfactory even though the flow is not fully resolved.

Table 9 Comparison of the vertical/horizontal components of the velocity along the segment x at $\textrm{Re}=1000$ with the results of [12] on single grid

The streamlines patterns obtain via our methods are shown in Figs. 1 and 2. All plots demonstrate the correct formation of eddies in the corners. Finally, the iteration count vs. error plots for $\textrm{Re} = 5000$ and 10000 are included in Fig. 3 which show overall smooth convergence to a steady state solution.

Table 10 Comparison of the vertical/horizontal components of the velocity along the segment x at $\textrm{Re}=10000$ with the results of [12] with two-grid scheme

It should be pointed out that the classical AH algorithm requires over 700 iterations even $\textrm{Re}=100$ case [6] and no convergence was obtained for the $\textrm{Re}=1000$ flow for $\alpha =\textrm{Re}$ and $\rho =1, 10, 20, 50$. Moreover, the grad-div stabilized Arrow-Hurzwich algorithm described in [11] could not achieve the convergence in any case with the Taylor-Hood finite element pair.

Fig. 1

Streamlines: $\textrm{Re}=1000$ (left) and $\textrm{Re}=3200$ (right)

Fig. 2

Streamlines: $\textrm{Re}=5000$ (left) and $\textrm{Re}=10000$ (right)

Fig. 3

Errors vs iteration count for the lid driven cavity problem: $\textrm{Re}=5000$ (top) and $\textrm{Re}=10000$ (bottom)

5.4 Channel Flow Over a Full Step

As a final qualitative numerical test, we consider a two dimensional flow in a channel with an obstacle step. The computational domain is a $30\times 10$ rectangle with a $1\times 1$ obstacle positioned at 5 units in the bottom of the channel. We use the Taylor-Hood finite element pair as in other tests with a total degree of freedom of 19177 for the mesh used in Algorithm 1. The coarse mesh scale is selected as $H=\sqrt{h}$ wherever Algorithm 2 is considered. We study with $\nu =0.01$ along with various $\rho$ selections and $\alpha =\frac{1}{\nu }$.

The streamlines over velocity contours obtained with our schemes are depicted in Fig. 4. The correct eddy formation behind the step is easily observable, which is key indicator for the accuracy of our schemes.

Fig. 4

Streamlines over velocity contours for the channel flow with $\nu =0.01$

Fig. 5

Errors vs iteration count for the channel flow: Algorithm 1 (left) and Algorithm 2 (right)

We also give iteration history for both schemes according to varying $\rho$ values in Fig. 5. The pictures reveals that, as the value of $\rho$ increases the number of iterations to reach the steady state decreases for both schemes. So the selection of $\rho$ plays a vital role when one use these algorithms to solve any problem. On the other hand, the number of iterations to converge is higher for Algorithm 2, especially for smaller $\rho$ values. This is due to the fact that two-grid schemes run on a coarser grid and is less resolved. However, as Table 11 reveals, although the number of iterations needed to convergence is higher for Algorithm 2, there is a meaningful difference in CPU times. Especially, for higher $\rho$ the two-grid scheme is 3 to 5 times faster than single-grid scheme which was also observed in the preceding examples.

Table 11 CPU times (in seconds) for varying $\rho$ values in channel flow example

6 Concluding Remarks

In this paper a novel Arrow–Hurwicz type method for solving the steady-state Navier–Stokes equations is proposed. Key of the idea is based on changing one term in momentum equation, that is inspired from artificial compressibility method. Uniform boundedness and convergence to the exact solution under reasonable assumptions were studied. We also presented its extension to a two-grid setting and proved the corresponding convergence result as well. A comprehensive numerical studies showed a significant efficiency in terms of computing times, accuracy and robustness over the existing methods for our proposed AH algorithms.